Open Access Article
Open Access Article“Amide − amine + alcohol = carboxylic acid.” chemical reactions as linear algebraic analogies in graph neural networks
Amer Marwan
El-Samman
*a and
Stijn
De Baerdemacker
 ab
ab
aUniversity of New Brunswick, Department of Chemistry. 30 Dineen Dr, Fredericton, Canada. E-mail: aelsamma@unb.ca
bUniversity of New Brunswick, Department of Mathematics and Statistics. 30 Dineen Dr, Fredericton, Canada. E-mail: stijn.debaerdemacker@unb.ca
First published on 23rd April 2025
Abstract
In deep learning methods, especially in the context of chemistry, there is an increasing urgency to uncover the hidden learning mechanisms often dubbed as “black box.” In this work, we show that graph models built on computational chemical data behave similar to natural language processing (NLP) models built on text data. Crucially, we show that atom-embeddings, a.k.a atom-parsed graph neural activation patterns, exhibit arithmetic properties that represent valid reaction formulas. This is very similar to how word-embeddings can be combined to make word analogies, thus preserving the semantic meaning behind the words, as in the famous example “King” − “Man” + “Woman” = “Queen.” For instance, we show how the reaction from an alcohol to a carbonyl is represented by a constant vector in the embedding space, implicitly representing “–H2.” This vector is independent from the particular carbonyl reactant and alcohol product and represents a consistent chemical transformation. Other directions in the embedding space are synonymous with distinct chemical changes (ex. the tautomerization direction). In contrast to natural language processing, we can explain the observed chemical analogies using algebraic manipulations on the local chemical composition that surrounds each atom-embedding. Furthermore, the observations find applications in transfer learning, for instance in the formal structure and prediction of atomistic properties, such as 1H-NMR and 13C-NMR. This work is in line with the recent push for interpretable explanations to graph neural network modeling of chemistry and uncovers a latent model of chemistry that is highly structured, consistent, and analogous to chemical syntax.
Neural networks in chemistry have gained tremendous traction in the past decade, carrying a broad range of applicability, from aiding drug and material discovery,1–11 to speeding up or bypassing the prediction of electronic structure properties.12–33 For each application, numerous approaches have been designed, including both graph-33–36 and text-based models3,37–44 where such techniques enjoy a varying degree of success.
In the context of text-based models, sophisticated text-based chemical inputs have been developed such as the Simplified Molecular Input Line Entry System (SMILES),43–46 the Self-Referencing Embedded Strings (SELFIES),47,48 and SMILES arbitrary-target specification (SMARTS).49,50 Though convolutional neural networks have been tried successfully on SMILES-based text for the detection of chemical motifs and on prediction of drug activity,39,43 Many so-called “linear graph models” have been fitted using recurrent neural networks (RNNs) due to their capacity of holding short- and long-term information about text.38,40,41,44 For example, SMILES2Vec is a deep RNN that learns important features from SMILES strings to predict toxicity, activity, solubility and solvation energy of chemical compounds.44 Text-based models also facilitate the design of generative architectures that predict the result of chemical reactions, generating the product strings from a reactant string input, or generating molecules of a desired property.37,38,40
Graph models,17–21,23,26–36 on the other hand, represent molecules as a collection of atoms in three-dimensional coordinate space. Generally speaking, the coordinates of the atoms serve as inputs to such models and the output is the target chemical property under investigation, often on energy. Permutational- and symmetry–invariant graph models have been designed successfully for the prediction of electronic energy within chemical accuracy.17–21,23 Notably, such graph-based methods in chemistry share important properties with text-based recurrent and transformer models making it instructive to examine the connection between these seemingly different approaches.
The central object shared in all these approaches is the “embedding” which is the feature-building quantity of the neural network in the latent space. For example, in text-based models, word-embeddings represent the latent features for each word in the context of the sentence after training.51–60 In chemistry, atom-embeddings, also optimized through training, are the features representing an atom in the context of a molecular graph.17–21,23 These neural activations for the word/atom are tuned to hold meaningful information about the context of the data (i.e. words, molecules) and the specific input. However, they are generally high-dimensional and obscure objects to analyze on their own. In previous works,61,62 we showed that the embeddings of chemical GNN models hold valuable information about chemistry. This information includes the ability to distinguish molecular environments and the ability to quantify molecular similarity.61 We also showed that the embedding space is a readily transferable representation for a wide array of properties such as for pKa, NMR, and solubility, underscoring the completeness of these representations.62 In this work, we go beyond the locality of the representation, and show that graph-embeddings behave similar to text-embeddings in that they have arithmetic properties that reveal meaningful combinations. This is akin to how word-embeddings can be combined to make word analogies in natural language models.51–55 Our methodology will naturally uncover the chemical syntactical organization of the embedding space.
The surprising property of word analogies using vector arithmetic has been observed first in natural language processing (NLP) models.51–55,63 In trained models such as skip-gram with negative sampling (SGNS), the word analogy “King is to X as Man is to Woman?” is solved by taking the closest vector to “King − Man + Woman” which happens to be the vector for X = “Queen.” The success of this is based loosely on the Pennington et al. conjecture,55 proven in ref. 51, which states that such word analogies are linear iff p(w|a)/p(w|b) ≈ p(w|x)/p(w|y). In simple terms, if words a and b are found in the same ratios as x and y across all words w of a vocabulary, then there must be a linear analogy between, a, b, x, and y. Despite the strong theoretical prior provided by the Pennington conjecture, experiments in word analogies for the assessment of social bias in NLP revealed that a distinction must be made between factual and semantic analogies.64 Whereas factual analogies with a unique answer can be drawn between words or entities with a clear distinct meaning, the situation is different for words with more semantic flexibility. Interestingly, experiments in social bias of NLPs have shown that the poster example “King − Man + Woman” = “Queen” is indeed prone to semantic bias and can lead to different analogies. We show in this work that similar mechanisms are at work in chemistry, where graph-embeddings of molecular graphs can provide a more factual and highly organized representation of chemical environments than more traditional vector encodings, such as Morgan Fingerprints.76.
The existence of linear algebraic analogies in chemical statistical models comes with some promising consequences. Firstly, it means that fundamental stoichiometric reactions can be modelled with vector algebra thereby opening a new way to traverse the chemical space in an algebraically structured way. In a related recent study65 these vector relations were not observed, but explicitly imposed as learning objective for chemical reaction formulae in a molecular GNN in order to ensure generalization or transferability of molecular representations by means of a global algebraic framework.
Most significantly, and in contrast to NLP, the structure of the chemical embedding space is not a consequence of the social construct of language. Rather, it relates quantitatively to the underlying chemical structure and formula. We demonstrate how this can be achieved using perturbational updates that are based on the neighbouring atoms' representation and a self-consistent framework. Simultaneously, this leads to a natural interpretation of GNN embedding space as vector algebra found between reactant and product states, which is synonymous with chemical formulaic language. Finally, we anticipate that the existence of a highly organized space around atomic chemical neighbourhood embeddings can facilitate contemporary development of generative models in chemistry.
This paper is organized as follows. In the Methodology Section, we first recapitulate the training of our pretrained GNN model on electronic energy,61,66 and our transfer learning models to other properties (1H-NMR and 13C-NMR).62 Details of the hyperparameters chosen for each architecture and the dataset used for training can all be found in Section 1.1. Following this, in Section 1.2 we discuss how we prepare our reaction datasets from the QM9 dataset67 using an algorithm that can query any class of reactants and transform them to products via a specified reaction. This dataset creation procedure will serve our observations on chemical reaction analogies in the embedding space which we present in Sections 2.1–2.3. Following our observations, we deduce an approximate replicate model of the embedding space based on layered atomic neighbourhood information in Section 2.4 which will explain our chemical analogy observations. Lastly, in Section 2.6 we show how linear analogies can reveal hidden relations in chemical properties such as 1H-NMR and 13C-NMR.
1 Methodology
1.1 GNN, pretraining and hyperparameters
We employed a pretrained graph neural network, SchNet,17–20 on electronic energy of the QM9 dataset.67 QM9 is a set of 134 K small-sized organic molecules (∼5–10 Å in size) with optimized conformations all computed using the B3LYP/6-31G(2df,p) level of density-functional theory. For the SchNet GNN model, the nodal features (i.e. the atom-embeddings) were chosen to have a 128-dimensional latent feature space. The edges that update the nodal features employ an initial expansion of interatomic distances using equally separated Gaussians with a cutoff of 50 Å. This provides the edges with enough parametric flexibility to update the nodal features via the convolutional operation described in ref. 17. More details on the GNN algorithm can also be found in ref. 17–20. Note that more efficient GNN training algorithms employ cutoff distances that are significantly shorter which allow for efficiently learning the neighbour interactions. However, this avenue was not chosen since a large cutoff distance is purposeful to maintain a global representation of molecules in the embedding space. We trained on 100 K molecules with total electronic energy at 0 kelvin as the target property. An additional 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 data points were used for validation during the training process. The rest of the set (20
000 data points were used for validation during the training process. The rest of the set (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) was leftover for testing and for the construction of our reactions datasets, see below. The trained model achieves a MAE of 0.2 meV and 1 meV on training and testing set's molecular energy, respectively. The trained model, details on all the hyperparameters, as well as the extracted embeddings for QM9 molecules can be found in ref. 66.
000) was leftover for testing and for the construction of our reactions datasets, see below. The trained model achieves a MAE of 0.2 meV and 1 meV on training and testing set's molecular energy, respectively. The trained model, details on all the hyperparameters, as well as the extracted embeddings for QM9 molecules can be found in ref. 66.
For the prediction of 1H-NMR and 13C-NMR, we employed a transfer learning model as introduced earlier in.62 Such models help to transfer the integrity of learned chemical representation from GNN models to new molecular properties and datasets. The transfer learning architecture used is a simple feed forward neural network (made up of one layer of 128 nodes, followed by “tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) h” activation, followed by another linear layer of 128 nodes), that intakes energy-trained embeddings (from SchNet) as inputs to transfer learn to other properties such as 1H-NMR, and 13C-NMR. This follows very closely to the transfer learning architecture used in previous works,62 only here the activation function has been replaced from linear or “Relu”, to “tan
h” activation, followed by another linear layer of 128 nodes), that intakes energy-trained embeddings (from SchNet) as inputs to transfer learn to other properties such as 1H-NMR, and 13C-NMR. This follows very closely to the transfer learning architecture used in previous works,62 only here the activation function has been replaced from linear or “Relu”, to “tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) h.”
h.”
For 1H-NMR and 13C-NMR data, we used the QM9NMR dataset,68 which has gas- and solvent-phase chemical shifts computed at the mPW1PW91/6-311+G(2d,p) for all QM9 molecules at geometry optimized conformations computed at the B3LYP/6-31G(2df,p) level. We used the hydrogen- and carbon-site embeddings as the input representation for training on the prediction of gas-phase 1H-NMR and 13C-NMR. The model was trained using an 8000 molecule randomized dataset from QM9NMR, achieving a RMSE of 2.69 ppm for carbon NMR and 0.20 ppm for proton NMR on 2000 molecule separate test set, which is comparable to full-fledged training on significantly larger datasets. For instance, the highly accurate kernel regression model that was applied at the inception of the QM9NMR dataset68 achieves a mean error of 1.9 ppm for carbon chemical shifts. Both carbon and proton NMR results are within the accuracy of density functional methods.
1.2 Reactions dataset creation
After training the model, we automated a dataset creation procedure mimicking the endpoints of reaction processes such as substitution, elimination, hydrolysis, Diels–Alder, and more. The procedure works as follows. First, we automate the identification of reactant functional groups across the hold-out test set of QM9 using a specified reactant label. The automation procedure can annotate every atom's environment up to any compositional depth (one, two, to several bonds away) in a bijective labelling representation. This is done by using atomic number priority to order neighbouring atoms which ensures uniqueness in the representation. The priority system is equivalent to the one used in well-established standards of ordering R/S or E/Z nomenclature.69 Ultimately, we obtain a local-centric label for each atom in the dataset that can be queried for long-range features. For instance, we query all straight-chain alcohols, alpha-positioned alkynes, or any other branching motif specified, or left unspecified (ex. all alcohols in QM9). Second, once reactants are isolated, a specified reaction is automated on the dataset. For instance, if the specified reaction is a methylation, this is carried out by removing a hydrogen and adding a methyl to mimic methylation on the alcohols. Lastly, we geometry optimize using two different force fields for comparison, MMFF94 and GAFF.70Note that due to limitations of training on the QM9 dataset which only involves equilibrium geometries, our current procedure only accounts for initial and product states but does not involve mechanistic transitions. This approach is analogous to state vector changes, similar to other state-dependent properties in chemistry (such as Gibbs free energy, enthalpy, and entropy) which depend on initial and final states without explicitly modeling transitions. While modeling transitions is an exiciting future direction, and there is ongoing work attempting to expand SchNet's trainability to include out-of-equilibrium geometries,71 our goal at this stage is to provide a tool for interpreting neural network models in terms of these reactant and product states.
Following the preparation of the reactant and product databases, we then run the reactants and products through the pretrained GNN model. Then we extract their atom-embeddings at the reaction-site. For instance, in hydrolysis, this would be the carbon on the carbonyl group. Finally, we obtain a complete database comprising the atom-embeddings of all molecules in the entire the QM9 dataset, completed with the reactant–product pairs of interest. The extensiveness of the database will reduce potential bias associated with small datasets in the retrieval approach described below. Our procedure is automated in a python workflow visualised in Fig. 1. The software for this procedure is open source and is referenced in the Data availability statement.
In order to visualize the embeddings as they change from reactants to products, we project the high-dimensional vectors of the embedding space to a lower-dimensional space while incurring minimal data loss. This can be done with Principal Component Analysis (PCA)72 which finds the lower-dimensional space that packs the largest variance in the data.
Ultimately, visualization techniques fall short from giving a comprehensive quantitative grasp of the chemical syntax in the embedding space. We will quantify our observations of linear analogies by means of cosine similarities in high-dimensional spaces, which will provide a measure on how well two different vectors are mutually aligned (see next section).
2 Results & discussion
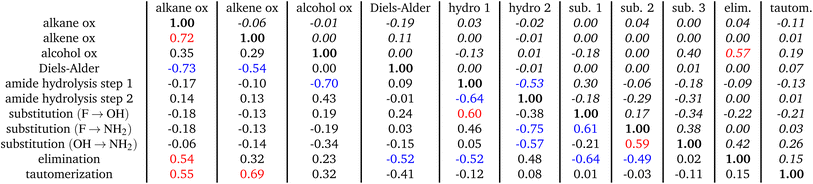
We investigate the chemical analogies in the embedding space with key reaction processes of increasing complexity that amount to all of the basic features of chemical reactions (adding/breaking bonds, one-step/multi-step). These reactions being (1) oxidation of alcohols/alkanes/alkenes, (2) Diels–Alder, (3) hydrolysis of amides to carboxylic acids, (4) tautomerization of alcohols to carbonyls, (5) substitution reactions, and (6) elimination reactions. While this set of reactions is definitely not exhaustive compared to the wide variety of reactions chemistry has to offer, it nevertheless is a balanced sample and will incur observations that can be easily extended to any reaction using the proposed methodology. The following subsections will delve into the first three reactions, whereas the rest of the reactions are explored in Tables 1 and 2, and in the following discussion.| Reaction | Force field | QM9| new| total | Density | % GNN | % MF | % MF\r |
|---|---|---|---|---|---|---|
| RCH2CH2R → RCHCHR | MMFF94 | 2062| 118 | 2180 | 5 × 10−4 | 62.8 | 0.0 | 13.3 |
| RCHCHR → RCCR | MMFF94 | 2285| 80 | 2365 | 4 × 10−4 | 71.1 | 0.0 | 80.0 |
| CH2OH → CHO | MMFF94 | 1749| 228 | 1977 | 5 × 10−4 | 62.7 | 48.0 | 48.0 |
| Dieneophile + diene → cyclohexene | MMFF94 | 7896| 112 | 8008 | 1 × 10−4 | 73.2 | 0.0 | 50.0 |
| RCONH2 → RCONH2OH | MMFF94 | 0| 127 | 127 | 8 × 10−3 | 60.9 | 24.4 | 24.4 |
| RCONH2OH → RCOOH | MMFF94 | 1787| 127 | 1914 | 5 × 10−4 | 60.2 | 33.1 | 33.1 |
| RF → ROH | GAFF | 22| 17 | 39 | 3 × 10−2 | 81.3 | 40.0 | 46.7 |
| RF → RNH2 | GAFF | 22| 17 | 39 | 3 × 10−2 | 81.3 | 0.0 | 6.7 |
| ROH → RNH2 | GAFF | 1916| 1395 | 3311 | 3 × 10−4 | 61.9 | 0.0 | 53.2 |
| RCHCHOH → RCH2CHO | GAFF | 29| 149 | 178 | 6 × 10−3 | 58.6 | 0.0 | 85.7 |
| RCH2CH2OH → RCHCH2 | GAFF | 25| 133 | 158 | 6 × 10−3 | 60.0 | 0.0 | 5.3 |
2.1 Oxidation reactions
We start with the simplest of the listed reactions, (a) the oxidation reaction of alkanes, alkenes and alcohols,| RCH2CH2R → RCHCHR + H2 | (1) |
| RCHCHR → RCCR + H2 | (2) |
| RCHOH → RCO + H2 | (3) |
Fig. 2 depicts the reaction process in the embedding space in the PCA projection for the oxidation of alkanes (2a), alkenes (2b), and alcohols (2c). In each, only the embedding vector of the reactant-center carbon Cr and product-center carbon Cp are depicted in color, and commented by an arrow representing the reaction. Note that the arrows only represent the reactant and product end-points and do not represent the full reaction process, for which QM9 is not designed. However, there has been some recent effort in exploring the success of transfer learning to real-space quantities of chemistry that would include any part of the chemical space.71 The scatterplot in the background of the arrows, consists of all the carbon embeddings of QM9 labelled according to chemical moiety as was shown in ref. 61. Other C embeddings in QM9 consisting of distinct functional groups from the reactant's functional group are shown in gray. Whereas the colored groups (annotated in the caption) represent atoms in QM9 that have same functional groups as the reactants and products of the reaction.
The first thing to notice from Fig. 2a is that the alkane and alkene carbons aggregate in different and well-separated clusters, as does every other carbon-centered chemical moiety in the database. This was already observed and discussed previously in ref. 23,61. The second observation is that all the vectors of the transformation appear to be equal to a large extent. The extent to which the vectors are equal can be quantified by considering the average “oxidation vector from alkane to alkene” and use this as a proxy to transform the embedding of any reactant alkane to its alkene counterpart, that is,
 | (4) |
 from its
from its  ,
, | (5) |
We investigate the validity of this approximation for each reaction in the dataset by means of the “neighbour test,” i.e. if the resulting  of eqn (5) leads closest to the true alkene embedding or not within the total compounded set of all alkenes (=2180, see Table 1). The neighbour test is analogous to the one carried out for the original word vector analogies where the word embedding for “King” − “Man” + “Woman” came out nearest to the vector for “Queen.” Here, the average oxidation vector serves the same role as the vector for ‘ − “Man” + “Woman”’ which transformed the word ”King” to ”Queen,” and similarly ”policeman” to ”policewoman” and ”boy” to ”girl”. In this case, the average oxidation vector can map 62.8% of reactant alkanes to be nearest their true product alkene C-embedding at the reaction center, see Table 1. This points towards a highly structured space, as more than 1 in 2 vectors are mapped exactly to the correct alkene using an average estimate reaction vector, opposed to a probability of 1 in Nalkenes (1/2180, see Table 1) if this would be random over a uniform distribution. In other words, the average <alkane oxidation> vector does not map to just any of the 2180 available alkenes, but lands exactly on the correct one 62.8% of the time. A noteworthy observation is that a 100% neighbour test can be achieved if the removal of hydrogen is performed without any subsequent force field optimization. Such discrepancy and the role of geometry optimization will be discussed later.
of eqn (5) leads closest to the true alkene embedding or not within the total compounded set of all alkenes (=2180, see Table 1). The neighbour test is analogous to the one carried out for the original word vector analogies where the word embedding for “King” − “Man” + “Woman” came out nearest to the vector for “Queen.” Here, the average oxidation vector serves the same role as the vector for ‘ − “Man” + “Woman”’ which transformed the word ”King” to ”Queen,” and similarly ”policeman” to ”policewoman” and ”boy” to ”girl”. In this case, the average oxidation vector can map 62.8% of reactant alkanes to be nearest their true product alkene C-embedding at the reaction center, see Table 1. This points towards a highly structured space, as more than 1 in 2 vectors are mapped exactly to the correct alkene using an average estimate reaction vector, opposed to a probability of 1 in Nalkenes (1/2180, see Table 1) if this would be random over a uniform distribution. In other words, the average <alkane oxidation> vector does not map to just any of the 2180 available alkenes, but lands exactly on the correct one 62.8% of the time. A noteworthy observation is that a 100% neighbour test can be achieved if the removal of hydrogen is performed without any subsequent force field optimization. Such discrepancy and the role of geometry optimization will be discussed later.
A different and more continuous measure to validate the performance of <alkane oxidation> is to compare the average distance between the predicted and the true value  , to the average pairwise distance of all alkenes
, to the average pairwise distance of all alkenes , or the average distance to the nearest neighbour of each alkene,
, or the average distance to the nearest neighbour of each alkene,  . It is evident that we are well within the ‘alkenes’ feature space bordering on the exact subspace that the alkene product lies in. It is also worth mentioning that in contrast to language models, the analogies ‘ − ‘‘Man” + “Woman”’ have not been learned explicitly as “H2” does not represent any single atomic embedding and is therefore categorically excluded from the dataset.
. It is evident that we are well within the ‘alkenes’ feature space bordering on the exact subspace that the alkene product lies in. It is also worth mentioning that in contrast to language models, the analogies ‘ − ‘‘Man” + “Woman”’ have not been learned explicitly as “H2” does not represent any single atomic embedding and is therefore categorically excluded from the dataset.
Similar results hold for the oxidation of alkenes to alkynes, and alkanes to alcohols, see Table 1 and Fig. 2b and c. Visually, it also appears that the average oxidation vectors, across reaction classes, i.e. for alkane, alkene, and alcohol oxidation in the PCA space appear to be largely colinear from the figures. To confirm that this colinearity is not a coincidence of the 2D projection space, we can measure the cosine similarity between the average vectors in the original high-dimensional space, see Table 2 (lower triangle). In the Table, the off-diagonal elements show the average cosine similarity between reaction classes (ex. between alkane oxidation and alkene oxidation) taken by considering the cosine similarity between the average reaction vectors of those classes,
 | (6) |
It is apparent from the Table that all oxidations share a high degree of cosine similarity, especially when compared to the other reactions studied. This is indeed significant, considering that in a high-dimensional space (128-D) it is increasingly likely that any two random vectors are orthogonal.73 It can be shown that the dot product of normally distributed vectors in D dimensions are strongly centered at cos(θ) = 0, with a standard deviation of σ = 1/D. For our 128-dimensional latent space, deviation from orthogonality of a normal distribution is 0.008. Thus the cosine similarity of 0.72, as shown in the Table, between alkane and alkene oxidation for instance, is an appreciable breach to orthogonality and implies significant colinearity in the 128-D latent space. There is also a breach of orthogonality between the oxidation reactions and elimination and tautomerization reactions, as these reactions also align considerably with oxidation with cosine similarities of 0.54 and 0.55, respectively, as Table 2 shows.
This result is significant in a number of ways. First, it suggests that oxidation is always in a similar direction in the embedding space with other oxidations and with other reactions that increase bond order. Explicitly, that means the opposite, reduction, must be in the exact opposite direction from oxidation and align with other reactions that decrease bond order, such as Diels–Alder as as we will later discuss. Whereas reactions that are distinct tend to be pointing in some near-orthogonal direction. Additionally, as Table 1 shows, this is not just the case for the simple case of bond-order changing reactions but all the other reactions studied (ex. substitutions and hydrolysis), presenting a highly interconnected space. It is apparent that the embedding space is organized based on chemical formulas considering only compositional changes between initial and end states. Thus, similar changes in chemical composition align, reverse changes anti-align, and distinct changes are orthogonal. Later, we will quantify that observation using a proposed replicate model of the embedding space based on neighbourhood composition. This replicate model will map all the trajectories of compositional changes for the embedding (adding carbons, removing nitrogens, …etc), up to several bonds away.
We mentioned previously that the neighbour test yields near perfect results when hydrogens are removed without the subsequent optimization step for any oxidation reaction. The difference in performance between the optimized and non-optimized results is chemically meaningful, and can be best illustrated in the case of oxidation of an alkane. In such a reaction, it is possible to have either the cis or the trans product, which are stereoisomers of each other. A closer look at the oxidation vectors to both isomers we find a difference in the cosine similarity of the reaction vector going to trans vs. going to cis. For the cis isomers, the high-dimensional cosine similarity of the embedding is consistently larger at an average cosine similarity of 0.95, whereas for the trans isomers, an average cosine similarity of 0.91 is obtained with respect to the mean reaction vector embedding. The difference between the cis and trans cosine similarities with respect to the mean reaction vector is significant according to an independent samples t-test which gave a p-value of 1 × 10−4. The neighbour test using the average reaction vector yields slightly better results on cis (67.1%) than on trans (54.9%), which implies that it is biased towards cis geometry, as QM9 has many alkanes inside rings.
The above analysis explains part of the discrepancy in the neighbour test going from non-optimized to optimized, as product alkenes determine which shape they will hold implies that a single average reaction vector approximation for all possible optimized states is a biased assumption. Additionally, we performed MMFF94 and GAFF geometry optimization on our new products for efficiency, whereas the QM9 dataset, and correspondingly the SchNet model, is optimized at the B3LYP/6-31G(2df,p) level of theory. While geometry optimizing using force fields may effectively be introducing non-equilibrium geometries from the perspective of the DFT-trained model thus providing a test of generalizability and robustness of the model, nevertheless, these discrepancies may be slightly affecting the results. However, even with these approximations it is clear that geometry optimization plays only a minor role to that of chemical composition in mapping out the chemical embedding space.
2.2 One-step reactions: Diels–Alder
The oxidation reactions discussed in the previous section demonstrate leaving group reactions whereby atoms leave the reaction center. The rational next question is about incoming groups making a bond at the reaction center. Can we still find linear analogies for this slightly increased complexity? The answer is affirmative. A class of such a reaction is the Diels–Alder reaction.Once again, we find a strong linear analogy for the reaction in the embedding space, whereby the neighbour test yields a 73% of the transformed Diels–Alder, using the average reaction vector estimate. See Fig. 2d for the PC projected reaction embedding vectors of the Diels–Alder reaction.
Diels–Alder also brings to light an additional corroborating observation. Diels–Alder shares similarities with reduction, because the double bond at the reaction center is reduced to a single bond as the ring closes to make the resulting product adduct. Evidently this makes the reaction vector for Diels–Alder face the opposite direction to oxidation reaction vectors as can be seen from Table 2, where the cosine similarity between Diels–Alder and for instance alkane oxidation is −0.73. Similarly Table 2 shows an opposite alignment with elimination and tautomerization reactions giving cosine similarities of −0.52 and −0.42, respectively, which are a considerable breach to orthogonality (< −0.008). This can also be seen in the PC projection of the reaction vectors in Fig. 2d when compared with that for oxidation, Fig. 2a. Therefore, even though Diels–Alder is not technically a reduction via adding hydrogens, it is highly colinear with reduction (and bond-order reducing reactions) which once again points to a highly organized space. It has been observed in past work74 that SchNet's modeling of chemistry is interpretable based on chemical bond-order. Our results put their findings in a larger framework based in the implicit chemical syntactical relationship between the embedding's various subspaces.
2.3 Multi-step reactions: hydrolysis
The hydrolysis of amides to make carboxylic acids is a two-step reaction process, first making a tetrahedral intermediate of a carboxylic acid through the imission of a water molecule.After a quick proton transfer step, an ammonia then leaves the tetrahedral intermediate.
Each of these processes comes with its own distinct embedding transformation, see Fig. 2e and f for the PC projected vectors for each step. The average reaction vector (in the original 128-D space), for each step, is once again a good proxy to transform any reactant as shown in Table 1.
Analyzing cosine similarity also proves insightful in the case of amide hydrolysis. For instance, in the first step of the hydrolysis, where the alcohol is being added to make the tetrahedral intermediate, there is considerable alignment with substitution of halogens with alcohols. Additionally, the second step of the reaction, when the ammonia leaves the reaction center and forms the carboxylic acid, shows similar alignment to the oxidation of alcohols. This is because as the ammonia leaves, a double bond is formed at the reaction center making a carbonyl product. Lastly, this second step of hydrolysis also aligns in the opposite direction with substitution of halogen to amine. This corresponds with the fact that amine is the leaving group in the second step of amide hydrolysis rather than the incoming group as it is in substitution of halogens. Reiterated, this points to a highly organized space with implicit relationship between its various subspaces.
We have restricted ourselves to just six types of elementary reactions, but similar conclusions can be drawn for other processes using the provided methodology. Our query software has been written with sufficient generality in mind, to quickly query any reactant (with any short- and long-range features), remove leaving groups, build any specified functional group, add/remove bonds at the reactions site, and extract embeddings at the reaction site, in a fully automated manner. The software is open source and the link can be found in the Data availability statement. Additionally, the repository also includes the reactions databases used for testing the linear algebraic analogies in this work.
2.4 Linear analogies from chemical neighbourhoods
Regardless of the multiple examples shown in the previous section alluding to a highly organized embedding space in terms of chemical analogies, this structure may still be perceived as a coincidence similar to the analogies found in natural language. However, in contrast to NLP, we can explain the approximate constant nature of the reaction vectors from chemical principles. We will show how it is possible to replicate the embedding space using a perturbative scheme, not much unlike a simplified proxy to the (k-hop) message passing or processes underpinning GNNs.75From our observations, and that of previous works,61,62 it is evident that the embedding space is a self-consistent framework. In other words, the atom's representations depends on the neighbourhood representation and the neighbourhood's representation in turn depends on the atom's representation. This self-consistency can be modeled using local neighbourhood composition and a crude initial guess. Then, by updating each atom's representation based on the neighbours, and in turn the neighbours based on the updated atoms in repeated successions, we reach a self-consistent framework that reproduces the embedding space.
The embedding replicates are based on introducing a crude guess of the chemical neighbourhood composition around each atom. This guess for each atom i is defined as just the average embedding in the entire dataset for that element-type, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) Zi, that is,
Zi, that is,
x(0)i = ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) Zi. Zi. | (7) |
So, our starting guess for the oxygen nodal vector is just the gross average of all oxygen embedding vectors in the set and does not contain any functional group representation. Following this, we define the local neighbourhood composition, the replicates are successively updated in an iterative self-consistent scheme using the embeddings corresponding to their neighbourhood atoms.
 | (8) |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) (0)j. The cj are the linear coefficients that fit the resulting replicate at first perturbation, for each atom-embedding, x(1)i, with the exact embedding vector. In other words, the updates for each distinct neighbourhood are learned by comparison with the true embeddings.
(0)j. The cj are the linear coefficients that fit the resulting replicate at first perturbation, for each atom-embedding, x(1)i, with the exact embedding vector. In other words, the updates for each distinct neighbourhood are learned by comparison with the true embeddings.
With only one update, such a crude representation cannot yet capture all the necessary neighbourhood information. However, by repeating our approach for a higher order perturbational updates we get deeper neighbourhood information,
 | (9) |
The only difference now is that we no longer rely on using the crude average neighbour-type embedding but rather here, x(1)j are the results of the previous perturbational update which took into account their direct neighbourhood. Since the direct neighbouring atoms also incorporated their own neighbourhood from the first order perturbation, then the atom-embedding for atom i is now recognizing the indirect neighbourhood layer that is two bonds away. This perturbational approach can now be repeated until self-consistency is reached, that is, until updates to the atom vectors provide no further neighbourhood information.
Table 3 show how well the perturbative replicates reproduce the true embedding vector for alkenes only using both the neighbour test and the mean distance to the true embedding. The latter needs to be compared with mean distance between neighbouring embeddings (1.79) and the average distance between embeddings of the same class (alkenes: 9.46). Additionally, the Table shows results for both the linear model mentioned before, and an added tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) h non-linearity (non-linear)
h non-linearity (non-linear)
 | (10) |
| Perturbation | Linear | Non-linear |
|---|---|---|
| 0 | 0.26% | 12.6 | 0.26% | 12.6 |
| 1 | 0.26% | 8.22 | 0.29% | 7.00 |
| 2 | 3.52% | 6.93 | 5.28% | 3.87 |
| 3 | 29.5% | 3.60 | 41.6% | 2.42 |
| 4 | 47.5% | 3.01 | 71.6% | 2.04 |
| 5 | 57.4% | 2.99 | 82.1% | 1.84 |
| 6 | 56.6% | 2.96 | 82.7% | 1.70 |
Using linear regression, the embedding replicate space is a near 56% replicate of the true embedding space based on the neighbour test after the sixth neighbourhood layer for the alkenes embeddings. Whereas the non-linear coefficients can provide a replicate of up to 82% success on the neighbour test by the fifth order replicate. Additionally, the mean distance to the true embedding (1.70) is near the minimum distance between embeddings (1.79). This means that it is nearing the neighbourhood density of the true embedding model underlining the limitations of the neighbour test. Comparing this distance with the average distance between any two alkene embeddings (9.46), we can see that we are well-within the alkene predictions, making fine-tuned replicates based on multiple bonds away.
With the perturbational replicates at hand, we are now in a position to prove the linear analogies up to first order perturbation. We first define a formal reaction vector, under any given perturbation. At a perturbation of m, for example, we can isolate a reaction vector as
 | (11) |
For an oxidation of an alcohol at a perturbation of 1, this would give the following
ΔX(1)ox,O = cC![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) (0)C − (cC (0)C − (cC![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) (0)C + cH (0)C + cH![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) (0)H), (0)H), | (12) |
ΔXox,(1)O = −cH![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) (0)H. (0)H. | (13) |
The key observation is that the reaction vector is proportional to the average ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) (0)H, a vector which is independent of the local neighbourhood of the oxygen. Similarly, the reaction vector for the oxidation from alkanes to alkenes is
(0)H, a vector which is independent of the local neighbourhood of the oxygen. Similarly, the reaction vector for the oxidation from alkanes to alkenes is
ΔX(1)ox,C = −cH![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) (0)H, (0)H, | (14) |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) (0)H and independent of the C environment. This explains how the perturbational replicates can reduce to the linear analogies found at the first order perturbation, and how similar changes whether on alkane or alcohol are colinear. As Table 3 shows, we obtain greater accuracy with greater perturbations on the neighbourhood embedding replicates. Of course, including the higher order corrections, will integrate long-range effects and provide a more fine-tuned reaction vector that will explain deviations from the exact constant vector.
(0)H and independent of the C environment. This explains how the perturbational replicates can reduce to the linear analogies found at the first order perturbation, and how similar changes whether on alkane or alcohol are colinear. As Table 3 shows, we obtain greater accuracy with greater perturbations on the neighbourhood embedding replicates. Of course, including the higher order corrections, will integrate long-range effects and provide a more fine-tuned reaction vector that will explain deviations from the exact constant vector.
2.5 Non-learned morgan fingerprint representation
An important question to consider is how specific the presented algebraic framework of cosine similarities and neighbourhood retrieval is to the GNN-learned representations. The uniform density of states in each cluster reported in Table 1 provides a naive baseline reference to appreciate the reported neighbourhood retrieval results on a quantitative level, alongside the qualitative picture in Fig. 2. Nevertheless, it is important to confront neighbourhood retrieval and cosine similarities with other molecular vector representations, and investigate whether similar algebraic relations exist. To this end, we confront the GNN embedding vectors with Morgan fingerprints (MF) bit encodings.76 The conceptual similarity between the GNN embedding vectors and MFs is that it encodes a chemical representation of atoms or molecules respectively in terms of chemical environments. A notable difference is that the GNN embedding vectors have been learned through a training procedures, whereas MFs encode the chemical environments explicitly. Additionally, and more importantly, the former provides a representation of an individual atom within its chemical environment, whereas the latter is a fully molecular property.For the baseline experiment, we have constructed the 2048 bit hydrogen-free radius-2 Morgan Fingerprints of all molecules involved in Table using the RDKit cheminformatics toolkit.77 The choice of hyperparameters corresponds to standard usage in cheminformatics applications,76 striking a balance between local and global molecular property encoding. With the MF constructed for both reactants and products in each reaction categories, it is possible to construct average reaction vectors in this 2048-dimensional space and perform neighbourhood retrieval and cosine similarity tests, just as before for the GCNN embedding vectors. The results are presented in Table 1 for the neighbourhood retrieval test (% MF and % MF\r) and Table 2 (upper triangle) for the cosine similarities.
It can be seen from Table 1 that the neighbour retrieval tests for % MF performed less than the GNN embedding vectors. An interesting observation for the % MF is that the product MF often scored second in the neighbourhood test, with the reactant vector being the closest. This leads to particularly low neighbourhood tests for % MF for the majority of reactions. Remarkably, when the reactant vector was removed from the pool of vectors, the product vector retrieval score increased considerably, denoted by % MF\r. This observation is reminiscent of the observations in NLP,64 where often the original vector (equivalent to the reactant vector in chemistry) is the closest to the analogy in situations situation where underlying semantics might lead to biased analogies. This points to an internal organization of the MF vector space that is less organized than the GNN, due to the fact that the MF vectors encode full molecular information, where multiple different chemical environments coexist, opposed to the GNN embedding vectors, which typically encode a single chemical environment around the single atom. These observations are corroborated by the cosine similarities in Table 2, which point to a less structured space compared to the GNN, even considering the highly dimensional space of the MF.
2.6 Applications of linear analogies
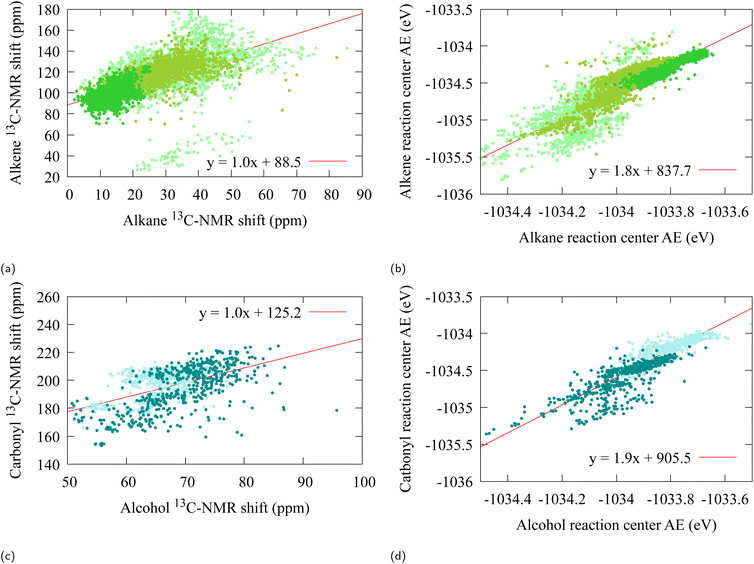
An other interesting question is to what extent these linear analogies in abstract latent space will provide imprints on real chemical observables. For instance, one can intuitively expect that chemical observables that are reasonably well described by a quasi-linear model in this organized latent space will display similar behaviour. Remarkably, it is possible to extract tangible relations for chemical observables based on fairly general assumptions. Consider an atom-wize chemical observable that can be obtained as a function f(x) of its chemical composition or atomic embedding vector, e.g.13C-NMR shifts, either from an end-to-end78 or transfer learning62,79 point of view. Our first assumption is that this function f(x) should be sufficiently smooth over each individual functional group class, so one can expand the function around the average![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) , or 0th order embedding vector x(0) for that functional group
, or 0th order embedding vector x(0) for that functional group | (15) |
| xr + Δ = xp, | (16) |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) , by construction. Furthermore, it implies that each δ specifying the individual end points of the reaction are necessarily equal
, by construction. Furthermore, it implies that each δ specifying the individual end points of the reaction are necessarily equal| δr = δp = :δ. | (17) |
As a result, one can write for both end points
 | (18) |
 | (19) |
Solving δ formally from the first equation, we obtain the simple linear relation
 | (20) |
| = αf(xr) + β. | (21) |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) r and
r and ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p, and not on the individual reaction end points. The relation becomes even stronger when considering a global linear transfer model
p, and not on the individual reaction end points. The relation becomes even stronger when considering a global linear transfer model| f(x) = a x + b, | (22) |
For which a quick insightful re-derivation of (21) yields
| f(xp) = a xp + b = a (xr + Δ)+b = f(xr) + a Δ, | (23) |
A fit on the atomization energies also yield linear relations (21) with α ≈ 1.8 [R2 = 0.79, R2 = 0.77] (see Fig. 3b and d). This deviation from α = 1 is to be expected from the architecture of SchNet, in which the final atomization energies are obtained from a fully connected feed-forward neural network. Furthermore, a closer scrutiny of Fig. 3b and d reveals a substructure into bands for which each individual α is closer to 1, which may point towards a more locally fine-tuned sub-classification of the alcohol/aldehyde and alkane/alkene groups for atomization energy.
3 Conclusions
In this work, we uncover a latent space of graph neural network models that maintains a high degree of structural integrity. The structure of the graph neural network latent space is largely based on a fine chemical syntax organization. We demonstrate this via the use of linear analogies, constant vectors that help transform from one chemical formula to another, a.k.a reaction vectors. We observed how linear analogies themselves form a coherent structure, in that similar reactions (ex. oxidations, eliminations) are colinear in the latent space. Thus, the structure of the embedding space can be thought of to have two levels of organization. The first level is that of molecular substructure composition; similar substructures are placed next to each other (alkanes and alkenes vs. aldehydes and ketones). The second level is that of changes to molecular substructure, similar chemical changes are in the same direction in the latent space. This is in line with previous observations in natural language models in which word analogies can be found in using vector arithmetic, such as ‘King’ − ‘Man’ + ‘Woman’ = ‘Queen’. In a similar vein, a chemist can write: ‘Amide’ − ‘Amine’ + ‘Alcohol’ = ‘Carboxylic Acid,’ only in a quantitative chemical compositional sense. Nevertheless, despite the apparent correlations in the vector algebraic relations, reflected in for instance the cosine similarities, a more in-depth analysis on a wider plethora of chemical reactions will be needed to confirm these relations in more generality.Our observations were largely explained by a replicate model of the latent space based on perturbational updates that integrate neighbourhood chemical compositions in successive layers until self-consistency is reached between atom representation and neighbourhood representation. This perturbational model relates the structure of the latent space to chemical composition. We showed how such a model can explain the approximately constant reaction vectors. Additionally, the reconstructed model demonstrates how linear analogies in the latent space carry over to chemical properties such as NMR and atomization energies. In other words, the integrity of linear analogies lies beyond just the latent space and can be used to explain quasi linear changes in chemical properties, such as constant NMR shifts, and near-constant changes in atomization energies.
Although many investigations into the interpretability of GNNs in chemical applications precede this work, this is among the first to uncover a structured, quantitative framework that connects GNN-learned embeddings to fundamental principles of chemical language at a global scale. In the past, explainability has been done locally, using extrinsic tools, and observing how the model responds to limited examples. However, our linear analogies structure, and perturbational replications sets the framework for a global explanation to the latent space of GNN chemistry. While the main frame is set, there is still much room to explore. One direction is to map out the trajectories of reactions in the latent space, and uncover what is happening between end-points of reactions, i.e. transition states. Another direction is to study how this global explanatory framework reduces to a local one and thus can give us explanations on a case-by-case basis. For example, we can study how the replicates improve prediction of chemical quantities (or changes in chemical quantities) based on finely tuning the neighbourhood composition. This also sets the stage for a global evaluation of model generalizability and transferability. Lastly, there is room for improving the replicates of the GNN model. For instance, the perturbational replicate model uses a neighbourhood composition feature space that ignores the exact layout of the graph, by incorporating the exact layout, and using the same geometry optimization as the GNN model, can lead to a finer replicate. Nonetheless, the findings in this paper set the stage for global explorations in GNN modeling of chemistry in a single coherent framework.
Data availability
The generated data set of “SchNet Model embedding vectors of QM9 atoms labeled according to functional group designation” for which the analysis has been published on UNB’s Dataverse server at https://doi.org/10.25545/EK1EQA.Author contributions
S. D. B. & A. E. S. with contributed equally to the conceptualization and methodology development of the project. A. E. S. implemented the methodology, data curation, and produced results. S. D. B. & A. E. S. contributed to the analysis of the results. A. E. S. wrote the manuscript and S. D. B. edit it. S. D. B. provided funding acquisition.Conflicts of interest
There are no conflicts to declare.4 Appendix
The reaction creation and analysis code can be found at: https://github.com/QuNB-Repo/DLCheM/tree/master. This automates reaction dataset creation. It is able to query a dataset for all reactants specified (with any long-range feature), remove leaving groups, build any functional group, and extract embeddings at the reaction site for analysis. The repository also contains all the prepared reaction datasets and analysis done in this study.4.1 Representing neighbourhood feature spaces
Practically, to represent equation 2.4, we must avoid problems of having a variant number of neighbours as we cannot handle data of various sizes without reverting back to graph neural networks. Additionally, we must ensure our representation for the neighbourhood is unique to each chemical neighbourhood. To avoid these problems we use a data structure whereby the chemical neighbourhood feature space is described by embedding-sized placeholders for the existence of H, C, N, O, and/or F neighbour, in that order. For instance, being an oxygen atom in an alcohol, will fill the carbon and the hydrogen embedding placeholders for each update (while leaving the rest as zero), with either some previous update or with the initial average for that neighbouring element. If, for instance, two carbons are found as neighbours, then their embeddings are added onto the same placeholder for the carbon neighbour. This practical approach avoids issues of variant neighbourhood sizes, as now at each update the number of features is the same, Dembedding × Delements. If there are multiple neighbourhood depths included in the representations, then the order of the neighbour elements is repeated for each depth such that we have Dembedding × Delements × Ddepth. This ensures uniqueness in the representation even across multiple layers of neighbourhood depth.Acknowledgements
Finanical support from NSERC, under the discovery grant program, CFI program and NBIF RAI program are acknowledged. SDB thanks the Canada Research Chair program for financial support.Notes and references
- A. C. Mater and M. L. Coote, J. Chem. Inf. Model., 2019, 59, 2545–2559 CrossRef CAS PubMed.
- G. B. Goh, N. O. Hodas and A. Vishnu, J. Comput. Chem., 2017, 38, 1291–1307 CrossRef CAS PubMed.
- M. Vogt, Expet Opin. Drug Discov., 2022, 17, 297–304 CrossRef PubMed.
- A. Mayr, G. Klambauer, T. Unterthiner and S. Hochreiter, Front. Environ. Sci., 2016, 3, 80 Search PubMed.
- J. Ma, R. P. Sheridan, A. Liaw, G. E. Dahl and V. Svetnik, J. Chem. Inf. Model., 2015, 55, 263 CrossRef CAS PubMed.
- T. Unterthiner, A. Mayr, G. Klambauer, M. Steijaert, J. K. Wegner, H. Ceulemans and S. Hochreiter, Proceedings of the Deep Learning Workshop at NIPS, 2014, p. 1 Search PubMed.
- G. E. Dahl, N. Jaitly and R. Salakhutdinov, arXiv, 2014, preprint, arXiv:1406.1231 Search PubMed.
- A. Korotcov, V. Tkachenko, D. P. Russo and S. Ekins, Mol. Pharm., 2017, 14, 4462 CrossRef CAS PubMed.
- T. Unterthiner, A. Mayr, G. Klambauer and S. Hochreiter, arXiv, 2015, preprint, arXiv:1503.01445 Search PubMed.
- J. Wenzel, H. Matter and F. Schmidt, J. Chem. Inf. Model., 2019, 59, 1253 CrossRef CAS PubMed.
- M. Li, H. Zhang, B. Chen, Y. Wu and L. Guan, Sci. Rep., 2018, 8, 1 Search PubMed.
- K. Mills, M. Spanner and I. Tamblyn, Phys. Rev. A, 2017, 96, 042113 CrossRef.
- K. Yao and J. Parkhill, J. Chem. Theory Comput., 2016, 12, 1139 CrossRef CAS PubMed.
- R. T. McGibbon, A. G. Taube, A. G. Donchev, K. Siva, F. Hernández, C. Hargus, K.-H. Law, J. L. Klepeis and D. E. Shaw, J. Chem. Phys., 2017, 147, 161725 CrossRef PubMed.
- S. Lorenz, A. Groß and M. Scheffler, Chem. Phys. Lett., 2004, 395, 210 CrossRef CAS.
- T. B. Blank, S. D. Brown, A. W. Calhoun and D. J. Doren, J. Chem. Phys., 1995, 103, 4129 CrossRef CAS.
- K. T. Schütt, P.-J. Kindermans, H. E. Sauceda, S. Chmiela, A. Tkatchenko and K.-R. Müller, arXiv, 2017, preprint, arXiv:1706.08566 Search PubMed.
- K. T. Schütt, F. Arbabzadah, S. Chmiela, K. R. Müller and A. Tkatchenko, Nat. Commun., 2017, 8, 1 CrossRef PubMed.
- K. Schutt, P. Kessel, M. Gastegger, K. Nicoli, A. Tkatchenko and K.-R. Muüller, J. Chem. Theory Comput., 2018, 15, 448 CrossRef PubMed.
- K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, J. Chem. Phys., 2018, 148, 241722 CrossRef PubMed.
- O. T. Unke and M. Meuwly, J. Chem. Theory Comput., 2019, 15, 3678 CrossRef CAS PubMed.
- J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192 RSC.
- R. Zubatyuk, J. S. Smith, J. Leszczynski and O. Isayev, Sci. Adv., 2019, 5, eaav6490 CrossRef CAS PubMed.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, International conference on machine learning, 2017, p. 1263 Search PubMed.
- J. Jo, B. Kwak, H.-S. Choi and S. Yoon, Methods, 2020, 179, 65 CrossRef CAS PubMed.
- J. Han, H. Kang, S. Kang, Y. Kwon, D. Lee and Y.-S. Choi, Phys. Chem. Chem. Phys., 2022, 24, 26870 RSC.
- Y. Kwon, D. Lee, Y.-S. Choi, M. Kang and S. Kang, J. Chem. Inf. Model., 2020, 60, 2024 CrossRef CAS PubMed.
- H. Rull, M. Fischer and S. Kuhn, arXiv, 2023, preprint, arXiv:2304.03361 Search PubMed.
- J. Xiong, Z. Li, G. Wang, Z. Fu, F. Zhong, T. Xu, X. Liu, Z. Huang, X. Liu and K. Chen, et al. , Bioinformatics, 2022, 38, 792 CrossRef CAS PubMed.
- D. Zhang, S. Xia and Y. Zhang, J. Chem. Inf. Model., 2022, 62, 1840 CrossRef CAS PubMed.
- Y. Pathak, S. Mehta and U. D. Priyakumar, J. Chem. Inf. Model., 2021, 61, 689 CrossRef CAS PubMed.
- K. Low, M. L. Coote and E. I. Izgorodina, J. Chem. Inf. Model., 2022, 62, 5457 CrossRef CAS PubMed.
- L. David, A. Thakkar, R. Mercado and O. Engkvist, J. Cheminf., 2020, 12, 1 Search PubMed.
- J. Zhou, G. Cui, S. Hu, Z. Zhang, C. Yang, Z. Liu, L. Wang, C. Li and M. Sun, AI Open, 2020, 1, 57 CrossRef.
- O. Wieder, S. Kohlbacher, M. Kuenemann, A. Garon, P. Ducrot, T. Seidel and T. Langer, Drug Discovery Today: Technol., 2020, 37, 1 CrossRef PubMed.
- Y. Wang, Z. Li and A. B. Farimani, arXiv, 2022, preprint, arXiv:2209.05582 Search PubMed.
- P. Schwaller, T. Gaudin, D. Lanyi, C. Bekas and T. Laino, Chem. Sci., 2018, 9, 6091–6098 RSC.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268–276 CrossRef PubMed.
- S. Jastrzebski, D. Leśniak and W. M. Czarnecki, arXiv, 2016, preprint, arXiv:1602.06289 Search PubMed.
- M. J. Kusner, B. Paige and J. M. Hernández-Lobato, International conference on machine learning, 2017, pp. 1945–1954 Search PubMed.
- E. J. Bjerrum, arXiv, 2017, preprint, arXiv:1703.07076 Search PubMed.
- M. H. Segler, T. Kogej, C. Tyrchan and M. P. Waller, ACS Cent. Sci., 2018, 4, 120–131 CrossRef CAS PubMed.
- M. Hirohara, Y. Saito, Y. Koda, K. Sato and Y. Sakakibara, BMC Bioinf., 2018, 19, 83–94 CrossRef PubMed.
- G. B. Goh, N. O. Hodas, C. Siegel and A. Vishnu, arXiv, 2017, preprint, arXiv:1712.02034 Search PubMed.
- D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CrossRef CAS.
- D. Weininger, A. Weininger and J. L. Weininger, J. Chem. Inf. Comput. Sci., 1989, 29, 97–101 CrossRef CAS.
- M. Krenn, Q. Ai, S. Barthel, N. Carson, A. Frei, N. C. Frey, P. Friederich, T. Gaudin, A. A. Gayle and K. M. Jablonka, et al. , Patterns, 2022, 3, 10 CrossRef PubMed.
- M. Krenn, F. Häse, A. Nigam, P. Friederich and A. Aspuru-Guzik, Mach. learn.: sci. technol., 2020, 1, 045024 Search PubMed.
- J. N. Wei, D. Duvenaud and A. Aspuru-Guzik, ACS Cent. Sci., 2016, 2, 725–732 CrossRef CAS PubMed.
- C. W. Coley, R. Barzilay, T. S. Jaakkola, W. H. Green and K. F. Jensen, ACS Cent. Sci., 2017, 3, 434–443 CrossRef CAS PubMed.
- K. Ethayarajh, D. Duvenaud and G. Hirst, arXiv, 2018, preprint, arXiv:1810.04882 Search PubMed.
- A. Gittens, D. Achlioptas and M. W. Mahoney, Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics, Long Papers, 2017, vol. 1, pp. 69–76 Search PubMed.
- S. Arora, Y. Li, Y. Liang, T. Ma and A. Risteski, Transactions of the Association for Computational Linguistics, 2016, vol. 4, pp. 385–399 Search PubMed.
- A. Drozd, A. Gladkova and S. Matsuoka, Proceedings of coling 2016, the 26th international conference on computational linguistics: Technical papers, 2016, pp. 3519–3530 Search PubMed.
- J. Pennington, R. Socher and C. D. Manning, Proceedings of the 2014 conference on empirical methods in natural language processing (EMNLP), 2014, pp. 1532–1543 Search PubMed.
- R. Bamler and S. Mandt, International conference on Machine learning, 2017, pp. 380–389 Search PubMed.
- M. Kusner, Y. Sun, N. Kolkin and K. Weinberger, International conference on machine learning, 2015, pp. 957–966 Search PubMed.
- M.-E. Brunet, C. Alkalay-Houlihan, A. Anderson and R. Zemel, International conference on machine learning, 2019, pp. 803–811 Search PubMed.
- R. Petrolito and F. Dell’Orletta, Word Embeddings in Sentiment Analysis, in Proceedings of 5th Italian Conference on Computational Linguistics (CLiC-it), Turin, Italy, 2018 Search PubMed.
- S. Wang, W. Zhou and C. Jiang, Computing, 2020, 102, 717–740 CrossRef.
- A. M. El-Samman, I. A. Husain, M. Huynh, S. De Castro, B. Morton and S. De Baerdemacker, Digital Discovery, 2024, 3, 544–557 RSC.
- A. M. El-Samman, S. De Castro, B. Morton and S. De Baerdemacker, Can. J. Chem., 2023, 102, 4 Search PubMed.
- T. Mikolov, K. Chen, G. Corrado and D. Jeffrey, arXiv, 2013, preprint, arXiv:1301.3781 Search PubMed.
- M. Nissim, R. van Noord and R. van der goot, Comput. Linguist., 2020, 46, 487 CrossRef.
- H. Wang, W. Li, X. Jin, K. Cho, H. Ji, J. Han and M. D. Burke, International Conference on Learning Representations, 2022 Search PubMed.
- A. M. El-Samman, SchNet Model Embedding Vectors of QM9 Atoms Labelled According to Functional Groups Designation, 2023, DOI:10.25545/EK1EQA.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. Von Lilienfeld, Sci. Data, 2014, 1, 1 Search PubMed.
- A. Gupta, S. Chakraborty and R. Ramakrishnan, Mach. learn.: sci. technol., 2021, 2, 035010 Search PubMed.
- I. Hunt, Basic IUPAC Organic Nomenclature: E- and Z-nomenclature of alkenes, https://www.chem.ucalgary.ca/courses/350/WebContent/orgnom/alkenes/alkenes-03.html, 2024.
- P. Tosco, N. Stiefl and G. Landrum, J. Cheminf., 2014, 6, 1–4 Search PubMed.
- M. Gallegos, V. Vassilev-Galindo, I. Poltavsky, Á. Martín Pendás and A. Tkatchenko, Nat. Commun., 2024, 15, 4345 CrossRef CAS PubMed.
- H. Abdi and L. J. Williams, Wiley Interdisciplinary Reviews: Computational Statistics, 2010, vol. 2, pp. 433 Search PubMed.
- T. Hastie, R. Tibshirani, J. H. Friedman and J. H. Friedman, The elements of statistical learning: data mining, inference, and prediction, Springer, 2009, vol. 2 Search PubMed.
- S. Letzgus, P. Wagner, J. Lederer, W. Samek, K.-R. Muller and G. Montavon, IEEE Signal Process. Mag., 2022, 39, 40 Search PubMed.
- G. Nikolentzos, G. Dasoulas and M. Vazirgiannis, Neural Netw., 2020, 130, 195–205 CrossRef PubMed.
- D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742 CrossRef CAS PubMed.
- RDKit: Open-source cheminformatics., doi: DOI:10.5281/zenodo.591637.
- Y. Guan, S. S. Sowndarya, L. C. Gallegos, P. C. S. John and R. S. Paton, Chem. Sci., 2021, 12, 12012–12026 RSC.
- Ž. Ivković, J. Jover and J. Harvey, Digital Discovery, 2024, 3, 2242–2251 RSC.
| This journal is © The Royal Society of Chemistry 2025 |