 Open Access Article
Open Access ArticleUnderstanding and mitigating noise in molecular quantum linear response for spectroscopic properties on quantum computers†
Karl Michael
Ziems
 *ab,
Erik Rosendahl
Kjellgren
*ab,
Erik Rosendahl
Kjellgren
 c,
Stephan P. A.
Sauer
c,
Stephan P. A.
Sauer
 d,
Jacob
Kongsted
d,
Jacob
Kongsted
 c and
Sonia
Coriani
c and
Sonia
Coriani
 a
a
aDepartment of Chemistry, Technical University of Denmark, Kemitorvet Building 207, DK-2800 Kongens Lyngby, Denmark. E-mail: kmizi@kemi.dtu.dk
bSchool of Chemistry, University of Southampton, Highfield, Southampton SO17 1BJ, UK. E-mail: K.M.Ziems@soton.ac.uk.
cDepartment of Physics, Chemistry and Pharmacy, University of Southern Denmark, Campusvej 55, DK-5230 Odense, Denmark
dDepartment of Chemistry, University of Copenhagen, DK-2100 Copenhagen Ø, Denmark
First published on 8th January 2025
Abstract
The promise of quantum computing to circumvent the exponential scaling of quantum chemistry has sparked a race to develop chemistry algorithms for quantum architecture. However, most works neglect the quantum-inherent shot noise, let alone the effect of current noisy devices. Here, we present a comprehensive study of quantum linear response (qLR) theory obtaining spectroscopic properties on simulated fault-tolerant quantum computers and present-day near-term quantum hardware. This work introduces novel metrics to analyze and predict the origins of noise in the quantum algorithm, proposes an Ansatz-based error mitigation technique, and reveals the significant impact of Pauli saving in reducing measurement costs and noise in subspace methods. Our hardware results using up to cc-pVTZ basis set serve as proof of principle for obtaining absorption spectra on quantum hardware in a general approach with the accuracy of classical multi-configurational methods. Importantly, our results exemplify that substantial improvements in hardware error rates and measurement speed are necessary to lift quantum computational chemistry from proof of concept to an actual impact in the field.
1 Introduction
Calculation of many spectroscopic properties of molecules requires not only the energy of the electronic ground state of the molecular system, but also information about the excited states. In the past decades, several formalisms have been developed to obtain such information without the need to explicitly construct the excited states. Arguably, the two most successful formalisms to this end are the equation of motion (EOM)1 and the linear response (LR)2,3 formulations.Conventionally, to predict the properties of systems with strong correlation, multi-configurational wave function methods such as complete active space (CAS)4–7 and restricted active space (RAS)8,9 self-consistent field (SCF) have been used in combination with LR.2,3,10–12 The drawback of these methods is that the scaling with respect to the system size scales exponentially, with the limit of current technology being 22 electrons in 22 orbitals13 or 26 electrons in 23 orbitals for “exact” implementations.14
A promising emerging technology to overcome the exponential scaling of these conventional multi-configurational methods are quantum processing units (QPUs). At present, fault-tolerant QPUs remain a future aspiration, while the available noisy intermediate-scale quantum (NISQ) devices face significant technological limitations. These limitations not only require extensive error suppression and mitigation strategies but also severely limit the range and quality of executable algorithms. For obtaining the molecular ground state wave function, several hybrid quantum-classical algorithms have been proposed, the most prominent examples being the variational quantum eigensolver (VQE)15,16 and approaches based on imaginary- or real-time evolution.17–19 To reduce the number of qubits, VQE has also been used within the active-space approximation.20–23
To utilize the wave function on a quantum device for property simulations, the EOM framework was extended to quantum EOM (qEOM).24,25 In the context of variational formulations, the EOM and LR formulations are identical for complete space unitary coupled cluster,26 and very similar for other Ansätze and in reduced spaces, hence qEOM and qLR were developed in parallel and are combined in the following. The qEOM formalism has been extended to many different use cases including multi-component-EOM,27 QED-EOM,28 spin-flip qEOM,29 qEOM for thermal averages of quantum states,30 and qEOM for non-adiabatic molecular dynamics.31 The original qEOM formulation has also seen improvements to its parameterizations as self-consistent (sc-qEOM/LR)32,33 and projected (proj-qEOM/LR) variant.33 Additionally, LR has been implemented by solving auxiliary response quantum states via VQE.34,35 A crucial step to near-term application, qEOM/LR were recently formulated within the active-space approximation with orbital-optimization (oo) as a powerful hybrid-classical algorithm opening for simulations beyond minimal basis on near-term devices. Apart from the naive implementation oo-qEOM36 and oo-qLR,37 eight different parametrizations were introduced by Ziems et al. using combinations of naive, self-consistent, state-transfer, and projected formalisms.37 The most suitable NISQ-era algorithms were found to be oo-qLR, oo-proj-qLR, and oo-allproj-qLR. Moreover, algorithmic improvements to the qEOM/LR formalism such as the Davidson solver sc-qEOM/LR38,39 and a reduced density matrix formulation of oo-qLR40 have recently been reported.
So far, the work in this field has mostly focused on algorithmic developments and testing on noise-free simulators that ignored not just the device noise of NISQ-QPUs but also the unavoidable quantum mechanical shot/sampling noise of fault-tolerant quantum computers. This work addresses these shortcomings and reports qLR results not only on a simulated fault-tolerant quantum computer (i.e., a shot-noise simulator) but also on currently available NISQ quantum hardware. Moreover, we analyze in detail how the quantum mechanical nature of quantum devices impacts the qLR/EOM algorithm and compare algorithms, systems, and excited state results using various (novel) metrics. For the mitigation of noise, we introduce our own Ansatz-based read-out and error mitigation and on-the-fly Pauli saving.
Importantly, we provide a proof of principle that absorption spectra can be obtained on a real quantum device using qLR/EOM formulations with a triple-zeta basis set. For this, we choose a small molecule, yet with a general and accurate Ansatz that can reproduce classic quantum chemistry. In that goal, this work diverges from many hardware studies that focus on large qubit number simulations using either approximated Ansätze, where the results often fall short of the accuracy achieved by classical quantum chemistry, sometimes merely replicating mean-field solutions, or are extremely dominated by classic costs, such as variants of quantum-select CI41 that use QPUs to just sample bitstrings in the computational basis.42–45 This study provides insight into the maturity of chemistry on quantum computers not from the viewpoint of a technical quantum advantage but of the possibilities and limitations for a chemist to obtain useful results on QPUs in the future.
2 Theory
Throughout the paper, we use p, q, r, s as general (spatial) orbital indices, a, b, c, d as virtual indices, i, j, k, l as inactive indices, and v, w, x, y as active indices. The notation va indicates an active index that is virtual in the Hartree–Fock reference, while vi stands for an active index that is inactive in the Hartree–Fock reference.2.1 Active space wave function
To reduce quantum computational costs and leverage the complementing strength of classic and quantum architecture at best, we employ an active space wave function with orbital optimization. The wave function is split according to| |0(θ)〉 = |I〉 ⊗ |A(θ)〉 ⊗ |V〉 | (1) |
| |A(θ)〉 = U(θ)|A〉 | (2) |
| Ô = ÔI ⊗ ÔA ⊗ ÔV | (3) |
| 〈0(θ)|Ô|0(θ)〉 = 〈I|ÔI|I〉 ⊗ 〈A(θ)|ÔA|A(θ)〉 ⊗ 〈V|ÔV|V〉 | (4) |
The active space unitary, U(θ), can utilize any common quantum computing wave function Ansatz such as k-UpCCGSD,46 QNP,47 tUPS,48 and variants of ADAPT.49–54 In this work, we use trotterized unitary coupled-cluster with singles and doubles (tUCCSD)
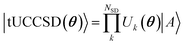 | (5) |
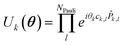 | (6) |
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) k,l being the l'th Pauli string resulting from the mapping of the k'th fermionic operator to Pauli strings with the mapping coefficient ck,l. The index k runs over all NSD number of singles and doubles excitation, and the index l over all NPauli Pauli strings for a given k. For the tUCCSD ansatz, the fermionic operators are constructed as
k,l being the l'th Pauli string resulting from the mapping of the k'th fermionic operator to Pauli strings with the mapping coefficient ck,l. The index k runs over all NSD number of singles and doubles excitation, and the index l over all NPauli Pauli strings for a given k. For the tUCCSD ansatz, the fermionic operators are constructed as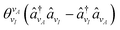 | (7) |
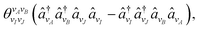 | (8) |
The orbital optimization is included via non-redundant rotations of the type inactive to active, inactive to virtual, and active to virtual, pq ∈ {vi, ai, av}. The orbital rotation parameters are
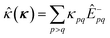 | (9) |
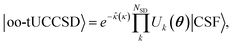 | (10) |
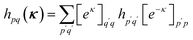 | (11) |
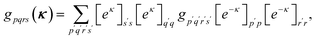 | (12) |
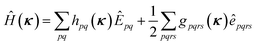 | (13) |
The ground state wave function and its energy can now be found by variational minimization of the parameters θ and κ,
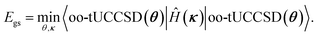 | (14) |
2.2 Quantum linear response
For sake of conciseness, we refer to the original quantum work37 or classic linear response literature3 for detailed information and only introduce the most important equations here.The qLR framework allows us to obtain excited state energies and properties within first-order time-dependent perturbation theory on top of any variationally obtained ground state wave function. Specifically, the generalized eigenvalue problem
| E[2]βk = ωkS[2]βk | (15) |
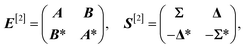 | (16) |
A = A†, AIJ = 〈0|[![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) †I, [Ĥ, †I, [Ĥ, ![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) J]]|0〉 J]]|0〉 | (17) |
B = BT, BIJ = 〈0|[![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) †I, [Ĥ, †I, [Ĥ, ![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) †J]]|0〉 †J]]|0〉 | (18) |
Σ = Σ†, ΣIJ = 〈0|[![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) †I, †I, ![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) J]|0〉 J]|0〉 | (19) |
Δ = −ΔT, ΔIJ = 〈0|[![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) †I, †I, ![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) †J]|0〉 †J]|0〉 | (20) |
![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) l ∈ {
l ∈ {![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) μ,
μ, ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) n}, with
n}, with ![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) μ being a generic orbital rotation operator and
μ being a generic orbital rotation operator and ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) n a generic active space excitation operator, exploiting, similar to what is done for the ground state wave function, an active space approach with orbital optimization (oo). Ziems et al.37 introduced eight different parameterizations to
n a generic active space excitation operator, exploiting, similar to what is done for the ground state wave function, an active space approach with orbital optimization (oo). Ziems et al.37 introduced eight different parameterizations to ![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) μ and
μ and ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) n and truncated the latter to the level of singles and doubles. Out of these, three were deemed near-term suitable, namely.
n and truncated the latter to the level of singles and doubles. Out of these, three were deemed near-term suitable, namely.
• Naive LR (oo-naive qLR), using ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) = Ĝ and
= Ĝ and ![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) =
= ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) ;
;
• Projected LR (oo-proj qLR), using ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) = Ĝ|0〉〈0| − 〈0|Ĝ|0〉 and
= Ĝ|0〉〈0| − 〈0|Ĝ|0〉 and ![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) =
= ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) ;
;
• All projected LR (oo-allproj qLR) using ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) = Ĝ|0〉〈0| − 〈0|Ĝ|0〉 and
= Ĝ|0〉〈0| − 〈0|Ĝ|0〉 and ![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) =
= ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) |0〉〈0|; with the naive orbital rotation operator
|0〉〈0|; with the naive orbital rotation operator
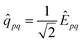 | (21) |
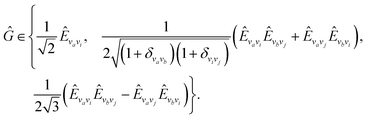 | (22) |
While eqn (15) is diagonalized classically, the matrix elements eqn (17)–(20) are obtained as expectation value measurements of the ground state wave function using the active space separation in the wave function and qLR operators introduced above.
Within this formalism, oscillator strengths for a given excited state k are obtained as
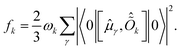 | (23) |
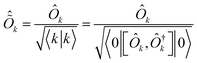 | (24) |
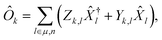 | (25) |
![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) l.
l.
In singles and doubles excitation, qLR leads to 14, 10 and 7 generic matrix element terms in the qLR equations for the naive, proj and allproj implementation, respectively, without significant change in the results.37 It will be part of this work to see whether this trend of saving elements on the fermionic level is reproduced in terms of Pauli string measurements. We point out that qLR with singles and doubles can also be implemented via reduced density matrices (RDM), where it represents a up to 6-RDM property for the proj qLR and allproj qLR, and a up to 4-RDM property for the naive qLR.40
2.3 Quantum computational workflow
Having briefly recapitulated the wave function ansatz and qLR parametrizations of interest, we now describe the methods we implemented in our in-house quantum computational software SlowQuant60 to understand and mitigate quantum errors in the qLR formalism and reduce computational costs.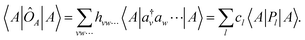 | (26) |
During the quantum computational workflow, from wave function optimization to molecular property, many expectation values are evaluated in order to assess energies, gradients, and second derivatives/hessians. These will have common Pauli strings. Thus, on an on-the-fly basis, every new Pauli string distribution is saved and stored in memory. This storage is accessed and updated during the computational workflow as new Pauli strings are needed. Importantly, only the most connected clique within qubit-wise commutation is stored and this only for a given parametrized circuit. Thus, the memory requirement will scale with the number of clique heads that in turn is proportional to the number of Pauli strings, e.g., O(N4qubit) for the electronic Hamiltonian.61
At its core, this approach means that a given Pauli string has always the same deviation from the true mean regardless of in which expectation value or where during the algorithm it appears. This is also true for measurement methods based on quantum tomography62 and approximations thereof, like classic shadows63 and matrix product state tomography.64 This implies that our findings below using Pauli saving apply to a wide range of (reduced and approximated) measurement schemes.
| pmitigated = M−1REMpraw | (27) |
| MREM,ij = Pr(bj|bi) | (28) |
Instead of only encoding read-out error as done in “traditional” REM, both read-out error and gate error can be encoded into the confusion matrix in our approach. This is achieved by including the ansatz when measuring the bit-strings, bj. To know what the prepared bit-string bi is, all parameters in the ansatz are set to zero, meaning that the ansatz does not modify the initial state but allows to encode gate error. The circuit preparation to construct bi takes the form,
| circ(bi) = U(0)Xi | (29) |
| pmitigated = M−1U0praw | (30) |
Using the ansatz with zero parameters to capture gate error makes the circuits Clifford-circuits. Thus, this error mitigation can also be seen as a form to combine REM with Clifford data regression.67 Especially, the add-and-subtract Clifford-based gate error mitigation68 also invokes a zero parameter ansatz to capture gate errors. These methods are for error mitigation of specific expectation values, in contrast to all distributions for a given Ansatz. A thorough comparison of these approaches will be part of future works.
Our approach can be combined with pre- and post-processing methods, as well as error suppression schemes. It should be noted that, in the form currently used in this work, this error mitigation technique is exponentially scaling in the number of required measurements.
The expectation value of an operator ÔA is obtained via measurements of Pauli strings on a wave function (cf.eqn (26)). Each measurement yields a bit-string distribution from which the expectation value is obtained as the sum of the means for each Pauli string distribution, i.e.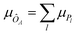 . Additionally, the standard deviation of an operator's expectation value, σÔA can be obtained from the distributions:
. Additionally, the standard deviation of an operator's expectation value, σÔA can be obtained from the distributions:
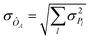 | (31) |
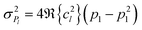 | (32) |
To analyze the noise in our qLR formalism we use various standard deviations.
First, we sample the qLR excitation energies for a given number of shots per Pauli string by performing many individual qLR simulations on a shot noise simulator, which provides the sampled standard deviation, σk, for each state k. This is the most accurate (yet expensive) and “black-box” insight into how each excited state is influenced by the quantum mechanical nature of quantum computers.
Second, we construct the qLR matrices, eqn (17)–(19), with the standard deviation for each matrix element obtained viaeqn (31). Then, each matrix is analyzed in terms of their average standard deviation, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) M with M ∈ A, B, Σ, which we will refer to as matrix std from here on. This tells us how the noise spreads through the various matrices of qLR and allows us to compare between different molecules and qLR parametrizations. Additionally, we construct a matrix standard deviation
M with M ∈ A, B, Σ, which we will refer to as matrix std from here on. This tells us how the noise spreads through the various matrices of qLR and allows us to compare between different molecules and qLR parametrizations. Additionally, we construct a matrix standard deviation ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) M,nc where we set the coefficient in eqn (32) to cl = 1 for all Pl. Comparing this to
M,nc where we set the coefficient in eqn (32) to cl = 1 for all Pl. Comparing this to ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) M allows us to assess whether the standard deviation is mainly driven by the deviation in the Pauli string or by large coefficients.
M allows us to assess whether the standard deviation is mainly driven by the deviation in the Pauli string or by large coefficients.
Third, we use the procedure above to obtain the average standard deviation in each row, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) M(
M(![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) l) of each matrix M. This corresponds to the standard deviation associated with each qLR operator
l) of each matrix M. This corresponds to the standard deviation associated with each qLR operator ![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) l in matrix M. Combining each operator's standard deviation with the contribution of each operator to a given excited state (extracted from the excitation vector, βk) allows us to obtain an expected standard deviation in each excited state from the qLR formalism,
l in matrix M. Combining each operator's standard deviation with the contribution of each operator to a given excited state (extracted from the excitation vector, βk) allows us to obtain an expected standard deviation in each excited state from the qLR formalism,
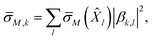 | (33) |
Additionally, the condition number and the average coefficient of variation (CV) of each matrix M are calculated as indicators of the matrix's susceptibility to noise.73 The CV is defined as the ratio of the standard deviation (calculated as in eqn (31)) and the mean. This is performed for each matrix element and averaged over.
Since device noise scales with shot noise, the information from this in-depth analysis will also help understand where algorithmic bottlenecks arise in noisy near-term machines. We note that such analysis can be performed for any quantum algorithm based on expectation value constructions.
3 Computational details
All simulations were performed using our in-house quantum computational chemistry software SlowQuant,60 where we implemented all methods and analysis tools described above, along with interfaces to Qiskit,74 IBM Quantum, and to PySCF75–77 for the integrals.On the shot noise simulator, we studied qLR of H2, LiH(2,2), H4 and BeH2(4,4) in a STO-3G78,79 basis set, while we run LiH(2,2) in both the STO-3G and cc-pVTZ80,81 basis sets on IBM Osaka. Here, a CAS-like active-space notation WF(n, o) was adopted, where n is the number of electrons in the active space and o is the number of spatial orbitals in the active space.
We used an oo-tUCCSD Ansatz for the wave function, qLR at the singles and doubles level (qLRSD), and Parity mapping for the fermionic-to-qubit mapping as it allows tapering off two qubits. Qubit-wise-commutativity (QWC)61,82 was employed in this work. The QWC algorithm used to find an approximate solution to the minimum clique coverage problem is a first-fit algorithm. For all simulations, the oo-VQE was performed classically with a shot-free simulator. The findings of this work, which focuses on qLR, are not reliant on having used oo-VQE for the ground state wave function optimization.
In the shot noise simulations we used a sampling of many qLR runs to obtain the sampled std. For this, 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 shots per Pauli string were used and 1000 individual runs for the sampling of H2 and LiH(2,2) and 250 individual runs for H4 and BeH2(4,4).
000 shots per Pauli string were used and 1000 individual runs for the sampling of H2 and LiH(2,2) and 250 individual runs for H4 and BeH2(4,4).
For the hardware experiments, we used the same specifications as for the shot noise simulations, apart from an increase of shots per Pauli to 500k (and 1m) representing a total shot budget of 4.5 million (9 million) for each qLR run and 2 million (4 million) for the error mitigation.
4 Results and discussion
4.1 Simulated quantum device and noise analysis
We first present results from runs on simulated fault-tolerant quantum computers, focusing on analyzing and understanding the error induced by the fundamental quantum nature of quantum computers (shot/sampling noise) on qLR. For qLR results on noise-free quantum computers (infinite shots limit) we refer to the literature.37,39,40| PS + QWC | QWC | None | |
|---|---|---|---|
| H 2 | |||
| naive | 9 | 35 | 42 |
| proj | 9 | 38 | 64 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| LiH(2,2) | |||
| naive | 9 | 1118 | 1774 |
| proj | 9 | 922 | 1491 |
| allproj | 9 | 447 | 715 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| H 4 | |||
| naive | 699 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 908 908 |
76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 406 406 |
| proj | 774 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 941 941 |
83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 041 041 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| BeH 2 (4,4) | |||
| naive | 822 | 104![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 096 096 |
420![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 132 132 |
| proj | 753 | 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 076 076 |
309![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 531 531 |
| allproj | 753 | 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 510 510 |
227![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 781 781 |
Using PS and QWC together leads to a dramatic reduction of the number of Pauli strings to be measured (which translates to a reduction in total shot budget), by 75–99% or up to two orders of magnitude. This saving increases with system (and thus qubit) size and will become even more advantageous for larger systems than the ones studied here. For the full space simulations, i.e., H2 and H4, proj qLR requires slightly more measurements than naive qLR comparing PS + QWC and none. This is expected as the proj qLR inserts projections onto the wave function that leads to more matrix elements and in turn Pauli strings to be evaluated (see working equations ref. 37). On the other hand, the active space simulations, i.e. LiH(2,2) and BeH2(4,4), have the opposite trend with allproj qLR and proj qLR needing significantly less measurements. This is again in line with the qLR working equations as naive, proj and allproj consist of 14, 10 and 7 generic matrix element terms, respectively, where the saving in terms comes from the orbital rotation parts that are not present in full space systems. Less generic matrix element terms leads to less Pauli string evaluations.
For brevity, we only show in the following the simulation results of LiH(2,2) and H4, and refer the reader to the ESI† for details on H2 and BeH2(4,4). These show mostly the same behaviour and at times similarities or differences will be highlighted in the text.
The sampled stds, σk, from shot noise simulation in Fig. 1 (top row or ESI Fig. S4†) and Fig. 2 show that Pauli saving leads to a reduction in shot-noise-induced deviation of up to a factor of 100 for selected excited states (solid vs. dotted lines). Interestingly, this effect is more pronounced for active space simulations. Even more dramatically, 13/11/9% of the shot noise runs of LiH(2,2) naive/proj/allproj qLR failed without PS, as they resulted in a negative eigenvalue from the Hessian and were removed in post-processing as non-physical results (cf. subsubsection 2.3.3). For BeH2(4,4), this increased to >90% without PS. This happening on shot noise simulator, i.e. a fault-tolerant quantum computer, for 100k shots per Pauli strings‡ for such small systems, shows how advances in measurement number and speed will be crucial for any useful application of quantum computing in chemistry in the future. We showed that schemes like PS can assist alongside hardware improvements, in this specific case reducing both the number of shots and noise-induced std by up to two orders of magnitude.
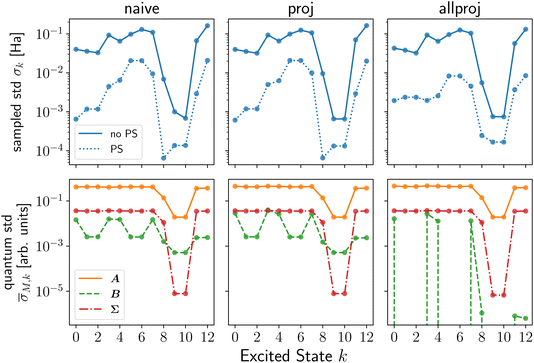 | ||
Fig. 1 Standard deviation (std) analysis of naive (left), proj (middle) and allproj (right) qLR of LiH. The top row shows the samples std, σk, with (dotted line) and without (solid line) Pauli saving (PS). The bottom row shows the state-specific std, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) M,k for the qLR matrices M = A (orange solid), M = B (green dashed) and M = Σ (red dashed-dotted). Recall subsubsection 2.3.4 and see ESI Section S1† for more details on the noise metrics and additional figures, respectively. In all simulations, 100 M,k for the qLR matrices M = A (orange solid), M = B (green dashed) and M = Σ (red dashed-dotted). Recall subsubsection 2.3.4 and see ESI Section S1† for more details on the noise metrics and additional figures, respectively. In all simulations, 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 shots per Pauli string were used. 000 shots per Pauli string were used. | ||
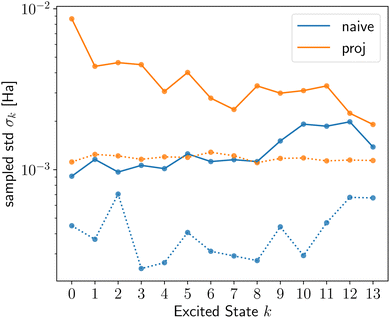 | ||
| Fig. 2 Sampled std σk with (dotted line) and without (solid line) Pauli saving for H4 naive (blue) and proj (orange) qLR. | ||
The reason behind the noise reduction obtained using PS is that it preserves symmetries even for noisy results since the same Pauli string has always the same noise. In ESI Section S2,† we provide a more mathematical reasoning for the example of a 2 × 2 matrix. Importantly, this finding holds for any hybrid quantum computing method that solves a (generalized) eigenvalue equation and is thus of importance for any quantum subspace diagonalization scheme.17,19,21,25,83–87
First, we contrast the qLR methods against each other before addressing the system- and state-dependent behaviour. For the full space systems, H2 (ESI Fig. S1†) and H4 (Fig. 2), proj qLR has a larger σk than naive qLR, while for active space simulations, LiH(2,2) (Fig. 1) and BeH2(4,4) (ESI Fig. S8†), the difference between the methods is much smaller. We can see this replicated in some of the metrics introduced in subsubsection 2.3.4 and shown in Tables S2, 2, 3 and S4† for H2, LiH(2,2), H4 and BeH2(4,4), respectively. For H4, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) M and CV reveal that proj qLR has much larger (up to a factor of 10) matrix stds, confirming the sampled std results from the shot noise simulator. For LiH(2,2), the metrics are very similar between the qLR methods, again aligning with the sampled results.
M and CV reveal that proj qLR has much larger (up to a factor of 10) matrix stds, confirming the sampled std results from the shot noise simulator. For LiH(2,2), the metrics are very similar between the qLR methods, again aligning with the sampled results.
| cond |
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) M
M
|
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) M,nc
M,nc
|
CV | |
|---|---|---|---|---|
| naive qLR | ||||
| A | 200 | 0.27 | 1.60 | 32.33 |
| B | 356 | 0.01 | 1.26 | 12.36 |
| Σ | 41 | 0.03 | 0.15 | 5.55 |
| E [2] | 232 | |||
| (S[2])−1E[2] | 49 | |||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| proj qLR | ||||
| A | 201 | 0.36 | 2.34 | 36.06 |
| B | large | 0.06 | 1.85 | large |
| Σ | 41 | 0.03 | 0.22 | 5.42 |
| E [2] | 232 | |||
| (S[2])−1E[2] | 49 | |||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| allproj qLR | ||||
| A | 202 | 0.37 | 3.00 | 36.69 |
| B | inf | 0.05 | 0.86 | inf |
| Σ | 41 | 0.03 | 0.22 | 5.42 |
| E [2] | 202 | |||
| (S[2])−1E[2] | 47 | |||
| cond |
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) M
M
|
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) M,nc
M,nc
|
CV | |
|---|---|---|---|---|
| naive qLR | ||||
| A | 4.37 | 0.15 | 20.78 | 2.78 |
| B | 12.27 | 0.04 | 14.90 | 2.83 |
| Σ | 1.07 | 0.15 | 6.25 | 257.27 |
| E [2] | 6.71 | |||
| (S[2])−1E[2] | 6.59 | |||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| proj qLR | ||||
| A | 4.52 | 0.75 | 258.49 | 25.33 |
| B | inf | 0.32 | 232.18 | inf |
| Σ | 1.08 | 0.14 | 25.11 | 436.17 |
| E [2] | 4.52 | |||
| (S[2])−1E[2] | 4.55 | |||
Interestingly, for all systems the matrix std, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) M, in A dominates. As evident from eqn (32), a matrix std's value comes from both the Pauli string variance and the coefficient. Comparing
M, in A dominates. As evident from eqn (32), a matrix std's value comes from both the Pauli string variance and the coefficient. Comparing ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) M with
M with ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) M,nc helps to differentiate this as the latter ignores the coefficient. From this, we can see that the dominance of A over B stems from the coefficient, while the dominance of A over Σ (if present) stems from the Pauli string variance. For example, for H4 naive (proj) qLR in Table 3,
M,nc helps to differentiate this as the latter ignores the coefficient. From this, we can see that the dominance of A over B stems from the coefficient, while the dominance of A over Σ (if present) stems from the Pauli string variance. For example, for H4 naive (proj) qLR in Table 3, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) M differs between A and B by a factor of 4 (2), while the coefficient free std,
M differs between A and B by a factor of 4 (2), while the coefficient free std, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) M,nc, are similar. On the other hand, A and Σ are identical (factor 2) in
M,nc, are similar. On the other hand, A and Σ are identical (factor 2) in ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) M, but differ by a factor of 3 (10) in
M, but differ by a factor of 3 (10) in ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) M,nc.
M,nc.
Second, comparing the sampled std σk between the four systems, one observes that (i) the full space systems have smaller std than their active space counterparts and (ii) that the std increases with qubit size. Thus, we observe that the sampled std increases from H2, to H4, LiH(2,2), and BeH2(4,4). While the condition number, cond, does not seem to be a reliable indicator for the subtle differences between qLR methods for a given system, it correctly predict this trend between systems. For example, for naive qLR the condition number of the Hessian, E[2], rises from 2.15, 6.71, 232, 960 for H2, H4, LiH(2,2), BeH2(4,4), respectively. The inter-system trend is also captured by the CV of the dominant A matrix.
Third, we come back to the state-dependent behaviour of the sampled std, σk, and focus on LiH(2,2) (see ESI† for others). In Fig. 1 (top row), we see the sampled std for each state. The most interesting feature is the dramatic decrease in std for excited states k = 8, 9, 10. In Fig. 1 (bottom row), we see the state-specific std, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) M,k, for LiH that reconstructs the noise contribution to each state stemming from each qLR matrix (cf. subsubsection 2.3.4). It reproduces the overall trends of the actual sampled std, σk, in the case of no PS (solid line, top row Fig. 1), importantly, including the dip for the excited states k = 8, 9, 10. This dip can now be explained as these excitation energies are dominated by transitions that originate from inactive-to-virtual orbital rotations. Our state-specific std approach can capture all this (see Section S1† for other systems) since it is based on classic quantum chemistry transition analysis of excited states, combined with the std of individual quantum operators based on their Pauli string decomposition.
M,k, for LiH that reconstructs the noise contribution to each state stemming from each qLR matrix (cf. subsubsection 2.3.4). It reproduces the overall trends of the actual sampled std, σk, in the case of no PS (solid line, top row Fig. 1), importantly, including the dip for the excited states k = 8, 9, 10. This dip can now be explained as these excitation energies are dominated by transitions that originate from inactive-to-virtual orbital rotations. Our state-specific std approach can capture all this (see Section S1† for other systems) since it is based on classic quantum chemistry transition analysis of excited states, combined with the std of individual quantum operators based on their Pauli string decomposition.
Not all subtle differences within one order of magnitude of std are captured, but large trends are perfectly reproduced (see also ESI Section S1†). To understand the discrepancies, we recall that the matrix and state-specific std (i) only account for trends in a given qLR matrix and not in the final excitation energies, and (i) assigns approximately a std to each quantum operator by row-wise integration of the qLR matrices.
As discussed in subsubsection 4.1.1, Pauli Saving leads to a reduction in measurement and noise, but Fig. 1 (top row) shows that, additionally, the trend between excited states is changed. This change cannot be captured by ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) M,k (bottom row). However, the overall std behaviour between the different qLR methods and different systems is preserved with PS.
M,k (bottom row). However, the overall std behaviour between the different qLR methods and different systems is preserved with PS.
In summary, this shows that the metrics that are directly based on the std of Pauli strings can explain how the quantum mechanical shot noise of quantum computers impact each level of the qLR algorithms differently and is parametrization-, system-, and excited state-dependent. It reveals that simple methods used so far like adding Gaussian distributed random numbers as noise to matrix elements32,33 cannot capture these subtleties and thus will not give results applicable to real quantum computers. We also note that the chosen 100k shots per Pauli string on simulated fault-tolerant quantum computers is not sufficient to reach chemical accuracy in the standard deviation for all excited states and systems presented. Again, it shows that even for small systems high measurement numbers (and speed) will be crucial and limiting even in the fault-tolerant regime. While the hardware will be the major restriction going forward, we note that the number of shots needed for a given accuracy might be reduced by using alternative measurement schemes. This includes: (i) different grouping algorithms, e.g. for QWC,61 variance based optimizations,88–90 full commutativity and fermionic approaches;82,91–93 (ii) classic shadow tomography;62 (iii) positive operator-valued measure (POVM) schemes;94 (iv) shot balancing;69–72 (v) mid-stream or feed-forwarding measurement;95,96 and (vi) shifting techniques.97,98 These approaches can incur classic and circuit depth overhead that have to be carefully studied for application on current noisy hardware. In the context of qLR, this is part of future works.
4.2 Hardware results
Having understood the impact of shot noise on the qLR results, we move to real hardware experiments on IBM Osaka for LiH(2,2). On near-term devices like this, we have additional device noise that leads to systematic and random noise. The latter is expected to broaden the standard deviation known from the shot noise study above, while systematic noise leads to a bias/shift away from the real mean of the expectation values. To mitigate these, we use our Ansatz-based read-out and gate error mitigation introduced in subsubsection 2.3.2.In Fig. 3, we present hardware results for all three qLR methods in the STO-3G basis set. The black line represents the ideal result (shot- and device-noise free) that is identical to classic CASSCF LR.37 In order to judge reproducibility, the hardware experiments were run 5 times. It shows that not all peaks are captured equally well. The peaks in the area of around 15–20 eV show the largest deviations, while the peaks around 55–60 eV are perfectly matched every time. This fully agrees with the shot noise study above (see Fig. 1 and ESI S4†), where these two areas have, respectively, the largest and smallest shot noise-induced deviations. This confirms that on near-term hardware the additional device noise leads to a broadening of the quantum mechanical shot noise. Between all three methods, none performs clearly better as expected from our quantum metrics analysis above. However, allproj qLR consists only of two runs as the three other runs were removed in post-processing as they had negative Hessian eigenvalues. Based on the analysis performed in the previous section and the low statistics count of only 5 hardware runs per qLR method, we do not believe that this is characteristic of allproj qLR but rather shows that the error rate of quantum computers can suddenly change between runs leading to nonphysical results even with error mitigation present.
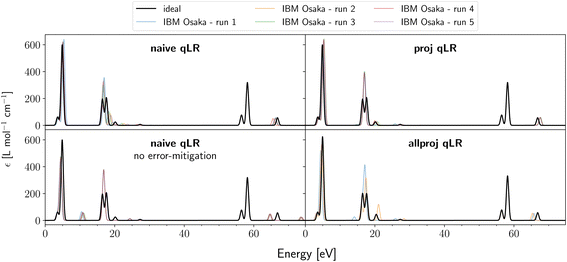 | ||
| Fig. 3 Absorption spectra of LiH(2,2)/STO-3G calculated on IBM Osaka with various qLR methods. The black line indicates the ideal (shot- and device-noise free) results that coincide with classic CASSCF. For each qLR method, five quantum hardware runs were performed and are shown in different colours. For allproj qLR, quantum run 1, 3, and 5 failed as they produced negative Hessian eigenvalues and were removed at post-processing. Detailed and zoomed-in results of each hardware run are found in ESI Section S3.† | ||
Furthermore, Fig. 3 also shows the effect of our Ansatz-based gate and read-out error mitigation. The first column reveals the effect for naive qLR. Systematic hardware errors that lead to shifts in peaks are clearly mitigated by this approach.
For each qLR run, the error mitigation had a cost of 2 million shots with a quantum runtime of 9 min, while the qLR simulation itself had a cost of 4.5 million shots taking 20 min each. This shows how costly and time-consuming even simple systems are on current near-term devices.
Lastly, in Fig. 4 (and in ESI Fig. S16†), we present naive qLR LiH(2,2) with cc-pVTZ basis set using 1m (500k) shots per Pauli string. The bottom panel show the sampled std, σk, for LiH(2,2)/cc-pVTZ on the shot noise simulator and correlates the dot size with the oscillator strength. As for the STO-3G case, there is a clear correlation between std from shot noise and deviation of the hardware runs from ideal results. In general, the STO-3G results show less deviation than the cc-pVTZ results (compare also Fig. S4 and S6 in the ESI†). We can reason this with our quantum metrics (see ESI Table S3†) as the triple-zeta simulation has larger cond (1199 for E[2], 111 for (S[2])−1E[2]) and CV (51 for A, 33 for B, 27 for Σ) than the single-zeta metrics in Table 2. This is due to the cc-pVTZ basis set being more diffuse than the STO-3G basis set. This causes some of the MO-coefficient to be small, which increases the sensitivity to noise.
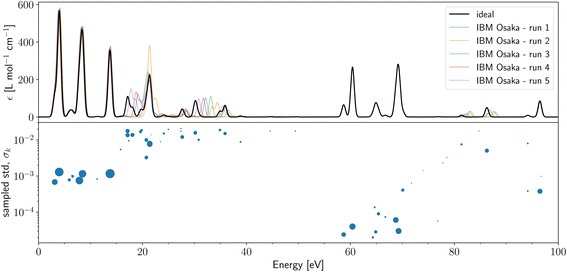 | ||
| Fig. 4 (Top) absorption spectra of LiH(2,2)/cc-pVTZ calculated on IBM Osaka with naive qLR and 1m shots per Pauli string. The black line indicates the ideal (shot- and device-noise free) results that coincide with classic CASSCF. Five quantum hardware runs were performed and are shown in different colours. Detailed results of each hardware run are found in S3.† (Bottom) sampled standard deviation, σk, for 1000 samples with 100k shots on shot noise simulator. The size of the dot correlates with the oscillator strength value. | ||
5 Summary
In this work, we presented a first-of-its-kind detailed study of quantum linear response theory on simulated fault-tolerant QPUs and current near-term quantum hardware. Specifically, we presented quantum metrics to understand and analyze the origin of noise in our algorithms, introduced Ansatz-based error mitigation, and revealed the impact of Pauli saving. Importantly, the findings reported are applicable to many hybrid quantum-classical algorithms in chemistry and provide guidance for choosing, understanding, and executing similar works in the future.To this end, we studied H2, H4, LiH and BeH2 on a shot noise simulator, i.e. a simulated fault-tolerant quantum computer, and discussed how the quantum mechanical shot noise of these devices impacts differently depending on the algorithm, system, and even the specific excited state. Using a standard deviation metric based on the individual Pauli string distribution, we reveal the coefficient of variation as a reliable indicator to compare algorithms across and within systems. Moreover, the unique standard deviation of each operator translates to different deviations in the individual excitation peak. Interestingly, we show that Pauli saving leads to a reduction in both measurement cost and noise by up to two orders of magnitude. This effect is likely to increase for larger systems.
The hardware results of LiH using up to cc-pVTZ basis set are a first small example of quantum simulations of spectroscopic properties towards useable results beyond the minimal basis approach commonly adopted in quantum computing for chemistry. The orbital-optimized qLR algorithm in combination with the chosen oo-tUCCSD ansatz can replicate classic quantum chemistry (CASSCF) for LiH. The results show that our Ansatz-based error mitigation and a large number of shots can capture most features of the absorption spectrum but accuracy still limited by measurement speed and error rates. We confirm that the excitation energy trend found in shot noise simulation and studied with our error metrics translates to quantum hardware.
This work is understood as a proof of principle to show that molecular excited state properties can be obtained on a quantum computer in a systematic and general fashion that is inspired by classic quantum chemistry and does not rely on approximated or hand-crafted circuits, pre-knowledge of the classic solution, massive classic post-processing or full state tomography allowing for density matrix clean-up. We show that for very small systems near-term hardware results can converge to classic state-of-the-art quantum chemistry accuracy. Importantly, this work also showcases that, in order for quantum computers to have any application in chemistry and scale simulations with accurate, multi-configurational results using proper basis sets to meaningful system sizes, let alone beyond classic capabilities, great improvements in hardware error rates and measurement speed are needed. Nonetheless, while quantum computing for chemistry is in its infancy, the prospect of circumventing the exponential scaling of quantum chemistry algorithms is highly impactful and motivates detailed fundamental research efforts.
Data availability
Data supporting this article have been included as part of the ESI.† The code used to generate the data can be found here.60Author contributions
Karl Michael Ziems: conceptualization (lead); investigation (lead); methodology (lead); visualization (lead); software (equal); writing – original draft (lead). Erik Rosendahl Kjellgren: investigation (supporting); methodology (supporting); software (equal); writing – original draft (supporting), writing – review & editing (equal). Stephan P. A. Sauer: funding acquisition (equal); writing – review & editing (equal). Jacob Kongsted: funding acquisition (equal); writing – review & editing (equal). Sonia Coriani: investigation (supporting); funding acquisition (equal); writing – review & editing (equal).Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
Financial Support from the Novo Nordisk Foundation (NNF) for the focused research project “Hybrid Quantum Chemistry on Hybrid Quantum Computers” (NNF grant NNFSA220080996) is acknowledged.References
- D. J. Rowe, Equations-of-Motion Method and the Extended Shell Model, Rev. Mod. Phys., 1968, 40, 153–166 CrossRef.
- J. Olsen and P. Jørgensen, Linear and nonlinear response functions for an exact state and for an MCSCF state, J. Chem. Phys., 1985, 82, 3235–3264 CrossRef CAS.
- T. Helgaker, S. Coriani, P. Jørgensen, K. Kristensen, J. Olsen and K. Ruud, Recent Advances in Wave Function-Based Methods of Molecular-Property Calculations, Chem. Rev., 2012, 112, 543–631 CrossRef CAS PubMed.
- P. Siegbahn, A. Heiberg, B. Roos and B. Levy, A Comparison of the Super-CI and the Newton-Raphson Scheme in the Complete Active Space SCF Method, Phys. Scr., 1980, 21, 323–327 CrossRef CAS.
- B. O. Roos, P. R. Taylor and P. E. M. Siegbahn, A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- P. E. M. Siegbahn, J. Almlöf, A. Heiberg and B. O. Roos, The complete active space SCF (CASSCF) method in a Newton–Raphson formulation with application to the HNO molecule, J. Chem. Phys., 1981, 74, 2384–2396 CrossRef.
- B. O. Roos, The Complete Active Space Self-Consistent Field Method and its Applications in Electronic Structure Calculations, in Advances in Chemical Physics, John Wiley & Sons, Ltd, 1987, pp 399–445 Search PubMed.
- J. Olsen, B. O. Roos, P. Jørgensen and H. J. A. Jensen, Determinant based configuration interaction algorithms for complete and restricted configuration interaction spaces, J. Chem. Phys., 1988, 89, 2185–2192 CrossRef CAS.
- P. A. Malmqvist, A. Rendell and B. O. Roos, The restricted active space self-consistent-field method, implemented with a split graph unitary group approach, J. Phys. Chem., 1990, 94, 5477–5482 CrossRef CAS.
- P. Jørgensen, H. J. A. Jensen and J. Olsen, Linear response calculations for large scale multiconfiguration self-consistent field wave functions, J. Chem. Phys., 1988, 89, 3654–3661 CrossRef.
- B. Helmich-Paris, CASSCF linear response calculations for large open-shell molecules, J. Chem. Phys., 2019, 150, 174121 CrossRef PubMed.
- M. G. Delcey, MultiPsi: A python-driven MCSCF program for photochemistry and spectroscopy simulations on modern HPC environments, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2023, 13, e1675 CAS.
- K. D. Vogiatzis, D. Ma, J. Olsen, L. Gagliardi and W. A. de Jong, Pushing configuration-interaction to the limit: Towards massively parallel MCSCF calculations, J. Chem. Phys., 2017, 147, 184111 CrossRef PubMed.
- H. Gao, S. Imamura, A. Kasagi and E. Yoshida, Distributed Implementation of Full Configuration Interaction for One Trillion Determinants, J. Chem. Theory Comput., 2024, 20, 1185–1192 CrossRef CAS PubMed.
- A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik and J. L. O'Brien, A variational eigenvalue solver on a photonic quantum processor, Nat. Commun., 2014, 5, 4213 CrossRef CAS PubMed.
- J. R. McClean, J. Romero, R. Babbush and A. Aspuru-Guzik, The theory of variational hybrid quantum-classical algorithms, New J. Phys., 2016, 18, 023023 CrossRef.
- K. Klymko, C. Mejuto-Zaera, S. J. Cotton, F. Wudarski, M. Urbanek, D. Hait, M. Head-Gordon, K. B. Whaley, J. Moussa and N. Wiebe, others Real-time evolution for ultracompact hamiltonian eigenstates on quantum hardware, PRX Quantum, 2022, 3, 020323 CrossRef.
- S. McArdle, T. Jones, S. Endo, Y. Li, S. C. Benjamin and X. Yuan, Variational ansatz-based quantum simulation of imaginary time evolution, npj Quantum Inf., 2019, 5, 75 CrossRef.
- M. Motta, C. Sun, A. T. Tan, M. J. O'Rourke, E. Ye, A. J. Minnich, F. G. Brandao and G. K.-L. Chan, Determining eigenstates and thermal states on a quantum computer using quantum imaginary time evolution, Nat. Phys., 2020, 16, 205–210 Search PubMed.
- W. Mizukami, K. Mitarai, Y. O. Nakagawa, T. Yamamoto, T. Yan and Y.-y. Ohnishi, Orbital optimized unitary coupled cluster theory for quantum computer, Phys. Rev. Res., 2020, 2, 033421 Search PubMed.
- T. Takeshita, N. C. Rubin, Z. Jiang, E. Lee, R. Babbush and J. R. McClean, Increasing the Representation Accuracy of Quantum Simulations of Chemistry without Extra Quantum Resources, Phys. Rev. X, 2020, 10, 011004 Search PubMed.
- I. O. Sokolov, P. K. Barkoutsos, P. J. Ollitrault, D. Greenberg, J. Rice, M. Pistoia and I. Tavernelli, Quantum orbital-optimized unitary coupled cluster methods in the strongly correlated regime: Can quantum algorithms outperform their classical equivalents?, J. Chem. Phys., 2020, 152, 124107 CrossRef CAS PubMed.
- J. Bierman, Y. Li and J. Lu, Improving the Accuracy of Variational Quantum Eigensolvers with Fewer Qubits Using Orbital Optimization, J. Chem. Theory Comput., 2023, 19, 790–798 CrossRef CAS PubMed.
- J. R. McClean, M. E. Kimchi-Schwartz, J. Carter and W. A. de Jong, Hybrid quantum-classical hierarchy for mitigation of decoherence and determination of excited states, Phys. Rev. A, 2017, 95, 042308 CrossRef.
- P. J. Ollitrault, A. Kandala, C.-F. Chen, P. K. Barkoutsos, A. Mezzacapo, M. Pistoia, S. Sheldon, S. Woerner, J. M. Gambetta and I. Tavernelli, Quantum equation of motion for computing molecular excitation energies on a noisy quantum processor, Phys. Rev. Res., 2020, 2, 043140 CrossRef CAS.
- A. G. Taube and R. J. Bartlett, New perspectives on unitary coupled-cluster theory, Int. J. Quantum Chem., 2006, 106, 3393–3401 CrossRef CAS.
- F. Pavošević and S. Hammes-Schiffer, Multicomponent Unitary Coupled Cluster and Equation-of-Motion for Quantum Computation, J. Chem. Theory Comput., 2021, 17, 3252–3258 CrossRef PubMed.
- F. Pavošević and J. Flick, Polaritonic Unitary Coupled Cluster for Quantum Computations, J. Phys. Chem. Lett., 2021, 12, 9100–9107 CrossRef PubMed.
- F. Pavošević, I. Tavernelli and A. Rubio, Spin-Flip Unitary Coupled Cluster Method: Toward Accurate Description of Strong Electron Correlation on Quantum Computers, J. Phys. Chem. Lett., 2023, 14, 7876–7882 CrossRef PubMed.
- D. Morrone, N. W. Talarico, M. Cattaneo and M. A. C. Rossi, Estimating molecular thermal averages with the quantum equation of motion and informationally complete measurements, Entropy, 2024, 26(9), 722 CrossRef CAS PubMed.
- A. Gandon, A. Baiardi, P. Ollitrault and I. Tavernelli, Nonadiabatic Molecular Dynamics with Fermionic Subspace-Expansion Algorithms on Quantum Computers, J. Chem. Theory Comput., 2024, 5951–5963 CrossRef CAS PubMed.
- A. Asthana, A. Kumar, V. Abraham, H. Grimsley, Y. Zhang, L. Cincio, S. Tretiak, P. A. Dub, S. E. Economou, E. Barnes and N. J. Mayhall, Quantum self-consistent equation-of-motion method for computing molecular excitation energies, ionization potentials, and electron affinities on a quantum computer, Chem. Sci., 2023, 14, 2405–2418 RSC.
- A. Kumar, A. Asthana, V. Abraham, T. D. Crawford, N. J. Mayhall, Y. Zhang, L. Cincio, S. Tretiak and P. A. Dub, Quantum Simulation of Molecular Response Properties in the NISQ Era, J. Chem. Theory Comput., 2023, 19, 9136–9150 CrossRef CAS PubMed.
- X. Cai, W.-H. Fang, H. Fan and Z. Li, Quantum computation of molecular response properties, Phys. Rev. Res., 2020, 2, 033324 CrossRef CAS.
- K. Huang, X. Cai, H. Li, Z.-Y. Ge, R. Hou, H. Li, T. Liu, Y. Shi, C. Chen, D. Zheng, K. Xu, Z.-B. Liu, Z. Li, H. Fan and W.-H. Fang, Variational quantum computation of molecular linear response properties on a superconducting quantum processor, J. Phys. Chem. Lett., 2022, 13, 9114–9121 CrossRef CAS PubMed.
- P. W. K. Jensen, E. R. Kjellgren, P. Reinholdt, K. M. Ziems, S. Coriani, J. Kongsted and S. P. A. Sauer, Quantum Equation of Motion with Orbital Optimization for Computing Molecular Properties in Near-Term Quantum Computing, J. Chem. Theory Comput., 2024, 20, 3613–3625 CrossRef CAS PubMed.
- K. M. Ziems, E. R. Kjellgren, P. Reinholdt, P. W. K. Jensen, S. P. A. Sauer, J. Kongsted and S. Coriani, Which Options Exist for NISQ-Friendly Linear Response Formulations?, J. Chem. Theory Comput., 2024, 20, 3551–3565 CrossRef CAS PubMed.
- Y. Kim and A. I. Krylov, Two Algorithms for Excited-State Quantum Solvers: Theory and Application to EOM-UCCSD, J. Phys. Chem. A, 2023, 127, 6552–6566 CrossRef CAS PubMed.
- P. Reinholdt, E. R. Kjellgren, J. H. Fuglsbjerg, K. M. Ziems, S. Coriani, S. P. A. Sauer and J. Kongsted, Subspace methods for the simulation of molecular response properties on a quantum computer, J. Chem. Theory Comput., 2024, 20, 3729–3740 CrossRef CAS PubMed.
- T. J. von Buchwald, K. M. Ziems, E. R. Kjellgren, S. P. Sauer, J. Kongsted and S. Coriani, Reduced density matrix formulation of quantum linear response, J. Chem. Theory Comput., 2024, 20, 7093–7101 CAS.
- K. Kanno, M. Kohda, R. Imai, S. Koh, K. Mitarai, W. Mizukami and Y. O. NakagawaQuantum-selected configuration interaction: Classical diagonalization of Hamiltonians in subspaces selected by quantum computers, arXiv, 2023, preprint, arXiv:2302.11320, DOI:10.48550/arXiv.2302.11320.
- J. Robledo-Moreno, M. Motta, H. Haas, A. Javadi-Abhari, P. Jurcevic, W. Kirby, S. Martiel, K. Sharma, S. Sharma and T. Shirakawa, et al., Chemistry beyond exact solutions on a quantum-centric supercomputer, arXiv, 2024, preprint, arXiv:2405.05068, DOI:10.48550/arXiv.2405.05068.
- L. Nützel, A. Gresch, L. Hehn, L. Marti, R. Freund, A. Steiner, C. D. Marciniak, T. Eckstein, N. Stockinger and S. Wolf, et al., Solving an Industrially Relevant Quantum Chemistry Problem on Quantum Hardware, Quantum Sci. Technol., 2025, 10, 015066 CrossRef.
- P. Ettenhuber, M. B. Hansen, I. Shaik, S. E. Rasmussen, P. P. Poier, N. K. Madsen, M. Majland, F. Jensen, L. Olsen and N. T. Zinner, Calculating the energy profile of an enzymatic reaction on a quantum computer, arXiv, 2024, preprint, arXiv:2408.11091, DOI:10.48550/arXiv.2408.11091.
- D. Kaliakin, A. Shajan, J. R. Moreno, Z. Li, A. Mitra, M. Motta, C. Johnson, A. A. Saki, S. Das, I. Sitdikov, et al., Accurate quantum-centric simulations of supramolecular interactions, arXiv, 2024, preprint, arXiv:2410.09209, DOI:10.48550/arXiv.2410.09209.
- J. Lee, W. J. Huggins, M. Head-Gordon and K. B. Whaley, Generalized Unitary Coupled Cluster Wave functions for Quantum Computation, J. Chem. Theory Comput., 2018, 15, 311–324 CrossRef PubMed.
- G.-L. R. Anselmetti, D. Wierichs, C. Gogolin and R. M. Parrish, Local, expressive, quantum-number-preserving VQE ansätze for fermionic systems, New J. Phys., 2021, 23, 113010 CrossRef CAS.
- H. G. A. Burton, Accurate and gate-efficient quantum Ansätze for electronic states without adaptive optimization, Phys. Rev. Res., 2024, 6, 023300 CrossRef CAS.
- H. R. Grimsley, S. E. Economou, E. Barnes and N. J. Mayhall, An adaptive variational algorithm for exact molecular simulations on a quantum computer, Nat. Commun., 2019, 10, 3007 CrossRef PubMed.
- H. L. Tang, V. Shkolnikov, G. S. Barron, H. R. Grimsley, N. J. Mayhall, E. Barnes and S. E. Economou, Qubit-ADAPT-VQE: An Adaptive Algorithm for Constructing Hardware-Efficient Ansätze on a Quantum Processor, PRX Quantum, 2021, 2, 020310 CrossRef.
- C. Feniou, M. Hassan, D. Traoré, E. Giner, Y. Maday and J.-P. Piquemal, Overlap-ADAPT-VQE: practical quantum chemistry on quantum computers via overlap-guided compact Ansätze, Commun. Phys., 2023, 6, 192 CrossRef CAS.
- H. G. A. Burton, D. Marti-Dafcik, D. P. Tew and D. J. Wales, Exact electronic states with shallow quantum circuits from global optimisation, npj Quantum Inf., 2023, 9, 75 CrossRef.
- M. Majland, P. Ettenhuber and N. T. Zinner, Fermionic adaptive sampling theory for variational quantum eigensolvers, Phys. Rev. A, 2023, 108, 052422 CrossRef CAS.
- P. G. Anastasiou, Y. Chen, N. J. Mayhall, E. Barnes and S. E. Economou, TETRIS-ADAPT-VQE: An adaptive algorithm that yields shallower, denser circuit Ansätze, Phys. Rev. Res., 2024, 6, 013254 CrossRef CAS.
- T. Helgaker, P. Jørgensen and J. Olsen, Molecular Electronic-Structure Theory, Wiley, 2000 Search PubMed.
- J. Paldus, B. G. Adams and J. Čížek, Application of graphical methods of spin algebras to limited CI approaches. I. Closed shell case, Int. J. Quantum Chem., 1977, 11, 813–848 CrossRef CAS.
- P. Piecuch and J. Paldus, Orthogonally spin-adapted coupled-cluster equations involving singly and doubly excited clusters. Comparison of different procedures for spin-adaptation, Int. J. Quantum Chem., 1989, 36, 429–453 CrossRef CAS.
- J. Oddershede, P. Jørgensen and N. H. F. Beebe, Determination of excitation energies and transition moments in a second order polarization propagator approach. Application to the Be atom and the CH + molecule, Int. J. Quantum Chem., 1977, 12, 655–670 CrossRef CAS.
- M. J. Packer, E. K. Dalskov, T. Enevoldsen, H. J. A. Jensen and J. Oddershede, A new implementation of the second-order polarization propagator approximation (SOPPA): The excitation spectra of benzene and naphthalene, J. Chem. Phys., 1996, 105, 5886–5900 CrossRef CAS.
- E. Kjellgren and K. M. Ziems, SlowQuant, 2024, https://github.com/erikkjellgren/SlowQuant/tree/master Search PubMed.
- V. Verteletskyi, T.-C. Yen and A. F. Izmaylov, Measurement optimization in the variational quantum eigensolver using a minimum clique cover, J. Chem. Phys., 2020, 152, 124114 CrossRef CAS PubMed.
- G. M. D'Ariano, M. G. Paris and M. F. Sacchi, Quantum tomography, Adv. Imaging Electron Phys., 2003, 128, S1076–S5670 Search PubMed.
- H.-Y. Huang, R. Kueng and J. Preskill, Predicting many properties of a quantum system from very few measurements, Nat. Phys., 2020, 16, 1050–1057 Search PubMed.
- M. Cramer, M. B. Plenio, S. T. Flammia, R. Somma, D. Gross, S. D. Bartlett, O. Landon-Cardinal, D. Poulin and Y.-K. Liu, Efficient quantum state tomography, Nat. Commun., 2010, 1, 149 Search PubMed.
- F. B. Maciejewski, Z. Zimborás and M. Oszmaniec, Mitigation of readout noise in near-term quantum devices by classical post-processing based on detector tomography, Quantum, 2020, 4, 257 Search PubMed.
- S. Bravyi, S. Sheldon, A. Kandala, D. C. Mckay and J. M. Gambetta, Mitigating measurement errors in multiqubit experiments, Phys. Rev. A, 2021, 103, 042605 CrossRef CAS.
- P. Czarnik, A. Arrasmith, P. J. Coles and L. Cincio, Error mitigation with Clifford quantum-circuit data, Quantum, 2021, 5, 592 CrossRef.
- M. Motta, G. O. Jones, J. E. Rice, T. P. Gujarati, R. Sakuma, I. Liepuoniute, J. M. Garcia and Y.-y. Ohnishi, Quantum chemistry simulation of ground-and excited-state properties of the sulfonium cation on a superconducting quantum processor, Chem. Sci., 2023, 14, 2915–2927 RSC.
- L. Zhu, S. Liang, C. Yang and X. Li, Optimizing Shot Assignment in Variational Quantum Eigensolver Measurement, J. Chem. Theory Comput., 2024, 20, 2390–2403 CrossRef CAS PubMed.
- O. Crawford, B. v. Straaten, D. Wang, T. Parks, E. Campbell and S. Brierley, Efficient quantum measurement of Pauli operators in the presence of finite sampling error, Quantum, 2021, 5, 385 CrossRef.
- D. Wecker, M. B. Hastings and M. Troyer, Progress towards practical quantum variational algorithms, Phys. Rev. A, 2015, 92, 042303 CrossRef.
- A. Arrasmith, L. Cincio, R. D. Somma and P. J. Coles, Operator Sampling for Shot-frugal Optimization in Variational Algorithms, arXiv, 2020, preprint, 10.48550/arXiv.2004.06252, DOI:10.48550/arXiv.2004.06252.
- E. R. Kjellgren, P. Reinholdt, K. M. Ziems, S. Sauer, S. Coriani and J. Kongsted, Divergences in classical and quantum linear response and equation of motion formulations, J. Chem. Phys., 2024, 161, 124112 CrossRef CAS PubMed.
- A. Javadi-Abhari, M. Treinish, K. Krsulich, C. J. Wood, J. Lishman, J. Gacon, S. Martiel, P. D. Nation, L. S. Bishop, A. W. Cross, B. R. Johnson and J. M. Gambetta, Quantum computing with Qiskit. 2024 Search PubMed.
- Q. Sun, Libcint: An efficient general integral library for Gaussian basis functions, J. Comput. Chem., 2015, 36, 1664–1671 CrossRef CAS PubMed.
- Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. Li, J. Liu, J. D. McClain, E. R. Sayfutyarova, S. Sharma, S. Wouters and G. K. Chan, PySCF: the Python-based simulations of chemistry framework, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 8, e1340 Search PubMed.
- Q. Sun, et al., Recent developments in the PySCF program package, J. Chem. Phys., 2020, 153, 024109 CrossRef CAS PubMed.
- W. J. Hehre, R. F. Stewart and J. A. Pople, Self-Consistent Molecular-Orbital Methods. I. Use of Gaussian Expansions of Slater-Type Atomic Orbitals, J. Chem. Phys., 1969, 51, 2657–2664 CrossRef CAS.
- W. J. Hehre, R. Ditchfield, R. F. Stewart and J. A. Pople, Self-Consistent Molecular Orbital Methods. IV. Use of Gaussian Expansions of Slater-Type Orbitals. Extension to Second-Row Molecules, J. Chem. Phys., 1970, 52, 2769–2773 CrossRef CAS.
- T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- B. P. Prascher, D. E. Woon, K. A. Peterson, T. H. Dunning and A. K. Wilson, Gaussian basis sets for use in correlated molecular calculations. VII. Valence, core-valence, and scalar relativistic basis sets for Li, Be, Na, and Mg, Theor. Chem. Acc., 2011, 128, 69–82 Search PubMed.
- P. Gokhale, O. Angiuli, Y. Ding, K. Gui, T. Tomesh, M. Suchara, M. Martonosi and F. T. Chong, O(N 3) Measurement Cost for Variational Quantum Eigensolver on Molecular Hamiltonians, IEEE Trans. Quantum Eng., 2020, 1, 1–24 Search PubMed.
- W. J. Huggins, J. Lee, U. Baek, B. O'Gorman and K. B. Whaley, A non-orthogonal variational quantum eigensolver, New J. Phys., 2020, 22, 073009 CrossRef CAS.
- R. M. Parrish and P. L. McMahon, Quantum filter diagonalization: Quantum eigendecomposition without full quantum phase estimation, arXiv, 2019, preprint, arXiv:1909.08925, DOI:10.48550/arXiv.1909.08925.
- N. H. Stair, R. Huang and F. A. Evangelista, A multireference quantum Krylov algorithm for strongly correlated electrons, J. Chem. Theory Comput., 2020, 16, 2236–2245 CrossRef CAS PubMed.
- C. L. Cortes and S. K. Gray, Quantum Krylov subspace algorithms for ground-and excited-state energy estimation, Phys. Rev. A, 2022, 105, 022417 CrossRef CAS.
- G. Lee, D. Lee and J. Huh, Sampling error analysis in quantum Krylov subspace diagonalization, Quantum, 2024, 8, 1477 CrossRef.
- T.-C. Yen, A. Ganeshram and A. F. Izmaylov, Deterministic improvements of quantum measurements with grouping of compatible operators, non-local transformations, and covariance estimates, npj Quantum Inf., 2023, 9, 14 CrossRef PubMed.
- S. Choi, T.-C. Yen and A. F. Izmaylov, Improving quantum measurements by introducing “ghost” pauli products, J. Chem. Theory Comput., 2022, 18, 7394–7402 CrossRef CAS PubMed.
- S. Choi, I. Loaiza and A. F. Izmaylov, Fluid fermionic fragments for optimizing quantum measurements of electronic Hamiltonians in the variational quantum eigensolver, Quantum, 2023, 7, 889 CrossRef.
- T.-C. Yen and A. F. Izmaylov, Cartan subalgebra approach to efficient measurements of quantum observables, PRX Quantum, 2021, 2, 040320 CrossRef.
- W. J. Huggins, J. R. McClean, N. C. Rubin, Z. Jiang, N. Wiebe, K. B. Whaley and R. Babbush, Efficient and noise resilient measurements for quantum chemistry on near-term quantum computers, npj Quantum Inf., 2021, 7, 23 CrossRef.
- J. Cohn, M. Motta and R. M. Parrish, Quantum filter diagonalization with compressed double-factorized hamiltonians, PRX Quantum, 2021, 2, 040352 CrossRef.
- G. García-Pérez, M. A. Rossi, B. Sokolov, F. Tacchino, P. K. Barkoutsos, G. Mazzola, I. Tavernelli and S. Maniscalco, Learning to measure: Adaptive informationally complete generalized measurements for quantum algorithms, PRX Quantum, 2021, 2, 040342 CrossRef.
- S. Patel, T.-C. Yen and A. F. Izmaylov, Extension of exactly-solvable Hamiltonians using symmetries of Lie algebras, J. Phys. Chem. A, 2024, 128, 4150–4159 CrossRef CAS PubMed.
- A. F. Izmaylov, T.-C. Yen and I. G. Ryabinkin, Revising the measurement process in the variational quantum eigensolver: is it possible to reduce the number of separately measured operators?, Chem. Sci., 2019, 10, 3746–3755 RSC.
- I. Loaiza, A. M. Khah, N. Wiebe and A. F. Izmaylov, Reducing molecular electronic hamiltonian simulation cost for linear combination of unitaries approaches, Quantum Sci. Technol., 2023, 8, 035019 CrossRef.
- G. Lee, S. Choi, J. Huh and A. F. Izmaylov, Reduction of Finite Sampling Error in Quantum Krylov Subspace Diagonalization, arXiv, 2024, preprint, arXiv:2409.02504, DOI:10.48550/arXiv.2409.02504.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc05839a |
| ‡ Note that we chose 100k shots as realistic number because this was the upper limit of shots per circuit on IBM hardware at the time. |
| This journal is © The Royal Society of Chemistry 2025 |
