Stacked-ring aromaticity from the viewpoint of the effective number of π-electrons

Abstract

In this study, we theoretically examined the mechanism of aromaticity induced in closely stacked cofacial π-dimers of 4nπ antiaromatic molecules, which is called stacked-ring aromaticity, in terms of the effective number of π-electrons (N_π) and Baird's rule. High-precision quantum chemical calculations combined with a multi-configurational wavefunction analysis revealed that double-triplet [¹(T₁T₁)] and intermolecular charge-transfer (CT) electron configurations mix substantially in the ground state wavefunctions of cyclobutadiene and Ni(II) norcorrole dimer models at small stacking distance (d). Since the T₁ configuration gives rise to two unpaired electrons, the remaining 4n − 2 π electrons still participate in the intramolecular conjugation, which can be interpreted as the origin of the aromaticity of each monomer. Consequently, the aromaticity of each T₁-like monomer was associated with Baird's rule. On the other hand, the increased weight of the CT configuration indicated the intermolecular delocalization of the formally unpaired four electrons derived from the ¹(T₁T₁) configuration, resulting in the intermolecular bonding interaction. This interaction contributed to the energy stabilization of the closely stacked π-dimers, even though the degree of the energy gain is considered insufficient for achieving self-aggregation of the π-dimers at d ∼3 Å. Our calculations have demonstrated that we should discuss the energy stabilization mechanism separately from the tropicity and structural changes within each monomer, although they are mutually linked through the appearance of ¹(T₁T₁) configuration.

---

1 Introduction

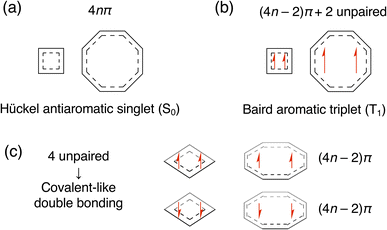
Aromaticity is one of the most important chemical concepts to understand the stabilities, reactivities, and physicochemical properties of circular π-conjugated organic molecules.¹ Although aromaticity itself is not observable, it is evaluated and analyzed based on the experimentally measured or theoretically estimated quantities, such as resonance energies,² geometric parameters (bond length alternations and planarity),³ mathematically derived indices,⁴ level structures of frontier molecular orbitals (MOs), magnetic responses (magnetically induced ring current and chemical shielding tensors),^5–7 and electron delocalization measures.^8,9 These indices help compare the degree of aromaticity of different molecular systems qualitatively and quantitatively.

The number of π-electrons (N_π) is the most fundamental index to classify the systems into aromatic or antiaromatic.¹⁰ According to Hückel's rule, (4n + 2)π and 4nπ electron systems in the singlet ground (S₀) state are classified into aromatic and antiaromatic systems, respectively.¹¹ In contrast to the S₀ states, 4nπ electron systems in the lowest ππ* excited states with the triplet (T₁) multiplicities are known to exhibit aromatic character, which is known as Baird's rule^12–14 and the MO and the valence bond (VB) theories have been successfully applied to understand its origin.¹⁴ Similar theoretical treatments in combination with computations of the aromaticity indices have been applied to understand the experimental and theoretical results for the S₁ state, suggesting aromatic character.^14–19 The S₁ state aromaticity concept helps discuss their unique photophysical and photochemical properties, although its interpretation is not as definite as that in the T₁ state.^14,20–22 Evaluating effective N_π contributing to the circular π-conjugation in the ground and low-lying excited states helps predict their geometries, stabilities, reactivities, properties, and functionalities qualitatively,¹⁰ even though it is not suitable for quantitative comparison of aromaticity between different systems. Our motivation is to extend the N_π-based understanding of aromaticity to π-stacked molecular assemblies in the S₀ state.

A theoretical analysis by Corminboeuf and coworkers suggested that aromatic character can appear in the S₀ state of cofacial π-stacked dimers consisting of 4nπ electron systems at sufficiently small stacking distances, even though formal N_π of the dimer is still a multiple of 4, which is sometimes referred to as stacked-ring aromaticity.²³ Molecular systems exhibiting stacked-ring aromaticity are expected to be candidates for a novel class of stimuli-responsive functional materials since such aromaticity-switching indicates drastic changes in their electronic structures and properties by aggregation. Recently, a series of covalently linked dimers of Ni(II) norcorroles, antiaromatic compounds bearing 16π electrons in their effective π-conjugation circuit, has been synthesized.^24–27 Experimental and computational analyses revealed that aromatic characters appeared in their S₀ state when closely π-stacked cofacial dimers were formed.^25–27 To date, however, molecular systems exhibiting stacked-ring aromaticity have been limited.

Mechanisms of the stacked-ring aromaticity have been examined from the viewpoints of the level structures of frontier MOs and the results of magnetic responses (i.e., diatropicity/paratropicity of each monomer).^23–35 Still, its N_π-based interpretation has been unclear. Establishing the N_π-based interpretation of the stacked-ring aromaticity will contribute to expanding candidate molecules for a novel class of stimuli-responsive functional materials. Since formal N_π is still a multiple of 4 in this case, we speculated that the stacked-ring aromaticity is related to Baird's rule.¹²

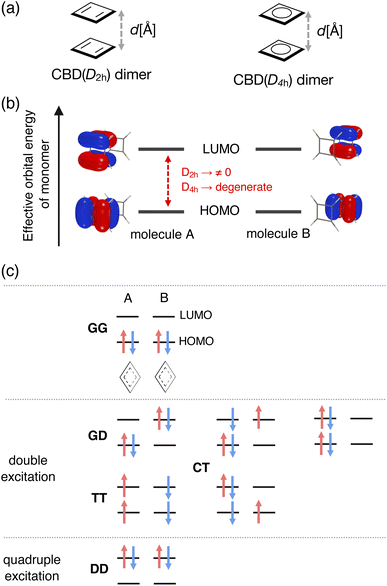
Fig. 1 summarizes our assumption for the electronic structures of stacked-ring aromatic systems. The starting point of this assumption is Baird's rule for 4nπ electron systems in the T₁ state. A clear and intuitive explanation for Baird's rule was given in the review paper by Rosenberg et al.¹⁴ We assumed that the aromatic nature in the closely stacked cofacial π-dimers of 4nπ electron systems is described by the electronic structures illustrated in Fig. 1c. We can find such an electronic structure, called the “double triplet [¹(T₁T₁)]” configuration, as an intermediate state of the singlet fission (SF) process.^36,37 In the ¹(T₁T₁) configuration, the unpaired electrons derived from the T₁-like monomers are coupled over the dimer (via exchange coupling) to exhibit the singlet spin multiplicity in total. We speculated that an increase of aromaticity (or a decrease of antiaromaticity) is attributed to the appearance of the Baird-aromatic T₁-like character of each monomer. During the preparation of this paper, we found a paper by Tsuji and coworkers in which the authors touched on the relationship between stacked-ring aromaticity and Baird's rule as a suggestion from an anonymous reviewer.³⁴ However, it was beyond the scope of their work based on the canonical MO theory. Another critical point is how Baird aromaticity in each T₁ monomer relates to the stabilization of dimers at the small stacking distance. The key to this point is the intermolecular delocalization of the four unpaired electrons, derived from two T₁-like monomers, caused by the charge-transfer interaction between the monomers. We assumed that the four unpaired electrons delocalized over the dimer, maintaining the unpaired T₁-like configuration within each monomer. A recent study on Ni(II) norcorrole dimer systems suggested the existence of a four-electron multicentered bonding interaction.^27,35 However, how it relates to the aromaticity-switching mechanism is still unclear.

Fig. 1 N _π-based illustrations of (a) Hückel's rule and (b) Baird's rule for the 4nπ electron systems, and (c) stacked-ring aromaticity for their π-dimers.

In this work, we performed theoretical analyses to relate the stacked-ring aromaticity in the S₀ state with Baird's rule and establish its N_π-based interpretation. However, such a ¹(T₁T₁) configuration can be typically found in the excited state wavefunctions. Therefore, analyzing energies and wavefunctions of both the ground and excited states of π-dimers at a given stacking distance (d) is necessary. We examined the validity of our assumption by employing π-dimer models consisting of cyclobutadienes and Ni(II) norcorroles.

2 Theory and computational methods

2.1 Cyclobutadiene π-dimer models

Although cyclooctatetraenes (COTs) have also been used as the theoretical models for examining the mechanism of stacked-ring aromaticity,²⁸ we considered cofacial π-dimer models composed of the simplest 4nπ systems, cyclobutadienes (CBDs) with planar local minimum geometries in both the S₀ and T₁ states. We should mention that several pioneering theoretical studies have explored the mechanism and locating the local minimum and transition state geometries on the full potential energy surface (PES) for the dimerization reaction of CBD.^23,38,39 In this study, on the other hand, we employed the CBD π-dimer system as a simple model to understand the mechanism of stacked-ring aromaticity.^23,28–34 We constructed two types of CBD π-dimer model: cofacial CBD π-dimers consisting of monomers with D_2h symmetry and those with D_4h symmetry (see Fig. 2a). First, we performed geometry optimization of the CBD monomer in the lowest-lying singlet state under the constraints of D_2h and D_4h symmetries at the state-specific n-electron valence state perturbation theory (NEVPT2) level based on the complete active space self-consistent field (CASSCF) wavefunction. The active orbital space employed in this step was CAS(4e, 4o), which includes all the valence π electrons and π orbitals of the CBD monomer. We used the cc-pVTZ basis set. Then, maintaining each monomer geometry fixed, π-dimer models in the face-to-face stacking configuration, consisting of the monomers with D_2h symmetry and the monomers with D_4h symmetry, were constructed at various stacking distances (2.2 Å ≤ d ≤ 5.0 Å). Hereafter, we call them the D_2h-dimer and D_4h-dimer models.

Fig. 2 (a) Molecular structures of cofacial π-dimer models composed of cyclobutadienes (CBDs) with D_2h and D_4h symmetry, (b) four localized active orbitals distributed primarily on each monomer, and (c) examples of electron configurations involved in the wavefunction of singlet ground state within CAS(4e, 4o) space. G, D, and T represent each monomer's ground singlet, doubly excited singlet, and singly excited triplet configuration, whereas CT means the charge-transfer configurations.

2.2 Multi-configurational wavefunction analysis based on a diabatic basis representation

Both the static and dynamical electron correlation effects are important to describe the electronic structures of the present π-dimers. The energies and wavefunctions of the lowest two A_g singlet states as a function of d were evaluated at the quasi-degenerate (QD-)NEVPT2 level based on the state-averaged (SA-)CASSCF reference wavefunctions.⁴⁰ The applications of the (QD-)NEVPT2 to the dimers of several π-conjugated systems have been reported.^41,42 We should note that it has been reported that the (multi-reference) second-order perturbation theory methods tend to overestimate the interaction energy of a pancake-bonded phenalenyl π-dimer system by a factor of 2–3 compared with the experimentally estimated values or theoretically predicted values at the higher electron correlated MR-AQCC level.^43,44 This kind of overestimating interaction energy may appear in the case of π-dimers of extended π-conjugated systems, like Ni(II) norcorroles.

Such multi-reference calculations are generally performed using the delocalized canonical orbital basis, and the adiabatic wavefunction can be obtained. In contrast, to extract the ¹(T₁T₁) character in the wavefunction, we, in this study, prepared localized active orbitals by rotating the canonical active orbitals obtained from the SA-CASSCF calculations. We took CAS(8e, 8o), constituting the full-π-valence CI space of the CBD dimer, which was necessary to discuss the relative energies of the A_g singlet states quantitatively. For simplicity, however, we here focused mainly on the electron configurations derived from the CAS(4e, 4o) composed of HOMOs and LUMOs of the monomers. Fig. 2b shows the four localized active orbitals in the D_2h-dimer model corresponding to the HOMO and LUMO of monomers A and B. In the D_4h-dimer model, these orbitals are degenerated regarding the effective orbital energy derived from the SA-CASSCF calculation. In Fig. 2c, we summarized examples of the electron configurations involved in the CAS(4e, 4o) contributing to the A_g singlet states. Here, G, D, and T represent the ground singlet, doubly excited singlet, and singly excited triplet configurations for each monomer. Thus, GG corresponds to the configuration where HOMO is doubly occupied in both the monomers. GD represents the configuration where HOMO is doubly occupied in one monomer, and LUMO is doubly occupied in the other. TT corresponds to the ¹(T₁T₁) configuration. Charge-transfer (CT) configurations, describing electron delocalization over the dimer, are crucial in the closely stacked case where the intermolecular orbital overlap becomes considerable. We obtained multi-configurational wavefunctions in such a diabatic representation to understand how the ¹(T₁T₁) configuration mixed in the ground state of the π-dimers at a given d. Detailed explanations of the electron configurations can be found in the ESI.†

This type of analysis is efficient if the wavefunction is characterized by a small number of electron configurations involved in the CAS space. Recently, Casanova and coworkers conducted a wavefunction analysis based on a diabatic basis and elucidated the relationship be-tween aromaticity and the electronic structure of excimers.^45,46 Considering the dynamical correlation effects is also essential to describe the energy profile of the π-dimers. Therefore, we obtained multi-configurational wavefunction expressions consistent with the QD-NEVPT2 energies. Based on the QD-NEVPT2, we constructed an effective Hamiltonian in the model (CAS) space. In the effective Hamiltonian, the diagonal and off-diagonal elements incorporate the dynamical correlation effects at the second-order perturbation theory level. By diagonalizing the effective Hamiltonian, we obtained the QD-NEVPT2 energies and the corresponding CASCI-type wavefunctions in the diabatic representation, which enabled us to analyze the ¹(T₁T₁) character in the ground state.

The lowest two A_g singlet states were analyzed at the QD-NEVPT2 level based on CAS(8e, 8o), in which the localized active orbitals (shown in Fig. S1†) were used. We employed an explicit Hermitian-type effective Hamiltonian construction and used the cc-pVTZ basis set. A detailed explanation of the methodology used to obtain the localized orbitals is provided in the ESI.† The ORCA 4.2 package⁴⁷ was used for these multi-reference calculations.

3 Results and discussion

3.1 Energies and weights of electron configurations in 1¹A_g and 2¹A_g states of the D_2h and D_4h-dimer models

Fig. 3a and b show the d dependences of the total energy and wavefunctions for the D_2h-dimer model. We observed an avoided crossing between the 1¹A_g and 2¹A_g states at d_cp ∼2.7 Å. When d is larger than d_cp, the GG configuration described the 1¹A_g state, whereas the TT configuration characterized the 2¹A_g. The characters of 1¹A_g and 2¹A_g states were exchanged when d < d_cp. We observed an energy minimum at d_min ∼2.3 Å for the TT-like 1¹A_g state, whereas the GG-like 2¹A_g state becomes unstable as d decreases. Again, we should note that these energy profiles were obtained under the constraint of fixed monomer geometries and face-to-face stacking configuration. Therefore, the obtained local minimum does not correspond to the local minimum on the full PES of the CBD dimer.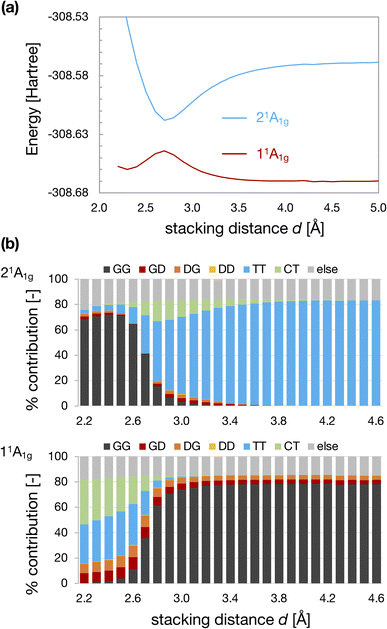

Fig. 3 Energies of 1¹A_g and 2¹A_g states of the D_2h-dimer model as a function of stacking distance d (a) and the weights of electron configurations (b).

Fig. 4 shows the results for the D_4h-dimer model. In contrast to the D_2h-dimer model, the 1¹A_g and 2¹A_g states are nearly degenerated even at large d because the effective orbital energies of HOMO and LUMO of the D_4h monomer are the same. In this situation, the ground state of the monomer is described by the superposition of G and D configurations on an equal footing because of its complete open-shell (diradical) nature. As a result, the four types of configurations, GG, GD, DG, and DD, contributed almost equally to the 1¹A_g state of the dimer. Again, the TT configuration characterized the 2¹A_g state for large d.

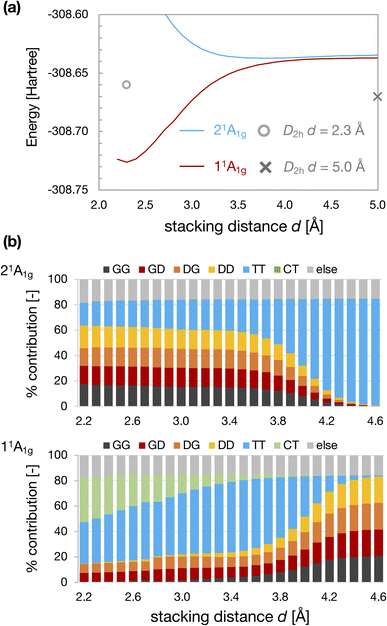Fig. 4 Energies of 1¹A_g and 2¹A_g states of D_4h-dimer model as a function of stacking distance d (a) and weight of electron configurations (b). The cross and circle in Fig. 4(a) represent the total energy calculated for the D_2h-dimer model at d = 5.0 Å and 2.3 Å.

Although the CBD monomer with D_4h symmetry exhibits degenerate HOMO and LUMO, it is known that the singlet state is stabilized due to electron correlation effects considering the CAS(4e, 4o) active space.⁴⁸ The singlet state was predicted to be lower than the triplet state for the D_4h structure at the highly accurate MR-AQCC and CCSDTQ levels.^49,50 The vertical S₀–T₁ energy gap (E(S₀)–E(T₁)) calculated at the QD-NEVPT2/cc-pVTZ level is also negative, indicating that the T₁ state is an excited state for the CBD monomer with D_4h symmetry (see Table S1†). Consequently, in the D_4h-dimer at sufficiently large d, the TT configuration appeared in the excited state.

On the other hand, TT configuration started to mix in the 1¹A_g state at d ∼4 Å. However, this mixing of TT at d > 3.4 Å may be related to underestimating the S₀–T₁ gap of D_4h cyclobutadiene at the NEVPT2 level⁵⁰ (see ESI†). Anyway, the weight of TT configuration becomes considerable in the 1¹A_g state for small d. The energy of the 1¹A_g state is stabilized as decreasing d, and there is an energy minimum at d_min ∼2.3 Å.

Another crucial point is the intermolecular delocalization of the four unpaired electrons derived from the TT configuration at small d. Theoretical analyses for the SF process indicated that the ¹(T₁T₁) configuration could efficiently mix with the intermolecular CT configurations, such as cation–anion (CA) and anion–cation (AC) pairs, via the CT–TT electronic coupling.^36,37 Such CT configurations are generated by single excitations from the GD or DG configuration as well as TT. In the VB picture, the energy stabilization of the closely π-stacked dimer is attributed to the stabilization of CT configurations in the ground state, taking along with the TT contributions via the CT–TT electronic coupling (see ESI†). The self-consistent field (SCF) procedure incorporates the contributions of CT configurations into the (de)stabilization of intermolecular (anti-)bonding MOs through the orbital optimization, resulting in closed-shell species at small d.^{23,26,27,32,34,51} Similar level structures and intermolecular (anti-)bonding characters of the canonical MOs were obtained for face-to-face dimer models of COTs with D_8h symmetry,²⁸ suggesting a similar mechanism of energy stabilization in the COT dimer cases, although the balance between the attractive and repulsive forces and the PES profile are expected to differ from those of CBD dimer cases to some extent. We expect that the intermolecular interaction between the CBDs at small d is regarded as a multi-center four-electron bonding-like interaction, i.e., a double pancake bonding interaction proposed by Kertesz and coworkers.^52,53

However, the degree of energy stabilization owing to this intermolecular interaction between the 4nπ units itself may not be sufficient to explain the formation of the self-aggregated π-dimers of actual systems. The energy of the 1¹A_g state of the D_4h-dimer model at d_min is lower than that of the non-interacting D_2h-dimer (d = 5.0 Å; see Fig. 4a). However, the energy of the 1¹A_g state of the D_4h-dimer model at d ∼3 Å is close to that of the non-interacting D_2h-dimer. Thus, the energy gain by stacking at d ∼3 Å would be insufficient to form a stable π-dimer. In addition, during the formation of the D_4h-dimer from the D_2h-dimer, maintaining the face-to-face alignment, there should be several competitive reaction pathways, as indicated in the previous works for CBD.^22,31,32 The total energy of the TT-like 2¹A_g state of the D_4h-dimer model is lower than that of the D_2h-dimer model at large d, which should be the direct contribution of Baird aromaticity of each 4nπ system to the energy stabilization.

3.2 Multi-configurational wavefunction analysis for Ni(II) norcorrole dimer models

Finally, we examined the ground state wavefunction of a Ni(II) norcorrole dimer exhibiting stacked-ring aromaticity to confirm the contribution of the ¹(T₁T₁) character in such an actual system. Ni(II) norcorrole is known to be a stable compound despite its antiaromatic character. We should note that, based on the calculation results of magnetic shielding properties, Karadakov has indicated that this stability arises because Ni(II) norcorrole contains a 14-membered cyclic conjugated antiaromatic system with 16 π electrons, as well as an 18-membered aromatic ring with 18 π electrons.⁵⁴ We focus on the Ni(II) norcorrole cyclophane tethered with two flexible alkyl chains synthesized recently by Shinokubo and coworkers²⁶ (A in Fig. 5). They obtained an almost ideal cofacial π-stacked structure in the crystal phase with an averaged intermolecular distance of ∼3.26 Å. They also observed an increased aromatic character owing to a considerable intermolecular orbital interaction. In this system, the substituent moieties at meso positions played a crucial role in the energy stabilization of the dimer with ideal face-to-face stacking. Applying the multi-reference calculations and wavefunction analyses to the full Ni(II) norcorrole cyclophane structure demands high computational resources. Therefore, we focus on the interaction between the Ni(II) norcorrole parts.

First, we constructed a Ni(II) norcorrole dimer model Nc(1) using the molecular geometry obtained from the X-ray crystallographic structure of A.²⁶ Then, we replaced all the substituent moieties at meso positions with hydrogen atoms and optimized only the positions of hydrogen atoms (see Fig. 5), maintaining other geometrical parameters fixed.

We prepared another Ni(II) norcorrole dimer model, Nc(2), for comparison. The monomer geometry of Nc(2) was taken from the X-ray crystallographic structure of meso-dimesitylnorcorrole (B in Fig. 5).⁵⁵B showed a herringbone packing structure in the crystal phase because of the bulky mesityl groups at meso positions. Again, we replaced the substituent groups with hydrogen atoms and optimized only the positions of hydrogen atoms. Then, we constructed a cofacial dimer model Nc(2) by setting the distance between nickel atoms to be 10 Å. No further geometry optimizations were performed. Namely, Nc(1) and Nc(2) modeled strongly interacting and non-interacting situations of Ni(II) norcorrole dimers.

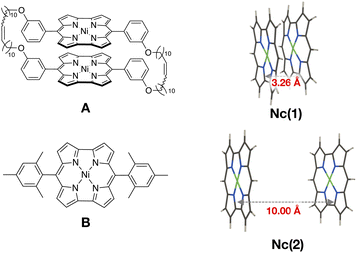Fig. 5 Structures of Ni(II) norcorrole cyclophane (A) and Ni(II) norcorrole with mesityl groups at meso positions (B), and Ni(II) norcorrole dimer models, Nc(1) and Nc(2), constructed from A and B.

The partial geometry optimizations for the positions of hydrogen atoms were performed at the RCAM-B3LYP level⁵⁶ using Gaussian 09 rev. D.⁵⁷ We employed the SDD basis set with the Stuttgart–Dresden effective core potential for Ni⁵⁸ and the minimally augmented⁵⁹ (ma-)def2-SVP⁶⁰ basis set for the other atoms (denoted as ma-def2-SVP-SDD). The auxiliary basis functions for the resolution-of-the-identity (RI) approximation were automatically generated using the AUTOAUX keyword implemented in the Orca program package.^47,61 Then, the CASCI-type wavefunctions for Nc(1) and Nc(2) were obtained by diagonalizing the effective Hamiltonian calculated at the QD-NEVPT2 level based on the SA-CASSCF(8e, 8o) with the ma-def2-SVP-SDD basis set. We performed the same procedure as the CBD dimer case to obtain the localized active orbitals and the multi-configurational wavefunctions in a diabatic representation. The active space orbitals consist of four π MOs of each monomer around the frontier MOs (see Fig. S2†).

Comparing the total energy of Nc(1) and Nc(2) at the QD-NEVPT2 level, the former was predicted to be about 79 kcal mol⁻¹ more stable. The interaction energy of Nc(1) would be overestimated by a factor of 2–3 compared with those estimated for several Ni(II) norcorrole dimers at density functional theory (DFT) levels.^25,26 We considered that this overestimation of the interaction energy is attributed to a similar reason to those reported for the phenalenyl π-dimer cases.^43,44 Nevertheless, we expect that even if we can apply higher levels of dynamical electron correlation treatment, the primal electron configurations in the ground state wavefunction will not change significantly when the choice of CAS appropriately describes the ground state wavefunction (see also Tables S2 and S3†).

Table 1 summarizes the weight of each electron configuration in the ground state of Nc(1) and Nc(2). The GG configuration primarily described the ground state of Nc(2) with a weight of 86.6%. In contrast, for Nc(1), the TT and CT configurations mixed in the ground state with weights of 37.2% and 26.7%, respectively, whereas the contribution of the GG configuration was negligibly small. The sum of the weight of TT and CT configurations was ∼64%, indicating that these configurations characterized the ground state of the closely π-stacked cofacial Ni(II) norcorrole dimers. Consequently, the experimental observations and computational results that suggest the aromaticity-switching in the cofacial Ni(II) norcorrole dimers are connected with each monomer's Baird-aromatic T₁-like electronic structure. On the other hand, to understand the overall energy stabilization mechanism of the actual π-dimers, we must analyze the potential energy surfaces around the crossing point, which is an ongoing project of our group in connection with the open-shell character⁶² and vibronic coupling,⁶³ as well as the role of the substituents.

Table 1 Weight [%] of each electron configuration in the ground state for Nc(1) and Nc(2)

	Nc(1)	Nc(2)
a The sum of the weights of TT and CT configurations.
GG	0.1	86.6
GD	9.1	1.1
DG	9.1	0.7
DD	0.0	0.0
TT	37.2	0.0
CT	26.7	0.0
Else	17.7	11.6
CT + TT^a	63.9	0.0

---

4 Conclusions

We performed a multi-configurational wavefunction analysis in a diabatic representation based on the high-precision quantum chemical calculations for cofacial π-dimer models consisting of CBDs and Ni(II) norcorroles. We demonstrated how the TT and CT configurations played crucial roles in the aromaticity-switching and energy stabilization in these dimer models. An increase in the diatropicity (or a decrease in the paratropicity), which has been evaluated from the magnetic response properties (such as the nucleus-independent chemical shift [NICS] calculations⁵), and the reduction in bond length alternation on each monomer in the closely π-stacked 4nπ-dimers is attributed to the appearance of the T₁-like character of each monomer in the TT configuration in the ground state at small d. Consequently, there is a connection between stacked-ring aromaticity and Baird's rule. The contributions of the CT configuration, describing the delocalization of the remaining four unpaired electrons over the dimer, contributed to the energy stabilization of the dimer at small d. In this sense, stacked-ring aromatic systems can be considered multicenter four-electron bonding systems. This is consistent with the results obtained by Shinokubo and coworkers based on the bond order of Ni(II) norcorrole dimer derived from the dimeric MOs.^27,35 Our analysis elucidated the relationship between the intermolecular bonding interaction and Baird's rule in the stacked-ring aromaticity. In this relation, how the degree of Baird aromaticity of each monomer affects the degree of the tropicity, structural parameters, and stabilization energy can be a topic to be investigated in the future.

However, the degree of energy stabilization between the 4nπ electron systems may still be insufficient for achieving the self-aggregation. The energy of the non-interacting D_2h-dimer is comparable to that of the D_4h-dimer model at d ∼3 Å, which is a typical stacking distance experimentally observed. The TT/CT-like characters begin to appear in the ground state at d ∼3 Å, which is not predicted as the energy minimum point. Thus, additional mechanisms stabilizing π-dimers are needed by introducing appropriate chemical modifications to the central 4nπ electron systems. Extending the π-systems and introducing direct linker connections between the monomers^24–26 can help realize the stable assembly in a proper stacking distance where the through-space electron delocalization occurs efficiently.

To analyze the energy stabilization mechanism in actual π-dimers, including Ni(II) norcorroles, we must consider the interaction between the substituents and the orbital interaction and dispersion forces between the antiaromatic units. In addition, structural reorganization induced by the intermolecular interactions should be analyzed in detail. Since the present analysis based on the QD-NEVPT2 level demands high computational resources to address these issues comprehensively, we need further study with less expensive calculations like the spin-restricted and unrestricted Kohn–Sham density functional theory (KS-DFT) methods while examining the validity of their solutions carefully.

In a perspective paper by Merino et al.,⁶⁴ the authors point out that the chemistry of aromaticity in recent years has reached a turning point. What to call aromatic and what not is the central topic in this community. Our calculations have demonstrated that we should discuss the energy stabilization mechanism separately from the in-plane tropicity and structural changes within each monomer in the π-dimers of antiaromatic molecules. However, they are mutually linked through the appearance of ¹(T₁T₁) configuration. Considering the current IUPAC definition,⁶⁵ this situation may not meet the energy criteria necessary to be called aromaticity in the usual sense. The magnetic and structural criteria for several Ni(II) norcorrole dimers of antiaromatic molecules indicate “Baird-aromatic” characters as a result of the appearance of the ¹(T₁T₁) character. On the other hand, several interacting molecular assembly systems have been reported to exhibit through-space contributions of MIC density.^66–69 It has also been reported that several Ni(II) norcorrole dimer systems also exhibit through-space MIC density between the monomers.²⁵ Such through-space currents would indicate the electron delocalization over the dimer via the contribution of the CT configuration and may relate to an aromatic characteristic that belongs to the entire dimer system. Of course, whether this phenomenon should be labeled as aromaticity may change when other new candidate systems are proposed and discovered. Ottosson pointed out another important perspective: who utilizes the aromaticity concept and who benefits from it.⁷⁰ In such discussions, the viewpoints presented in this study will provide valuable information to the various stakeholders of the aromaticity concept.

Since the electron configurations in both the ground and excited states change substantially with d, the dissociation and relaxation processes of the excited states are interesting topics to investigate theoretically and experimentally. Recent advances in experimental techniques can expand the potential applications of strongly π–π interacting molecular assemblies to future molecular electronics. In this regard, it would also be interesting to clarify the relationship between the effective radius of the circular conjugation circuit (R) and the stacking distance region where the tropicity-switching or unique magnetic and other response phenomena occur, as was theoretically examined by Orozco-Ic et al. for suggestion of molecular Helmholtz coils.³¹ We expect that the present results will contribute to further progress in the design and synthesis of novel stimuli-responsive molecular assemblies and pioneer attractive applications of 4nπ electron systems in the photochemistry, photophysics, and quantum information fields, controlling the spin-entangled ¹(T₁T₁) configurations,^71–73 which also contributes to expanding the numbers of different users of the aromaticity concept.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

Conceptualization, simulations, and analyses were performed by R. S. and K. O. All the authors discussed and interpreted the theoretical results. All authors contributed to writing the article.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by Japan Society for the Promotion of Science (JSPS) KAKENHI Grant Number JP19H00912, JP21K04995, JP22H04974, JP22H02050, a Grant-in-Aid for Transformative Research Areas (A) “Condensed Conjugation” (Grant No. JP21H05489), and the International Collaborative Research Program of Institute for Chemical Research, Kyoto University (grant #2023-60 and #2024-53). R.S. acknowledges support from the Quantum LEAder Resource (QLEAR) fellowship program (Osaka University) and Murata Science and Education Foundation. K. O. acknowledges support from JSPS Fellowship (JP23KJ1474). The authors thank Prof. Hiroshi Shinokubo (Nagoya University) for his valuable comments on the structures and properties of Ni(II) norcorrole dimers. Theoretical calculations were partly performed using Research Center for Computational Science, Okazaki, Japan (Project: 23-IMS-C004 and 24-IMS-C004).

Notes and references

1. I. Fernandez, Aromaticity, Elsevier, 2021,  DOI:10.1016/C2019-0-04193-3.
2. M. K. Cyranski, Chem. Rev., 2005, 105, 3773–3811.
3. T. M. Krygowski and M. K. Cyrański, Chem. Rev., 2001, 101, 1385.
4. J. Aihara, J. Am. Chem. Soc., 1976, 98, 2750–2758.
5. Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. v. R. Schleyer, Chem. Rev., 2005, 105, 3842.
6. D. Geuenich, K. Hess, F. Köhler and R. Herges, Chem. Rev., 2005, 105, 3758.
7. H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500.
8. J. Poater, M. Duran, M. Solà and B. Silvi, Chem. Rev., 2005, 105, 3911.
9. F. Feixas, E. Matito, J. Poater and M. Solà, Chem. Soc. Rev., 2015, 44, 6434.
10. M. Solà, Nat. Chem., 2022, 14, 585.
11. E. Hückel, Z. Phys., 1931, 70, 204.
12. N. C. Baird, J. Am. Chem. Soc., 1972, 94, 4941.
13. H. Ottosson, Nat. Chem., 2012, 4, 969.
14. M. Rosenberg, C. Dahlstrand, K. Kilså and H. Ottosson, Chem. Rev., 2014, 114, 5379.
15. P. B. Karadakov, J. Phys. Chem. A, 2008, 112, 7303.
16. P. B. Karadakov, J. Phys. Chem. A, 2008, 112, 12707.
17. F. Feixas, J. Vandenbussche, P. Bultinck, E. Matitoc and M. Solà, Phys. Chem. Chem. Phys., 2011, 13, 20690.
18. P. B. Karadakov, P. Hearnshaw and K. E. Horner, J. Org. Chem., 2016, 81, 11346.
19. J. Toldo, O. E. Bakouri, M. Solà, P. O. Norrby and H. Ottosson, ChemPlusChem, 2019, 84, 712.
20. R. Papadakis and H. Ottosson, Chem. Soc. Rev., 2015, 44, 6472.
21. J. Kim, J. Oh, A. Osuka and D. Kim, Chem. Soc. Rev., 2022, 51, 268.
22. J. Yan, T. Slanina, J. Bergman and H. Ottosson, Chem.–Eur. J., 2023, 29, e202203748.
23. C. Corminboeuf, P. v. R. Schleyer and P. Warner, Org. Lett., 2007, 9, 3263.
24. R. Nozawa, H. Tanaka, W.-Y. Cha, Y. Hong, I. Hisaki, S. Shimizu, J.-Y. Shin, T. Kowalczyk, S. Irle, D. Kim and H. Shinokubo, Nat. Commun., 2016, 7, 13620.
25. R. Nozawa, J. Kim, J. Oh, A. Lamping, Y. Wang, S. Shimizu, I. Hisaki, T. Kowalczyk, H. Fliegl, D. Kim and H. Shinokubo, Nat. Commun., 2019, 10, 3576.
26. H. Kawashima, S. Ukai, R. Nozawa, N. Fukui, G. Fitzsimmons, T. Kowalczyk, H. Fliegl and H. Shinokubo, J. Am. Chem. Soc., 2021, 143, 10676.
27. S. Kino, S. Ukai, N. Fukui, R. Haruki, R. Kumai, Q. Wang, S. Horike, Q. M. Phung, D. Sundholm and H. Shinokubo, J. Am. Chem. Soc., 2024, 146, 9311.
28. D. E. Bean and P. W. Fowler, Org. Lett., 2008, 10, 5573.
29. M. Alonso, J. Poater and M. Solà, Struct. Chem., 2007, 18, 773.
30. J. Aihara, J. Phys. Chem. A, 2009, 113, 7945.
31. M. Orozco-Ic, A. Restrepo, A. Muñoz-Castro and G. Merino, J. Chem. Phys., 2019, 151, 014102.
32. K. Okazawa, Y. Tsuji and K. Yoshizawa, J. Phys. Chem. A, 2023, 127, 4780.
33. M. Orozco-Ic and D. Sundholm, Phys. Chem. Chem. Phys., 2023, 25, 12777.
34. Y. Tsuji, K. Okazawa and K. Yoshizawa, J. Org. Chem., 2023, 88, 14887.
35. Q. Wang, D. Sundholm, J. Gauss, T. Nottoli, F. Lipparini, S. Kino, S. Ukai, N. Fukui and H. Shinokubo, Phys. Chem. Chem. Phys., 2024, 26, 14777.
36. M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891.
37. M. B. Smith and J. Michl, Annu. Rev. Phys. Chem., 2013, 64, 361.
38. Y. Li and K. N. Houk, J. Am. Chem. Soc., 1996, 118, 880.
39. C. S. Wannere, A. Paul, R. Herges, K. N. Houk, H. F. Schaefer III and P. v. R. Schleyer, J. Comput. Chem., 2007, 28, 344.
40. C. Angeli, S. Borini, M. Cestari and R. Cimiraglia, J. Chem. Phys., 2004, 121, 4043.
41. R. A. Krueger and G. Blanquart, J. Phys. Chem. A, 2019, 123, 1796.
42. A. G. Graham, F. Mota, E. Shurdha, A. L. Rheingold, J. J. Novoa and J. S. Miller, Chem.–Eur. J., 2015, 21, 13240.
43. B. Kolb, M. Kertesz and T. Thonhauser, J. Phys. Chem. A, 2013, 117, 3642.
44. Z. Cui, H. Lischka, H. Z. Beneberu and M. Kertesz, J. Am. Chem. Soc., 2014, 136, 5539.
45. A. Diaz-Andres and D. Casanova, J. Phys. Chem. Lett., 2021, 12, 7400.
46. A. Krishnan, A. Diaz-Andres, K. P. Sudhakaran, A. T. John, M. Hariharan and D. Casanova, J. Phys. Org. Chem., 2022, 36, e4438.
47. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327.
48. A. F. Voter and W. A. Goddard, J. Am. Chem. Soc., 1986, 108(11), 2830.
49. M. Eckert-Maksić, M. Vazdar, M. Barbatti, H. Lischka and Z. B. Maksić, J. Chem. Phys., 2006, 125, 064310.
50. E. Monino, M. Boggio-Pasqua, A. Scemama, D. Jacquemin and P.-F. Loos, J. Phys. Chem. A, 2022, 126, 4664.
51. J.-Y. Fujiyoshi, T. Tonami, M. Yamane, K. Okada, R. Kishi, S. Muhammad, A. G. Al-Sehemi, R. Nozawa, H. Shinokubo and M. Nakano, ChemPhysChem, 2018, 19, 2863.
52. Z. Cui, H. Lischka, H. Z. Beneberu and M. Kertesz, J. Am. Chem. Soc., 2014, 136, 12958.
53. Z. Mou and M. Kertesz, Angew. Chem., Int. Ed., 2017, 56, 10188.
54. P. B. Karadakov, Org. Lett., 2020, 22, 8676.
55. T. Ito, Y. Hayashi, S. Shimizu, J.-Y. Shin, N. Kobayashi and H. Shinokubo, Angew. Chem., Int. Ed., 2012, 51, 8542.
56. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51.
57. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, Gaussian, Inc., Wallingford, CT, 2009.
58. M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866.
59. J. Zheng, X. Xu and D. G. Truhlar, Theor. Chem. Acc., 2011, 128, 295.
60. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
61. G. L. Stoychev, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2017, 13, 554.
62. M. Nakano, Top. Curr. Chem., 2017, 375, 47.
63. I. B. Bersuker and V. Z. Polinger, Vibronic interactions in Molecules and Crystals, Springer-Verlag: Berlin and Heidelberg, Germany, 1989,  DOI:10.1007/978-3-642-83479-0.
64. G. Merino, M. Solà, I. Fernández, C. Foroutan-Nejad, P. Lazzeretti, G. Frenking, H. L. Anderson, D. Sundholm, F. P. Cossío, M. A. Petrukhina, J. Wu, J. I. Wu and A. Restrepo, Chem. Sci., 2023, 14, 5569.
65. V. I. Minkin, Pure Appl. Chem., 1999, 71, 1919.
66. M. Orozco-Ic, R. R. Valievab and D. Sundholm, Phys. Chem. Chem. Phys., 2022, 24, 6404.
67. Q. Wang, M. Orozco-Ic and D. Sundholm, Phys. Chem. Chem. Phys., 2023, 25, 19207.
68. T. Nishiuchi, Y. Makihara, R. Kishi, H. Sato and T. Kubo, J. Phys. Org. Chem., 2023, 36, e4451.
69. V. Vijay, M. Madhu, R. Ramakrishnan, A. Benny and M. Hariharan, Chem. Commun., 2020, 56, 225.
70. H. Ottosson, Chem. Sci., 2023, 14, 5542.
71. K. E. Smyser and J. D. Eaves, Sci. Rep., 2020, 10, 18480.
72. S. Matsuda, S. Oyama and Y. Kobori, Chem. Sci., 2020, 11, 2934.
73. Y. Kawashima, T. Hamachi, A. Yamauchi, K. Nishimura, Y. Nakashima, S. Fujiwara, N. Kimizuka, T. Ryu, T. Tamura, M. Saigo, K. Onda, S. Sato, Y. Kobori, K. Tateishi, T. Uesaka, G. Watanabe, K. Miyata and N. Yanai, Nat. Commun., 2023, 14, 1056.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc07123a

---