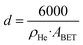Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A descriptor guiding the selection of catalyst supports for ammonia synthesis†
Andreas Weilharda,
Ilya Popova,
Emerson C. Kohlrauscha,
Gazi N. Alievb,
L. Scott Blankenship a,
Luke T. Normana,
Sadegh Ghaderzadeha,
Louise Smith
a,
Luke T. Normana,
Sadegh Ghaderzadeha,
Louise Smith c,
Mark Isaacs
c,
Mark Isaacs e,
James O'Shead,
Anabel E. Lanternaa,
Wolfgang Theis
e,
James O'Shead,
Anabel E. Lanternaa,
Wolfgang Theis b,
David Morgan
b,
David Morgan c,
Graham J. Hutchings
c,
Graham J. Hutchings c,
Elena Besley
c,
Elena Besley a,
Andrei N. Khlobystov
a,
Andrei N. Khlobystov a and
Jesum Alves Fernandes
a and
Jesum Alves Fernandes *a
*a
aSchool of Chemistry, University of Nottingham, NG7 2RD, Nottingham, UK. E-mail: jesum.alvesfernandes@nottingham.ac.uk
bSchool of Physics & Astronomy, University of Birmingham, B15 2TT, Birmingham, UK
cCardiff Catalysis Institute, School of Chemistry, Cardiff University, CF10 3AT, Cardiff, UK
dSchool of Physics and Astronomy, University of Nottingham, NG7 2RD, Nottingham, UK
eDepartment of Chemistry, University College London, London, UK
First published on 4th February 2025
Abstract
The efforts to increase the active surface area of catalysts led to reduction of metal particle size, down to single metal atoms. This results in increasing importance of support–metal interactions. We demonstrate the mechanisms through which the support influences catalytic activity of nanoclusters: the support electronics, described by the O 2p energy level, and the support surface chemistry, determined by the density of Lewis base sites. Using Ru nanoclusters, our study shows that these parameters can be effectively captured within a single catalyst support descriptor (CSD). The apparent activation energy and turnover frequency (TOF) for the ammonia synthesis correlates strongly with CSD measured for the series Ru/MgO, Ru/Sc2O3, Ru/CeO2, Ru/La2O3, and Ru/Y2O3. Furthermore, the study demonstrates that CSD correlates linearly with the binding strength of N–Ru in nanocluster, thereby providing a direct link between the catalyst's surface chemistry and the nature of the support. The catalyst support descriptor developed in this study serves as a simple yet powerful tool for selecting the optimal support material to maximise the activity of metal nanoclusters without altering the metal itself.
1 Introduction
Over the past 20 years, the focus in heterogeneous catalysis has shifted from using bulk metals and particles to nanoclusters and, ultimately, single atoms.1–3 This change was driven by the desire to maximise the metal's surface area, which in turn increased the interaction and bonding between the metal and its support due to the sheer increase of the fraction of surface atoms as metal particles become smaller.4 As a result, there is now a greater dependence on the electronic structure of catalytic centres on the local environment provided by the support material.3 In this context, metal nanoclusters and single atoms can be seen as homogeneous catalysts, where the support functions like a ligand towards the metal centres, strongly modifying their chemical state and thus the activation energy required for a specific reaction.3,5For example, Ru nanoclusters with a size range of 2–3 nm are considered the most effective catalysts for ammonia synthesis because of the maximum concentration of B5 sites.6–9 In such cases, improving the catalytic performance depends on changing the electronic environment of Ru catalysts.7–9 This can be accomplished by carefully selecting a catalyst support, known as Electronic Metal-Supported Interaction (EMSI).2 Numerous reports show support's effect on catalytic performance in various reactions, but there is no clear understanding of the fundamental aspects of this effect,10–14 and even more importantly, there are no universal rules to guide the choice of ligand–support for a specific metal. Ideally, such a guide would embed the properties of the support into the classical framework of the Sabatier principle, which relates the binding strength of the crucial intermediate on the catalyst surface to the reaction rate via the Bell–Evans–Polanyi principle.15–19 Examples include ammonia synthesis (intermediate = surface nitride N*),7,16,20–25 CO hydrogenation (intermediate = surface carbonyl CO*)26 and CO2 hydrogenation (oxygen and carbon binding strengths).22,27,28 In ammonia synthesis, the N2 activation is generally accepted to be rate-controlling, and consequently, the crucial intermediate is the surface-adsorbed nitride (*N). Assuming a simplified single-atom model, the activation of nitrogen can be mainly driven by the π-backdonation from the filled metal d-orbitals to the π*-orbitals of dinitrogen, which destabilises the N2 triple bond. This effect is stronger for the higher-lying d-states of the metal.23,29,30 How can higher-lying d-states be achieved without changing the metal, which in turn would decrease the N2 activation energy?
In this work, we use the support to achieve this. We developed a catalyst support descriptor (CSD) for ligand–support selection for heterogeneous catalysis based on support band structure and surface chemistry. The CSD was experimentally validated for the ammonia synthesis reaction, the Haber–Bosch process considered the most important chemical reaction in industry. A series of metal oxides CeO2, La2O3, Y2O3, Sc2O3, and MgO were investigated due to their differences in the valence band energy, mainly comprised of O 2p, and surface density of Lewis basic sites. Ru nanoclusters of 2–3 nm in diameter were produced by magnetron sputtering, where metal atoms are deposited onto metal oxides' surfaces in vacuum. This enables direct contact between the metal atom catalyst and support surface without any impurities in between, which allows a direct comparison between these materials' activity for an accurate validation of the CSD.
2 Results and discussion
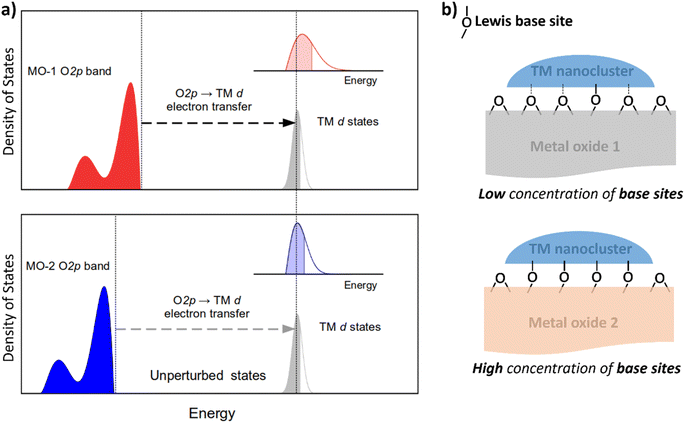
Nanocluster–support interactions affecting the electronic structure of d-manifold include two main contributions: (i) pure Coulomb interactions, which do not mix states of the subsystems and are substantial for ionic supports, and (ii) electron transfer, ET (also known as resonance coupling) between band states of the support and d-states of nanoclusters (Fig. 1a). The first contribution provides a constant shift of d-states (crystal field shift), but the effect on the metal internal structure is minor compared to the ET term.31 Therefore, ET is the most crucial factor to consider when analyzing the support's effect on catalytic properties.Because ET can be viewed as a hybridization of orbitals for the transition metal (TM) and the atoms of the support material, its magnitude depends on the energy difference of the states involved and their coupling parameter. In the context of metal oxides, density functional theory and Hartree–Fock calculations have demonstrated that their valence band has a relatively narrow peak just below the Fermi level, with a significant contribution of O 2p atomic orbitals.32 Metal oxides' surfaces are terminated by oxygen atoms, whose orbitals are strongly coupled with the d-orbitals of TM nanoclusters. Therefore, the ET from the O 2p band to the TM-d orbital (O 2p band → TM-d) contributes significantly to the resonance interaction between the transition metal nanocluster and the metal oxide support.
To tune the ET contribution for a given transition metal, we must vary the energy of the O 2p band of the supporting oxide. As the energy of the O 2p is lower than the energy of the d-orbitals of the TM, the ET effect will be more prominent for the oxide having the O 2p band located higher on the energy scale (Fig. 1a). The position of the O 2p band in any metal oxide can be experimentally determined from the energy of O-KL23L23 Auger lines.33 The kinetic energy, Ekin, of the O-KL23L23 line observed in Auger electron spectroscopy (AES) is related to the energy of the O 2p band as:
| Ekin = −E1s + 2E2p | (1) |
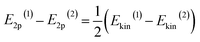 | (2) |
This equation shows that higher kinetic energies of O-KL23L23 correspond to higher-lying O 2p bands, resulting in a bigger ET effect (Fig. 1a).
In addition to the support's electronic structure, we must consider its surface chemistry. The most relevant aspect is the surface density of Lewis base sites (LBS) responsible for coupling to the nanoclusters' d-states (Fig. 1b). For example, the density of LBS on the support's surface has been shown to be a relatively good descriptor for predicting the catalytic activity of Ru nanoclusters in ammonia synthesis.35,36 However, this descriptor works well only for a limited range of oxides and fails for higher concentrations of LBS, such as in Y2O3.35,36
In this work, we unify the two parameters of metal oxides, the energy of the valence band (E2p) and surface density of LBS (C), within a single catalyst support descriptor (CSD), making it applicable to a broader range of metal oxides. Based on the perturbation theory, the Hamiltonian of the metal d-orbitals coupling with O 2p-band is proportional to the concentration of LBS and inversely proportional to their energy difference (see details in ESI, Section 1†). This allows us to propose the following equation for the CSD:
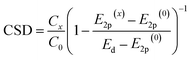 | (3) |
To test CSD, we selected five metal oxides with different stoichiometries (i.e. Y2O3, La2O3, CeO2, Sc2O3 and MgO), as supports for Ru nanoclusters and investigated their catalytic activity in the ammonia synthesis reaction. To measure E2p and concentration of LBS of the supports, we used X-ray photoelectron spectroscopy (XPS) and temperature programmed desorption (TPD) of CO2, respectively (Fig. 2a and b, see details in ESI, Sections 2 and 3†). The O-KL23L23 peak was used to determine the relative values of E2p (eqn (2)). XPS measurements show the lowest kinetic energy for MgO (510.2 eV) and the highest for La2O3 (513.4 eV) (Fig. 2c and Table S1†). MgO was used as a reference point as it has the deepest valence band within this series of supports which allows to estimate Ed–E2p which was found 3.15 eV (see details in ESI, Section 1†). Therefore, for MgO CO2 TPD measurements, normalised to their surface areas (Table S2†), show that Y2O3 displays the highest surface density of LBS in the series, which is in line with previous reports,37 followed by La2O3 and CeO2, Sc2O3 and then MgO (Fig. 2c and S12†). Using eqn (3), we calculate the values of the CSD for the catalysts in the series, predicting the following order of the activation energies Ru/Y2O3 < Ru/La2O3 < Ru/CeO2 < Ru/Sc2O3 < Ru/MgO (Fig. 2c and d).
 | ||
| Fig. 2 Properties of supports and catalysts. (a) The kinetic energy of the O-KL23L23 peaks for the metal oxides after signal processing (see details in ESI, Section 2†). (b) CO2 desorption normalised by the surface area of the support from the metal oxides measured between 50 °C and 600 °C at atmospheric pressure in a flux of 30 mL per min He (*due to the active redox behaviour of CeO2, CO2 desorption measurements were carried out after the H2 reduction treatment of CeO2; see details in ESI, Section 3†). (c) A table containing kinetic energy of O-KL23L23, the concentration of LBS and the corresponding CSD values calculated according to eqn (3). (d) Schematic depiction of CSD values and predicted Ea. (e) Aberration Corrected Scanning Transmission Electron Microscopy (AC-STEM) of Ru/metal oxide catalysts with size distribution histograms. No sintering of Ru nanoclusters was observed after catalysis (Fig. S18†). | ||
To test this prediction and ensure that the observed catalytic parameters are dominated by the effects of supports, it is critical to ensure that the size distributions of Ru nanoclusters are uniform across the metal oxides series. Our methodology, based on the on-surface formation of metal nanoclusters directly from a flux of atoms generated by magnetron sputtering, enables the growth of nanoclusters with accurate size control on different supports.32–35 Furthermore, this approach provides direct contact between Ru nanoclusters and the support, without any solvent and impurities associated with traditional wet impregnation methods.34,36 Aberration-corrected scanning transmission electron microscopy (AC-STEM) imaging of Ru nanoclusters on the metal oxides after catalysis shows the mean diameter ca. 2–3 nm with a narrow size distribution (Fig. 2e), except in Ru@La2O3 where the average diameter is 3.4 nm. This size range of nanoclusters is optimal for ammonia synthesis because the density of B5 sites is maximised, which are largely responsible for N2 activation.6–9
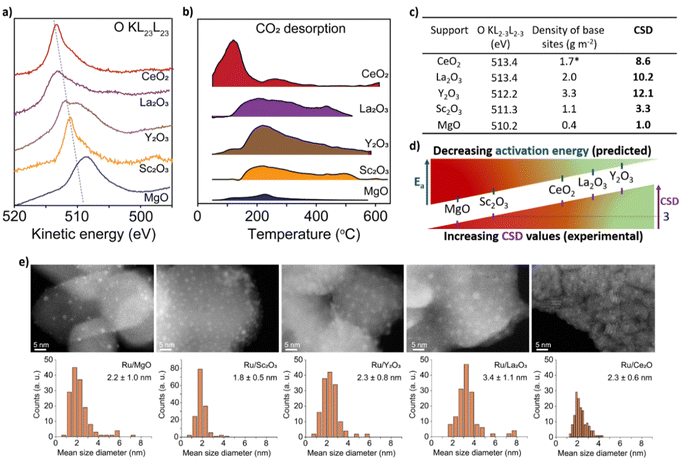
To investigate the electronic effects imposed by the support onto the catalyst, the apparent activation energy, Eapp, of ammonia synthesis was determined (Fig. 3a, see details in ESI†). We found a linear dependence between Eapp and CSD (R2 = 0.94) with a slope of −20.0 ± 3.5 kJ mol−1. This trend captures a wide range of Eapp varying from Ru@MgO (153 kJ mol−1 ± 8 kJ mol−1) to Ru@Y2O3 (76 kJ mol−1 ± 10 kJ mol−1). Noteworthy, the Eapp found for Ru@MgO in our work is in agreement with previous computational predictions for Eapp.38 Furthermore, an Eapp of ca. 70 kJ mol−1 (note the similarity to the Eapp found for Ru@Y2O3 76 kJ mol−1) has been predicted for the Sabatier optimum under low N2 conversions.16,20,39
 | ||
| Fig. 3 Validation of catalyst support descriptor – CSD. Activation energies (a) and turnover frequency (TOF) at 400 °C (b) for the catalysts plotted against the values of CSD. Catalysts stability was tested over 58 hours of reaction (Fig. S13†). TOF was calculated by dividing the rate of NH3 (mmol h−1) production by the amount of Ru surface atoms (mmol). | ||
Inspecting the turnover frequency (TOF) dependency with CSD, a linear correlation was found for MgO, Sc2O3, La2O3 and Y2O3 (R2 = 0.99, Fig. 3b). As expected, the lowest turnover frequency is found for Ru/MgO with 6 h−1, whilst the highest for Ru/Y2O3 with 37 h−1. Interestingly, Ru/CeO2 is an outlier that outperforms its predicted catalytic activity. This effect is most likely due to the reducibility of the CeO2 surface (Ce4+ vs. Ce3+), mitigating hydrogen poisoning.40–42 To elucidate the effect of H2 on the catalytic performance, the partial pressure of H2 was varied. This does not only give information about H2 poisoning but also about the degree of rate control.20
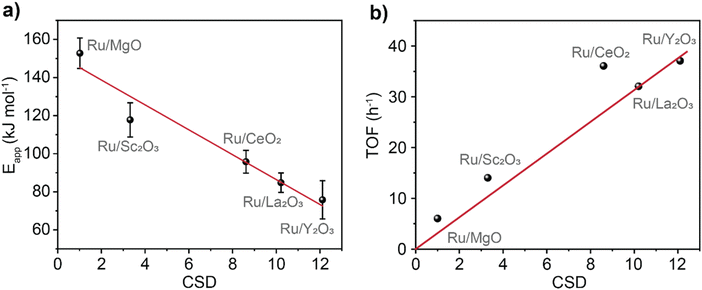
Upon inspecting the effects of the partial pressure of H2 on the reaction rate for Ru/La2O3, Ru/Sc2O3 and Ru/MgO we observed a decrease in the rate indicating the dissociative N2 adsorption being rate controlling step (Fig. 4a and b and S14†). In contrast, Ru/Y2O3 exhibits a non-monotonic behaviour indicative of a fluctuation of the rate controlling typical for the Sabatier optimum (see details in ESI, Section 5†). The rate-controlling step fluctuates from dissociative N2 adsorption to NH3* formation depending on the partial pressure of H2 (Fig. 4a and c). Finally, the reaction rate on Ru/CeO2 shows no dependence on H2 partial pressure (Fig. 4d). This confirms the spillover effect of H* from the nanocluster to the support in Ru/CeO2, explaining that this catalyst is an outlier on the TOF vs. CSD trend (Fig. 3b).40,42 Furthermore, all the metal oxides exhibit N2 order close to 1, which confirms the dissociative N2 adsorption being rate-controlling under the conditions used in our experiments (Fig. 4c and d insets and S14†).25
 | ||
| Fig. 4 Rate control and H2 poisoning mitigation. (a) Schematic depiction of the N2 to NH3 transformation in the presence of H2 on a surface site S. Green highlights the dissociative adsorption of N2 onto S, whilst purple highlights the recombinative desorption of NH3, and red highlights the surface nitride as the crucial intermediate. (b) Effect of the partial pressure of H2 on Ru/La2O3 and an inset shows the dependence for Ru/MgO. (c) Effect of the partial pressure of H2 and N2 (inset) onto Ru/Y2O3. (d) Effect of the partial pressure of H2 and N2 (inset) onto Ru/CeO2. (b–d) All experiments are at 10 bar total pressure a total flow of 40 mL min−1 and 400 °C. The total flow was kept constant by the additional flux of Ar in the reaction mixture (see details in ESI, Section 4†). | ||
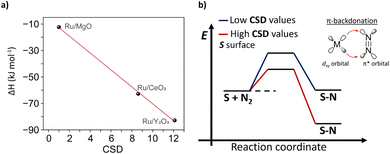
To relate CSD with traditional descriptors, such as binding energy of N*, we conducted temperature-programmed adsorption (TPA) and temperature-programmed desorption (TPD) studies (see details in ESI, Section 4†) and estimated thermodynamic parameters for formation N* for Ru/MgO, Ru/CeO2 and Ru/Y2O3 (Tables S4 and S5†). We then demonstrated that CSD correlates linearly with the binding strength and formation enthalpy of N*, i.e. higher CSD leads to a more exothermic (and thus exergonic) adsorption of N2 (Fig. 5). Consequently, our CSD based on the electronic structure (O 2p band energy) and surface chemistry of the support (LBS surface density) can be linked to previous descriptors, such as the binding strength of N*, and thus regarded as a powerful tool to predict catalytic activity.
3 Conclusions
In summary, this work introduces a catalyst support descriptor (CSD) as a powerful tool for optimising support materials in heterogeneous catalysis. By combining the metal oxide O 2p energy level and the surface density of Lewis base sites (LBS), the CSD effectively predicts catalytic performance across a range of metal oxides. We demonstrated a strong correlation between the CSD and catalytic activity, with Ru/Y2O3 showing the best performance in ammonia synthesis. This work highlights the importance of electron transfer due to resonance coupling in enhancing catalytic activity, offering a unified framework for selecting support materials. By bridging traditional descriptors with the CSD, the study provides a comprehensive methodology for catalyst design, paving the way for advancements in ammonia synthesis and beyond. The CSD offers a novel approach to understanding and improving the electronic environment of catalytic centres, ensuring more efficient and targeted catalyst development This is especially important for the Haber–Bosch process, which is highly energy-intensive and polluting, with high CO2 emissions. Our descriptor offers a robust methodology to guide the search for the future efficient catalysts to alleviate the environmental impact of the ammonia synthesis in industry.4 Experimental
4.1. General information
MgO, CeO2, La2O3, Sc2O3 and Y2O3 were purchased from Sigma Aldrich used without further purification. All solvents were of analytical grade, and all water used in this work was Millipore Milli-Q 18 MΩ ultrapure and deionised. HCl (37% v/v) and HNO3 (69% v/v) are ARISTAR™ grade and purchased from VWR Chemicals. Research grade hydrogen (99.999%) and nitrogen (99.999%) was supplied by BOC – LINDE GROUP. Aberration corrected scanning transmission electron microscopy (AC-STEM) measurements were performed using a JEOL 2100F scanning transmission electron microscope with a CEOS aberration corrector operated with an accelerating voltage of 200 kV. Ru nanoclusters were prepared by producing a flow of Ru atoms deposited on metal oxides using magnetron sputtering technique (Table 1).43,44 Ru content was measured by Inductively Coupled Plasma Optical Emission Spectrometer (ICP-OES) using a PerkinElmer Optima 2000 DV (Table 1). Catalytic experiments were undertaken in Plug flow reactor provided by micromeritics. Effluent NH3 concentrations were measured using GC-TCD analysis provided by Agilent. Microkinetic measurements were measured using CATLAB-PCS Microreactor with an integrated mass spectrometer.| Catalyst | Deposition time (min) | Applied power (W) | Ru content (wt%) |
|---|---|---|---|
| Ru/CeO2 | 50 | 60 | 1.5 |
| Ru/Y2O3 | 40 | 50 | 0.8 |
| Ru/La2O3 | 40 | 50 | 2.0 |
| Ru/MgO | 50 | 60 | 1.7 |
| Ru/Sc2O3 | 40 | 50 | 1.7 |
4.2. Metal oxides X-ray photoelectron spectroscopy (XPS) measurements
XPS measurements were performed using Thermo Fisher K-Alpha X-ray Photoelectron Spectrometer using a monochromatic Al Kα radiation source operating at 72 W (6 mA × 12 kV) which defines an analysis area of approximately 400 × 400 microns. An analyser pass energy of 160 eV was used for wide energy range survey scans, and 50 eV for elemental regions (C 1s, O 1s, O KLL, Y 3d, La 3d, Ce 3d, Sc 2p and Mg 1s), all samples were recorded using a dual ion-electron charge compensation detector, operating with an argon background pressure of ca. 10−7 mbar. Samples were mounted by pressing onto silicone-free double-sided adhesive tape. Depth profiling was performed with an Argon ion gun operating at 1000 eV and rastered over a 2 × 1 mm area for 10 seconds per cycle. The data were processed with CASAXPS (Version 2.3.17). The data was charge corrected to the reference C 1s signal at 285.0 eV.4.3. Thermal programmed desorption (TPD) of CO2
To measure the concentration of Lewis basic sites (LBS) on the supports, temperature-programmed desorption (TPD) of CO2 was performed. The measurements were normalized by metal oxides BET area.Helium pycnometry experiments were conducted on a Micromeritics Accupyc, following degassing at 300 °C for 1 hour using a Micromeritics Smart VacPrep. A total of 200 helium purges were performed at room temperature before conducting 50 volume measurements. The helium density (ρHe) was determined as the average of these 50 measurements. The average particle diameter (d) was calculated from ABET and ρHe, assuming non-agglomerated, non-porous spherical particles according to the formula:
4.4. Catalytic experiments
Catalytic experiments were conducted in a stainless steel PFR reactor supplied by Micromeritics, PID Microactivity effi, and the effluent NH3 concentration was measured using Agilent 8890 GC system. In a typical experiment 1.7 mg of Ru was employed to ensure the same catalyst loading throughout the catalytic experiments. Furthermore, the volume of Ru/metal-oxide support and the employed support were kept constant to keep the contact time the same. The samples were furthermore diluted in 2.3 g of SiC. Both, the catalytic material and the SiC were mixed and loaded into the reactor. The reactor is pressurized to 20 bar and the catalysts are reduced in a flow of H2 (30 mL min−1) for 6 h at 450 °C. Afterwards, the reactor is cooled to 400 °C and a N2 is added to the feed (10 mL min−1). After, 10 h samples of the exhaust feed are measured by GC-TCD (Table S3 and Fig. S13†).To determine the rate orders, all other parameters were kept the same, but the pressure was reduced to 10 bar. To vary the partial pressures of H2 and N2, Ar was introduced to the feed and the total gas flow was kept constant at 40 mL min−1 (Fig. S14†).
The activation energy was measured by changing the total flow of reagents to the reactor at various temperatures. The rate was approximated by measuring the linear regression of the inverse total flow (H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N2 = 3
N2 = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) against the effluent NH3 concentration (Fig. S15†).
1) against the effluent NH3 concentration (Fig. S15†).
4.5. N* binding strength
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
A. W. performed the catalytic experiments. I. P., S. G. and E. B. were responsible for the theoretical framework. E. K. and L. N. prepared the metal catalysts and performed part of their characterisation. G. N. A. and W. T. performed and analysed the AC-STEM images. L. S. B. and L. S. have performed the base sites and surface area measurements and analysis. M. I., J. O., A. E. L. and D. M. were responsible for the XPS measurements and data analysis. G. J. H, A. N. K. and J. A. F. provided funding acquisition and project supervision. The work was written and edited by all co-authors.Conflicts of interest
The authors declare no competing interests.Acknowledgements
The authors acknowledge support of EPSRC Metal Atoms on Surfaces and Interfaces (MASI) for Sustainable Future programme grant (EP/V000055/1) for the financial support; and Dr Tom Pike for the scientific discussions.References
- Y. Guo, M. Wang, Q. Zhu, D. Xiao and D. Ma, Ensemble effect for single-atom, small cluster and nanoparticle catalysts, Nat. Catal., 2022, 5(9), 766–776 CrossRef CAS.
- L. Liu and A. Corma, Metal Catalysts for Heterogeneous Catalysis: From Single Atoms to Nanoclusters and Nanoparticles, Chem. Rev., 2018, 118(10), 4981–5079 CrossRef CAS PubMed.
- X. Cui, W. Li, P. Ryabchuk, K. Junge and M. Beller, Bridging homogeneous and heterogeneous catalysis by heterogeneous single-metal-site catalysts, Nat. Catal., 2018, 1(6), 385–397 CrossRef CAS.
- L. C. Caballero, N. E. Thornburg and M. M. Nigra, Catalytic ammonia reforming: alternative routes to net-zero-carbon hydrogen and fuel, Chem. Sci., 2022, 13(44), 12945–12956 RSC.
- X. Peng, M. Zhang, T. Zhang, Y. Zhou, J. Ni, X. Wang and L. Jiang, Single-atom and cluster catalysts for thermocatalytic ammonia synthesis at mild conditions, Chem. Sci., 2024, 15(16), 5897–5915 RSC.
- F. R. García-García, A. Guerrero-Ruiz and I. Rodríguez-Ramos, Role of B5-Type Sites in Ru Catalysts used for the NH3 Decomposition Reaction, Top. Catal., 2009, 52(6), 758–764 CrossRef.
- K. Honkala, A. Hellman, I. N. Remediakis, A. Logadottir, A. Carlsson, S. Dahl, C. H. Christensen and J. K. Nørskov, Ammonia Synthesis from First-Principles Calculations, Science, 2005, 307(5709), 555–558 CrossRef CAS PubMed.
- S. Shetty, A. P. J. Jansen and R. A. van Santen, Active Sites for N2 Dissociation on Ruthenium, J. Phys. Chem. C, 2008, 112(46), 17768–17771 CrossRef CAS.
- J. A. Herron, S. Tonelli and M. Mavrikakis, Atomic and molecular adsorption on Ru(0001), Surf. Sci., 2013, 614, 64–74 CrossRef CAS.
- M. Ravi and J. W. Makepeace, Facilitating green ammonia manufacture under milder conditions: what do heterogeneous catalyst formulations have to offer?, Chem. Sci., 2022, 13(4), 890–908 RSC.
- X. Peng, H.-X. Liu, Y. Zhang, Z.-Q. Huang, L. Yang, Y. Jiang, X. Wang, L. Zheng, C. Chang, C.-t. Au, L. Jiang and J. Li, Highly efficient ammonia synthesis at low temperature over a Ru–Co catalyst with dual atomically dispersed active centers, Chem. Sci., 2021, 12(20), 7125–7137 RSC.
- Y. Ogura, K. Sato, S.-i. Miyahara, Y. Kawano, T. Toriyama, T. Yamamoto, S. Matsumura, S. Hosokawa and K. Nagaoka, Efficient ammonia synthesis over a Ru/La0.5Ce0.5O1.75 catalyst pre-reduced at high temperature, Chem. Sci., 2018, 9(8), 2230–2237 RSC.
- M. Kitano, Y. Inoue, H. Ishikawa, K. Yamagata, T. Nakao, T. Tada, S. Matsuishi, T. Yokoyama, M. Hara and H. Hosono, Essential role of hydride ion in ruthenium-based ammonia synthesis catalysts, Chem. Sci., 2016, 7(7), 4036–4043 RSC.
- S. Kamiguchi, K. Asakura, T. Shibayama, T. Yokaichiya, T. Ikeda, A. Nakayama, K.-i. Shimizu and Z. Hou, Catalytic ammonia synthesis on HY-zeolite-supported angstrom-size molybdenum cluster, Chem. Sci., 2024, 15(8), 2914–2922 RSC.
- S. Ichikawa, Volcano-shaped curves in heterogeneous catalysis, Chem. Eng. Sci., 1990, 45(2), 529–535 CrossRef CAS.
- T. Bligaard, J. K. Nørskov, S. Dahl, J. Matthiesen, C. H. Christensen and J. Sehested, The Brønsted–Evans–Polanyi relation and the volcano curve in heterogeneous catalysis, J. Catal., 2004, 224(1), 206–217 CrossRef CAS.
- M. G. Evans and M. Polanyi, Further considerations on the thermodynamics of chemical equilibria and reaction rates, Trans. Faraday Soc., 1936, 32, 1333–1360 RSC.
- M. G. Evans and M. Polanyi, Inertia and driving force of chemical reactions, Trans. Faraday Soc., 1938, 34, 11–24 RSC.
- M. G. Evans and M. Polanyi, Some applications of the transition state method to the calculation of reaction velocities, especially in solution, Trans. Faraday Soc., 1935, 31, 875–894 RSC.
- S. Dahl, A. Logadottir, C. J. H. Jacobsen and J. K. Nørskov, Electronic factors in catalysis: the volcano curve and the effect of promotion in catalytic ammonia synthesis, Appl. Catal., A, 2001, 222(1), 19–29 CrossRef CAS.
- A. Vojvodic, A. J. Medford, F. Studt, F. Abild-Pedersen, T. S. Khan, T. Bligaard and J. K. Nørskov, Exploring the limits: A low-pressure, low-temperature Haber–Bosch process, Chem. Phys. Lett., 2014, 598, 108–112 CrossRef CAS.
- A. J. Medford, A. Vojvodic, J. S. Hummelshøj, J. Voss, F. Abild-Pedersen, F. Studt, T. Bligaard, A. Nilsson and J. K. Nørskov, From the Sabatier principle to a predictive theory of transition-metal heterogeneous catalysis, J. Catal., 2015, 328, 36–42 CrossRef CAS.
- F. Abild-Pedersen, J. Greeley, F. Studt, J. Rossmeisl, T. R. Munter, P. G. Moses, E. Skúlason, T. Bligaard and J. K. Nørskov, Scaling Properties of Adsorption Energies for Hydrogen-Containing Molecules on Transition-Metal Surfaces, Phys. Rev. Lett., 2007, 99(1), 016105 CrossRef CAS.
- G. Xu, C. Cai and T. Wang, Toward Sabatier Optimal for Ammonia Synthesis with Paramagnetic Phase of Ferromagnetic Transition Metal Catalysts, J. Am. Chem. Soc., 2022, 144(50), 23089–23095 CrossRef CAS PubMed.
- C. M. Goodwin, P. Lömker, D. Degerman, B. Davies, M. Shipilin, F. Garcia-Martinez, S. Koroidov, J. Katja Mathiesen, R. Rameshan, G. L. S. Rodrigues, C. Schlueter, P. Amann and A. Nilsson, Operando probing of the surface chemistry during the Haber–Bosch process, Nature, 2024, 625(7994), 282–286 CrossRef CAS PubMed.
- A. O. Elnabawy, J. Schumann, P. Bothra, A. Cao and J. K. Nørskov, The Challenge of CO Hydrogenation to Methanol: Fundamental Limitations Imposed by Linear Scaling Relations, Top. Catal., 2020, 63(7), 635–648 CrossRef CAS.
- A. A. Peterson and J. K. Nørskov, Activity Descriptors for CO2 Electroreduction to Methane on Transition-Metal Catalysts, J. Phys. Chem. Lett., 2012, 3(2), 251–258 CrossRef CAS.
- F. Studt, I. Sharafutdinov, F. Abild-Pedersen, C. F. Elkjær, J. S. Hummelshøj, S. Dahl, I. Chorkendorff and J. K. Nørskov, Discovery of a Ni-Ga catalyst for carbon dioxide reduction to methanol, Nat. Chem., 2014, 6(4), 320–324 CrossRef CAS.
- B. Hammer and J. K. Nørskov, Electronic factors determining the reactivity of metal surfaces, Surf. Sci., 1995, 343(3), 211–220 CrossRef CAS.
- B. Hammer and J. K. Norskov, Why gold is the noblest of all the metals, Nature, 1995, 376(6537), 238–240 CrossRef CAS.
- I. Popov, E. Plekhanov, A. Tchougréeff and E. Besley, Effective hamiltonian of crystal field method for periodic systems containing transition metals, Mol. Phys., 2023, 121(9–10), e2106905 CrossRef.
- I. Fongkaew, B. Yotburut, W. Sailuam, W. Jindata, T. Thiwatwaranikul, A. Khamkongkaeo, N. Chuewangkam, N. Tanapongpisit, W. Saenrang, R. Utke, P. Thongbai, S. Pinitsoontorn, S. Limpijumnong and W. Meevasana, Effect of hydrogen on magnetic properties in MgO studied by first-principles calculations and experiments, Sci. Rep., 2022, 12(1), 10063 CrossRef CAS PubMed.
- C. Wagner, D. Zatko and R. Raymond, Use of the oxygen KLL Auger lines in identification of surface chemical states by electron spectroscopy for chemical analysis, Anal. Chem., 1980, 52(9), 1445–1451 CrossRef CAS.
- D. J. Morgan, Photoelectron spectroscopy of ceria: Reduction, quantification and the myth of the vacancy peak in XPS analysis, Surf. Interface Anal., 2023, 55(11), 845–850 CrossRef CAS.
- K. Sato and K. Nagaoka, Boosting Ammonia Synthesis under Mild Reaction Conditions by Precise Control of the Basic Oxide–Ru Interface, Chem. Lett., 2021, 50(4), 687–696 CrossRef CAS.
- S.-i. Miyahara, K. Sato, Y. Kawano, K. Imamura, Y. Ogura, K. Tsujimaru and K. Nagaoka, Ammonia synthesis over lanthanoid oxide–supported ruthenium catalysts, Catal. Today, 2021, 376, 36–40 CrossRef CAS.
- S. Sato, R. Takahashi, M. Kobune and H. Gotoh, Basic properties of rare earth oxides, Appl. Catal., A, 2009, 356(1), 57–63 CrossRef CAS.
- A. Hellman, K. Honkala, I. N. Remediakis, Á. Logadóttir, A. Carlsson, S. Dahl, C. H. Christensen and J. K. Nørskov, Insights into ammonia synthesis from first-principles, Surf. Sci., 2006, 600(18), 4264–4268 CrossRef CAS.
- S. Kozuch and S. Shaik, Kinetic-Quantum Chemical Model for Catalytic Cycles: The Haber−Bosch Process and the Effect of Reagent Concentration, J. Phys. Chem. A, 2008, 112(26), 6032–6041 CrossRef CAS PubMed.
- B. Lin, B. Fang, Y. Wu, C. Li, J. Ni, X. Wang, J. Lin, C.-t. Au and L. Jiang, Enhanced Ammonia Synthesis Activity of Ceria-Supported Ruthenium Catalysts Induced by CO Activation, ACS Catal., 2021, 11(3), 1331–1339 CrossRef CAS.
- C. Li, M. Li, Y. Zheng, B. Fang, J. Lin, J. Ni, B. Lin and L. Jiang, Revealing hydrogen migration effect on ammonia synthesis activity over ceria-supported Ru catalysts, Appl. Catal. B Environ., 2023, 320, 121982 CrossRef CAS.
- B. Lin, Y. Wu, B. Fang, C. Li, J. Ni, X. Wang, J. Lin and L. Jiang, Ru surface density effect on ammonia synthesis activity and hydrogen poisoning of ceria-supported Ru catalysts, Chin. J. Catal., 2021, 42(10), 1712–1723 CrossRef CAS.
- I. Cano, A. Weilhard, C. Martin, J. Pinto, R. W. Lodge, A. R. Santos, G. A. Rance, E. H. Åhlgren, E. Jónsson, J. Yuan, Z. Y. Li, P. Licence, A. N. Khlobystov and J. Alves Fernandes, Blurring the boundary between homogenous and heterogeneous catalysis using palladium nanoclusters with dynamic surfaces, Nat. Commun., 2021, 12(1), 4965 CrossRef CAS.
- E. C. Kohlrausch, H. A. Centurion, R. W. Lodge, X. Luo, T. Slater, M. J. L. Santos, S. Ling, V. R. Mastelaro, M. J. Cliffe, R. V. Goncalves and J. Alves Fernandes, A high-throughput, solvent free method for dispersing metal atoms directly onto supports, J. Mater. Chem. A, 2021, 9(47), 26676–26679 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc08253b |
| This journal is © The Royal Society of Chemistry 2025 |