Thermodynamic insights into the self-assembly of zeolitic imidazolate frameworks from computer simulations

Abstract

New metal–organic frameworks (MOFs) are periodically synthesized all over the world due to the wide range of societally and environmentally relevant applications they possess. However, the mechanisms and thermodynamics associated with MOF self-assembly are poorly understood because of the difficulties in studying such a multi-scale process with molecular-level resolution. In this work, we performed well-tempered metadynamics simulations of the early nucleation and late growth steps of the self-assembly of ZIF-4 using a partially reactive force field. We found that the formation of building blocks is a complex, multi-step process that involves changes in the coordination of the metal ion. Saturating the ligand coordination of a metal ion is more energetically favorable during growth than during early formation of building blocks. The addition of a fourth ligand is less exergonic than it is for the first three and the associated free energy is highly dependent on the local environment of the undercoordinated metal ion. The stability of this bond depends on the strength of the solvent–metal ion interaction. Incorporating a ligand to a ZIF-1 crystal is less favorable compared to the more stable ZIF-4 polymorph. Milder differences were found when comparing the growth of (100), (010) and (001) ZIF-4 surfaces.

---

Introduction

Zeolitic Imidazolate Frameworks (ZIFs) are a family of metal–organic frameworks (MOFs) characterized by their high chemical and thermal stability.¹ These porous solids are formed by a metal ion (typically Zn²⁺, Co²⁺, Fe²⁺ or Cd²⁺) tetrahedrally coordinated to a bidentate imidazolate(Im)-based ligand. The metal ion–N(Im) coordination bonds lead to metal–ligand–metal angles of 145°, equivalent to the T–O–T angles encountered in zeolites. As a consequence, ZIFs tend to share topology with some zeolites (sod and rho are the most common ones). Moreover, the flexibility afforded by these coordination bonds together with the high stability in water that results from their hydrophobicity,² confer ZIFs an enormous potential for stimuli-responsive applications.³

Even though almost twenty years have passed since the initial discovery of six Zn(Im)₂ porous polymorphs (ZIF-1, ZIF-2, ZIF-3, ZIF-4, ZIF-6 and ZIF-10) by Park and coworkers,⁴ their phase diagram, as well as the chemistry underlying their synthesis mechanisms are still largely unknown. These six polymorphs were all synthesized in solvothermal conditions, all with dimethylformamide (DMF) as a solvent, except for ZIF-2, which was made in a 2 : 1 DMF/N-methyl-2-pyrrolidone mixture. Reactants were Zn(NO₃)₂ and imidazole in all cases. The main difference between the synthesis conditions leading to these different polymorphs lies in the metal : ligand and reactants : solvent ratio as well as in the temperature and synthesis times.⁴ The size and morphology of a particular polymorph can also be modified by changing synthesis conditions.^5,6 Clearly, as for many other families of materials, the synthesis of ZIFs depends on a delicate balance between thermodynamic and kinetic aspects.^7,8 In cases where the synthesis is under thermodynamic control, the denser, enthalpically favored phases are typically obtained (including ZIF-zni and ZIF-coi),^9,10 while when under kinetics control, less stable polymorphs could be favored.^11,12 It is worth mentioning though that the enthalpy difference between porous polymorphs can sometimes be very low.⁷

The thermodynamically most favorable porous Zn(Im)₂ polymorph, ZIF-4, crystallizes in the cag topology, which has not yet been found in zeolites. In an in-depth study of the phase diagram of this MOF,¹³ none of the other five polymorphs found by Park and coworkers were detected. Whether this is a matter of lack of stability of certain polymorphs¹⁴ or due to limitations in the experimental measures remains yet to be elucidated. Instead, five other crystalline polymorphs were found, including the less porous, high pressure phases ZIF-cp-II and ZIF-cp-III, the high temperature phases ZIF-hpt-I and ZIF-hpt-II and the dense ZIF-zni form. In addition, two amorphous phases and a liquid-like phase were detected.¹⁵ Yet another crystalline porous phase, ZIF-4-cp was also experimentally obtained in another study,¹⁶ and its place in the phase diagram has been recently determined via computer simulations.¹⁷

Despite the vast amount of research works dedicated to better understanding the complex landscape of Zn(Im)₂ and other zeolitic MOFs,^13,16–30 we still lack fundamental knowledge on their self-assembly energetics and mechanisms. This is due to the intrinsic multiscale nature of self-assembly: from the formation of the very first metal–organic complexes in solution that act as building blocks, to nucleation, which may involve collective motions of metal–organic clusters and solvent aggregates, up to the growth of new pore layers at the surface of a stable nuclei to form macroscopic MOF crystals. It is impossible to sample the large variety of characteristic time and length scales involved in the whole process with a single experimental or computational technique. Moreover, the MOF synthesis field has traditionally been an experiment-only domain, due to the high complexity of the system under study (solvent, reactants, additives, pH, temperature, agitation, among many other synthesis variables). Nonetheless, simulation techniques can bring a crucial added value to the field, as they have already done in other cases including clathrates, atmospheric ice formation, zeolites, pharmaceutical organic solids, electronic devices and clays,^31–39 since they allow to study reactivity at molecular level resolution.

Recent advances in computational techniques have made it possible to model the early stages of self-assembly of MOFs.^40–48 Yoneya and coworkers pioneered the field by modeling the complexation between Ru²⁺ and Pd²⁺ and 4,4′-bipyridine within an implicit solvent.⁴⁰ Biswal and Kusalik went even farther by adding an explicit solvent and proposing the use of cationic dummy atom models (CDA) to take into account the anisotropy in charge distribution around Zn²⁺ ions to better understand the formation of rings within MOF-2.^41,42

Colón and coworkers were the first to apply enhanced sampling methods to accelerate the dynamics of coordination bonds thus enabling to reach later stages of the nucleation process.⁴³ Kollias and coworkers relied on well-tempered metadynamics⁴⁹ to explore changes in free energies associated with early nucleation stages of MIL-101(Cr) as a function of the solvent and ionic force.⁴⁴ Balestra and Semino combined CDA models with well-tempered metadynamics simulations for the first time to study the early stages of the nucleation of ZIF-8.⁴⁷ Later on, Filez and collaborators have combined simulations and experiments to gain insight into the nucleation mechanism of ZIF-67(Co), focusing on changes in the coordination symmetry of the Co²⁺ ion.⁴⁶ Following a different philosophy based on a Monte Carlo approach, Wells and colleagues have modeled the formation of different polymorphs as a function of the composition of the system.⁴⁵

Despite all these simulation efforts and the fact that the thermodynamics of the metal–ligand coordination bonds have been widely studied,^48,50–53 their dynamics and role in the mechanisms of synthesis and phase transitions of these materials are still poorly understood. In this contribution, we bridge this gap by first focusing on the mechanism of formation of a [Zn(Im)₄]²⁻ complex in solution, starting from a fully solvated Zn²⁺ ion. We tackle crucial questions, such as whether the successive ligand additions are equally favorable in terms of the free energy or not, and how does this process compare with adding a new Zn²⁺ or Im⁻ ion onto a preformed ZIF surface (which can be thought of as a model of the growth stages of the self-assembly process). In addition, we study the mechanism and thermodynamics of adding these extra-ions to the surface and look at whether they depend on the hkl indices and/or on the polymorph studied.

Methods

Simulation setup

All the simulations were performed using the LAMMPS open source software⁵⁴ coupled with the PLUMED package.⁵⁵ Among the existing reactive force fields for ZIFs, nb-ZIF-FF, ReaxFF and machine learning potentials, we selected the nb-ZIF-FF force field.⁴⁷ ReaxFF raised concerns in what respects to its adequacy for modelling ZIFs⁵⁶ and the machine learning potentials that are currently available for ZIFs^28–30 are not developed for modeling species in solution and thus would require further refinements. In nb-ZIF-FF, the Zn–N interactions are represented by a Morse potential that allows bond formation and breaking events. This force field also incorporates flexible dummy atoms attached to the Zn and N species to correctly reproduce the angular distribution of ligands around a Zn centre. nb-ZIF-FF adequately reproduces the properties of several ZIF-4 polymorphs, including those that result from its thermal amorphization and melting²⁷ (ZIF-amorphous and ZIF-liquid), its high pressure phases¹⁷ (ZIF-4-cp and ZIF-4-cp-II) and the ZIF-1 crystal.⁴⁷ For the DMF solvent we employed a flexible version of the CS2 potential developed by Chalaris and Samios.⁵⁷ The intramolecular bond, angular and dihedral parameters were taken from the CHARMM general force field.⁵⁸ In order to model the Zn–N(Im) and Zn–O(DMF) interactions on an equal footing, we replaced the Lennard-Jones term of this last pair for a Morse potential. Since the original nb-ZIF-FF was not parameterized considering the interaction with DMF, we had to re-optimize simultaneously the Morse depth parameters of both Zn–O(DMF) and Zn–N(Im) pairs. The final parameters of the force field are summarized in Tables 1–3 of the “Force field parameters” section of the ESI.† We validated the new version of the force field as done in the original nb-ZIF-FF article⁴⁷ by computing cell parameters, interatomic distances and angles, radial distribution functions and the relative stability of the ZIF polymorphs (see Tables 4–6 in the ESI†). These observables are in good agreement with their experimental and ab initio counterparts.^4,47,59,60 We also validated the force field for the modeling of isolated [Zn(DMF)_n(Im)_m]^2−m clusters with varying m and n values by comparison with density functional theory calculations. Stability trends and energy differences are reasonably well captured by our model (see section “Force field validation: electronic structure calculations” in the ESI†).

All the results were obtained from simulations made at the NPT ensemble at T = 400 K and P = 1 bar, which reproduces the experimental solvotermal synthesis conditions of ZIF-4.⁴ The time step was set to 0.5 fs. Nosé–Hoover thermostats and barostats were used with damping times of 100× and 1000× time steps respectively. Periodic boundary conditions were always employed in all directions. Long range electrostatics were treated with the pppm algorithm, using a relative error threshold for the forces of 10⁻⁶. Additional details of the simulations are included in the “Well-tempered metadynamics setup” section of the ESI.†

Metadynamics

Well-tempered metadynamics⁴⁹ enables the exploration of a selected collective variable (CV) space in a reversible fashion. As a result, it is possible to recover the free energy surface as a function of the CV values when convergence is reached. The selection of CVs has to be done in such a way that the two or more states that are being compared are located at different points in this reduced coordinate representation. Nevertheless, this necessary condition is often not sufficient to force the system to visit all the desired states; it is also mandatory that the selected reaction coordinates capture the slowest or activated degrees of freedom of the reaction.

The process of going from a free Zn to a fully-coordinated Zn(Im)₄²⁻ (see section “Formation of early [Zn(Im)_n]²⁻ⁿ complexes” below) was divided in two steps because performing metadynamics simulations with more than three CVs is not recommended due to convergence problems. First, we simulated a single, solvated Zn ion with two ligand moieties considering three CVs. The first two CVs correspond to the minimum distance between the Zn and the two N atoms (d_min = min{d_N1, d_N2}) of each imidazolate that is interchanged. In this way, the Zn may bind with any of the available N sites of each of the two ligands. The functional form of the minimum distance d_min⁽ⁱ⁾ to the i-th ligand was selected so that it has continuous derivatives by using the following formula:

dmin(i) = (dN1(i)−6 + dN2(i)−6)−1/6 i = 1, 2 (1)

Since the bottleneck of the reaction is the dissociation of a DMF molecule from the solvation shell of the Zn ion, we chose the coordination number between Zn and the O atoms of the solvent (n_Zn–O) as the third CV, which was calculated by the following sum over all the O atoms (O_i):

where f(r_i) is a function that takes the value of 1 if the Zn–O_i distance r_i is lower than a threshold value of d₀ = 2.1 Å similar to the bond length and decays to zero afterwards with a characteristic width of r₀ = 0.5 Å. In this case:

For the second stage of ligand additions, which implied going from [Zn(Im)₂] to [Zn(Im)₄]²⁻, the same set of CVs was used, except that in this case the Zn–ligand distances correspond to the two new ligand moieties that are interchanged, while the previous two imidazolates were kept connected to the Zn through a harmonic constraint. An extra Zn ion was included in the box to maintain the electroneutrality of the system, with a constraint that ensures that it always remains far away from the reactive sites.

For the Zn-surface adsorption–desorption process (see section “ZIF crystal growth” below) a slightly different set of CVs was used. Since it was not possible to control the three Zn–N distances and the Zn–O coordination number at the same time due to the low scaling convergence of metadynamics, we employed the following reaction coordinates: (i) the coordination number between the tagged Zn and all oxygen atoms, (ii) the coordination number between the tagged Zn and all nitrogen atoms, and (iii) the distance between the Zn and the center of mass of the three reactive nitrogen sites. This last CV was introduced to probe the slow diffusive motion of the tagged Zn ion from the vicinity of the crystal slab to the bulk region, given that the second CV takes the value of zero immediately after it abandons the surface vicinity.

Finally, the lack of multiple reactive sites allowed us to employ only two CVs for the study of the ligand–surface interchange: (i) the coordination number between the reactive Zn and the O(DMF) atoms and (ii) the minimum distance between the tagged ligand nitrogen sites and the reactive Zn, in the same fashion as explained in eqn (1). Again, the connectivity between the mobile ligand and any other surface Zn was kept fixed and equal to zero and a upper boundary of 10 Å was imposed to the distance CV to avoid exploring spurious regions of the free energy surface.

It is worth noting that the choice of CV has a direct impact on the numerical value of the free energy difference between two states and its corresponding activation free energy. This is a consequence of the different amount of phase space volume assigned to each minima by selecting a particular CV. For this reason, we will focus in comparing free energies associated with the same kind of CV (coordination number). The observed qualitative tendencies should remain consistent if a change in CV is performed, provided that the chosen CV represents the self-assembly process reasonably well. On the contrary, the obtained activation energies should only be considered as estimates of the true thermodynamic quantities.

For the visualization of the obtained free energy surfaces it is often necessary to perform a dimensionality reduction over the full CV space, keeping either one or two relevant coordinates or a function of them. The procedure used to compute these transformations, as well as further details of the metadynamics simulations including convergence criteria and error calculations, are given in the ESI.†

Results

Formation of early [Zn(Im)_n]²⁻ⁿ complexes

We start our analysis by studying the fundamental reaction steps that take place at the very beginning of the synthesis process. In particular, we focused on the formation of the [Zn(Im)₄]⁻² complex from the dissociated ions, that will serve as building unit for the ZIF structures. In order to gain insight into the free energy associated with this transformation, we ran well-tempered metadynamics simulations in which the ligands reversibly attach and detach to the Zn center thanks to the partially reactive force field nb-ZIF-FF.⁴⁷ This allowed us to compute free energy differences between all the possible intermediate species that are formed along this process. These simulations also offer molecular-level information concerning the mechanism of these reactions.

We divided this process into two steps:

(I) Zn²⁺ + 2Im⁻ ⇌ [Zn(Im)₂]

(II) [Zn(Im)₂] + 2Im⁻ ⇌ [Zn(Im)₄]²⁻

This was done to guarantee reasonable convergence times, as a new collective variable is needed to treat each coordination bond, and the cost of a metadynamics simulation scales rapidly with the number of CVs. The distances between each reactive imidazolate and the Zn ion and the coordination number between the Zn ion and O(DMF) atoms were used as CVs for both steps. The imidazolates that were interchanged in the first step were kept connected to the Zn ion via a harmonic restraint for the addition of the two last ligands. All simulations were performed at the experimental ZIF-4 solvothermal synthesis temperature of 400 K.⁴

From an octahedral to a tetrahedral Zn ion

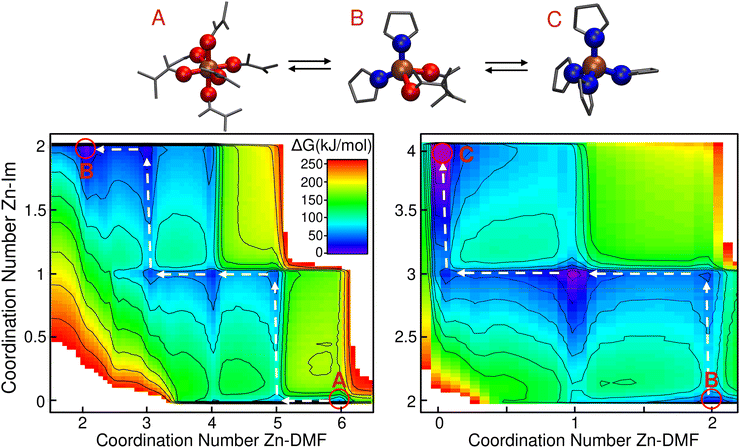
It is known that the most stable Zn²⁺ complex in DMF solution comprises six solvent molecules.⁶¹ On the other hand, the coordination of Zn with imidazolate in all ZIF crystals is tetrahedral. In what follows, we delve into the question of how this change of coordination takes place.

In the left panel of Fig. 1 we plotted the free energy as a function of the Zn–O(DMF) and Zn–N(Im) coordination numbers (n_Zn–DMF and n_Zn–Im respectively) for the addition of the first two imidazolates. To do so, we reduced the dimension of the original four-dimensional free energy surface obtained from metadynamics via a transformation of coordinates explained in the “Transformations of the collective variable space” section of the ESI.† The zero of free energy was arbitrarily assigned to the global minimum located at n_Zn–Im = n_Zn–DMF = 2.

Fig. 1 Free energy surface in the space given by n_Zn–DMF and n_Zn–Im for reactions (I) (left) and (II) (right). In the left panel, the white arrows indicate the most favorable sequence of steps that connect the fully solvated octahedral complex (state A) with the [Zn(Im)₂(DMF)₂] tetrahedral complex (state B). In the right panel, the arrows indicate the optimal path for transforming B into the 4-imidazolate-coordinated Zn (state C). The zero of free energy in both plots was located in the absolute minima within each of them. Typical configurations of the three states A, B and C are shown in the upper part of the plot. Zn ions are displayed in ochre, Zn-bonded O and N atoms are displayed in red and blue respectively. All other atoms are plotted in gray. H atoms of imidazolate ions are omitted for clarity purposes.

In the lower part of the plot at which n_Zn–Im = 0 we identified three minima that correspond to the [Zn(DMF)₄]²⁺ (ΔG = 84 ± 3 kJ mol⁻¹), [Zn(DMF)₅]²⁺ (ΔG = 60 ± 3 kJ mol⁻¹) and [Zn(DMF)₆]²⁺ (ΔG = 56 ± 4 kJ mol⁻¹) species. The [Zn(DMF)₆]²⁺ complex is the most stable one, as expected. In the n_Zn–Im = 1 region, we found three other stable complexes: [Zn(Im)(DMF)₃]⁺ (ΔG = 38 ± 4 kJ mol⁻¹), [Zn(Im)(DMF)₄]⁺ (ΔG = 28 ± 5 kJ mol⁻¹) and [Zn(Im)(DMF)₅]⁺ (ΔG = 43 ± 4 kJ mol⁻¹). All error bars were calculated following the procedure detailed in the “Convergence and uncertainty calculation” section of the ESI.† From these results we can infer that after the addition of the first ligand molecule, the hexacoordinated structures are already destabilized. This can be explained by steric effects: the presence of five DMF molecules together with a larger imidazolate ion in the coordination shell of the Zn ion is not favorable. Entropic effects that favor the lower coordinated structures could also be relevant at this high temperature condition. Finally, when the second ligand is incorporated at n_Zn–Im = 2, the three observed minima are assigned to the [Zn(Im)₂(DMF)₂] (ΔG = 0 ± 6 kJ mol⁻¹), [Zn(Im)₂(DMF)₃] (ΔG = 15 ± 6 kJ mol⁻¹) and [Zn(Im)₂(DMF)₄] (ΔG = 46 ± 5 kJ mol⁻¹) species. At this point the tetrahedral coordination starts being the most stable. With this information, we can establish the minimum energy path that connects the states A and B, which is marked with white arrows in Fig. 1. The identified mechanism involves the following steps: (i) [Zn(DMF)₆]²⁺ loses one solvent molecule, (ii) this allows the incorporation of the first ligand yielding a [Zn(Im)(DMF)₅]⁺ complex. (iii) Two consecutive solvent detachment events lead to the first tetracoordinated species: [Zn(Im)(DMF)₃]⁺. (iv) Finally, a second ligand is incorporated followed by another solvent loss, giving as result the most stable complex [Zn(Im)₂(DMF)₂] (state B in the figure).

In the right part of Fig. 1 we plotted the free energy surface for reaction (II). From this figure we can observe that once the first two imidazolates bind to the Zn ion, the most stable structures for the next additions will retain the tetrahedral geometry. For the incorporation of the third imidazolate, the new bond is first formed, followed by the loss of a solvent molecule, as it was the case for the second one. For the fourth imidazolate addition, the solvent detachment happens before, due to the fact that the high volume of the ligand prevents the possibility of accommodating one DMF in addition of the four imidazolates.

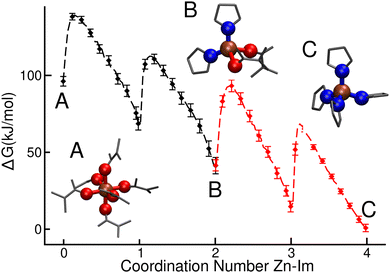
Overall reaction free energy profile

The free energy landscape for the overall process is shown in Fig. 2. In this case n_Zn–DMF was integrated out in order to allow for a more clear visualization. The black and red curves represent results obtained from the well-tempered metadynamics simulations associated reactions (I) and (II) respectively, and they were aligned so that the free energy of the common state, [Zn(Im)₂(DMF)₂], matches.

Fig. 2 Free energy as a function of n_Zn–Im for the full process involving reactions (I) (black curve) and (II) (red curve). Both curves were aligned to match in the common state (labelled as B). The zero of free energy was arbitrarily assigned to the C species. Representative snapshots of the states A, B and C are also shown.

From this plot we can see that free energy changes that involve the first, second and third ligand additions are virtually identical (ΔG = −28 ± 4 kJ mol⁻¹ for the first imidazolate incorporation and ΔG = −27 ± 4 kJ mol⁻¹ for the other two). We also know from the previous analyses that the first two additions involve the loss of two solvent molecules each, while the third one only involves a single Zn–O(DMF) bond breaking. This last observation would lead us to expect a greater free energy drop for the third ligand addition compared to the other two. Nevertheless, this difference in the number of Zn–O(DMF) broken bonds could be compensated by the entropy gain and the lowering of steric repulsion that take place when the total coordination number of the complex is reduced. This argument can be tested by analyzing the free energy differences between the [Zn(DMF)_n]⁺² species with n = 4, 5, 6 extracted from Fig. 1. The free energy drop caused by the loss of the first solvent molecule is much lower than the one that corresponds to the second one (ΔG_Zn(DMF)6→5 = 4 kJ mol⁻¹ vs. ΔG_Zn(DMF)5→4 = 24 kJ mol⁻¹), thus confirming our hypothesis.

Compared to the addition of the first, second and third ligands, the magnitude of the free energy drop that corresponds to the last step is reduced by a half, yielding a value of ΔG = −14 ± 3 kJ mol⁻¹. This difference can be explained by the steric repulsion between the large imidazolates in [Zn(Im)₄]⁻² as well as the coulombic repulsion between the negatively charged complex and the newly added ligand. This trend was also observed by Balestra and coworkers by means of DFT studies for the case of water and ethanol acting as solvents.⁴⁸ The binding free energy of the fourth ligand will turn out to be an important feature when comparing this case with the setup studied in next section, in which the tagged Zn starts as part of the surface of a crystalline slab instead of as a dissolved ion.

ZIF crystal growth

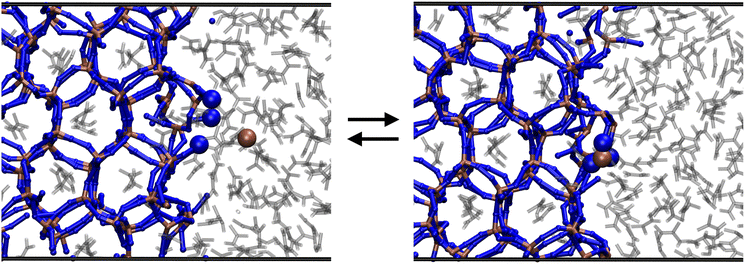
In this section, we will tackle the question on whether the energetics of forming a new Zn–N(Im) bond depends on the self-assembly stage or not. In particular, we aim to compare the Zn–Im recombination reactions that occur during the formation of the [Zn(Im)₄]⁻² building units with those occurring at the interface of an already formed ZIF crystal slab and an electrolyte solution, which serves as a model of the late growth stages.

The growth of the ZIF surface will be decomposed into two fundamental reactions: (i) a solvated Zn ion adsorbs into a crystal site composed by three undercoordinated surface ligands (see Fig. 3) and (ii) a similar process but with the ligand acting as the adsorbed species, this time binding with an undercoordinated surface Zn.

Fig. 3 Scheme of the model system employed to study the energetics and mechanisms of ZIF crystal growth. The (001) surface of ZIF-4 is shown. The Zn and N atoms involved in the reaction are displayed as spheres. The solvent molecules are plotted in gray. For clarity purposes, only the Zn and N atoms of the crystal slab are shown.

Zn adsorption–desorption on a ZIF surface

We computed the free energy changes that operate during the reaction shown in Fig. 3 via well-tempered metadynamics simulations, as described above for the study of the formation of the [Zn(Im)₄]⁻² complex. This time, we used another set of CVs to properly sample the process (see Methods section). For quantifying the influence of the surface local structure on the free energy of the reaction, we compared results obtained for four different slabs: three of them correspond to a ZIF-4 crystal but differ in their (hkl) Miller indices. Specifically, the surfaces studied were cut in the directions perpendicular to the x, y and z axes (equivalent to the crystallographic a, b and c directions), resulting in Miller indices of (100), (010) and (001) respectively. The fourth surface was obtained by cutting a ZIF-1 crystal in a plane perpendicular to the y direction (lattice vector b), that corresponds to (010). The reason behind this choice was to study the effect of changing (i) the Miller indices of the exposed face by comparing results from the three ZIF-4 surface slabs and (ii) the topology of the crystalline structure by comparing results coming from two different polymorphs. ZIF-1 was chosen because it is the second most stable porous polymorph after ZIF-4.⁷ This crystal was cut perpendicular to the y direction to avoid oblique surfaces, given the triclinic nature of the ZIF-1 unit cell. The produced systems were charge neutral, as the total amount of ligands was twice the amount of Zn ions in the whole simulation box. The procedure for generating all the surface slabs is detailed in the “ZIF surface generation” section of the ESI.† In all cases, the binding site for the Zn comprises three free ligand molecules, as shown in Fig. 3.

In Fig. 4 we show the free energy landscapes for these processes as a function of the coordination number between the Zn and imidazolate ions, in the same spirit as in Fig. 2. The other two CVs employed in the well-tempered metadynamics procedure were integrated out to make this plot. The zero of free energy was located at the absolute free energy minimum in all cases.

Fig. 4 Free energy vs. n_Zn–Im for the reaction schematized in Fig. 3 for ZIF-4 surfaces with Miller indices (100) (black) (010) (green) and (001) (orange) and for a ZIF-1 (010) surface (turquoise). Images of the surfaces are displayed at the top of the figure.

There are some common features between plots, for example, there are always four minima that correspond to the Zn ion bonded to zero, one, two or three surface ligands. The free energy differences between the four minima are shown in Table 1. The corresponding errors are obtained following the procedure explained in the ESI,† as previously mentioned.

Table 1 Values of ΔG_i in kJ mol⁻¹ for each of the surfaces studied with the corresponding errors. The index i represents the change in the coordination number of the tagged Zn

	ΔG0→1	ΔG1→2	ΔG2→3
ZIF-4 (100)	−38 ± 11	−58 ± 10	−49 ± 5
ZIF-4 (010)	−41 ± 12	−41 ± 10	−29 ± 4
ZIF-4 (001)	−41 ± 12	−46 ± 9	−49 ± 4
ZIF-1 (010)	−42 ± 10	−59 ± 8	−51 ± 4

---

An average value of ΔG_0→1 = −40 kJ mol⁻¹ was registered for the first Zn–N(Im) bond formation while for the other two, the observed free energy difference was about ΔG_1→2 = −51 and ΔG_2→3 = −45 kJ mol⁻¹ on average. This difference is explained by the fact that the Zn has to diffuse from the bulk to the surface vicinity during the first step. All the free energies are higher in absolute value than their counterparts from the [Zn(Im)₄]⁻² complex formation, meaning that the crystal growth is more exergonic than the first bond formation steps, as predicted by nucleation theories from surface tension arguments.⁶²

All of the free energy differences between consecutive steps lie within the uncertainty bars of the others, meaning that we cannot state that the nature of the surface has an important influence in the Zn adsorption process. An exception to this behavior was found in the plot that corresponds to ZIF-4 (010), which presents a lower energy drop than the other two ZIF-4 surfaces for the step that goes from forming two Zn–N(Im) bonds to three (see ΔG_2→3). In order to explain this behavior we can consider the original description of the process in terms of n_Zn–Im and n_Zn–DMF. The mechanism of the third imidazolate bond formation involves, as explained in the ‘Formation of early [Zn(Im)_n]²⁻ⁿ complexes’ section, the bond formation itself followed by a detachment of a DMF molecule from the Zn ion. We found that the main difference between the (010) surface and the others lies in the step of solvent detachment, which is about ∼10 kJ mol⁻¹ less exergonic in this case. By visual inspection of the trajectories, we found that this tagged solvent molecule lies inside the ZIF pore in the case of the (010) surface. As a consequence, it is harder for this DMF molecule to diffuse far from the Zn than in the other surfaces, in which the solvent molecule to be detached is pointing towards the liquid region. Snapshots of these pentacoordinated intermediate structures for the ZIF-4 (010) and ZIF-4 (001) surfaces are shown in the ESI.†

Ligand adsorption–desorption on a ZIF surface

Our analysis concludes with the study of another adsorption process that takes place during the growth stage of the synthesis: the addition of a ligand molecule to an undercoordinated surface Zn. Since in this case only one bond has to be formed, it was possible to use only two CVs instead of three to properly sample the reaction (see Methods section). In order to compare with the previous results, we plotted the free energy as a function of the coordination number in Fig. 5, which in this case goes from three to four, as the newly added ligand completes the coordination of the undercoordinated surface Zn. We also include the results for the last ligand addition to the Zn ion in solution that was discussed in section ‘Formation of early [Zn(Im)_n]²⁻ⁿ complexes’ in the figure, for comparison.

Fig. 5 Free energy vs. Zn–N coordination number of the reactive Zn ion at the ZIF-4 (100) (black), (010) (green) and (001) (orange) and ZIF-1 (010) (turquoise) surfaces and for an isolated [Zn(Im)₃]⁻ complex (red). In the inset we highlight the zero coordination region. Typical snapshots of the non-bonded (left) and bonded (right) species are also shown.

For the ZIF-4 surfaces, values of ΔG = −41 ± 3 kJ mol⁻¹ were registered for the (100) and (010) surfaces, while ΔG = −47 ± 3 kJ mol⁻¹ for the (001) one. The value that corresponds to the ZIF-1 surface slab was ΔG = −28 ± 3 kJ mol⁻¹ and finally for the [Zn(Im)₃]⁻ a value of ΔG = −14 ± 3 kJ mol⁻¹ was found, as stated above. The addition of the fourth ligand is less energetically favorable than the previous ones in all cases (see Fig. 2 and 4), because of the already mentioned steric effects, with the exception of the (010) case analyzed above. This suggests that the ligand adsorption could be the limiting step of the process, which would also be in line with the empirical observation made by synthesis experts that an excess concentration of imidazole with respect to the stoichiometric value is required for the synthesis to be successful.⁴ Nevertheless, this difference is much more subtle for growth than for the formation of the [Zn(Im)₄]⁻² building units. The fact that the reactive Zn is already part of the crystal in the growth stages seems to promote a more adequate geometry for the addition of the last ligand. This makes the formation of the [Zn(Im)₄]²⁻ species the least favorable step, which highlights the importance of the stability of these initial building blocks in the formation of ZIFs. This stability can be modulated by changes in synthesis conditions, such as the nature of the solvent, temperature and ligand : metal ratio among others.

With respect to the free energy of binding a ligand for different surface slabs, we found the following trend: ZIF-4(001) > ZIF-4(100) = ZIF-4(010) > ZIF-1(010). The lowest value, that corresponds to ZIF-1, can be associated to the fact that this polymorph is less stable than ZIF-4. This is due to its lower density, which results in the reduction the intensity of van der Waals interactions.⁷ In order to explain the difference found between ZIF-4 surface slabs, we characterized the solvation structure of each surface, since breaking a Zn–O(DMF) bond is the bottleneck of this reaction, as explained above.

In Fig. 6, we plotted the average orientation (top) and density (bottom) of solvent molecules as a function of their distance to the surface. Orientations were measured by computing the cosine of the angle θ between the C(DMF)–O(DMF) bond and the vector perpendicular to the surface plane. Densities were normalized by the bulk value of ρ₀ = 6.80 nm⁻³. The position of the surface was assigned to the average position of the outermost Zn layer, while that of solvent molecules was described by their central C atom. From the top panel we observe that in all cases the orientation reaches a minimum at distances around d ∼ 3 Å, which correspond to the Zn–C(DMF) distance in a bonded Zn–O(DMF) pair, which means that the solvent is oriented perpendicular to the surface in this region. In the (010) and (001) cases, this is accompanied by the presence of a maximum in the density plot (see bottom panel), that comprises the first solvation layer of the surface. For the (100) surface, the density does not reach a maximum at this point, suggesting that the solvent penetrates less the vicinity of the surface slab. Nevertheless, the trend observed in Fig. 5, seems to suggest that the orientation of the solvent molecules plays a more important role than local density in the ligand binding process. For the (100) and (010) surfaces, the average orientation reaches a minimum of −0.4, while for the (001) plane this minimum is reduced to −0.2. This indicates that the solvent is less strongly aligned to the normal vector of the plane in the case of the (001) surface, which makes it easier to detach. This argument can be reinforced by comparing the free energy cost of the DMF removal from a surface Zn, which can be obtained from the same well-tempered metadynamics simulations as the ones that correspond to Fig. 5. The obtained DMF detachment free energies were ΔG₍₁₀₀₎ = 48 ± 3 kJ mol⁻¹, ΔG₍₀₁₀₎ = 42 ± 3 kJ mol⁻¹ and ΔG₍₀₀₁₎ = 29 ± 3 kJ mol⁻¹ for the ZIF-4 (100), (010) and (001) surfaces, respectively. This trend confirms that the DMF is detached more frequently from a (001) surface than from the (100) and (010) ones. Even though it was found that the ZIF-4 planes present some differences in these aspects, it is clear that the magnitude of the discrepancies in Fig. 5 are not enough to make the ZIF-4 crystals grow faster in c direction than in a and b. Experimentally this is also confirmed by the fact that the average ZIF-4 crystal shape is not elongated in any preferential direction.⁹

Fig. 6 Average orientation of DMF molecules (top) and average DMF density (bottom) as a function of the distance to the outermost Zn layer of ZIF-4 (100) (black), (010) (green) and (001) (orange) surfaces. Orientations were measured by computing the cosine of the angle θ between the C(DMF)–O(DMF) bond and the vector perpendicular to the surface plane. Densities were normalized by the bulk value.

Conclusions

In this work we studied the energetics and mechanisms underlying the formation of [Zn(Im)₄]⁻² building units and late growth stages of the self-assembly of ZIFs by means of well-tempered metadynamics simulations carried out with a partially reactive force field. We describe a ten-steps mechanism that leads from an octahedral, fully solvated, Zn ion to a tetrahedral complex featuring four ligands:

(i) [Zn(DMF)₆]²⁺ ⇌ [Zn(DMF)₅]²⁺ + DMF

(ii) [Zn(DMF)₅]²⁺ + Im⁻ ⇌ [Zn(Im)(DMF)₅]⁺

(iii) [Zn(Im)(DMF)₅]⁺ ⇌ [Zn(Im)(DMF)₄]⁺ + DMF

(iv) [Zn(Im)(DMF)₄]⁺ ⇌ [Zn(Im)(DMF)₃]⁺ + DMF

(v) [Zn(Im)(DMF)₃]⁺ + Im⁻ ⇌ [Zn(Im)₂(DMF)₃]

(vi) [Zn(Im)₂(DMF)₃] ⇌ [Zn(Im)₂(DMF)₂] + DMF

(vii) [Zn(Im)₂(DMF)₂] + Im⁻ ⇌ [Zn(Im)₃(DMF)₂]⁻

(viii) [Zn(Im)₃(DMF)₂]⁻ ⇌ [Zn(Im)₃(DMF)]⁻ + DMF

(ix) [Zn(Im)₃(DMF)]⁻ ⇌ [Zn(Im)₃]⁻ + DMF

(x) [Zn(Im)₃]⁻ + Im⁻ ⇌ [Zn(Im)₄]²⁻

In light of this mechanism, we conclude that the change of coordination number is a complex process involving intermediate pentacoordinated species. This kind of Zn hybrid complexes has been already characterized both experimentally and theoretically.^63–67

The incorporation of the first three ligands is equally favorable in terms of free energy in the formation of the [Zn(Im)₄]⁻² complex. During the late growth, however, it is less favorable to form the first Zn–N(Im) bond than forming the next two. This is associated with the local environment of the ZIF surface, which offers easy access to undercoordinated ligands. Conversely, adding a fourth ligand is the least exergonic step in the process of formation of Zn–ligand complexes. When this reaction is compared with its analogous of forming a Zn–N(Im) bond between a tri-coordinated surface Zn and a free, solvated, Im ion, the latter is more exergonic. This suggests that the formation of the fully-coordinated Zn ion is a crucial part in the self-assembly mechanism. This process can be modulated by changing synthesis conditions, including nature of solvent and reactants, temperature and Zn : Im and reactant : solvent ratios.

The free energy associated with the addition of a fourth ligand to a surface Zn, a late growth step, depends on the local environment surrounding the tagged Zn. This effect is more important when comparing the growth of two polymorphs than when comparing the growth of ZIF-4 crystal faces with different Miller indices. The differences found in this latter case are associated with the ease of removing the solvent molecules that bind to the surface Zn. Even more subtle differences take place when adding a Zn to a ZIF surface. These are also associated with the removal of solvent molecules and seem to be related to whether the solvent molecules competing with the Zn lie in the solution or whether they are adsorbed in the outermost pore layer of the surface.

This work sheds light into important thermodynamic and mechanistic aspects of the self-assembly of ZIFs. Our methodology can be extended to study the formation of building units and late growth processes that characterize the self-assembly of other MOFs and thus contribute to coming closer to the holy grail of MOF rational design. The intermediate nucleation and growth steps that were not covered in this study will be the object of further work.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

E. M. ran the well-tempered metadynamics simulations and curated the data. R. S. conceived the project and methodology, provided the funding and supervised the investigation. Both authors analyzed the results and wrote the manuscript.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was funded by the European Union ERC Starting grant MAGNIFY, grant number 101042514. This work was granted access to the HPC resources of IDRIS under the allocation A0150911989 made by GENCI.

Notes and references

1. B. Chen, Z. Yang, Y. Zhu and Y. Xia, J. Mater. Chem. A, 2014, 2, 16811–16831.
2. A. U. Ortiz, A. P. Freitas, A. Boutin, A. H. Fuchs and F.-X. Coudert, Phys. Chem. Chem. Phys., 2014, 16, 9940–9949.
3. P. Iacomi and G. Maurin, ACS Appl. Mater. Interfaces, 2021, 13, 50602–50642.
4. K. S. Park, Z. Ni, A. P. Côté, J. Y. Choi, R. Huang, F. J. Uribe-Romo, H. K. Chae, M. O'Keeffe and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10186–10191.
5. Y. Yu, A. Qiao, A. M. Bumstead, T. D. Bennett, Y. Yue and H. Tao, Cryst. Growth Des., 2020, 20, 6528–6534.
6. Y. V. Kaneti, S. Dutta, M. S. A. Hossain, M. J. A. Shiddiky, K. Tung, F. Shieh, C. Tsung, K. C. Wu and Y. Yamauchi, Adv. Mater., 2017, 29, year.
7. D. W. Lewis, A. R. Ruiz-Salvador, A. Gómez, L. M. Rodriguez-Albelo, F.-X. Coudert, B. Slater, A. K. Cheetham and C. Mellot-Draznieks, CrystEngComm, 2009, 11, 2272.
8. A. K. Cheetham, G. Kieslich and H. H.-M. Yeung, Acc. Chem. Res., 2018, 51, 659–667.
9. J. Zhang, A. Qiao, H. Tao and Y. Yue, J. Non-Cryst. Solids, 2019, 525, 119665.
10. C. A. Schröder, I. A. Baburin, L. van Wüllen, M. Wiebcke and S. Leoni, CrystEngComm, 2013, 15, 4036–4040.
11. R. A. Van Santen, J. Phys. Chem., 1984, 88, 5768–5769.
12. P. T. Cardew, Cryst. Growth Des., 2023, 23, 3958–3969.
13. R. N. Widmer, G. I. Lampronti, S. Chibani, C. W. Wilson, S. Anzellini, S. Farsang, A. K. Kleppe, N. P. M. Casati, S. G. MacLeod, S. A. T. Redfern, F.-X. Coudert and T. D. Bennett, J. Am. Chem. Soc., 2019, 141, 9330–9337.
14. L. Bouëssel du Bourg, A. U. Ortiz, A. Boutin and F.-X. Coudert, APL Mater., 2014, 2, 124110.
15. J. Fonseca, T. Gong, L. Jiao and H.-L. Jiang, J. Mater. Chem. A, 2021, 9, 10562–10611.
16. S. Henke, M. T. Wharmby, G. Kieslich, I. Hante, A. Schneemann, Y. Wu, D. Daisenberger and A. K. Cheetham, Chem. Sci., 2018, 9, 1654–1660.
17. E. Méndez and R. Semino, J. Mater. Chem. A, 2024, 12, 31108–31115.
18. M. Eddaoudi, D. F. Sava, J. F. Eubank, K. Adil and V. Guillerm, Chem. Soc. Rev., 2015, 44, 228–249.
19. M. J. Van Vleet, T. Weng, X. Li and J. Schmidt, Chem. Rev., 2018, 118, 3681–3721.
20. V. Guillerm and D. Maspoch, J. Am. Chem. Soc., 2019, 141, 16517–16538.
21. R. Freund, S. Canossa, S. M. Cohen, W. Yan, H. Deng, V. Guillerm, M. Eddaoudi, D. G. Madden, D. Fairen-Jimenez, H. Lyu, L. K. Macreadie, Z. Ji, Y. Zhang, B. Wang, F. Haase, C. Wöll, O. Zaremba, J. Andreo, S. Wuttke and C. S. Diercks, Angew. Chem., Int. Ed., 2021, 60, 23946–23974.
22. H. Wang, X. Pei, M. J. Kalmutzki, J. Yang and O. M. Yaghi, Acc. Chem. Res., 2022, 55, 707–721.
23. M. Barsukova, A. Sapianik, V. Guillerm, A. Shkurenko, A. C. Shaikh, P. Parvatkar, P. M. Bhatt, M. Bonneau, A. Alhaji, O. Shekhah, S. R. G. Balestra, R. Semino, G. Maurin and M. Eddaoudi, Nat. Synth., 2023, 3, 33–46.
24. C. Castillo-Blas, A. M. Chester, D. A. Keen and T. D. Bennett, Chem. Soc. Rev., 2024, 53, 3606–3629.
25. K. Mu, J. Wang, M. Gao, Y. Wu, Q. Shi and J. Dong, ACS Omega, 2024, 9, 34777–34786.
26. S. Lee, D. Nam, D. C. Yang and W. Choe, Small, 2023, 19, year.
27. E. Méndez and R. Semino, J. Mater. Chem. A, 2024, 12, 4572–4582.
28. T. Du, S. Li, S. Ganisetti, M. Bauchy, Y. Yue and M. M. Smedskjaer, Natl. Sci. Rev., 2024, 11, nwae023.
29. Z. Shi, B. Liu, Y. Yue, A. Arramel and N. Li, J. Am. Ceram. Soc., 2024, 107, 3845–3856.
30. N. Castel, D. André, C. Edwards, J. D. Evans and F.-X. Coudert, Digital Discovery, 2024, 3, 355–368.
31. L. C. Jacobson and V. Molinero, J. Am. Chem. Soc., 2011, 133, 6458–6463.
32. C. Chu-Jon, E. Martinez, A. A. Bertolazzo, S. Banik, J. D. Rimer, S. K. R. S. Sankaranarayanan and V. Molinero, J. Am. Chem. Soc., 2024, 146, 33204–33213.
33. A. Hudait and V. Molinero, J. Am. Chem. Soc., 2016, 138, 8958–8967.
34. S.-C. Chien, S. M. Auerbach and P. A. Monson, Langmuir, 2015, 31, 4940–4949.
35. C. Bores, S. Luo, J. David Lonergan, E. Richardson, A. Engstrom, W. Fan and S. M. Auerbach, Phys. Chem. Chem. Phys., 2022, 24, 142–148.
36. G. C. Sosso, M. Salvalaglio, J. Behler, M. Bernasconi and M. Parrinello, J. Phys. Chem. C, 2015, 119, 6428–6434.
37. V. Marinova, G. P. F. Wood, I. Marziano and M. Salvalaglio, Cryst. Growth Des., 2022, 22, 3034–3041.
38. L. Li, M. Paloni, A. R. Finney, A. Barducci and M. Salvalaglio, J. Phys. Chem. Lett., 2023, 14, 1748–1755.
39. T. T. B. Le, A. R. Finney, A. Zen, T. Bui, W. J. Tay, K. Chellappah, M. Salvalaglio, A. Michaelides and A. Striolo, J. Chem. Theory Comput., 2023, 20, 1612–1624.
40. M. Yoneya, S. Tsuzuki and M. Aoyagi, Phys. Chem. Chem. Phys., 2015, 17, 8649–8652.
41. D. Biswal and P. G. Kusalik, ACS Nano, 2016, 11, 258–268.
42. D. Biswal and P. G. Kusalik, J. Chem. Phys., 2017, 147, 044702.
43. Y. J. Colón, A. Z. Guo, L. W. Antony, K. Q. Hoffmann and J. J. de Pablo, J. Chem. Phys., 2019, 150, 104502.
44. L. Kollias, D. C. Cantu, M. A. Tubbs, R. Rousseau, V.-A. Glezakou and M. Salvalaglio, J. Am. Chem. Soc., 2019, 141, 6073–6081.
45. S. A. Wells, N. F. Cessford, N. A. Seaton and T. Düren, RSC Adv., 2019, 9, 14382–14390.
46. M. Filez, C. Caratelli, M. Rivera-Torrente, F. Muniz-Miranda, M. Hoek, M. Altelaar, A. J. Heck, V. Van Speybroeck and B. M. Weckhuysen, Cell Rep. Phys. Sci., 2021, 2, 100680.
47. S. R. G. Balestra and R. Semino, J. Chem. Phys., 2022, 157, 184502.
48. S. R. G. Balestra, B. Martínez-Haya, N. Cruz-Hernández, D. W. Lewis, S. M. Woodley, R. Semino, G. Maurin, A. R. Ruiz-Salvador and S. Hamad, Nanoscale, 2023, 15, 3504–3519.
49. A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 020603.
50. J. T. Hughes, T. D. Bennett, A. K. Cheetham and A. Navrotsky, J. Am. Chem. Soc., 2012, 135, 598–601.
51. K. Boussouf, T. Khairat, M. Prakash, N. Komiha, G. Chambaud and M. Hochlaf, J. Phys. Chem. A, 2015, 119, 11928–11940.
52. D. Wu and A. Navrotsky, J. Solid State Chem., 2015, 223, 53–58.
53. J. J. Calvin, P. F. Rosen, S. J. Smith and B. F. Woodfield, J. Chem. Thermodyn., 2019, 132, 129–141.
54. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171.
55. G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613.
56. N. Castel and F.-X. Coudert, J. Phys. Chem. C, 2022, 126, 19532–19541.
57. M. Chalaris and J. Samios, J. Chem. Phys., 2000, 112, 8581–8594.
58. K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes, I. Vorobyov and A. D. Mackerell, J. Comput. Chem., 2009, 31, 671–690.
59. N. Castel and F.-X. Coudert, Chem. Mater., 2023, 35, 4038–4047.
60. R. Gaillac, P. Pullumbi, K. A. Beyer, K. W. Chapman, D. A. Keen, T. D. Bennett and F.-X. Coudert, Nat. Mater., 2017, 16, 1149–1154.
61. S.-i. Ishiguro, M. Miyauchi and K. Ozutumi, J. Chem. Soc., Dalton Trans., 1990, 2035–2041.
62. M. Volmer and A. Weber, Z. Phys. Chem., 1926, 119U, 277–301.
63. J. Aduriz-Arrizabalaga, J. M. Mercero, D. De Sancho and X. Lopez, Phys. Chem. Chem. Phys., 2023, 25, 27618–27627.
64. J. E. H. Pucheta, D. Prim, J. M. Gillet and J. Farjon, ChemPhysChem, 2016, 17, 1034–1045.
65. M. Sola, A. Lledos, M. Duran and J. Bertran, Inorg. Chem., 1991, 30, 2523–2527.
66. A. V. Piskunov, A. V. Maleeva, G. K. Fukin, V. K. Cherkasov and A. S. Bogomyakov, Inorg. Chim. Acta, 2017, 455, 213–220.
67. C. Kirchner and B. Krebs, Inorg. Chem., 1987, 26, 3569–3576.

---

Footnote

† Electronic supplementary information (ESI) available: Metadynamics setup and data treatment, surfaces preparation protocols, force field parameters and validation details and additional figures. See DOI: https://doi.org/10.1039/d5sc00807g

---