Ability of strained C atoms to act as an electron donor

Abstract

There is a great deal of strain within the propellane and pyramidane hydrocarbon molecules. Quantum chemical calculations evaluate how this strain affects the ability of the bridgehead C atom to act as an electron donor in hydrogen, halogen, chalcogen, pnicogen, and tetrel bonds, despite the absence of a formal C lone pair or C=C multiple bond. The strain induces the formation of a substantial region of negative electrostatic potential on this C atom which can attract the σ-hole of an electrophile. Each such molecule also contains an occupied molecular orbital that can be described as either a C lone pair or C–C bond, which is spatially disposed to align with, and transfer charge to, a σ* antibonding orbital of an approaching Lewis acid. The degree of strain within the hydrocarbon is closely correlated with the magnitude of the negative electrostatic potential, which is in turn connected with the strength of the ensuing bond. Tetrel bonds are strongest, followed by halogen, both of which contain a significant degree of covalency.

---

Introduction

The decades of research on the H-bond (HB) from both experimental and theoretical perspectives have provided a wealth of insights about its underlying nature, factors that control its strength, and a list of experimental markers of its presence.^1–10 Somewhat more recent has been the rediscovery of a number of closely related bonding patterns that generally fall under the umbrella title of sigma (and pi) hole bonds. These HB analogues substitute the central proton by any of a diverse list of larger atoms, many of which are more electronegative than the H that they replace.^11–26 The anisotropy of the electron density around these bridging atoms leads to regions of both negative and positive electrostatic potential, the latter of which comprise these so-called holes. The first of these bonds to receive wide scale attention was the halogen bond (XB) where the H is replaced by any of the group 17 atoms. But it is becoming readily apparent that other families can be involved as well, leading to the chalcogen (YB), pnicogen (ZB), and tetrel (TB) bonds that are stimulating increased study. This idea has propagated to the transition metals as well, leading to the more recently christened matere, osme, and spodium bonds,^27–38 among others.

The cumulative research into these bonds has culminated in a wider understanding of the contributing forces. There is first the coulombic attraction derived from the interaction between these positive holes and the partial negative charge on the partner nucleophile. As a second major contributor, the alignment of the lone pair on the nucleophile with the σ*(XR) antibonding orbital of the Lewis acid promotes a charge transfer from the former to the latter which helps stabilize the system. Certain guiding principles have also been unveiled regarding the strength of these bonds. For example, as one moves down any column in the periodic table, the lowered electronegativity and rising polarizability leads to more intense σ-holes, and thence to stronger bonding. It is also now understood that this hole can be intensified by the presence of electron-withdrawing substituents on the Lewis acid that enhance the deficit of density in the σ-hole area.

There has been much less concentrated effort to determine how the properties of the nucleophile affect the bonding. Indeed, the vast majority of work has considered the source of electron density to be a lone pair on a molecule such as NH₃ or H₂O.^39–44 As such, it is understood that its efficacy is enhanced by electron-donating substituents, such as alkyl or amino groups, but little beyond this general concept. While there has been some consideration of other electron sources such as π-clouds or σ-bonds,^45–53 this work has been relatively meager when compared to the careful dissection of the factors affecting the Lewis acid.

Carbon is of course a highly prevalent atom throughout the realm of chemistry and biochemistry. Given its common bonding patterns, there would rarely be any opportunity for C to contain a lone pair to serve as electron donor in any of these noncovalent bonds. When involved in multiple bonds, there would be a π-cloud above the C–C bond of an alkene or alkyne, which might act as an electron source. The same would be true of the more extended π-cloud hovering over an aromatic phenyl group. However, these π-clouds have been shown in the past to furnish comparatively weak bonding opportunities. The situation is different for carbenes. Their divalent R–C–R bonding around the central C leaves them with a lone pair that can be utilized for this purpose. But such carbenes are rather unusual so would not represent a major player in these sorts of bonds.

An interesting question arises concerning how placing strain on a central C atom might influence its electronic structure. There is some precedent for this idea, as it was recently shown that inducing strain into the three Z–R bonds surrounding the central Z pnicogen atom of ZR₃ can very substantially strengthen the Z⋯N pnicogen bond to a nucleophile.⁵⁴ In the case of carbon, there are available systems which contain a great deal of strain. The propellanes are hydrocarbons where each C is formally bonded to four substituents, but the internal strain leaves these bonds far from the 109° separation one might expect from a saturated system.^55–59 And indeed, some earlier work confirms that this strain imparts to the bridgehead atom a substantial negative charge, which promotes its ability to participate in a noncovalent bond, despite the absence of a formal lone pair.^60–65

The present work is designed to probe this issue much more fully and systematically and to determine whether the strained propellanes are capable of engaging in noncovalent bonds, and if so, which particular sorts of bonds and how strong might they be. The types of bonds considered cover the full range from the HB to XB, YB, ZB and TB. The Lewis acid atom with which the propellane C might interact spans from the second row down to the much larger and electropositive atoms of the fourth row. (1,1,1) propellane is compared with its larger and less strained (2,2,2) variant. Added to this mix is pyramidane, in the shape of a square pyramid, where the single apex C atom is under an especially high degree of strain.⁶⁶ It is found that the bonds involving these C atoms can be quite strong, even in the absence of a true lone pair. This work has implications that extend beyond the particular systems examined here, to any molecule where the central C atom is under a certain degree of strain.

Methods

Full optimizations of isolated monomers and dimers were performed at the M06-2X/def2-tzvpp^67–70 level of theory using the Gaussian 16 (Rev. C.01) package.⁷¹ Harmonic frequency analysis of normal modes verified them as true minima. The counterpoise approach proposed by Boys and Bernardi⁷² corrected the basis set superposition error (BSSE). MEP (molecular electrostatic potential) analysis identified the extrema on the 0.001 au electronic isodensity contour on the isolated monomers utilizing the MultiWFN software.^73,74 Graphical post-processing of MEP results was performed using the VMD software.⁷⁵ Using the AIMAll program,⁷⁶ QTAIM topological analysis of the scalar field of electron density^77,78 provided bond paths and bond critical points (saddle points of the electron density function). NBO analysis⁷⁹ allowed elucidation of interorbital interactions within the complexes, via the NBO 7.0 set of codes. Decomposition of interaction energy into its components was achieved using the ALMO-EDA scheme^80,81 within Q-Chem 6 software.

The triplet states of the monomers were higher in energy than the singlets by 98.25, 11,50 and 75.16 kcal mol⁻¹ for 111P, 222P and pyramidane, respectively, as listed in Table S1,† so calculations were focused on the singlets. The same much higher triplet energies characterized the complexes, with triplet–singlet separations between 58 and 166 kcal mol⁻¹. With respect to the application of a single electron configuration, Table S1† shows that the T1 diagnostic⁸² falls well below the 0.02 threshold suggested by these authors that would signal multiconfiguration involvement, and even more comfortably below the 0.05 level suggested by others.⁸³ The same may be said of the complexes, with T1 values also displayed in Table S1.†

Results

The first section below describes the salient properties of the monomers, particularly those aspects that are relevant to their mutual interactions. The way in which the Lewis acids and bases fit together, and the energetics are contained in the next section. The unique properties of these complexes are probed through analysis of their electronic structures in the succeeding section.

Monomer properties

First with regard to the shapes of the three strained C systems, 111P contains two bridgehead or apical C_a atoms, that are linked together by three CH₂ groups as may be seen in Fig. 1a. The internal distance between the two apical C_a atoms is 1.544 Å, and the bonds between apical and methylene or equatorial C_e atoms is slightly shorter at 1.506 Å. The strain at the apical C atoms can be measured by the C_e–C_a–C_e angles of 96.1°. Even smaller is the C_a–C_a–C_e angle of only 59.2°. The two apical C_a atoms in 222P in Fig. 1b are bridged by three CH₂CH₂ chains. The C_a–C_a distance in 222P is 1.532 Å, slightly shorter than in 111P, and r(C_aC_e) is 1.543 Å, considerably longer than these same bonds in 111P. One may view 222P as a pair of planar equilateral triangular C(CH₂)₃ units, each with internal θ(C_eC_aC_e) angles of 120°. The C_a–C_a–C_e angles in 222P are equal to 90.3°, so this larger propellane is less strained than is 111P. As its name implies, pyramidane takes the shape of a square pyramid. Each of the four bondlengths to the apical C atom are 1.619 Å, longer than any of the other strained molecules. There is a great deal of strain at the central C_a atom, with θ(C_eC_aC_e) angles equal to 52.8°.

Fig. 1 Geometries of (a) 111P, (b) 222P, and (c) pyramidane, with distances in Å and angles in degs. Molecular electrostatic potentials of (d) 111P, (e) 222P, and (f) pyramidane, where red and blue regions indicate negative and positive regions, respectively.

The strain within these systems has major repercussions for their electronic structure. The molecular electrostatic potential (MEP) surrounding each of the three strained molecules is illustrated in Fig. 1d–f. The red and blue colors indicate negative and positive sign of the MEP. A prominent negative red area is located to the right of the apical C atom of each of these units. The value of the minimum of the MEP on the 0.001 au isodensity surface is listed in Table 1 where it may be seen to be smallest for 222P at −6.2 kcal mol⁻¹. The magnitude of this negative charge rises to −20.8 kcal mol⁻¹ for 111P, and is most negative for pyramidane at −42.3 kcal mol⁻¹. As such, this apical C atom would be prone to attract an electrophilic center of a partner molecule, particularly so for the two latter systems.

Table 1 MEP extrema (kcal mol⁻¹) on the 0.001 au electron isodensity surface for isolated monomers

	V s,min
111P	−20.8
222P	−6.2
Pyramidane	−42.3
	V s,max
HF	69.8
HCl	45.2
HBr	38.8
HI	28.9
HCN	52.9
ClF	42.0
BrF	50.4
IF	60.8
SF2	35.9
SeF2	46.2
TeF2	56.4
PF3	28.4
AsF3	40.6
SbF3	50.0
GeF4	52.6
SnF4	69.5
PbF4	70.2

---

The series of pairing partners with these strained C systems contains the elements of a HB, XB, YB, ZB or TB. Inspection of the MEP of each of these molecules indeed verifies the presence of a so-called σ-hole of positive potential. The maximum of the MEP on the 0.001 au isodensity surface on the leftmost atom in the name of the electrophile is listed in Table 1 as V_s,max, these quantities follow the usual pattern of increasing in magnitude as one drops down in any column of the periodic table, e.g. Cl < Br < I. With regard to different families, the tetrel atoms contain the deepest σ-hole, followed by halogen, chalcogen, and finally pnicogen.

In addition to a coulombic attraction between the electrostatic potentials of the two units, formation of a bond would be supplemented by a charge transfer component. Such a phenomenon would be facilitated if there is a pair of electrons available in the region to which the electrophile is attracted. There is indeed such an orbital for each of these strained C systems, as may be seen in the top row of Fig. 2 which displays the appropriate localized NBO orbital for each strained C molecule. This orbital is denoted by NBO as a C–C bond for the two propellanes, and a C lone pair for pyramidane. The salient point is the prominent purple region to the immediate right of each apical C atom, whose electrons would be available to an incoming electrophile. For purposes of completeness, the lower row of Fig. 2 depicts the unoccupied orbital of each system that could in principle accept electrons that might flow in the reverse direction. Note the substantial green lobe to the right of each apical C. The import of these orbitals is discussed below. While there is a single orbital of this type for the two propellanes, that for pyramidane exists as three symmetrically disposed orbitals, each of which lies along a C–C bond axis.

Fig. 2 NBO orbital of (a) 111P, (b) 222P, and (c) pyramidane, that corresponds to a σ(C_aC_a) bond or C_a lone pair. (d–f) The corresponding vacant σ* orbitals.

Another indicator of the ability to attract a Lewis acid is the availability of an electron pair in the proper alignment. The electron localization function (ELF) of each of the strained hydrocarbons is presented in Fig. 3. Both 111P and pyramidane contain a prominent region to the immediate right of the apical C, indicated by the red arrow. 222P, on the other hand, contains no such ELF region, the absence of which has implications for bonding as discussed below.

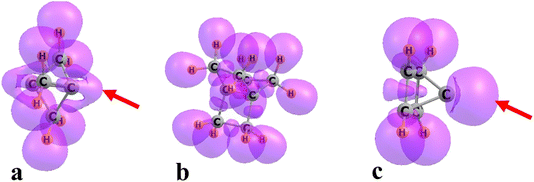Fig. 3 ELF diagrams of (a) 111P, (b) 222P, and (c) pyramidane. Red arrows in a and c point to ELF extension close to bridgehead C atom.

Geometries and energetics of dyads

Each of the hydrocarbon nucleophiles was paired with a set of potential Lewis acids, as catalogued in Table 2. The geometries of the various complexes are illustrated in Fig. 4 for the particular case of SbF₃ as the Lewis acid. R refers to the distance from the apical C_a atom of each hydrocarbon base to the central atom A of each acid, Sb in Fig. 1. The degree of linearity of the C_a⋯AF alignment which relates to the σ-hole on the acid is designated by θ. The position of the A atom relative to the C HOMO/lone pair direction is represented by α which is referenced to the indicated C_a–C_a axis within the propellanes, connecting the two apical C atoms. In the case of pyramidane, the second point of reference is indicated by the small red ball in Fig. 1c which is located at the center of the pyramid's square floor. The internal C–C bond lengths are first r_e, between the apical and equatorial C atoms. The distance between the pair of apical C atoms in the propellanes is measured as r_a. The height of the square pyramid is taken as r_a for pyramidane.

Table 2 Intermolecular geometric parameters (Å and degs) of dyads^a

	111P			222P			Pyramidane
	R	θ	α	R	θ	α	R	θ	α
a Proton is transferred from Br/I to pyramidane.
HF	1.932	179.5	178.5	2.025	179.7	179.8	1.754	179.4	178.7
HCl	2.074	177.1	171.4	2.128	179.8	179.8	1.737	178.6	177.5
HBr	2.017	175.8	171.5	2.139	178.3	179.9	—^a
HI	2.033	179.3	178.5	2.186	178.3	179.8	—^a
HCN	2.317	178.5	175.4	2.242	179.2	178.5	2.183	179.9	180.0
ClF	2.570	180.0	178.6	2.151	180.0	180.0	1.962	180.0	179.9
BrF	2.475	179.9	179.0	2.299	180.0	180.0	2.138	180.0	179.9
IF	2.591	179.6	177.6	2.509	180.0	180.0	2.338	179.9	179.8
SF2	2.874	175.2	152.8	2.897	179.8	175.6	2.305	169.6	164.2
SeF2	2.751	171.0	157.1	2.911	176.3	175.5	2.287	164.0	165.0
TeF2	2.714	164.6	160.2	2.987	171.3	175.7	2.416	158.4	162.4
PF3	3.141	169.3	146.7	3.088	173.6	175.1	2.921	165.8	142.3
AsF3	2.988	167.9	149.6	3.044	171.5	174.9	2.631	162.0	150.2
SbF3	2.876	162.5	153.2	3.065	166.7	175.1	2.596	153.7	152.0
GeF4	2.257	180.0	180.0	2.117	180.0	180.0	2.096	179.7	179.5
SnF4	2.320	179.7	179.1	2.268	179.8	179.8	2.244	179.9	178.9
PbF4	2.365	179.8	179.3	2.261	179.9	179.9	2.280	179.6	176.7

---

Fig. 4 Geometries of SbF₂ with (a) 111P, (b) 222P, and (c) pyramidane, defining geometrical parameters.

The values of the intermolecular parameters are listed in Table 2 for the dyads involving 111P, 222P, and pyramidane. The H-bond distances for the propellanes vary between 1.9 and 2.3 Å, shortest for the strongest acid HF and somewhat longer for HCN. In most cases, R is shorter for 111P than for 222P. These HB lengths are considerably shorter for pyramidane, between 1.7 and 2.2 Å. It might be noted that neither HBr nor HI engages in a HB complex with pyramidane. When paired with either of these acids, pyramidane extracts the proton to form an ion pair. The θ angles are very close to linearity for these HBs, as are the α angles. So these HBs are well disposed for the lone pair/HOMO of the apical C to align with the dipole moment of the proton donor, and its σ*(HX) antibonding orbital.

The same linearity of θ and α is noted in the halogen and tetrel bonded complexes, a function of their symmetry. These angles deviate from 180° for the chalcogen and pnicogen bonds, a common observation in these sorts of bonds, resulting in part from the deviation of their σ-holes from their internal axes of symmetry. R is shorter for 222P as compared to 111P for the XBs and TBs, but this trend is nearly reversed for the YBs and ZBs. The shortest distances occur for the pyramidane complexes.

The interaction energies of each complex are compiled in Table 3, computed at both the M062X and CCSD(T) levels of theory. There is general agreement between the two. The latter tends to offer a small reduction in the interaction energy but the trends are the same for both. There are some patterns which are common for all complexes. TB complexes at the bottom of the table are clearly most strongly bound, with some quantities exceeding 60 kcal mol⁻¹. With the exception of these TBs, the pyramidane engages in the strongest bonding, but the ordering of the two propellanes depends upon the type. The 222P variety forms much stronger XBs than 111P, comparable to the bonds with pyramidane, but the two are roughly equivalent for the other sorts of bonding. Within a given subset with the same sort of bonding, the interaction energy tends to grow with A atom size, as for example S < Se < Te. But this pattern is not followed for the halogen bonds with 222P or pyramidane. It is worth noting that the trends discussed here for the interaction energy are reproduced in the bond dissociation energies, which take the optimized geometries of the monomers as their reference. These quantities are listed in Table S2.†

Table 3 Interaction energies of optimized dimers (kcal mol⁻¹)

	111P		222P		Pyramidane
Dimer	M062X	CCSD(T)	M062X	CCSD(T)	M062X	CCSD(T)
HF	−7.05	−6.22	−4.37	−3.07	−14.65	−13.13
HCl	−4.42	−4.28	−3.49	−2.84	−11.83	−10.24
HBr	−4.16	−4.03	−3.41	−2.95	—	—
HI	−3.18	−3.04	−3.07	−2.74	—	—
HCN	−3.84	−3.90	−3.04	−2.73	−7.70	−7.51
ClF	−6.32	−4.72	−24.20	−16.95	−27.95	−21.23
BrF	−10.02	−8.16	−25.20	−18.80	−28.53	−23.84
IF	−12.90	−10.86	−23.79	−18.82	−28.97	−25.65
SF2	−5.10	−3.35	−4.74	−2.46	−13.89	−9.90
SeF2	−8.21	−6.14	−6.22	−3.69	−22.07	−18.03
TeF2	−12.47	−9.84	−8.07	−5.10	−27.42	−23.99
PF3	−3.90	−2.23	−4.16	−1.87	−6.72	−4.53
AsF3	−6.71	−4.49	−5.58	−2.98	−13.56	−10.35
SbF3	−10.78	−7.88	−7.58	−4.55	−21.63	−17.86
GeF4	−26.48	−21.56	−62.01	−51.15	−53.13	−48.63
SnF4	−35.99	−30.80	−64.45	−54.32	−56.72	−52.37
PbF4	−33.48	−28.20	−72.93	−60.02	−53.92	−48.84

---

The addition of each Lewis acid induces certain geometrical perturbations within each of the strained C nucleophiles. Of particular interest are the bondlengths involving the apical C atom. As explained in Fig. 4, r_e refers to the bond to any of the equatorial C atoms. The distance to the other apical C atom in the propellanes is designated as r_a. This same label is applied in the pyamidane for the pyramid height, i.e. distance between the apical C and the center of the 4 equatorial atoms on the pyramid floor (indicated by the small red ball in Fig. 4c).

The adjustments in these internal distances are contained in Table 4 which show some interesting patterns. Formation of any of the bonds causes the internal C–C bondlengths r_e of 111P to lengthen by between 0.009 and 0.043 Å. The changes within 222P are a bit more nuanced as there are stretches for some interactions, while contracting for others. It is the halogen and tetrel bonds which are responsible for these latter bond shortenings. The pyramidane reacts in the opposite way to 111P, with all bonds undergoing a sizable contraction in all complexes. These reductions are quite sizable, up to as much as 0.05 Å.

Table 4 Modifications of internal interatomic distances (Å) caused by complexation and total charge transferred to Lewis acid unit (e)

	111P			222P			Pyramidane
	Δre	Δra	CT	Δre	Δra	CT	Δre	Δra	CT
HF	0.015	−0.008	0.024	0.007	0.001	−0.002	−0.020	−0.027	0.077
HCl	0.010	−0.005	0.030	0.004	0.002	0.000	−0.020	−0.028	0.130
HBr	0.010	−0.005	0.043	0.004	0.003	0.001	—	—	—
HI	0.009	−0.003	0.048	0.003	0.004	0.001	—	—	—
HCN	0.010	−0.005	0.016	0.004	0.000	0.002	−0.010	−0.013	0.037
ClF	0.012	−0.005	0.071	−0.079	0.936	0.354	−0.042	−0.060	0.593
BrF	0.021	−0.006	0.121	−0.079	0.938	0.301	−0.039	−0.056	0.623
IF	0.026	−0.008	0.113	−0.082	0.943	0.225	−0.036	−0.051	0.225
SF2	0.008	−0.004	0.020	0.004	0.007	−0.011	−0.028	−0.040	0.166
SeF2	0.015	−0.006	0.044	0.006	0.010	−0.008	−0.035	−0.049	0.200
TeF2	0.023	−0.008	0.070	0.009	0.012	−0.006	−0.036	−0.050	0.179
PF3	0.006	−0.002	0.002	0.003	0.005	−0.019	−0.010	−0.014	0.020
AsF3	0.011	−0.005	0.015	0.005	0.006	−0.013	−0.022	−0.031	0.079
SbF3	0.020	−0.007	0.034	0.008	0.009	−0.012	−0.029	−0.041	0.115
GeF4	0.039	−0.019	0.130	−0.052	0.907	0.250	−0.051	−0.072	0.226
SnF4	0.043	−0.023	0.155	−0.057	0.903	0.256	−0.050	−0.070	0.230
PbF4	0.041	−0.022	0.190	−0.050	0.868	0.400	−0.053	−0.076	0.289

---

111P and 222P respond in opposite ways with respect to r_a. The former becomes somewhat “flatter” as r_a is reduced, while this parameter grows larger in 222P. The magnitude of this distance is particularly intriguing. While Δr_a is small for several of the interactions, it is quite large for the XBs and TBs, nearly a full Å. Like 111P, pyramidane also flattens when bonded, but by a greater amount. The height of this pyramid drops by between 0.013 and 0.076 Å, with the largest changes occasioned by the XBs and TBs.

Analysis of electronic structure

AIM analysis of the topology of the electron density of each of these complexes provides a clear bond path between the apical C and the A atom to which it is connected, as is clear from inspection of the molecular diagrams of all of these dyads contained in Fig S1 of the ESI.† Several of the features of the critical point on this bond path provide a measure of the bond strength. The electron density at this point, the potential energy density V, and the total energy density H are all reported in Table 5. These quantities mirror the energetics in most respects. Focusing first on the electron density, this quantity is as low as 0.01 au but rises to nearly 0.10 au for the stronger XBs and TBs, even reaching 0.12 au for pyramidane⋯ClF. These large values suggest a substantial degree of covalency has crept into the interaction. V is another quantity that is sometimes taken as a direct indicator of bond energy. These values in Table 5 follow a similar pattern as both ρ and E_int. The sign of H is commonly taken as a measure of the degree of covalency. A number of the complexes have a slightly negative H, but of only a small magnitude. The exceptions with a substantially negative H are the tetrel bonds, and the XBs with 222P and pyramidane. It is also these systems that have the largest ρ, most negative V, and the highest interaction energies.

Table 5 AIM parameters (au) within dyads

	111P			222P			Pyramidane
	ρ	V	H	ρ	V	H	ρ	V	H
HF	0.030	−0.022	−0.005	0.020	−0.016	−0.001	0.051	−0.043	−0.017
HCl	0.024	−0.015	−0.001	0.018	−0.013	0.000	0.057	−0.045	−0.019
HBr	0.028	−0.018	−0.003	0.019	−0.013	0.000	—	—	—
HI	0.028	−0.017	−0.002	0.018	−0.012	0.000	—	—	—
HCN	0.014	−0.008	0.001	0.014	−0.009	0.002	0.021	−0.013	0.000
ClF	0.029	−0.020	0.001	0.083	−0.064	−0.023	0.123	−0.123	−0.053
BrF	0.043	−0.031	−0.004	0.070	−0.051	−0.017	0.094	−0.093	−0.036
IF	0.040	−0.030	−0.005	0.054	−0.038	−0.012	0.071	−0.068	−0.021
SF2	0.016	−0.010	0.001	0.014	−0.010	0.001	0.062	−0.046	−0.014
SeF2	0.024	−0.015	0.000	0.016	−0.010	0.001	0.069	−0.058	−0.021
TeF2	0.031	−0.021	−0.003	0.016	−0.011	0.000	0.060	−0.053	−0.016
PF3	0.011	−0.006	0.000	0.011	−0.007	0.000	0.018	−0.009	0.001
AsF3	0.016	−0.008	0.001	0.013	−0.008	0.000	0.035	−0.022	−0.006
SbF3	0.023	−0.013	−0.001	0.015	−0.009	0.000	0.041	−0.030	−0.008
GeF4	0.058	−0.057	−0.019	0.091	−0.098	−0.041	0.087	−0.105	−0.033
SnF4	0.062	−0.063	−0.014	0.080	−0.080	−0.026	0.079	−0.088	−0.022
PbF4	0.066	−0.063	−0.015	0.094	−0.087	−0.032	0.085	−0.089	−0.024

---

A summary view of the data at this point suggests the following. The majority of the interactions would be categorized as almost purely noncovalent. AIM densities are fairly small, H hovers around zero, and interaction energies are less than 10 kcal mol⁻¹. There are other dyads where covalency enters to a significant degree. Most of the halogen bonds, particularly with 222P and pyramidane have rather large interaction energies, some approaching 30 kcal mol⁻¹; ρ_BCP is in the neighborhood of 0.1 au and H is clearly negative. The same is true for all of the tetrel bonds, even including 111P. The chalcogen and pnicogen bonds behave otherwise. These bonds are clearly noncovalent for the two propellanes. It is only for pyramidane, that these bonds contain a significant share of covalency, with negative H and large interaction energy.

Partitioning of the total interaction energy into its component parts offers supplementary insights into the nature of the interactions. ALMO-EDA decomposition yields the electrostatic interaction (ES) between the positive charge of the Lewis acid and the negative charge cloud of the Lewis base. The polarization (POL) and charge transfer (CT) terms arise when each subunit perturbs the electron density of its partner, and the dispersion (DISP) term represents the standard London formulation involving instantaneous interactions. Pauli exchange (EX) between the clouds of the two molecules prevents them from collapsing into a single unit. These terms are compiled in Tables S3–S5† for the various dyads, and follow trends not unlike the full energetics. Most quantities are largest for the tetrel and halogen bonds. For example, ES exceeds 100 kcal mol⁻¹ for some of the complexes involving TF₄.

Perhaps most revealing of the nature of the bonding in some ways are the relative contributions of each term. Table 6 lists each component as its percentage contribution to the total attractive force. In other words the ES percentage is equal to that term, divided by the sum (ES + POL + CT + DISP). It is immediately clear that the electrostatic component accounts for a major segment of the attraction. Its share is typically larger than half, although there are systems where it is reduced slightly, to less than 40%. There is some variability in terms of the relative contributions of the other terms. For example, DISP is the second leading contributor for HBs, YBs, and ZBs, but this percentage is reduced quite a bit for the XBs and TBs. The former has quite a large CT, larger than ES in some cases. It is POL that is second only to ES for the TBs. This pattern fits the idea that CT and POL would be expected to play a larger role as the bonds become shorter and more covalent in the XB and TB systems, while DISP would be more important as the bonding becomes more purely noncovalent.

Table 6 Percentage contributions of ALMO-EDA decomposition terms of interaction energies. ES = electrostatic term, POL = polarization, CT = charge transfer, DISP = dispersion, percentage contributions are defined as fraction of sum of attractive elements

	111P				222P				Pyramidane
	ES	POL	CT	DISP	ES	POL	CT	DISP	ES	POL	CT	DISP
HF	62	13	16	10	49	16	13	22	67	11	16	7
HCl	59	9	20	12	46	11	16	28	56	12	25	7
HBr	55	9	24	12	45	10	17	29	—	—	—	—
HI	41	9	30	20	32	10	20	38	—	—	—	—
HCN	66	10	12	12	47	14	12	27	71	8	12	9
FCl	52	6	28	14	35	9	48	8	37	19	40	5
FBr	48	9	31	11	38	12	42	8	43	17	34	5
FI	47	13	25	15	46	12	29	13	54	15	23	8
SF2	59	6	13	21	50	7	11	32	52	10	29	9
SeF2	57	9	16	18	50	9	11	30	51	15	26	8
TeF2	49	13	19	19	34	15	13	38	56	15	20	10
PF3	62	5	6	26	53	6	6	35	65	7	9	19
AsF3	62	8	8	21	53	9	6	32	62	11	14	13
SbF3	50	14	14	22	35	16	10	39	58	14	15	13
GeF4	55	23	12	10	49	32	11	8	60	23	11	6
SnF4	51	25	16	9	51	24	18	8	61	20	14	6
PbF4	50	20	21	9	49	20	24	7	59	17	18	6

---

The foregoing Lewis bases all possess a certain degree of symmetry. 211P has rings with different numbers of C atoms, as does 221P. Table S6† lists the ALMO-EDA percentage contributions of the various components when each of these rings is combined with HF, ClF, SF₂, PF₃, and GeF₄, so as to cover each of the different noncovalent bonds. These tables also contain the same quantities for the symmetric 111P and 222P bases for purposes of comparison. Fig S2† illustrates the percentage contributions of each element graphically. It is immediately clear that the asymmetry introduced into the propellanes has only a small influence on these quantities. In terms of the overall interaction energies, for the stronger XB and TB bonds, Fig S3† shows that this parameter rises in the following order: 111P < 211P < 221P, a trend that continues to 222P with the tetrel bond. For the weaker bonds, this pattern reverses, such that 211P provides the strongest bonding and 222P the weakest, although the variation is not very great.

To ensure that the insights arising from the ALMO-EDA analysis are not dependent upon that particular approach, the alternative Interacting Quantum Atoms (IQA) energy decomposition scheme⁸⁴ was also applied to all complexes. The results presented in Table S7† yields an exchange–correlation component (V_xc), which is thought to be its covalent equivalent, and a classical term (V_cl), which is usually connected⁸⁵ to the electrostatic contribution of the interaction. It can be deduced from these results that in the most stable complexes, namely those stabilized by the tetrel bond, the classic component dominates over the exchange–correlation term, being even up to 7 times larger. Similar situations arise for weaker, albeit still quite stable, dimers stabilized by chalcogen and pnicogen bonds. The electrostatic term is predominant here although there are two exceptions: the SF₂ and SeF₂ complexes with pyramidane. The role of V_xc increases greatly for halogen bonded complexes which are comparable in energy with those characterized by chalcogen and pnicogen bonds. Within this group the xc term surpasses the classic term. Among hydrogen bonded dimers the balance between these two contributions is shifted once to one side and once to the other. For example, for the dimers with HF as Lewis acid the classic term is significantly higher while the reverse is true for the HI dimers with 111P and 222P.

The bulk of the charge transfer stabilization of these complexes is predicated on the idea that the occupied orbitals of the strained C systems can overlap with and transfer a certain amount of electron density into the vacant σ* antibonding orbitals of the approaching Lewis acid. The energetic aspect of this transfer is quantified via NBO second order perturbation theory into the E2 values listed in the first column of Table 7 for transfer originating in the σ(C_aC_a) orbital of the hydrocarbon. This transfer is complemented by transfer from the C_aC_e bonding orbitals between the apical C and its immediate equatorial neighbors. But there is another appreciable contribution from charge transferring in the opposite direction, from a lone pair of the A atom to the vacant σ*(CC) orbitals depicted in the lower half of Fig. 2. The third column of Table 7 shows that these contributions can be sizable, even if smaller than the prior set. Given the smaller values of the reverse charge transfers it is not surprising that the net transfer brings excess density to the Lewis acid, consistent with the positive values of CT in Table 4 for the 111P complexes.

Table 7 NBO E2 energies (kcal mol⁻¹) for interorbital transfers

	111P			222P
a From σ(HX). b Donation from Ca lone pair. c Sum of donations from 4σ(TF). d NBO conflates X atom with 222P. e NBO treats F atoms as separate molecular units.
Dimer	CaCa → σ*AF	ΣCaCe → σ*AF	Alp → σ*CC	CaCa → σ*AF	ΣCaCe → σ*AF	Alp → σ*CC
HF	5.1	2.2	1.6^a	0.7	1.0	1.5^a
HCl	4.1	2.4	1.6^a	0.5	1.9	1.6^a
HBr	5.2	3.9	2.6^a	0.5	2.5	1.9^a
HI	5.4	4.3	3.4^a	0.4	2.5	2.0^a
HCN	2.0	0.8	0.7^a	0.2	0.9	1.2^a
FCl	4.9	3.0	5.4	—^d	—	—
FBr	10.8	7.4	10.1	—^d	—	—
FI	10.7	8.1	9.3	—^d	—	—
SF2	1.6	1.0	1.6	0.3	0.8	2.8
SeF2	3.6	2.2	4.0	0.4	1.2	3.0
TeF2	5.4	2.5	6.1	0.4	1.2	1.2
PF3	0.5	0.1	1.3	0.1	—	1.9
AsF3	1.5	1.0	2.3	0.1	0.5	2.3
SbF3	2.8	1.2	4.2	0.2	0.4	2.6
GeF4	15.5^b	5.0	2.1^c	24.0^b	4.8	—
SnF4	12.3^b	5.6	1.1^c	15.7^b	2.9	—
PbF4	9.9^b	4.1	1.1^c	—^e	—	—

---

The situation is a bit different for 222P. The transfer energies for charge shift to the Lewis acid are generally much smaller. And there are cases where the reverse transfer in the last column outweighs the forward transfers, it is consequently sensible that the CT values for 222P in Table 4 are quite small, and indeed several are negative in sign, suggesting more charge moving in the reverse than in the forward direction.

One can achieve a more visual picture of the charge shifts occurring within the complexes via electron density shift diagrams. Such diagrams are presented in Fig. 5 for the halogen-bonded IF complexes in the top row, and the AsF₃ pnicogen bonds in the lower section. Each diagram was generated by subtracting the densities of the two component subunits from that of the full dyad, without moving any of the atoms. Purple regions denote electron density accrual, and losses are signaled by green. So as to be consistent, all diagrams visualize the same ±0.002 au contour.

Fig. 5 Electron density shift diagrams of FI with (a) 111P, (b) 222P, and (c) pyramidane. Purple and green colors indicate regions of gain and loss of density, respectively. (d–f) Complexes with AsF₃. Contour shown is ±0.002 au.

In general, the density shift patterns are consistent with the standard mappings anticipated for halogen and pnicogen bonds. There is an internal polarization within both molecules from left to right consistent with the overall direction of charge shift. A purple charge buildup occurs between the C and I/As atom, commensurate with the formation of a noncovalent bond. There is a certain level of agreement between the magnitudes of the charge shifts signaled by the sizes of the green and purple domains, and the total charge transfer CT listed in Table 4. CT is fairly small for 111P⋯AsF₃ and the colored regions in Fig. 5d are reduced accordingly. These areas nearly vanish entirely in Fig. 4e for the 222P dyad, which is consistent with the small negative CT quantity. The pyramidane complex with AsF₃ has a larger CT which is reflected in the enlarged domains in Fig. 5f.

Discussion

The ability of the C atom to serve as electron donor, particularly within the context of a hydrocarbon with nonpolar C–C and C–H bonds is quite limited. With no lone pair, the source of any electron donation from C is usually limited to the C–C π bonds of alkenes and alkynes. Also available to some extent would be the spatially extended π-clouds of conjugated systems or aromatic rings. The noncovalent bonding of these systems are usually dominated by London dispersion, as the lack of polar bonds limits any coulombic contribution. The hydrocarbon systems examined here do not have the benefit of either of these possibilities. The fully saturated bonding pattern provides no π-bonding, nor does it contain a lone pair on any of the C atoms. The ability of these systems to act as effective electron donor in a variety of different noncovalent bonds is thus highly notable.

There are several aspects of these strained systems that are responsible. In the first place, a substantial negative region of electrostatic potential appears on the bridgehead C that is capable of attracting an electrophile. The magnitude of this negative MEP rises along with the degree of strain imposed on the C. This strain is quite large for the apex of the square pyramidane, reduced somewhat for 111P, but is even significant for 222P, which contains the least strain. A second manifestation of the internal strain is the appearance of an orbital that is ideally disposed to transfer charge to an electrophile. This orbital has all the characteristics of a C lone pair for pyramidane. Indeed, NBO characterizes this orbital as a lone pair with 1.976 e occupancy. This orbital is best characterized as a σ(C_aC_a) bond in 111P, but with prominent lobes that extend some distance from each C, which mimics in some ways the disposition of lone pairs. This orbital looks much the same in 222P, but its effect is a bit muted in that it does not appear as an ELF, as it does in the other two systems. For these reasons, this electron-donating orbital can be collectively thought of as a pseudo lone pair, or perhaps as a σ(CC) bond.

It would thus be of interest to draw comparisons with a class of molecules which contain a bona fide lone pair on a C atom. The CR₂ carbene class of molecules fulfills this role with a true lone pair on its central C. The ability of carbenes to serve as electron donor has engendered a significant body of computational literature⁸⁶ with which to compare the data here. Early on, Alkorta et al.⁸⁷ had shown the importance of charge transfer and polarization when carbenes are paired with CO₂ and NCCN, with interaction energies as high as 4 kcal mol⁻¹. Li et al.⁸⁸ considered carbenes as electron donor within the context of a Br⋯C XB, with interaction energies reaching as high as 5.1 kcal mol⁻¹, and found orbital interactions supply a fair share of the binding, not unlike the halogen bonds described here. Halogen bonding by CH₂ was reexamined more thoroughly considering Cl, Br, and I as electron acceptor atoms soon thereafter,⁸⁹ with interaction energies ranging between 2 and 10 kcal mol⁻¹, generally smaller than the values approaching 30 kcal mol⁻¹ for 222P and pyramidane. The carbene was enlarged to N-heterocyclic⁹⁰ where it was found that in some cases the XB could shorten and strengthen into a covalent C–X bond. A variety of carbenes engaged in a XB with Cl,⁹¹ with strengths up to about 6 kcal mol⁻¹. Grabowski⁹² has recently shown that imidazol-2-yliden forms XBs with XCCH, XCN, and X₂ through the C lone pair, and that some can cross the borderline into covalent bonding, with interaction energies exceeding 60 kcal mol⁻¹, even larger than the XB strengths found here. These XBs involving carbenes have some potential applications, e.g. producing a strong reduction of isocyanide odor.⁹³

Carbenes are not limited to halogen bonds. It was shown⁹⁴ that CH₂ could engage in a chalcogen bond with the S center of several molecules, but with only fairly small interaction energies, less than 2 kcal mol⁻¹, much smaller than the YBs discussed above. Chalcogen bonds of this type were later verified⁹⁵ experimentally in the context of N-heterocyclic carbenes (NHCs). Tetrel atoms heavier than C also contain a lone pair in the corresponding metallylenes. The YBs they form with OCY vary in strength up to a maximum of 23 kcal mol⁻¹.

The possibility of a Si⋯N tetrel bond between a NHC and SiR₄ was suggested in 2016,⁹⁶ leading to energies as high as 20 kcal mol⁻¹, smaller than the 26–57 kcal mol⁻¹ range of the pseudo lone pairs considered above. The theme of tetrel bonding to carbenes was expanded soon thereafter,^97,98 in this case C⋯C TBs to the central atom of CO₂, leading to binding of up to 6 kcal mol⁻¹. If able to overcome an energy barrier, these bonds can morph into shorter and stronger covalent bonds. Similar calculations⁹⁹ found NHCs as particularly potent in this regard, binding by some 25 kcal mol⁻¹ to the heavier tetrel atoms, with a particularly high degree of charge transfer. There is a heavy dependence upon dispersion for the weaker bonds which shifts toward polarization energy as the bond gains strength. The TB formed by the NHC imidazol-2-ylidene to various tetrel atoms lies in the range between 11 and 17 kcal mol⁻¹;¹⁰⁰ the C lone pair is more attractive to the incoming Lewis acid than are the N lone pairs on the adjacent atoms. As a further point of comparison, the C lone pair is also more attractive to an electrophile than is the 3-center BCB bond of boron-substituted carbenes.¹⁰¹

This list of noncovalent bonding has expanded to encompass pnicogen bonds,¹⁰² again with NHCs, and these bond energies could exceed 20 kcal mol⁻¹, placing them a bit stronger than the ZBs to the strained hydrocarbons. Consideration of other aspects of the interaction suggested a high degree of covalency in several of them. Work following soon thereafter¹⁰³ verified these pnicogen bonds, this time in the context of P⋯C, with binding energies also in the 20 kcal mol⁻¹ range for the C(NH₂)₂ carbene. Lin et al.¹⁰⁴ had compared pnicogen and tetrel bonds to carbenes, finding the latter tend to be stronger, consistent with our own findings.

Carbenes are not limited to these particular noncovalent bonds, but can function as electron donor within triel¹⁰⁵ and spodium bonds,^106,107 with interaction energies in the 18–27 kcal mol⁻¹ range. And like all noncovalent bonds in this category, interactions with carbenes can also be enhanced by charge assistance if the electron acceptor is positively charged¹⁰⁸ which can ramp the energy up to 12–27 kcal mol⁻¹. Grabowski¹⁰⁹ showed that as the C atom of a carbene is replaced by heavier tetrel atoms in that family, the negative potential in its lone pair area is replaced by a positive region, preventing them from serving as electron donors.

Altogether then, it would appear that the pseudo lone pairs of the strained tetravalent C atoms are capable of forming bonds of all types. These bonds are every bit as strong, and frequently stronger, than those involving the C lone pairs of divalent carbenes. In either case, there are certain interactions, e.g. those with tetrel atoms as electron acceptors where the bond borders on covalency. This bond strengthening arising from strain around the central atom is of a piece with other recent work^54,110 that has documented a similar phenomenon that occurs when the three substituents attached to a central pnicogen atom are drawn in toward one another. However, there are distinct differences as well. The central pnicogen atom contains positive σ-holes that are deepened by the strain, allowing a stronger interaction with a base. The bending of the bonds around the central C atom here from their optimum locations yields a higher negatively charged region, and the appearance of an orbital that closely resembles a C lone pair, which can in turn overlap with the σ* orbital of an approaching electrophile.

With regard to the propellanes, early calculations^{59,60,62,63,111} had confirmed the orbital between the two bridgehead C atoms of 111P to have the spatial distribution illustrated in Fig. 2a. Other calculations by Joy et al.⁶⁵ had earlier noted the negative potentials that accumulate near their bridgehead C atoms, as well as the characteristics of their HOMOs that agree with our own Fig. 2a and b. These authors had considered halogen bonding simultaneously by two Lewis acids, one on each bridgehead C, finding the bonding to 222P considerably stronger than that to 111P, in line with the data in Table 3. One difference between the two sets of calculations concerns the 222P molecule. Joy et al. had found two minima, which they designated as o and c, where the distance between bridgehead C atoms is 1 Å longer in the former. Our own calculations found that the former collapsed into the latter upon optimization, and that the o form only appears for the triplet state, which is higher in energy than the c singlet by 12 kcal mol⁻¹. More recently, Veljković et al.⁶⁶ examined the interaction of water with pyramidane, and observed a strong OH⋯C HB to the strained C at the apex of the pyramid. The interaction energy of 6.4 kcal mol⁻¹ is somewhat weaker than the XH⋯C HBs examined here. Our findings that electrostatics offer a large share of the full interaction energy are in full agreement with both of these earlier works. There is also precedent for the 111P molecule acting as electron donor to a coinage metal atom¹¹² with a mechanism very much like that described above, with interaction energies in the range between 13 and 45 kcal mol⁻¹. These authors also found evidence of a certain amount of back transfer from a lone pair of the M to σ*(CC) antibonding orbitals within the propellane.

As in many situations of this type, drawing a clear distinction between a covalent and noncovalent bond can be a nettlesome problem. This categorization is sometimes based on the distance between the atoms, or perhaps rests on certain of the AIM parameters. Other thresholds have been proposed that are based on Pauli energy^113,114 or certain bond indices such as Wiberg¹¹⁵ or BNI and USI.¹¹⁶ Another set of criteria considers the distance along the bond path between the minima of the density and the molecular electrostatic potential.¹¹⁷ There is also the question of polarity and how that influences the balance between wave function interference and coulomb attraction of the charge that might accumulate in the region between the nuclei.¹¹⁸ It should be understood that regardless of its technical classification, chemical bonding arises chiefly from constructive interference between the wavefunctions which leads to an accumulation of electron density in the region between the nuclei. Rioux¹¹⁹ describes this phenomenon in terms of a balance between kinetic and potential energy. The finding here that these interactions contain a large electrostatic component does not necessarily point toward noncovalency, as it arises mainly from interactions between the positive charge of the Lewis acid and the negative charge cloud of the Lewis base, and accompanying overlapping of the charge distribution. As such, one would not categorize the interaction here as ionic, which occurs primarily in ionic solids and in ionic solution. Further, there are arguments to be made that there is really no distinction between covalent and noncovalent bonds.¹²⁰

Conclusions

The strain placed on the bridgehead C atom of 111 and 222 propellane leads to the development of a negative electrostatic potential on this atom, with an occupied molecular orbital that resembles a C lone pair, even though each C is tetravalently bonded. The same is true for pyramidane which takes on a square pyramid shape. Each of these three molecules is able to act as electron donor in a host of interactions, including hydrogen, halogen, chalcogen, pnicogen, and tetrel bonds. The latter are particularly strong, on the border of covalent bonding, and the halogen bonds are quite strong as well. In general, pyramidane has the most intensely negative potential, followed by 111 and then 222 propellane. The bond strengths generally follow this same pattern.

With regard to internal geometric perturbations, the CC bond of the 111 propellane between the two bridgehead C atoms shortens as a result of the intermolecular interaction, while the bonds to the equatorial atoms grow longer. Pyramidane is different in that all internal C–C bonds contract due to the interaction. 222 propellane is unique in that the bond between bridgehead atoms is lengthened in all cases, but by a great deal, nearly a full Å, for the halogen and tetrel bonds.

Careful analysis of the electronic structure within the complexes suggests that the electron transfer from the C pseudo lone pair to the various Lewis acids is present in all complexes. However, there is a second bonding phenomenon, in which charge is transferred in the reverse direction, from a lone pair of the Lewis acid central atom to σ*(CC) antibonding orbitals within the propellanes. The former is much stronger than the latter for 111 propellane, but there are several cases involving the 222 variant where the latter reverse transfer outcompetes the former.

It should be reiterated that the strong bonding arises in the context of a tetravalent C atom. Since this atom has no formal lone pair, nor is it part of a π-system, such bonding is quite remarkable. While this C is under a good deal of strain in the context of these particular systems, it is expected that lesser degrees of strain will facilitate such bonding, even if not quite as strong.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

Conceptualization – S. S. data curation – M. M., W. Z., investigation – S. S., M. M., W. Z., visualization – S. S., M. M., W. Z., supervision – S. S., W. Z., funding acquisition – S. S., W. Z., validation – M. M., W. Z., writing – original draft – S. S., writing – review & editing – S. S., M. M., W. Z.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge Polish high-performance computing infrastructure PLGrid (HPC Centers: ACK Cyfronet AGH) for providing computer facilities and support within computational grant no. PLG/2023/016853, Wrocław Center for Networking and Supercomputing (WCSS). This material is also based upon work supported by the U.S. National Science Foundation under Grant No. 1954310 to SS. This work was financed in part by a statutory activity subsidy from the Polish Ministry of Science and Higher Education for the Faculty of Chemistry of Wroclaw University of Science and Technology.

References

1. G. C. Pimentel and A. L. McClellan, The Hydrogen Bond, Freeman, San Francisco, 1960.
2. S. N. Vinogradov and R. H. Linnell, Hydrogen Bonding, Van Nostrand-Reinhold, New York, 1971.
3. M. D. Joesten and L. J. Schaad, Hydrogen Bonding, Marcel Dekker, New York, 1974.
4. E. Arunan, G. R. Desiraju, R. A. Klein, J. Sadlej, S. Scheiner, I. Alkorta, D. C. Clary, R. H. Crabtree, J. J. Dannenberg, P. Hobza, H. G. Kjaergaard, A. C. Legon, B. Mennucci and D. J. Nesbitt, Pure Appl. Chem., 2011, 83, 1637–1641.
5. S. J. Grabowski, Hydrogen Bonding – New Insights, Springer, Dordrecht, Netherlands, 2006.
6. A. Chand, D. K. Sahoo, A. Rana, S. Jena and H. S. Biswal, Acc. Chem. Res., 2020, 53, 1580–1592.
7. K. K. Mishra, S. K. Singh, S. Kumar, G. Singh, B. Sarkar, M. S. Madhusudhan and A. Das, J. Phys. Chem. A, 2019, 123, 5995–6002.
8. H. S. Biswal and S. Wategaonkar, J. Chem. Phys., 2011, 135, 134306.
9. E. A. Hillenbrand and S. Scheiner, J. Am. Chem. Soc., 1984, 106, 6266–6273.
10. S. M. Cybulski and S. Scheiner, Chem. Phys. Lett., 1990, 166, 57–64.
11. E. Gougoula, C. Medcraft, I. Alkorta, N. R. Walker and A. C. Legon, J. Chem. Phys., 2019, 150, 084307.
12. I. Alkorta and A. Legon, Molecules, 2018, 23, 2250.
13. S. J. Grabowski, Struct. Chem., 2019, 30, 1141–1152.
14. S. Grabowski, Molecules, 2018, 23, 1183.
15. S. Scheiner, Phys. Chem. Chem. Phys., 2024, 26, 27382–27394.
16. A. Franconetti and A. Frontera, Chem.–Eur. J., 2019, 25, 6007–6013.
17. A. Frontera and A. Bauzá, Chem.–Eur. J., 2018, 24, 16582–16587.
18. T. Clark, J. S. Murray and P. Politzer, Phys. Chem. Chem. Phys., 2018, 20, 30076–30082.
19. K. E. Riley and K.-A. Tran, Faraday Discuss., 2017, 203, 47–60.
20. W. Zierkiewicz, M. Michalczyk, R. Wysokiński and S. Scheiner, Molecules, 2019, 24, 376.
21. W. Dong, Y. Wang, J. Cheng, X. Yang and Q. Li, Mol. Phys., 2019, 117, 251–259.
22. R. Sedlak, S. M. Eyrilmez, P. Hobza and D. Nachtigallova, Phys. Chem. Chem. Phys., 2018, 20, 299–306.
23. M. Esrafili and P. Mousavian, Molecules, 2018, 23, 2642.
24. S. Scheiner and U. Adhikari, J. Phys. Chem. A, 2011, 115, 11101–11110.
25. G. Chalasinski, S. M. Cybulski, M. M. Szczesniak and S. Scheiner, J. Chem. Phys., 1989, 91, 7809–7817.
26. Z. Latajka and S. Scheiner, J. Chem. Phys., 1984, 81, 407–409.
27. A. Bauzá, I. Alkorta, J. Elguero, T. J. Mooibroek and A. Frontera, Angew. Chem., Int. Ed., 2020, 59, 17482–17487.
28. A. Daolio, A. Pizzi, M. Calabrese, G. Terraneo, S. Bordignon, A. Frontera and G. Resnati, Angew. Chem., Int. Ed., 2021, 60, 20723–20727.
29. S. Burguera, R. M. Gomila, A. Bauzá and A. Frontera, Crystals, 2023, 13, 187.
30. A. Daolio, A. Pizzi, G. Terraneo, A. Frontera and G. Resnati, ChemPhysChem, 2021, 22, 2281–2285.
31. R. M. Gomila and A. Frontera, Molecules, 2022, 27, 6597.
32. M. Calabrese, A. Pizzi, A. Daolio, R. Beccaria, C. Lo Iacono, S. Scheiner and G. Resnati, Chem.–Eur. J., 2024, e202304240.
33. X. Wang, Q. Li and S. Scheiner, Molecules, 2024, 29, 79.
34. H. S. Biswal, A. Kumar Sahu, A. Frontera and A. Bauzá, J. Chem. Inf. Model., 2021, 61, 3945–3954.
35. V. R. Boro, B. K. Saha and G. Rangazhvar, Chem. Commun., 2025, 61, 945–948.
36. A. V. Rozhkov, E. Y. Tupikina, K. I. Tugashov and V. Y. Kukushkin, CrystEngComm, 2024, 26, 5607–5616.
37. S. Burguera, A. K. Sahu, M. J. Chávez Romero, H. S. Biswal and A. Bauzá, Phys. Chem. Chem. Phys., 2024, 26, 18606–18613.
38. R. M. Gomila and A. Frontera, Dalton Trans., 2025, 54, 3095–3105.
39. H. Yu, Q. Zhao, K. Wang, M. Fu, L. Ning, W. Chen, M. Guan, Z. Han, Y. Yang, H. Li and M. Gao, ChemistrySelect, 2025, 10, e202401049.
40. A. Frontera and S. Emamian, J. Phys. Chem. A, 2025, 129, 1368–1385.
41. M. U. Engelhardt, M. O. Zimmermann, M. Dammann, J. Stahlecker, A. Poso, T. Kronenberger, C. Kunick, T. Stehle and F. M. Boeckler, J. Chem. Theory Comput., 2024, 20, 10716–10730.
42. R. D. Parra, Inorganics, 2024, 12, 161.
43. R. D. Parra, Inorganics, 2024, 12, 16.
44. Z. Wang, Z. Cao, A. Hao and P. Xing, Chem. Sci., 2024, 15, 6924–6933.
45. Y. V. Torubaev and I. V. Skabitsky, Cryst. Growth Des., 2024, 24, 8319–8333.
46. H. Wang, J. Chen, M. Hong, J. Kang, Y. Jiang, Q. Tian, X. Xu, H. Wang, Z. Zhang, X. Liu, X. Wen and Q. Gou, J. Phys. Chem. Lett., 2024, 15, 8636–8641.
47. C. R. Travis, R. G. Dumais, J. W. Treacy, K. M. Kean, K. N. Houk and M. L. Waters, J. Am. Chem. Soc., 2024, 146, 20678–20684.
48. S. Burguera, M. d. l. N. Piña and A. Bauzá, Phys. Chem. Chem. Phys., 2024, 26, 20522–20529.
49. S. J. Grabowski, J. Phys. Org. Chem., 2013, 26, 452–459.
50. S. J. Grabowski, Understanding Hydrogen Bonds: Theoretical and Experimental Views, Royal Society of Chemistry, Cambridge, 2021.
51. S. J. Grabowski, ChemPhysChem, 2019, 20, 565–574.
52. I. Alkorta, C. Martín-Fernández, M. M. Montero-Campillo and J. Elguero, J. Phys. Chem. A, 2018, 122, 1472–1478.
53. J. Echeverría, CrystEngComm, 2017, 19, 6289–6296.
54. S. Scheiner, M. Michalczyk and W. Zierkiewicz, Inorg. Chem., 2023, 62, 20209–20218.
55. K. B. Wiberg, Chem. Rev., 1989, 89, 975–983.
56. M. D. Levin, P. Kaszynski and J. Michl, Chem. Rev., 2000, 100, 169–234.
57. R. Gianatassio, J. M. Lopchuk, J. Wang, C.-M. Pan, L. R. Malins, L. Prieto, T. A. Brandt, M. R. Collins, G. M. Gallego, N. W. Sach, J. E. Spangler, H. Zhu, J. Zhu and P. S. Baran, Science, 2016, 351, 241–246.
58. I. S. Makarov, C. E. Brocklehurst, K. Karaghiosoff, G. Koch and P. Knochel, Angew. Chem., Int. Ed., 2017, 56, 12774–12777.
59. A. J. Sterling, A. B. Dürr, R. C. Smith, E. A. Anderson and F. Duarte, Chem. Sci., 2020, 11, 4895–4903.
60. M. D. Newton and J. M. Schulman, J. Am. Chem. Soc., 1972, 94, 773–778.
61. K. B. Wiberg, J. Am. Chem. Soc., 1983, 105, 1227–1233.
62. J. E. Jackson and L. C. Allen, J. Am. Chem. Soc., 1984, 106, 591–599.
63. W. Wu, J. Gu, J. Song, S. Shaik and P. C. Hiberty, Angew. Chem., Int. Ed., 2009, 48, 1407–1410.
64. S. Shaik, D. Danovich, W. Wu and P. C. Hiberty, Nat. Chem., 2009, 1, 443–449.
65. J. Joy, E. Akhil and E. D. Jemmis, Phys. Chem. Chem. Phys., 2018, 20, 25792–25798.
66. I. S. Veljković, M. Malinić and D. Ž. Veljković, Phys. Chem. Chem. Phys., 2025, 27, 2563–2569.
67. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
68. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
69. Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167.
70. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
71. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Wallingford, CT, 2016.
72. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
73. T. Lu and F. Chen, J. Mol. Graphics Modell., 2012, 38, 314–323.
74. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
75. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
76. T. A. Keith, TK Gristmill Software, Overland Park KS2013.
77. R. F. W. Bader, Atoms in Molecules, A Quantum Theory, Clarendon Press, Oxford, 1990.
78. R. F. W. Bader, J. Phys. Chem. A, 1998, 102, 7314–7323.
79. F. Weinhold, C. R. Landis and E. D. Glendening, Int. Rev. Phys. Chem., 2016, 35, 399–440.
80. P. R. Horn, Y. Mao and M. Head-Gordon, Phys. Chem. Chem. Phys., 2016, 18, 23067–23079.
81. P. R. Horn, Y. Mao and M. Head-Gordon, J. Chem. Phys., 2016, 144, 114107.
82. T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., 1989, 36, 199–207.
83. A. Obeng and J. Autschbach, J. Chem. Theory Comput., 2024, 20, 4965–4976.
84. M. A. Blanco, A. Martín Pendás and E. Francisco, J. Chem. Theory Comput., 2005, 1, 1096–1109.
85. A. M. Pendás, J. L. Casals-Sainz and E. Francisco, Chem.–Eur. J., 2019, 25, 309–314.
86. S. Scheiner, Polyhedron, 2021, 193, 114905.
87. I. Alkorta, F. Blanco, J. Elguero, J. A. Dobado, S. M. Ferrer and I. Vidal, J. Phys. Chem. A, 2009, 113, 8387–8393.
88. Q. Li, Y. Wang, Z. Liu, W. Li, J. Cheng, B. Gong and J. Sun, Chem. Phys. Lett., 2009, 469, 48–51.
89. M. D. Esrafili and N. Mohammadirad, J. Mol. Model., 2013, 19, 2559–2566.
90. H. Lv, H.-Y. Zhuo, Q.-Z. Li, X. Yang, W.-Z. Li and J.-B. Cheng, Mol. Phys., 2014, 112, 3024–3032.
91. J. E. Del Bene, I. Alkorta and J. Elguero, Chem. Phys. Lett., 2017, 685, 338–343.
92. S. J. Grabowski, Phys. Chem. Chem. Phys., 2023, 25, 9636–9647.
93. A. S. Mikherdov, A. S. Novikov, V. P. Boyarskiy and V. Y. Kukushkin, Nat. Commun., 2020, 11, 2921.
94. Q. Zhao, D. Feng, Y. Sun, J. Hao and Z. Cai, Int. J. Quantum Chem., 2011, 111, 3881–3887.
95. P. Komorr, M. Olaru, E. Hupf, S. Mebs and J. Beckmann, Chem.–Eur. J., 2022, 28, e202201023.
96. D. Pathak, S. Deuri and P. Phukan, J. Phys. Chem. A, 2016, 120, 128–138.
97. J. E. Del Bene, I. Alkorta and J. Elguero, J. Phys. Chem. A, 2017, 121, 4039–4047.
98. J. E. Del Bene, I. Alkorta and J. Elguero, J. Phys. Chem. A, 2017, 121, 8136–8146.
99. M. Liu, Q. Li, W. Li and J. Cheng, Struct. Chem., 2017, 28, 823–831.
100. Y. Chen, L. Yao and F. Wang, Mol. Phys., 2023, 121, e2211906.
101. Y. Chen, L. Yao and F. Wang, Struct. Chem., 2024, 35, 485–496.
102. M. D. Esrafili, F. Mohammadian-Sabet and E. Vessally, Mol. Phys., 2016, 114, 2115–2122.
103. J. E. Del Bene, I. Alkorta and J. Elguero, ChemPhysChem, 2017, 18, 1597–1610.
104. H. Lin, L. Meng, X. Li, Y. Zeng and X. Zhang, New J. Chem., 2019, 43, 15596–15604.
105. Z. Chi, W. Dong, Q. Li, X. Yang, S. Scheiner and S. Liu, Int. J. Quantum Chem., 2019, 119, e25867.
106. M. Jabłoński, Materials, 2021, 14, 6147.
107. M. Jabłoński, Molecules, 2021, 26, 2275.
108. M. de las Nieves-Piña, A. Frontera, T. J. Mooibroek and A. Bauzá, ChemPhysChem, 2021, 22, 2478–2483.
109. S. J. Grabowski, Crystals, 2022, 12, 112.
110. S. Moaven, O. H. Villanueva, D. K. Unruh and A. F. Cozzolino, Dalton Trans., 2022, 51, 11335–11339.
111. D. Feller and E. R. Davidson, J. Am. Chem. Soc., 1987, 109, 4133–4139.
112. R. Wang, S. Yang and Q. Li, Molecules, 2019, 24, 2601.
113. S. Liu, C. Rong, T. Lu and H. Hu, J. Phys. Chem. A, 2018, 122, 3087–3095.
114. W. Zhang, X. He, M. Li, J. Zhang, D. Zhao, S. Liu and C. Rong, J. Chem. Phys., 2023, 159, 184104.
115. Y. Ge, A. Le, G. J. Marquino, P. Q. Nguyen, K. Trujillo, M. Schimelfenig and A. Noble, ACS Omega, 2019, 4, 18809–18819.
116. S. Zhong, X. He, S. Liu, B. Wang, T. Lu, C. Rong and S. Liu, J. Phys. Chem. A, 2022, 126, 2437–2444.
117. E. Bartashevich and V. Tsirelson, ChemPlusChem, 2025, 90, e202400617.
118. L. Zhao, S. Pan and G. Frenking, J. Chem. Phys., 2022, 157, 034105.
119. F. Rioux, Chem. Educ., 2003, 8, 1–3.
120. G. Roos, D. E. P. Vanpoucke and J. S. Murray, ChemPhysChem, 2025, 26, e202401065.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sc01632k

---