 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Molecular beam scattering of neon from flat jets of cold salty water†
Walt Yang ab,
Madison M. Foreman
ab,
Madison M. Foreman ab,
Tiffany C. Ly
ab,
Tiffany C. Ly a,
Kevin R. Wilson
a,
Kevin R. Wilson b and
Daniel M. Neumark
b and
Daniel M. Neumark *ab
*ab
aDepartment of Chemistry, University of California, Berkeley, CA 94720, USA. E-mail: dneumark@berkeley.edu
bChemical Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
First published on 30th May 2025
Abstract
Molecular beam scattering experiments are carried out to study collisions between Ne atoms (Ei = 24.3 kJ mol−1) and the surface of a cold salty water (8 m LiBr(aq), 230 K) flat jet. Translational energy distributions are collected as a function of scattering angle using a rotatable mass spectrometer. Impulsive scattering and thermal desorption contribute to the overall scattering distributions, but impulsive scattering dominates at all three incidence angles explored. Highly super-specular scattering is observed in the impulsive scattering channel that is attributed to anisotropic momentum transfer to the liquid surface. The thermal desorption channel exhibits a cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ angular distribution. Compared to Ne scattering from dodecane, fractional energy loss in the impulsive scattering channel is much larger across a wide range of deflection angles. A soft-sphere model is applied to investigate the kinematics of energy transfer between the scatterer and liquid surface. Fitting to this model yields an effective surface mass of 250−60+100 amu and internal excitation of 11.8 ± 1.6 kJ mol−1, both of which are considerably larger than for Ne/dodecane. It thus appears that energy transfer to cold salty water is more efficient than to a dodecane liquid surface, a result attributed to the extensive hydrogen-bonded network of liquid water and roughness of the liquid surface.
θ angular distribution. Compared to Ne scattering from dodecane, fractional energy loss in the impulsive scattering channel is much larger across a wide range of deflection angles. A soft-sphere model is applied to investigate the kinematics of energy transfer between the scatterer and liquid surface. Fitting to this model yields an effective surface mass of 250−60+100 amu and internal excitation of 11.8 ± 1.6 kJ mol−1, both of which are considerably larger than for Ne/dodecane. It thus appears that energy transfer to cold salty water is more efficient than to a dodecane liquid surface, a result attributed to the extensive hydrogen-bonded network of liquid water and roughness of the liquid surface.
1. Introduction
The air–water interface is an important chemical environment for a wide array of chemistries that occur in everyday life. Examples that impact the environment on a global scale include treatment of amine gases,1 formation of acid rain,2–4 and heterogeneous chemistry on aerosols such as the reactive uptake of N2O5 that, in turn, modulates ozone concentrations in the atmosphere.5–9 These considerations have motivated the development of novel surface-specific experimental methods to study chemical kinetics and dynamics at this unique interface.10–12Several spectroscopic techniques have been designed to characterize the surface region of aqueous solutions.13–15 Deep ultraviolet electronic sum frequency generation can probe the presence and photodynamics of ions at the interface through symmetry breaking considerations.16–24 Time-resolved second-harmonic generation spectroscopy has uncovered the dynamics of hydrated electrons at the air–water interface,25 while vibrational sum frequency generation spectroscopy has been applied to a wide range of problems including charged water structures at the interface,26–31 the interfacial assembly of proteins,32 and electric double layer dynamics.33 Extreme ultraviolet photoelectron spectroscopy has determined interfacial densities of aromatic compounds,34,35 while X-ray photoemission spectroscopy has been used to elucidate specific ion effects at aqueous solution–vapor interfaces.36,37 Augmented reaction rates compared to those in bulk liquids have been reported through studies on thin liquid films and microdroplets.38–40
Molecular beam scattering serves as a complementary method to these techniques and has been incorporated by Nathanson, Minton, McKendrick, Nesbitt, and others into experiments that probe interfacial interactions on a wide variety of liquid surfaces. These experiments were enabled by the development of the wetted wheel by Fenn and Siegbahn as a method to introduce continually-refreshed liquid surfaces into high-vacuum environments.41,42 Experiments by Faubel and others on liquid microjets43–45 further advanced the field, unlocking the ability to investigate interfacial interactions on more volatile liquids46 and thus the vapor–water interface.47 Relevant experiments include scattering of HCl, DCl, and N2O5 from highly concentrated salty water microjets.48–50 More complex studies have also been undertaken, including observing solvated electron chemistries at the surface of water using a microjet.51 Additionally, surface structures of fluorinated and ionic liquids on a wetted wheel have been deduced through reactive-atom scattering combined with laser-induced fluorescence52–55 and rotationally resolved scattering studies.56,57
We have recently utilized commercially available microfluidic chips58 to create flat jets of volatile liquids in a molecular beam scattering apparatus. Compared to a cylindrical jet, for which the diameter is typically 30 μm, flat jets present a larger scattering target that is more compatible with the dimensions of a molecular beam. Moreover, the well-defined surface normal of a flat jet facilitates the measurement of angular distributions in a scattering experiment.
We have previously performed molecular beam scattering from dodecane flat liquid jets59–62 (Pvap = 1.5 × 10−2 Torr at 275 K), in which we reported the angular and translational energy distributions of Ne, CD4, ND3, and D2O evaporating and scattering from dodecane at various scattering geometries.59–61 In a recent review article,62 we also presented preliminary findings on the evaporation and scattering of Ar from a cold aqueous 8 molal LiBr flat jet (Pvap = 4.2 × 10−2 Torr at 223 K).
For both solvents, the evaporation experiments indicated that the vapor jacket surrounding the jet was sufficiently dilute for scattering experiments to be feasible. Using precedent set by prior gas–solid63,64 and gas–liquid65 scattering experiments, we characterized two scattering mechanisms at the gas–liquid interface: impulsive scattering (IS) and thermal desorption (TD). Key characteristics for each of these channels are expected in angle-resolved measurements, where IS exhibits near-specular scattering governed by initial conditions while TD yields cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ angular distributions with respect to the surface normal.63,65–67
θ angular distributions with respect to the surface normal.63,65–67
In our dodecane studies, we determined that the physical properties of the scatterers heavily influenced the observed branching ratios between IS and TD. Extracted TD fractions correlated with solubility trends from literature values, and all four scatterers exhibited slightly super-specular scattering behavior in the IS channel. Ne scattering from squalane was previously simulated using classical trajectory calculations,68 and our Ne scattering results from dodecane were semiquantitatively produced through molecular dynamics (MD) simulations by Li and co-workers.69 From the exploratory results of Ar scattering from cold salty water, the TD channel was favored more than in Ne scattering from dodecane, which may be due to a higher trapping probability at the cold salty water interface, the scatterer identity, or both.
In this work, we extend our capabilities to molecular beam scattering from aqueous solutions and present the first angle-resolved scattering measurements of Ne from a flat jet of cold salty water. Highly super-specular scattering behavior dominates at each scattering geometry that is attributed to anisotropic momentum transfer to the surface. The TD channel exhibits a characteristic cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ angular distribution and the TD fractions are similar to those reported for dodecane. Fitting the fractional energy loss in the IS channel to a soft-sphere kinematic model as a function of deflection angle shows that energy transfer to internal modes of the salty water surface is larger compared to the internal excitation of dodecane at similar beam energies.
θ angular distribution and the TD fractions are similar to those reported for dodecane. Fitting the fractional energy loss in the IS channel to a soft-sphere kinematic model as a function of deflection angle shows that energy transfer to internal modes of the salty water surface is larger compared to the internal excitation of dodecane at similar beam energies.
2. Experimental methods
The scattering experiments are conducted with a crossed molecular beam apparatus70,71 modified for gas–liquid scattering as described previously.59,62 Briefly, the apparatus comprises three vacuum regions: a source chamber in which the molecular beam is created, a collision chamber where scattering with the liquid sample takes place, and a rotatable detector chamber housed within the collision chamber that contains an electron impact ionizer (80 eV electron kinetic energy), a quadrupole mass filter, and an ion detection assembly. The incidence angle θi of the beam with respect to the liquid surface normal is chosen to be 45°, 60°, or 75° by rotation of the chip holder. The scattering angle θf is also defined with respect to the surface normal, and the deflection angle follows as χ = 180° − (θi + θf). The scattering angle is confined to a range between 90° − θi and 90° due to the geometry of the apparatus.A pulsed supersonic (SS) molecular beam of 10% Ne seeded in He is produced by a piezoelectric valve (MassSpecpecD BV, Enschede).72,73 Stagnation conditions are typically 295 K and 3000 Torr, resulting in a beam velocity of 1572 ± 185 m s−1 (FWHM) with a mean Ne translational energy of 24.3 kJ mol−1. These values are derived from beam characterization via time-of-flight (TOF) measurements with a rotating (200 Hz) chopper wheel (two slits, 14 μs open time).
The cold salty water flat jet is formed in the collision chamber using a commercially available microfluidic chip.58 The liquid sample is initially prepared by vacuum-degassing 8 m LiBr dissolved in H2O (Milli-Q, MilliporeSigma) with pure He. This is done in a 2.3 L glass cylinder housed in a high-pressure stainless-steel reservoir. To deliver the solution with a flow rate of ∼2 mL min−1 and a temperature of ∼225 K at the interaction region, the reservoir is pressurized with pure helium to between 80 and 90 bar. A high-resolution camera captures calibrated images of the jet in operation, and typical dimensions of the first flat jet leaf are 0.4 × 1.2 mm2 (W × H). The thickness of the jet is not directly measured, but is estimated to be ∼1.5 μm at the center and thicker at the rims for pure water.45 These experimental conditions lead to a flow velocity of ∼7 m s−1. This velocity and the length of the jet leaf limit the detector viewing time to ∼150 μs. A 1.5 mm circular aperture is used at the detector entrance for all scattering experiments. Much of the collision chamber interior is covered with a liquid nitrogen-cooled copper wall that serves to both reduce the pressure inside the chamber by adsorbing gas particles on its surface and function as a heat sink for the liquid jet assembly through a connected Cu framework.
Numerous modifications to the liquid delivery setup were made since performing the dodecane experiments. The liquid passes through an in-line stainless-steel counter-current precooling stage ∼1 m in length held at 235 K by the use of a circulating LN2-cooled ethanol bath (Xylem Rule iL280P). In the collision chamber, the liquid is further cooled at the stainless-steel/marine-grade 464 brass chip holder to which flexible tinned Cu braids are attached. The braids are mounted to an extension of the cryogenically cooled Cu wall within the collision chamber and are designed such that they do not hinder rotation of the chip. The temperature of the chip holder Tholder is recorded by a thermocouple, and the temperature difference Tholder − Tliq (the true liquid temperature at the interaction region) is estimated to be less than 3 °C due to the relatively low vapor pressure of the solution at Tholder.47,49 For Ne scattering at θi = 45°, 60°, and 75°, Tholder was measured to be 230 ± 1 K (Pvap = 7.6 × 10−2 Torr).
TOF measurements determine the translational energy distributions of scattered species at each scattering angle. Time zero is defined as the moment when the most intense part of the pulsed molecular beam reaches the interaction region. The temporal resolution of these measurements is then limited by the duration of the pulsed beam. For the Ne beam, the valve opening time is set to 15 μs, resulting in a measured temporal width at the detector of 29 μs. “Beam-off” data are subtracted from “beam-on” data, and TOF profiles are measured in a back-and-forth manner to achieve background-subtracted scattering spectra and thus intensity-calibrated angular distributions by calibrating to the θf = 90° spectra due to the high signal-to-noise ratio present at that angle. When generating the angular distributions, the first set of spectra collected when the detector is initially exposed to the scattered products is typically discarded due to substantial improvement in detector signal stability over time. Total acquisition times in the case of Ne scattering are typically between 20 and 40 min for a single spectrum.
3. Results and analysis
3.1. Scattering
TOF spectra of Ne scattered from a cold salty water jet are shown in Fig. 1a–c at incidence angles θi = 45°, 60°, and 75° for select detector angles. TOF spectra for other detector angles are shown in Fig. S1.† Angular distributions are shown in Fig. 2a–c for these three incidence angles and are derived from integrating the fitted TOF spectra. As θf increases, the TOF spectra shift toward earlier arrival times for all incidence angles. Additionally, the TOF spectra overall shift slightly toward earlier arrival times as θi increases across similar values of θf.The TOF profiles are fitted using two components assigned to a faster contribution from IS and a slower one from TD following our previous work on scattering from a dodecane jet.62 The IS mechanistic channel is modeled by a flux distribution for a supersonic (SS) molecular beam,74,75
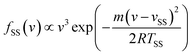 | (1) |
 | (2) |
This fitting methodology is supported by measurements demonstrating Maxwellian behavior of Ar atoms evaporating from a salty water cylindrical jet at 237 K76 and was used to interpret our results on Ar evaporation from a cold salty water flat jet at 226 K, where near-Maxwellian behavior was observed at various values of θf with an overall cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θf angular distribution.62 Further, we assume a sticking coefficient of unity66 and limited interaction with the vapor sheath around the jet, consistent with scattering experiments that sample nascent scattering signal.
θf angular distribution.62 Further, we assume a sticking coefficient of unity66 and limited interaction with the vapor sheath around the jet, consistent with scattering experiments that sample nascent scattering signal.
The scattering TOF spectra are fitted with a linear combination of SS and MB distributions describing the IS and TD scattering pathways, respectively.65,77 In the TD channel, Tliq is assumed to be equal to Tholder, the value of which is reported in the previous section. Convolution with the molecular beam temporal profiles is carried out in the fitting procedure. The resulting best-fit SS and MB contributions are shown as red and blue traces, respectively, in Fig. 1a–c. These fits are also shown in Fig. S1† for other detector angles. Across all incidence angles θi, the relative contribution from TD decreases as θf increases. This trend, and the narrowing of the TOF distributions as θf increases, reflect the cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θf angular distribution for TD. Additionally, as θi increases toward more grazing incoming trajectories for a given θf, the IS/TD ratio increases, once again leading to narrower TOF profiles.
θf angular distribution for TD. Additionally, as θi increases toward more grazing incoming trajectories for a given θf, the IS/TD ratio increases, once again leading to narrower TOF profiles.
Fig. 2a–c shows the angular dependencies of the integrated IS and TD fits for θi = 45°, 60°, and 75°. The TD angular distributions are easier to discern in the zoomed-in angular plots shown in Fig. S2.† For all three incidence angles, the IS channel exhibits a strong deviation from the specular scattering expected for elastic collisions. Instead, super-specular scattering is observed, where the maximum intensity of the IS channel is at θf = 90°. However, for θi = 75°, where the effective target area of the flat jet is smallest, the TOF profiles for θf = 85° and 90° are contaminated from signal due to part of the molecular beam passing by the edge of the jet and subsequently entering the detector chamber; this “beam leakage” artificially enhances the signal near 90°. This is also observed for θi = 60° and θf = 90°.
Inspecting the angular dependence of the TD channel at θi = 45° shows that it follows a cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θf angular distribution, demonstrating that trapped Ne atoms undergo thermal equilibration with the liquid surface prior to desorption, akin to evaporation. Similar but less definitive results are observed for θi = 60° and 75° (see Fig. S2†). The cos
θf angular distribution, demonstrating that trapped Ne atoms undergo thermal equilibration with the liquid surface prior to desorption, akin to evaporation. Similar but less definitive results are observed for θi = 60° and 75° (see Fig. S2†). The cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θf angular distributions for TD imply that the vapor sheath around the jet does not significantly distort the nascent scattering signal. Overall, the increase in IS/TD ratios as both θi and θf increase is consistent with other gas–liquid scattering experiments.62,78–80
θf angular distributions for TD imply that the vapor sheath around the jet does not significantly distort the nascent scattering signal. Overall, the increase in IS/TD ratios as both θi and θf increase is consistent with other gas–liquid scattering experiments.62,78–80
The TD fraction, defined as TD/(TD + IS) using the integrated intensities of each fitted curve, is plotted as a function of incidence angle θi and deflection angle χ for Ne scattering from cold salty water in Fig. 3 and 4, respectively. Our previous results scattering from dodecane62 are also shown for reference. As was reported for dodecane, the TD fraction decreases as θi increases. This was also observed for other gas–liquid scattering studies78–80 and differs from previous gas–solid experiments.81–83 For all three incidence angles, the TD fraction for Ne scattering from cold salty water is similar to that for Ne scattering from dodecane. This trend continues at each deflection angle for scattering at θi = 60° in Fig. 4. In addition, the TD fraction increases as χ increases for both systems.
 | ||
| Fig. 3 TD fraction at θf = 60° as a function of incidence angle θi for Ne scattered from cold salty water and dodecane flat jets, and CD4, ND3, and D2O scattered from a dodecane flat jet. For scattering from cold salty water at θi = 75°, TD fractions are plotted for θf = 55° and 65°. The dodecane data are taken from ref. 62. | ||
 | ||
| Fig. 4 TD fraction as a function of deflection angle χ for Ne scattered from cold salty water and dodecane flat jets, and CD4, ND3, and D2O scattered from a dodecane flat jet at θi = 60°. Open symbols denote TD fraction values that are contaminated with beam leakage. The dodecane data are taken from ref. 62. | ||
3.2. Kinematic models
We analyze energy transfer at the gas–liquid interface in the IS channel using the fits to the scattering TOF profiles and the incident beam energy. A description of the average fractional energy loss in the IS channel as a function of deflection angle then follows according to the well-established62,84,85 “soft-sphere” kinematic model,86,87
 | (3) |
Fig. 5 shows the measured fractional translational energy loss as a function of deflection angle for Ne scattering from both cold salty water and dodecane flat jets. As in Fig. 2, angles at which the fractional energy loss values are affected by contamination from beam leakage, and thus anomalously low, are denoted by open symbols and omitted from the soft-sphere model fitting procedure. As χ increases, ΔE/Ei also increases, and there is minimal dependence on the incidence angle. For θi = 60°, the energy loss values for Ne scattering from cold salty water increase from 0.48 to 0.52 between χ = 40° and 90°. Compared to Ne scattering from dodecane, with analogous values ranging from 0.20 to 0.46, the fractional energy loss values are higher overall but exhibit a weaker dependence on χ. This trend persists for the other two incidence angles.
 | ||
| Fig. 5 Average fractional energy loss as a function of deflection angle χ for impulsively scattered Ne from cold salty water and dodecane flat jets, with incident beam energies of 24.3 and 23.7 kJ mol−1, respectively. Open symbols denote fractional energy loss values that are contaminated with beam leakage. The solid curves give predictions for the soft-sphere model, where the incident particle interacts with a localized region of the surface with an effective mass, meff, and this may increase its internal energy, Eint, during a collision. The fitting results for Ne scattering from cold salty water and dodecane with the soft-sphere model are meff = 250 and 61 amu and Eint = 11.8 and 2.1 kJ mol−1, respectively. The dodecane data are taken from ref. 62. | ||
The parametric fits from the soft-sphere model on the fractional energy loss data are also shown in Fig. 5, yielding values for meff and Eint. The hard-sphere model fit, where Eint has been set to zero, is shown in Fig. S3.† As an approximation, the gas–surface interaction potential is estimated to be equivalent to the Lennard-Jones well depth between Ne and water, or 1.1 kJ mol−1.88,89 If the system is assumed to be noninteracting and V is set to zero, the fits do not change substantially. After implementing the soft-sphere model, meff is found to be 250 amu and Eint 11.8 kJ mol−1, compared to values of 61 amu and 2.1 kJ mol−1 for Ne scattering from dodecane. The high degree of correlation between meff and Eint complicates the reliable determination of their error bars; the procedure outlined in the SI yields estimated error bars of +100/−60 amu and ±1.6 kJ mol−1, respectively, for the two parameters.
The soft-sphere model provides an adequate fit to the fractional energy loss from cold salty water, although the fit was better for dodecane. However, the effective surface mass is much larger than the mass of a single water molecule or any ionic species that may be present at the surface. This result may indicate that collisions in the IS channel are more complex than simple two-body collisions, a scenario that goes beyond the soft-sphere model and indicates a potential breakdown of the model. We take care not to overinterpret this fitted value, since the soft-sphere model does not appropriately account for more complex scenarios such as multiple-bounce collisions. For such trajectories, an effective surface mass of 250 amu may not be representative of the kinematics at play. Further discussion on this point follows in the next section.
4. Discussion
Major findings in this work include super-specular scattering observed at all three incidence angles that were investigated, facile energy transfer in the IS channel, and the branching ratios between IS and TD mechanistic channels. We compare these results to our recent work on dodecane62 and work done by Saecker and Nathanson90 in which Ne was scattered from both squalane and glycerol surfaces at a fixed deflection angle of 90°.In Fig. 2a–c, we observed a high degree of super-specular scattering at θi = 45°, 60°, and 75°, where the IS channel intensity reaches its maximum at an outgoing angle of 90°, albeit less sharply for 45° than for the other two incidence angles. This phenomenon has been seen to a considerably smaller extent in select gas–solid scattering systems91,92 and our prior scattering experiments from dodecane jets where the IS distribution peaked at an outgoing angle of 70° for θi = 60°.62 It contrasts with CO2 and OH scattering from a perfluorinated liquid surface in which sub-specular scattering was seen.57,80 Based on the gas–solid scattering literature, we attribute this effect to the anisotropic loss of momentum favored parallel to the surface normal.
The high degree of super-specular scattering seen here is consistent with the large fractional translational energy loss values, exceeding 40% for all deflection angles (Fig. 5), when compared to dodecane. Analyzing the fractional energy loss values for θi = 60° and assuming these values contribute to momentum transfer entirely along the surface normal (no momentum transfer parallel to the surface), we find that trajectories with ΔE/Ei ≥ 0.25 lead to a value of 90° for θf. For a range of χ = 40° to 60° (the range over which most of the IS flux lies), the fractional energy loss values for cold salty water and dodecane are 0.48 to 0.45 and 0.20 to 0.31, respectively. These considerations imply that Ne scattering from cold salty water but not dodecane can be highly super-specular, in agreement with experiment.
While these kinematics offer a possible mechanism for the observed angular distribution, they do not explain this phenomenon, and a dynamical understanding of why momentum transfer to the surface is so anisotropic has yet to be formulated. In this regard, a possible microscopic mechanism lies in multiple-bounce collisions, which are enhanced for rough surfaces like liquids.93 MD simulations have shown that multiple-bounce collisions lead to a higher degree of energy loss,68,69 resulting in trajectories that are super-specular in nature.
The fractional translational energy loss in the IS channel plotted in Fig. 5 shows a higher degree of energy transfer to cold salty water than to dodecane at comparable beam energies. Overall, for both systems, fractional energy loss depends exclusively on χ and not independently on θi and θf. The slight deviations in the θi = 45° data (where the IS and TD distributions temporally overlap to a greater degree) from the θi = 60° and 75° data at smaller values of χ is likely due to the conventional scattering mechanistic dichotomy failing to capture more nuanced scattering behavior such as multiple-bounce collisions, which have been shown to contribute to scattering signal for liquid surfaces.68,93,94
Comparing Ne scattering across the four different surfaces at hand, we find the trend for fractional energy loss in the IS channel at χ = 90° to be cold salty water (0.52) > dodecane (0.46) > squalane (0.42) > glycerol (0.38); note that the squalane and glycerol experiments were performed at Ei = 25 kJ mol−1.90 While results for squalane and glycerol are available only at χ = 90°, Fig. 5 shows that the deviation between water and dodecane results is considerably larger at smaller values of χ, e.g. 0.48 and 0.20 at χ = 40° for cold salty water and dodecane, respectively.
The fitted values for the internal excitation of the surface of Eint = 11.8 and 2.1 kJ mol−1 for cold salty water and dodecane, respectively, reveal that the cold salty water surface is internally excited to a greater degree. Without the presence of strong attractive forces, fractional energy loss (and the effective surface mass, which will be discussed later) has been previously used as a metric for determining the “softness” of a surface, or to what degree collisions with a surface are soft-spherelike.90 Here, Eint is a direct measure of surface softness, since Eint = 0 for a hard-sphere model. With this argument, we find that cold salty water is a softer surface than dodecane.
Contrasting with dodecane62 and squalane,90 the greater internal excitation energy of cold salty water suggests that the hydrogen-bonded network of liquid water allows for multiple low-frequency intermolecular modes to be excited by the incident Ne atoms. For example, THz spectroscopy of liquid water shows that there is a high density of intermolecular vibrational modes below 300 cm−1.95 Additionally, several librational modes of liquid water could be excited, including the twisting libration band at 485 cm−1 and rocking–wagging libration bands at 707 and 743 cm−1.96 Although the internal excitation is large compared to dodecane, the lowest lying vibrational mode for water, ν2 (1595 cm−1),97 is unlikely to be populated to a significant degree. Note that the hydrogen-bonded network, and thus these librational modes, are likely to be perturbed by the high ion concentration. Previous infrared spectroscopy data of highly concentrated (up to 12 M) LiBr salt solutions have shown shifts in the librational band maximum on the order of 100 cm−1 compared to pure water.98
The relative insensitivity of fractional energy loss with respect to χ is consistent with the large effective surface mass for cold salty water of 250 amu within the framework of the soft-sphere model.84,86,87 In prior work, large effective surface masses correlated with harder surfaces in the absence of attractive forces.90 This is not always the case, however. For example, Ar scattering at 80 kJ mol−1 from squalane and perfluoropolyether wetted wheels at 290 K led to effective surface mass and internal excitation values of 162 and 142 amu and 33.6 and 9.6 kJ mol−1, respectively.78,84 Within this context, the relatively large meff of 250 amu would suggest that collisions in the IS channel couple strongly with the hydrogen-bonded network present in the liquid. This counterintuitive result, where large energy transfer values are accompanied by a large meff, was observed previously for oxygen and argon atomic scattering from liquid and self-assembled monolayer surfaces, referenced above, and attributed to the number of surface atoms participating in a collision event.84,93 However, such an interpretation must be considered with caution in light of the possible breakdown of the soft-sphere model discussed at the end of Section 3.
The relatively large meff may also suggest the presence of ions, specifically bromide anions, at the interface. Although recent vibrational sum-frequency generation work has shown that anions are not enhanced at the interface of salty water solutions, larger halide anions were found to have a higher propensity to concentrate at the interface.99 Further, this study was confined to lower concentrations of salt (≤1.0 M) and NaBr, not LiBr, for investigating bromide behavior. The relatively high concentration of Br− in our solution, together with the large effective surface mass and fractional energy loss values, make it plausible that Ne interacts with Br− at the interface. Further studies must be conducted in tandem with MD simulations on highly concentrated salty water solutions to determine the degree of anion enhancement at the interface.
The similar TD fractions for cold salty water compared to dodecane suggest that, surprisingly, cold salty water is a similarly accommodating surface as dodecane with respect to incident Ne atoms.90 Moreover, the TD fractions for Ne scattering from the two liquids are notably less than those for CD4, ND3, and D2O from dodecane (Fig. 4). While scattering from cold salty water results in larger energy transfer values compared to scattering from dodecane, our findings suggest that energy transfer and TD fraction reflect two different aspects of the gas–solvent interaction. In particular, Nathanson has proposed that the TD fraction correlates with the free energy of solvation for the scatterer in the solvent,90 whereas energy transfer in the IS channel more likely reflects interfacial dynamics. To our knowledge, there are no reliable free energy of solvation values for Ne in cold salty water, so it remains to be seen whether this correlation holds across the two liquids under the rather different conditions of the two experiments (Tliq = 230 K for cold salty water vs. 269 K for dodecane). However, recent results in our group show that there is essentially no IS channel for ND3 scattering from cold salty water, a result consistent with the high solubility of ND3 in water, while the TD fraction for CD4 scattering is similar to Ne.100 It thus seems reasonable that the TD fraction for scattering from cold salty water is in fact strongly correlated with solubility.
Examining the TD fractions plotted as a function of incidence angle in Fig. 3, more grazing collisions (i.e., larger θi) result in less TD, consistent with other gas–liquid scattering experiments.78–80 In gas–solid scattering,81–83,86 the opposite trend is observed. The relationship between normal energy scaling and the likelihood of trapping at the interface does not hold for liquid surfaces, presumably due to the increased roughness and corrugation which converts incident kinetic energy in large θi collisions into translational motion away from the surface.80
5. Conclusions
Herein, we have conducted the first angle-resolved scattering measurements of Ne from a cold salty water flat jet. This expands upon our previous work scattering from a dodecane flat jet and demonstrates advancement of the technique to probe dynamics that occur at volatile liquid surfaces. We have also elucidated mechanistic branching ratios and energy transfer across a wide range of deflection angles at the vapor–water interface. Key results include the super-specular angular distributions derived from the TOF profiles, the related energy transfer in the IS channel, and similar TD fractions between cold salty water and dodecane.The angular distributions for Ne scattering from cold salty water at θi = 45°, 60°, and 75° all exhibit an approximately cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θf distribution in the TD channel and highly super-specular scattering in the IS channel, contrasting with our previous work scattering from dodecane jets. The former observation validates the presence of nascent scattering conditions, while the latter is attributed to anisotropic momentum transfer along the surface normal, mediated by the high degree of fractional energy loss in the IS channel.
θf distribution in the TD channel and highly super-specular scattering in the IS channel, contrasting with our previous work scattering from dodecane jets. The former observation validates the presence of nascent scattering conditions, while the latter is attributed to anisotropic momentum transfer along the surface normal, mediated by the high degree of fractional energy loss in the IS channel.
Fitting the measured fractional energy loss values as a function of deflection angle with a soft-sphere kinematic model yields internal excitation and effective surface mass values. The relatively large internal excitation value of 11.8 kJ mol−1 for cold salty water shows that it is a softer surface than dodecane. The amount of internal excitation present can populate multiple collective intermolecular modes of the hydrogen-bonded network but not discrete vibrational modes of single water molecules.
The large effective surface mass of 250 amu is consistent with the relatively small dependence of fractional energy loss values on χ for cold salty water and suggests that IS trajectories couple strongly with the hydrogen-bonded network present in the liquid. It may also indicate the presence of bromide ions at the surface of cold salty water. However, as discussed above, the possible contribution of multiple-collision trajectories to the IS channel complicates the interpretation of meff. The TD fractions for Ne scattering from cold salty water are similar to those for dodecane, indicating somewhat surprisingly that cold salty water is a similarly accommodating surface as dodecane.
The scattering results presented here provide a fundamental understanding of scattering dynamics at the vapor–water interface and continue to show the unique ability of the flat liquid jet technique in uncovering interfacial gas–liquid interactions. This work will serve as the foundation for future angle-resolved scattering studies on aqueous systems. Studies on nonreactive and reactive scattering from cold salty water flat jets, including polyatomic scattering, are currently underway, and experiments to investigate the effect of surfactants on scattering dynamics are in development.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Author contributions
Walt Yang: conceptualization (equal); data curation (lead); formal analysis (lead); investigation (lead); methodology (equal); software (equal); writing – original draft (lead); writing – review & editing (equal). Madison M. Foreman: conceptualization (equal); data curation (equal); formal analysis (equal); investigation (equal); methodology (equal); software (supporting); writing – review & editing (equal). Tiffany C. Ly: data curation (supporting); formal analysis (supporting); investigation (supporting); methodology (supporting); software (supporting); writing – review & editing (supporting). Kevin R. Wilson: conceptualization (supporting); supervision (supporting). Daniel M. Neumark: conceptualization (lead); methodology (equal); project administration (lead); resources (lead); supervision (lead); validation (lead); writing – review & editing (equal).Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
The authors acknowledge the support by the Office of Basic Energy Science, Chemical Sciences Division of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. MMF additionally acknowledges support from the Arnold and Mabel Beckman Foundation through the Arnold O. Beckman Postdoctoral Fellowship in Chemical Sciences (http://dx.doi.org/10.13039/100000997). We thank Alec M. Wodtke, Steven Saric, Chin Lee, and Marvin N. Pohl for their contributions to the development of the salty water experiments.References
- R. Littel, W. P. M. Van Swaaij and G. F. Versteeg, Kinetics of carbon dioxide with tertiary amines in aqueous solution, AIChE J., 1990, 36, 1633–1640 CrossRef CAS.
- A. Singh and M. Agrawal, Acid rain and its ecological consequences, J. Environ. Biol., 2008, 29, 15–24 CAS.
- R. Putikam and M.-C. Lin, A novel mechanism for the isomerization of N2O4 and its implication for the reaction with H2O and acid rain formation, Int. J. Quantum Chem., 2018, 118, e25560 CrossRef.
- M. F. Ruiz-López, M. T. C. Martins-Costa, J. M. Anglada and J. S. Francisco, A New Mechanism of Acid Rain Generation from HOSO at the Air–Water Interface, J. Am. Chem. Soc., 2019, 141, 16564–16568 CrossRef PubMed.
- R. Atkinson, A. M. Winer and J. N. Pitts Jr, Estimation of night-time N2O5 concentrations from ambient NO2 and NO3 radical concentrations and the role of N2O5 in night-time chemistry, Atmos. Environ., 1986, 20, 331–339 CrossRef CAS.
- F. J. Dentener and P. J. Crutzen, Reaction of N2O5 on tropospheric aerosols: Impact on the global distributions of NOx, O3, and OH, J. Geophys. Res.:Atmos., 1993, 98, 7149–7163 CrossRef CAS.
- N. Riemer, H. Vogel, B. Vogel, B. Schell, I. Ackermann, C. Kessler and H. Hass, Impact of the heterogeneous hydrolysis of N2O5 on chemistry and nitrate aerosol formation in the lower troposphere under photosmog conditions, J. Geophys. Res.:Atmos., 2003, 108, 4144 Search PubMed.
- W. L. Chang, P. V. Bhave, S. S. Brown, N. Riemer, J. Stutz and D. Dabdub, Heterogeneous atmospheric chemistry, ambient measurements, and model calculations of N2O5: A review, Aerosol Sci. Technol., 2011, 45, 665–695 CrossRef.
- H. Wang, X. Chen, K. Lu, R. Hu, Z. Li, H. Wang, X. Ma, X. Yang, S. Chen and H. Dong, NO3 and N2O5 chemistry at a suburban site during the EXPLORE-YRD campaign in 2018, Atmos. Environ., 2020, 224, 117180 CrossRef CAS.
- X.-F. Gao and G. M. Nathanson, Exploring Gas-Liquid Reactions with Microjets: Lessons We Are Learning, Acc. Chem. Res., 2022, 55, 3294–3302 CrossRef CAS PubMed.
- D. J. Nesbitt, A. M. Zolot, J. R. Roscioli and M. Ryazanov, Nonequilibrium Scattering/Evaporation Dynamics at the Gas-Liquid Interface: Wetted Wheels, Self-Assembled Monolayers, and Liquid Microjets, Acc. Chem. Res., 2023, 56, 700–711 CrossRef CAS PubMed.
- S. W. Devlin, F. Bernal, E. J. Riffe, K. R. Wilson and R. J. Saykally, Spiers Memorial Lecture: Water at interfaces, Faraday Discuss., 2024, 249, 9–37 RSC.
- G. L. Richmond, Molecular Bonding and Interactions at Aqueous Surfaces as Probed by Vibrational Sum Frequency Spectroscopy, Chem. Rev., 2002, 102, 2693–2724 CrossRef CAS PubMed.
- J. A. McGuire and Y. R. Shen, Ultrafast Vibrational Dynamics at Water Interfaces, Science, 2006, 313, 1945–1948 CrossRef CAS PubMed.
- P. B. Petersen and R. J. Saykally, On the Nature Of Ions at the Liquid Water Surface, Annu. Rev. Phys. Chem., 2006, 57, 333–364 CrossRef CAS PubMed.
- S. Yamaguchi and T. Tahara, Development of electronic sum frequency generation spectroscopies and their application to liquid interfaces, J. Phys. Chem. C, 2015, 119, 14815–14828 CrossRef CAS.
- A. M. Rizzuto, S. Irgen-Gioro, A. Eftekhari-Bafrooei and R. J. Saykally, Broadband Deep UV Spectra of Interfacial Aqueous Iodide, J. Phys. Chem. Lett., 2016, 7, 3882–3885 CrossRef CAS PubMed.
- H. Mizuno, A. M. Rizzuto and R. J. Saykally, Charge-Transfer-to-Solvent Spectrum of Thiocyanate at the Air/Water Interface Measured by Broadband Deep Ultraviolet Electronic Sum Frequency Generation Spectroscopy, J. Phys. Chem. Lett., 2018, 9, 4753–4757 CrossRef CAS PubMed.
- D. Bhattacharyya, H. Mizuno, A. M. Rizzuto, Y. Zhang, R. J. Saykally and S. E. Bradforth, New Insights into the Charge-Transfer-to-Solvent Spectrum of Aqueous Iodide: Surface versus Bulk, J. Phys. Chem. Lett., 2020, 11, 1656–1661 CrossRef CAS PubMed.
- H. Mizuno, K. J. Oosterbaan, G. Menzl, J. Smith, A. M. Rizzuto, P. L. Geissler, M. Head-Gordon and R. J. Saykally, Revisiting the π → π* transition of the nitrite ion at the air/water interface: A combined experimental and theoretical study, Chem. Phys. Lett., 2020, 751, 137516 CrossRef CAS.
- S. W. Devlin, D. L. McCaffrey and R. J. Saykally, Characterizing Anion Adsorption to Aqueous Interfaces: Toluene–Water versus Air–Water, J. Phys. Chem. Lett., 2021, 13, 222–228 CrossRef PubMed.
- C. J. C. Jordan and J. R. R. Verlet, Time-resolved electronic sum-frequency generation spectroscopy with fluorescence suppression using optical Kerr gating, J. Chem. Phys., 2021, 155, 164202 CrossRef CAS PubMed.
- C. J. C. Jordan, E. A. Lowe and J. R. R. Verlet, Photooxidation of the phenolate anion is accelerated at the water/air interface, J. Am. Chem. Soc., 2022, 144, 14012–14015 CrossRef CAS PubMed.
- F. Bernal, A. Dodin, C. Kyprianou, D. T. Limmer and R. J. Saykally, Strong Adsorption of Guanidinium Cations to the Air–Water Interface, Proc. Natl. Acad. Sci. U. S. A., 2025, 122, e2418443122 CrossRef CAS PubMed.
- D. M. Sagar, C. D. Bain and J. R. R. Verlet, Hydrated Electrons at the Water/Air Interface, J. Am. Chem. Soc., 2010, 132, 6917–6919 CrossRef CAS PubMed.
- D. Liu, G. Ma, L. M. Levering and H. C. Allen, Vibrational Spectroscopy of Aqueous Sodium Halide Solutions and Air–Liquid Interfaces: Observation of Increased Interfacial Depth, J. Phys. Chem. B, 2004, 108, 2252–2260 CrossRef CAS.
- Y. R. Shen and V. Ostroverkhov, Sum-frequency vibrational spectroscopy on water interfaces: polar orientation of water molecules at interfaces, Chem. Rev., 2006, 106, 1140–1154 CrossRef CAS PubMed.
- X. Chen and H. C. Allen, Water structure at aqueous solution surfaces of atmospherically relevant dimethyl sulfoxide and methanesulfonic acid revealed by phase-sensitive sum frequency spectroscopy, J. Phys. Chem. B, 2010, 114, 14983–14988 CrossRef CAS PubMed.
- W. Hua, X. Chen and H. C. Allen, Phase-sensitive sum frequency revealing accommodation of bicarbonate ions, and charge separation of sodium and carbonate ions within the air/water interface, J. Phys. Chem. A, 2011, 115, 6233–6238 CrossRef CAS PubMed.
- M. Bonn, Y. Nagata and E. H. G. Backus, Molecular Structure and Dynamics of Water at the Water–Air Interface Studied with Surface-Specific Vibrational Spectroscopy, Angew. Chem., 2015, 54, 5560–5576 CrossRef CAS PubMed.
- Y.-C. Wen, S. Zha, X. Liu, S. Yang, P. Guo, G. Shi, H. Fang, Y. R. Shen and C. Tian, Unveiling Microscopic Structures of Charged Water Interfaces by Surface-Specific Vibrational Spectroscopy, Phys. Rev. Lett., 2016, 116, 016101 CrossRef PubMed.
- S. Alamdari, S. J. Roeters, T. W. Golbek, L. Schmüser, T. Weidner and J. Pfaendtner, Orientation and Conformation of Proteins at the Air–Water Interface Determined from Integrative Molecular Dynamics Simulations and Sum Frequency Generation Spectroscopy, Langmuir, 2020, 36, 11855–11865 CrossRef CAS PubMed.
- A. Greco, S. Imoto, E. H. G. Backus, Y. Nagata, J. Hunger and M. Bonn, Ultrafast aqueous electric double layer dynamics, Science, 2025, 388, 405–410 CrossRef CAS PubMed.
- C. W. West, J. Nishitani, C. Higashimura and T. Suzuki, Extreme ultraviolet time-resolved photoelectron spectroscopy of aqueous aniline solution: enhanced surface concentration and pump-induced space charge effect, Mol. Phys., 2021, 119, e1748240 CrossRef.
- Y.-i. Yamamoto, T. Hirano, T. Ishiyama, A. Morita and T. Suzuki, Gas–Liquid Interface of Aqueous Solutions of Surface Active Aromatic Molecules Studied Using Extreme Ultraviolet Laser Photoelectron Spectroscopy and Molecular Dynamics Simulation, J. Am. Chem. Soc., 2025, 147, 4026–4037 CrossRef CAS PubMed.
- R. K. Lam, J. W. Smith, A. M. Rizzuto, O. Karslıoğlu, H. Bluhm and R. J. Saykally, Reversed interfacial fractionation of carbonate and bicarbonate evidenced by X-ray photoemission spectroscopy, J. Chem. Phys., 2017, 146, 094703 CrossRef.
- K. A. Perrine, K. M. Parry, A. C. Stern, M. H. Van Spyk, M. J. Makowski, J. A. Freites, B. Winter, D. J. Tobias and J. C. Hemminger, Specific cation effects at aqueous solution–vapor interfaces: Surfactant-like behavior of Li+ revealed by experiments and simulations, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 13363–13368 CrossRef CAS PubMed.
- Y. Li, X. Yan and R. G. Cooks, The Role of the Interface in Thin Film and Droplet Accelerated Reactions Studied by Competitive Substituent Effects, Angew. Chem., 2016, 55, 3433–3437 CrossRef CAS PubMed.
- M. E. Diveky, M. J. Gleichweit, S. Roy and R. Signorell, Shining New Light on the Kinetics of Water Uptake by Organic Aerosol Particles, J. Phys. Chem. A, 2021, 125, 3528–3548 CrossRef CAS PubMed.
- R. A. LaCour, J. P. Heindel, R. Zhao and T. Head-Gordon, The Role of Interfaces and Charge for Chemical Reactivity in Microdroplets, J. Am. Chem. Soc., 2025, 147, 6299–6317 CrossRef CAS PubMed.
- S. L. Lednovich and J. B. Fenn, Absolute evaporation rates for some polar and nonpolar liquids, AIChE J., 1977, 23, 454–459 CrossRef CAS.
- H. Siegbahn, Electron spectroscopy for chemical analysis of liquids and solutions, J. Phys. Chem., 1985, 89, 897–909 CrossRef CAS.
- M. Faubel, S. Schlemmer and J. P. Toennies, A molecular beam study of the evaporation of water from a liquid jet, Z. Phys. D:At., Mol. Clusters, 1988, 10, 269–277 CrossRef CAS.
- M. Faubel and T. Kisters, Non-equilibrium molecular evaporation of carboxylic acid dimers, Nature, 1989, 339, 527–529 CrossRef CAS.
- M. Ekimova, W. Quevedo, M. Faubel, P. Wernet and E. T. J. Nibbering, A liquid flatjet system for solution phase soft-x-ray spectroscopy, Struct. Dyn., 2015, 2, 054301 CrossRef PubMed.
- D. K. Lancaster, A. M. Johnson, D. K. Burden, J. P. Wiens and G. M. Nathanson, Inert Gas Scattering from Liquid Hydrocarbon Microjets, J. Phys. Chem. Lett., 2013, 4, 3045–3049 CrossRef CAS.
- J. A. Faust and G. M. Nathanson, Microjets and coated wheels: versatile tools for exploring collisions and reactions at gas–liquid interfaces, Chem. Soc. Rev., 2016, 45, 3609–3620 RSC.
- S. M. Brastad and G. M. Nathanson, Molecular beam studies of HCl dissolution and dissociation in cold salty water, Phys. Chem. Chem. Phys., 2011, 13, 8284 RSC.
- J. A. Faust, T. B. Sobyra and G. M. Nathanson, Gas–Microjet Reactive Scattering: Collisions of HCl and DCl with Cool Salty Water, J. Phys. Chem. Lett., 2016, 7, 730–735 CrossRef CAS PubMed.
- T. B. Sobyra, H. Pliszka, T. H. Bertram and G. M. Nathanson, Production of Br2 from N2O5 and Br– in Salty and Surfactant-Coated Water Microjets, J. Phys. Chem. A, 2019, 123, 8942–8953 CrossRef CAS PubMed.
- X.-F. Gao, D. J. Hood, X. Zhao and G. M. Nathanson, Creation and Reaction of Solvated Electrons at and near the Surface of Water, J. Am. Chem. Soc., 2023, 145, 10987–10990 CrossRef CAS PubMed.
- R. H. Bianchini, M. A. Tesa-Serrate, M. L. Costen and K. G. McKendrick, Collision-Energy Dependence of the Uptake of Hydroxyl Radicals at Atmospherically Relevant Liquid Surfaces, J. Phys. Chem. C, 2018, 122, 6648–6660 CrossRef CAS.
- E. J. Smoll, M. A. Tesa-Serrate, S. Purcell, L. D'Andrea, D. W. Bruce, J. M. Slattery, M. L. Costen, T. K. Minton and K. G. McKendrick, Determining the composition of the vacuum–liquid interface in ionic-liquid mixtures, Faraday Discuss., 2018, 206, 497–522 RSC.
- S. M. Purcell, P. D. Lane, L. D'Andrea, N. S. Elstone, D. W. Bruce, J. M. Slattery, E. J. Smoll Jr, S. J. Greaves, M. L. Costen and T. K. Minton, et al., Surface Structure of Alkyl/Fluoroalkylimidazolium Ionic–Liquid Mixtures, J. Phys. Chem. B, 2022, 126, 1962–1979 CrossRef CAS PubMed.
- P. D. Lane, T. Gstir, S. M. Purcell, M. Swierczewski, N. S. Elstone, D. W. Bruce, J. M. Slattery, M. L. Costen and K. G. McKendrick, Superthermal Al Atoms as a Reactive-Atom Probe of Fluorinated Surfaces, J. Phys. Chem. A, 2023, 127, 5580–5590 CrossRef CAS PubMed.
- J. R. Roscioli and D. J. Nesbitt, Quantum State Resolved Scattering from Room-Temperature Ionic Liquids: The Role of Cation versus Anion Structure at the Interface, J. Phys. Chem. A, 2011, 115, 9764–9773 CrossRef CAS PubMed.
- M. J. Roman, A. G. Knight, D. R. Moon, P. D. Lane, S. J. Greaves, M. L. Costen and K. G. McKendrick, Inelastic scattering of OH from a liquid PFPE surface: Resolution of correlated speed and angular distributions, J. Chem. Phys., 2023, 158, 244704 CrossRef CAS PubMed.
- J. D. Koralek, J. B. Kim, P. Brůža, C. B. Curry, Z. Chen, H. A. Bechtel, A. A. Cordones, P. Sperling, S. Toleikis and J. F. Kern, et al., Generation and characterization of ultrathin free-flowing liquid sheets, Nat. Commun., 2018, 9, 1353 CrossRef PubMed.
- C. Lee, M. N. Pohl, I. A. Ramphal, W. Yang, B. Winter, B. Abel and D. M. Neumark, Evaporation and Molecular Beam Scattering from a Flat Liquid Jet, J. Phys. Chem. A, 2022, 126, 3373–3383 CrossRef CAS PubMed.
- W. Yang, C. Lee, S. Saric, M. N. Pohl and D. M. Neumark, Evaporation and scattering of neon, methane, and water from a dodecane flat liquid jet, J. Chem. Phys., 2023, 159, 054704 CrossRef CAS PubMed.
- S. Saric, W. Yang and D. M. Neumark, Molecular beam scattering of ammonia from a dodecane flat liquid jet, Faraday Discuss., 2024, 251, 382–394 RSC.
- W. Yang, M. M. Foreman, S. Saric, A. M. Wodtke, K. R. Wilson and D. M. Neumark, Molecular beam scattering from flat jets of liquid dodecane and water, Nat. Sci., 2024, 4, e20240009 CrossRef.
- J. E. Hurst, C. A. Becker, J. P. Cowin, K. C. Janda, L. Wharton and D. J. Auerbach, Observation of Direct Inelastic Scattering in the Presence of Trapping-Desorption Scattering: Xe on Pt(111), Phys. Rev. Lett., 1979, 43, 1175–1177 CrossRef CAS.
- K. C. Janda, J. E. Hurst, J. Cowin, L. Wharton and D. J. Auerbach, Direct-inelastic and trapping-desorption scattering of N2 and CH4 from Pt(111), Surf. Sci., 1983, 130, 395–409 CrossRef CAS.
- M. E. Saecker, S. T. Govoni, D. V. Kowalski, M. E. King and G. M. Nathanson, Molecular Beam Scattering from Liquid Surfaces, Science, 1991, 252, 1421–1424 CrossRef CAS PubMed.
- G. Comsa and R. David, Dynamical parameters of desorbing molecules, Surf. Sci. Rep., 1985, 5, 145–198 CrossRef CAS.
- I. Kinefuchi, H. Yamaguchi, S. Shiozaki, Y. Sakiyama and Y. Matsumoto, Out-of-plane Scattering Distribution of Nitrogen Molecular Beam on Graphite (0001) Surface, AIP Conf. Proc., 2005, 762, 947–952 CrossRef CAS.
- Y. Peng, L. Liu, Z. Cao, S. Li, O. A. Mazyar, W. L. Hase and T. Yan, Chemical Dynamics Simulation of Ne Atom Scattering off a Squalane Surface, J. Phys. Chem. C, 2008, 112, 20340–20346 CrossRef CAS.
- J. Li, H. Guo and J. Li, Energy- and Angle-Resolved Scattering of Ne from Dodecane Liquid Surfaces: Theory Corroborating Experiment, J. Phys. Chem. Lett., 2024, 15, 5824–5830 CrossRef CAS PubMed.
- Y. T. Lee, J. D. McDonald, P. R. Lebreton and D. R. Herschbach, Molecular Beam Reactive Scattering Apparatus with Electron Bombardment Detector, Rev. Sci. Instrum., 1969, 40, 1402–1408 CrossRef CAS.
- Y. T. Lee, Molecular Beam Studies of Elementary Chemical Processes (Nobel Lecture), Angew. Chem., 1987, 26, 939–951 CrossRef.
- D. Irimia, D. Dobrikov, R. Kortekaas, H. Voet, D. A. Van Den Ende, W. A. Groen and M. H. M. Janssen, A short pulse (7 μs FWHM) and high repetition rate (dc-5kHz) cantilever piezovalve for pulsed atomic and molecular beams, Rev. Sci. Instrum., 2009, 80, 113303 CrossRef PubMed.
- C. Meng and M. H. M. Janssen, Measurement of the density profile of pure and seeded molecular beams by femtosecond ion imaging, Rev. Sci. Instrum., 2015, 86, 023110 CrossRef PubMed.
- M. D. Morse, in Atomic, Molecular, and Optical Physics: Atoms and Molecules, ed. F. B. Dunning, and R. G. Hulet, Academic Press, 1996, vol. 29B, pp. 21–47 Search PubMed.
- A. Lebehot, J. Kurzyna, V. Lago, M. Dudeck and R. Campargue, in Atomic and Molecular Beams, ed. R. Campargue, Springer, 2001, pp. 237–251 Search PubMed.
- C. Hahn, Z. R. Kann, J. A. Faust, J. Skinner and G. M. Nathanson, Super-Maxwellian helium evaporation from pure and salty water, J. Chem. Phys., 2016, 144, 044707 CrossRef PubMed.
- I. Kinefuchi, Y. Kotsubo, K. Osuka, Y. Yoshimoto, N. Miyoshi, S. Takagi and Y. Matsumoto, Incident energy dependence of the scattering dynamics of water molecules on silicon and graphite surfaces: the effect on tangential momentum accommodation, Microfluid. Nanofluid., 2017, 21, 15 CrossRef.
- M. E. King, G. M. Nathanson, M. Hanning-Lee and T. K. Minton, Probing the microscopic corrugation of liquid surfaces with gas–liquid collisions, Phys. Rev. Lett., 1993, 70, 1026–1029 CrossRef CAS PubMed.
- M. E. King, K. M. Fiehrer, G. M. Nathanson and T. K. Minton, Effects of Thermal Roughening on the Angular Distributions of Trapping and Scattering in Gas–Liquid Collisions, J. Phys. Chem. A, 1997, 101, 6556–6561 CrossRef CAS.
- B. G. Perkins and D. J. Nesbitt, Toward Three-Dimensional Quantum State-Resolved Collision Dynamics at the Gas–Liquid Interface: Theoretical Investigation of Incident Angle, J. Phys. Chem. A, 2009, 113, 4613–4625 CrossRef CAS PubMed.
- C. B. Mullins, C. T. Rettner, D. J. Auerbach and W. H. Weinberg, Variation of the trapping probability of Ar on Pt(111) with kinetic energy and angle of incidence: The changing role of parallel momentum with surface temperature, Chem. Phys. Lett., 1989, 163, 111–115 CrossRef CAS.
- C. T. Rettner, C. B. Mullins, D. S. Bethune, D. J. Auerbach, E. K. Schweizer and W. H. Weinberg, Molecular beam studies of trapping dynamics, J. Vac. Sci. Technol., A, 1990, 8, 2699–2704 CrossRef CAS.
- M. Head-Gordon, J. C. Tully, C. T. Rettner, C. B. Mullins and D. J. Auerbach, On the nature of trapping and desorption at high surface temperatures. Theory and experiments for the Ar–Pt(111) system, J. Chem. Phys., 1991, 94, 1516–1527 CrossRef CAS.
- W. A. Alexander, J. Zhang, V. J. Murray, G. M. Nathanson and T. K. Minton, Kinematics and dynamics of atomic-beam scattering on liquid and self-assembled monolayer surfaces, Faraday Discuss., 2012, 157, 355 RSC.
- N. Andric and P. Jenny, Molecular dynamics investigation of energy transfer during gas-surface collisions, Phys. Fluids, 2018, 30, 077104 CrossRef.
- C. T. Rettner and M. N. R. Ashfold, in Dynamics of Gas-Surface Interactions, Royal Society of Chemistry, 1991 Search PubMed.
- G. M. Nathanson, Molecular Beam Studies of Gas–Liquid Interfaces, Annu. Rev. Phys. Chem., 2004, 55, 231–255 CrossRef CAS PubMed.
- D. Berthelot, Sur le mélange des gaz, C. R. Hebd, Seances Acad. Sci., 1898, 126, 1703–1855 Search PubMed.
- F. M. Mourits and F. H. A. Rummens, A critical evaluation of Lennard-Jones and Stockmayer potential parameters and of some correlation methods, Can. J. Chem., 1977, 55, 3007–3020 CrossRef CAS.
- M. E. Saecker and G. M. Nathanson, Collisions of protic and aprotic gases with hydrogen bonding and hydrocarbon liquids, J. Chem. Phys., 1993, 99, 7056–7075 CrossRef CAS.
- R. B. Subbarao and D. R. Miller, Velocity distribution measurements of 0.06–1.4 eV argon and neon atoms scattered from the (111) plane of a silver crystal, J. Chem. Phys., 1973, 58, 5247–5257 CrossRef CAS.
- C. T. Rettner, L. A. Delouise and D. J. Auerbach, Effect of incidence kinetic energy and surface coverage on the dissociative chemisorption of oxygen on W(110), J. Chem. Phys., 1986, 85, 1131–1149 CrossRef CAS.
- M. A. Tesa-Serrate, E. J. Smoll, T. K. Minton and K. G. McKendrick, Atomic and Molecular Collisions at Liquid Surfaces, Annu. Rev. Phys. Chem., 2016, 67, 515–540 CrossRef CAS PubMed.
- N. Lipkin, R. Gerber, N. Moiseyev and G. Nathanson, Atom scattering studies of liquid structure and dynamics: Collisions of Xe with a model of squalane, J. Chem. Phys., 1994, 100, 8408–8417 CrossRef.
- M. Heyden, J. Sun, S. Funkner, G. Mathias, H. Forbert, M. Havenith and D. Marx, Dissecting the THz spectrum of liquid water from first principles via correlations in time and space, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 12068–12073 CrossRef CAS PubMed.
- D. P. Shelton, Correlated libration in liquid water, J. Chem. Phys., 2024, 160, 114507 CrossRef CAS PubMed.
- T. Shimanouchi, Tables of molecular vibrational frequencies, National Bureau of Standards, Washington, DC, 1972 Search PubMed.
- D. James and R. Armishaw, Structure of aqueous solutions: Infrared spectra of the water librational mode in solutions of monovalent halides, Aust. J. Chem., 1975, 28, 1179–1186 CrossRef CAS.
- Y. Litman, K.-Y. Chiang, T. Seki, Y. Nagata and M. Bonn, Surface stratification determines the interfacial water structure of simple electrolyte solutions, Nat. Chem., 2024, 16, 644–650 CrossRef CAS PubMed.
- M. M. Foreman, W. Yang, T. C. Ly and D. M. Neumark, Molecular Beam Scattering of Methane and Ammonia from Flat Jets of Cold Salty Water, 2025, in preparation Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sc01636c |
| This journal is © The Royal Society of Chemistry 2025 |


