Local coordination geometry within cobalt spinel oxides mediates photoinduced polaron formation

Abstract

Understanding the photophysics of transition metal oxides is crucial for these materials to realize their considerable potential in applications such as photocatalysis and optoelectronics. Recent studies suggest that formation of localized excited states consisting of polarons (quasi-particles comprising a charge carrier strongly coupled to a proximal lattice distortion) plays a crucial role in the photophysics of these materials. Cobalt-containing spinel oxides (Co₃O₄ and ZnCo₂O₄) offer a unique opportunity to investigate the influence of local geometry, and cation inversion on photoinduced polaron formation. Here, we use Hubbard-corrected density functional theory (DFT + U) paired with resonance Raman and temperature-dependent optical spectroscopies to demonstrate that low-energy transitions observed in Co₃O₄ are associated with d–d transitions involving cobalt ions occupying tetrahedral sites within the spinel lattice. These low-energy optical transitions exhibit strong coupling to phonon modes associated with tetrahedral sites. Replacing most tetrahedral cobalt ions with zinc produces the slightly inverted ternary spinel material, ZnCo₂O₄, in which we observe a phonon-coupled optical transition that occurs at the same energy as observed in Co₃O₄. We propose that these phonon-coupled optical transitions enable direct access to a polaronic state upon photoexcitation; however, the intensity of this optical transition depends on temperature in Co₃O₄, whereas no significant temperature dependence is observed in ZnCo₂O₄. We therefore hypothesize that in Co₃O₄ the mechanism of polaron formation is coupling of the optical transition to dynamic, thermally-gated lattice distortions, whereas, in ZnCo₂O₄, the transition couples to static lattice defects that arise from the presence of a small population of tetrahedrally-coordinated cobalt ions.

---

Introduction

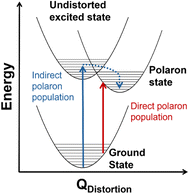
Transition metal oxides have promising characteristics for solar energy conversion technologies because of their visible band gap energies, stability, abundance, cost-effectiveness and low toxicity.^1,2 However, these materials contain weakly dispersive bands originating from the metal 3d orbitals that lead to low charge-carrier mobility,^3,4 rapid charge recombination,^5,6 and formation of localized, “self-trapped” states near the band-edges.⁷ These states, which comprise one or more localized charge carriers coupled to proximal lattice distortions arising from one or more phonons, are known as polarons.^7,8 Small polarons, first described by Holstein,^9,10 are described by a short-range carrier–phonon interaction (radius_polaron ∼ lattice parameter) and carrier mobility that increases with increased temperature.¹¹ Conversely, large polarons have long-range carrier–phonon interactions (radius_polaron ≫ lattice parameter) with carrier mobility that decreases with increased temperature.^12,13 Many transition metal oxides are reported to host small polarons,^7,14–19 and in many cases the performance of these materials for electrocatalytic, photoelectrocatalytic, and optoelectronic applications is impacted by small polaron formation.^20–25

Although conductivity studies have contributed to a thorough understanding of polaron transport mechanisms in transition metal oxides,^{11,15,17,26,27} there is still a limited understanding of the mechanisms by which polarons form in photoexcited states. In hematite (α-Fe₂O₃), for example, one proposed mechanism involves indirect population of polaron states via relaxation from an initially excited, higher-energy non-polaronic state.^20,28 Our group recently identified an additional mechanism involving the direct population of polaronic excited states at room temperature upon band-edge excitation in α-Fe₂O₃.^29,30 Fig. 1 depicts the difference between indirect and direct population of polaronic states via photoexcitation. Importantly, optical population of polaronic states in α-Fe₂O₃ is proposed to occur even in a pristine, defect-free lattice: the optical transitions couple to intrinsic, thermally-activated phonon distortions within the crystal.^29,30 There is also evidence of polaron formation arising from charge carriers coupling to intrinsic lattice distortions in rutile TiO₂ and LiNbO₄.^16,31 These self-trapping mechanisms differ from other descriptions of small polarons forming via charge carriers coupling to dopants or lattice defects.^32–35 Distinguishing the mechanism of photoinduced polaron formation (mediated by dynamic thermally activated lattice distortions or static lattice defects) is fundamentally important to the development of strategies for engineering metal oxide materials for photoapplications.

Fig. 1 Conceptual configuration coordinate diagram depicting mechanisms of photoexcited polaron formation. The red arrow illustrates direct photoexcitation from a thermally distorted ground state into a polaronic state and the blue arrow shows relaxation into a polaronic state via an undistorted ground state.

Spinel oxides (AB₂O₄) offer a unique opportunity to understand how the mechanism of photoinduced polaron formation depends on orbital composition of the band edge, coordination geometry of metal centers, and the presence of substitutional defects. These materials are mixed-valent with Fd3̄m symmetry and two different site symmetries for metals: tetrahedral (T_d) and octahedral (O_h). Ternary spinel oxides, in which A and B are different metals, are described by an inversion parameter x (0.0 < x < 1.0) that quantifies the percentage of the A cations that occupy octahedral sites. When x = 0.0, meaning all of the A cations are in tetrahedral sites, the spinel is considered “normal,” whereas when x = 1.0, meaning all of the A cations are in octahedral sites, the spinel is fully inverted. Intermediate values of x correspond to population of A cations in both tetrahedral and octahedral sites. Spinel oxides containing cobalt are of particular interest because of the difference in crystal field splittings of Co²⁺ T_d and Co³⁺ O_h (Fig. 2A). Transitions between the e and t₂ states within the T_d sites are allowed by the Laporte selection rule whereas this rule forbids transitions between the t_2g and e_g states within the O_h sites. Normal Co₃O₄, which contains both Co²⁺ T_d and Co³⁺ O_h, exhibits optical transitions associated with localized d–d transitions at 0.8, 0.9 and 1.6 eV, in addition to an optical transition at 2.5 eV associated with a ligand-to-metal-charge transfer (LMCT) transition.^36–40 Normal ZnCo₂O₄, with only Co³⁺ O_h, is reported to have only the LMCT-type transition at 2.5 eV.²⁷ The coordination geometry of cobalt in spinel oxides thus impacts their optical spectra; we aim to understand how this coordination geometry impacts photoinduced polaron formation.

Fig. 2 (A) The Co₃O₄ unit cell (Fd3̄m) with associated d-splitting diagrams for Co³⁺ (O_h) and Co²⁺ (T_d). (B) Electronic band structure and projected density of states of Co₃O₄ calculated with Hubbard-corrected DFT. (C) Plot of experimentally (solid blue line) and computationally (dashed black line) determined imaginary dielectric spectra of Co₃O₄. Labels a–e correlate with arrows in (D), the spin-symmetrized projected density of states arising from the primitive cell of Co₃O₄.

The formation of small polarons in Co spinel oxides (Co₃O₄ and ZnCo₂O₄) has been inferred from the observation of thermally activated charge transport in these materials;^26,27 however, as with other transition metal oxides, descriptions of photoinduced polarons in these materials are scarce. Transient absorption (TA) studies of Co₃O₄ have reported that the strongest TA signal is induced by thermal effects,^41,42 which mirrors the behavior of hematite, a material known to undergo photoinduced polaron formation.^29,30,43,44 In other work using extreme ultraviolet (XUV) spectroscopy, Zhang, et al. describe indirect formation of small polarons from self-trapped photocarriers in Co₃O₄.⁴⁵ Using a combined approach of resonance Raman spectroscopy, temperature-dependent optical spectroscopy and Hubbard-corrected density functional theory, we investigate the influence of cobalt coordination geometry on photoinduced polaron formation in Co₃O₄ and ZnCo₂O₄. We report evidence that T_d Co in Co₃O₄ mediates resonance Raman enhancement of specific phonon modes, indicating the presence of phonon-coupled optical transitions that lead to polaron formation. Parallel studies of partially inverted ZnCo₂O₄, in which the majority of the T_d Co ions are replaced with Zn, confirm the involvement of T_d Co in phonon-coupled transitions; however, in ZnCo₂O₄ these transitions do not depend on temperature. This observation suggests that photoinduced polarons in ZnCo₂O₄ form at static defects rather than dynamic lattice distortions. The fundamental understanding of photophysical properties as a function of coordination geometry presented here is crucial to designing transition metal oxides for optical applications.

Results and discussion

Assignment of the optical spectra of Co₃O₄

Co₃O₄ adopts a spinel crystal structure (space group Fd3̄m) with two different metal sites: Co³⁺ ions occupy octahedral sites and Co²⁺ ions occupy tetrahedral sites (Fig. 2A). The two coordination sites give rise to two distinct crystal field splittings of the 3d orbitals as shown in Fig. 2A. Transitions between the e and t₂ states within the T_d sites are allowed by the Laporte selection rule whereas this rule forbids transitions between the t_2g and e_g states within the O_h sites. The unpaired electrons of adjacent T_d Co²⁺ atoms in Co₃O₄ are antiferromagnetically coupled.⁴⁶ Density Functional Theory with Hubbard and Hund corrections (DFT + U + J) was used to calculate the ground-state electronic structure of Co₃O₄ within the Born–Oppenheimer approximation, in which nuclear motion is neglected. Hubbard (electron correlation correction)⁴⁷ and Hund (local magnetization correction)⁴⁸ corrections are used in highly correlated materials such as Co₃O₄ to mitigate self-interaction errors.³⁰ Using a linear response method,^30,47 U and J parameters were calculated for Co₃O₄ from first principles via perturbation of the local environments of open-shell ions (T_d Co²⁺ and O_h Co³⁺ in the case of Co₃O₄, see ESI† for more computational details). The DFT + U + J-computed band structure and projected density of states (pDOS) shown in Fig. 2B indicate that 3d orbitals associated with Co²⁺ T_d atoms are the primary contributors to an energetically isolated band at the valence band maximum (VBM), whereas both Co²⁺ T_d and Co³⁺ O_h 3d orbitals contribute to the conduction band minimum (CBM). These computed results suggest isolated valence bands with Co²⁺ T_d character participate in the low-energy transitions observed in the experimental imaginary dielectric spectrum at 0.82 and 0.92 eV (labeled a, b in Fig. 2C).

Fig. 2C plots the DFT + U + J-computed dielectric spectrum overlaid with the experimental dielectric spectrum extracted from transmission and reflection spectra measured from a 53.7-nm thick Co₃O₄ film (see ESI† for details of dielectric spectrum determination and powder X-ray diffraction pattern). We applied a rigid shift of +0.3 eV to all conduction band eigenvalues to bring the computed dielectric function into alignment with the measured spectrum. Herein, this shift is applied to all electronic band diagrams and electronic density of states plots of Co₃O₄. In order to fulfill the f-sum rule governing total oscillator strength, all computed optical spectra are subsequently renormalized by a factor of (1 − (0.3 eV/ħω)).^49,50 The computed single-particle dielectric spectrum shows good agreement with the measured spectrum, confirming the features at 0.82, 0.92 and 1.64 eV involve Co²⁺ T_d bands (a–c). From the spin-resolved density of states separated into band contributions from t_2g and e_g (O_h), e and t₂ (T_d) and O 2p (Fig. 2D), optical transitions are assigned while also considering spatial wavefunction overlap. The onsets of the conduction bands derived from O_h Co³⁺ e_g, T_d Co²⁺ t₂, and O 2p orbitals occur at the same energy; however, the largest projected density of states comes from O_h Co³⁺ e_g. Thus, when considering transitions from T_d Co²⁺ e to the conduction band, these DFT + U + J computations exhibit no energetic difference among transitions to O_h Co³⁺ e_g, T_d Co²⁺ t₂, and O 2p. The oscillator strength of the experimental dielectric peak at 0.82 eV is higher than the 0.92 shoulder, indicating the higher likelihood of the 0.82-eV transition; however, the shoulder is not resolved in the imaginary dielectric computed by DFT + U + J. Therefore, to assign this shoulder, we qualitatively assessed the spatial overlap of orbital wavefunctions by mapping the contributions of specific atoms to specific projected densities of states (Fig. S10†). This approach reveals that the most probable transition contributing to the 0.82 eV feature is an intra-atomic transition of Co²⁺ T_d that satisfies the spin transition selection rule (Fig. S10A and B†). The spatial overlap of the orbitals involved in an intra-atomic transition is greater than the overlap of orbitals between a T_d Co and an O_h Co (inter-sublattice charge transfer), further supporting the assignment of the 0.82-eV optical transition to an intra-atomic d-to-d transition in T_d Co²⁺ (e → t₂). From the spin-resolved density of states combined with our spatial overlap analysis, the feature at 0.92 eV is best described as a charge transfer transition from the tetrahedral sublattice to the octahedral sublattice (T_d Co²⁺ e → O_h Co³⁺ e_g). Similarly, the transition at 1.62 eV can be described as an inter-sublattice charge transfer from O_h Co³⁺ t_2g → T_d Co²⁺ t₂. The covalency between T_d Co²⁺ and O 2p, as well as O_h Co³⁺ and O 2p, allows these metal-to-metal (inter-sublattice charge transfer) transitions to occur. The feature at 2.55 eV and its shoulder at 2.90 eV arise from ligand-to-metal charge transfer (LMCT) type transitions. The assignment of these two LMCT transfers is resolved from comparing the experimental spectrum of Co₃O₄ with ZnCo₂O₄, which has majority O_h Co³⁺ (Fig. S12†). It becomes apparent that the O 2p → O_h Co³⁺ e_g transition is slightly higher in energy than the O 2p → T_d Co²⁺ t₂ transition, leading to the following assignments: O 2p → T_d Co²⁺ t₂ (2.55 eV) and O 2p → O_h Co³⁺ e_g (2.90 eV). All transitions are spin-conserved (Fig. 2D and Table 1).

Table 1 Assignment of optical transitions in Co₃O₄

Peak center (eV)	Label	Transition	Description
0.82	a	Td Co^2+ e → t2	Intra-atomic transition
0.92	b	Td Co^2+ e → Oh Co^3+ eg	Inter-sublattice charge transition
1.64	c	Oh Co^3+ t2g → Td Co^2+ t2	Inter-sublattice charge transition
2.55	d	O 2p → Td Co^2+ t2	Ligand-to-metal charge transition
2.90	e	O 2p → Oh Co^3+ eg	Ligand-to-metal charge transition

---

The electronic density of states and band structure of Co₃O₄ have been previously calculated using many approaches including, but not limited to GGA + U, hybrid functional PBE0, range-separated exchange–correlation functional HSE06, and many-body Green's function GW approximation.^27,51,52 Commonly, the density of states shows some degree of Co 3d and O 2p wavefunction overlap at the band edges; however, depending on the computational approach, the band gap varies from 0.78 to 1.6 eV.^27,51,52 Singh, et al. explored many different DFT approaches to calculating the electronic structure of Co₃O₄, including PBE, PBE + U_eff, HSE06, and many-body Green's function using the GW approximation (Sc-GW0).⁵² Of these, the Sc-GW0 method produces the most accurate representation of the electronic structure of Co₃O₄ based on computed electronic bands, density of states, and absorption spectra.⁵² Although the absorption spectrum computed with Sc-GW0 exhibits a high oscillator strength between ∼0.5 and 2.0 eV,⁵² unlike our DFT + U + J approach, it cannot resolve the two distinct transitions at 0.8 and 1.6 eV reported in experimental optical spectra.^{27,36,37,41,45}

The experimental presence of the 0.8-eV optical transition and discrepancies in the band gap energies computed with various approaches has led to debate over defining the optical band gap of Co₃O₄: some report it as 0.8 eV,^27,39,53 while others define it to be 1.6 eV.^41,54 The incongruity in reported band gap energies is scrutinized by Smart, et al. in their work modelling Co₃O₄ optical transitions with DFT + U and a hybrid functional that includes a fraction of Hartree–Fock exchange.⁵⁵ They propose the 0.8-eV optical transition arises from photoinduced formation of a small hole polaron, and that this transition becomes most apparent upon application of uniaxial lattice strain.⁵⁵ Our calculation of the ground-state electronic structure of Co₃O₄ using a Hubbard- and Hund- corrected plane-wave pseudopotential approach demonstrates that the low-energy transition at 0.8 eV (and its 0.9-eV shoulder) originate from localized Co²⁺ T_d valence bands (e). Additionally, the corresponding empty Co²⁺ T_d conduction bands (t₂) participate in the observed transition at 1.64 eV, indicating the importance of T_d Co²⁺ electronic character to this transition as well. Although the computational approach used here is a single-particle method that neglects many-body perturbations and nuclear motion, its ability to capture all the features observed in the experimental dielectric spectrum supports its accuracy in describing the nature of the bands that contribute to optical transitions in Co₃O₄. Because the dielectric spectrum reported here is calculated within the Born–Oppenheimer approximation, transitions originating from ground states containing nuclear displacements are not captured, contrasting the description of the 0.8 eV transition as involving a lattice strain-induced small hole polaron by Smart, et al.⁵⁵

Optical phonon enhancement in Co₃O₄

We assess phonon coupling to various optical transitions in Co₃O₄ using Stokes resonance Raman spectroscopy. Fig. 3A plots a series of resonance Raman spectra collected for a 428-nm thick Co₃O₄ film deposited on a sapphire substrate using a variety of excitation lasers with photon energies ranging from 1.49 to 3.06 eV, which spans the Co₃O₄ absorption spectrum (Fig. 3B). These Raman spectra of Co₃O₄ each contain five phonon modes, consistent with previous reports.^56,57 The phonon mode at 86 meV (oxygen breathing about T_d Co²⁺, Fig. 4D) is the most intense at all excitation energies, except hν_exc = 1.88 eV, which corresponds to the inter-sublattice charge transfer transition (O_h Co³⁺ t_2g → T_d Co²⁺ t₂). When Co₃O₄ is excited with a photon energy of 1.58 eV, which correspond to the lower-energy edge of this inter-sublattice charge transfer peak, the 86 meV phonon mode becomes most intense again. Fig. 3C plots the excitation spectrum for each phonon mode corrected for scattering cross section and sample absorption, which enables the comparison of phonon mode intensities across different excitation energies. This quantitative analysis of relative intensities reveals that there is amplified resonance enhancement of all modes upon excitation at 1.49 eV, indicating strong phonon coupling to this optical transition. This analysis was repeated on a thin film of Co₃O₄ deposited on quartz, and the same trends are apparent (Fig. S7†). Given that the 86-meV phonon mode is most intense at an excitation energy of 1.49 eV, we propose it is this phonon mode that most strongly couples to the optical transition at 1.49 eV.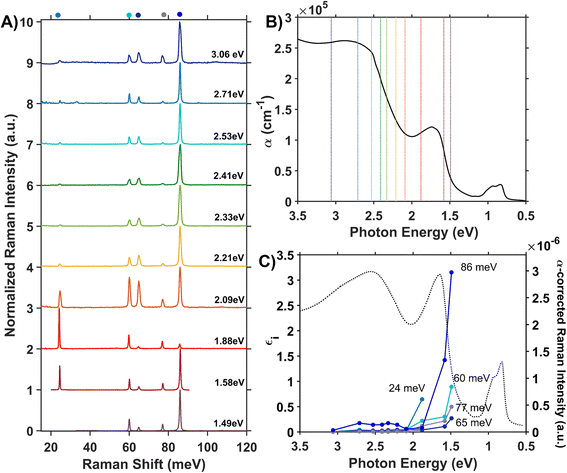

Fig. 3 (A) Internally normalized Stokes Raman spectra of Co₃O₄ collected with various excitation energies that span the absorption spectrum plotted in (B). Raman spectra are vertically offset for clarity. Because the spectra are internally normalized, only relative changes in phonon mode intensity can be assessed as a function of excitation energy. Note that the spectrum excited with 1.49 eV begins at a Raman shift of 30 meV due to instrumental constraints, primarily the bandwidth of the filter used to remove Rayleigh scattering. (C) Plot of the intensities of the various Raman modes shown in part A corrected for scattering cross section and sample absorption superimposed on the imaginary dielectric spectrum. Note the corresponding color point of each phonon mode indicated above the relevant Raman peak in A. For the full correction, see ESI Fig. S5.†

Fig. 4 (A) Raman spectrum of Co₃O₄ collected with a excitation photon energy of 1.58 eV overlaid with the energies of DFT + U + J-computed Raman-active phonon modes. The atomic displacements corresponding to the modes at 24 meV (B), 60 meV (C) and 86 meV (D) are shown. The circled atoms demonstrate the vector displacements of the phonon modes in a 2 × 2 × 1 super cell, where T_d sites are most shifted at 24 meV, O_h sites at 60 meV and oxygens surrounding T_d sites at 86 meV. Note that the extra oxygen atoms in the 24 meV and 86 meV vector-displacement images appear from the displacement of the neighboring super-cell.

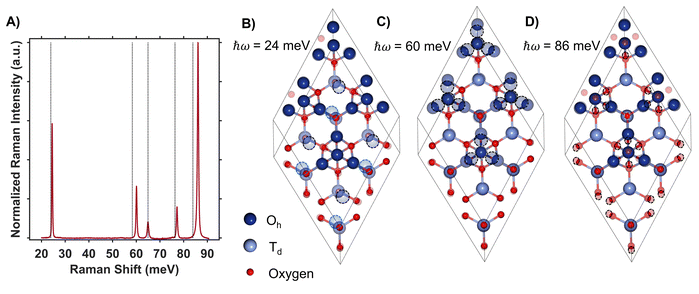
DFT + U + J was used to calculate the displacement vectors of all 39 optical phonon modes in Co₃O₄ at k-point Γ (Table S2†). White and DeAngelis determined through evaluating the Raman selection rules that there are five Raman active modes in normal spinel oxides.⁵⁸ The symmetry of these modes was compared with the displacement vectors computed with DFT + U + J to identify the Raman active modes, the energies of which are overlaid with the Raman spectrum in Fig. 4A. From the resonance Raman profile (Fig. 3A and C), the phonon modes with energies of 24, 60, and 86 meV exhibit the most significant resonance enhancement upon excitation at 1.49 eV, corresponding to the onset of the absorption feature centered at 1.64 eV. These modes correspond to motion of tetrahedral Co²⁺ (24 meV), octahedral Co³⁺ (60 meV), and oxygen stretching symmetrically about Co²⁺ T_d atoms (86 meV, Fig. 4B–D).

The observed enhancement of the 24-meV (T_d Co²⁺motion) and 60-meV (O_h Co³⁺ motion) phonons at a Raman excitation energy of 1.49 eV is related to the contribution of both T_d Co²⁺ and O_h Co³⁺ electronic character to this optical transition, which corresponds to population of empty T_d Co²⁺ t₂ conduction band states from O_h Co³⁺ t_2g valence band states. Although both T_d Co²⁺ and O_h Co³⁺ phonon modes exhibit resonance enhancement because of associated electronic character in the optical transition centered at 1.64 eV, it is the oxygen breathing mode about Co²⁺ T_d ions at 86 meV that exhibits the most enhancement. The degree of energetic overlap between the O 2p and Co²⁺ T_d projected density of states in the conduction band at the energy of the O_h Co³⁺ t_2g →T_d Co²⁺ t₂ transition is significant (Fig. 2B and D) and supports the observed enhancement of the 86-meV phonon, which corresponds to motion of oxygen atoms along their bond axes to T_d Co²⁺.

Temperature dependence of optical transitions

To further understand the role of phonon coupling in the optical transitions of Co₃O₄, we measured the dependence of its dielectric spectrum on temperature between 82 and 470 K. Fig. 5A and B plot the resulting thermal difference spectra (TDS) calculated according to eqn (1).

Δε_i(T) = ε_i,T − ε_i,294K (1)

Fig. 5 Thermal difference imaginary dielectric spectra of Co₃O₄ collected at temperatures above (A) and below (B) room temperature (294 K). (C) Absolute value of the thermal difference spectra integrated from 0.68 to 1.86 eV and normalized to the integrated intensity of the spectrum collected at 82 K plotted versus temperature (black circles). The solid blue line plots the temperature-dependent change in Bose–Einstein population of a phonon with an energy of 24 meV. Bose–Einstein distributions corresponding to the energies of the other Raman active phonon modes are plotted as dotted lines.

We assessed the impact of temperature on the dielectric spectrum by integrating the intensity of the thermal difference spectra. Fig. 5C (blue) plots the absolute value of the thermal difference spectra integrated from 0.68 to 1.86 eV and normalized to the integrated intensity obtained from the spectrum collected at 82 K. To account for sign changes, the integrands of spectra collected below room temperature are shown as negative, and those collected above room temperature are positive. For phonon-coupled optical transitions, we expect the change in intensity with changing temperature to be proportional to the change in population of the coupled phonons. The thermal population of phonon modes is dictated by the Bose–Einstein distribution shown in eqn (2), where ħΩ is the phonon energy. Normalization of the differential spectra to an arbitrary temperature, in this case 82 K, leads to eqn (3), where we compare the change in intensity of the dielectric spectrum (Δε defined in eqn (1)) to the change in population of the Raman active phonon modes at various temperatures.

The temperature dependence of the TDS intensity overlays well with the change in population of the 24-meV Raman-active phonon with temperature predicted by the Bose–Einstein distribution (eqn (3)). This agreement suggests that the low energy optical transitions (1.64 eV, 0.96 eV and 0.82 eV) are coupled strongly to the thermal population of this phonon. Interestingly, the 24-meV phonon mode is not the most enhanced in resonance Raman spectra collected with an excitation photon energy of 1.49 eV; however, both the 24-meV and 86-meV phonon modes are described by displacement vectors primarily of or around T_d Co²⁺ions (Fig. 4B and D). Evidence of thermally activated optical transitions combined with strong phonon coupling to optical transitions observed in resonance Raman spectra (vide supra) suggests an optically accessed polaronic state related to T_d Co²⁺. Compared to resonance Raman measurements, thermal difference spectra are not as precise in determining the energies of the specific phonon modes coupling to the optical transition, as there may be multiple phonon modes contributing to thermal activation. However, the Bose–Einstein distribution corresponding to a phonon energy of 24 meV overlays the temperature-dependent TDS intensities much better than the distributions corresponding to other Raman-active phonon modes (Fig. 5C). We therefore interpret the threshold phonon energy of 24 meV to be where thermal activation occurs. Similar temperature-dependent behavior is observed in α-Fe₂O₃: at the excitation energy where maximal Raman enhancement is observed (∼2.2 eV), the strongest temperature-dependence in the optical spectrum is also present.²⁹ Thermal activation of optical transitions in α-Fe₂O₃ is the proposed mechanism by which direct excitation into intrinsic polaronic states occurs.^29,30 The similarities in the trends of Raman enhancement and the temperature-dependence of the dielectric spectrum observed for Co₃O₄ and α-Fe₂O₃ support the presence of an optically accessible polaronic state in Co₃O₄ arising from coupling to intrinsic, dynamic lattice distortions (phonons) (Fig. 1, red arrow).

Co₃O₄ compared to ZnCo₂O₄: assessing the role of T_d Co in spinel oxides

The resonance Raman and thermal difference spectra of Co₃O₄ suggest that Co²⁺ ions occupying T_d sites are involved in the phonon-coupled optical transitions. To further understand the role of T_d Co²⁺ in the optical spectra of Co₃O₄, we assessed the optical properties of ZnCo₂O₄, where Zn²⁺ replaces T_d Co²⁺ (Fig. 6A). We computed the imaginary dielectric spectrum for normal ZnCo₂O₄ with DFT + U (see ESI for details†). Within normal ZnCo₂O₄, the T_d Zn²⁺ 3d orbitals are completely filled, and the O_h Co³⁺ 3d orbitals have a low-spin configuration, termed “quasi close-shelled”.^59,60 With no unpaired electrons present, the Hund parameter, J, is not implemented in these calculations. The DFT + U calculations of normal ZnCo₂O₄ reveal two absorption bands at and above ∼2.5 eV, while the experimental spectrum only has one transition in this region. Literature reports assign the experimentally observed feature at 3.0 eV to an LMCT-type transition,^27,38 which matches the lower energy peak (2.5 eV) observed in the DFT + U dielectric spectrum. The 3.5 eV peak in the DFT + U dielectric spectrum computed here is associated with an intra-sublattice charge transfer (O_h Co³⁺ t_2g → O_h Co³⁺ e_g). Because this is a charge transfer between two different lattice sites, the Laporte selection rule does not apply. Due to the hybridized nature of the Co 3d and O 2p orbitals in both the valence and conduction bands, we assign the experimental dielectric peak at 3.0 eV to a combination of LMCT and intra-sublattice charge transfer transitions (see Fig. S11 in the ESI†). Interestingly, when comparing the experimental peak shape of the dielectric transition at 3.0 eV in ZnCo₂O₄ (Fig. 6B) to the analogous transition in Co₃O₄ (Fig. 2C and S12†), it becomes apparent that the shoulder in Co₃O₄ (labeled e in Fig. 2C) is at the same energy as the peak center of the experimental ZnCo₂O₄ transition. This energetic alignment in the experimental dielectric spectra, used to assign the 2.90-eV shoulder in Co₃O₄ as excitation into O_h Co³⁺ e_g bands, has been observed previously in a Zn dopant study of Co₃O₄.³⁸

Fig. 6 (A) Unit cell of normal ZnCo₂O₄ with associated crystal field splitting diagrams of Co³⁺ in octahedral and tetrahedral coordination. (B) Plot of experimentally (solid green line) and computationally (dashed black line) determined imaginary dielectric spectra of ZnCo₂O₄. The computed dielectric spectrum was calculated for normal ZnCo₂O₄. (C) The electronic density of states calculated with Hubbard-corrected DFT for normal Co₃O₄ (top), ZnCo₂O₄ with an inversion factor of 0.125 (middle), and normal ZnCo₂O₄ (bottom).

The lower-energy region of the experimental dielectric spectrum of ZnCo₂O₄ contains broad and weak features at 1.79, 0.98 and 0.82 eV, which coincide with where Co₃O₄ has transitions associated with Co²⁺ T_d. X-ray fluorescence analysis indicates the stoichiometry of the ZnCo₂O₄ film used to produce the dielectric spectrum is 1.94 ± 0.04 Co : Zn, and the powder X-ray diffraction pattern indicates the film is phase-pure spinel (Fig. S3†). We therefore suspected that our ZnCo₂O₄ film may be slightly inverted and contain a small population of cobalt in tetrahedral sites, consistent with previous reports.⁶¹ In an effort to control cation distribution in ZnCo₂O₄, we changed the temperature at which ZnCo₂O₄ films were annealed following spin-coating. We observe that annealing above 600 °C induces phase separation as features associated with ZnO become apparent in the X-ray diffraction pattern and Raman spectra (Fig. S13 and S14†). Additionally, as annealing temperature increases, the low energy peaks observed in the dielectric spectrum increase in intensity (Fig. S15†). We therefore suspect that the films containing ZnO also contain Co₃O₄, which accounts for the presence of the intense low-energy peaks in the dielectric spectrum (Fig. S15†). With no ZnO peaks present in X-ray diffraction or ZnO phonon modes observed in Raman for the films annealed at 600 °C, we hypothesize that the weak, low-intensity features observed in the dielectric spectra of these films arise from cation inversion, whereby a fraction of the Co ions occupy T_d sites and a fraction of the Zn ions occupy O_h sites. We describe the Co ions in T_d sites as substitutional lattice defects.

To investigate the impact of cation inversion on the optical spectra of ZnCo₂O₄, we computed the electronic structure of inverted ZnCo₂O₄ using DFT + U + J (see ESI for details†). Inverted ZnCo₂O₄ (i-ZnCo₂O₄) was modeled by switching two O_h Co³⁺ ions with two T_d Zn²⁺ ions within a 2×2×2 supercell of normal ZnCo₂O₄ to produce an inversion factor of x = 0.125 while maintaining charge balance and stoichiometry. The resulting two T_d Co³⁺ ions were modeled to be antiferromagnetically coupled to maintain net-zero magnetization. Compared to normal ZnCo₂O₄ (n-ZnCo₂O₄), i-ZnCo₂O₄ contains an isolated state at the valence band-edge with primarily T_d Co and O 2p character (Fig. 6C, middle and bottom). The conduction band edge in i-ZnCo₂O₄ appears at a lower energy than that in n-ZnCo₂O₄ (similar to Co₃O₄), and i-ZnCo₂O₄ contains an isolated region at the conduction band-edge of primarily O_h Co and O 2p character (Fig. 6C, middle and top). The band-edge character of i-ZnCo₂O₄, despite the 3+ oxidation state of the cobalt ion in T_d sites, has more similarities to that of Co₃O₄ than n-ZnCo₂O₄ (Fig. 6C). Thus, the presence of Co (T_d) in spinel oxides results in low-energy d-to-d transitions, regardless of its oxidation state (+2 or +3). Because there is no evidence of phase separation (i.e. presence of Co₃O₄) to describe the low-energy features in the dielectric, we conclude the synthesized ZnCo₂O₄ contains at least a small degree of inversion.

The Raman spectrum of ZnCo₂O₄ has five distinct modes (Fig. 7A and B) consistent with previous reports.^62,63 The phonon mode frequencies are similar to those observed in Co₃O₄, which is expected, as both materials adopt the spinel crystal structure. Additionally, the 23-meV, 61-meV, and 89-meV phonon modes in ZnCo₂O₄ are described by the same phonon motions as in Co₃O₄: motion of T_d metal center motion of O_h metal center, and oxygen stretching about T_d sites respectively (Fig. 4B–D). Fig. 7B (top) plots the experimental Raman spectrum of ZnCo₂O₄ overlaid with the computed phonon modes of normal ZnCo₂O₄. While the five prominent phonon modes are accounted for by DFT + U phonon calculations, there are two broad and weak features at 26 meV and 85 meV that do not appear in calculations. Both phonons have similar energies to corresponding modes observed in Co₃O₄, which are both related predominantly to T_d sites (Fig. 7B, bottom). The discrepancy between the energies of experimentally observed Raman-active optical phonon modes and the computed modes of normal ZnCo₂O₄ can be explained by the sample crystallizing with a degree of inversion. With a small percentage of tetrahedral sites occupied by Co³⁺, and the rest by Zn²⁺, the phonon modes dominated by tetrahedral motion (∼24 meV and ∼89 meV) split into two distinct distributions. This phenomenon has been observed in other inverted spinel oxides⁶⁴ and is further evidence of the ZnCo₂O₄ films crystallizing with a small percent occupation of cobalt in tetrahedral sites (Fig. 7B).

Fig. 7 (A) Internally normalized Raman spectra of a ZnCo₂O₄ thin film deposited on a sapphire substrate collected with excitation photon energies that span its absorption spectrum. Because the spectra are internally normalized, only relative changes in phonon mode intensity can be assessed as a function of excitation energy (see ESI† for full work-up of Raman data). (B) Raman spectra of ZnCo₂O₄ (top) and Co₃O₄ (bottom) excited at a photon energy of 1.58 eV are overlaid with the Raman-active phonon modes computed for normal ZnCo₂O₄ and Co₃O₄, respectively. (C) Plot of the intensities of the various Raman modes shown in part A corrected for scattering cross section and sample absorption superimposed on the imaginary dielectric spectrum of ZnCo₂O₄. Note the corresponding color point of each phonon mode indicated above the relevant Raman peak in A.

Unlike Co₃O₄, the resonance Raman profile of ZnCo₂O₄ does not exhibit increased resonance enhancement of the phonons associated with T_d motion (23 and 89 meV) with decreasing excitation energy. In contrast, the 61-meV phonon, related to Co O_h motion (described by Fig. 4B), exhibits enhanced intensity in ZnCo₂O₄ relative to all the other modes as excitation photon energy decreases (Fig. 7A). Interestingly, when the Raman profile is corrected for scattering cross section and sample absorption, the 61-meV mode is most enhanced at an excitation photon energy of 1.49 eV – the same excitation photon energy at which the most significant resonance enhancement is observed in Co₃O₄ (Fig. 3C and Fig. 7C). This analysis was repeated on a thin film of ZnCo₂O₄ deposited on quartz, and the same trends are apparent (Fig. S8†). The similarity in excitation photon energy where resonance enhancement is observed in ZnCo₂O₄ and Co₃O₄ indicates that the onset of the optical transition centered at ∼1.6 eV is significant for both materials.

Based on the calculated density of states of inverted ZnCo₂O₄ (Fig. 6C), the experimental optical transition observed at 1.6 eV is assigned to metal-to-metal charge transfer (MMCT) from bands with T_d Co³⁺ character (arising from the T_d Co substitutional defects) to bands with O_h Co³⁺ character. The most enhanced Raman spectrum (hν_exc = 1.49 eV) occurs upon excitation at the onset of the 1.6-eV transition, implying that the presence of the Co³⁺ T_d substitutional defect is crucial for the observed enhancement of the O_h phonon in ZnCo₂O₄. The conduction band character associated with the 1.6-eV transition arises from 3d orbitals associated with Co³⁺ O_h, the same site associated with the main vibrational motion of the 61-meV phonon (Fig. 4C). Although the strong resonance enhancement observed for the 61-meV phonon in ZnCo₂O₄ is evidence of strong coupling between this mode and the optical transition at 1.6 eV, we do not observe significant temperature dependence of this transition in thermal difference spectra when compared to Co₃O₄ (see Fig. S16 in ESI†). In fact, unlike Co₃O₄, the thermal difference spectra collected for ZnCo₂O₄ at elevated temperatures do not exhibit any well-defined features corresponding to spectral features observed in the dielectric spectrum at room temperature.

The spectral and computational results reported here for ZnCo₂O₄ and Co₃O₄ indicate that Co 3d character at the band edge mediates phonon-coupled optical transitions (Fig. 3C, 4C, D and 7C). However, the contrast in temperature-dependence of the optical transition where both materials exhibit the strongest phonon coupling (1.6 eV) suggests fundamentally different processes dictating the observed enhancement. We interpret our findings in Co₃O₄ as direct population of an intrinsic polaronic state via photoexcitation, which is strongly influenced by the contributions of Co²⁺ T_d ions to band-edge states. In ZnCo₂O₄, we interpret the experimental ZnCo₂O₄ sample to have a small percent occupation of tetrahedral sites by Co based on the presence of low-energy optical transitions associated with T_d Co. Although the occupation of Co³⁺ in tetrahedral sites enables the optical transition and phonon enhancement at 1.6 eV, the lack of significant temperature dependence of this optical transition indicates that the phonon-coupled optical transitions leading to Raman enhancement in ZnCo₂O₄ are fundamentally different from those observed in Co₃O₄.

We suspect that the differences observed in the thermal difference spectra of Co₃O₄ and ZnCo₂O₄ are related to the disruption in the translational symmetry of the lattice induced by cation inversion in ZnCo₂O₄. From assignment of optical transitions in Co₃O₄, the low-energy optical transitions are either highly localized transitions between neighboring Co atoms or intra-atomic transitions in T_d Co (Table 1). With fewer Co atoms in T_d sites, these optical transitions become suppressed, as observed in ZnCo₂O₄ (Fig. 6B); however, the localized transitions still exhibit phonon coupling, leading to the observed resonance Raman enhancements (Fig. 7C). The lack of temperature dependence of these transitions in ZnCo₂O₄ suggests that, although these transitions access localized phonon-coupled states, the localization is related to the static lattice defect of tetrahedral cobalt rather than thermally induced dynamic lattice displacements within a pristine, translationally symmetric lattice. The lack of thermal dependence in ZnCo₂O₄, but presence of resonance Raman enhancement of O_h phonon modes upon excitation of a transition from T_d Co to O_h Co, is strong evidence of an optically accessed polaronic state. We therefore conclude that in both Co₃O₄ and ZnCo₂O₄ there is evidence of an optically accessible polaronic state. However, in Co₃O₄ formation of the polaronic state is due to intrinsic, dynamic lattice deformations caused by thermally activated phonons (exactly analogous to the mechanism we observe in hematite), whereas in ZnCo₂O₄, photoinduced polaron formation is mediated by static lattice defects arising from cation inversion.

Conclusions

The optical characterization of Co₃O₄ and ZnCo₂O₄ reported here shows that low energy transitions at 0.8, 0.9 eV and 1.6 eV arise from tetrahedrally coordinated cobalt ions, regardless of oxidation state (Co²⁺, Co³⁺). The d–d transition observed at 1.6 eV in both Co₃O₄ and ZnCo₂O₄ is a phonon-coupled optical transition. In Co₃O₄, the combination of temperature-dependent intensity and resonance Raman enhancement at the onset of the O_h Co³⁺ → T_d Co²⁺ optical transition (1.64 eV) is evidence that this transition directly populates an intrinsic polaron state coupled to thermally activated phonons. Although the resonance Raman profile of ZnCo₂O₄ exhibits a similar Raman enhancement upon excitation of the 1.6-eV transition, the observed inversion and lack of temperature dependence suggests that this photoexcited polaron forms due to the presence of tetrahedral cobalt substitutional defects within the lattice. We conclude that T_d-coordinated cobalt is a significant factor in phonon-coupled transitions for cobalt-containing spinel oxides. The contrast in the mechanism of polaron formation (intrinsic or self-trapped polaron vs. defect-mediated polaron) observed for these similar materials is an important insight that we anticipate will help uncover mechanisms of photoinduced polaron formation in other oxide materials. Although both mechanisms of polaron formation observed here have been previously reported, understanding the spectral signatures that distinguish them is crucial for further development of oxide materials for photo-applications.

Data availability

Data supporting this article have been included as part of the ESI.† Primary data are available from the authors upon reasonable request.

Author contributions

E. P. C., J. L. S., and K. E. K. contributed to conceptualization of the project and interpretation of the data; K. E. K. supervised the project. E. P. C. performed most experiments and computations. J. L. S. contributed to some computations for Co₃O₄. M. T. R. collected low-frequency Raman spectra. E. P. C. wrote the manuscript. All authors reviewed the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support for this work was provided by the University of Rochester via a University Research Award. M. T. R. thanks the USA National Science Foundation for financial support (DMR-2348765). The authors acknowledge the University of Rochester Raman Facility and thank David McCamant for discussion about Raman collection. We are grateful to the computational resources and technical assistance from the University of Rochester Center for Integrated Research Computing. For X-ray diffraction and energy dispersive X-ray emission measurements, we acknowledge the Chemical Analysis Laboratory Material Science Facilities at Rochester Institute of Technology and thank Tom Allston for guidance on measurements. We thank Todd Krauss and URNano for access to atomic force microscopes (AFM) and thank Alex Searle for collection and processing of AFM data, as well as Sean O'Neill and Lisbeth Compton for discussions regarding AFM collection and work-up. We acknowledge URNano for profilometry measurements and thank Gregory Madjeski for discussions regarding data collection.

References

1. D. Franchi and Z. Amara, Applications of Sensitized Semiconductors as Heterogeneous Visible-Light Photocatalysts in Organic Synthesis, ACS Sustainable Chem. Eng., 2020, 8(41), 15405–15429.
2. J. Luo, S. Zhang, M. Sun, L. Yang, S. Luo and J. C. Crittenden, A Critical Review on Energy Conversion and Environmental Remediation of Photocatalysts with Remodeling Crystal Lattice, Surface, and Interface, ACS Nano, 2019, 13(9), 9811–9840.
3. F. J. Morin, Electrical Properties of α-Fe₂O₃, Phys. Rev., 1954, 93(6), 1195–1199.
4. F. J. Morin, Electrical Properties of NiO, Phys. Rev., 1954, 93(6), 1199–1204.
5. J. Husek, A. Cirri, S. Biswas and L. R. Baker, Surface Electron Dynamics in Hematite (α-Fe₂O₃): Correlation between Ultrafast Surface Electron Trapping and Small Polaron Formation, Chem. Sci., 2017, 8(12), 8170–8178.
6. S. Biswas, J. Husek, S. Londo and L. R. Baker, Ultrafast Electron Trapping and Defect-Mediated Recombination in NiO Probed by Femtosecond Extreme Ultraviolet Reflection–Absorption Spectroscopy, J. Phys. Chem. Lett., 2018, 9(17), 5047–5054.
7. C. Franchini, M. Reticcioli, M. Setvin and U. Diebold, Polarons in Materials, Nat. Rev. Mater., 2021, 6(7), 560–586.
8. L. Landau, Über die Bewegung der Elektronen im Kristallgitter, Phys. Z. Sowjetunion, 1933, 3, 644–645.
9. T. Holstein, Studies of Polaron Motion: Part I. The Molecular-Crystal Model, Ann. Phys., 1959, 8(3), 325–342.
10. T. Holstein, Studies of Polaron Motion: Part II. The “Small” Polaron, Ann. Phys., 1959, 8(3), 343–389.
11. P. Nagels, M. Denayer and J. Devreese, Electrical Properties of Single Crystals of Uranium Oxide, Solid State Commun., 1963, 1(2), 35–40.
12. H. Fröhlich, Electrons in Lattice Fields, Adv. Phys., 1954, 3(11), 325–361.
13. X. Mettan, J. Jaćimović, O. S. Barišić, A. Pisoni, I. Batistić, E. Horváth, S. Brown, L. Rossi, P. Szirmai, B. Farkas, H. Berger and L. Forró, Tailoring Thermal Conduction in Anatase TiO₂, Commun. Phys., 2019, 2(1), 123.
14. M. Reticcioli, U. Diebold, G. Kresse, and C. Franchini, Small Polarons in Transition Metal Oxides, in Handbook of Materials Modeling, W. Andreoni, and S. Yip, Springer International Publishing, Cham, 2020, pp 1035–1073.
15. I. G. Austin, A. J. Springthorpe, B. A. Smith and C. E. Turner, Electronic Transport Phenomena in Single-Crystal NiO and CoO, Proc. Phys. Soc., 1967, 90(1), 157–174.
16. S. Yang, A. T. Brant, N. C. Giles and L. E. Halliburton, Intrinsic Small Polarons in Rutile TiO₂, Phys. Rev. B, 2013, 87(12), 125201.
17. H. L. Tuller and A. S. Nowick, Small Polaron Electron Transport in Reduced CeO₂ Single Crystals, J. Phys. Chem. Solids, 1977, 38(8), 859–867.
18. F. Esch, S. Fabris, L. Zhou, T. Montini, C. Africh, P. Fornasiero, G. Comelli and R. Rosei, Electron Localization Determines Defect Formation on Ceria Substrates, Science, 2005, 309(5735), 752–755.
19. R. Karsthof, M. Grundmann, A. M. Anton and F. Kremer, Polaronic Interacceptor Hopping Transport in Intrinsically Doped Nickel Oxide, Phys. Rev. B, 2019, 99(23), 235201.
20. S. Biswas, S. Wallentine, S. Bandaranayake and L. R. Baker, Controlling Polaron Formation at Hematite Surfaces by Molecular Functionalization Probed by XUV Reflection-Absorption Spectroscopy, J. Chem. Phys., 2019, 151(10), 104701.
21. N. Mansourian-Hadavi, S. Wansom, N. H. Perry, A. R. Nagaraja, T. O. Mason, L. Ye and A. J. Freeman, Transport and Band Structure Studies of Crystalline ZnRh₂O₄, Phys. Rev. B, 2010, 81(7), 075112.
22. T. Feng, L. Li, Q. Shi, S. Dong, B. Li, K. Li and G. Li, Evidence for the Influence of Polaron Delocalization on the Electrical Transport in LiNi_0.4+x Mn_0.4−x Co_0.2 O₂, Phys. Chem. Chem. Phys., 2020, 22(4), 2054–2060.
23. N. C. Verissimo, F. A. Pires, I. Rodríguez-Gutiérrez, J. Bettini, T. E. R. Fiuza, C. A. Biffe, F. E. Montoro, G. R. Schleder, R. H. R. Castro, E. R. Leite and F. L. Souza, Dual Modification on Hematite to Minimize Small Polaron Effects and Charge Recombination for Sustainable Solar Water Splitting, J. Mater. Chem. A, 2024, 12(11), 6280–6293.
24. S. Bandaranayake, A. Patnaik, E. Hruska, Q. Zhu, S. Das and L. R. Baker, Effect of Surface Electron Trapping and Small Polaron Formation on the Photocatalytic Efficiency of Copper(I) and Copper(II) Oxides, ACS Appl. Mater. Interfaces, 2024, 16(31), 41616–41625.
25. H. Gajapathy, S. Bandaranayake, E. Hruska, A. Vadakkayil, B. P. Bloom, S. Londo, J. McClellan, J. Guo, D. Russell, F. M. F. de Groot, F. Yang, D. H. Waldeck, M. Schultze and L. R. Baker, Spin Polarized Electron Dynamics Enhance Water Splitting Efficiency by Yttrium Iron Garnet Photoanodes: A New Platform for Spin Selective Photocatalysis, Chem. Sci., 2024, 15(9), 3300–3310.
26. C.-S. Cheng, M. Serizawa, H. Sakata and T. Hirayama, Electrical Conductivity of Co₃O₄ Films Prepared by Chemical Vapour Deposition, Mater. Chem. Phys., 1998, 53(3), 225–230.
27. X. C. Huang, J. Y. Zhang, M. Wu, S. Zhang, H. Y. Xiao, W. Q. Han, T.-L. Lee, A. Tadich, D.-C. Qi, L. Qiao, L. Chen and K. H. L. Zhang, Electronic Structure and p-Type Conduction Mechanism of Spinel Cobaltite Oxide Thin Films, Phys. Rev. B, 2019, 100(11), 115301.
28. L. M. Carneiro, S. K. Cushing, C. Liu, Y. Su, P. Yang, A. P. Alivisatos and S. R. Leone, Excitation-Wavelength-Dependent Small Polaron Trapping of Photoexcited Carriers in α-Fe₂O₃, Nat. Mater., 2017, 16(8), 819–825.
29. J. L. Shelton and K. E. Knowles, Thermally Activated Optical Absorption into Polaronic States in Hematite, J. Phys. Chem. Lett., 2021, 12(13), 3343–3351.
30. J. L. Shelton and K. E. Knowles, Polaronic Optical Transitions in Hematite (α-Fe₂O₃) Revealed by First-Principles Electron–Phonon Coupling, J. Chem. Phys., 2022, 157(17), 174703.
31. F. Freytag, G. Corradi and M. Imlau, Atomic Insight to Lattice Distortions Caused by Carrier Self-Trapping in Oxide Materials, Sci. Rep., 2016, 6(1), 36929.
32. Y. Yamada, O. Hino, S. Nohdo, R. Kanao, T. Inami and S. Katano, Polaron Ordering in Low-Doping La_1−xSr_xMnO₃, Phys. Rev. Lett., 1996, 77(5), 904–907.
33. G. Allodi, M. Cestelli Guidi, R. De Renzi, A. Caneiro and L. Pinsard, Ultraslow Polaron Dynamics in Low-Doped Manganites from ¹³⁹La NMR-NQR and Muon Spin Rotation, Phys. Rev. Lett., 2001, 87(12), 127206.
34. S. X. Zhang, D. C. Kundaliya, W. Yu, S. Dhar, S. Y. Young, L. G. Salamanca-Riba, S. B. Ogale, R. D. Vispute and T. Venkatesan, Niobium Doped TiO₂: Intrinsic Transparent Metallic Anatase versus Highly Resistive Rutile Phase, J. Appl. Phys., 2007, 102(1), 013701.
35. E. Possenriede, H. Kröse, T. Varnhorst, R. Scharfschwerdt and O. F. Schirmer, Shallow Acceptor and Electron Conduction States in BaTiO₃, Ferroelectrics, 1994, 151(1), 199–204.
36. J. G. Cook and M. P. van der Meer, The Optical Properties of Sputtered Co₃O₄ Films, Thin Solid Films, 1986, 144(2), 165–176.
37. K. M. E. Miedzinska, B. R. Hollebone and J. G. Cook, An Assignment of the Optical Absorption Spectrum of Mixed Valence Co₃O₄ Spinel Films, J. Phys. Chem. Solids, 1987, 48(7), 649–656.
38. K. J. Kim and Y. R. Park, Optical Investigation of Charge-Transfer Transitions in Spinel Co₃O₄, Solid State Commun., 2003, 127(1), 25–28.
39. L. Qiao, H. Y. Xiao, H. M. Meyer, J. N. Sun, C. M. Rouleau, A. A. Puretzky, D. B. Geohegan, I. N. Ivanov, M. Yoon, W. J. Weber and M. D. Biegalski, Nature of the Band Gap and Origin of the Electro-/Photo-Activity of Co₃O₄, J. Mater. Chem. C, 2013, 1(31), 4628–4633.
40. C.-M. Jiang, L. R. Baker, J. M. Lucas, J. Vura-Weis, A. P. Alivisatos and S. R. Leone, Characterization of Photo-Induced Charge Transfer and Hot Carrier Relaxation Pathways in Spinel Cobalt Oxide (Co₃O₄), J. Phys. Chem. C, 2014, 118(39), 22774–22784.
41. M. M. Waegele, H. Q. Doan and T. Cuk, Long-Lived Photoexcited Carrier Dynamics of d–d Excitations in Spinel Ordered Co₃O₄, J. Phys. Chem. C, 2014, 118(7), 3426–3432.
42. P. Aroonratsameruang, P. Chakthranont and P. Pattanasattayavong, The Cause of Limited Photoelectrochemical Water Reduction Performance of Co₃O₄ Photocathodes, Mater. Chem. Phys., 2021, 270, 124834.
43. D. Hayes, R. G. Hadt, J. D. Emery, A. A. Cordones, A. B. F. Martinson, M. L. Shelby, K. A. Fransted, P. D. Dahlberg, J. Hong, X. Zhang, Q. Kong, R. W. Schoenlein and L. X. Chen, Electronic and Nuclear Contributions to Time-Resolved Optical and X-Ray Absorption Spectra of Hematite and Insights into Photoelectrochemical Performance, Energy Environ. Sci., 2016, 9(12), 3754–3769.
44. A. S. M. Ismail, Y. Uemura, S. H. Park, S. Kwon, M. Kim, H. Elnaggar, F. Frati, Y. Niwa, H. Wadati, Y. Hirata, Y. Zhang, K. Yamagami, S. Yamamoto, I. Matsuda, U. Halisdemir, G. Koster, B. M. Weckhuysen and F. M. F. de Groot, Direct Observation of the Electronic States of Photoexcited Hematite with Ultrafast 2p3d X-Ray Absorption Spectroscopy and Resonant Inelastic X-Ray Scattering, Phys. Chem. Chem. Phys., 2020, 22(5), 2685–2692.
45. Y. Zhang, C. Zhang, X. Huang, Z. Yang, K. H. L. Zhang and Y. Yang, Barrierless Self-Trapping of Photocarriers in Co₃O₄, J. Phys. Chem. Lett., 2021, 12(50), 12033–12039.
46. W. L. Roth, The Magnetic Structure of Co₃O₄, J. Phys. Chem. Solids, 1964, 25(1), 1–10.
47. M. Cococcioni and S. de Gironcoli, Linear Response Approach to the Calculation of the Effective Interaction Parameters in the LDA + U Method, Phys. Rev. B, 2005, 71(3), 035105.
48. B. Himmetoglu, R. M. Wentzcovitch and M. Cococcioni, First-Principles Study of Electronic and Structural Properties of CuO, Phys. Rev. B, 2011, 84(11), 115108.
49. M. Zacharias, C. E. Patrick and F. Giustino, Stochastic Approach to Phonon-Assisted Optical Absorption, Phys. Rev. Lett., 2015, 115(17), 177401.
50. Y. Kang, H. Peelaers, K. Krishnaswamy and C. G. Van De Walle, First-Principles Study of Direct and Indirect Optical Absorption in BaSnO₃, Appl. Phys. Lett., 2018, 112(6), 062106.
51. J. Chen, X. Wu and A. Selloni, Electronic Structure and Bonding Properties of Cobalt Oxide in the Spinel Structure, Phys. Rev. B, 2011, 83(24), 245204.
52. V. Singh, M. Kosa, K. Majhi and D. T. Major, Putting DFT to the Test: A First-Principles Study of Electronic, Magnetic, and Optical Properties of Co₃O₄, J. Chem. Theory Comput., 2015, 11(1), 64–72.
53. C. Lohaus, J. Morasch, J. Brötz, A. Klein and W. Jaegermann, Investigations on RF-Magnetron Sputtered Co₃O₄ Thin Films Regarding the Solar Energy Conversion Properties, J. Phys. D: Appl. Phys., 2016, 49(15), 155306.
54. A. F. Lima, Interpretation of the Optical Absorption Spectrum of Co₃O₄ with Normal Spinel Structure from First Principles Calculations, J. Phys. Chem. Solids, 2014, 75(1), 148–152.
55. T. J. Smart, T. A. Pham, Y. Ping and T. Ogitsu, Optical Absorption Induced by Small Polaron Formation in Transition Metal Oxides: The Case of Co₃O₄, Phys. Rev. Mater., 2019, 3(10), 102401.
56. V. G. Hadjiev, M. N. Iliev and I. V. Vergilov, The Raman Spectra of Co₃O₄, J. Phys. C: Solid State Phys., 1988, 21(7), L199–L201.
57. B. Rivas-Murias and V. Salgueiriño, Thermodynamic CoO–Co₃O₄ Crossover Using Raman Spectroscopy in Magnetic Octahedron-shaped Nanocrystals, J. Raman Spectrosc., 2017, 48(6), 837–841.
58. W. B. White and B. A. DeAngelis, Interpretation of the Vibrational Spectra of Spinels, Spectrochim. Acta, Part A, 1967, 23(4), 985–995.
59. Z. Wang, P. K. Nayak, J. A. Caraveo-Frescas and H. N. Alshareef, Recent Developments in p-Type Oxide Semiconductor Materials and Devices, Adv. Mater., 2016, 28(20), 3831–3892.
60. S. Lany, Semiconducting Transition Metal Oxides, J. Phys.: Condens. Matter, 2015, 27(28), 283203.
61. M. Dekkers, G. Rijnders and D. H. A. Blank, ZnIr₂O₄, a p-Type Transparent Oxide Semiconductor in the Class of Spinel Zinc-d⁶-Transition Metal Oxide, Appl. Phys. Lett., 2007, 90(2), 021903.
62. V. Venkatachalam, A. Alsalme, A. Alswieleh and R. Jayavel, Double Hydroxide Mediated Synthesis of Nanostructured ZnCo₂O₄ as High Performance Electrode Material for Supercapacitor Applications, Chem. Eng. J., 2017, 321, 474–483.
63. W. Wang, Facile Hydrothermal Synthesis of ZnCo₂O₄ Nanostructures: Controlled Morphology and Magnetic Properties, J. Mater. Sci.: Mater. Electron., 2021, 32(12), 16662–16668.
64. Z. Ž. Lazarević, Č. Jovalekić, A. Milutinović, D. Sekulić, V. N. Ivanovski, A. Rečnik, B. Cekić and N. Ž. Romčević, Nanodimensional Spinel NiFe₂O₄ and ZnFe₂O₄ Ferrites Prepared by Soft Mechanochemical Synthesis, J. Appl. Phys., 2013, 113(18), 187221.

---

Footnotes

† Electronic supplementary information (ESI) available: Details of experimental procedures for film fabrication and structural characterization, computational methods, additional resonance Raman spectra, thermal difference spectra of ZnCo₂O₄, and tables of computed phonon energies. See DOI: https://doi.org/10.1039/d5sc01909e

‡ Current address: National Renewable Energy Laboratory, Chemistry and Nanoscience Center, Golden, CO, 80401, USA.

---