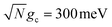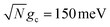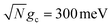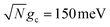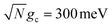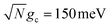Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Polariton mediated electron transfer under the collective molecule–cavity coupling regime†
Eric R. Koessler*a,
Arkajit Mandal b,
Andrew J. Musser
b,
Andrew J. Musser c,
Todd D. Kraussade and
Pengfei Huo
c,
Todd D. Kraussade and
Pengfei Huo *ade
*ade
aDepartment of Chemistry, University of Rochester, 120 Trustee Road, Rochester, NY 14627, USA. E-mail: ekoessle@ur.rochester.edu
bDepartment of Chemistry, Texas A&M University, College Station, TX 77842, USA
cDepartment of Chemistry and Chemical Biology, Cornell University, Ithaca, NY 14853, USA
dThe Institute of Optics, Hajim School of Engineering, University of Rochester, Rochester, NY 14627, USA
eCenter for Coherence and Quantum Optics, University of Rochester, Rochester, NY 14627, USA. E-mail: pengfei.huo@rochester.edu
First published on 19th May 2025
Abstract
We investigate polariton-mediated electron transfer (PMET) under the collective molecule–cavity coupling regime, with the presence of dark state transfer, cavity loss, and continuous-wave (CW) laser driving using quantum dynamics simulations and analytic rate constant theories. We demonstrate how the PMET rate constant can be enhanced by the collective coupling effect, where the light–matter coupling strength is small, yet there are many molecules collectively coupled to the cavity. We first show how reactions initialized in the collective upper polariton (UP) state can significantly enhance the PMET rate constant by decreasing the reaction driving force of an otherwise uphill ET reaction with collective strong coupling and positive detuning. We further show how the PMET rate constant is affected by dark states and cavity loss, which are often regarded as obstacles, and how to overcome them to provide a significant cavity-induced rate constant enhancement under the collective coupling regime. In particular, we show that by driving the UP state with a CW laser in a positively detuned cavity, the effective PMET rate constant can be several orders of magnitude larger than outside the cavity, even with significant molecular disorder and cavity loss. These results reveal a promising approach to realize photochemical rate enhancement with collective strong coupling in disordered and lossy polariton systems, as well as enabling otherwise impractical uphill ET reactions.
1 Introduction
The possibility of modifying and enhancing the rates of photochemical reactions by strong coupling to optical cavities has attracted the excitement of the polariton chemistry community in recent years.1–5 Following experimental demonstrations of chemical rate modification under the vibrational strong coupling (VSC) regime,6–11 recent works in the electronic strong coupling (ESC) regime have demonstrated the modification and enhancement of photochemical reactions inside optical cavities.12–17 While these recent polariton photochemistry experiments have yet to be fully understood with detailed microscopic theory,18–20 there have been numerous theoretical proposals that predict ESC photochemical and photophysical rate modifications inside the cavity for a variety of model systems, such as photoinduced charge transfer,21–33 singlet fission,34–36 intersystem crossing,37,38 exciton energy transfer,39,40 photodissociation,41–49 excited state proton transfer,50 and photoisomerization.51–56While these recent experimental and theoretical polariton photochemistry works are exciting, there has also been concern expressed about the extent to which these proposed modifications can be realized when many (N ∼ 103–109) molecules are collectively coupled to the cavity.20,57 Some polariton photochemistry experiments in the collective coupling regime have failed to observe cavity rate modifications with theoretical explanations typically assigning blame to the presence of the dense manifold of the dark states or cavity loss.17,58–60 Many of the previous theoretical works predicting cavity modification of photochemistry used simplified model systems with only a single strongly-coupled molecule, a set of disorderless molecules, or assume a perfect lossless cavity for analytic and computational convenience and consequentially cannot address the issues of dark states and cavity loss.
Our work builds off of previous theoretical work on PMET,21,22,26,29,31,61–63 particularly the work of Mandal et al. in ref. 21, who performed explicit quantum dynamics simulations and described analytic Marcus theory rate constant expressions for PMET with a single molecule strongly coupled to a lossless cavity mode. Mauro et al. in ref. 22 described analytic Marcus and Fermi's golden rule (FGR) rate constant expressions for PMET with many identical molecules strongly coupled to a lossless cavity mode, as well as simulated PMET population dynamics with a kinetics model that included cavity loss and dark state transfer with FGR.
In this work, we investigate polariton-mediated electron transfer (PMET) in the collective coupling regime under the influence of dark states, cavity loss, and continuous-wave (CW) laser driving. We extend these previous works by performing explicit quantum dynamics simulations of many donor–acceptor molecules with donor states collectively coupled to a lossy cavity mode with CW laser driving. By focusing on the transfer from the polariton manifold of states to the excited acceptor states (i.e. without the influence of transfer to acceptor ground states), the monotonic population dynamics in this work (as opposed to the non-monotonic population dynamics observed in ref. 22) can be accurately fit with effective rate constants. Furthermore, the use of explicit quantum dynamics simulations in this work allows for accurate descriptions of bright polariton to dark state transfer rates in the disordered molecule regime. These effective rate constants fitted from explicit quantum dynamics simulations can describe the effects of cavity loss and dark state transfer on PMET in an intuitive fashion, which allows for a clear understanding of which parameter regimes and experimental approaches allow for significant PMET rate enhancement due to collective strong coupling.
We theoretically show how collective quantities, such as the Rabi splitting ΩR, manifest in the change of the PMET rate constant by rigorously deriving a Marcus-type rate constant. This rate theory suggests a possible mechanism that only depends on the 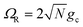 , even though the light–matter coupling strength per emitter gc is small. We numerically verify the validity of this rate constant expression using the numerical simulations. Further, by driving the UP state with a CW laser in a positively detuned cavity, the effective PMET rate constant can be several orders of magnitude larger than outside the cavity even with significant molecular disorder (that causes transition to the dark states) and cavity loss (that causes population decay from UP to the ground state). These results reveal a promising mechanism to realize photochemical rate enhancement with collective strong coupling in disordered and lossy polariton systems, as well as enable otherwise impractical uphill ET reactions by using the higher energy of the UP. Note that uphill ET reactions could also be enhanced by coupling to the visible light field64 or by use a plasmonic effect.65 Here, our work demonstrates a promising principle based on polariton effects, and how delocalized light–matter interactions between one cavity mode and N molecules can induce changes in the rate constant for local chemical transformation.
, even though the light–matter coupling strength per emitter gc is small. We numerically verify the validity of this rate constant expression using the numerical simulations. Further, by driving the UP state with a CW laser in a positively detuned cavity, the effective PMET rate constant can be several orders of magnitude larger than outside the cavity even with significant molecular disorder (that causes transition to the dark states) and cavity loss (that causes population decay from UP to the ground state). These results reveal a promising mechanism to realize photochemical rate enhancement with collective strong coupling in disordered and lossy polariton systems, as well as enable otherwise impractical uphill ET reactions by using the higher energy of the UP. Note that uphill ET reactions could also be enhanced by coupling to the visible light field64 or by use a plasmonic effect.65 Here, our work demonstrates a promising principle based on polariton effects, and how delocalized light–matter interactions between one cavity mode and N molecules can induce changes in the rate constant for local chemical transformation.
2 Theory and model
2.1 Model Hamiltonian
A illustration of the model system is provided in Fig. 1a, and the schematic energy diagrams for the model system are depicted in panels (b) and (c). We consider a model photoinduced ET system that is coupled to a single-mode cavity at the Tavis–Cummings (TC) level of approximation. A relevant photoinduced ET system example is CdSe nanoplatelets (NPLs) as the photoinduced charge transfer donor molecules and organic molecules (such as viologen molecules) as the charge acceptor. The CdSe NPLs and viologen molecules outside the cavity have been previously synthesized and reported in the literature,66 and the photoinduced charge transfer kinetics have also been investigated. We consider each donor to be coupled to an acceptor molecule through chemically local electronic coupling VDA. We further consider that the cavity mode couples collectively to a total of N donor–acceptor molecule pairs, through the transition dipole of the donor (CdSe NPL), which has been accomplished in our recent experimental work.67–70 The light–matter interactions, as opposed to the electronic coupling, are highly non-local between the cavity mode and N molecules.The total system Hamiltonian for the model is
| Ĥ = Ĥm + Ĥp + Ĥmp + Ĥl, | (1) |
The molecular Hamiltonian 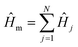 describes a total of N non-interacting molecules. Each Ĥj contains three electronic states: ground state |G〉, donor state |D〉, and acceptor state |A〉, with an ET reaction coordinate R (Marcus coordinate71). The model Hamiltonian for a single donor–acceptor pair is21
describes a total of N non-interacting molecules. Each Ĥj contains three electronic states: ground state |G〉, donor state |D〉, and acceptor state |A〉, with an ET reaction coordinate R (Marcus coordinate71). The model Hamiltonian for a single donor–acceptor pair is21
Ĥj = ½mSωS2Rj2|Gj〉〈Gj| + (ΔED + ½mSωS2(Rj − R0D)2)|Dj〉〈Dj| + (ΔEA + ½mSωS2(Rj − R0A)2)|Aj〉〈Aj| + VDA(|Dj〉〈Aj| + |Aj〉〈Dj|) + ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) S,j + Ĥsb,j, S,j + Ĥsb,j,
| (2) |
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) S,j = Pj2/2mS is the kinetic energy of the reaction coordinate with momentum Pj, and Ĥsb,j is the Caldeira–Leggett system-bath interaction72 of the reaction coordinate with a phonon bath
S,j = Pj2/2mS is the kinetic energy of the reaction coordinate with momentum Pj, and Ĥsb,j is the Caldeira–Leggett system-bath interaction72 of the reaction coordinate with a phonon bath
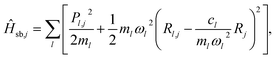 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−ω/ω0. The friction parameter ζ determines the overall system-bath coupling strength and the high frequency cut-off is ω0 ≫ ωS.
e−ω/ω0. The friction parameter ζ determines the overall system-bath coupling strength and the high frequency cut-off is ω0 ≫ ωS.
We focus on the single excitation subspace.1,22 This includes the collective ground state |G〉 and singly excited states |Dj〉 and |Aj〉 (where j ∈ [1, N] labels the molecules), defined as
| |G〉 ≡ |G1〉 ⊗…⊗ |GN〉, | (4a) |
| |Dj〉 ≡ |G1〉 ⊗…⊗ |Dj〉 ⊗…⊗ |GN〉, | (4b) |
| |Aj〉 ≡ |G1〉 ⊗…⊗ |Aj〉 ⊗…⊗ |GN〉. | (4c) |
The photonic Hamiltonian of a single quantized cavity mode is described as
| Ĥp = ℏωc(â†â + ½), | (5) |
 | (6) |
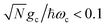 (before entering into the ultra-strong coupling regime21). Additionally, each molecule's transition dipole is assumed to be aligned with the cavity field polarization and identical in magnitude such that each molecule's coupling gc is identical and static.
(before entering into the ultra-strong coupling regime21). Additionally, each molecule's transition dipole is assumed to be aligned with the cavity field polarization and identical in magnitude such that each molecule's coupling gc is identical and static.
The CW laser Hamiltonian Ĥl describes a continuous driving between the cavity states of the system67 and is expressed as
Ĥl(t) = Vl(â![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eiωlt + ↠eiωlt + â†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−iωlt), e−iωlt),
| (7) |
In addition to the Hamiltonian dynamics, the effect of cavity loss is included in the system through the Lindblad master equation77–79
 | (8) |
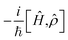 describes the Hermitian evolution of the reduced density matrix
describes the Hermitian evolution of the reduced density matrix ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) due to Ĥ and the dissipator
due to Ĥ and the dissipator 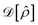 is
is
 | (9) |
The cavity mode in the single excitation subspace is treated as a two-level system with states |0〉, which is the vacuum 0-photon Fock state whose energy is set to 0 for convenience, and |1〉, which is the 1-photon Fock state with energy ℏωc. In the combined molecule–cavity Hilbert space, which is restricted to zero and single-excitation states (see Fig. 1b), we label the states in a condensed fashion (e.g., |G〉 ⊗ |1〉 ≡ |G, 1〉). For brevity, further labels of excited molecular states without a Fock state label are assumed to have 0 photons (e.g., |Aj〉 implies |Aj, 0〉).
We further define the polaritonic Hamiltonian as
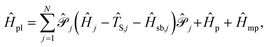 | (10) |
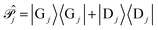 is the projection operator that projects onto the ground and donor molecular states which excludes the acceptor states from Ĥpl.
is the projection operator that projects onto the ground and donor molecular states which excludes the acceptor states from Ĥpl.
The eigenstates of Ĥpl are the so-called polariton states of the system. For a given nuclear configuration R ≡ {Rj}, these polariton states |ψn(R)〉 and their corresponding eigenenergies En(R) can be determined by the following eigenvalue equation
| Ĥpl(R)|ψn(R)〉 = En(R)|ψn(R)〉, | (11) |
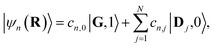 | (12) |
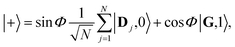 | (13a) |
 | (13b) |
 | (14) |
 | (15) |
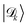 (not to be confused with the donor exciton states |Dj, 0〉) which are superpositions of only {|Dj, 0〉} states that can be expressed as follows1,75,80
(not to be confused with the donor exciton states |Dj, 0〉) which are superpositions of only {|Dj, 0〉} states that can be expressed as follows1,75,80
 | (16) |
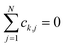 which renders them optically dark (i.e. having no transition dipole from the ground state |G〉). As a reminder, the above definitions of the bright polariton and dark states do not have explicit static disorder taken into account. Generally, static disorder can significantly impact polariton dynamics81 and polariton delocalization.82 Our bath model in this work is equivalent to a Brownian oscillator spectral density83 with a peak frequency at ℏωS ≈ 9.54 meV thus most of the effective phonon modes are low frequency and can be expected to behave similarly to explicit static disorder with a standard deviation of84
which renders them optically dark (i.e. having no transition dipole from the ground state |G〉). As a reminder, the above definitions of the bright polariton and dark states do not have explicit static disorder taken into account. Generally, static disorder can significantly impact polariton dynamics81 and polariton delocalization.82 Our bath model in this work is equivalent to a Brownian oscillator spectral density83 with a peak frequency at ℏωS ≈ 9.54 meV thus most of the effective phonon modes are low frequency and can be expected to behave similarly to explicit static disorder with a standard deviation of84  .
.
When the cavity is in resonance with the donor energy (Φ = π/4), the UP and LP states without disorder simplify to
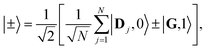 | (17) |
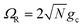 . For λD ≠ 0, the donor state energies may not be identical (i.e. disordered) for R ≠ 0 which causes the polariton eigenstates to no longer be perfectly bright or dark.68,85,86 In particular, there may be quasi-dark eigenstates67 with small amounts of photonic character, as well as eigenstates similar to the disorderless UP and LP states but with different amounts of donor character for different molecules.67
. For λD ≠ 0, the donor state energies may not be identical (i.e. disordered) for R ≠ 0 which causes the polariton eigenstates to no longer be perfectly bright or dark.68,85,86 In particular, there may be quasi-dark eigenstates67 with small amounts of photonic character, as well as eigenstates similar to the disorderless UP and LP states but with different amounts of donor character for different molecules.67
2.2 Origin of the collective effect in PMET
Here, we develop an analytic theory to describe the collective PMET rate constant. The details of the derivations are provided in the ESI.† For a reaction occurring across a large number of nuclear coordinates R among a set of electronic–photonic states, a collective reaction coordinate RRCab(X) from state |a〉 to state |b〉 can be defined as a function of the energy difference X. For a fixed X = ΔEab(R), the collective reaction coordinate RRCab(X) is the nuclear configuration that minimizes the donor energy Ea(R).87 This collective reaction coordinate can be used to derive reaction parameters such as the driving force and reorganization energy.For a collective PMET reaction from the UP state |+〉 with mixing angle Φ to an individual acceptor state |Aj〉, the collective reaction coordinate can be shown to be
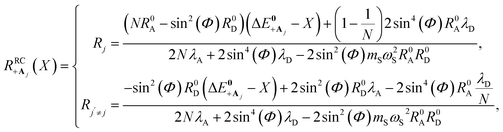 | (18) |
 is the energy difference between states |Aj〉 and |+〉 at R = 0 (see the ESI† for a detailed derivation). In the collective limit N → ∞ (with a fixed collective light–matter coupling
is the energy difference between states |Aj〉 and |+〉 at R = 0 (see the ESI† for a detailed derivation). In the collective limit N → ∞ (with a fixed collective light–matter coupling 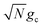 ), the collective reaction coordinate simplifies to be
), the collective reaction coordinate simplifies to be
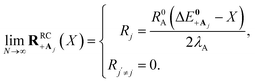 | (19) |
To determine reaction parameters such as the reorganization energy and the driving force, the energy differences 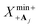 and
and 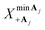 that minimize the energies of states |+〉 and |Aj〉, respectively, along
that minimize the energies of states |+〉 and |Aj〉, respectively, along 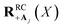 can be used. The corresponding reorganization energy λ+Aj between states |+〉 and |Aj〉 is
can be used. The corresponding reorganization energy λ+Aj between states |+〉 and |Aj〉 is
 | (20a) |
 | (20b) |
The polaron decoupling effect24 of the |+〉 state can be seen in the collective limit 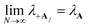 where the contribution of the |+〉 state to the reorganization energy goes to 0. A similar calculation shows that the reorganization energy between the collective ground state |G, 0〉 and |+〉 is
where the contribution of the |+〉 state to the reorganization energy goes to 0. A similar calculation shows that the reorganization energy between the collective ground state |G, 0〉 and |+〉 is
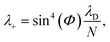 | (21a) |
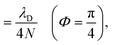 | (21b) |
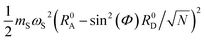 , which would be expected based on identifying
, which would be expected based on identifying  as the collective nuclear displacement of the |+〉 state;24 however, the difference is that the cross-term in λ+Aj has an extra factor of
as the collective nuclear displacement of the |+〉 state;24 however, the difference is that the cross-term in λ+Aj has an extra factor of 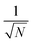 compared to the cross-term in the expression ½mSωS2(R0A − R0+)2. Regardless, this difference becomes negligible in the collective limit.
compared to the cross-term in the expression ½mSωS2(R0A − R0+)2. Regardless, this difference becomes negligible in the collective limit.
The driving force ΔG+Aj between states |+〉 and |Aj〉 is
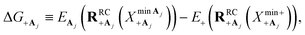 | (22a) |
 | (22b) |
The collective limit of the driving force is
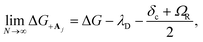 | (23a) |
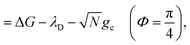 | (23b) |
 , which is observed in the single molecule case,21 is also seen in the collective limit.22 In addition, the driving force is modified by the detuning, where positive detuning decreases the driving force (decreasing the value of ΔG+Aj).
, which is observed in the single molecule case,21 is also seen in the collective limit.22 In addition, the driving force is modified by the detuning, where positive detuning decreases the driving force (decreasing the value of ΔG+Aj).
Another consequence of the result in eqn (23a) and (23b) is that the driving force is affected by the donor reorganization energy λD even in the collective limit such that there is no complete polaron decoupling effect for the driving force. At resonance, this is due to the increase in the minimum energy of the |+〉 state by λD which reduces the driving force by λD.
2.3 Collective PMET rates
In the collective limit, the reorganization energy of the |+〉 state relative to the collective ground state |G, 0〉 is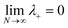 which implies the |+〉 state has the same equilibrium geometry as |G, 0〉 (given that |G, 0〉 has a unique equilibrium geometry). This allows for equilibrium rates from the |+〉 state to an acceptor state to be calculated when the reaction is initiated with an FC excitation.
which implies the |+〉 state has the same equilibrium geometry as |G, 0〉 (given that |G, 0〉 has a unique equilibrium geometry). This allows for equilibrium rates from the |+〉 state to an acceptor state to be calculated when the reaction is initiated with an FC excitation.
The traditional Marcus theory of nonadiabatic ET71,87,89–91 describes the reaction rate between a donor and acceptor state assuming a weak donor–acceptor coupling and a reaction initiated in the thermal equilibrium geometries of the donor state. The general Marcus rate constant expression is
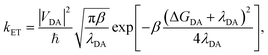 | (24) |
 | (25) |
 | (26) |
 | (27) |
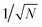 “dilution” factor (normalization factor) in V+Aj. For an FGR type of estimation of rate constant, this results in a 1/N normalization factor, which often causes difficulties in theoretically observing any collective modification for polariton photophysics dynamics59 or in VSC rate constant changes.63,94,95 Nevertheless, the collective PMET rate can naturally avoid such a pitfall by considering the total rate constant
“dilution” factor (normalization factor) in V+Aj. For an FGR type of estimation of rate constant, this results in a 1/N normalization factor, which often causes difficulties in theoretically observing any collective modification for polariton photophysics dynamics59 or in VSC rate constant changes.63,94,95 Nevertheless, the collective PMET rate can naturally avoid such a pitfall by considering the total rate constant 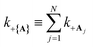 between the |+〉 state and all possible acceptor states {|Aj〉}, which can be can be expressed as
between the |+〉 state and all possible acceptor states {|Aj〉}, which can be can be expressed as
 | (28) |
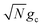 which reduces the driving force (and alters the mixing angle Φ when detuning is present). For the case λD = 0, this total rate constant k+{A} is equivalent to the Marcus PMET rate constant between the UP and acceptor for a single molecule with a light–matter coupling strength equal to
which reduces the driving force (and alters the mixing angle Φ when detuning is present). For the case λD = 0, this total rate constant k+{A} is equivalent to the Marcus PMET rate constant between the UP and acceptor for a single molecule with a light–matter coupling strength equal to 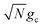 .21 Note that for the case λD ≠ 0, the disorderless |+〉 state defined in eqn (13a) is not an exact eigenstate of Ĥpl but may instead be an approximation of an eigenstate whose expansion coefficients are similar to that of |+〉 but whose acceptor couplings may differ from V+Aj at
.21 Note that for the case λD ≠ 0, the disorderless |+〉 state defined in eqn (13a) is not an exact eigenstate of Ĥpl but may instead be an approximation of an eigenstate whose expansion coefficients are similar to that of |+〉 but whose acceptor couplings may differ from V+Aj at 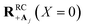 and whose driving force may differ from ΔG+Aj. For a thermal Boltzmann distribution of nuclear positions, this approximation should be reasonable when the donor energy disorder84
and whose driving force may differ from ΔG+Aj. For a thermal Boltzmann distribution of nuclear positions, this approximation should be reasonable when the donor energy disorder84  (low molecular disorder relative to collective coupling strength1,60) and
(low molecular disorder relative to collective coupling strength1,60) and 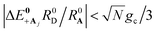 (small detuning of donor state energy EDj versus EDj′≠j at
(small detuning of donor state energy EDj versus EDj′≠j at 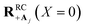 relative to collective coupling strength to ensure the UP eigenstate has significant character |c+,j|2 ≈ sin2(Φ)/N of state |Dj〉 in order to couple to state |Aj〉 at
relative to collective coupling strength to ensure the UP eigenstate has significant character |c+,j|2 ≈ sin2(Φ)/N of state |Dj〉 in order to couple to state |Aj〉 at 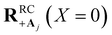 ).
).
As shown in Fig. 1c, when any of the parameters λD, Γ, or Vl are non-zero the dynamics of the polariton and acceptor states are affected by factors beyond those of the PMET rates in eqn (28). More specifically, a non-zero λD can allow for dynamical disorder among the polariton states which causes population transfer58,67,68,74,80,85,96–101 between the UP, LP, and dark states; a non-zero value of Γ causes population decay from photonic polariton states to |G, 0〉; and Vl causes population transfer between |G, 0〉 and photonic polariton states. While these factors create challenges for describing the population dynamics of the polariton and acceptor states with analytic expressions, explicit quantum dynamics simulations of the molecular–cavity system can provide these population dynamics beyond the limitations of analytic expressions. In this work, we calculate effective rate constants between the donor manifold of states (|G, 0〉 and the polariton states) and the acceptor manifold of states ({|Aj〉}) by fitting the simulated explicit population dynamics of the acceptor states to a simple two-state ET model with fitted forward and backward rate constants. In particular, for a system initialized among the donor manifold of states, we fit the simulated population dynamics of the acceptor states  to the following equation
to the following equation
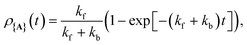 | (29) |
2.4 Simulation details
The reduced density matrix dynamics![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (t) of the molecule–cavity PMET system in this work were propagated at the wavefunction level using the Lindblad mean-field Ehrenfest
(t) of the molecule–cavity PMET system in this work were propagated at the wavefunction level using the Lindblad mean-field Ehrenfest 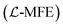 approach.79 MFE is a mixed quantum-classical dynamics method that propagates a quantum subsystem (electrons and photons) alongside a classical subsystem (nuclei) which feel a mean-field force based on the quantum state.102–104 MFE has been shown to be accurate for model systems in the non-adiabatic regime (κ ≪ 1), including ET and other charge transfer processes.21
approach.79 MFE is a mixed quantum-classical dynamics method that propagates a quantum subsystem (electrons and photons) alongside a classical subsystem (nuclei) which feel a mean-field force based on the quantum state.102–104 MFE has been shown to be accurate for model systems in the non-adiabatic regime (κ ≪ 1), including ET and other charge transfer processes.21 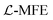 incorporates Lindblad decay dynamics into MFE at the wavefunction level which allows for efficient and accurate simulation of cavity loss68,70,79,105 even in the presence of coherent laser pumping.
incorporates Lindblad decay dynamics into MFE at the wavefunction level which allows for efficient and accurate simulation of cavity loss68,70,79,105 even in the presence of coherent laser pumping.
The state-independent phonon bath, described by Ĥsb,j, was treated implicitly using a Langevin dynamics approach, which is equivalent to the reduced dynamics of the harmonic ET coordinate under the influence of an ohmic bath in the Markovian regime.21,83,106,107 This Langevin description reduces the computational cost of the many-molecule PMET simulation by reducing the number of propagated nuclear DOFs to one per molecule91,108,109 (see the ESI† for details). The computational cost of the simulation was further reduced by manually coding the result of the matrix–vector operation of Ĥ acting on the wavefunction (by taking advantage of the symmetry of the TC type Hamiltonian) in a way that scales linearly with N, see details in ref. 110. These approaches to reduce the computational cost allowed for N = 1000 molecules to be efficiently simulated on the nanosecond timescale. The number of trajectories was Ntraj = 10, 000/N such that 10 trajectories were averaged over for the N = 1000 molecule simulations. This small number of trajectories required to reach convergence was possible due to the self-averaging of the population dynamics of the UP and the sum of the acceptor states when multiple molecules are coupled to the cavity. The nuclear time step was dtN = 0.125 fs and the electronic time step was dtE = dtN/4. The friction parameter used in this work was ζ = 1.066 × 106 au and the mass was mS = 4.529 × 108 au for consistency with previous works on ET.21,106
3 Results and discussions
In this section, we explore the population dynamics and rates of our PMET model system in the collective coupling regime and compare them to the dynamics and rates outside the cavity. In all cases inside the cavity, we focus on cavities in resonance with the donor excited state in the FC configuration (ℏωc = ΔED + λD = 3 eV) and reactions initiated in, or coherently pumped to, the UP state. This regime of focus allows us to examine the extent to which PMET reaction rates can be significantly enhanced, particularly in the presence of dark state transfer and cavity loss.Fig. 1d and e present PMET in the Marcus regime for varying numbers of coupled molecules inside the cavity. The reaction inside the cavity is initiated as an FC excitation to the resonant |+〉 state. The ET parameters are λA = 200 meV, VDA = 5 meV, and ΔG = 0 at room temperature T = 300 K. The nonadiabatic parameter for a single donor–acceptor pair is κ ≈ 0.032 ≪ 1 with ℏωS ≈ 9.54 meV < kBT ≈ 25.8 meV and λD = Γ = Vl = 0 which confirms the dynamics are in the Marcus regime. Fig. 1d shows the propagated and fitted acceptor state populations for a variety of N with a fixed gc = 4 meV. The system was propagated for 1 ps and kf and kb were fitted based on eqn (29) with the corresponding fitted populations from the right-hand side of eqn (29) plotted as dashed lines. The dynamics show a strong, non-monotonic dependence on N that accumulates acceptor population most rapidly near N = 2500 with reduced acceptor populations for larger or smaller N. Notably, the fitted populations show excellent agreement with the propagated populations which demonstrates that the short-time acceptor dynamics are well-captured by a 2-state rate constant model even when thousands of molecules are coupled to the cavity.
Fig. 1e shows the corresponding analytic Marcus forward rate constants and fitted forward rate constants based on the explicit quantum dynamics propagation. The Marcus rate constants based on eqn (28) are plotted (solid red line) over a continuous range of N ∈ [1, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000] molecules while the fitted rate constants (red dots) are plotted based on simulations for various N in the same range. The Marcus rate constant for a single donor–acceptor pair outside the cavity is also shown for comparison (black dashed line). The Marcus and fitted rate constants show excellent agreement, especially for N ≫ 1. The rate constant dependence on N inside the cavity appears as an inverted parabola (when the N axis scales as
000] molecules while the fitted rate constants (red dots) are plotted based on simulations for various N in the same range. The Marcus rate constant for a single donor–acceptor pair outside the cavity is also shown for comparison (black dashed line). The Marcus and fitted rate constants show excellent agreement, especially for N ≫ 1. The rate constant dependence on N inside the cavity appears as an inverted parabola (when the N axis scales as 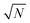 and the kf axis scales logarithmically) due to the collective coupling
and the kf axis scales logarithmically) due to the collective coupling 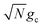 effect on the driving force ΔG+Aj (eqn (23b)). From N = 1 to N = 2500, the UP energy increases with N which decreases
effect on the driving force ΔG+Aj (eqn (23b)). From N = 1 to N = 2500, the UP energy increases with N which decreases  and increases the rate constant until the reaction is barrier-less and the rate is maximized at N = 2500. For N > 2500, the UP energy continues to increase with N but the reaction is now in the inverted Marcus regime which decreases the rate as ΔG+Aj becomes more negative. For 100 < N < 8100, the reaction inside the cavity is enhanced by up to a factor of 4 relative to outside the cavity due to the more favorable driving force ΔG+Aj compared to the bare ΔG = 0 outside the cavity. Although the purpose of this panel is to validate our theory and the accuracy of our quantum dynamics simulations, it is nevertheless interesting to show one can selectively achieve the Marcus normal, activation less, and inverted regime with the same type of molecules by only varying N. Note that due to the large transition dipole of the CdSe NPL, we estimate that N = 103–104 NPLs coupled to the cavity can generate ΩR ∼ 102 meV Rabi splitting.67,69,70
and increases the rate constant until the reaction is barrier-less and the rate is maximized at N = 2500. For N > 2500, the UP energy continues to increase with N but the reaction is now in the inverted Marcus regime which decreases the rate as ΔG+Aj becomes more negative. For 100 < N < 8100, the reaction inside the cavity is enhanced by up to a factor of 4 relative to outside the cavity due to the more favorable driving force ΔG+Aj compared to the bare ΔG = 0 outside the cavity. Although the purpose of this panel is to validate our theory and the accuracy of our quantum dynamics simulations, it is nevertheless interesting to show one can selectively achieve the Marcus normal, activation less, and inverted regime with the same type of molecules by only varying N. Note that due to the large transition dipole of the CdSe NPL, we estimate that N = 103–104 NPLs coupled to the cavity can generate ΩR ∼ 102 meV Rabi splitting.67,69,70
It should be emphasized that the mechanism of enhancement in PMET demonstrated in Fig. 1 based on modifying the driving force relies on initiating the system in the UP state, which is a quantum state whose particular combination of energy and donor character does not exist outside the cavity near the FC region. A different mechanism for collective cavity-enhanced photochemistry was described in ref. 20 and 60 where the cavity filtered an initial FC cavity excitation into donor states with higher energy vibrational states during a series of early-time Rabi oscillations, where the higher energy vibrations allowed faster transfer to the acceptor state. This filtering mechanism, described for T = 0, relied on a non-zero λD and the observed enhancement vanished for λD = 0. In contrast, the enhancement mechanism in Fig. 1 based on increasing the energy of the electronic–photonic UP state using collective coupling does not fundamentally depend on filtering the donor vibrational states and does not diminish at λD = 0.
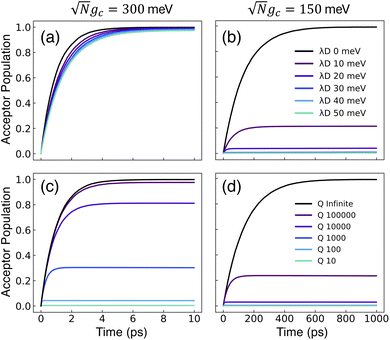
Fig. 2 presents the influence of dark state transfer and cavity loss on PMET population dynamics for an uphill reaction with N = 1000. The reaction inside the cavity is initiated as a FC excitation to the resonant |+〉 state. The ET parameters are λA = 100 meV, VDA = 10 meV, and ΔG − λD = 300 meV uphill at room temperature T = 300 K. In this parameter regime, the forward rate constant outside the cavity is very small (koutsidef ≈ 10−6 ps−1) due to the uphill ΔG that is more than 10 times larger than kBT. As a result, population that resides in the dark states (or |G, 0〉) will not appreciably transfer to the acceptor states on the plotted timescales (up to 1000 ps). Any visible accumulation of acceptor population must come directly from the UP state due to its more favorable ΔG+Aj. Similarly, the backward rate from the acceptor to the donor states outside the cavity is also very small (for nuclear distributions in the FC region). Notably, in contrast to the forward transfer direction, the total backward rate from the acceptor states to the donor manifold is directly influenced by the density of states in the donor manifold. Consequentially, the contribution of the acceptor-to-dark transfer to the total backward rate is (N − 1)/(N + 1) ≈ 1 which means population transferred to the acceptor states will not appreciably transfer backward to the donor manifold on the plotted timescales. The acceptor population dynamics in Fig. 2 can thus be understood as a result of two competing pathways: the UP to acceptor transfer which appreciably accumulates acceptor population, and the UP to dark or UP to |G, 0〉 transfer which becomes effectively “trapped” in the dark or |G, 0〉 states and does not lead to appreciable acceptor state population.
Fig. 2a and b show the acceptor population dynamics for varying λD from 0 to 50 meV and for collective coupling strengths 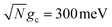 and
and 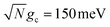 , respectively, with Γ = Vl = 0. Note that by setting Vl = 0, the CW laser excitation is not active in these simulations. Instead, the system is initially prepared as a Franck–Condon excitation where the initial state is the |+〉 state. The bare driving force ΔG is adjusted such that ΔG − λD = 300 meV is fixed for all values of λD in order to put the forward rates from the UP to acceptor states on equal footing (i.e. so that the driving force in eqn (23) is equal for all values of λD aside from the collective coupling
, respectively, with Γ = Vl = 0. Note that by setting Vl = 0, the CW laser excitation is not active in these simulations. Instead, the system is initially prepared as a Franck–Condon excitation where the initial state is the |+〉 state. The bare driving force ΔG is adjusted such that ΔG − λD = 300 meV is fixed for all values of λD in order to put the forward rates from the UP to acceptor states on equal footing (i.e. so that the driving force in eqn (23) is equal for all values of λD aside from the collective coupling 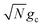 effect). The primary effect of increasing λD in this case is an increase in the transfer rate from the UP to the dark states. One perspective to understand this effect is that increasing λD increases the coupling strength of the phonon bath that transfers population between the UP and the dark states.80,88,99 Another perspective is that increasing λD increases the spectral linewidth of the donor states (i.e. adds disorder to the donor energies) which increases the spectral overlap between the UP and dark states resulting in increased transfer between these states. For a Gaussian sampling of nuclear configurations in the FC region, this spectral disorder has a standard deviation of
effect). The primary effect of increasing λD in this case is an increase in the transfer rate from the UP to the dark states. One perspective to understand this effect is that increasing λD increases the coupling strength of the phonon bath that transfers population between the UP and the dark states.80,88,99 Another perspective is that increasing λD increases the spectral linewidth of the donor states (i.e. adds disorder to the donor energies) which increases the spectral overlap between the UP and dark states resulting in increased transfer between these states. For a Gaussian sampling of nuclear configurations in the FC region, this spectral disorder has a standard deviation of  . While the dark states can also transfer to the UP (and LP), this rate scales as 1/N which becomes negligible in the collective limit.80
. While the dark states can also transfer to the UP (and LP), this rate scales as 1/N which becomes negligible in the collective limit.80
The acceptor population dynamics in Fig. 2a do not show a strong dependence on λD ≤ 50 meV. For a collective coupling strength of  , the reaction is almost barrier-less due to the favorable driving force ΔG+Aj = 0. The initial UP population can thus fully transfer to the acceptor states in only a few ps while the transfer rate from the UP to the dark states is suppressed by the large energy gap between these states even for λD = 50. On the other hand, in Fig. 2b, there is a strong dependence on λD due to the smaller collective coupling strength of
, the reaction is almost barrier-less due to the favorable driving force ΔG+Aj = 0. The initial UP population can thus fully transfer to the acceptor states in only a few ps while the transfer rate from the UP to the dark states is suppressed by the large energy gap between these states even for λD = 50. On the other hand, in Fig. 2b, there is a strong dependence on λD due to the smaller collective coupling strength of 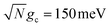 which both reduces the UP to acceptor rate constant and allows for a significant spectral overlap between the UP and dark states. As a result, a modest λD = 10 meV causes most population to transfer to the dark states before it can transfer to the acceptor states and λD = 50 meV prevents any visible accumulation of acceptor population on these timescales. Thus the magnitude of effect that dark states have on suppressing UP-to-acceptor PMET depends on the competing rates of the UP-to-acceptor pathway and the UP-to-dark pathway, the latter of which is very sensitive to the spectral gap (or lack thereof) between the UP and dark states. As a result, the presence of dark states in PMET must be seriously considered when the timescale of the UP-to-acceptor transfer is similar to or longer than the timescale of UP-to-dark transfer.80 Similar consequences of dark state transfer have also been described in other related works on cavity-modified photochemistry.31,111
which both reduces the UP to acceptor rate constant and allows for a significant spectral overlap between the UP and dark states. As a result, a modest λD = 10 meV causes most population to transfer to the dark states before it can transfer to the acceptor states and λD = 50 meV prevents any visible accumulation of acceptor population on these timescales. Thus the magnitude of effect that dark states have on suppressing UP-to-acceptor PMET depends on the competing rates of the UP-to-acceptor pathway and the UP-to-dark pathway, the latter of which is very sensitive to the spectral gap (or lack thereof) between the UP and dark states. As a result, the presence of dark states in PMET must be seriously considered when the timescale of the UP-to-acceptor transfer is similar to or longer than the timescale of UP-to-dark transfer.80 Similar consequences of dark state transfer have also been described in other related works on cavity-modified photochemistry.31,111
Fig. 2c and d show the acceptor population dynamics for varying cavity loss rates with quality factors Q ≡ ωc/Γ ranging from lossless Q = ∞ (Γ = 0) down to Q = 10 (Γ = 300 meV) and for collective coupling strengths  and
and 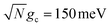 , respectively, with λD = Vl = 0. The effect of increasing Γ in this case is an increase in the transfer rate from the UP to the |G, 0〉 state. Due to Vl = 0, once population is transferred to |G, 0〉, it remains trapped there as there are no transfer pathways from |G, 0〉 to other states. For λD = 0, the resonant UP state experiences cavity loss at a rate of Γ/2 due to the UP possessing half photonic character. In contrast to the dark state transfer rate dependence on λD, the cavity loss rate that the UP experiences in this model is not strongly dependent on the energy of the UP or the energy gap between the UP and the dark states. As a result, the acceptor population dynamics in Fig. 2c are visibly suppressed across the entire range of finite Q, even for Q = 100
, respectively, with λD = Vl = 0. The effect of increasing Γ in this case is an increase in the transfer rate from the UP to the |G, 0〉 state. Due to Vl = 0, once population is transferred to |G, 0〉, it remains trapped there as there are no transfer pathways from |G, 0〉 to other states. For λD = 0, the resonant UP state experiences cavity loss at a rate of Γ/2 due to the UP possessing half photonic character. In contrast to the dark state transfer rate dependence on λD, the cavity loss rate that the UP experiences in this model is not strongly dependent on the energy of the UP or the energy gap between the UP and the dark states. As a result, the acceptor population dynamics in Fig. 2c are visibly suppressed across the entire range of finite Q, even for Q = 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, which corresponds to a minuscule Γ = 0.03 meV. The accumulated acceptor population steadily decreases with lower Q and higher Γ until there is no visible acceptor accumulation for Q = 10. In contrast to Fig. 2a, the dynamics in Fig. 2c are not protected from cavity loss by the large collective coupling of the UP. The acceptor population dynamics in Fig. 2d are similarly impacted by lower Q factors with decreasing accumulated acceptor population as Q is decreased. Due to the lack of energy dependence on the UP cavity loss rate, the difference in the amount of suppression observed between Fig. 2c and d is not as large as that between Fig. 2a and b. Overall, the presence of cavity loss in PMET must be seriously considered when the timescale of the UP-to-acceptor transfer is similar to or longer than the timescale of cavity loss, which is the case for many realistic strongly-coupled molecule–cavity designs67–70 whose Q are often less than Q = 1000, and this cavity loss effect cannot be easily protected against by increasing the collective coupling strength. Similar consequences of cavity loss have also been described in other related works on cavity-modified photochemistry.58,96
000, which corresponds to a minuscule Γ = 0.03 meV. The accumulated acceptor population steadily decreases with lower Q and higher Γ until there is no visible acceptor accumulation for Q = 10. In contrast to Fig. 2a, the dynamics in Fig. 2c are not protected from cavity loss by the large collective coupling of the UP. The acceptor population dynamics in Fig. 2d are similarly impacted by lower Q factors with decreasing accumulated acceptor population as Q is decreased. Due to the lack of energy dependence on the UP cavity loss rate, the difference in the amount of suppression observed between Fig. 2c and d is not as large as that between Fig. 2a and b. Overall, the presence of cavity loss in PMET must be seriously considered when the timescale of the UP-to-acceptor transfer is similar to or longer than the timescale of cavity loss, which is the case for many realistic strongly-coupled molecule–cavity designs67–70 whose Q are often less than Q = 1000, and this cavity loss effect cannot be easily protected against by increasing the collective coupling strength. Similar consequences of cavity loss have also been described in other related works on cavity-modified photochemistry.58,96
Fig. 3 presents the influence of CW laser driving and cavity loss on PMET population dynamics and rate constants for an uphill reaction with N = 1000. The ET parameters are the same as those used in Fig. 2 and λD = 0. The laser pumping strength was set to Vl = 10 meV and the laser frequency was tuned to 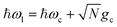 which is the energy difference between the resonant |+〉 state and |G, 0〉 in the FC region. Isolated from other dynamics, this CW laser will coherently drive population between |G, 0〉 and the UP due to the photonic character of the UP. Instead of an FC excitation, the reaction inside the cavity is initiated in the |G, 0〉 state, which will coherently pump to the UP state and then experience transfer to the acceptor states. The LP state, while also possessing half photonic character, is significantly detuned from ℏωl in this case and does not experience any appreciable pumping from |G, 0〉.
which is the energy difference between the resonant |+〉 state and |G, 0〉 in the FC region. Isolated from other dynamics, this CW laser will coherently drive population between |G, 0〉 and the UP due to the photonic character of the UP. Instead of an FC excitation, the reaction inside the cavity is initiated in the |G, 0〉 state, which will coherently pump to the UP state and then experience transfer to the acceptor states. The LP state, while also possessing half photonic character, is significantly detuned from ℏωl in this case and does not experience any appreciable pumping from |G, 0〉.
Fig. 3a and b show the propagated and fitted acceptor population dynamics in the presence of CW laser driving to the UP for varying cavity loss rates from Q = 50 to Q = ∞ and for collective coupling strengths 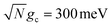 and
and 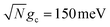 , respectively. As Q is decreased in Fig. 3a, the propagated acceptor population (solid lines) accumulates slower yet still approaches ρ{A} = 1 during the 50 ps of propagation. This stands in sharp contrast to Fig. 2c where lower Q factors significantly reduced the plateau acceptor populations. This difference is due to the CW laser in Fig. 3a, which allows for population that was trapped in |G, 0〉 due to cavity loss to be repopulated into the UP and continue transfer to the acceptor states. Fig. 3b shows a similar dependence on Q where the plateau acceptor populations are much larger than those in Fig. 2d for finite Q.
, respectively. As Q is decreased in Fig. 3a, the propagated acceptor population (solid lines) accumulates slower yet still approaches ρ{A} = 1 during the 50 ps of propagation. This stands in sharp contrast to Fig. 2c where lower Q factors significantly reduced the plateau acceptor populations. This difference is due to the CW laser in Fig. 3a, which allows for population that was trapped in |G, 0〉 due to cavity loss to be repopulated into the UP and continue transfer to the acceptor states. Fig. 3b shows a similar dependence on Q where the plateau acceptor populations are much larger than those in Fig. 2d for finite Q.
While these dynamics in Fig. 3a and b involve multiple non-ET pathways due to cavity loss and laser driving, the fitted acceptor populations (dashed lines, based on the right-hand side of eqn (29)) still show excellent agreement with the propagated populations. This demonstrates that the combined effect of cavity loss and CW laser driving to the UP can be accurately captured by fitting effective forward kf and backward kb rate constants to the acceptor population dynamics. These effective rate constants will change based on the cavity loss Γ and laser pumping Vl even though the bare rate constants (such as eqn (28)) between the UP and the acceptor states are unchanged by Γ and Vl.
Fig. 3c shows the corresponding fitted forward rate constants from the dynamics in Fig. 3a (red) and b (blue) for a range of Q ∈ [10, ∞]. The fitted forward rate constant for a single molecule reaction initiated in |G〉 outside the cavity with a CW laser coupling states |G〉 and |D〉 together with ℏωl = ΔED, Vl = 10 meV, and the same ET parameters is plotted as a black dashed line for comparison. The fitted rate constants demonstrate that the PMET reaction is enhanced by orders of magnitude relative to outside the cavity, even for Q = 10 and 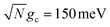 . The shape of the rate constant dependence on Q is similar for both
. The shape of the rate constant dependence on Q is similar for both  and
and 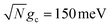 where the rates are mostly unaffected for Q ≥ 500 (Γ ≤ 6 meV) and begin to decrease as Q decreases below 500. This transition point between affected and unaffected rates along Q corresponds to the regime where ℏΓ ≈ Vl because for ℏΓ ≪ Vl, the laser pumping can rapidly replenish any UP population lost through cavity loss while for ℏΓ ≫ Vl, the UP population is lost faster than the laser pumping can replenish it. In particular, the effective forward rate constant in this case can be approximated as
where the rates are mostly unaffected for Q ≥ 500 (Γ ≤ 6 meV) and begin to decrease as Q decreases below 500. This transition point between affected and unaffected rates along Q corresponds to the regime where ℏΓ ≈ Vl because for ℏΓ ≪ Vl, the laser pumping can rapidly replenish any UP population lost through cavity loss while for ℏΓ ≫ Vl, the UP population is lost faster than the laser pumping can replenish it. In particular, the effective forward rate constant in this case can be approximated as
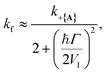 | (30) |
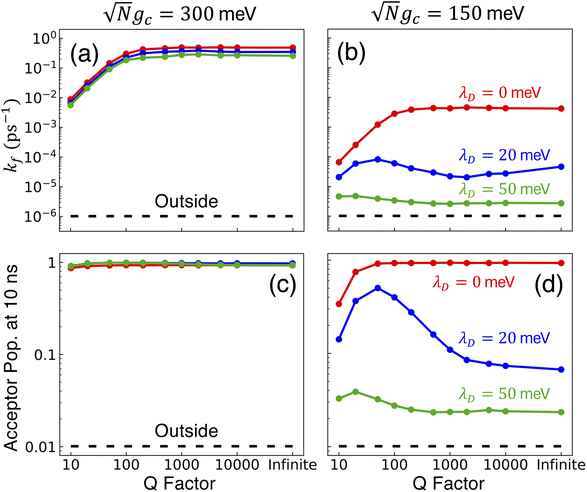
Fig. 4 presents the influence of dark state transfer in addition to CW laser driving and cavity loss on PMET population dynamics and rate constants for an uphill reaction with N = 1000. The ET and CW laser parameters are the same as those used in Fig. 3. Simulations were performed for λD = 0 (red), λD = 20 meV (blue), and λD = 50 meV (green) over a range of Q ∈ [10, ∞]. The simulations were propagated for t = 10 ns because the reaction rates between the dark donor and acceptor states begin to appreciably affect the dynamics around this time and, more broadly, additional dynamics pathways such as non-radiative molecular decay begin to become relevant on these timescales.
Fig. 4a and b show the fitted forward rate constants from the propagated acceptor populations for collective coupling strengths 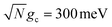 and
and 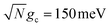 , respectively. For the larger collective coupling simulations in Fig. 4a, the fitted rate constants are only slightly affected by λD, where the rates decreased slightly with larger values of λD over the entire range of Q. This trend is similar to the dynamics seen in Fig. 2a where the acceptor populations only slightly decreased with increasing λD. As discussed before, this is due to the large spectral gap between the UP and the dark states58 for
, respectively. For the larger collective coupling simulations in Fig. 4a, the fitted rate constants are only slightly affected by λD, where the rates decreased slightly with larger values of λD over the entire range of Q. This trend is similar to the dynamics seen in Fig. 2a where the acceptor populations only slightly decreased with increasing λD. As discussed before, this is due to the large spectral gap between the UP and the dark states58 for  which greatly reduces the transfer rate from the UP to the dark states compared to smaller collective couplings due to the emergence of the phonon bottleneck effect. As a result, when coherently pumping the UP with a CW laser, the fitted rate constants in Fig. 4a are several orders of magnitude larger than those outside the cavity, even for λD = 50 meV and Q = 10.
which greatly reduces the transfer rate from the UP to the dark states compared to smaller collective couplings due to the emergence of the phonon bottleneck effect. As a result, when coherently pumping the UP with a CW laser, the fitted rate constants in Fig. 4a are several orders of magnitude larger than those outside the cavity, even for λD = 50 meV and Q = 10.
The fitted rate constants in Fig. 4b have a more complicated dependence on λD than those in Fig. 4a. As demonstrated previously in Fig. 2b, the spectral gap between the UP and dark states for 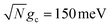 is small enough that the transfer rate to dark states is significant and the acceptor populations are more sensitive to differences in λD. This is observed in the Q = ∞ rate constants in Fig. 4b where increasing λD up to 50 meV can reduce the rate constants by up to 3 orders of magnitude compared to λD = 0. Regardless, the fitted rate constants are still significantly larger than those outside the cavity, even for λD = 50 meV. When Q is decreased and the cavity loss rate increases, one might expect the fitted rate constants to monotonically decrease as well due to the extra loss channel from the UP to |G, 0〉. However, the largest fitted rates for λD = 20 meV and λD = 50 meV are not found at Q = ∞ but instead at much smaller, finite values of Q (Q = 50 for λD = 20 meV and Q = 20 for λD = 50 meV). This surprising result can be understood by recognizing that for λD > 0, the dark states are dynamically disordered, which causes them to gain some non-zero photonic character. This photonic character causes the dark states to directly experience cavity loss, which transfers population from the dark states to |G, 0〉. With the CW laser tuned to the UP, this population that previously was in the dark states can then be pumped back to the UP, which can then experience enhanced transfer to the acceptor states. In other words, the cavity loss experienced by the disordered dark states allows population previously trapped in these dark states (for Q = ∞) to be recycled back into the UP. This mechanism allows for the effective forward rate constant for smaller values of Q to be significantly larger than expected based on the Q dependence seen in λD = 0 and, in some cases, even be larger than the rate constants for Q = ∞. This is a promising result for realizing enhanced PMET experimentally since the Q < 1000 attained in many current cavity designs67–70 may not be a significant hindrance.
is small enough that the transfer rate to dark states is significant and the acceptor populations are more sensitive to differences in λD. This is observed in the Q = ∞ rate constants in Fig. 4b where increasing λD up to 50 meV can reduce the rate constants by up to 3 orders of magnitude compared to λD = 0. Regardless, the fitted rate constants are still significantly larger than those outside the cavity, even for λD = 50 meV. When Q is decreased and the cavity loss rate increases, one might expect the fitted rate constants to monotonically decrease as well due to the extra loss channel from the UP to |G, 0〉. However, the largest fitted rates for λD = 20 meV and λD = 50 meV are not found at Q = ∞ but instead at much smaller, finite values of Q (Q = 50 for λD = 20 meV and Q = 20 for λD = 50 meV). This surprising result can be understood by recognizing that for λD > 0, the dark states are dynamically disordered, which causes them to gain some non-zero photonic character. This photonic character causes the dark states to directly experience cavity loss, which transfers population from the dark states to |G, 0〉. With the CW laser tuned to the UP, this population that previously was in the dark states can then be pumped back to the UP, which can then experience enhanced transfer to the acceptor states. In other words, the cavity loss experienced by the disordered dark states allows population previously trapped in these dark states (for Q = ∞) to be recycled back into the UP. This mechanism allows for the effective forward rate constant for smaller values of Q to be significantly larger than expected based on the Q dependence seen in λD = 0 and, in some cases, even be larger than the rate constants for Q = ∞. This is a promising result for realizing enhanced PMET experimentally since the Q < 1000 attained in many current cavity designs67–70 may not be a significant hindrance.
To further examine the interesting PMET dependence on λD, Fig. 4c and d show the propagated acceptor populations after t = 10 ns of propagation for collective coupling strengths 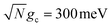 and
and 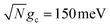 , respectively. These long-time populations are affected not only by the effective forward rate constants shown in Fig. 4a and b but by the effective backward rate constants as well. Simulations with similar forward rate constants but different backward rate constants can have different long-time populations, such that the simulation with a larger backward rate constant can have a smaller long-time acceptor population than the simulation with a smaller backward rate constant. Fig. 4c, like 4a, does not show a strong dependence on λD due to the small rate of transfer to the dark states and, as a result, the long-time acceptor populations are all nearly 1 for all simulated Q and λD.
, respectively. These long-time populations are affected not only by the effective forward rate constants shown in Fig. 4a and b but by the effective backward rate constants as well. Simulations with similar forward rate constants but different backward rate constants can have different long-time populations, such that the simulation with a larger backward rate constant can have a smaller long-time acceptor population than the simulation with a smaller backward rate constant. Fig. 4c, like 4a, does not show a strong dependence on λD due to the small rate of transfer to the dark states and, as a result, the long-time acceptor populations are all nearly 1 for all simulated Q and λD.
On the other hand, Fig. 4d demonstrates the consequence of the disordered dark states cavity loss mechanism seen in Fig. 4b for 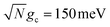 in an even more striking fashion. Not only are the largest long-time acceptor populations for λD = 20 meV and λD = 50 meV located at smaller values of Q, but the smallest long-time acceptor populations are seen at Q = ∞, even smaller than those at Q = 10. Further, the long-time acceptor population for λD = 20 meV at Q = 50 is over 7 times larger than that at Q = ∞. While simulations with Q = ∞ may have a relatively fast rate of transfer to acceptor states at short times, much of the UP population quickly transfers to and becomes trapped in the dark states for λD > 0 which forbids any appreciable transfer to the acceptor states during the rest of the 10 ns of propagation (we assume the dark exciton lifetime will be longer than this time scale, which is the case for CdSe NPL67). When λD > 0 and Q is small, on the other hand, the recycling of population from the disordered dark states to the UP allows for acceptor population to continue accumulating for the entire 10 ns of propagation even if the rate of accumulation at the start of the simulation is slower than for Q = ∞. This explains why the peaks in long-time acceptor population along Q in Fig. 4d are more pronounced than the peaks in forward rate constant in Fig. 4b.
in an even more striking fashion. Not only are the largest long-time acceptor populations for λD = 20 meV and λD = 50 meV located at smaller values of Q, but the smallest long-time acceptor populations are seen at Q = ∞, even smaller than those at Q = 10. Further, the long-time acceptor population for λD = 20 meV at Q = 50 is over 7 times larger than that at Q = ∞. While simulations with Q = ∞ may have a relatively fast rate of transfer to acceptor states at short times, much of the UP population quickly transfers to and becomes trapped in the dark states for λD > 0 which forbids any appreciable transfer to the acceptor states during the rest of the 10 ns of propagation (we assume the dark exciton lifetime will be longer than this time scale, which is the case for CdSe NPL67). When λD > 0 and Q is small, on the other hand, the recycling of population from the disordered dark states to the UP allows for acceptor population to continue accumulating for the entire 10 ns of propagation even if the rate of accumulation at the start of the simulation is slower than for Q = ∞. This explains why the peaks in long-time acceptor population along Q in Fig. 4d are more pronounced than the peaks in forward rate constant in Fig. 4b.
Fig. 5 presents the influence of cavity detuning in the presence of the CW laser driving, λD-induced transition to dark states, and cavity loss on PMET fitted rate constants for an uphill reaction with N = 1000. The ET and CW laser parameters are the same as those used in Fig. 3 and 4. Simulations were performed for λD = 0 (red), λD = 20 meV (blue), and λD = 50 meV (green) over t = 10 ns with collective coupling 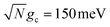 .
.
Fig. 5a shows the fitted forward rate constants from the propagated acceptor populations with a fixed Q = 100 and detuning ranging over δc ∈ [−100, 500] meV. For positive detunings, the rate constant increases up until δc ≈ 350 meV and begins to decrease for larger detunings. The rate constant is maximized near δc ≈ 350 meV because the shoulder of the exponential in eqn (28) is nearly 0 (ΔG − λD − (δc + ΩR)/2 + λA ≈ 0) for this detuning which can be considered a nearly barrier-less transfer from the UP to the acceptor states. While there is some rate reduction at positive detunings due to the decrease of UP matter character sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Φ, this reduction is only sin2
Φ, this reduction is only sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Φ (δc = 350 meV)/
Φ (δc = 350 meV)/![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2
sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Φ (δc = 0 meV) ≈ 0.24 which is much less than the several orders of magnitude increase of rate due to the more favorable driving force around δc ≈ 350 meV. The rate constant begins to decrease for detunings larger than δc ≈ 350 meV due to both the further reduction of matter character and a driving force that is now in the inverted Marcus regime. For negative detunings, the rate constants decrease for all λD, which is expected based on eqn (28) because the UP energy is decreased, which makes the driving force larger and the reaction from the UP to the acceptors slower.
Φ (δc = 0 meV) ≈ 0.24 which is much less than the several orders of magnitude increase of rate due to the more favorable driving force around δc ≈ 350 meV. The rate constant begins to decrease for detunings larger than δc ≈ 350 meV due to both the further reduction of matter character and a driving force that is now in the inverted Marcus regime. For negative detunings, the rate constants decrease for all λD, which is expected based on eqn (28) because the UP energy is decreased, which makes the driving force larger and the reaction from the UP to the acceptors slower.
Perhaps the most notable observation from Fig. 5a is that the effective rate constants for all three values of λD become nearly identical for larger positive detunings. This is in stark contrast to the negative detunings, where the non-zero λD rate constants are orders of magnitude smaller than the λD = 0 rate constant. The reasons for this effect at large detunings are similar to the reasons why the effective rate constants for the 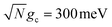 case in Fig. 4a are nearly the same for all three λD values. The large positive detunings increase the spectral gap between the UP and the dark states, which significantly decreases the transfer rate from the UP to the dark states. In addition, the decrease of UP matter character at positive detunings also decreases the transfer rate from the UP to the dark states since that rate is proportional to the UP matter character. This significantly decreased transfer rate from the UP to the dark states at large positive detunings becomes negligible compared to the increased rate from the UP to the acceptor states, which essentially eliminates the effect of the dark states on the PMET process for large positive detunings. As such, our theoretical work suggests that future experimental work uses positive detunings to (1) enhance the effective driving force of PMET, and at the same time, (2) decrease the transition rate from UP to the dark states.
case in Fig. 4a are nearly the same for all three λD values. The large positive detunings increase the spectral gap between the UP and the dark states, which significantly decreases the transfer rate from the UP to the dark states. In addition, the decrease of UP matter character at positive detunings also decreases the transfer rate from the UP to the dark states since that rate is proportional to the UP matter character. This significantly decreased transfer rate from the UP to the dark states at large positive detunings becomes negligible compared to the increased rate from the UP to the acceptor states, which essentially eliminates the effect of the dark states on the PMET process for large positive detunings. As such, our theoretical work suggests that future experimental work uses positive detunings to (1) enhance the effective driving force of PMET, and at the same time, (2) decrease the transition rate from UP to the dark states.
Fig. 5b shows the fitted forward rate constants from the propagated acceptor populations with a fixed δc = 350 meV and Q ranging over Q ∈ [10, ∞]. The rate constant's lack of dependence on λD that was seen in Fig. 5a for Q = 100 is also seen in Fig. 5b across all values of Q. This further supports the idea that the dark states do not significantly impact the overall PMET process from the UP to the acceptor states with large positive detunings. The dependence of the rate constant across Q is similar to that seen in Fig. 3c. Additionally, the rate constants in Fig. 5b (with collective coupling 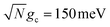 ) are almost as large as those rate constants at resonance with
) are almost as large as those rate constants at resonance with 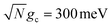 in Fig. 3c. Notably, the rate constant for λD = 50 meV and Q = 10 is 103 times larger than outside the cavity, exemplifying how the cavity can still significantly enhance PMET reactivity even with significant molecular disorder and cavity loss by CW driving to a positively detuned UP state.
in Fig. 3c. Notably, the rate constant for λD = 50 meV and Q = 10 is 103 times larger than outside the cavity, exemplifying how the cavity can still significantly enhance PMET reactivity even with significant molecular disorder and cavity loss by CW driving to a positively detuned UP state.
4 Conclusions
In this work, we theoretically examined enhancing PMET rates in the collective light–matter coupling regime in the presence of dark state transfer and cavity loss. We extended a simple ET model to include collective cavity coupling as well as dark state transfer, cavity loss, and coherent CW laser pumping. We derived the collective reaction coordinate of a PMET reaction between the UP and acceptor states and used it to prove that the driving force from the UP state is decreased by the collective light–matter coupling. We demonstrated the effect of this driving force modification by simulating PMET rate enhancement over a large range of N molecules in the Marcus regime and confirmed the excellent agreement between fitted rate constants from simulation and Marcus theory rate constants. We then showed how a CW laser tuned to the UP can partially or entirely avoid these suppressing effects of dark states and cavity loss and allow for orders of magnitude PMET rate enhancement in the collective limit. In particular, we demonstrated that using CW laser driving can effectively reduce the deleterious effect of cavity loss by replenishing the UP populations. Further, a reasonable size of Rabi splitting (larger than the reorganization energy) can reduce the rate of population decay from the UP to the dark states (due to the phonon bottleneck effect80,99). Many of the parameters recorded in this work are experimentally relevant to the system of CdSe NPLs coupled to the cavity,67–70 and can thus be experimentally tested in the near future. It may be worth mentioning that CW laser driving is often easier to implement than a pulsed laser, and most of photo-driven chemistry is performed under a powerful CW laser source or other continuous narrow-band light source such as a light-emitting diode.We further considered cavity detuning and found that the effective rate constants can be substantially increased with large positive detuning which also nearly eliminates the suppressing effects of the dark states. Encouragingly, this enhancement can be several orders of magnitude larger than the rate constant outside the cavity even when λD and Γ are large. The positive cavity detuning also significantly reduces the magnitude of the population transfer from the UP to the dark states, due to the enlarged energy gap and phonon bottleneck effect. These results demonstrate that significant cavity enhancement may be achievable for uphill ET-like reactions by CW driving to the UP in a cavity that has been positively detuned to optimize the driving force from the UP to the acceptor states and avoid dark state transfer.
These results show that the significant cavity enhancement is enabled by collective coupling to the cavity and depends sensitively on the collective Rabi splitting ΩR. The collective PMET rate constant depends on 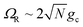 , and thus is collective. Despite individual molecules being weakly coupled to the cavity mode with strength gc, as long as there are a large enough number of molecules N collectively coupled to the cavity, there will be a significant modification of the rate constant. This mechanism relies on the non-local light–matter interactions and local chemical couplings (between donor to acceptor through VDA). This rate dependence on the collective Rabi splitting in this work could offer insight into the apparent Rabi splitting dependence of existing polariton photochemistry experiments1,12–15 such as the rate enhancement observed in ref. 12. Future work includes analyzing the effects of multiple k – dispersed cavity modes on the PMET process68–70,97,101 as well as investigating both the electron–photon population dynamics and nuclear wave packet dynamics of different photochemical model systems51,58 in the collective coupling regime.
, and thus is collective. Despite individual molecules being weakly coupled to the cavity mode with strength gc, as long as there are a large enough number of molecules N collectively coupled to the cavity, there will be a significant modification of the rate constant. This mechanism relies on the non-local light–matter interactions and local chemical couplings (between donor to acceptor through VDA). This rate dependence on the collective Rabi splitting in this work could offer insight into the apparent Rabi splitting dependence of existing polariton photochemistry experiments1,12–15 such as the rate enhancement observed in ref. 12. Future work includes analyzing the effects of multiple k – dispersed cavity modes on the PMET process68–70,97,101 as well as investigating both the electron–photon population dynamics and nuclear wave packet dynamics of different photochemical model systems51,58 in the collective coupling regime.
Data availability
Data for this article, including source code and data are available on Github at [https://github.com/ericrkoessler/PMET-LMFE].Author contributions
All authors designed the project. E. R. K., A. M., and P. H. derived the analytic expressions of PMET. E. R. K. performed the quantum dynamics simulations. All authors wrote and edited the manuscript.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was supported by the National Science Foundation Award under Grant No. CHE-2244683. The development of the analytic PMET rate constant expression and the PMET mechanism was supported by the Department of Energy under Grant No. DE-SC0022171. We appreciate the initial seed funding from the University Research Award (URA) of the University of Rochester that enabled this work. P. H. appreciates the support of the Cottrell Scholar Award (a program by the Research Corporation for Science Advancement). Computational resources were provided by the Center for Integrated Research Computing (CIRC) at the University of Rochester. We appreciate valuable discussions with Theta Chen, Jillian Dempsey, Dan Weix, and Nick Vamivakas.Notes and references
- A. Mandal, M. A. Taylor, B. M. Weight, E. R. Koessler, X. Li and P. Huo, Chem. Rev., 2023, 123, 9786–9879 CrossRef CAS.
- R. F. Ribeiro, L. A. Martínez-Martínez, M. Du, J. C. Gonzalez-Angulo and J. Yuen-Zhou, Chem. Sci., 2018, 9, 6325–6339 RSC.
- R. Bhuyan, J. Mony, O. Kotov, G. W. Castellanos, J. Gómez Rivas, T. O. Shegai and K. Börjesson, Chem. Rev., 2023, 123, 10877–10919 CrossRef CAS.
- K. Hirai, J. A. Hutchison and H. Uji-i, Chem. Rev., 2023, 123, 8099–8126 CrossRef CAS PubMed.
- J. Fregoni, F. J. Garcia-Vidal and J. Feist, ACS Photonics, 2022, 9, 1096–1107 CrossRef CAS PubMed.
- A. Thomas, L. Lethuillier-Karl, K. Nagarajan, R. M. A. Vergauwe, J. George, T. Chervy, A. Shalabney, E. Devaux, C. Genet, J. Moran and T. W. Ebbesen, Science, 2019, 363, 615–619 CrossRef CAS PubMed.
- A. Thomas, J. George, A. Shalabney, M. Dryzhakov, S. J. Varma, J. Moran, T. Chervy, X. Zhong, E. Devaux, C. Genet, J. A. Hutchison and T. W. Ebbesen, Angew. Chem., Int. Ed., 2016, 55, 11462–11466 CrossRef CAS.
- J. Lather, P. Bhatt, A. Thomas, T. W. Ebbesen and J. George, Angew. Chem., Int. Ed., 2019, 58, 10635–10638 CrossRef CAS.
- A. Thomas, A. Jayachandran, L. Lethuillier-Karl, R. M. A. Vergauwe, K. Nagarajan, E. Devaux, C. Genet, J. Moran and T. W. Ebbesen, Nanophotonics, 2020, 9, 249–255 CrossRef CAS.
- R. M. A. Vergauwe, A. Thomas, K. Nagarajan, A. Shalabney, J. George, T. Chervy, M. Seidel, E. Devaux, V. Torbeev and T. W. Ebbesen, Angew. Chem., Int. Ed., 2019, 58, 15324–15328 CrossRef CAS PubMed.
- J. Lather, A. N. K. Thabassum, J. Singh and J. George, Chem. Sci., 2022, 13, 195–202 RSC.
- H. Zeng, J. B. Pérez-Sánchez, C. T. Eckdahl, P. Liu, W. J. Chang, E. A. Weiss, J. A. Kalow, J. Yuen-Zhou and N. P. Stern, J. Am. Chem. Soc., 2023, 145, 19655–19661 CrossRef CAS.
- I. Lee, S. R. Melton, D. Xu and M. Delor, J. Am. Chem. Soc., 2024, 146, 9544–9553 CrossRef CAS.
- J. A. Hutchison, T. Schwartz, C. Genet, E. Devaux and T. W. Ebbesen, Angew. Chem., Int. Ed., 2012, 51, 1592–1596 CrossRef CAS PubMed.
- B. Munkhbat, M. Wersäll, D. G. Baranov, T. J. Antosiewicz and T. Shegai, Sci. Adv., 2018, 4, eaas9552 CrossRef.
- C. Ng, S. Dligatch, H. Amekura, T. J. Davis and D. E. Gómez, Adv. Opt. Mater., 2015, 3, 1582–1590 CrossRef CAS.
- J. Mony, C. Climent, A. U. Petersen, K. Moth-Poulsen, J. Feist and K. Börjesson, Adv. Funct. Mater., 2021, 31, 2010737 CrossRef CAS.
- P. A. Thomas, W. J. Tan, V. G. Kravets, A. N. Grigorenko and W. L. Barnes, Adv. Mater., 2024, 36, 2309393 CrossRef CAS.
- T. Schwartz and J. A. Hutchison, arXiv, 2024, preprint, arXiv:2403.06001, DOI:10.48550/arXiv.2403.06001.
- K. Schwennicke, A. Koner, J. B. Pérez-Sánchez, W. Xiong, N. C. Giebink, M. L. Weichman and J. Yuen-Zhou, arXiv, 2024, preprint, arXiv:2408.05036, DOI:10.48550/arXiv.2408.05036.
- A. Mandal, T. D. Krauss and P. Huo, J. Phys. Chem. B, 2020, 124, 6321–6340 CrossRef CAS.
- L. Mauro, K. Caicedo, G. Jonusauskas and R. Avriller, Phys. Rev. B, 2021, 103, 165412 CrossRef CAS.
- B. M. Weight, T. D. Krauss and P. Huo, J. Phys. Chem. Lett., 2023, 14, 5901–5913 CrossRef CAS.
- F. Herrera and F. C. Spano, Phys. Rev. Lett., 2016, 116, 238301 CrossRef PubMed.
- A. Semenov and A. Nitzan, J. Chem. Phys., 2019, 150, 174122 CrossRef PubMed.
- S. N. Chowdhury, A. Mandal and P. Huo, J. Chem. Phys., 2021, 154, 044109 CrossRef CAS PubMed.
- M. A. C. Saller, Y. Lai and E. Geva, J. Phys. Chem. Lett., 2022, 13, 2330–2337 CrossRef CAS.
- D. Wellnitz, G. Pupillo and J. Schachenmayer, J. Chem. Phys., 2021, 154, 054104 CrossRef CAS.
- N. T. Phuc, J. Chem. Phys., 2021, 155, 014308 CrossRef.
- C. Schäfer, M. Ruggenthaler, H. Appel and A. Rubio, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 4883–4892 CrossRef PubMed.
- S. K. Sharma and H.-T. Chen, J. Chem. Phys., 2024, 161, 104102 CrossRef CAS.
- Y. Gu, B. Gu, S. Sun, H. Yong, V. Y. Chernyak and S. Mukamel, J. Am. Chem. Soc., 2023, 145, 14856–14864 CrossRef CAS.
- G. D. Scholes, C. A. DelPo and B. Kudisch, J. Phys. Chem. Lett., 2020, 11, 6389–6395 CrossRef CAS PubMed.
- C. Climent, D. Casanova, J. Feist and F. J. Garcia-Vidal, Cell Rep. Phys. Sci., 2022, 3, 100841 CrossRef CAS PubMed.
- B. Gu and S. Mukamel, J. Phys. Chem. Lett., 2021, 12, 2052–2056 CrossRef CAS.
- L. A. Martínez-Martínez, M. Du, R. F. Ribeiro, S. Kéna-Cohen and J. Yuen-Zhou, J. Phys. Chem. Lett., 2018, 9, 1951–1957 CrossRef.
- Q. Ou, Y. Shao and Z. Shuai, J. Am. Chem. Soc., 2021, 143, 17786–17792 CrossRef CAS PubMed.
- B. Zhang and Z. Shuai, J. Phys. Chem. Lett., 2022, 13, 9279–9286 CrossRef CAS.
- K. Peng and E. Rabani, J. Chem. Phys., 2024, 161, 154107 CrossRef CAS PubMed.
- M. Du, L. A. Martínez-Martínez, R. F. Ribeiro, Z. Hu, V. M. Menon and J. Yuen-Zhou, Chem. Sci., 2018, 9, 6659–6669 RSC.
- M. Kowalewski, K. Bennett and S. Mukamel, J. Phys. Chem. Lett., 2016, 7, 2050–2054 CrossRef CAS PubMed.
- M. H. Farag, A. Mandal and P. Huo, Phys. Chem. Chem. Phys., 2021, 23, 16868–16879 RSC.
- D. S. Wang, T. Neuman, S. F. Yelin and J. Flick, J. Phys. Chem. Lett., 2022, 13, 3317–3324 CrossRef CAS PubMed.
- A. Csehi, O. Vendrell, G. J. Halász and Á. Vibók, New J. Phys., 2022, 24, 073022 CrossRef.
- A. Csehi, Á. Vibók, G. J. Halász and M. Kowalewski, Phys. Rev. A, 2019, 100, 053421 CrossRef CAS.
- E. Davidsson and M. Kowalewski, J. Chem. Phys., 2020, 153, 234304 CrossRef CAS PubMed.
- M. Gudem and M. Kowalewski, J. Phys. Chem. A, 2021, 125, 1142–1151 CrossRef CAS.
- J. Torres-Sánchez and J. Feist, J. Chem. Phys., 2021, 154, 014303 CrossRef PubMed.
- E. Davidsson and M. Kowalewski, J. Phys. Chem. A, 2020, 124, 4672–4677 CrossRef CAS PubMed.
- T. E. Li, Z. Tao and S. Hammes-Schiffer, J. Chem. Theory Comput., 2022, 18, 2774–2784 CrossRef CAS.
- A. Mandal and P. Huo, J. Phys. Chem. Lett., 2019, 10, 5519–5529 CrossRef CAS.
- J. Galego, F. Garcia-Vidal and J. Feist, Nat. Commun., 2016, 7, 13841 CrossRef CAS PubMed.
- J. Galego, F. J. Garcia-Vidal and J. Feist, Phys. Rev. Lett., 2017, 119, 136001 CrossRef.
- J. Feist, J. Galego and F. J. Garcia-Vidal, ACS Photonics, 2018, 5, 205–216 CrossRef CAS.
- J. Fregoni, G. Granucci, E. Coccia, M. Persico and S. Corni, Nat. Commun., 2018, 9, 4688 CrossRef CAS.
- J. Fregoni, G. Granucci, M. Persico and S. Corni, Chem, 2020, 6, 250–265 CAS.
- E. Michail, K. Rashidi, B. Liu, G. He, V. M. Menon and M. Y. Sfeir, Nano Lett., 2024, 24, 557–565 CrossRef CAS PubMed.
- A. Dutta, V. Tiainen, I. Sokolovskii, L. Duarte, N. Markešević, D. Morozov, H. A. Qureshi, S. Pikker, G. Groenhof and J. J. Toppari, Nat. Commun., 2024, 15, 6600 CrossRef CAS.
- E. Eizner, L. A. Martínez-Martínez, J. Yuen-Zhou and S. Kéna-Cohen, Sci. Adv., 2019, 5, eaax4482 CrossRef CAS.
- J. B. Pérez-Sánchez, F. Mellini, N. C. Giebink and J. Yuen-Zhou, Phys. Rev. Res., 2024, 6, 013222 CrossRef.
- S. N. Chowdhury, P. Zhang and D. N. Beratan, J. Phys. Chem. Lett., 2022, 13, 9822–9828 CrossRef CAS.
- N. T. Phuc, P. Q. Trung and A. Ishizaki, Sci. Rep., 2020, 10, 7318 CrossRef CAS PubMed.
- J. A. Campos-Gonzalez-Angulo, R. F. Ribeiro and J. Yuen-Zhou, Nat. Commun., 2019, 10, 4685 CrossRef.
- K. Uosaki, T. Kondo, X.-Q. Zhang and M. Yanagida, J. Am. Chem. Soc., 1997, 119, 8367–8368 CrossRef CAS.
- K. Uosaki, T. Kondo, X.-Q. Zhang and M. Yanagida, Angew. Chem., 2011, 123, 1316–1320 CrossRef.
- Q. Li, S. He and T. Lian, Nano Lett., 2020, 20, 6162–6169 CrossRef CAS.
- L. Qiu, A. Mandal, O. Morshed, M. T. Meidenbauer, W. Girten, P. Huo, A. N. Vamivakas and T. D. Krauss, J. Phys. Chem. Lett., 2021, 12, 5030–5038 CrossRef CAS PubMed.
- M. Amin, E. R. Koessler, O. Morshed, F. Awan, N. M. B. Cogan, R. Collison, T. M. Tumiel, W. Girten, C. Leiter, A. N. Vamivakas, P. Huo and T. D. Krauss, ACS Nano, 2024, 18, 21388–21398 CrossRef CAS PubMed.
- O. Morshed, M. Amin, N. M. B. Cogan, E. R. Koessler, R. Collison, T. M. Tumiel, W. Girten, F. Awan, L. Mathis, P. Huo, A. N. Vamivakas, T. W. Odom and T. D. Krauss, J. Chem. Phys., 2024, 161, 014710 CrossRef CAS PubMed.
- F. Freire-Fernández, N. G. Sinai, M. J. Hui Tan, S.-M. Park, E. R. Koessler, T. Krauss, P. Huo and T. W. Odom, ACS Nano, 2024, 18, 15177–15184 CrossRef.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- A. O. Caldeira and A. J. Leggett, Phys. Rev. Lett., 1981, 46, 211–214 CrossRef.
- M. Tavis and F. W. Cummings, Phys. Rev., 1968, 170, 379–384 CrossRef.
- J. B. Pérez-Sánchez, A. Koner, N. P. Stern and J. Yuen-Zhou, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2219223120 CrossRef PubMed.
- T. E. Li, B. Cui, J. E. Subotnik and A. Nitzan, Annu. Rev. Phys. Chem., 2022, 73, 43–71 CrossRef CAS PubMed.
- F. Herrera and F. C. Spano, Phys. Rev. A, 2017, 95, 053867 CrossRef.
- D. Manzano, AIP Adv., 2020, 10, 025106 CrossRef.
- G. Lindblad, Commun. Math. Phys., 1976, 48, 119–130 CrossRef.
- E. R. Koessler, A. Mandal and P. Huo, J. Chem. Phys., 2022, 157, 064101 CrossRef CAS PubMed.
- Y. Lai, W. Ying and P. Huo, J. Chem. Phys., 2024, 161, 104109 CrossRef CAS PubMed.
- H.-T. Chen, Z. Zhou, M. Sukharev, J. E. Subotnik and A. Nitzan, Phys. Rev. A, 2022, 106, 053703 CrossRef CAS.
- T. Liu, G. Yin and W. Xiong, Chem. Sci., 2025, 16, 4676–4683 RSC.
- A. Garg, J. N. Onuchic and V. Ambegaokar, J. Chem. Phys., 1985, 83, 4491–4503 CrossRef CAS.
- S. Mukamel, Principles of Nonlinear Optical Spectroscopy, Oxford University Press, 1995, p. 222 Search PubMed.
- T. Khazanov, S. Gunasekaran, A. George, R. Lomlu, S. Mukherjee and A. J. Musser, Chem. Phys. Rev., 2023, 4, 041305 CrossRef CAS.
- A. George, T. Geraghty, Z. Kelsey, S. Mukherjee, G. Davidova, W. Kim and A. J. Musser, Adv. Opt. Mater., 2024, 12, 2302387 CrossRef CAS.
- A. Warshel, J. Phys. Chem., 1982, 86, 2218–2224 CrossRef CAS.
- W. Ying, M. E. Mondal and P. Huo, J. Chem. Phys., 2024, 161, 064105 CrossRef CAS PubMed.
- N. B. Taylor and I. Kassal, Chem. Sci., 2018, 9, 2942–2951 RSC.
- D. W. Small, D. V. Matyushov and G. A. Voth, J. Am. Chem. Soc., 2003, 125, 7470–7478 CrossRef CAS PubMed.
- J. E. Lawrence, J. R. Mannouch and J. O. Richardson, J. Phys. Chem. Lett., 2024, 15, 707–716 CrossRef CAS PubMed.
- B. Hou, M. Thoss, U. Banin and E. Rabani, Nat. Commun., 2023, 14, 3073 CrossRef CAS PubMed.
- M. D. Newton and N. Sutin, Annu. Rev. Phys. Chem., 1984, 35, 437–480 CrossRef CAS.
- W. Ying, M. Taylor and P. Huo, Nanophotonics, 2024, 13, 2601–2615 CrossRef PubMed.
- W. Ying and P. Huo, Commun. Mater., 2024, 5, 110 CrossRef CAS.
- G. Groenhof, C. Climent, J. Feist, D. Morozov and J. J. Toppari, J. Phys. Chem. Lett., 2019, 10, 5476–5483 CrossRef CAS PubMed.
- R. H. Tichauer, J. Feist and G. Groenhof, J. Chem. Phys., 2021, 154, 104112 CrossRef CAS PubMed.
- D. Hu, B. Chng, W. Ying and P. Huo, ChemRxiv, 2024, preprint, DOI:10.26434/chemrxiv–2024–t818f.
- B. X. K. Chng, W. Ying, Y. Lai, A. N. Vamivakas, S. T. Cundiff, T. D. Krauss and P. Huo, J. Phys. Chem. Lett., 2024, 15, 11773–11783 CrossRef CAS PubMed.
- R. Pandya, A. Ashoka, K. Georgiou, J. Sung, R. Jayaprakash, S. Renken, L. Gai, Z. Shen, A. Rao and A. J. Musser, Adv. Sci., 2022, 9, 2105569 CrossRef CAS PubMed.
- E. Hulkko, S. Pikker, V. Tiainen, R. H. Tichauer, G. Groenhof and J. J. Toppari, J. Chem. Phys., 2021, 154, 154303 CrossRef CAS PubMed.
- A. Kirrander and M. Vacher, in Ehrenfest Methods for Electron and Nuclear Dynamics, John Wiley & Sons, Ltd, 2020, ch. 15, pp. 469–497 Search PubMed.
- J. C. Tully, J. Chem. Phys., 2012, 137, 22A301 CrossRef PubMed.
- M. Vacher, D. Mendive-Tapia, M. J. Bearpark and M. A. Robb, Theor. Chem. Acc., 2014, 133, 1505 Search PubMed.
- M. E. Mondal, E. R. Koessler, J. Provazza, A. N. Vamivakas, S. T. Cundiff, T. D. Krauss and P. Huo, J. Chem. Phys., 2023, 159, 094102 CrossRef CAS PubMed.
- C. A. Schwerdtfeger, A. V. Soudackov and S. Hammes-Schiffer, J. Chem. Phys., 2014, 140, 034113 CrossRef PubMed.
- A. Mandal, F. A. Shakib and P. Huo, J. Chem. Phys., 2018, 148, 244102 CrossRef PubMed.
- N. Grønbech-Jensen and O. Farago, Mol. Phys., 2013, 111, 983–991 CrossRef.
- M. Paterlini and D. M. Ferguson, Chem. Phys., 1998, 236, 243–252 CrossRef CAS.
- M. E. Mondal, A. N. Vamivakas, S. T. Cundiff, T. D. Krauss and P. Huo, J. Chem. Phys., 2025, 162, 014114 CrossRef CAS PubMed.
- S. Pannir-Sivajothi, J. A. Campos-Gonzalez-Angulo, L. A. Martínez-Martínez, S. Sinha and J. Yuen-Zhou, Nat. Commun., 2022, 13, 1645 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sc01911g |
| This journal is © The Royal Society of Chemistry 2025 |