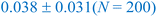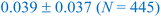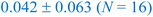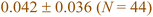A structural similarity based data-mining algorithm for modeling multi-reactant heterogeneous catalysts

Abstract

First-principles-based Density Functional Theory (DFT) simulations are powerful tools for studying heterogeneous catalyst systems. However, their high computational cost and large configuration space hinder their application in understanding multi-reactant catalysis on geometrically diverse surfaces. This work introduces an innovative similarity algorithm that quantifies the structural differences between atomic configurations to address this challenge. The quantification effectively identifies structurally dissimilar configurations with minimal human intervention. Consequently, data mining the configurational phase-space through this similarity algorithm drastically reduces the number of DFT simulations required to identify stable atomic models relevant to key multi-reactant chemistries. In this work, the similarity algorithm is utilized to understand CO*–OH* co-adsorption at varying adsorbate coverages on a stepped Pt surface by DFT simulating only 2% of possible unique configurations. Furthermore, the versatility of the similarity algorithm is showcased by analyzing bidentate adsorption on a stepped Pt surface. This work serves as a crucial steppingstone towards understanding important multi-reactant heterogeneous catalytic chemistries.

---

Introduction

First-principles atomic simulations, such as those based on Density Functional Theory (DFT), are powerful tools for understanding interactions and reaction mechanisms in heterogeneous catalytic systems.^1–3 These methods have been successfully applied to study key reaction chemistries, especially involving a single type of adsorbate on various catalytic surfaces, resulting in fundamental mechanistic insights and the discovery of more efficient catalytic materials. However, extending these techniques to more complex reactions—such as the electro-catalytic conversion of carbon and nitrogen-based feedstocks,^4–8 biomass-based reactions in solvent environments,⁹ and alcohol steam reforming¹⁰—remains a significant challenge. The difficulty lies in constructing accurate atomic models that incorporate multiple types of reaction intermediates on geometrically diverse catalytic surfaces under varying adsorbate coverages, a crucial characteristic of such reactions. This challenge arises from the vast configurational space created by the combinatorial explosion of unique binding sites and different adsorbate molecules. Consequently, the number of required DFT simulations increases by two to three orders of magnitude compared to scenarios with a single type of adsorbate. Therefore, novel data-driven methods capable of sampling such large phase spaces with significantly reduced computational demands are essential to tackle these challenges.

Data-driven statistical learning methods such as machine learning (ML)/deep learning (DL) and graph theory-based algorithms hold the potential to overcome challenges associated with large phase spaces.^11–28 On this front, efforts have been made to reduce the DFT calculations by adopting a surrogate ML/DL model for prediction of physical properties, such as adsorption energy of reaction intermediates.^{11,12,14,17–20} Alternatively, ML/DL algorithms have been designed to output interatomic potentials for atomistic simulations to achieve faster configuration sampling compared to ab initio molecular dynamic simulations.^15,16,21 On the other hand, graph-theory based enumeration methods have been proposed that characterize catalytic configurations into ego graphs.^13,22–25 Graph theory based algorithms are then used to remove duplicate configurations through isomorphism checking to identify the unique configurations. These unique configurations are then combined with an energy-based evolutionary algorithm and/or training a surrogate model for adsorption energy estimation. These methods are then used to study catalysis on metallic surfaces considering varying adsorbate coverages by utilizing a small number of DFT calculations. All these different approaches have successfully achieved high prediction accuracy. However, these state-of-the-art algorithms have been efficiently applied only to systems involving (1) single adsorbate in the unit cell,^{11,12,14–19,26–28} or (2) multiple types of adsorbates with fixed coverage and surface binding sites,²⁰ or (3) systems featuring a single type of adsorbate,^13,21–25 or (4) systems with fixed adsorbate patterns.²⁹ Extending these methods to accurately model systems with various types of adsorbates on geometrically diverse surfaces, such as defective surfaces under varying coverages, remains a significant challenge. A key bottleneck is the current frameworks' inability to quantify structural differences between various atomic configurations without assuming fixed patterns between adsorbate configurations. Consequently, DFT simulations are either performed on numerous similar atomic configurations or assuming fixed adsorbate patterns, resulting in oversampling structures with comparable physics. Hence, the primary objective of this work is to develop a new method that can universally assess structural similarity among different atomic structures and apply it to modeling heterogeneous catalytic systems that involve multiple reactants.

Here, we present a unique similarity-determining algorithm to quantify the structural differences between pairs of atomic configurations. The calculated similarity scores are shown to form clusters that represent the degree of structural similarity in the adsorbate binding sites. This leads to a scalable and fully automated data-mining algorithm for identifying the most structurally diverse configurations. These diverse atomic models can then be combined with a configuration sampling method, such as the energy-based evolutionary algorithm (called the Evo-Sim algorithm),^22,30 resulting in a significant reduction of the required DFT simulations to identify the most stable atomic configurations. We demonstrate the utility of the Evo-Sim algorithm by determining the most stable configurations for seventeen different coverages of mixed CO*–OH* co-adsorbed on stepped Pt(553) and terrace Pt(111) surfaces. These configurations are key to understanding the electro-oxidation chemistry of important carbon feedstocks, and Evo-Sim identifies the stable configurations by DFT simulating only about 2% of all possible unique configurations. Furthermore, bidentate ethylene adsorption on a stepped Pt surface is analyzed, showcasing the versatility of the similarity algorithm. Our method now provides a foundation for developing detailed atomic models for the important cases of multi-reactant heterogeneous catalytic reactions.

Results and discussion

In this section, we first present the workflow of the similarity algorithm in detail. Next, we showcase the utility of the similarity algorithm in constructing (i) combined phase diagrams of CO* and OH* co-adsorbed on the Pt(553) and the Pt(111) surfaces and (ii) estimating the phase diagram for multidentate ethylene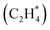 adsorption on Pt(553). A novel method combining the similarity algorithm, energy-based evolutionary algorithm, and cluster detection methods is used. The identified configurations shed light on key, previously unknown features driving CO electro-oxidation and temperature-dependent desorption of ethylene on metallic Pt catalysts.

Similarity algorithm

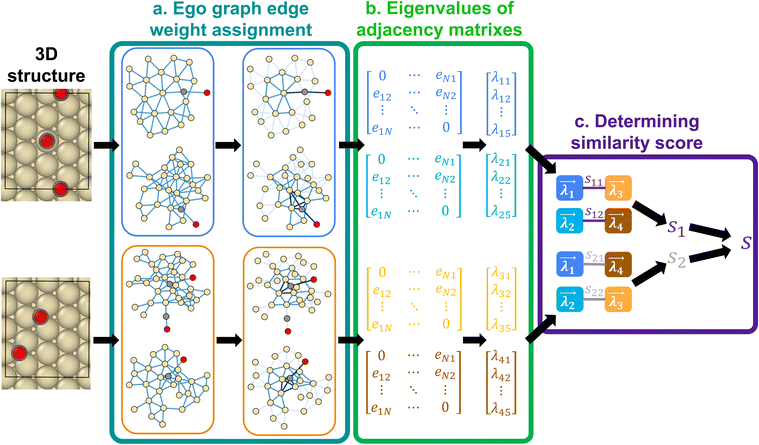
Fig. 1 illustrates the similarity algorithm framework. The framework estimates configurational similarity by implementing a newly developed eigenvalue-driven protocol that computes the similarity between two configurations with the same number of adsorbates using the adjacency matrix of their respective graph representations. The algorithm first creates N_ad (number of adsorbates in the configuration) ego graphs for each configuration (Fig. 1a). The ego graph places the adsorbate as the central node and then captures the chemical environment of the given adsorbate using the SURFGRAPH python package.²² The adjacency matrix of a given ego graph is a N × N symmetric matrix with zeros on the diagonal, where N is the number of atoms captured in the ego graph. The off-diagonal elements of the adjacency matrix are the edges e_ij between atoms ‘i’ and ‘j’ present in the ego graph. In step two (Fig. 1b), the edge weight is determined by the characteristics of the atoms and their distance, r, from the center adsorbate of the ego graph, as described by the following mathematical relation: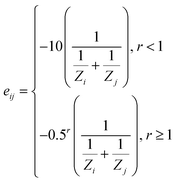 The Z_i denotes the atomic number of the atom of interest. Utilization of atomic numbers ensures that the identity of the active site structure's elements is well-captured in the graph representation, making it versatile. The distance from the center adsorbate, r, is defined as the number of edges along the shortest path between the node of interest and a node of the center adsorbate. The −10 prefactor enhances the edge weights of the center adsorbate and nearby adsorbate-metal edges in the associated adjacency matrix, giving the most importance to the interactions closest to the binding site. The −0.5^r prefactor decreases the weight of edges with r > 1, as the bonding interactions of atoms lying away from the adsorbate have significantly less influence on the binding energy than the atoms closer to the adsorbate binding site. The proposed edge weight assignments align with the physical intuition that active site atoms nearest to the adsorbate will contribute the most to the binding energetics.^3,31–34 Further, the dependence of the edge weight as a function of distance from the adsorbate node serves as the attention mechanism, which can also be modified based on the catalyst material.^17,35,36

Fig. 1 Similarity algorithm. (a) Ego graph edge weight assignment based on the distance from the center adsorbate. (b) Computation of the significant eigenvalues of the adjacency matrix of a given ego-graph. (c) Determining similarity score by combining a pairing protocol with the Normalized Euclidean Distance (NED) calculation between two configurations.

After assigning edge weights, the eigenvalues of the adjacency matrix are calculated (Fig. 1b). The eigenvalues of the adjacency matrix of the ego graph of interest are ranked in ascending order, and the top five largest magnitude eigenvalues are chosen to constitute the eigenvalue vector of the adjacency matrix of the ego graph. Our analysis shows that these top five eigenvalues most optimally capture structural differences for adsorbates on metal surfaces. The number of eigenvalues can be tuned for other materials. Hence, for a given configuration, there are N_ad eigenvalue vectors, each sized 5 × 1. Each vector characterizes the chemical environment of a given adsorbate. The similarity score between two ego graphs is then computed as the vector distance between the two eigenvalue vectors. The score is calculated using the normalized Euclidean distance (NED), defined as 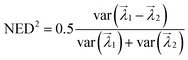, where var is the variance of a number array, and are the two eigenvalue vectors subjected to the calculation.

As a given configuration would have ‘N_ad’ chemical environments, multiple ways exist to estimate the vector distance. For example, as shown in Fig. 1, for the case of two adsorbates on the surface, configurations (1) and (2) would both have two chemical environment graphs each (G₁, G₂ and G₃, G₄, as shown in inset a, for the first and second configuration, respectively). Corresponding to these graphs and their adjacency matrices, eigenvalue vectors 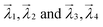are estimated for configurations (1) and (2) respectively. To estimate the smallest vector distance, NED estimates will then be performed by permuting all possible pairings between the eigenvectors of configuration (1) and configuration (2). For the case of two adsorbates, the pairings would be, 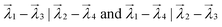, as shown in Fig. 1 inset c respectively. These two pairings would then result in similarity scores S₁ and S₂, and the smaller of the two scores will be the similarity score between configuration (1) and (2). Hence, an important challenge in estimating the vector distance accurately is identifying the most optimal pairing of adsorbate chemical environments between two configurations, which is unknown a priori. Therefore, multiple vector calculation groups representing all possible pairings of the eigenvalue vectors from the two configurations are initially generated, as shown in Fig. 1c. Vector distance calculation groups are then obtained by pairing the eigenvalue vectors of the first configuration to each one of the permutations of the eigenvalue vectors of the other configuration. Consequently, the number of calculation groups is N_group = P(N_ad, N_ad), with each group containing N_ad pairs of eigenvalues. In each group, the chemical environment of a given adsorbate of the first configuration is compared to only one of the chemical environments of the second configuration. For each pair of eigenvalue vectors in the group, the average of the NED values is computed and is stored as N_group. The N_group possessing the minimum averaged NED values is then reported as the similarity (see ESI S1.1† for an example). Thus, the similarity score is always computed from the most optimal pairing of the feature vectors from the two configurations of interest, and the smaller the magnitude of the similarity score, the more similar the two configurations. The utility of the similarity algorithm to identify the most stable atomic configurations for a multi-adsorbate system on a stepped metal surface is discussed next.

Understanding combined CO* and OH* adsorption on a stepped metal surface

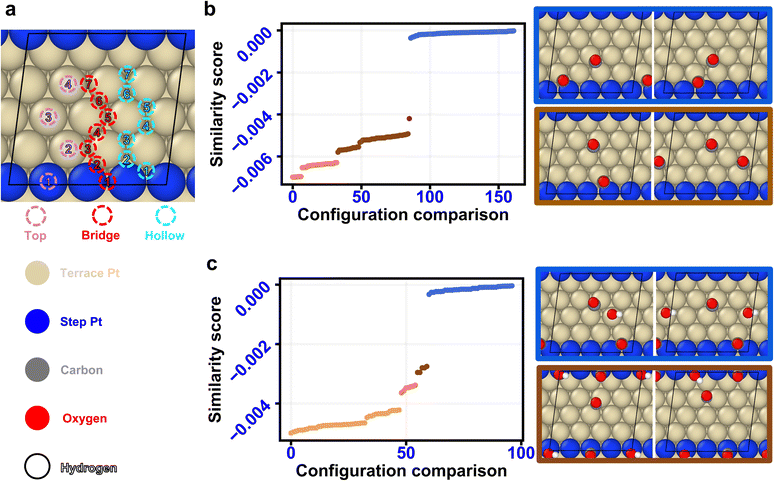
A fundamental understanding of the role of surface adsorbates and defects is critical in advancing various electro-catalytic carbon feedstock-based chemistries, including electro-oxidation of methanol,^4,5,37 ethanol, glycerol, and formic acid, amongst others.^7,8 A key reaction common to these chemistries is the CO-electro-oxidation reaction, which is considered a bottleneck to reduce the overpotential needed to fully oxidize the carbon feedstock.³⁷ A lack of fundamental understanding of the collective behavior of CO* and oxygenated species, such as OH*, especially in the presence of defects such as edges and kinks on the catalyst surface, constrains the discovery of an optimal CO electro-oxidation catalyst. The presence of a large phase space of possible unique atomic configurations remains the critical bottleneck to enable such an understanding. Herein, we utilize the similarity algorithm combined with an energy-driven evolutionary algorithm to study combined CO* and OH* adsorption on a stepped Pt(553) and a terrace Pt(111) surfaces under electrochemical conditions. We first utilize the similarity algorithm to discover structurally dissimilar configurations. These configurations are then fed into an energy-driven evolutionary algorithm, incorporating DFT simulations, to identify structures containing dominant governing interactions. Finally, the structures obtained from these two steps are used to plot a voltage-dependent phase diagram.

The binding sites on the Pt(553) surface are characterized by the coordination number of the Pt atoms and the proximity of the well-coordinated Pt atoms to the step edge, denoted by the row number in Fig. 2a. The characterization identifies four, seven, and seven top, bridge, and hollow unique adsorption sites, respectively. Considering the number and variability in binding sites, the number of configurations increases exponentially as adsorbate coverage rises, especially when more than one type of adsorbate is considered (ESI Fig. 1†). The structurally dissimilar configurations are identified using the similarity algorithm to navigate the large phase space of possible configurations. Fig. 2b and c demonstrate the method for the cases of 2CO* and 2CO*–1OH* co-adsorbed on Pt(553). The similarity algorithm discussed in Fig. 1 is first used to obtain the pairwise similarity scores. The obtained similarity scores for the scenario involving 2CO* on Pt(553) are plotted in Fig. 2b. Remarkably, the similarity scores exhibit clustering behavior, with each cluster categorizing the configuration pairs based on the degree of similarity in binding site information. The clusters are automatically detected and labeled employing the DBSCAN algorithm from the SKLEARN Python package, requiring no human intervention.^38,39 Fig. 2b further illustrates two configuration pairs for the case of 2CO* belonging to the most similar blue and second most similar brown clusters, respectively. All pairs of configurations in the blue cluster possess an identical set of binding sites. As shown in the blue inset, both CO* in the two configurations occupy bridge sites, and both CO* are positioned in the 2nd row and the 4th row, respectively. However, while possessing the same types of binding sites (bridge sites, in this particular example), a representative configuration pair in the brown cluster demonstrates a variation in the coordination number of the Pt atoms forming these sites. As shown in the brown inset in Fig. 2b, CO* in the left configuration occupies bridge sites on the 2nd and 6th rows, while the right configuration has CO* on bridge sites on the 4th and 6th rows, respectively. Hence, the similarity algorithm captures the similarity based on the structural similarity of the binding sites between two different configurations. The case of multiple types of adsorbates is discussed next.

Fig. 2 Pairwise similarity scores identify highly similar configuration pairs. (a) Unique binding sites (top, bridge, hollow) on Pt(553) are labeled. Similarity scores profile (score < 0.01) for (b) 2CO* and (c) 2CO*–1OH* on Pt(553) surface configurations. Examples of configuration pairs in the topmost (blue) and second topmost (brown) similar clusters are shown.

Fig. 2c illustrates the case of 2CO*–1OH* adsorbed on the Pt(553). Analogous to the case of 2CO* on Pt(553), the similarity scores can successfully identify structural similarity between pairs of configurations. As shown in the blue highlighted pairs in Fig. 2c, both configurations have the OH* molecule adsorbed at the top site on the 3rd row, and the two CO* molecules occupy the hollow site on the 1st row and the bridge site on the 6th row, respectively. Therefore, the adsorbate-specific binding sites between the configurations in the blue pair possess the same binding site type and coordination number for each binding site. Conversely, the configuration pairs in the second topmost brown cluster differ by a single adsorbate binding site. As depicted by the two configurations in the brown pair in Fig. 2c, in the left configuration, a CO* occupies the bridge site of the 6th row, whereas in the right configuration, a CO* occupies the bridge site of the 7th row. Therefore, the observations pertaining to the 2CO* and 2CO*–1OH* scenarios demonstrate that the similarity algorithm effectively estimates quantitative similarity between pairs of non-isomorphic configurations based on the type and coordination number of the active site structure. Importantly, these observations consistently apply to all CO*–OH* coverages simulated in this study and indicate a robust ability of the similarity scores to quantitatively identify similar configurations. Further, to showcase the versatility of the similarity algorithm, we have also tested the algorithm on 1CO*–1OH* adsorbed on a Pt(553) surface with W₃O₇ as reported recently by Deshpande et al.,^30,40 and on the NO* adsorption on Pt3Sn(111) surface. The algorithm successfully clusters configuration pairs based on structural similarity for both these cases. Additional discussion on the similarity score clustering is presented in ESI Section 1.5.†

To further understand the relationship between the binding energetics of the adsorbates and the assessed structural similarity, we compute the average values and standard deviations of the absolute binding energy difference among the configuration pairs within each of the blue and brown clusters across all coverages of CO* and OH* estimated on Pt(553) (Table 1). The findings demonstrate that the configuration pairs within the blue, as well as the brown clusters, consistently exhibit small mean binding energy differences (most cases <0.1 eV), indicating that configurations sharing identical binding site information tend to possess similar binding energy values.^3,31–34 The utility of the identified similarity clusters to substantially minimize the required DFT calculations for estimating stable configurations at varying CO*–OH* coverages is discussed in the next section.

Table 1 The average and standard deviation of the absolute binding energy differences among the configuration pairs in the topmost blue similarity scores cluster and the second topmost brown similarity scores cluster under all CO*–OH* coverages on the Pt(553) surface. Configuration pairs are obtained by applying the similarity algorithm on non-isomorphic configurations within 0.3 eV from the most stable one

Coverage
0.1 ML (2CO*)
0.15 ML (3CO*)
0.2 ML (4CO*)
0.15 ML (2CO*–1OH*)
0.2 ML (2CO*–2OH*)
0.25 ML (3CO*–2OH*)
0.3 ML (3CO*–3OH*)
0.3 ML (4CO*–2OH*)
0.35 ML (4CO*–3OH*)

---

Similarity-incorporated evolutionary algorithm

Having demonstrated the effectiveness of the similarity algorithm in identifying structurally similar configurations, we now explore its application to determine the most stable CO* and OH* configurations at different coverages on the Pt(553) surface. A state-of-the-art sampling method to achieve this is the evolutionary algorithm.^22,30,41 The evolutionary algorithm initially ranks the stable non-isomorphic configurations according to their DFT-derived energies and then populates a subset of configurations with low formation energy. This iterative process continues until the desired coverage is attained. However, the evolutionary algorithm cannot successfully scale for the case of multiple types of adsorbates due to an order of magnitude larger phase space of atomic configurations. Further, the evolutionary algorithm only relies on non-isomorphic unique configurations to sample the phase space and lacks information regarding the structural and physical similarity of configurations. This leads to DFT simulation of configurations with similar physics and structures. We propose a new method to solve these issues, integrating the evolutionary algorithm with the similarity algorithm. The workflow of the similarity-incorporated evolutionary algorithm (Evo-Sim) is presented in Fig. 3a. Initially, the isomorphic configurations are removed, and then the top 0.3 eV DFT relaxed configurations at a given coverage are filtered (evolutionary algorithm step).^22,30 Thereafter, this subset of configurations is input to the similarity algorithm to calculate similarity scores. The top two most similar clusters are first determined using the DBSCAN algorithm. Then, using the similarity score in conjunction with the DFT energy, only the structure with the lower binding energy is kept from a given pair of configurations in the top two clusters. This step adds an additional layer that removes configurations that are structurally similar to each other, hence drastically reducing the size of the phase space by only retaining the structures with key dissimilar interactions. Only this small subset is then populated with an additional adsorbate. We further tested the ability of the proposed approach to identify the most stable atomic configurations by considering different groups of most similar clusters to determine the dis-similar configurations. The most stable configurations obtained for all the different CO*–OH* coverages using only the topmost similar blue cluster (Evo-Sim-1) were the same as those obtained using the top two most similar (blue and brown clusters) for configuration removal (Evo-Sim-2). However, the required DFT simulations were 25% less for the second case. Hence, we adopted the latter approach to determine the stable configurations. More details are presented in ESI Section 1.6.†

Fig. 3 Evo-Sim algorithm significantly reduces the computational demand for identifying stable configurations. (a) The workflow for Evo-Sim algorithm. (b) The number of DFT simulations required to determine stable configurations of four different coverages of CO*–OH* on the Pt(553) surface using three different sampling methods: brute force enumeration (Brute-force), evolutionary algorithm (Evo), and Evo-Sim.

To assess the effectiveness of the configuration reduction achieved through Evo-Sim, a comparative analysis of the number of DFT simulations required to identify the most stable configuration at a given coverage using three different sampling methods (brute-force enumeration, evolutionary algorithm, and Evo-Sim) is then conducted (see ESI S1.2† for more details). The brute-force enumeration is conducted using Surfgraph algorithm. ²² For a given coverage, adsorbates are placed on all unique binding sites on the surface, and the duplicate configurations are removed using isomorphism. Four different CO*–OH* coverages (3CO*, 2CO*–1OH*, 2CO*–2OH*, and 3CO*–2OH*) on the Pt(553) surface are considered for this comparative analysis, as depicted in Fig. 3b. The results obtained from the brute-force method reveal that the overall configurational space experiences an exponential increase as coverage increases. In contrast, applying the evolutionary algorithm achieves a significant configuration reduction compared with the brute-force results. The reduction in configurations is shown to fit the power-law 1−0.6^{min(N_ads, N_ads,max−N_ads)}; where, N_ads denotes the number of adsorbates adsorbed on the surface and N_{ads, max} signifies the adsorbate coverage at saturation. Whereas, the overall configuration reduction of Evo-Sim is scaled by a power law given by 1−0.5^{min(N_ads, N_ads,max−N_ads)} in comparison with the brute-force results. Hence, Evo-Sim achieves a performance gain of 0.6^{min(N_ads, N_ads,max−N_ads)}−0.5^{min(N_ads, N_ads,max−N_ads)} vs. the evolutionary algorithm. Consequently, using the Evo-Sim algorithm, we estimated the most stable configurations for the nine different CO*–OH* coverages on Pt(553) by DFT simulating less than 2% of all possible unique configurations. Additionally, to check for the accuracy of Evo-Sim, we performed DFT calculations on all possible configurations of 2CO*–1OH* and 2CO*–2OH* on the Pt(553) surface acquired by the evolutionary algorithm. The most stable configurations and their energy values acquired from the two methods match exactly. To test the versatility of the approach on an alloyed system, we used the Evo-Sim algorithm on a previously studied NO* adsorption on Pt3Sn(111) system.²² Results showed that Evo-Sim can significantly reduce the DFT calculations, while maintaining high accuracy. More details are presented in ESI Section 3.2.† The agreement of the Evo-Sim and evolutionary algorithm results highlights the effectiveness of utilizing the proposed similarity algorithm, compared to the current state-of-the-art methods, in significantly reducing the DFT calculations to accurately estimate the atomic structures of complex heterogeneous catalytic surfaces consisting of defects and multiple types of adsorbates at varying coverages. The relevance of the Evo-Sim algorithm in estimating the surface phase diagram for combined CO* and OH* on Pt surfaces is discussed next.

Phase diagram of CO*–OH* co-adsorption on Pt(553) and Pt(111) surfaces

In this section, we now utilize the stable configurations derived through the Evo-Sim algorithm to elucidate the combined role of co-adsorbed CO* and OH*, terrace-like coordinated sites, and undercoordinated step sites in determining the state of Platinum catalyst under CO electro-oxidation reaction. Similar to the case of Pt(553), Evo-Sim is used to estimate eight different coverages of CO*–OH* configurations on Pt(111). More details are presented in the ESI S1.3.† A coverage-dependent phase diagram for CO* and OH* on the Pt(553) and Pt(111) surfaces is then used to quantitatively compare CO-electro-oxidation potential on the defected and terrace-like Pt surfaces. Coverages of mixed CO*–OH* between 0.1-0.35 ML and 0.2–0.67 ML are considered on the Pt(553) and Pt(111) surfaces respectively, as shown in ESI Fig. 5.† Coverages above 0.35 ML are not explored on Pt(553), as only the terrace-like coordinated sites remain, and analysis shows that the energetics on such sites are well captured by results on Pt(111). The free energy of a given phase is plotted vs. standard hydrogen electrode (SHE).⁴²

The phase diagrams are shown in Fig. 4. We observe that at a fixed CO* coverage, OH* adsorption becomes favorable when the potential is above ∼0.6 V vs. SHE on Pt(553) and above ∼1 V vs. SHE on Pt(111). As observed in Fig. 4a and b, at a fixed CO* coverage, the adsorption-free energy curve associated with a higher OH* coverage intersects with the curve of a lower OH* coverage at certain applied potentials for Pt(553) and Pt(111). This intersection, ΔG_{iCO*, mOH*}(V) = ΔG_{iCO*, nOH*}(V) with condition m ≠ n marks the oxidation potential corresponding to the oxidation of CO* to CO₂ (CO* + OH* → CO₂(g) + ½H₂(g)) for a given CO* coverage. Our key assumption here is that CO* oxidation is limited by the activation of oxygenated intermediates such as OH*. Hence, the intersection associated with the lowest free energy in the phase diagram identifies the CO* oxidation potential. The calculated oxidation potential on Pt(553) (∼0.6 V) agrees with previous experimental cyclic voltammetry (CV) reports on Pt nanoparticles (0.5–0.76 V) and nanowires (0.4–0.7 V), that possess many undercoordinated Pt sites.^43,44 In addition, the oxidation potential on Pt(111) (∼1 V) also agrees with the previous experimental CV study on Pt(111) (0.8–0.9 V).³⁷ The lower oxidation potential on Pt(553) suggests that the Pt surfaces with defects are more effective than terrace surfaces in mitigating CO poisoning.

Fig. 4 Coverage-dependent phase diagram of CO*–OH* co-adsorption on (a) Pt(553) and (b) Pt(111) surfaces. The adsorption free energy is plotted as a function of the applied potential relative to the standard hydrogen electrode (SHE). Top-view snapshots of the most stable configurations under all coverages are shown. Estimated CO* oxidation potentials on both surfaces are marked by black circles.

The analysis of energetically stable configurations of CO*–OH* on Pt(553) and Pt(111) surfaces provides insights into the superior performance of Pt(553). As shown in Fig. 4a, the orientation of OH* molecules on both surfaces indicates that OH* is stabilized through hydrogen bonding. Hence, configurations possessing at least a pair of OH* molecules are essential to capture this effect. Further, the configurations of CO*–OH* on the Pt(553) surface consistently indicate that OH* molecules occupy the step sites, and the number of CO* molecules at step sites decreases as the OH* coverage increases. This serves as the key distinction between OH* on the two surfaces, such that OH* molecules are predominantly located on step sites on Pt(553), whereas on Pt(111), they occupy terrace sites. Thus, our analysis shows that under-coordinated Pt sites are primarily responsible for reducing CO electro-oxidation potential on metallic Pt catalyst by favorably activating oxygenated intermediates at lower potentials.^43–45 The detailed mechanism underlying CO electro-oxidation on Pt surfaces is beyond the scope of this work.

In summary, our analysis of CO*–OH* adsorption on the Pt surface showcases an application of the similarity algorithm on a mixed reactant monodentate adsorption system. By drastically reducing the number of DFT simulations (∼98%) through the similarity algorithm, we, for the first time, systematically sampled the configurations varying across seventeen mixed coverages of CO* and OH* on Pt(553) and Pt(111) surfaces. The resulting phase diagram elucidates the adsorption behavior and the role of different geometric features that drive CO-electro-oxidation on Pt catalysts. We discuss the case of multi-dentate ethylene adsorption on stepped Pt surfaces next.

Ethylene adsorption on Pt(553)

Modeling bidentate adsorbate adsorption at varying coverages on geometrically diverse surface sites is important to study metal-catalyzed hydrocarbon hydrogenation. One of the key reactions that has been analyzed is ethylene adsorption on various metal surfaces.^46–56 However, the lack of understanding of co-adsorbate effects obstructs the understanding of the catalytic mechanism. The main bottleneck for gaining this understanding is the vast configurational space (ESI Fig. 9†). Herein, we demonstrate the utility of the Evo-Sim algorithm in filling this gap by modeling ethylene (C₂H₄) adsorption on the Pt(553) surface at varying coverages. Previous studies have reported that a single ethylene adsorbate has two binding modes on a Pt surface, σ and π,^49,51–53 as shown in ESI Fig. 10.† To quantify the chemisorption behavior of ethylene on Pt(553), we generate configurations at different ethylene coverages (0.1–0.65 ML) with the adsorbed ethylene molecules either adopting σ (σ-batch) or π (π-batch) mode, as illustrated in Fig. 5a. A 0.1 ML coverage is initially considered by modeling configurations adopting the two binding modes. Afterward, the Evo-Sim algorithm with a 0.3 eV energy cutoff is used to retain one configuration among the configuration pairs within the most similar cluster to achieve the subsequent ethylene coverage. The process is continued until the saturation 0.65 ML coverage 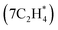is achieved. For more details, refer to the ESI S2.1.† The similarity profiles for the different ethylene coverages considered are found to show clustering behavior, similar to the CO*–OH* cases, and the configuration pairs are categorized based on the type and coordination number of the binding sites (See ESI S2.2† for more details).

Fig. 5 Coverage-dependent phase diagram of ethylene adsorption on Pt(553). (a) Workflow to achieve the seven coverages. (b) Coverage-dependent phase diagram of ethylene adsorbed on Pt(553) surface. The adsorption free energy is plotted as a function of the surface temperature. Snapshots of the most stable configurations at different coverages are shown. The dashed vertical lines mark the calculated lower and upper limits of the desorption temperature range.

The phase diagram (Fig. 5b) illustrates the chemisorption behavior of ethylene on the Pt(553) surface under an ultra-high vacuum condition (10⁻¹⁰ torr)⁵⁶ for the seven coverages considered. Results in Fig. 5b show that the surface temperature of ∼180 K marks the starting point of ethylene desorption. At 180 K, the saturated coverage of 0.6 ML starts to destabilize and reduces to 0.4 ML . Then, at ∼280 K, the surface coverage is further reduced to 0.1 ML 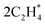, which is the lowest ethylene coverage before all ethylene molecules are desorbed at ∼340 K. Considering the atomic structures of the energetically stable configurations, as shown in Fig. 5b, the on well-coordinated terrace sites desorb before the on the under-coordinated step sites as the temperature increases. Consequently, our results suggest that ethylene adsorption is more stable on step sites than on terrace sites. For the discussion relating to the ethylene binding mode, see ESI S2.3.† Furthermore, the calculated desorption temperature range (∼180–340 K) is consistent with experimental temperature programmed desorption spectra of ethylene on Pt surfaces.^54–56 In conclusion, our analysis of ethylene adsorption on the Pt surface exemplifies the application of the similarity algorithm on a bidentate adsorption system. Using the Evo-Sim algorithm, for the first time, systematic sampling of ethylene configurations at seven coverages is performed. The generated phase diagram thus qualitatively elucidates the adsorption behavior of ethylene on metallic Pt consisting of both well-coordinated and under-coordinated sites.

Conclusions

In summary, we present a novel similarity algorithm to quantify the structural difference between two catalytic models to enable the identification of structurally distinct atomic configurations. The combination of structurally distinct configurations with an energy-driven evolutionary algorithm, termed Evo-Sim, is shown to model highly complex catalytic systems involving multiple types of adsorbate molecules under varying coverages on a defected metal surface. A substantial reduction (∼98%) in the total number of required DFT simulations to estimate the stable atomic configurations is reported using Evo-Sim. The most stable configurations for seventeen different mixed coverages of CO*–OH* co-adsorbed on the Pt(553) and Pt(111) surfaces are estimated. The resulting phase diagram showcases the role of uncoordinated edge sites in improving CO electro-oxidation activity on Pt surfaces. Furthermore, to demonstrate the universal applicability of Evo-Sim, bidentate adsorption of ethylene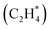 on the Pt(553) surface system is reported. The developed method now provides a powerful stepping stone to model complex multi-reactant heterogeneous catalyst systems.

Methods

DFT simulation settings

The simulations are performed within the framework of periodic DFT with the VASP code.⁵⁷ The energies and geometries of the most stable configurations on the Pt(553) surface are obtained through the minimization of the total energy with respect to geometry by generalized gradient approximation calculations (GGA–PBE).⁵⁸ The projected augmented wave (PAW) method is used to account for the effect of core electrons on the valence electron density.⁵⁹ A PBE-calculated lattice constant of 3.97 Å for pure Pt is employed. The Pt(553) surface is represented by a 5 × 4 unit cell with three layers (total of 60 atoms per unit cell). Convergence of relative adsorption energies for a given coverage was tested with respect to slab thickness (more information is presented in the ESI Section 4†). A vacuum equivalent to 13 Å is applied between any two successive slabs, and surface relaxation is allowed in the top 2 layers. For the size of vacuum chosen, dipole corrections were tested to have negligible influence. All the calculations use a plane wave energy cutoff of 400 eV. A minimum k-point grid sampling of 3 × 3 × 1 is employed. The electronic occupancies are determined using a Methfessel–Paxton scheme with an energy smearing of 0.2 eV. Configurations are relaxed until the Hellmann–Feynman forces acting on the atoms are smaller than 0.05 eV Å⁻¹. For the gas phase CO, H₂O, H₂ and ethylene calculations, we use a simulation cell with dimensions (10 Å, 10 Å, 10 Å).

Thermodynamic derivation of phase diagrams

For the CO*–OH* adsorption on the Pt(553) surface, ΔG_CO* and ΔG_OH* free energies are estimated. ΔG_CO* is given by:

ΔG_xCO* = E_xCO*,yOH* − E* + ZPE_CO* − TS_CO* − x × μ_CO(g),

where E_xCO*,yOH* is the DFT calculated energy of the most stable configuration containing ‘x’ CO* and ‘y’ OH*. ‘E*’ is the DFT calculated energy of the clear Pt(553) surface used in this work. is the zero point energy of adsorbed CO* on the surface, calculated through the summation of the ZPE energy of each CO* given its binding sites (top, bridge, or hollow). ZPE_sitei values are calculated using the normal mode frequencies reported in the DFT study of CO* adsorption on Pt(111),⁶⁰ assuming the vibrational behavior of adsorbed CO is insensitive to the surface structure. The entropy of the CO*, TS_CO*, is taken to be zero assuming translation, rotation and vibrational entropic contributions are negligible, as CO* is known to bind strongly on Pt surfaces. E_CO(g) is the DFT calculated energy of gas phase CO. ZPE_CO(g) and TS_CO(g) are zero point energy of the gas phase CO and the entropy of the gas phase CO, respectively, and the values are taken from the standard table.⁶¹ is the pressure correction. For the partial pressure of CO, P_CO, we used the Henry's law to correlate to the equilibrium water solubility under 1 atm and 298K, P_CO = Mol frac × Henry^'s constant, where Mol frac and Henry^' constant are taken from the CO solubility database,⁶² which are 1.775 × 10⁻⁵ and 56336 atm, respectively. The solvation effect on CO molecules is neglected, assuming the interactions between OH* molecules and solvents (water) are much stronger than those of CO*.

For the OH binding free energy, we use the formula derived by Norskov et al.⁴²

ΔG_yOH* = E_xCO*,yOH* − E* + y × (½E_H2(g) − E_H2O(g) + ΔZPE_OH* − TΔS_OH* + E_{solv, OH*} − eU),

where E_H2(g) and E_H2O(g) are calculated through DFT. ΔZPE_OH* and TΔS_OH* are obtained from a previous computational study on the oxidation–reduction reaction,⁴² which are −0.12 eV and −0.47 eV, respectively. TS_OH*, is taken to be zero assuming translation, rotation and vibrational entropic contributions are negligible as OH* is known to bind strongly on Pt surfaces. U is the applied potential relative to the reversible hydrogen electrode potential. Given that the study reports configurations involving OH* clusters, we adopt the solvation corrections as reported by Morankar et al.⁶³ The solvation correction in an aqueous environment, E_{solv, OH*}, depends on the relative position of OH* molecules, according to Morankar et al.⁶³ Therefore, we use −0.51 eV for 1OH* cases, −0.75 eV for 2OH* cases, and −1.03 eV for 3OH* cases, adopted from Morankar et al.⁶³

By combining ΔG_OH* and ΔG_CO*, and remove the duplicated E_{xCO*, yOH*} − E* term, we obtained the formula for the ΔG_{yOH*, xCO*}.

ΔG_{yOH*, xCO*} = E_{xCO*, yOH*} − E* + ZPE_CO* − TS_CO* − x × μ_CO(g) + y × (½E_H2(g) − E_H2O(g) + ΔZPE_OH* − TΔS_OH* + E_{solv, OH*} − eU)

For the ethylene adsorption on the Pt(553) surface, the adsorption free energy of a given coverage was plotted as a function of the temperature using the formula:

The total zero point energy , and the total entropy, . The adsorbed are calculated by summing configuration-specific terms. The configuration-specific zero point energy and entropy are categorized into the σ and π binding configuration and calculated using the VASP vibrational analysis. To obtain the configuration specific entropy, we applied the harmonic approximation on all the vibrational modes output from the VASP corresponding to the binding configuration of interest. Configuration specific ZPE and entropy values are listed in ESI Table 2.† ZPE_C2H4(g) and TS_C2H4(g) are obtained through the standard table,⁶¹ which are 1.34 eV and 0.68 eV respectively. P_C2H4(g) value is adopted from an experiential study performing temperature programmed desorption in an ultra-high vacuum chamber.⁵⁶

Determining ethylene desorption temperature range

In Fig. 5b, an intersection of the free energy curves corresponding to higher and lower ethylene coverages signifies that ethylene is desorbed from the surface, with the condition i ≠ j. The temperature at this intersection is designated as the ethylene desorption temperature, whereas the intersection associated with the lowest free energy marks the temperature at which desorption occurs. When all the free energy curves pass above the ΔG = 0 line, , there will be no ethylene adsorbed on the surface, marking the temperature at which the desorption ends.

Code availability

The similarity calculation code is available from: https://github.com/jinzengur/similarity-calculation.git, and is made available under MIT license.

Data availability

All DFT calculation data for this article are available in the Zenodo repository system. https://doi.org/10.5281/zenodo.15048286. Any queries related to materials or any other content of the work should be addressed to the corresponding author.

Author contributions

S. D. supervised the project. J. Z. and S. D. developed the similarity algorithm. J. Z. and J. G. conducted the surface adsorption calculations. J. Z. and S. D. performed the analysis on the calculation results. J. Z. and S. D. contributed to the writing of the paper.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

The authors would like to acknowledge computing resources from the Argonne Leadership Computing Facility through the Director Discretionary grant system.

References

1. J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Towards the computational design of solid catalysts, Nat. Chem., 2009, 1(1), 37–46.
2. J. Greeley, I. Stephens, A. Bondarenko, T. P. Johansson, H. A. Hansen, T. Jaramillo, J. Rossmeisl, I. Chorkendorff and J. K. Nørskov, Alloys of platinum and early transition metals as oxygen reduction electrocatalysts, Nat. Chem., 2009, 1(7), 552–556.
3. B. W. Chen, L. Xu and M. Mavrikakis, Computational methods in heterogeneous catalysis, Chem. Rev., 2020, 121(2), 1007–1048.
4. B. A. Sexton, Methanol decomposition on platinum (111), Surf. Sci., 1981, 102(1), 271–281.
5. B. Sexton, K. Rendulic and A. Huges, Decomposition pathways of C1–C4 alcohols adsorbed on platinum (111), Surf. Sci., 1982, 121(1), 181–198.
6. C. Tang, Y. Zheng, M. Jaroniec and S. Z. Qiao, Electrocatalytic refinery for sustainable production of fuels and chemicals, Angew. Chem., Int. Ed., 2021, 60(36), 19572–19590.
7. A. Capon and R. Parson, The oxidation of formic acid at noble metal electrodes: I. Review of previous work, J. Electroanal. Chem. Interfacial Electrochem., 1973, 44(1), 1–7.
8. J.-Y. Wang, H.-X. Zhang, K. Jiang and W.-B. Cai, From HCOOH to CO at Pd electrodes: a surface-enhanced infrared spectroscopy study, J. Am. Chem. Soc., 2011, 133(38), 14876–14879.
9. D. A. Chipoco Haro, L. Barrera, H. Iriawan, A. Herzog, N. Tian, A. J. Medford, Y. Shao-Horn, F. M. Alamgir and M. C. Hatzell, Electrocatalysts for Inorganic and Organic Waste Nitrogen Conversion, ACS Catal., 2024, 14(13), 9752–9775.
10. A. De la Osa, A. Calcerrada, J. Valverde, E. Baranova and A. de Lucas-Consuegra, Electrochemical reforming of alcohols on nanostructured platinum-tin catalyst-electrodes, Appl. Catal., B, 2015, 179, 276–284.
11. K. Tran and Z. W. Ulissi, Active learning across intermetallics to guide discovery of electrocatalysts for CO₂ reduction and H₂ evolution, Nat. Catal., 2018, 1(9), 696–703.
12. Z. W. Ulissi, A. J. Medford, T. Bligaard and J. K. Nørskov, To address surface reaction network complexity using scaling relations machine learning and DFT calculations, Nat. Commun., 2017, 8(1), 14621.
13. P. G. Ghanekar, S. Deshpande and J. Greeley, Adsorbate chemical environment-based machine learning framework for heterogeneous catalysis, Nat. Commun., 2022, 13(1), 5788.
14. J. A. Esterhuizen, B. R. Goldsmith and S. Linic, Theory-guided machine learning finds geometric structure-property relationships for chemisorption on subsurface alloys, Chem, 2020, 6(11), 3100–3117.
15. H. Jung, L. Sauerland, S. Stocker, K. Reuter and J. T. Margraf, Machine-learning driven global optimization of surface adsorbate geometries, npj Comput. Mater., 2023, 9(1), 114.
16. S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, E (3)-equivariant graph neural networks for data-efficient and accurate interatomic potentials, Nat. Commun., 2022, 13(1), 2453.
17. W. Xu, K. Reuter and M. Andersen, Predicting binding motifs of complex adsorbates using machine learning with a physics-inspired graph representation, Nat. Comput. Sci., 2022, 2(7), 443–450.
18. Y. Huang, S.-H. Wang, X. Wang, N. Omidvar, L. E. Achenie, S. E. Skrabalak and H. Xin, Unraveling Reactivity Origin of Oxygen Reduction at High-Entropy Alloy Electrocatalysts with a Computational and Data-Driven Approach, J. Phys. Chem. C, 2024, 128(27), 11183–11189.
19. M. Zhong, K. Tran, Y. Min, C. Wang, Z. Wang, C.-T. Dinh, P. De Luna, Z. Yu, A. S. Rasouli and P. Brodersen, Accelerated discovery of CO₂ electrocatalysts using active machine learning, Nature, 2020, 581(7807), 178–183.
20. H. S. Pillai, Y. Li, S.-H. Wang, N. Omidvar, Q. Mu, L. E. Achenie, F. Abild-Pedersen, J. Yang, G. Wu and H. Xin, Interpretable design of Ir-free trimetallic electrocatalysts for ammonia oxidation with graph neural networks, Nat. Commun., 2023, 14(1), 792.
21. J. Vandermause, Y. Xie, J. S. Lim, C. J. Owen and B. Kozinsky, Active learning of reactive Bayesian force fields applied to heterogeneous catalysis dynamics of H/Pt, Nat. Commun., 2022, 13(1), 5183.
22. S. Deshpande, T. Maxson and J. Greeley, Graph theory approach to determine configurations of multidentate and high coverage adsorbates for heterogeneous catalysis, npj Comput. Mater., 2020, 6(1), 79.
23. Z. Lian, F. Dattila and N. López, Stability and lifetime of diffusion-trapped oxygen in oxide-derived copper CO₂ reduction electrocatalysts, Nat. Catal., 2024, 7(4), 401–411.
24. J. Xu, W. Xie, Y. Han and P. Hu, Atomistic insights into the oxidation of flat and stepped platinum surfaces using large-scale machine learning potential-based grand-canonical Monte Carlo, ACS Catal., 2022, 12(24), 14812–14824.
25. V. Sumaria and P. Sautet, CO organization at ambient pressure on stepped Pt surfaces: first principles modeling accelerated by neural networks, Chem. Sci., 2021, 12(47), 15543–15555.
26. S.-H. Wang, H. S. Pillai, S. Wang, L. E. Achenie and H. Xin, Infusing theory into deep learning for interpretable reactivity prediction, Nat. Commun., 2021, 12(1), 5288.
27. Y. Chang, I. Benlolo, Y. Bai, C. Reimer, D. Zhou, H. Zhang, H. Matsumura, H. Choubisa, X.-Y. Li and W. Chen, High-entropy alloy electrocatalysts screened using machine learning informed by quantum-inspired similarity analysis, Matter, 2024, 7(11), 4099–4113.
28. J. Lan, A. Palizhati, M. Shuaibi, B. M. Wood, B. Wander, A. Das, M. Uyttendaele, C. L. Zitnick and Z. W. Ulissi, AdsorbML: a leap in efficiency for adsorption energy calculations using generalizable machine learning potentials, npj Comput. Mater., 2023, 9(1), 172.
29. S. Han, S. Lysgaard, T. Vegge and H. A. Hansen, Rapid mapping of alloy surface phase diagrams via Bayesian evolutionary multitasking, npj Comput. Mater., 2023, 9(1), 139.
30. S. Deshpande and D. G. Vlachos, A Data and DFT-Driven Framework for Predicting the Microstructure of Submonolayer Inverse Metal Oxide on Metal Catalysts, J. Phys. Chem. Lett., 2024, 15, 2715–2722.
31. F. Abild-Pedersen, J. Greeley, F. Studt, J. Rossmeisl, T. R. Munter, P. G. Moses, E. Skulason, T. Bligaard and J. K. Nørskov, Scaling Properties of Adsorption Energies for Hydrogen-Containing Molecules on Transition-Metal Surfaces, Phys. Rev. Lett., 2007, 99(1), 016105.
32. J. Greeley and M. Mavrikakis, Alloy catalysts designed from first principles, Nat. Mater., 2004, 3(11), 810–815.
33. N. İnoğlu and J. R. Kitchin, Simple model explaining and predicting coverage-dependent atomic adsorption energies on transition metal surfaces, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(4), 045414.
34. J. Kitchin, J. K. Nørskov, M. Barteau and J. Chen, Modification of the surface electronic and chemical properties of Pt (111) by subsurface 3d transition metals, J. Chem. Phys., 2004, 120(21), 10240–10246.
35. Y. Bai, H. Ding, S. Bian, T. Chen, Y. Sun and W. S. Wang, A neural network approach to fast graph similarity computation, in Proceedings of the twelfth ACM international conference on web search and data mining, 2019, pp. 384–392.
36. G. H. Gu, J. Noh, S. Kim, S. Back, Z. Ulissi and Y. Jung, Practical deep-learning representation for fast heterogeneous catalyst screening, J. Phys. Chem. Lett., 2020, 11(9), 3185–3191.
37. H. A. Gasteiger, N. Markovic, P. N. Ross Jr and E. J. Cairns, Carbon monoxide electrooxidation on well-characterized platinum-ruthenium alloys, J. Phys. Chem., 1994, 98(2), 617–625.
38. M. Ester, H.-P. Kriegel, J. Sander and X. Xu in A density-based algorithm for discovering clusters in large spatial databases with noise, 1996, vol. 96, pp. 226–231.
39. E. Schubert, J. Sander, M. Ester, H. P. Kriegel and X. Xu, DBSCAN revisited, revisited: why and how you should (still) use DBSCAN, ACM Trans. Database Syst., 2017, 42(3), 1–21.
40. J. Marlowe, S. Deshpande, D. G. Vlachos, M. M. Abu-Omar and P. Christopher, Effect of dynamic and preferential decoration of Pt catalyst surfaces by WO_x on hydrodeoxygenation reactions, J. Am. Chem. Soc., 2024, 146(20), 13862–13874.
41. G. L. Hart, V. Blum, M. J. Walorski and A. Zunger, Evolutionary approach for determining first-principles hamiltonians, Nat. Mater., 2005, 4(5), 391–394.
42. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, Origin of the overpotential for oxygen reduction at a fuel-cell cathode, J. Phys. Chem. B, 2004, 108(46), 17886–17892.
43. J. Solla-Gullón, F. Vidal-Iglesias, V. Montiel and A. Aldaz, Electrochemical characterization of platinum–ruthenium nanoparticles prepared by water-in-oil microemulsion, Electrochim. Acta, 2004, 49(28), 5079–5088.
44. A. Ponrouch, S. Garbarino and D. Guay, Effect of the nanostructure on the CO poisoning rate of platinum, Electrochem. Commun., 2009, 11(4), 834–837.
45. G. Tomaschun and T. Klüner, Methanol oxidation on the Pt (321) surface: a theoretical approach on the role of surface morphology and surface coverage effects, Phys. Chem. Chem. Phys., 2019, 21(33), 18227–18239.
46. F. Zaera and G. Somorjai, Hydrogenation of ethylene over platinum (111) single-crystal surfaces, J. Am. Chem. Soc., 1984, 106(8), 2288–2293.
47. Y. Wang, X. Dong, Y. Yu and M. Zhang, Ethylene decomposition over Pt (100): A mechanism study from first principle calculation, Appl. Surf. Sci., 2016, 390, 984–992.
48. J.-F. Paul and P. Sautet, Influence of the surface atom metallic coordination in the adsorption of ethylene on a platinum surface: a theoretical study, J. Phys. Chem., 1994, 98(42), 10906–10912.
49. C. J. Heard, S. Siahrostami and H. Gronbeck, Structural and energetic trends of ethylene hydrogenation over transition metal surfaces, J. Phys. Chem. C, 2016, 120(2), 995–1003.
50. J. Andersin, N. Lopez and K. Honkala, Dft study on the complex reaction networks in the conversion of ethylene to ethylidyne on flat and stepped Pd, J. Phys. Chem. C, 2009, 113(19), 8278–8286.
51. T. Miura, H. Kobayashi and K. Domen, Density functional study of ethylene hydrogenation on Pt (111) surface, J. Phys. Chem. B, 2000, 104(29), 6809–6814.
52. T. Ohtani, J. Kubota, J. N. Kondo, C. Hirose and K. Domen, Suppression of formation of ethylidyne on Pt (111) by reversibly adsorbed di-σ-bonded ethylene studied by in situ IRAS, Surf. Sci., 1998, 415(1–2), L983–L987.
53. J. Kubota, T. Ohtani, J. N. Kondo, C. Hirose and K. Domen, IRAS study of π-bonded ethylene on a Pt (111) surface in the presence of gaseous ethylene and hydrogen, Appl. Surf. Sci., 1997, 121, 548–551.
54. P. Berlowitz, C. Megiris, J. Butt and H. Kung, Temperature-programmed desorption study of ethylene on a clean, a hydrogen-covered, and an oxygen-covered platinum (111) surface, Langmuir, 1985, 1(2), 206–212.
55. B. Vermang, M. Juel and S. Raaen, Temperature programed desorption of C₂H₄ from pure and graphite-covered Pt (111), J. Vac. Sci. Technol., A, 2007, 25(6), 1512–1518.
56. Y.-L. Tsai, C. Xu and B. E. Koel, Chemisorption of ethylene, propylene and isobutylene on ordered Sn/Pt (111) surface alloys, Surf. Sci., 1997, 385(1), 37–59.
57. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169.
58. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865.
59. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758.
60. P. J. Feibelman, B. Hammer, J. K. Nørskov, F. Wagner, M. Scheffler, R. Stumpf, R. Watwe and J. Dumesic, The co/pt (111) puzzle, J. Phys. Chem. B, 2001, 105(18), 4018–4025.
61. R. D. Johnson III, Computational chemistry comparison and benchmark database, 1999.
62. W. R. Cargill, Solubility Data Series Volume 43 Carbon Monoxide, IUPAC Solubility Data Ser., 1990, 43(4).
63. A. Morankar, S. Deshpande, Z. Zeng, P. Atanassov and J. Greeley, A first principles analysis of potential-dependent structural evolution of active sites in Fe-NC catalysts, Proc. Natl. Acad. Sci. U. S. A., 2023, 120(49), e2308458120.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sc02117k

---