 Open Access Article
Open Access ArticleCollective motions in the primary coordination sphere: a critical functional framework for catalytic activity of the oxygen-evolving complex of photosystem II†
Hiroshi Isobe *a,
Takayoshi Suzuki
*a,
Takayoshi Suzuki a,
Michihiro Suga
a,
Michihiro Suga a,
Jian-Ren Shen
a,
Jian-Ren Shen a and
Kizashi Yamaguchi
a and
Kizashi Yamaguchi b
b
aResearch Institute for Interdisciplinary Science, Okayama University, Okayama 700-8530, Japan. E-mail: h-isobe@cc.okayama-u.ac.jp
bCenter for Quantum Information and Quantum Biology, Osaka University, Toyonaka, Osaka 560-0043, Japan
First published on 3rd June 2025
Abstract
Photosynthetic water oxidation, vital for dioxygen production and light energy conversion, is catalyzed by the oxygen-evolving complex of photosystem II, where the inorganic Mn4CaO5 cluster acts as the catalytic core. In this study, we investigate the functional significance of collective motions of amino acid side chains within the primary coordination sphere of the Mn cluster, focusing on their role in modulating the energetic demands for catalytic transformations in the S3 state. We applied regularized canonical correlation analysis to quantitatively correlate the three-dimensional arrangement of coordinating atoms with catalytic driving forces computed via density functional theory. Our analysis reveals that distinct collective side chain motions profoundly influence the energetic requirements for structural reconfigurations of the Mn cluster, achieved through expansion and contraction of the ligand cavity while fine-tuning its geometry to stabilize key intermediates. Complementary predictions from a neural network-based machine learning model indicate that the coordination sphere exerts a variable energetic impact on the catalytic transformations of the Mn cluster, depending on the S-state environment. Integrated computational analyses suggest that the extended lifetime of the S3YZ˙ state, consistently observed after three flash illuminations, may result from slow, progressive protein dynamics that continuously reshape the energy landscape, thereby shifting the equilibrium positions of rapid, reversible chemical processes over time. Overall, our findings demonstrate that collective motions in the primary coordination sphere constitute an active, dynamic framework essential for the efficient execution of multi-electron catalysis under ambient conditions, while simultaneously achieving a high selectivity with irreversible nature required for effective 3O2 evolution.
1 Introduction
Photosynthesis is the fundamental biochemical process through which green plants, algae, and cyanobacteria convert solar energy into chemical energy, simultaneously releasing oxygen as a by-product.1–3 This process constitutes the cornerstone of the global energy economy, continuously supplying the biosphere with essential organic substrates and oxygen that sustain the metabolic functions, growth, and adaptability of living organisms, thereby underpinning the intricate network of biological interactions that define life on Earth. A distinctive aspect of photosynthesis is its reliance on water as an abundant electron donor. The thermodynamically demanding water-splitting reaction is mediated by photosystem II (PSII), a complex assembly of proteins and cofactors embedded in the thylakoid membranes.4–8 PSII serves as the entry point for the light-dependent reactions of photosynthesis, using sophisticated pigment-protein antenna systems to capture and funnel solar energy efficiently. Upon light absorption by the P680 chlorophyll dimer, a highly oxidizing excited state is generated, which is capable of extracting electrons from water, with these electrons subsequently shuttled via the redox-active tyrosine residue (D1-Tyr161, also known as YZ) to the oxidized P680, thereby sustaining a continuous electron flow through the photosynthetic electron transport chain. Central to the water oxidation process within PSII is the oxygen-evolving complex (OEC), which harbors an inorganic Mn4CaO5 cluster as its catalytic core. This unique metal cluster, consisting of four manganese atoms and one calcium atom linked by five μ-oxo bridges and arranged in a distorted chair-like geometry,9 is critical for enabling water oxidation. During its catalytic cycle, the cluster sequentially advances through a series of defined S-states (from S0 to S4, with S4 being transient), as illustrated in Fig. 1A.10,11 Each photon-induced transition contributes the accumulation of one oxidizing equivalent, effectively bridging the gap between individual single-electron photochemical events and the overall four-electron water-splitting reaction. Concomitantly, these sequential S-state transitions are coupled with the release of four protons into the thylakoid lumen, a mechanism that moderates the redox potential of the Mn cluster and contributes to the proton gradient required for ATP synthesis. | ||
| Fig. 1 (A) S-state cycle of the OEC, driven by sequential flash illuminations, illustrating stepwise one-electron oxidations via the proximal tyrosyl radical (YZ˙), each coupled to proton release and substrate water binding. (B) Molecular structures of the S3-state hydroxo–oxo and oxyl–oxo intermediates in both open and closed cubane conformations, with the formal oxidation states of Mn indicated in Roman numerals. (C) Overlay of experimentally observed conformations of seven amino acid side chains within the primary coordination sphere of the Mn4CaO5 cluster during the S2 to S3 transition:26 1F state (green) and time points at 150 μs (pink), 400 μs (cyan), and 200 ms (gold) after 2F. The Mn cluster is depicted in wireframe, coordinating residues as sticks, and directly bound O and N atoms (OA–OL and Nε) highlighted in blue. | ||
The remarkable catalytic efficiency of the Mn4CaO5 cluster is intrinsically tied to its structural and electronic flexibility. This flexibility allows for dynamic modulation of the coordination geometry, thereby facilitating efficient electron transfer during sequential oxidation events and optimizing substrate water binding and activation. This dynamic behavior is augmented by an extensive network of amino acid residues in the D1 protein (and one in CP43) that constitute the primary coordination sphere of the cluster, which includes six carboxylate ligand groups from D1-Asp170, D1-Glu189, D1-Glu333, D1-Asp342, D1-Ala344, CP43-Glu354 and one additional N-donor group from D1-His332. These residues have been recognized as critical determinants in preserving the structural stability of the cluster and fine-tuning its redox properties throughout the S-state cycle. Before high-resolution structural data of the OEC in its dark-stable (S1) state became available in 2011,9 site-directed mutagenesis studies were instrumental in mapping the functional roles of these ligand residues.12–23 These early investigations demonstrated that each primary sphere residue has a specific function. For instance, some (D1-Asp170, D1-Asp342, and D1-Ala344) are indispensable for the assembly and stabilization of the cluster,13–17 while others (D1-His332, D1-Glu333, and CP43-Glu354) directly coordinate the metal ions and influence the redox equilibrium and substrate water dynamics.18–22 Certain second-sphere residues (D1-Glu189 and the hydrogen-bond partners of the primary coordination sphere residues) contribute to proton egress and tune the reaction kinetics.23 Mechanistic insights gained include the identification of proton-coupled electron transfer steps (involving YZ–D1-His190–D1-Glu189),23 the assignment of fast versus slow substrate water binding (Ca-bound water influenced by CP43-Glu354),22 and evidence suggesting that O–O bond formation involves a μ-oxo bridge (O5) and an inserted water molecule (affected by D1-Glu333).21
The advent of X-ray free-electron laser (XFEL)-based serial femtosecond crystallography has finally enabled both determination of high-resolution static structures of the OEC in flash-generated states (S2, S3, and S0) and real-time monitoring of concerted structural changes in the metal cluster and its surrounding protein matrix under near-physiological conditions immediately following each flash of light.24–32 These structural insights have corroborated many of the mutagenesis-derived hypotheses, validating the ligation scheme and revealing a flexible water insertion channel involving D1-Glu189 and neighboring water molecules. A particularly illustrative example is the transition from S2 to S3, during which the side chain of D1-Glu189 shifts markedly away from Ca, as illustrated in Fig. 1C, accompanied by the emergence of a new oxygen density at the MnD site, designated O6 or OX.25–29,31,32 This identification indicates that PSII does not start with all substrate oxygens pre-bound; instead, the complex actively takes up an additional water-derived ligand during the cycle. However, such localized structural changes alone do not fully account for all the results obtained from mutagenesis experiments. For example, kinetic analyses in the S3 state using H218O revealed that the CP43-E354Q mutant exhibits substrate water exchange rates that are approximately 8.5-fold faster in the fast phase (attributed to exchangeable substrate water, O6) and about 1.8-fold faster in the slow phase (associated with tightly bound substrate water, O5) compared to the wild type. The CP43-E354Q cores also exhibited an unusually prolonged S2 state lifetime, with a substantial fraction of centers remaining in S2 for over 10 hours at room temperature. Considering that CP43-Glu354 is a bidentate ligand to MnB and MnC, but is neither directly coordinated to MnD nor does it engage in hydrogen bonding with O6, these findings imply that the effects of the CP43-Glu354 mutation extend beyond a mere static alteration of the coordination environment. Significant conformational dynamics observed across all coordinating side chains, as depicted in Fig. 1C, suggest that OEC function and substrate water exchange may be regulated by complex, collective interplay among multiple residues rather than by the isolated action of a single ligand. The intricate nature of these interactions calls for a comprehensive investigation into the collective motions within the primary coordination sphere to fully elucidate the mechanisms governing the OEC function and the overall process of photosynthetic water oxidation.
To confront these challenges, we implemented a comprehensive analytical framework that integrates statistical methodologies, machine learning models, and conventional density functional theory (DFT) calculations. Specifically, we applied regularized canonical correlation analysis (rCCA) to systematically correlate the collective motions of coordinating residues with the energetic demands for catalysis in the S3 state. Complementing this, our neural network-based machine learning model, trained on extensive datasets spanning a diverse range of physiologically relevant conditions, captures complex nonlinear dependencies inherent in the system. This integrated computational approach allows for a quantitative assessment of how side chain dynamics influence the catalytic progression of the OEC in the state immediately preceding O2 evolution, thereby advancing our understanding of the mechanisms that underpin optimal catalytic performance and overall function.
2 Computational methods
2.1. OEC model construction
Structural models of the OEC were constructed using monomeric units (A and B) extracted from high-resolution XFEL crystallography data of PSII, as reported by Kern et al.26 and Suga et al.27 An overall view of the OEC models employed in this study is illustrated in Fig. S1.† The models represent various S-states, with the corresponding PDB codes as follows: 6DHE, 6JLJ, and 6JLM for the dark-stable (S1) state; 6DHF, 6JLK, and 6JLN for the one-flash (1F, corresponding to S2) state; 6DHG for two flashes (2F) + 150 μs; 6DHH for 2F + 400 μs; 6DHO, 6JLL, and 6JLO for the 2F (S3) state; 6DHP and 6JLP for the three-flash (3F, corresponding to S0) state. Each structural model comprises 348 atoms, including the Mn4CaO5 inorganic cluster, four terminal aqua/hydroxo ligands coordinated to Ca and MnA, an additional O6 (or OX) ligand at MnD, 12 crystal water molecules, a chloride ion (Cl−), and specific amino acid residues: D1-Asp61, D1-Asn87, D1-Tyr161 (TyrZ), D1-Gln165, D1-Ser169, D1-Asp170, D1-Asn181, D1-Val185, D1-Phe182 (backbone only), D1-Glu189, D1-His190, D1-Asn298 (fragment), D2-Lys317 (fragment), D1-His332, D1-Glu333, D1-Ala336, D1-His337, D1-Asp342, D1-Ala344 (C-terminus), CP43-Glu354, and CP43-Arg357.2.2 Dataset preparation
The construction and preparation of datasets constitute critical components of any machine learning workflow and statistical data analysis. In our study, we carefully balanced consistency with diversity to develop models that are both highly reliable and widely applicable. Consistency was ensured by constraining the backbone coordinates to experimentally determined positions and maintaining chemical plausibility, thereby avoiding the generation of physically or chemically unrealistic conformations. Conversely, diversity was introduced by extensively sampling ligand configurations, thereby capturing the intrinsic structural flexibility and dynamic adaptability of the OEC. This dual focus on consistency and diversity is essential for enhancing the model's generalization capacity, i.e., its ability to make accurate predictions on novel, previously unseen data.33,34To elucidate the relationship between the collective motion within the primary coordination sphere and the catalytic function of the OEC, we employed supervised machine learning, complemented by rCCA as an additional statistical tool. The input feature dataset (X) was derived from the three-dimensional (3D) coordinates of coordinating atoms, while the target variable dataset (Y) corresponds to the energetic driving forces computed via DFT for two chemical species, hydoroxo–oxo (Stotal = 3)35–38 and oxyl–oxo (EPR silent, Stotal = 6)39–44 in the S3 state, as depicted in Fig. 1B. The driving force (ΔE) is quantitatively defined as the energy difference between the ‘open cubane’ and ‘closed cubane’ conformations45–47 after water binding in the S3 state, i.e., ΔE = E(open) − E(closed). All target data (Y) were generated using a consistent computational protocol, as detailed in the subsequent section, thereby minimizing potential biases and ensuring uniform data quality across diverse conformational states. Initial structural configurations were obtained from the aforementioned XFEL crystallographic data. Given the ambiguity surrounding the Mn oxidation states in the experimental structures,48,49 all Mn cluster geometries were fully optimized under the assumption of a high oxidation state scenario.50,51 Validation of the optimized clusters was achieved by calculating Mulliken spin densities for each Mn ion, which converged to approximately 4 for MnIII and 3 for MnIV, thereby confirming that the optimized clusters correspond to the intended oxidation states. It is important to note that the structural parameters of the optimized Mn clusters were not directly used as input features (dataset X) for the rCCA and machine learning models. Instead, our focus is on the spatial arrangement of the amino acid side chains within the primary coordination sphere, which enabled an in-depth investigation of how dynamic adjustments in these side chains influence the relative stability of the open and closed cubane conformations. To prevent overfitting to a specific conformational state, the final training dataset was balanced to represent coordination environments corresponding to both the open cubane and closed cubane structures. Ligand positions within the primary coordination sphere were sampled in three distinct manners: (1) by retaining the experimental coordinates, (2) by optimizing the open cubane conformation via DFT, and (3) by optimizing the closed cubane conformation via DFT. These sampling approaches were applied across a broad range of physiologically relevant S-states of PSII (including both monomeric units A and B), covering states with smaller cavities (S0 and S2) as well as those with larger cavities (S1, S3, and the S2 → S3 transient states) as discussed later, while also accounting for both the hydroxo–oxo and oxyl–oxo species. The resulting dataset comprises 130 entries, with extensive sampling details provided in Table S1 and visualized in Fig. S2.† This comprehensive sampling procedure enabled both the machine learning and rCCA models to learn intricate patterns and interdependencies between the ligand arrangements (feature set X) and the associated catalytic driving forces (target variable Y).
2.3 DFT calculations
Geometry optimizations were carried out using the B3LYP functional52–54 augmented with Grimme's D3 empirical dispersion correction and the Becke–Johnson (BJ) damping function,55,56 as implemented in Gaussian 16.57 For Ca and Mn, the Los Alamos (LANL2DZ) pseudopotential basis set58–60 was used, while all remaining atoms were treated with the 6-31G(d) basis set; together, these are referred to as BS1. To maintain steric constraints imposed by the protein matrix, the backbone and selected peripheral residues (D1-Gln165, D1-Asn298, and D2-Lys317) were fixed at their crystallographic coordinates during the optimizations. These constraints ensure a realistic representation of the protein environment while allowing the active site sufficient freedom to relax within its local structural context. Unless otherwise noted, single-point energy calculations were performed using a modified B3LYP functional in which the Hartree–Fock (HF) exchange component (wHF) was reduced from 20% to 15%.61 These calculations employed an extended basis set designated BS2, comprising the Stuttgart/Dresden (SDD) pseudopotential basis set62,63 for Ca and Mn, and the 6-311G(d,p) basis set for all remaining atoms. An implicit solvent model (IEFPCM)64 with a dielectric constant of 5.7 (approximating chlorobenzene) was used to simulate the low-polarizability environment characteristic of the protein interior. Following the DFT computations, rCCA and supervised machine learning were applied to investigate the interplay between ligand movements and catalytic driving forces. These analyses were executed using a combination of Python libraries (NumPy, pandas, SciPy,65 scikit-learn,66 Chainer,67 Optuna68) and R (mixOmics).69 Additional technical details are provided in the ESI.†3 Results and discussion
3.1 Assessing ligand cavity variability in the OEC
Understanding the collective motion of primary ligands surrounding the Mn cluster in the OEC is essential for elucidating the mechanism of water oxidation. In this study, we introduce a robust framework to characterize the ligand environment by modeling the cavity as an effective sphere with a radius R. This radius quantitatively represents the spatial extent of the coordination environment, providing a global metric for the distribution of ligands, which is a critical factor when comparing different states within the catalytic cycle. The cavity size is estimated via the inertial radius of 13 coordinating atoms belonging to seven first-shell ligands, as highlighted in blue in Fig. 1C. Mathematically, the effective radius R can be defined as
 | (1) |
![[r with combining macron]](https://www.rsc.org/images/entities/b_char_0072_0304.gif) is their mean position. The notation ‖A‖ signifies the l2-norm of the vector A, implying that ‖A‖2 = ATA. The first formulation defines R as the square root of the mean squared deviation of the ligand positions from their centroid, providing a global measure of the overall dispersion. In contrast, the second formulation expresses R in terms of the average of all pairwise distances among the ligand atoms ‖rK − rL‖, hereafter referred to as XK.L. This alternative representation is derived from a fundamental identity that relates the variance of a set of points to the sum of their pairwise separations. While the variance-based formulation is intuitive for understanding the overall spread relative to a central point, the pairwise distance approach offers a more detailed view of interatomic spacing, thereby revealing subtle local variations that might otherwise be averaged out in a global variance measure.
is their mean position. The notation ‖A‖ signifies the l2-norm of the vector A, implying that ‖A‖2 = ATA. The first formulation defines R as the square root of the mean squared deviation of the ligand positions from their centroid, providing a global measure of the overall dispersion. In contrast, the second formulation expresses R in terms of the average of all pairwise distances among the ligand atoms ‖rK − rL‖, hereafter referred to as XK.L. This alternative representation is derived from a fundamental identity that relates the variance of a set of points to the sum of their pairwise separations. While the variance-based formulation is intuitive for understanding the overall spread relative to a central point, the pairwise distance approach offers a more detailed view of interatomic spacing, thereby revealing subtle local variations that might otherwise be averaged out in a global variance measure.
Application of this analysis to structural datasets from the Protein Data Bank (PDB codes: 3WU2,9 5B5E, 5B66,70 4UB6, 4UB8,71 5WS5, 5WS6,25 6DHE, 6DHF, 6DHG, 6DHH, 6DHO, 6DHP,26 6JLJ, 6JLK, 6JLL, 6JLM, 6JLN, 6JLO, 6JLP,27 6W1O, 6W1P, 6W1Q, 6W1R, 6W1T, 6W1U, 6W1V,28 7RF2, 7RF3, 7RF4, 7RF5, 7RF6, 7RF7, 7RF8,29 7COU, 7CJI, 7CJJ,30 8EZ5, 8F4C,31 8IR5, 8IRC, 8IRD, 8IRE, 8IRF, 8IRG, 8IRH, and 8IRI32) enabled us to compute ligand cavity sizes for the various oxidation states (S0, S1, S2, and S3) as well as during the S2 to S3 transition (S2→3). The resulting distributions of these cavity sizes, illustrated as box plots in Fig. 2, exhibit notable variability. Standard deviations (Std) ranging from 0.027 to 0.042 Å likely reflect differences in resolution, heterogeneity of S-state populations, experimental noise, and variations in sample preparation and measurement temperature. Importantly, even when applying the conservative bounds of Hoeffding's inequality72 to account for experimental uncertainties, the observed shifts in median cavity sizes across the S-states remain statistically significant, as indicated in Fig. 2. This analysis reveals a clear trend: smaller cavity sizes in the lower oxidation states (S0 and S2 excluding S1) and larger sizes in the higher oxidation states (S2→3 and S3). Two observations merit particular attention. First, the S1 state shows a median cavity size (3.68 Å) that is unexpectedly larger than those in the S0 and S2 states (both 3.64 Å). Although the mechanism behind this expansion is not fully understood, one plausible explanation is that the observed increase may reflect equilibrium processes such as protonation isomerism or tautomerism within the OEC. For example, variations in the protonation states of water-derived ligands (e.g., W1 and W2 as H2O versus OH−, and O4 and O5 as OH− versus O2−),73,74 as well as Jahn–Teller distortions at the MnIII site,75 could be responsible for these subtle differences. While this finding highlights the need for further investigation, our current investigation does not address this issue further. Second, during the S2 to S3 transition, the median cavity size (3.67 Å) lies between those of S2 (3.64 Å) and S3 (3.71 Å) and exhibits substantial variability. Time-resolved XFEL data (Fig. 3A), derived from studies by Kern et al. (6DHF, 6DHG, 6DHH, and 6DHO)26 and Suga et al. (6JLK, 6JLL, 6JLN, and 6JLO),27 demonstrate a progressive cavity enlargement following the second flash (2F). Mechanistically, this suggests that the effective radius R serves as a rough indicator for monitoring structural changes during the S2 to S3 transition. However, we recognize that this model assumes a ligand distribution that is uniform in all directions, which may not adequately capture anisotropic fluctuations that can occur under dynamic conditions. Indeed, our analysis of selected pairwise distances (XK.L) in Fig. 3B shows that while the majority of distances increase over time, consistent with an overall expansion of the ligand cavity, some specific pairs show transient decreases at certain time intervals. This observation highlights the importance of incorporating higher-order moments of the spatial distribution, for example through the pair-specific formalism presented in eqn (1), to achieve a more detailed characterization of the ligand environment.
 | ||
Fig. 2 Box plots of experimentally determined ligand cavity sizes, represented by inertial radii R, for the S0, S1, S2, and S3 states, as well as during the S2 to S3 transition (S2→3). The experimental data are sourced from the following PDB codes: 6DHP and 6JLP for S0; 3WU2, 5B5E, 5B66, 4UB6, 4UB8, 5WS5, 6DHE, 6JLJ, 6JLM, 6W1O, 7RF2, 7COU, 7CJI, and 8IR5 for S1; 6DHF, 6JLK, 6JLN, 6W1P, 7RF3, 7CJJ, and 8IRC for S2; 6DHG, 6DHH, 6W1Q, 6W1R, 6W1T, 6W1U, 7RF4, 7RF5, 7RF6, 7RF7, 8IRD, 8IRE, 8IRF, 8IRG, 8IRH, and 8IRI for S2→3; and 5WS6, 6DHO, 6JLL, 6JLO, 6W1V, 7RF8, 8EZ5, and 8F4C for S3. For details regarding the box plot construction, see Fig. 7. Std denotes the standard deviation. Conservative bounds based on Hoeffding's inequality72 were computed under the assumption that each measurement is confined to its observed minimum (Mix) and maximum (Max). For a 95% confidence interval, the deviation t is calculated as 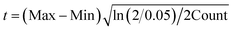 , yielding lower and upper bounds of mean − t and mean + t, respectively. , yielding lower and upper bounds of mean − t and mean + t, respectively. | ||
 | ||
| Fig. 3 (A) Variations in the inertial radius (R) during the S2 to S3 transition. The experimental data are sourced from the XFEL results reported by Kern et al. (6DHF, 6DHG, 6DHH, and 6DHO)26 and from Suga et al. (6JLK, 6JLL, 6JLN, and 6JLO).27 (B) Alterations in specific pairwise interatomic distances during the S2 to S3 transition. Eight distances that exhibit large coefficients in the canonical variate (see Fig. 5A) were selected, with the experimental data taken from monomer A as reported by Kern et al.26 | ||
Importantly, the expansion of the ligand cavity in the S3 state is not permanent, as it reverts to its original dimensions during the subsequent S3 to S0 transition (Fig. 2). This reversible behavior implies that critical catalytic processes, such as substrate binding and activation, and the formation and release of dioxygen, likely occur within an environment that cyclically undergoes both expansion and contraction. This observation raises an intriguing question: to what extent are these dynamic changes in the coordination environment linked to the catalytic reactions within the Mn cluster? To explore this inquiry, our study employs a complementary approach that combines statistical analyses, machine learning techniques, and quantum chemical calculations. Statistical analyses are used to identify patterns and correlations across multi-dimensional datasets, machine learning methods provide predictive models linking ligand motions to catalytic function, and quantum chemical calculations offer detailed molecular and electronic insights into reaction mechanisms. By cross-referencing evidence from these complementary methods, we aim to uncover the functional interplay between structural dynamics and catalytic activity in the OEC.
3.2 Structural–energetic mapping of ligand motions using rCCA
To investigate the interplay between ligand dynamics and catalytic activity, we initiated our study with a quantitative analysis employing canonical correlation analysis (CCA).76 CCA is a robust multivariate statistical method that reduces the dimensionality of two complex datasets while simultaneously identifying the maximal correlations between their linear combinations. By transforming these high-dimensional datasets into a smaller set of canonical variates, CCA allows us to extract underlying interaction patterns that might be obscured when variables are considered individually. In our analysis, two primary datasets were constructed from the same N entries. The first dataset, represented by an N × P matrix X = (X1, X2, …, XP), consists of P pairwise distances between atoms that directly coordinate with three critical catalytic manganese ions (MnA, MnB, MnD). P is equal to 19 as it excludes the distances between oxygen atoms within the same carboxyl group. These pairwise distances were chosen as features instead of the global ligand cavity radius R, as they more effectively capture subtle local distortions and anisotropic deformations within the coordination sphere that are critical for elucidating the catalytic function. The second dataset, stored in an N × Q matrix Y = (Y1, Y2, …, YQ), comprises Q variables that represent the driving forces for the interconversion between closed and open cubane configurations. In our case, Q is set to 2, corresponding to the hydroxo–oxo and oxyl–oxo species.35–44 These datasets are derived from the XFEL data reported by Kern et al.26 and includes a total of 60 samples for N (entries 1–60 in Table S1†). Prior to the application of CCA, each column vector in the X and Y matrices was standardized using Z-score normalization to ensure that all variables contribute equally. Specifically, the standardization was performed as follows:
 | (2) |
 | (3) |
![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) i and Ȳi represent the mean values of the ith variable in the X and Y datasets, while σXi and σYi denote their corresponding standard deviations. The tilde symbol (∼) signifies the standardized values. The objective of CCA is to find linear combinations of these standardized variables that maximize the correlation between the two datasets. These combinations, referred to as canonical variates, are defined as:
i and Ȳi represent the mean values of the ith variable in the X and Y datasets, while σXi and σYi denote their corresponding standard deviations. The tilde symbol (∼) signifies the standardized values. The objective of CCA is to find linear combinations of these standardized variables that maximize the correlation between the two datasets. These combinations, referred to as canonical variates, are defined as:
f = ![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) a = a1 a = a1![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) 1 + a2 1 + a2![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) 2+…+aP 2+…+aP![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) P P
| (4) |
| g = Ỹb = b1Ỹ1 + b2Ỹ2+…+bQỸQ | (5) |
 | (6) |
The highest canonical correlation ρ1 corresponds to the first canonical variates f1 and g1, which capture the dominant correlated pattern between the standardized datasets ![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) and Ỹ. In subsequent dimension, CCA identifies the second canonical correlation (ρ2) with its associated variates f2 and g2, subject to the condition that ρ1 ≥ ρ2 and the orthogonality constraints corr(f1, f2) = corr(g1, g2) = 0. A key advantage of using the linear combinations of pairwise distances (the f variates) is that they provide insight into the collective motions within the primary coordination sphere and their connection to catalytic activity, as captured by the driving forces represented in the g variates.
and Ỹ. In subsequent dimension, CCA identifies the second canonical correlation (ρ2) with its associated variates f2 and g2, subject to the condition that ρ1 ≥ ρ2 and the orthogonality constraints corr(f1, f2) = corr(g1, g2) = 0. A key advantage of using the linear combinations of pairwise distances (the f variates) is that they provide insight into the collective motions within the primary coordination sphere and their connection to catalytic activity, as captured by the driving forces represented in the g variates.
The outcomes of the rCCA analysis are illustrated in Fig. 4, with detailed numerical values provided in Table S5.† The original 19-dimensional space, defined by pairwise distance vectors derived from 10 coordinating atoms of the first-shell ligands (![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) OB.OC,
OB.OC, ![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) OB.OD, …,
OB.OD, …, ![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) OJ.Nε), together with the two energy vectors corresponding to the hydroxo and oxyl species (Ỹhydroxo and Ỹoxyl) (Fig. 4A), can be effectively compressed into a two-dimensional canonical space (Fig. 4B and C). The first canonical correlation coefficient ρ1 = 0.91 indicates a remarkably strong correlation between f1 and g1 (Fig. 4B), suggesting that the collective movement of the amino acid side chains captured by f1 is closely linked to the catalytic driving force represented by g1. In contrast, the second canonical correlation coefficient ρ2 = 0.29 (Fig. 4C) suggests a relatively weak association for the second mode, which is therefore not considered in further analyses.
OJ.Nε), together with the two energy vectors corresponding to the hydroxo and oxyl species (Ỹhydroxo and Ỹoxyl) (Fig. 4A), can be effectively compressed into a two-dimensional canonical space (Fig. 4B and C). The first canonical correlation coefficient ρ1 = 0.91 indicates a remarkably strong correlation between f1 and g1 (Fig. 4B), suggesting that the collective movement of the amino acid side chains captured by f1 is closely linked to the catalytic driving force represented by g1. In contrast, the second canonical correlation coefficient ρ2 = 0.29 (Fig. 4C) suggests a relatively weak association for the second mode, which is therefore not considered in further analyses.
 | ||
Fig. 4 (A) Graphical representation of the correlation matrices within and between two datasets ![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) and Ỹ. The upper-left and lower-right sections depict the autocorrelation matrices for and Ỹ. The upper-left and lower-right sections depict the autocorrelation matrices for ![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) and Ỹ, while the off-diagonal sections are mirror images of the cross-correlation matrix. The distance and energy vectors ( and Ỹ, while the off-diagonal sections are mirror images of the cross-correlation matrix. The distance and energy vectors (![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) OB.OC, OB.OC, ![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) OB.OD, …, Ỹhydroxo, Ỹoxyl) are arranged along both axes in the same order as in Fig. 5A. (B) And (C) scatter plots of the first and second pairs of canonical variates, overlaid with linear regression fits (solid lines) and 95% confidence intervals (shaded regions). For detailed definitions of the regularization parameters λ1 and λ2, as well as CV-score, see the ESI.† OB.OD, …, Ỹhydroxo, Ỹoxyl) are arranged along both axes in the same order as in Fig. 5A. (B) And (C) scatter plots of the first and second pairs of canonical variates, overlaid with linear regression fits (solid lines) and 95% confidence intervals (shaded regions). For detailed definitions of the regularization parameters λ1 and λ2, as well as CV-score, see the ESI.† | ||
The strong correlation between f1 and g1 implies the existence of common underlying factors that simultaneously influence the structural and energetic aspects of the system. To elucidate these factors, we examined the canonical coefficients a and b associated with f and g, as demonstrated in Fig. 5. This analysis enables us to identify the variables that contribute to the observed canonical correlations and to assess both the magnitude and the direction of their effects. For instance, the coefficients corresponding to g1 indicate that this variate is predominantly determined by the energy difference of the hydroxo species Ỹhydroxo The negative sign of this coefficient implies that an increase in any f1 variable with a positive coefficient will amplify the catalytic driving force promoting the transition from the closed to the open cubane structure in its hydroxo form, while increases in f1 variables with negative coefficients are expected to counteract this driving force.
 | ||
| Fig. 5 (A) Coefficients a and b in the canonical variates f and g, as defined in eqn (4) and (5). (B and C) Potential causal factors underlying the strong correlation between the collective motion of side chains and the catalytic driving force in the first canonical variates f1 and g1: changes in intermetallic distances within the Mn cluster (B) and alterations in the coordination geometries of MnA, MnB, and MnD associated with the movements of O5 and O6 (C). | ||
In Fig. 5A, distances highlighted in red exhibit large coefficients in f1 suggesting potential links to variations in the separations among the catalytic Mn ions. For example, the distance ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) OB.OE has a strongly negative coefficient, indicating that a reduction in this distance, representing the separation between the OB and OE oxygen atoms that directly coordinate to MnA and MnB, leads to a contraction of the MnA⋯MnB distance. This contraction stabilizes the open cubane configuration, which is characterized by a shorter MnA⋯MnB distance, while destabilizing the closed cubane that favors a longer separation. Similarly, distances such as
OB.OE has a strongly negative coefficient, indicating that a reduction in this distance, representing the separation between the OB and OE oxygen atoms that directly coordinate to MnA and MnB, leads to a contraction of the MnA⋯MnB distance. This contraction stabilizes the open cubane configuration, which is characterized by a shorter MnA⋯MnB distance, while destabilizing the closed cubane that favors a longer separation. Similarly, distances such as ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) OD.OL,
OD.OL, ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) OD.Nε,
OD.Nε, ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) OE.OL, and
OE.OL, and ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) OE.Nε exhibit positive coefficients, likely reflecting elongation between MnB and MnD that energetically supports the open cubane configuration characterized by extended MnB⋯MnD distances, while suppressing the closed cubane that requires shorter MnB⋯MnD distances.
OE.Nε exhibit positive coefficients, likely reflecting elongation between MnB and MnD that energetically supports the open cubane configuration characterized by extended MnB⋯MnD distances, while suppressing the closed cubane that requires shorter MnB⋯MnD distances.
The interpretation of changes in distances marked within blue boxes (specifically, ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) OB.OL,
OB.OL, ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) OB.Nε, and
OB.Nε, and ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) OD.OE) is more complex. Initially, one might hypothesize that changes in
OD.OE) is more complex. Initially, one might hypothesize that changes in ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) OB.OL and
OB.OL and ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) OB.Nε reflect variations in the spatial relationship between MnA⋯MnD, as depicted in Fig. 5B. However, the impact of water binding complicates this interpretation. Prior to water binding, the MnA⋯MnD distances differ substantially between configurations (approximately 4.8 Å in the open cubane versus 5.2 Å in the closed cubane); however, following water binding, these distances change only marginally (around 5.2 Å and 5.3 Å, respectively). This minimal alteration does not fully account for the pronounced coefficients observed in f1, and the positive coefficients for
OB.Nε reflect variations in the spatial relationship between MnA⋯MnD, as depicted in Fig. 5B. However, the impact of water binding complicates this interpretation. Prior to water binding, the MnA⋯MnD distances differ substantially between configurations (approximately 4.8 Å in the open cubane versus 5.2 Å in the closed cubane); however, following water binding, these distances change only marginally (around 5.2 Å and 5.3 Å, respectively). This minimal alteration does not fully account for the pronounced coefficients observed in f1, and the positive coefficients for ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) OB.OL and
OB.OL and ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) OB.Nε contradict the expected contraction associated with the open cubane. Consequently, we propose an alternative interpretation: these changes may arise from the motions of ligands in response to variations in the coordination geometries of MnA, MnB, and MnD, influenced by the movements of O5 and O6. This hypothesis is corroborated by the overlay of amino acid side chains corresponding to the open and closed cubane structures, as illustrated in Fig. 5C. Specifically, with reference to the page orientation, the transition from the closed to the open cubane configuration following water binding involves MnA moving backward, MnB shifting to the left, and MnD remaining largely stationary. As a result, D1-Asp170 is displaced backward, while D1-Glu333 and CP43-Glu354 adjust in response to the altered coordination environment of MnB. Although MnD remains largely static after water binding, the alteration in its coordination geometry causes OL to move outward. These side chain movements, manifesting as elongations in the OB⋯OL and OB⋯Nε distances and a contraction in the OD⋯OE distance, are consistent with the observed signs of the coefficients for
OB.Nε contradict the expected contraction associated with the open cubane. Consequently, we propose an alternative interpretation: these changes may arise from the motions of ligands in response to variations in the coordination geometries of MnA, MnB, and MnD, influenced by the movements of O5 and O6. This hypothesis is corroborated by the overlay of amino acid side chains corresponding to the open and closed cubane structures, as illustrated in Fig. 5C. Specifically, with reference to the page orientation, the transition from the closed to the open cubane configuration following water binding involves MnA moving backward, MnB shifting to the left, and MnD remaining largely stationary. As a result, D1-Asp170 is displaced backward, while D1-Glu333 and CP43-Glu354 adjust in response to the altered coordination environment of MnB. Although MnD remains largely static after water binding, the alteration in its coordination geometry causes OL to move outward. These side chain movements, manifesting as elongations in the OB⋯OL and OB⋯Nε distances and a contraction in the OD⋯OE distance, are consistent with the observed signs of the coefficients for ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) OB.OL,
OB.OL, ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) OB.Nε, and
OB.Nε, and ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) OD.OE.
OD.OE.
We now broaden our interpretation of the results. Based on eqn (1), the substantial increase in the majority of distances between the coordinating atoms is closely associated with the expansion of the ligand cavity, characterized by the inertial radius R. Considering the predominance of positive coefficients within the red and blue boxes in Fig. 5A, we propose the following interpretation, as illustrated in Fig. 6A: the expansion of the cavity defined by first-shell residues inherently amplifies the catalytic reaction in the guest cofactor. This provides a clear illustration of how coordinated ligand movements actively drive and enhance catalytic activity, a process that can be effectively approximated by a spherical model using a single parameter, R. However, the enlargement of the cavity is not uniformly distributed. Counteracting driving forces appear to become significant during the interval from 150 to 400 μs after 2F, potentially stabilizing the closed cubane before the onset of water binding, although they are insufficient to overcome the primary force that triggers the transition to the open cubane conformation after water binding. This interpretation is supported by the negative coefficients attributed to the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) OB.OE and
OB.OE and ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) OD.OE distances (Fig. 5A), along with the experimentally observed irregular shortening of the
OD.OE distances (Fig. 5A), along with the experimentally observed irregular shortening of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) OE.OL and
OE.OL and ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) OE.Nε distances (Fig. 3B). Notably, these distances involve the OE atom of Glu354 (Fig. 1C), the sole OEC ligand contributed by the CP43 subunit that coordinates the Mn cluster on the side opposite D1-Asp170/Glu189. This collective motion appears to be driven primarily by a positional shift of CP43-Glu354 relative to D1-Asp170, D1-Glu189, D1-Glu333, and D1-His332, as depicted in Fig. 6B. Such a shift leads to a deformation in the cavity geometry that cannot be adequately represented by a simplified spherical model. An alternative interpretation is therefore plausible: while the backbone movement that enlarges the cavity promote the catalytic reaction, the slower side chain motions, tracking the structural changes in the Mn cluster, may manifest in the deformation of the cavity. This dynamic interplay between backbone and side chains movements indicates that the cavity can both expand to facilitate catalysis and adapt its shape to stabilize intermediate states. The cooperative nature of primary coordination sphere movements may also explain why certain observations from site-directed mutagenesis studies cannot be fully accounted for by examining the isolated action of any single residue.12,22,80
OE.Nε distances (Fig. 3B). Notably, these distances involve the OE atom of Glu354 (Fig. 1C), the sole OEC ligand contributed by the CP43 subunit that coordinates the Mn cluster on the side opposite D1-Asp170/Glu189. This collective motion appears to be driven primarily by a positional shift of CP43-Glu354 relative to D1-Asp170, D1-Glu189, D1-Glu333, and D1-His332, as depicted in Fig. 6B. Such a shift leads to a deformation in the cavity geometry that cannot be adequately represented by a simplified spherical model. An alternative interpretation is therefore plausible: while the backbone movement that enlarges the cavity promote the catalytic reaction, the slower side chain motions, tracking the structural changes in the Mn cluster, may manifest in the deformation of the cavity. This dynamic interplay between backbone and side chains movements indicates that the cavity can both expand to facilitate catalysis and adapt its shape to stabilize intermediate states. The cooperative nature of primary coordination sphere movements may also explain why certain observations from site-directed mutagenesis studies cannot be fully accounted for by examining the isolated action of any single residue.12,22,80
 | ||
| Fig. 6 Schematic representation of dual functions within the primary coordination sphere, identified by comparing the first canonical variates f1 and g1 (Fig. 5A) with experimentally observed variations in pairwise distances (Fig. 3B). (A) Expansion of the ligand cavity to promote the transition from the closed to open cubane conformations, which can be represented using a spherical model with a radius R. (B) Adjustment of the ligand cavity geometry to stabilize the closed cubane intermediate, a motion that cannot be modeled by a sphere. Dashed lines indicate pairwise distances that contribute significantly to this stabilization, all involving the OE atom from CP43-Glu354. The color scheme for CP43-Glu354, D1-Asp170, D1-Glu189, D1-Glu333, and D1-His332 is consistent with that in Fig. 1C. | ||
Before concluding this section, we would like to address the question of causal directionality. In the present study, we have adopted a “structure-first” scenario, in which the backbone movement is interpreted as the primary determinant of the thermodynamic driving direction within the OEC. However, this is only one possible interpretation. An alternative “electron-first” scenario suggests that redox-driven changes in the electronic configuration of the Mn cluster act as the initial trigger for coordinating side-chain rearrangements, with backbone shifts and cavity resizing subsequently occurring. Indeed, as shown in Fig. 2, increases in cluster oxidation state appear to induce corresponding expansions and contractions of the ligand cavity, intuitively supporting this electron-first view. However, time-resolved XFEL studies have demonstrated that flash illumination provokes extensive, multi-layered conformational changes across the entire PSII complex, including inter-subunit interface reorganization and dynamic hydrogen-bond network rearrangements that extend into the OEC region.27 This complexity underscores the difficulty of unambiguously assigning cause and effect. Thus, whether electron movement or structural rearrangement comes first remains an open question that cannot be resolved by the current first-shell-focused analytical approach alone.
3.3 Nonlinear modeling of catalytic energy landscapes with DNN
The rCCA analysis yielded a notably small second canonical correlation coefficient (ρ2 = 0.29), indicating that the second set of canonical variates (f2 and g2) contains little meaningful information. Moreover, the energy vector corresponding to the oxyl–oxo Ỹoxyl contributes only marginally to the first canonical variate g1, thereby complicating direct comparisons between the driving forces of the oxyl–oxo and hydroxo–oxo species. A key limitation of rCCA is its inherent linearity: while this facilitates the interpretability of causal factors, which is a primary motivation for our choice of rCCA, it restricts the model's capacity to capture complex, nonlinear relationships that are likely intrinsic to the OEC system. To address this limitation, we implemented a supervised learning approach based on the hypothesis that the mapping between the input distance matrix and the output energy matrix is fundamentally nonlinear. Accordingly, we designed a deep neural network (DNN) architecture comprising three layers, in which each layer first applies an affine (linear) transformation to the input data, followed by a nonlinear activation function (the rectified linear unit, ReLU).81 The architecture concludes with a fully connected layer that integrates the learned features into the final output.One major challenge in developing our DNN model was achieving robust generalization while mitigating overfitting. Initially, we employed Z-score normalization, as indicated in eqn (2) and (3), to standardize both the distance (![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) ) and energy (Ỹ) matrices across the training and testing datasets. However, this approach consistently resulted in near–perfect correlations (approaching unity) between Ỹ and the predicted energies, clearly indicating that the model was overfitting to the training data. Despite various modifications, including changes to the DNN architecture, alternative optimizers, and additional regularization techniques, the overfitting issue persisted (Fig. S4A–C†). Ultimately, replacing Z-score normalization with min–max scaling, as defined in eqn (7) and (8), resolved the problem.
) and energy (Ỹ) matrices across the training and testing datasets. However, this approach consistently resulted in near–perfect correlations (approaching unity) between Ỹ and the predicted energies, clearly indicating that the model was overfitting to the training data. Despite various modifications, including changes to the DNN architecture, alternative optimizers, and additional regularization techniques, the overfitting issue persisted (Fig. S4A–C†). Ultimately, replacing Z-score normalization with min–max scaling, as defined in eqn (7) and (8), resolved the problem.
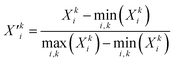 | (7) |
 | (8) |
Here, the prime symbol (′) signifies that min–max scaling has been applied. This change enabled effective hyperparameter optimization via 10-fold cross-validation (Table S4†), as evidenced by concurrent reductions in both training and testing loss curves during training (Fig. S4D†), indicating that the model successfully captured meaningful patterns without overfitting. The fundamental difference between the standardized data (![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) ) and the min–max scaled data (X′) lies in the distance metric employed. The min–max scaling preserves the Euclidean metric within the distance matrix, thereby maintaining the spatial relationships (relative distances and angles) present in the original dataset (X), while the Z-score normalization converts the metric into a variant of the Mahalanobis distance characterized by a diagonal variance–covariance matrix (Table S3†). Although the Z-score normalization equalizes the contributions of each variable, it can distort intrinsic spatial relationships critical to understanding the physical or chemical properties of the system, particularly when the original 3D configurations of coordinating residues in the input feature dataset (X) are closely linked to catalytic processes in the target variable dataset (Y).
) and the min–max scaled data (X′) lies in the distance metric employed. The min–max scaling preserves the Euclidean metric within the distance matrix, thereby maintaining the spatial relationships (relative distances and angles) present in the original dataset (X), while the Z-score normalization converts the metric into a variant of the Mahalanobis distance characterized by a diagonal variance–covariance matrix (Table S3†). Although the Z-score normalization equalizes the contributions of each variable, it can distort intrinsic spatial relationships critical to understanding the physical or chemical properties of the system, particularly when the original 3D configurations of coordinating residues in the input feature dataset (X) are closely linked to catalytic processes in the target variable dataset (Y).
Fig. 7A displays a scatter plot comparing driving forces computed via DFT [Y = (Yhydroxo, Yoxyl)] with those predicted by the DNN model [Ypred = (Ypred, hydroxo, Ypred, oxyl)] for 130 samples (Table S1†), with hydroxo–oxo results depicted in red and oxyl–oxo results in blue. The DNN predictions (Ypred) were obtained by applying the inverse transformation of eqn (8) to the scaled outputs  , thereby restoring the energy values to units of kcal mol−1. The horizontal and vertical axes further depict the distribution curves for Y and Ypred. The results demonstrate a good correlation between the DFT-computed and DNN-predicted driving forces; for the hydroxo–oxo species, the correlation coefficient is 0.95 with a regression slope of 0.90, while for the oxyl–oxo species, the coefficient is 0.92 with a slope of 0.83. Notably, the hydroxo–oxo species exhibit considerably larger standard deviations (19.1 kcal mol−1 for Yhydroxo and 18.2 kcal mol−1 for Ypred, hydroxo) compared to the oxyl–oxo species (11.2 and 10.2 kcal·mol−1, respectively). These differences in variability are consistent with the latent factors uncovered by rCCA, i.e., underlying sources not explicitly represented in either X or Y, which appear to be closely linked to structural modifications within the Mn cluster. In particular, variations in the coordination geometries of three catalytic metals (MnA, MnB, and MnD) and changes in their intermetallic distances MnA⋯MnB (rAB) and MnB⋯MnD (rBD) seem to govern the driving forces. The ratio rAB/rBD, which effectively distinguishes between the open and closed cubane configurations,41 serves as a sensitive metric in this context; for the hydroxo–oxo species, this ratio is lower in the open cubane conformation (0.78) compared to the oxyl–oxo species (0.85), while in the closed cubane conformation, the hydroxo–oxo species exhibits a higher ratio (1.12) than the oxyl–oxo species (1.03). This distinct trend suggests that the hydroxo–oxo species is more responsive to subtle changes in the coordination environment, particularly those driven by the collective motion of coordinating side chains, consistent with the results presented in Fig. 7A.
, thereby restoring the energy values to units of kcal mol−1. The horizontal and vertical axes further depict the distribution curves for Y and Ypred. The results demonstrate a good correlation between the DFT-computed and DNN-predicted driving forces; for the hydroxo–oxo species, the correlation coefficient is 0.95 with a regression slope of 0.90, while for the oxyl–oxo species, the coefficient is 0.92 with a slope of 0.83. Notably, the hydroxo–oxo species exhibit considerably larger standard deviations (19.1 kcal mol−1 for Yhydroxo and 18.2 kcal mol−1 for Ypred, hydroxo) compared to the oxyl–oxo species (11.2 and 10.2 kcal·mol−1, respectively). These differences in variability are consistent with the latent factors uncovered by rCCA, i.e., underlying sources not explicitly represented in either X or Y, which appear to be closely linked to structural modifications within the Mn cluster. In particular, variations in the coordination geometries of three catalytic metals (MnA, MnB, and MnD) and changes in their intermetallic distances MnA⋯MnB (rAB) and MnB⋯MnD (rBD) seem to govern the driving forces. The ratio rAB/rBD, which effectively distinguishes between the open and closed cubane configurations,41 serves as a sensitive metric in this context; for the hydroxo–oxo species, this ratio is lower in the open cubane conformation (0.78) compared to the oxyl–oxo species (0.85), while in the closed cubane conformation, the hydroxo–oxo species exhibits a higher ratio (1.12) than the oxyl–oxo species (1.03). This distinct trend suggests that the hydroxo–oxo species is more responsive to subtle changes in the coordination environment, particularly those driven by the collective motion of coordinating side chains, consistent with the results presented in Fig. 7A.
In our DFT calculations, we fixed the backbone coordinates of all residues to their experimentally determined positions (Table S1†), thereby preserving the essential structural features of the OEC unique to each S-state and incorporating the effects of oxidation-induced backbone conformational changes into the computational results. This approach allowed us to categorize the ligand environments into distinct oxidation states (S0, S1, S2, and S3), as well as the transient state (S2→3), and to investigate how oxidation-induced modifications, primarily in the backbone region, impact the catalytic driving forces governing structural transformations within the Mn cluster. Fig. 7B presents a scatter plot that applies this categorization to both the DFT-computed and DNN-predicted driving forces, with S0, S1, S2, S2→3, and S3 color-coded as red, blue, green, purple, and ocher, respectively. Because of inherent data variability, differences among individual S-state environments may not be immediately apparent. Therefore, we incorporated box plots along the horizontal and vertical axes of the scatter plot, providing a visual summary of the distributions based on a five-number summary, as illustrated in the bottom right of Fig. 7. The median is emphasized as a robust measure of central tendency that is relatively insensitive to outliers. Analysis of the median values reveals a marked contrast between low and high oxidation environments. In the high oxidation (S3) environment, both DFT and DNN results exhibit remarkably strong driving forces (−10.2 and −9.3 kcal mol−1), while in the low oxidation (S0, S1, and S2) environment, the driving forces are much weaker, ranging from −1.6 to +1.9 kcal mol−1 for DFT and −1.8 to +2.6 kcal mol−1 for DNN. During the transition from the low to high oxidation environment (S2→3), the median driving forces are comparable to (−11.1 kcal mol−1 as computed by DFT) or even stronger than (−13.1 kcal mol−1 as predicted by DNN) those in the high oxidation (S3) environment. Interestingly, subtle differences between monomers A and B, potentially arising from sample preparation and crystal packing,82 appear to influence the driving forces. As illustrated in Fig. 7C, the median driving forces are higher in monomer A (−8.7 and −5.1 kcal mol−1 for DFT and DNN, respectively) than in monomer B (−2.1 and −0.7 kcal mol−1). These inter-monomer variations may mirror differences, as seen in high-resolution X-ray diffraction structures of the OEC in its dark-stable state,70 further underscoring the sensitivity of the catalytic process to even subtle structural perturbations.
To further substantiate the predictive capabilities of our DNN model, we applied the pre-trained network to independent experimental data that were not included in the previous 10-fold cross-validation tests. This dataset comprises experimental structural data of PSII across various S states, obtained from the following PDB ID codes: 6DHP and 6JLP for S0; 3WU2, 5B5E, 5B66, 4UB6, 4UB8, 5WS5, 6DHE, 6JLJ, 6JLM, 6W1O, 7RF2, 7COU, 7CJI, and 8IR5 for S1; 6DHF, 6JLK, 6JLN, 6W1P, 7RF3, 7CJJ, and 8IRC for S2; 6DHG, 6DHH, 6W1Q, 6W1R, 6W1T, 6W1U, 7RF4, 7RF5, 7RF6, 7RF7, 8IRD, 8IRE, 8IRF, 8IRG, 8IRH, and 8IRI for S2→3; and 5WS6, 6DHO, 6JLL, 6JLO, 6W1V, 7RF8, 8EZ5, and 8F4C for S3. The dataset, comprising data from both monomers A and B, includes 94 samples. Of these, 26 samples (derived from 6DHE, 6DHF, 6DHG, 6DHH, 6DHO, 6DHP, 6JLJ, 6JLK, 6JLL, 6JLM, 6JLN, 6JLO, and 6JLP) were previously incorporated into the training/validation sets, while the remaining 68 samples were entirely new to the model. The cavity size distributions for these 94 samples are visualized in Fig. 2. Prior to input into the model, these data were normalized using the min–max scaling method described in eqn (7) and (8). Following prediction, an inverse scaling transformation was applied to restore the driving force values to their original physical units (kcal mol−1).
Fig. 8A displays box plots of the predicted driving forces for the OEC under different oxidation state environments. In this panel, the data for the hydroxo–oxo and oxyl–oxo species have been merged, effectively doubling the number of data points compared to those in Fig. 2; see S5† for individual species results. The predicted driving forces exhibit considerable variability, with standard deviations of 2.9, 4.4, 4.7, 12.9, and 14.5 kcal mol−1 for S0, S1, S2, S2→3, and S3, respectively. This variability likely arises from a combination of random and systematic errors inherent in the experimental measurements, as previously noted, which contribute to the dispersion in ligand cavity size and other related structural parameters (Fig. 2), as well as additional uncertainties introduced during the machine learning process. Two potential sources of error may become particularly evident in the S3 state. The first arises from incomplete separation of the S2 and S3 states in the XFEL structural data, such that nominal S3 models may still carry S2-derived ligand arrangements. This state-contamination provides a straightforward explanation for why our DNN model continues to predict S3 driving-force fluctuations with amplitudes comparable to those seen in the S2 to S3 transition. The second source of error lies in the limited scope of our current X data, which may simply lack critical S3-specific descriptors, such as the detailed topology of hydrogen-bonding network surrounding the Mn cluster and interactions with distal residues beyond the primary coordination sphere, thereby limiting the model's ability to capture key environmental influences and to fully eliminate any residual S2 memory effects. Despite these variabilities, the differences in the median driving force between low (S0, S1, and S2) and high (S2→3, and S3) oxidation environments are both pronounced and statistically significant. For instance, the Hoeffding upper bounds for the S2→3, and S3 states (−6.6 and −8.7 kcal mol−1) are substantially lower than the Hoeffding lower bounds for the S0, S1, and S2 states (−1.8, −2.1, and −3.4 kcal mol−1). As Hoeffding's inequality yields conservative, wide confidence intervals,72 the clear separation between these bounds suggests that significant differences exist in the central tendencies and variances between the two groups. In the low oxidation environments, the median driving forces remain slightly positive, ranging from 1.4 to 2.3 kcal mol−1. Interestingly, although the S1 state exhibits a considerably larger cavity size relative to S0 and S2, its driving force (1.7 kcal mol−1) is comparable to those of S0 (2.3 kcal mol−1) and S2 (1.4 kcal mol−1). In stark contrast, the transition to higher oxidation states is accompanied by a dramatic reversal in the driving force; for S2→3 and S3, the median values shift to strongly negative levels (−14.5 and −20.2 kcal·mol−1). This dramatic change implies a previously unrecognized, fundamental reorganization within the catalytic landscape of the OEC that distinguishes the high (S2→3 and S3) from the low (S0, S1, and S2) oxidation environments.
 | ||
| Fig. 8 (A) Box plots of the driving forces predicted by the DNN model trained on the full dataset of 130 samples listed in Table S1.† The input data are identical to those listed in Fig. 2: 6DHP and 6JLP for S0; 3WU2, 5B5E, 5B66, 4UB6, 4UB8, 5WS5, 6DHE, 6JLJ, 6JLM, 6W1O, 7RF2, 7COU, 7CJI, and 8IR5 for S1; 6DHF, 6JLK, 6JLN, 6W1P, 7RF3, 7CJJ, and 8IRC for S2; 6DHG, 6DHH, 6W1Q, 6W1R, 6W1T, 6W1U, 7RF4, 7RF5, 7RF6, 7RF7, 8IRD, 8IRE, 8IRF, 8IRG, 8IRH, and 8IRI for S2→3; and 5WS6, 6DHO, 6JLL, 6JLO, 6W1V, 7RF8, 8EZ5, and 8F4C for S3. The outcomes for the hydroxo–oxo and oxyl–oxo species have been combined, effectively doubling the number of data points compared to those in Fig. 2. Std denotes the standard deviation. For details regarding the derivation of the Hoeffding upper and lower bounds, see the caption of Fig. 2. (B) Box plots of the driving forces predicted by the DNN model trained on a reduced dataset of 78 samples, generated by excluding entries corresponding to closed cubane coordination environments from Table S1.† The input data remain the same as those described above. For details regarding the box plot construction, see Fig. 7. | ||
Experimental evidence indicates that, across all S states (S0, S1, S2, S2→3, and S3), the observed crystal structures consistently adopt open-cubane-like configurations characterized by low rAB/rBD ratios.9,24–32,70,71 This observation questions the necessity of including features representing the closed cubane coordination environment in our neural network model. Although such features are indispensable for rCCA to resolve the collective motions of side chains involved in transient closed cubane formation, as illustrated in Fig. 6B, their inclusion is debatable when the DNN model relies solely on experimentally observed information (i.e., the coordination environments stabilizing the open cubane) for its predictions. To address this issue, we constructed an alternative dataset by excluding samples corresponding to the closed cubane environments from the training set provided in Table S1,† resulting in a total of 78 samples. A new DNN model trained on this reduced dataset produced prediction results for the above 94 experimental structures (Fig. 8B) that are qualitatively identical to those obtained with the full dataset (Fig. 8A). Specifically, the model predicted weak or negligible driving forces for the low oxidation environments and pronounced driving forces for the high oxidation environments. Over 100 training trials with different random seeds confirmed that the predictions consistently generalized (Fig. S6†), demonstrating that the performance of our DNN model is robust and not driven by isolated outliers. This reproducibility not only underscores the extraordinary learning capabilities of neural networks but also offers significant insights into the functional mechanisms of PSII. Notably, the reorganization observed during the S2 to S3 transition appears to be driven predominantly by large-scale structural alterations in the protein, such as shifts in backbone positioning or variations in ligand cavity size, as depicted in Fig. 2, rather than by relatively modest side chain movements that accompany changes in the cluster structure, as illustrated in Fig. 6B.
3.4 Implications of the S3YZ˙ lag phase
The energy landscape changes predicted by our DNN model on an experimental dataset including previously unseen data, as illustrated in Fig. 8, could serve as critical markers for the dynamic chemical processes induced by protein reorganization. By correlating these predictions with established experimental observations, we can both validate the predictive performance of our model and enhance our understanding of the underlying reaction mechanisms. However, current experimental techniques remain insufficient for directly measuring subtle thermodynamic shifts, thereby complicating any rigorous evaluation based on the ‘energy landscape’ concept. Over the past decade, numerous theoretical studies have postulated the involvement of a putative S4 state, the highest metal oxidation state in the S-state cycle formally expresses as MnVO or MnIVO˙, as an essential intermediate in oxygen evolution.35,83–87 However, at present, the inability of current experimental techniques to directly probe the S3 to S0 chemistry has largely confined these proposals to purely theoretical conceptualizations. In this context, the consistently observed extended lifetime (1.2–2.5 ms) of the S3YZ˙ state following 3F emerges as the sole critical benchmark. A variety of experiments have reported distinct biphasic kinetic behavior during this transition;88–92 the fast phase (approximately 50–250 μs), attributed to the expulsion of a proton from the protongate residues D1-Glu65 and D2-Glu312,92 (but see also ref. 93), is accompanied by a pronounced delay in electron transfer kinetics that characterizes the subsequent slower phase extending from 1.2 to 2.5 ms. Our study focuses on this prolonged lifetime of the S3YZ˙ state as a means to enhance the reliability and chemical interpretability of the predictions generated by our DNN model, by verifying their consistency with this universally observed phenomenon. To this end, we performed quantum chemical calculations and cross-referenced the results with insights obtained from both the rCCA and DNN models, as discussed in the preceding sections. It should be noted that determining which of the previously proposed reaction mechanisms35,83–87 is correct is beyond the scope of the present study, as such an identification is currently unachievable without further experimental evidence.Fig. 9 illustrates the relative stabilities of open and closed conformations for various intermediates in the S3YZ˙, S4YZ, and ‘S4’YZ states, with hydroxo–oxo denoted as H, oxyl–oxo as O*, peroxo as P, superoxol as S; note that ‘S4’YZ represents nominal S4YZ configurations in which an internal electron relocation occurs within the Mn cluster, thereby lowering the metal oxidation state from its highest level. These intermediates are modeled with (W1, W2) = (H2O, OH−) for H and (W1, W2) = (H2O, H2O) for the other structures, assuming a spin multiplicity of 14. The backbone structure is anchored using the PDB coordinates of 6JLL (monomer A) corresponding to the S3-enriched state and 6JLP (monomer A) corresponding to the S0-enriched state, while the orientations of amino acid side chains were fully relaxed using DFT. The choice of these specific coordinates is motivated by our interest in understanding the effects of different cavity sizes formed by coordinating ligands, with measured radii (R) of 3.72 Å for 6JLL and 3.64 Å for 6JLP. To accurately assess the energetics of the structures with markedly different unpaired electron counts, such as the peroxo (P) and superoxo (S) intermediates, the wHF parameter was reduced to 10% in combination with the D4 dispersion correction model,94 a methodological choice shown to closely reproduce the energy differences calculated via the DLPNO-CCSD(T) method.95 Detailed Mulliken spin densities for all structures in Fig. 9 are listed in Table S7.† The justification for adopting the protonation states (W1, W2) = (H2O, OH−) for H(open) and (W1, W2) = (H2O, H2O) for O*(open) as representations of the S3YZ˙ state can be clarified by comparing the stability of the high-valent Mn species. Notably, the MnIVO˙ (or MnVO) species in S4YZ, with a spin multiplicity of 12 featuring an antiferromagnetically coupled MnDIV–O6˙ unit, is calculated to be 6–10 kcal mol−1 less stable than the H(open) and O*(open) species in S3YZ˙.
 | ||
| Fig. 9 Relative stabilities of various intermediates and transition structures in the S3YZ˙, S4YZ, and ‘S4’YZ states calculated at the IEFPCM-B3LYP(wHF15%)-D3(BJ)/BS2//B3LYP-D3(BJ)/BS1 level, using the PDB coordinates 6JLL (A) and 6JLP (B), except for S, P, and Spre, which, owing to their significantly different unpaired electron counts compared to H, were assessed using IEFPCM-B3LYP(wHF10%)-D4/BS2//B3LYP-D3(BJ)/BS1, as recommended by Drosou et al.95 Graphical representations and key interatomic distances for the transition structures TSPT and TSOO are provided in Fig. 10. The assumed protonation states for water ligands were (W1, W2) = (H2O, OH−) for H and (W1, W2) = (H2O, H2O) for all other structures. Ligand cavity sizes (R) were determined from the experimental data using eqn (1). Values in parentheses represent the distance ratios between MnA⋯MnB (rAB) and MnB⋯MnD (rBD), based on the 6JLL coordinates. The following color codes are used: yellow, calcium; red, oxygen; white, hydrogen; purple, MnIV; orange, MnIII. | ||
The computational results are consistent with the predictions from the rCCA and DNN models, confirming that the driving force for the closed-to-open structural change is significantly dependent on the crystal structure employed. Altering the crystal structure from S3 to S0 leads to a marked decrease in the driving force for hydroxo–oxo Y#hydroxo [where the sharp symbol (#) denotes the incorporation of reorganization energy], reducing it from 15.3 to 8.6 kcal mol−1. All structures, except for O*(closed), also experience stabilization relative to H(open), with energy reductions ranging from 1 to 7 kcal mol−1. These findings suggest that a reduced cavity size facilitates the conversion of H(open), which exhibits the lowest rAB/rBD ratio (0.77), into more closed-cubane-like configurations, such as P(3444), Spre(3444), S(closed), and H(closed), which are characterized by longer MnA⋯MnB and shorter MnB⋯MnD distances compared to H(open). For clarity, the distance ratio rAB/rBD for each structure is provided in parentheses in Fig. 9, and based on these results, we tentatively classify structures with rAB/rBD > 0.9 as ‘closed-cubane-like.’
Why is there a measurable delay between the formation of the YZ radical and the onset of electron transfer from the Mn cluster to YZ˙? One hypothesis is that the system requires additional time to surmount a high energy barrier associated with deprotonating the hydroxo ligand at MnD of H(open), a process that would yield the oxyl–oxo species O*(open). Fig. 10A displays the optimized transition structure (TSPT) that captures a proton relay involving the transfer of three protons between O6 (OH−) and W2 (OH−) via W3 and W5 during the conversion from H(open) to O*(open). The calculated activation energy for this proton relay is in the range of 15–18 kcal mol−1, a value that remains within acceptable limits considering inherent uncertainties in DFT calculations and the possibility of proton tunneling through the barrier. However, this interpretation is contradicted by the experimentally observed small kinetic isotope effects (1.2–1.4),91,96 which suggest that proton movement is unlikely to be the rate limiting. Moreover, if O*(open) is the predominant species in the S3 state,39–44 this explanation makes no sense. An alternative hypothesis that the lag phase is a consequence of O–O bond formation preceding electron transfer has also been proposed.97 However, our calculations show that the energy barriers for O–O bond formation in the S3YZ˙ state are very low (4–7 kcal mol−1), as demonstrated by the optimized transition structure TSOO in Fig. 10B. This discrepancy between the low calculated barriers and the observed kinetic delay suggests that neither mechanism alone can adequately account for the emergence of the lag phase.
 | ||
| Fig. 10 Graphical representations and key interatomic distances for two transition structures in the S3YZ˙ state. TSPT represents a transition structure involving the relayed movement of three protons during the conversion from H(open) to O*(open). TSOO depicts a transition structure corresponding to the formation of a peroxide bond between O5 and O6 originating from O*(open) featuring a partially formed O–O bond. Mulliken spin densities for these transition structures (Table S7†) are consistent with the electronic configurations and hole distributions characteristic of the S3 state. Interatomic distances, calculated using the coordinates from 6JLL (6JLP), are given in angstroms outside (inside) the parentheses. | ||
In our view, the observed lag phase may reflect a fundamental mechanism within the PSII enzyme that governs the thermodynamic pathway of the catalytic reaction. We propose that flash illumination initiates two distinct relaxation processes within the OEC: one involving the slower, progressive reorganization of the protein backbone and side chains, and another characterized by the rapid equilibration of the Mn cluster. The interplay between these processes appears to modulate the overall progression of the catalytic reaction, with the slower structural dynamics ultimately contributing to the lag phase. Our hypothesis is based on an analysis of the cavity-size-dependent relative stabilities of two key intermediates in the nominal ‘S4’YZ state compared to the S3YZ˙ state, specifically, the intermediates P(3444) and Spre(3443), where the numbers in parentheses denote the oxidation states of MnA, MnB, MnC, and MnD. For example, in a protein environment with a larger cavity (3.72 Å), the relatively stable peroxo intermediate P(3444) in ‘S4’YZ35,83–87 is calculated to be approximately 3–4 kcal mol−1 less stable than both H(open) and O*(open) in S3YZ˙, This finding suggests that under these conditions the driving force for electron transfer from the Mn cluster to YZ˙ is insufficient to promote the transition to the ‘S4’YZ state. Furthermore, the formation of Spre(3443), regarded as a superoxo precursor to dioxygen formation,83 is an endothermic process requiring 12–13 kcal mol−1, indicating that even if P(3444) were to form, the energetic penalty associated with 3O2 release would remain substantial. Conversely, in a protein environment characterized by a smaller cavity (3.64 Å), closed-cubane-like structures are significantly stabilized, as previously noted. Both P(3444) and Spre(3443) in ‘S4’YZ contain a trivalent MnAIII ion, which is associated with an extended MnA⋯MnB distance (3.02 and 3.17 Å) and a high rAB/rBD ratio (0.91 and 0.94), features typical of the closed cubane configuration. Consequently, P(3444) and Spre(3443) in ‘S4’YZ become stabilized by 7.3 and 4.5 kcal mol−1 relative to H(open) in S3YZ˙, as shown in Fig. 9B, with P(3444) emerging as a significant energy sink within the combined S3YZ˙ and ‘S4’YZ states.
Our scenario is as follows: the third flash triggers the rapid establishment of both electronic and structural equilibrium within the Mn cluster of the S3 state. This equilibration leads to the formation of a transient O–O peroxide bond that, rather than manifesting as a discrete, readily observable intermediate, effectively prepares the Mn cluster for subsequent proton-coupled electron transfer processes. In contrast, the complete structural reorganization of the protein matrix, accompanied by a reduction in the ligand cavity (Fig. 2), is expected to occur on a markedly slower timescale relative to the rapid adjustments within the Mn cluster, thereby gradually shifting the equilibrium positions of the fast, reversible chemical processes in the S3 state over time. Although the precise role of this delayed structural relaxation remains to be fully elucidated, we hypothesize that it serves as a regulatory checkpoint within the catalytic cycle, seamlessly integrating efficient multi-electron chemistry with the overall thermodynamic control required for the irreversible release of 3O2 under mild conditions,98 as illustrated in Fig. S7.† Such regulation may be critical for ensuring that the catalytic reaction proceeds in a controlled and orderly manner, thereby minimizing the risk of stalling or progressing in unexpected directions that might lead to inefficient catalysis or incomplete water oxidation.
4. Conclusions
In this study, we combined rCCA, neural network-based machine learning, and DFT calculations to elucidate the functional role of collective amino acid side chain motions within the primary coordination sphere in directing the catalytic processes at the Mn4CaO6 cofactor of PSII. By correlating two multidimensional datasets, one detailing the relative positions of coordinating atoms and the other representing the energetic demands for catalysis in the S3 state, we have been able to effectively characterize the collective motion that underpins catalytic transformations. Our findings reveal that the primary coordination sphere plays a dual role: it undergoes expansion or contraction to drive necessary structural rearrangements of the Mn cluster, and it concurrently adjusts its cavity geometry to effectively stabilize crucial reaction intermediates. Complementary predictions from our neural network-based machine learning model further suggest that the coordination sphere imposes an energetic modulation on the structural changes of the Mn cluster, with the magnitude of this effects varying across different S-state environments. This modulation appears to be associated with extensive, light-induced structural reorganizations within PSII, as manifested in experimentally observed variations in the ligand cavity across various S states, a behavior that is distinct from transient side chain motions typically accompanying the formation of unstable intermediates, thereby underscoring a more fundamental role for the coordination sphere in shaping the catalytic energy landscape. Additionally, our integrated approach suggests that the extended lifetime of the S3YZ˙ state consistently observed after 3F may be ascribed to gradual protein dynamics that continually reshape the energy landscape, thereby shifting the equilibrium positions of rapid, reversible chemical events over time. Such dynamic adjustment implies that the thermodynamic balance among various intermediates within the combined S3YZ˙ and ‘S4’YZ states is not fixed but may be continually tuned by protein motion. Ultimately, our findings redefine the primary coordination sphere as an active, modulating framework that might be essential for energetic optimization of multi-electron chemistry under ambient conditions, while seamlessly reconciling the dual demands of the strict selectivity and irreversibility necessary for robust 3O2 evolution.Data availability
Data supporting this article have been included as part of the ESI.† Additional codes and datasets used in this study are publicly available via our GitHub repository at https://github.com/h-isobe379/CCA-DNN-analysis-for-OEC.Author contributions
Hiroshi Isobe: conceptualization, formal analysis, investigation, writing – original draft, writing – review & editing. Takayoshi Suzuki: critical discussion from a coordination-chemistry perspective. Michihiro Suga: critical discussion from a structural-biology perspective. Jian-Ren Shen: project administration, writing – review & editing. Kizashi Yamaguchi: critical discussion from a theoretical-chemistry perspective.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by JSPS KAKENHI Grant Number JP22K05317. The computation was performed using Research Center for Computational Science, Okazaki, Japan.References
- R. E. Blankenship, Molecular Mechanisms of Photosynthesis, 2nd edn, Wiley-Blackwell, Chichester, UK, 2014 Search PubMed.
- M. P. Johnson, Essays Biochem., 2016, 60, 255–273 CrossRef PubMed.
- G. C. Dismukes, V. V. Klimov, S. V. Baranov, Y. N. Kozlov, J. DasGupta and A. M. Tyryshkin, Proc. Natl. Acad. Sci. U.S.A., 2001, 98, 2170–2175 CrossRef CAS PubMed.
- Photosystem II: The Light Driven Water: Plastoquinone Oxidoreductase, ed. T. J. Wydrzynski and K. Satoh, Springer, Dordrecht, The Netherlands, 2005 Search PubMed.
- J. P. McEvoy and G. W. Brudvig, Chem. Rev., 2006, 106, 4455–4483 CrossRef CAS PubMed.
- N. Cox, D. A. Pantazis, F. Neese and W. Lubitz, Acc. Chem. Res., 2013, 46, 1588–1596 Search PubMed.
- J. Yano and V. K. Yachandra, Chem. Rev., 2014, 114, 4175–4205 CrossRef CAS PubMed.
- J.-R. Shen, Annu. Rev. Plant Biol., 2015, 66, 23–48 CrossRef CAS PubMed.
- Y. Umena, K. Kawakami, J.-R. Shen and N. Kamiya, Nature, 2011, 473, 55–60 CrossRef CAS PubMed.
- P. Joliot, G. Barbieri and R. Chabaud, Photochem. Photobiol., 1969, 10, 309–329 CrossRef CAS.
- B. Kok, B. Forbush and M. McGloin, Photochem. Photobiol., 1970, 11, 457–475 CrossRef CAS PubMed.
- R. J. Debus, Biochim. Biophys. Acta, 2015, 1847, 19–34 CrossRef CAS PubMed.
- R. J. Boerner, A. P. Nguyen, B. A. Barry and R. J. Debus, Biochemistry, 1992, 31, 6660–6672 CrossRef CAS PubMed.
- R. J. Debus, C. Aznar, K. A. Campbell, W. Gregor, B. A. Diner and R. D. Britt, Biochemistry, 2003, 42, 10600–10608 CrossRef CAS PubMed.
- M. A. Strickler, L. M. Walker, W. Hillier, R. D. Britt and R. J. Debus, Biochemistry, 2007, 46, 3151–3160 Search PubMed.
- N. Mizusawa, Y. Kimura, A. Ishii, T. Yamanari, S. Nakazawa, H. Teramoto and T. Ono, J. Biol. Chem., 2004, 279, 29622–29627 CrossRef CAS PubMed.
- K. Cser, B. A. Diner, P. J. Nixon and I. Vass, Photochem. Photobiol. Sci., 2005, 4, 1049–1054 Search PubMed.
- R. J. Debus, K. A. Campbell, J. M. Peloquin, D. P. Pham and R. D. Britt, Biochemistry, 2000, 39, 470–478 CrossRef CAS.
- M. Sugiura, F. Rappaport, W. Hillier, P. Dorlet, Y. Ohno, H. Hayashi and A. Boussac, Biochemistry, 2009, 48, 7856–7866 Search PubMed.
- T. A. Stich, G. J. Yeagle, R. J. Service, R. J. Debus and R. D. Britt, Biochemistry, 2011, 50, 7390–7404 CrossRef CAS PubMed.
- R. J. Service, J. Yano, P. L. Dilbeck, R. L. Burnap, W. Hillier and R. J. Debus, Biochemistry, 2013, 52, 8452–8464 Search PubMed.
- R. J. Service, J. Yano, I. McConnel, H. J. Hwang, D. Niks, R. Hille, T. Wydrzynski, R. L. Burnap, W. Hillier and R. J. Debus, Biochemistry, 2011, 50, 63–81 CrossRef CAS PubMed.
- R. J. Debus, K. A. Campbell, D. P. Pham, A.-M. Hays and R. D. Britt, Biochemistry, 2000, 39, 6275–6287 CrossRef CAS PubMed.
- I. D. Young, M. Ibrahim, R. Chatterjee, S. Gul, F. D. Fuller, S. Koroidov, A. S. Brewster, R. Tran, R. Alonso-Mori, T. Kroll, T. Michels-Clark, H. Laksmono, R. G. Sierra, C. A. Stan, R. Hussein, M. Zhang, L. Douthit, M. Kubin, C. de Lichtenberg, L. V. Pham, H. Nilsson, M. H. Cheah, D. Shevela, C. Saracini, M. A. Bean, I. Seuffert, D. Sokaras, T.-C. Weng, E. Pastor, C. Weninger, T. Fransson, L. Lassalle, P. Bräuer, P. Aller, P. T. Docker, B. Andi, A. M. Orville, J. M. Glownia, S. Nelson, M. Sikorski, D. Zhu, M. S. Hunter, T. J. Lane, A. Aquila, J. E. Koglin, J. Robinson, M. Liang, S. Boutet, A. Y. Lyubimov, M. Uervirojnangkoorn, N. W. Moriarty, D. Liebschner, P. V. Afonine, D. G. Waterman, G. Evans, P. Wernet, H. Dobbek, W. I. Weis, A. T. Brunger, P. H. Zwart, P. D. Adams, A. Zouni, J. Messinger, U. Bergmann, N. K. Sauter, J. Kern, V. K. Yachandra and J. Yano, Nature, 2016, 540, 453–457 Search PubMed.
- M. Suga, F. Akita, M. Sugahara, M. Kubo, Y. Nakajima, T. Nakane, K. Yamashita, Y. Umena, M. Nakabayashi, T. Yamane, T. Nakano, M. Suzuki, T. Masuda, S. Inoue, T. Kimura, T. Nomura, S. Yonekura, L.-J. Yu, T. Sakamoto, T. Motomura, J.-H. Chen, Y. Kato, T. Noguchi, K. Tono, Y. Joti, T. Kameshima, T. Hatsui, E. Nango, R. Tanaka, H. Naitow, Y. Matsuura, A. Yamashita, M. Yamamoto, O. Nureki, M. Yabashi, T. Ishikawa, S. Iwata and J.-R. Shen, Nature, 2017, 543, 131–135 CrossRef CAS PubMed.
- J. Kern, R. Chatterjee, I. D. Young, F. D. Fuller, L. Lassalle, M. Ibrahim, S. Gul, T. Fransson, A. S. Brewster, R. Alonso-Mori, R. Hussein, M. Zhang, L. Douthit, C. de Lichtenberg, M. H. Cheah, D. Shevela, J. Wersig, I. Seuffert, D. Sokaras, E. Pastor, C. Weninger, T. Kroll, R. G. Sierra, P. Aller, A. Butryn, A. M. Orville, M. Liang, A. Batyuk, J. E. Koglin, S. Carbajo, S. Boutet, N. W. Moriarty, J. M. Holton, H. Dobbek, P. D. Adams, U. Bergmann, N. K. Sauter, A. Zouni, J. Messinger, J. Yano and V. K. Yachandra, Nature, 2018, 563, 421–425 CrossRef CAS.
- M. Suga, F. Akita, K. Yamashita, Y. Nakajima, G. Ueno, H. Li, T. Yamane, K. Hirata, Y. Umena, S. Yonekura, L.-J. Yu, H. Murakami, T. Nomura, T. Kimura, M. Kubo, S. Baba, T. Kumasaka, K. Tono, M. Yabashi, H. Isobe, K. Yamaguchi, M. Yamamoto, H. Ago and J.-R. Shen, Science, 2019, 366, 334–338 CrossRef CAS PubMed.
- M. Ibrahim, T. Fransson, R. Chatterjee, M. H. Cheah, R. Hussein, L. Lassalle, K. Sutherlin, I. D. Young, F. D. Fuller, S. Gul, I.-S. Kim, P. S. Simon, C. de Lichtenberg, P. Chernev, I. Bogacz, C. C. Pham, A. M. Orville, N. Saichek, T. Northen, A. Batyuk, S. Carbajo, R. Alonso-Mori, K. Tono, S. Owada, A. Bhowmick, R. Bolotovsky, D. Mendez, N. W. Moriarty, J. M. Holton, H. Dobbek, A. S. Brewster, P. D. Adams, N. K. Sauter, U. Bergmann, A. Zouni, J. Messinger, J. Kern, V. K. Yachandra and J. Yano, Proc. Natl. Acad. Sci. U.S.A., 2020, 117, 12624–12635 CrossRef CAS PubMed.
- R. Hussein, M. Ibrahim, A. Bhowmick, P. S. Simon, R. Chatterjee, L. Lassalle, M. Doyle, I. Bogacz, I.-S. Kim, M. H. Cheah, S. Gul, C. De Lichtenberg, P. Chernev, C. C. Pham, I. D. Young, S. Carbajo, F. D. Fuller, R. Alonso-Mori, A. Batyuk, K. D. Sutherlin, A. S. Brewster, R. Bolotovsky, D. Mendez, J. M. Holton, N. W. Moriarty, P. D. Adams, U. Bergmann, N. K. Sauter, H. Dobbek, J. Messinger, A. Zouni, J. Kern, V. K. Yachandra and J. Yano, Nat. Commun., 2021, 12, 6531 CrossRef CAS.
- H. Li, Y. Nakajima, T. Nomura, M. Sugahara, S. Yonekura, S. K. Chan, T. Nakane, T. Yamane, Y. Umena, M. Suzuki, T. Matsuda, T. Motomura, H. Naitow, Y. Matsuura, T. Kimura, K. Tono, S. Owada, Y. Joti, R. Tanaka, E. Nango, F. Akita, M. Kubo, S. Iwata, J.-R. Shen and M. Suga, IUCrJ, 2021, 8, 431–443 CrossRef CAS PubMed.
- A. Bhowmick, R. Hussein, I. Bogacz, P. S. Simon, M. Ibrahim, R. Chatterjee, M. D. Doyle, M. H. Cheah, T. Fransson, P. Chernev, I.-S. Kim, H. Makita, M. Dasgupta, C. J. Kaminsky, M. Zhang, J. Gätcke, S. Haupt, I. I. Nangca, S. M. Keable, A. O. Aydin, K. Tono, S. Owada, L. B. Gee, F. D. Fuller, A. Batyuk, R. Alonso-Mori, J. M. Holton, D. W. Paley, N. W. Moriarty, F. Mamedov, P. D. Adams, A. S. Brewster, H. Dobbek, N. K. Sauter, U. Bergmann, A. Zouni, J. Messinger, J. Kern and J. Yano, Nature, 2023, 617, 629–636 Search PubMed.
- H. Li, Y. Nakajima, E. Nango, S. Owada, D. Yamada, K. Hashimoto, F. Luo, R. Tanaka, F. Akita, K. Kato, J. Kang, Y. Saitoh, S. Kishi, H. Yu, N. Matsubara, H. Fujii, M. Sugahara, M. Suzuki, T. Masuda, T. Kimura, T. N. Thao, S. Yonekura, L.-J. Yu, T. Tosha, K. Tono, Y. Joti, T. Hatsui, M. Yabashi, M. Kubo, S. Iwata, H. Isobe, K. Yamaguchi, M. Suga and J.-R. Shen, Nature, 2024, 626, 670–677 CrossRef CAS PubMed.
- I. Goodfellow, Y. Bengio and A. Courville, Deep Learning, MIT Press, Cambridge, MA, 2016 Search PubMed.
- K. Kawaguchi, Y. Bengio and L. Kaelbling, in Mathematical Aspects of Deep Learning, ed. P. Grohs and G. Kutyniok, Cambridge University Press, Cambridge, 2022, pp. 112–148 Search PubMed.
- P. E. M. Siegbahn, Biochim. Biophys. Acta, 2013, 1827, 1003–1019 Search PubMed.
- N. Cox, M. Retegan, F. Neese, D. A. Pantazis, A. Boussac and W. Lubitz, Science, 2014, 345, 804–808 CrossRef CAS PubMed.
- M. Retegan, V. Krewald, F. Mamedov, F. Neese, W. Lubitz, N. Cox and D. A. Pantazis, Chem. Sci., 2016, 7, 72–84 RSC.
- P. E. M. Siegbahn, Phys. Chem. Chem. Phys., 2018, 20, 22926–22931 RSC.
- A. Boussac, A. W. Rutherford and M. Sugiura, Biochim. Biophys. Acta, 2015, 1847, 576–586 CrossRef CAS PubMed.
- H. Isobe, M. Shoji, J.-R. Shen and K. Yamaguchi, Inorg. Chem., 2016, 55, 502–511 Search PubMed.
- H. Isobe, M. Shoji, T. Suzuki, J.-R. Shen and K. Yamaguchi, J. Chem. Theory Comput., 2019, 15, 2375–2391 Search PubMed.
- H. Isobe, M. Shoji, T. Suzuki, J.-R. Shen and K. Yamaguchi, J. Photochem. Photobiol., A, 2021, 405, 112905 Search PubMed.
- H. Isobe, M. Shoji, T. Suzuki, J.-R. Shen and K. Yamaguchi, J. Phys. Chem. B, 2022, 126, 7212–7228 CrossRef CAS PubMed.
- F. Rummel and P. J. O'Malley, J. Phys. Chem. B, 2022, 126, 8214–8221 CrossRef CAS PubMed.
- H. Isobe, M. Shoji, S. Yamanaka, Y. Umena, K. Kawakami, K. Kamiya, J.-R. Shen and K. Yamaguchi, Dalton Trans., 2012, 41, 13727–13740 RSC.
- D. A. Pantazis, W. Ames, N. Cox, W. Lubitz and F. Neese, Angew. Chem., Int. Ed., 2012, 51, 9935–9940 CrossRef CAS PubMed.
- D. Bovi, D. Narzi and L. Guidoni, Angew. Chem., Int. Ed., 2013, 52, 11744–11749 CrossRef CAS PubMed.
- M. Amin, Photosynth. Res., 2023, 156, 89–100 CrossRef CAS PubMed.
- M. Drosou, G. Comas-Vila, F. Neese, P. Salvador and D. A. Pantazis, J. Am. Chem. Soc., 2023, 145, 10604–10621 CrossRef CAS PubMed.
- V. Krewald, M. Retegan, N. Cox, J. Messinger, W. Lubitz, S. DeBeer, F. Neese and D. A. Pantazis, Chem. Sci., 2015, 6, 1676–1695 RSC.
- M. H. Cheah, M. Zhang, D. Shevela, F. Mamedov, A. Zouni and J. Messinger, Proc. Natl. Acad. Sci. U.S.A., 2020, 117, 141–145 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B:Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, M. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J.-L. Sonnenberg, D. W. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, T. Throssell, J. A. Montgomery, J. E. Peralta, F. Ogliaro, F. Bearpark, M. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, A. P. Burant, J. C. Iyengar, S. S. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. Martin, R. L. Morokuma, K. Farkas, O. Foresman, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS.
- W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
- M. Reiher, O. Salomon and B. A. Hess, Theor. Chem. Acc., 2001, 107, 48–55 Search PubMed.
- M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866–872 CrossRef CAS.
- M. Kaupp, P. v. R. Schleyer, H. Stoll and H. Preuss, J. Chem. Phys., 1991, 94, 1360–1366 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, I. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa and P. van Mulbregt, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and É. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- S. Tokui, K. Oono, S. Hido and J. Clayton, in Proc. Workshop on Machine Learning Systems (LearningSys) in the 29th Annual Conference on Neural Information Processing Systems, (NIPS), 2015 Search PubMed.
- T. Akiba, S. Sano, T. Yanase, T. Ohta and M. Koyama, arXiv, 2019, arXiv: 1907.10902 [cs.LG] Search PubMed.
- K.-A. Lê Cao and Z. Welham, Multivariate Data Integration Using R: Methods and Applications with the mixOmics Package, CRC Press, Boca Raton, FL, 2021 Search PubMed.
- A. Tanaka, Y. Fukushima and N. Kamiya, J. Am. Chem. Soc., 2017, 139, 1718–1721 CrossRef CAS PubMed.
- M. Suga, F. Akita, K. Hirata, G. Ueno, H. Murakami, Y. Nakajima, T. Shimizu, K. Yamashita, M. Yamamoto, H. Ago and J.-R. Shen, Nature, 2015, 517, 99–103 CrossRef CAS PubMed.
- S. Boucheron, G. Lugosi and P. Massart, Concentration Inequalities: A Nonasymptotic Theory of Independence, Oxford University Press, Oxford, 2013 Search PubMed.
- D. Narzi, G. Mattioli, D. Bovi and L. Guidoni, Chem.–Eur. J., 2017, 23, 6969–6973 CrossRef CAS PubMed.
- K. Miyagawa, T. Kawakami, H. Isobe, M. Shoji, S. Yamanaka, K. Nakatani, M. Okumura, T. Nakajima and K. Yamaguchi, Chem. Phys. Lett., 2019, 732, 136660 CrossRef CAS.
- M. Drosou, G. Zahariou and D. A. Pantazis, Angew. Chem., Int. Ed., 2021, 60, 13493–13499 CrossRef CAS PubMed.
- H. Hotelling, Biometrika, 1936, 28, 321–377 CrossRef.
- A. E. Hoerl and R. W. Kennard, Technometrics, 1970, 12, 55–67 CrossRef.
- H. D. Vinod, J. Econom., 1976, 4, 147–166 CrossRef.
- S. E. Leurgans, R. A. Moyeed and B. W. Silverman, J. R. Stat. Soc. B., 1993, 55, 725–740 CrossRef.
- Y. Shimada, H. Suzuki, T. Tsuchiya, T. Tomo, T. Noguchi and M. Mimuro, Biochemistry, 2009, 48, 6095–6103 Search PubMed.
- V. Nair and G. E. Hinton, in Proceedings of the 27th International Conference on Machine Learning, 2010, pp. 807–814 Search PubMed.
- M. Zhang, M. Bommer, R. Chatterjee, R. Hussein, J. Yano, H. Dau, J. Kern, H. Dobbek and A. Zouni, eLife, 2017, 6, e26933 CrossRef PubMed.
- M. Shoji, H. Isobe, S. Shigeta, T. Nakajima and K. Yamaguchi, J. Phys. Chem. B, 2018, 122, 6491–6502 CrossRef CAS PubMed.
- D. Narzi, M. Capone, D. Bovi and L. Guidoni, Chem.–Eur. J., 2018, 24, 10820–10828 CrossRef CAS PubMed.
- F. Allgower, A. P. Gamiz-Hernandez, A. W. Rutherford and V. R. Kaila, J. Am. Chem. Soc., 2022, 144, 7171–7180 CrossRef PubMed.
- X. Song and B. Wang, J. Chem. Theory Comput., 2023, 19, 2684–2696 Search PubMed.
- Y. Guo, L. He, Y. Ding, L. Kloo, D. A. Pantazis, J. Messinger and L. Sun, Nat. Commun., 2024, 15, 5982 CrossRef CAS.
- F. Rappaport, M. Blanchard-Desce and J. Lavergne, Biochim. Biophys. Acta, 1994, 1184, 178–192 CrossRef CAS.
- M. R. Razeghifrad and R. J. Pace, Biochemistry, 1999, 38, 1252–1257 Search PubMed.
- M. Haumann, P. Liebisch, C. Muller, M. Barra, M. Grabolle and H. Dau, Science, 2005, 310, 1019–1021 CrossRef CAS PubMed.
- A. Klauss, M. Haumann and H. Dau, Proc. Natl. Acad. Sci. U.S.A., 2012, 109, 16035–16040 CrossRef CAS PubMed.
- P. Greife, M. Schönborn, M. Capone, R. Assunção, D. Narzi, L. Guidoni and H. Dau, Nature, 2023, 617, 623 CrossRef CAS PubMed.
- T. Noguchi, J. Phys. Chem. B, 2024, 128, 1866–1875 CrossRef CAS PubMed.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122 CrossRef PubMed.
- M. Drosou and D. A. Pantazis, Chem.–Eur. J., 2021, 27, 12815–12825 CrossRef CAS PubMed.
- I. Zaharieva, H. Dau and M. Haumann, Biochemistry, 2016, 55, 6996–7004 CrossRef CAS PubMed.
- K. M. Davis, B. T. Sullivan, M. C. Palenik, L. Yan, V. Purohit, G. Robinson, I. Kosheleva, R. W. Henning, G. T. Seidler and Y. Pushkar, Phys. Rev. X, 2018, 8, 041014 CAS.
- H. Nilsson, L. Cournac, F. Rappaport, J. Messinger and J. Lavergne, Biochim. Biophys. Acta, 2016, 1857, 23–33 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sc02386f |
| This journal is © The Royal Society of Chemistry 2025 |

