Open Access Article
Open Access ArticlePrivileged metal cluster complexes†
Shiquan Lin‡
ac,
Dan Li‡b,
Dandan Zhangb,
Lijun Geng a,
Yuhan Jiaa,
Weizhe Wanga,
Longjiu Cheng
a,
Yuhan Jiaa,
Weizhe Wanga,
Longjiu Cheng *b,
Shiv N. Khanna
*b,
Shiv N. Khanna d and
Zhixun Luo
d and
Zhixun Luo *ac
*ac
aBeijing National Laboratory for Molecular Sciences (BNLMS), State Key Laboratory for Structural Chemistry of Unstable and Stable Species, Institute of Chemistry, Chinese Academy of Sciences, Beijing, 100190, China. E-mail: zxluo@iccas.ac.cn
bDepartment of Chemistry, Anhui University, Hefei, 230601, China. E-mail: clj@ustc.edu
cSchool of Chemistry, University of Chinese Academy of Sciences, Beijing, 100190, China
dDepartment of Physics, Virginia Commonwealth University, Richmond, VA 23284-2000, USA
First published on 27th May 2025
Abstract
Clusters are a prominent subject of interest in modern chemistry research, bridging atoms and materials or catalysts. Metal coordination and metal–metal bonding are crucial in determining the chemical structures and properties of metal clusters; however, formulating a universal principle for assessing their electronic activity remains challenging. Utilizing self-developed mass spectrometry, this study examines the gas-phase reactions of rhodium and platinum clusters with common ligand molecules in forming metal complexes. We find that the Rhn± (n = 1–35) and Ptn± (n = 3–20) clusters readily react with CO and NO to form highly-selective products of cluster complexes. This illustrates the size-dependent saturable effect of sequential coordination, which is rooted in cluster stability alongside concurrent electron delocalization and local bonding. We introduce a new electronic rule, termed the electronic “Aā” rule, to understand the adaptive balance of electron delocalization and averaged local bonding in stabilizing metal clusters, whether they are coordinated with ligands or not.
Introduction
Material innovations like metal complexes, metal–organic frameworks, and ligand-protected metal clusters illustrate how bonding principles shape the development of materials for a wide range of applications. The integration of chemical bonding theory with predictive modelling enables the rational design and creation of high-performance materials, advancing frontiers in nanotechnology, catalysis, chemo sensing, and beyond. The octet rule, or 8-electron rule, elucidates how atoms interact to attain a stable electron configuration by gaining, losing, or sharing electrons via chemical bonds, including multicentre-bonds and orbital hybridization. Similarly, the effective atomic number (EAN) rule, also known as the 18-electron rule, offers a crucial framework for understanding the stability of transition metal (TM) complexes.1–4 Expanding on these fundamental bonding principles, additional rules such as Lauher's rule and 9N-L rule,5,6 as well as Wade's rule derived from polyhedral skeletal electron pair theory,7,8 have been introduced to provide a rational basis for understanding the stability of polynuclear TM complexes. These electronic rules successfully explained the coordination and stability of bi-, tri-, and tetra-nuclear TM complexes by assuming full occupancy of their cluster valence molecular orbitals (CVMOs).9,10 For instance, Co4(CO)12 features a Td-symmetric Co4 core stabilized by twelve carbonyl ligands, yielding a total of 60 valence electrons allocated across 30 orbitals. However, challenges remain when applied to high-nuclearity complexes or core–shell metal clusters.11–13 A simple example is the trigonal bipyramidal complex [Ni5(CO)12]2− which contains 76 valence electrons but only 36 valence orbitals. This discrepancy becomes particularly evident when the metallic core exhibits multi-centre bonding or when ligands adopt bidentate or bridging coordination, which are common in ligand-protected metal clusters.14On the other hand, early studies have firmly established the jellium model to explain the electronic shell structures15–19 in metal clusters and superatoms.20–24 On this basis, Häkkinen and colleagues25 presented a perspective on coinage metal nanoclusters by emphasizing the delocalized valence electrons (n*) of a superatomic metal core, defined as n* = N − α − β, where N is the number of valence electrons from metal atoms, α denotes the number of electrons captured by electrophilic ligands, and β indicates the total charge carried by the cluster. This perspective elucidates the fundamental principles of electronic delocalization and the superatomic nature of metal clusters; nevertheless, it overlooks the role of local bonding.26 A more comprehensive electron-counting rule is needed, one that integrates both electron delocalization and local bonding, to better predict structures and deepen the understanding of cluster stability.27 However, the preparation of pure metal clusters and their selective conversion into cluster complexes remains challenging. The challenges stem from the stringent conditions required to form metal–metal bonds, as well as the high surface energy of subnano metals, which makes them susceptible to collision-induced dissociation and unwanted contamination.
In this work, we employed a custom-designed mass spectrometer to investigate the reactions of Rhn± (n = 1–35) and Ptn± (n = 3–20) clusters with CO and NO. Our findings show that both rhodium and platinum clusters exhibit high reactivity with CO and NO, forming highly-selective carbonyl and nitrosyl complexes indicative of saturable coordination. To elucidate the structural stability and bonding characteristics of the resulting dominant complexes Mn(CO)m± and Mn(NO)m± (M = Rh, Pt), we performed quantum chemistry calculations. The results reveal size-dependent ligand coordination and electron delocalization on metal clusters. Based on this, we propose an new electron rule to elucidate the adaptive balance of delocalized electrons and averaged local bonding, referred to as the electronic “Aā” rule. This rule highlights the self-adaptability of delocalized and localized electrons in stabilizing metal clusters of varying sizes.
Experimental and computational methods
The instrument leading to the findings in this study was described in detail elsewhere.28 In brief, a homemade reflection time-of-flight mass spectrometer (Re-TOFMS) is combined with a laser vaporization (LaVa) source together with a compact tube reactor (Φ = 6 mm, L = 60 mm). Rhn+ clusters were produced by laser ablation of a finely polished clean Rh disk (99.95% purity, Φ = 16 mm). A pulsed 532 nm laser (Nd:YAG) with an average energy of 15–35 mJ per pulse at a repetition rate of 10 Hz was used for the experiments. The pulsed laser was well focused onto the surface of the Rh target which was installed on a motor-driven sample holder capable of both translational and rotational movement. A tube nozzle (Φ = 1.35 mm, L = 35 mm) was installed at the outlet of the waiting room where the generated clusters were cooled by supersonic expansion under He buffer gas (99.999%) with a background pressure of 1.0 MPa. Both the buffer gas and reactant gas (0.1 MPa) were controlled by a pulse valve (10 Hz) respectively with the on-time at 150–250 μs (Series 9, General Valve).All the structures were fully relaxed using density functional theory (DFT) calculations at the PBE/def2tzvpp level of theory via the Gaussian 16 package.29–32 All energy calculations were corrected by zero-point vibrations, and frequency analyses were conducted to ensure that the structures at energy minima. Chemical bonding analyses were performed using the AdNDP method at the same level of theory, which enables an electron pair to delocalize over n atoms of the cluster. Molecular orbitals, nucleus-independent chemical shifts (NICS)33 and DOS were calculated by using the Multiwfn program.34 The PBE0 functional at the def2tzvpp level of theory was used to simulate photoelectron spectra.35 Molecular visualization was accomplished using the VMD software,36 and colouring of the structures was conducted using the VESTA software.37
Results and discussion
Fig. 1 presents the mass spectra of Ptn+ and Ptn− (n = 3–20) clusters in the absence and presence of varying doses of NO reactants. These Ptn± clusters were well controlled to exhibit a comparable size distribution centred at n = 11–13, and they exhibited comparable NO coordination reactions in the presence of small dose of NO reactants. However, when introducing sufficient NO reactants into the flow tube reactor, all the nascent Ptn± clusters react to form a highly selective coordination product for each. Specifically, the cationic Ptn+ clusters react to yield Pt3(NO)3+, Pt4(NO)4+, Pt5(NO)5+, Pt6(NO)6+, Pt7(NO)7+, Pt8(NO)8+, Pt9(NO)9+, Pt10(NO)9+, Pt11(NO)10+, Pt12(NO)11+, Pt13(NO)12+, etc. These products remain consistent even when the size distribution of the nascent clusters changes (Fig. S1–S4, ESI†), with a few exceptions for Pt4+ and Pt8,9+ which form Pt4(NO)4,5+, Pt8(NO)7,8+ and Pt9(NO)8,9+ respectively, likely due to the critical points of the transition from planar to three-dimensional structure, and to the core–shell structure of the metallic cores. Similarly, the anionic Ptn− clusters demonstrate comparable NO reactivity, exclusively generating Ptn(NO)n− (n ≤ 7) with a strict 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 metal-to-ligand ratio. This stoichiometric correspondence where each Pt atom coordinates one NO molecule mirrors the monolayer protection phenomenon observed in wet-chemically synthesized nanoclusters. This 1
1 metal-to-ligand ratio. This stoichiometric correspondence where each Pt atom coordinates one NO molecule mirrors the monolayer protection phenomenon observed in wet-chemically synthesized nanoclusters. This 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometric ratio in these Ptn(NO)n− clusters is reminiscent of the face-centered cubic (fcc) packing arrangement seen in AB-type ionic crystals for certain simple metal complexes, as well as NO adsorption on each Pt atom site of a Pt surface (Fig. S17, ESI†). Also, it bears similarity to the monolayer-protected metal clusters. Notably, the larger Ptn− clusters (n ≥ 8) adsorb one fewer NO molecule to form Ptn(NO)n−1−, which could be associated with the formation of core–shell structures.
1 stoichiometric ratio in these Ptn(NO)n− clusters is reminiscent of the face-centered cubic (fcc) packing arrangement seen in AB-type ionic crystals for certain simple metal complexes, as well as NO adsorption on each Pt atom site of a Pt surface (Fig. S17, ESI†). Also, it bears similarity to the monolayer-protected metal clusters. Notably, the larger Ptn− clusters (n ≥ 8) adsorb one fewer NO molecule to form Ptn(NO)n−1−, which could be associated with the formation of core–shell structures.
We have also analysed the reactions of Rhn± clusters with NO and CO gases to form complexes. Significantly, in the presence of sufficient CO reactant, the Rhn+ clusters exhibit remarkable reaction selectivity to form a predominant cluster complex for each, seen as Rh3(CO)9+, Rh4(CO)12+, Rh5(CO)14+, Rh6(CO)16+, Rh7(CO)17+, Rh8(CO)18+, Rh9(CO)19+, Rh10(CO)18+, Rh11(CO)19+, Rh12(CO)20+, and Rh13(CO)22+ (Fig. S5–S7, ESI†). Further increase of CO doses did not form complexes of a larger coordination number, indicating saturation effect of the CO coordination on the Rhn+ clusters. Although the observed Rh(CO)4+, Rh3(CO)9+, Rh4(CO)12+, and Rh5(CO)14+ species match previously reported carbonyl complexes,38–45 the larger clusters Rhn(CO)m+ (n ≥ 6)—including Rh6(CO)16+, Rh7(CO)17+, Rh8(CO)18+, Rh9(CO)19+, and Rh10(CO)18+—offer new insights into electron delocalization and multicentre bonding in polynuclear complexes. Similarly, the Rhn+ clusters in reacting with NO also form highly-selective metal cluster complexes Rhn(NO)m+ (Fig. S8 and S9, ESI†). It is important to note that in these cluster complexes, not all metal atoms achieve 18-electron coordination. Instead, the entire system reflects a dynamic coordination equilibrium, which is accompanied by electron delocalization.
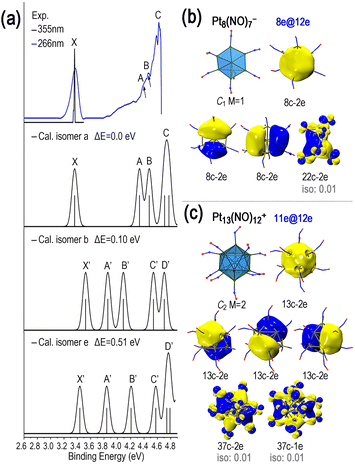
Using density functional theory (DFT) calculations, we determined the lowest energy structures of the Ptn(NO)m± clusters. For small Ptn± clusters (n < 8), favourable coordination of all metal atoms is achieved, allowing partial electron delocalization. We focused particularly on the Pt8(NO)7− cluster within a critical size. To validate its structure, we conducted photoelectron spectroscopy (PES) experiments using both 266 nm and 355 nm laser ionization, as shown in Fig. 2a. The simulated PES spectrum of the lowest energy structure (isomer a) aligns well with the experimental data, verifying the core–shell structure of Pt8(NO)7−. In contrast, the other low-lying isomers (isomers b and e) exhibit significantly different vertical ionization energy values (X′) and PES profiles. This supports the prediction that larger Ptn± clusters (n ≥ 8) adsorb one less NO molecule to form Ptn(NO)n−1± products simply due to their core–shell structures.
Fig. 2b illustrates the chemical bonding analysis for Pt8(NO)7− using adaptive natural density partitioning (AdNDP).46 The AdNDP analysis shows that each Pt atom (5d96s1) in the cluster possesses five d-type lone pairs (d10), indicating that the unpaired π* electron of the NO molecule is coupled with the 5d electrons of the Pt atom within symmetry-matching regulation. This behaviour is consistent across other Ptn(NO)m± cluster complexes, although the extent of delocalization depends on the number of Pt atoms and NO molecules. Notably, the Pt8(NO)7− cluster exhibit two types of 8c–2e bonds, displaying distinct superatomic characteristics of S and P orbitals. Furthermore, a multi-centre bonding (22c–2e) pattern is observed, indicating weak global electron delocalization across the entire Pt8(NO)7− cluster. Similarly, we conducted AdNDP analysis for the Pt13(NO)12± cluster, whose metallic core (Pt13) has been previously shown to adopt a core–shell structure.47,48 Notably, the Pt13(NO)12+ cluster also exhibit two types of 13c–2e bonds (Fig. 2c), reflecting superatomic S and P orbitals, along with weak global delocalization through a 37c–2e bond spanning the entire cluster.
The geometric structures and AdNDP analyses of the small Ptn(NO)m± clusters are presented in Fig. 3a and b (more details in Fig. S10–S39, ESI†). Among them, the lowest energy structures of Pt3(NO)3±, Pt4(NO)4±, Pt5(NO)5±, Pt6(NO)6±, and Pt7(NO)7± exhibit either planar or polyhedral geometry for their metallic cores, with each surface platinum atom bonded to a single terminal nitrosyl ligand. Interestingly, these Ptn(NO)m± clusters (n = 3–7) all demonstrate electron localization and delocalization, showing diverse multi-centre bonds such as 3c–2e, 4c–2e, 5c–2e, etc., as well as weak global delocalization involving all-atom multicentre bonds. The delocalized electrons not only form multicentre bonds but also contribute to superatomic features, resulting in balanced coordination and enhanced stability. What is more interesting is that each Pt atom on the surface of these Ptn(NO)m± clusters achieve a 12-electron coordination, which could be favoured for the six 5d·6s valence orbitals of Pt. This is reasonable as the 6p orbital is significantly higher in energy, with a substantial energy gap (>6 eV) between the 6 s and 6p orbital levels. The electron delocalization and localization in these clusters were further verified by analyses on density of states (DOS) and canonical molecular orbitals (Fig. S40–S48, ESI†).
For comparison, Fig. 3c illustrates the geometries and AdNDP analyses of the Rhn(NO)m+ (n = 1–6) clusters. These Rhn(NO)m+ clusters exhibit a variety of isomers (Fig. S49−S53, ESI†). Only the most stable ones are selected for bonding analysis (Fig. S54–S60, ESI†). The NO molecule contains an unpaired electron in its antibonding π* orbital, and this unpaired single electron can engage with the electrons of the Rh atom, facilitating a favourable d10 electron configuration. Among the Rhn(NO)m+ clusters, the larger ones (n ≥ 6) display pronounced electron delocalization, reflecting their superatomic nature; in comparison, the smaller clusters (n = 1–5) exhibit π-electron delocalization,49 with metal–metal bond lengths extended due to ligand interactions. Specifically, Rh(NO)3+ features a 6c–1e multi-centre bond associated with π delocalization, and there are 16 electrons (16e) contributed by the Rh atom and three NO ligands. The delocalized orbitals in these Rhn(NO)m+ primarily consist of antibonding π* orbitals of NO, resulting in full occupation of the five d-type lone pairs.
Comprehensive DFT calculations were also performed to analyse the structures and bonding characteristics of the Rhn(CO)m+ (n = 1–7) clusters (Fig. S61−S71, ESI†). Because of the primary distinction between carbonyl and nitrosyl complexes in the bonding and antibonding orbitals of the CO and NO molecules (Fig. S72, ESI†), all Rhn(CO)m+ species exhibit four d-type lone pairs, which differs from that of the Rhn(NO)m+ clusters. The lowest energy structures of Rh(CO)4+, Rh2(CO)7+, Rh3(CO)9+, Rh4(CO)12+, Rh5(CO)14+, Rh6(CO)16+, Rh7(CO)17+, and Rh8(CO)18+ reveal that carbonyl ligands bind to Rh atoms through two distinct modes: bridging and terminal. Previous studies have unveiled the stability of Rh(CO)4+ as a stable 16e Rh-complex with a planar tetragonal configuration.50,51 This also aligns with the aforementioned 16e-stability of Rh(NO)3+.
For these polynuclear complexes, the cluster valence electrons are distributed across the entire cluster, enabling the formation of multicentre bonds. For example, Rh3(CO)9+ features a 3c–2e bond, with each Rh atom attaining 14 electrons through covalent bonds and coordination interaction. Likewise, Rh2(CO)7+ exhibits a 6c–1e bond derived from the d orbitals of Rh atoms and a π* antibonding orbital of CO. The Rh4(CO)12+ and Rh5(CO)14+ species also demonstrate multi-centre bonding defined by orbital hybridization; while Rh6(CO)16+ adopts an octahedral Rh6 core, with multicentre bonds reflecting electron delocalization and aromaticity (Fig. S73 and S74, ESI†). We have also studied the anionic Rhn(CO)m− systems (Fig. S75–S81, ESI†), which find similar structures and AdNDP patterns pertaining to multicenter-bonding and electron delocalization especially for n ≥ 6. Additionally, the DOSs and orbital analyses align with the results of the AdNDP analysis (Figs. S82–S84, ESI†).
The formation of predominant carbonyl and nitrosyl complexes motivated us to further study the high selectivity of NO and CO coordination with Pt and Rh clusters. Among them, nitrosyl complexes exhibit significant electron delocalization due to the involvement of half-filled antibonding π* orbitals along the molecular axis. In contrast, the π* orbitals of CO remain vacant, facilitating backdonation from the metal to the CO ligands and promoting favourable local coordination.10 Considering that these cluster complexes exhibit delocalized electrons and distinct local coordination preferences, we propose the electronic “A@ā” or “Aā” rule. This rule integrates adaptive delocalized electrons (A) and localized electrons on average (ā) to assess the stability of metal clusters. In this “Aā” rule, the total number of valence electrons (NCVE) for a metal cluster complex is determined by the sum of delocalized and localized valence electrons, i.e.,
| NCVE =A + ā·n′ +c | (1) |
| Rhn(CO)m+ | CVMO | 9N-L | CVE | Aā | Rhn(NO)m+ | CVMO | 9N-L | CVE | Aā |
|---|---|---|---|---|---|---|---|---|---|
| a CVE is the total number of cluster valence electrons; CVMO is the number of cluster valence molecular orbitals; 9N-L denotes the estimated quantity of cluster valence molecular orbitals, excluding the count of relative antibonding orbitals associated with the polyhedral skeleton edges of metal–metal bonds; “Aā” values relate to the delocalized electrons (A) and averaged local electrons (ā) for surface metal atoms. | |||||||||
| Rh(CO)4+ | 9 | 9 | 16e | 16e | Rh(NO)3+ | 9 | 9 | 17e | 1e@16e |
| Rh2(CO)7+ | 17 | 17 | 31e | 1e@15e | Rh2(NO)5+ | 17 | 17 | 32e | 2e@15e |
| Rh3(CO)9+ | 24 | 24 | 44e | 2e@14e | Rh3(NO)6+ | 24 | 24 | 44e | 2e@14e |
| Rh4(CO)12+ | 30 | 30 | 59e | 3e@14e | Rh4(NO)8+ | 30 | 30 | 59e | 3e@14e |
| Rh5(CO)14+ | 36 | 36 | 72e | 4e@14e | Rh5(NO)9+ | 36 | 36 | 71e | 3e@14e |
| Rh6(CO)16+ | 43 | 42 | 85e | 5e@14e | Rh6(NO)9+ | 43 | 42 | 80e | 2e@13e |
| Ptn(NO)m+ | CVMO | 9N-L | CVE | Aā | Ptn(NO)m− | CVMO | 9N-L | CVE | Aā |
|---|---|---|---|---|---|---|---|---|---|
| Pt3(NO)3+ | 24 | 24 | 38e | 2e@12e | Pt3(NO)3− | 24 | 24 | 40e | 4e@12e |
| Pt4(NO)4+ | 30 | 30 | 51e | 3e@12e | Pt4(NO)4− | 30 | 30 | 53e | 5e@12e |
| Pt5(NO)5+ | 36 | 36 | 64e | 4e@12e | Pt5(NO)5− | 36 | 36 | 66e | 6e@12e |
| Pt6(NO)6+ | 43 | 42 | 77e | 5e@12e | Pt6(NO)6− | 43 | 42 | 79e | 7e@12e |
| Pt7(NO)7+ | 49 | 48 | 90e | 6e@12e | Pt7(NO)7− | 49 | 48 | 92e | 8e@12e |
| Pt8(NO)8+ | — | 57 | 103e | 8e@12e | Pt8(NO)7− | — | 57 | 102e | 8e@12e |
| Pt13(NO)12+ | — | 82 | 165e | 11e@12e | Pt13(NO)12− | — | 82 | 167e | 13e@12e |
| Run(CO)m+ | CVMO | 9N-L | CVE | Aā | Con(CO)m+ | CVMO | 9N-L | CVE | Aā |
|---|---|---|---|---|---|---|---|---|---|
| Ru(CO)5+ | 9 | 9 | 17e | 17e | Co(CO)5+ | 9 | 9 | 18e | 18e |
| Ru2(CO)9+ | 17 | 17 | 33e | 2e@16e | Co2(CO)8+ | 17 | 17 | 33e | 1e@16e |
| Ru3(CO)12+ | 24 | 24 | 47e | 5e@14e | Co3(CO)10+ | 24 | 24 | 46e | 2e@15e |
| Ru4(CO)14+ | 30 | 30 | 59e | 7e@13e | Co4(CO)12+ | 30 | 30 | 59e | 3e@14e |
| Ru5(CO)16+ | 36 | 36 | 71e | 9e@12e | Co5(CO)14+ | 36 | 36 | 72e | 4e@14e |
According to the “Aā” rule, we have examined the electronic configurations and structure stability of the Con(CO)m+ and Run(CO)m+ clusters in previous investigations,52–54 as well as a recently reported Fe6C(CO)16 cluster,55 all of which adhere to the xe@ne regulation (Fig. S85−S89, ESI†). Considering the number of ligands that act as monodentate (μ1, 2e or 3e donor, including the single-site, bridge-site and hollow-site modes) and bidentate (μ2, e.g., 4e donor) in a MnXm (M, metal; X, ligand) cluster to be represented by x and y respectively, the relationship for stable cluster complexes (e.g., CO) can be expressed as:
 | (2) |
Conclusions
To summarize, we report an investigation in exploring and understanding the privileged metal cluster complexes. We systematically studied the gas-phase reactivity of Rhn± (n = 1–35) and Ptn± (n = 3–20) clusters with CO and NO. Interestingly, these metal clusters exhibit remarkable selectivity in the NO- and CO-coordination reactions when exposed to sufficient gas reactants, leading to the formation of saturable carbonyl and nitrosyl complexes. Typical examples include a series of Ptn(NO)n± (n = 3–8) and Ptn(NO)n-1± (n = 8–14) products, as well as several Rh cluster complexes such as Rh4(CO)12+, Rh4(NO)8+; Rh5(CO)14+, Rh5(NO)9+; Rh6(CO)16+, Rh6(NO)9+; Rh7(CO)17+, and Rh7(NO)10+. Notably, the NO complexes favour significant electron delocalization pertaining to the involvement of half-filled antibonding π* orbitals along the NO molecule axis. In contrast, the π* orbitals of CO are vacant, which facilitates metal-to-ligand backdonation and reinforces local coordination. We introduce an electronic “Aā” rule to evaluate the structural stability of metal cluster complexes, clarifying adaptive balance of delocalized electrons and averaged local bonding.Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
The manuscript was written through contributions of all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Prof. Gernot Frenking in Philipps-Universität Marburg, Prof. Jinlong Yang in University of Science and Technology of China, Prof. Mingfei Zhou and GuanJun Wang in Fudan University, for their helpful discussions. This work was supported by the National Natural Science Fundation of China (Grant No. 92261113 and 22272180), CAS Project for Young Scientists in Basic Research (Grant No. YSBR-050), CAS Key Research Program of Frontier Sciences (QYZDBSSW-SLH024). SNK was supported by a grant from US Department of Energy (DOE) under the award DE-SC0006420.Notes and references
- G. Frenking and N. Fröhlich, Chem. Rev., 2000, 100, 717–774 CrossRef CAS PubMed.
- L. Andrews and A. Citra, Chem. Rev., 2002, 102, 885–912 CrossRef CAS PubMed.
- X. Jiang, Z. Xiao, W. Zhong and X. Liu, Coord. Chem. Rev., 2021, 429, 213634 CrossRef CAS.
- A. Fielicke, Chem. Soc. Rev., 2023, 52, 3778–3841 RSC.
- J. W. Lauher, J. Am. Chem. Soc., 1978, 100, 5305–5315 CrossRef CAS.
- A. Tang and S. Li, Chin. Sci. Bull., 1982, 28, 25–27 CrossRef.
- F. Lips and S. Dehnen, Angew. Chem., Int. Ed., 2011, 50, 955–959 CrossRef CAS PubMed.
- D. M. P. Mingos, 50th Anniversary of Electron Counting Paradigms for Polyhedral Molecules: Bonding in Clusters, Intermetallics and Intermetalloids, University of Oxford, Oxford, UK, 2021 Search PubMed.
- R. Bau, M. H. Drabnis, L. Garlaschelli, W. T. Klooster, Z. W. Xie, T. F. Koetzle and S. Martinengo, Science, 1997, 275, 1099–1102 CrossRef CAS PubMed.
- X. Wu, L. Zhao, J. Jin, S. Pan, W. Li, X. Jin, G. Wang, M. Zhou and G. Frenking, Science, 2018, 361, 912–916 CrossRef CAS PubMed.
- E. Kapiloff and K. M. Ervin, J. Phys. Chem. A, 1997, 101, 8460–8469 CrossRef CAS.
- E. K. Parks, K. P. Kerns and S. J. Riley, J. Chem. Phys., 2000, 112, 3384–3393 CrossRef CAS.
- Z. Lin, Chin. J. Struct. Chem., 2024, 43, 100254 CAS.
- G. Pacchioni and N. Roesch, Inorg. Chem., 1990, 29, 2901–2908 CrossRef CAS.
- I. Katakuse, T. Ichihara, Y. Fujita, T. Matsuo, T. Sakurai and H. Matsuda, Int. J. Mass Spectrom. Ion Processes, 1985, 67, 229–236 CrossRef CAS.
- W. Ekardt, Phys. Rev. Lett., 1984, 52, 1925–1928 CrossRef CAS.
- W. D. Knight, K. Clemenger, W. A. De Heer, W. A. Saunders, M. Y. Chou and M. L. Cohen, Phys. Rev. Lett., 1984, 52, 2141–2143 CrossRef CAS.
- W. A. De Heer, Rev. Mod. Phys., 1993, 65, 611–676 CrossRef CAS.
- M. Brack, Rev. Mod. Phys., 1993, 65, 677–732 CrossRef CAS.
- X. Zhang, Y. Wang, H. Wang, A. Lim, G. Gantefoer, K. H. Bowen, J. U. Reveles and S. N. Khanna, J. Am. Chem. Soc., 2013, 135, 4856–4861 CrossRef CAS PubMed.
- Z. Luo and A. W. Castleman Jr, Acc. Chem. Res., 2014, 47, 2931–2940 CrossRef CAS PubMed.
- A. C. Reber and S. N. Khanna, Acc. Chem. Res., 2017, 50, 255–263 CrossRef CAS PubMed.
- E. A. Doud, A. Voevodin, T. J. Hochuli, A. M. Champsaur, C. Nuckolls and X. Roy, Nat. Rev. Mater., 2020, 5, 371–387 CrossRef.
- P. Jena, H. Fang and Q. Sun, in Superatoms: Principles, Synthesis and Applications, 2021, pp. 15–51 Search PubMed.
- M. Walter, J. Akola, O. Lopez-Acevedo, P. D. Jadzinsky, G. Calero, C. J. Ackerson, R. L. Whetten, H. Groenbeck and H. Hakkinen, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 9157–9162 CrossRef CAS PubMed.
- Z. Luo, A. C. Reber, M. Jia, W. H. Blades, S. N. Khanna and A. W. Castleman Jr, Chem. Sci., 2016, 7, 3067–3074 RSC.
- Z. Luo, A. W. Castleman Jr and S. N. Khanna, Chem. Rev., 2016, 116, 14456–14492 CrossRef CAS PubMed.
- H. Zhang, H. Wu, Y. Jia, L. Geng, Z. Luo, H. Fu and J. Yao, Rev. Sci. Instrum., 2019, 90, 073101 CrossRef PubMed.
- J. Paier, R. Hirschl, M. Marsman and G. Kresse, J. Chem. Phys., 2005, 122, 234102 CrossRef PubMed.
- W. Florian and A. Reinhart, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. B.01, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- Z. F. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. V. Schleyer, Chem. Rev., 2005, 105, 3842–3888 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graph., 1996, 14, 33–38 CrossRef CAS PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- C. Chi, J. Cui, Z. H. Li, X. Xing, G. Wang and M. Zhou, Chem. Sci., 2012, 3, 1698–1706 RSC.
- G. Wang, J. Cui, C. Chi, X. Zhou, Z. H. Li, X. Xing and M. Zhou, Chem. Sci., 2012, 3, 3272–3279 RSC.
- J. Cui, X. Zhou, G. Wang, C. Chi, Z. H. Li and M. Zhou, J. Phys. Chem. A, 2014, 118, 2719–2727 CrossRef CAS PubMed.
- P. Ferrari, J. Vanbuel, N. M. Tam, M. T. Nguyen, S. Gewinner, W. Schollkopf, A. Fielicke and E. Janssens, Chem.–Eur. J., 2017, 23, 4120–4127 CrossRef CAS PubMed.
- A. Fielicke, G. Von Helden, G. Meijer, B. Simard, S. Dénommée and D. M. Rayner, J. Am. Chem. Soc., 2003, 125, 11184–11185 CrossRef CAS PubMed.
- A. Fielicke, G. Von Helden, G. Meijer, D. B. Pedersen, B. Simard and D. M. Rayner, J. Am. Chem. Soc., 2005, 127, 8416–8423 CrossRef CAS PubMed.
- I. Swart, F. M. F. D. Groot, B. M. Weckhuysen, D. M. Rayner, G. Meijer and A. Fielicke, J. Am. Chem. Soc., 2008, 130, 2126–2127 CrossRef CAS PubMed.
- Q. Xu, S. Inoue, Y. Souma and H. Nakatani, J. Organomet. Chem., 2000, 606, 147–150 CrossRef CAS.
- D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217 RSC.
- N. Watari and S. Ohnishi, J. Chem. Phys., 1997, 106, 7531–7540 CrossRef CAS.
- T. Imaoka, H. Kitazawa, W.-J. Chun, S. Omura, K. Albrecht and K. Yamamoto, J. Am. Chem. Soc., 2013, 135, 13089–13095 CrossRef CAS PubMed.
- Y. Gao, X. Lei, R. Cheng, S. Lin and Z. Luo, Phys. Chem. Chem. Phys., 2024, 26, 28019–28024 RSC.
- A. D. Brathwaite, H. L. Abbott-Lyon and M. A. Duncan, J. Phys. Chem. A, 2016, 120, 7659–7670 CrossRef CAS PubMed.
- R. Crabtree, The Organometallic Chemistry of the Transition Metals, John Wiely & Sons Inc., Hoboken, New Jersey, 2001 Search PubMed.
- S. Fedrigo, T. L. Haslett and M. Moskovits, Chem. Phys. Lett., 1999, 307, 333–338 CrossRef CAS.
- K. P. Kerns, E. K. Parks and S. J. Riley, J. Chem. Phys., 2000, 112, 3394–3407 CrossRef CAS.
- D. Yubero Valdivielso, C. Kerpal, W. Schollkopf, G. Meijer and A. Fielicke, Dalton Trans., 2023, 52, 9929–9939 RSC.
- C. R. Cobb, R. K. Ngo, E. J. Dick, V. M. Lynch and M. J. Rose, Chem. Sci., 2024, 15, 11455–11471 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sc02924d |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |