Unusual differential cross sections for the H + D₂O → D + HOD exchange reaction induced by the C_3V transition state and quantum interference

Abstract

Previous experimental and theoretical studies have shown that direct reactive systems typically exhibit backward-peaked differential cross sections (DCS) at relatively low collision energies, while complex-forming reactive systems tend to display forward-backward symmetric DCS. Is this a universal phenomenon in all direct reactions, especially those proceeding through non-collinear transition states? In this work, we developed the quantum wave packet method to calculate the full-dimensional state-to-state DCSs for the title exchange reaction with D₂O in the ground rovibrational state on a highly accurate neural network potential energy surface. For the first time, we obtain a sideward-scattered angle distribution just above the threshold, which directly reflects the C_3V transition state geometry of this reaction. As the collision energy increases, the DCS broadens and undergoes a series of notable changes, culminating in the dominance of backward scattering at E_c = 1.4 eV, accompanied by an early-sideward scattering peak. Although trajectory analysis can explain most of the DCS variations, significant differences persist between the quantum and quasiclassical trajectory DCSs, arising from quantum interference between the contributions from low and high partial waves. Additionally, the collision energy dependent DCSs at the scattering angle of 107° exhibit two clear step-like features around E_c = 0.91 and 1.16 eV, which can be attributed to the shape resonance states trapped in the C_3V well. In the energy region considered here, the majority of the available energy goes into the translational motion of the products, and the reaction exhibits low vibrational mode-specific behavior.

---

The state-to-state differential cross sections (DCSs) are reactant and product fully quantum state-resolved quantity, characterizing the scattering angle distribution of the reaction. They provide the most intuitive reflection of the reaction mechanism and are therefore the fundamental goal of both experimental and theoretical studies in chemical reaction dynamics. According to previous experimental and theoretical studies, the DCSs for a direct reactive system are backward peaked at relatively low collision energies, as observed in abstract reactions such as H + H₂, H + H₂O, and H + CH₄,^1–3 as well as the H + HCl and H + HBr exchange reactions.^4,5 As the collision energy increases, the peak width broadens, or the peak gradually shifts to a smaller angle. The situation becomes complicated in hydrogen abstraction reactions involving the F atom, where the HF vibrational excited adiabatic potential wells in the post-barrier region support dynamical resonances that can affect the product scattering behavior.^6–13 Moreover, for complex-forming reactive systems dominated by barrierless reaction pathways through deep wells, the DCS is typically forward–backward symmetric due to the long-lived reaction intermediates, such as those in the insertion reactions of O(¹D), C(¹D), and S(¹D) with the ground state H₂ molecule,^14,15 and in the H + O₂ and O(¹D) + CO₂ reactions.^16–18 Nonstatistical effects have also been observed in many complex-forming reactions, stemming from the relatively short lifetime of the reaction intermediate.^{14,16,19–24}

However, we wonder: are the DCSs of the direct reactions always backward peaked at low collision energies in all cases, especially in reactions with non-collinear transition states? The experiments and quasiclassical trajectory (QCT) studies of the oxygen isotope exchange reaction O(³P) + CO₂ have provided some clues; however, the energies they studied were so high that they still led to backward scattering.²⁵ The H + H₂O exchange reaction and its isotopic analogue, which features a saddle point close to a C_3V geometry, present another opportunity for investigation.

The H + H₂O reaction is the prototype for tetra-atomic reactions, in much the same way that the H + H₂ reaction served as the prototype for triatomics. Theoretically, because three of the four atoms are hydrogens, the system is an ideal candidate for high quality ab initio calculations of a PES, as well as for accurate quantum reactive scattering calculations. Our group has calculated the fully converged DCS for the abstract channel H + H₂O → H₂ + OH and its isotopic analogue for both the initial ground and vibrational excited states.^2,26,27 However, studies of the exchange channel have been limited to the total cross sections for an extended period. The integral cross sections (ICS) of the H + D₂O → D + HOD reaction were first reported 25 years ago, in which the reaction probabilities were calculated with one OD bond in the D₂O reactant treated as a spectator bond, and under the centrifugal sudden (CS) approximation for total angular momentum J > 0.²⁸ It was later demonstrated that the CS approximation was inadequate for the H + H₂O reaction.²⁹ And although the spectator bond assumption works well for the H + H₂O → H₂ + OH abstraction reaction, both OH bonds should be treated as reactive bonds in order to accurately investigate the exchange process, due to the C_3V saddle point.³⁰ In 2012, a full-dimensional quantum dynamics study for the H + D₂O → D + HOD reaction was presented without any dynamical approximations. The exact coupled-channel (CC) ICSs agree well with the experimental results and show a distinct step-like feature just above the threshold, which provides the first evidence for a shape resonance in this reaction.³¹ In 2016, Zhao et al. performed a state-to-state quantum dynamics study for the H′ + H₂O → H + H′OH reaction using the reactant-coordinate-based (RCB) method, but it was limited to total angular momentum J = 0.³²

Here, we report the full-dimensional (6D) DCS for the H + D₂O → D + HOD exchange reaction. To the best of our knowledge, this is the first quantum DCS for a polyatomic exchange reaction, although the state–state quantum dynamics calculations have been performed on many polyatomic reactions, with the development of both the initial state-selected^2,32–38 and transition-state^39–41 time-dependent wave packet (TDWP) methods. We observe a sideward-scattered angle distribution just above the threshold, which directly reflects the C_3V transition state geometry of this reaction. Moreover, the quantum interference effects are responsible for the significant difference between quantum mechanical (QM) and quasi-classical trajectory (QCT) DCS. Additionally, the shape resonances in this reaction lead to distinct step-like features in the collision-energy-dependent DCS at the scattering angle of 107°.

We utilized the multistep reactant-product-decoupling (MRPD) method^33,34 to carry out the full-dimensional state-to-state quantum calculation on the CXZ potential energy surface (PES),⁴² which is the most accurate and smooth PES available for the OH₃ reaction system, constructed by using the neural network (NN) method. To converge DCSs for collision energies up to 1.5 eV, we calculate state-to-state reaction probabilities for all total angular momenta J up to 20. For details of the numerical parameters, please refer to the ESI.† It should be noted that both OD bonds in the D₂O reactant were treated as reactive in our calculations; that is, they were fully vibrationally excited in the interaction region. Moreover, the dividing surface used to extract the S-matrix elements is placed far enough in the product asymptotic region, where the two exchange channels are fully separated. Since the two D + HOD channels are equivalent, the reaction probabilities and cross sections presented in this study correspond to a single D exchange and should be doubled when compared to the experimental results.

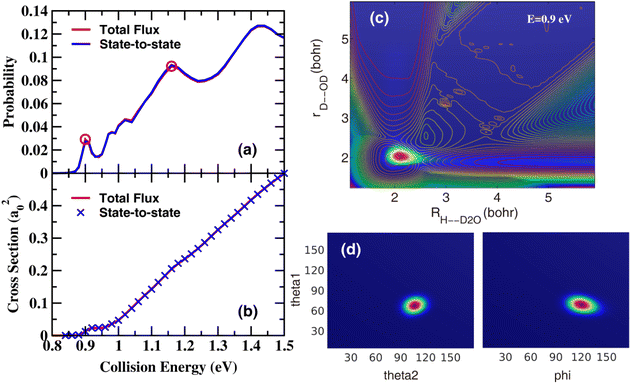
Fig. 1(a) and (b) shows the total reaction probabilities for J = 0 and ICSs as a function of collision energy on the CXZ PES from the MRPD state-to-state calculations, compared with those obtained from the initial state selected wave packet (ISSWP) approach using only the reactant Jacobi coordinates. As can be seen, the agreement between these two results is excellent in the entire energy region considered, indicating the RPD partition of the wave function, as well as the continuous propagation, is highly accurate. The reaction probabilities exhibit a sharp peak just above the threshold, which remains as a clear step-like feature in the ICS, along with several broad peaks at higher energies that are nearly washed out in the ICS.

Fig. 1 (a) Total reaction probabilities for J = 0 and (b) ICS for the title reaction on the CXZ PES obtained from the MRPD state-to-state calculations, in comparison with those obtained using the ISSWP approach. (c) Reactive scattering wave functions at the collision energy of 0.9 eV in the two Jacobi coordinates R_H-D2O and r_D-OD with other coordinates integrated. The contour lines are the corresponding 2D PESs along R_H-D2O and r_D-OD with other coordinates optimized. (d) Reactive scattering wave in the angle coordinates with R, r₁, and r₂ fixed at the peak position.

Fig. 1(c) displays the two-dimensional contour of the J = 0 scattering wave functions at the collision energy of 0.9 eV—the position of the sharp peak—obtained by Fourier transformation of the time-dependent (TD) wave functions after 4000 a.u. of propagation time. It can be seen that the scattering wave functions are localized in the C_3V well along the reaction coordinate. Examination of the wave function in the bending and torsion degrees of freedom, shown in Fig. 1(d), reveals no nodal structure. Furthermore, the Argand diagram for the ground state product, presented in Fig. S2,† shows a continuous counterclockwise motion without any kink. So the peak at 0.9 eV arises from a shape resonance, corresponding to a quasibound state trapped in the C_3V well—formed by the topography of the PES—on the ground-state vibrationally adiabatic potential (VAP), which decays into products by tunneling through the barrier. Fig. S3† shows the scattering wave functions at the collision energy of 1.16 eV, which are also localized in the C_3V well, with clear nodes along the θ₁ and φ coordinates. So the broad peaks at higher energies originate from shape resonance states supported by the C_3V well on bending/torsion excited VAP.

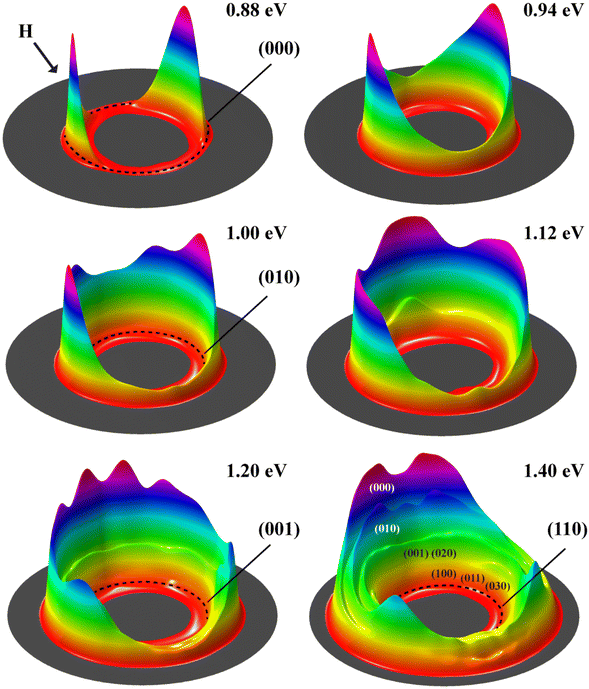
Fig. 2 shows the DCSs at six collision energies, in terms of surface plots for the product translational energy and angle distributions for the reaction. The scattering angle is defined as the angle between the direction of the incoming H atom and the outgoing direction of the HOD product molecule. Unlike other direct reactions previously studied, the most intriguing observation in the title reaction is the sideward scattered DCS at the lowest energy of 0.88 eV, which peaked at 109° with a half-maximum width of 45°. As the collision energy increases, the DCS broadens, undergoing a series of remarkable changes and eventually becoming dominated by backward scattering at E_c = 1.4 eV, accompanied by an early-sideward scattering peak. Additionally, Fig. 2 provides an overview of the product vibrational state distributions. As shown, almost all HOD products populate in the (000) state below E_c = 1.0 eV. At E_c = 1.12 eV, the population of the (010) state increases considerably, although the (000) state still dominates the distribution. At E_c = 1.4 eV, the vibrational distribution broadens further. In addition to some populations in the first OD stretching (001) and (020) states, a few populations are also observed in states with excitation energy corresponding to the first OH stretching (100), as well as the (011) and (030) levels. The vibrational energy levels of the HOD, along with the collision energies at which they become populated, are summarized in Table S1.†

Fig. 2 Surface plots for the product translational energy and angle distributions for the title reaction at the collision energy of 0.88, 0.94, 1.00, 1.12, 1.20, and 1.40 eV. The forward scattering direction for HOD corresponds to the direction of the incoming H atom. Dashed circles represent the maximum translational energies of the products in the indicated HOD vibrational states, which are labeled by (n₁, n₂, n₃), where n₁ is the quantum number for the OH stretching mode, n₂ is for the bending mode, and n₃ is for the OD stretching mode.

To quantitatively examine the variation of angle distribution with collision energy, we present the total DCSs, summed over all HOD rovibrational states, at a series of energies in Fig. 3. From 0.88 to 1.0 eV, the angular distribution broadens, with the peak shifting to a smaller angle. Meanwhile, the backward scattering components increase substantially, and the forward components also rise slightly. Subsequently, part of sideward scattering shifts toward the forward direction, while another part moves toward the backward direction, resulting in a flattening of the sideward peak at E_c = 1.12 eV. Between 1.16 and 1.2 eV, the sideward scattering component near 95° remains unchanged, while the forward- and backward-shifted components continue to grow, resulting in a concave shape in the sideward DCS. At collision energy above 1.2 eV, the backward scattered products, arising from two distinct sources, gradually become dominant. The peak position of early-sideward scattering shifts to 59° at E_c = 1.4 eV.

Fig. 3 Total DCSs, summed over all HOD rovibrational states, for collision energies from 0.88 to 1.0 eV (a); from 1.0 to 1.2 eV (b); and from 1.2 to 1.4 eV (c).

To analyze the reaction mechanism, we also performed the QCT calculations on the CXZ PES. The details of QCT methodology are described in the ESI.† Fig. 4 compares the QM and QCT total DCSs at the collision energies of 0.90, 1.00, 1.20, and 1.40 eV. At 0.9 eV, the two scattering angle distributions are quite similar, both peaking near 107°. As the collision energy increases, the QCT DCS also broaden and develop pronounced backward scattering components. However, the QM and QCT scattering angle distributions show significant differences at higher collision energies. It can be seen that sideward scattering remains dominant in the QCT DCS at 1.2 and 1.4 eV, although the peak position shifts to 130° at 1.4 eV. Notably, the QCT DCSs do not reproduce the oscillatory structures observed in the QM results.

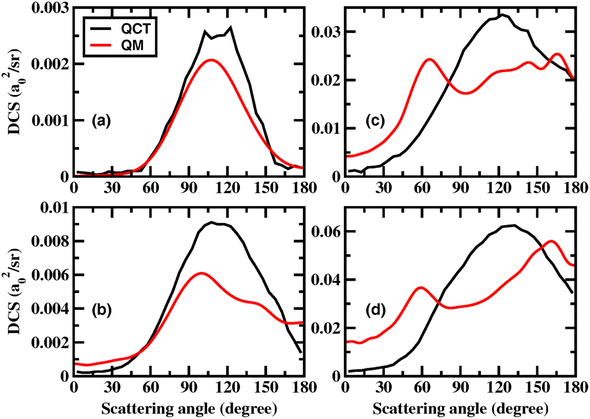Fig. 4 Total DCSs at the collision energy of (a) 0.90, (b) 1.00, (c) 1.20, and (d) 1.40 eV obtained by both QM and QCT calculations.

Fig. 5(a) and (b) show the QCT and QM deflection functions, which reveal the correlation between the total angular momentum J (or the impact parameter) and the scattering angle, for all product rovibrational states at E_c = 1.2 eV. To better correspond with the trajectories, the functions are presented without multiplication by sin θ. The QM generalized deflection function (GDF), which is additive over J and contains coherences between different values of J, was proposed by Prof. Jambrinato and Prof. Aoiz as⁴³

K is the projection of J on the product body-fixed z axis. Unlike the typical band-shaped profile of a direct reaction (where low J corresponds to backward scattering and high J to forward scattering), the classical deflection function for the title reaction shows a distinctive heart-shaped pattern. The initial sideward scattering peak is correlated with low J, while the backward and early-sideward scattering components are correlated with high J. The QM GDFs closely resemble their classical counterparts, indicating that most variations in the QM DCS can be accounted for by the trajectories.

Fig. 5 The QCT (a) and QM (b) deflection functions (not weighted by sin θ) for all the product rovibrational states at the collision energy of 1.20 eV. (c–e) The comparisons between the partially summed QM DCSs and partial QM deflection functions.

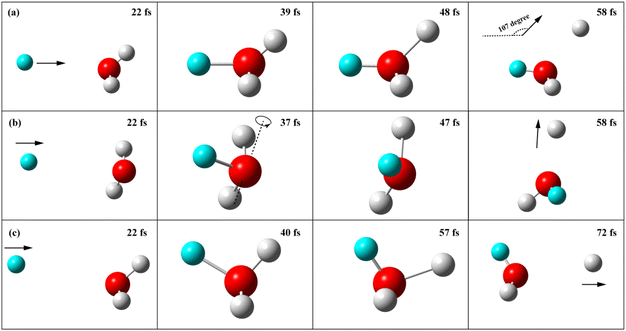
Analysis of the reactive trajectories at E_c = 1.2 eV revealed the reaction mechanisms during the collision process. (The snapshots and animations of the typical trajectories for each case are depicted in Fig. 6 and ESI Text.†) First, nearly all the reactive trajectories are direct, with the OH₃ intermediate existing for less than one vibrational period. With small total angular momentum J, the direct exchange trajectories behave like nearly head-on collision with the shortest lifetime, where the angle between the directions of outgoing D atom and incoming H atom is close to the bending angle of 107° in the C_3V transition state. So the sideward-scattered HOD we obtained just above the threshold is a direct reflection of the transition state geometry in this exchange reaction. In contrast, the direct trajectories with large total angular momentum J lead to more glancing collision. In some of these glancing collisions, the incident H direction forms an angle with the OH bond of the transition state, causing the HOD to rotate and the sideways-scattered DCS to broaden in both the backward and forward directions. In the remaining glancing collision, the product D atom departs along the direction of the incoming H regent, which lies in the D_3h plane of the transition state, producing a backward-scattered HOD product.

Fig. 6 Snapshots of trajectories at E_c = 1.2 eV resulting in the sideward scattering with a small initial impact parameter of 0.24 bohr (J = 3) (a); the backward scattering with large impact parameters of 1.194 bohr (J = 15) (b) and 1.206 bohr (J = 15) (c). Each panel shows the geometry at the reaction time indicated (fs).

Despite their overall similarity to the QCT deflection functions, the QM GDFs also display noticeable oscillations and negative values (shown in red) across all scattering angles as shown in Fig. 5(b). These features are associated with constructive and destructive interference and are likely responsible for the oscillatory structures observed in the QM DCS. Fig. 5(c) and (d) depict the partially summed QM DCS, DCS([J_i,J_k]), representing the angular distribution calculated for a selected subset of partial waves, in comparison with the partial QM GDFQ_r(θ,[J_i,J_k]), obtained by summing Q_r(θ,J) over the same J range. While the partially summed DCS includes only the coherences among partial waves within the selected range, the partial QM GDF also includes coherences outside this range.⁴³ Consistent with the reaction mechanism analyzed by trajectories, the low-J range (J = 0–10) primarily contributes to sideways scattering, whereas the high-J range (J = 11–20) is associated with backward and early-sideward scattering. However, for both these J ranges, Q_r is smaller than the partial DCS in the sideways region but larger in the forward and backward regions, reflecting interference cancellation and interference growth, respectively. Fig. 5(e) presents the incoherent sum of DCS(J = 0–10) and DCS(J = 11–20), which is similar to the QCT DCS at 1.2 eV, featuring a sideward scattering peak around 122°. Therefore, the peaks and dips in the total QM DCSs, which are absent in the corresponding QCT ones, are the results of quantum interference between contributions from low and high partial waves.

In addition to quantum interference, we also want to study the influence of shape resonance on the DCS of the reaction. In our previous study,^10,35 the collision-energy-dependent DCS in the backward scattering direction were successfully used to detect Feshbach resonances and heavy–light–heavy reactivity oscillations, as they are dominated by a small number of low J and can largely retain the oscillatory structures in the J = 0 reaction probabilities. For the title reaction, because the HOD product is first sideward scattered just above the threshold, we present the collision-energy-dependent DCS at the scattering angle of 107° in Fig. 7(a). As seen, the total DCS exhibits two clear step-like features around E_c = 0.91 and 1.16 eV, consistent with two prominent resonance peaks in the J = 0 reaction probability in Fig. 1(a), which are attributed to the shape resonance states supported by the shallow C_3V well along the reaction path. As shown in Fig. 3, the step-like feature around E_c = 0.91 eV, which is characterized by minimal changes in DCS with increasing collision energy, can be observed across all scattering angles. However, the step-like feature around E_c = 1.16 eV can only be found in a small range of sideward angles.

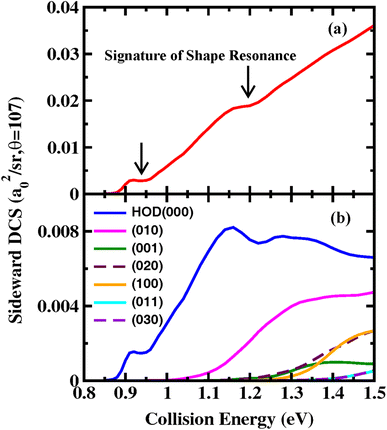Fig. 7 Collision energy dependent (a) total DCS and (b) product HOD vibrational state-resolved DCS at the scattering angle of 107°.

Fig. 7(b) shows the product vibrational state-resolved DCSs at the scattering angle of 107°. As can be seen, only the first seven vibrational states are populated in the energy region considered here. The majority of HOD is in the ground state, and the step-like features observed in the total DCS are primarily due to the ground state. As the collision energy increases, the contributions from vibrationally excited states increase. For HOD, because the OD stretching vibrational frequency is nearly double the bending frequency, there are strong Fermi resonances between levels (001) and (020), and their corresponding overtones. It is impossible to clearly distinguish between the strongly mixed states, therefore it is more appropriate to combine the populations of (001) and (020) states, as well as the (011) and (030) states, when comparing with experimental results. Our calculations predict that the ratio of population is 39.7 : 28.7 : 18.6(= 4.3 + 14.3) : 6.9 : 4.1(= 1.8 + 2.3) of (000) : (010) : [(001) + (020)] : (100) : [(011) + (030)] at E_c = 1.5 eV. Therefore, the reaction exhibits a low mode-specific behavior in the energy region considered here, with no clear preference for particular HOD bending or stretching modes. HOD is predicted to be distributed according to the sequence of the vibrational energy levels. This result clearly reflects the fact that the HOD angle and the newly formed OH bond in the C_3V transition state are only slightly smaller and slightly longer, respectively, than those in the HOD product.

Fig. 8 shows the fraction of the total available energy in the product channel that goes into the internal motion of HOD as a function of collision energy. As observed, the majority of the total available energy is directed into the translational motion of the products. The fraction of energy deposited into the vibrational motion first changes slowly, then increases considerably from 3% at E_c = 1.08 eV to 17.5% at E_c = 1.5 eV. Assuming that the HOD rotational constant remains relatively unchanged across different vibrational states, we can get the approximate fraction of rotational motion, which slightly increases and stays below 7% in the entire energy region.

Fig. 8 The fraction of the total available energy in the product channel going into the internal, rotation and vibration excitations of HOD as a function of the collision energy.

Therefore, our full-dimensional state-to-state quantum dynamics study reveals that the DCS of direct reactive systems are not always backward-peaked at relatively low collision energies. In the title exchange reaction, it directly reflects the non-collinear transition state geometry. We anticipate that this phenomenon exists in other non-collinear reactions and requires accurate theoretical and experimental investigations near the threshold. Moreover, the variations of the DCS with collision energy clearly reveal quantum effects in the reaction, including both interferences and shape resonances.

Data availability

All data are available in the main text, in the ESI†, or upon requests to the corresponding author.

Author contributions

S. L. and D. H. Z. conceived the research and wrote the manuscript. S. L. performed the quantum dynamical calculation. Q. C., K. S. and B. F. performed the QCT calculation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Strategic Priority Research Program of the Chinese Academy of Sciences (grant no. XDB0450202, XDB0970202, XDB0970203), the National Natural Science Foundation of China (Grant No. 22288201, 22022306), the Innovation Program for Quantum Science and Technology (Grant No. 2021ZD0303305), Liaoning Revitalization Talents Program (XLYC2203062), and the Dalian Innovation Support Program (Grant No. 2021RD05).

References

1. G. C. Schatz and A. Kuppermann, Quantum mechanical reactive scattering for three-dimensional atom plus diatom systems. II. Accurate cross sections for H + H₂, J. Chem. Phys., 1976, 65, 4668–4692.
2. S. Liu and D. H. Zhang, A local mode picture for H atom reaction with vibrationally excited H₂O: a full dimensional state-to-state quantum dynamics investigation, Chem. Sci., 2016, 7, 261–265.
3. W. Zhang, Y. Zhou, G. Wu, Y. Lu, H. Pan, B. Fu, Q. Shuai, L. Liu, S. Liu, L. Zhang, B. Jiang, D. Dai, S. Lee, Z. Xie, B. Braams, J. Bowman, M. Collins, D. H. Zhang and X. Yang, Depression of reactivity by the collision energy in the single barrier H + CD₄ → HD + CD₃ reaction, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 12782–12785.
4. B. Fu, Y. Zhou and D. H. Zhang, A state-to-state quantum dynamical study of the H + HBr reaction, J. Theor. Comput. Chem., 2008, 7, 777–791.
5. H. Song, S.-Y. Lee, Z. Sun and Y. Lu, Time-dependent wave packet state-to-state dynamics of H/D + HCl/DCl reactions, J. Chem. Phys., 2013, 138, 054305.
6. R. T. Skodje, D. Skouteris, D. E. Manolopoulos, S. Lee, F. Dong and K. Liu, Resonance-mediated chemical reaction: F + HD → HF + D, Phys. Rev. Lett., 2000, 85, 1206–1209.
7. M. Qiu, Z. Ren, L. Che, D. Dai, S. A. Harich, X. Wang, X. Yang, C. Xu, D. Xie, M. Gustafsson, R. T. Skodje, Z. Sun and D. H. Zhang, Observation of Feshbach resonances in the F + H₂ → HF + H reaction, Science, 2006, 311, 1440–1443.
8. Z. Ren, L. Che, M. Qiu, X. Wang, W. Dong, D. Dai, X. Wang, X. Yang, Z. Sun, B. Fu, S.-Y. Lee, X. Xu and D. H. Zhang, Probing the resonance potential in the F atom reaction with hydrogen deuteride with spectroscopic accuracy, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 12662–12666.
9. W. Dong, C. Xiao, T. Wang, D. Dai, X. Yang and D. H. Zhang, Transition-state spectroscopy of partial wave resonances in the F + HD reaction, Science, 2010, 327, 1501–1502.
10. T. Wang, J. Chen, T. Yang, C. Xiao, Z. Sun, L. Huang, D. Dai, X. Yang and D. H. Zhang, Dynamical resonances accessible only by reagent vibrational excitation in the F + HD → HF + D reaction, Science, 2013, 342, 1499–1502.
11. T. Yang, L. Huang, C. Xiao, J. Chen, T. Wang, D. Dai, F. Lique, M. H. Alexander, Z. Sun, D. H. Zhang, X. Yang and D. M. Neumark, Enhanced reactivity of fluorine with para-hydrogen in cold interstellar clouds by resonance-induced quantum tunnelling, Nat. Chem., 2019, 11, 744–749.
12. W. Shiu, J. J. Lin and K. Liu, Reactive resonance in a polyatomic reaction, Phys. Rev. Lett., 2004, 92, 103201.
13. J. Zhou, J. J. Lin and K. Liu, Deciphering the nature of the reactive resonance in F + CHD₃: correlated differential cross-sections of the two isotopic channels, Mol. Phys., 2010, 108, 957–968.
14. X. Liu, J. J. Lin, S. Harich, G. C. Schatz and X. Yang, A quantum state-resolved insertion reaction: O(¹D) + H₂(J = 0) → OH(²П,v,N) + H(²S), Science, 2000, 289, 1536–1538.
15. F. J. Aoiz, L. Bañares and V. J. Herrero, Dynamics of insertion reactions of H₂ molecules with excited atoms, J. Phys. Chem. A, 2006, 110, 12546–12565.
16. Z. Sun, D. H. Zhang, C. Xu, S. Zhou, D. Xie, G. Lendvay, S.-Y. Lee, S. Y. Lin and H. Guo, State-to-state dynamics of H + O₂ reaction, evidence for nonstatistical behavior, J. Am. Chem. Soc., 2008, 130, 14962.
17. M. J. Perri, A. L. Van Wyngarden, K. A. Boering, J. J. Lin and Y. T. Lee, Dynamics of the O(¹D) + CO₂ oxygen isotope exchange reaction, J. Chem. Phys., 2003, 119, 8213–8216.
18. M. J. Perri, A. L. Van Wyngarden, J. J. Lin, Y. T. Lee and K. A. Boering, Energy dependence of oxygen isotope exchange and quenching in the O(¹D) + CO₂ reaction: a crossed molecular beam study, J. Phys. Chem. A, 2004, 108, 7995–8001.
19. A. L. Van Wyngarden, K. A. Mar, K. A. Boering, J. J. Lin, Y. T. Lee, S. Lin, H. Guo and G. Lendvay, Nonstatistical behavior of reactive scattering in the ¹⁸O + ³²O₂ isotope exchange reaction, J. Am. Chem. Soc., 2007, 129, 2866–2870.
20. Z. Sun, L. Liu, S. Lin, R. Schinke, H. Guo and D. H. Zhang, State-to-state quantum dynamics of O + O₂ isotope exchange reactions reveals nonstatistical behavior at atmospheric conditions, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 555–558.
21. T. Martínez, M. L. Hernández, J. M. Alvariño, F. J. Aoiz and V. S. Rábanos, A detailed study of the dynamics of the O(¹D) + HCl → OH + HCl, ClO + H reactions, J. Chem. Phys., 2003, 119, 7871–7886.
22. P. G. Jambrina, I. Montero, F. J. Aoiz, J. Aldegunde and J. M. Alvariño, Elucidation of the O(¹D) + HF → F + OH mechanism by means of quasiclassical trajectories, Phys. Chem. Chem. Phys., 2012, 14, 16338–16348.
23. C. Xie, J. Li, D. Xie and H. Guo, Quasi-classical trajectory study of the H + CO₂ → HO + CO reaction on a new ab initio based potential energy surface, J. Chem. Phys., 2012, 137, 024308.
24. J. Yang, K. Shao, D. Zhang, Q. Shuai, B. Fu, D. H. Zhang and X. Yang, Trapped abstraction in the O(¹D) + CHD₃ → OH + CD₃ reaction, J. Phys. Chem. Lett., 2014, 5, 3106–3111.
25. L. Y. Yeung, M. Okumura, J. Zhang, T. K. Minton, J. T. Paci, A. Karton, J. M. L. Martin, J. P. Camden and G. C. Schatz, O(³P) + CO₂ collisions at hyperthermal energies: dynamics of nonreactive scattering, oxygen isotope exchange, and oxygen-atom abstraction, J. Phys. Chem. A, 2011, 116, 64–84.
26. Z. Zhao, S. Liu and D. H. Zhang, Differential cross sections for the H + D₂O → HD + OD reaction: a full dimensional state-to-state quantum dynamics study, Chin. J. Chem. Phys., 2017, 30, 16–24.
27. X. Xu, J. Chen, S. Liu and D. H. Zhang, Differential cross-sections for the vibrationally excited H + HOD(v_OH = 1–4) → H₂ + OD reactions, J. Phys. Chem. A, 2024, 128, 10395–10403.
28. D. H. Zhang, M. A. Collins and S.-Y. Lee, First-principles theory for the H + H₂O, D₂O reactions, Science, 2000, 290, 961–963.
29. D. H. Zhang, M. Yang and S.-Y. Lee, Accuracy of the centrifugal sudden approximation in the H + H₂O reaction and accurate integral cross sections for the H + H₂O → H₂ + OH abstraction reaction, J. Chem. Phys., 2002, 117, 10067–10072.
30. D. H. Zhang, M. Yang and S.-Y. Lee, Breakdown of the spectator model for the OH bonds in studying the H + H₂O reaction, Phys. Rev. Lett., 2002, 89, 103201.
31. B. Fu, Y. Zhou and D. H. Zhang, Shape resonance in the H + D₂O → D + HOD reaction: a full-dimensional quantum dynamics study, Chem. Sci., 2011, 3, 270–274.
32. B. Zhao, Z. Sun and H. Guo, A reactant-coordinate-based wave packet method for full-dimensional state-to-state quantum dynamics of tetra-atomic reactions: application to both the abstraction and exchange channels in the H + H₂O reaction, J. Chem. Phys., 2016, 144, 064104.
33. M. T. Cvitaš and S. C. Althorpe, State-to-state reactive scattering in six dimensions using reactant-product decoupling: OH + H₂ → H₂O + H(J = 0), J. Chem. Phys., 2011, 134, 024309.
34. S. Liu, X. Xu and D. H. Zhang, Time-dependent wave packet theory for state-to-state differential cross sections of four-atom reactions in full dimensions: application to the HD + OH → H₂O + D reaction, J. Chem. Phys., 2012, 136, 144302.
35. Z. Chen, J. Chen, R. Chen, T. Xie, X. Wang, S. Liu, G. Wu, D. Dai, X. Yang and D. H. Zhang, Reactivity oscillation in the heavy–light–heavy Cl + CH₄ reaction, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 9202–9207.
36. S. Liu, J. Chen, X. Zhang and D. H. Zhang, Feshbach resonances in the F + CHD₃ → HF + CD₃ reaction, Chem. Sci., 2023, 14, 7973–7979.
37. X. Xu, J. Chen, S. Liu and D. H. Zhang, Differential cross sections for the H + H₂S → H₂ + SH reaction: a full-dimensional state-to-state quantum dynamics study, J. Phys. Chem. A, 2023, 127, 9513–9519.
38. S. Liu and D. H. Zhang, State-to-state integral cross sections for the Cl + CHD₃(v_CH = 0, 1) → HCl + CD₃ reaction, J. Chem. Phys., 2025, 162, 074307.
39. B. Zhao, Z. Sun and H. Guo, Calculation of state-to-state differential and integral cross sections for atom-diatom reactions with transition-state wave packets, J. Chem. Phys., 2014, 140, 234110.
40. B. Zhao, Z. Sun and H. Guo, Calculation of the state-to-state matrix for tetra-atomic reactions with transition-state wave packets: H₂/D₂ + OH → H/D + H₂O/HOD, J. Chem. Phys., 2014, 141, 154112.
41. R. Welsch and U. Manthe, Loss of memory in H + CH₄ → H₂ + CH₃ state-to-state reactive scattering, J. Phys. Chem. Lett., 2015, 6, 338–342.
42. J. Chen, X. Xu and D. H. Zhang, A global potential energy surface for the H₂ + OH → H₂O + H reaction using neural networks, J. Chem. Phys., 2013, 138, 154301.
43. P. G. Jambrina, M. Menéndez and F. J. Aoiz, Angular momentum-scattering angle quantum correlation: a generalized deflection function, Chem. Sci., 2018, 9, 4837.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sc03277f

‡ These authors contributed equally to this work.

---