 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Vacancy enhanced Li, Na, and K clustering on graphene†
Jonathon
Cottom
 ac,
Qiong
Cai
ac,
Qiong
Cai
 b and
Emilia
Olsson
b and
Emilia
Olsson
 *ac
*ac
aAdvanced Research Center for Nanolithography, Science Park 106, Amsterdam, 1098 XG, The Netherlands
bSchool of Chemistry and Chemical Engineering, University of Surrey, Guildford, GU2 7XH, UK
cInstitute of Theoretical Physics, Institute of Physics, University of Amsterdam, Science Park 904, Amsterdam, 1098 XH, The Netherlands. E-mail: k.i.e.olsson@uva.nl
First published on 16th April 2025
Abstract
The formation of metallic dendrites during battery cycling is a persistent challenge for alkali metal-ion batteries, reducing cycle life and posing safety risks. Although surface defects are often implicated in inhomogeneous metal nucleation, the atomic-scale mechanisms by which they promote metal clustering and subsequent dendrite formation remain poorly understood. Here, we use first-principles calculations to investigate how carbon monovacancies (VC) influence the clustering behaviour of alkali metals (Li, Na, and K) on graphene – a common basal-plane motif in graphite, hard carbons, and graphene-based anodes. Clusters of Li, Na, and K of varying size (Mn for n ∈ {1–12}) are characterised on pristine and defective graphene to understand their stability. On pristine graphene, cluster formation is hindered for Li due to the instability of small clusters (n ≤ 3) and significant Li–Li repulsion, and suppressed for K due to weak K–K binding and its larger ionic radius. In contrast, Na exhibits spontaneous clustering, suggesting a higher propensity for dendrite formation even in the absence of defects. The introduction of a VC dramatically alters these trends: it stabilises small (n ≤ 3) clusters across all three metals by enhancing binding strength with the surface and modifying charge localisation. For Li, the vacancy overcomes the barrier to early-stage nucleation; for Na, it promotes growth at even lower metal loadings; and for K, clustering becomes locally favoured albeit only for the smallest cluster sizes (n ≤ 3). These results clarify the defect-facilitated pathways to metal clustering, offering atomistic insight that can inform the development of more dendrite-resistant carbon architectures.
1. Introduction
As human society seeks sustainable energy solutions, the development of efficient storage technologies has become pivotal in reducing the dependency on fossil fuels. Lithium-ion batteries (LIBs) have long been central to this effort due to their high energy density and efficiency across a wide range of applications.1–3 However, with growing demand straining global lithium (Li) resources, exploring viable alternatives and complementary technologies is essential.4–9 Sodium (Na) and potassium (K), situated alongside lithium in the periodic table, offer promising pathways toward cost-effective, large-scale energy storage systems that can alleviate pressure on lithium supplies. Sodium-ion (NIBs) and potassium-ion batteries (KIBs) are emerging as feasible options for applications where weight constraints are less critical, enabling LIBs to be prioritized for weight-sensitive applications.10–13Alkali metal-ion batteries (MIBs), including lithium, sodium, and potassium, share common design elements: a layered cathode, a liquid electrolyte, and (typically) a carbon-based anode. A wide range of carbonaceous anode materials—graphite, graphene, hard and soft carbons, and carbon nanotubes—have been implemented across these systems with varying degrees of success, each offering distinct surface morphologies, porosities, and electronic properties.14–17 In parallel, carbon materials are increasingly being explored as interlayer components in solid-state battery architectures, where they facilitate alkali metal plating and stripping while improving mechanical contact with solid electrolytes.12,18,19 Despite their morphological diversity, these materials exhibit sp2-hybridized frameworks of six-membered carbon rings, forming planar or quasi-planar basal surfaces reminiscent of graphene.16,18,20–24 This structural commonality establishes graphene both as a candidate anode material and as a prototypical model for investigating alkali metal interactions on carbon surfaces.25–31
The electrochemical performance of MIBs remains constrained by persistent challenges related to stability and cycle life, particularly under fast-charging conditions.8,12,32,33 A critical bottleneck is the uncontrolled nucleation of metal at the anode, which initiates dendritic growth and irreversible plating.34–38 These filamentary structures, resulting from inhomogeneous deposition at the anode–electrolyte interface, pose severe safety risks through potential short-circuiting.16,19,39,40 Although solid-state batteries (ASSBs) were conceived to suppress dendrite formation by replacing liquid electrolytes with mechanically rigid solids, Li and Na dendrites continue to emerge in practice, limiting commercial viability despite the appeal of high energy density and improved safety.18,19,41–47 Recent evaluations of solid-state Na systems suggest that hard carbon remains the most practically deployable anode material due to its interface compatibility and cycling stability.48 These persistent issues point to an incomplete understanding of early-stage alkali metal deposition and motivate atomic-scale studies of nucleation and clustering on representative carbon surfaces.
Graphene, due to its exceptional electrical conductivity, chemical inertness, and structural similarity to the basal planes of graphite and hard carbon, serves as a relevant and widely adopted model for carbon-based battery anodes.22,25,26,28–30,49,50 While pristine graphene exhibits weak interactions with alkali metals (Li, Na, and K), intrinsic defects such as carbon vacancies (VC), Stone–Wales rearrangements, and extended grain boundaries substantially alter local electronic and chemical reactivity.22,51–53 These defects introduce localized states near the Fermi level, promoting partially covalent metal–carbon bonding and enabling the nucleation of metal clusters.51,52,54–56 A range of defect and structural modifications have been explored as avenues for tuning alkali metal adsorption, including double vacancies, hydrogen-vacancy networks in graphane, and substitutional doping.29,30,50 These strategies further underscore the broader relevance of defect engineering for tailoring metal–surface interactions in graphene and structurally analogous carbon anode materials.
Previous work has investigated the interactions of single alkali metal atoms (Li, Na, and K) with both pristine and defective graphene within MIBs.29,56–59 These studies highlighted the important role played by intrinsic defects, particularly carbon vacancies (VC), in single-ion binding and migration, identifying VC as a primary source of irreversible capacity loss.11,53,60,61 The metal–vacancy (M–VC) binding is dominated by the strong interaction between the alkali metal and the unsaturated carbon dangling bonds, a feature common to all carbon vacancy-containing defects provided one or more dangling bonds remain.49,59 Such localized interactions significantly enhance the stability and reduce the mobility of adsorbed metal atoms. Furthermore the VC forms the simplest building block of many important defect clusters with other vacancies in the form of di-vacancy and extended defect pores and with hetero-atoms such as (NC)nVC, (OC)nVC and as a result of doping. Other computational studies on lithium clustering demonstrated that small Li clusters adsorb more favorably on graphene compared to bulk Li metal surfaces,54 exhibiting concentration-dependent binding energies that influence charging behavior.62 Additionally, lattice-gas cluster expansion analyses have explored the equilibrium stability of Li coverages on graphene.63 Despite these insights into lithium, corresponding studies addressing Na and K clustering remain limited, leaving significant gaps in understanding their nucleation behavior on graphene and motivating further systematic investigation.
Liang et al.51 conducted a comparative study on Na clusters, showing that Na weakly adsorbs on pristine graphene but that double vacancies significantly enhance Na adsorption—a result aligned with our previous findings on defect-enhanced Na storage.13,49,58,59 Collectively, these studies offer insights into the deposition and clustering of Li on graphene, though several questions remain. Experimental investigations into metallic Li nucleation on basal-plane graphene, for instance, indicate that the pristine surface is lithiophobic, with nucleation barriers too high to overcome,52 whereas basal plane defects are believed to serve as nucleation sites, rendering the surface lithiophilic.52 In practical MIB applications, such defects may arise from synthesis conditions or cycling-induced wear, linking them to suboptimal performance and non-ideal behavior. However, the role of defects remains largely undefined, posing an open question as to what drives Li and Na clustering tendencies, while K demonstrates no such effect.
This study systematically assesses the impact of a single vacancy on Li, Na, and K clustering behavior. Through density functional theory (DFT) calculations, we provide atomic-scale insights into M nucleation and cluster growth on graphene, for both pristine and vacancy systems. This approach offers a focused test case to elucidate the critical role of vacancy defects in M-clustering, clarifying the link between surface and cluster morphology and the propensity for dendrite formation.
2. Methodology
All density functional theory (DFT) calculations were performed spin-polarized using the CP2K code64–68 at the Γ-point, employing DZVP-SR-MOLOPT basis sets65 for valence electrons and GTH pseudopotentials69–71 for core electrons. A plane-wave cutoff of 750 Ry and a relative cutoff of 60 Ry were used, yielding total energy convergence within 0.1 meV per formula unit. Initial defect-free relaxations were carried out on a 308-atom graphene supercell, generated via an 11 × 7 orthohexagonal expansion of the primitive cell (see Fig. S1 in the ESI†). For the pristine cell, both the in-plane lattice vectors and atomic positions were fully relaxed using the quasi-Newton BFGS algorithm.72–75 In defect-containing calculations, only the atomic positions were optimized. A vacuum spacing of 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Å was applied in the out-of-plane direction to eliminate spurious interlayer interactions.66,68,76 The Perdew–Burke–Ernzerhof (PBE) functional77,78 with D3-BJ dispersion corrections79–83 was used, consistent with previous studies.13,24,49,58,59,84,85 Geometry optimizations were deemed converged when the total energy changed by less than 1 × 10−7 eV and the maximum atomic force was below 0.005 eV Å−1.
Å was applied in the out-of-plane direction to eliminate spurious interlayer interactions.66,68,76 The Perdew–Burke–Ernzerhof (PBE) functional77,78 with D3-BJ dispersion corrections79–83 was used, consistent with previous studies.13,24,49,58,59,84,85 Geometry optimizations were deemed converged when the total energy changed by less than 1 × 10−7 eV and the maximum atomic force was below 0.005 eV Å−1.
Using the lowest energy M adsorption sites previously identified in ref. 49, the lowest-energy cluster configurations were determined via a stepwise sampling scheme.86 Starting with a single metal atom (M1), atoms were sequentially added to form each Mn+1 cluster from Mn. To efficiently identify sites where a significant M–M interaction occurs as a prerequisite for cluster growth, any incremental interaction energy greater than −0.05 eV is treated as negligible and therefore non-interacting with respect to cluster growth. In effect, for a given neighboring site, if ΔE ≥ −0.05 eV, the corresponding binding interaction is considered statistically insignificant, as this value is on the order of (or below) twice the thermal energy at ambient conditions (kBT ≈ 0.025 eV). Consequently, only sites exhibiting ΔEpair ≤ −0.05 eV are included in the initial sampling. In practice the search space is constrained to those sites that are predicted to result in either lateral or vertical growth of the cluster. The total number of configurations considered at each iteration is given by
To evaluate nucleation behavior, interaction energies were calculated using three key metrics: the formation energy Ef, using Zhang and Northrup's standard formalism87 (eqn (1)), the binding energy Ebind (eqn (2)), and the cohesive energy Ecoh (eqn (3)):
 | (1) |
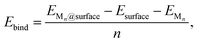 | (2) |
 | (3) |
The formation energy Ef quantifies the average energetic cost of assembling the adsorbed cluster from isolated atoms. The binding energy Ebind captures the net interaction between the cluster and the surface, where negative values indicate attractive interactions and positive values imply repulsion. The cohesive energy Ecoh describes the intrinsic metal–metal bonding within the cluster in vacuum; more negative values correspond to stronger cohesion. These metrics are interdependent. In particular, strong metal–surface interactions (large negative Ebind) often weaken intra-cluster cohesion (less negative Ecoh) due to geometric or electronic frustration. This antagonistic relationship provides insight into whether cluster formation is favored over dispersion.
Thermodynamic stability was further assessed using the incremental formation energy relative to the M1 representing a disperse coverage with no M–M interactions:
| ΔEf = Ef(n) − Ef(n = 1). | (4) |
Clusters with ΔEf < 0 are energetically favored to form and grow, whereas ΔEf > 0 implies instability and the clustering is unfavoured with respect to the disperse coverage. Note that kinetic effects are not considered in this analysis. For consistency with prior studies, free-energy corrections are omitted here, although several works62,88–90 have extended energy-based analyses to incorporate entropic and zero-point contributions. All structural visualizations were prepared using VESTA.91
We employ two complementary approaches to elucidate the evolution of the charge transfer. First, we analyze the local coordination environment of the metal atoms by applying directional filtering to classify atoms based on their bonding configurations. This enables us to group metal atoms into distinct categories, such as those with surface coordination or those bonded only to other metal atoms, and to compute the average partial charges within each group as a function of cluster size. Second, we compute the total metal charge Qtotal by summing the Mulliken charges92 of all metal atoms in a cluster:
 | (5) |
 | (6) |
 | (7) |
3. Results and discussion
To investigate metal (M) nucleation and clustering on graphene, we systematically examine two systems: (1) the pristine basal plane providing our defect-free reference, and (2) the basal plane containing a carbon vacancy (VC). This comparative approach addresses the following key question: How does the presence of a VC defect impact the binding energy (Ebind) and cohesive energy (Ecoh) of metal clusters, and consequently, the morphology and stability of the clusters? By analyzing these systems the role of defect-induced surface modifications in promoting or suppressing metal clustering is elucidated.3.1. Metal clustering on the pristine basal plane: trends in stability and morphology
To investigate the formation of Mn clusters (n = 1–12), we calculated the cluster binding energies on the defect-free graphene basal plane. Ebind, Ecoh, and Ef are shown in Fig. 1, along with the associated cluster geometries. In all cases, the isolated metal atom preferentially adsorbs at the hole site (above the centre of the C6 ring), consistent with previous studies.29,49,93,94 For clusters with n ≥ 2, short-range M–M repulsive interactions distort the geometry, displacing metal atoms from the high-symmetry adsorption site. The degree of distortion is dictated by the inter-site distance between neighbouring hole sites (2.46 Å) in the graphene basal plane and the extent to which M–M separations can be accommodated on the carbon surface.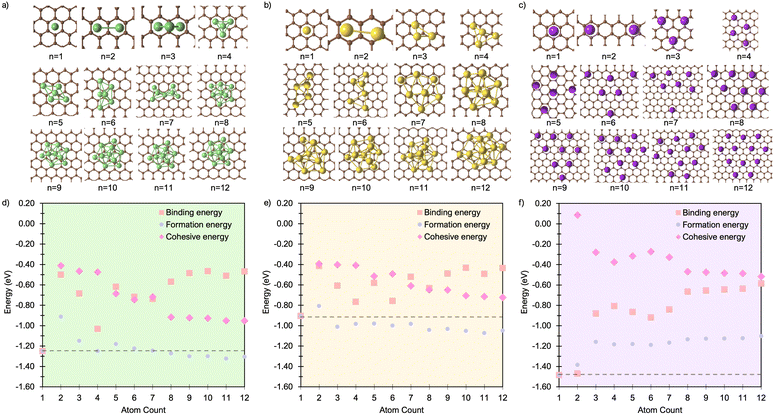 | ||
| Fig. 1 Lowest energy cluster configurations on the pristine basal plane for (a) Li (green spheres represent Li atoms and brown spheres represent C atoms), (b) Na (yellow spheres represent Na atoms), and (c) K (purple spheres represent K atoms). Side views of the lowest energy cluster configurations are included in the ESI (Fig. S3–S5).† The interaction energies decomposed into binding energy (Ebind), cohesive energy (Ecoh), and formation energy (Ef) are plotted for Li in (d), Na in (e), and K in (f), with the atom count denoting the number of M atoms in the Mn clusters. | ||
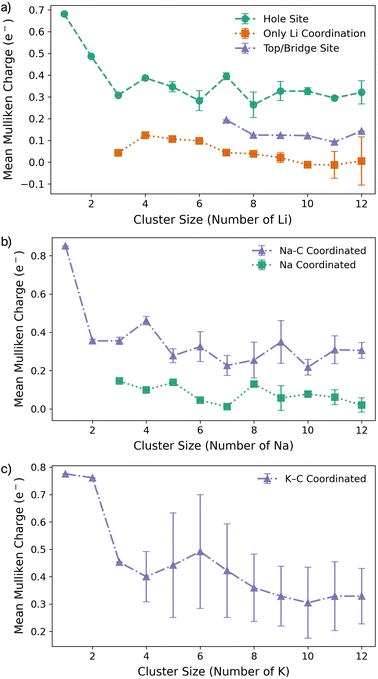
For Li2 (Fig. 1a and d), the addition of a second Li atom to Li1 induces a notable distortion, with a Li–Li separation of 3.12 Å. This displacement from the high-symmetry site (0.33 Å) leads to a number of Li–C bond lengths, replacing the single bond observed in the Li1 (Fig. 2a). Na2 adopts a similar configuration to Li2 but with a greater distortion (3.47 Å) (Fig. 1b), reflecting the larger ionic radius of Na. The increased displacement gives the Na2 significant top-site character, driving an increase in the Na–C bond length (Fig. 2b). In contrast, K2 shows greater relaxation than either Li or Na, relaxing into a configuration with atoms located at distorted next-next-nearest-neighbour hole sites (Fig. 1c). No stable neighbour or next-neighbour minima were found without applying constraints; upon releasing the constraint, the system relaxed to the next-next-neighbour geometry, corresponding to a K–K separation of 7.86 Å (Fig. 2c).
 | ||
| Fig. 2 Bond lengths as a function of M cluster size (atom count) for (a) Li, (b) Na, and (c) K clusters on the pristine basal plane, showing the C–M and M–M distances. | ||
For all Li1 and Li2 configurations, the dominant interaction is between the metal atom and the surface, as reflected by charge transfer trends (Fig. 3a–c). As previously reported, adsorption of an isolated metal atom results in the transfer of its valence s-electron to the underlying C6 ring, following the reaction:
| M0 + C06(graphene) → M+ + C6−(graphene), |
 | ||
| Fig. 3 Mean Mulliken charges as a function of M cluster size for (a) Li, (b) Na, and (c) K clusters on the pristine basal plane. | ||
The reduction in partial charge arises from the emergence of partially occupied metal states at the Fermi energy, as shown in the projected density of states (PDOS) (Fig. S11 in the ESI†), and from charge redistribution between the metal centres, evident in the Δρ(r) plots (Fig. S12–S14 in the ESI†). Energetically, M2 formation is unfavoured in all cases, with ΔEf of +0.34 eV per atom for Li2, +0.05 eV per atom for Na2, and no stable configuration identified for K2; even the relaxed next-next-neighbour geometry remains +0.15 eV per atom higher in energy than the K1. While Ecoh for both Li2 and Na2 is moderately stabilising at −0.40 eV per atom, it is insufficient to counteract the ∼50% reduction in Ebind relative to the M1 reference (Fig. 1d and e).
For K3, the trends described previously continue, with two important differences (Fig. 1f). Firstly, Ecoh becomes negative (−0.2 eV per atom), indicating the onset of an attractive K–K interaction. The K–K separation is reduced to 4.8 Å, with next-neighbour top sites occupied (Fig. 2c). Secondly, as observed for Li2 and Na2, the attractive interaction is driven by the emergence of K-derived states at the Fermi energy (Fig. S11 in the ESI†), which in turn leads to a notable reduction in partial charge (Fig. 3c and S14 in the ESI†).
In contrast, the behaviour of Li3 and Na3 differs markedly. In both cases, the M2 configuration is preserved, with the additional metal atom binding preferentially to the existing metal ions, without direct interaction with the carbon surface (Fig. 1a and b). The influence of M–M interactions is pronounced. Firstly, there is a significant decrease in the M–M bond lengths (Fig. 2b and c), due to the absence of meaningful geometric constraints from the surface lattice. Secondly, Ecoh becomes substantially more favourable for both Li and Na (Fig. 1d and e), while Ebind remains comparable to that of the dimer, indicating that the energetic benefit arises primarily from the metal–metal interaction.
Finally, analysis of the partial charges reveals the presence of two distinct coordination environments: cationic, surface-adsorbed metal ions (as observed for M2), and metal-coordinated sites with no direct C-interaction. The trend established with Li2 continues, with a further reduction in the partial charge to 0.33e− for surface-bound sites, accompanied by an increased density of Li states at the Fermi level. For Na3, the partial charges and associated electronic states remain essentially unchanged relative to Na2, indicating that no additional charge redistribution occurs. It is noteworthy that the total reduction in partial charge from Li1 to Li3 mirrors that observed between Na1 and Na2, via the intermediate Li2 configuration. For both Li and Na, the metal-coordinated sites are electronically distinct, exhibiting near-neutral character: approximately 0e− for Li and 0.2e− for Na (Fig. 3, S12 and S13 in the ESI†). Despite the onset of attractive interactions, cluster formation at n = 3 remains strongly disfavoured for Li and K, with ΔEf values of +0.20 eV per atom and +0.22 eV per atom, respectively. In contrast, Na cluster formation becomes energetically favourable at this size, with ΔEf = −0.11 eV per atom.
The formation of M4 clusters marks the point at which the clustering behaviour begins to diverge significantly between the metals. For Li, Li4 forms via lateral addition to an adjacent hole site, accompanied by relaxation of the previously Li-coordinated atom into the central threefold symmetry site. This structure serves as the fundamental building block for larger clusters, with subsequent growth proceeding by lateral addition to distorted hole, top, or bridge sites (depending on size), followed by vertical growth through the Li-coordinated site. This stepwise occupation is illustrated in Fig. S3 in the ESI.† The mean Li–Li and Li–C bond lengths, shown in Fig. 2a, exhibit a gradual increase in Li–Li separation with cluster size, reaching a maximum spread at Li6, where partial formation of a second layer occurs (see Fig. S6 and S7 in the ESI†). The introduction of the threefold-coordinated Li site has a notable effect on the electronic structure, introducing a state deep in the valence band and shifting the charge character towards a more neutral Li0 configuration, as evident in Fig. 3 and visualised in the Δρ(r) plots (Fig. S12 in the ESI†).
As cluster size increases, the variation across sites of a given type also increases, reducing the precision with which associated geometric and charge-based descriptors can be defined. Ecoh becomes markedly more favourable with increasing cluster size, although this is partially offset by a reduction in Ebind. Consequently, ΔEf becomes increasingly favourable for cluster sizes n > 7, with the clustered and dispersed forms becoming energetically degenerate at n = 4 and n = 7. For lithium, this suggests that clustering can occur under high deposition rates, potentially contributing to the observed plating, with the nucleation probability distributed equally across a degenerate set of surface sites.52
Na follows a similar clustering pattern to Li, but with two important differences. Firstly, its larger ionic radius leads to a greater mismatch between the Na–Na bond length and the spacing between surface adsorption sites, resulting in a significantly larger distortion compared to Li (Fig. 2, S8 and S9 in the ESI†). Secondly, Ebind and Ecoh exhibit substantial overlap, producing a fine balance between metal–metal and metal–carbon interactions (Fig. 1e).
While the general trends mirror those observed for Li, Na clusters consistently exhibit a marked degree of structural distortion at all sizes, a behaviour only seen in Li for the largest clusters (n > 10). This structural variability affects the electronic structure: instead of discrete states, the PDOS (Fig. S11 in the ESI†) appears smeared, reflecting the range of geometries present within each cluster. This in turn manifests in the partial charges, where the Na–C interactions span a wide range even in the smallest clusters. Unlike Li, these charges cannot be cleanly distinguished by adsorption site due to the relatively weaker binding of Na (Fig. 3b).
As previously noted, Ecoh and Ebind lie within a narrow window of approximately 0.4 eV, with Ecoh becoming gradually more favourable and Ebind increasingly less so as cluster size increases. The resulting formation energy, ΔEf, indicates that cluster formation becomes energetically favourable for n > 2, with Na2 already exhibiting a slightly positive ΔEf of +0.05 eV per atom. This suggests that Na dendrite formation may occur even on pristine basal plane structures, consistent with experimental observations.95–98 However, given the relatively weak binding energy of these Na clusters, further investigation is needed to determine whether they remain anchored to the surface or desorb as isolated entities.
K continues to form a single-layer structure, with atoms spaced to balance metal–metal repulsion against emerging lateral interactions. As the number of K atoms increases, there is a corresponding increase in the spread of K–K distances and the diversity of adsorption sites occupied (Fig. 2c). This variation in site occupancy and degree of lateral interaction leads to a range of partial charges, although the spread remains narrower than that observed for Li and Na, where vertical cluster growth occurs (Fig. 1c, S5 and S10 in the ESI†). Electronically, the behaviour remains consistent with that of K3, showing an increase in the density of K-derived states as the cluster size increases. These states remain confined to the Fermi level and above, indicating no significant occupation of lower-energy states (Fig. S11 in the ESI†). Finally, although Ecoh increases modestly with cluster size, this is more than offset by a corresponding decrease in the binding energy (Ebind). As a result, ΔEf remains positive across all cluster sizes considered (Fig. 1f). This persistent absence of favourable K clustering supports the conclusion that K nucleation and dendrite formation are energetically unfavourable on pristine basal plane surfaces, consistent with experimental observations in carbon-based KIBs.97,99,100
In summary, the formation and stability of metal clusters on the pristine basal plane are governed by a delicate interplay between geometric accommodation, electronic delocalisation, and charge transfer. Li, Na, and K exhibit qualitatively distinct behaviours driven by their ionic radii and their ability to match the spatial periodicity of adsorption sites. Li forms compact clusters with clear layer-by-layer growth beyond n = 3, enabled by moderate geometric distortion and strong M–C binding. This growth leads to partial charge redistribution and the emergence of low-lying valence states, although cluster formation remains energetically unfavourable until n ≥ 7. Na follows a similar motif, but its larger ionic size imposes greater geometric frustration, resulting in persistent distortion, smeared electronic states, and a complex distribution of partial charges. Despite these distortions, Na cluster formation becomes energetically favourable from n = 3, indicating a thermodynamic driving force for nucleation and potential dendrite formation, even in the absence of defects. In contrast, K displays fundamentally different behaviour: the weak M–C binding, strong M–M repulsion, and poor geometric compatibility inhibit both vertical growth and electron localisation. K remains in a dispersed monolayer configuration with minimal electronic perturbation and positive formation energies across all sizes, consistent with the absence of dendrite formation observed experimentally.97,99,100
Together, these results highlight how subtle differences in atomic size and metal–surface coupling give rise to distinct clustering pathways, offering mechanistic insight into the conditions under which metal dendrites may nucleate or be suppressed on carbon-based substrates.
3.2. Influence of carbon vacancies on metal clustering and stability
Building on the insights from pristine graphene, we now examine the influence of a single carbon vacancy (VC) on metal cluster formation and stability. Fig. 4a–c presents the lowest-energy Mn cluster geometries on the VC surface for Li, Na, and K (for side views, see Fig. S16–S18 in the ESI†). In all three cases, M1 binds preferentially at the vacancy, coordinating to the under-coordinated carbon atom, while the remaining two carbons reconstruct to form a five-membered ring, consistent with earlier work on isolated metal adsorption.49 The binding energies (Fig. 4d–f) at n = 1 are notably enhanced compared to pristine graphene (Fig. 1d–f), with Ebind values of −3.23 eV for Li, −2.52 eV for Na, and −2.84 eV for K. This enhancement reflects the strong interaction with the unsaturated carbon atom (Fig. 4a–c). | ||
| Fig. 4 Lowest energy cluster configurations on the defective basal plane for (a) Li (green spheres represent Li atoms and brown spheres represent C atoms), (b) Na (yellow spheres represent Na atoms), and (c) K (purple spheres represent K atoms). Side views of the lowest energy cluster configurations are included in the ESI (Fig. S16–S18).† The interaction energies decomposed into binding energy (Ebind), cohesive energy (Ecoh), and formation energy (Ef) are plotted for Li in (d), Na in (e), and K in (f), with the atom count denoting the number of M atoms in the Mn clusters. | ||
The corresponding M–C bond lengths, shown in Fig. 5, are significantly shorter than those in the pristine system (Fig. 2). This shift is driven by the formation of a strong M–C* bond, with distances of 2.03 Å, 2.36 Å, and 2.81 Å for Li1, Na1, and K1, respectively. The presence of the dangling bond alters the charge transfer mechanism: the transferred charge is now predominantly localised on the under-coordinated carbon rather than delocalised over the C6 ring (see Fig. S26–S28 in the ESI†). The reaction
| C01 + M0 → C1− + M+ |
 | ||
| Fig. 5 Bond lengths as a function of M cluster size (atom count) for (a) Li, (b) Na, and (c) K clusters on the defective basal plane, showing the C–M and M–M distances. | ||
 | ||
| Fig. 6 Mean Mulliken charges as a function of M cluster size for (a) Li, (b) Na, and (c) K clusters on the defective basal plane. Δρ(r) plots are presented in Fig. S26–S28 in the ESI.† | ||
For M2, the added atom occupies the adjacent vacancy hole site in the case of Li2 and Na2, and the next-neighbour hole site for K2, with both metal centres interacting with the unsaturated carbon atom. The Li and Na atoms occupy equivalent sites and exhibit negligible extension relative to M1 (M–C* distances: Li2, 2.05 Å; Na2, 2.36 Å) (Fig. 5a and b). In contrast, K2 adopts a more asymmetric configuration, with one atom at the vacancy and the other on the next-neighbour hole site, giving K–C* distances of 2.81 Å and 3.68 Å, respectively (Fig. 5c). The partial charges (Fig. 6) remain largely consistent for Li2, while Na2 and K2 exhibit a small decrease of approximately 0.1e−. In all cases, the charge transfer extends beyond the under-coordinated carbon to neighbouring C atoms, as shown in Fig. S26–S28 in the ESI.† Inspection of the PDOS (Fig. S25 in the ESI†) highlights a key distinction from the pristine system: the metal-derived states remain unoccupied and lie well above the Fermi level, whereas in the pristine case, these states are partially filled. Ef is dominated by the strong binding of M2 to the vacancy site (Ebind), although it is reduced compared to the M1 case. Ecoh is marginally more favourable than on the pristine surface, but its impact on ΔEf is negligible (Fig. 4). All M2 configurations remain strongly stabilised, with ΔEf values of −1.2 eV per atom, −1.0 eV per atom, and −0.75 eV per atom for Li2, Na2, and K2, respectively.
At M3, Li exhibits markedly different behaviour. At Li3, the five-membered carbon ring begins to open, with the C–C bond extending beyond 1.9 Å. This structural change is reflected in the partial charges (Fig. 6), where the Li atom interacting with the breaking C–C bond exhibits a significantly reduced Mulliken charge. At Li4, the ring fully ruptures, enabling one Li atom to coordinate to three equivalent dangling carbon atoms with a short C–Li bond length of 1.85 Å. These under-coordinated carbon atoms are displaced upwards by approximately 1.2 Å from the graphene plane (Fig. 4a). The partial charge on this vacancy-bound Li site drops further −0.1e−, while the Li atoms occupying nearby hole sites retain a consistent charge of 0.5e− (Fig. 6a). Following this reconstruction, additional Li atoms preferentially occupy adjacent hole sites and, beyond Li5, begin to adsorb vertically, initiating second-layer growth. This growth pathway mirrors that seen on the pristine surface, with the vacancy acting as an anchoring centre. The transition observed at Li3 and Li4 marks a shift from formation energy (Ef) dominated by strong metal–surface binding (Ebind) to one increasingly governed by metal–metal cohesion (Ecoh). Beyond Li4, Ebind becomes progressively less favourable with cluster size, while Ecoh continues to increase. Nevertheless, all Lin configurations remain energetically stabilised, with ΔEf negative across the entire size range considered.
For both Na and K, the five-membered carbon ring (C5) remains intact across all cluster sizes (Fig. 4b and c). For Na, clustering follows the same intermediate configurations as observed on the pristine surface, with small clusters (n ≤ 3) anchored at the vacancy site, rendering their formation significantly more favourable. The presence of the vacancy leads to an increased spread in bond lengths (Fig. 5b) and partial charges (Fig. 6b), although the mean values remain comparable to those on the pristine surface. This broadened distribution arises from the combination of local distortion induced by the vacancy and the fixed nature of tightly bound atoms in the small clusters, which are energetically costly to displace. Consequently, additional atoms must accommodate these anchored positions, introducing greater structural distortion within the growing cluster, as illustrated schematically in Fig. S22 and S23 in the ESI.† The PDOS shows a similar trend to the pristine case: Na–Na interactions produce states degenerate with the Fermi level, while non-carbon-coordinated Na atoms contribute deeper-lying valence band states (Fig. S25 in the ESI†).
For all Nan clusters considered, ΔEf remains negative, indicating favourable clustering. As with Li, a gradual transition is observed from an initial regime dominated by strong local vacancy interactions (Ebind) to a regime where Ecoh and Ebind contributions are of comparable magnitude, approaching the energetic balance seen on the pristine surface.
For K, clustering proceeds in a manner broadly similar to the pristine system, with two notable exceptions. First, there is a marked energetic antagonism between the vacancy-bound K atom and additional K atoms occupying non-vacancy sites during vertical growth. This competition results in favourable multilayer configurations emerging only at K8, K11, and K12, though isoenergetic lateral configurations exist at each of these sizes. Second, the formation energy ΔEf is negative only for clusters up to K5, where the strong local vacancy interaction dominates. The comparatively weak Ecoh of potassium limits the transition to a surface-anchored growth mode seen for both Li and Na. As a result, while the vacancy can stabilise small Kn clusters, it does not promote sustained growth. This reinforces the conclusion that potassium remains resistant to nucleation and dendrite formation, even in the presence of surface defects.
3.3. Discussion
The introduction of a carbon vacancy (VC) dramatically alters the thermodynamics of metal clustering on the graphene basal plane. For all three metals, the presence of an unsaturated carbon at the vacancy enhances the local binding energy (Ebind) of the initial adsorbed atom, leading to stronger anchoring and the stabilisation of otherwise unfavourable small clusters. As cluster size increases, however, this effect becomes localised: the vacancy contribution is diluted on a per-atom basis, and Ebind converges toward the pristine values. Concurrently, Ecoh grows steadily more favourable, approaching the bulk metal limit. This crossover from vacancy-dominated to cluster-internal energetics provides a natural scale for predicting cluster size thresholds for nucleation and vertical growth.Geometrically, the vacancy site introduces a strong asymmetry that constrains early-stage cluster morphology. For Li, the vacancy drives a structural transformation: the five-membered ring opens at n = 3, enabling a central Li atom to coordinate to three under-coordinated carbon atoms at n = 4. This geometry stabilises the cluster and defines the onset of vertical growth. In contrast, Na and K preserve the five-membered ring across all cluster sizes. This rigidity, combined with the larger equilibrium M–M distances, limits the accessible surface adsorption geometries and restricts metal-carbon relaxation. These trends are mirrored in both the metal–carbon bond lengths and partial charge distributions: Li exhibits shorter bonds and enhanced covalent character at the vacancy, while Na and K maintain the single dangling bond interaction.
The evolution of the electronic structure reflects the transition from localised surface binding to collective metallic behaviour. For Li and Na, small clusters exhibit sharp distinctions in the PDOS, with surface-bound atoms contributing states near the Fermi level, while interior or second-layer atoms retain deeper-lying, metal-like character. This evolution is accompanied by a progressive reduction in Mulliken partial charge with increasing cluster size, consistent with charge delocalisation and the emergence of quasi-metallic behaviour. For Li, the partial charge on the vacancy-bound site drops from ∼0.5e− at n = 1 to ∼0.1e− at n = 4, and reaches ∼–0.2e− at n = 5. Na exhibits a more gradual reduction, with the vacancy-bound site stabilising near ∼0.2e− by n = 6. In both cases, the emergence of metal-derived states degenerate with the Fermi level coincides with lateral metal–metal interaction, while vertical growth introduces deeper-lying valence band states associated with non-surface-bound atoms.
To further quantify the interplay between electron transfer and cluster growth, we calculate the total cluster charge Qtotal (Fig. 7a–c) and the fractional ionic character f(n) (Fig. 7d–f). Qtotal represents the summed Mulliken charge of all metal atoms in a given cluster, while f(n) = Qtotal/(nq1) normalizes this value relative to the ideal ionic limit, defined by the charge q1 of the isolated surface adsorbed metal (M1). For all metals on the pristine surface, Qtotal increases sublinearly with n, indicating a progressive departure from predominantly ionic behavior (Fig. 7a–c). This deviation is most pronounced for Li and Na, where f(n) drops rapidly from unity to approximately 0.3 by n = 6–8, consistent with the emergence of strong metal–metal bonding within the cluster (Fig. 7d and e). In contrast, K exhibits weaker charge transfer overall, with f(n) remaining above 0.4 even at the largest cluster sizes studied (Fig. 7f). The presence of a carbon vacancy primarily influences the smallest clusters (n = 1–3), where electron transfer is enhanced through interaction with the vacancy's dangling bond. At n = 1, f(n) increases to 0.71, 0.82, and 0.85 for Li, Na, and K respectively. However, beyond n = 4, the influence of the vacancy saturates, and f(n) converges toward the pristine trend. These trends confirm that electron donation to the surface is rapidly exhausted, and that beyond a critical cluster size, excess charge remains within the cluster itself – consistent with the development of delocalized metallic states near, and eventually below, the Fermi level (Fig. S11 and S25 in the ESI†). Importantly, the vacancy has only a modest effect on f(n) beyond the smallest sizes, reinforcing its role as a local defect that governs early-stage nucleation without significantly altering the longer-range electronic character of the cluster.
 | ||
| Fig. 7 Total metal cluster charge (Qtotal) for (a) Li, (b) Na, and (c) K, and their fractional character (f(n)) for (d) Li, (e) Na, and (f) K. | ||
Overall, these findings highlight the dual role of carbon vacancies in mediating early-stage metal nucleation. Vacancies not only stabilise small clusters that are otherwise unfavourable on pristine graphene, but also imprint distinct structural and electronic fingerprints on the growing ensemble. The vacancy acts as an anchor point, localising charge and stabilising low-coordinate geometries, while facilitating a controlled transition to extended, metallic clusters through lateral and vertical addition. The extent to which this anchoring effect persists depends sensitively on the balance between vacancy–metal binding, metal–metal cohesion, and the geometric constraints imposed by ionic radius. As a result, the vacancy-driven nucleation landscape is element-specific: Li benefits from strong, directional bonding and cohesive growth; Na occupies an intermediate regime where distortion accommodates nucleation; and K remains largely non-nucleating, even with defect assistance. These distinctions offer a predictive framework for interpreting alkali metal behaviour on defective carbon and for designing anode materials that control clustering through tailored surface chemistry.
4. Conclusions
This study systematically examines the nucleation and growth of Li, Na, and K clusters on both pristine graphene and defective surfaces featuring a single carbon vacancy (VC), elucidating the thermodynamic pathways underlying dendrite formation in alkali metal-ion batteries.On the pristine basal plane, cluster growth is hindered for Li due to strong M–M repulsion and the unfavourable energetics of small clusters. K exhibits minimal clustering across all sizes, reflecting its weak binding and large ionic radius. In contrast, Na clusters readily form, with ΔEf becoming favourable as early as n = 3, suggesting an inherent propensity for dendrite nucleation even in the absence of defects. The introduction of a vacancy site dramatically alters this picture. For Li, the VC stabilises otherwise unstable small clusters, enabling stepwise growth anchored at the defect. For Na, already favourable clustering is further enhanced by the vacancy, reinforcing inhomogeneous nucleation pathways. K, while weakly bound overall, shows modest cluster stabilisation at small sizes, but fails to achieve favourable vertical growth, maintaining resistance to dendrite formation.
These behaviours arise from the interplay between metal–carbon binding, metal–metal cohesion, and electronic structure evolution, with the vacancy shifting the balance from surface-limited to metal-dominated growth. Importantly, the findings reveal that even a single point defect can serve as a nucleation hotspot, transforming otherwise uniform growth into spatially heterogeneous clustering. Given the diversity of intrinsic and extrinsic defects in real carbonaceous anodes, extending this analysis beyond vacancies will be essential. Such insights will inform strategies for defect-engineered electrode design aimed at suppressing dendrite formation and enhancing long-term electrochemical stability.
Data availability
Data for this article are available at Zenodo at https://doi.org/10.5281/zenodo.14747737.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was conducted at the Advanced Research Center for Nanolithography, a public-private partnership between the University of Amsterdam (UvA), Vrije Universiteit Amsterdam (VU), Rijksuniversiteit Groningen (RUG), the Netherlands Organization for Scientific Research (NWO), and the semiconductor equipment manufacturer ASML. This work made use of the Dutch national e-infrastructure with the support of the SURF Cooperative using grant no. EINF-2434 and EINF-5451. The authors thank SURF (https://www.surf.nl/) for the support in using the Lisa Compute Cluster and National Supercomputer Snellius. Q. C. would like to acknowledge funding support from the Faraday Institution through the LiSTAR programme (FIRG014, Grant FIRG083), and funding support from Horizon Europe via the OPERA consortium (Grant No. 101103834) under the UK Research and Innovation (UKRI)'s Horizon Europe funding guarantee (Grant No. 10078555). E. O. is grateful for a WISE Fellowship from the NWO and support via Holland High Tech through a public–private partnership in research and development within the Dutch top sector of High-Tech Systems and Materials (HTSM).References
- M. Armand and J. M. Tarascon, Building better batteries, Nature, 2008, 451, 652 CrossRef CAS PubMed.
- K. Yuan, Y. Lin, X. Li, Y. Ding, P. Yu, J. Peng, J. Wang, H. K. Liu and S. Dou, High-Safety Anode Materials for Advanced Lithium-Ion Batteries, Energy Environ. Mater., 2024, 7(5), e12759 CrossRef CAS.
- S. Tagliaferri, L. Gaspard, H. Au, C. Mattevi, M. M. Titirici and M. Crespo-Ribadeneyra, Nature-inspired batteries: from biomaterials to biomimetic design strategies, Green Chem., 2024, 26, 6944 RSC.
- M. Titirici, S. G. Baird, T. D. Sparks, S. M. Yang, A. Brandt-Talbot, O. Hosseinaei, D. P. Harper, R. M. Parker, S. Vignolini, L. A. Berglund, Y. Li, H. L. Gao, L. B. Mao, S. H. Yu, N. Díez, G. A. Ferrero, M. Sevilla, P. Ã. Szilágyi, C. J. Stubbs, J. C. Worch, Y. Huang, C. K. Luscombe, K. Y. Lee, H. Luo, M. J. Platts, D. Tiwari, D. Kovalevskiy, D. J. Fermin, H. Au, H. Alptekin, M. Crespo-Ribadeneyra, V. P. Ting, T. P. Fellinger, J. Barrio, O. Westhead, C. Roy, I. E. Stephens, S. A. Nicolae, S. C. Sarma, R. P. Oates, C. G. Wang, Z. Li, X. J. Loh, R. J. Myers, N. Heeren, A. Grégoire, C. Périssé, X. Zhao, Y. Vodovotz, B. Earley, G. Finnveden, A. Björklund, G. D. Harper, A. Walton and P. A. Anderson, The sustainable materials roadmap, JPhys Mater., 2022, 5, 032001 CrossRef.
- N. Tapia-Ruiz, A. R. Armstrong, H. Alptekin, M. A. Amores, H. Au, J. Barker, R. Boston, W. R. Brant, J. M. Brittain, Y. Chen, M. Chhowalla, Y. S. Choi, S. I. Costa, M. C. Ribadeneyra, S. A. Cussen, E. J. Cussen, W. I. David, A. V. Desai, S. A. Dickson, E. I. Eweka, J. D. Forero-Saboya, C. P. Grey, J. M. Griffin, P. Gross, X. Hua, J. T. Irvine, P. Johansson, M. O. Jones, M. Karlsmo, E. Kendrick, E. Kim, O. V. Kolosov, Z. Li, S. F. Mertens, R. Mogensen, L. Monconduit, R. E. Morris, A. J. Naylor, S. Nikman, C. A. O'Keefe, D. M. Ould, R. G. Palgrave, P. Poizot, A. Ponrouch, S. Renault, E. M. Reynolds, A. Rudola, R. Sayers, D. O. Scanlon, S. Sen, V. R. Seymour, B. Silván, M. T. Sougrati, L. Stievano, G. S. Stone, C. I. Thomas, M. M. Titirici, J. Tong, T. J. Wood, D. S. Wright and R. Younesi, 2021 roadmap for sodium-ion batteries, JPhys Energy, 2021, 3, 031503 CrossRef CAS.
- A. Eftekhari and D. W. Kim, Sodium-ion batteries: New opportunities beyond energy storage by lithium, J. Power Sources, 2018, 395, 336–348 CrossRef CAS.
- H. Au, M. Crespo-Ribadeneyra and M.-M. Titirici, Beyond Li-ion batteries: performance, materials diversification, and sustainability, One Earth, 2022, 5, 207 CrossRef.
- J. Zhang, X. Yao, R. K. Misra, Q. Cai and Y. Zhao, Progress in electrolytes for beyond-lithium-ion batteries, J. Mater. Sci. Technol., 2020, 44, 237 CrossRef CAS.
- R. C. Massé, E. Uchaker and G. Cao, Beyond Li-ion: electrode materials for sodium- and magnesium-ion batteries, Sci. China Mater., 2015, 58, 715 CrossRef.
- W. Li, H. Wang, E. Matios and J. Luo, Combining theories and experiments to understand the sodium nucleation behavior towards safe sodium metal batteries, Chem. Soc. Rev., 2020, 49, 3783 RSC.
- H. Au, H. Alptekin, A. C. S. Jensen, E. Olsson, C. A. O'Keefe, T. Smith, M. Crespo-Ribadeneyra, T. F. Headen, C. P. Grey, Q. Cai, A. J. Drew and M.-M. M. Titirici, A revised mechanistic model for sodium insertion in hard carbons, Energy Environ. Sci., 2020, 13, 3469 RSC.
- S. Chen, T. Hu, T. Yu, X. Luo, L. Zhang and F. Li, Structural Feature Design for Carbon Materials toward Sodium Storage: Insights and Prospects, ACS Energy Lett., 2025, 10(4), 1931–1952 CrossRef CAS.
- E. Olsson, J. Cottom, H. Au, Z. Guo, A. C. S. Jensen, H. Alptekin, A. J. Drew, M.-M. Titirici and Q. Cai, Elucidating the Effect of Planar Graphitic Layers and Cylindrical Pores on the Storage and Diffusion of Li, Na, and K in Carbon Materials, Adv. Funct. Mater., 2020, 30, 1908209 CrossRef CAS.
- E. Buiel and J. R. Dahn, Li-insertion in hard carbon anode materials for Li-ion batteries, Electrochim. Acta, 1999, 45, 121 CrossRef CAS.
- L. F. Zhao, Z. Hu, W. H. Lai, Y. Tao, J. Peng, Z. C. Miao, Y. X. Wang, S. L. Chou, H. K. Liu and S. X. Dou, Hard Carbon Anodes: Fundamental Understanding and Commercial Perspectives for Na-Ion Batteries beyond Li-Ion and K-Ion Counterparts, Adv. Energy Mater., 2021, 11, 1 Search PubMed.
- R. A. Adams, A. Varma and V. G. Pol, Carbon Anodes for Nonaqueous Alkali Metal-Ion Batteries and Their Thermal Safety Aspects, Adv. Energy Mater., 2019, 9, 1900550 CrossRef.
- Y. Li, Y. Lu, P. Adelhelm, M.-M. Titirici and Y.-S. Hu, Intercalation chemistry of graphite: alkali metal ions and beyond, Chem. Soc. Rev., 2019, 48, 4655 RSC.
- J. Xiao, N. Xiao, K. Li, L. Zhang, J. Chang, X. Ma, H. Li, J. Bai, Q. Jiang and J. Qiu, Ultra-High Fluorine Enhanced Homogeneous Nucleation of Lithium Metal on Stepped Carbon Nanosheets with Abundant Edge Sites, Adv. Energy Mater., 2022, 12, 2103123 CrossRef CAS.
- F. Flatscher, J. Todt, M. Burghammer, H. S. Søreide, L. Porz, Y. Li, S. Wenner, V. Bobal, S. Ganschow, B. Sartory, R. Brunner, C. Hatzoglou, J. Keckes and D. Rettenwander, Deflecting Dendrites by Introducing Compressive Stress in Li7La3Zr2O12 Using Ion Implantation, Small, 2024, 20, 2307515 CrossRef CAS PubMed.
- R. Mukherjee, A. V. Thomas, D. Datta, E. Singh, J. Li, O. Eksik, V. B. Shenoy and N. Koratkar, Defect-induced plating of lithium metal within porous graphene networks, Nat. Commun., 2014, 5, 3710 CrossRef CAS PubMed.
- A. Rajkamal and R. Thapa, Carbon Allotropes as Anode Material for Lithium-Ion Batteries, Adv. Mater. Technol., 2019, 4, 1900307 CrossRef CAS.
- E. Olsson, J. Yu, H. Zhang, H. Cheng and Q. Cai, Atomic-Scale Design of Anode Materials for Alkali Metal (Li/Na/K)-Ion Batteries: Progress and Perspectives, Adv. Energy Mater., 2022, 12, 2200662 CrossRef CAS.
- Y. Li, Y. Lu, P. Adelhelm, M.-M. Titirici and Y.-S. Hu, Intercalation chemistry of graphite: alkali metal ions and beyond, Chem. Soc. Rev., 2019, 48, 4655 RSC.
- S. Payá, N. Díez, J. Cottom, E. Olsson and M. Sevilla, MgSO4 as an Effective, Low-Temperature Sulfur Dopant for Carbon Materials Enabling Fast Sodium Storage, ACS Appl. Energy Mater., 2024, 7, 10061 CrossRef.
- M. S. Balogun, Y. Luo, W. Qiu, P. Liu and Y. Tong, A review of carbon materials and their composites with alloy metals for sodium ion battery anodes, Carbon, 2016, 98, 162 CrossRef CAS.
- J. C. Pramudita, D. Sehrawat, D. Goonetilleke and N. Sharma, An Initial Review of the Status of Electrode Materials for Potassium-Ion Batteries, Adv. Energy Mater., 2017, 7, 1602911 CrossRef.
- Y. Han, Y. Ni, X. Guo and T. Jiao, Insights into the mechanism of electric field regulating hydrogen adsorption on Li-functionalized N-doped defective graphene: A first-principles perspective, Fuel, 2024, 357, 129655 CrossRef CAS.
- E. Olsson, T. Hussain, A. Karton and Q. Cai, The adsorption and migration behavior of divalent metals (Mg, Ca, and Zn) on pristine and defective graphene, Carbon, 2020, 163, 276 CrossRef CAS.
- R. E. Mapasha, S. P. Kgalema, H. Mapingire and E. Igumbor, Lithium on CH Divacancy Self-Healed Graphane: A First-Principles Study, Nanoenergy Adv., 2024, 4, 122–132 CrossRef.
- S. P. Kgalema, M. Diale, E. Igumbor and R. E. Mapasha, Enhancement of lithiation on a graphane monolayer through extended H vacancy pathways: An ab initio study, Phys. B, 2024, 673, 415490 CrossRef CAS.
- Q. Wang, H. Sun, Q. Li, X. Yang, W. Chen, J. Yan, Y. Lyu, G. Yan, H. Zhao, Z. Meng, Z. Yang and Y. Wang, Enhanced hydrogen storage in K and Na decorated DHP-graphene monolayer: DFT and GCMC study, Chem. Phys. Lett., 2025, 865, 141932 CrossRef CAS.
- W. Cai, Y.-X. Yao, G.-L. Zhu, C. Yan, L.-L. Jiang, C. He, J.-Q. Huang and Q. Zhang, A review on energy chemistry of fast-charging anodes, Chem. Soc. Rev., 2020, 49, 3806 RSC.
- T. Liu, J. P. Vivek, E. W. Zhao, J. Lei, N. Garcia-Araez and C. P. Grey, Current Challenges and Routes Forward for Nonaqueous Lithium-Air Batteries, Chem. Rev., 2020, 120, 6558 CrossRef CAS PubMed.
- B. J. Landi, M. J. Ganter, C. D. Cress, R. A. DiLeo and R. P. Raffaelle, Carbon nanotubes for lithium ion batteries, Energy Environ. Sci., 2009, 2, 638 RSC.
- L. M. Morgan, M. P. Mercer, A. Bhandari, C. Peng, M. M. Islam, H. Yang, J. Holland, S. W. Coles, R. Sharpe, A. Walsh, B. J. Morgan, D. Kramer, M. S. Islam, H. E. Hoster, J. S. Edge and C.-K. Skylaris, Pushing the boundaries of lithium battery research with atomistic modelling on different scales, Prog. Energy, 2022, 4, 012002 CrossRef.
- W. Liu, P. Liu and D. Mitlin, Review of Emerging Concepts in SEI Analysis and Artificial SEI Membranes for Lithium, Sodium, and Potassium Metal Battery Anodes, Adv. Energy Mater., 2020, 10, 2002297 CrossRef CAS.
- F. Wu, J. Maier and Y. Yu, Guidelines and trends for next-generation rechargeable lithium and lithium-ion batteries, Chem. Soc. Rev., 2020, 49, 1569 RSC.
- S. Moharana, G. West, M. Walker, X. S. Yan and M. Loveridge, Controlling Li Dendritic Growth in Graphite Anodes by Potassium Electrolyte Additives for Li-Ion Batteries, ACS Appl. Mater. Interfaces, 2022, 14, 42078 CrossRef CAS PubMed.
- X. Yao, Interface Engineering and Advanced Characterisation for Solid-State Li Metal Batteries, 2022 Search PubMed.
- J. Wang, Q. Ma, S. Sun, K. Yang, Q. Cai, E. Olsson, X. Chen, Z. Wang, A. M. Abdelkader, Y. Li, W. Yan, S. Ding and K. Xi, Highly aligned lithiophilic electrospun nanofiber membrane for the multiscale suppression of Li dendrite growth, eScience, 2022, 2, 655 CrossRef.
- G. Li and C. W. Monroe, Dendrite nucleation in lithium-conductive ceramics, Phys. Chem. Chem. Phys., 2019, 21, 20354 RSC.
- X. Xing, Y. Li, S. Wang, H. Liu, Z. Wu, S. Yu, J. Holoubek, H. Zhou and P. Liu, Graphite-Based Lithium-Free 3D Hybrid Anodes for High Energy Density All-Solid- State Batteries, ACS Energy Lett., 2021, 6, 1831 CrossRef CAS.
- J. Duan, W. Wu, A. M. Nolan, T. Wang, J. Wen, C. Hu, Y. Mo, W. Luo and Y. Huang, Lithium-Graphite Paste: An Interface Compatible Anode for Solid-State Batteries, Adv. Mater., 2019, 31, 1807243 CrossRef PubMed.
- C. Niu, H. Pan, W. Xu, J. Xiao, J.-G. G. Zhang, L. Luo, C. Wang, D. Mei, J. Meng, X. Wang, Z. Liu, L. Mai and J. Liu, Self-smoothing anode for achieving high-energy lithium metal batteries under realistic conditions, Nat. Nanotechnol., 2019, 14, 594 CrossRef CAS PubMed.
- F. Mo, J. Ruan, S. Sun, Z. Lian, S. Yang, X. Yue, Y. Song, Y. N. Zhou, F. Fang, G. Sun, S. Peng and D. Sun, Inside or Outside: Origin of Lithium Dendrite Formation of All Solid-State Electrolytes, Adv. Energy Mater., 2019, 9, 1902123 CrossRef CAS.
- W. Liu, Y. Xia, W. Wang, Y. Wang, J. Jin, Y. Chen, E. Paek and D. Mitlin, Pristine or Highly Defective? Understanding the Role of Graphene Structure for Stable Lithium Metal Plating, Adv. Energy Mater., 2019, 9, 1802918 CrossRef.
- Y. Gu, Y. He, L. Wei, Y. Lian, W. Pan, X. Li, Y. Su, Y. Peng, Z. Deng and Z. Liu, Fast-charging and dendrite-free lithium metal anode enabled by partial lithiation of graphene aerogel, Nano Res., 2022, 15, 9792 CrossRef.
- X. Yu, S. Chen, B. Tang, X. L. Li, J. Zhou, Y. Ren, J. Wei, C. Yang, Y. Guo, Z. Zhou and S. H. Bo, The Debate over Hard Carbon and Alloy Anodes Continues for Solid-State Sodium Batteries, ACS Energy Lett., 2024, 9, 4441 CrossRef CAS.
- E. Olsson, G. Chai, M. Dove and Q. Cai, Adsorption and migration of alkali metals (Li, Na, and K) on pristine and defective graphene surfaces, Nanoscale, 2019, 11, 5274 RSC.
- O. Olaniyan, R. E. Maphasha, M. J. Madito, A. A. Khaleed, E. Igumbor and N. Manyala, A systematic study of the stability, electronic and optical properties of beryllium and nitrogen co-doped graphene, Carbon, 2018, 129, 207 CrossRef CAS.
- H. Liang, J. Ni and L. Li, Bio-inspired engineering of Bi2S3-PPy yolk-shell composite for highly durable lithium and sodium storage, Nano Energy, 2017, 33, 213 CrossRef CAS.
- Q. Meng, B. Deng, H. Zhang, B. Wang, W. Zhang, Y. Wen, H. Ming, X. Zhu, Y. Guan, Y. Xiang, M. Li, G. Cao, Y. Yang, H. Peng, H. Zhang and Y. Huang, Heterogeneous nucleation and growth of electrodeposited lithium metal on the basal plane of single-layer graphene, Energy Storage Mater., 2019, 16, 419 CrossRef.
- S. K. Saju, S. Chattopadhyay, J. Xu, S. Alhashim, A. Pramanik and P. M. Ajayan, Hard carbon anode for lithium-, sodium-, and potassium-ion batteries: Advancement and future perspective, Cell Rep. Phys. Sci., 2024, 5, 101851 CrossRef CAS.
- X. Fan, W. T. Zheng, J.-L. L. Kuo and D. J. Singh, Adsorption of single Li and the formation of small Li clusters on graphene for the anode of lithium-ion batteries, ACS Appl. Mater. Interfaces, 2013, 5, 7793 CrossRef CAS PubMed.
- H. Lv, Y. Yao, M. Yuan, G. Chen, Y. Wang, L. Rao, S. Li, U. I. Kara, R. L. Dupont, C. Zhang, B. Chen, B. Liu, X. Zhou, R. Wu, S. Adera, R. Che, X. Zhang and X. Wang, Functional nanoporous graphene superlattice, Nat. Commun., 2024, 15(1), 1295 CrossRef CAS PubMed.
- T. Hussain, E. Olsson, K. Alhameedi, Q. Cai and A. Karton, Functionalized Two-Dimensional Nanoporous Graphene as Efficient Global Anode Materials for Li-, Na-, K-, Mg-, and Ca-Ion Batteries, J. Phys. Chem. C, 2020, 124, 9734 CrossRef CAS.
- P. C. Tsai, S. C. Chung, S. K. Lin and A. Yamada, Ab initio study of sodium intercalation into disordered carbon, J. Mater. Chem. A, 2015, 3, 9763 RSC.
- E. Olsson, J. Cottom and Q. Cai, Defects in Hard Carbon: Where Are They Located and How Does the Location Affect Alkaline Metal Storage?, Small, 2021, 17, 2007652 CrossRef CAS PubMed.
- E. Olsson, J. Cottom, H. Au, M.-M. Titirici and Q. Cai, Investigating the effect of edge and basal plane surface functionalisation of carbonaceous anodes for alkali metal (Li/Na/K) ion batteries, Carbon, 2021, 177, 226 CrossRef CAS.
- Z. Jian, C. Bommier, L. Luo, Z. Li, W. Wang, C. Wang, P. A. Greaney and X. Ji, Insights on the Mechanism of Na-Ion Storage in Soft Carbon Anode, Chem. Mater., 2017, 29, 2314 CrossRef CAS.
- L.-F. Zhao, Z. Hu, W.-H. Lai, Y. Tao, J. Peng, Z.-C. Miao, Y.-X. Wang, S.-L. Chou, H.-K. Liu, S.-X. Dou, L.-F. Z. Zhao, C. Miao, L.-F. Zhao, Z. Hu, W.-H. Lai, Y. Tao, J. Peng, Y.-X. Wang, S.-L. H. Chou, K. Liu and S.-X. Dou, Hard Carbon Anodes: Fundamental Understanding and Commercial Perspectives for Na-Ion Batteries beyond Li-Ion and K-Ion Counterparts, Adv. Energy Mater., 2021, 11, 2002704 CrossRef CAS.
- M. Liu, A. Kutana, Y. Liu and B. I. Yakobson, First-principles studies of Li nucleation on graphene, J. Phys. Chem. Lett., 2014, 5, 1225 CrossRef CAS PubMed.
- E. Lee and K. A. Persson, Li absorption and intercalation in single layer graphene and few layer graphene by first principles, Nano Lett., 2012, 12, 4624 CrossRef CAS PubMed.
- J. Vandevondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach, Comput. Phys. Commun., 2005, 167, 103 CrossRef CAS.
- J. VandeVondele and J. Hutter, Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases, J. Chem. Phys., 2007, 127, 114105 CrossRef PubMed.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. Vandevondele, Cp2k: Atomistic simulations of condensed matter systems, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15 CAS.
- K. Burke, F. G. Cruz and K.-C. Lam, Unambiguous exchange-correlation energy density, J. Chem. Phys., 1998, 109, 8161 CrossRef CAS.
- T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, CP2K: An electronic structure and molecular dynamics software package - Quickstep: Efficient and accurate electronic structure calculations, J. Chem. Phys., 2020, 152, 194103 CrossRef PubMed.
- M. Krack, Pseudopotentials for H to Kr optimized for gradient-corrected exchange-correlation functionals, Theor. Chem. Acc., 2005, 114, 145 Search PubMed.
- S. Goedecker, M. Teter and J. Hutter, Separable dual-space Gaussian pseudopotentials, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 1703 CrossRef CAS PubMed.
- C. Hartwigsen, S. Goedecker and J. Hutter, Relativistic separable dual-space Gaussian pseudopotentials from H to Rn, Phys. Rev. B:Condens. Matter Mater. Phys., 1998, 58, 3641 CrossRef CAS.
- C. G. Broyden, The convergence of a class of double-rank minimization algorithms 1. General considerations, IMA J. Appl. Math., 1970, 6, 76 CrossRef.
- D. Goldfarb, A Family of Variable-Metric Methods Derived by Variational Means, Math. Comput., 1970, 24, 23 CrossRef.
- D. F. Shanno, Conditioning of Quasi-Newton Methods for Function Minimization, Math. Comput., 1970, 24, 647 CrossRef.
- R. Fletcher, A new approach to variable metric algorithms, Comput. J., 1970, 13, 317 CrossRef.
- J. D. Head and M. C. Zerner, A Broyden-Fletcher-Goldfarb-Shanno optimization procedure for molecular geometries, Chem. Phys. Lett., 1985, 122, 264 CrossRef CAS.
- J. Perdew, K. Burke and M. Ernzerhof, Errata: Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1997, 77, 3865 CrossRef PubMed.
- J. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- A. D. Becke and E. R. Johnson, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 2005, 123, 154108 CrossRef PubMed.
- E. R. Johnson and A. D. Becke, A post-Hartree-Fock model of intermolecular interactions: Inclusion of higher-order corrections, J. Chem. Phys., 2006, 124, 174104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, J. Antony, T. Schwabe and C. Mück-Lichtenfeld, Density functional theory with dispersion corrections for supramolecular structures, aggregates, and complexes of (bio)organic molecules, Org. Biomol. Chem., 2007, 5, 741 RSC.
- E. Olsson, J. Cottom, H. Alptekin, H. Au, M. Crespo-Ribadeneyra, M. M. Titirici and Q. Cai, Investigating the Role of Surface Roughness and Defects on EC Breakdown, as a Precursor to SEI Formation in Hard Carbon Sodium-Ion Battery Anodes, Small, 2022, 18, 2200177 CrossRef CAS PubMed.
- J. Jiao, R. Xiao, M. Han, Z. Wang and L. Chen, Impact of Hydrogen on Lithium Storage on Graphene Edges, Appl. Surf. Sci., 2020, 145886 CrossRef CAS.
- J. Cottom, S. van Vliet, J. Meyer, R. Bliem and E. Olsson, Coverage-dependent stability of Ru x Si y on Ru(0001): a comparative DFT and XPS study, Phys. Chem. Chem. Phys., 2024, 26, 28793 RSC.
- S. Zhang and J. Northrup, Chemical potential dependence of defect formation energies in GaAs: Application to Ga self-diffusion, Phys. Rev. Lett., 1991, 67, 2339 CrossRef CAS PubMed.
- J. Gaberle, D. Z. Gao, M. B. Watkins and A. L. Shluger, Calculating the Entropy Loss on Adsorption of Organic Molecules at Insulating Surfaces, J. Phys. Chem. C, 2016, 120, 3913 CrossRef CAS.
- C. Sutton and S. V. Levchenko, First-Principles Atomistic Thermodynamics and Configurational Entropy, Front. Chem., 2020, 8, 757 CrossRef CAS PubMed.
- F. Friedrich, S. Pieper and H. A. Gasteiger, Entropy Measurements of Li-Ion Battery Cells with Li- and Mn-Rich Layered Transition Metal Oxides via Linear Temperature Variation, J. Electrochem. Soc., 2021, 168, 120502 CrossRef CAS.
- K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- R. S. Mulliken and J. Chem Phys, Electronic Population Analysis on LCAO-MO Molecular Wave Functions. I, J. Chem. Phys., 1955, 23, 1833 CrossRef CAS.
- K. Nakada and A. Ishii, DFT Calculation for Adatom Adsorption on Graphene, in Graphene Simulation, ed. J. Gong, InTech, 2011, ch. 1, pp. 3–19 Search PubMed.
- S. Yang, S. Li, S. Tang, W. Dong, W. Sun, D. Shen and M. Wang, Sodium adsorption and intercalation in bilayer graphene from density functional theory calculations, Theor. Chem. Acc., 2016, 135, 1 Search PubMed.
- D. Shpalter, Z. V. Bobyleva, G. P. Lakienko, A. R. Safiullina, A. Jablanovic, D. S. Lutsenko, O. A. Drozhzhin and E. V. Antipov, Hard carbon anode materials for hybrid sodium-ion/metal batteries with high energy density, J. Power Sources, 2024, 624, 235547 CrossRef CAS.
- F. Xie, Z. Xu, Z. Guo and M.-M. Titirici, Hard carbons for sodium-ion batteries and beyond, Prog. Energy, 2020, 2(4), 042002 CrossRef.
- Z. Jian, Z. Xing, C. Bommier, Z. Li and X. Ji, Hard Carbon Microspheres: Potassium-Ion Anode Versus Sodium-Ion Anode, Adv. Energy Mater., 2016, 6, 1501874 CrossRef.
- D. Chen, W. Zhang, K. Luo, Y. Song, Y. Zhong, Y. Liu, G. Wang, B. Zhong, Z. Wu and X. Guo, Hard carbon for sodium storage: Mechanism and optimization strategies toward commercialization, Energy Environ. Sci., 2021, 14, 2244 RSC.
- J. Zhao, X. Zou, Y. Zhu, Y. Xu and C. Wang, Electrochemical Intercalation of Potassium into Graphite, Adv. Funct. Mater., 2016, 26, 8103 CrossRef CAS.
- Z. Chen, L. Wang, J. Zheng, Y. Huang, H. Huang, C. Li, Y. Shao, X. Wu, X. Rui, X. Tao, H. Yang and Y. Yu, Unraveling the Nucleation and Growth Mechanism of Potassium Metal on 3D Skeletons for Dendrite-Free Potassium Metal Batteries, ACS Nano, 2024, 18, 8496 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5se00130g |
| This journal is © The Royal Society of Chemistry 2025 |

