Online reprogramming electronic bits for N dimension fractal soft deformable structures†
Fengjiao
Bin‡
 a,
Jiaxu
Meng‡
a,
Wei
Chen
bc,
Ruishen
Lou
a,
Xu
Li
a,
Jiangman
Sun
d,
Shikai
Jing
*a and
Dengbao
Xiao
*a
a,
Jiaxu
Meng‡
a,
Wei
Chen
bc,
Ruishen
Lou
a,
Xu
Li
a,
Jiangman
Sun
d,
Shikai
Jing
*a and
Dengbao
Xiao
*a
aBeijing Institute of Technology, Beijing 100021, P. R. China. E-mail: Jingshikai@bit.edu.cn; xdbhangtian@163.com
bBeijing University of Technology, Beijing 100124, P. R. China
cBeijing Aire Intech Eye Hospital, Beijing 100041, P. R. China
dBeijing University of Chemical Technology, Beijing 100029, P. R. China
First published on 15th November 2024
Abstract
Inspired by the complex fractal morphologies and deformations observed in animals and plants, an N-dimensional soft structure composed of stretchable electronic bits has been developed. This soft structure, capable of independent and cooperative motion, can be manipulated through the programming of bits using a machine language based on instruction encoding. This method simplifies the process of changing the bit's step temperature to control its binary state. Theoretical analysis demonstrates that the fractal dimensions and deformation morphologies of the soft structure achieve stability and extremity when the total number of programming bits exceeds eighteen. Considering strip-shaped soft structures as a case study, their ultimate deformation morphologies, covering the reachable regions of all bits, can achieve complexity comparable to that of dandelion tufts and tree crowns. Moreover, the deformation process exhibits agility akin to that of an octopus. We have prepared samples that include strip-shaped soft structures, each containing multiple pairs of bits, and a hand-shaped soft structure equipped with five pairs of bits, intended for conducting deformation programming experiments. These experimental results validated the correctness of the online reprogramming method for soft structures, showing their capability to perform a range of complex deformations, such as the “OK” gesture, and highlighting potential applications in surgical contexts. This design strategy contributes to the development of soft structures, offering contributions from both theoretical and practical perspectives.
1. Introduction
Soft structures have seen increasing research and application in robotics, wearable devices, and medical instruments in recent years. Compared with traditional rigid structures, soft structures possess excellent flexibility and adaptability, enabling complex movements and deformations in unstructured and dynamic environments. This makes them particularly suitable for human–robot interaction, soft grippers, and soft surgical instruments.1 Research on flexible structures has focused on two critical aspects: the control of deformation magnitude and capabilities for deformation, and the programmable nature of deformation modes. These studies have not only expanded the application of flexible materials but also provided new insights into intelligent structure design.2–4Flexible structures have shown substantial promise in robotic applications, particularly in tasks requiring adaptability and precision.5 Their flexibility allows them to perform complex tasks such as gripping and grasping various objects by adjusting their shape and movement.6 Techniques such as pneumatic-driven soft grippers have gained significant attention for their ability to precisely control deformation by modulating air pressure.7–9 These systems offer tunable force and movement, making them particularly well-suited for handling delicate or irregularly shaped objects.10 Research by various groups has demonstrated the versatility of pneumatic3 and hydraulic actuation,11 which has been extensively applied in flexible gripping systems due to their responsiveness and adaptability. For instance, by adjusting the pressure within the actuator,12,13 these systems can grasp a wide range of objects with varying stiffness. The integration of multi-modal sensing technologies, such as strain and pressure sensors, has further advanced control capabilities in soft robotic systems.14–16 These sensors enable real-time monitoring of deformation states, providing critical feedback that allows for adaptive adjustments during the gripping process.17 As a result, the gripping forces can be precisely controlled, enhancing the interaction with objects of different shapes and stiffness. Notably, flexible tactile sensors have been a game-changer in this area, significantly improving the finesse of robotic systems when handling delicate or sensitive materials. In terms of motion control, flexible robots have made great strides by incorporating advanced materials such as shape memory materials (SMMs)18,19 and electroactive polymers (EAPs).2,20 These materials, when exposed to external stimuli like heat or electric fields, enable the robots to perform complex motions, including bending and twisting. The dynamic response of these materials allows flexible robots to move effectively in highly dynamic or challenging environments, making them ideal for bio-inspired applications.
Advancements in flexible materials have enabled programmable deformation through both intrinsic material properties and external stimuli, significantly broadening their applications in various fields.21 Shape memory alloys (SMA) and liquid crystal elastomers (LCE)22–25 have emerged as key materials in systems requiring programmable deformation.26 These materials enable complex, multi-modal shape changes through controlled structural design and phase transitions when exposed to heat, light, or other external stimuli. For instance, LCEs, with their inherent anisotropic properties, offer precise control over deformation, making them particularly suitable for adaptive and reconfigurable systems. Yang et al. demonstrated how such properties allow LCEs to achieve diverse deformation modes, paving the way for their use in various bio-inspired applications.21 In addition, programmable deformation via multi-physical field coupling has become a focus of extensive research. By combining stimuli such as photothermal,27 magnetothermal,28 and electrothermal4 effects, flexible structures can achieve more versatile and complex deformation modes within a single system. Seong et al.29 illustrated the use of magnetically responsive materials, which can rapidly respond to magnetic fields, making them ideal for tasks requiring precise manipulation or targeted grasping. This approach enriches the functional scope of flexible materials, particularly in applications demanding high adaptability.30 The advent of 4D printing technology31 has further expanded the potential of programmable deformation by introducing a time-dependent dimension. This enables flexible materials to dynamically reshape in response to environmental changes, opening up new possibilities in drug delivery systems and biomimetic devices.
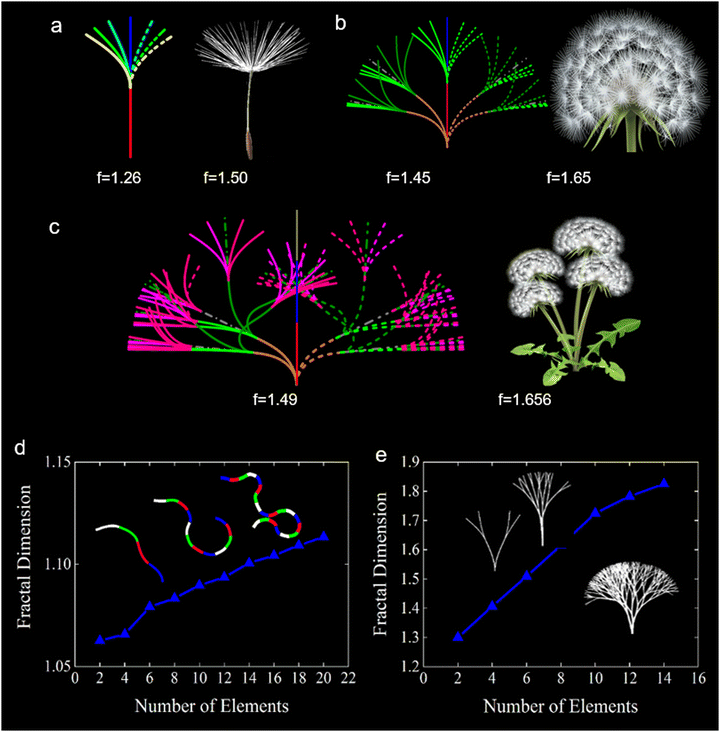
Despite the significant advancements in deformation control, there remains a gap in achieving more diverse and intricate deformation capabilities. While current technologies excel in improving grasping efficiency and stiffness control, more research is needed to expand the range of programmable deformations and to enhance precision in complex tasks. In reconsidering this problem from a reverse-engineering perspective, one could explore whether it is possible to deduce the basic forms required by such structures based on known complex spatial morphologies. For instance, natural woody plants like banyan trees in Fig. 1a are composed of trunks and branches, while herbaceous plants such as dandelions from the Asteraceae family exhibit complex spatial geometric structures (Fig. 1b). In Fig. 1c, the stiffness of mimosa leaf32 adjusts in response to external stimuli, leading to imprecise motion through predetermined deformation. This lack of precision in deformation has also been observed in arabidopsis.33 It is well-known that the octopus34 (Fig. 1d) possesses eight soft tentacles, viewed as components or bits, which can be independently controlled and coordinated with each other, representing an ideal model for deformable soft structures.35 Consider the possibility of controlling the geometric states of all bits through an online program, we can develop soft structures with complex deformation morphologies.
Hence, drawing inspiration from computer programming bits and the static/dynamic deformations observed in plants and animals, we have designed a soft structure made of online-reprogramming electronic bits that can achieve complex dynamic deformations. This bit possesses two distinct physical states composed of stretchable electronics and SMPs with magnetic particles. The mechanical properties of the soft electronic bits vary between the two states, allowing for information to be dynamically and recurrently programmed in real-time, which results in diverse deformation responses. The programming operation of the bit does not interfere with its own deformation, enabling deformation responses to occur concurrently with online programming.
2. Results and discussion
2.1. Reprogramming stretchable electronic bits
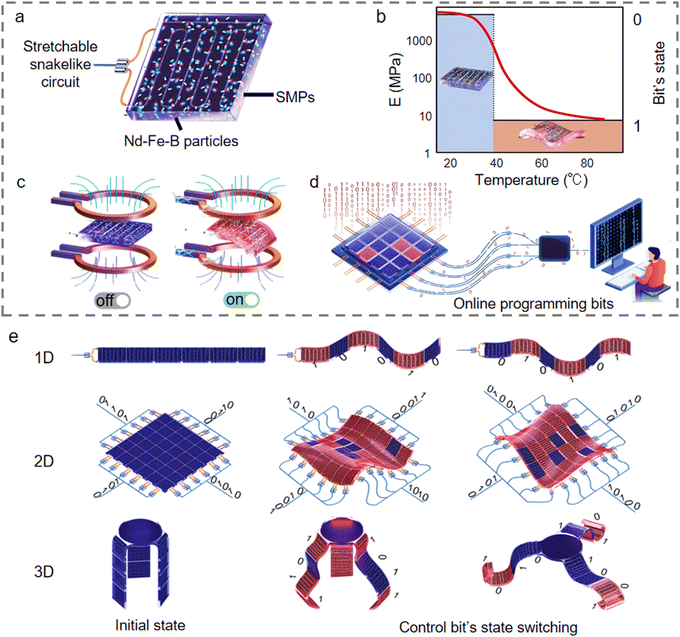
In this case, SMPs composed of magnetized NdFeB particles serve as the soft constituent, combining with the stretchable snakelike heater circuit fabricated through laser etching (refer to Fig. S1, ESI†), to construct the online reprogramming stretchable electronic bits (Fig. 2a). Notably, the snakelike circuit does not significantly affect the mechanical properties or the deformation behavior of the bit. The length and thickness of each programmable bit are 25 mm and 2 mm, respectively. These dimensions can be customized based on specific requirements for length, width, and geometry, as detailed in Section S1 of the ESI.† Contrary to the offline magnetization programming method,36 the online programming approach in this study involves applying voltage to the circuit within the bit, which raises the temperature from 20 °C to 80 °C and maintains it at a steady level. As a result, a notable change in the Young's module E of the programmable bit was achieved. The Young's modulus of the bits can be varied from 20 MPa to approximately 1000 MPa by independently applying or not applying voltage to the snakelike circuit. This modification corresponds to the binary states 1 and 0, reflecting the circuit's off and on states, respectively (Fig. 2b). Furthermore, due to the heating capability of the control circuit, the bit can be rapidly softened. This demonstrates that the response speed of the stretchable electronic bit can be modulated by the power supplied to the control circuit.As shown in Fig. 2c, the reprogrammable bit in state 1, indicating the activation of the stretchable snakelike heater circuit, can perform large bending deformation under a magnetic field. In contrast, when the circuit is deactivated (state 0), the bit exhibits negligible deformation. Thus, guided by the principles of binary coding, the deformations of the bits were reprogrammed, providing promising opportunities for achieving online shape manipulation in soft structures (see Fig. 2d). In Fig. 2a and c, a single bit is shown, while Fig. 2d includes a 4 × 4 matrix, consisting of a total of 16 bits. In this study, each bit can function independently as well as collaboratively within soft structures, like the motions observed in octopuses.34 As illustrated in Fig. 2e, the integration of multiple bits capable of independent and cooperative motion enables the creation of a soft N-dimensional fractal (N ∈ (1, 3)) structure that can be programmed online, thus supporting the intelligent execution of complex deformation tasks. It is noteworthy that this method does not require pre-programming of the bit offline, a task that is impractical for most current soft materials.37
2.2. Large deformation of reprogramming electronic bits
This section explores the impact of the number of bits on the deformation morphology and the accessible regions of the soft structure. Focusing on a 1D strip-shaped soft structure with n bits, as illustrated in Fig. 2e, this study investigates morphology prediction based on the theory of large deformations.38 The objective is to gain a comprehensive understanding of the deformation process and to facilitate the informed design of rational 2D/3D soft structures. The detailed derivation process can be found in the second section of the ESI† titled Theoretical analysis, where the governing equation for large deformation is given by: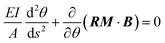 | (1) |
The deformation of each bit can be equivalent to that of a cantilever beam under concentrated load, as described by the theory of small deformation in beams.39,40 The deformation governing equation could be presented as follows:
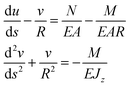 | (2) |
From eqn (1) and (2), the deformation capacity and accessible region of a 1D strip-shaped soft structure are determined by the strength and direction of the magnetic field, the number of bits n, and the geometry of the sections. Given the two programming states for each bit, it becomes clear that the total number of programming combinations for the soft structure can amount to n2. With an increase in n, both the deformation morphology and the fractal dimensions of the soft structure become increasingly complex, indicating a stronger deformable capability. The fractal dimension thoroughly investigated in numerous studies,41 denoted by f, is introduced to characterize deformation capability and its associated morphology.
| N(d) = Cd±f | (3) |
Fig. 3a demonstrates that the accessible region of a single bit, with two programming combinations, forms a sector region when the magnetic strength is set. This morphology resembles the white villi of dandelion seeds. Fig. 3b depicts the morphology and accessible region of a soft structure constructed from two bits, featuring four programming combinations. Due to the independent control of the two bits, the resultant morphology is more intricate, like a single dandelion cluster. Fig. 3c shows that the morphology and accessible region of the soft structure, consisting of three bits with nine programming combinations, have flourished to mimic clusters of dandelions. Additionally, the fractal dimension (f) becomes stable when the number of bits (n) exceeds 18 (Fig. 3d and e), indicating that the deformation capability of the soft structure has reached its maximum. Video 1 (ESI†) captures the deformation progression of the soft structure as n increases, where labels B1, B2, B3, and B4 represent the applied magnetic strength and direction on the bits. These findings show that by modifying the number and geometric parameters of the bits, along with the applied magnetic field, desired deformation morphologies can be realized.
2.3. Online reprogramming experiment for soft structure
For specific morphing tasks, it is essential to program the state information of all bits systematically and controllably in soft structures. The design process involves inversely determining the number of bits and their state information, reflecting the idea that interpretations can differ greatly among individuals. Likewise, numerous combinations of bit numbers and deformation sequences are possible. In contemporary computer science, program development entails algorithm design and the use of programming languages for sequential programming and compilation. Accordingly, a methodology for programming and compiling soft structures is introduced in this work. In this approach, the algorithmic flow is designed based on the deformation control equation and its numerical solutions, with each bit's state being manually programmed using machine language (the details of the experimental procedure are outlined in Section S4.2 and S4.3 of the ESI†). Concurrently, the stretchable, snakelike circuit heaters within the bits are used to execute the programming.Fig. 4 shows both the deformation simulation and experimental results for the 1D strip-shaped soft structure, in which the colors in the simulation diagram represent displacement, while the colors in the experimental diagram represent two bits. The experimental setup features a yellow grid background, with each square in the grid having a side length of 10 mm. Additionally, the length of each flexible bit is 25 mm. The procedure and parameter settings for the simulation are provided in Section S3 of the ESI.† The model and specific arrangement of the experimental equipment can be found in Section S4.1 (ESI†). Programming codes ‘01’, ‘10’, and ‘11’ have been assigned to represent deformation states 1, 2, and 3, respectively, enabling the realization of three distinct deformations with two bits. Furthermore, we can also achieve the deformation of a soft structure by changing the direction of the magnetic field. Specifically, reversing the magnetic direction from that used in states 1 to 3 led to the observation of two additional deformations, coded as ‘11’ for state 4 and ‘01’ for state 5 (Fig. 4a). All deformation processes are documented in Movie 2 (ESI†) illustrating that the soft structure can change its programming state in real time to control its deformation. Additionally, the programming experiments and simulation results for soft structures with two and three strips are showcased in Fig. 4b and c. These findings not only reveal the independent deformation capabilities of each bit but also their capacity for programmable collaboration. The deformation process is illustrated in Movie 2 (ESI†). As depicted in Fig. 4b, the soft structure comprising two strips can achieve two-dimensional deformations, controlled by four codes. For instance, ‘1110’ corresponds to deformation state 6, and ‘1100’ to deformation state 7. More complex collaborative deformations have been demonstrated by soft structures consisting of three strips, which can be programmed with six codes (Fig. 4c). We compared the experimental deformation results shown in Fig. 4 with the simulation data by calculating the error based on the maximum displacement at the end of the flexible strip. The comparison between the experimental results and the error is presented in Fig. S9 (ESI†), with detailed quantitative error calculations provided in Table S2 (ESI†). As shown, the maximum displacement error at the strip's end is less than 15%.
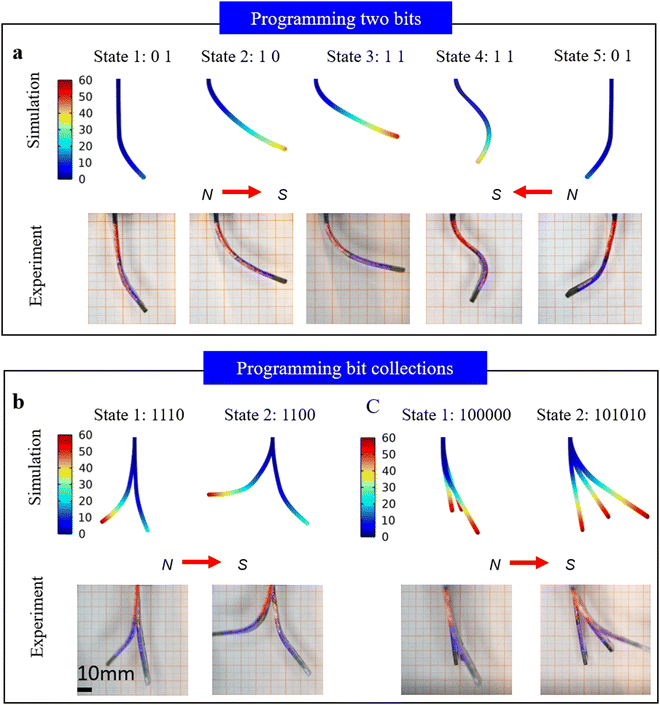 | ||
| Fig. 4 Online programming of soft structures: (a) one strip with 2-bits, (b) two strips with 4-bits, and (c) three strips with 6-bits. | ||
We have also developed a hand-shaped soft structure comprising five strips with two bits each, which can be programmed in real-time online. The human hand has 27 degrees of freedom, enabling it to execute complex movements within a quarter-sphere directed towards the palm's center, whereas a typical manipulator is limited to fewer than 7 degrees of freedom.42 In the hand-shaped soft structure, each strip, equipped with two bits to simulate a finger, allows for achieving 2 × 516 degrees of freedom. The degrees of freedom increase dramatically with the number of bits, and this advanced programming capability deformation exceeds that of all existing rigid and soft robot hands or manipulators.43Fig. 5a illustrates an “OK” gesture and a controlled clench, with the bit length consistent with that in Fig. 4. These deformation processes are demonstrated in Movie 4 (ESI†). To demonstrate the soft structure's potential for more promising and complicated movements, we have also executed the action of grasping a lens during cataract surgery. In cataract surgery, the lens is emulsified using ultrasound, and the resulting debris is removed with special instruments before an artificial lens is implanted (Fig. 5b) showcased in Movie 5 (ESI†). Based on the lens contour, the hand-shaped soft structure is programmed online to progressively enclose and grasp the lens. This forms a protective barrier that assists in shielding surrounding tissues from the ultrasonic emulsification shock wave during cataract surgery. Fig. 5c preliminary displays how the programmed soft structure deforms to wrap a lens model in vitro. Programming deformation is an inverse problem that does not have a single solution regarding the number of bits and their programming sequence. This design strategy can be further extended to hydrogels, artificial muscles, phase change alloys, and other materials that react to external stimuli.
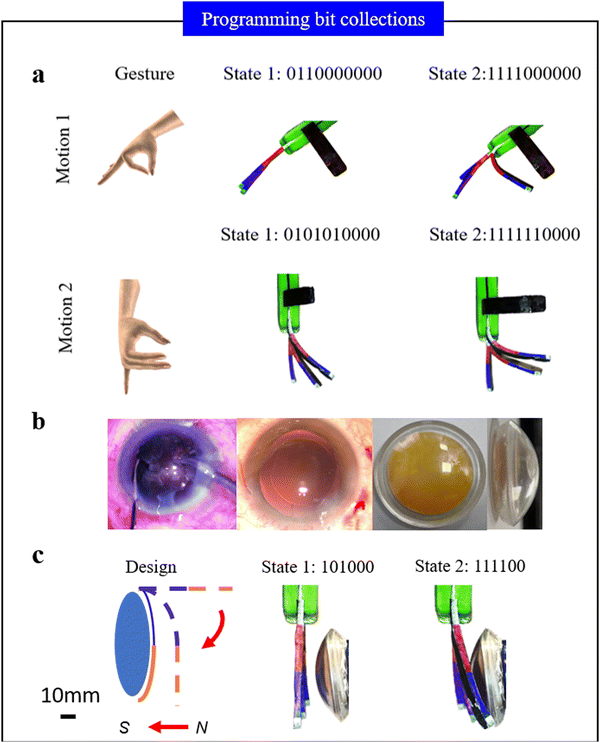 | ||
| Fig. 5 Online programming for hand-shaped soft structures: (a) “OK” gesture, (b) cataract extraction surgery, and (c) cover and grasp lens. | ||
3. Experimental
3.1. Preparation of the SMP material
The stretchable electronic bits are prepared by the solution polymerization method. Table S1 (ESI†) shows a list of materials involved. The process for preparing the magnetotropic SMP solutions is illustrated in Fig. S1 (steps ① to ②) (ESI†).3.2. Fabrication of reprogramming electronic bits
The procedure for fabricating the soft structure is detailed in Fig. S1 (steps ③ to ⑤) (ESI†). The dimensions of a single bit are 25 mm in length, 25 mm in width, and 2 mm in thickness. The specific fabrication steps are outlined as follows:Firstly, fix the stretchable snakelike heater circuit within the mold, ensuring the circuit is positioned flatly at the mold's center. Next, place the beaker with the freshly mixed solution in a vacuum oven to remove any form, then gradually pour the solution into the model in four increments using a burette. Due to the presence of the electric heater circuit, some of the SMP solution may adhere to the circuit when introduced into the mold, potentially reintroducing bubbles during this process. Therefore, after each addition, the mold should be shaken on the table multiple times to ensure the solution is evenly distributed between the mold and the circuit. This action also helps disperse some air bubbles, while others will rise to the surface and escape. Secondly, transfer the solution to a vacuum box for a second defoaming step, aimed at removing the air bubbles introduced during the solution's addition to the model. Before activating the heating switch of the drying oven, the vacuum balance valve should be opened. It is advisable not to maintain the vacuum drying oven in a vacuum state throughout the curing process.
To ensure the soft structure possesses sufficient magnetic properties for responding to external magnetic fields, the embedded NdFeB particles must be magnetized. The direction of magnetization aligns the length of the soft structure, and the underlying principle is as follows:
The charge stored in the capacitor is charged by a boost circuit and then instantaneously discharged to the inductive coil via a control circuit, generating a high current. When the magnetic field is large enough to overcome the internal coercivity of the magnetic material and the external magnetic field is subsequently removed, the magnetic material retains a residual magnetization, thereby concluding the magnetization process. After the completion of the magnetization process, the magnetization strength of a single soft structure piece is measured to be approximately 38 mT.
3.3. Deformation simulation of a soft structure
COMSOL Multiphysics® software is used to simulate the force-magnetic coupling field within the soft structure, examining its deformation. Detailed settings and calculations can be found in the third section of the ESI,† “Numerical simulation”.3.4. Steps for online programming of a soft structure containing n bits
Step 1: begin by identifying the desired shape of the soft structure to preliminarily determine the potential deformation profile, final deflection, and inclination angles.Step 2: according to the length of the bit, divide the deformation contour's length to determine the deformation state of the nth bit, including both bending contour and rotation angle. Segment the deformation contour in alignment with the lengths of the bits, and then specify the deformation state for all n bits, including their bending deformation contours and rotation angles.
Step 3: determine the sequence of potential deformations based on the rotation angles of the bits. For those bits requiring state adjustments, set the value of Young's modulus and the operating duration of the temperature control system according to the deformation control eqn (S19) in the ESI.†
Step 4: establish the potential deformation sequences by evaluating the rotation angles of all bits. Assign a binary value of 1 to bits identified for deformation and a value of 0 to those that remain undeformed. Lastly, manually manipulate the stretchable snakelike heater circuit to encode this information, thereby preserving the binary state for online reprogramming of the electronic bits. The details of the experimental procedure are outlined in Sections S4.2 and S4.3 of the ESI.†
4. Conclusions
In summary, we propose a reprogrammable soft electronic bit whose mechanical properties can be digitally, independently, and reversibly programmed. All bits’ binary information is constantly read and written following binary codes, demonstrating the ability for real-time online programming. This enables the bits not only to perform independent deformation but also to cooperate with one another. The deformation morphology and accessible regions of the strip-shaped soft structure resemble dandelion clusters and octopus’ movements. Furthermore, online programming experiments involving a hand-shaped soft structure, which possesses far more degrees of freedom than both a human hand and a manipulator, have highlighted its complex deformation capabilities, validated the effectiveness of this design strategy.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Key R&D Program of China (2021YFB1715100, 2023YFB4604800), the National Natural Science Foundation of China (Grant No. 11802031, 12172055), and the opening fund of State Key Laboratory of Mechanical Structure Strength and Vibration (SV2020-KF-11).References
- H. Liu, W. Zhang, X. Guo and S. Zhang, IEEE Rob. Autom. Lett., 2024, 9, 390 Search PubMed.
- S. Yin, D. R. Yao, Y. Song, W. Heng, X. Ma, H. Han and W. Gao, Chem. Rev., 2024, 124, 11585–11636 CrossRef CAS PubMed.
- S. K. Talas, B. A. Baydere, T. Altinsoy, C. Tutcu and E. Samur, Soft Rob., 2020, 7, 521–533 CrossRef PubMed.
- J. Zhang, H. Tian, H. Liu, D. Wang, Y. Wu, X. Li, C. Wang, X. Chen and J. Shao, Adv. Funct. Mater., 2024, 34, 2309800 CrossRef CAS.
- Z. Tian, B. Xu, G. Wan, X. Han, Z. Di, Z. Chen and Y. Mei, Nat. Commun., 2021, 12, 509 CrossRef CAS PubMed.
- X. Hu, I. C. Yasa, M. Mastrangeli and Z. Ren, Sci. Adv., 2021, 7, eabe8436 CrossRef CAS.
- Q. Zhao, L. Dong, M. Ren and Y. Wang, Sci. Adv., 2022, 8, eabm5616 CrossRef.
- T. Sun, Y. Chen, T. Han, C. Jiao, B. Lian and Y. Song, Rob. Comput. Integr. Manuf., 2020, 61, 101848 CrossRef.
- S. Xu, S. Zhang, R. Lei, Y. Liu, W. Bu, X. Wei and Z. Zhang, Prog. Nat. Sci.: Mater. Int., 2023, 17, 9565–9574 Search PubMed.
- L. Blanc, A. Delchambre and P. Lambert, Actuators, 2017, 6, 23 CrossRef.
- G. L. Smith, J. B. Tyler, N. Lazarus, H. Tsang, L. Viornery, J. Shultz and S. Bergbreiter, Adv. Funct. Mater., 2023, 33, 2207435 CrossRef CAS.
- G. Shin, Y. Choi, B. Jeon, I. Choi, S. Song and Y. L. Park, Adv. Funct. Mater., 2024, 34, 2302895 CrossRef CAS.
- A. I. Acevedo-Velazquez, Z. Wang, A. Winkler, N. Modler and K. Röbenack, J. Phys. Conf. Ser., 2024, 2716, 012049 CrossRef.
- O. Gul, J. Kim, K. Kim, H. J. Kim and I. Park, Adv. Mater. Technol., 2024, 2302134 CrossRef CAS.
- S. E. Navarro, S. Nagels, H. Alagi, L.-M. Faller, O. Goury, T. Morales-Bieze, H. Zangl, B. Hein, R. Ramakers and W. Deferme, IEEE Rob. Autom. Lett., 2020, 5, 5621–5628 Search PubMed.
- A. B. da Silva, G. E. Mendes, E. S. Bragato, G. L. Novelli, M. Monjardim and R. M. Andrade, Biomimetics, 2024, 9, 110 CrossRef CAS.
- J. Lee, T. Kim, H. Kim, S. Im, J. Park, I. Park, D. H. Park, B. Han, D. Kang and G. Lee, Adv. Intell. Syst., 2024, 2400624 CrossRef.
- B. Jin, H. Song, R. Jiang, J. Song, Q. Zhao and T. Xie, Sci. Adv., 2018, 4, eaao3865 CrossRef.
- X. Li, Y. Ma, C. Wu, Y. Wang, S. Zhou, X. Gao and C. Cao, Smart Mater. Struct., 2024, 33, 045011 CrossRef CAS.
- F. Hartmann, L. Penkner, D. Danninger, N. Arnold and M. Kaltenbrunner, Sci. Adv., 2021, 8, 2003104 CrossRef CAS PubMed.
- Y. Yang, Y. Wang, M. Lin, M. Liu and C. Huang, Mater. Horiz., 2024, 11, 2180–2190 RSC.
- S. Li, H. Bai, Z. Liu, X. Zhang, C. Huang, L. W. Wiesner, M. Silberstein and R. F. Shepherd, Sci. Adv., 2021, 7, eabg3677 CrossRef CAS PubMed.
- W. Li and X. S. Zhang, Comput. Methods Appl. Mech. Eng., 2023, 417, 116393 CrossRef.
- C. Wang, K. Sim, J. Chen, H. Kim, Z. Rao, Y. Li, W. Chen, J. Song, R. Verduzco and C. Yu, Adv. Mater., 2018, 30, 1706695 CrossRef PubMed.
- X. Li, Y. Ma, C. Wu, Y. Wang, S. Zhou, X. Gao and C. Cao, Smart Mater. Struct., 2024, 33, 045011 CrossRef CAS.
- Z. Jiao, Z. Hu, Z. Dong, W. Tang, H. Yang and J. Zou, Sci. Adv., 2024, 11, 2305501 CrossRef CAS.
- S. Yang, H. Zhang, X. Sun, J. Bai and J. Zhang, ACS Nano, 2024, 18, 5847–5863 CAS.
- J. Tang and B. Sun, Appl. Phys. Lett., 2022, 120 Search PubMed.
- M. Seong, K. Sun and S. Kim, et al. , Nat. Commun., 2024, 15, 7929 CrossRef CAS PubMed.
- Y. Kim, H. Yuk, R. Zhao, S. A. Chester and X. Zhao, Nature, 2018, 558, 274–279 CrossRef CAS PubMed.
- H. Yao, Y. Wen, H. Tian, Z. Zhou, Y. Di, Y. Zhang, X. Luo and J. Shao, IEEE Trans. Ind. Electron., 2023, 71, 7413–7423 Search PubMed.
- Z. Tian, B. Xu, G. Wan, X. Han, Z. Di, Z. Chen and Y. Mei, Nat. Commun., 2021, 12, 509 CrossRef CAS.
- Y. Kim, H. Yuk, R. Zhao, S. A. Chester and X. Zhao, Nature, 2018, 558, 274–279 CrossRef CAS PubMed.
- B. Jin, H. Song, R. Jiang, J. Song, Q. Zhao and T. Xie, Sci. Adv., 2018, 4, eaao3865 CrossRef PubMed.
- O. M. Wani, H. Zeng and A. Priimagi, Nat. Commun., 2017, 8, 15546 CrossRef CAS PubMed.
- H. Kim, J. Choi, K. K. Kim, P. Won, S. Hong and S. H. Ko, Nat. Commun., 2021, 12, 4658 CrossRef CAS PubMed.
- L. Hines, K. Petersen, G. Z. Lum and M. Sitti, Adv. Mater., 2017, 29, 1603483 CrossRef.
- N. J. Provart, J. Alonso, S. M. Assmann, D. Bergmann, S. M. Brady, J. Brkljacic, J. Browse, C. Chapple, V. Colot and S. Cutler, New Phytol., 2016, 209, 921–944 CrossRef CAS PubMed.
- C. Larson, B. Peele, S. Li, S. Robinson, M. Totaro, L. Beccai, B. Mazzolai and R. Shepherd, Science, 2016, 351, 1071–1074 CrossRef CAS.
- J. A. Fan, W.-H. Yeo, Y. Su, Y. Hattori, W. Lee, S.-Y. Jung, Y. Zhang, Z. Liu, H. Cheng and L. Falgout, Nat. Commun., 2014, 5, 3266 CrossRef PubMed.
- C. Laschi, M. Cianchetti, B. Mazzolai, L. Margheri, M. Follador and P. Dario, Adv. Rob., 2012, 26, 709–727 CrossRef.
- J. Gagnepain and C. Roques-Carmes, Wear, 1986, 109, 119–126 CrossRef.
- K. Kreutz-Delgado, M. Long and H. Seraji, Int. J. Rob. Res., 1992, 11, 469–481 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01051e |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |