Open Access Article
Open Access ArticleTheoretical study of the impact of dilute nanoparticle additives on the shear elasticity of dense colloidal suspensions†
Subhasish
Chaki
 ade,
Benito
Román-Manso
f,
Larissa
Senatus
f,
Jennifer A.
Lewis
f and
Kenneth S.
Schweizer
ade,
Benito
Román-Manso
f,
Larissa
Senatus
f,
Jennifer A.
Lewis
f and
Kenneth S.
Schweizer
 *abcd
*abcd
aDepartment of Materials Science, University of Illinois, Urbana, IL 61801, USA. E-mail: kschweiz@illinois.edu
bDepartment of Chemistry, University of Illinois, Urbana, IL 61801, USA
cDepartment of Chemical & Biomolecular Engineering, University of Illinois, Urbana, IL 61801, USA
dMaterials Research Laboratory, University of Illinois, Urbana, IL 61801, USA
eInstitut für Theoretische Physik II-Soft Matter, Heinrich-Heine-Universität, Düsseldorf 40225, Germany
fSchool of Engineering and Applied Sciences, Harvard University, Cambridge, Massachusetts 02138, USA
First published on 29th January 2025
Abstract
Motivated by basic issues in soft matter physics and new experimental work on granule–nanoparticle mixtures, we systematically apply naive mode coupling theory with accurate microstructural input to investigate the elastic shear modulus of highly size asymmetric, dense, chemically complex, colloid–nanoparticle mixtures. Our analysis spans four equilibrium microstructural regimes: (i) entropic depletion induced colloid clustering, (ii) discrete adsorbed nanoparticle layers that induce colloid spatial dispersion, (iii) nanoparticle-mediated tight bridging network formation, and (iv) colloidal contact aggregation via direct attractions. Each regime typically displays a distinctive mechanical response to changing colloid–nanoparticle size ratio, packing fractions, and the strength and spatial range of interparticle attractive and repulsive interactions. Small concentrations of nanoparticles can induce orders of magnitude elastic reinforcements typically involving single or double exponential growth with increasing colloid and/or nanoparticle packing fraction. Depending on the system, the elementary stress scale can be controlled by the colloid volume, the nanoparticle volume, or a combination of both. Connections between local microstructural organization and the mixture elastic shear modulus are established. The collective structure factor of the relatively dilute nanoparticle subsystem exhibits strong spatial ordering and large osmotic concentration fluctuations imprinted by the highly correlated dense colloidal subsystem. The relevance of the theoretical results for experimental mixtures with large size asymmetry, particularly in the context of 3D ink printing and additive manufacturing, are discussed.
I. Introduction
Nanoparticles (NP) are frequently used as dilute additives to enhance the mechanical and other properties of dense colloidal suspensions via manipulation of their concentration, size, and tunable attractive and repulsive NP–NP and NP–colloid interactions.1–6 A significant challenge lies in the rational control of such multi-faceted modifications, how the colloid spatial organization is modified, and its impact on bulk properties. The NP (or small nonadsorbing polymer) induced entropic depletion attraction between colloids due to excluded volume repulsions7–9 is always present in mixtures with large size asymmetry, and its impact on structure, phase transitions, and emergent amorphous solid states (glasses, gels) has been extensively studied.10–24 However, at high colloid packing fractions, complex many body effects emerge25 that introduce new physics not present in the classic depletion scenario formulated for dilute colloidal suspensions and non-interacting small objects. For example, if colloids are at very high concentration, the nanoparticles can less efficiently explore the interstitial regions between colloids and must exhibit nontrivial spatial correlations.In many synthetic and biological systems, multiple competing and tunable energetic interactions can qualitatively modify suspension microstructure and mechanical properties. These include not only the classic DVLO26,27 van der Waals attraction due to dielectric property mismatch and Coulomb repulsion if the colloid surface is charged, but also NP-mediated interactions. The latter include attractions of diverse chemical origins such as NP–colloid van der Waals, Coulomb, hydrophobic, and polymer brush coatings in poor solvents. Such attractions can drive colloid and/or NP clustering, physical bonding, and gelation or “attractive glass” formation at ultra-high concentrations.21–24,28,29 In addition, NP–colloid interfacial attractions can lead to NP adsorption on the colloid surface, possibly inducing steric stabilization of the large colloids, and/or NP-mediated tight bridging of colloids which can result in a network-like amorphous solid.5,30–34 Complexity can also arise from repulsive NP–NP and NP–colloid interactions.
In many real materials of diverse chemical constitution and solution conditions, multiple interactions are simultaneously present. Their consequences on mixture microstructure and mechanical properties is in general not additive, and depends on size asymmetry and packing fractions. A similar complexity arises in polymer nanocomposite (PNC) melts,12,35,36 though the nature of interactions is somewhat simpler since such materials typically do not involve solvent and the fillers and polymers are uncharged. Moreover, the nanoparticles in PNCs are present at high concentrations, rather than as dilute additives, to achieve the desired property modification.
The most elementary mechanical property is the linear elastic shear modulus. For very dense size asymmetric mixtures it remains poorly understood at the microscopic level, despite its high engineering importance for 3D printing and additive manufacturing,37–41 and high relevance to the yield stress required to induce a solid-to-fluid transition. Though nonequilibrium cluster formation via irreversible aggregation and fractal geometry considerations are important in lower solids packing fraction suspensions,42–48 these are not leading order effects for the highly concentrated colloidal systems of present interest.
Progress in understanding the structure and dynamics of dense size asymmetric mixtures has been made using molecular dynamics (MD) and Monte Carlo (MC) simulations,4,49–55 although computation of the amorphous solid shear modulus is rare. Moreover, such tools become increasingly difficult or intractable to employ for systems with large size asymmetry, especially in very dense mixtures in the presence of strong attractive interactions where additional equilibration issues often arise. Theoretical advances have been made in developing a microscopic understanding of the shear modulus of quiescent (undeformed) kinetically arrested size asymmetric dense mixtures based on force-level statistical mechanical approaches such as the microscopic ideal mode coupling theory (MCT)56–58 and its single particle naive analog (NMCT).31,59,60 These approaches can be predictive since the time persistent forces and stresses underlying emergent elasticity are quantified using integral equation theory (IET)13,17,61 to determine the necessary structural correlation input. However, the accuracy of IET depends on the choice of approximate closure relations for the Ornstein–Zernike (OZ) equations, which can significantly affect the elastic modulus predictions.
The crucial importance of having accurate microstructural information to theoretically predict the elastic shear modulus has been recently demonstrated for 1-component ultra-dense hard sphere fluids and colloidal suspensions.62,63 Adoption of the classic Percus–Yevick (PY) closure61 for computing the structural input to NMCT leads to the prediction of a single exponential growth law for the shear modulus at high packing fractions. This agrees with experiments64 up to a high packing fraction of ∼60%, then qualitatively fails since a second, much steeper exponential growth regime emerges at higher concentrations but well below random close packing (RCP). Two of the present authors have shown63 this can be understood as a consequence of qualitative structural changes upon approaching the RCP state as captured by adopting the modified Verlet (MV) closure.65,66 The MV closure incorporates longer range correlation effects arising from a many-body entropic attraction between hard particles. The predictions of NMCT combined with OZ–MV theory are in excellent agreement with experiments and simulations for the equation of state, compressibility, radial distribution function, and dynamic elastic modulus.62,63 The superior accuracy of OZ–MV theory for the equilibrium properties of size asymmetric dense colloidal mixtures and melt polymer nanocomposites in the presence of strong short range attractive interactions has also been validated based on comparison to simulations of model systems.32,67
Building on the above theoretical advances, we aim to broaden and deepen understanding of the elastic shear modulus in kinetically arrested, globally homogenous, amorphous solid states (dense gels, attractive glasses, repulsive glasses) of size asymmetric colloid–NP mixtures. We focus on dilute NP concentrations, and show they can induce orders of magnitude enhancement of the mixture elastic modulus at high packing fractions.
The high-level motivation of this study stems from both the fundamental soft matter science, and its relevance to 3D printing applications using Brownian colloidal and also non-Brownian granular mixtures.68–73 For the latter systems, it is interesting to note that recent experimental studies have found intriguing effects of nm-scale local chemistry and temperature despite their granular nature.39,74–77 Here, we present elastic shear modulus data for a new experimental realization of a dense granular suspension in the presence of dilute Brownian nanoparticles relevant to printing applications. We believe our theoretical analysis provides qualitative insights relevant to this system which consists of a low concentration of polymer-coated 30 nm silica nanoparticles in dense suspensions of glass granules. Specifically, we have experimentally discovered that the shear modulus exhibits a bi-exponential increase with granule loading, with a crossover around a packing fraction of 50% to a much steeper exponential growth. Such behavior is qualitatively similar to the recent experimental and theoretical studies of Brownian hard sphere colloid suspensions.63,64 More generally, our new experimental system is chemically and structurally complex with many competing interactions. The present theoretical study seeks to explore the connection between tunable interactions, structure, size asymmetry, NP composition, and colloid concentration on shear elasticity.
Section II briefly describes new motivating experimental results for the linear elastic shear modulus of a granular-nanoparticle mixture. Section III presents the theoretical methods and interaction potential models employed. A systematic numerical study of the elastic modulus across a broad chemical parameter space at a fixed large size asymmetry is given in Section IV. Section V examines the effect of size ratio. Example results for the microstructural correlations, and their relation to the elastic modulus trends, are presented in Section VI. The paper concludes in Section VII with a summary and future outlook. The Appendix summarizes a technical theory aspect. The ESI† presents additional theory and experimental figures that complement or buttress our scientific statements and conclusions, and a review of the derivation of the theoretical expression for the elastic shear modulus of mixtures.
II. Experiments
A. Suspension formulation
Dense granular-nanoparticle suspensions were created using the following materials and procedure. First, a stock suspension of polyethylenimine (PEI, branched, Mw = 1200, polysciences) coated silica nanoparticles (NPs) at pH ∼ 6 was created. PEI was dissolved in a commercially available NP suspension [LUDOX TM-50 colloidal silica (Sigma-Aldrich), which has a specific surface area of 140 m2 g−1, an average diameter of d = 30 nm, and particle loading of 50 wt% in water at pH ∼ 9] to achieve a surface coverage of 1 mg of PEI per m2 of SiO2 NPs. The resulting suspension is then sonicated (Ultrasonic cleaning bath, M series 2800, Branson Ultrasonics) for 60 s prior to adjusting its pH in a stepwise fashion with a HCl solution (6 M hydrochloric acid, VWR) to a final value of pH ∼ 6. After each HCl aliquot is added, the suspension is sonicated for 300 s followed by speed mixing (SpeedMixer DAC 600.2; FlackTek, Inc.) for 180 s at 2100 rpm.Granular–NP suspensions were then prepared by adding an appropriate amount of an aqueous hydroxyethyl cellulose solution (HEC, 2-hydroxyethyl cellulose, Mw = 1.3 × 106, 5 wt% in DI water) to the PEI-coated NP stock suspension. This dilute polymeric additive increases the solution viscosity, which is necessary to enable 3D printing of granular–NP inks. The resulting suspension is then speed mixed for 120 s at 1800 rpm. Next, granular particles (GPs, silica-based glass spheres, average diameter of D = 40 μm, MO-SCI) are added to this suspension in two steps, followed by speed mixing at 2100 rpm after each step. The polydispersity of the granular particles is relatively low, with 80% of the particle diameters ranging from 38–53 microns. At pH ∼ 6, bare GPs and PEI-coated NPs are oppositely charged; hence, it is expected that PEI-coated NPs will strongly absorb onto GPs forming a monolayer coating that drives their charge reversal. Finally, a divalent salt (ammonium sulfate (NH4)2SO4, ultrapure 99+%, ThermoFisher Scientific) is added to the suspension to induce an attractive interaction between PEI-coated NPs (both those NPs that are free in suspension as well as those adsorbed on the GPs), followed by speed mixing for 60 s at 2100 rpm. A schematic of the experimental system is shown in Fig. 1.
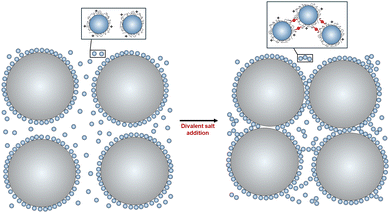 | ||
| Fig. 1 Schematic silicate glass granules and PEI-coated silica NP mixtures before (left) and after (right) the addition of a divalent salt. | ||
Using the above approach, we have produced GP–NP suspensions composed of varying GP packing fractions ϕG = 0.20–0.60, at a fixed NP packing fraction of 0.015, a (NH4)2SO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PEI weight ratio of 0.2, a PEI
PEI weight ratio of 0.2, a PEI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SSANP ratio of 1 mg m−2, and a HEC
SSANP ratio of 1 mg m−2, and a HEC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water weight ratio of 0.02. We expect these mixtures will influenced by (a) van der Waals attractions and Coulomb repulsions between GPs resulting from dielectric mismatch and GP surface charge, respectively, (b) GP–NP Coulomb attractions, and (c) salt-mediated NP–NP attractions.
water weight ratio of 0.02. We expect these mixtures will influenced by (a) van der Waals attractions and Coulomb repulsions between GPs resulting from dielectric mismatch and GP surface charge, respectively, (b) GP–NP Coulomb attractions, and (c) salt-mediated NP–NP attractions.
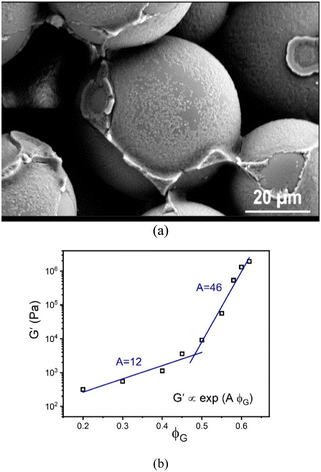
In all cases studied, there is no evidence of macroscopic phase separation or gravitational-induced sedimentation. An example optical micrograph is shown in Fig. 2a which provides evidence for the adsorption of nanoparticles on, and bridging of them between, the large granular particles.
Though not studied experimentally here, the GP–NP and NP–NP attractions can be reversed to a Coulomb repulsion by removing the cationic polyelectrolyte and salt, respectively. The direct DVLO-like interactions can be potentially turned off in an oily solvent or polymer melt. Additionally, the 40-micron GP can be replaced by Brownian colloids of the same chemistries. These systematic variations will be studied in future experimental work, and here serve to motivate the diverse interaction models studied theoretically.
B. Rheological measurements
Oscillatory shear measurements are carried out on the suspensions at 22 °C using a hybrid rheometer (discovery HR-3 hybrid rheometer; TA Instruments) equipped with a customized 8-bladed vane (15 mm diameter, 38.5 mm height, 1.3 mm blade thickness, 4 mm gap) and a solvent trap to prevent evaporation. After the suspensions are loaded into the cup, a 300 s equilibration step is carried out. The storage (G′) and loss (G′′) moduli are measured as function of applied stress (ranging from 0.1 to 3000 Pa) at an oscillation frequency of 1 Hz. Our focus here is only the linear elastic modulus measured from the low stress plateau of G′. For all granule packing fractions, the material responds as an elastic solid in that G′ > G′′. Fig. S1 (ESI†) shows representative frequency sweeps that illustrate the rather weak evolution of the elastic modulus over the range from 0.01–1000 Hz, especially for the highest granular packing fractions systems of most interest. This near frequency-independence in the high packing fraction range is important when discussing how the experimental findings compare to the theoretical results discussed below.Our results for the linear shear modulus are shown in Fig. 2b as a function of GP packing fraction. Interestingly, it exhibits a bi-exponential dependence, following G′ ∝ exp(AϕG), where A is defined as an “elastic fragility index”. For the data in Fig. 2b, we find A ∼ 12 and 46, with a crossover around ϕG ≈ 0.47.
Although not the focus of the present article, the shear modulus is found to evolve in a weakly non-monotonic manner with NP volume fraction at very high granular particle loading (see Fig. S2, ESI†). Such behavior is reminiscent of the so-called “elastic glass melting” of ultra-dense hard sphere colloids mixed with low concentrations of small nonadsorbing polymers.22,24 This phenomenon has been recently predicted and understood based on microscopic statistical mechanical theory.78 But athermal depletion systems are controlled entirely by repulsive forces and entropic considerations, which differs from our granular–NP mixture. Hence, the physical mechanism for the non-monotonic shear modulus evolution in Fig. S2 (ESI†) may be different, and is also not captured in the model theoretical calculations discussed below.
We emphasize that the primary goal of the present paper is a broad theoretical exploration of the impact of many controllable variables on the elastic shear modulus of size asymmetric dense colloid–nanoparticle mixtures. The specific granular-nanoparticle mixture discussed above serves as a motivation and has guided at a high level our choice of theoretical model parameters related to the system chemistry. More directly, we believe the presented results are broadly applicable to size asymmetric chemically complex Brownian colloid–nanoparticle mixtures. Our major theoretical objectives include addressing several key questions. (i) Can the behavior of Brownian colloids and nanoparticles be relevant to our experiments on non-Brownian granules mixed with Brownian nanoparticles? (ii) Is the appearance of two regimes of elastic modulus growth with granule packing fraction related to the mechanism observed in recent experiments,64 and to the theoretical understanding we developed, for ultra-dense Brownian hard sphere colloidal suspensions?63 (iii) How sensitive is the mixture elastic modulus to NP concentration in the dilute “additive” regime? (iv) What governs the elementary absolute scale of elastic energy storage in the mixture: the diameter of the large colloids, the small nanoparticles, or some combination of both?
III. Model and theories
The basic theoretical tools employed have been previously discussed in detail in the literature60,79 and are only briefly recalled here.A. Binary mixture model and equilibrium structure
We consider a binary mixture of size asymmetric hard spheres where species i and j interact via the model pair potentials with distances of closest approach of rc: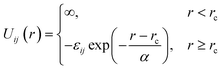 | (1) |
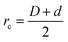 . The “chemistry” variables are encoded in the pair potentials Uij beyond the contact distance, which are modeled using the two-parameter exponential form in eqn (1). The variable strength parameter at contact
. The “chemistry” variables are encoded in the pair potentials Uij beyond the contact distance, which are modeled using the two-parameter exponential form in eqn (1). The variable strength parameter at contact 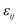 (in thermal energy units, kBT) can be positive or negative depending on whether it represents an attraction or repulsion, respectively. The corresponding spatial range parameter α is fixed to be the same for all species and expressed in units of the colloid diameter. We note that α can vary in magnitude relative to the NP size depending on the physical origin of the attraction or repulsion, but in all cases remains small compared to the colloid diameter. The force scale between two species is simply
(in thermal energy units, kBT) can be positive or negative depending on whether it represents an attraction or repulsion, respectively. The corresponding spatial range parameter α is fixed to be the same for all species and expressed in units of the colloid diameter. We note that α can vary in magnitude relative to the NP size depending on the physical origin of the attraction or repulsion, but in all cases remains small compared to the colloid diameter. The force scale between two species is simply 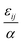 . Initially we treat the colloids as hard spheres (εmm = 0) to focus on NP-related effects (variable εmn, εnn), thereby defining our family of “baseline” systems. We shall also briefly consider the effects of direct colloid–colloid attraction and repulsion. A schematic of the theoretical model is shown in Fig. 3.
. Initially we treat the colloids as hard spheres (εmm = 0) to focus on NP-related effects (variable εmn, εnn), thereby defining our family of “baseline” systems. We shall also briefly consider the effects of direct colloid–colloid attraction and repulsion. A schematic of the theoretical model is shown in Fig. 3.
The mixture pair structure is determined using OZ integral equation theory,61
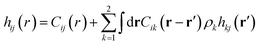 | (2) |
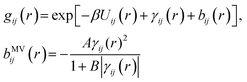 | (3) |
B. Quiescent naïve mode coupling theory of mixtures
NMCT is a self-consistent, force-level, microscopic theory for single particle dynamic localization into an amorphous Einstein solid.80 Each particle dynamically vibrates in a harmonic manner around its mean spatial location with an amplitude that defines its localization length. For a binary sphere mixture in the absence of external forces, the well-known two coupled NMCT localization equations can be written as:79,81| KααrLα2/2 = 3kBT/2. | (4) |
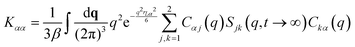 | (5) |
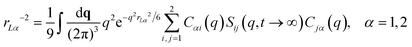 | (6) |
The elastic shear modulus for a sphere mixture is computed based on the well known exact statistical mechanical expression evaluated with the approximate MCT projection of stresses onto pair collective density fluctuation variables and factorization of 4-point correlations into products of 2-point correlations. The result is:79,82
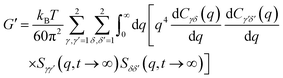 | (7) |
The above binary mixture model is characterized by 9 control parameters: the colloid to nanoparticle diameter size ratio (D/d, where D > d), NP packing fraction ϕn ≪ 1 (per the “additive” cases of interest), colloid packing fraction ϕm, and the 6 parameters that define the strength and spatial range of exponential interactions between all species beyond contact.
Colloid–NP and NP–NP attractions are often strong and short-range, which motivates our “baseline” model choice of parameters: contact interaction strength of 3kBT and 4kBT with the range parameter α = 0.002D. Our major focus is on hard colloids where interactions beyond contact are solely nanoparticle-mediated, although a few model calculations are presented where there is a direct non-contact interaction between the larger colloids.
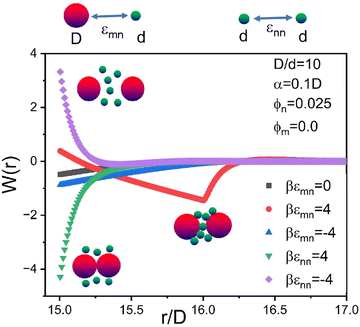
To illustrate in the simplest context how the energetic “chemistry variables” impact the effective colloid–colloid organization, Fig. 4 shows calculations of the NP-mediated potential of mean force (PMF) between two dilute hard sphere colloids dissolved in a NP fluid of ϕn = 0.025. Results are shown for 5 choices of interactions: the athermal depletion system (εmn = εnn = 0), a NP–colloid short range attraction or repulsion (εmn = ±4kBT, εnn = 0), and a NP–NP short range attraction or repulsion (εnn = ±4kBT, εmn = 0). The form of the PMF can be repulsive, weakly contact attractive, strongly contact attractive, or repulsive at contact with a strong non-contact bridging minimum. These diverse forms of the PMF illustrate the qualitatively sensitivity of the NP-mediated colloid effective interaction to the tunable microscopic interaction energies.
IV. Chemistry driven variations of the shear elastic modulus
The numerical solution of coupled nonlinear integral equations becomes increasingly difficult, and eventually impossible, as the size asymmetry gets larger. This difficulty is more pronounced at the very high packing fractions, and for systems with very short-range strong non-contact interactions, of primary interest in this work. Thus, a size ratio of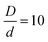 is chosen as the largest we can broadly study. The NP packing fraction is varied in the dilute additive regime, with a focus on ϕn = 0.025. These parameters define the “baseline” system for exploring the consequences of changing the chemistry variables.
is chosen as the largest we can broadly study. The NP packing fraction is varied in the dilute additive regime, with a focus on ϕn = 0.025. These parameters define the “baseline” system for exploring the consequences of changing the chemistry variables.
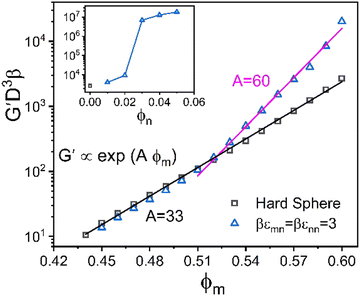
As a reference state for assessing how nanoparticles can provide elastic reinforcement, Fig. 5 shows results for the elastic shear modulus of the pure hard sphere system. The theory predicts it grows exponentially with packing fraction, G′ ∝ exp(Aϕm), up to ϕm = 0.6 with an “elastic fragility index” of A ≈ 33. The structural origin of this behavior83 has been theoretically shown to arise from the scaling of the shear modulus as the inverse 6th power of the equilibrium structural correlation length, ξ, associated with medium range order. The latter is determined from the non-random part of the pair-correlation function, h(r) = g(r) − 1, with ξ growing exponentially with packing fraction. At even higher packing fractions, but still well below RCP, a second stronger exponential regime is predicted and observed64 (not shown) for ϕ > 0.60 with A ≈ 60. These two regimes, and the location of the crossover, are in good agreement with experiment.63 The present study does not focus on this second ultra-high packing regime.
A. Baseline mixtures
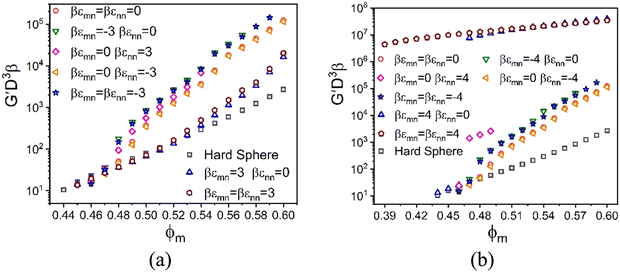
We begin by examining in detail the dependence of the elastic shear modulus on the chemistry variables in the baseline mixtures where the direct colloid–colloid interaction is pure hard sphere. The main frame of Fig. 5 demonstrates that introducing a small amount of nanoparticles (ϕn = 0.025) with colloid–NP and NP–NP attraction strengths of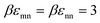 of a short range αmn = αnn = 0.002D (2% the NP diameter) results in a shear modulus exhibiting two exponential growth regimes. The nanoparticles are dynamically delocalized (i.e., fluid), while the colloids are a localized solid. This double exponential behavior is distinct from that of 1-component hard spheres63 which emerges beyond ϕ = 0.60, as discussed above. In the present colloid–NP mixtures, the double exponential behavior is driven by interfacial NP–colloid attractions that favor NP adsorption and NP-mediated tight bridge formation between colloids. Interestingly, up to ϕm ∼ 0.51, the mixture shear modulus closely matches that of the 1-component hard sphere system. Beyond a crossover at ϕm ∼ 0.52, a much steeper exponential growth regime is predicted with an elastic fragility index nearly twice as large as that of hard spheres, A ≈ 60. This clearly illustrates the strong effect on elasticity of adding a low concentration of nanoparticles. Hence, mechanistically, a double exponential form for the modulus can be realized at lower packing fractions and via a different microscopic mechanism than for dense hard sphere suspensions.
of a short range αmn = αnn = 0.002D (2% the NP diameter) results in a shear modulus exhibiting two exponential growth regimes. The nanoparticles are dynamically delocalized (i.e., fluid), while the colloids are a localized solid. This double exponential behavior is distinct from that of 1-component hard spheres63 which emerges beyond ϕ = 0.60, as discussed above. In the present colloid–NP mixtures, the double exponential behavior is driven by interfacial NP–colloid attractions that favor NP adsorption and NP-mediated tight bridge formation between colloids. Interestingly, up to ϕm ∼ 0.51, the mixture shear modulus closely matches that of the 1-component hard sphere system. Beyond a crossover at ϕm ∼ 0.52, a much steeper exponential growth regime is predicted with an elastic fragility index nearly twice as large as that of hard spheres, A ≈ 60. This clearly illustrates the strong effect on elasticity of adding a low concentration of nanoparticles. Hence, mechanistically, a double exponential form for the modulus can be realized at lower packing fractions and via a different microscopic mechanism than for dense hard sphere suspensions.
The packing fraction dependence of the elastic modulus in Fig. 5 resembles the experimental data in Fig. 2. However, it is unclear whether this a causal connection. Nonetheless, the possibility it could be cannot be dismissed given that the experimental mixture does involve attractions between the large and small particles and also between nanoparticles. Recall that Fig. 2 shows a representative optical micrograph that indicates there is nanoparticle adsorption on, and bridging between, the large granules.
The inset of Fig. 5 shows the evolution of the shear modulus with NP concentration at fixed ϕm = 0.60. Interestingly, the mixture is predicted to undergo an abrupt dynamic transition for NP loadings beyond ϕn = 0.025, resulting in the localization of both colloids and nanoparticles, and the formation of a bridged network solid. This transition is the origin of the predicted discontinuous jump in the shear modulus.
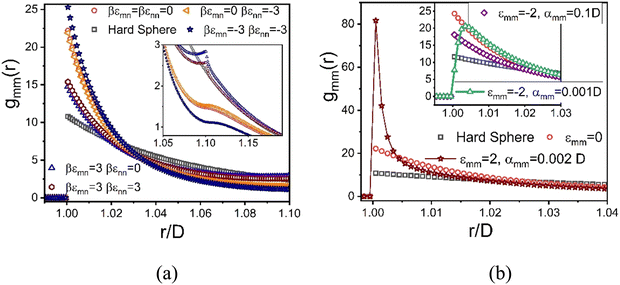
To further investigate the rich chemical space of this size asymmetric mixture, we study the evolution of its elastic modulus at fixed NP packing fraction (ϕn = 0.025) and size ratio of 10 at the same absolute magnitude of the energy scale and spatial range of non-contact interactions (if present) in eqn (1). Fig. 6 shows results for 8 distinct systems based on different choices of the competing interactions, where the (repulsive or attractive) energy scale is 3kBT and 4kBT for a spatial range of 2% the NP diameter. Our goal is to study the consequences of the presence of only one (4 examples) or two (2 examples) non-contact interactions, with the specific choices motivated by the many possibilities inherent to the experimental system of Section II. Results are also shown for the athermal entropic depletion mixture to illustrate the consequences of pure excluded volume interactions, and the reference pure hard sphere system.
We first discuss the results in Fig. 6a. For all systems and colloid packing fractions, the larger colloids are localized beyond a threshold value of packing fraction where solidity first emerges (as indicated by where the curves begin), while the nanoparticles remain fluidized. Hence, for these partially localized systems, all elastic energy is stored in the colloidal subsystem. Consider first the athermal depletion mixture. The large size asymmetry induces a strong entropic attraction between colloids, resulting in a shear modulus that becomes up to two decades larger than the reference hard sphere system at high ϕm. A detailed analysis of the shear modulus (Fig. S3, ESI†) reveals two exponential regimes, G′ ∝ exp(Aϕm) with elastic fragility indices of A = 82 and A = 58, and a crossover at ϕm = 0.52. Physically, at the highest ϕm values there is little open space between colloids for the nanoparticles to explore and gain entropy in contrast to the classic picture of the driving force for depletion. The classic depletion mechanism is thus frustrated, resulting in a reduction of the rate of growth of modulus reinforcement with packing fraction as indicated by a weak bending over of the curve in Fig. 6a. Notably, the direction of this change in slope is opposite to that in the data of Fig. 2.
The other mixtures in Fig. 6a are characterized by entropic depletion effects and the competing consequences of non-contact energetic interactions: (1) colloid–NP repulsion, (2) NP–NP attraction, (3) NP–NP repulsion, and (4) symmetric colloid–NP and NP–NP repulsions. Remarkably, the growth of the shear modulus with ϕm for all 4 systems is quite similar to each other in magnitude and functional form, and closely resembles the depletion system. Such a “degeneracy of consequences” behavior seems surprising. A physical interpretation is that what the different chosen microscopic interactions have in common is they all favor colloid–colloid contacts, as we have verified by examining the predicted structural correlations.
Fig. 6a also shows results for two other model mixtures that are qualitatively distinct from the ones discussed above. Their behavior is controlled by attractive colloid–NP interactions that promote NP adsorption on, and tight bridges between, the colloids. The simultaneous presence of NP–NP attractions has minor effects, but does result in additional reinforcement that can plausibly be physically interpreted as strengthening of NP-mediated tight bridges. The shear moduli of these two systems are lower at high packing fractions than in the athermal depletion and other 4 systems discussed above. Two exponential growth regimes are predicted with a crossover at ϕm = 0.52. At the lower packing fractions, the elastic fragility index is similar to that of the hard-sphere system, while at high packing fractions it quite similar to the depletion mixture and systems (1)–(4) above. This overall behavior indicates that bridge formation is predominantly driven by cross-attraction between colloids and nanoparticles, and resembles the experimental dependence of the elastic shear modulus on granule particle packing fraction in Fig. 2.
We now increase the dimensionless energy scale by only one thermal energy increment from 3kBT to 4kBT. Fig. 6b shows the corresponding shear moduli of systems (1)–(4) remain largely unaffected. In qualitative contrast, this modest increase of colloid–NP attraction leads to a dramatic double localization transition of colloids and nanoparticles, resulting in a tight bridging network solid. This network-like solid has a shear modulus four decades larger than that of hard spheres at high colloid concentrations. On the other hand, the shear modulus for the doubly localized state is much less elastically fragile compared to the analogous systems in Fig. 6a. Furthermore, introducing a larger NP–NP attraction does not significantly alter the behavior for mixtures with only a colloid–NP cross attraction, only modestly augmenting the elastic strength of the bridging network, similar to the trends observed in Fig. 6a.
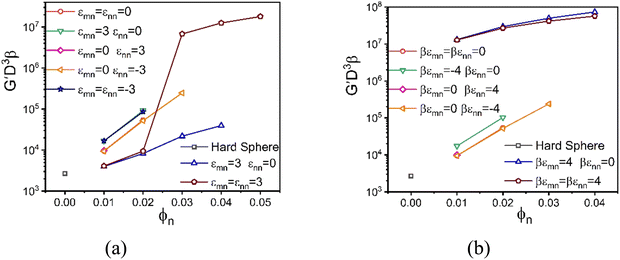
Fig. 7a and b explore the impact of varying NP packing fraction, ϕn, in the dilute NP regime at a fixed high ϕm = 0.60, corresponding to the same chemical systems in Fig. 6a and b, respectively. Fig. 7a shows that the elastic modulus for the depletion system grows roughly exponentially with ϕn, with a very steep elastic fragility index of A ≈ 173 (Fig. S5, ESI†) that remains largely unaffected for the interactions that define systems (1)–(4). In all these mixtures, the colloids are localized but the nanoparticles remain fluid. The presence of a colloid–NP attraction reduces the depletion effect, leading to a slower modulus growth with colloid packing fraction with an elastic fragility index of A ≈ 78 (Fig. S5, ESI†), and a lower absolute magnitude. A transition from single to double localization emerges beyond ϕn = 0.025 when both colloid–NP and NP–NP attractions of 3kBT strength are present. In the doubly localized solid state, the shear modulus becomes very high, but shows a much weaker dependence on ϕn. In the language of glass physics, this system is “elastically strong”.
Fig. 7b shows the analogous shear moduli results as a function of NP concentration for the larger attraction strength of 4kBT, again at ϕm = 0.60. A much weaker change with ϕn is now found for systems (1)–(4) compared to the pure athermal depletion system. Notably, these mixtures exhibit double localization when attraction exists only between the colloids and nanoparticles, and this behavior remains unaffected by NP–NP attraction.
In both Fig. 6 and 7, we find that the interaction models with only an attraction between the nanoparticles leads to spinodal phase separation at intermediate colloid packing fractions (these states are not studied dynamically). But we emphasize that the emergence of glass or gel-like solids predicted by NMCT (driven by caging or bonding), and the corresponding shear modulus, is not casually coupled to the long wavelength concentration fluctuations that emerge close to the phase separation.84
B. Effect of direct colloid–colloid interactions
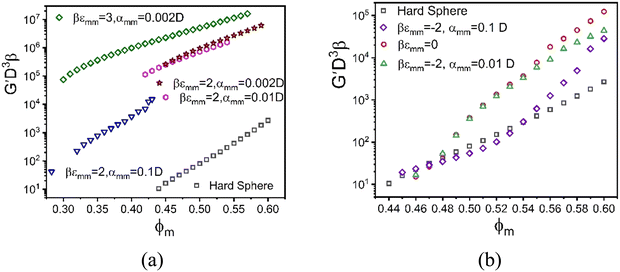
In experimental systems, there can be a direct van der Waals attraction between large particles due to dielectric constant mismatch, and/or a direct repulsion which could be, for example, of a Coulomb origin if the surfaces are charged or of a steric origin if the surfaces are coated with grafted polymers brushes under good solvent conditions. Of course, if the silica-based granules (or large colloids more generally) are dissolved in an oily solvent or a polymer melt so they remain neutral and the dielectric constant and refractive indices are (nearly) matched, these interactions can potentially be turned off. The latter situation is effectively what was analyzed in the preceding subsection, and can be studied experimentally by adjustment of the chemical system.A direct large particle attraction favors contact aggregation that will compete with the NP-mediated interfacial attraction that promotes bridges. To isolate the role of the former, we consider in Fig. 8 a mixture model where there is a direct exponential attraction between colloids while all other interactions (NP–NP and colloid–NP) are purely excluded volume. The size ratio 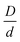 and NP packing fraction ϕn are taken to be essentially identical with those in Fig. 6. All such model systems are found to be singly localized where the nanoparticles remain a fluid and do not directly contribute to the elastic shear modulus.
and NP packing fraction ϕn are taken to be essentially identical with those in Fig. 6. All such model systems are found to be singly localized where the nanoparticles remain a fluid and do not directly contribute to the elastic shear modulus.
The elastic modulus predictions for different inter-colloid direct attraction strengths and spatial ranges are shown in Fig. 8a. Interestingly, the results for a 2kBT attraction are parallel to that of pure hard spheres for the longest-range attraction. The combined effects of depletion and direct bond formation results in a much stronger solid by orders of magnitude, with the onset of solidity shifting to much lower packing fractions. This reflects the tendency for strong contact aggregation and physical bond formation, but in a manner that the growth of the shear modulus with densification remains nearly the same as in the absence of this direct attraction. On the other hand, the formation of direct bonds between colloidal particles for a stronger 3kBT attraction reduces the elastic fragility of the mixture, a rather generic trend associated with a large increase of the absolute magnitude of the shear rigidity via introduction of stronger interparticle attractions or physical bonds. Fig. 8a also shows that the modulus systematically increases with decreasing attraction range expressed in units of colloid diameter, D. This trend could be interpreted as a consequence of minimizing local free energy since entropy can be gained via looser bonding without sacrificing much energetic stabilization as the attraction range grows. Moreover, a shorter attraction range at fixed strength implies a stronger attractive force associated with bond formation, which is relevant since it is effective forces that enter the NMCT calculation of particle localization and arrested stress correlations.85
Generically, and in the experiments of Section II, the large particles can experience short range repulsions which may locally result in more accessible voids, thereby allowing nanoparticles to more easily explore the interstitial regions between the large particle surfaces in a dense suspension. Fig. 8b shows example calculations of the elastic modulus motivated by this scenario for different strengths and ranges of a direct exponential repulsion between colloids with all other interactions taken to be hard core excluded volume. The size ratio 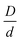 and value of ϕn are the same as in Fig. 8a. All systems are singly localized where the nanoparticles remain fluid.
and value of ϕn are the same as in Fig. 8a. All systems are singly localized where the nanoparticles remain fluid.
We find that the direct short-range repulsion renders the mixture more elastically fragile compared to the analogous system with a direct attraction, and it displays a double exponential like dependence of the shear modulus on colloid packing fraction. From the perspective of depletion, colloids tend to be pushed into contact with nanoparticles expelled from the contact region, but NPs can still be present in the interstitial region and form steric bridges (or “entropic bonds”) at very high colloid packing fractions. Therefore, the overall behavior of the elastic modulus in this mixture behaves similarly to the depletion system, but its absolute magnitude is smaller at high packing fractions. As the range of the direct repulsion grows, the modulus becomes smaller than in the corresponding athermal depletion system, with the initial slope less than at high packing fractions, in contrast to the behavior for the pure depletion system.
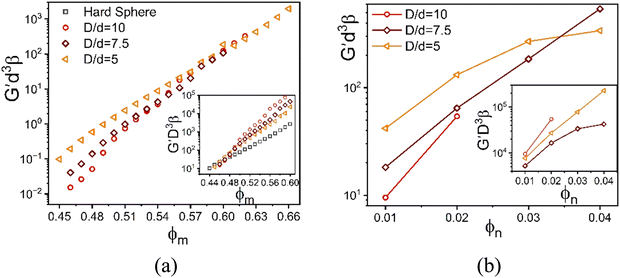
V. Effect of size ratio on shear modulus
How the results of Section IV depend on the colloid to NP size ratio is of high interest. For 1-component Brownian hard colloid systems the natural unit of elastic energy storage is thermal energy divided by the particle volume or diameter cubed. But for a size asymmetric mixture, with or without the beyond contact energetic interactions, the analogous stress scale is not obvious. Varying large particle diameter at fixed NP diameter may affect not only the absolute magnitude of the mixture shear modulus, but also change the dimensionless spatial range for non-contact interactions and/or the strength of the van der Waals interactions.We briefly explore the above question within our computational limitations by studying size ratios of 5, 7.5, and 10. The two most different chemistry scenarios are considered: (i) an athermal depletion mixture where NPs remain fluid-like but induce colloid contacts, and (ii) strong colloid–NP interfacial attraction where NPs mediate bridges between colloids resulting in doubly localized network-like solids. To isolate the role of size asymmetry, we perform calculations for different size ratios at a fixed attraction range and strength for case (ii).
For the baseline NP packing fraction of 0.025, the elastic moduli of the depletion mixture is plotted in Fig. 9 as a function of colloid packing fraction for three size ratios. All systems show single localization, where the NPs remain fluid. The shear moduli non-dimensionalized by the colloid volume collapse onto that of the 1-component HS system up to ϕm = 0.48 (inset Fig. 9a). However, upon replotting the same calculations but non-dimensionalized by the smaller NP volume, an intriguing collapse is found beyond ϕm = 0.56. This suggests the elastic modulus is a weak function of size ratio at both lower and higher colloidal packing fractions (all high in an absolute sense), with an elastic energy storage scale governed by the colloid and NP diameters or volumes, respectively.
To further investigate the stress scale issue, Fig. 9b shows how the elastic modulus depends on NP packing fraction at a very high colloid concentration for three size ratios. The elastic modulus grows significantly with NP concentration, in an exponential (larger size ratio) or sub-exponential (smallest size ratio) manner. To probe the size ratio scaling question, the main panel and inset show the same calculations non-dimensionalized by the volume of the nanoparticle and colloid, respectively. Although the collapse is not perfect, the differences diminish in the same manner as found in Fig. 9a. This suggests a crossover from elastic energy storage controlled by colloids at lower NP packing fractions, to being controlled by the nanoparticles at very high NP packing fractions.
The above crossover of the elastic energy storage scale for the depletion mixtures is an intriguing finding. Determining its physical origin from our ensemble-averaged numerical calculations is challenging. Based on the dilute large particle limit of the depletion problem for the classic Asakura–Oosawa (AO) model,7 the strength of the entropic attraction induced by a dilute fluid of small nonadsorbing particles scales linearly with both D/d and dilute NP concentration, with a spatial range set by d. Of course, the ultra-dense colloids studied here involve many body physics effects not present in the doubly dilute (colloids and nanoparticles) AO model. Below we offer a speculative scenario for our prediction of a change of the elastic energy storage scale based on geometric considerations and a length scale crossover.
In a simplified picture, the mean surface-to-surface separation of a pair of large particles is 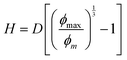 where ϕmax is a maximum colloid packing fraction in the mixture with dilute nanoparticles. For the latter value, we adopt the pure hard sphere RCP value predicted by63 OZ–MV theory of ∼0.78. As ϕm increases from 0.44 to 0.66 in Fig. 9, we estimate H decreases from 0.21D to 0.06D, corresponding to mean surface-to-surface separations of 2.1d to 0.6d for D/d = 10, and 1.05d to 0.3d for D/d = 5. These numbers suggest a geometric crossover: as the colloid packing fraction increases, the mean inter-colloid separation changes from being larger than, to smaller than, the NP diameter. This change in packing geometry implies that at lower colloid packing fractions, nanoparticles can more freely explore the spaces between large colloids. However, as the colloid packing fraction becomes large enough, nanoparticles become largely confined to the interstitial spaces between densely packed colloids. This argument is speculative, but we believe provides some insight for understanding the crossover in the stress scale at high colloid packing fractions where the NP size dominates the mixture shear modulus.
where ϕmax is a maximum colloid packing fraction in the mixture with dilute nanoparticles. For the latter value, we adopt the pure hard sphere RCP value predicted by63 OZ–MV theory of ∼0.78. As ϕm increases from 0.44 to 0.66 in Fig. 9, we estimate H decreases from 0.21D to 0.06D, corresponding to mean surface-to-surface separations of 2.1d to 0.6d for D/d = 10, and 1.05d to 0.3d for D/d = 5. These numbers suggest a geometric crossover: as the colloid packing fraction increases, the mean inter-colloid separation changes from being larger than, to smaller than, the NP diameter. This change in packing geometry implies that at lower colloid packing fractions, nanoparticles can more freely explore the spaces between large colloids. However, as the colloid packing fraction becomes large enough, nanoparticles become largely confined to the interstitial spaces between densely packed colloids. This argument is speculative, but we believe provides some insight for understanding the crossover in the stress scale at high colloid packing fractions where the NP size dominates the mixture shear modulus.
Fig. 10 examines a very different mixture system. Specifically, the elastic shear modulus for two size ratios, 5 and 10, in the presence of an interfacial attraction of 4kBT. Here the mixture is doubly localized and the solid is a bridged network, in qualitative contrast to the depletion mixture. The main frames of Fig. 10 use the colloid diameter to nondimensionalize the modulus, while the insets employ the NP diameter. In both cases, we do not find a collapse of the calculations. However, the deviations are relatively modest, far less than the factor of 8 if colloid diameter was the controlling factor. This suggests the possibility of collapsing the theoretical results with a mixed volumetric scale. Indeed, Fig. S7 (ESI†) shows that a perfect collapse can be achieved by using a mixed stress scale of 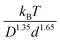 which combines the colloid and NP diameters. Remarkably, this same mixed scaling (non-integer dependence on the two particle diameters) collapses the results in both panels of Fig. 10 which examine the effect of size ratio on how the modulus grows with colloid packing fraction and with NP packing fraction.
which combines the colloid and NP diameters. Remarkably, this same mixed scaling (non-integer dependence on the two particle diameters) collapses the results in both panels of Fig. 10 which examine the effect of size ratio on how the modulus grows with colloid packing fraction and with NP packing fraction.
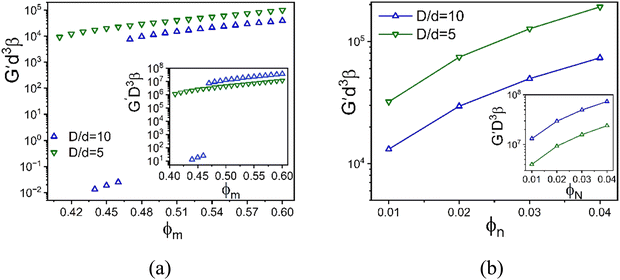 | ||
| Fig. 10 Log–linear plot of the dimensionless elastic shear modulus scaled by the NP diameter cubed as a function of (a) colloid packing fraction at fixed NP packing fraction 0.025, and (b) NP packing fraction at fixed colloid packing fraction 0.60 with a colloid–NP interfacial attraction of 4kBT and range 0.002D. Insets: Analogous plots but with the dimensionless elastic modulus scaled by the colloid diameter cubed. The collapse of the presented results based on a mixed stress scale is shown in Fig. S7 (ESI†). | ||
A fundamental understanding of the exponents in the above mixed stress scale behavior of the shear modulus (roughly 4/3 and 5/3) remains to be determined. The depletion attraction between the colloidal particles is always present for large size asymmetric mixture. On the other hand, NP–colloid attractions promote bridging. We speculate that these two opposing effects change the structural organization in a nontrivial manner, leading to a mixed effective volume for elastic energy storage. Regardless of its microscopic origin, this intriguing result may be relevant to understanding why granular-nanoparticle mixtures, where the overwhelming majority species is the large particles, can still exhibit a high MPa level shear modulus at very high loadings as seen in the experimental data in Fig. 2.
VI. Structural correlations
The dramatic variation of the mixture shear modulus for different interactions strengths and ranges documented above invites the examination of the colloid pair correlation function at high-packing fractions. Recall this information serves as the critical input to the NMCT predictions for the shear modulus. In this section we present selected structural results motivated by some of our key findings in Sections IV and V.Fig. 11a shows gmm(r) for the 5 homogeneous mixtures in Fig. 6a which all display large modulus reinforcements at fixed values of ϕm = 0.59 and ϕn = 0.025. Recall that nanoparticles are not localized for these systems and do not contribute directly to the elastic modulus. This motivates examining the colloidal microstructure. The contact values of gmm(r) in Fig. 11a exhibit 3 different values, which correlates with their corresponding moduli in Fig. 5a. These structural results support our view that the similarity of the shear moduli of these systems is strongly related to colloid contacts.
For the case of moderate interfacial attraction of ε = 3kBT, the inset of Fig. 11a shows that the contact value of gmm(r) becomes smaller due to the emergence of a secondary near contact peak at r = 1.11D associated with NP adsorption and bridging. This structural change may explain the higher shear modulus of the depletion system than predicted for the moderate interfacial attraction mixture. However, the appearance of a relatively weak secondary bridging peak at r = 1.11D exists even in the athermal depletion limit as shown in the inset of Fig. 11a. This reflects an interesting steric frustration effect at high colloid packing fractions, where a NP appears to form an “entropic bridge” due to the unavailability of sufficient free volume to achieve the classic depletion configuration. Fig. 11a also shows that NP attraction or repulsion has a relatively weak effect on the depletion or interfacial attractive systems. Recall again that nanoparticles are not localized for the systems studied, and they affect elastic energy storage only via depletion induced contact colloid clustering or NP-mediated bridging.
In Fig. 11b, a very large contact value of gmm(r) of 80 is predicted when there is a direct short-range attraction between colloids of strength 2kBT with no competing colloid–NP and NP–NP attractions. The inset shows that for a short-ranged direct repulsion of strength −2kBT and range 0.01d, the location of the first peak of the gmm(r) shifts to slightly higher values beyond the colloid diameter. This indicates the absence of direct contacts between colloids and the importance of steric stabilization due to NPs. A secondary bridging peak also appears for both the short and longer ranged direct repulsion. The comparable importance of entropic and energetic effects is likely the origin of the double-exponential dependence of the elastic modulus on colloid packing fraction. In contrast, a single exponential dependence is predicted when strong physical bonding dominates.
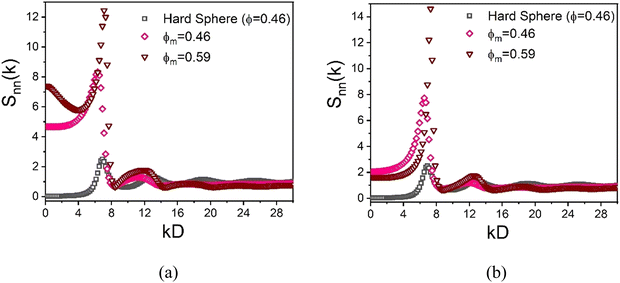
Although the nanoparticles are dilute, the presence of a very high density of large colloids significantly restricts the free space available for nanoparticles. Moreover, the high degree of local short range order of the dense colloidal subsystem can be “imprinted” on the spatial organization of the nanoparticles which populate the small interstitial regions and thus are highly correlated with the colloids and with themselves.86 This effect can be probed by calculating the NP–NP collective structure factor in Fourier space, a quantity that is potentially measureable using labelled scattering or optical methods. Representative results are shown in Fig. 12 at a high and lower colloid packing fraction, and display distinctive imprinting and other features. For example, a large value of the dimensionless osmotic compressibility, Snn(0), of the NP subsystem is predicted which indicates NP segregation into the spatially correlated interstitial regions.
In detail, the increasing first peak of the NP–NP structure factor with growing colloid packing fraction implies the nanoparticles become more spatially correlated as they become more confined. Similar large increases of the first peak of the structure factor have been recently reported for ultra-dense equilibrated hard sphere systems, in both simulation62 and in theory.63 At lower colloid packing fraction (ϕm = 0.46 and ϕn = 0.025), the large size ratio allows nanoparticles to relatively easily explore the region between interstitial spaces. Consequently, the first peak of the NP–NP structure factor in this mixture does not align well with the first peak of the hard sphere structure factor at ϕ = 0.46, as shown in Fig. 12(a). At higher colloid packing fractions (ϕm = 0.59 and ϕn = 0.025), the depletion mixture shows bridging, as evidenced by the radial distribution function in inset of Fig. 10(a). Here, the first peak of the NP–NP structure factor aligns well with the first peak of the hard sphere structure factor, reflecting how the short-range order of colloids is imprinted on the interstitial space occupied by NPs, as highlighted in Fig. 12(a).
Now, in the presence of a colloid–NP cross-attraction with a strength of 4kBT, NP-mediated bridging between colloids becomes more prominent, even at lower colloid packing fractions (ϕm = 0.46 and ϕn = 0.025). This results in an alignment of the first peak of the NP–NP and hard sphere structure factors, as seen in Fig. 12(b). At larger colloid packing fractions (ϕm = 0.59 and ϕn = 0.025) with a colloid–NP cross-attraction, the first peak of the NP–NP structure factor also aligns well with the hard sphere structure factor, reflecting the imprinting of the colloidal short-range order on the interstitial space occupied by nanoparticles. Notably, the shape of the second peak at high colloid packing fraction is unconventional in form (almost resembling a jump discontinuity) compared to dense hard sphere fluids. This feature becomes more pronounced as colloid concentration increases, and may be the origin of the strong fragility response of the elastic shear modulus in Fig. 6a.
VII. Summary and future outlook
Motivated by the general problem of shear rigidity in size asymmetric, dense, chemically complex colloid–nanoparticle mixtures, as well as the new experimental work in Section II, we have systematically applied NMCT with the accurate MV closure for structural input to numerically investigate the elastic modulus of suspensions of spherical colloids and nanoparticles. The effects of size ratio, colloid and NP packing fractions, and diverse interparticle attractive and repulsive interactions on the mixture elastic modulus were explored. A concise summary of our findings in Sections IV–VI for a fixed size ratio and interaction range, and the distinct scenarios elucidated with increasing packing fractions, are as follows.Athermal entropic depletion
At low NP concentrations, the elastic shear modulus exhibits a bi-exponential growth law with increasing colloid packing fraction, with a steeper initial slope or elastic fragility index. At very high colloid concentrations, the modulus becomes strongly dependent on NP packing fraction even in the dilute additive regime of interest. Colloids are localized, whereas nanoparticles are delocalized.High cross attraction (ε = 4kBT)
At lower NP concentrations, the shear modulus is very high but relatively weakly dependent on colloidal packing fraction (low elastic fragility). Conversely, at high colloid volume fractions, the shear modulus remains significantly elevated and strongly dependent on NP packing fractions. Both colloids and nanoparticles are localized, store elastic energy, and the microstructure is akin to a bridged network solid.Moderate cross attraction (ε = 3kBT)
At lower nanoparticle concentrations, the shear modulus increases markedly with colloid packing fraction and shows a double exponential, elastically fragile behavior. At high colloid packing fractions, the shear modulus strongly depends on NP loading. The colloids are localized, while nanoparticles remain a fluid.Moderate cross attraction and nanoparticle attraction (ε = 3kBT)
At lower NP concentrations, the shear modulus grows significantly with colloid packing fraction, displaying two exponential regimes with a smaller elastic fragility index at lower colloid packing fractions. At high colloid concentrations, beyond a NP packing fraction of ∼0.02 the shear modulus weakly depends on NP concentration. The mixture displays only single colloid localization when varying colloid packing fraction, but abruptly transitions from single to double localization beyond a NP packing fraction of 0.02.Direct colloidal attraction
Strong contact aggregation between colloids amplifies the effect of depletion driven attraction. This results in a less elastically fragile, but significantly higher, elastic modulus than that of dense hard sphere colloidal suspensions.Direct colloidal repulsion
The amount of colloid contact aggregation is reduced via a steric stabilization like mechanism. Double exponential dependence of the mixture shear modulus on colloidal packing fraction is predicted.The observed two-exponential growth form of the shear modulus with colloid packing fraction with a steeper slope at higher colloid concentrations is fascinating. It is theoretically predicted not only for mixtures with colloid–NP and NP–NP attractions, but also mixtures where there are longer range direct repulsions between the colloids in the presence of a small amount of nanoparticles. This is another indication that at the high colloid packing fractions critical to applications such as direct ink writing, the elastic stress scale is influenced not only by entropic depletion effects via size asymmetry, but also by NP concentration, colloid–NP attraction, and/or direct colloid–colloid repulsion strength and range. Hence, one may engineer the form of the elastic modulus growth with colloid loading in many chemistry distinct manners. On the other hand, the response of the mixture shear modulus to adding nanoparticles at fixed colloid high packing fraction does depend significantly on the chemistry variables.
Our theoretical analysis of the shear modulus is based on an approach that directly relates it to the microscopic interactions and pair correlations between all species in the mixture. At a high level, the choice of interaction models corresponds to four qualitatively different microstructural regimes: (i) entropic depletion induced colloid clustering, (ii) discrete adsorbed NP layers that induce good colloidal dispersion, (iii) a NP-mediated tight bridging network formation, and (iv) colloidal contact aggregation via direct attractive interactions. These regimes are associated with changes in the strength of the interfacial colloid–nanoparticle attraction from zero (entropy dominated) to an intermediate level where energetic and entropic effects are comparable and compete, to a strong interfacial attraction energetic bonding controlled regime. At high colloid packing fractions, a secondary-bridging structural feature is predicted for the entropy dominated depletion system and the direct short-ranged inter-colloid repulsion system. This reflects nanoparticles being sterically forced to be close to colloidal surfaces at very high density due to the lack of available open space. For the doubly localized state induced by a strong short-ranged interfacial attraction, the colloids and nanoparticles form a tightly bridged network, with a collective elastic energy storage mechanism. On the other hand, systems with singly localized colloids and fluid-like nanoparticles exhibit different elastic behaviors since nanoparticles modulate the spatial organization of the colloids without directly contributing to the stress. The collective structure factor of the relatively dilute NP subsystem reveals strong spatial ordering and large osmotic concentration fluctuations. This behavior is likely linked to the significant role of NP size in determining the stress-scale of the modulus.
Beyond the rich dependence of the elastic shear modulus dependence on colloid and NP packing fractions, the colloid–NP size asymmetry ratio is also important. At a fixed low concentration of nanoparticles, the athermal depletion mixture modulus data collapses as a function of the colloid packing fraction for various size ratios if scaled by the diameter cubed of the colloid at lower colloid packing fractions, or the NP diameter cubed at higher colloid packing fractions. This suggests a transition from a regime of elastic energy storage dominated by colloid caging, to a regime dominated by tightly localized or confined nanoparticles. The latter perhaps suggests a basis for understanding our experimental observation of a large MPa magnitude shear modulus in the granular-nanoparticle mixtures discussed in Section II.
The above stress scale and collapse behaviors are not general to significant variation of NP packing fraction at high colloid concentrations for different size ratios. Most importantly, in the presence of strong colloid–NP attractions that promote double localization, bridging, and a network solid formation, the growth of the now much higher elastic modulus becomes of a far weaker exponential form than for the depletion mixtures, and exhibits a qualitatively different dependence on size ratio. Specifically, a combination of the NP and colloid diameters enters the relevant volume that dimensionalizes the elastic modulus leading to a rather remarkable collapse of both the modulus growth with colloid packing fraction at fixed NP loading, and its growth with NP packing fraction at high values of colloid packing fraction.
Finally, we return to our motivating experiments for granular-nanoparticle mixtures in Section II. Our present theoretical work has only scratched the surface of the underlying physics of this system which is characterized by a vast tunable parameter space of high relevance to ink printing. One issue is the attractive and repulsive interactions between the granules, the granules and nanoparticles, and even between nanoparticles, remain challenging to precisely know. A second complicating issue is the non-Brownian nature of the granule subsystem in experiment, versus the Brownian nature of the colloidal subsystem in our theoretical analysis. Despite these complexities, our simple theoretical model based on a two-parameter (strength and range) beyond contact exponential interaction does capture the experimentally observed double exponential dependence of the elastic shear modulus on the large particle packing fraction, including the steeper slope under ultra-concentrated conditions. However, our broad theoretical exploration of parameter space shows this double exponential dependence can arise from different microscopic mechanisms.
Another issue is at high granular volume fractions, the experimental elastic shear modulus reaches very high magnitudes on the order of MPa, suggesting the elastic energy storage is predominantly governed by the nanoparticles. In our theoretical model, the size ratio reaches only a value of 10, compared to experimental ratio of order 1000. Consequently, the elementary stress scale associated with our theoretical results for the elastic modulus cannot generally be literally mapped onto the experimental systems. On the other hand, at high colloidal packing fractions in athermal depletion mixtures, the theory does predict a collapse of the elastic shear modulus results across different size ratios where the elementary stress scale involves only the smaller nanoparticle diameter. This suggests a surprising emergent irrelevance of the large particle diameter for determining the modulus stress scale. However, this collapse behavior does not persist when colloid–nanoparticle and nanoparticle–nanoparticle attractions are included. Further exploration of this issue is crucial for better connecting our theoretical work with the discussed experiments.
The presented theoretical results are guiding the formulation of new rationally designed mixture formulations and rheology experiments using modifications of the experimental system introduced in this article. Ongoing measurements combined with our theoretical efforts hold the promise of revealing a broad physical understanding of engineering relevance. Extension of the present theoretical and experimental work to address the nonlinear rheology of such size asymmetric ultra-dense mixtures, especially the yield stress and strain, is also underway.
Data availability
The main text, or ESI† contains all the data.Conflicts of interest
There are no conflicts to declare.Appendix
Collective Debye–Waller factors
The determination of the required Debye–Waller factors in eqn (6) for a binary mixture within NMCT is well known.60,79 The starting point is the evolution equation for the time domain partial collective dynamic structure factor matrix S(q, t):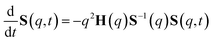 | (A1) |
| S−1(q) = (I − C*)−1 | (A2) |
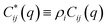 Defining a 2 × 2 matrix Ω(q), eqn (A1) then becomes
Defining a 2 × 2 matrix Ω(q), eqn (A1) then becomes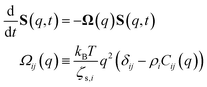 | (A3) |
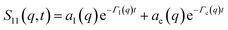 | (A4) |
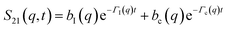 | (A5) |
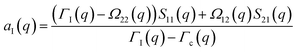 | (A6) |
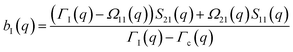 | (A7) |
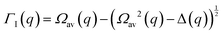 | (A8) |
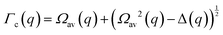 | (A9) |
Acknowledgements
The authors acknowledge support from the Army Research Office via a MURI grant with contract no. W911NF-21-0146. We thank Anoop Mutneja, Heinrich Jaeger, and Alice Pelosse for discussions.References
- E. Dickinson, Soft Matter, 2006, 2, 642–652 RSC.
- A. Albanese, P. S. Tang and W. C. W. Chan, Annu. Rev. Biomed. Eng., 2012, 14, 1–16 CrossRef CAS PubMed.
- M. A. El-Sayed, Acc. Chem. Res., 2004, 37, 326–333 CrossRef CAS PubMed.
- C. J. Martinez, J. Liu, S. K. Rhodes, E. Luijten, E. R. Weeks and J. A. Lewis, Langmuir, 2005, 21, 9978–9989 CrossRef CAS PubMed.
- J. F. Gilchrist, A. T. Chan, E. R. Weeks and J. A. Lewis, Langmuir, 2005, 21, 11040–11047 CrossRef CAS PubMed.
- A. T. Chan and J. A. Lewis, Langmuir, 2005, 21, 8576–8579 CrossRef CAS.
- S. Asakura and F. Oosawa, J. Chem. Phys., 1954, 22, 1255–1256 CrossRef CAS.
- A. V. Vrij, Pure Appl. Chem., 1976, 48, 471–483 CAS.
- K. Miyazaki, K. S. Schweizer, D. Thirumalai, R. Tuinier and E. Zaccarelli, J. Chem. Phys., 2022, 156, 80401 CrossRef CAS.
- P. Bartlett, R. H. Ottewill and P. N. Pusey, J. Chem. Phys., 1990, 93, 1299–1312 CrossRef CAS.
- P. D. Kaplan, J. L. Rouke, A. G. Yodh and D. J. Pine, Phys. Rev. Lett., 1994, 72, 582 CrossRef CAS PubMed.
- J. B. Hooper and K. S. Schweizer, Macromolecules, 2005, 38, 8858–8869 CrossRef CAS.
- J. A. Perera-Burgos, J. M. Méndez-Alcaraz, G. Pérez-Ángel and R. Castañeda-Priego, J. Chem. Phys., 2016, 145, 104905 CrossRef PubMed.
- S. M. Ilett, A. Orrock, W. C. K. Poon and P. N. Pusey, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 1344 CrossRef CAS PubMed.
- P. N. Segrè, V. Prasad, A. B. Schofield and D. A. Weitz, Phys. Rev. Lett., 2001, 86, 6042 CrossRef.
- Y. L. Chen and K. S. Schweizer, J. Chem. Phys., 2004, 120, 7212 CrossRef CAS PubMed.
- R. Castañeda-Priego, A. Rodríguez-López and J. M. Méndez-Alcaraz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 051404 CrossRef PubMed.
- S. A. Shah, Y. L. Chen, S. Ramakrishnan, K. S. Schweizer and C. F. Zukoski, J. Phys.: Condens. Matter, 2003, 15, 4751 CrossRef CAS.
- R. Tuinier, J. Rieger and C. G. De Kruif, Adv. Colloid Interface Sci., 2003, 103, 1–31 CrossRef CAS PubMed.
- M. Fuchs and K. S. Schweizer, Europhys. Lett., 2000, 51, 621 CrossRef CAS.
- G. L. Hunter and E. R. Weeks, Rep. Prog. Phys., 2012, 75, 066501 CrossRef PubMed.
- E. Zaccarelli and W. C. K. Poon, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15203–15208 CrossRef CAS.
- E. Zaccarelli, G. Foffi, K. A. Dawson, F. Sciortino and P. Tartaglia, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 031501 CrossRef CAS.
- K. N. Pham, A. M. Puertas, J. Bergenholtz, S. U. Egelhaaf, A. Moussaïd, P. N. Pusey, A. B. Schofield, M. E. Cates, H. Fuchs and W. C. K. Poon, Science, 2002, 296, 104–106 CrossRef CAS PubMed.
- V. Tohver, J. E. Smay, A. Braem, P. V. Braun and J. A. Lewis, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 8950–8954 CrossRef CAS PubMed.
- E. J. W. Verwey and J. T. G. Overbeek, Theory of the stability of lyophobic colloids, Elsevier, Amsterdam, 1948 Search PubMed.
- B. Derjaguin and L. Landau, Acta Physicochim. URSS, 1941, 14, 633 Search PubMed.
- V. Tohver, A. Chan, O. Sakurada and J. A. Lewis, Langmuir, 2001, 17, 8414–8421 CrossRef CAS.
- K. N. Pham, S. U. Egelhaaf, P. N. Pusey and W. C. K. Poon, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 011503 CrossRef CAS PubMed.
- E. N. Scheer and K. S. Schweizer, J. Chem. Phys., 2008, 128, 164905 CrossRef PubMed.
- Y. Zhou and K. S. Schweizer, J. Chem. Phys., 2020, 153, 114901 CrossRef CAS PubMed.
- Y. Zhou and K. S. Schweizer, J. Chem. Phys., 2019, 150, 214902 CrossRef PubMed.
- S. M. Morozova, L. López-Flores, A. Gevorkian, H. Zhang, V. Adibnia, W. Shi, D. Nykypanchuk, T. G. Statsenko, G. C. Walker, O. Gang, M. O. de la Cruz and E. Kumacheva, ACS Nano, 2023, 17, 15012–15024 CrossRef CAS PubMed.
- R. B. Jadrich, D. J. Milliron and T. M. Truskett, J. Chem. Phys., 2023, 159, 090401 CrossRef CAS PubMed.
- S. Cheng, S. J. Xie, J. M. Y. Carrillo, B. Carroll, H. Martin, P. F. Cao, M. D. Dadmun, B. G. Sumpter, V. N. Novikov, K. S. Schweizer and A. P. Sokolov, ACS Nano, 2017, 11, 752–759 CrossRef CAS.
- S. Gong, Q. Chen, J. F. Moll, S. K. Kumar and R. H. Colby, ACS Macro Lett., 2014, 3, 773–777 CrossRef CAS.
- M. Diba, G. L. Koons, M. L. Bedell and A. G. Mikos, Biomaterials, 2021, 274, 120871 CrossRef CAS.
- T. Jiang, C. F. Zukoski and C. F. Zukoski, J. Rheol., 2014, 58, 1277–1299 CrossRef CAS.
- F. J. Müller, L. Isa and J. Vermant, Nat. Commun., 2023, 14, 5309 CrossRef PubMed.
- R. L. Truby and J. A. Lewis, Nature, 2016, 540, 371–378 CrossRef CAS.
- J. A. Lewis, Adv. Funct. Mater., 2006, 16, 2193–2204 CrossRef CAS.
- A. Zaccone, H. Wu and E. Del Gado, Phys. Rev. Lett., 2009, 103, 208301 CrossRef PubMed.
- S. Ramakrishnan, Y. L. Chen, K. S. Schweizer and C. F. Zukoski, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 040401(R) CrossRef PubMed.
- H. A. Vinutha, F. D. Diaz Ruiz, X. Mao, B. Chakraborty and E. Del Gado, J. Chem. Phys., 2023, 158, 114104 CrossRef CAS.
- M. Bantawa, W. A. Fontaine-Seiler, P. D. Olmsted and E. Del Gado, J. Phys.: Condens. Matter, 2021, 33, 414001 CrossRef CAS.
- P. K. Kao, M. J. Solomon and M. Ganesan, Soft Matter, 2022, 18, 1350–1363 RSC.
- K. A. Whitaker, Z. Varga, L. C. Hsiao, M. J. Solomon, J. W. Swan and E. M. Furst, Nat. Commun., 2019, 10, 2237 CrossRef.
- C. Ferreiro-Córdova, E. Del Gado, G. Foffi and M. Bouzid, Soft Matter, 2020, 16, 4414–4421 RSC.
- J. Liu, Y. Gao, D. Cao, L. Zhang and Z. Guo, Langmuir, 2011, 27, 7926–7933 CrossRef CAS PubMed.
- D. Meng, S. K. Kumar, S. Cheng and G. S. Grest, Soft Matter, 2013, 9, 5417–5427 RSC.
- V. Ganesan and A. Jayaraman, Soft Matter, 2014, 10, 13–38 RSC.
- S. K. Kumar, B. C. Benicewicz, R. A. Vaia and K. I. Winey, Macromolecules, 2017, 50, 714–731 CrossRef CAS.
- J. Liu and E. Luijten, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 061401 CrossRef PubMed.
- J. Liu, N. B. Wilding and E. Luijten, Phys. Rev. Lett., 2006, 97, 115705 CrossRef PubMed.
- D. J. Ashton, J. Liu, E. Luijten and N. B. Wilding, J. Chem. Phys., 2010, 133, 194102 CrossRef PubMed.
- E. M. Zirdehi, T. Voigtmann and F. Varnik, J. Phys.: Condens. Matter, 2020, 32, 275104 CrossRef CAS PubMed.
- E. Lázaro-Lázaro, J. A. Perera-Burgos, P. Laermann, T. Sentjabrskaja, G. Pérez-Ángel, M. Laurati, S. U. Egelhaaf, M. Medina-Noyola, T. Voigtmann, R. Castañeda-Priego and L. F. Elizondo-Aguilera, Phys. Rev. E, 2019, 99, 042603 CrossRef PubMed.
- D. Truzzolillo, D. Marzi, J. Marakis, B. Capone, M. Camargo, A. Munam, F. Moingeon, M. Gauthier, C. N. Likos and D. Vlassopoulos, Phys. Rev. Lett., 2013, 111, 208301 CrossRef PubMed.
- R. Zhang and K. S. Schweizer, J. Phys. Chem. B, 2018, 122, 3465 CrossRef CAS PubMed.
- R. Jadrich and K. S. Schweizer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 061503 CrossRef PubMed.
- J. P. Hansen and I. R. McDonald, Theory of Simple Liquids, Elsevier, 2006 Search PubMed.
- Y. Zhou, B. Mei and K. S. Schweizer, Phys. Rev. E, 2020, 101, 042121 CrossRef CAS PubMed.
- S. Chaki, B. Mei and K. S. Schweizer, Phys. Rev. E, 2024, 110, 034606 CrossRef CAS PubMed.
- N. Koumakis, A. Pamvouxoglou, A. S. Poulos and G. Petekidis, Soft Matter, 2012, 8, 4271–4284 RSC.
- L. Verlet, Mol. Phys., 1981, 42, 1291–1302 CrossRef CAS.
- L. Verlet, Mol. Phys., 1980, 41, 183–190 CrossRef CAS.
- Y. Zhou and K. S. Schweizer, Macromolecules, 2020, 53, 9962–9972 CrossRef CAS.
- K. A. Deo, A. Murali, J. J. Tronolone, C. Mandrona, H. P. Lee, S. Rajput, S. E. Hargett, A. Selahi, Y. Sun, D. L. Alge, A. Jain and A. K. Gaharwar, Adv. Healthcare Mater., 2024, 2303810 CrossRef CAS PubMed.
- Y. Li, J. R. Royer, J. Sun and C. Ness, Soft Matter, 2023, 19, 1342–1347 RSC.
- J. C. Conrad, S. R. Ferreira, J. Yoshikawa, R. F. Shepherd, B. Y. Ahn and J. A. Lewis, Curr. Opin. Colloid Interface Sci., 2011, 16, 71–79 CrossRef CAS.
- G. D’Oria, D. Z. Gunes, F. Lequeux, C. Hartmann, H. J. Limbach and L. Ahrné, Food Hydrocolloids, 2023, 137, 108401 CrossRef.
- Y. Xu and T. G. Mason, Sci. Adv., 2023, 9, 10 Search PubMed.
- S. Pradeep, P. E. Arratia and D. J. Jerolmack, Nat. Commun., 2024, 15, 7432 CrossRef CAS PubMed.
- K. Farain and D. Bonn, Phys. Rev. Lett., 2024, 133, 028203 CrossRef CAS PubMed.
- N. M. James, C. P. Hsu, N. D. Spencer, H. M. Jaeger and L. Isa, J. Phys. Chem. Lett., 2019, 10, 1663–1668 CrossRef CAS PubMed.
- H. Kim, M. van der Naald, N. D. Dolinski, S. J. Rowan and H. M. Jaeger, Soft Matter, 2023, 19, 6797–6804 RSC.
- C. Chen, M. van der Naald, A. Singh, N. D. Dolinski, G. L. Jackson, H. M. Jaeger, S. J. Rowan and J. J. de Pablo, ACS Cent. Sci., 2023, 9, 639–647 CrossRef CAS PubMed.
- A. Mutneja and K. S. Schweizer, Soft Matter, 2024, 20, 7284 RSC.
- D. C. Viehman and K. S. Schweizer, J. Chem. Phys., 2008, 128, 8 CrossRef PubMed.
- T. R. Kirkpatrick and P. G. Wolynes, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 35, 3072 CrossRef CAS PubMed.
- R. Jadrich and K. S. Schweizer, J. Chem. Phys., 2011, 135, 234902 CrossRef PubMed.
- G. Nägele and J. Bergenholtz, J. Chem. Phys., 1998, 108, 9893 CrossRef.
- B. Mei, Y. Zhou and K. S. Schweizer, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2025341118 CrossRef CAS PubMed.
- W. Götze, Complex Dynamics of Glass-Forming Liquids: A Mode-Coupling Theory, Oxford University Press, 2009 Search PubMed.
- K. S. Schweizer, J. Chem. Phys., 2005, 123, 244501 CrossRef PubMed.
- M. P. Lettinga, C. M. Kats and A. P. Philipse, Langmuir, 2000, 16, 6166–6172 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01193g |
| This journal is © The Royal Society of Chemistry 2025 |