Open Access Article
Open Access ArticleFine-tuning the architecture of microgels by varying the initiator addition time†
Elena
Buratti‡
 a,
Fabrizio
Camerin‡
a,
Fabrizio
Camerin‡
 b,
Valentina
Nigro
b,
Valentina
Nigro
 c,
Silvia
Franco
c,
Silvia
Franco
 de,
José
Ruiz-Franco
de,
José
Ruiz-Franco
 fg,
Lionel
Porcar
h,
Roberta
Angelini
fg,
Lionel
Porcar
h,
Roberta
Angelini
 de,
Barbara
Ruzicka
de,
Barbara
Ruzicka
 de,
Yuri
Gerelli
de,
Yuri
Gerelli
 de and
Emanuela
Zaccarelli
de and
Emanuela
Zaccarelli
 *de
*de
aDepartment of Chemical, Pharmaceutical and Agricultural Sciences, University of Ferrara, via L. Borsari 46, 44121 Ferrara, Italy
bPhysical Chemistry, Department of Chemistry, Lund University, SE-22100 Lund, Sweden
cPhotonics Micro and Nanostructures Laboratory, Nuclear Department, ENEA Frascati Research Centre, Via E. Fermi 45, 00044 Frascati, Italy
dItalian National Research Council, Institute for Complex Systems (CNR-ISC), Sapienza University of Rome, Piazzale Aldo Moro 5, 00185 Rome, Italy. E-mail: emanuela.zaccarelli@cnr.it
eDepartment of Physics, Sapienza University of Rome, P.le A. Moro 2, 00185 Roma, Italy
fDepartment of Condensed Matter Physics, University of Barcelona, Carrer de Martí i Franqués 1, Barcelona 08028, Spain
gInstitute of Complex Systems (UBICS), University of Barcelona, Carrer de Martí i Franqués 1, Barcelona, 08028, Spain
hInstitut Laue-Langevin, 71 avenue des Martyrs, Grenoble 38000, France
First published on 27th January 2025
Abstract
Poly-N-isopropylacrylamide (PNIPAM) microgels are versatile colloidal-scale polymer networks that exhibit unique responsiveness to external stimuli, such as temperature. While the synthesis of PNIPAM microgels is well-documented, there is limited exploration of how their structural properties can be modified by subtle changes in the polymerization process. In this work, we carefully investigate how varying the time of addition of a common initiator, such as potassium persulfate, during the polymerization process allows a precise control over microgel architecture. Our findings, based on a combination of numerical simulations, scattering, and rheology experiments, reveal that delayed initiator addition results in a more heterogeneous network, characterized by a less extended corona. In contrast, more homogeneous microgels are obtained by adding the initiator all at the start of the synthesis. In this way, the internal mass distribution of the particles can be tuned, highlighting the importance of synthesis timing for optimizing microgel conformation and functionality in tailored applications.
1 Introduction
Microgels are colloidal-scale polymer networks that represent the prototype model system for soft repulsive particles.1–4 Their ability to respond to external control parameters, such as temperature in the case of the widely investigated poly-N-isopropylacrylamide (PNIPAM), makes them very valuable for a wide range of applications,5,6 from nanosensing7 to biomedicine.8The experimental synthesis of PNIPAM microgels is well-documented in the literature9,10 and follows a general recipe, that is used by the large majority of the research groups worldwide. It is well-known that such a synthesis protocol gives rise to polymer networks, that are not homogeneous. Rather, they are characterized by a so-called core–corona structure, due to the fact that crosslinkers, usually N,N-methylenebisacrylamide (BIS) molecules, react significantly faster than NIPAM monomers in the polymerization process. In this way, microgels comprise a denser, inner part that is richer in crosslinkers (the core), and a fluffier, external shell (the corona), where only few crosslinkers are present. This characteristic structure has been revealed by neutron and X-ray small-angle scattering experiments at high dilution, measuring the microgels form factors, that are well-described by the celebrated fuzzy sphere model.11,12
The synthesis protocol can also be adapted to modify the overall internal conformation of the particles. To this aim, some studies have focused on the possibility to obtain more homogeneous microgels. This can either be achieved by starting with oligomers rather than monomers in the reaction batch13 or via continuous monomer feeding.14 Another possibility is to act on the initiator of the polymerization process. However, no specific differences in structure or swelling properties have been reported if different types of initiators, such as potassium persulfate (KPS) or ammonium persulfate (APS), were employed.15,16 Similarly, for anionic or cationic initiators like 2,2-azobis(2-methylpropionamidine) dihydrochloride (AIBA), it was shown that the microgel properties are largely unaffected.17
Nevertheless, a less investigated aspect is the addition time of the initiator, which is typically introduced into the reaction batch either in a single shot or in a controlled way within a fixed amount of time. This subtle change in the protocol could have non-trivial effects on the resulting particles, since one could expect that a drop-by-drop addition would create more nuclei, leading to smaller microgels, as compared to a one-time addition that could form a lower number of polymerization centers. In addition to size modifications, the initiator time could also favor a different internal organization of crosslinkers and monomers, thus affecting the features of the core–corona structure. Expectations would be in favor of more homogeneous microgels with a more controlled drop-by-drop addition, while a more heterogeneous structure could be expected with the initiator being added altogether.
In this work, we aim to systematically explore this effect by preparing microgels with different amounts of initiator time tadd, leaving unaltered all the other parameters in the synthesis. The parameter tadd represents the duration of the continuos feeding of the KPS initiator, ranging from tadd = 0.2 min, where all KPS is added at the same time, up to tadd = 9 min, where KPS is added at an approximate rate of 0.27 mM min−1. The microgels hydrodynamic size and internal structure are determined by means of dynamic light scattering (DLS) and small angle neutron scattering (SANS) techniques, respectively. To interpret the results, we rely on computer simulations based on a monomer-resolved microgel model, recently established in our group,12,18 which was shown to be able to capture the internal structure of microgels at different crosslinker concentration.19 To capture the subtle variation of the structure with different initiator addition times, we slightly modify our in silico assembly procedure to account for modifications of the core–corona ratio within the particles. The microgel modeling is further aided by rheological measurements from which we extracted relevant information on the number of polymerization nuclei in the reaction batch. In this way, we are able to fully describe the observed experimental variations given by the addition of KPS from tadd = 0.2 min up to tadd = 9 min.
Our findings reveal interesting features for the obtained microgels. Specifically, we find that when the initiator is added during a very short time interval, polymerization occurs on few nuclei in the reaction batch, following our initial expectations, giving rise to overall larger microgels. At the same time, such particles present a quite extended core with respect to the total size of the microgels and thus a more homogeneous structure. On the contrary, our analysis evidences the tendency for the formation of smaller particles when initiator is included within longer times. This is related to the possibility of creating multiple polymerization centers over time so that, at fixed amount of added monomer, the particles have a smaller hydrodynamic radius. In the latter case, crosslinkers are more confined within the inner part of the microgels, resulting in a more heterogeneous structure with a smaller core as compared to the former scenario. The interpretation of the experimental results, which only show a moderate variation with increasing addition time, is facilitated by the adopted simulations. These complement the measurements by offering an insightful microscopic perspective.
Overall, these results provide a better understanding of the processes taking place during the experimental synthesis, and offer a guide on how to leverage the initiator addition time for obtaining microgels with different sizes and architectures.
2 Materials and methods
2.1 Experimental section
For each sample, the scattering intensity I(q) was obtained from the radial averaging of the 2-D detector images using the GRASP22 software. Absolute scattering units (i.e. cm−1) normalisation was achieved by accounting for the measured neutron flux and for the sample and empty cell transmission values.
Experimental data acquired for the empty cell and for the pure D2O were subtracted from those of the sample to the data analysis, which was then performed using the SasView software.23 SANS intensity versus q curves were analyzed using a model based on the fuzzy sphere form-factor.11 This model includes the fuzzy-sphere form factor Pinho(q) (eqn (1)), the gel network density fluctuations contribution Pfluct(q) (eqn (2)) and a flat, q-independent, background (bkg).
In detail, the fuzzy-sphere form-factor was expressed as11
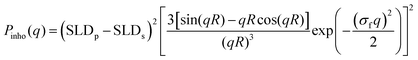 | (1) |
It is worth noticing that for σf = 0, Pinho(q) corresponds to the form-factor of a homogeneous spherical particle of radius R.
The gel network contribution was modeled using a Lorentzian function
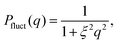 | (2) |
| Im(q) = c·Pinho(q) + Ifluct(0)·Pfluct(q) + bkg | (3) |
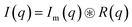 | (4) |
The resulting expression (eqn (4)) was fitted to the experimental data using a least-squares minimization method. This procedure led to the determination of R, σf, ξ, c, Ifluct(0), and bkg. Importantly, this model does not include any polydispersity function to account for size variations, thus assuming a monodisperse particle population.
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 500 s−1 for 30 seconds to obtain a reproducible initial state by erasing any previous mechanical history. After loading, the sample was allowed to equilibrate thermally for a few minutes before starting the measurement. The flow curves of viscosity as a function of shear rate are described by means of the Cross model:24
= 500 s−1 for 30 seconds to obtain a reproducible initial state by erasing any previous mechanical history. After loading, the sample was allowed to equilibrate thermally for a few minutes before starting the measurement. The flow curves of viscosity as a function of shear rate are described by means of the Cross model:24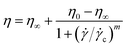 | (5) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c is a critical shear rate and m is a positive power exponent. To estimate an effective packing fraction ϕeff, viscosity measurements were performed in dilute conditions as a function of the weight concentration Cw. Specifically, the dependence of the relative viscosity ηr = η/ηs, with ηs the solvent viscosity in the absence of the microgels, on the packing fraction ϕeff is given at low concentrations by the Einstein–Batchelor equation:25
c is a critical shear rate and m is a positive power exponent. To estimate an effective packing fraction ϕeff, viscosity measurements were performed in dilute conditions as a function of the weight concentration Cw. Specifically, the dependence of the relative viscosity ηr = η/ηs, with ηs the solvent viscosity in the absence of the microgels, on the packing fraction ϕeff is given at low concentrations by the Einstein–Batchelor equation:25| ηr(ϕeff) = 1 + 2.5ϕeff + 5.9ϕeff2. | (6) |
2.2 Numerical section
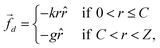 | (7) |
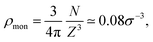 | (8) |
In this work, for capturing the dependence on the initiator addition time tadd, we introduce a few differences with respect to this previously established assembly protocol. First of all, we change the value of C with respect to Z in order to vary the confinement of the crosslinkers. Secondly, we act on the short-time (bare) diffusion coefficient D0 of the Brownian thermostat in the simulations used for the assembly. In fact, we observed that by setting 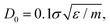 as in the previously established method,12 the results were rather independent of C. The use of
as in the previously established method,12 the results were rather independent of C. The use of 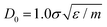 appears to fix this issue. For consistency, we note that the method put forward in ref. 12 with C = Z/2 and
appears to fix this issue. For consistency, we note that the method put forward in ref. 12 with C = Z/2 and 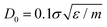 yields statistically identical assembly results to the case where C = 0.65Z and
yields statistically identical assembly results to the case where C = 0.65Z and 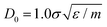 reported in this work. This choice, as shown below, corresponds to the experimental case tadd = 9 minutes.
reported in this work. This choice, as shown below, corresponds to the experimental case tadd = 9 minutes.
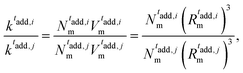
In addition, in order to be consistent with rheological measurements, which provide indirect information on the packing fractions of the different samples, as discussed in detail below, we also vary the number of monomers N, and thus Z, ensuring the validity of eqn (8). For convenience, all relevant assembly parameters for the microgels discussed in the present work are summarized in Table 1, together with the assigned names to the samples. In this respect, the subscript refers to the size of the microgel based on the number of particles (s = small, m = medium, l = large), while the apex, where present, is related to the size of the spherical region defined by C, that is roughly the core radius. We note that the experimental value of tadd is not present for the cases that cannot be directly compared to experiments, due to the lack of neutron scattering and viscosity measurements for the intermediate samples.
| Name | t add [min] | N | C [σ] | Z [σ] | C/Z |
|---|---|---|---|---|---|
| M s | 9.0 | 168k | 51.6 | 79.4 | 0.65 |
| M m | 1.0 | 230k | 66.1 | 88.1 | 0.75 |
| M c50l | — | 336k | 50 | 100 | 0.50 |
| M c60l | — | 336k | 60 | 100 | 0.60 |
| M c70l | — | 336k | 70 | 100 | 0.70 |
| M l | 0.2 | 336k | 80 | 100 | 0.80 |
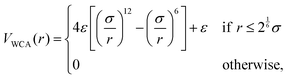 | (9) |
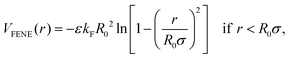 | (10) |
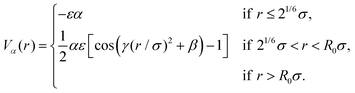 | (11) |
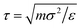 the unit of time. A subsequent production run is carried out for at least 5 × 106δt. All microgels simulations are performed using the LAMMPS package.32
the unit of time. A subsequent production run is carried out for at least 5 × 106δt. All microgels simulations are performed using the LAMMPS package.32
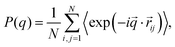 | (12) |
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) . In real space, we calculate the radial density profiles of the microgel as
. In real space, we calculate the radial density profiles of the microgel as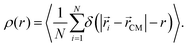 | (13) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) CM the distance from the microgel center of mass. Finally, we estimate the hydrodynamic radius of our microgels to compare with DLS measurements, exploiting the method recently put forward in ref. 16. In brief, the hydrodynamic radius is calculated following Hubbard and Douglas as done in ref. 33:
CM the distance from the microgel center of mass. Finally, we estimate the hydrodynamic radius of our microgels to compare with DLS measurements, exploiting the method recently put forward in ref. 16. In brief, the hydrodynamic radius is calculated following Hubbard and Douglas as done in ref. 33: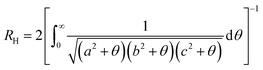 | (14) |
3 Results and discussion
3.1 Experimental characterization
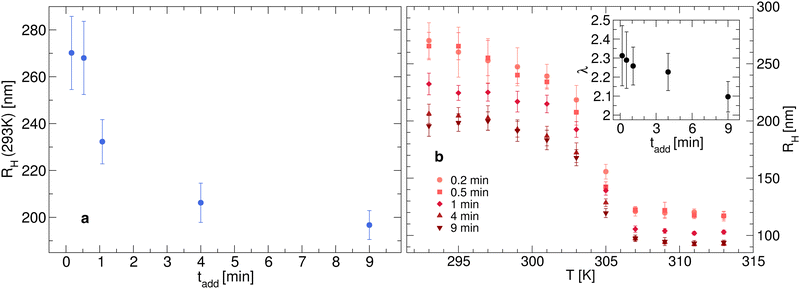
We synthesize five different microgel batches by adding N-isopropylacrylamide (NIPAM) as monomer, N,N-methylenebisacrylamide (BIS) as crosslinking agent, and potassium persulfate (KPS) as initiator of the polymerization process. The five batches differ for the rate of addition of KPS, which is carried out in 0.2, 0.5, 1, 4 and 9 minutes, respectively. The detailed procedure for the microgel synthesis is described in the Methods section.For characterizing the obtained microgels, we first investigate their hydrodynamic size by DLS. The hydrodynamic radius RH as a function of KPS addition time tadd is shown in Fig. 1(a) and (b) at 293 K and as a function of temperature T, respectively. It is clear how the inclusion of the initiator at different times has a strong effect on the overall size of the particles, since RH drops by about 25% if the addition is carried out in less than a minute or in 4 minutes. Smaller differences are instead noted at longer addition times, with RH that changes from 206 to 197 nm for tadd = 4 and 9 minutes, respectively.
The response to temperature is typical of other responsive PNIPAM microgels, with a swollen state at low temperatures and a collapsed state at high temperatures. However, we observe a more subtle temperature dependence for different microgel batches. In fact, as shown in Fig. 1(b), different size ranges are explored for different addition times. This is reflected in the overall swelling ratio λ = RH(T = 293 K)/RH(T = 313 K) (see inset in Fig. 1(b)) which goes from about 2.3 for small tadd to about 2.1 when the addition of KPS is carried out for longer times, indicating an increasingly reduced shrinking capability. Despite this, we note that the synthesis procedure does not affect the volume phase transition temperature of the microgels, which remains close to 305 K, as expected.
For three of the five samples we also carry out rheological measurements. The relative viscosity ηrel as a function of weight concentration Cw is reported in Fig. 2 for batches with initiator addition time tadd = 0.2, 1 and 9 minutes. In all cases we note a similar trend, with the viscosity growing for increasing concentrations. Coherently with expectations, the highest value of viscosity is reached for the sample with tadd = 0.2 and with the greatest hydrodynamic radius. As shown in Fig. 2, the relative viscosity data can be fitted by means of eqn (6), which allows us to extract the conversion parameter k, reported in the inset for the three investigated samples. Its decreasing trend as a function of tadd is similar to that observed for RH shown in Fig. 1(a).
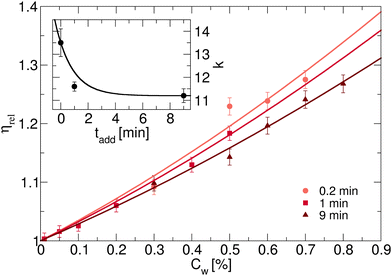 | ||
| Fig. 2 (a) Relative viscosity ηrel for dispersions containing PNIPAM microgels synthesised with KPS added in tadd = 0.2,1 and 9 min, as a function of weight concentration Cw. Inset: Shift parameter k, obtained by fitting ηrel according to eqn (6). The solid black line is a guide to the eye. | ||
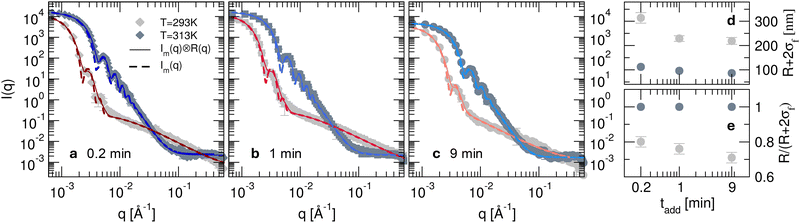 | ||
Fig. 3 (a)–(c) Experimental scattering intensity measured on the D22 diffractometer for microgels synthesised in D2O with KPS added in tadd = 0.2, 1 and 9 min in the collapsed (313 K, dark grey symbols) and in the swollen (293 K, light grey symbols) states. Thin solid lines represent the best fits obtained using eqn (4) with the resolution-free Im(q) curves, shown as thick dashed lines. (d) Total particle radius (R + 2σf) as a function of KPS addition time tadd obtained from the fits of the SANS data (panels a–c) for the microgels in the collapsed (313 K, dark grey circles) and in the swollen (293 K, light grey circles) state. (e) Core–corona ratio, 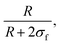 as a function of the KPS addition time tadd obtained from the fits of the SANS data for the microgels for the two analysed temperatures. as a function of the KPS addition time tadd obtained from the fits of the SANS data for the microgels for the two analysed temperatures. | ||
As derived from the analysis of the SANS data reported in Fig. 3(a)–(c), in the collapsed state all microgels can be described as homogeneous spheres with a total radius11 decreasing from 112 ± 3 nm for the sample prepared at tadd = 0.2 min to 86 ± 2 nm for the sample prepared at tadd = 9 min (Fig. 3(d)). In this model, the fuzziness and the presence of a detectable gel network can be suppressed by setting σf = 0 in eqn (1) and Ifluct(0) = 0 in eqn (3). At T = 293 K, the microgel form factors are well described by eqn (3). For these swollen microgels, SANS experiments allows us to determine the extension of the corona and that of the core radius, respectively, thanks to the use of the fuzzy sphere model. Also in this case the total radius (R + 2σf) of the particles decreases as the addition time increases. The opposite trend is found for the core–corona ratio, 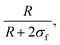 shown in Fig. 3(e). Indeed, the extension of the corona, σf, is found to be similar for all investigated samples, while larger changes are observed in the extension of the microgel core radius, R. Such decreasing trend in the core–corona ratio reveals that the structure of the microgel gets more heterogeneous as tadd increases. For the samples in the swollen state it is also possible to detect the presence of the Lorentzian contribution (eqn (2)) originated by the gel network density fluctuations. Because of the explored q-range, the correlation length ξ could not be determined with high accuracy, resulting ∼4 ± 2 nm for all investigated samples.
shown in Fig. 3(e). Indeed, the extension of the corona, σf, is found to be similar for all investigated samples, while larger changes are observed in the extension of the microgel core radius, R. Such decreasing trend in the core–corona ratio reveals that the structure of the microgel gets more heterogeneous as tadd increases. For the samples in the swollen state it is also possible to detect the presence of the Lorentzian contribution (eqn (2)) originated by the gel network density fluctuations. Because of the explored q-range, the correlation length ξ could not be determined with high accuracy, resulting ∼4 ± 2 nm for all investigated samples.
To assess size effects, we also report form factors measured by SANS for the surfactant-free microgels synthesized with tadd = 9 minutes in the ESI.† The results, reported in Fig. S1 (ESI†) are very similar to those of Fig. 3, particularly from the core–corona ratio extracted from the fits and reported for the surfactant-free microgels in Table S1 (ESI†) and for all other samples in Table S2 (ESI†). This indicates that the resulting microgels internal architecture is independent on the amount of added surfactant.
3.2 Establishing a microgel model for describing the role of the initiator addition time tadd
Computer simulations represent an important tool for gaining more detailed information on the architecture of the microgels at the single-particle level. In silico synthesis in fact allows for a one-to-one comparison with the form factors of the microgel samples measured experimentally, with the advantage of being able to directly study the effect of a change in a parameter on the structure of the particle. In brief, a realistic model for microgels can be obtained by the self-assembly of N patchy particles under spherical confinement in such a way that a crosslinked gel-like structure is obtained. The higher reactivity of crosslinkers compared to monomers, which is typically observed in experiments, can be mimicked by concentrating specific particles in the center of the sphere during assembly by means of an additional designing force![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) d, see eqn (7). Therefore, by applying
d, see eqn (7). Therefore, by applying ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) d within a radius C, we are able to effectively obtain a more extended or restricted microgel core. Additional details on the microgel assembly are reported in Methods.
d within a radius C, we are able to effectively obtain a more extended or restricted microgel core. Additional details on the microgel assembly are reported in Methods.
It is important to note that the in silico synthesis we carry out does not aim to reproduce the standard chemical protocol followed in experiments. Rather, it is designed for describing the overall structure of the particles, independently of the followed procedure. For the case being, this does not translate into having specific particles with the role of “initiator” in the computational synthesis. Rather, the focus is centered to the effect that the addition of initiator at different times has on the final structure, and thus on crosslinker distribution, of the individual microgels. Specifically, here we find that two parameters in the computational synthesis are particularly relevant for reproducing correctly the microgel architecture obtained experimentally upon changing tadd, namely the size of the core compared to the overall size of the particle and the ratio between the number of monomers among different microgel batches, as discussed in more detail in the following.
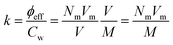 | (15) |
 | (16) |
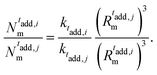 | (17) |
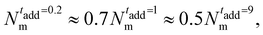 | (18) |
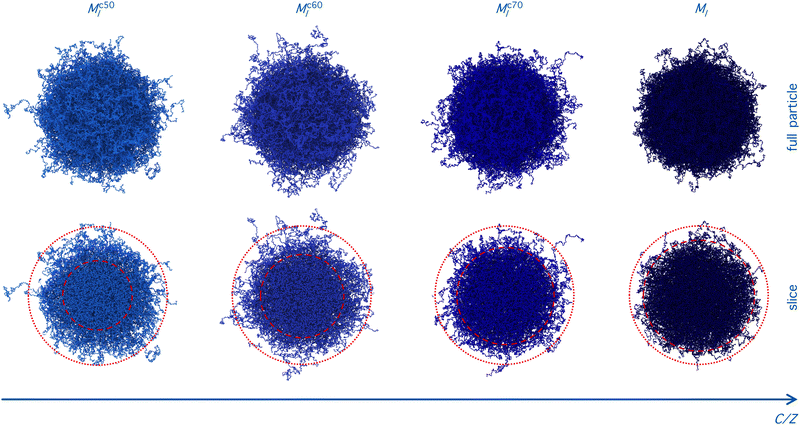
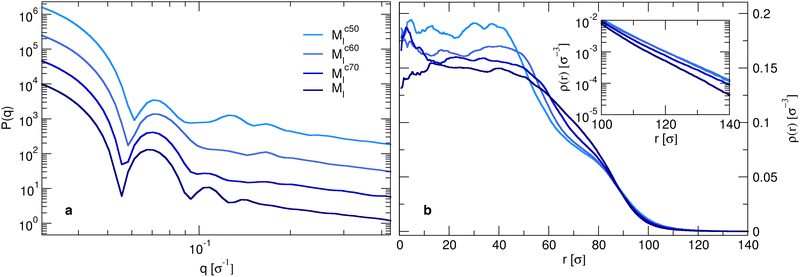
Although the number of monomers is fixed, the microgels exhibit a slight increase in total size as the core size decreases, as indicated by distance where the radial density profile approaches zero (inset in Fig. 5(b)). The position of the first peak of P(q) remains roughly constant, which is an indication that the radius of gyration of the microgels is also quite constant (not shown). This observation is not in contradiction with the increase in total size, as for smaller cores, the particle becomes denser toward its center and the overall extension of the particle can still be larger, driven by the presence of a less dense, but more extended corona. Indeed, the structure and extension of the corona change, as evidenced by the appearance of two distinct gradient regions in the radial density profiles. These correspond to the shift, toward higher wavenumbers of the second and third peaks in the form factors for the Mc60l and Mc50l samples reported in Fig. 5(a).
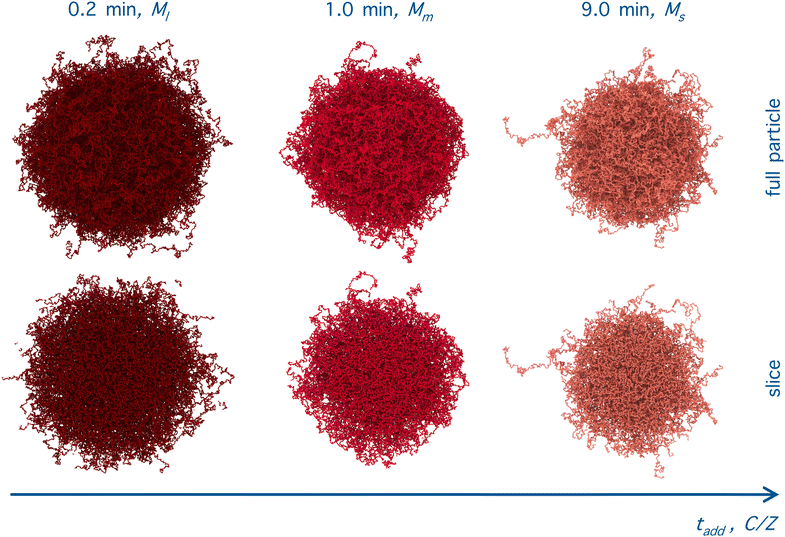
This picture suggests that if the crosslinkers are concentrated in a larger and larger volume, the overall size of the particle tends to be smaller than for the opposite case, where a more spread and swollen structure is retained. This is confirmed by the radial density profiles ρ(r) shown in Fig. 5(b), which provide the same information in real space but allowing for a better visualization of the variation of the core size with C. In addition, the inset shows that the smaller the core, the greater the long-distance tail of the profiles, indicating the growing size of the particles. These results can also be visually detected by looking at the snapshots of the corresponding microgels, where an overall fluffier structure with longer outer chains is consistently observed for microgels with a smaller core.
3.3 Comparison between in silico microgels and experiments
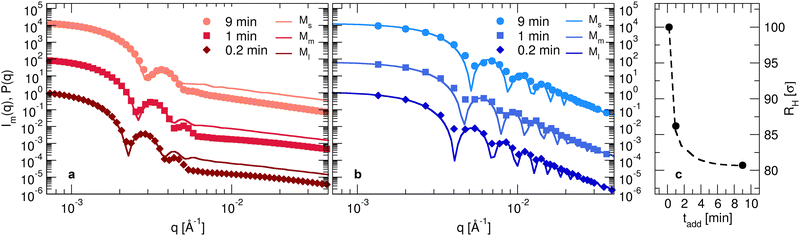
By combining the information derived in the previous sections, it is now possible to obtain detailed models for each of the synthesized batches. In order to do so, it is straightforward to compare the Im(q) derived from the analysis of the experimental data to the form factors calculated numerically. The determination of the Im(q) data is reported in the Methods section. In order to determine the conversion unit between simulations and experiments, we superimpose the first peak of the numerical form factor onto the experimental one at the lowest investigated temperature.12 Then, the same scaling factor, corresponding to the measure of the bead size σ used in simulations, is retained for all other temperatures.Experimental and numerical form factors for initiator addition times of 0.2,1.0 and 9.0 minutes are shown with symbols and full lines, respectively, in Fig. 6(a) for T = 293 K and in Fig. 6(b) for 313 K. The numerical form factors are calculated for microgels Ml, Mm and Ms, as discussed in the previous section, in order to account for the smaller amount of monomers present in each of the experimental microgels for longer tadd. The size of the core C is here adjusted as the main fit parameter for matching at best the experimental measurements. A remarkable agreement with the experiments is obtained for a progressively smaller size of the core as the initiator addition time increases. Correspondingly, the ratio between the core and the microgel radii C/Z also decreases, going from around 0.8 to 0.65 from 0.2 to 9 minutes of initiator addition time. These findings are in qualitative agreement with the analysis of the neutron scattering data, showing that the core extension decreases as tadd increases, as reported in Table S2 (ESI†). It is important to note that the same microgel model is also able to reproduce the form factors of the surfactant-free microgel for tadd = 9 minutes, as reported in Fig. S1 (ESI†). This reassures us that the model is robust toward size effects, independently on the internal microgel architecture. Referring back to Fig. 3, it is evident that the form factors exhibit a shift of the first peak towards higher wavenumbers as tadd increases, consistent with a reduction in the size of the particles. Besides, we also note a progressive disappearance of the second peak of the form factors in the swollen state that becomes almost invisible for the smallest microgels. The deviations between numerical and experimental form factors found at high wavenumbers are a consequence of the finite size of the beads for in silico microgels as compared to the actual laboratory ones.12 The situation improves at high temperatures, where we observe many characteristic oscillations of a fully collapsed spherical microgel network.
Importantly, the present modeling is also able to reproduce the experimental trend of hydrodynamic radius RH observed in the experiments. This quantity, calculated from molecular dynamics trajectories of single microgels as described in Methods, is shown in Fig. 6(c) for the cases under investigation. Consistently with DLS results (Fig. 1(a)), we find that RH of the simulations significantly drops from the value it retains at the smallest initiator addition time to the intermediate one (at 1 minute), and then slightly decreases further when KPS addition occurs over 9 minutes. The relative decrease in RH is also in qualitative agreement with DLS experiments, showing a first reduction by around 15% and a subsequent one by another 5–10%. The change in size of the investigated microgels can also be visualized by means of the simulation snapshots reported in Fig. 7.
4 Conclusions
In this work, we analyzed in detail the modifications of the microgel conformation upon changing the time in which the initiator is added to the standard chemical synthesis. Variations at this stage in the protocol are expected to influence the distribution of the crosslinkers within microgel particles and, in turn, the overall microgel architecture. Despite being a small variation in the synthesis procedure, the importance of this study stems from the fact that in the literature microgels are prepared almost interchangeably with either the addition of the initiator in one-shot (low tadd) or with the drop-by-drop (high tadd) protocol. This variation of the synthesis protocol determines subtle changes in the observed microgel structure, previously undocumented, thus requiring a careful modeling effort.Therefore, the present work analyzes the effect of initiator addition time by combining experiments and simulations. Our findings show a non-trivial phenomenology. First of all, we find that a fast addition time results in microgels having a larger core with respect to the total size of the network, hence denoting a more homogeneous structure. Instead, a longer addition time yields a more marked difference between core and corona and thus microgels with a more heterogeneous network. To model this in simulations, we use a more compact distribution of crosslinkers and thus a smaller core radius, which naturally yields a more stretched corona. On the other hand, an almost instantaneous addition of the initiator gives rise to a large core, as also confirmed by simulations. Interestingly, it is the first type of microgels—the more heterogeneous one in terms of core–corona structure—to be larger in size according to DLS, while the second ones are significantly smaller.
To shed light on these interesting features, we analysed the experimental synthesis in terms of the number of microgel nuclei that are formed during the polymerisation reaction, which is found to vary significantly with the addition time of the initiator. This was indirectly observed by means of viscosity measurements in dilute conditions. By combining all these elements together, it was possible to capture the evolution of the microgel structure with different initiator addition times, which results from two distinct contributions. On the one hand, there is a tendency for the microgels to become more and more heterogeneous in terms of core–corona ratio as tadd increases and, on the other hand, we observe a decrease in microgel size due to a reduced capacity to incorporate monomers within the network. Although it might be expected that a slower addition would result in a more homogeneous structure, this is not confirmed by the data. Actually, it is the microgels with the initiator added all at once to have a larger core with respect to the corona, and thus being overall more homogeneous. However, this results in fewer microgel nuclei being generated, which has a significant impact on the polymerisation process. In this respect, it would be interesting to monitor the kinetics of reaction for the formation of these particles. In addition, attenuation studies similar to those recently performed in ref. 35, could be valuable to confirm the present results.
It is important to note that the present findings are obtained with the complementary addition of a fixed amount of surfactant. Nonetheless, we have repeated the synthesis in its absence for the case of initiator addition time of 9 minutes, and we found no substantial differences. The corresponding form factors, reported in the ESI,† are also captured by the numerical model with the same core-to-corona ratio as for the smaller experimental microgels. Hence, we can conclude that the current findings do not appear to be affected by the presence of surfactant in the experimental synthesis.
In summary, we have shown that the addition of the initiator at different times has relevant effects on the polymerization process of microgels, and can be exploited for fine-tuning the particles internal architectures and sizes. These findings are found to be independent on the use of surfactants in the synthesis protocol and thus unaffected by microgel size. This provides a straightforward, additional parameter in the experimental synthesis, enabling the optimization of microgel preparation for specific applications. In the future, it will be interesting to extend this study to different types of microgels, also based on different monomeric units, such as PVCL,36 and crosslinking agents,37,38 in order to investigate how these factors influence the internal structure. By combining experimental and simulation approaches, future work could aim to identify conditions that promote either maximal structural homogeneity or inhomogeneity, further advancing the understanding of microgel design.
Author contributions
E. B. and F. C. contributed equally to this work. Conceptualization: E. Z.; formal analysis: E. B., F. C., V. N., S. F., Y. G., E. Z.; funding acquisition: E. Z.; investigation: E. B., F. C., V. N., S. F., J. R.-F., Y. G., E. Z.; methodology: Y. G., E. Z.; project administration: E. Z.; software: Y. G.; supervision: R. A., B. R., E. Z.; validation: F. C., V. N., Y. G., E. Z.; visualization: F. C.; writing – original draft: F. C., Y. G., E. Z.; writing – review and editing: E. B., F. C., V. N., S. F., J. R.-F., L. P., R. A., B. R., Y. G., E. Z.Data availability
Data for this article are available on the online repository Zenodo (https://doi.org/10.5281/zenodo.14267285). SANS experimental data can be accessed at https://doi.ill.fr/10.5291/ILL-DATA.EASY-1060.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We dedicate this manuscript to the memory of our colleague Stefan Egelhaaf, a great scientist and a dear friend. We are deeply grateful for the fruitful collaborations and interactions we had with him throughout the years. We also thank Giovanni Del Monte for sharing the code for the calculation of the hydrodynamic radius in simulations and Andrea Ninarello for useful discussions. We thank the Institut Laue – Langevin for the awarded neutron beamtime (doi: https://doi.org/10.5291/ILL-DATA.EASY-1060). This work benefited from the use of the SasView application, originally developed under NSF award DMR-0520547. SasView contains code developed with funding from the European Unions Horizon 2020 research and innovation programme under the SINE2020 project, grant agreement no. 654000. EB and EZ acknowledge financial support by the Italian Ministry of University and Research (MUR) under the National Recovery and Resilience Plan (NRRP), Mission 4, Component 2, Investment 1.1, Call for tender no. 104 published on 2.2.2022 by the Italian Ministry of University and Research (MUR), funded by the European Union – NextGenerationEU-Project Co-MGELS, contract nr. 2022PAYLXW.Notes and references
- Z. Zhang, N. Xu, D. T. Chen, P. Yunker, A. M. Alsayed, K. B. Aptowicz, P. Habdas, A. J. Liu, S. R. Nagel and A. G. Yodh, Nature, 2009, 459, 230–233 CrossRef CAS PubMed.
- D. Paloli, P. S. Mohanty, J. J. Crassous, E. Zaccarelli and P. Schurtenberger, Soft Matter, 2013, 9, 3000–3004 RSC.
- P. J. Yunker, K. Chen, M. D. Gratale, M. A. Lohr, T. Still and A. Yodh, Rep. Prog. Phys., 2014, 77, 056601 CrossRef PubMed.
- G. Del Monte and E. Zaccarelli, Phys. Rev. X, 2024, 14, 041067 CAS.
- M. Karg, A. Pich, T. Hellweg, T. Hoare, L. A. Lyon, J. Crassous, D. Suzuki, R. A. Gumerov, S. Schneider and I. I. Potemkin, et al. , Langmuir, 2019, 35, 6231–6255 CrossRef CAS PubMed.
- J. Brijitta and P. Schurtenberger, Curr. Opin. Colloid Interface Sci., 2019, 40, 87–103 CrossRef CAS.
- S. Kumari, M. Avais and S. Chattopadhyay, ACS Appl. Polym. Mater., 2023, 5, 1626–1645 CrossRef CAS.
- J. Zheng, C. Zhu, X. Xu, X. Wang and J. Fu, J. Mater. Chem. B, 2023, 11, 6265–6289 RSC.
- R. Pelton, Adv. Colloid Interface Sci., 2000, 85, 1–33 CrossRef CAS.
- A. Fernandez-Nieves, H. Wyss, J. Mattsson and D. A. Weitz, Microgel suspensions: fundamentals and applications, John Wiley & Sons, 2011 Search PubMed.
- M. Stieger, W. Richtering, J. S. Pedersen and P. Lindner, J. Chem. Phys., 2004, 120, 6197–6206 CrossRef CAS PubMed.
- A. Ninarello, J. J. Crassous, D. Paloli, F. Camerin, N. Gnan, L. Rovigatti, P. Schurtenberger and E. Zaccarelli, Macromolecules, 2019, 52, 7584–7592 CrossRef CAS PubMed.
- E. Mueller, R. J. Alsop, A. Scotti, M. Bleuel, M. C. Rheinstädter, W. Richtering and T. Hoare, Langmuir, 2018, 34, 1601–1612 CrossRef CAS.
- T. Kyrey, J. Witte, A. Feoktystov, V. Pipich, B. Wu, S. Pasini, A. Radulescu, M. U. Witt, M. Kruteva and R. von Klitzing, et al. , Soft Matter, 2019, 15, 6536–6546 RSC.
- O. Virtanen, A. Mourran, P. Pinard and W. Richtering, Soft Matter, 2016, 12, 3919–3928 RSC.
- G. Del Monte, D. Truzzolillo, F. Camerin, A. Ninarello, E. Chauveau, L. Tavagnacco, N. Gnan, L. Rovigatti, S. Sennato and E. Zaccarelli, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2109560118 CrossRef.
- S. Sennato, E. Chauveau, S. Casciardi, F. Bordi and D. Truzzolillo, Polymers, 2021, 13, 1153 CrossRef CAS PubMed.
- N. Gnan, L. Rovigatti, M. Bergman and E. Zaccarelli, Macromolecules, 2017, 50, 8777–8786 CrossRef CAS PubMed.
- N. Hazra, A. Ninarello, A. Scotti, J. E. Houston, P. Mota-Santiago, E. Zaccarelli and J. J. Crassous, Macromolecules, 2023, 57, 339–355 CrossRef.
- B. J. Frisken, Appl. Opt., 2001, 40, 4087–4091 CrossRef CAS.
- J. W. White, Proc. R. Soc. London, Ser. A, 1975, 345, 119–143 CAS.
- C. D. Dewhurst, J. Appl. Crystallogr., 2023, 56, 1595–1609 CrossRef CAS.
- SasView, https://www.sasview.org/.
- H. A. Barnes, in Rheology: Principles, Measurements and Applications, ed. C. W. Macosko, published by VCH Publishers, Weinheim, Germany, 1996, p. 550 Search PubMed.
- G. K. Batchelor, J. Fluid Mech., 1977, 83, 97–117 CrossRef.
- H. Senff and W. Richtering, J. Chem. Phys., 1999, 111, 1705–1711 CrossRef CAS.
- S. Franco, E. Buratti, B. Ruzicka, V. Nigro, N. Zoratto, P. Matricardi, E. Zaccarelli and R. Angelini, J. Phys.: Condens. Matter, 2021, 33, 174004 CrossRef CAS.
- L. Rovigatti, P. Šulc, I. Z. Reguly and F. Romano, J. Comput. Chem., 2015, 36, 1–8 CrossRef CAS.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS.
- H. R. J. Warner, Ind. Eng. Chem. Fundam., 1972, 11, 379–387 CrossRef CAS.
- T. Soddemann, B. Dünweg and K. Kremer, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 6, 409–419 CrossRef CAS.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in 't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- J. B. Hubbard and J. F. Douglas, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 47, R2983 CrossRef CAS.
- R. Elancheliyan, G. Del Monte, E. Chauveau, S. Sennato, E. Zaccarelli and D. Truzzolillo, Macromolecules, 2022, 55, 7526–7539 CrossRef CAS.
- M. Otten, M. Hildebrandt, B. Pfeffing, V. C. Voigt, F. Scheffold, T. Hellweg and M. Karg, Langmuir, 2024, 40, 14515–14526 CrossRef CAS PubMed.
- F. Schneider, A. Balaceanu, A. Feoktystov, V. Pipich, Y. Wu, J. Allgaier, W. Pyckhout-Hintzen, A. Pich and G. J. Schneider, Langmuir, 2014, 30, 15317–15326 CrossRef CAS PubMed.
- K. Kratz, A. Lapp, W. Eimer and T. Hellweg, Colloids Surf., A, 2002, 197, 55–67 CrossRef CAS.
- J. Ruiz-Franco, R. Rivas-Barbosa, M. A. Lara-Peña, J. R. Villanueva-Valencia, A. Licea-Claverie, E. Zaccarelli and M. Laurati, Soft Matter, 2023, 19, 3614–3628 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental, model, and numerical form factors for the surfactant-free sample together with tables summarising the main structural parameters derived from the analysis of SANS data for all investigated samples. Parameters related to the analysis of DLS data according to the modified cumulant expansion method. See DOI: https://doi.org/10.1039/d4sm01200c |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |