Open Access Article
Open Access ArticleStructure, dynamics and phase transitions in electric field assembled colloidal crystals and glasses†
Indira
Barros
a,
Sayanth
Ramachandran
ab and
Indrani
Chakraborty
 *a
*a
aDepartment of Physics, Birla Institute of Technology and Science, Pilani-K K Birla Goa Campus, Zuarinagar, Goa 403726, India. E-mail: indranic@goa.bits-pilani.ac.in
bMax-Planck Institute for Polymer Research Mainz, Ackermannweg 10, 55128 Mainz, Germany
First published on 3rd February 2025
Abstract
Field-induced assembly of colloidal particles into structures of desired configurations is extremely relevant from the viewpoint of producing field-assembled micro-swimmers and reconfigurable smart materials. However, the behaviour of colloidal particles under the influence of alternating current (AC) electric fields remains a topic of ongoing investigation due to the complex and nuanced effects of various control parameters. Here, we examine the role of several factors including particle size, zeta potential, voltage and frequency of the applied field in the formation of different structural configurations in an intermediate frequency range (5–50 kHz) and very low conductivity solutions. We observe a wide range of configurations ranging from crystals to glasses that are normally observed at frequency ranges below 1 kHz. Additionally, we investigate the dynamics: the nature of diffusion and active motion in these out-of-equilibrium systems and show how that is directly interlinked with the formation of close-packed or open (non close-packed) structures. Lastly, we investigate the frequency-driven disorder–order–disorder phase transition in colloidal crystals, which is a starting point for building reconfigurable systems. Our findings contribute to a deeper understanding of interlinked roles of various factors in electric field-induced assembly of colloidal particles in the intermediate frequency-low conductivity regime, which is significant for potential applications in micro-robotics and next generation materials.
1 Introduction
Programmable self-assembly of colloidal particles into desired configurations has recently become an area of intense interest due to its tremendous application potential in new-age manufacturing of smart, reconfigurable materials, construction of microbots for targeted drug delivery and fabrication of next-generation biomedical devices.1–5 Colloids are an excellent choice as building blocks in the micrometer and nanometer scales for a controlled assembly of several complex architectures, ranging from colloidal oligomers and reconfigurable ‘molecules’ to colloidal crystals with different symmetries and structural configurations.6–14 Several different interactions, ranging from capillary,15,16 depletion,13 and DNA mediated,8–10,17 to field-induced18,19 interactions have been used to produce a wide variety of architectures using colloidal building blocks. Field-induced assembly, where colloids are assembled into structures of desired configurations using an electric field,20–22 magnetic field23,24 or light25 induced activation, has also been studied extensively in the last few years.18 The major advantages of field induced assembly are: (a) the morphology of the produced structures can be made fully controllable and the configurations can be switched from one to another by varying the field parameters, (b) magnetic fields can penetrate live tissues, leading to assembly, control and propulsion of such a structure inside biological systems,26 and (c) electric field-based activation is easy to set up, and has a low cost.Electric field-induced assembly offers remarkable versatility in assembling colloidal particles, thanks to the multitude of controllable parameters within the system. However, this versatility also entails a wide spectrum of phenomena and structural configurations achievable by small changes in the control parameters. Trau et al. observed the formation of two-dimensional colloidal crystals on electrode surfaces for both micrometer and nanometer-sized particles upon the application of a DC electric field.27 They were also able to produce multilayers by controlling the DC field and by field-induced annealing with a low-frequency AC field. Using an out-of-plane AC electric field, Ma et al. observed the formation of colloidal oligomers of different valences in the low-frequency regime (0.5–1.5 kHz) and the formation of honeycomb-like open structures at higher frequencies.20 By superimposing a DC electric field with an AC electric field, Maestas et al. controlled the number ratio of particles in different planes, thereby producing square and triangular bilayers, rectangular bands, zig-zagged stripes, sigma lattice and honeycomb-Kagome structures.28 Ordered, non-close packed colloidal arrays were produced by Jingjing et al. using a combination of a low-frequency AC electric field and a sequence of DC pulses in a solution of appropriate particle concentrations.21 Yakovlev et al. made two-dimensional crystalline structures with a rotating electric field.29 Biaxial fields were used by Leunissen et al.30 to produce chains at moderate fields and one-particle thick sheet-like structures at higher fields. Moving one step further, Vissers et al. showed a distinct separation of binary particle species with opposing charges into bands perpendicular to the applied AC electric field at low frequencies (∼1.5 Hz).31 Heatley et al. produced colloidal molecules of tunable size and bond length using a binary mixture of colloidal particles of different types and sizes under a perpendicularly applied AC electric field.32 ‘Active colloidal molecules’ utilizing binary colloids, patchy particles and even live cells were produced by Wang et al.33 Other than isotropic particles, anisotropic particles like colloidal dimers were observed to align perpendicular to the substrate to form close-packed crystals under an AC electric field.34 Using colloidal dimers actuated by a perpendicularly applied AC electric field, Yang et al. obtained stable planar clusters with handedness,35 while Katzmeier et al. used asymmetric dimer particles to demonstrate propulsion under AC electric fields for potential applications as micro-swimmers.36
In spite of the sheer diversity of phenomena in electric field-induced colloidal assembly, and the extensive amount of existing literature on field-induced assembly of isotropic particles,37–41 the difficulty of controlling the sensitivity to minor parameter variations and understanding the nuanced interplay of several influencing factors that determine the outcome of the final structure makes field-induced assembly challenging. The outcome of the assembly often depends strongly on the surface properties of the synthesized particles, showing drastically different results even for similar systems at similar frequency values/salt concentrations. Additionally, the formation of crystalline/glassy structures is often observed at low-frequency regimes (10 Hz–1 kHz) and high conductivity solutions where dielectrophoresis dominates over electroosmosis. Beyond a frequency of 100 kHz, electroosmotic flow becomes insignificant, and electrothermal effects dominate the fluid flow. In the intermediate frequency range of 1–100 kHz, AC electroosmotic fluid flow is the dominant mechanism and the dielectrophoretic manipulation of micrometer-sized particles is challenging, leading to the observation of conflicting results. All of this emphasizes the necessity for a detailed exploration of the various influencing parameters, and understanding the complex dynamics of structure formation.
In our work, we systematically study the dependence of the electric field (AC) induced structure formation of isotropic colloids on various parameters such as the particle size, zeta potential, frequency and voltage of the applied electric field in the 5–50 kHz frequency regime and very low conductivity solutions. We show that slight changes in parameters such as the zeta potential can lead to a wide variety of structural configurations at this frequency regime and connect our observations with existing theories on the electrokinetic assembly of colloids. Furthermore, we perform a detailed study of the diffusion dynamics of the particles as they assemble into a structure. We show that the dynamics of motion of the particles is directly interlinked with the geometry and order of the structures produced. Thirdly, we probe the frequency-induced phase transition of the colloidal particles from an open glassy structure to an ordered crystalline structure and finally to a disordered, bulk structure. This is an extremely relevant attribute for building reconfigurable colloidal crystals, which have garnered a lot of interest over the last few years because of their potential use in switchable photonic crystals and smart materials for sensing.42–44 Additionally, field-assembled and field-driven micro-swimmers can be used for targeted drug delivery.36,45 Therefore this study not only bridges the gap in our understanding of colloidal assembly and dynamics under electric fields, but also helps in engineering complex structures with tailored functionalities.
2 Experimental details
2.1 Sample preparation and imaging
Polystyrene colloidal particles of 1 μm size were purchased from Bangs Laboratories and Sigma-Aldrich. The particles had different functionalizations as given in Table 1 as a result of which they had different zeta potential values. A suspension of the desired particles dispersed in de-ionized water was prepared with a solid concentration of 0.01%. At lower concentrations, the cluster growth would be much slower, while at a higher concentration, the particles might exhibit jamming, or in certain dense areas close-packed crystalline zones might be formed purely from geometrical constraints. Additionally, there might be a tendency to form multilayers or columnar structures if the system is overcrowded. A small concentration (4.33 mM) of a surfactant SDS was added to ensure a smooth transfer to the capillary chamber. In the case where salt was added to the suspension, a solution of 0.01 mM NaCl and 4.33 mM SDS was prepared in de-ionized water and the dispersion of the particles was made in this solution.| Sample name | Details | Zeta potential (mV) |
|---|---|---|
| Bare-PS | 1 μm polystyrene | −82.9 ± 1.0 |
| Amine-PS | 1 μm amine functionalized polystyrene | −94.6 ± 1.7 |
| Mag-PS | 1 μm polystyrene spheres embedded with magnetic nanoparticles | −42.5 ± 1.7 |
| Salt-PS | Bare-PS with 10−5 M NaCl | −102.8 ± 3.1 |
To prevent non-specific interactions between the particles and the substrate, indium tin oxide (ITO)-coated glass coverslips (thickness #1) were cleaned by sequential ultrasonic treatment in isopropyl alcohol for 15 minutes, acetone for 15 minutes, and again in isopropyl alcohol for 15 minutes. The coverslips were then rinsed with de-ionized water and dried in an oven at 80 °C.
A capillary chamber was fabricated by sandwiching two cleaned ITO coated coverslips which serve as the electrodes. The electrodes were placed in a slightly displaced manner (see Fig. 1a) to enable smooth contact fabrication. Spacing of 150 μm between the electrodes was achieved using a plastic spacer, which also prevents shorting of the electrodes. Electrical contacts were made with copper tape and silver paste. The colloidal dispersion was then carefully pipetted into the capillary and all ends were sealed using UV-curable adhesive, ensuring the containment of the particle dispersion within the capillary chamber. An AC electric field was applied using a function generator (METRAVI DDS-1010) in the sinusoidal mode. A time gap of 15 minutes was kept between consecutive experiments where the field was switched off to ensure that the particles re-dispersed to a randomized configuration, as well as lose any charge build-up due to the field before the start of the next experiment. The experimental setup was observed under an optical microscope, utilizing a 100× objective lens in bright-field mode. Videos were recorded using a high-speed camera. The zeta potential measurements were made using a Particulate Systems – NanoPlus zetasizer. The final zeta potential values were obtained after averaging over three separate measurements.
2.2 Analysis
Trackpy,46 a Python-based implementation of the Crocker–Grier algorithm47 was used to track the particle positions from the sequence of recorded images. In many of the figures of this paper, the tracked particles are annotated with red circles for clarity. The trajectories of the particles were determined over thousands of frames and from the trajectories, mean square displacement (MSD) vs. lag time plots and displacement distributions were generated. Subsequently, the diffusion exponent values (n) were calculated from the MSD analysis. To analyze the formed structure, Voronoi diagrams were constructed in Python from which the number of nearest neighbours, nearest-neighbour distances and areas of the Voronoi cells were calculated.3 Results
3.1 Factors influencing structural configurations under AC electric field
We studied the formation of colloidal crystals and glasses under AC electric fields, as a function of different structural and field parameters. The sample chamber was composed of two ITO-coated cover glasses with a spacer of 150 μm thickness (Fig. 1a). An AC electric field of desired peak-to-peak voltage (Vpp) and frequency was given in a direction perpendicular to the plane of the coverslips. A representative image of the formation of colloidal crystals composed of 1 μm polystyrene particles at a frequency of 5 kHz, Vpp = 20 V, and a salt concentration of 10−5 M as a function of time is shown in Fig. 1b–e and Video V1 (ESI†). The crystals majorly show a hexagonal close-packed configuration with a packing fraction of 74% in the inner regions. Over the span of 24 hours, the crystals formed could span large areas of the order of 100 × 100 μm2. Without the presence of any salt, we observed the formation of planar glassy structures with 1 μm diameter particles rather than ordered crystals (Fig. 1f). However, size played a major role in determining the final structure. In contrast to the planar glassy structures formed by the 1 μm polystyrene particles, the 3 μm diameter particles strongly preferred the formation of vertical columns along the direction of the applied electric field (Fig. 1h). The intermediate case was that of the 2 μm diameter particles, which showed simultaneous formation of columns and chains of these columns (Fig. 1g) indicating that the assembly occurs both in horizontal and vertical planes in this case. If we represent the applied AC electric field with frequency ω as the real part of the complex phasor E(t) = E0eiωtêz, then the time-averaged dipole–dipole interaction force on a particle at position r exerted by another particle residing at the coordinate origin is given as:21,48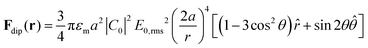 | (1) |
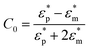 where
where 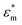 and
and 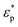 are the complex permittivities of the medium and the particle, respectively, εm is the permittivity of the medium, a is the particle radius, r is the center-to-center distance between the particles, E0,rms is the rms value of the applied electric field and θ is the angle between the field direction and the line joining the centers of the particles. When θ = 0°, the inter-particle force due to dipolar interactions is attractive, and when θ = 90°, the force is repulsive. We can clearly see that as the dipolar force varies as a6, the dipolar contribution will dominate for larger particles. This leads to the formation of columns parallel to the field and chains of columns in 3 μm and 2 μm particles, respectively, in contrast to crystals and glassy structures for 1 μm particles.
are the complex permittivities of the medium and the particle, respectively, εm is the permittivity of the medium, a is the particle radius, r is the center-to-center distance between the particles, E0,rms is the rms value of the applied electric field and θ is the angle between the field direction and the line joining the centers of the particles. When θ = 0°, the inter-particle force due to dipolar interactions is attractive, and when θ = 90°, the force is repulsive. We can clearly see that as the dipolar force varies as a6, the dipolar contribution will dominate for larger particles. This leads to the formation of columns parallel to the field and chains of columns in 3 μm and 2 μm particles, respectively, in contrast to crystals and glassy structures for 1 μm particles.
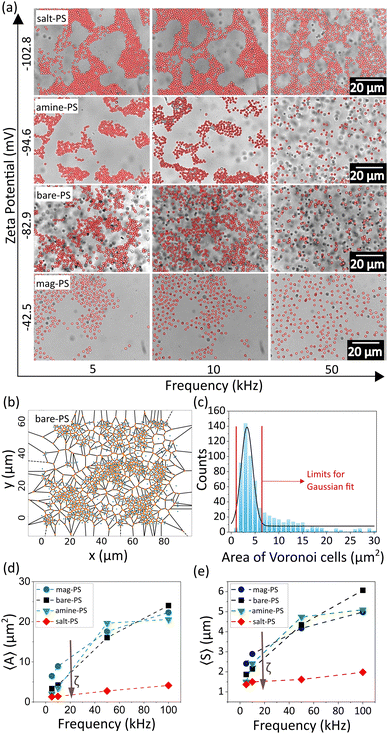
The configuration of the assembled colloidal crystals and glasses was found to be strongly dependent on three parameters: (a) applied voltage, (b) frequency of the AC field and (c) zeta potential of the particles. The zeta potential (ζ) of the particles is obviously expected to play a major role in the electric field-induced assembly of the particles. To examine this, we used a set of particles with different functionalizations and therefore different zeta potential values as given in Table 1. We tabulated the structures formed as a function of ζ and applied field frequency (Fig. 2a). In the low-frequency regime (∼5 kHz), for the lowest value of the zeta potential in our experiments, that is ζ = −42.5 mV, we observed the formation of planar glassy structures with the highest nearest neighbour distances. In this case at higher frequencies, the particles covered the entire viewing plane with relatively fewer localized clusters. As the ζ increased to −82.9 mV, the nearest-neighbour distances between the particles started to decrease and at ζ = −94.6 mV, the formation of more packed configurations of localized clusters was observed. The highest value of ζ in our experiments was obtained with the addition of 10−5 M NaCl to the sample bare-PS, which counter-intuitively increased the ζ value. This is due to the adsorption of ions on the surface of the colloids and the consequent increase in the surface charge as demonstrated by Manilo et al.49 At the highest value of ζ, the formation of close-packed nearly-crystalline structures was observed. This scenario changes with increasing values of the applied frequency. Firstly, with an increase in frequency, an overall increase of separation between the constituent particles of a cluster was observed, while lower frequencies (5–10 kHz) led to more packed configurations. Secondly, even for high (negative) ζ values, a large fraction of the particles tended to be dispersed in the bulk medium. At frequencies higher than 50 kHz, the majority of the particles remained dispersed in the bulk rather than forming planar structures.
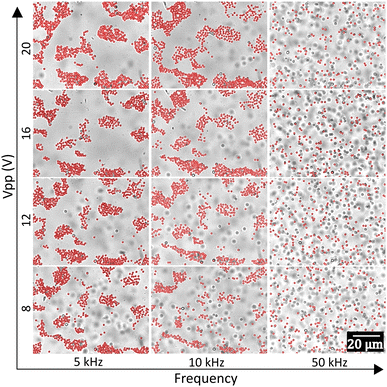
To quantify the effects of changing ζ and frequency on the structural organization of the clusters, we constructed Voronoi cell diagrams for each of the images. A representative Voronoi cell diagram of structures formed from 1 μm polystyrene particles is given in Fig. 2b. For each frequency value, a histogram was plotted for the area of the Voronoi cells followed by a Gaussian fitting (Fig. 2c). The extended tail of the histogram at higher values of the Voronoi cell area was excluded by introducing a window of fitting, in order to ignore the larger cells at the edges and empty areas (Fig. 2c). The value at the peak of the Gaussian was taken as the average value of the cell areas (〈A〉) for the corresponding frequency, and a plot of 〈A〉 as a function of frequency was made (Fig. 2d). The nearest-neighbour distances were obtained by calculating the average centre-to-centre distances of the Voronoi cells, and then these distances were averaged (〈S〉) as before and plotted as a function of frequency (Fig. 2e). 〈A〉 was observed to increase with the applied frequency, as shown in Fig. 2d. In agreement with our observations, at lower frequencies (∼5 kHz) particles with higher (negative) values of ζ showed smaller 〈A〉 indicating more compact clusters while particles with smaller (negative) ζ values showed larger 〈A〉 indicating more spread out clusters (Fig. 2d). The sample with the highest (negative) ζ (marked in red symbol in Fig. 2d) showed the smallest 〈A〉. This is in stark contrast to previous observations where the structures were observed to become more close-packed with a decrease in the absolute zeta value.50,51 There was a general trend of increase in 〈A〉 with an increasing frequency, indicating that the particles were more spread out in the bulk for all ζ values. All these observations were also supported by the increase in 〈S〉 with decreasing ζ and increasing frequency (Fig. 2e). 〈A〉 and 〈S〉 at high frequencies (>50 kHz) and even at intermediate frequencies (10–50 kHz) deviate from the trend shown in lower frequencies as the particles tend to get increasingly dispersed in the bulk than confined to a plane at these frequencies (Fig. 2d and e). Other than frequency, the applied voltage also plays a major role in determining the structural configuration as seen in Fig. 3 and Fig. S1 (ESI†). As the applied voltage is changed from a peak-to-peak value of 8 V to 20 V, the colloidal clusters tend to increase in size. The effect is most pronounced at intermediate frequencies (∼10 kHz), whereas there is no significant difference at low and high frequencies. Consequently, 〈A〉 also shows a gradual decrease with an increase in the peak-to-peak voltage (Fig. S1, ESI†).
The formation of planar structures perpendicular to the field direction for 1 μm particles implies that the dominant mechanism in this case is not dipolar interactions, but electrohydrodynamic flow (EHD) between the particles and the substrate. This is basically induced charge electro-osmotic (ICEO) flow on the polarizable surface of an electrode. According to Ristenpart et al.,37 the tangential velocity ut due to EHD flow scales as:
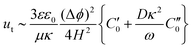 | (2) |
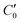 and
and 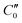 are the real and imaginary parts of C0 which is a function of frequency, particle properties like zeta potential and radius, solution properties like ionic strength, ion valences and mobilities, and the dielectric constant. κ−1 is the Debye length, μ is the fluid's shear viscosity, D is the ion diffusivity, Δϕ is the applied potential difference between the two parallel electrodes separated by a distance 2H, ω is the angular frequency of the applied AC field, ε is the dielectric constant of the medium and ε0 is the permittivity of free space respectively. When
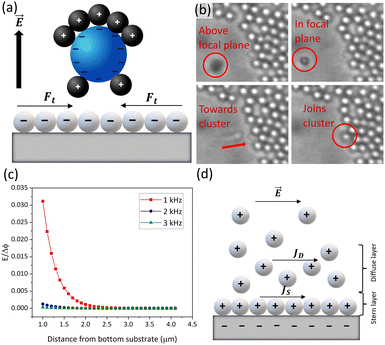
are the real and imaginary parts of C0 which is a function of frequency, particle properties like zeta potential and radius, solution properties like ionic strength, ion valences and mobilities, and the dielectric constant. κ−1 is the Debye length, μ is the fluid's shear viscosity, D is the ion diffusivity, Δϕ is the applied potential difference between the two parallel electrodes separated by a distance 2H, ω is the angular frequency of the applied AC field, ε is the dielectric constant of the medium and ε0 is the permittivity of free space respectively. When 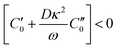 , the EHD flow will be contractile (directed towards the particle), and if >0, the flow will be extensile (directed away from the particle). An extensile EHD flow will lead to non-close packed structures while a contractile flow will lead to crystal formation. Fig. 4a shows a schematic diagram representing the contractile EHD flow generated due to the force Ft generated on the ions (near the electrode surface) by the tangential component of the local electric field of the particle along with its electric double layer. This force results in the horizontal translation of the particles across the surface of the electrode. Even while imaging, the particles were observed to sediment to the bottom electrode and translate horizontally across the electrode surface to attach to a larger cluster (Fig. 4b).
, the EHD flow will be contractile (directed towards the particle), and if >0, the flow will be extensile (directed away from the particle). An extensile EHD flow will lead to non-close packed structures while a contractile flow will lead to crystal formation. Fig. 4a shows a schematic diagram representing the contractile EHD flow generated due to the force Ft generated on the ions (near the electrode surface) by the tangential component of the local electric field of the particle along with its electric double layer. This force results in the horizontal translation of the particles across the surface of the electrode. Even while imaging, the particles were observed to sediment to the bottom electrode and translate horizontally across the electrode surface to attach to a larger cluster (Fig. 4b).
Our observation that the increase in voltage increases the cluster size at intermediate frequencies for a given value of ζ also becomes clear from eqn (2). As Δϕ increases, ut increases, leading to a faster growth of the clusters under a more rapid contractile flow (Fig. 3). On the other hand, the time-averaged dielectrophoretic (DEP) force on a colloidal particle is given as:
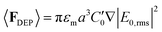 | (3) |
In the frequency range in our experiments (5–50 kHz), the relative dominance of dielectrophoresis and electro-osmosis is unclear. While for a typical maximum value of ∇|E0,rms|2 ∼ 1016 V2 m−3 the steady state DEP velocity for a 1 μm diameter particle is ∼30 μm s−1, the maximum AC electro-osmotic velocity can be an order of magnitude larger depending on the solution conductivity.52 So the dielectrophoretic manipulation of the micrometer-sized particles in this frequency regime is more complicated. At similar frequency range and conductivity as in our experiments, the structures produced previously were either randomly dispersed particles on the substrate or in bulk, or honeycomb lattice structures.20 The formation of glassy and crystalline structures was observed in most cases at much lower frequencies (100 Hz–1 kHz) and much higher conductivities.
The disappearance of the crystalline or open structures at high values of the frequency ≥50 kHz (Fig. 2a) is obvious from the 1/ω frequency dependence in eqn (2) (the frequency dependence of C0 is negligible in our relevant frequency range). As the frequency increases, the tangential velocity of the EHD flow decreases, and therefore the particles tend to remain suspended in bulk and are not brought together. On the other hand, at very low frequencies (∼1 kHz) the particles neither form columns, nor remain suspended in bulk like the 50 kHz case, but they remain separate on the observation plane as we show later in Section 3.3 and Fig. 6a. The sedimentation of the particles to the bottom electrode plane is due to the presence of a high electric field at the surface of the polarizable bottom electrode. For the frequency range relevant to us, Ristenpart et al. gave the electric field E near an electrode as:38
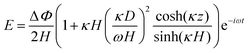 | (4) |
The role of ζ is however more complex. At ζ = 0, the effective induced dipole moment of the dielectric particle in a polar solvent like water is directed opposite to the applied field, so the dipole coefficient has a large negative value and a contractile EHD flow is obtained. As ζ becomes more negative, the concentration of ions around the particles increases, and their surface conductivity comes to play a role, making the dipole moment smaller and less negative. Consequently, the contractile EHD flow becomes smaller. Beyond a certain ζ value, the particle becomes more polarizable than the medium due to the contribution of the surface conductivity of mobile ions in the diffuse layer, leading to an extensile EHD flow.53 With an increasing (absolute) value of ζ, Woehl et al.50 demonstrated a decreasing aggregation rate in colloidal clusters, while Luo et al.51 observed a larger separation between constituent particles in a cluster. In both cases, the zeta potential was varied by using a wide range of electrolytes at different concentrations and the experiments were performed in a frequency range from 100–400 Hz. In our observations, we however see a completely opposite picture. A higher negative value of ζ produces more close-packed or crystalline structures while a lower negative value produces more open structures. The primary reason behind this is that we are working in a different electrokinetic regime: a frequency range from 5 kHz to 50 kHz. As outlined by Prieve et al.,39 in frequency regimes above 1 kHz and in a very low conductivity solution, the ohmic resistance introduced by the particle will have a dominating role in determining the current distribution in its vicinity as compared to the capacitive impedance associated with the electrode. This is in contrast to the frequency regime below 1 kHz where both faradaic processes and electrode polarization play a role in cluster formation. This might lead to a drastically different structural configuration as a function of the ζ. A second possible reason behind the trend in ζ might be the fact that the surface conductivity of the particle consists of not just the diffuse layer conductivity, but also the Stern layer conductivity. The schematic in Fig. 4d shows the two different current densities: JS due to the Stern layer conductivity and JD due to the diffuse layer conductivity.52 The Stern layer conductivity produces drastically different structures in particles even with nearly similar zeta potentials; for example, Yang et al. showed that polystyrene and silica spheres with nearly the same zeta potential (−43.8 mV and −41.5 mV) produce non-close packed and crystalline structures, respectively, due to different Stern layer conductivities.53 It was also shown that if the Stern layer conductivity (σp) is high enough, polystyrene particles with ζ = −40 mV (σp = 15 pS) will show extensile flow (positive velocity), while particles with ζ = −60 mV (σp = 100 pS), will show contractile flow, contrary to expectations. Therefore even a higher negative value of ζ can produce close-packed structures. We suspect that in our case also, the difference in Stern layer conductivities for the different sets of particles has led to an opposite trend in structure formation as a function of ζ. Further theoretical analysis needs to be done to give an exact explanation behind this observed phenomenon. In summary, size, ζ, frequency and voltage all play a complex and interlinked role in determining the final structure of the colloidal crystals and glasses.
3.2 Diffusion dynamics in active clusters
Palacci et al. have shown the formation of light-activated living crystals formed from Janus particles.25 In this case, the crystals were called ‘living’ as each constituent colloid was activated by an external optical field and the formation of clusters or crystals was an inherently out-of-equilibrium phenomenon. In our system also, electric field-activated colloids form crystals or glassy structures where they become a constituent part of that dynamic structure. Particles constantly break off and join growing clusters, as the clusters themselves span large areas if allowed to grow for sufficient time (Fig. S2, ESI†). For this reason, we intended to study the dynamical behaviour, that is diffusion and active motion characteristics of the constituent colloids of a large cluster, once the cluster has grown to a considerable size. The particles are expected to show active dynamics, with coupled rotational and translation motion described by the following equations: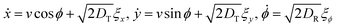 | (5) |
| MSD = 4DTt + v2t2 | (6) |
log(MSD) ∝ n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(t) log(t) | (7) |
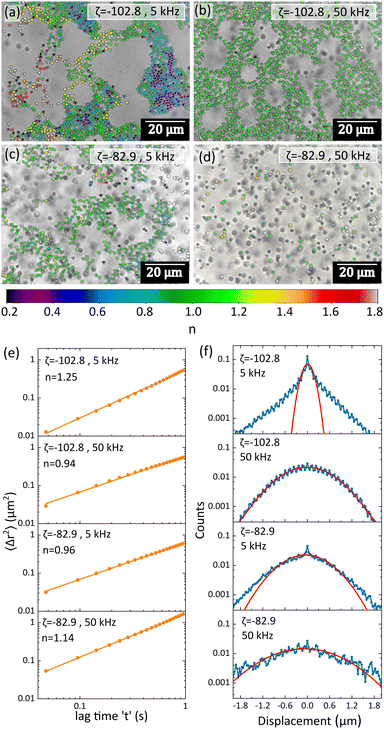
The distribution of n values was found to be strongly dependent on the applied frequency, indicating different degrees of caging. For example, in the case of salt-PS, there was a wide distribution in the n values at lower frequencies (5 kHz), as seen in Fig. 5a. Particles that were located at the core region of the clusters showed subdiffusion (n < 1) indicating a high degree of caging from their immediate neighbours. Particles on the outer edge of the clusters, in more sparse regions or singlets showed superdiffusion (n > 1). In the intermediate regions between these two extremes, we observed pure Brownian motion from the particles as indicated in light green. This is in sharp contrast to the case of 50 kHz (Fig. 5b) where firstly more open clusters were formed, and secondly, n was overwhelmingly close to 1 indicating pure Brownian motion with little to no sub or superdiffusion. This shows that at lower frequencies, there is more caging, and more open areas for the particles, leading to the formation of more packed structures. At higher frequencies particles tend to remain relatively more separated from each other, showing predominantly Brownian diffusion, although the applied electric field is present. Similar behaviour was also observed at lower ζ values: for the sample bare-PS. We again observed a larger distribution of n values at 5 kHz (Fig. 5c) compared to 50 kHz (Fig. 5d), but the effect was less pronounced than salt-PS. Since even in field-activated systems like ours a large number of particles showed pure Brownian motion, we plotted the MSD vs. lag time (t) plots for all the particles and calculated the time-ensemble averaged MSD (〈Δr2〉), as well as plotted the displacement distributions. The log–log plots of 〈Δr2〉 vs. t for all four cases showed a similar overall linear trend (Fig. 5e), with the slope n being very close to 1 indicating predominantly Brownian motion. This indicates that once the crystalline or glassy structures are formed, the dynamics of a large part of the system shifts towards pure Brownian, each constituent particle being locked into the system either physically or due to the electric double layer repulsion from the neighbouring particles. The displacement distributions, however, were more indicative of the system's inner dynamics. For 5 kHz the displacement distributions were distinctly non-Gaussian, the non-Gaussianity being more pronounced for salt-PS (Fig. 5f). For 50 kHz, the displacement distributions were observed to be nearly Gaussian (Fig. 5f). The shift towards pure Brownian dynamics at higher frequencies strongly points to the presence of stronger repulsive barriers among the particles, while lower frequencies lead to areas with stronger and weaker electric field distributions.
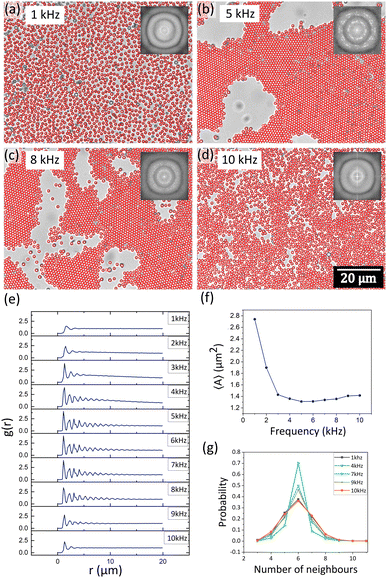
3.3 Frequency-induced phase transition in colloidal crystals
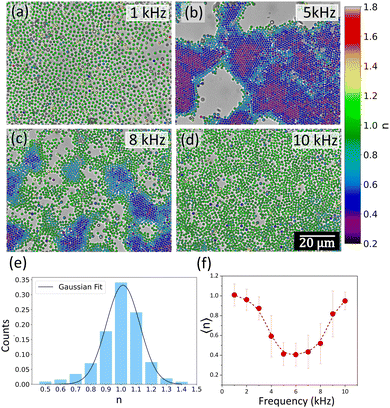
The strong dependence of the morphology of the formed structures on the applied field frequency, as well as the different diffusion dynamics at lower and higher frequencies, prompted us to do a detailed structural study across the frequency-induced phase transition from disordered to ordered and back to disordered state of the colloidal crystals. Interestingly, we observed the formation of the most crystalline structure at an intermediate frequency of 5 kHz for 1 μm polystyrene particles. At lower values of the frequency (1 kHz), destruction of the crystalline order and an increase in the nearest-neighbour distances between the constituent particles were observed (Fig. 6a and Video V2, ESI†). From 1 kHz to 5 kHz, the colloids began to crystallize reaching maximum packing and ordering at 5 kHz (Fig. 6b). Beyond 5 kHz, the larger crystals started breaking up into smaller crystallites, as well as individual particles started to break off from the parent crystal (Fig. 6c). Complete destruction of the crystalline order was observed at 10 kHz (Fig. 6d), although the inter-particle distance was observed to be less than the case of 1 kHz, and more bulk suspensions were observed. The fast Fourier transforms (FFTs) shown in the inset of the images of Fig. 6a–d show a clear ring pattern superposed with spots for 5 kHz, which slowly fades off to a smudged pattern at 10 kHz as well as at 1 kHz, indicating the destruction of the crystalline order. The radial distribution function g(r) plotted in steps of frequency of 1 kHz in Fig. 6e clearly indicates the gradual creation and destruction of the crystalline order as a function of the applied field frequency. At the intermediate frequencies (5–6 kHz), several peaks in the g(r) are observed whereas both at 1 kHz and 10 kHz, a smooth curve is observed with very few peaks. It should be noted here that in this structural reconfiguration, there is a possibility that crystalline order persists, but the packing fraction changes as the frequency is varied. This means that the close-packed crystalline structure becomes more open with a lower value of the packing fraction. To examine this, we again constructed Voronoi diagrams and calculated the Voronoi cell areas. The average Voronoi cell area (〈A〉) showed a minimum near 5 kHz, with a gradual increase between 5 and 10 kHz indicating spreading out of the clusters (Fig. 6f). There is a rapid change in the configuration below 4 kHz where 〈A〉 rapidly increases and the particles form a planar, glassy structure with large separations from each other. Note that this situation at 1 kHz is drastically different from the case of 10 kHz: in both cases, glassy structures are formed but they are essentially different as indicated by the value of 〈A〉 in these two frequency regimes (Fig. 6f). We also observed that at all frequencies, the most probable number of nearest neighbours was 6 (Fig. 6g). However, there is an overall trend of an increase in the probability between 1 kHz and 7 kHz followed by a decrease till 10 kHz. Interestingly, 1 kHz had a slightly higher probability of having six neighbours than 10 kHz. This again implies that at low frequencies, planar, non-close-packed glassy structures are formed, which tend to get packed into large crystalline, close-packed regions at intermediate frequencies, and again pass over to a disordered, bulk suspension at higher frequencies. As described in Section 3.1, in eqn (4) and (Fig. 4c), the non-uniform electric field is very high near the surface of the electrode at lower frequencies (∼1 kHz) and has a sharp decrease with distance, while for higher frequencies, the electric field even near the electrode surface is much lower. This indicates that the particles will tend to stay close to the surface at lower frequencies and will not come together to form crystalline or open structures (Fig. 6(a)).It was also observed that multiple frequency sweeps anneal the defects in the growing crystal. Additionally, smaller regions of crystals join with the larger regions, indicating that constant frequency sweeps can give us very large areas of defect-free colloidal crystals (Fig. S3, ESI†). The dynamics of these particles depend strongly on their local environment, as shown in Fig. 7a–d and Fig. S4 (ESI†). In the interior regions of the large crystalline structures, the diffusion exponent n values are close to 0.5, indicating arrested diffusion due to the presence of neighbouring colloids. On the other hand, the outer regions show n close to 1 or higher, indicating Brownian or superdiffusive behaviours, respectively. This indicates that particles in the outer regions have a significant probability to break off from one crystalline zone and join an adjacent growing zone. This was observed multiple times in crystallization experiments (see Fig. S2, ESI†). As we go from an ordered to a disordered state at higher frequencies, the diffusion dynamics clearly become more Brownian (indicated by n values close to 1) (Fig. 7d). A calculation of the mean value of the diffusion exponent 〈n〉 was done by fitting a Gaussian to the n distribution plots for each frequency (Fig. 7e). A plot of the 〈n〉 values as a function of frequency (Fig. 7f) showed a gradual decrease and a subsequent increase with a minimum near 6 kHz.
A comparison between Fig. 6f (variation of 〈A〉 with frequency) and Fig. 7f (variation of 〈n〉 with frequency) indicates the direct interlink between the diffusion dynamics and structural configuration of the colloidal crystals. Both the curves show a minimum near 5–6 kHz indicating arrested diffusion and a greater degree of packing. While 〈n〉 shows a gradual rise at both high and low-frequency regimes, 〈A〉 has a steeper response in the low-frequency regime. The increase of 〈A〉 and 〈n〉 for the two extreme frequency regimes indicates that the repulsive barrier between the particles tends to dominate locking them into an open, glassy structure and producing predominantly Brownian diffusion dynamics.
4 Conclusions
In summary, we investigated three important aspects of electric field (AC) driven assembly of isotropic colloidal particles in the intermediate frequency (5–50 kHz)-low conductivity regime: (a) the role of several influencing factors including size, zeta potential, frequency and voltage of the applied field in determining the final structural configuration of the colloidal crystals and glasses, (b) the dynamics of diffusion and active motion and how that is interlinked with structure formation and (c) the frequency driven disorder–order–disorder phase transition in colloidal crystals. Initially, we explored the formation of colloidal crystals and glasses under AC electric fields, observing distinct configurations ranging from columnar structures to hexagonal close-packed crystals and planar glassy structures. While larger particle sizes led to the formation of more vertically oriented (parallel to the field) structures, smaller sizes led to in-plane structure formation (perpendicular to the field). Using Voronoi diagram analysis we showed that higher frequencies lead to the formation of more open structures while higher voltages lead to the formation of more close-packed structures. At low frequencies (∼5 kHz), a higher value of the zeta potential leads to close-packed structures, while lower values lead to open structures. An examination of the dynamical behaviour of the constituent particles in a colloidal cluster demonstrated a complex interplay of Brownian motion, subdiffusion, and superdiffusion at lower frequencies, which evolved into predominantly Brownian motion at higher frequencies. The variation of the diffusion exponent n indicated different degrees of particle caging and mobility within the clusters at different frequencies. Lastly, we studied the frequency-induced phase transition in colloidal crystals where an open two-dimensional configuration was seen at very low frequencies, and an increase in the frequency led to a gradual development of crystalline order until 6 kHz. Beyond this, the crystalline order began to disappear leading to a completely disordered state at 10 kHz. An analysis of the average diffusion exponent and Voronoi cell area with frequency showed that there is a direct interlink between the nature of diffusion and the structural configuration of the colloidal crystals. Overall, our findings contribute to a systematic, deeper understanding of the complex behaviour of colloidal systems under AC electric fields beyond the 1 kHz frequency regime, in very low conductivity solutions. This is significant for applications in various fields including the fabrication of reconfigurable, smart materials and field-assembled/driven micro-swimmers for targeted drug delivery.Author contributions
IB and SR fabricated the sample chambers and did the electric field-based experiments. IB performed the data analysis. IB, SR, and IC contributed to the planning of the experiments and writing of the paper.Data availability
Most of the data used in this work are either in the main paper or the ESI.† Additional data will be available from the authors upon request as most of these are video data and are too bulky to store in a repository.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the Start-up grant (SRG/2021/001696) of the Science and Engineering Research Board (SERB) (at present the Anusandhan National Research Foundation (ANRF)), Government of India and the additional competitive research grant (GOA/ACG/2021-2022/Nov/03) from BITS-Pilani for this work. We also acknowledge the central sophisticated instrumentation facility (CSIF) at BITS-Goa for the zeta-potential measurements.Notes and references
- B. J. Nelson, I. K. Kaliakatsos and J. J. Abbott, Annu. Rev. Biomed. Eng., 2010, 12, 55–85 CrossRef CAS.
- D. Dasgupta, S. Peddi, D. K. Saini and A. Ghosh, Adv. Healthcare Mater., 2022, 11, 2200232 CrossRef CAS PubMed.
- J. Wang and W. Gao, ACS Nano, 2012, 6, 5745–5751 CrossRef CAS PubMed.
- D. Patra, S. Sengupta, W. Duan, H. Zhang, R. Pavlick and A. Sen, Nanoscale, 2013, 5, 1273–1283 RSC.
- K. Han, Micromachines, 2023, 14, 661 CrossRef PubMed.
- O. D. Velev and S. Gupta, Adv. Mater., 2009, 21, 1897–1905 CrossRef CAS.
- F. Li, D. P. Josephson and A. Stein, Angew. Chem., Int. Ed., 2011, 50, 360–388 CrossRef CAS.
- I. Chakraborty, V. Meester, C. van der Wel and D. J. Kraft, Nanoscale, 2017, 9, 7814–7821 RSC.
- I. Chakraborty, D. J. Pearce, R. W. Verweij, S. C. Matysik, L. Giomi and D. J. Kraft, ACS Nano, 2022, 16, 2471–2480 CrossRef CAS.
- Y. Wang, Y. Wang, X. Zheng, É. Ducrot, J. S. Yodh, M. Weck and D. J. Pine, Nat. Commun., 2015, 6, 7253 CrossRef CAS PubMed.
- M. He, J. P. Gales, É. Ducrot, Z. Gong, G.-R. Yi, S. Sacanna and D. J. Pine, Nature, 2020, 585, 524–529 CrossRef CAS PubMed.
- J. S. Oh, G.-R. Yi and D. J. Pine, ACS Nano, 2020, 14, 4595–4600 CrossRef CAS.
- S. Sacanna, W. T. Irvine, P. M. Chaikin and D. J. Pine, Nature, 2010, 464, 575–578 CrossRef CAS PubMed.
- K. S. Khalil, A. Sagastegui, Y. Li, M. A. Tahir, J. E. Socolar, B. J. Wiley and B. B. Yellen, Nat. Commun., 2012, 3, 794 CrossRef.
- H. Wang, W. Chen, B. Chen, Y. Jiao, Y. Wang, X. Wang, X. Du, Y. Hu, X. Lv and Y. Zeng, et al. , Small, 2020, 16, 1905480 CrossRef CAS.
- I. B. Liu, N. Sharifi-Mood and K. J. Stebe, Annu. Rev. Condens. Matter Phys., 2018, 9, 283–305 CrossRef CAS.
- Y. Wang, Y. Wang, D. R. Breed, V. N. Manoharan, L. Feng, A. D. Hollingsworth, M. Weck and D. J. Pine, Nature, 2012, 491, 51–55 CrossRef CAS PubMed.
- V. Liljeström, C. Chen, P. Dommersnes, J. O. Fossum and A. H. Gröschel, Curr. Opin. Colloid Interface Sci., 2019, 40, 25–41 CrossRef.
- A. A. Harraq, B. D. Choudhury and B. Bharti, Langmuir, 2022, 38, 3001–3016 CrossRef CAS PubMed.
- F. Ma, D. T. Wu and N. Wu, J. Am. Chem. Soc., 2013, 135, 7839–7842 CrossRef CAS PubMed.
- J. Gong and N. Wu, Langmuir, 2017, 33, 5769–5776 CrossRef CAS.
- J. G. Lee, A. M. Brooks, W. A. Shelton, K. J. Bishop and B. Bharti, Nat. Commun., 2019, 10, 2575 CrossRef PubMed.
- T. Yang, B. Sprinkle, Y. Guo, J. Qian, D. Hua, A. Donev, D. W. Marr and N. Wu, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 18186–18193 CrossRef CAS PubMed.
- K. Han, C. W. Shields IV, B. Bharti, P. E. Arratia and O. D. Velev, Langmuir, 2020, 36, 7148–7154 CrossRef CAS PubMed.
- J. Palacci, S. Sacanna, A. P. Steinberg, D. J. Pine and P. M. Chaikin, Science, 2013, 339, 936–940 CrossRef CAS.
- S. Rotundo, D. Brizi, A. Flori, G. Giovannetti, L. Menichetti and A. Monorchio, Sensors, 2022, 22, 5132 CrossRef CAS.
- M. Trau, D. Saville and I. A. Aksay, Science, 1996, 272, 706–709 CrossRef CAS PubMed.
- J. R. Maestas, F. Ma, N. Wu and D. T. Wu, ACS Nano, 2021, 15, 2399–2412 CrossRef CAS PubMed.
- E. V. Yakovlev, K. A. Komarov, K. I. Zaytsev, N. P. Kryuchkov, K. I. Koshelev, A. K. Zotov, D. A. Shelestov, V. L. Tolstoguzov, V. N. Kurlov and A. V. Ivlev, et al. , Sci. Rep., 2017, 7, 1–10 CrossRef CAS.
- M. E. Leunissen, H. R. Vutukuri and A. van Blaaderen, Adv. Mater., 2009, 21, 3116–3120 CrossRef CAS.
- T. Vissers, A. van Blaaderen and A. Imhof, Phys. Rev. Lett., 2011, 106, 228303 CrossRef PubMed.
- K. L. Heatley, F. Ma and N. Wu, Soft Matter, 2017, 13, 436–444 RSC.
- Z. Wang, Z. Wang, J. Li, C. Tian and Y. Wang, Nat. Commun., 2020, 11, 2670 CrossRef CAS PubMed.
- F. Ma, S. Wang, L. Smith and N. Wu, Adv. Funct. Mater., 2012, 22, 4334–4343 CrossRef CAS.
- X. Yang and N. Wu, Langmuir, 2018, 34, 952–960 CrossRef CAS PubMed.
- F. Katzmeier and F. C. Simmel, Nat. Commun., 2023, 14, 6247 CrossRef CAS.
- W. Ristenpart, I. A. Aksay and D. Saville, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2004, 69, 021405 CrossRef CAS PubMed.
- W. Ristenpart, I. A. Aksay and D. Saville, J. Fluid Mech., 2007, 575, 83–109 CrossRef CAS.
- D. C. Prieve, P. J. Sides and C. L. Wirth, Curr. Opin. Colloid Interface Sci., 2010, 15, 160–174 CrossRef CAS.
- A. Ramos, Electrokinetics and Electrohydrodynamics in Microsystems, Springer, Vienna, 2011 Search PubMed.
- T. M. Squires and M. Z. Bazant, J. Fluid Mech., 2004, 509, 217–252 CrossRef.
- S. O. Lumsdon, E. W. Kaler and O. D. Velev, Langmuir, 2004, 20, 2108–2116 CrossRef CAS.
- Y. Hu, Z. Tian, D. Ma, C. Qi, D. Yang and S. Huang, Adv. Colloid Interface Sci., 2024, 324, 103089 CrossRef CAS PubMed.
- H. Namigata, K. Watanabe, T. A. Welling, K. Suga and D. Nagao, Colloid Interface Sci. Commun., 2024, 62, 100806 CrossRef CAS.
- M. Hu, X. Ge, X. Chen, W. Mao, X. Qian and W.-E. Yuan, Pharmaceutics, 2020, 12, 665 CrossRef CAS.
- D. Allan, T. Caswell, N. Keim, C. Wel and R. Verweij, soft-matter/trackpy: Trackpy v0. 5.0. Zenodo, 2021.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310 CrossRef CAS.
- F. Katzmeier, B. Altaner, J. List, U. Gerland and F. C. Simmel, Phys. Rev. Lett., 2022, 128, 058002 CrossRef CAS PubMed.
- M. V. Manilo, N. I. Lebovka and S. Barany, J. Mol. Liq., 2019, 276, 875–884 CrossRef CAS.
- T. J. Woehl, K. L. Heatley, C. S. Dutcher, N. H. Talken and W. D. Ristenpart, Langmuir, 2014, 30, 4887–4894 CrossRef CAS PubMed.
- L. Luo, Z. Yan, M. Yang, H. Yin, H. Fu, M. Jin, H. Feng, G. Zhou and L. Shui, J. Phys. D: Appl. Phys., 2021, 54, 475302 Search PubMed.
- H. Morgan and N. Green, AC Electrokinetics: Colloids and Nanoparticles, Research Studies Press, 2003 Search PubMed.
- X. Yang, S. Johnson and N. Wu, Adv. Intell. Syst., 2019, 1, 1900096 CrossRef.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- B. Cui and A. Zaccone, Phys. Rev. E, 2018, 97, 060102 CrossRef CAS.
- I. Chakraborty and Y. Roichman, Phys. Rev. Res., 2020, 2, 022020 CrossRef CAS.
- J. R. Howse, R. A. L. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Phys. Rev. Lett., 2007, 99, 048102 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01242a |
| This journal is © The Royal Society of Chemistry 2025 |


![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif)