Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Impact of charge distribution on the stability of ferroelectric nematic liquid crystals
Matheus
de Mello
 *a,
Mark Richard
Wilson
*a,
Mark Richard
Wilson
 b and
Takeaki
Araki
b and
Takeaki
Araki
 *c
*c
aDepartment of Physics, Kyoto University, Kyoto 606-8502, Japan. E-mail: de.matheus.42h@st.kyoto-u.ac.jp
bDepartment of Chemistry, Durham University, Durham, DH1 3LE, UK. E-mail: mark.wilson@durham.ac.uk
cDepartment of Physics, Kyoto University, Kyoto 606-8502, Japan. E-mail: araki.takeaki.5a@kyoto-u.ac.jp
First published on 21st January 2025
Abstract
This study explores the influence of charge distribution and molecular shape on the stability of ferroelectric nematic liquid crystalline phases through atomistic simulations of DIO molecules. We demonstrate the role of dipole–dipole interactions and molecular shape in achieving polar ordering by simulating charged and chargeless topologies, and analysing positional and orientational pair-distribution functions. The charged DIO molecules exhibit head-to-tail and side-by-side parallel alignments conducive to long-range polar order, whereas the chargeless molecules show no polar ordering. The 2D x–y cross-section of the correlation pair-distribution function shows that lateral local dipoles in the molecular structure are critical for the formation of the ferroelectric phase, highlighting the importance of charge asymmetry and electrostatic interactions in stabilizing long-range polar order.
1 Introduction
Display and sensor devices widely use nematic liquid crystals, taking advantage of their unique rheological and optical properties.1,2 The uniaxial nematic phase is the least ordered mesophase of liquid crystals and occurs at higher temperatures in comparison to other mesophases of the same compound. Within this phase, molecules typically align along a preferred direction called the nematic director.3 This alignment is observed in rod-like or elongated particles,4 and can also be induced in systems with disc-like particles through an external electric field.5 The uniaxial nematic phase exhibits inversion symmetry, meaning the director vector n is equivalent to −n, resulting in no net polar ordering even in polar mesogens.3In contrast to the conventional nematic phase, Born conjectured the existence of a globally polarised mesophase if the dipole–dipole interactions between molecules could counteract thermal fluctuations.6 This phase is called the ferroelectric nematic phase (NF) and displays polar ordering along the director P = Pn, breaking centrosymmetric inversion and establishing a preferred orientation. This feasibility depends on the strength of the intrinsic molecular dipole moment; the interaction of the order μ2/Vm needs to surpass kBT, where μ is the dipole moment strength, Vm represents the molecular volume, kB stands for the Boltzmann constant, and T is the equilibrium temperature. A rough estimate at room temperature dictates that the dipole moment of mesogenic molecules should exceed 6 D for significant stability. Nevertheless, at that time, empirical evidence for a polar nematic mesophase remained absent, prompting the exploration of other mesophases featuring weakly polar or entirely nonpolar molecules.
In 2017—101 years after Born's seminal paper, Nishikawa et al.7 and Mandle et al.8,9 experimentally realised and identified two distinct low-molecular-mass materials, namely DIO and RM734, which was later confirmed to be ferroelectric nematic phases by Chen et al.10 in 2020. Ferroelectric nematic liquid crystals have large spontaneous polarisation (P = 4.4 μC cm−2 in DIO), maintain fluidity, exhibit giant dielectric permittivity, and possess non-linear optical properties. They can be reoriented by weak electric fields, making them valuable for low-voltage displays, memory devices, energy harvesting applications, and more.7,9,10
This groundbreaking experimental achievement of the ferroelectric nematic liquid crystalline phases has spurred extensive research regarding the origin, mechanism, and nature of the phase transition.10–24 Li et al.25 systematically studied some of the molecular features required for ferroelectric phase stability and presented statistical guidelines for the molecular design of novel materials with ferroelectric properties. Guided by machine learning algorithms, the most statistically significant features for achieving high polarity and liquid crystalline behaviour were that: (i) dipole moment μ greater than 9 D, (ii) low geometrical aspect ratio L/W < 2.5, and (iii) an oblique dipole angle of about 20°.
If the dipole moment falls below the threshold, the material transitions into a traditional nonpolar nematic phase, following Born's 1916 prediction. The geometrical aspect ratio of the mesogen plays a role in preventing crystallisation before reaching the ferroelectric nematic phase and expanding the temperature range at which the phase remains stable at lower temperatures.25 Notably, nitrile-containing molecules with large dipoles (μ > 10 D) fail to form NF phases, unlike planar nitro groups, due to dimerization tendencies attributed to the small cross-sectional area and linear shape among nitriles.
Berardi et al.26 investigated the role of molecular shape in the formation of polar nematics. They noted that pear-shaped mesogens with non-equal head–tail interactions, interacting via a generalized Gay–Berne potential with both attractive and repulsive interactions, can also form globally polar nematic phases. However, if a longitudinal dipole moment is added, a sufficiently large dipole will destabilize the polar nematic. Thus, the combination of molecular shape and attractive forces appears (in combination with dipoles) to be fundamental to the stability of the ferroelectric nematic phase.
Unfortunately, the key molecular ingredients for the stabilization of the ferroelectric nematic liquid crystalline phase remain elusive. However, computer simulations provide a way of unravelling the complex interactions in liquid crystal systems.27,28 Enabled by recent advancements in computation power, simulations have become integral in liquid crystal research. Driven by both fundamental understanding and technological applications,12,18 simulations enable detailed visualization and analysis of both molecular structure and properties in a way that can enhance basic knowledge by validating theoretical frameworks and providing insight for experimental setups.29–31
To elucidate the origins of polar ordering in these systems, and the significance of molecular shape and charge distribution in maintaining the stability of the ferroelectric nematic phase, we study the spatial correlations, microscopic behaviour, and properties of DIO molecules via atomistic simulations. Our results aim to illuminate the interplay between molecular shape and the intermolecular dipole–dipole interaction that drives the transition to the long-range polar-ordered nematic phase. We hope our results will help further advance novel technological devices in ferroelectric liquid crystals through fundamental understanding.
2 Computational methods
This study examines the orientational and positional distribution, and the dynamic properties of DIO molecules with and without electric charges. Using atomistic simulations, we capture molecular ordering and phase behaviour as a function of temperature, focusing on isotropic, nematic, and ferroelectric liquid crystalline states. We conducted all-atom molecular dynamics simulations using GROMACS 202332 with the General Amber Force Field (GAFF).33 The pair-wise energy interaction is defined by: | (1) |
Here, req and θeq are the equilibrium bond lengths and angles, while Kr, Kθ, and kd are the force constants. The parameters nd and ωd describe the torsional angle properties. Lennard-Jones parameters σij and εij represent non-bonded interactions, and qi is the partial charge of the ith atom.
We generated molecular topologies using the AmberTools package.34 Atomic charges were obtained using the RESP (Restrained ElectroStatic Potential) method35 employing the B3LYP/6-31G(d,p) level of density functional theory36 carrying out the quantum chemical calculations with Gaussian 16.37Fig. 1(a) and (b) show the chemical structure of the DIO molecule and its electrostatic isopotential surface, respectively. The molecular topology was generated using the AmberTools “tleap”' program and converted to the GROMACS form using the ACPYPE script.38 Following Boyd and Wilson,39 the torsional energy parameters were optimised to eliminate non-physical conformations. The LINCS method of holonomic constraints (4th order) maintained all bond lengths,40 while non-bonded interactions were truncated at 1.2 nm for short-range electrostatic and van der Waals cutoffs. The long-range electrostatic interactions were computed using the Particle Mesh Ewald (PME)41 method with 4th-order cubic interpolation and a grid spacing of 0.25 nm.
In addition to DIO, we prepared the same molecular structure but with partial atomic charges manually set to zero (named chargeless DIO in this work) to study the effects of molecular shape and Lennard-Jones interactions alone on the stability of the NF phase. Instead of modifying the GROMACS force field definition files directly, we take a practical workaround approach by manually setting all partial charges to zero to effectively eliminate Coulombic interactions. Accordingly, for the chargeless system, GROMACS can only run if a plain cutoff scheme for long-range electrostatics is used in the mdp input file. We simulated systems composed of 1000 charged and 2048 chargeless DIO molecules, corresponding to 56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 114
000 and 114![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 688 atoms, respectively, considerably higher than the previous literature studies. Molecules were initialized with random positions and orientations at 450 K in the isotropic state, with velocities following a Maxwell distribution at the prescribed temperature. Also, an aligned ferroelectric nematic state at 330 K was prepared using Packmol42 where the majority of DIO molecules were initially ordered over the molecular long-axis, along the positive z-axis of the simulation box (named “Manually Aligned (MA)” in this work).
688 atoms, respectively, considerably higher than the previous literature studies. Molecules were initialized with random positions and orientations at 450 K in the isotropic state, with velocities following a Maxwell distribution at the prescribed temperature. Also, an aligned ferroelectric nematic state at 330 K was prepared using Packmol42 where the majority of DIO molecules were initially ordered over the molecular long-axis, along the positive z-axis of the simulation box (named “Manually Aligned (MA)” in this work).
For all simulations, we used the following equilibration procedure and input parameters. After energy minimization using the Steep Descent and Conjugate Gradients methods, the system underwent a 50 ns equilibration period in the constant-NVT (constant number of particles, volume, and temperature) ensemble. Temperature coupling was achieved using the V-rescale algorithm, and a leap-frog integrator was used with a time step of 0.001 ps. Next, the system was equilibrated for an additional 250 ns in the constant-NPT (constant number of particles, pressure, and temperature) ensemble, totalling 300 ns. Isotropic pressure coupling was performed using the C-rescale algorithm at a reference pressure of 1 bar and a water compressibility reference of 4.5 × 10−5 bar−1 within a cubic simulation box. The robustness of the initial condition was confirmed by matching the macroscopic average density with experimental results in the literature at each respective temperature.
A cooling protocol was applied, decreasing the temperature in steps of 10 K with equilibration intervals of 10–20 ns between each step. The previous temperature initialized each sub-sequential annealing configuration to explore the minimal energy landscape. The MA system underwent a heating protocol from 330 K to 420 K.
The well-equilibrated system at a specific temperature was subjected to a production run of 250–750 ns in the constant-NPT ensemble, during which physical observables were analyzed. The temperature was controlled using the Nosé–Hoover thermostat,43 and pressure was controlled using the Parrinello–Rahman barostat.44 All simulations were conducted under 3D periodic boundary conditions, with trajectory data recorded at 10 ps intervals. Fig. 1(c) shows a typical configuration snapshot of the weakly aligned ferroelectric nematic phase at 330 K. Numerical analysis of the simulation results was performed using the MDAnalysis45 python package and molecular visualization with OVITO Pro.46
3 Numerical results and discussion
This section presents the key results of the atomistic simulations and provides a comprehensive discussion of the microscopic dynamics, auto-correlation functions, and orientational and positional distribution functions of the ferroelectric nematic phase of DIO molecules.3.1 Nematic and polar order parameter
To characterize the molecular organization in the LC system, the nematic order tensor Qαβ was calculated and diagonalized. Here, | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉 is calculated as the average orientation of the molecules in the sample, where θ is the angle between the axis defining the individual molecular long-axis and the director n.
θ〉 is calculated as the average orientation of the molecules in the sample, where θ is the angle between the axis defining the individual molecular long-axis and the director n.
Fig. 2(a) shows the temperature dependence of the average value of the nematic order parameter P2. It demonstrates the formation of nematic order as the temperature decreases for both charged and chargeless systems. The clearing point temperature for the charged DIO molecule is approximately TNI ≈ 425 K, which is in good agreement with the experimental clearing point of 446 K observed in the literature.7 The chargeless system develops nematic order due to the anisotropy of molecular shape and excluded volume interactions and has a slightly lower transition temperature.
Fig. 2(b) shows the temperature dependence of the average P1 order parameter, indicating a small but finite polar order formation in the charged system due to an asymmetric distribution of molecular ordering along the director vector. For the DIO molecules, the formation of the ferroelectric phase is preceded by the nematic phase.7 Above or near below TNI ≈ 425 K, the average value of the scalar P1 order parameter fluctuates around zero, as the orientation is evenly distributed around the direction of the pair of vectors (n, −n). However, for a lower temperature, the average value of P1 > 0 indicates the onset of polar ordering with some degree of molecules aligning along the director vector. According to Fig. 2(b), we estimate that the phase transition towards a polar phase starts at T = 420 K. Although this temperature is higher than the experimental observation (≈338 K),7 we consider our simulations can capture the phase transition to NF. Visualization of the instantaneous spatial configuration snapshot in Fig. 1(c) reveals small, locally ordered nanodomains at 330 K. Despite the average value of P1 being small in the weakly aligned configuration, it remains non-zero throughout the trajectory, indicating the formation of locally ordered domains with correlated orientations.
On the other hand, as evidenced in Fig. 2(b), we observed neither long-range nor nanodomains of polar ordering in the spontaneously ordered configuration of chargeless topologies, with the instantaneous configuration resembling a conventional nematic phase. These indicate, as expected, that the molecular charge distribution plays a key role in the spontaneous formation of the polar order. We should note that our observed polar order P1 is considerably smaller than those observed in the experiments.7 The difficulty in achieving a spontaneously large polar order comparable to experiments stems from slow reorientational dynamics in the NF phase at lower temperatures. Once the system transitions into the nematic phase, the mesogens become restricted due to insufficient thermal energy, making it computationally expensive to increase polar order comparable to experimental values. We discuss this challenge in more depth in Section 3.3 (see Fig. 4).
3.2 Pair-distribution and correlation functions
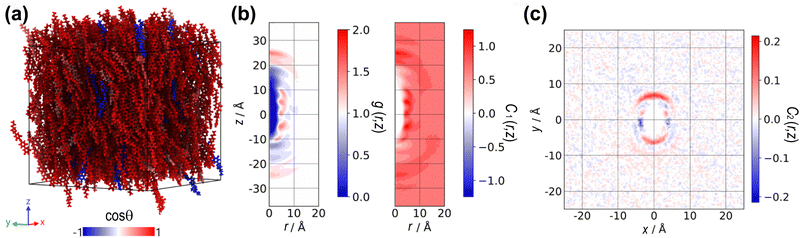
Sequentially, we calculated the cylindrical distribution and orientational correlation functions to investigate the spatial and orientational alignment in the NF phase of DIO. These functions delineate the orientational ordering and probability density of finding pairs of molecules at specific distances within defined cylindrical dimensions and provide details of close contacts arising from preferred molecular interactions. The expression for the cylindrical distribution function g(r,z) is given as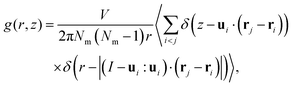 | (3) |
Also, we computed the pair-orientational correlation function C1(r,z) following the expression
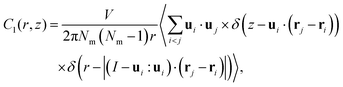 | (4) |
Fig. 3(a) presents the cylindrical distribution functions g(r,z), derived from the spontaneously ordered configurations at a temperature of T = 350 K for the charged (weakly polar) and chargeless (nonpolar) DIO systems, respectively. At this temperature, the orientational order parameter, P2 is identical to both systems, but the charged DIO model has entered the NF. Regions where the distribution function is dark blue indicate steric repulsion between molecules and can be interpreted as the excluded volume of the molecular shape, as the probability of finding molecules in those regions is zero. Additionally, the plot shows darker red areas, corresponding to points along the aromatic rings, suggesting that (on average) the molecules tend to be positioned at specific radial distances within the cylindrical cross-section relative to the reference molecule at the centre.
The orientational correlation function C1(r,z) in Fig. 3(b) reveals distinct peaks of positive (red) and negative (blue) correlations, closely tied to the alignment of molecules along both the axial and radial axes. Peaks along the z-axis indicate a pronounced head-to-tail (or head-to-head if blue) alignment. In contrast, peaks along the radial axis denote a parallel (or antiparallel) side-by-side alignment. The results show that the orientational correlation functions of the charged and chargeless DIOs are fundamentally different. The charged DIO topology exhibits parallel alignment over most of the region, especially around r = 5 Å, evident as peaks of intense positive alignment. In contrast, the chargeless DIO topology displays antiparallel alignment, visible as alternating peaks of positive and negative orientations along a fixed radial distance throughout the axial extension of the simulation box.
The lack of parallel alignment through the simulation box is a sign of the absence of long-range polar ordering in the chargeless system (see Fig. 2(b)). On average, the distribution of molecular ordering (measured through the order parameter P1) is symmetrical due to the balance between the parallel and antiparallel alignments. For the charged DIO topology, even though the P1 value is small (P1 ≈ 0.2) in the spontaneous configuration, peaks of positive correlation indicate a preference for local parallel ordering of dipoles.
As previously discussed, Berardi et al.26 noted that materials composed of constituents lacking head-to-tail symmetry, such as axially symmetric tapered molecules, can also form a nematic phase with local polar order, even if they are electrically apolar. The shape of these constituents influences the positional and orientational correlations among neighbouring particles, facilitating or hindering the development of the polar phase. Moreover, if the mesogens are tapered or pear-shaped, splay deformation can occur, linking it with the polar order in the system. Mertelj et al.48 and Sebastián et al.18 demonstrated that at the phase transition between the nematic and the splay-nematic phase, growing ferroelectric order occurs as the splay deformation coupling constant softens, driving a polarization via flexoelectric coupling. However, this is not a proper ferroelectric order, as the polar order is simply coupled to the splay of the director field.49 One of the current challenges of molecular simulations is implementing splay deformation within the confines of the simulation box, as the length scale of the phase modulation is on the micro-scale. Overcoming this barrier would test the hypothesis that splay deformation enhances polar ordering and is a fundamental ingredient for forming the NF phase.49–51 Though we note, in the case of chargeless DIO, that the molecular shape can be regarded as a simple rod, and here we have not observed local ordering due to the shape asymmetry. This suggests that the charge distribution is required for the stability and onset of ferroelectric order, at least for DIO.
3.3 Dynamics and auto-correlation of molecular axis
To further investigate the stability of the ferroelectric phase in charged DIO, we examine the correlation dynamics to verify the extensive equilibration time needed to achieve polar order following the onset of nematic ordering in the sample. Our analysis begins with the fluctuations of the auto-correlation function for the primary axis (long axis) ui as,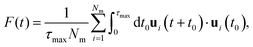 | (5) |
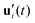 . Fig. 4 shows a comparison of the auto-correlation functions for the primary and the secondary axes.
. Fig. 4 shows a comparison of the auto-correlation functions for the primary and the secondary axes.
 | ||
| Fig. 4 Plots of the auto-correlation functions of the primary and secondary axes of inertia for the charged (red) and chargeless (blue) topologies. | ||
We find that the auto-correlation function for the primary axis decays quite slowly over the simulation time for the charged DIO, even compared to that for the chargeless system. It is considered that decay in the auto-correlation function for the primary axis in the nematic phase is caused by both the slow and flip-flop rotation of rod-like molecules. This slow decay indicates that the molecules become locally trapped in local domains by the electrostatic interactions, preventing them from rotating into a configuration that would enhance the values of the P1 order parameter. This behaviour suggests that once the system is “locked” into a meta-stable paraelectric nematic state or developed a weakly ordered ferroelectric phase, it becomes computationally prohibitive to either establish, enlarge, or disrupt polar order within the system, even within the temperature range of the NF phase. Even after our extensive equilibration and successive production runs totalling over 900 ns, the increase in polar order towards a long-range with large P1 values was not observed. Due to the expensive computational time required, we suggest implementing other simulation techniques, such as Hamiltonian replica exchange or parallel tempering, to overcome local minima and glassy behaviour.52,53 Another suggestion is to investigate if refining the atomic charges using a self-consistent modelling scheme with density functional theory under periodic boundary conditions can increase the self-diffusion coefficients of the molecules and improve the reorientational correlation times.54,55
Notably, the secondary axis auto-correlation function for the charged system (light red line in Fig. 4) decays significantly slower than the chargeless topology (light blue line). This signifies that the charge distribution also impacts the rotational motion of the molecules. We will discuss this in more detail later.
3.4 Manually aligned NF configuration
Here we consider the stability of the highly polar-ordered configuration for the charged DIO. We prepared a sample formed from the initially aligned configuration of molecules (MA). Fig. 5(a) is a snapshot of a typical configuration of the charged DIO at T = 400 K. Most molecules remain oriented in the same direction after a long annealing process. Fig. 5(b) illustrates the orientational correlation function C2(r,z) for the NF phase of charged DIO. In the MA configuration, the average value of P1 is considerably higher than in the weakly aligned spontaneously grown phase considered above, approximately P1 ≈ 0.8. We can achieve higher orientational order due to the initial condition that favours equilibration towards the strongly aligned state. This polar order is further evidenced by the positive (red) values of orientational correlation observed in Fig. 5(b), displaying long-range order, even far from the molecule located at the central reference position. These positive values extend throughout the simulation box, showing a uniform alignment across the system.Our result reveals that the pair-distribution peaks in both plots of Fig. 5(b) for the MA configuration match those of the spontaneously aligned charged configuration shown in Fig. 3(a). This matching suggests that the weakly aligned state observed in the spontaneously aligned configuration is a meta-stable or glassy state of the highly polar configuration. The concept of a meta-stable or glassy state here implies that while the weakly aligned state is not the most stable configuration, it is still stable under certain conditions and can persist for extended periods due to the slow decay of the primary axis correlation function.
A chargeless, manually aligned configuration was prepared to explore further alignment stability in favoured initial conditions. However, the chargeless system lost its initial polar alignment after heating and equilibration within the ferroelectric nematic temperature range at 400 K. It remained in a normal nematic phase with head-to-tail symmetry, confirming that charges are essential for stabilising the polar order. This highlights the role of electrostatic interactions in the stability of the ferroelectric order within our system.
Additionally, we calculated the transverse correlation function for the secondary axis of inertia  in the x–y plane over a range Δz = 0.2 nm, as described by the following equation:
in the x–y plane over a range Δz = 0.2 nm, as described by the following equation:
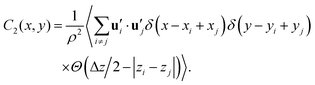 | (6) |
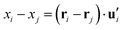 . This calculation was performed over an average of all time steps in the trajectory.
. This calculation was performed over an average of all time steps in the trajectory.
In Fig. 5(c), this function reveals an asymmetry in the correlation distribution in the x–y plane, indicating a preferred lateral direction of alignment, i.e. local biaxial order. The asymmetry suggests that the molecules within the system tend to align more strongly along one lateral direction than others. This preferred alignment direction could be influenced by a combination of structural factors and charge distribution, highlighting the complex interplay between molecular structure, charge distribution, and short-range electrostatic interactions.
3.5 Interaction energy and charge distribution
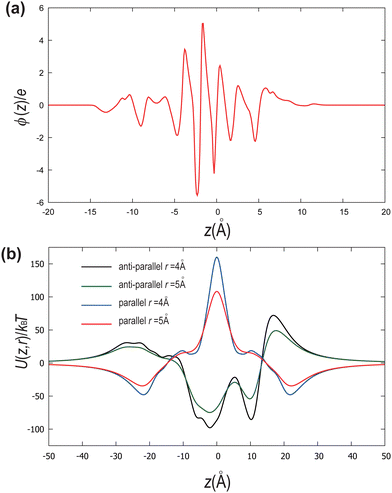
Let us conclude by addressing the role of charge distribution along and perpendicular to the molecular length. Madhusudana14 demonstrates that electrostatic interactions, which typically favour antiparallel alignment, can be modified by adjusting the amplitudes of the charge density waves along the rod length. They assume that rotational motion around the long axis is sufficiently fast that molecules can be idealized as cylindrical rods with longitudinal surface charge density waves. Furthermore, alternating charge densities along the molecular length, with lower charge densities at the ends, favour the NF phase through short-range electrostatic interactions. The model highlights that stability below a critical inter-rod separation and the weakly first-order nature of the paraelectric-to-ferroelectric nematic transition is due to the coupling between the density of the medium (molecular packing) and polar order. Thus, the local structure of the molecules directly impacts the short-range electrostatic interactions responsible for stabilizing the NF phase.In Fig. 6(a), we illustrate the charge density profile along the molecular length, identifying how charges are spatially arranged. Following the assumption of the fast rotational motion around the long axis, the charge density profile ϕ(z) is calculated as
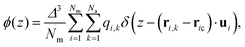 | (7) |
In Fig. 6(b), we measure the dependence of the interaction energy on the distance z between a pair of DIO molecules separated by distances r = 4 Å and r = 5 Å for both parallel and antiparallel configurations. The interaction energy is calculated as
 | (8) |
3.6 Highly electrically charged ester site analysis
As evidenced by Fig. 5(c), the asymmetry in the transverse axis correlation distribution function, as seen in the x–y plane, suggests that there is a lateral preferred alignment. Having analysed the distribution functions to the centre of mass of the DIO molecules, we now turn our attention to the highly negatively charged ester region, a strong lateral dipole moment in the molecule, as illustrated in the ESP diagram in Fig. 1(b) and highlighted in the chemical structure shown in Fig. 7. Although We have not categorized and compared specific molecular structures in DIO, we focused our attention to this ester site in this work.We start the analysis by calculating the pair-distribution (ge) and correlation functions for the primary (Ce1) and secondary axes (Ce2) of the ester groups. The primary axis is along the C–C bond of its ester group, while the secondary one lies in the plane containing the C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O angle and perpendicular to the primary axis. The correlation functions are defined in similar manners of eqn (3), (4) and (6). Fig. 7(a) illustrates a preference for a side-by-side distribution of molecules rather than a longitudinal distribution, evident from the low-density region along the cylindrical axis. For the charged system, the distribution shows asymmetry, with a higher probability of finding molecules around (z = 0, r = 0.5 nm), which diminishes as the radial distance between the molecules increases. This indicates an influence of the charge distribution on molecular alignment at short ranges. In contrast, the chargeless system displays a symmetrical distribution along the centre reference position of z = 0, demonstrating no preferred directional alignment without charge.
O angle and perpendicular to the primary axis. The correlation functions are defined in similar manners of eqn (3), (4) and (6). Fig. 7(a) illustrates a preference for a side-by-side distribution of molecules rather than a longitudinal distribution, evident from the low-density region along the cylindrical axis. For the charged system, the distribution shows asymmetry, with a higher probability of finding molecules around (z = 0, r = 0.5 nm), which diminishes as the radial distance between the molecules increases. This indicates an influence of the charge distribution on molecular alignment at short ranges. In contrast, the chargeless system displays a symmetrical distribution along the centre reference position of z = 0, demonstrating no preferred directional alignment without charge.
Additionally, Fig. 8(a) shows the primary axis correlation distribution functions Ce1(x,y) in the x–y plane. For the charged system, there is a strong positive head-to-tail and side-by-side correlation, a feature that is notably absent in the chargeless system, indicated by weak correlation distribution. This suggests that the charged system favours lateral molecular alignment, likely due to electrostatic interactions between negatively charged ester groups.
 | ||
| Fig. 8 Plots of the 2D x–y cross-section of (a) primary axis correlation function, and (b) transverse (secondary) axis pair-distribution correlation function. | ||
In terms of the secondary (transverse) axis correlation distribution function Ce2(x,y), as depicted in Fig. 7(c) and 8(b), the chargeless system shows no correlation for the highly charged ester group. However, the charged system clearly prefers side-by-side positive alignment, although the long-range correlation of the secondary axis is not observed (as one would expect to see in a biaxial nematic phase). This further supports the notion that electrostatic forces are key in promoting and stabilizing specific alignment patterns in the charged DIO model. In usual nematic liquid crystals, the rotational motion along the long axis is sufficiently fast and has been neglected when the stability of the nematic phase is considered. Our simulations reveal that the rotational motion of the secondary axis is relatively slow, as shown in Fig. 4, and non-negligible correlations among them for the charged DIO.
As noted above, it was discussed that the large angle between the dipole moment and the long axis of the rod shape is a significant factor for the formation of the NF phase.25 We consider that the lateral component of the oblique dipole moment leads to the local parallel alignment between the DIO molecules, and this local alignment induces the global ferroelectric ordering. Overall, these findings underscore the impact of charge distribution on molecular alignment and interaction. The charged systems exhibit distinct side-by-side correlations and asymmetries in their pair-distribution functions, driven by electrostatic interactions, whereas the chargeless systems lack such preferential alignment. This comprehensive analysis provides deeper insights into molecular organization mechanisms in systems with varying charge distributions.
4 Conclusion
This study examined the role of charge distribution and molecular shape in the stability of ferroelectric nematic phases through detailed atomistic simulations of DIO molecules. Our results discuss the importance of dipole–dipole interactions and the intrinsic charge distribution along the molecular length in achieving and maintaining polar ordering. Charged DIO molecules tend to align head-to-tail and side-by-side in parallel, with weak, short-range polar order highlighting the necessity of charge asymmetry for phase stability. In contrast, chargeless DIO configurations fail to demonstrate polar ordering, reaffirming the role of electrostatic interactions in forming the NF phase.The pair-distribution and orientational correlation function of charged systems showed pronounced peaks indicative of polar ordering, while chargeless systems displayed no such preference, with anti-parallel alignment. For charged DIO topologies, we found that the molecules preferred a head-to-tail and parallel shifted side-by-side alignment while maintaining a rod-like shape that favours the polar ordering. The manually aligned configuration results further validated the role of electrostatic interactions in stabilizing the ferroelectric order due to the presence of long-range polar order in the system. We suggest that the spatial electrical structure of the lateral dipoles plays an important role in stabilizing the ferroelectric nematic order due to the asymmetry in the x–y 2D cross-section peaks in the pair-distribution and pair-correlation functions.
Due to slow dynamics, as the system reaches the nematic phase, future research should explore advanced simulation techniques such as Hamiltonian replica exchange or parallel tempering to overcome the challenges posed by the glassy behaviour observed in the spontaneously aligned system. We also suggest improving theoretical models that consider the local lateral dipoles in the molecular structure to study the relationship between the charge distribution and the feasibility of the NF phase. Continued exploration of ferroelectric nematic liquid crystal simulations can provide invaluable insights into advancing this novel field of nematics with potential technological applications in low-voltage displays, memory devices, and energy harvesting technologies.
Data availability
The data supporting the findings of this study are available from KURENAI under DataCite DOI. The data can be accessed at https://hdl.handle.net/2433/290133. No restrictions apply to the availability of the data, and all interested parties are encouraged to access it for further research.Author contributions
MdM, TA, and MRW performed the numerical simulations and formal analysis and wrote the original draft.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to G. Watanabe (Kitasato University), and H. Nishikawa (RIKEN) for helpful discussions. This work is supported from the Japanese Government Monbukagakusho Scholarship (MEXT), JST CREST Grant Number JPMJCR2095, JSPS KAKENHI 21K03486 and 24K00592, Kyoto University Graduate School of Science under GINPU Fund, and The University of Tokyo ISSP for the provision of computer time.Notes and references
- I. Khoo and Y. Shen, Opt. Eng., 1985, 24, 579–585 CrossRef CAS.
- G. S. He, Nonlinear optics and photonics, OUP, Oxford, 2014 Search PubMed.
- P.-G. De Gennes and J. Prost, The physics of liquid crystals, Oxford University Press, 1993 Search PubMed.
- J. V. Selinger, Introduction to the theory of soft matter: from ideal gases to liquid crystals, Springer, 2016 Search PubMed.
- N. H. Tinh, C. Destrade and H. Gasparoux, Phys. Lett. A, 1979, 72, 251–254 CrossRef.
- M. Born, Ueber anisotrope Flüssigkeiten: Versuch einer Theorie der flüssigen Kristalle und des elektrischen Kerr-Effekts in Flüssigkeiten, 1916.
- H. Nishikawa, K. Shiroshita, H. Higuchi, Y. Okumura, Y. Haseba, S.-I. Yamamoto, K. Sago and H. Kikuchi, Adv. Mater., 2017, 29, 1702354 CrossRef.
- R. J. Mandle, S. J. Cowling and J. W. Goodby, Chem. – Eur. J., 2017, 23, 14554–14562 CrossRef CAS.
- R. J. Mandle, S. J. Cowling and J. W. Goodby, Phys. Chem. Chem. Phys., 2017, 19, 11429–11435 RSC.
- X. Chen, E. Korblova, D. Dong, X. Wei, R. Shao, L. Radzihovsky, M. A. Glaser, J. E. Maclennan, D. Bedrov, D. M. Walba and N. A. Clark, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 14021–14031 CrossRef CAS PubMed.
- S. K. Gupta, D. Budaszewski and D. P. Singh, Eur. Phys. J.: Spec. Top., 2022, 231(4), 673–694 CAS.
- O. D. Lavrentovich, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 14629–14631 CrossRef CAS.
- E. I. Kats, Phys. Rev. E, 2021, 103, 012704 CrossRef CAS PubMed.
- N. V. Madhusudana, Phys. Rev. E, 2021, 104, 014704 CrossRef CAS.
- A. Manabe, M. Bremer and M. Kraska, Liq. Cryst., 2021, 48, 1079–1086 CrossRef CAS.
- M. T. Máthé, A. Buka, A. Jákli and P. Salamon, Phys. Rev. E, 2022, 105, L052701 CrossRef PubMed.
- K. Perera, R. Saha, P. Nepal, R. Dharmarathna, M. S. Hossain, M. Mostafa, A. Adaka, R. Waroquet, R. J. Twieg and A. Jákli, Soft Matter, 2023, 19(3), 347–354 RSC.
- N. Sebastián, M. Čopič and A. Mertelj, Phys. Rev. E, 2022, 106, 021001 CrossRef.
- N. Sebastián, M. Lovšin, B. Berteloot, N. Osterman, A. Petelin, R. J. Mandle, S. Aya, M. Huang, I. Drevenšek-Olenik, K. Neyts and A. Mertelj, Nat. Commun., 2023, 14, 3029 CrossRef.
- J. Thoen, G. Cordoyiannis, W. Jiang, G. H. Mehl and C. Glorieux, Phys. Rev. E, 2023, 107, 014701 CrossRef CAS PubMed.
- J. Yang, Y. Zou, W. Tang, J. Li, M. Huang and S. Aya, Nat. Commun., 2022, 13, 7806 CrossRef CAS.
- H. Nishikawa, K. Sano, S. Kurihara, G. Watanabe, A. Nihonyanagi, B. Dhara and F. Araoka, Commun. Mater., 2022, 3, 89 CrossRef CAS.
- M. A. Osipov, Liq. Cryst., 2024, 1–7 CrossRef.
- M. A. Osipov, Liq. Cryst. Rev., 2024, 12, 14–29 CrossRef CAS.
- J. Li, H. Nishikawa, J. Kougo, J. Zhou, S. Dai, W. Tang, X. Zhao, Y. Hisai, M. Huang and S. Aya, Sci. Adv., 2021, 7, eabf5047 CrossRef CAS PubMed.
- R. Berardi, M. Ricci and C. Zannoni, Ferroelectrics, 2004, 309, 3–13 CrossRef CAS.
- M. R. Wilson, Int. Rev. Phys. Chem., 2005, 24, 421–455 Search PubMed.
- M. R. Wilson, G. Yu, T. D. Potter, M. Walker, S. J. Gray, J. Li and N. J. Boyd, Crystals, 2022, 12, 685 Search PubMed.
- J. Peláez and M. R. Wilson, Phys. Rev. Lett., 2006, 97, 267801 CrossRef.
- M. R. Wilson, Chem. Soc. Rev., 2007, 36, 1881–1888 RSC.
- G. Yu and M. R. Wilson, Soft Matter, 2022, 18, 3087–3096 RSC.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1, 19–25 CrossRef.
- K. Sprenger, V. W. Jaeger and J. Pfaendtner, J. Phys. Chem. B, 2015, 119, 5882–5895 CrossRef CAS.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Am. Chem. Soc., 2001, 222, U403–U446 Search PubMed.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1992, 96, 2155–2160 CrossRef CAS.
- M. Frisch, G. Trucks, H. B. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. Petersson and H. Nakatsujiet al., Gaussian 16, 2016 Search PubMed.
- A. W. Sousa da Silva and W. F. Vranken, BMC Res. Notes, 2012, 5, 1–8 CrossRef.
- N. J. Boyd and M. R. Wilson, Phys. Chem. Chem. Phys., 2015, 17, 24851–24865 RSC.
- B. Hess, H. Bekker, H. J. Berendsen and J. G. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- L. Martnez, R. Andrade, E. G. Birgin and J. M. Martnez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- S. Nosé, Mol. Phys., 1984, 52, 255–268 CrossRef.
- S. Melchionna, G. Ciccotti and B. Lee Holian, Mol. Phys., 1993, 78, 533–544 CrossRef CAS.
- N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, J. Comput. Chem., 2011, 32, 2319–2327 CrossRef CAS.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2009, 18, 015012 CrossRef.
- R. Eppenga and D. Frenkel, Mol. Phys., 1984, 52, 1303–1334 CrossRef CAS.
- R. J. Mandle, N. Sebastián, J. Martinez-Perdiguero and A. Mertelj, Nat. Commun., 2021, 12, 4962 CrossRef CAS PubMed.
- M. P. Rosseto and J. V. Selinger, Phys. Rev. E, 2020, 101, 052707 CrossRef CAS.
- A. Mertelj, L. Cmok, N. Sebastián, R. J. Mandle, R. R. Parker, A. C. Whitwood, J. W. Goodby and M. Čopič, Phys. Rev. X, 2018, 8, 041025 CAS.
- N. Sebastián, L. Cmok, R. J. Mandle, M. R. de la Fuente, I. Drevenšek Olenik, M. Čopič and A. Mertelj, Phys. Rev. Lett., 2020, 124, 037801 CrossRef PubMed.
- H. Fukunishi, O. Watanabe and S. Takada, J. Chem. Phys., 2002, 116, 9058–9067 CrossRef CAS.
- D. J. Earl and M. W. Deem, Phys. Chem. Chem. Phys., 2005, 7, 3910–3916 RSC.
- Y. Ishii, N. Matubayasi, G. Watanabe, T. Kato and H. Washizu, Sci. Adv., 2021, 7, eabf0669 CrossRef CAS.
- Y. Ishii, N. Matubayasi and H. Washizu, J. Phys. Chem. B, 2022, 126, 4611–4622 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2025 |