Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Viscotaxis of beating flagella†
Shubham
Anand
 ,
Jens
Elgeti
,
Jens
Elgeti
 * and
Gerhard
Gompper
* and
Gerhard
Gompper
 *
*
Theoretical Physics of Living Matter, Institute for Advanced Simulation and Institute of Biological Information Processing, Forschungszentrum Jülich, 52425 Jülich, Germany. E-mail: s.anand@fz-juelich.de; j.elgeti@fz-juelich.de; g.gompper@fz-juelich.de
First published on 19th March 2025
Abstract
Many biological microorganisms and artificial microswimmers react to external cues of environmental gradients by changing their swimming directions. We study here the behavior of eukaryotic flagellated microswimmers in linear viscosity gradients. Motivated by the near-surface motion of many microswimmers, we consider flagellar swimming in two spatial dimensions. We employ a model of flagellum consisting of a semi-flexible filament with a travelling wave of spontaneous curvature to study generic aspects of viscotaxis of actively beating flagella. The propulsion of the flagellum in a fluid due to a hydrodynamic friction anisotropy is described by resistive-force theory. Using numerical simulations and analytical theory, we show that beating flagella exhibit positive viscotaxis, reorienting themselves toward higher viscosity areas. We quantify this behavior by characterization of the dependence of the rotational velocity on gradient strength, beat amplitude, swimming speed, and wave length. We also examine the effects of asymmetric flagellar wave forms, which imply circular trajectories in the absence of viscosity gradients; here, large asymmetry leads to trochoid-like trajectories perpendicular to the gradient in the form of drifting circles. Flagellar deformability strongly reduce the beat amplitude and the viscotatic response. The viscotatic response is shown to be captured by a universal function of the sperm number.
1 Introduction
Sperm cells move in complex environments to find and reach the egg, such as the female reproductive tract for species with internal fertilization, or open water for species with external fertilization, where both eggs and sperm are released into the bulk fluid. This process poses several key challenges for sperm motion: how do sperm steer? How do they change their swimming direction? How do sperm sense and react to different environmental cues? How do environmental patterns such as flow or viscosity gradients influence their trajectory? These are important issues to be clarified in order to understand how sperm can navigate their tortuous journey towards the egg.1,2For an active steering response, two mechanisms have been proposed:3 an average intrinsic curvature of the flagellum (which leads to a curved or helical trajectory4,5) and higher harmonic-beat frequencies.6 Also, buckling of the flagellum under the load of the propulsion force of the flagellum has been suggested.7 This steering response can be purposefully employed by the cell for spatial orientation, for example in chemical gradients.8–11 This chemotactic behavior is typically controlled by biochemical processes in the cell.
In general, the movement of biological microswimmers, such as sperm, can also be significantly influenced by changes in the physical properties of their environment,12,13 where microswimmers can reorient in external gradients by physical forces exerted on their bodies. Such physical mechanisms – which of course also apply to synthetic microswimmers – include phenomena like rheotaxis,14–16 where microswimmers can swim upstream in flow through microchannels, and gravitaxis,17 where they move against the gravitational field.
We focus here on the much less explored effect of viscotaxis, the motion of microswimmers in viscosity gradients. Several recent theoretical and numerical studies18,19 have demonstrated that various kinds of microswimmers respond to the viscosity gradients, depending on their shape or hydrodynamic propulsion mechanisms. Three-bead model microswimmers have been shown to display positive viscotaxis due to a friction imbalance,18 while squirmers display negative viscotaxis due to enhanced surface-propulsion forces in high-viscosity fluids.19,20 Experimental studies of viscotactic behavior have been performed already in the late 1970s for the prokaryotes Leptospira and Spiroplasma,21,22 and more recently for the green algae Chlamydomonas rheinhardtii using modern microfluidic techniques.23,24 Significant attention has been paid, both theoretically and experimentally, to the behavior at sharp viscosity changes, as they occurs at soft, penetrable interfaces in binary mixtures of two fluids with different viscosities.24–26
In our study, we numerically and theoretically investigate the movement of active eukaryotic flagella, with a snake-like beat pattern, in fluids with spatially varying viscosity. Here, the flagellum is modelled as a semi-flexible filament subject to a traveling bending wave.27 Our explicit modelling of the beating flagellum allows detailed predictions of viscotaxis in terms of the physical properties of the flagellum, such as bending rigidity of the flagellum, average spontaneous curvature, beat frequency, and wave length, as well as the magnitude of the viscosity gradient.
Here, it is interesting to note that the inherent spontaneous curvature of flagella is an important parameter in sperm navigation. Indeed, sperm cells of various species exhibit a range of morphological shapes, which are often not symmetrical. This asymmetry of some sperm cells facilitates directional steering toward favorable environments, e.g. sea urchin sperm have been shown to utilize spontaneous curvature to actively adjust their movement in chemotactic response.3,28,29
Sperm often move along surfaces, as their propulsion and hydrodynamic interactions imply an effective, dynamic attraction to surfaces.30–32 We model this swimming-near-surfaces behavior by considering flagellar motion in two spatial dimensions. Our simulations reveal that individual, symmetrically beating flagella generally exhibit positive viscotaxis, i.e. they reorient to align with a viscosity gradient, moving toward regions with higher viscosity. However, asymmetrically beating flagella, with average spontaneous curvature, can swim at finite angles with the gradient or move in drifting circles perpendicular to the gradient direction. These results are valuable for controlling sperm motion in microfluidic devices.33–37
2 Model and methods
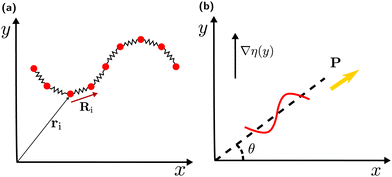
The sperm flagellum is modelled as an actively beating semi-flexible filament in two dimensions, constructed of N beads connected by bonds to form a linear chain, see Fig. 1(a). The structure and dynamics of the flagellum is described by the position vectors ri and velocity vectors vi of each bead. The total force fi acting on each bead includes the bond force, a curvature-elastic force, and a viscous force due to friction with the embedding medium. The dynamics of each bead within the flagellum is then governed by the equation of motion | (1) |
A constant separation between neighboring beads is determined by a harmonic bond potential,
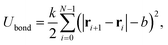 | (2) |
 | (3) |
The local spontaneous curvature Cflag is incorporated by the rotation matrix  in eqn (3), which rotates a vector anti-clockwise by an angle of bCflag. A time-dependent local spontaneous curvature27
in eqn (3), which rotates a vector anti-clockwise by an angle of bCflag. A time-dependent local spontaneous curvature27
Cflag(s,t) = C0 + Ac![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(−ωt + qs) sin(−ωt + qs) | (4) |
In previous studies, it was observed that the beating pattern of bull sperm40 and of human sperm6 can be well approximated by a single beating mode. Thus, the single mode in eqn (4) captures the essential characteristics of the beat motion.
The bending wave propagates along the flagellum, creating backward fluid motion in the embedding viscous medium, and thereby simultaneously propelling the flagellum forward. We do not model the fluid explicitly in our simulations, but employ resistive force theory (RFT) instead. Here, propulsion is facilitated by the fact that a slender object in a viscous fluid with viscosity η experiences unequal friction coefficients ξ‖ and ξ⊥ (both depending linearly on η) for motion tangential and perpendicular to its contour. In the limit of large aspect ratio, the friction anisotropy of a stiff filament is ξ⊥/ξ‖ = 2.41–46 Experimental data for bull sperm5 yields a somewhat smaller value of ξ⊥/ξ‖ = 1.81, which we adopt in our simulations. We apply resistive force theory to each bead in our chain, where the force depends on the local tangent and normal directions of the flagellum, with
fri= − (ξ⊥![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) i i![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) Ti + ξ‖ Ti + ξ‖![[t with combining circumflex]](https://www.rsc.org/images/entities/b_char_0074_0302.gif) i i![[t with combining circumflex]](https://www.rsc.org/images/entities/b_char_0074_0302.gif) Ti)vi, ξ⊥, ξ‖ ∼ η Ti)vi, ξ⊥, ξ‖ ∼ η | (5) |
We employ flagellum length L = Nb and beat period τ as the basic length and time scales in the simulations, respectively. To ensure a realistic representation of sperm flagella, we select parameters that imitate the shape of the natural flagellum beat. A large spring constant kb2 is employed to keep the bond length nearly constant. To ensure that the dominant deformation is bending rather than stretching, we choose κ/L ≪ kb2, typically κ/L = 3.18 × 10−4kb2. A curvature amplitude AcL = 6.28 generates beat amplitudes Ab of about 15% of the flagellum length L. For more details about the parameter selection in the simulations, see (ESI†),39 in particular Table S1. Using these parameters, symmetrically beating flagella propel with constant velocity, as expected.
For small enough beat amplitudes, the velocity is well described by42
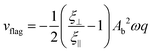 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(−ωt + qx), where Ab is the beat amplitude (see ESI† for details39). In addition, Ac and Ab are related by Ab = λ2Ac/4π2 for small beat amplitudes.
sin(−ωt + qx), where Ab is the beat amplitude (see ESI† for details39). In addition, Ac and Ab are related by Ab = λ2Ac/4π2 for small beat amplitudes.
3 Flagellar motion in viscosity gradients
The main focus of our study is the dynamics of flagellar motion within spatially varying viscosity fields. We model a slowly varying viscosity as a simple linear gradient in viscosity,| η(y) = η0(1 + α(y − ycm)/L), ξ⊥, ξ‖ ∼ η(y), | (7) |
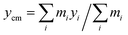 represents the y-coordinate of the center of mass. Here, α is the (dimensionless) viscosity gradient coefficient and α < 1. The spatial variation in viscosity is small on the scale of flagellum length L.
represents the y-coordinate of the center of mass. Here, α is the (dimensionless) viscosity gradient coefficient and α < 1. The spatial variation in viscosity is small on the scale of flagellum length L.
3.1 Symmetric flagellar beat
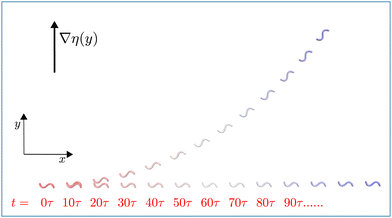 | ||
| Fig. 2 Flagellum motion in viscosity gradient. Superimposed snapshots of a symmetric beating flagellum under stroboscopic illumination demonstrating the progressive motion of the flagellum in viscosity gradient, with α = 0.4, C0 = 0 and AcL = 6.28, compared to the motion without gradient (α = 0.0). Snapshot are separated by 10 beat periods τ. See also Movie M1 (ESI†).39 | ||
To quantify the viscotactic behavior, we study the time dependence of the orientation angle θ(t), which is the angle between the polarity vector (swimming direction) P and the positive x-axis, as shown in Fig. 1(b). For a flagellum, which is initiated to swim in the positive x-direction, perpendicular to the gradient, i.e. θ(0) = 0, the orientation angle (averaged over the periodic oscillations due to beating) increases roughly linearly in time – until it saturates at θ = π/2 for very long times (see Fig. S2(a) in ESI†).39 We define the rate of reorientation (or angular velocity) Ω(θ,α) = dθ/dt. The orientation rate Ω increases with increasing viscosity gradient α (see Fig. S2(b) in ESI†),39 as expected.
Symmetry dictates that Ω(θ,α) must be an odd function in α and a 2π-periodic even function in θ—mirror symmetry to the gradient (sperm facing “left” or “right” of the gradient both rotate towards the gradient) implies Ω(θ) = −Ω(π–θ)—hence Ω(θ,α) can be expressed as a cosine expansion, i.e.,
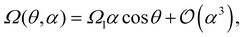 | (8) |
 | ||
| Fig. 3 Quantifying visotactic behavior. Rotational velocity Ω(θ) as a function of orientation angle θ for various viscosity gradients α. Solid points are the simulation data, dashed lines are fits to eqn (8). The single fit parameter Ω1τ = 0.02196 is the viscotactic response coefficient. Error bars are smaller than the symbol size. | ||
3.2 Viscotaxis mechanism and analytical estimate of reorientation rate
We conjecture that the main underlying mechanism for reorientation in viscotaxis is the drag imbalance of the high- and low-viscosity sides of the swimming flagellum, as illustrated in Fig. 4. This imbalance in forces results in a torque, causing the flagellum to rotate. To calculate this torque analytically, we imagine the beating filament as its sinusoidal shape traveling at constant speed v. This calculation is performed in a body-fixed reference frame, denoted by (x′,y′), where the x′-axis is the long axis of the flagellum. In this reference frame, the viscosity gradient appears with a tilt angle θ, which results in a reduced viscosity difference between the two sides of the flagellum in the body-fixed y′-direction, i.e. an effective gradient coefficient α′ = α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ). The drag forces acting on the flagellum dependent on the local viscosity, and are dominated by ξ‖ for small beating amplitudes, as the motion through the fluid is such that the local tangent is essentially always almost parallel to velocity vector and thus to the x′-axis. The torque around the center of mass then reads
cos(θ). The drag forces acting on the flagellum dependent on the local viscosity, and are dominated by ξ‖ for small beating amplitudes, as the motion through the fluid is such that the local tangent is essentially always almost parallel to velocity vector and thus to the x′-axis. The torque around the center of mass then reads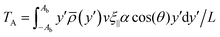 | (9) |
 | (10) |
Combining eqn (9) and (10), we obtain
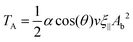 | (11) |
This torque is balanced by the viscous rotational drag ξR,FΩ of the flagellum. For small beat amplitudes, the rotational drag coefficient of the flagellum is approximately equal to that of a rod of the same length, ξR,rod = ξ⊥L3/12. It is important to note that as long as the pivot point for the rotation is the geometric midpoint of the flagellum, the rotational drag is not affected by the viscosity gradient, as the increased friction on one half is exactly balanced by the reduced friction on the other half. However, the pivot point shifts toward the higher viscosity side, by a distance proportional to α. Therefore, gradient effects contribute only to the higher-order terms in α, which are not considered here. By generalizing the Gray–Hancock calculation to the case of a viscosity gradient along the flagellar swimming (x′) direction, we can also show analytically that gradient contributions cancel out, so that the swimming speed v in eqn (11) is independent of α. Moreover, if the polarity vector P (swim direction) is not perpendicular to the gradient, but is inclined at an angle θ, then it is the projection of mass distribution onto the axis perpendicular to the gradient direction (∇η)/η0 which is relevant. The balance of these two torques finally results in (see ESI† for details39)
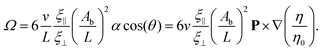 | (12) |
The approximation of the rotational drag coefficient ξR of the flagellum by ξrod of a stiff rod can be improved for larger beat amplitudes Ab by a correction factor for the rotational drag coefficients ξR,rod/ξR,F, which is obtained directly from simulations. We calculate the rotational torque for a simulated configuration to obtain an angular velocity Ω, and relate it to the rotational friction as
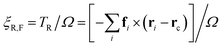 | (13) |
Finally, this is averaged over one beat period, 〈ξR,F〉τ. The rotational friction coefficient ξR,F is smaller than ξR,rod, because the beating flagellum is less extended, and some parts have orientational components parallel to the rotational velocity. Thus, for further analysis and quantitative comparison with simulation data, we use a modified form of Ω with an additional factor ξR,rod/ξR,F, i.e.,
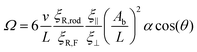 | (14) |
This rotational velocity is influenced by three key factors: (i) the magnitude of the viscosity gradient α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ) ∝ ∇η, as already shown above to nicely agree with the simulations, (ii) the beat amplitude Ab, and (iii) via the velocity, on the wavelength λ.
cos(θ) ∝ ∇η, as already shown above to nicely agree with the simulations, (ii) the beat amplitude Ab, and (iii) via the velocity, on the wavelength λ.
In order to test the validity and accuracy of our analytical prediction (14) for Ω, we compare it with simulation data. We consider first the dependence of Ω1 on the beat amplitude Ab, while keeping all other parameters constant. Taking into account that the velocity depends quadratically on Ab and inversely on wavelength λ, see eqn (6), the rotational velocity (14) is expected to scale as
| Ω1τ ∼ ωτ(Ab/L)4L/λ. | (15) |
The simulations results (see Fig. 5(a) and Fig. S3 in ESI†)39 demonstrate that indeed Ω ∼ Ab4. Thus, viscotaxis is predicted to display a very pronounced dependence on the beat amplitude.
Fig. 5 illustrates the dependence of the reorientation rate Ω1 on the flagellar length L. Here, the flagellar length is varied for constant wavelength λ. For L > λ (L < λ) there is more (less) than a single wave on the flagellum. The comparison in Fig. 5(a) demonstrates that there is in general good agreement between the analytical results (14) and simulation for L > λ. For L < λ, the observed deviations can be attributed to the assumptions inherent during the derivation of the analytical model; in this regime, the flagellar shape is no longer a travelling sine wave, but rather a short rod-like filament oriented in the swimming direction, which bends left and right periodically. This dependence of Ω1 on L/λ can be seen more clearly in Fig. 5(b). For L/λ > 1, the decrease of Ω1 with increasing L is due to the increasing rotational drag ξR,F ∝ L3, as described by eqn (14). For L/λ < 1, swimming is impaired due to the absence of a travelling wave, as explained above, so that Ω1 → 0 for L/λ → 0. This implies that the wave length for optimal viscotasis is λ ≃ L, as confirmed by the simulation results in Fig. 5(b).
3.3 Asymmetric flagellar beat
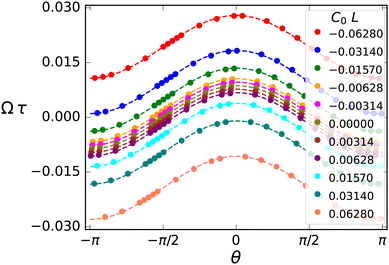
We examine the effect of beat asymmetry on the viscotactic response. The simulation results in Fig. 6 illustrate that the rotational velocity curve Ω(θ) is shifted upwards or downwards for C0L < 0 or C0L > 0, respectively. Therefore, the total rotational velocity Ω can be described as a superposition of the contributions from C0 and  ,
,
Ω = Ω0 + Ω1α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ). cos(θ). | (16) |
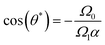 | (17) |
 | ||
| Fig. 8 Phase diagram of trajectory types. Regions of linear and trochoid-like trajectories in a parameter space defined by dimensionless quantities |Ω0|L/v and |Ω1α|L/v. The separatrix |Ω0|/|Ω1α| = 1, as indicated by the black dashed line, separates the two distinct regimes. For |Ω0|/|Ω1α| > 1 the system exhibits trochoid-like47 motion, while for |Ω0|/|Ω1α| < 1 the system remains stationary. | ||
To illustrate this behavior, we select two curves from Fig. 6, with two spontaneous curvatures C0L = − 0.0157 with Ω0 < Ω1α and two fixed points, and C0L = −0.0628 with (Ω0 > Ω1α) and no fixed point. The corresponding trajectories are shown in Fig. 9. At the stable fixed point, cos(θ*) = −Ω0/Ω1α, the two curvature mechanisms oppose each other, and the flagellum moves on an asymptotically straight trajectory with inclination θ*. For large Ω0, the spontaneous curvature dominates, and a trochoid-like trajectory emerges, with drifting circular motion perpendicular to the gradient.
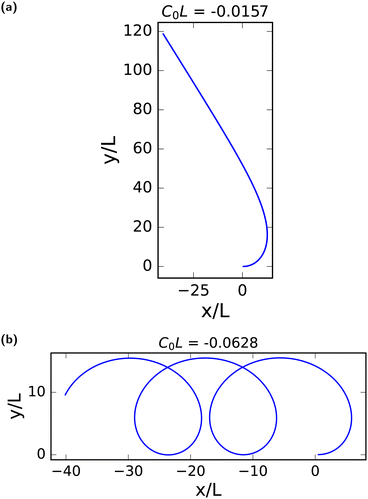 | ||
| Fig. 9 Trajectory of flagella with spontaneous curvature. Trajectory for the center of mass of beating flagella with average spontaneous curvature (a) C0L = −0.0157 with a stable fixed point, moving on an asymptotically straight trajectory, and (b) C0L = −0.0628 with no fixed point, showing period motion on a trochoid-like47 trajectory. In both cases, α = 0.4. See also Movies M2 and M3 (ESI†).39 | ||
The dynamics described by eqn (16) is the motion of a self-propelled particle (SPP) in the non-thermal limit, with constant speed v and a propulsion direction e(t), which in polar coordinates is e = (cos(θ),sin(θ)) with inclination angle θ. Under the effect of a redirectional torque, the orientational motion of this particle is governed by
![[small theta, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a7.gif) = Ω0 + Ω1α = Ω0 + Ω1α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ) cos(θ) | (18) |
The particle position r(t) is then obtained from the equation of motion
| ṙ(t) = ve(t) | (19) |
The trochoid-like motion is a periodic motion, compare Fig. 9(b), with time period ΔT. The pitch, denoted as P, defined in analogy with the pitch of a helix, is the distance between two equivalent points on the periodic trajectory along the drift direction. It is calculated over one complete cycle or one time period, from θ = 0 to 2π, i.e.,
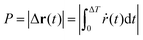 | (20) |
The time period ΔT of each cycle can be calculated from eqn (18) as
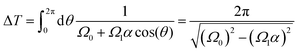 | (21) |
To quantify the pitch, we employ perturbation theory, with expansion parameter ε = Ω1α/Ω0, which measures the deviation from purely circular motion. Thus, we study the equation
 | (22) |
 | (23) |
The solution θ1(t) = sin(Ω0t) is used to calculate the translational drift
 | (24) |
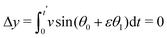 | (25) |
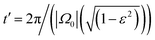 . This results demonstrates two important features of the trochoid-like motion: (i) there is no drift along the y-axis, which shows that the particle always drifts perpendicular to the gradient direction, and (ii) the resulting pitch is P = −vπε/|Ω0| = −αvπΩ1/(Ω0|Ω0|).
. This results demonstrates two important features of the trochoid-like motion: (i) there is no drift along the y-axis, which shows that the particle always drifts perpendicular to the gradient direction, and (ii) the resulting pitch is P = −vπε/|Ω0| = −αvπΩ1/(Ω0|Ω0|).
Note that the α → −α inversion symmetry implies that Δx, Δy, and P are odd functions of α. Therefore next-leading terms in eqn (24) and (25), and in the pitch, are of order  .
.
We can generalize this solution for the pitch by combining the first-order perturbation theory with the observation that the pitch must diverge for Ω1α → Ω0, and vanishes for Ω1α = 0, Ω0 ≠ 0, which results in the approximation
 | (26) |
To investigate the quality of this analytical approximation, we compare it with the simulation results, as shown in Fig. 10. The agreement is quite satisfactory over the whole accessible range of Ω1α/Ω0 values.
3.4 Effect of flagellar elasticity on viscotaxis
A flagellum is not a rigid object, but has a finite elasticity and deformability. The elasto-dynamics of a flexible filament can be conveniently characterized by a single dimensionless parameter, the sperm number Sp,48,49| Sp4 = Tv/τ = L4ξ⊥ω/κ, | (27) |
The effect of flagellar deformability has been studied previously for end-actuated flexible filaments44,49,50 and for trypanosome parasites.51 However, these cases are more complicated, either due to the highly inhomogeneous wave form, or the large deformable body attached to the flagellum. Some numerical results are also available for sperm.50
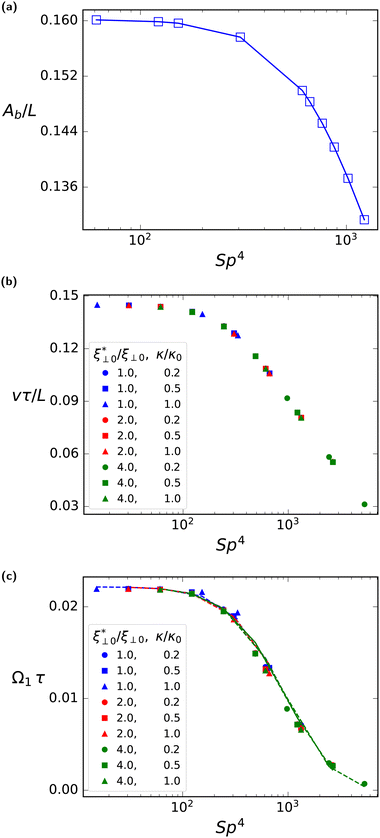
In order to investigate the dependence of the rotational velocity on the activity-induced deformations of the flagellum, we study the relation between the rotational velocity Ω1 and the sperm number Sp by variation of the beat frequency ω for several combinations of bending rigidity κ and perpendicular friction coefficient ξ⊥. In the limit of Sp → 0, rigidity dominates, and the shape of the flagellum follows exactly the prescribed curvature pattern, whereas at large Sp, viscosity dominates, resulting in additional deformations of the filament.
These additional deformations of the filament change the effective beating amplitude of the flagellum. In order to predict this dependence, we employ the curvature energy for the flexible worm-like filament as a function of its conformation,52
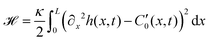 | (28) |
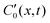 denotes the local spontaneous curvature, where a non-zero value means the filament would spontaneously relax to
denotes the local spontaneous curvature, where a non-zero value means the filament would spontaneously relax to  , which is a minimum-energy state. The local spontaneous curvature has the same role as described in eqn (4). We ignore contributions from boundary terms, as they do not influence the subsequent physics. The dynamics of the filament is then governed by the local viscous drag and bending force, derived from eqn (28), and is described by the equation of motion
, which is a minimum-energy state. The local spontaneous curvature has the same role as described in eqn (4). We ignore contributions from boundary terms, as they do not influence the subsequent physics. The dynamics of the filament is then governed by the local viscous drag and bending force, derived from eqn (28), and is described by the equation of motion | (29) |
To solve eqn (29) with a travelling spontaneous-curvature wave,  , we use a travelling-wave ansatz also for the deflection, h(x,t) = h0ei(qx−ωt), where h0 = |h0|eiϕ represents the (complex) beating amplitude. This implies
, we use a travelling-wave ansatz also for the deflection, h(x,t) = h0ei(qx−ωt), where h0 = |h0|eiϕ represents the (complex) beating amplitude. This implies
ξ⊥iωh0 = κ(q4h0 + q2![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) 0) 0) | (30) |
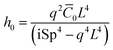 | (31) |
Therefore, the beating amplitude for the beating flagellum is
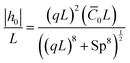 | (32) |
Eqn (32) shows that the beating amplitude increases linearly with ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) 0L and decreases monotonically as a function of Sp4. In the limit of small sperm number (Sp → 0), |h0|/L = π2λ
0L and decreases monotonically as a function of Sp4. In the limit of small sperm number (Sp → 0), |h0|/L = π2λ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) 0L/4. A strong decrease of the beat amplitude with increasing Sp, as predicted by eqn (32), is indeed observed in the simulations, see Fig. 11(a). From eqn (31), we can also extract the phase-lag ϕ of the beat wave relative to the spontaneous curvature wave,
0L/4. A strong decrease of the beat amplitude with increasing Sp, as predicted by eqn (32), is indeed observed in the simulations, see Fig. 11(a). From eqn (31), we can also extract the phase-lag ϕ of the beat wave relative to the spontaneous curvature wave,
 | (33) |
This implies that ϕ = 0 for Sp → 0, i.e. the beat and spontaneous-curvature waves are in phase, while 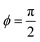 for Sp → ∞, i.e. the two waves have the maximum phase shift.
for Sp → ∞, i.e. the two waves have the maximum phase shift.
The reduction of beat amplitude with increasing Sp implies a qualitatively similar behavior for the swimming speed, as indicated by the low-amplitude approximation42v ∼ Ab2, compare eqn (6). This is well confirmed by our simulation results for α = 0.0, (Fig. 11(b)), in qualitative agreement with the earlier numerical results for sperm.50
Furthermore, the analytical dependence of beating amplitude on Sp4, eqn (32), can be combined with the swimming speed as a function of Sp4, to theoretically predict (by employing eqn (14)) the viscotactic response coefficient Ω1 as a function of Sp4. The simulation results in Fig. 11(c) show that Ω1τ for various beat frequencies ω and friction coefficients ξ⊥ all fall onto a single master curve, which is described by a universal scaling function Γ, with
| Ω1τ = Γ(Sp4). | (34) |
Note that the existence of a master curve already follows from a simple dimensional analysis, as the sperm number Sp is the only dimensionless combination of the parameters ω, κ, ξ⊥, and L.
Moreover, the simulation results closely match the analytical result for the shape of the master curve, see Fig. 11(b). In addition, Ω1τ is found to approach a finite value in the limit Sp → 0, achieved by decreasing the beat frequency ω → 0. This is a non-trivial limit, because the rotation frequency vanishes, while the beat period diverges. The fact that the product Ωτ remains finite indicates that the rotation of the flagella does not require a dynamic deformation of the flagellum, i.e. the rotational motion is not a consequence of changes in the shape during its beating motion, but due to the friction asymmetry discussed in Section 3.2 above, see eqn (12).
The reduced viscotatic response of the flagellum due to elasticity and deformability is mainly due to a decreasing beat amplitude, which leads to a decreasing friction asymmetry and also a reduced propulsion speed (Gray and Hancock estimate v/ω ∼ Ab2). The combined effect on the viscotactic response is very pronounced due to the strong dependence Ω1 ∼ Ab4 on the beat amplitude, compare eqn (15). This effect also manifests itself in the angular dependence of the rotation rate Ω(θ) in Fig. 12, where the magnitude of Ω decreases both at the minima and maxima – in contrast to the case of spontaneous curvature, where the whole Ω(θ) curve shifts upwards. This implies that for elastic flagella, motion perpendicular to the gradient in either direction implies a slower reorientation in the gradient direction due to deformability.
 | ||
| Fig. 12 Rotational velocity vs. orientation. Rotational velocity Ωτ as a function of orientation θ at different Sp4 for C0L = 0 and α = 0.4. | ||
The deformability of the flagellum also affects rotational friction coefficient ξR. The results (see Fig. S4 in ESI†)39 show that ξR,F increases with increasing flexibility. This contributes to the decrease of Ω1, because Ω1 ∼ 1/ξR,F, compare eqn (14). In analogy with the rotational friction of a stiff rod, ξR,rod ∼ L3, we can attribute the increase of ξR,F to an increment of the projected length, i.e. ξR,F ∼ Leff3, where Leff is end-to-end length of the flagellum due to its deformation. Of course, the increases of the projected length of the flagellum and the decrease of the beat amplitude are geometrically related for fixed contour length of the flagellum, with L − Leff = π2(Ab/L)2 for λ = L to leading order in Ab/L (see ESI† for details39).
4 Discussion and conclusions
We have studied the viscotactic behavior of flagella by simulating semi-flexible filaments with an active bending wave in two spatial dimensions. Our theoretical and simulation study focuses on the motion of the flagellum in an environment with a linear viscosity gradient. The flagellum is found to reorient toward regions of higher viscosity, where the rotational velocity increases for steeper gradients. We derive an approximate analytical expression for the reorientation rate, which matches our simulation data very well. Additionally, flagella with asymmetric beat determined by an average spontaneous curvature exhibit enhanced viscotaxis. For strong spontaneous curvature, positive viscotaxis is replaced by a trochoid-like drift motion perpendicular to the gradient direction. Flagellar deformability, characterized by the dimensionless sperm number Sp, is found to reduce the beat amplitude, swimming speed, and the viscotactic response.It is now of course interesting to see which threshold viscosity gradient indices α* = Ω0/Ω1, which correspond to the boundary between linear (positive viscotaxis) and trochoid (neutral viscotaxis) trajectories in Fig. 8, are predicted for sperm of various species – under the assumption that our flagella results provide reasonable estimates for sperm. Experimental characteristics and resulting estimates are collected in Table 1. These numbers imply the following conclusions and speculations: (i) for circling sperm (bull, sea urchin), the threshold viscosity coefficient α* is quite large, so that large viscosity gradients are required to induce positive viscotaxis; it is therefore unlikely that viscotaxis plays a significant role in fertilization. In fact, it is known that for sea urchin the circling is intimately connected to the sensing of chemotactic gradients. (ii) In contrast, for human sperm, the threshold viscosity coefficient α* is small, so that already small viscosity gradients can have a significant effect on guiding the sperm motion. Note, however, that human sperm is also spinning around its long axis, which makes the behavior more complex. (iii) It is tempting to speculate that the likely trochoid motion of circling sperm might also play a role in fertilization, as it might prevent positive viscotaxis, and rather make sperm to move “side-wise” in a viscosity gradient, thereby avoiding regions of high viscosity where they may get stuck. In fact, this avoidance effect of high-viscosity regions of trochoid motion may also be an interesting design criterion for microbots.13
| L/μm | v 0/(μm s−1) | η/ηw (20 °C) | A b/L | Ω 0 L/v0 | Ω 1 L/v0 | α* = Ω0/Ω1 | Ref. | |
|---|---|---|---|---|---|---|---|---|
| Bull | ||||||||
| In water (36 °C) | 60 | 117 | 0.7 | 0.34 | 1.59 | 0.385 | 4.2 | 5 and 53 |
| In Ficoll 400 | 60 | 43 | 10 | 0.27 | 0.84 | 0.242 | 3.5 | |
| Sea urchin | ||||||||
| In water | 50 | 200 | 1.0 | 0.2 | 1.5 | 0.133 | 11.3 | 54 and 55 |
| Human | ||||||||
| In water (36 °C) | 50 | 62 | 0.7 | 0.13 | 0–0.05 | 0.056 | 0–0.9 | 7 and 56 |
An important aspect of low-Reynold-number hydrodynamics and overdamped dynamics in a viscous environment is the time reversibility of motion. This may not seem to be the case in viscotaxis – as swimming up-gradient turns in to swimming down-gradient upon time reversal or inversion of swimming direction. However, a closer look reveals that there is no contradiction, as some time is required for flagella to reorient from arbitrary initial condition and to turn up-gradient. Mathematically, this is reflected in the invariance of eqn (8) under time reversal. We denote time-inverted variables with a prime. Under time reversal, velocity is inverted, i.e. θ′ = θ + π, and Ω′ = −Ω. Then, it follows from eqn (8) that −Ω′ = −Ω1α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ′ − π) = −Ω1α
cos(θ′ − π) = −Ω1α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ′), i.e. Ω′ = Ω1α
cos(θ′), i.e. Ω′ = Ω1α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ′).
cos(θ′).
It is important to note that the viscosity gradient and the local viscosity is kept constant in our study. This is of course not possible in a real system, when the flagellum shows positive viscotaxis. In a real system, with constant viscosity gradient ∂yη and initial conditions corresponding to the “positive viscotaxis” region of the phase diagram of Fig. 8, the flagellum moves to regions of higher viscosity, which implies that α = L(∂yη)/η in eqn (12) decreases along the trajectory, until it reaches θ = 0 (or θ = π) and moves perpendicular to the gradient. This happens when the separatrix in Fig. 8 – equivalent to the condition α = |Ω0/Ω1| – is reached. This uniquely determines the asymptotic y*-position given implicitly through
| η(y*) = L(∂yη)|Ω1/Ω0|. | (35) |
This implies, in particular, that for deep penetration into a region of higher viscosity, it is advantageous to have a small Ω0, i.e. a small spontaneous curvature and an nearly symmetrical beat.
This study can be extended in several directions. First, sperm has not only a flagellum but also a head, which adds a frictional load to the flagellar propulsion. This affects the motion in a viscosity gradient in several ways. As the head reduces the beat amplitude in the front part of the flagellum, the amplitude increases from front to tail. Also, pushing the head down-gradient becomes easier than up-gradient (compare ref. 18). Preliminary simulation results show that negative viscotaxis becomes indeed possible in such a case. More studies are required to characterize this behavior in detail. Second, sperm move in the vicinity of surfaces, which is one of the motivation for our modelling in two spatial dimensions. However, motion in two spatial dimensions of course cannot capture all relevant effects of swimming near surfaces, where the head is typically close to the wall and the beating plane can assume various orientations with respect the wall.4 Third, most biological fluid are not Newtonian, but often highly viscoelastic. For example shear-thinning could have a significant effect on viscotaxis, as it can modify the local viscosity gradient. Forth, sperm (and many microswimmers) often swim near surfaces, but of course not always. Therefore, it would be very interesting to investigate and characterize the motion in linear viscosity gradients in three dimensions. This case is significantly more complex compared to viscotaxis in two dimensions, as the behavior now depends on the orientation of the beating plane relative to the viscosity-gradient direction. Finally, it would be important to study sperm motion in more complex viscosity landscapes.
Author contributions
G. G. and J. E. designed the research project. S. A. performed the simulations and analysed the obtained data. All authors performed analytic calculations, participated in the discussions and writing of the manuscript.Data availability
All data are available on zenodo, DOI: 10.5281/zenodo.14059510.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We gratefully acknowledge funding from the ETN PHYMOT (“Physics of Microbial Motility”) within the European Union's Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement no 955910. We also acknowledge a computing time grant on the supercomputer JURECA at the Jülich Supercomputer Centre.Notes and references
- L. Alvarez, B. M. Friedrich, G. Gompper and U. B. Kaupp, Trends Cell Biol., 2014, 24, 198–207 CrossRef CAS PubMed.
- K. Miki and D. E. Clapham, Curr. Biol., 2013, 23, 443–452 CrossRef CAS PubMed.
- A. Gong, S. Rode, U. B. Kaupp, G. Gompper, J. Elgeti, B. M. Friedrich and L. Alvarez, Philos. Trans. R. Soc., B, 2020, 375, 20190149 CAS.
- J. Elgeti, U. B. Kaupp and G. Gompper, Biophys. J., 2010, 99, 1018–1026 CrossRef CAS PubMed.
- B. M. Friedrich, I. H. Riedel-Kruse, J. Howard and F. Jülicher, J. Exp. Biol., 2010, 213, 1226–1234 CrossRef CAS PubMed.
- G. Saggiorato, L. Alvarez, J. F. Jikeli, U. B. Kaupp, G. Gompper and J. Elgeti, Nat. Commun., 2017, 8, 1–9 CrossRef CAS PubMed.
- D. J. Smith, E. Gaffney, H. Gadêlha, N. Kapur and J. Kirkman-Brown, Cytoskeleton, 2009, 66, 220–236 CrossRef CAS PubMed.
- M. Yoshida, Y. Hiradate, N. Sensui, J. Cosson and M. Morisawa, Biol. Bull., 2013, 224, 156–165 CAS.
- J. F. Jikeli, L. Alvarez, B. M. Friedrich, L. G. Wilson, R. Pascal, R. Colin, M. Pichlo, A. Rennhack, C. Brenker and U. B. Kaupp, Nat. Commun., 2015, 6, 7985 CAS.
- T. Strünker, L. Alvarez and U. Kaupp, Curr. Opin. Neurobiol., 2015, 34, 110–116 Search PubMed.
- Y. Hong, N. M. Blackman, N. D. Kopp, A. Sen and D. Velegol, Phys. Rev. Lett., 2007, 99, 178103 Search PubMed.
- J. Elgeti, R. G. Winkler and G. Gompper, Rep. Prog. Phys., 2015, 78, 056601 CrossRef CAS PubMed.
- G. Gompper, H. A. Stone, C. Kurzthaler, D. Saintillan, F. Peruani, D. A. Fedosov, T. Auth, C. Cottin-Bizonne, C. Ybert, E. Clément, T. Darnige, A. Lindner, R. E. Goldstein, B. Liebchen, J. Binysh, A. Souslov, L. Isa, R. di Leonardo, G. Frangipane, H. Gu, B. J. Nelson, F. Brauns, M. C. Marchetti, F. Cichos, V.-L. Heuthe, C. Bechinger, A. Korman, O. Feinerman, A. Cavagna, I. Giardina, H. Jeckel and K. Drescher, J. Phys.: Condens. Matter, 2025, 37, 143501 CrossRef CAS PubMed.
- A. Zöttl and H. Stark, Phys. Rev. Lett., 2012, 108, 218104 CrossRef PubMed.
- Marcos, H. Fu, T. Powers and R. Stocker, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 4780–4785 CrossRef CAS PubMed.
- K. Qi, H. Annepu, G. Gompper and R. G. Winkler, Phys. Rev. Res., 2020, 2, 033275 CrossRef CAS.
- B. ten Hagen, F. Kümmel, R. Wittkowski, D. Takagi, H. Löwen and C. Bechinger, Nat. Commun., 2014, 5, 4829 CrossRef CAS PubMed.
- B. Liebchen, P. Monderkamp, B. Ten Hagen and H. Löwen, Phys. Rev. Lett., 2018, 120, 208002 CrossRef CAS PubMed.
- V. A. Shaik and G. J. Elfring, Phys. Rev. Fluids, 2021, 6, 103103 CrossRef.
- C. Datt and G. J. Elfring, Phys. Rev. Lett., 2019, 123, 158006 CrossRef CAS PubMed.
- G. Kaiser and R. Doetsch, Nature, 1975, 255, 656 CrossRef CAS PubMed.
- M. J. Daniels, J. M. Longland and J. Gilbart, J. Gen. Microbiol., 1980, 118, 429–436 CAS.
- M. R. Stehnach, N. Waisbord, D. M. Walkama and J. S. Guasto, Nat. Phys., 2021, 17, 926–930 Search PubMed.
- S. Coppola and V. Kantsler, Sci. Rep., 2021, 11, 399 Search PubMed.
- C. Feng, J. J. Molina, M. S. Turner and R. Yamamoto, Phys. Rev. Res., 2022, 4, 043202 Search PubMed.
- J. Gong, V. A. Shaik and G. J. Elfring, Sci. Rep., 2023, 13, 596 Search PubMed.
- Y. Yang, J. Elgeti and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 061903 CrossRef PubMed.
- B. M. Friedrich and F. Jülicher, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 13256–13261 CrossRef CAS PubMed.
- B. Friedrich and F. Jülicher, New J. Phys., 2008, 10, 123025 CrossRef.
- A. P. Berke, L. Turner, H. C. Berg and E. Lauga, Phys. Rev. Lett., 2008, 101, 038102 CrossRef PubMed.
- J. Elgeti and G. Gompper, EPL, 2009, 85, 38002 CrossRef.
- J. Elgeti and G. Gompper, Eur. Phys. J.: Spec. Top., 2016, 225, 2333–2352 Search PubMed.
- V. Kantsler, J. Dunkel, M. Polin and R. E. Goldstein, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 1187–1192 CrossRef CAS PubMed.
- P. Denissenko, V. Kantsler, D. J. Smith and J. Kirkman-Brown, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 8007–8010 CrossRef CAS PubMed.
- R. Nosrati, P. J. Graham and D. Sinton, MNF 2014, 2014, p. 181 Search PubMed.
- R. Nosrati, P. J. Graham, Q. Liu and D. Sinton, Sci. Rep., 2016, 6, 26669 CrossRef CAS PubMed.
- S. Rode, J. Elgeti and G. Gompper, New J. Phys., 2019, 21, 013016 CrossRef.
- R. E. Isele-Holder, J. Jäger, G. Saggiorato, J. Elgeti and G. Gompper, Soft Matter, 2016, 12, 8495–8505 RSC.
- URL_will_be_inserted_by_publisher.
- I. H. Riedel-Kruse, A. Hilfinger, J. Howard and F. Jülicher, HFSP J., 2007, 1, 192–208 CrossRef PubMed.
- C. Brennen and H. Winet, Annu. Rev. Fluid Mech., 1977, 9, 339–398 CrossRef.
- J. Gray and G. Hancock, J. Exp. Biol., 1955, 32, 802–814 CrossRef.
- S. Lighthill, SIAM Rev., 1976, 18, 161–230 CrossRef.
- T. S. Yu, E. Lauga and A. Hosoi, Phys. Fluids, 2006, 18, 091701 CrossRef.
- E. Lauga and T. R. Powers, Rep. Prog. Phys., 2009, 72, 096601 Search PubMed.
- R. Johnson and C. Brokaw, Biophys. J., 1979, 25, 113–127 CrossRef CAS PubMed.
- In geometry, a trochoid (from Greek trochos ‘wheel’) is a roulette curve formed by a circle rolling along a line. It is the curve traced out by a point fixed to a circle (where the point may be on, inside, or outside the circle) as it rolls along a straight line, see https://en.wikipedia.org/wiki/Trochoid.
- K. Machin, J. Exp. Biol., 1958, 35, 796–806 CrossRef.
- E. Lauga, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 041916 CrossRef PubMed.
- C. P. Lowe, Philos. Trans. R. Soc., B, 2003, 358, 1543–1550 CrossRef PubMed.
- D. Alizadehrad, T. Krüger, M. Engstler and H. Stark, PLoS Comput. Biol., 2015, 11, e1003967 CrossRef PubMed.
- M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Clarendon Press, Oxford, 1986 Search PubMed.
- R. Rikmenspoel, J. Exp. Biol., 1984, 108, 205–230 CrossRef CAS PubMed.
- M. Böhmer, Q. Van, I. Weyand, V. Hagen, M. Beyermann, M. Matsumoto, M. Hoshi, E. Hildebrand and U. B. Kaupp, EMBO J., 2005, 24, 2741–2752 CrossRef PubMed.
- D. Woolley and G. Vernon, J. Exp. Biol., 2001, 204, 1333–1345 CrossRef CAS PubMed.
- J. A. Mossman, J. T. Pearson, H. D. Moore and A. A. Pacey, Hum. Reprod., 2013, 28, 22–32 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Model parameters, validation of simulation code, details of analytical calculations, and movie captions. See DOI: https://doi.org/10.1039/d4sm01328j |
| This journal is © The Royal Society of Chemistry 2025 |