Open Access Article
Open Access ArticleOptothermally induced active and chiral motion of colloidal structures†
Rahul
Chand
*,
Ashutosh
Shukla
,
Sneha
Boby
and
G. V. Pavan
Kumar
 *
*
Department of Physics, Indian Institute of Science Education and Research (IISER) Pune, Pune, 411008, India. E-mail: rahul.chand@students.iiserpune.ac.in; pavan@iiserpune.ac.in
First published on 5th May 2025
Abstract
Artificial soft matter systems have proven to be important tools to harness mechanical motion for microscale manipulation. Typically, this motion is driven either by external fields or by mutual interactions between the colloids. In the latter scenario, dynamics arise from non-reciprocal interactions among colloids within a chemical environment. In contrast, we eliminate the need for a chemical environment by utilizing a large area of optical illumination to generate thermal fields. The resulting optothermal interactions introduce non-reciprocity to the system, enabling active motion of the colloidal structure. Our approach involves two types of colloids: passive and thermally active. The thermally active colloids contain absorbing elements that capture energy from the incident optical beam, creating localized thermal fields around them. In a suspension of these colloids, the thermal gradients generated drive nearby particles through attractive thermo-osmotic forces. We investigate the resulting dynamics, which lead to various swimming modes, including active propulsion and chiral motion. We have also simulated the dynamics of the colloidal structures by solving the coupled Langevin equations to gain insight into the emerging motion. By exploring the interplay between optical forces, thermal effects, and particle interactions, we aim to gain insights into controlling colloidal behavior in non-equilibrium systems. This research has significant implications for directed self-assembly, microfluidic manipulation, and the study of active matter.
Introduction
Out-of-equilibrium soft matter systems display a range of complex behaviors including active propulsion,1–12 self-organization,13–15 and other emergent dynamics.16–20 These phenomena arise as a result of the mutual interaction between the individual element and external stimuli.21,22 Artificial synthetic colloidal systems provide a controlled test bed for studying this behavior.23 Various external fields such as optical,24–32 chemical,28,29,33 electrical34–38 and magnetic fields37–40 are commonly used as manipulation techniques. Most of the studies are based on inherently asymmetric systems where the structural or compositional asymmetry induces force imbalance leading to the active motion of the structure.25,41–48In contrast, researchers have proposed the use of symmetrical colloids with different chemical reactivities to enable active motion without inherent asymmetry.49–54 In these cases, the dynamics of the colloidal structures are powered by non-reciprocal interactions. However, these methods require chemical environments such as hydrogen peroxide49 or water–lutidine mixtures.50,51 Such requirements restrict the usability of these platforms.
Regarding this, some recent studies have shown that in an aqueous medium, colloidal particles can be dragged to the heat center by the thermo-osmotic slip flow produced by it.55–57 One can utilize this process to harness non-reciprocal attractive interactions without any chemical environment. In systems with absorbing and non-absorbing colloids, these interactions induce imbalance and drive the motion.58 Recently, we have reported the directional motion obtained through such thermo-osmotic interactions in various optical confinements (such as Gaussian, line, and ring beam).58,59 The interaction between the absorbing and non-absorbing colloids fuels the dynamics. However, the induction of similar dynamics in an unconfined environment is yet to be explored in detail. These may have widespread applications in areas such as directed self-assembly,60 microfluidic manipulation,61–64 and the exploration of non-equilibrium processes in active matter.65
Motivated by this, in this article, we experimentally investigated the dynamics of colloidal structures made of absorbing thermally active (A) and non-absorbing passive (P) colloids under broad-area optical illumination (see Fig. 1(a)). In a suitable large area, with uniform optical illumination, the gradient optical forces are insignificant and the optical field only enables selective heating of the colloidal particles depending on their absorbing characteristics. Thus, such illumination generates temperature gradients without any confinement potential. We examine how these temperature gradients affect particle motion and interactions, leading to different swimming modes (see Fig. 1(b)). Our simulation results support these findings. In our study, we used the optically generated thermal field instead of its chemical counterpart because it is measurable and controllable as a result of various recent advancements.66 In addition, optothermal interactions provide promising applications for micromanipulation and self-assembly in various other emergent phenomena.67–71
Experimental method
The colloidal particles used in our experiment are melamine formaldehyde (MF) colloids of diameter 2 μm as passive (P) colloids and nano-particulate iron–oxide infused polystyrene (PS) colloids of diameter 1.3 μm as thermally active (A) colloids. These colloids are obtained from microParticles GmbH. The calculated absorption and scattering cross-sections of these colloidal particles are shown in Supplementary information 1 (ESI†). We used a dilute aqueous suspension of these colloids in our sample cell. As shown in Fig. 2(a), a dual-channel optical microscopy setup is used for the experiments. A 532 nm continuous-wave Gaussian laser beam was coupled to the sample plane using a 50×, 0.5 NA objective lens. Since our laser diode provides limited optical output (<120 mW), the low power output of our laser diode limits the ability to create an appropriate, large area of uniform optical illumination. Thus, we employed a defocused optical beam instead of optical plane wave illumination. For that, the sample plane was positioned away from the objective lens's focal plane (F, dashed line in Fig. 2(a)). Additionally, a white light source was integrated into the setup via a beam splitter to facilitate visualization of the dynamics. Most of the experiments are performed with a laser power of 45 mW at the back aperture of the objective lens, and the illumination extent in the sample plane is ≃32 μm diameter leading to an optical intensity of 56 μW μm−2 in the sample plane. The intensity of the optical illumination can be altered by changing the power of the laser beam or by modulating the extent of the defocused beam. To ensure that under such optical illumination, the colloidal systems do not experience a lot of variation in intensity over their trajectory, we have considered the shorter experimental trajectories, approximately 10 μm. Within such a span of the trajectories, the intensity variation experienced by the colloidal system is <18%. If we consider a longer span of the trajectories, then the intensity variation will be significant, and the role of direct optical forces cannot be ruled out. The image of the sample plane is then collected using a 50×, 0.8 NA objective lens and then projected onto a CCD/fast camera sensor. The CCD/fast camera captures the dynamics at a rate of 30/500 frames per second. The trajectories of the colloidal particles were extracted from the recorded video files using the TrackMate72 extension of Fiji software.73Results and discussion
Active motion of the dimer structure
Under such optical illumination, thermally active colloids effectively harness laser energy and dissipate heat. Typically, in the water medium, the transient heating of the system occurs on the timescale of microseconds. The temperatures reach a steady state at the timescales relevant to our study. This process generates a localized temperature distribution around the thermally active colloids. This thermal field results in thermo-osmotic slip fluid flow, which acts as an environmental cue to manipulate the motion of nearby colloidal particles. Specifically, when the thermally active colloids interact with their passive counterpart, these thermo-osmotic interactions become non-reciprocal, forming various bound structures. The simplest possibility is a dimer structure composed of one thermally active (A) and passive (P) colloid. Due to the non-reciprocity of the interactions, these dimer structures exhibit propulsion behavior as illustrated in the trajectory depicted in Fig. 2(b). We have calculated the mean-squared displacement (MSD) to quantify these dynamics, as presented in Fig. 2(c). The MSD analysis reveals a diffusive followed by a ballistic motion within our experimental timescale. The ballistic behavior is emblematic of typical active systems.74 Generally, active structures exhibit three different timescales in MSD: diffusive behavior and ballistic behavior, followed by diffusive behavior with increasing lagtime (τ) (for details, see Supplementary information 2, ESI†). The large time-scale diffusive behavior generally appears beyond the rotational diffusive time scale τr of the colloidal particles, which is generally of the order of 102 s. Since, in our case, the experimental time duration is ≃10 s, in our experimental MSD, we do not observe the large time scale diffusive behavior.Furthermore, we can associate a specific orientation direction with this active dimer structure, represented by a black arrow connecting the centers of the two colloids as shown in the inset of Fig. 2(b). To investigate how the orientation of this active dimer structure evolves, we estimated the mean squared angular displacement (MSAD) of this directional vector, as shown in Fig. 2(c). Slope 1 suggests that the orientation of the active dimer lacks any inherent rotational bias. In contrast, if we replace the thermally active colloid with a passive colloid (P′) of the same composition and size, then no tightly bound dimer structure exhibiting active motion is formed. The colloids exhibit independent diffusive motion, as can be seen from Fig. 2(d) (also see the ESI,† Video S1). The calculated MSD of the individual colloids, in Fig. 2(e), scales linearly with the lagtime, further emphasizing the colloids' unbiased Brownian motion. This observation suggests the vital role of slip flow-induced non-reciprocal attractive interactions in enabling the activity. We note that the dimer structure propels without any additional chemical environment.
Inducing rotational bias
To gain deeper insights into the dynamics that emerge from evolving colloidal structures due to temperature differences, we experimentally studied the dynamics of trimer and quadromer structures. There are two distinct configurations, AT1 and AT2. (i) AT1 contains one thermally active colloid (A1) paired with two passive colloids (P1) and (P2) and (ii) AT2 contains two thermally active colloids (A1) and (A2) alongside one passive colloid (P1). In both these trimer configurations, the non-reciprocal thermo-osmotic interaction can only lead to an imbalance of effective force along the structure's symmetry line. As a result, both of them exhibit propulsion behavior similar to the active dimer structure (see the ESI,† Video S2). Fig. 3(a) and (b) show the corresponding time-evolving trajectories of these two trimer configurations. We can clearly observe from the trajectory that although these trimer structures undergo active propulsion, they also do not show any preferred angular motion (see Supplementary information 3, ESI†).In contrast, if we consider a quadromer structure composed of two passive and thermally active colloids (as shown in Fig. 3(c)), due to the respective arrangement of the colloids, passive colloid P1 is relatively more distant than passive colloid P2 from thermally active colloid A2. This leads to different magnitudes of attractive thermo-osmotic force acting on the passive colloids. The thermo-osmotic force on P2 is greater than that on P1. As a result, P2 tends to move faster than P1. But since the quadromer moves together, the trajectory tends to move toward colloid P1, resulting in a tendency of anticlockwise chiral motion, as depicted in Fig. 3(c) (also see the ESI,† Video S2). Since our optical illumination is within a limited spatial extent, we experimentally did not observe a full curling trajectory. We have recorded the dynamics with a 30 fps CCD camera. We can define an orientation vector of the colloidal quadromer along the line joining from the center of mass of passive colloids P1 and P2 to the center of mass of thermally active colloids A1 and A2. The time evolution of the orientation vector clearly indicates the persistent angular motion in the case of chiral quadromers, as indicated in the inset of Fig. 3(c). The calculated MSD and MSAD for such a chiral quadromer structure are shown in Fig. 3(d). In contrast to the active dimer and trimer structure, in this case, we observed a ballistic trend in both the MSD and the MSAD. Similar chiral motion is also observed in natural active systems75–78 and artificial colloidal systems with inherent asymmetry mostly in chemical environments.24,42,50,79–83 But here, we show the dynamics in symmetric colloids with a non-chemical environment purely due to the optothermal interaction.
To understand the influence of thermo-osmotic interactions in the active and chiral motion, we have simulated the dynamics of the colloidal structures as given below.
Simulation of the dynamics of the colloidal structures
To simulate the dynamics of the colloids due to the temperature difference, we considered thermally active (A) and passive (P) colloids of diameters 1.3 μm and 2 μm, respectively. To model the absorbing nature of the thermally active colloids, we considered that they are at a higher temperature compared to their passive counterparts. In such a situation, the dynamics of colloid i will be determined using the Langevin equation given by | (1) |
![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) i and γi are the instantaneous velocity and viscous drag coefficient of colloid i. The last term
i and γi are the instantaneous velocity and viscous drag coefficient of colloid i. The last term  is the stochastic noise-induced random force term, where kB is the Boltzmann constant and Ti is the temperature of colloid i. All other forces are considered in the external force term
is the stochastic noise-induced random force term, where kB is the Boltzmann constant and Ti is the temperature of colloid i. All other forces are considered in the external force term ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) exti. Details of these forces are given below.
exti. Details of these forces are given below.
The large area optical field is modeled as plane wave illumination. This idealized the optical field as infinitely extended in simulation, in contrast to the experiments with a limited illumination region. In such a situation, no confining gradient optical force acts on the colloids (see Supplementary information 4, ESI†). Besides, the scattering optical force on the colloids acts in the propagation direction that pushes the colloids towards the bottom glass coverslip (see Supplementary information 4, ESI†). Due to the collective effect of gravity and the scattering optical forces, the dynamics of the colloids become two-dimensional. Since there is no in-plane component of the optical forces, we have not considered any optical force in our two dimensional simulation. The optical field is only used to create temperature differences between the colloids, which further harnesses temperature-mediated interactions between them. Secondary optical interactions between the colloids, such as optical binding, may play some role. However, the thermo-osmotic flow-induced forces are dominant within our experimental parameters, as can be seen from Supplementary information 5 (ESI†).
Being at an elevated temperature (TA = Ts + ΔT) compared to the surroundings, the thermally active colloids set up a thermal field in the surrounding medium as given by
 | (2) |
 | (3) |
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) TOij) on colloid i due to colloid j can be written as
TOij) on colloid i due to colloid j can be written as![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) TOij = γi TOij = γi![[small nu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0ea.gif) j. j. | (4) |
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) TOij = 0, if j = passive colloids, and
TOij = 0, if j = passive colloids, and ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) TOij = γi
TOij = γi![[small nu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0ea.gif) j ≠ 0, if j = thermally active colloids.
j ≠ 0, if j = thermally active colloids.
In addition to the above-mentioned forces, we have also considered the Lennard Jones forces (![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) Jij) between the colloids to ensure the exclusion region for one colloid due to the presence of the others. These
Jij) between the colloids to ensure the exclusion region for one colloid due to the presence of the others. These ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) Jij forces acting on colloid i due to the presence of colloid j can be written as
Jij forces acting on colloid i due to the presence of colloid j can be written as
 | (5) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij is the unit vector along the position of colloid i with respect to colloid j.
ij is the unit vector along the position of colloid i with respect to colloid j.
Taking the above-mentioned forces into account, the coupled Langevin equations involving passive and thermally active colloids can be written as
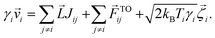 | (6) |
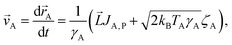 | (7a) |
 | (7b) |
Control over the dynamics
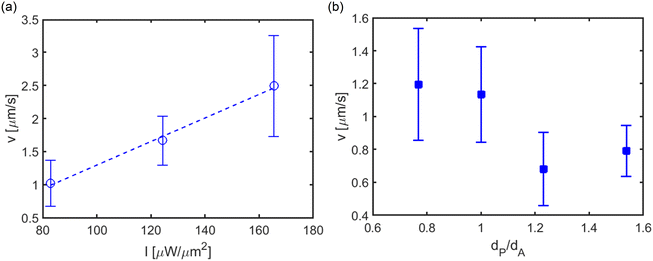
In the previous sections, we have shown how the temperature difference between the colloids and the resulting thermo-osmotic interaction leads to active propulsion and chiral motion in different colloidal structures. In this section, we experimentally try to understand the role of the intensity of the incident optical field and the size of the colloidal constituents in the dynamics of colloidal structures. Fig. 5(a) shows the velocity of the active dimer and trimer structure at various laser intensities. The thermal field and the thermo-osmotic interaction between the colloids can be controlled using the intensity of the incident optical field. We have also observed a similar trend in simulation (see Supplementary information 7, ESI†). One can also tune the dynamics by changing the constituent colloids' size. Fig. 5(b) shows the active velocity of the dimer structures as a function of the ratio of the diameter of the passive to thermally active colloids. In this case, we have only changed the passive colloid's diameter dP = 1, 1.3, 1.6, 2 μm, keeping the diameter of the thermally active colloid fixed (dA = 1.3 μm). Since the thermally active colloid is unchanged, the extent of heating and thermo-osmotic fluid flow remains unchanged, and the variation of the velocity is due to the passive colloid. The velocity shows a decreasing trend with increasing diameter of the passive colloid. A qualitatively similar trend is also observed in simulation (see Supplementary information 8, ESI†).Conclusions
Thus, in this study, we have experimentally explored the intricate behaviors of colloidal structures composed of thermally active and passive colloids. Our investigation revealed various emergent swimming modes, including active propulsion and chiral handedness. Such dynamics are primarily driven by temperature differences between the constituent colloids, resulting from an attractive nonreciprocal interaction between the colloids, as we found that these emerging dynamics are absent when the non-reciprocal attractive interactions are ignored.In contrast to the available literature, we did not rely on any chemical environment, such as hydrogen peroxide or 2,6-lutidine, to harness the nonreciprocal interaction.49–53 In our study, the non-reciprocal interaction between the colloids is employed by the thermo-osmotic slip fluid flow due to the temperature difference of the colloids. These interactions result in an inherent force imbalance within the structures, leading to both propulsion and chiral motion influenced by the constituent colloidal particles. Additionally, we observed that the dynamics of the colloidal structures can be enhanced or diminished by tuning the magnitude of the temperature mismatch, achievable through the intensity of optical illumination. We have also solved Langevin equations to validate the active dynamics of colloidal structures resulting from temperature differences between colloids.
In addition, since the dynamics emerge due to thermo-osmotic flow produced by the heated colloid in an aqueous solution, this platform is potentially useful for cargo transport. This study may also contribute valuable insights into the dynamics of colloidal structures, paving the way for potential applications in micro-engineering84–86 and microfluidic devices.61–64
Author contributions
R. C., A. S., and G. V. P. K. designed the study. R. C., A. S., and S. B. performed the experiments and analysis. A. S. has helped in the Brownian dynamics simulations. R. C. wrote the manuscript draft. All the authors reviewed the manuscript.Data availability
All the data including the simulation logic and experimental validation along with the analysis are included in the manuscript and ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
R. C. thanks Diptabrata Paul and Sumant Pandey for the fruitful discussion. This work was partially funded by AOARD (grant number FA2386-23-1-4054) and the Swarnajayanti fellowship grant (DST/SJF/PSA-02/2017-18) to G. V. P. K.Notes and references
- É. Fodor, C. Nardini, M. E. Cates, J. Tailleur, P. Visco and F. Van Wijland, Phys. Rev. Lett., 2016, 117, 038103 CrossRef PubMed.
- T. Speck, Europhys. Lett., 2016, 114, 30006 CrossRef.
- S. C. Takatori and J. F. Brady, Phys. Rev. E, 2015, 91, 032117 CrossRef CAS PubMed.
- M. J. Bowick, N. Fakhri, M. C. Marchetti and S. Ramaswamy, Phys. Rev. X, 2022, 12, 010501 CAS.
- D. Needleman and Z. Dogic, Nat. Rev. Mater., 2017, 2, 1–14 Search PubMed.
- J. Van der Gucht, Grand challenges in soft matter physics, Front. Phys., 2018, 6, 87 CrossRef.
- O. Hallatschek, S. S. Datta, K. Drescher, J. Dunkel, J. Elgeti, B. Waclaw and N. S. Wingreen, Nat. Rev. Phys., 2023, 5, 407–419 CrossRef PubMed.
- G. De Magistris and D. Marenduzzo, Phys. A: Stat. Mech. Appl., 2015, 418, 65–77 CrossRef.
- É. Fodor and M. C. Marchetti, Phys. A: Stat. Mech. Appl., 2018, 504, 106–120 CrossRef.
- S. Ramaswamy, Annu. Rev. Condens. Matter Phys., 2010, 1, 323–345 CrossRef.
- T. Sanchez, D. T. Chen, S. J. DeCamp, M. Heymann and Z. Dogic, Nature, 2012, 491, 431–434 CrossRef CAS PubMed.
- C. Weber, P. K. Radtke, L. Schimansky-Geier and P. Hänggi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 011132 CrossRef PubMed.
- T. H. Tan, A. Mietke, J. Li, Y. Chen, H. Higinbotham, P. J. Foster, S. Gokhale, J. Dunkel and N. Fakhri, Nature, 2022, 607, 287–293 CrossRef CAS PubMed.
- D. P. Singh, U. Choudhury, P. Fischer and A. G. Mark, Adv. Mater., 2017, 29, 1701328 CrossRef PubMed.
- N. A. Araújo, L. M. Janssen, T. Barois, G. Boffetta, I. Cohen, A. Corbetta, O. Dauchot, M. Dijkstra, W. M. Durham and A. Dussutour, et al. , Soft Matter, 2023, 19, 1695–1704 RSC.
- E. O. Budrene and H. C. Berg, Nature, 1995, 376, 49–53 CrossRef CAS PubMed.
- Q. Yang, M. Jiang, F. Picano and L. Zhu, Nat. Commun., 2024, 15, 2874 CrossRef CAS PubMed.
- A. Curatolo, N. Zhou, Y. Zhao, C. Liu, A. Daerr, J. Tailleur and J. Huang, Nat. Phys., 2020, 16, 1152–1157 Search PubMed.
- E. B. Steager, C.-B. Kim and M. J. Kim, Phys. Fluids, 2008, 20, 073601 Search PubMed.
- L. Theeyancheri, S. Chaki, T. Bhattacharjee and R. Chakrabarti, Phys. Rev. Res., 2024, 6, L012038 Search PubMed.
- T. Speck, Soft Matter, 2020, 16, 2652–2663 RSC.
- S. C. Takatori and J. F. Brady, Soft Matter, 2014, 10, 9433–9445 RSC.
- W. Wang, X. Lv, J. L. Moran, S. Duan and C. Zhou, Soft Matter, 2020, 16, 3846–3868 RSC.
- X. Peng, Z. Chen, P. S. Kollipara, Y. Liu, J. Fang, L. Lin and Y. Zheng, Light: Sci. Appl., 2020, 9, 141 CrossRef PubMed.
- T. Raj, S. Roy, A. Kumar, B. Roy, E. Mani and S. Sudhakar, J. Colloid Interface Sci., 2025, 677, 986–996 CrossRef CAS PubMed.
- S. Nedev, S. Carretero-Palacios, P. Kühler, T. Lohmüller, A. S. Urban, L. J. Anderson and J. Feldmann, ACS Photonics, 2015, 2, 491–496 CrossRef CAS PubMed.
- G. Tkachenko, V. G. Truong, C. L. Esporlas, I. Sanskriti and S. Nic Chormaic, Nat. Commun., 2023, 14, 1691 CrossRef CAS PubMed.
- S. Simoncelli, J. Summer, S. Nedev, P. Kühler and J. Feldmann, Small, 2016, 12, 2854–2858 CrossRef CAS PubMed.
- I. Buttinoni, G. Volpe, F. Kümmel, G. Volpe and C. Bechinger, J. Phys.: Condens. Matter, 2012, 24, 284129 CrossRef PubMed.
- A. Haldar, S. B. Pal, B. Roy, S. D. Gupta and A. Banerjee, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 033832 CrossRef.
- R. N. Kumar, A. D. Ranjan, S. Roy, S. D. Gupta, N. Ghosh and A. Banerjee, Phys. Rev. A, 2024, 110, 023512 CrossRef CAS.
- B. Roy, N. Ghosh, S. Dutta Gupta, P. K. Panigrahi, S. Roy and A. Banerjee, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 87, 043823 CrossRef.
- P. Kumar, L. Theeyancheri and R. Chakrabarti, Soft Matter, 2022, 18, 2663–2671 RSC.
- L. Zhang and Y. Zhu, Langmuir, 2012, 28, 13201–13207 CrossRef CAS PubMed.
- S. Erez, E. Karshalev, Y. Wu, J. Wang and G. Yossifon, Small, 2022, 18, 2101809 CrossRef CAS PubMed.
- Y.-L. Chen, C.-X. Yang and H.-R. Jiang, Sci. Rep., 2018, 8, 5945 CrossRef CAS PubMed.
- A. F. Demirörs, M. T. Akan, E. Poloni and A. R. Studart, Soft Matter, 2018, 14, 4741–4749 RSC.
- Y. Komazaki, H. Hirama and T. Torii, J. Appl. Phys., 2015, 117, 154506 CrossRef.
- P. Tierno, R. Golestanian, I. Pagonabarraga and F. Sagués, Phys. Rev. Lett., 2008, 101, 218304 CrossRef PubMed.
- P. Tierno, R. Golestanian, I. Pagonabarraga and F. Sagués, J. Phys. Chem. B, 2008, 112, 16525–16528 CrossRef CAS PubMed.
- H. Moyses, J. Palacci, S. Sacanna and D. G. Grier, Soft Matter, 2016, 12, 6357–6364 RSC.
- H.-R. Jiang, N. Yoshinaga and M. Sano, Phys. Rev. Lett., 2010, 105, 268302 CrossRef PubMed.
- L. Wang, M. N. Popescu, F. Stavale, A. Ali, T. Gemming and J. Simmchen, Soft Matter, 2018, 14, 6969–6973 RSC.
- M. M. Stanton, J. Simmchen, X. Ma, A. Miguel-López and S. Sánchez, Adv. Mater. Interfaces, 2016, 3, 1500505 CrossRef.
- J. Simmchen, J. Katuri, W. E. Uspal, M. N. Popescu, M. Tasinkevych and S. Sánchez, Nat. Commun., 2016, 7, 10598 CrossRef CAS PubMed.
- F. Kümmel, B. Ten Hagen, R. Wittkowski, I. Buttinoni, R. Eichhorn, G. Volpe, H. Löwen and C. Bechinger, Phys. Rev. Lett., 2013, 110, 198302 CrossRef PubMed.
- A. Mondal, B. Roy and A. Banerjee, Opt. Express, 2015, 23, 8021–8028 CrossRef CAS PubMed.
- L. Theeyancheri, S. Chaki, N. Samanta, R. Goswami, R. Chelakkot and R. Chakrabarti, Soft Matter, 2020, 16, 8482–8491 RSC.
- T. Yu, P. Chuphal, S. Thakur, S. Y. Reigh, D. P. Singh and P. Fischer, Chem. Commun., 2018, 54, 11933–11936 RSC.
- F. Schmidt, B. Liebchen, H. Löwen and G. Volpe, J. Chem. Phys., 2019, 150, 094905 CrossRef PubMed.
- J. Grauer, F. Schmidt, J. Pineda, B. Midtvedt, H. Löwen, G. Volpe and B. Liebchen, Nat. Commun., 2021, 12, 6005 CrossRef CAS PubMed.
- A. Varma, T. D. Montenegro-Johnson and S. Michelin, Soft Matter, 2018, 14, 7155–7173 RSC.
- J. Codina, H. Massana-Cid, P. Tierno and I. Pagonabarraga, Soft Matter, 2022, 18, 5371–5379 RSC.
- S. Kumar, M. Gunaseelan, R. Vaippully, A. Kumar, M. Ajith, G. Vaidya, S. Dutta and B. Roy, Biomed. Opt. Express, 2020, 11, 3555–3566 CrossRef CAS PubMed.
- A. P. Bregulla, A. Würger, K. Günther, M. Mertig and F. Cichos, Phys. Rev. Lett., 2016, 116, 188303 CrossRef PubMed.
- M. Fränzl and F. Cichos, Nat. Commun., 2022, 13, 656 CrossRef PubMed.
- D. Quinn and F. Cichos, Front. Nanotechnol., 2023, 5, 1135408 CrossRef.
- R. Chand, C. E. Rani, D. Paul and G. V. P. Kumar, ACS Photonics, 2023, 10, 4006–4013 CrossRef CAS.
- R. Chand, A. Shukla and G. V. P. Kumar, ACS Photonics, 2025, 12, 855–863 CrossRef CAS.
- S. E. Chung, W. Park, S. Shin, S. A. Lee and S. Kwon, Nat. Mater., 2008, 7, 581–587 CrossRef CAS PubMed.
- K. Jae-Sung and J. H. Oh, Appl. Sci., 2018, 8, 992 CrossRef.
- S. Hettiarachchi, H. Cha, L. Ouyang, A. Mudugamuwa, H. An, G. Kijanka, N. Kashaninejad, N.-T. Nguyen and J. Zhang, Lab Chip, 2023, 23, 982–1010 RSC.
- M. Rhee and M. A. Burns, Lab Chip, 2008, 8, 1365–1373 RSC.
- T. M. Schneider, S. Mandre and M. P. Brenner, Phys. Rev. Lett., 2011, 106, 094503 CrossRef PubMed.
- L. K. Davis, K. Proesmans and É. Fodor, Phys. Rev. X, 2024, 14, 011012 CAS.
- M. Fränzl, S. Muinos-Landin, V. Holubec and F. Cichos, ACS Nano, 2021, 15, 3434–3440 CrossRef PubMed.
- P. S. Kollipara, Z. Chen and Y. Zheng, ACS Nano, 2023, 17, 7051–7063 CrossRef CAS PubMed.
- Y. Liu and A. W. Poon, Opt. Express, 2010, 18, 18483–18491 CrossRef CAS PubMed.
- J. H. Shin, J. Seo, J. Hong and S. K. Chung, Sens. Actuators, B, 2017, 246, 415–420 CrossRef CAS.
- S. Ghosh, A. Biswas, B. Roy and A. Banerjee, Soft Matter, 2019, 15, 4703–4713 RSC.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- J.-Y. Tinevez, N. Perry, J. Schindelin, G. M. Hoopes, G. D. Reynolds, E. Laplantine, S. Y. Bednarek, S. L. Shorte and K. W. Eliceiri, Methods, 2017, 115, 80–90 CrossRef CAS PubMed.
- J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld and B. Schmid, et al. , Nat. Methods, 2012, 9, 676–682 CrossRef CAS PubMed.
- G. Volpe, S. Gigan and G. Volpe, Am. J. Phys., 2014, 82, 659–664 CrossRef.
- B. Vincenti, G. Ramos, M. L. Cordero, C. Douarche, R. Soto and E. Clement, Nat. Commun., 2019, 10, 5082 CrossRef PubMed.
- E. Lauga, W. R. DiLuzio, G. M. Whitesides and H. A. Stone, Biophys. J., 2006, 90, 400–412 CrossRef CAS PubMed.
- K. Ērglis, Q. Wen, V. Ose, A. Zeltins, A. Sharipo, P. A. Janmey and A. Cēbers, Biophys. J., 2007, 93, 1402–1412 CrossRef PubMed.
- C. N. Dominick and X.-L. Wu, Biophys. J., 2018, 115, 588–594 CrossRef CAS PubMed.
- B. Liebchen and D. Levis, Europhys. Lett., 2022, 139, 67001 CrossRef CAS.
- F. Schmidt, A. Magazzù, A. Callegari, L. Biancofiore, F. Cichos and G. Volpe, Phys. Rev. Lett., 2018, 120, 068004 CrossRef CAS PubMed.
- L. Caprini, H. Löwen and U. M. B. Marconi, Soft Matter, 2023, 19, 6234–6246 RSC.
- P. L. Muzzeddu, H. D. Vuijk, H. Löwen, J.-U. Sommer and A. Sharma, J. Chem. Phys., 2022, 157, 134902 CrossRef CAS PubMed.
- M. Donato, A. Mazzulla, P. Pagliusi, A. Magazzù, R. Hernandez, C. Provenzano, P. Gucciardi, O. Maragò and G. Cipparrone, Sci. Rep., 2016, 6, 31977 CrossRef CAS PubMed.
- B. Xu, Y. Zhao, X. Chen, R. Fu, H. Li, S. Xie, H. Liu, Y. Li, S. Zhang and B. Li, Laser Photonics Rev., 2024, 2400791 Search PubMed.
- P. Galajda and P. Ormos, Appl. Phys. Lett., 2001, 78, 249–251 CrossRef CAS.
- H. Rubinsztein-Dunlop and M. E. Freise, Opt. Photonics News, 2002, 13, 22–26 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01348d |
| This journal is © The Royal Society of Chemistry 2025 |