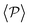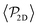Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Sedimentation and structure of squirmer suspensions under gravity†
C. Miguel
Barriuso G.‡
 *ab,
Horacio
Serna‡
*ab,
Horacio
Serna‡
 ab,
Ignacio
Pagonabarraga
ab,
Ignacio
Pagonabarraga
 cd and
Chantal
Valeriani
cd and
Chantal
Valeriani
 *ab
*ab
aDepartamento de Estructura de la Materia, Física Térmica y Electrónica, Universidad Complutense de Madrid, 28040 Madrid, Spain. E-mail: carbarri@ucm.es; cvaleriani@ucm.es
bGISC – Grupo Interdisciplinar de Sistemas Complejos, 28040 Madrid, Spain
cDepartament de Física de la Matèria Condesada, Facultat de Física – Universitat de Barcelona, Carrer de Martí i Franquès, 1, 11, 08028 Barcelona, Spain
dUniversitat de Barcelona Institute of Complex Systems (UBICS), Universitat de Barcelona, 08028 Barcelona, Spain
First published on 15th January 2025
Abstract
The effect of gravity on the collective motion of living microswimmers, such as bacteria and micro-algae, is pivotal to unravel not only bio-convection patterns but also the settling of bacterial biofilms on solid surfaces. In this work, we investigate suspensions of microswimmers under the influence of a gravitational field and hydrodynamics, simulated via the dissipative particle dynamics (DPD) coarse-grained model. We first study the collective sedimentation of passive colloids and microswimmers of the puller and pusher types upon increasing the imposed gravitational field and compare them with previous results. Once sedimentation occurs, we observe that, as the gravitational field increases, the bottom layer undergoes a transition to an ordered state compatible with a hexagonal crystal. In comparison with passive colloids, both pullers and pushers easily rearrange at the bottom layer to anneal defects. Specifically, pullers are better than pushers in preserving the hexagonal order of the bottom mono-layer at high gravitational fields.
1 Introduction
In the last decade, many research efforts have been put forward to understand the effects of external fields of different kinds on the motion of active agents, paying special attention to cases in which the hydrodynamic interactions (HIs) between active agents are relevant.1–3 When acting concomitantly, external fields and hydrodynamics might induce new motion patterns in microswimmers. In particular, the influence of gravity on the collective motion of biological microswimmers, such as bacteria and micro-algae, is crucial to understand bio-convection patterns,4–9 as well as the settling and growth of bacterial biofilms on solid surfaces.10–12 When dealing with synthetic systems, it has been shown that confinement plus gravity plays a crucial role in the motion of catalytic Janus microswimmers, for which understanding its influence is key to controlling their trajectories,13–17 or in experiments dealing with active droplets,18–20 where clusters present a rich dynamics. The collective motion of microswimmers affected by gravity has promising technological applications such as stirring of bioreactors,21 transport of fluid and small objects at the micro-scale,22 biomedicine,23 and water remediation.24A topic that has recently attracted attention is the sedimentation of active agents, with interest in not only the single-agent but also the collective dynamics. In the past 15 years, numerous theoretical investigations have reported the study of sedimentation of dry25–29 and wet30–33 active matter. Correspondingly, a great deal of numerical research has also been carried out. The sedimentation dynamics of a single squirmer at high Péclet numbers under the influence of gravity is considered in ref. 34, where multi particle collision dynamics (MPCD) was used. In this work the authors found different regimes such as cruising and sliding states, and proposed an expression for the sedimentation velocity as a function of height, self-propulsion and rotational velocities. Using the same model as in the present work, a recent numerical and experimental study revealed that the complex dynamics of a single Janus catalytic microswimmer swimming near a wall can be captured by a minimal squirmer-like model, including bottom heaviness and mass asymmetry.17 By means of dissipative particle dynamics (DPD), it was shown that the dynamics resulting from the interplay between hydrodynamics and chemical fields in this type of system has been overcome by inertial and gravitational effects. A recent numerical work has focused on the effects of the microswimmer's shape and vertical walls on the sedimentation dynamics:35 a two dimensional elliptical squirmer under a gravitational field is simulated inside a vertical channel employing the lattice Boltzmann (LB) method. The observed dynamics, consisting of tilted motion and oscillations, depends on both the swimming mode (pusher, neutral or puller) and the squirmers' aspect ratio. The sedimentation dynamics of two squirmers of similar and different types has also been studied in narrow vertical channels using the LB method,36,37 finding several motion patterns like steady and oscillatory settling.
Regarding collective sedimentation dynamics, HIs have been considered in simulations of squirmer suspensions under the LB scheme,38 revealing that active stresses are responsible for flocking, swimming coherence and formation of band-like structures similar to those observed in systems of self-propelled particles with explicit alignment interactions.39–43 LB simulations of squirmer suspensions with an additional tumbling rate and under the action of gravitational fields44 have demonstrated that for strong enough pullers/pushers, the hydrodynamic flows produced by their collective motion affect the sedimentation in a way that cannot be explained by the behavior of a single swimmer under gravity. On the other side, using MPCD, the authors of ref. 45 have observed that most of the squirmers settle under a moderate gravitational field, forming a multi-layered structure at the bottom. However, squirmers on the surface of the sedimented layers form convection patterns. The authors found that the sedimentation length depends on the gravitational field applied and the squirmer type. In similar simulation studies of bottom heavy squirmers, complex convective patterns were found,46 due to the torque that orients the squirmers upwards. The same behaviour was observed in gyrotactic clusters.47 The influence of biological microswimmers (E. coli) on the settling of passive colloids has revealed that the bacterial active bath enhances the effective diffusion coefficient of the colloidal particles.48
Following the MPCD method, the collective dynamics of a monolayer of squirmers under strong gravitational fields was also investigated, finding a complex dynamical phase behaviour in terms of the swimming mode and the packing fraction of the monolayer that includes a hydrodynamic Wigner fluid, fluctuating chains, and swarms.49 MPCD has also been used to study the sedimentation of attractively interacting colloids,50 determining that clustering induced by strong attractions modified the linear relation between the sedimentation velocity and colloids' packing fraction. In the same spirit, experiments with colloidal beads51 not only revealed the same non-linear behaviour but also reported that attractive interactions increase particle settling.
Apart from these studies on sedimented monolayers, few works have been devoted to suspensions of microswimmers under tight confinement in slit pores. The restriction to quasi two-dimensional motion promoted structural features similar to those observed in monolayers under strong gravity. In Ref. 52 the effects of confinement in thin slit pores on the collective behavior of microswimmer suspensions are studied, finding that the most relevant variable was the self-propelling mechanism and suggesting that to improve the prediction of collective states the near-field approximation of the flow field should be considered. In a recent numerical article, the authors investigated the combined effects of tight confinement and (LB) hydrodynamics on the collective motion of microswimmers, concluding that the patterns largely differed from their bulk counterparts.53
In recent years considerable effort has been devoted to clarify how hydrodynamics affects the interaction of a microswimmer with bounding walls, taking into account the influence of swimmer pairwise/collective interactions and the walls’ boundary conditions. In particular, some studies show that pullers aggregate more at walls when solving Navier–Stokes equations using finite volume methods,54 considering stability arguments using boundary element methods,32 analyzing squirmer detention times at walls using MPCD simulations55 and more recently considering pair-wise interactions.56 On the other side, works based on LB methods57,58 and a recent study (DPD-based) of ellipsoidal microswimmers confined in thin films59 have shown an opposite trend with pushers being effectively more attracted to walls than pullers. Depending on the volume fraction and the squirmer type (puller, neutral or pusher), swimmers exist in a gas-like phase, undergo swarming or motility induced phase separation. Additionally, LB simulations of a sedimented squirmer layer60 also show swarming for pushers and the formation, at low area fractions, of chiral spinners composed of two or three squirmers stabilized by near-field HIs.
In the present work, we consider the collective sedimentation of squirmer-like microswimmers embedded in DPD solvent following an improved version of the model presented in ref. 61. Apart from gaining insights into the interplay between gravity, thermal fluctuations and hydrodynamics, we aim to validate the model contrasting it with previous simulation studies using different techniques.44,45 Once the sedimentation has occurred, we study the structure of the formed bottom layer, paying special attention to the transition to an ordered structure with hexagonal symmetry as the gravitational field increases. Although previous studies have also shown hexagonal order in a monolayer of squirmers,49 we show that this order is compatible with a hexagonal crystal and that activity favors the repairing of defects observed in sedimented mono-layers of passive colloids.
We organize the article as follows. In Section 2, we introduce the model, the simulation details and the analysis tools. In Section 3, we first present the results of the sedimentation of microswimmers, and then we characterize the structure of the formed bottom monolayer of microswimmers. In Section 4, we summarize the main findings of the article and present the conclusions.
2 Numerical details
2.1 Model and simulation details
The system under study is composed of N = 500 “raspberry” colloids (swimming or not), composed of Nc = 19 particles each, embedded in a solvent composed of Ns = 948![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 073 particles and confined between two parallel walls made out of Nw = 168
073 particles and confined between two parallel walls made out of Nw = 168![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 particles describing a square lattice with lattice constant, lw = 0.3Rss, in the presence of a gravitational field only affecting the colloids (see Fig. 1a). The system is simulated with an in-house extension§ of the open source package LAMMPS62 (patch_2Jul2021) implementing colloid self-propulsion via a squirmer-like force field applied to the solvent particles, as in ref. 61. All particles present in the system interact via DPD pairwise interactions (DPD-BASIC package¶) except particles forming the colloids which are joined together by rigid interactions (RIGID package||). The minimum length scale that we take as the unit reference for all lengths present in the system is the DPD cutoff for solvent–solvent interactions Rss = 1 (see Fig. 1). The dimensions of the simulation box are Lx = Ly = 87Rss and Lz = 43.5Rss. Periodic boundary conditions are applied along x and y axes. The solvent number density ρs = N/(Vbox − Vcols) = N/[LxLyLz − N(4/3)πRc3] = 2.981, and the colloid volume fraction is ϕc = N(4/3)πRH3/LxLyLz ≈ 0.099, where Rc = 1.75Rss and RH = 2.5Rss are the colloid radii with respect to the DPD cutoff for colloid–solvent and colloid–colloid interactions respectively (see Fig. 1b).
200 particles describing a square lattice with lattice constant, lw = 0.3Rss, in the presence of a gravitational field only affecting the colloids (see Fig. 1a). The system is simulated with an in-house extension§ of the open source package LAMMPS62 (patch_2Jul2021) implementing colloid self-propulsion via a squirmer-like force field applied to the solvent particles, as in ref. 61. All particles present in the system interact via DPD pairwise interactions (DPD-BASIC package¶) except particles forming the colloids which are joined together by rigid interactions (RIGID package||). The minimum length scale that we take as the unit reference for all lengths present in the system is the DPD cutoff for solvent–solvent interactions Rss = 1 (see Fig. 1). The dimensions of the simulation box are Lx = Ly = 87Rss and Lz = 43.5Rss. Periodic boundary conditions are applied along x and y axes. The solvent number density ρs = N/(Vbox − Vcols) = N/[LxLyLz − N(4/3)πRc3] = 2.981, and the colloid volume fraction is ϕc = N(4/3)πRH3/LxLyLz ≈ 0.099, where Rc = 1.75Rss and RH = 2.5Rss are the colloid radii with respect to the DPD cutoff for colloid–solvent and colloid–colloid interactions respectively (see Fig. 1b).
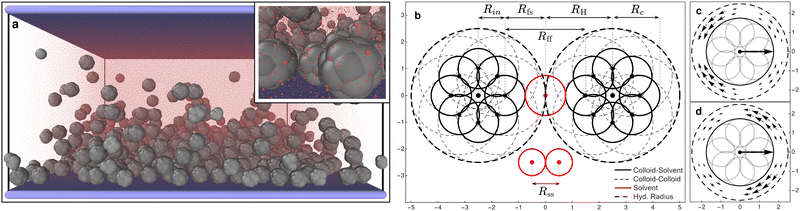 | ||
| Fig. 1 (a) Snapshot of the full simulation box (inset: zoom on some bottom colloids). The raspberry colloids (gray) over the bounding substrate made of frozen particles (blue) surrounded by the solvent particles (transparent red). See the ESI† for an animated version of this figure (video1.avi). (b) Schematic representation of a 2D section of two raspberry colloids (black) and three solvent particles (red). We see 8 of the 18 DPD filler particles—distributed on the surface of a sphere of radius Rin = 1.0Rss—each colloid is made of. The filler particles have two DPD cutoffs, Rff = 3 when interacting with other filler particles (solid thick circles), and Rfs = Rff/2 when interacting with solvent particles (dashed thin circles). This allows solvent particles to flow between colloids while these are interacting and results in effective radius of Rcs ≡ Rc = 1.75 for colloid–solvent interactions and Rcc ≡ RH = 2.5 for colloid–colloid interactions. Solvent particles interact with each other with a DPD cutoff Rss = 1. The interactions with the walls are also modelled as DPD with Rwf = Rff for wall–filler interactions and Rws = Rfs for wall–solvent. A central particle (not visible), placed at the center of the colloid, defines the origin of the generated force fields shown in panels (c) and (d) in the region between spheres of radii Rc and RH. These emanate from the center of mass of the colloid, are fixed with its internal frame of reference, and are consistent with a pusher (c) and a puller (d) type squirmer, producing a net self-propulsion force along the axis of symmetry of the force field. Graphics presented here and elsewhere were generated in part using the visualisation software Ovito.63 | ||
FDPD(rij) = (FCij + FDij + FRij)![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij if rij < rc, ij if rij < rc, | (1) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij = (ri − rj)/rij being the unit vector between the i-th and j-th particles. The conservative term is FCij = Aw(rij), where A is the amplitude and w(rij) = 1 − rij/rc is a weighting factor varying between 0 and 1.64 The dissipative contribution reads FDij = −γw2(rij)(
ij = (ri − rj)/rij being the unit vector between the i-th and j-th particles. The conservative term is FCij = Aw(rij), where A is the amplitude and w(rij) = 1 − rij/rc is a weighting factor varying between 0 and 1.64 The dissipative contribution reads FDij = −γw2(rij)(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij·
ij·![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_char_0076_20d1.gif) ij) with friction coefficient γ. Finally, the thermal contribution
ij) with friction coefficient γ. Finally, the thermal contribution 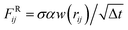 is a random force, where α is a Gaussian random number with zero mean and unit variance, Δt is the chosen time-step for the time integration and
is a random force, where α is a Gaussian random number with zero mean and unit variance, Δt is the chosen time-step for the time integration and 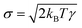 is related to the mean of the random force via fluctuation–dissipation, T being the temperature of the system. The values of the chosen DPD parameters are shown in Table 1.
is related to the mean of the random force via fluctuation–dissipation, T being the temperature of the system. The values of the chosen DPD parameters are shown in Table 1.
| ss | ff | fs | ws | wf | c* | |
|---|---|---|---|---|---|---|
| A | 20 | 50 | 20 | 150 | 150 | 0 |
| γ | 200 | 0 | 200 | 450 | 0 | 0 |
| R | 1 | 3 | 1.5 | 1.5 | 3 | 0 |
| k B T | 1 | 1 | 1 | 1 | 1 | 0 |
The chosen values ensure a low Reynolds number (Re ≤ 0.105), the lowest slip velocity at the wall boundaries that kept the simulation stable, impermeability of the walls and colloids by solvent particles and avoidance of depletion interactions between colloids and between colloids and walls.** To minimize the impact of these interactions, we prescribe the different DPD cutoffs between interactions of solvent, colloidal and wall particles to allow solvent to flow in between colloids or between colloids and walls; see Fig. 1. In practice, it means that the interaction radius of the colloids when interacting with each other is RH = 2.50, but when interacting with solvent particles, their interaction radius is Rc = 1.75, and so the solvent particles with a diameter determined by the cutoff Rfs = 1.50 can fit in between two colloids at contact. The same occurs when colloid, wall and solvent particles interact. To the best of our knowledge, this approach has not yet been studied, although it bears similarities with previous DPD studies, using virtual walls66 or dissipative “coats”,68 and MPCD approaches using virtual particles for modelling flow past obstacles71 and squirmers.72
Regarding the self-propulsion, we implement a variation of the squirmer model76,77 where, instead of prescribing a velocity boundary condition at the microswimmer surface, we apply a force field acting on the solvent particles located within a spherical shell surrounding the microswimmer. The resulting hydrodynamic force field only considering the two first surface modes of the polar component (neglecting the radial component) reads
FH(r,θ) = (B1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + B2 θ + B2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)êθ if Rc < r < RH θ)êθ if Rc < r < RH | (2) |
The parameter B1 determines the propulsion force along the prescribed orientation of the colloid, and B2 accounts for the swimming mode. The sign of the parameter β = B2/B1 (determined by that of B2) defines the self-propulsion mechanism: pusher (β < 0), neutral (β = 0) or puller (β > 0). Rather than prescribing the propulsion force, Fp, we prescribe B1 and compute the propulsion force Fp = 2B1/3 through the functional relation for the squirmer velocity. A suspension of passive colloids, B1 = 0, will be used as a reference system.
The colloid is not a perfect sphere and steric effects might modulate the orientational behavior of the colloid at close interactions (see the ESI†). Larger sphericity can be achieved by increasing the number of fillers. A perfect spherical colloid with steric interactions is achievable with the current model considering the conservative interaction of only the central particle, whose DPD cutoff would be increased so as to include the remaining 18 filler particles. The conservative interactions of the fillers have to be switched off, as they are only needed for interchanging dissipative, thermal and thrust forces with the rest of the solvent particles. Even though simulations of more complex colloid geometries might be not as direct as with the raspberry model, both the model and the DPD scheme are versatile enough to consider either spherical swimmers or swimmers with complex structures in ref. 61.
The implementation of the DPD boundary conditions is a relevant and widely discussed topic.78–84 Following ref. 79, we increase the wall density (4 times the solvent density) and independently tune the solvent–wall particle friction coefficient γws (to ensure the lowest slip velocity and no density fluctuations near the wall, we separately perform simulations of steady solvent flow). However, in the simulations presented here (where a steady flow is not present) a slip velocity was measured for passive colloids and walls (see the ESI†).
As in any other coarse-grained method, we capture hydrodynamics down to the coarse-graining scale Rss. This approach describes near-field hydrodynamics,31,85–87 but we do not take into account the asymptotic behavior of near-field hydrodynamics when r → 0 (lubrication). The role of the asymptotic lubrication and far-field interactions has been previously addressed for pairs of squirmers.30,34,52 Specifically, when interacting with walls, the far-field approximation predicts velocities that agree within a 10% error up to a distance of 0.5 body lengths from the wall.31 In our case, using the data from the radial distribution functions (see Fig. S10 of the ESI†), we estimate the minimum gap between the colloid and the wall to be δRDFw ≈ 0.7DRDFcs and between colloids to be δRDFc ≈ DRDFcs, where DRDFcs ≈ 2Rss is the estimated minimum swimmer body length with respect to solvent interactions††. The lubrication torque correction34,87 at the mentioned distance from the wall is found to be 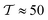 , while the average torque felt by the colloids is ≈600. Therefore, although not dominant, lubrication forces should be included to make accurate predictions. The aim of this work is not to make quantitative predictions but to validate and assess how the model captures the known phenomenology, exploring its limitations when applied to current non-trivial systems (sedimentation of a suspension of swimmers) and gaining insight into the behavior of such systems.
, while the average torque felt by the colloids is ≈600. Therefore, although not dominant, lubrication forces should be included to make accurate predictions. The aim of this work is not to make quantitative predictions but to validate and assess how the model captures the known phenomenology, exploring its limitations when applied to current non-trivial systems (sedimentation of a suspension of swimmers) and gaining insight into the behavior of such systems.
| Fg = −mgẑ | (3) |
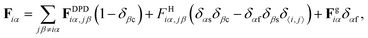 | (4) |
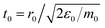 .
.
2.2 Analysis tools
Once colloids have sedimented and the mean colloid height reached a stationary regime, we compute their sedimentation profile via their 2D packing fraction in the xy-plane, ϕ2D, together with their orientational profile (i.e. their mean vertical orientation) along the z-axis, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α. For the latter calculation, we divide the z direction in 200 bins of height Δz ≈ 0.22Rss and compute the number of colloids in each bin, together with their mean vertical orientation. Finally, we take the temporal average over the last 400 configurations for τ > 3000.
α. For the latter calculation, we divide the z direction in 200 bins of height Δz ≈ 0.22Rss and compute the number of colloids in each bin, together with their mean vertical orientation. Finally, we take the temporal average over the last 400 configurations for τ > 3000.
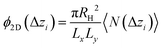 | (5) |
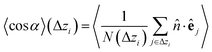 | (6) |
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) is the normal vector from the bottom to the top wall, parallel to the z axis unit vector, and e is the colloid orientation.
is the normal vector from the bottom to the top wall, parallel to the z axis unit vector, and e is the colloid orientation.
All reported quantities refer to colloids at the bottom layer. To characterize the structure of the bottom layer, we compute the pair correlation function, g(r), and the static structure factor (SSF) in two dimensions
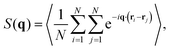 | (7) |
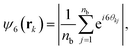 | (8) |
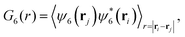 | (9) |
To study colloids' alignment with respect to their closest neighbours, we compute each colloid k local polar order parameter
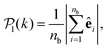 | (10) |
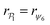 for each colloid k, including itself. For isolated swimmers,
for each colloid k, including itself. For isolated swimmers, 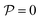 . Although
. Although 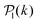 is calculated at the bottom layer, we consider the three-dimensional orientation of the colloids since they might point either towards the wall or away from the wall. Next, we compute the probability distribution of the local polar order parameter,
is calculated at the bottom layer, we consider the three-dimensional orientation of the colloids since they might point either towards the wall or away from the wall. Next, we compute the probability distribution of the local polar order parameter, 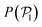 . The total alignment of the bottom layer can be described by the global polar order parameter39
. The total alignment of the bottom layer can be described by the global polar order parameter39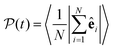 | (11) |
To complete the analysis of colloids' alignment, we study the spatial velocity correlation function (SVCF) and the spatial orientation correlation function (SOCF)
SVCF(r) = 〈![[v with combining circumflex]](https://www.rsc.org/images/entities/b_char_0076_0302.gif) i· i·![[v with combining circumflex]](https://www.rsc.org/images/entities/b_char_0076_0302.gif) j〉r=|ri−rj| j〉r=|ri−rj| | (12) |
| SOCF(r) = 〈êi·êj〉r=|ri−rj| | (13) |
![[v with combining circumflex]](https://www.rsc.org/images/entities/b_char_0076_0302.gif) i
and
i
and ![[v with combining circumflex]](https://www.rsc.org/images/entities/b_char_0076_0302.gif) j are the three-dimensional unit velocities of particles i and j, êi and êj are the unit orientations, and r = |ri − rj| is the scalar distance between the two particles. Thus, both correlations adopt values in the range of [−1,1].
j are the three-dimensional unit velocities of particles i and j, êi and êj are the unit orientations, and r = |ri − rj| is the scalar distance between the two particles. Thus, both correlations adopt values in the range of [−1,1].
The presence of the wall influences the orientation of the colloids close to it. Hence, we define the angle α between the colloid orientation and the normal vector of the bottom wall, ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) = [0,0,1], and calculate its distribution, P(α).
= [0,0,1], and calculate its distribution, P(α).
3 Results and discussion
We first report briefly the results for sedimenting passive colloids and compare with previous results. Once sedimentation takes place, we analyze the sedimentation profiles of puller/pusher squirmers and characterize the structural features of the sedimented bottom layer using the passive case as a reference and comparing with previous studies.3.1 Sedimentation velocity of passive colloids
Passive colloids sediment falling, on average, along linear trajectories in the vertical direction (see Fig. 2). The measured sedimentation velocity, vg, is proportional to Fg = 6πηRcvg. Increasing the packing fraction of the colloidal dispersion leads to a decrease in the sedimentation velocity due to HIs. Using Rc,RDF = 1.46 the packing fraction is ϕ = N(4/3)πRc,RDF3/LxLyLz ≈ 0.02. According to Fig. 12.3 of ref. 90, such a packing fraction has the effect of reducing the sedimentation velocity by 5%: in our case 100·(Rc,eff − Rc,RDF)/Rc,RDF ≈ 6%. It should be noted that hydrodynamic theory predicts a varying friction coefficient depending on the distance to the wall (see ref. 34 and 91 and eqn (7)–(2.15) of ref. 92). The approximation in ref. 34 for the system under study predicts a decrease in the sedimentation velocity of a single colloid, although barely distorting the linearity of the trajectory for 10 ≲ z/Rss ≲ 35. The disentanglement of these two effects (the varying sedimentation velocity due to walls and due to collective sedimentation) lies outside the scope of the present work and is left for future study.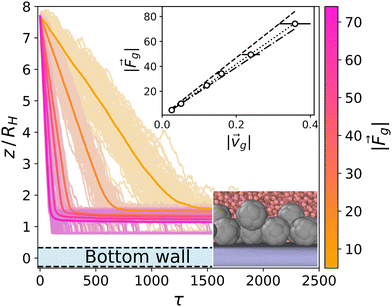 | ||
| Fig. 2 Trajectories for the sedimentation of the top layer of passive colloids (light colors) and average (dark colors) for Fg = {5,10,25,34,50,74}. The y-axis is scaled to the body length of the colloids DH = 2RH. The bounding wall is displayed in light blue at the bottom. Top inset: The data points correspond to the obtained sedimentation velocities by fitting the averaged z trajectories (dark color curves), and the error bars show the ensemble standard deviation. The dashed line corresponds to the Stokes law for a colloid with radius R = Rin + Rss/2 = 1.75 (see Fig. 1). The dotted line corresponds to a fit to the data points corresponding to a colloid radius of R = 1.55. The dashed-dotted line corresponds to the Stokes law for a colloid with radius R = 1.46 estimated from the RDF. Bottom inset: Snapshot of the sedimented colloids at the highest gravity Fg = 74.1. | ||
3.2 Squirmer sedimentation and orientational profiles
Fig. 3 reports the sedimentation and orientational profile of the squirmer dispersions.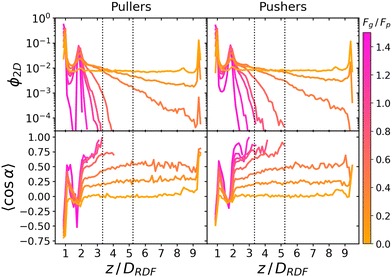 | ||
Fig. 3 Top: Sedimentation profile as the 2D packing fraction ϕ2D for pullers (left) and pushers (right) for Fg/Fp = {0.0,0.15,0.3,0.5,0.7,0.75,1.0,1.5} (color bar). The x-axis is scaled to the colloid body length DRDF = 2RRDF ≈ 4.2 regarding colloid–colloid interactions estimated by the RDF (see the ESI†). The region between the dotted lines corresponds to the exponential regime in the two lowest nonzero Fg/Fp ratios. Bottom: Mean vertical orientation along the z direction. α is the angle between the vertical and the squirmer orientation (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α = 1 corresponds to an upward (positive z) orientation and cos α = 1 corresponds to an upward (positive z) orientation and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α = −1 corresponds to an downward (negative z) orientation). Refer to Fig. 3 of ref. 45 for comparison. See the ESI† for a zoom on the layers. α = −1 corresponds to an downward (negative z) orientation). Refer to Fig. 3 of ref. 45 for comparison. See the ESI† for a zoom on the layers. | ||
In the absence of gravity, Fg = 0, squirmers are uniformly distributed in the bulk, as expected. Near the walls, the characteristic accumulation of active particles54,93–96 appears as two peaks at z ≈ DRDF and z ≈ 9.4DRDF reaching ϕ2D ≈ 0.14 and ϕ2D ≈ 0.09 for pullers and pushers, respectively (see the ESI,† Fig. S3 for a zoom on the peaks). This implies that pullers tend to stick slightly more to walls than pushers. Since these packing fractions are not far from the dilute limit, if we assume that the difference in aggregation of pullers and pushers at the wall is mostly controlled by HIs of a single squirmer with the wall, the difference in packing fractions qualitatively agrees with the theory:33,97 when swimming towards the bottom wall, α ∈ (π/2,3π/2), pullers tend to reorient towards the wall and align perpendicularly to it (α = π), while pushers tend to reorient away from the wall and align parallel to it (α = ±π/2). Thermal fluctuations on a pusher swimming parallel to the wall will favor with equal probability that the squirmer approaches or moves away from the wall. Since pullers are oriented preferentially towards the wall, thermal fluctuations will not help the squirmer to displace away from the wall. This is also consistent with the higher residence times exhibited by pullers55 and can be correlated with the fluctuations of the flux of particles to or from the first layer (Fig. S7 of the ESI†).
As gravity increases, the packing fraction maximum of the first layer also increases, reaching ϕ2D ≈ 0.82 for pullers and ϕ2D ≈ 0.78 for pushers, being in all cases slightly higher for pullers than for pushers (see Fig. S4 of the ESI†)‡‡. The same effect is more clearly visible at the top wall (z ≈ 9.4DRDF) for the Fg/Fp = 0.3 case, where the pullers' packing fraction presents a peak near the wall (that is absent for pushers).
Away from the walls, at z = 2DRDF and z = 8.4DRDF, two secondary peaks are visible reaching ϕ2D ≈ 0.0050 and ϕ2D ≈ 0.0057 for pullers and pushers, respectively. As gravity increases, the packing fraction of the second bottom layer for both pullers and pushers remains similar and increases linearly, until Fg/Fp ≈ 0.7 when it reaches a maximum and starts decreasing (see the ESI†). This maximum appears when the gravity is strong enough to confine all colloids below z = 3DRDF. Thus, increasing gravity beyond this value does not increase the second layer packing fraction, since there are no more colloids above z = 3DRDF. Instead, increasing gravity decreases the packing fraction, since colloids from the second layer are pushed down to the first, which is not yet fully populated. Additionally, since pushers can leave the first layer more easily than pullers,59 as we increase gravity beyond this value, the packing fraction for pushers is higher than for pullers at all 0.7 < Fg/Fp < 1.5 values. Thus, if gravity is large enough, it is slightly more probable to find pushers than pullers in the second layer, as opposed to what happens in the first sedimented layer.
In the region between the first and the second layers we also observe a non-monotonic behaviour of the 2D packing fraction (see the ESI†). It increases for pullers and pushers (being larger for pullers than for pushers) until it reaches a maximum around Fg/Fp ≈ 0.3. Then, it starts decreasing for pullers and pushers and starting from Fg/Fp ≥ 0.7 a crossover appears (with pushers overtaking pullers).
Moving away from the bottom layers, z > 2.5DRDF, a decay of the 2D packing fraction is observed, always faster for pullers than for pushers. At the two lowest gravitational forces, this decay seems exponential: thus, the corresponding sedimentation lengths, δ, is obtained by fitting the packing fraction to ϕ2D = ez/δ between two chosen heights (the dotted lines in Fig. 3) as described in ref. 45, to minimize the influence of the walls. The corresponding sedimentation lengths are (see the ESI†)
| δpull = 5.27RRDF, δpush = 9.96RRDF for Fg/Fp = 0.15, |
| δpull = 2.5RRDF, δpush = 3.41RRDF for Fg/Fp = 0.3, |
The bottom panels of Fig. 3 show the squirmers' mean vertical orientation at different heights. In the absence of gravity, Fg = 0, the alignment is dominated by steric and hydrodynamic interactions,97 and thus subject to the squirmer shape and type. Although the description of the squirmer through a raspberry model does not correspond to a perfect spherical shape, the deviations in sphericity it introduces, e.g. wall alignment due to the short-range structure of the steric interaction, are small (see the ESI†). Moreover, when comparing the relative behavior of pullers and pushers, the effects due to weak departure from sphericity are the same in both, so the differences in the observed behavior can be attributed solely to hydrodynamics. In the far-field approximation, a single squirmer interacting will tend to align perpendicularly or parallel to a wall for a puller or pusher respectively. The Fg/Fp = 0 curve of the bottom panels of Fig. 3 displays two opposing peaks near the top and bottom walls at z ≈ DRDF and z ≈ 9.4DRDF reaching 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α〉 ≈ ±0.7 for pullers and 〈cos
α〉 ≈ ±0.7 for pullers and 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α〉 ≈ ±0.5 for pushers (≈135° and ≈120° w.r.t each wall normal respectively). To gain further information, the distribution P(α) for the squirmers close to the bottom wall and the full joint probability distributions P(z,cos
α〉 ≈ ±0.5 for pushers (≈135° and ≈120° w.r.t each wall normal respectively). To gain further information, the distribution P(α) for the squirmers close to the bottom wall and the full joint probability distributions P(z,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α) also for higher z are reported in the bottom panel of Fig. 5 and in Fig. S5 of the ESI† respectively. They display the different shapes of the distributions for pullers and pushers and show that the most probable values near walls are cos
α) also for higher z are reported in the bottom panel of Fig. 5 and in Fig. S5 of the ESI† respectively. They display the different shapes of the distributions for pullers and pushers and show that the most probable values near walls are cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α ≈ ±0.9 and cos
α ≈ ±0.9 and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α ≈ ±0.4 respectively (≈155° and ≈115° w.r.t each wall normal). Therefore, both pullers and pushers are oriented towards the wall but pullers are more tilted towards it. The detailed discussion of the results for squirmers close to the bottom wall (z < 1.5DRDF) will be addressed in the next section (Section 3.3). Two secondary peaks are observed around z = 2DRDF and z = 8.4DRDF (zoom available in the ESI†) that also show a mean orientation slightly tilted towards the nearest wall 〈cos
α ≈ ±0.4 respectively (≈155° and ≈115° w.r.t each wall normal). Therefore, both pullers and pushers are oriented towards the wall but pullers are more tilted towards it. The detailed discussion of the results for squirmers close to the bottom wall (z < 1.5DRDF) will be addressed in the next section (Section 3.3). Two secondary peaks are observed around z = 2DRDF and z = 8.4DRDF (zoom available in the ESI†) that also show a mean orientation slightly tilted towards the nearest wall 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α〉 ≈ ±0.1. Further into the bulk a constant 〈cos
α〉 ≈ ±0.1. Further into the bulk a constant 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α〉 ≈ 0 is observed that stems from an isotropic distribution (see the ESI,† the first column of Fig. S5).
α〉 ≈ 0 is observed that stems from an isotropic distribution (see the ESI,† the first column of Fig. S5).
For the lowest gravities considered, Fg/Fp ≤ 0.3, the orientations in the bulk region tilt upwards for both pullers and pushers until the top wall is reached as squirmers more aligned with the vertical direction can travel a wider span of heights. Although both pullers and pushers reach the top wall, only pullers display an upward peak at z ≈ 9.4DRDF concurring with their tendency to reorient perpendicular to the wall via HIs, in agreement with ref. 45. As gravity increases, squirmers need a more upward orientation to access the same heights than for weaker gravity. For Fg/Fp = 1/2, heights above z ≳ 4DRDF and z ≳ 5DRDF become unreachable for pullers and pushers respectively. Pushers access slightly higher regions than pullers, since they tend to align parallel to each other (decreasing α) while pullers tend to align perpendicularly (increasing α) thus sinking.56 Close to the second layer, at z ≈ 2DRDF, a depletion as particles swim away from the bottom wall is observed for all Fg/Fp. As we increase z, particles start reorienting upwards consistently with previous predictions100 (see also Fig. S5 of the ESI† for a more direct comparison).
Our results for Fg/Fp = 0.15 are in agreement to those reported in ref. 44, since we also detect a bimodal P(z,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) for close to the wall pullers, for which negative orientations are more likely than positive ones (Fig. S5 of the ESI,† 2nd column). However, for pushers, P(z,cos
θ) for close to the wall pullers, for which negative orientations are more likely than positive ones (Fig. S5 of the ESI,† 2nd column). However, for pushers, P(z,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) is unimodal and more centered (in our case the most likely orientations do not exactly match probably due to the colloid's asphericity). Our bulk distribution for pullers is also alike, with a noticeable bias towards positive orientations, although the one for pushers does not differ from pullers as much as those reported in ref. 44.
θ) is unimodal and more centered (in our case the most likely orientations do not exactly match probably due to the colloid's asphericity). Our bulk distribution for pullers is also alike, with a noticeable bias towards positive orientations, although the one for pushers does not differ from pullers as much as those reported in ref. 44.
3.3 Characterization of the bottom layer
Fig. 4 represents the formation and structure of the bottom layer once sedimentation has occurred for B1 = 50 and β = ±10, corresponding to Fp = 2B1/3 = 100/3, with 0.00 ≤ Fg ≤ 75 and the passive case as a reference system.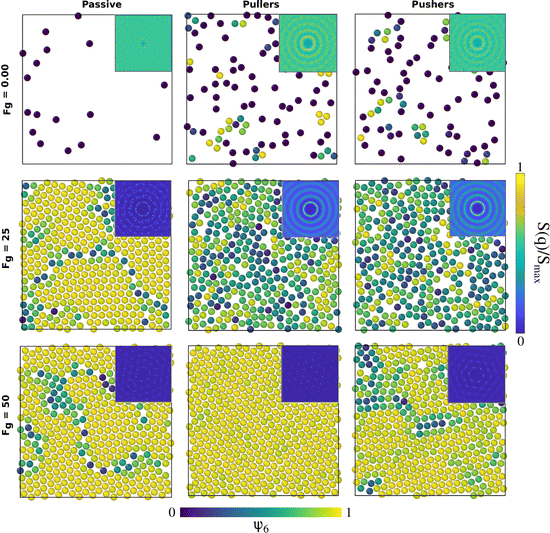 | ||
| Fig. 4 Configurations of the colloids' centres of mass at the bottom layer in the steady state for passive colloids, pullers and pushers at different Fg values. The microswimmers' propulsion force is Fp = 33.33. Colloids are represented with a radius of RC,eff = 1.85, 2RC,eff being the contact distance between colloids according to the pair correlation function in the top row of Fig. 8. The colloids' color code is the value of the hexagonal order parameter, ψ6, as in the color bar. The insets are the two-dimensional static structure factor (SFF) measured for the colloids at the bottom layer (the color bar represents the normalized intensity, S(q)/Smax, of the SFF). The axes of the insets (not shown) are the components of the wave vectors qx and qy and range from −2π to 2π. An animated version of this figure is provided in the ESI.† | ||
Upon increasing gravity, Fg, in both active and passive systems, colloids deposited at the bottom layer undergo a transition to a phase with hexagonal order, which depends on the systems activity. The hydrodynamic signature of the squirmers affects not only when the transition takes place but also the structural properties of the crystalline phase. Steady state snapshots of the colloids at the bottom layer at three selected gravitational fields, Fg, are shown in Fig. 4, where the colloids are represented in different colors depending on the values of their hexagonal order parameter, ψ6. The insets of the snapshots contain the two-dimensional SSF (see eqn (7)).
In the absence of gravity, Fig. 4 top row, the SSF of the passive system exhibits a rather homogeneous intensity, meaning that the structure is disordered and resembles a gas. The SSF for both pullers and pushers shows signatures of a liquid structure but not fully developed. The almost-liquid structure of the active systems is also reflected in the fact that both pullers and pushers tend to accumulate close to the walls even without gravity, as reported in the packing fraction profiles of Fig. 3. Visual inspection of the colloids close to the wall (see supplementary videos, ESI†) shows that as gravity increases the system undergoes a transition from a kissing-like state49 to a weak dynamic clustering phase. At an intermediate gravity, Fg = 25 (central row), passive colloids form a solid structure and the SFF shows features of a defective hexagonal crystal as defects appear at short and long ranges. Squirmers, both pullers and pushers, display an SSF of a fully developed liquid. Finally, at a high gravitational field, Fg = 50 (bottom row), all SFFs display the features of a hexagonal ordered phase, with defects present for passive colloids and pushers, whereas pullers form an almost perfect hexagonal crystal. Once passive colloids are deposited at the bottom, they do not change their positions due to thermal motion, and thus the bottom layer is kinetically trapped as a crystal with defects. For long enough simulations, the bottom layer of passive systems should reach a perfect hexagonal order. In contrast, due to activity, the suspensions of pullers and pushers easily overcome the kinetically trapped states forming an ordered hexagonal phase on a much shorter time-scale. From the snapshots and the SFF, it is already visible that pullers tend to maintain the hexagonal order better than pushers. An animated version of Fig. 4 is provided in the ESI.† The observed phases bear resemblance to those reported in ref. 49 and 60 although in our case we do not see a clear formation of dimers, trimers, chains or swarming. We ascribe this to the fluctuations induced by temperature and the high fluid vorticity produced by the large |β| values studied. It should also be noted that in our case the packing fraction is coupled to the gravitational strength (Fig. S4 of the ESI†), so at null and low gravities swimmers are able to escape from the wall.
To better understand the formation of the hexagonal phase and its characteristics, we present in Fig. 5 the probability distributions of the hexagonal order parameter (see eqn (8)), P(ψ6), the local polar order parameter (see eqn (10)), 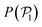 , and the angle between colloids' orientations and the normal vector of the bottom wall, P(α), for suspensions of pullers and pushers for all Fg/Fp values considered.
, and the angle between colloids' orientations and the normal vector of the bottom wall, P(α), for suspensions of pullers and pushers for all Fg/Fp values considered.
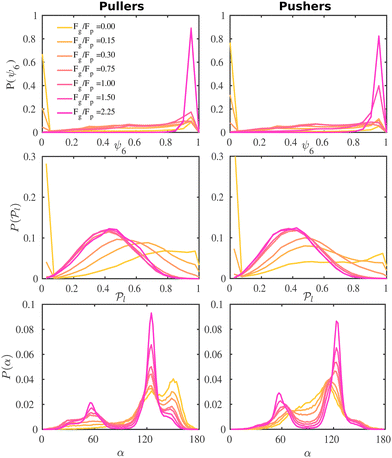 | ||
Fig. 5 Probability distribution functions of the hexagonal order parameter, P(ψ6) (top row), the local polar order parameter, 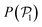 (central row), and the angle between the prescribed orientation of the microswimmers and the bottom wall's normal vector, P(α) (bottom row), for puller (β = 10) and pushers (β = −10) at different Fg/Fp. The bin size to calculate P(ψ6) and (central row), and the angle between the prescribed orientation of the microswimmers and the bottom wall's normal vector, P(α) (bottom row), for puller (β = 10) and pushers (β = −10) at different Fg/Fp. The bin size to calculate P(ψ6) and 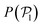 is 0.05 and to calculate P(α) is π/100. See the ESI† for P(α) distributions at different heights. is 0.05 and to calculate P(α) is π/100. See the ESI† for P(α) distributions at different heights. | ||
For weak gravities, Fg/Fp ≤ 0.30, P(ψ6) (top row in Fig. 5) suspensions of pullers and pushers display a very similar behavior, featuring a peak around ψ6 = 0.0 that decreases as Fg increases. This peak is due to the presence of many isolated colloids with no neighbours for which hexagonal order cannot be defined and thus ψ6 is assigned to zero. Otherwise, the distributions are spread rather uniformly up to high values of ψ6 where a small peak is already visible. For Fg/Fp = 0.75, there are enough colloids in the bottom layer and thus ψ6 is defined for all the squirmers. The distributions flatten and the small peak around high values of ψ6 decreases. At high gravities, (Fg/Fp > 1.00), the distributions for both pullers and pushers display a pronounced peak around ψ6 = 0.95. Nevertheless, the distributions for pullers are virtually overlapping for the two highest gravities (Fg/Fp = 1.50, 2.25), whereas the distributions for pushers indicate that the fully-developed hexagonal phase is only observed at the highest gravitational field of Fg/Fp = 2.25 and the distribution for Fg/Fp = 1.50 only shows a small peak. This points out that pullers favour the formation of hexagonal order and thus the transition develops at smaller gravities than for pushers.
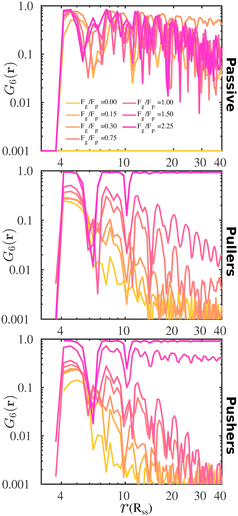
To complement the analysis of the P(ψ6) and be able to qualitatively classify the hexagonal phases at the bottom layer, we compute the hexagonal order correlation function, G6(r) (see eqn (9)), and display them in Fig. 6. For passive colloids, the correlations decay slowly and are noisy due to the defects on the hexagonal structure. For pullers, at high gravitational fields, G6(r) does not decay, as expected for a hexagonal crystal. At smaller gravitational fields, G6(r) shows the typical exponential decay of liquids. Pushers display the signature of a hexagonal crystal for the highest gravity, Fg/Fp = 2.25, and probably a power law decay indicating a hexatic phase for Fg/Fp = 1.50. At smaller gravitational fields, the correlations decay exponentially.
We now investigate the local polar order which has been observed in experiments of active droplets,101 Janus particles102 and even vibrated active disks103 in which hydrodynamics is not present. Computing the distributions of the local polar order parameter, 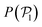 (central row in Fig. 5) allows us to determine the alignment of colloids with respect to their first neighbors. In the absence of gravity
(central row in Fig. 5) allows us to determine the alignment of colloids with respect to their first neighbors. In the absence of gravity 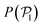 displays a pronounced peak around zero both for pullers and pushers, because many colloids do not have neighbors. The distribution for pullers is shifted to higher values of
displays a pronounced peak around zero both for pullers and pushers, because many colloids do not have neighbors. The distribution for pullers is shifted to higher values of 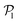 than for pushers, consistently with previous results.104,105 Both distributions also feature a small peak around
than for pushers, consistently with previous results.104,105 Both distributions also feature a small peak around 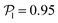 , corresponding to the alignment of colloids with few neighbors. Local alignment decreases with gravity, leading to a left shift of
, corresponding to the alignment of colloids with few neighbors. Local alignment decreases with gravity, leading to a left shift of 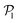 . For Fg/Fp = 0.15 and 0.30,
. For Fg/Fp = 0.15 and 0.30, 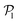 exhibits wide peaks at
exhibits wide peaks at 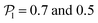 , for pullers and pushers respectively, indicating, on average, an alignment between neighbors coming from the local interactions between microswimmers. In the supplementary video (ESI†) video4_local-pol.avi it can be observed how microswimmers (both pullers and pushers) within
, for pullers and pushers respectively, indicating, on average, an alignment between neighbors coming from the local interactions between microswimmers. In the supplementary video (ESI†) video4_local-pol.avi it can be observed how microswimmers (both pullers and pushers) within 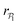 align with themselves when gravity is absent. In the case of pullers, the local alignment occurs when groups of swimmers form small clusters rapidly disappearing due to swimmers moving in different directions. In the case of pushers, besides the formation of high local polar-order clusters, we often observe that, after an encounter, swimmers move together along the bottom wall during short times before moving apart. To confirm that local polarization is not only produced by squirmers aligning with the wall but also by squirmers aligning with each other, we show the local polar order parameter distributions,
align with themselves when gravity is absent. In the case of pullers, the local alignment occurs when groups of swimmers form small clusters rapidly disappearing due to swimmers moving in different directions. In the case of pushers, besides the formation of high local polar-order clusters, we often observe that, after an encounter, swimmers move together along the bottom wall during short times before moving apart. To confirm that local polarization is not only produced by squirmers aligning with the wall but also by squirmers aligning with each other, we show the local polar order parameter distributions, 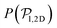 , calculated using the 2D projections of the swimmers' orientation onto the bottom wall's plane (see Fig. S6 of the ESI†). These display a peak around 0.95, for both pullers and pushers, which is higher for pushers, consistently with their tendency to align parallel to the bottom wall and between each other. For pushers, at Fg/Fp = 0.15 and 0.30, the distributions feature peaks around
, calculated using the 2D projections of the swimmers' orientation onto the bottom wall's plane (see Fig. S6 of the ESI†). These display a peak around 0.95, for both pullers and pushers, which is higher for pushers, consistently with their tendency to align parallel to the bottom wall and between each other. For pushers, at Fg/Fp = 0.15 and 0.30, the distributions feature peaks around 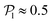 . For Fg/Fp ≥ 0.75, the distributions peak at
. For Fg/Fp ≥ 0.75, the distributions peak at 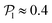 . As gravity becomes stronger, the packing fraction at the bottom layer increases and local alignment is hindered due to the increase of squirmer interactions that randomize the orientations because of the high strength of the stresslets. The resulting distribution approaches the expected one for uniformly distributed 3D orientations, although slightly shifted to higher
. As gravity becomes stronger, the packing fraction at the bottom layer increases and local alignment is hindered due to the increase of squirmer interactions that randomize the orientations because of the high strength of the stresslets. The resulting distribution approaches the expected one for uniformly distributed 3D orientations, although slightly shifted to higher 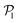 values because of the induced vertical alignment coming from the steric interactions due to the swimmers asphericity. This is further confirmed since the 2D distributions
values because of the induced vertical alignment coming from the steric interactions due to the swimmers asphericity. This is further confirmed since the 2D distributions 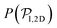 are in very good agreement with the expected one for uniformly distributed 2D orientations.
are in very good agreement with the expected one for uniformly distributed 2D orientations.
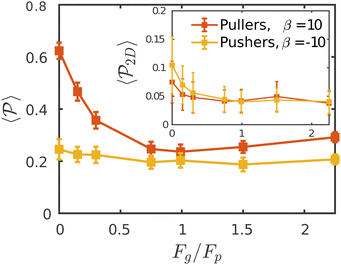
Having studied the probability distribution of the local polar order parameter, we now report the global polar order parameter, 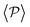 in Fig. 7 for pullers and pushers at the bottom layer, as a function of gravity.
in Fig. 7 for pullers and pushers at the bottom layer, as a function of gravity.
Although local alignment as a function of gravity is similar for pullers and pushers, 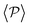 shows a qualitatively different behavior. For pullers, it decreases as gravity increases, which can be attributed to the hindrance of polar order with packing fraction,105 and the more frequent pairwise interactions. The observed modest increase for Fg/Fp > 1 might be due to the asphericity of the raspberry structure that might promote certain angles when steric interactions with the bottom wall become stronger (see Fig. S8 in the ESI†). There are two contributions to the global polar order at the bottom layer, the direct interactions among swimmers and indirectly, their alignment with the wall. The inset of Fig. 7 shows that although the interaction among squirmers produces some polarization, the dominant contribution is the alignment with the wall. Similar to what happened previously with the local alignment, for Fg/Fp < 0.75, the 2D polarization
shows a qualitatively different behavior. For pullers, it decreases as gravity increases, which can be attributed to the hindrance of polar order with packing fraction,105 and the more frequent pairwise interactions. The observed modest increase for Fg/Fp > 1 might be due to the asphericity of the raspberry structure that might promote certain angles when steric interactions with the bottom wall become stronger (see Fig. S8 in the ESI†). There are two contributions to the global polar order at the bottom layer, the direct interactions among swimmers and indirectly, their alignment with the wall. The inset of Fig. 7 shows that although the interaction among squirmers produces some polarization, the dominant contribution is the alignment with the wall. Similar to what happened previously with the local alignment, for Fg/Fp < 0.75, the 2D polarization 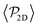 is higher for pushers than for pullers, contrary to what happens in the 3D case. This is so since pushers swim side-by-side more stably than pullers (and thus contribute more to
is higher for pushers than for pullers, contrary to what happens in the 3D case. This is so since pushers swim side-by-side more stably than pullers (and thus contribute more to 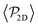 ) and pullers have a more stable orientation when facing the wall than pushers (thus contributing more to
) and pullers have a more stable orientation when facing the wall than pushers (thus contributing more to 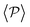 ). Although both
). Although both 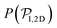 and
and 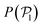 are of the same magnitude, the same is not true for
are of the same magnitude, the same is not true for 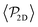 and
and 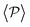 , since the alignment with the wall contributes both to local and global polarizations, whereas the direct squirmer interactions contribute less to the global than to the local polarization (as different local polarizations cancel between each other).
, since the alignment with the wall contributes both to local and global polarizations, whereas the direct squirmer interactions contribute less to the global than to the local polarization (as different local polarizations cancel between each other).
Regarding 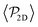 similar, albeit larger, polar order has been found in ref. 49 and 60 in which swarming is found for pushers but not for pullers. Regarding
similar, albeit larger, polar order has been found in ref. 49 and 60 in which swarming is found for pushers but not for pullers. Regarding 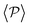 , although global polar order has also been found in previous studies in squirmer suspensions either in bulk,30,38,105 in confinement104 and under gravity,100 in our system, the behavior of
, although global polar order has also been found in previous studies in squirmer suspensions either in bulk,30,38,105 in confinement104 and under gravity,100 in our system, the behavior of 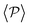 is mostly controlled by the interplay between the hydrodynamic coupling to the wall and the fluctuations induced by temperature106 and stresslets.38 The increased puller polarization induced by the wall (
is mostly controlled by the interplay between the hydrodynamic coupling to the wall and the fluctuations induced by temperature106 and stresslets.38 The increased puller polarization induced by the wall (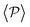 in Fig. 7) correlates with their aggregation at the bottom layer (ϕ2D in Fig. S4 of ESI†) for low gravitational fields.34
in Fig. 7) correlates with their aggregation at the bottom layer (ϕ2D in Fig. S4 of ESI†) for low gravitational fields.34
Although previous studies have argued that asymptotic near-field hydrodynamics strongly determines squirmer interactions and alignment,30,34,52,86 in our case we see some global polar order in 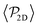 without the need of lubrication corrections. In ref. 38 large global polar order is also found for bulk suspensions of pullers also without lubrication corrections.
without the need of lubrication corrections. In ref. 38 large global polar order is also found for bulk suspensions of pullers also without lubrication corrections.
In order to analyze in more detail the alignment of squirmers with the wall, we calculate the distribution, P(α), of the angle between the colloid orientation and the normal vector to the bottom wall (Fig. 5, bottom row); hence α = 0° corresponds to the squirmer pointing upwards, α = 180° pointing downwards, and α = 90° oriented parallel to the wall in the xy plane.
In the absence of gravity, the distribution for pullers displays two peaks, as they tend to align with the wall forming angles α ≈ 125° and 155°. Additionally, a valley around α = 90° shows the low probability of pullers being oriented parallel to the wall. For pushers the distribution takes non-negligible values around α = 90° as expected, and we also note how a peak develops at α ≈ 115° while the one at 155° is absent. This difference in the wall alignment both for pullers and pushers has also been observed in LB simulations.107 Not surprisingly, the most probable angles are far from the theoretical prediction for a single squirmer.97 In ref. 58 the authors find tilt angles of α = 132° for pullers and α = 62° for pushers of strength β = ±9.6 in LB simulations of a single squirmer interacting with a wall. Our work is in a qualitative agreement for pullers, although the angles for pushers are in sharp contrast. Again, this is not surprising since in our case interactions between squirmers, thermal fluctuations and asphericity of the swimmers need to be taken into account. In ref. 54 the authors carry out computational fluid dynamics simulations (CFD) for a single and multiple squirmers between walls and find that although a single squirmer with β < 1 is scattered by the wall with α < 90° (in contrast to ref. 58 where squirmers scatter for |β| < 2), when multiple squirmers are present, they aggregate near the wall and their orientation is tilted towards it with 〈α〉 ≈ 135° (for β = 3) and ≈120° (for β = −3), which is in better agreement with our results.
As gravity increases, the probability of finding a pusher parallel to the wall decreases, reaching values close to zero for the highest gravitational fields applied. Unlike pullers, pushers are rarely oriented towards the wall forming angles around α = 155°. Instead, when pointing towards the wall, pushers form a preferred angle around α = 125°, as can be observed from the peak in the distributions. Such a peak becomes more pronounced as the gravitational field increases. Similar to pullers, when pointing away from the wall pushers also form angles around α = 60°, but in this case the peak in the distributions is present for all gravitational fields considered. These peaks can be seen in the bottom left panel of Fig. 3 (see Fig. S3 of the ESI† for a zoom): the two first peaks correspond to the negative peak 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α〉 = −0.7, that shrinks to 〈cos
α〉 = −0.7, that shrinks to 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α〉 = −0.5 when increasing gravity, and the third one to the positive peak 〈cos
α〉 = −0.5 when increasing gravity, and the third one to the positive peak 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α〉 = 0.5 at slightly higher z. As displayed in Fig. S3 of the ESI,† the variation of 〈cos
α〉 = 0.5 at slightly higher z. As displayed in Fig. S3 of the ESI,† the variation of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α〉 with height is smooth for pullers, even reaching a minimum at z ≈ 0.95DRDF, and sharper for pushers, departing from a non-zero derivative and increasing almost linearly without passing through any minimum.
α〉 with height is smooth for pullers, even reaching a minimum at z ≈ 0.95DRDF, and sharper for pushers, departing from a non-zero derivative and increasing almost linearly without passing through any minimum.
At the highest gravitational fields, the P(α) distributions for pullers and pushers are very similar, suggesting that hydrodynamics plays a smaller role in the orientation of microswimmers with respect to the wall. This is clear since hexagonal symmetry of the bottom layer is close-packed and thus the microswimmers can barely move under such conditions. The distributions feature a short peak around α = 60° and a high peak around α = 125°, indicating that although the preferred orientation of the squirmers is still pointing towards the wall, some point away, unlike orientations observed at low gravity. This feature can also be detected in Fig. S3 of the ESI† where the peak in ϕ2D happens at heights where 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α〉 is negative, while the maximum values of 〈cos
α〉 is negative, while the maximum values of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α〉 correspond to a ϕ2D an order of magnitude lower. The preferred angles at these high gravitational fields are also related to the swimmers' raspberry structures. Although the DPD cut-off radius makes the swimmers approximately spherical, there is still a steric contribution to the settled positions of the colloids on the bottom wall (see Fig. S8 of the ESI†).
α〉 correspond to a ϕ2D an order of magnitude lower. The preferred angles at these high gravitational fields are also related to the swimmers' raspberry structures. Although the DPD cut-off radius makes the swimmers approximately spherical, there is still a steric contribution to the settled positions of the colloids on the bottom wall (see Fig. S8 of the ESI†).
For completeness, we briefly review the possible mechanisms contributing to the vertical squirmer orientation. In a recent simulation work on ellipsoidal squirmers confined in thin layers, angles around 60° and 120° with respect to the normal axis of the wall were also observed.59 For purely spherical squirmers, a more pronounced upward orientation is seen in ref. 49 that is the highest for neutral squirmers and decreases with increasing |β|, the authors also find that pushers tilt away from the vertical and their height increases as, they argue, they move through a “transitional region between the upright orientation at the wall as calculated in lubrication theory and the parallel far-field orientation”. The effect of the interplay between far-field and lubrication in the swimmers orientation is also analyzed in ref. 55 and 56.
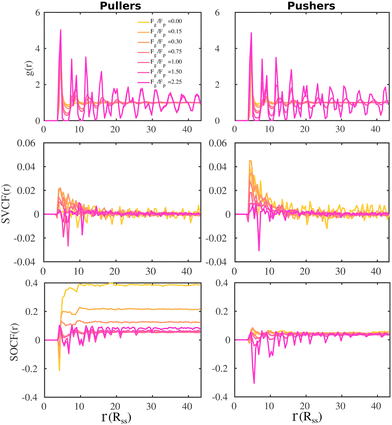
To gain further information on the alignment of the microswimmers at the bottom layer, we compute the SVCF and SOCF. In Fig. 8 we present the pair correlation function, g(r) (top panels), the SVCF(r) (middle panels) and the SOCF(r) (bottom panels).
As already noted from the SSF (see Fig. 4), the g(r) (top panels) show how swimmers at the bottom layer form a hexagonal array as the gravitational field increases for both suspensions of pullers and pushers. The SVCF(r) (middle panels) for both pullers and pushers show a positive correlation at short distances that rapidly decays for Fg/Fp ≤ 1.0. Upon increasing gravity, the correlation for pushers monotonically decreases to negative values at the highest imposed gravitational field. However, for pullers the behavior is non-monotonic, first increasing up to Fg/Fp = 0.15 and then decreasing, assuming negative values for Fg/Fp ≥ 1.50.
It is noteworthy that the g(r) (top panels) and the SOCF(r) (bottom panels) are correlated, especially at high gravitational fields, indicating that positive and negative correlations of the swimmer orientation are somehow correlated at the same time with the hexagonal structure of the bottom layer. For low gravitational fields (Fg/Fp ≤ 0.30), the first peak of the SOCF(r) for pullers is negative, being less pronounced as the gravitational field decreases. This means that at short-range pullers tend to orient in a partially anti-parallel way with each other. At longer distances, we observe how the contributions of the SOCF(r) becomes positive (squirmers are oriented partially parallel) and then reach a constant value, being the case with no gravity the one corresponding to the highest positive correlation. For the highest Fg/Fp, the SOCF(r) reveals that pullers orientation positively contribute to the correlation at short-range. Then, at longer distances, the SOCF(r) describes the hexagonal structure of the layer in such a way the peaks of the g(r) coincide with the regions of positive correlation, while the minima of the g(r) with regions of negative correlation. Finally, the SOCF(r) of pusher suspensions also correlate well with the hexagonal structure of the bottom layer at high gravitational fields, with the difference that now the regions of negative correlations are more pronounced than those of the SOCF(r) for pullers. Additionally, at low gravitational fields, the SOCF(r) for pushers acquires small positive values at long-range.
The results shown for the SOCF(r) (bottom panels in Fig. 8) match with the results of 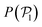 and P(α) presented in Fig. 5. The highest positive correlations are obtained for suspensions of pullers at low gravitational fields, where they are mainly oriented towards the wall; whereas suspensions of pushers exhibit rather small positive correlations at long-range, since their local alignment is low and their orientation with respect to the wall is distributed over a wider range of angles. The SOCF(r) of pullers can also be correlated with the global polar order
and P(α) presented in Fig. 5. The highest positive correlations are obtained for suspensions of pullers at low gravitational fields, where they are mainly oriented towards the wall; whereas suspensions of pushers exhibit rather small positive correlations at long-range, since their local alignment is low and their orientation with respect to the wall is distributed over a wider range of angles. The SOCF(r) of pullers can also be correlated with the global polar order 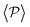 (Fig. 7). Although the SOCF(r) displays a constant value spawning the full simulation box, computing it for the projected orientations onto the xy plane parallel to the wall, SOCF2D(r) (ESI,† Fig. S6), shows that the correlations vanish, suggesting that the observed correlations are due to the vertical alignment of squirmers and are modulated by squirmer interactions, whose relevance increases with gravity.
(Fig. 7). Although the SOCF(r) displays a constant value spawning the full simulation box, computing it for the projected orientations onto the xy plane parallel to the wall, SOCF2D(r) (ESI,† Fig. S6), shows that the correlations vanish, suggesting that the observed correlations are due to the vertical alignment of squirmers and are modulated by squirmer interactions, whose relevance increases with gravity.
4 Conclusions
In summary, DPD simulations have been performed to study sedimentation of raspberry-like colloidal suspensions bounded between parallel walls (Fig. 1). When colloids are passive, the observed sedimentation velocity (Fig. 2) is qualitatively well captured by the Stokes law considering a height-independent friction coefficient, with a small overestimation ascribable to the packing fraction correction for collective sedimentation90 and to the varying friction coefficient induced by the walls.34 When passive colloids are replaced by squirmers, in the absence of gravity they accumulate at walls due to activity, as expected (e.g.Fig. 3). This aggregation is greater for pullers than for pushers due to the interplay between hydrodynamics and temperature, agreeing with previous studies32,54,55 (although other works report different results57,58). Near the walls, the orientation for both pullers and pushers is tilted to the wall, more prominently for pullers than for pushers, consistently with far-field hydrodynamics.97 We noted that the characteristic orientation angles observed are also influenced by squirmer interactions, the absence of lubrication corrections and the asphericity of the colloid. Far from the walls, the swimmers vertical orientations distribute isotropically. Consistently with previous studies,44,45 at moderate gravitational fields, where swimmers can still reach the top wall, we observe an exponential decay of the squirmer packing fraction (Fig. 3) with sedimentation lengths that are always higher than for passive colloids, being greater for pushers than for pullers and decreasing with increasing gravity. We argued that pushers are able to access higher regions due to pairwise far-field HIs near a boundary described in a recent work.56 We observed no sign of previously reported bioconvenction45 and argued that the geometry of the simulation domain and the strength of the stresslet may be responsible. However, polar order is observed in the bulk region where swimmers’ orientations tilt upwards as we increase the gravitational field. As gravity is increased further, certain heights become inaccessible to swimmers, the exponential regime is broken and two well defined bottom layers begin to develop.Once colloids have settled, the structure of the bottom layer was analyzed. It was observed that the bottom layer undergoes a transition from an isotropic liquid to a hexagonal crystal as gravity is increased (see Fig. 4, 5, first row, and Fig. 6). To the best of our knowledge, this is the first time that such transition has been described in the context of a sedimented monolayer of squirmers. Previous works have reported phases with hexagonal symmetry,49,60 but none of them compatible with a hexagonal crystal as shown here. In the reference case of passive colloids, the hexagonal crystal contains many defects, due to the fact that the system is kinetically trapped in states that thermal motion is not able to overcome. For pullers and pushers there was no observation of any kinetically trapped state, since their activity allows their rearrangement into more ordered structures. However, pullers tend to preserve the hexagonal order better than pushers: this is reflected in the fact that a perfect hexagonal crystal is obtained for pullers at lower gravitational fields. This is related to the hydrodynamic field generated by pullers and pushers. For the former, hydrodynamics favours the orientation of the swimmers pointing towards the wall with a certain persistence that hinders their mobility; whereas in the latter it favours orientations of the swimmers parallel to the wall, making them more motile and thus more prone to alter the order of the bottom layer.
It was also observed that, although the local polar alignment is similar in both pullers and pushers despite the gravitational field (see Fig. 5, central row), the global polar alignment is higher for pullers than for pushers for all Fg/Fp and shows a non-monotonic behaviour with a minimum at Fg/Fp = 1.0. While pushers always display a low global polar alignment (see Fig. 7). In the absence of gravity, the dominant contribution to the high polar order exhibited by pullers comes from their interactions with the wall and is modulated by squirmer pairwise interactions. The reduction in this polar order, when gravity is increased, was explained taking into account the increase of the packing fraction at the bottom layer, which has been shown to hinder polar order. The difference in polar order between pullers and pushers was explained through the interplay of hydrodynamics and thermal fluctuations, being pullers more stable under reorientations.
It was found that at high gravitational fields, both pullers and pushers not only are mainly oriented towards the wall, forming an angle with respect to the wall's normal vector of about 120°, but are also oriented pointing away from the wall with a preferred angle of about 60° (see Fig. 5, bottom row). As described above, this preferred orientations with respect to the wall do not correlate with the polar alignment of the microswimmers at high gravitational fields. However, from low to moderate gravitational fields, pushers tend to align parallel to the wall (high values of P(α) around α = 90°) whereas pullers tend to align towards the wall forming angles of 125° and 155°, which explains the high polar order exhibited by pullers and the low polar order of pushers.
This picture becomes clearer when analysing the spatial correlation functions at the bottom layer (see Fig. 8). Apart from the transition from an isotropic liquid to a hexagonal crystal also observed from the pair correlation functions (see Fig. 8, top row), we confirm that the orientations of the pullers are correlated throughout the entire system from low to intermediate gravitational fields, whereas pushers display low correlation (see Fig. 8, bottom row). Interestingly, at high gravitational fields, although the SOCF(r) are rather low at long distances for pullers and pushers, at short distances they correlate with the g(r), showing positive correlations at the g(r) maxima and negative correlations at the g(r) minima, being this effect more pronounced for pushers. Regarding the SVCF(r), the behaviour is very similar for both microswimmer types, showing positive correlations for low to intermediate gravitational fields at short distances, and negative correlations at short distances for high gravitational fields.
To conclude, there are many possible extensions with the possibility of practical applications of the presented study. Few possible studies to develop in the coming future include: an analysis of the dynamics of the deposited bottom layer, the study of the effects of including lubrication corrections, the effects of multilayers' formation on the structure of the bottom layer, broader scans of parameters such as propulsion force, squirmer parameter or temperature to promote pair-wise squirmer alignment, sedimentation of mixtures of active and passive colloids and different colloid and/or bounding geometry.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
C. V. acknowledges funding IHRC22/00002 and PID2022-140407NB-C21 from MINECO. This project has received funding from the European Union's Horizon research and innovation programme under the Marie Skłodowska-Curie grant agreement no 101108868 (BIOMICAR). I. P. acknowledges financial support from DURSI under Project No. 2021SGR-673, Ministerio de Ciencia, Innovación y Universidades MCIU/AEI/FEDER under grant agreement PID2021-126570NB-100 AEI/FEDER-EU and Generalitat de Catalunya for financial support under Program Icrea Acadèmia. We acknowledge MARENOSTRUM-BSC (grant FI-2024-2-0044). C. M. B. G. acknowledges enriching discussions with José Martín-Roca, Juan Pablo Miranda López and Rodrigo Fernandez-Quevedo.Notes and references
- G. Gompper, R. G. Winkler, T. Speck, A. Solon, C. Nardini, F. Peruani, H. Löwen, R. Golestanian, U. B. Kaupp and L. Alvarez, et al. , J. Phys.: Condens. Matter, 2020, 32, 193001 CrossRef CAS PubMed.
- M. C. Marchetti, J.-F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143 CrossRef CAS.
- H. Stark, Eur. Phys. J.:Spec. Top., 2016, 225, 2369–2387 Search PubMed.
- A. Javadi, J. Arrieta, I. Tuval and M. Polin, Philos. Trans. R. Soc., A, 2020, 378, 20190523 CrossRef CAS PubMed.
- M. A. Bees, Annu. Rev. Fluid Mech., 2020, 52, 449–476 CrossRef.
- T. Pedley and J. Kessler, Sci. Prog., 1992, 105–123 Search PubMed.
- Z. Alloui, T. Nguyen and E. Bilgen, Int. J. Heat Mass Transfer, 2007, 50, 1435–1441 CrossRef CAS.
- A. Ramamonjy, P. Brunet and J. Dervaux, J. Fluid Mech., 2023, 971, A29 CrossRef.
- A. Kage, C. Hosoya, S. A. Baba and Y. Mogami, J. Exp. Biol., 2013, 216, 4557–4566 Search PubMed.
- S. Lynch, K. Mukundakrishnan, M. Benoit, P. Ayyaswamy and A. Matin, Appl. Environ. Microbiol., 2006, 72, 7701–7710 CrossRef CAS PubMed.
- R. J. McLean, J. M. Cassanto, M. B. Barnes and J. H. Koo, FEMS Microbiol. Lett., 2001, 195, 115–119 CrossRef CAS PubMed.
- D. R. Korber, J. R. Lawrence, L. Zhang and D. E. Caldwell, Biofouling, 1990, 2, 335–350 CrossRef.
- S. J. Ebbens and D. A. Gregory, Acc. Chem. Res., 2018, 51, 1931–1939 CrossRef CAS PubMed.
- P. Sharan, Z. Xiao, V. Mancuso, W. E. Uspal and J. Simmchen, ACS Nano, 2022, 16, 4599–4608 CrossRef CAS PubMed.
- D. P. Singh, W. E. Uspal, M. N. Popescu, L. G. Wilson and P. Fischer, Adv. Funct. Mater., 2018, 28, 1706660 CrossRef.
- M. R. Bailey, F. Grillo, N. D. Spencer and L. Isa, Adv. Funct. Mater., 2022, 32, 2109175 CrossRef CAS.
- M. R. Bailey, C. M. B. Gutiérrez, J. Martín-Roca, V. Niggel, V. Carrasco-Fadanelli, I. Buttinoni, I. Pagonabarraga, L. Isa and C. Valeriani, Nanoscale, 2024, 16, 2444–2451 RSC.
- C. Krüger, C. Bahr, S. Herminghaus and C. C. Maass, Eur. Phys. J. E:Soft Matter Biol. Phys., 2016, 39, 64 CrossRef PubMed.
- S. Thutupalli, D. Geyer, R. Singh, R. Adhikari and H. A. Stone, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5403–5408 CrossRef CAS PubMed.
- B. V. Hokmabad, A. Nishide, P. Ramesh, C. Krüger and C. C. Maass, Soft Matter, 2022, 18, 2731–2741 RSC.
- G. D. M. Carvajal, B. Taidi and M. Jarrahi, Algal Res., 2024, 77, 103350 CrossRef.
- J. Dervaux, M. Capellazzi Resta and P. Brunet, Nat. Phys., 2017, 13, 306–312 Search PubMed.
- H. Chen, H. Zhang, T. Xu and J. Yu, ACS Nano, 2021, 15, 15625–15644 CrossRef CAS PubMed.
- Y. Fu, H. Yu, X. Zhang, P. Malgaretti, V. Kishore and W. Wang, Micromachines, 2022, 13, 295 CrossRef PubMed.
- J. Tailleur and M. E. Cates, Europhys. Lett., 2009, 86, 60002 CrossRef.
- K. Wolff, A. M. Hahn and H. Stark, Eur. Phys. J. E:Soft Matter Biol. Phys., 2013, 36, 43 CrossRef CAS PubMed.
- C. G. Wagner, M. F. Hagan and A. Baskaran, J. Stat. Mech.:Theory Exp., 2017, 2017, 043203 CrossRef.
- S. Hermann and M. Schmidt, Soft Matter, 2018, 14, 1614–1621 RSC.
- J. Vachier and M. G. Mazza, Eur. Phys. J. E:Soft Matter Biol. Phys., 2019, 42, 11 CrossRef PubMed.
- T. Ishikawa, J. T. Locsei and T. J. Pedley, J. Fluid Mech., 2008, 615, 401–431 CrossRef.
- S. E. Spagnolie and E. Lauga, J. Fluid Mech., 2012, 700, 105–147 CrossRef.
- K. Ishimoto and E. A. Gaffney, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2013, 88, 062702 CrossRef PubMed.
- E. Lauga, The Fluid Dynamics of Cell Motility, Cambridge University Press, 1st edn, 2020 Search PubMed.
- F. Rühle, J. Blaschke, J.-T. Kuhr and H. Stark, New J. Phys., 2018, 20, 025003 CrossRef.
- Y. Ying, T. Jiang, S. Li, D. Nie and J. Lin, Phys. Scr., 2024, 99, 025304 CrossRef CAS.
- D. Nie, Y. Ying, G. Guan, J. Lin and Z. Ouyang, J. Fluid Mech., 2023, 960, A31 CrossRef CAS.
- G. Guan, J. Lin and D. Nie, Entropy, 2022, 24, 1564 CrossRef PubMed.
- F. Alarcón and I. Pagonabarraga, J. Mol. Liq., 2013, 185, 56–61 CrossRef.
- T. Vicsek, A. Czirók, E. Ben-Jacob, I. Cohen and O. Shochet, Phys. Rev. Lett., 1995, 75, 1226 CrossRef CAS PubMed.
- H. Chaté, F. Ginelli, G. Grégoire, F. Peruani and F. Raynaud, Eur. Phys. J. B, 2008, 64, 451–456 CrossRef.
- H. Chaté, Annu. Rev. Condens. Matter Phys., 2020, 11, 189–212 CrossRef.
- R. Kürsten and T. Ihle, Phys. Rev. Lett., 2020, 125, 188003 CrossRef PubMed.
- A. P. Solon, H. Chaté and J. Tailleur, Phys. Rev. Lett., 2015, 114, 068101 CrossRef PubMed.
- A. Scagliarini and I. Pagonabarraga, Soft Matter, 2022, 18, 2407–2413 RSC.
- J.-T. Kuhr, J. Blaschke, F. Rühle and H. Stark, Soft Matter, 2017, 13, 7548–7555 RSC.
- F. Rühle and H. Stark, Eur. Phys. J. E:Soft Matter Biol. Phys., 2020, 43, 1–17 CrossRef PubMed.
- F. Rühle, A. W. Zantop and H. Stark, Eur. Phys. J. E:Soft Matter Biol. Phys., 2022, 45, 26 CrossRef PubMed.
- B. O. T. Maldonado, S. Pradeep, R. Ran, D. Jerolmack and P. E. Arratia, J. Fluid Mech., 2024, 988, A9 CrossRef.
- J.-T. Kuhr, F. Rühle and H. Stark, Soft Matter, 2019, 15, 5685–5694 RSC.
- A. Moncho-Jordá, A. Louis and J. Padding, Phys. Rev. Lett., 2010, 104, 068301 CrossRef PubMed.
- E. Lattuada, S. Buzzaccaro and R. Piazza, Phys. Rev. Lett., 2016, 116, 038301 CrossRef PubMed.
- J.-B. Delfau, J. Molina and M. Sano, Europhys. Lett., 2016, 114, 24001 CrossRef.
- D. Bárdfalvy, V. Škultéty, C. Nardini, A. Morozov and J. Stenhammar, Commun. Phys., 2024, 7, 93 CrossRef.
- G.-J. Li and A. M. Ardekani, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2014, 90, 013010 CrossRef PubMed.
- K. Schaar, A. Zöttl and H. Stark, Phys. Rev. Lett., 2015, 115, 038101 CrossRef PubMed.
- A. Théry, C. C. Maaß and E. Lauga, R. Soc. Open Sci., 2023, 10, 230223 CrossRef PubMed.
- I. Llopis and I. Pagonabarraga, J. Non-Newtonian Fluid Mech., 2010, 165, 946–952 CrossRef CAS.
- Z. Shen, A. Würger and J. S. Lintuvuori, Eur. Phys. J. E:Soft Matter Biol. Phys., 2018, 41, 1–9 CrossRef CAS PubMed.
- B. Wu-Zhang, D. A. Fedosov and G. Gompper, Soft Matter, 2024, 20, 5687–5702 RSC.
- Z. Shen and J. S. Lintuvuori, Phys. Rev. Fluids, 2019, 4, 123101 CrossRef.
- C. M. Barriuso Gutiérrez, J. Martn-Roca, V. Bianco, I. Pagonabarraga and C. Valeriani, Front. Phys., 2022, 10, 926609 CrossRef.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2009, 18, 015012 CrossRef.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS.
- E. S. Boek and P. Van Der Schoot, Int. J. Mod. Phys. C, 1998, 09, 1307–1318 CrossRef.
- J. B. Gibson, K. Zhang, K. Chen, S. Chynoweth and C. W. Manke, Mol. Simul., 1999, 23, 1–41 CrossRef CAS.
- M. Whittle and E. Dickinson, J. Colloid Interface Sci., 2001, 242, 106–109 CrossRef CAS.
- M. Whittle and K. P. Travis, J. Chem. Phys., 2010, 132, 124906 CrossRef PubMed.
- E. I. Barcelos, S. Khani, A. Boromand, L. F. Vieira, J. A. Lee, J. Peet, M. F. Naccache and J. Maia, Comput. Phys. Commun., 2021, 258, 107618 CrossRef CAS.
- T. Curk, J. Chem. Phys., 2024, 160, 174115 CrossRef CAS PubMed.
- A. Lamura, G. Gompper, T. Ihle and D. M. Kroll, Europhys. Lett., 2001, 56, 319–325 CrossRef CAS.
- A. Zöttl and H. Stark, Eur. Phys. J. E:Soft Matter Biol. Phys., 2018, 41, 61 CrossRef PubMed.
- V. Lobaskin and B. Dünweg, New J. Phys., 2004, 6, 54 CrossRef.
- J. de Graaf, H. Menke, A. J. T. M. Mathijssen, M. Fabritius, C. Holm and T. N. Shendruk, J. Chem. Phys., 2016, 144, 134106 CrossRef PubMed.
- A. I. Campbell, S. J. Ebbens, P. Illien and R. Golestanian, Nat. Commun., 2019, 10, 3952 CrossRef PubMed.
- M. J. Lighthill, Commun. Pure Appl. Math., 1952, 5, 109–118 CrossRef.
- J. R. Blake, J. Fluid Mech., 1971, 46, 199–208 CrossRef.
- M. Revenga, I. Zúñiga, P. Español and I. Pagonabarraga, Int. J. Mod. Phys. C, 1998, 09, 1319–1328 CrossRef.
- S. M. Willemsen, H. C. J. Hoefsloot and P. D. Iedema, Int. J. Mod. Phys. C, 2000, 11, 881–890 Search PubMed.
- I. V. Pivkin and G. E. Karniadakis, J. Comput. Phys., 2005, 207, 114–128 CrossRef.
- A. Mehboudi and M. S. Saidi, Sci. Iran., 2011, 18, 1253–1260 CrossRef.
- S. K. Ranjith, B. S. V. Patnaik and S. Vedantam, J. Comput. Phys., 2013, 232, 174–188 CrossRef.
- Z. Li, X. Bian, Y.-H. Tang and G. E. Karniadakis, J. Comput. Phys., 2018, 355, 534–547 CrossRef CAS.
- Y. Wang, J. She and Z. Zhou, Appl. Math. Mech., 2021, 42, 467–484 CrossRef.
- T. Ishikawa, M. P. Simmonds and T. J. Pedley, J. Fluid Mech., 2006, 568, 119 CrossRef.
- I. O. Götze and G. Gompper, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2010, 82, 041921 CrossRef PubMed.
- J. S. Lintuvuori, A. T. Brown, K. Stratford and D. Marenduzzo, Soft Matter, 2016, 12, 7959–7968 RSC.
- B. Halperin and D. R. Nelson, Phys. Rev. Lett., 1978, 41, 121 CrossRef CAS.
- D. R. Nelson and B. Halperin, Phys. Rev. B:Condens. Matter Mater. Phys., 1979, 19, 2457 CrossRef CAS.
- W. B. Russel, D. A. Saville and W. R. Schowalter, Colloidal Dispersions, Cambridge University Press, 1989 Search PubMed.
- G. Perkins and R. Jones, Phys. A, 1992, 189, 447–477 CrossRef CAS.
- J. Happel and H. Brenner, Low Reynolds number hydrodynamics: with special applications to particulate media, Springer Netherlands, Dordrecht, 1983, vol. 1 Search PubMed.
- Rothschild, Nature, 1963, 198, 1221–1222 CrossRef.
- A. P. Berke, L. Turner, H. C. Berg and E. Lauga, Phys. Rev. Lett., 2008, 101, 038102 CrossRef PubMed.
- G. Li and J. X. Tang, Phys. Rev. Lett., 2009, 103, 078101 CrossRef PubMed.
- M. Molaei, M. Barry, R. Stocker and J. Sheng, Phys. Rev. Lett., 2014, 113, 068103 CrossRef PubMed.
- E. Lauga and T. R. Powers, Rep. Prog. Phys., 2009, 72, 096601 CrossRef.
- J. Palacci, C. Cottin-Bizonne, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2010, 105, 088304 CrossRef PubMed.
- F. Ginot, I. Theurkauff, D. Levis, C. Ybert, L. Bocquet, L. Berthier and C. Cottin-Bizonne, Phys. Rev. X, 2015, 5, 011004 CAS.
- M. Enculescu and H. Stark, Phys. Rev. Lett., 2011, 107, 058301 CrossRef PubMed.
- S. Thutupalli, R. Seemann and S. Herminghaus, New J. Phys., 2011, 13, 073021 CrossRef.
- D. Nishiguchi and M. Sano, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2015, 92, 052309 CrossRef PubMed.
- J. Deseigne, O. Dauchot and H. Chaté, Phys. Rev. Lett., 2010, 105, 098001 CrossRef PubMed.
- N. Oyama, J. J. Molina and R. Yamamoto, Phys. Rev. E, 2016, 93, 043114 CrossRef PubMed.
- A. A. Evans, T. Ishikawa, T. Yamaguchi and E. Lauga, Phys. Fluids, 2011, 23, 111702 CrossRef.
- A. Zöttl and H. Stark, Phys. Rev. Lett., 2014, 112, 118101 CrossRef PubMed.
- Z. Ouyang, J. Lin and X. Ku, Rheol. Acta, 2018, 57, 655–671 CrossRef CAS.
Footnotes |
† Electronic supplementary information (ESI) available: The present manuscript is accompanied by a document supp_info.pdf with additional results and 4 video files: video1.avi: realistic animations of 9 of the studied simulations showing the time evolution of passive, puller and pusher systems under null, moderate and strong gravitational force. The orientation of the colloids is displayed as a red bead in each of the raspberry colloids. video2_psi6.avi: the video file contains an animated version of Fig. 4 without the SSF insets. video3_cos-alpha.avi: the same as video2_psi6.avi but the color code shows the vertical orientation of swimmers measured as cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α. video4_local-pol.avi: the same as video2_psi6.avi but the color code shows the local polarization. See DOI: https://doi.org/10.1039/d4sm01356e α. video4_local-pol.avi: the same as video2_psi6.avi but the color code shows the local polarization. See DOI: https://doi.org/10.1039/d4sm01356e |
| ‡ The authors equally contributed to this work. |
| § https://gitlab.com/hyperactivematter/acdpdh. |
| ¶ https://docs.lammps.org/Packages_details.html#pkg-dpd-basic. |
| || https://docs.lammps.org/Packages_details.html#pkg-rigid. |
| ** Pathological depletion interactions stemming from the coarse-grained nature of DPD are well known and have been studied and tackled in different ways from the origins of the DPD framework until very recently.65–70 |
| †† Since we choose a larger DPD filler–wall interaction cutoff than the filler–solvent one, there will always be a gap between the colloid–wall effective surfaces with respect to the solvent interactions. If there was no overlap, this gap would be δw = Rwf − Rfs/2 − Rws/2 = 1.5Rss = 0.43Dcs, where Dcs = 2Rcs = 2Rin + Rfs = 3.5Rss is the swimmer's body-length with respect to filler–solvent interactions (see Fig. 1). However, due to the softness of the DPD interaction, there is some overlap: thus, the minimum effective gap (estimated via the radial distribution functions, see the ESI†) is δRDFw ≈ 1.4Rss = 0.7DRDFcs. Likewise, when colloids interact with each other, without overlap, the gap is δc = Rff − Rfs = 1.5Rss = 0.43Dcs and estimating distances via RDFs, δRDFc ≈ DRDFcs. The reason the gap, measured in body lengths, is larger when the RDFs are considered (which might seem counter-intuitive) is because the overlap between filler and solvent particles is greater than that between fillers or between wall and filler particles, since Afs < Aff < Awf (see Table 1). Thus, the overlap in the measuring unit (the body length), Dcs − DRDFcs = 1.5Rss, is greater than in the measured quantities (the gaps), δc − δRDFc = 0.5Rss and δw − δRDFw = 0.1Rss. |
| ‡‡ It should be noted that these values were obtained by computing the 2D packing fraction for the first layer with a wide bin size of Δz = RRDF = 2.1Rss. In the ESI,† Fig. S3, we study the peaks for a smaller bin size (Δz = 0.044Rss): the height difference of the peaks between pullers and pushers is reduced as gravity increases. The peaks' widths and tails are also affected by gravity; thus, when we compute the packing fraction with Δz = RRDF, the difference between pullers and pushers appears constant. |
| This journal is © The Royal Society of Chemistry 2025 |