DOI:
10.1039/D4SM01390E
(Paper)
Soft Matter, 2025,
21, 1373-1381
One- and two-particle microrheology of soft materials based on optical-flow image analysis†‡
Received
22nd November 2024
, Accepted 9th January 2025
First published on 14th January 2025
Abstract
Particle-tracking microrheology probes the rheology of soft materials by accurately tracking an ensemble of embedded colloidal tracer particles. One-particle analysis, which focuses on the trajectory of individual tracers is ideal for homogeneous materials that do not interact with the particles. By contrast, the characterization of heterogeneous, micro-structured materials or those where particles interact directly with the medium requires a two-particle analysis that characterizes correlations between the trajectories of distinct particle pairs. Here, we propose an optical-flow image analysis as an alternative to the tracking-based algorithms to extract one and two-particle microrheology information from video microscopy images acquired using diverse imaging contrast modalities. This technique, termed optical-flow microrheology (OFM), represents a high-throughput, operator-free approach for the characterization of a broad range of soft materials, making microrheology accessible to a wider scientific community.
1 Introduction
Microrheology is an invaluable tool to study the rheological properties of a large variety of soft matter systems, including cells and other biological samples.1–7 Compared to traditional rheometry, microrheology requires small sample volumes, enables local measurements, spans a broad frequency range, and works with extremely soft samples. In its simplest implementation, passive microrheology, the thermal Brownian motion of colloidal tracer particles is analyzed to probe the linear viscoelastic properties of the host material. In the one-particle (1P) analysis scheme this is done by quantifying the thermally-induced positional fluctuations of individual particles,8 yielding the mean square displacement (MSD) 〈Δr2(t)〉, from which the complex shear modulus of the material G*(ω) = G′(ω) + iG′′(ω) is obtained through the generalized Stokes–Einstein relation| | 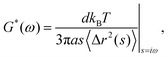 | (1) |
with d the dimensionality, kBT the thermal energy, a the tracer radius, i the imaginary unit, and 〈Δr2(s)〉 the Laplace transform of the MSD.
Over the years, several 1P microrheology techniques have been developed, based on either particle tracking,9 dynamic light scattering,10,11 diffusing wave spectroscopy,8 or, more recently, on differential dynamic microscopy.12–14 However, for mechanically heterogeneous media or when the particle directly influences the local environment of the medium in which it is embedded, all these approaches fail to properly measure the bulk mechanical properties of the material. This challenge is overcome by two-particle (2P) microrheology,15 which minimizes local effects by analyzing correlated displacements between particle pairs separated by distances larger than the sample microstructural heterogeneities. Repeating this operation over a large collection of particle pairs permits for the determination of the bulk rheological material response.16 It is worth noting that, since 2P microrheology probes the mechanical properties of the sample over length scales much larger than the tracer size, the exact tracer size does not need to be known, and the tracers do not need to be monodisperse.
In practice, 2P microrheology relies on the evaluation of the two-particle displacement cross-correlation tensor
| | | Dμν(r,Δt) = 〈Δx(n)μΔx(m)νδ(r − r(nm))〉, | (2) |
where the indices
μ and
ν denote spatial components,
m and
n indicate distinct particles, Δ
x(n)μ corresponds to the displacement of a particle
n along the direction
μ between time
t and
t + Δ
t, while
r(nm) =
x(n) −
x(m) is their relative position vector at time
t. The averages 〈⋯〉 are taken over all the particles
n and the pairs of distinct particles
n and
m and, in the case of stationary samples, they can also be taken over different initial time points
t and over different realizations.
15 Usually,
Dμν is expressed in a reference frame with one axis parallel to the line connecting the centers of the particles (see also Fig. S1 in ESI
†), where it becomes diagonal with eigenvalues
D‖ (non degenerate) and
D⊥ (two-fold degenerate).
17 For an incompressible medium, the flow field generated by a point-like stress source decays for large distances
r ≫
a as 1/
r,
18 and it can be shown that the two-particle displacement spatial cross-correlation tensor can be expressed in terms of the frequency-dependent bulk modulus
![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif)
(
s)
¶.
16,19,20 Specifically, one has
| | 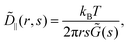 | (3) |
where
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ‖
‖(
r,
s) is the Laplace transform of
D‖(
r,Δ
t), which does not depend on the tracer radius. The above equation can also be expressed in terms of the perpendicular component
D⊥, exploiting the fact that
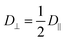
. Comparing
eqn (1) and (3) suggests to define a distinct or two-particle (2P) MSD, 〈Δ
r2(Δ
t)〉
2P as
15| | 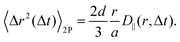 | (4) |
While for a perfectly homogeneous medium 1P MSD and 2P MSD are expected to coincide, in environments presenting heterogeneities on the scale of the tracer size, systematic deviations from the generalized Stokes–Einstein relation (eqn (1)) can occur and a significant difference is expected.20 The above definition enables generalizing eqn (1) to the case of non-homogeneous materials, providing a unified recipe to obtain rheological information from the MSD.
Historically, all implementations of 2P microrheology have relied on particle-tracking analysis using optical microscopy. A fundamental limitation of this approach is the rapid decay of the cross-correlation signal with increasing interparticle distance, necessitating continuous monitoring of a large number of particles over extended time periods. This requirement poses significant computational challenges. In addition, the extreme sensitivity to tracking artifacts often demands meticulous parameter optimization and supervision by a skilled operator. It was recently demonstrated that 2P information can also be obtained in diffusing wave spectroscopy microrheology experiments probing the correlated motion of concentrated colloidal particles.21 However, extending this approach to enable tracking-free 2P microrheology in samples seeded with a relatively small number of tracer particles remains a significant challenge to date.
In this work, we introduce a tracking-free method to determine the one- and two-particle mean square displacements, which form the basis for one-particle (eqn (1)) and two-particle (eqn (3)) microrheology, respectively. This method, termed optical flow microrheology (OFM), builds on optical flow, an image processing concept designed to capture motion by analyzing spatio-temporal intensity changes at each pixel.22,23 In our approach, optical flow images are generated from the difference between two image frames separated by a short time interval Δt, multiplied by a spatial derivative of the image intensity distribution. We demonstrate that the spatial correlations of these optical flow images provide robust estimates of both one- and two-particle MSDs of tracer particles. The validity of OFM is tested with a model Newtonian fluid as well as a viscoelastic solution of entangled semiflexible biopolymers (actin filaments). The latter is known to require the 2P microrheology scheme to obtain a correct estimate of the bulk rheological properties, due to the effects of tracer particles on the structure of nearby actin filaments.15,24,25 To further highlight the capabilities of OFM, we also study the hydrodynamic interactions between colloidal particles in quasi-2D confinement.26,27
2 Materials and methods
Throughout this work, we will assume that, while particles move in three dimensions, those contributing to the optical signal are positioned approximately within the object plane of the microscope. This assumption implies that the depth of field of the imaging setup is small compared to the typical interparticle distance, such that the “real” distance between two particles can be reliably estimated as the distance between their projections on the image plane.28 Formally, this enables us to reduce the problem to a two-dimensional one, with x and r indicating positions and relative positions within the plane, respectively, and Dμν representing a two-dimensional rank-two tensor. Moreover, hereafter, the one- and two-particle MSDs, denoted as 〈Δr2〉 and 〈Δr2〉2P, respectively, are assumed to refer to the motion along a single spatial dimension. This choice corresponds to set d = 1 in eqn (1) and (4).
2.1 Basics of OFM
To understand how OFM works it is useful to introduce the displacement map| | 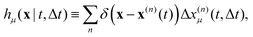 | (5) |
which is non-zero at the positions of each particle n at time t, where it assumes the displacement value Δx(n)μ(t,Δt) along the direction μ during the interval Δt. Using eqn (2) it is straightforward to obtain the identity| | 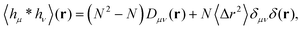 | (6) |
where 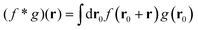 is the spatial cross-correlation. Here, N is the number of particles, and 〈Δr2〉 represents the one-particle MSD. To simplify the notation, we omitted the time dependence in the above equation. Eqn (6) shows that knowing hμ provides immediate access to both Dμν(r) and 〈Δr2〉. Let us now outline how to obtain an excellent approximation of hμ by using an image analysis scheme as the one illustrated for a simplified 1D implementation in Fig. 1. We assume that the intensity in the image can be written as
is the spatial cross-correlation. Here, N is the number of particles, and 〈Δr2〉 represents the one-particle MSD. To simplify the notation, we omitted the time dependence in the above equation. Eqn (6) shows that knowing hμ provides immediate access to both Dμν(r) and 〈Δr2〉. Let us now outline how to obtain an excellent approximation of hμ by using an image analysis scheme as the one illustrated for a simplified 1D implementation in Fig. 1. We assume that the intensity in the image can be written as 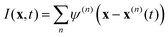 , where ψ(n)(x) represents the intensity distribution of the n-th particle in a reference frame with the origin in the particle's centroid (Fig. 1a). For simplicity, we will assume that all particles share the same intensity distribution ψ(n) = ψ. In a manner similar to optical flow methods,22 we define the map
, where ψ(n)(x) represents the intensity distribution of the n-th particle in a reference frame with the origin in the particle's centroid (Fig. 1a). For simplicity, we will assume that all particles share the same intensity distribution ψ(n) = ψ. In a manner similar to optical flow methods,22 we define the map| | | fμ(x|t,Δt) ≡ −∂μI(x,t)·ΔI(x|t,Δt), | (7) |
where ∂μI denotes the partial derivative of the image intensity with respect to the spatial coordinate μ (Fig. 1d) and ΔI(x|t,Δt) ≡ I(x,t + Δt) − I(x,t) is the variation of the image intensity during a time interval Δt (Fig. 1b and c).
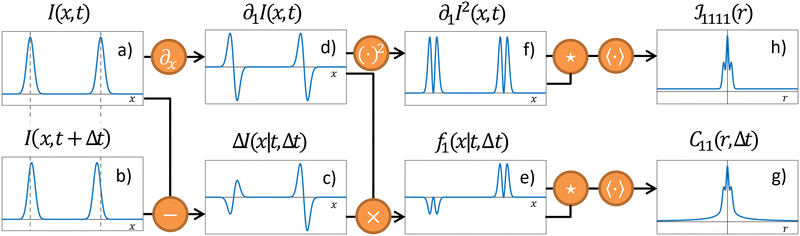 |
| | Fig. 1 Schematic of the OFM algorithm in 1D. (a) Intensity profile I(x,t) at time t. For clarity, only two “particles” are shown. (b) Intensity profile I(x,t + Δt) at a later time t + Δt. Compared to time t the particles are slightly displaced. (c) The difference ΔI(x|t,Δt) shows two distinct “swings”. The amplitude (with sign) of each swing is proportional to the displacement of the corresponding particle, while the overall shape closely mirrors the spatial gradient ∂1I(x,t) of the intensity profile, shown in panel (d). (e) Multiplying ΔI(x|t,Δt) by ∂1I(x,t) provides a spatial map f1(x|t,Δt) where each particle is replaced by a positive definite, compactly supported function, that is centered at the particle position and whose amplitude (with sign) is proportional to the corresponding displacement. (f) The squared gradient [∂xI(x,t)]2 provides a reference map, as [∂xI(x,t)]2Δx corresponds to the f1(x|t,Δt) map when each particle performs the same displacement Δx. (g) and (h) Time- and ensemble-averaged autocorrelation function of fx and of the squared gradient, respectively. Eventually, the one-particle MSD and the displacement cross-correlation tensor are obtained from (g) and (h), exploiting eqn (13) and (14), respectively. | |
If Δt is sufficiently short to ensure that displacements remain small relative to the particle size, then we can approximate
| | 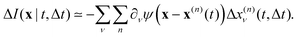 | (8) |
For dilute tracers, image overlap is negligible, so ψ(x − x(n))ψ(x − x(m)) ≃ 0 for n ≠ m. Thus, we derive
| | 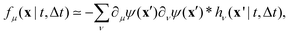 | (9) |
where
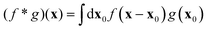
is the spatial convolution, and
hν is as defined in
eqn (5) (
Fig. 1e). In contrast to standard optical flow velocimetry,
29 our objective is not to reconstruct the instantaneous velocity field but to reliably capture its spatiotemporal correlations. To this end, we consider the expectation value of the cross-correlation function
| | 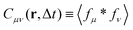 | (10) |
(Fig. 1g) and we obtain
| | 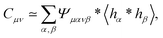 | (11) |
where
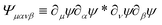
. As shown in detail in the appendix,
eqn (11) can be written directly in terms of the cross-correlation of the products of the partial spatial derivative of the image intensity
| | 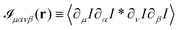 | (12) |
(Fig. 1f and h). For distances r much shorter than the radius a of the particles, we obtain
| | 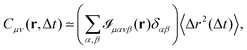 | (13) |
whereas for large distances,
r ≫
a, we get
| | 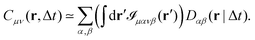 | (14) |
Eqn (13) and (14) represent our main theoretical results, revealing how both the one-particle MSD and the spatial cross-correlation tensor of displacements can be derived through relatively simple image processing. Explicitly, Cμν(r,Δt) is calculated (see eqn (10)) as the mean value of the cross-correlation function of the map fμ(x|t,Δt) defined in eqn (7), whereas the quantities in round brackets in eqn (13) and (14) are computed from the spatial map ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) μανβ, which is obtained from the image intensity distribution according to eqn (12). A detailed derivation of eqn (13) and (14) can be found in the appendix. It is worth noting that the calculation of both Cμν and
μανβ, which is obtained from the image intensity distribution according to eqn (12). A detailed derivation of eqn (13) and (14) can be found in the appendix. It is worth noting that the calculation of both Cμν and ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) μανβ involves the numerical evaluation of spatial derivatives of the image, an operation whose accuracy crucially depends on spatial sampling. Loosely speaking, the digital image of a single particle must be sufficiently “smooth” to ensure that the expansion in eqn (8) provides consistent results. Empirically, we find that this condition is fulfilled whenever the sampling density is above the Nyquist limit, i.e. when the resolution limit of the objective is at least twice as large as the effective pixel size of the camera sensor.30 An illustrative example of the impact of digitation artifacts due to undersampling on the results is reported in ESI† (Fig. S6).
μανβ involves the numerical evaluation of spatial derivatives of the image, an operation whose accuracy crucially depends on spatial sampling. Loosely speaking, the digital image of a single particle must be sufficiently “smooth” to ensure that the expansion in eqn (8) provides consistent results. Empirically, we find that this condition is fulfilled whenever the sampling density is above the Nyquist limit, i.e. when the resolution limit of the objective is at least twice as large as the effective pixel size of the camera sensor.30 An illustrative example of the impact of digitation artifacts due to undersampling on the results is reported in ESI† (Fig. S6).
The eigenvalues D‖ and D⊥ can be extracted from the components Dμν of the cross-correlation tensor, obtained by inverting eqn (14). As schematically illustrated in Fig. S1 (ESI†), for each pair of particles separated by r, the displacements along the two axes can be decomposed in the parallel and the perpendicular direction as Δx1 = Δx‖![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − Δx⊥
θ − Δx⊥![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and Δx2 = Δx‖
θ and Δx2 = Δx‖![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + Δx⊥
θ + Δx⊥![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, respectively, with θ the polar angle of r relative to the x-axis. According to eqn (2), the tensor components Dμν can be expressed in terms of eigenvalues D‖ and D⊥ as
θ, respectively, with θ the polar angle of r relative to the x-axis. According to eqn (2), the tensor components Dμν can be expressed in terms of eigenvalues D‖ and D⊥ as
| | D11 = D⊥ + (D‖ − D⊥)cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ | (15) |
| | D22 = D⊥ + (D‖ − D⊥)sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ | (16) |
| | D12 = D⊥ + (D‖ − D⊥)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, θ, | (17) |
The typical appearance of D11(r,Δt) for an incompressible Newtonian fluid is shown in Fig. 2a. Inspection of eqn (15) suggests two methods for estimating D‖ and D⊥ from the two-dimensional map D11. One option is to perform an azimuthal average of D11(r,Δt) over narrow angular sectors oriented along θ = 0 and θ = π/2, respectively. Alternatively, for each distance r one can fit eqn (15) to the angular profile D11(r,θ,Δt), and simultaneously estimate D‖ and D⊥ as best-fitting parameters (Fig. 2b and c). We found this latter approach to be more reliable and used it for all the analyses presented in this work. The approach illustrated above for D11 can also be applied, with slight modifications, to D22 and D12, by using eqn (16) and (17), respectively. Inverting eqn (13) for each r enables extracting a value for 〈Δr2(Δt)〉, which is then averaged over a small circle of radius r0 ≪ a around the origin to provide the best estimate for the one-particle MSD||. For each r, 〈Δr2(Δt)〉2P is estimated using eqn (4) and the resulting values are averaged over a suitable interval r1 ≤ r ≤ r2, with r1 ≫ a. Sufficiently far from boundaries the equality D‖ = 2D⊥ holds for an incompressible fluid. Therefore D⊥ can be used to estimate independently the 2P MSD, calculated as 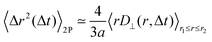 .
.
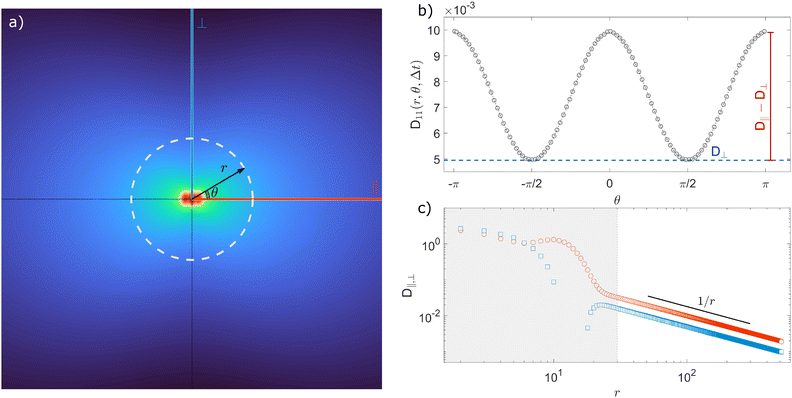 |
| | Fig. 2 Schematic illustration of the procedure for extracting the parallel (D‖) and the perpendicular (D⊥) eigenvalues of the displacement cross-correlation tensor. (a) Pictorial representation of the component D11(r,Δt) of the displacement cross-correlation tensor Dμν(r,Δt) for an incompressible fluid, obtained inverting eqn (14). (b) Angular dependence of D11(r,Δt) (white dashed line in (a)). (c) D‖ and D⊥ as a function of distance r for a fixed delay time Δt. Red circles (blue squares) represent D‖ (D⊥) obtained as a best-fitting parameter to the angular profile using the model in eqn (15). The gray shaded area marks the region r < a where D11 is dominated by same-particle correlations. | |
A MATLAB® implementation of the proposed algorithm is openly available in Zenodo at https://doi.org/10.5281/zenodo.14038680.
In the above presentation, the image of each tracer particle is represented by a time-independent function ψ(r). While this formalism, in principle, is compatible with non-circularly symmetric particle shapes, it does not account for particle rotations, which are expected to contribute to the OFM signal in the case of anisotropic tracers.31 The extension of the OFM framework to include the rotational degree of freedom of the tracer particles is beyond the aim of the present work.
2.2 Particle tracking and differential dynamics microscopy
Particle tracking analysis for the Newtonian fluid was performed using a customized version of the MATLAB® script developed and made freely available by the group of Maria Kilfoil at UPEI (projects.upei.ca/kilfoillab/).32 Particle tracking and two-particle analysis for the actin solution and the quasi-2D colloidal suspension were performed using a MATLAB® implementation33 of the original IDL routines by John Crocker, David Grier, and Eric Weeks.15 Differential dynamic microscopy is used as an independent probe of the diffusive motion of diluted colloidal particles dispersed in a Newtonian fluid. Details on the method and its implementation can be found in ref. 34–36.
2.3 Sample preparation and acquisition
To experimentally validate OFM, we examine three different systems: a Newtonian fluid (a glycerol–water mixture), a solution of entangled semiflexible actin filaments, and colloidal particles confined between two closely spaced parallel rigid surfaces in a quasi-2D geometry. While the first two cases represent typical microrheology applications, the third one allows us to study hydrodynamic interactions.
Newtonian fluid.
Our Newtonian sample is a glycerol–water mixture at a glycerol mass fraction of 95%, which is maintained at a temperature of T = (22 ± 1) °C. Fluorescently labeled polystyrene particles (abs/ems = 530/607 nm) with nominal radius a = 0.49 μm (microParticles GmbH), are dispersed at a volume fraction of ϕ ≃ 0.05%. The sample is loaded in a rectangular glass capillary (Vitrocom, CM Scientific) with a path length of 200 μm along the microscope optical axis. Particle motion is observed at the midplane of the sample using an inverted microscope (Nikon Eclipse Ti-E) equipped with a 20× long-working-distance objective (NA = 0.54), under epifluorescent illumination (Nikon Intenselight C-HGFIE) and using a TRITC filter cube. Sequences of 8000 square images (image size: 520 × 520 pixel2) are acquired at a frame rate of 20 frames per second with a sCMOS camera (Hamamatsu Orca Flash 4.0 v2) with an effective pixel size of dpix = 0.325 μm.
Entangled actin solution.
The entangled solution of actin filaments is prepared by polymerizing Mg-ATP-actin monomers at a concentration of 0.5 mg ml−1. Fluorescent carboxylate-modified polystyrene beads (a = 0.5 μm and ϕ ≃ 0.0004) are embedded within the solution as tracers. Full details on the sample preparation can be found in ref. 37. The sample is sealed in a custom-made sample cell with a path length of 1 mm along the optical axis, and imaging begins 95 minutes after initiating polymerization of actin monomers at ∼24 °C. Under these conditions, the mechanical response is stable for at least 1 hour. The typical mesh size of the actin solution is ∼420 nm and the mean filament length is (15 ± 15) μm. Fluorescence imaging is performed at λ = 650 nm on an inverted microscope (Nikon Ti Eclipse) equipped with a confocal scan head (Yokogawa CSU-X), using a 20× Plan Fluor objective (NA = 0.75) immersed in mineral oil. An additional 1.5× lens (optivar) in the microscope body is engaged to give a final magnification of 30×. To avoid edge effects, the focus is set at 150 μm above the bottom coverglass of the sample cell. Two sets of images with dimensions of 1226 × 1704 pixel2 and effective pixel size of dpix = 0.217 μm are acquired with a sCMOS camera (Andor Zyla 4.2); the first set consists of 2401 frames acquired at 25 Hz, the second of 1081 frames acquired at 1 Hz. Combining the two datasets enables the determination of the particle mean squared displacements over a wide range of delay times Δt.
Quasi-2D colloidal suspension.
To demonstrate the ability of OFM to characterize hydrodynamic interactions in confined environments, we use an aqueous suspension of sulfate latex particles of radius a = 1.4 μm (Molecular Probes), sealed within quasi-two-dimensional (2D) sample cells, which are prepared as follows: 2.3 μl of the colloidal suspension at ϕ = 8% w/v is first deposited onto a microscope slide. A second microscope slide is then carefully placed on top, and the two slides are bonded using UV-curing glue (NOA61, Norland Products Inc.). The assembled cell is mounted on a microscope slide for analysis. The final cell thickness w = 3.2 ± 0.2 μm is determined by a small fraction of particles in the upper tail of the size distribution, which remain trapped between the two glass slides and effectively act as spacers. Visual inspection reveals that the fraction of immobile particles acting as spacers is about 1%. We probe particle motion by acquiring four different series of 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 square images each (image size: 520 × 520 pixel2) at a rate of 500 frames per second. Imaging is performed on a bright field optical microscope equipped with a 20× objective (NA = 0.5) and a digital camera with an effective pixel size of dpix = 0.24 μm.
000 square images each (image size: 520 × 520 pixel2) at a rate of 500 frames per second. Imaging is performed on a bright field optical microscope equipped with a 20× objective (NA = 0.5) and a digital camera with an effective pixel size of dpix = 0.24 μm.
3 Results and discussion
Let us first consider the results obtained for the glycerol–water mixture, a sample expected to exhibit ideal Newtonian behavior. Following the method outlined in Section 2.1, we calculate the parallel (D‖) and perpendicular (D⊥) components of the two-particle displacement spatial cross-correlation tensor from D11 (eqn (15)), as shown in the inset of Fig. 3, both D‖ and D⊥ display for a fixed Δt the expected 1/r scaling at large r.
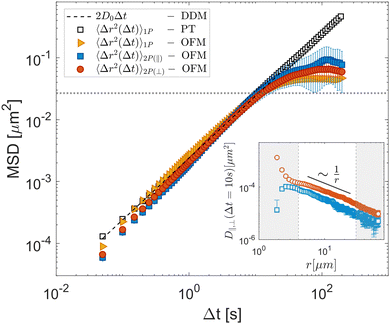 |
| | Fig. 3 Experimental results obtained for a Newtonian fluid (glycerol–water mixture). OFM results for 1P MSD (orange triangles) and 2P MSD computed from the parallel (D‖, orange circles) and perpendicular (D⊥, blue squares) eigenvalues of the displacement tensor are shown as full symbols. Open square symbols represent the one-particle MSD obtained with particle tracking. The dashed line corresponds to 2D0Δt, where D0 = (1.20 ± 0.15) × 10−3 μm2 s−1 is the diffusion coefficient determined by differential dynamic microscopy analysis of the same data. The horizontal dotted line corresponds to (a/3)2, the square of the estimated largest displacement for which the OFM analysis is expected to provide reliable information. Inset: D‖ (red circles) and D⊥ (blues squares) for Δt = 10 s as a function of r. The white area denotes the interval 4.0 μm < r < 30 μm, where D‖,⊥ exhibits 1/r scaling, and from which the two-particle MSD is computed. Error bars represent the standard error estimated over five independent repetitions. | |
Repeating the OFM calculation for different lag times Δt (see ESI†) enables us to determine the time dependences of the 1P and 2P MSD, the latter being independently evaluated from both D‖ and D⊥. These are shown in Fig. 3, where the yellow triangles denote the 1P MSD, the orange circles denote the 2P MSD derived from D‖ and the blue squares that derived from D⊥. Both one- and two-particle MSDs scale linearly with Δt and are mutually consistent, as expected for homogeneous fluids.15 The OFM results also align with the MSDs obtained from particle-tracking analysis (black open squares) in the range of small delay times. Systematic deviations, however, appear for larger delays, where the OFM results converge to a plateau value. This is because OFM relies on a linear expansion of the intensity profile that assumes that particle displacements remain smaller than the particle image size, as discussed in detail in Section 2.1. Based on our experiments we estimate that reliable OFM results are obtained for displacements up to approximately a/3, indicated by the horizontal dotted line in Fig. 3. Let us note that, while the 2P MSD closely approximates the 1P MSD, it is systematically smaller. This minor discrepancy can be attributed to the finite depth of focus of our optical system, which allows slight misalignments along the optical axis. Consequently, the interparticle distance is systematically underestimated, resulting in a lower two-particle MSD value, according to eqn (4).28
A significant advantage of OFM compared to tracking-based 2P microrheology is its capability to independently estimate D‖ and D⊥ through spatial derivatives of the image intensity and displacement along horizontal (x or 1) and vertical (y or 2) directions, as outlined in eqn (15) and (16). In our setup, a non-uniform mechanical drift occurred along the capillary long axis (y-axis), inducing a global shift of root mean square amplitude of about 100 nm during acquisition. Although small, this drift notably influences the D22 component of the displacement cross-correlation tensor. However, the directional independence of OFM permits for an accurate estimation of D11 even when an orthogonal drift is present (see Fig. S2 and S3 in ESI†).
To test OFM on a sample where the individual particle motion fails to reflect the average mechanical properties,3 we use the entangled solution of actin filaments as a typical example of a system where only the 2P MSD properly reflects the bulk mechanical properties due to a direct interaction of the tracer particles with the actin filament.15,24,38 As shown in the inset of Fig. 4, the OFM analysis reveals that D‖ and D⊥ display a 1/r scaling within the range of 4.0 μm < r < 30 μm. Averaging over this range, 2P MSD displays a completely different time dependence compared to the time dependence of the 1P MSD, as shown in the main graph of Fig. 4. Because the particles interact directly with the actin solution, the 1P MSD reaches a plateau at long times, characteristic of arrested motion. By contrast, the 2P MSD increases continuously in time, displaying a sublinear behavior, which reflects the average mechanical response of the system.24 The results obtained with OFM are in excellent agreement with the equivalent quantities calculated based on particle-tracking (black symbols in Fig. 4).39 The corresponding moduli G′ and G′′, estimated using the algebraic form of the generalized Stokes–Einstein equation proposed in ref. 11, are shown in ESI† (Fig. S4). This demonstrates the capability of OFM to provide accurate 2P microrheological characterization of heterogeneous complex fluids without the need for tracking algorithms.
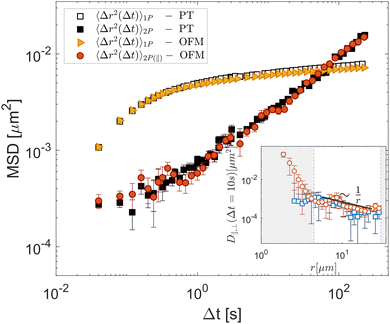 |
| | Fig. 4 Experimental results for a heterogeneous viscoelastic sample (entangled solution of actin filaments). OFM results for 1P MSD (yellow triangles) and 2P MSD (orange circles), the latter obtained by exploiting the parallel component of the displacement tensor (eqn (4)). Squares: 1P MSD (open symbols) and 2P MSD (filled symbols) obtained with particle-tracking. Inset: D‖ (red circles) and D⊥ (blues squares) for Δt = 10 s as a function of r. The white area marks the region 4.5 μm < r < 30 μm, where D‖,⊥ exhibits 1/r scaling. Error bars represent the standard error estimated over six non-overlapping portions of the field of view. | |
Finally, we use our optical flow approach to study the correlated motion of micron-sized particles confined between parallel flat walls, closely spaced by a distance w, in a so-called quasi-2D geometry. Consistently with the results of previous studies,40,41 we find positive correlations along the parallel direction and negative correlations in the transverse direction, as evidenced in the two-dimensional displacement cross-correlation tensor D11 shown in Fig. 5a. This mirrors the fact that in 2D the flow field generated by a point-like moving particle is parallel to the particle's displacement along the direction of motion (the ‖ axis in Fig. 5a), and antiparallel in the transverse direction (the ⊥ axis in Fig. 5a).40 Upon estimating the two eigenvalues of the displacement cross-correlation tensor, we note that both D‖ and D⊥ exhibit a 1/r2 scaling for r > 3w (Fig. S5 in ESI†). This decay is faster compared to the unconfined 3D case, where D‖ and D⊥ scale as ∼1/r for large distances (see insets of Fig. 3 and 4). Our results can be directly compared with those in ref. 40 as the confinement condition, captured by the ratio between particle radius a and cell thickness w, is almost the same in the two studies: a/w = 0.45 ± 0.02 and a/w = 0.44 ± 0.03, in ref. 40 and the present work, respectively. In Fig. 5bD‖(r,Δt) and D⊥(r,Δt), normalized by the one-particle MSD 〈Δr2(Δt)〉, are plotted as a function of r for fixed Δt = 0.002 s (orange circles and blue squares, respectively). As can be appreciated from the figure, for large r our data are in good quantitative agreement with the asymptotic behavior ±0.31(w/r)2 reported for the same quantities in ref. 40 (dashed lines). As with the previous data sets, OFM results closely match particle tracking data, further confirming the validity of our approach.
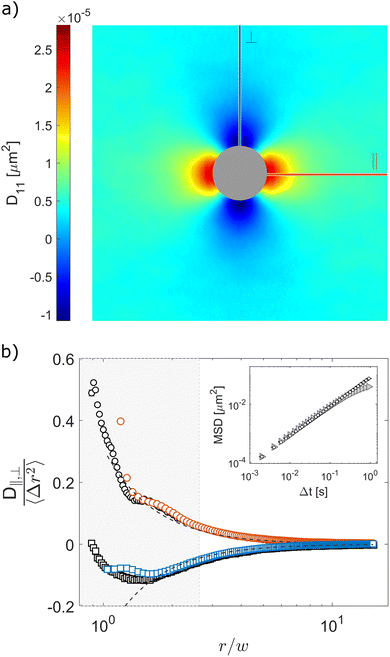 |
| | Fig. 5 Experimental determination of hydrodynamic interactions of micron-sized particles confined between parallel plates. (a) Displacement cross-correlation tensor D11(r,Δt = 0.002 s), with positive (negative) values for displacements parallel (perpendicular) to the x-axis. The central region is patched for better visualization. (b) D‖ (circles) and D⊥ (squares) at time Δt = 0.002 s normalized by the one-particle MSD 〈Δr2〉 obtained from OFM (colored symbols) and particle tracking (black and white symbols) as a function of r/w, where w is the cell thickness. Dashed lines correspond to the large-r asymptotic behavior ±0.31(w/r)2 reported in ref. 40 for the same quantities. Inset: One-particle MSD from OFM (triangles) and particle tracking (circles). Error bars represent the standard error estimated over four independent repetitions. | |
4 Conclusions
In this work, we have introduced optical-flow microrheology (OFM) as a robust method for microrheological analysis. We have demonstrated that OFM applied to microscope images acquired across various contrast modalities (bright-field microscopy for the quasi-2D suspension, wide-field fluorescence microscopy for the Newtonian sample, and confocal fluorescence microscopy for the actin solution) yields reliable one-particle (1P) and two-particle (2P) microrheology results. The core principle of OFM is that the change between two images taken at times t and t + Δt can be modeled as a convolution of the displacement map during Δt and the spatial gradient of the particle intensity profile. This formulation enables the calculation of both the one-particle mean square displacement (MSD) and the displacement cross-correlation tensor components, D‖ and D⊥, representing longitudinal and transverse particle interactions, respectively.
We validated our approach using three distinct samples and found excellent agreement with traditional particle tracking analysis in all cases, attesting to the accuracy and reliability of OFM. This study also identifies an inherent limitation of OFM in its current form: it is optimal for probing small displacements, typically those smaller than the probe particle radius a. While this is advantageous in highly viscoelastic systems, such as the entangled actin network studied here, where particle motion is strongly confined, it hampers the use of OFM to very soft samples, or cases involving small tracers. Moreover, the number density of tracer particles must be low enough to prevent significant particle superpositions in the images, a limitation that also holds for particle tracking-based microrheology.
Nevertheless, OFM offers distinct advantages over conventional tracking-based 2P microrheology. First, the computation time in OFM is determined by image size rather than the number of tracer particles N, contrasting with tracking-based methods where computational demands increase rapidly with N2. This feature can be particularly relevant for applications requiring quasi-real-time monitoring of processes during which the rheological properties of a sample or product rapidly evolve over time and actions are required in response to these changes. Furthermore, OFM requires no operator-dependent inputs for particle selection or identification, reducing the likelihood of user-induced biases. Additionally, the ability of OFM to independently evaluate displacement correlations along orthogonal directions (via D11 and D22) facilitates the detection and correction of artifacts stemming from global drifts or displacements within the sample.
OFM thus represents an easily accessible, high-throughput, operator-independent tool with broad potential for studying the microrheology of diverse soft materials, investigating actively generated stresses in biological systems,42 and exploring fluid-mediated interactions between colloidal particles in complex, confined environments.
Author contributions
Conceptualization (FG, RC), data curation (MB, MAES, FG), formal analysis (MB, FG), funding acquisition (YR, VT, MAES, YR, SUE, FG, RC), investigation (MB, MAES, PMM), methodology (FG), project administration (RC), software (MB, MAES, FG), resources (YR, MLG), supervision (YR, VT, MLG, SUE, FG, RC), visualization (MB), writing – original draft (MB, FG, RC), writing – review and editing (all authors).
Data availability
The data that support the findings of this study and the MATLAB OFM code are openly available on the Zenodo repository https://doi.org/10.5281/zenodo.14038680.
Conflicts of interest
There are no conflicts to declare.
Appendix
Derivation of cross-correlation function Cμν from the image intensity
Here, we derive an expression for the cross-correlation function 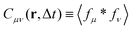 in terms of the cross-correlation of the product of the image partial derivatives
in terms of the cross-correlation of the product of the image partial derivatives 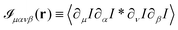 . Throughout the derivation, we will assume that the fluctuation δN in the number N of particles within the field of view is negligible. In other terms, we do not consider the possibility that a particle could enter or exit the field of view during the considered time interval. We start considering the product of the partial derivatives of the image
. Throughout the derivation, we will assume that the fluctuation δN in the number N of particles within the field of view is negligible. In other terms, we do not consider the possibility that a particle could enter or exit the field of view during the considered time interval. We start considering the product of the partial derivatives of the image| | 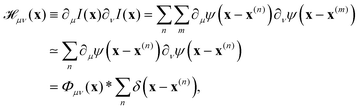 | (18) |
where Φμν(x) ≡ ∂μψ(x)∂νψ(x) and we assume diluted non-overlapping particles. In the above expressions, the time dependence has been omitted to lighten the notation. If we now consider the cross-correlation function  we get
we get| | 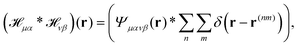 | (19) |
where 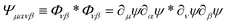 and r(nm) = x(n) − x(m). Taking the expectation value of both sides of the above equation and defining, consistently with eqn (12),
and r(nm) = x(n) − x(m). Taking the expectation value of both sides of the above equation and defining, consistently with eqn (12), 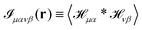 , we obtain
, we obtain| | 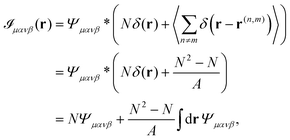 | (20) |
where N is the number of particles and we made use of the fact that 〈δ(r)〉 = 1/A, where A is the area of the region considered. By exploiting the relation| | 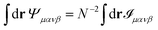 | (21) |
we can write Ψμανβ(r) in terms of ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) μανβ(r) as
μανβ(r) as| | 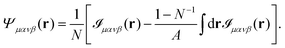 | (22) |
Substituting eqn (6) and (22) in eqn (11) yields in the limit of small distances (r ≪ a)
| | 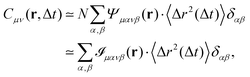 | (23) |
where the second equality is valid up to corrections of order
N−1. In contrast, in the limit of large
r (
r ≫
a) we obtain
| | 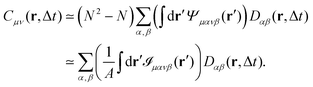 | (24) |
Acknowledgements
We acknowledge support by: Associazione Italiana per la Ricerca sul Cancro (AIRC), Grant No. MFAG-22083 (FG), the Italian Space Agency (ASI), Grant No. 2023-19-U.0 and Grant 2023-20-U.0 (MB, FG), the Swiss National Science Foundation Grant No. 197340 (VT). VT, FG, and RC also would like to thank the Erwin Schrodinger International Institute for Mathematics and Physics (ESI), University of Vienna (Austria) for funding the 2024 Thematic Program “Linking Microscopic Processes to the Macroscopic Rheological Properties in Inert and Living Soft Materials” where part of this work has been carried out.
Notes and references
- T. A. Waigh, Rep. Prog. Phys., 2005, 68, 685 CrossRef.
- P. Cicuta and A. M. Donald, Soft Matter, 2007, 3, 1449–1455 RSC.
- J. C. Crocker and B. D. Hoffman, Methods Cell Biol., 2007, 83, 141–178 CAS.
- D. Wirtz, Annu. Rev. Biophys., 2009, 38, 301–326 CrossRef CAS PubMed.
- T. M. Squires and T. G. Mason, Annu. Rev. Fluid Mech., 2010, 42, 413–438 CrossRef.
- T. A. Waigh, Rep. Prog. Phys., 2016, 79, 074601 CrossRef PubMed.
-
E. M. Furst and T. M. Squires, Microrheology, Oxford University Press, 2017 Search PubMed.
- T. Mason and D. Weitz, Phys. Rev. Lett., 1995, 74, 1250 CrossRef CAS PubMed.
- T. G. Mason, K. Ganesan, J. H. Van Zanten, D. Wirtz and S. C. Kuo, Phys. Rev. Lett., 1997, 79, 3282 CrossRef CAS.
- T. Mason, H. Gang and D. Weitz, J. Mol. Struct., 1996, 383, 81–90 CrossRef CAS.
- B. R. Dasgupta, S. Y. Tee, J. C. Crocker, B. J. Frisken and D. A. Weitz, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2002, 65, 051505 CrossRef PubMed.
- A. V. Bayles, T. M. Squires and M. E. Helgeson, Rheol. Acta, 2017, 56, 863–869 CrossRef CAS.
- P. Edera, D. Bergamini, V. Trappe, F. Giavazzi and R. Cerbino, Phys. Rev. Mater., 2017, 1, 073804 CrossRef.
- M. Escobedo-Sánchez, J. P. Segovia-Gutiérrez, A. Zuccolotto-Bernez, J. Hansen, C.-C. Marciniak, K. Sachowsky, F. Platten and S. U. Egelhaaf, Soft Matter, 2018, 14, 7016–7025 RSC.
- J. C. Crocker, M. T. Valentine, E. R. Weeks, T. Gisler, P. D. Kaplan, A. G. Yodh and D. A. Weitz, Phys. Rev. Lett., 2000, 85, 888–891 CrossRef CAS PubMed.
- A. J. Levine and T. C. Lubensky, Phys. Rev. Lett., 2000, 85, 1774–1777 CrossRef CAS PubMed.
-
L. D. Landau, L. Pitaevskii, A. M. Kosevich and E. M. Lifshitz, Theory of elasticity, Elsevier, 2012, vol. 7 Search PubMed.
-
L. D. Landau and E. M. Lifshitz, Fluid Mechanics, Addison-Wesley, 1959 Search PubMed.
- J.-C. Meiners and S. R. Quake, Phys. Rev. Lett., 1999, 82, 2211 CrossRef CAS.
- A. M. Puertas and T. Voigtmann, J. Phys.: Condens. Matter, 2014, 26, 243101 CrossRef CAS PubMed.
- Q. Li, K. A. Dennis, Y.-F. Lee and E. M. Furst, J. Rheol., 2023, 67, 1107–1118 CrossRef CAS.
- B. K. P. Horn and B. G. Schunck, Artif. Intell., 1981, 17, 185–203 CrossRef.
-
B. D. Lucas and T. Kanade, Proceedings of the 7th International Joint Conference on Artificial Intelligence, San Francisco, CA, USA, 1981, vol. 2, pp. 674–679.
- M. L. Gardel, M. T. Valentine, J. C. Crocker, A. R. Bausch and D. A. Weitz, Phys. Rev. Lett., 2003, 91, 158302 CrossRef CAS PubMed.
- A. Sonn-Segev, A. Bernheim-Groswasser, H. Diamant and Y. Roichman, Phys. Rev. Lett., 2014, 112, 088301 CrossRef.
- B. Cui, H. Diamant, B. Lin and S. A. Rice, Phys. Rev. Lett., 2004, 92, 258301 CrossRef PubMed.
- J. Santana-Solano, A. Ramírez-Saito and J. L. Arauz-Lara, Phys. Rev. Lett., 2005, 95, 198301 CrossRef PubMed.
-
M. L. Gardel, M. T. Valentine and D. A. Weitz, Microscale diagnostic techniques, Springer, 2005, pp. 1–49 Search PubMed.
-
B. D. Lucas and T. Kanade, Proceedings of the 7th International Joint Conference on Artificial Intelligence, San Francisco, CA, USA, 1981, vol. 2, pp. 674–679.
-
J. Pawley, Handbook of biological confocal microscopy, Springer Science & Business Media, 2006, vol. 236 Search PubMed.
- M. A. Kamal, M. Brizioli, T. Zinn, T. Narayanan, R. Cerbino, F. Giavazzi and A. Pal, J. Colloid Interface Sci., 2024, 660, 314–320 CrossRef CAS PubMed.
- V. Pelletier, N. Gal, P. Fournier and M. L. Kilfoil, Phys. Rev. Lett., 2009, 102, 188303 CrossRef PubMed.
- A. Sonn-Segev, A. Bernheim-Groswasser and Y. Roichman, Soft Matter, 2014, 10, 8324–8329 RSC.
- R. Cerbino and V. Trappe, Phys. Rev. Lett., 2008, 100, 188102 CrossRef PubMed.
- F. Giavazzi, D. Brogioli, V. Trappe, T. Bellini and R. Cerbino, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2009, 80, 031403 CrossRef PubMed.
- R. Cerbino and P. Cicuta, J. Chem. Phys., 2017, 147, 110901 CrossRef PubMed.
- P. M. McCall, F. C. MacKintosh, D. R. Kovar and M. L. Gardel, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 12629–12637 CrossRef CAS PubMed.
- J. Liu, M. Gardel, K. Kroy, E. Frey, B. D. Hoffman, J. C. Crocker, A. Bausch and D. Weitz, Phys. Rev. Lett., 2006, 96, 118104 CrossRef CAS PubMed.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310 CrossRef CAS.
- B. Cui, H. Diamant, B. Lin and S. A. Rice, Phys. Rev. Lett., 2004, 92, 258301 CrossRef PubMed.
- J. Santana-Solano, A. Ramírez-Saito and J. L. Arauz-Lara, Phys. Rev. Lett., 2005, 95, 198301 CrossRef PubMed.
- F. Mura, G. Gradziuk and C. P. Broedersz, Soft Matter, 2019, 15, 8067–8076 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01390e |
| ‡ This article is dedicated to the memory of our coauthor, Stefan U. Egelhaaf (17 June 1963–22 November 2023). Stefan was a brilliant scientist, a great teacher, and an esteemed colleague whose significant contributions have greatly enriched the field of experimental soft matter physics. His passion and dedication inspired us all. |
| § Deceased. |
¶ Formally, the complex modulus G*(ω) is given by G*(ω) = ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) (s = iω).8 (s = iω).8 |
| || In our numerical implementation, this spatial average is performed by excluding the pixel at the origin. This expedient prevents the inclusion of a spurious additive term due to noise in the detection chain, which affects the intensity recorded by each pixel of the camera sensor. |
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Manuel A.
Escobedo-Sánchez
a,
Manuel A.
Escobedo-Sánchez
 b,
Patrick M.
McCall
c,
Yael
Roichman
d,
Veronique
Trappe
e,
Margaret L.
Gardel
b,
Patrick M.
McCall
c,
Yael
Roichman
d,
Veronique
Trappe
e,
Margaret L.
Gardel
 c,
Stefan U.
Egelhaaf§
c,
Stefan U.
Egelhaaf§
 b,
Fabio
Giavazzi
b,
Fabio
Giavazzi
 *a and
Roberto
Cerbino
*a and
Roberto
Cerbino
 *f
*f
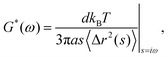
![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) (s)¶.16,19,20 Specifically, one has
(s)¶.16,19,20 Specifically, one has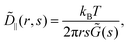
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ‖(r,s) is the Laplace transform of D‖(r,Δt), which does not depend on the tracer radius. The above equation can also be expressed in terms of the perpendicular component D⊥, exploiting the fact that
‖(r,s) is the Laplace transform of D‖(r,Δt), which does not depend on the tracer radius. The above equation can also be expressed in terms of the perpendicular component D⊥, exploiting the fact that 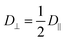 . Comparing eqn (1) and (3) suggests to define a distinct or two-particle (2P) MSD, 〈Δr2(Δt)〉2P as15
. Comparing eqn (1) and (3) suggests to define a distinct or two-particle (2P) MSD, 〈Δr2(Δt)〉2P as15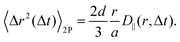
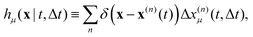
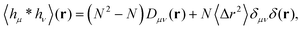
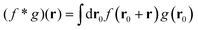 is the spatial cross-correlation. Here, N is the number of particles, and 〈Δr2〉 represents the one-particle MSD. To simplify the notation, we omitted the time dependence in the above equation. Eqn (6) shows that knowing hμ provides immediate access to both Dμν(r) and 〈Δr2〉. Let us now outline how to obtain an excellent approximation of hμ by using an image analysis scheme as the one illustrated for a simplified 1D implementation in Fig. 1. We assume that the intensity in the image can be written as
is the spatial cross-correlation. Here, N is the number of particles, and 〈Δr2〉 represents the one-particle MSD. To simplify the notation, we omitted the time dependence in the above equation. Eqn (6) shows that knowing hμ provides immediate access to both Dμν(r) and 〈Δr2〉. Let us now outline how to obtain an excellent approximation of hμ by using an image analysis scheme as the one illustrated for a simplified 1D implementation in Fig. 1. We assume that the intensity in the image can be written as 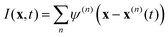 , where ψ(n)(x) represents the intensity distribution of the n-th particle in a reference frame with the origin in the particle's centroid (Fig. 1a). For simplicity, we will assume that all particles share the same intensity distribution ψ(n) = ψ. In a manner similar to optical flow methods,22 we define the map
, where ψ(n)(x) represents the intensity distribution of the n-th particle in a reference frame with the origin in the particle's centroid (Fig. 1a). For simplicity, we will assume that all particles share the same intensity distribution ψ(n) = ψ. In a manner similar to optical flow methods,22 we define the map
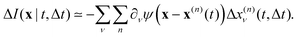
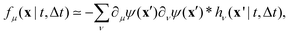
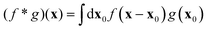 is the spatial convolution, and hν is as defined in eqn (5) (Fig. 1e). In contrast to standard optical flow velocimetry,29 our objective is not to reconstruct the instantaneous velocity field but to reliably capture its spatiotemporal correlations. To this end, we consider the expectation value of the cross-correlation function
is the spatial convolution, and hν is as defined in eqn (5) (Fig. 1e). In contrast to standard optical flow velocimetry,29 our objective is not to reconstruct the instantaneous velocity field but to reliably capture its spatiotemporal correlations. To this end, we consider the expectation value of the cross-correlation function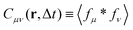
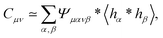
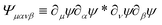 . As shown in detail in the appendix, eqn (11) can be written directly in terms of the cross-correlation of the products of the partial spatial derivative of the image intensity
. As shown in detail in the appendix, eqn (11) can be written directly in terms of the cross-correlation of the products of the partial spatial derivative of the image intensity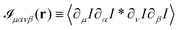
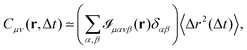
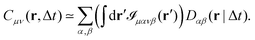
![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) μανβ, which is obtained from the image intensity distribution according to eqn (12). A detailed derivation of eqn (13) and (14) can be found in the appendix. It is worth noting that the calculation of both Cμν and
μανβ, which is obtained from the image intensity distribution according to eqn (12). A detailed derivation of eqn (13) and (14) can be found in the appendix. It is worth noting that the calculation of both Cμν and ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) μανβ involves the numerical evaluation of spatial derivatives of the image, an operation whose accuracy crucially depends on spatial sampling. Loosely speaking, the digital image of a single particle must be sufficiently “smooth” to ensure that the expansion in eqn (8) provides consistent results. Empirically, we find that this condition is fulfilled whenever the sampling density is above the Nyquist limit, i.e. when the resolution limit of the objective is at least twice as large as the effective pixel size of the camera sensor.30 An illustrative example of the impact of digitation artifacts due to undersampling on the results is reported in ESI† (Fig. S6).
μανβ involves the numerical evaluation of spatial derivatives of the image, an operation whose accuracy crucially depends on spatial sampling. Loosely speaking, the digital image of a single particle must be sufficiently “smooth” to ensure that the expansion in eqn (8) provides consistent results. Empirically, we find that this condition is fulfilled whenever the sampling density is above the Nyquist limit, i.e. when the resolution limit of the objective is at least twice as large as the effective pixel size of the camera sensor.30 An illustrative example of the impact of digitation artifacts due to undersampling on the results is reported in ESI† (Fig. S6).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − Δx⊥
θ − Δx⊥![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and Δx2 = Δx‖
θ and Δx2 = Δx‖![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + Δx⊥
θ + Δx⊥![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, respectively, with θ the polar angle of r relative to the x-axis. According to eqn (2), the tensor components Dμν can be expressed in terms of eigenvalues D‖ and D⊥ as
θ, respectively, with θ the polar angle of r relative to the x-axis. According to eqn (2), the tensor components Dμν can be expressed in terms of eigenvalues D‖ and D⊥ as![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,
θ,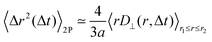 .
.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 square images each (image size: 520 × 520 pixel2) at a rate of 500 frames per second. Imaging is performed on a bright field optical microscope equipped with a 20× objective (NA = 0.5) and a digital camera with an effective pixel size of dpix = 0.24 μm.
000 square images each (image size: 520 × 520 pixel2) at a rate of 500 frames per second. Imaging is performed on a bright field optical microscope equipped with a 20× objective (NA = 0.5) and a digital camera with an effective pixel size of dpix = 0.24 μm.


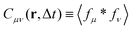 in terms of the cross-correlation of the product of the image partial derivatives
in terms of the cross-correlation of the product of the image partial derivatives 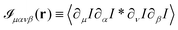 . Throughout the derivation, we will assume that the fluctuation δN in the number N of particles within the field of view is negligible. In other terms, we do not consider the possibility that a particle could enter or exit the field of view during the considered time interval. We start considering the product of the partial derivatives of the image
. Throughout the derivation, we will assume that the fluctuation δN in the number N of particles within the field of view is negligible. In other terms, we do not consider the possibility that a particle could enter or exit the field of view during the considered time interval. We start considering the product of the partial derivatives of the image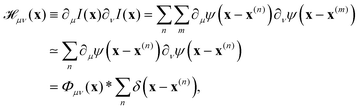
 we get
we get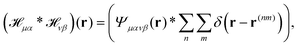
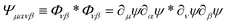 and r(nm) = x(n) − x(m). Taking the expectation value of both sides of the above equation and defining, consistently with eqn (12),
and r(nm) = x(n) − x(m). Taking the expectation value of both sides of the above equation and defining, consistently with eqn (12), 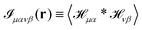 , we obtain
, we obtain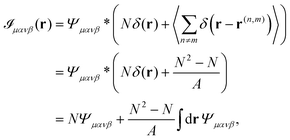
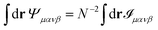
![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) μανβ(r) as
μανβ(r) as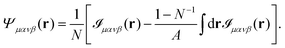
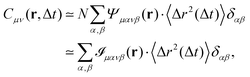
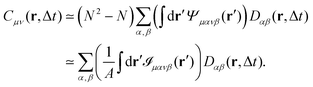
![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) (s = iω).8
(s = iω).8
