Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Capturing the impact of protein unfolding on the dynamic assembly of protein networks†
Matt D. G. Hughes a,
Sophie Cussons
a,
Sophie Cussons bc,
Ahmad Borumand
bc,
Ahmad Borumand a,
Arwen I. I. Tyler
a,
Arwen I. I. Tyler d,
David J. Brockwell
d,
David J. Brockwell bc and
Lorna Dougan
bc and
Lorna Dougan *ab
*ab
aSchool of Physics and Astronomy, Faculty of Engineering and Physical Sciences, University of Leeds, UK. E-mail: L.Dougan@leeds.ac.uk
bAstbury Centre for Structural Molecular Biology, University of Leeds, UK
cSchool of Molecular and Cellular Biology, Faculty of Biological Sciences, University of Leeds, UK
dSchool of Food Science and Nutrition, Faculty of Environment, University of Leeds, UK
First published on 5th February 2025
Abstract
The rapid assembly of molecular or nanoscale building blocks into extended arrays is crucial to the construction of functional networks in vivo and in vitro and depends on various factors. One factor seldom considered is the dynamic changes of the building block shape. Folded protein building blocks offer a unique system to investigate dynamic shape changes due to their intrinsic ability to change from a compact and specific folded structure to an extended unfolded structure in response to a perturbation such as force. Here, we use photochemically crosslinked folded protein hydrogels constructed from force labile protein building blocks as a model dynamic shape-changing network system and characterise them by combining time-resolved rheology and small-angle X-ray scattering (SAXS). This approach probes both the load-bearing network structures, using rheology, and network architectures, using SAXS, thereby providing a crosslength scale understanding of the network formation. We propose a triple assembly model for the structural evolution of networks constructed from force labile protein building block consisting of: primary formation where monomeric folded proteins create the preliminary protein network scaffold; a subsequent secondary formation phase, where larger oligomers of protein diffuse to join the preliminary network scaffold; and finally in situ unfolding and relaxation which leads to the mature network structure of connected larger and denser fractal-like clusters. The time-resolved SAXS data provides evidence that protein unfolding occurs on the edges of the fractal-like clusters, resulting in a population of unfolded proteins in the space between clusters. Identifying the key stages of assembly in protein networks constructed from force labile proteins provides a greater understanding of the importance of protein unfolding in hierarchical biomechanics in vivo and creates future opportunities to develop bespoke biomaterials for novel biomedical applications.
Introduction
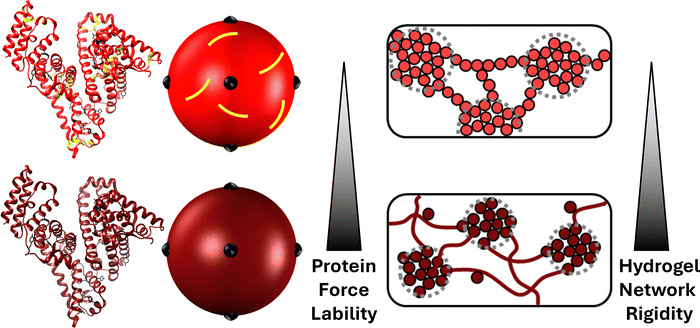
The mechanical unfolding of proteins in vivo is essential to the function of some protein assemblies in living systems.1–3 Within muscles, the PEVK and immunogloblin regions of the giant muscle protein titin act as entropic and enthalpic springs, respectively to ensure energy dissipation and protect muscle fibres from rupture.4–8 Other examples include: bacteria adhesion, in which pathologenic bacteria strongly adhere to their host with adhesin protein which are designed to unfold in response to shear and ensure the bacterium remains attached;9,10 and cellular mechano-transduction caused by the cytoskeletal protein talin unfolding under force, revealing binding sites and allowing the binding of vinculin. This process imbues cells with force-sensing (i.e. greater applied force, more talin unfolding and more vinculin binding).11,12 Proteins are ideal for these roles due to their specific and highly conserved mechanically resistant 3D folded structures, allowing them to unfold at specific forces and orientations.13–18 Over the last three decades, single molecule force spectroscopy experiments have provided a wealth of knowledge and understanding on the mechanical behaviour of individual protein folds.19 These studies identified specific structural motifs which lead to mechanical responses from the folded structure of individual proteins.17,20–22 More recently these experimental studies have been complimented with elastic network modelling23,24 and other computational approaches25,26 to provide insight into the unfolding pathways and force propagation within protein networks. This large body of work has provided an understanding of the force resistant and force labile properties of protein folded structures. Such mechanical properties have made folded proteins extremely attractive as building blocks for engineered biomaterials such as hydrogels.27–32 Indeed, folded proteins have been exploited for their unique nanoscale properties to produce hydrogel matrices, swollen by large volumes of water, with a range of properties including: tuneable swelling behaviour through the protein-folding nanomechanics either via reagent ratios/pH33 or engineered chimeric proteins with mutually exclusive folds;34 shape-morphing and -memory via unfolding or degradation of protein building block domains;35–37 and high stretchability, resilience and toughness achieved by the low unfolding force of the selected/designed protein building block.38–40Protein unfolding defines the mechanics and architecture of protein networks.28,41 Using bovine serum albumin (BSA) as a model protein, a combined cross-lengthscale approach of circular dichroism (CD), small-angle neutron scattering (SANS) and rheology showed that in situ unfolding altered the network topology from dendritic sparse clusters connected by folded protein to larger denser clusters connected via unfolded protein. This change in network morphology resulted in enhanced network mechanical rigidity, demonstrating that protein force lability plays a key role in defining key network properties (Fig. 1). BSA is an ideal model protein due to its native 17 structural disulphide bonds which act as mechanical ‘nano-staples’ preventing BSA from unfolding during network gelation. The protein can be made force labile by chemical reduction of the disulphide bonds allowing unfolding and control of hydrogel networks via protein force lability.
Further corroboration includes coarse-grained simulations and force-clamp rheology which showed that unfolding of proteins defines the load behaviour of folded protein hydrogels.42 Studies have highlighted the role of in situ unfolding and entanglement of unfolded protein strands in defining hydrogel network mechanics.43,44 Entanglement of unfolded protein can be further promoted and manipulated by tuning the thermodynamic and kinetic stabilities of the folded protein building block, resulting in a relative stiffening of the network.44 By exploiting these entanglements, protein hydrogels can be produced with high stiffness (E = 0.70 ± 0.11 MPa) and compressibility (K = 1.7 MPa at 10–20% strain) similar to tissues like cartilage.43 Such control of in situ unfolding provides a powerful route for the design of robust and tuneable biomaterials for medical and healthcare applications. However, despite growing interest in protein hydrogels, including light-based fabrication of biomaterials and de novo design of modular protein hydrogels with programmable viscoelasticity,45,46 the formation pathway of protein networks and the role of in situ protein unfolding remains poorly understood. Such understanding of protein network formation is a complex problem, given the dynamic mechanical properties of the protein building block, and requires careful accounting of time and relaxation parameters to accurately model.47
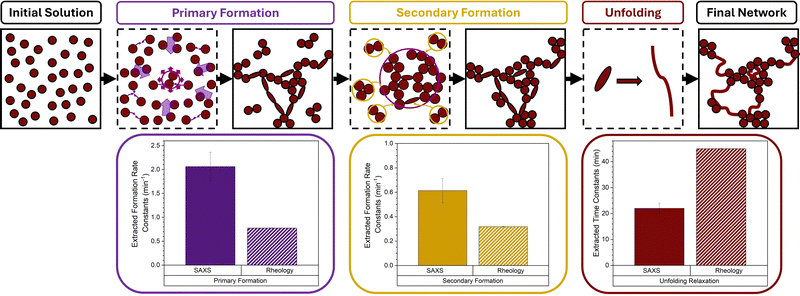
The power of a combined rheology and SAXS approach to study cluster-driven dynamical arrest in concentrated protein solutions has previously been demonstrated.48 Recently we completed the first time-resolved study49 of folded protein hydrogel network formation using small-angle X-ray scattering (SAXS) and rheology to capture the structural and mechanical formation of photochemically crosslinked hydrogels formed from mechanically robust BSA building blocks (∼6 nm in diameter). These results showed that folded proteins undergo a dual modal formation mechanism (Fig. 2): a primary formation phase consisting of monomer units diffusing and crosslinking to form a preliminary self-supporting network; and a secondary phase characterised by both the formation of new intra-network crosslinks and isolated protein oligomers diffusing and crosslinking to the preliminary network, enabling growth.
 | ||
| Fig. 2 Network formation of mechanically robust and force labile proteins. (left) Colloidal representations of mechanical robust (light red) and force labile (dark red) BSA, with tyrosine residues highlighted in black and disulphide bond “nano-staples” shown in yellow. (top) Schematic showing the transition from free protein in solution through preliminary self-supporting network phase to mature protein network, highlighting the two formation processes for mechanically robust BSA.49 The Primary Formation (purple) which is the formation of the preliminary network resulting from the diffusion of protein building blocks. The Secondary Formation (dark yellow) due to the slower diffusion of high-order crosslinked protein oligomers (formed during the primary formation) joining the network as well as the formation of ‘intra’-network crosslinks both resulting in the densification of the network. (bottom) Schematic of the unknown transition between pre-gel solution of force labile BSA and the previously determined final network structure of force labile protein hydrogels (right), where fractal-like clusters of crosslinked BSA are connected by an inter-cluster region of unfolded protein. | ||
This type of two-phase formation has been observed in colloidal systems,50,51 for example, large colloids (∼3 μm in diameter) made from poly(methyl methacrylate), which showed the initial formation of a percolated network.50 After this initial phase, there is volume fraction dependant rearrangement of the preliminary network driven by either stress or entropy (high and low volume fraction, respectively) resulting in the formation of the final arrested structure of isostatic clusters of colloids. Dual mechanism formation has been observed in biological systems such as amyloid fibrils,52 where primary nucleation produces oligomers which form into fibrillar aggregates, or amyloid fibrils, in proteins such as α-synuclein (∼8 nm in diameter). The presence of these amyloid fibrils can catalyse the formation of new oligomers in a process known as secondary nucleation.53 Another example is the formation of fibrin fibers in blood clots in which initial proto-fibers form from individual fibrin molecules (∼50 nm in length) via knob–hole interactions before undergoing a secondary process, laterally aggregating and bundling together to form mature fibrin fibers.54,55
Such examples from soft matter and biological systems demonstrate the broad applicability of dual formation models for networks composed of building blocks of different sizes and types. However, those mentioned above can all be reasonably modelled as colloidal systems in which the key timescale is diffusion, whereas the assembly of polymer networks is heavily influenced by the dynamics of the polymer chains and as such the relaxation timescales of the polymer chains must also be considered and not simply the diffusion of the polymer.56 An example of this is a class of materials termed dynamic covalent polymer networks,57,58 in which the formation/rupture rates of the covalent crosslinking as well as the polymer's innate dynamic properties lead to visco-elastic materials with strongly time-dependent properties. When probed at timescales longer than the characteristic relaxation time, these systems behave as viscoelastic fluids whereas at timescales shorter than the characteristic relaxation time they behave as rigid highly elastic solids.58 This demonstrates the importance of intrinsic building block dynamic timescales in polymeric systems. Current approaches to understand protein networks have assumed folded proteins behave as colloids so have included limited or no ability to dynamically alter the building block geometry during formation, i.e. shape dynamics is absent.
Indeed, it has previously been shown that colloidal models59–63 fit well to hydrogels constructed from mechanically robust proteins like native BSA, with its disulphide nano-staples preventing unfolding. However these models failed to model the behaviour of force labile BSA hydrogels.64 This was demonstrated by controlling the reaction rate of photochemical crosslinking at which mechanically robust and force labile BSA hydrogels were formed. The hydrogel rigidity and architecture of mechanically robust BSA hydrogels showed trends expected for a colloidal system, i.e. decreasing network rigidity and increasing cluster density with decreasing reaction rate, due to the regime change from diffusion-limited cluster aggregation to reaction-limited cluster aggregation.65–67 These trends in reaction rate were not observed in force labile BSA hydrogels (i.e. unfolding allowed to occur within the network), and instead the opposite was observed with the network rigidity increasing with decreasing reaction rate. These studies demonstrated that current colloidal modelling approaches are not able to capture the complexity exhibited by folded protein networks due, in part, to dynamic shape changes of the building block i.e. unfolding. It is therefore interesting to consider how an evolving building block shape, as observed during protein unfolding, might impact the dynamic evolution of the network formation process.
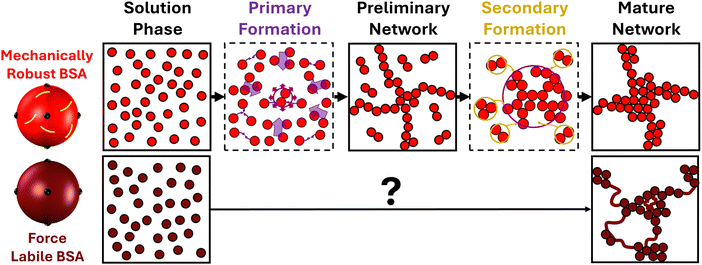
Here, to address this lack of understanding, we utilise time-resolved SAXS and rheology to study the gelation behaviour of force labile BSA protein in the presence of DTT (Methods) to ensure reduction and removal of the disulphide nano-staples and allow unfolding. The results of force labile BSA experiments are compared to the previously obtained results for mechanically robust BSA, to establish the effect of building block shape changing through in situ unfolding on the formation phases of protein networks and the emergence of local in situ unfolding in the architecture of protein networks.
Results
In situ unfolding enhances rigidity during formation
Time-resolved rheology experiments were performed to measure the formation mechanism of force labile folded protein hydrogel networks. We monitored the mechanical formation of photochemically crosslinked force labile and mechanically robust BSA hydrogels using a previously developed LED rig68 for the in situ photochemical gelation of folded protein hydrogels on the rheometer. Fig. 3a shows how the storage modulus, G′, (the elastic solid-like component of the material's shear modulus) of force labile and mechanically robust BSA hydrogels evolves as a function of gelation time (defined as the time the sample is illuminated by the blue light) at a fixed frequency.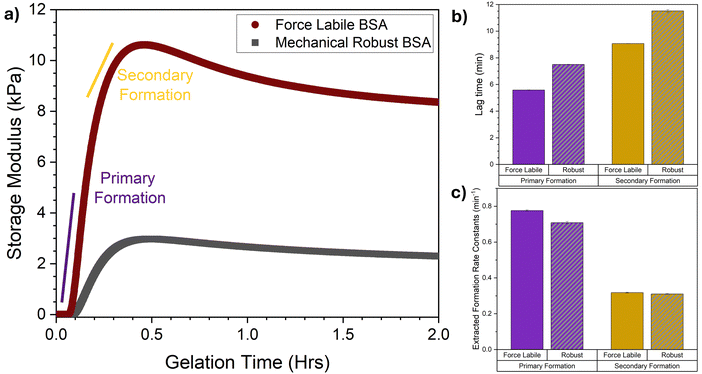 | ||
| Fig. 3 Rheology reveals that allowing in situ unfolding results in earlier load-bearing formation but with equal fundamental formation rate constants. (a) Average gelation curves, showing the storage modulus as a function of gelation time of force labile (dark red) and mechanically robust (grey) BSA hydrogels (final concentrations: 100 mg mL−1 BSA, 50 mM NaPS, 100 μM Ru(BiPy)3, in the presence (dark red) and absence (grey) of 3 mM DTT). Illuminated at t = 0 until t = 2 hours. (b) Lag times and (c) formation rate constants of the primary (purple) and secondary (dark yellow) formation for both force labile (solid column) and mechanically robust (striped, grey column) BSA hydrogels, extracted via fitting the gelation curves in panel (a) with eqn (1). All error bars show the standard error, N = 3. | ||
These gelation curves, both for force labile and mechanically robust BSA, show an initial lag phase followed by a sharp increase in G′ rising to a peak. As gelation continues, the G′ decreases as a function of time relaxing down to a plateau G′ value. These curves can be broken into two regions: the formation phase before the peak in G′; and the relaxation phase after the peak in G′. Comparison of the force labile and mechanically robust BSA hydrogels shows higher G′ values for force labile BSA hydrogels. Additionally, we observe a larger amount of relaxation after the G′ peak in force labile BSA hydrogels. These results are consistent with previous results, in which we observe force labile BSA hydrogels have approximately 3–4 times higher rigidity (i.e. G′) than mechanically robust BSA hydrogels.41,64 This was suggested to be due to a higher level of crosslinking between the unfolded protein in the network. Furthermore, our previous work using circular dichroism spectroscopy (CD) demonstrated that the relaxation in G′ is due to the unfolding of protein building blocks.41 Using CD to monitor the folded fraction of force labile and mechanically robust BSA over time found there is significant (∼30%) unfolding of force labile BSA during the relaxation phase, while only minimal unfolding was observed in mechanically robust BSA hydrogels (∼7%). Additionally, using CD we have previously demonstrated that decreasing the stability of the protein results in faster unfolding kinetics.69 Similarly our results here show a characteristic relaxation time for force liable BSA of 3200 ± 100 s and 4200 ± 100 s for robust BSA. Looking at the formation phase of the gelation curves (i.e. t = 0 to t ∼ 24 min) a lag phase is observed followed by a sharp increase in G′, the rate of which increases and then begins to slow as network formation continues until the peak in G′ is reached. This profile is suggestive of an initial fast network growth followed by a slower growth mode. Indeed, previous combined rheology and SAXS on mechanically robust BSA networks demonstrated the presence of two formation modes: a primary and secondary formation mode. Here, a similar dual modal formation is observed in the gelation curves of force labile BSA hydrogels. To further understand the impact of in situ unfolding on network formation, key parameters of the formation phase are extracted, namely the lag time (i.e. the time between initiation of crosslinking and the start of the primary and secondary formation processes) and the formation rate constant (i.e. the characteristic rate of the primary or secondary formation processes). To extract these parameters, the gelation curves in Fig. 3a are fitted with a previously developed fitting function (eqn (1), Methods, example fitting shown in Fig. S1, ESI†). The extracted lag times and formation rate constants are shown in Fig. 3b and c, respectively. Firstly, in both force labile and mechanically robust BSA hydrogels the lag time for the primary formation is shorter than secondary formation and the rate of primary formation is faster than the rate of secondary formation. This is consistent with previous results on mechanically robust BSA hydrogels which showed that formation consists of an initial faster growth mode followed by a subsequent secondary growth mode.49 Interestingly, while the lag times for force labile BSA are shorter than mechanically robust BSA, the rates of these processes are essentially identical (primary formation: kα(force labile) = 0.78 ± 0.01 min−1 cf. kα(mechanically robust) = 0.71 ± 0.01 min−1, secondary formation: kβ (force labile) = 0.32 ± 0.01 min−1 cf. kβ (mechanically robust) = 0.31 ± 0.01 min−1). The similarity in the rates is likely a result of the low gelation lamp intensity (2.8 mW cm−2 at 450 nm) leading to the system being in the reaction limited cross-linking regime rather than the diffusion limited regime i.e. the key driver to photochemical crosslink formation is probability of crosslink formation rather than diffusion and collision of particles.64,65,68 The shorter lag time shows that force labile BSA more rapidly forms a preliminary self-supporting network, which may be due to an increase in overall size of the protein building block when the staples are removed. However, SAXS data on force labile and mechanically robust BSA in solution shows no difference in the size of the protein monomer (Fig. S2, ESI†). Another possible reason for the shorter lag time could be the increased malleability of force labile BSA compared to mechanically robust BSA providing a more dynamic protein building block with a greater effective size, allowing for a greater connectivity between network elements. Coarse-grained simulation approaches have shown that increasing the flexibility of a 5-monomer chain building block resulted in an increase in the coordination (i.e. number of bonding partners) of the building block, demonstrating increased network connectivity.70 This increased connectivity through building block malleability would also explain why, despite the similar formation rates between force labile and mechanically robust BSA hydrogels, much higher storage moduli are observed for the more malleable and force labile BSA. This is consistent with an increased network connectivity which would lead to stronger overall networks. Buehler et al.47 showed in a recent simulation approach that increasing the network connectivity resulted in a decreased network convoluted-ness (i.e. how much of the network must be explored to travel from one end to the other) and an enhanced mechanical response. It is interesting to consider the present study in the context of literature on polymer-linked colloidal networks.71,72 For example a recent study observed that increasing the flexibility of a bivalent linker polymer results in an increase in loop formation (a non-load bearing defect) thereby reducing the number of mechanical relevant connections.73 In the context of the present study, this suggests that while the fold of force labile BSA is more flexible than robust BSA, it is still behaving as a short rigid linker during the early stages of network formation.
The rheology results show that networks formed from force labile protein building blocks exhibit two growth modes in their formation phase and have a higher storage modulus and shorter lag times compared to equivalent networks formed from mechanically robust proteins. A change in the connectivity of the network is likely to influence structural formation of the force labile protein network.
Structural in situ unfolding alters the formation of protein networks
Time-resolved small-angle scattering is employed to directly probe the structure of folded proteins as they evolve and assemble into mature networks through photochemical crosslinking. We make use of a bespoke LED light apparatus enabling gelation of the sample in situ in the SAXS instrument. Fig. 4a shows the scattering curves of force labile BSA in the pre-gel solution at 100 mg mL−1 and their evolution over the first 23 minutes of photochemical gelation time. Looking at the initial SAXS curve at gelation time, t = 0, the expected shape for repulsive globular colloids at high concentrations (protein volume fraction = 7.4%) is observed i.e. a power law decrease at high-q with an exponent of approximately −4 with a ‘peak’ in the curve in the mid-q range and a depressed I(0). This scattering profile is consistent with monomeric electrostatic BSA protein at 100 mg mL−1 previously observed with SAXS.74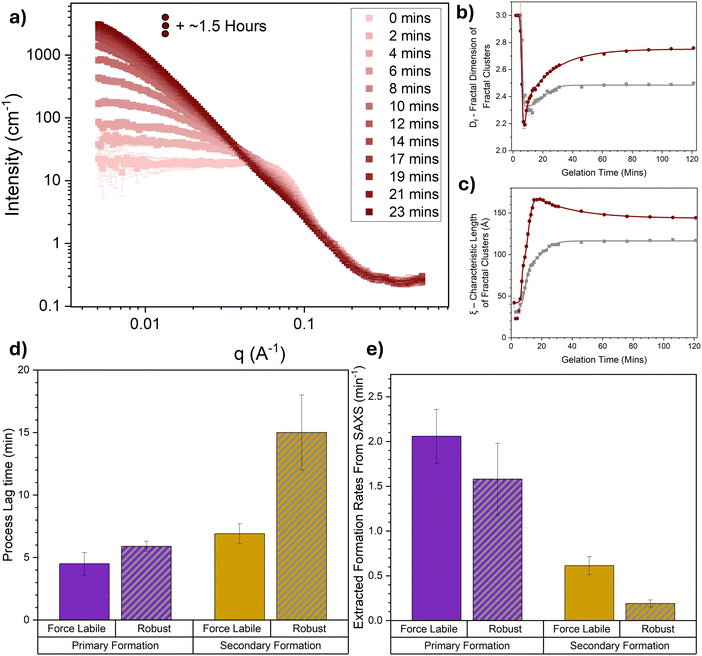 | ||
| Fig. 4 Time resolved SAXS captures in situ unfolding in the architecture of folded protein hydrogel networks. (a) SAXS curves of BSA hydrogel networks (final concentrations: 100 mg mL−1 BSA, 50 mM NaPS, 100 μM Ru(BiPy)3, 3 mM DTT) as a function of gelation time. For clarity, SAXS curves are shown at 2 min intervals and data collected beyond 23 minutes and up to 2 hours are shown in Fig. S3 (ESI†). (b) Fractal dimension and (c) characteristic correlation length of fractal-like clusters in force labile (dark red) and mechanically robust (grey) BSA hydrogels as a function of the gelation time, extracted from the SAXS curves in panel (a) and previous work49 using eqn (4). The solid lines show fits using eqn (6). (d) Lag times and (e) formation rate constants of the primary (purple) and secondary (dark yellow) formation for both force labile (solid column) and mechanically robust (striped, grey column) BSA hydrogels, extracted via fitting the curves in panels (b) and (c) with eqn (6). All error bars show the standard error, N = 2. | ||
As the gelation time increases the profile of the scattering curves evolves, especially in the low-q region, where a dramatic increase in the intensity at low q is observed. This increase in the intensity in the low-q region is indicative of large structures forming in the system and increasing in size over time, as expected for chemically crosslinked BSA protein. Furthermore, a change in the slope of the mid-q region is observed, which is indicative of a change in the geometry of the largest scattering object. This suggests that not only are the crosslinked structures in the system growing in size but also altering in their geometry, i.e. how they are put together, over time. To further explore this data, a fractal structure model is applied (eqn (5), Methods) which describes the protein network as fractal-like clusters of folded protein linked together by an inter-cluster region populated by folded and unfolded proteins. This model has been developed and successfully applied to hydrogels constructed from several different folded proteins.41,44,69,75,76 From this model two key structural parameters are extracted: the fractal dimension, Df, which is a measure of the space-filling capacity of an object and can be intuitively thought of as the density of a cluster; and the characteristic length of the fractal-like clusters, ξ, which is related to the overall size of the clusters. The extracted parameters, Df and ξ, for force labile BSA hydrogels are shown in Fig. 4b and c, respectively, additionally, the previously determined extracted parameters for mechanically robust BSA49 are also plotted for comparison. In both hydrogel systems a short lag phase is observed before a sharp drop in the Df accompanied by a sharp increase in ξ. At gelation time, t ∼ 10 min, there is a turning point with Df instead increasing with gelation time, meanwhile ξ continues to increase but at a slower rate. Model independent analysis shows Porod exponent and radius of gyration (Fig. S4, ESI†) resemble similar evolutions with time to Df and ξ, respectively. The profiles of Df and ξ with time suggest that as proteins begin to crosslink, they initially form dendritic branching structures with lower fractal dimensions which are growing in size, then as gelation continues and these structures continue to grow in size they begin to densify, increasing in fractal dimension with time. These observations are expected and are consistent with a proposed dual modal formation model of folded protein networks. A primary formation is characterized by rapid crosslinking of monomeric protein to form percolating clusters leading to a dendritic spanning network. A secondary formation is characterised by an increase in the size and density of the percolated crosslinked clusters of folded protein within the network. This results from the slower diffusion of crosslinked aggregates formed during the primary phase (e.g. dimers, trimers etc.) that join the network after gelation, and additional intra-cluster crosslinks formed when thermal excitation of network elastic modes bring different protein branches into contact.
Comparing the force labile and stapled BSA hydrogels interesting differences are observed in the evolution of their extracted structural parameters, Df and ξ. These differences include: (i) Df of force labile BSA hydrogels increases for a longer time and plateaus at a higher value (Df (force labile, t = ∞) = 2.75 ± 0.01) compared to mechanically robust BSA (Df (mechanically robust, t = ∞) = 2.48 ± 0.01); (ii) ξ of clusters in force labile BSA hydrogels are larger than those present in mechanically robust BSA; and (iii) the evolution of ξ in force labile BSA hydrogels follows a different profile at longer gelation times (t > 18 min) compared to mechanically robust BSA hydrogels, namely while ξ (mechanically robust) increases up to a constant plateau (ξ (mechanically robust) = 116 ± 1 Å at t ∼ 30 min), the profile of ξ (force labile) increases up to a peak of 166 ± 1 Å at t ∼ 18 min before decreasing down to a plateau value of 144 ± 2 Å. These differences suggest that hydrogels constructed from the more malleable force labile BSA, which allow protein unfolding, consist of larger denser fractal-like clusters compared to hydrogels constructed from more mechanically robust BSA, consistent with our previous study.41 The decrease in cluster size in force labile BSA hydrogels at longer gelation times (t > 18 min) resembles the relaxation phase observed in the rheological gelation curve (Fig. 3a). This similarity suggests that the shrinking cluster size is due to the unfolding of the protein building block, demonstrating that in situ unfolding has a key role in the assembly and evolution of the structure of folded protein networks. Furthermore, our ξ (force labile) data suggests the unfolding occurs at the edges of clusters rather than in the centre of clusters. If unfolding were to occur in the centre of clusters, it might be expected to observe an increase in cluster size due to the increased volume of an unfolded protein compared to a tightly folded protein, or a bimodal distribution of cluster sizes as some clusters break in half due to unfolding. The data shows neither of these outcomes, suggesting that unfolding occurs at the edges of clusters and thereby populates the inter-cluster region with unfolded protein as we have previously hypothesised.41 Additionally unfolding on the edges of clusters provides an explanation for the increased Df values observed in force labile BSA hydrogels at long gelation times, i.e. as the dendritic branching edges of clusters unfold the denser ‘core’ of the cluster is left behind leading to a measurable increase in Df.
To further interrogate the alteration to the hydrogel network assembly caused by increased protein malleability and in situ unfolding, the data in Fig. 4b and c, is fitted with a bespoke fitting function (eqn (7), Methods) of a similar form used to fit our rheology data, allowing for the extraction of key kinetic parameters of the primary and secondary formation. Fig. 4d and e show the primary and secondary formation average lag times, tigel (eqn (8)) and average formation rate constants, ki (eqn (7)), respectively for force labile BSA hydrogels. Additionally, previously determined lag time and formation rate constants for mechanically robust BSA49 have been added for comparison. Similarly with the rheology data (Fig. 3b and c) shorter lag times and faster rates are observed for primary formation and longer lag times and slower rates for secondary formation. Furthermore, the lag times of force labile BSA hydrogels are shorter than those of mechanically robust BSA hydrogels in agreement with the rheology data. The primary formation rate constants extracted from SAXS are in reasonable agreement between force labile and mechanically robust BSA and suggests that there is a minimal effect of protein malleability and in situ unfolding on the initial formation of the preliminary network. This is likely due to the system being in the reaction limited crosslinking regime meaning the rate limiting step is not protein dependent but rather chemical reaction probability dependent. However, despite this, a 3-fold increase in the structural secondary formation rate in force labile BSA hydrogels is seen compared to mechanically robust BSA, suggesting the protein building block malleability and in situ unfolding are significant to the secondary formation mode. This is likely due to increased protein malleability and in situ unfolding allowing both for: easier reconfiguration of clusters leading to more rapid formation of ‘intra’-crosslinks; and an increase in solvent accessibility of crosslinking site thus effectively increasing the reaction rate.
The SAXS results show that protein hydrogel networks constructed from malleable, force labile BSA exhibit dual formation processes in agreement with rheology results (Fig. 3) and also seen in networks constructed from mechanically robust BSA.49 Furthermore, the SAXS results show that increasing the malleability of the protein building and allowing in situ unfolding results in more rapid secondary formation and unfolding at the edges of fractal-like clusters populating the inter-cluster region with unfolded proteins.
Discussion
Here, we have utilised time-resolved mechanical and structural measurements combined with a previously proposed dual modal formation model to disentangle the complex assembly of a model force labile protein network. Three distinct phases are observed in the assembly of protein networks constructed from force labile folded proteins which lead to a mature protein network (Fig. 5), namely: a primary formation, a secondary formation and post formation in situ unfolding. Our previous study49 identified the primary and secondary formation as: (i) an initial primary formation which is characterized by the diffusion and crosslinking of protein monomer into a dendritic, system-spanning, self-supporting network consisting of percolated cross-linked clusters; and (ii) a subsequent secondary formation characterized by additional crosslinking due to internal network deformation modes bringing regions into contact for additional crosslinking, or the incorporation of freely-diffusing aggregates into the system-spanning cluster, resulting in growth and densification of the clusters already embedded in the network. In this work, we expand this dual formation model to a triple modal assembly model to include the in situ unfolding of the building block after the primary formation of the preliminary network. The time-resolved SAXS data showed that this in situ unfolding occurs at the edges of the fractal-like clusters present in the system and thereby populates the inter-cluster with unfolded protein, confirming our previous hypothesis.41Furthermore, by comparing the results on force labile BSA hydrogels with previous results on mechanically robust BSA proteins, we demonstrate that while protein building block malleability has a minimal effect on the structural and mechanical primary formation rate, it leads to a 3-fold increase in the structural secondary formation. This increase is attributed to the protein malleability and in situ unfolding allowing for: an easier configuration of fractal-like cluster allowing for ‘intra’-crosslinks to more readily form within the network; and increased solvent accessibility of the crosslinking site effectively increasing the reaction rate. A similar increase in the rate of the structural primary formation is not observed, likely due to the system being in the reaction limited crosslinking regime meaning the rate of reaction is the limiting step rather than the diffusion or dynamics of the protein building blocks. In order to further understand the design space of folded protein network formation, experiments could be completed at higher reaction rates (via gelation lamp intensity) which will allow for characterisation of the importance of differing diffusion and building block dynamics on the primary formation to be observed. It is interesting to consider how mixtures of mechanically robust and force labile proteins would tune the formation behaviour. Previously, we have demonstrated that increasing the thermodynamic stability of a proportion of protein (via ligand binding) results in a complex non-linear increase in the network rigidity.69 This provides an interesting avenue to explore protein systems of mixed stabilities to further explore the proposed formation model we have proposed here and tune hydrogel properties.
Comparing the SAXS and rheology results, we find that the lag times extracted from SAXS results, for both force labile and robust BSA hydrogels (e.g. tαgel(SAXS) ∼ 5 min, Fig. 4d), are shorter than those extracted from rheological measurements (e.g. tαgel(Rheo) ∼ 6 min, Fig. 3b). This difference reflects the behaviour of protein monomers during the initial gelation, where monomers begin to form cross-links to form clusters. Such clusters are observable with SAXS and are present immediately before the preliminary self-supporting network forms, with mechanics measurable using rheology.
Interestingly, the structural formation rates (primary and secondary) extracted from SAXS data do not match the mechanical formation rates (primary and secondary) extracted from the rheology data (Fig. 5). The SAXS values are approximately 2-fold higher than the rheology values. While SAXS probes the distribution of ‘mass’ in the protein network, rheology probes only the load-bearing protein network, which is related to the elastic connectivity of the system. The different formation rates observed in Fig. 5 suggests the dynamic evolution of the mass network is 2 times faster than the evolution of the load-bearing network. One explanation could be that approximately half of the protein is contributing to the loading-bearing network. This estimation is corroborated by the two-fold difference in the unfolding relaxation time constants extracted from SAXS (τunfolding(SAXS) = 22 ± 2 min) and rheology (τunfolding(Rheo) = 45 ± 1 min) (Fig. 5). Recent modelling work by del Gado et al. has identified the concept of a rigidity network within colloidal networks. Del Gado et al. show that this rigidity network, which defines the mechanical response of the colloidal network, is the result of connectivity between clusters (of crosslinked colloids) rather than the connection between individual colloids within clusters.60,77 In this context, the present study suggests that 50% of protein is mechanically relevant in the load-bearing network. Additionally, Del Gado et al. work has suggested that this rigidity network is the result of a combination of a bond network (i.e. connectivity between network elements) and repulsive contacts (e.g. electrostatic repulsion of network building blocks).78 However, these are strictly colloidal-based models so do not contain the necessary polymeric components to capture the hybrid behaviour of folded/unfolded protein biomaterials, such as the force labile protein hydrogels presented here. So, to more deeply understand the interplay between the ‘mass’ network probed by SAXS and the elastic connectivity network probed by rheology, computational simulations are required which take into account the hybrid colloidal nature of the system. The ability to predict the properties of protein-based biomaterials is crucial for their development in medical and healthcare applications, such as cell scaffolds. Recent studies are demonstrating the potential of these novel hydrogels. For example, Alegre-Cebollada et al.79 exploited protein engineering to create stiff viscoelastic protein hydrogels which exhibited viscous energy dissipation which attenuated mechanosensing. Interestingly, this mechanosensing was present even when cells were exposed to higher effective rigidity. It has been demonstrated that competing elastic and viscous gradients determine directional cell migration80 and that the synergistic relationship between protein dynamics and polymer hydrogel engineering can be exploited to create a highly transparent protein–polymer actuator. The potential of this composite system was explored as a tuneable protein-driven hydrogel lens.33 Furthermore, the formation behaviour of protein networks has been explored for the controlled release of therapeutics. For example, the inclusion of microbubbles and other large micron-sized fillers into hydrogel matrices is being explored as a method to imbue triggered drug release.76,81 These examples, and others,82,83 highlight the importance of developing predictive design rules so that the potential of protein biomaterials can be fully realised.
Materials and methods
Materials
Bovine serum albumin (heat shock fraction, protease free, fatty acid free, and essentially immunoglobulin free), tris(2,2′-bipyridyl)dichlororuthenium(II)hexahydrate (Ru(BiPy)3), sodium persulfate (NaPS), dithiothreitol (DTT), sodium phosphate dibasic, and sodium phosphate monobasic were obtained from Sigma-Aldrich, and used without further treatment.Sample preparation
As previously published41,68,76 and outlined here, hydrogel samples are prepared by mixing in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio a 200 mg mL−1 stock of either BSA protein and 2× cross-link reagent stock for final protein and reagent concentrations of 100 mg mL−1 BSA, 50 mM NaPS, 100 μM Ru(BiPy)3, and 3 mM DTT.
1 ratio a 200 mg mL−1 stock of either BSA protein and 2× cross-link reagent stock for final protein and reagent concentrations of 100 mg mL−1 BSA, 50 mM NaPS, 100 μM Ru(BiPy)3, and 3 mM DTT.
Rheometry
Mechanical characterization experiments of BSA hydrogel samples were performed on an Anton Paar MCR 302 stress-controlled rheometer (Anton Paar GmbH, Austria) in parallel plate configuration (with a plate diameter of 8 mm). Samples of pre-gel solutions were added to the parallel plate with a gap height of 1.48 mm. Photochemical cross-linking was initiated and controlled via illumination by blue LED at a current of 0.03 Amps. To prevent evaporation, during this process low viscosity silicone oil (approximately 5 ct) was placed around the geometry. The silicone oil should present no schematic error on rheometric data as this is below the rheometer's torque range. Time sweep gelation measurements were conducted at a frequency and shear strain of 1 Hz and 0.5%, respectively.Rheometry analysis
The rheological gelation curves were fitted in accordance with eqn (7),| G′(t) = G′(∞)·F(t)·R(t) | (1) |
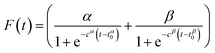 | (2) |
The relaxation factor, R(t), is defined as:
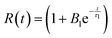 | (3) |
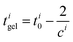 | (4) |
Small angle X-ray scattering (SAXS)
SAXS measurements were conducted on a Xeuss 3.0 offline SAXS instrument (Xenocs Inc., France) using a gallium rich alloy liquid metal jet X-ray source, (Ga Kα = 9.2 keV (1.3 Å)) (Excillum, Sweden). Samples were loaded into 1.48 mm path length capillary tubes (Capillary Tube Supplies Ltd), sealed with manuscript sealing wax. Sealed capillary tubes were loaded into a Xenocs Peltier capillary holder and held at a constant temperature of 20 °C. The detector was run at two distances from the sample at 4.5 m and 0.5 m giving the investigated q-range of 0.005 Å−1 to 0.5 Å−1. Samples were photo-initiated and gelated in situ in the X-ray sample chamber using previously developed bespoke blue LED lighting rig.49 2-D SAXS patterns were recorded on an Eiger2 R 1 M detector (Dectris, Switzerland). Silver behenate (a = 58.38 Å) was used to calibrate the SAXS data and glassy carbon calibration was performed to convert data to absolute intensities. SAXS curves were acquired over multiple frames. Frame times began at 1 min (52 s acquisition time + 8 s processing time) for the first 15 min of gelation, then increased to 2 min (108 s acquisition time + 12 s processing time) until the gelation time t = 31 min. After 31 min of the sample being illuminated by the blue light the frame time was set at 15 min (850 s acquisition time + 50 s processing time). Note, control experiments were done to ensure that there was no radiation damage to the protein, nor did X-rays alone activate the photochemical crosslinking (Fig. S5, ESI†). SAXS data were processed using the DAWN software.84SAXS analysis
SAXS curves obtained were fitted using SASview (https://www.sasview.org). Model-independent fits were performed and consisted of a Guinier-Porod fit11 over the entire data range, to extract the Porod exponent and the radius of gyration at specific time point for the evolving system. Model-dependant fits were performed in accordance with eqn (1).| I(q) = Scale·P(q)[(1 − pc) + pcS(q)] + Background | (5) |
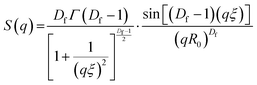 | (6) |
To fit the time evolution of the fractal dimension and correlation length extracted from the SAXS curves we used eqn (7):
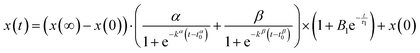 | (7) |
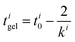 | (8) |
Data availability
Data for this article, including rheology and scattering data are available at the University of Leeds data repository at https://doi.org/10.5518/1632.Conflicts of interest
The authors declare no conflicts of interests.Acknowledgements
The project was supported by a grant from the European Research Council (ERC) (UKRI EP/X023524/1) to L. Dougan. We acknowledge Diamond Light Source for access to the DL-SAXS equipment (experiment number SM32045) supported by an EPSRC grant (EP/R042683/1), and instrument scientists Drs Sam Burholt, Tim Snow, Paul Wady for their help and support during beamtime. This work benefitted from the SasView software, originally developed by the DANSE project under NSF award DMR-0520547. We would like to thank Dr Sophie Ayscough and the European Spallation Source for sharing their LED lamp designs. Many thanks to all members of the Dougan group for helpful discussion and feedback.References
- S. Prakash and A. Matouschek, Trends Biochem. Sci., 2004, 29, 593–600 CrossRef CAS.
- A. Matouschek, Curr. Opin. Struct. Biol., 2003, 13, 98–109 CrossRef CAS PubMed.
- S. Sharma, S. Subramani and I. Popa, FEBS J., 2020, febs.15508 Search PubMed.
- H. Li, W. A. Linke, A. F. Oberhauser, M. Carrion-Vazquez, J. G. Kerkvliet, H. Lu, P. E. Marszalek and J. M. Fernandez, Nature, 2002, 418, 998–1002 CrossRef CAS.
- P. E. Marszalek, H. Lu, H. Li, M. Carrion-Vazquez, A. F. Oberhauser, K. Schulten and J. M. Fernandez, Nature, 1999, 402, 100–103 CrossRef CAS.
- Z. Mártonfalvi and M. Kellermayer, PLoS One, 2014, 9, e85847 CrossRef PubMed.
- C. Squarci, P. Bianco, M. Reconditi, I. Pertici, M. Caremani, T. Narayanan, Á. I. Horváth, A. Málnási-Csizmadia, M. Linari, V. Lombardi and G. Piazzesi, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2219346120 CrossRef CAS.
- C. M. Loescher, J. K. Freundt, A. Unger, A. L. Hessel, M. Kühn, F. Koser and W. A. Linke, Nat. Cardiovasc. Res., 2023, 2, 991–1002 CrossRef CAS.
- L. F. Milles, E. M. Unterauer, T. Nicolaus and H. E. Gaub, Nat. Commun., 2018, 9, 4764 CrossRef PubMed.
- T. J. Foster, J. A. Geoghegan, V. K. Ganesh and M. Höök, Nat. Rev. Microbiol., 2014, 12, 49–62 CrossRef CAS PubMed.
- B. T. Goult, N. H. Brown and M. A. Schwartz, J. Cell Sci., 2021, 134, jcs258749 CrossRef CAS PubMed.
- H. Wang, R. Said, C. Nguyen-Vigouroux, V. Henriot, P. Gebhardt, J. Pernier, R. Grosse and C. Le Clainche, Nat. Commun., 2024, 15, 9497 CrossRef CAS.
- T. Hoffmann, K. M. Tych, M. L. Hughes, D. J. Brockwell and L. Dougan, Phys. Chem. Chem. Phys., 2013, 15, 15767 RSC.
- M. Bertz and M. Rief, J. Mol. Biol., 2009, 393, 1097–1105 CrossRef CAS.
- I. Mesbah, B. Habermann and F. Rico, Database, 2024, 2024, baae047 CrossRef.
- N. Luchetti, K. M. Smith, M. A. G. Matarrese, A. Loppini, S. Filippi and L. Chiodo, Sci. Rep., 2024, 14, 27658 CrossRef CAS.
- D. J. Brockwell, E. Paci, R. C. Zinober, G. S. Beddard, P. D. Olmsted, D. A. Smith, R. N. Perham and S. E. Radford, Nat. Struct. Mol. Biol., 2003, 10, 731–737 CrossRef CAS PubMed.
- M. Carrion-Vazquez, A. F. Oberhauser, T. E. Fisher, P. E. Marszalek, H. Li and J. M. Fernandez, Prog. Biophys. Mol. Biol., 2000, 74, 63–91 CrossRef CAS PubMed.
- M. L. Hughes and L. Dougan, The physics of pulling polyproteins: a review of single molecule force spectroscopy using the AFM to study protein unfolding, Institute of Physics Publishing, 2016, vol. 79 Search PubMed.
- E. A. Shank, C. Cecconi, J. W. Dill, S. Marqusee and C. Bustamante, Nature, 2010, 465, 637–640 CrossRef CAS PubMed.
- B. Jagannathan, P. J. Elms, C. Bustamante and S. Marqusee, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 17820–17825 CrossRef CAS PubMed.
- H. Dietz and M. Rief, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 1244–1247 CrossRef CAS.
- R. Kumar and S. Dutta, Sci. Rep., 2024, 14, 23905 CrossRef CAS.
- J. Schönfelder, R. Perez-Jimenez and V. Muñoz, Nat. Commun., 2016, 7, 11777 CrossRef.
- A. M. R. de Graff, G. Shannon, D. W. Farrell, P. M. Williams and M. F. Thorpe, Biophys. J., 2011, 101, 736–744 CrossRef CAS.
- B. Ni, D. L. Kaplan and M. J. Buehler, Sci. Adv., 2024, 10 DOI:10.1126/sciadv.adl4000.
- S. Lv, D. M. Dudek, Y. Cao, M. M. Balamurali, J. Gosline and H. Li, Nature, 2010, 465, 69–73 CrossRef CAS.
- M. a Da Silva, S. Lenton, M. Hughes, D. J. Brockwell and L. Dougan, Biomacromolecules, 2017, 18, 636–646 CrossRef CAS.
- A. Sanchez-Fernandez, J.-F. Poon, A. E. Leung, S. F. Prévost and C. Dicko, ACS Nano, 2024, 18, 18314–18326 CrossRef CAS PubMed.
- Y. Fu, Q. Lin, R. Lan and Z. Shao, Small, 2024, 20, 2403376 CrossRef CAS PubMed.
- S. Nikfarjam, R. Gibbons, F. Burni, S. R. Raghavan, M. A. Anisimov and T. J. Woehl, Biomacromolecules, 2023, 24, 1131–1140 CrossRef CAS.
- A. Dutta, G. Vasilyev and E. Zussman, Biomacromolecules, 2023, 24, 2575–2586 CrossRef CAS.
- M. Kaeek and L. R. Khoury, Adv. Sci., 2023, 10(36), e2306862 CrossRef PubMed.
- N. Kong, L. Fu, Q. Peng and H. Li, ACS Biomater. Sci. Eng., 2017, 3, 742–749 CrossRef CAS PubMed.
- L. R. Khoury and I. Popa, Nat. Commun., 2019, 10, 5439 CrossRef.
- Y. Liu and L. R. Khoury, Small Sci., 2024, 4, 2400214 CrossRef CAS.
- Q. Bian, L. Fu and H. Li, Nat. Commun., 2022, 13, 137 CrossRef CAS.
- J. Wu, P. Li, C. Dong, H. Jiang, B. Xue, X. Gao, M. Qin, W. Wang, B. Chen and Y. Cao, Nat. Commun., 2018, 9, 620 CrossRef.
- H. Lei, L. Dong, Y. Li, J. Zhang, H. Chen, J. Wu, Y. Zhang, Q. Fan, B. Xue, M. Qin, B. Chen, Y. Cao and W. Wang, Nat. Commun., 2020, 11, 4032 CrossRef CAS PubMed.
- J. Fang, A. Mehlich, N. Koga, J. Huang, R. Koga, X. Gao, C. Hu, C. Jin, M. Rief, J. Kast, D. Baker and H. Li, Nat. Commun., 2013, 4, 2974 CrossRef.
- M. D. G. Hughes, B. S. Hanson, S. Cussons, N. Mahmoudi, D. J. Brockwell and L. Dougan, ACS Nano, 2021, 15, 11296–11308 CrossRef CAS.
- J. Nowitzke, S. Bista, S. Raman, N. Dahal, G. Stirnemann and I. Popa, ACS Nano, 2024, 18, 31031–31043 CrossRef CAS PubMed.
- L. Fu, L. Li, Q. Bian, B. Xue, J. Jin, J. Li, Y. Cao, Q. Jiang and H. Li, Nature, 2023, 618, 740–747 CrossRef CAS.
- M. D. G. Hughes, S. Cussons, N. Mahmoudi, D. J. Brockwell and L. Dougan, ACS Nano, 2022, 16, 10667–10678 CrossRef CAS PubMed.
- I. Kopyeva, R. P. Brady and C. A. DeForest, Nat. Rev. Bioeng., 2024, 2, 159–180 Search PubMed.
- R. Mout, R. C. Bretherton, J. Decarreau, S. Lee, N. Gregorio, N. I. Edman, M. Ahlrichs, Y. Hsia, D. D. Sahtoe, G. Ueda, A. Sharma, R. Schulman, C. A. DeForest and D. Baker, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2309457121 CrossRef CAS.
- E. Khare, A. C. S. de Alcântara, N. Lee, M. S. Skaf and M. J. Buehler, Mater. Adv., 2024, 5, 1991–1997 RSC.
- F. Cardinaux, E. Zaccarelli, A. Stradner, S. Bucciarelli, B. Farago, S. U. Egelhaaf, F. Sciortino and P. Schurtenberger, J. Phys. Chem. B, 2011, 115, 7227–7237 CrossRef CAS.
- M. D. G. Hughes, K. R. Cook, S. Cussons, A. Boroumand, A. I. I. Tyler, D. Head, D. J. Brockwell and L. Dougan, Small, 2024, 21, 2407090 CrossRef.
- H. Tsurusawa, M. Leocmach, J. Russo and H. Tanaka, Sci. Adv., 2019, 5 DOI:10.1126/sciadv.aav6090.
- Y. Huang, C. Wu, J. Chen and J. Tang, Angew. Chemie, 2023, 63, e202313885 CrossRef PubMed.
- A. K. Buell, C. Galvagnion, R. Gaspar, E. Sparr, M. Vendruscolo, T. P. J. Knowles, S. Linse and C. M. Dobson, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 7671–7676 CrossRef CAS.
- S. I. A. Cohen, S. Linse, L. M. Luheshi, E. Hellstrand, D. A. White, L. Rajah, D. E. Otzen, M. Vendruscolo, C. M. Dobson and T. P. J. Knowles, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9758–9763 CrossRef CAS PubMed.
- J. W. Weisel and R. I. Litvinov, Fibrin Formation, Structure and Properties, Springer, Cham, 2017 Search PubMed.
- B. E. Vos, C. Martinez-Torres, F. Burla, J. W. Weisel and G. H. Koenderink, Acta Biomater., 2020, 104, 39–52 CrossRef CAS.
- M. J. Webber and M. W. Tibbitt, Nat. Rev. Mater., 2022, 7, 541–556 CrossRef.
- D. Montarnal, M. Capelot, F. Tournilhac and L. Leibler, Science, 2011, 334, 965–968 CrossRef CAS.
- B. Marco-Dufort, R. Iten and M. W. Tibbitt, J. Am. Chem. Soc., 2020, 142, 15371–15385 CrossRef CAS PubMed.
- K. A. Whitaker, Z. Varga, L. C. Hsiao, M. J. Solomon, J. W. Swan and E. M. Furst, Nat. Commun., 2019, 10, 2237 CrossRef.
- A. Zaccone, H. Wu and E. Del Gado, Phys. Rev. Lett., 2009, 103, 208301 CrossRef.
- S. Alexander, Phys. Rep., 1998, 296, 65–236 CrossRef CAS.
- S. Ramakrishnan, Y.-L. Chen, K. S. Schweizer and C. F. Zukoski, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 040401 CrossRef CAS.
- M. Nabizadeh, F. Nasirian, X. Li, Y. Saraswat, R. Waheibi, L. C. Hsiao, D. Bi, B. Ravandi and S. Jamali, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2316394121 CrossRef CAS PubMed.
- M. D. G. Hughes, D. West, R. Wurr, S. Cussons, K. R. Cook, N. Mahmoudi, D. Head, D. J. Brockwell and L. Dougan, J. Colloid Interface Sci., 2025, 698, 1259–1269 CrossRef PubMed.
- K. R. Cook, D. Head and L. Dougan, Soft Matter, 2023, 19, 2780–2791 RSC.
- S. Jungblut, J.-O. Joswig and A. Eychmüller, Phys. Chem. Chem. Phys., 2019, 21, 5723–5729 RSC.
- M. Kolb and R. Jullien, J. Phys. Lett., 1984, 45, 977–981 CrossRef CAS.
- A. Aufderhorst-Roberts, M. D. G. Hughes, A. Hare, D. A. Head, N. Kapur, D. J. Brockwell and L. Dougan, Biomacromolecules, 2020, 21, 4253–4260 CrossRef CAS.
- M. D. G. Hughes, S. Cussons, N. Mahmoudi, D. J. Brockwell and L. Dougan, Soft Matter, 2020, 16, 6389–6399 RSC.
- B. S. Hanson and L. Dougan, Biomacromolecules, 2021, 22, 4191–4198 CrossRef CAS PubMed.
- C. Zhao, G. Yuan, D. Jia and C. C. Han, Soft Matter, 2012, 8, 7036 RSC.
- L. Feng, B. Laderman, S. Sacanna and P. Chaikin, Nat. Mater., 2015, 14, 61–65 CrossRef CAS.
- M. P. Howard, R. B. Jadrich, B. A. Lindquist, F. Khabaz, R. T. Bonnecaze, D. J. Milliron and T. M. Truskett, J. Chem. Phys., 2019, 151, 124901 CrossRef PubMed.
- F. Zhang, M. W. A. Skoda, R. M. J. Jacobs, R. A. Martin, C. M. Martin and F. Schreiber, J. Phys. Chem. B, 2007, 111, 251–259 CrossRef CAS PubMed.
- M. D. G. Hughes, S. Cussons, B. S. Hanson, K. R. Cook, T. Feller, N. Mahmoudi, D. L. Baker, R. Ariëns, D. A. Head, D. J. Brockwell and L. Dougan, Nat. Commun., 2023, 14, 5593 CrossRef CAS PubMed.
- C. P. Brown, M. D. G. Hughes, N. Mahmoudi, D. J. Brockwell, P. L. Coletta, S. Peyman, S. D. Evans and L. Dougan, Biomater. Sci., 2023, 11, 2726–2737 RSC.
- S. Zhang, L. Zhang, M. Bouzid, D. Z. Rocklin, E. Del Gado and X. Mao, Phys. Rev. Lett., 2019, 123, 058001 CrossRef CAS.
- C. S. Dias, J. C. Neves, M. M. T. da Gama, E. del Gado and N. A. M. Araujo, 2023, 59–62.
- C. Huerta-López, A. Clemente-Manteca, D. Velázquez-Carreras, F. M. Espinosa, J. G. Sanchez, Á. Martínez-del-Pozo, M. García-García, S. Martín-Colomo, A. Rodríguez-Blanco, R. Esteban-González, F. M. Martín-Zamora, L. I. Gutierrez-Rus, R. Garcia, P. Roca-Cusachs, A. Elosegui-Artola, M. A. del Pozo, E. Herrero-Galán, P. Sáez, G. R. Plaza and J. Alegre-Cebollada, Sci. Adv., 2024, 10 DOI:10.1126/sciadv.adf9758.
- P. Saez, P. U. Shirke, J. R. Seth, J. Alegre-Cebollada and A. Majumder, Math. Biosci., 2025, 380, 109362 CrossRef PubMed.
- V. Calabrese, M. A. da Silva, L. Porcar, S. J. Bryant, K. M. Z. Hossain, J. L. Scott and K. J. Edler, Soft Matter, 2020, 16, 3303–3310 RSC.
- D. Mangal, G. S. Vera, S. Aime and S. Jamali, Soft Matter, 2024, 20, 4692–4698 RSC.
- M. C. Pedersen, S. Mukherjee, A. Doostmohammadi, C. Mondal and K. Thijssen, Phys. Rev. Lett., 2024, 133, 228301 CrossRef CAS PubMed.
- J. Filik, A. W. Ashton, P. C. Y. Chang, P. A. Chater, S. J. Day, M. Drakopoulos, M. W. Gerring, M. L. Hart, O. V. Magdysyuk, S. Michalik, A. Smith, C. C. Tang, N. J. Terrill, M. T. Wharmby and H. Wilhelm, J. Appl. Crystallogr., 2017, 50, 959–966 CrossRef CAS PubMed.
- G. Beaucage, J. Appl. Crystallogr., 1996, 29, 134–146 CrossRef CAS.
- G. Beaucage, J. Appl. Crystallogr., 1995, 28, 717–728 CrossRef CAS.
- J. Teixeira, J. Appl. Crystallogr., 1988, 21, 781–785 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: ESI is provided in additional document. See DOI: https://doi.org/10.1039/d4sm01413h |
| This journal is © The Royal Society of Chemistry 2025 |