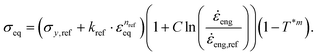Experimental and FEM simulation study of compressive deformation of solder microballs and particle chains

Abstract

Beaded microstructures, formed by side-by-side alignment of spherical microparticles, offer a promising approach for creating micropaths with pre-determined electrical and thermal conductivity. Post-processing through mechanical compression effectively modulates the structural and conductive properties, enabling precise control over conductivity by applying defined compressive forces and calibrating strain levels. To investigate the mechanical properties of these beaded structures, this study begins with an in-depth analysis of the compressive response of unconstrained individual solder microballs, representative of malleable soft materials. The study examines the influence of particle size, engineering strain rate, and temperature on compressive force and deformation characteristics. Results from single-particle experiments are then systematically compared with those from beaded structures, revealing distinct mechanical responses. In particular, particle chains require higher compressive forces due to lateral constraints introduced by neighbouring particles, with differences in force values dependent on strain level and also on the number of microballs in the chain. FEM simulations were employed to model stress distributions, contact pressures, and deformation profiles, extending the analysis to deformation scenarios beyond experimental limits. The Johnson–Cook (J–C) model proved to be a robust predictor of compressive behaviour under varying strain rates and elevated temperatures, with temperature exerting a more significant influence than strain rate. Parameterization of the model allowed for accurate replication of empirical scaling behaviours, with strain rate and temperature dependencies from the J–C model closely matching experimental observations. These results expand our understanding of single solder microparticle deformation and offer valuable insights into the deformation of beaded structures, which could be beneficial for practical applications such as the fabrication of electronic components.

---

Introduction

Beaded micropaths, consisting of side-by-side aligned microparticles, possess intriguing properties, including mesoscale periodicity and a high surface-to-volume ratio. Such structures—resembling a pearl necklace by appearance—may also conduct electricity very effectively, thus serving as a new type of conductive micro-track.¹ The key to achieving high electrical conductivity in these structures lies in ensuring robust interconnections between the individual particles. To accomplish this, various post-processing techniques have been explored, including contact heating,² laser treatment,³ and electric-current-induced-fusing,⁴ each employing heat in a distinct manner.

For malleable materials, which can be easily shaped without breaking, uniaxial mechanical compression can be a straightforward alternative method. Pressing the line of microparticles deposited on a substrate, in a direction normal to the surface of the substrate, leads to an increase in contact between adjacent particles. This process enables the conduction of electric current, with the resultant electrical conductivity depending on the level of compressive strain applied;¹ see also exemplary experimental results in Fig. S1 (ESI†).

From a practical standpoint, understanding the specific compressive force values required for a given level of compression is essential for several reasons, including process scaling in different operating conditions, improving the durability of microstructures, enhancing repeatability and consistency in production, and facilitating adaptation to different materials. This normal force (F_N) is intrinsically dependent on particle size, the quantity of particles undergoing compression, and material properties. Additionally, it is influenced by the compressive strain (ε), strain rate ([small epsi, Greek, dot above]), and process temperature (T).

In this research, we first investigate the mechanical properties of an individual spherical microparticle, focusing on its material mechanics and rheological properties to provide foundational insights. We then examine the more complex interactions within a single-particle-thick structure, where particles are aligned side-by-side to form a beaded path. Solder materials, which are readily available and widely used in electronics, are our focus here, serving as representative examples of malleable soft materials. Our study utilizes microspheres ranging in size from 200 to 760 μm, which fall within the typical range used for these particles in various electronic applications.

Numerous studies have examined the deformation of individual solder balls^5–12 and microballs composed of other conductive and non-conductive materials,^13–15 though typically within limited ranges of deformation and temperature. Our work broadens this research by investigating microspheres under more extensive compressive strains and temperatures, providing a deeper understanding of the material's dynamic properties under complex interactions.

In the case of more complex systems, such as chains of adjacent microparticles, we found no comprehensive studies on beaded paths, where side-by-side aligned spherical particles undergo a distinct deformation process compared to single-particle compression. This difference arises because particles in a path have limited freedom to deform along the chain's direction, leading to uneven lateral deformation. In contrast, an isolated spherical particle, unconstrained by neighbours, can deform more uniformly in all lateral directions under compression. Consequently, the distribution of forces and pressures in a particle chain differs significantly from that in a single particle. It remains uncertain how force values compare between physically constrained and unconstrained microspheres across a broad range of compressive strains. We hypothesize that compressing particles in a chain will require greater force than compressing the same number of separated particles, with this difference becoming more pronounced at higher compression levels and with more particles in the chain. This study aims to verify this hypothesis through experimental research and computer simulations, quantifying the compression differences between these two microparticle arrangements. To facilitate collaboration and progress in materials research, all simulation files are available in the ESI,† inviting further analysis and validation by the scientific community.

Methods

Materials and experimental setups

In this study, we used both leaded (Sn₆₃Pb₃₇) and lead-free (Sn_96.5Ag₃Cu_0.5) solder ball microparticles sourced from PMTC, Taiwan, via Reball, Poland. The particle sizes ranged from 200 to 760 μm, with a tolerance of ±15 μm. These particles exhibit a melting point of 183 °C for the leaded solder material, and 217 °C for the lead-free solder material.

The mechanical properties of the solder balls were analysed using an MCR302e Anton Paar rheometer configured in a plate-plate setup, as depicted in Fig. 1a. This equipment allowed for the precise measurement and control of normal force, compressive strain, and compression velocity. The rheometer's specifications include a maximum normal force capacity of 50 N and a maximum compression velocity of 1 mm s⁻¹. For particle positioning, we consistently placed the solder balls in the central part of the measuring shaft. When aligning the particles in a line, a minimal quantity of ethanol was applied to facilitate the particles' proximity and physical contact. This approach utilized attractive capillary forces arising from liquid bridges formed between neighbouring particles, as detailed in ref. 16. Following the evaporation of the solvent, the testing was initiated.

Fig. 1 (a) 3D computer graphics of the experimental setup. This setup is used for measurements of a particle/particle chain under mechanical compression. The thermal insulation and compressing shaft are presented in cross-section to enhance the clarity and comprehensibility of the setup. The black arrow indicates the direction of compression. During the experiments, temperature, compression rate, and normal force were the variables. (b) 2D geometry and triangular mesh used in FEM studies on the compression of a single sphere. Taking advantage of system symmetries, the model represents a single sphere constrained between two rigid plates. (c) 3D geometry and tetrahedral mesh applied in simulations involving two or more compressed spheres. In the left image, the vertically positioned plate serves as a symmetry plane, while the right image illustrates the actual modelled system.

Temperature control during the experiments was achieved using a Peltier device with active heating capabilities, allowing precise adjustment from −25 to 220 °C. To reduce heat loss from the measuring shaft, thermal foam insulation was applied (see Fig. 1a). Prior to each experiment, the position along the compression direction was calibrated by lowering the shaft until it contacted the heated base plate, establishing the zero position. Additionally, the normal force was zeroed by monitoring any increase in force during the heating phase, caused by the thermal expansion of the metal shaft. Once the normal force stabilized, both the ‘zero gap’ between the measuring shaft and the base, as well as the normal force itself, were reset to ensure accurate measurements. Subsequently, the shaft was raised, and the solder ball microparticles were swiftly positioned on the lower base of the rheometer for measurement. After positioning, the shaft was lowered to a height corresponding to the diameter of the measured particles. Typically, a waiting period of approximately one minute was allowed for the stabilization of the micro-particles' temperature and their surroundings before initiating the designated measurement program.

The data represented as closed circles in Fig. 2–4 is processed experimental data, with each experimental measurement repeated three times. Due to the use of a stepper motor, the measured deformation was slightly different for each experiment (though the differences were practically negligible). To average the data, a polynomial curve was fitted to the raw data points, ensuring identical values on the X-axis. In the final step, the data were averaged. Standard deviations were not added to Fig. 2–4 for clarity but are included in Fig. 5.

Theoretical model

Theoretical calculations were performed using COMSOL Multiphysics 6.1 with structural mechanics and nonlinear structural materials modules. Particle deformation was modelled using the Solid Mechanics interface in a time-dependent study. This approach facilitated accurate simulations of particle behaviour under load, focusing on key metrics such as contact area, deformation profiles, and applied forces.

To analyse the compression behaviour of a single sphere, a 2D axisymmetric model was utilized, as illustrated in Fig. 1b. This approach simplified the geometry, significantly reducing computational time by leveraging system symmetry. The pressing plate was modelled as a rigid domain with a prescribed displacement, determined by the product of constant velocity and time. The particle mesh was composed of triangular elements, with the element size set to the predefined 'extremely fine' setting. Manual adjustments to the minimum element size were applied to ensure precision. The pressing plate was meshed with a single brick element, as shown in the right panel of Fig. 1b.

The solder particle, composed of Sn₆₃Pb₃₇ alloy, was treated as a plastic material. Three material hardening models were implemented and compared: perfect plastic, Ludwik, and Johnson–Cook (J–C). The simplest among these, the perfectly plastic model describes a material that deforms elastically up to a specific yield stress value, referred to as the initial yield stress (σ_γ). Beyond this point, the material deforms plastically without any further increase in stress. This behavior can be expressed mathematically as:

σ_eq(ε_eq) = E·ε_eq for ε_eq ≤ ε_γ

,

σ_eq(ε_eq) = σ_γ for ε_eq > ε_γ

where σ_eq is the equivalent (local) plastic stress, ε_eq is the equivalent (local) plastic strain, E is Young’s modulus (elastic modulus), σ_γ is the yield stress, ε_γ = σ_γ/E is the yield strain.

A more comprehensive model is the Ludwik model, which includes strain-hardening effects and is given by the following expression:

σ_eq = σ_y + k·εⁿ_eq,

where k is the hardening modulus, and n is the strain-hardening exponent. Lastly, the model most extensively used here, was the J–C model, which extends the Ludwik model by incorporating both strain-rate and temperature effects into the deformation description. It is expressed by the following equation:
where C is the strain-rate sensitivity coefficient, [small epsi, Greek, dot above]_eq is the equivalent (local) plastic strain rate, [small epsi, Greek, dot above]_ref is the reference strain rate, T* is the dimensionless temperature and m is the temperature exponent.

It is important to note that in the COMSOL simulations, σ represents the equivalent local stress (not the global stress that would be calculated as the average stress across the entire material or structure). Equivalent stress, often referred to as von Mises stress in finite element analysis, is a scalar value derived from the stress tensor at each point in the material. Similarly, the equivalent plastic strain rate, [small epsi, Greek, dot above]_eq, represents the rate of change of plastic deformation over time, specific to each mesh element. Therefore, the reference strain rate parameter should not be treated as a global parameter, a common mistake that can occur when modelling in COMSOL. To clarify, we denote the reference strain rate as [small epsi, Greek, dot above]_eq,ref to emphasize that it is a local value, ensuring a constant logarithmic relation for a specific compression rate. This raises the question of how to define and input [small epsi, Greek, dot above]_eq,ref, into COMSOL, as it is a matrix of values in space and time rather than a single value defined by the engineering strain rate as [small epsi, Greek, dot above] = υ/D. Our solution was to manually implement the J–C model equation in COMSOL, where we directly specify the values obtained from the logarithmic ratio of the engineering strain rate to the reference engineering strain rate. We can do this because we assume in our calculations that the deformation shape is independent of the strain rate, i.e., the simulated deformation shapes of the initially spherical sample remain the same regardless of the compression speed. This assumption is approximately consistent with real conditions. Therefore, we do not require a matrix of [small epsi, Greek, dot above]_eq,ref values, as we know that each value in this matrix will change in the same way, expressed as the logarithm of [small epsi, Greek, dot above]_eng/[small epsi, Greek, dot above]_eng,ref. Thus, the final equation for the J–C model used has the following formula:

Additionally, we discovered that the J–C model in COMSOL version 6.1 does not correctly simulate stress values for structures compressed at rates slower than the reference strain rate. Specifically, regardless of how low the strain rate was set, the simulation yielded stress values as if the reference strain rate had been applied. This behaviour results from COMSOL's implementation of the model, where the argument of the logarithmic function is shifted by 1, ln(1 + [small epsi, Greek, dot above]_eq/[small epsi, Greek, dot above]_ref) to enhance calculation stability. Ultimately, we resolved the convergence issue by manually implementing the modified J–C model, as described above.

Each model predicted the particle's shape, contact area with the pressing plate, and applied load. The accuracy of these predictions was validated by comparing simulation results to experimental data (see Fig. 6b in the Results section).

Once the J–C model (including isotropic hardening and Coulomb friction between the pressing plate and the surface of each individual sphere, with a friction coefficient of 0.15) was identified as the most accurate for predictions (see Section 3.2 for detailed reasoning), the Optimization Module, coupled with a parametric study, was used to fine-tune the model parameters to match the experimental data. The optimization study using the Nelder–Mead method was conducted in cycles, with the optimality tolerance parameter set to 0.001. In each cycle, a parametric sweep was performed, varying simulation input parameters such as strain rate or temperature. After each cycle, the discrepancy between the experimental data and the simulated curves was estimated based on residual sum of squares (RSS). The ultimate goal of optimization was to minimize the summed RSS for the considered experimental parameter values. Model parameters were then adjusted, and the next cycle commenced. This iterative process continued until the optimality tolerance was achieved (Fig. S2 shows the reduction in the objective function across cycles, ESI†). The final set of optimized parameters was applied to all subsequent simulations.

Due to the limitations of the 2D axisymmetric model for single-particle scenarios, interactions between multiple particles in contact were simulated using a 3D model with the symmetry-based geometry shown in Fig. 1c. To further reduce computational complexity, one-quarter of the system was simulated, leveraging both the contact plane symmetry and the symmetry of the compressed objects.

Results and discussion

Laboratory results for single-ball compression

We begin our measurements by compressing individual solder balls and studying how the compressive force (F_N)–strain (ε) relation depends on ball diameter (d), engineering strain rate ([small epsi, Greek, dot above]), and solder ball temperature (T).

Fig. 2 illustrates the relation between applied compressive force and compressive strain for single solder balls of varying diameters. The strain is defined as ε = ΔL/L₀ × 100, where ΔL is the change in length, i.e., axial shortening due to compression, and L₀ is the initial length of the sample, which in this case is the ball diameter. The experiment involved compressing the solder balls at a constant engineering strain rate of 0.005 s⁻¹ ([small epsi, Greek, dot above] = υ/d, where compression velocity υ is divided by sphere diameter d), with each trial lasting approximately 3 minutes.

Fig. 2 Compression behaviour of Sn₆₃Pb₃₇ single solder balls. (a) Force–strain relation: graph illustrating applied force (F_N) versus compressive strain (ε) for single solder balls of different sizes. (b) The normalized (by ball size) force–strain relation. A constant strain rate of 0.005 s⁻¹ was used. The presented data are processed experimental results, with each experimental measurement repeated three times (for details, see the Methods section).

As shown in Fig. 2, the compressive force increases rapidly at low strain values (a few percent), then grows more gradually at intermediate strains (up to about 60%), and finally rises sharply at higher strains, exhibiting a near-divergent trend as strain approaches 100%. The changes in F_N values are the result of changes in the contact area A₁ (plate-ball contact), the transition from elastic to plastic deformation, and the strain hardening. Additionally, at high strain values, friction is likely becoming significant. As the contact area between the deformed particle and the plates increases, the amount of material sliding along the contact surface grows, and the compressive force applied perpendicular to the contact surfaces increases, all of which contribute to an increase in tangential friction.

When compressing a spherical bead, the stress σ induced by the force F_N is distributed over the contact area perpendicular to the applied force. In the purely elastic regime (strains <1%), Hertzian contact theory predicts a scaling of F_N ∼ d^1/2x^3/2, where x represents the contact radius. However, in the plastic deformation regime relevant to our study (1–80% strain), the force scales as F_N ∼ d². This transition occurs because plastic flow constrains further stress increase, shifting the governing mechanism from elastic deformation to contact area dominance. Specifically, the contact area grows proportionally to d², as opposed to the Hertzian model, which assumes elastic material behaviour. In Fig. 2b, the experimental results are normalized by dividing F_N values by d² for each data series. The resulting data collapse confirms the quadratic scaling relationship, validating that the plastic regime governs the deformation behaviour at these strain levels.

In the subsequent experiment, force–strain characteristics were determined for different strain rates. Notably, force is reported instead of stress, as calculating stress is challenging for a spherical object, requiring assumptions about which cross-sectional area to consider. From an experimental perspective, measuring force provides a more direct parameter. Fig. 3a presents the experimental data for five measurements, where the engineering strain rate (defined as the velocity of the compressive rod moving only in the Z-direction divided by the sphere diameter) varied from 3.1 × 10⁻⁵ to 1.5 s⁻¹. For microparticles with a size of 650 μm, this corresponds to a pressing plate displacement speed ranging from 0.025 to 1000 μm s⁻¹. At the lowest strain rate, the experiment lasted 7 hours, allowing for deformation up to 84%. In contrast, at the highest strain rate, the experiment lasted approximately 0.4 seconds, with deformation reaching 64%, limited by the maximum permissible force of 50 N imposed by the measurement apparatus.

Fig. 3 Strain rate dependency of 650-μm single Sn₆₃Pb₃₇ solder balls. (a) Force–strain relation at different strain rates varying from 3.1 × 10⁻⁵ to 1.5 s⁻¹. (b) The normalized force–strain relation reveals that a simple power-law relation can be used to scale the force. The power-law exponent of 0.12 indicates a very weak dependence of force on strain rate.

Fig. 3b presents the same force–strain relation as Fig. 3a, with the additional normalization of the force value. We found that within the studied range of strain rate values, a power law with an exponent of 0.12 can describe the strain rate dependence of the compressive force. Nevertheless, this dependence is very weak, suggesting that in practical industrial applications, solder microparticles can be compressed at higher strain rates without a significant increase in force. This is particularly relevant for calendering or rolling processes, where typical strain rates during compression range from 0.01 to 10 s⁻¹. However, if the compressive force – and thus the pressure at the particle–substrate interface – becomes too high, leading to substrate indentation or cracking, the compression speed should be reduced. Alternatively, increasing the process temperature remains an option.

In the next experiment, we investigate how temperature (T) affects the compressive force–strain relationship. A series of experiments were conducted over a broad temperature range, from 5 °C to 210 °C. Note that the melting temperature of Sn₆₃Pb₃₇ solder is approximately 183 °C, thus the final measurement involves the compression of a molten solder droplet.

The experimental data presented in Fig. 4a reveal a strong temperature-dependent trend in the mechanical properties of the solder material, i.e., the material's resistance to deformation decreases with increasing temperature. This behaviour can be represented mathematically using a temperature-dependent scaling factor. Specifically, the force–strain curves for different temperatures were normalized using a factor that accounts for thermal softening: 1 − T*^m, where T* = (T − T_RT)/(T_melt − T_RT). This relation is widely used in material science to predict the performance of materials under varying thermal conditions,¹⁷ where T_RT is the reference temperature used as a baseline for normalizing the temperature T in relation to the melting temperature T_melt. To determine the parameter m, we tested various values and observed which value resulted in the best collapse of the data onto a single curve. Through this empirical process, we found that the value of m is approximately 0.7. In Fig. 4b, the scaled data from Fig. 4a is plotted. In Fig. 4b, we did not plot the results for the experiment conducted at 210 °C, which is above the melting temperature. For the molten solder droplet, F_N is nearly constant and is in the range of mN for strain values up to around 70%, after which it starts to increase, reaching 0.3 N at a strain of 95%. This is still very small to be observed in Fig. 4a.

In this section of the research, we identified an empirical relation between the compressive force and the parameters of particle diameter, compression strain rate, and process temperature, which can be expressed as: F_N ∝ d²·[small epsi, Greek, dot above]^0.12·[1 − T*^0.7].

Fig. 4 Temperature dependency of 650-μm single Sn₆₃Pb₃₇ balls. (a) Force–strain relation at different temperatures in the range 5–210 °C. A constant strain rate of 4.0 × 10⁻⁴ s⁻¹ was used. (b) The normalized force–strain relation reveals that a temperature-dependent scaling factor 1 − T*^m can be used to describe the behavior, with the parameter m determined to be 0.7. The results indicate a strong dependence of force on temperature.

In the final part of the laboratory studies on the compression of a single microparticle, we compare two solder particle materials, namely the leaded alloy Sn₆₃Pb₃₇ and the lead-free alloy SAC305 (96.5% Sn, 3% Ag, 0.5% Cu). Although Sn₆₃Pb₃₇ remains widely used in many applications due to its excellent wetting properties and reliable joint strength, the lead-free solders are increasingly favoured. This shift is driven by environmental and health regulations, as well as the need for sustainable alternatives. Spherical microparticles, each 650 μm in diameter were compressed at strain rates of 1.5 × 10⁻³ s⁻¹ and 4 × 10⁻¹ s⁻¹ at room temperature. The experiment for each type of microparticle was repeated three times.

Fig. 5 illustrates the averaged results along with the standard deviation. As shown in the graph, the leaded particles deform more easily, requiring slightly less force. This is expected, given that leaded solders generally exhibit lower yield strength and greater ductility compared to lead-free solders^18,19 due to the presence of lead, which imparts greater malleability and reduces the resistance to deformation. Additionally, stress–strain curves for these experiments are provided in Fig. S3 (ESI†).

Fig. 5 Comparison of compression behaviour of leaded (Sn₆₃Pb₃₇) and lead-free (SAC305) solder beads. The force–strain relation shows that the leaded particles deform more easily, requiring slightly less force. The measurements of lead-free particles were less consistent, as evidenced by the error bars, which are larger for measurements of lead-free particles at strain rates of 1.5 × 10⁻³ and 4 × 10⁻¹ s⁻¹. The inset images show views taken from above in the direction of compression. The contact area of the compressed lead-free particles is typically less spherical than that of the leaded solder particles.

It is interesting to note that for the measurement of lead-free microparticles, there is consistently a greater spread in the measurements, as shown by the error bars. Under the microscope, the contact area of the compressed lead-free particles always appears less spherical, displaying more irregular deformation shapes. The greater spread and irregular deformation in lead-free microparticles like SAC305 can be explained by the differences in microstructure. Lead-based solders (e.g., Sn₆₃Pb₃₇) are eutectic alloys with a uniform structure that leads to more regular, predictable deformation. SAC305, a hypoeutectic alloy, has a heterogeneous structure with tin-rich phases and hard intermetallic compounds (Ag₃Sn, Cu₆Sn₅), resulting in uneven mechanical behaviour and less spherical deformation.²⁰

Two-dimensional axisymmetric simulation results of single ball compression

Numerical simulations were conducted using the finite element analysis methodology. The primary goals were to verify experimental results and ensure the accuracy of the obtained data. Additionally, simulations helped extend the range of deformations, particularly for larger or rapidly compressed spheres, where equipment limitations prevented compressive forces exceeding 50 N. The simulations also provided data that are challenging to acquire in laboratory settings, such as true strain rates (as opposed to engineering strain rates), enabled parametric analyses to identify appropriate material parameters, and allowed examination of the impact of friction on the results.

We will begin with several general simulations to illustrate the differences between commonly used compression models for microballs of various materials. Fig. 6 shows the results for a lead solder microparticle with a size of 650 μm subjected to compression with an engineering strain rate of 0.1 s⁻¹ (arbitrarily chosen). The simulations started with perfect plastic material model. In general, when compressing a material with a constant cross-section at small strain levels, the changes in cross-sectional area can be considered negligible. Under these conditions, the stress–strain curve for an idealized, perfectly plastic material initially appears as a straight line with a positive slope, corresponding to elastic deformation. This elastic regime typically dominates up to relatively large strains in elastic and viscoelastic materials. However, in the case of soft metals, elastic deformation occurs only at the very beginning of the loading process—typically up to strains around 0.2%,^8,9,21 a value barely discernible in practice and therefore neglected in our analysis.

Fig. 6 (a) 2D axisymmetric COMSOL simulations depicting the equivalent (local) stress distributions within a quarter-sphere subjected to uniaxial compression. The left column illustrates results for a perfect plastic model, while the right column corresponds to a Ludwik material model, under 5%, 50%, and 70% strain. The perfect plastic model exhibits a uniform stress distribution capped at approximately 33 MPa, signifying no further stress increase post-yield. Conversely, the Ludwik model demonstrates stress heterogeneity, indicative of a more accurate representation of material behaviour under deformation. See also corresponding Movie S1 (ESI†). (b) The force-compression response is shown for three models: perfect plastic, Ludwik without friction, and Ludwik with friction. The model incorporating Ludwik material behaviour with friction exhibits the closest alignment with experimental data, obtained from compression testing of a 650-μm Sn₆₃Pb₃₇ solder ball at an engineering strain rate of approximately 0.1 s⁻¹. (c) 2D axisymmetric COMSOL illustrations of a quarter-sphere under compression, showing equivalent local strain rate distributions at 5%, 50%, and 70% strain. These strain rate distributions are used in the J–C model to calculate the resulting equivalent stress values, and eventually the global compressive force F_N. See also corresponding Movie S2 (ESI†).

Beyond this point, the curve transitions sharply to a horizontal line at the yield stress, indicating a regime of constant stress characteristic of plastic deformation. Above this level it sharply transitions to a horizontal line at the yield stress level, indicating constant stress during plastic deformation. However, in the case of compressing an object with a non-uniform cross-section (such as a sphere) or where the values of this cross-section vary significantly, the perfect plastic model (or any other model used here) cannot be directly applied to analytically find a solution. This is because, at a given time step (overall engineering strain, ε), different points within the compressed object experience different equivalent (local) stresses, σ_eq (Fig. 6a). Consequently, the results on the graph represent an effective force–strain response that accounts for the heterogeneous distribution of stresses and strains throughout the object. The simulation graph for the perfect plastic model (Fig. 6b, purple colour) is therefore a curve with varying force values. As expected, the simulation results are far from the actual data, which is understandable since solder is a viscoplastic material with hardening.

The results from simulations based on the Ludwik model indicate that hardening behaviour of the material, influences both the values of the equivalent stress and its distribution, as illustrated in Fig. 6a (second column). The simulated curve (Fig. 6b, teal colour) shows a close approximation to the actual laboratory data. With appropriate parameter selection, the simulation can accurately replicate experimental results, particularly in the low to mid-range deformation levels. For large deformation values, the friction of the sliding material on the plane of the compressing slabs can play a role. Thus, in the last simulation presented in Fig. 6b (pink colour), frictional force was added (friction coefficient μ = 0.15), increasing the effective compressive force. As can be seen, this allows for a better fit of the numerical data to the experimental data.

However, to determine the appropriate (not arbitrarily chosen) model parameters, it is necessary to perform parameterization firstly for the reference data and then for a family of experimental curves. The material model used for parameterization is the J–C plasticity model.

Fig. 7 presents the results of parameterization using the J–C model. Panel (a) shows a set of experimental curves as a function of strain rates, along with the corresponding simulations. The fitting process began by fitting the force-deformation curve at a strain rate of 1.5 s⁻¹, where the most extensive data was available from five independent experiments conducted by two researchers. Based on this curve, key material parameters such as σ_y,ref, k_ref and n_ref were determined, enabling further parameterization to find C by fitting the simulations to the full set of experimental curves. The parameters used in the calculations are provided in Table 1, panel (a). Once all parameters were identified, the complete set of curves was plotted. Additionally, knowing C enables calculation of strain rate-dependent yield stress values σ_y using the equation σ_y = σ_y,ref × (1 + C·ln([small epsi, Greek, dot above]_eng/[small epsi, Greek, dot above]_eng,ref)) for the corresponding strain rates. For example, at an engineering strain rate of 4.0 × 10⁻¹ s⁻¹, the calculation is: σ_y = 34 × (1 + 0.07·ln(0.267) = 30.8 MPa. Yield stress values for different strain rates are provided in Table 2.

Fig. 7 Force–strain curves for (a) different engineering strain rates from 4 × 10⁻⁵ to 1.5 s⁻¹, and (b) different temperatures from 5 °C to 165 °C. Open circles represent experimental data, while solid lines show simulated results using the J–C model. In panel (a), the simulated curves agree well with the experimental data across the entire strain range, with only slight deviations at higher strains, which are within the typical variation range (as shown in Fig. 5). Notably, although the J–C model is typically applied to dynamic situations and does not account for material relaxation, it effectively describes the behaviour of solder microparticles across the tested strain rates and deformations. Panel (b) illustrates the temperature-dependent softening of the material, where higher temperatures lead to a decrease in compressive force for the same strain level, with simulations accurately reflecting this trend.

Table 1 Material parameters used for initial curve fitting and parameterization of [small epsi, Greek, dot above] and T dependencies. The parameters for σ_y,ref, k, n in panel (a) were obtained from fitting data from experiments conducted at a strain rate of 1.5 s⁻¹ and at a temperature of 23 °C, while the parameters in panel (b) were obtained from data fitting for an experiment conducted at a strain rate of 4.0 × 10⁻⁴ s⁻¹ and a temperature of 5 °C

	σ y,ref [MPa]	k ref [MPa]	n ref [—]	C [—]	m [—]	Mesh size [m]	Poisson ratio [—]	YM [GPa]
Panel (a)	34	39	0.2	0.07	0	5 × 10^−4	0.39	35
Panel (b)	19	21	0.2	0	0.7	1 × 10^−5	0.39	35

---

Table 2 Calculated σ_y values for various [small epsi, Greek, dot above], based on the C-parameter obtained from the J–C model parameterization

[small epsi, Greek, dot above] [s^−1]	1.5 × 10^0	4.0 × 10^−1	1.0 × 10^−1	6.0 × 10^−3	4.0 × 10^−4	4.0 × 10^−5
σ y [MPa]	34	30.8	27.5	20.7	14.3	8.78

---

Subsequently, parameterization was performed to find the optimal values of C and m to best fit the additional experimental data series. Fig. 7b presents a set of experimental curves as a function of temperature, along with the corresponding simulations. Similar to the strain rate parameterization in Fig. 7a, an iterative approach was applied here. Initially, model parameters were adjusted to minimize the difference between simulated and experimental curves at 5 °C, establishing a baseline parameter set (see Table 1, panel b). This allowed further parameterization to determine m, which was set at 0.7. This value aligns with the scaling parameter obtained from data collapsing in Fig. 4b. With all parameters identified, the full set of curves was plotted. Additionally, knowing m allows calculation of temperature-dependent yield stress values σ_y using the equation: σ_y = σ_y,ref × (1 − T*^m) for the corresponding temperatures. For instance, at temperature 50 °C, the calculation is: σ_y = 19 × (1 − [(50 − 5)/(183 − 5)]^0.7) = 11.74 MPa. Yield stress values for different temperatures are provided in Table 3.

Table 3 Calculated σ_y values for various T, based on the m-parameter obtained from the J–C model parameterization

T [°C]	5	25	50	75	100	125	150	165
σ y [MPa]	19	14.9	11.7	9.11	6.76	4.58	2.54	1.37

---

Experimental and 3D simulation results of particle chain compression

In this section, we investigated the compression of assembled microballs. We conducted experiments where the balls were arranged linearly, as well as experiments where the balls were freely dispersed, meaning they did not touch each other during the compression. Fig. 8a shows the experimental results, illustrating the relation between normal force (F_N) and strain (ε) for different configurations of particle chains. The data were processed through averaging and polynomial fitting. The curves indicate that linearly arranged particle systems exhibit greater resistance to deformation, requiring more force to reach the same strain level compared to systems with freely dispersed particles. The difference in force values becomes noticeable for strains above approximately 20%. At this level of strain, the contact surface between the particles becomes substantial, and the shape of the particles during deformation begins to deviate from symmetry, transitioning from spherical to disc-like, and eventually to an elongated form (see Fig. 8b, c and Movie S3, ESI†).

Fig. 8 (a) Experimental results depicting the relation between normal force (F_N) and strain (ε) for various particle configurations. Linearly arranged particle systems exhibit greater resistance to deformation, requiring higher forces to achieve equivalent strain levels compared to systems with freely dispersed particles. The experiments were conducted at an engineering strain rate of 0.0015 s⁻¹. The magnitudes of error bars (typically <5% relative error) are smaller than the symbol sizes and are not visible. (b) and (c) Shape deformation stages of particles under compression at different strain levels (10%, 30%, and 70%), showing the contrast between two-particle systems (b) and a segment of an infinitely long particle chain (c). The two-particle system exhibits asymmetrical deformation, while the infinite chain shows symmetrical deformation due to balanced forces from neighbouring particles. Blue colour indicates contact areas between neighbouring particles (A₂).

Fig. 8b and c show the deformation stages of a pair of particles (panel b) and a segment of an infinitely long particle chain under compression (panel c). The images illustrate how the particles undergo shape changes at different strain levels: 10%, 30%, and 70%. At low strains, the particles remain nearly spherical, indicating minimal deformation and a small contact area between neighbouring microparticles (A₂), represented by the blue regions. As the strain increases, the particles begin to flatten, transitioning into a disc-like shape. At high strains, this deformation becomes even more pronounced, with the particles adopting an elongated, oblong form. This visual progression underscores the mechanical behaviour of particles within a chain configuration and demonstrates how their interactions contribute to the overall deformation process.

In the configuration with only two particles (Fig. 8b), there are no constraints on the side opposite to the contact, which leads to asymmetric deformation relative to the axis passing through the centre of the particle. In contrast, in the segment of an infinitely long chain (Fig. 8c), constraints are present on both sides, resulting in symmetrical deformation, with the microparticles elongating somewhat faster in the direction parallel to the chain axis due to the balanced forces exerted by neighbouring particles.

To simulate the response of different microparticle configurations under compressive force, it was necessary to perform 3D simulations. A 2D axisymmetric approach (used in Section 3.2) would be insufficient due to the inability to accurately capture the full geometrical and mechanical behaviour of the spherical particles, especially in cases involving asymmetric deformation, complex contact interactions, and variations in force distribution across the surface of the microparticle, which are inherently three-dimensional phenomena. Importantly, the best-matched parameters for the J–C model obtained from the 2D axisymmetric simulations were applied directly to the 3D simulations, providing a well-calibrated basis for this expanded analysis. The appropriate symmetries used for efficient simulations are provided in the COMSOL mph files, included as ESI.†

Fig. 9a presents the experimental results and the corresponding simulations (represented by dashed and solid lines) for various ball configurations (2, 3, and 4 balls, both in-line and separated). As observed, the simulated results closely match the experimental data, indicating the accuracy of the model. It is noteworthy that the difference in force values between the separated and in-line configurations increases as the number of balls is increased. In Fig. 9b, we present the percentage difference in simulated compression forces between the ‘in line’ ball configuration and the ‘separated’ configuration. As can be observed, this difference increases with the number of balls but stops rising significantly for a particle chain consisting of around 10 balls. The curve begins to approach the theoretically predicted value for an infinite chain of balls.

Fig. 9 (a) Experimental data (symbols) and simulation results (lines) for 2, 3, and 4 balls, arranged either in-line or separated, showing normal force (F_N) as a function of strain (ε). Both the experiments and simulations were conducted at an engineering strain rate of 0.0015 s⁻¹. The magnitudes of error bars (typically <5% relative error) are smaller than the symbol sizes and are not visible. (b) Percentage difference in simulated normal force (ΔF) for different numbers of balls in the in-line configuration, where the force is normalized by dividing the total applied force by the number of particles.

The observed difference in compression forces for systems with varying numbers of balls, as shown in Fig. 9b, is due to the deformation constraints that arise as the number of particles in the system increases. In the case of two balls, each can deform in multiple directions, as the compression forces are not restricted solely to the balls' contact direction. In a system of three balls, the central particle experiences constraints from both sides, which reduces its freedom to deform and leads to higher compression forces compared to the two-ball system. In the case of four balls, the two central particles are further constrained, increasing the difference between the forces in the in-line and separated configurations. For very long chains, the number of neighbouring particles drives the system closer to the behaviour predicted theoretically for an infinite chain, where additional balls no longer introduce significant changes in the force distribution.

Fig. 10a presents the simulated relationship between average plate-particle contact pressure (F_N/A₁) and compressive strain for three configurations: unconfined microparticles, two microparticles in contact, and a segment of two microparticles in an infinite chain. The values for all configurations are normalized per particle. Initially, the contact pressure is high due to the small contact area between the microparticle and plate; however, as the contact area increases with strain, the pressure decreases. This trend is followed by a subsequent rise beyond around 50% strain, driven by the effects of tangential friction and material hardening.

Fig. 10 (a) Average plate-sphere contact pressure as a function of compressive strain for three configurations: single sphere, two spheres in contact, and an infinite chain. (b) Average interparticle contact pressure versus compressive strain for two configurations: two spheres in contact and an infinite chain. (c) Temperature effect on interparticle contact pressure as a function of compressive strain, evaluated at different temperatures. (d) Simulated contact pressure distribution maps at 70% compressive strain for three configurations: unconfined microparticles, two microparticles in contact, and a segment of two microparticles in an infinite chain, generated in COMSOL. Note that the results are normalized per particle. All simulations were conducted at an engineering strain rate of 0.0015 s⁻¹.

In Fig. 10b, the average interparticle contact pressure is plotted against compressive strain for two configurations: two microparticles in contact and a segment of two microparticles in an infinite chain. The pressure values for small strains (up to approximately 20%) exhibit oscillations, which are numerical artifacts caused by the mesh resolution used in the 3D simulation and are not of physical origin. A finer mesh could smooth these results, though it would significantly increase simulation time. However, this is not critical, as the overall trend remains clear, and the data values are relatively accurate.

The curves exhibit a similar trend to those in panel (a), though the initial rise in pressure is more gradual and extends over a broader range of strains (to around 10%). The interparticle contact pressures are roughly 40% lower than the plate-particle contact pressures. As in panel (a), the chain configuration exhibits higher pressure values. This is attributed to the geometric constraints imposed within the compressed chain: each microparticle is restricted from lateral deformation by adjacent particles, resulting in a more concentrated load at the contact points. In contrast, in the two-microparticle configuration, each particle can deform laterally in directions other than the contact point, leading to lower overall contact pressures.

Fig. 10c illustrates the results of simulations examining the effect of temperature on interparticle contact pressure within an infinite chain under compression. The plots display contact pressures across a range of temperatures, from 25 °C to 150 °C. As temperature increases, a decrease in interparticle contact pressure is observed, aligning with expectations. This relationship highlights the temperature dependence of mechanical interactions between particles, which is critical for understanding potential mechanisms of mechanical solid-state bonding within particle chains and, consequently, for enhancing electrical contact.

In Fig. 10d, simulated contact pressure distribution maps at 70% compressive strain show detailed pressure distributions for the three particle configurations. These color-mapped images visually capture how pressure is concentrated at contact points within each configuration. In the chain configuration, a repetitive, regular pattern of high-pressure zones is observed along the compression axis. For the single sphere, the pressure is centrally concentrated, with deformation symmetrically spreading around the contact point with the plate. In the two-sphere configuration, there are two regions of high pressure—at the contact point between the spheres and at the points where they contact the plate. Notably, in the infinite chain configuration, local pressure values are nearly twice as high as the average pressure values, both for plate-particle and interparticle pressures. This may have implications for the mechanical stability of the chain, such as stronger adhesion to the substrate and enhanced bonding between particles.

Discussion and conclusions

One of the main motivations for conducting this study was to understand the differences in deformation between unconstrained individual particles of malleable materials, such as solder, and particles arranged side-by-side in a linear structure.

We began our research with experiments on the deformation of individual unconstrained solder microparticles, studying the compressive force across a wide range of strains (0 to 80%), strain rates (0.000031 to 1.5 s⁻¹), particle diameters (200–650 μm), and temperatures (5–165 °C). To our knowledge, this is one of the most comprehensive experimental studies on the deformation of solder (Pb₆₃Sn₃₇ and Sn_96.5Ag₃Cu_0.5). By employing a systematic data collapse approach on the experimental results, we derived an empirical relationship that correlates compressive force with particle size, strain rate, and temperature. To supplement the experimental findings, we conducted simulations, which not only validated the empirical data but also allowed us to extend the parameter space beyond hardware-imposed limitations of strain rate and maximum compressive force.

For the simulations, we used the J–C model, which accurately reflected the experimental data across the full range of strain rates, strains, and temperatures. In implementing this model, we also incorporated the friction coefficient to account for interfacial effects. Thus, for the material examined within the specified parameter ranges, we conclude that the J–C model is sufficiently robust, making the application of more complex models²² unnecessary for this case.

The results of the study show that temperature exhibited a more pronounced effect on the applied force compared to strain rate. As temperature increased, material strength decreased significantly, attributed to the heightened mobility of dislocations within the material at elevated temperatures. In contrast, the influence of strain rate was relatively weak, suggesting that a wide range of compression rates can be utilized in industrial applications without substantially impacting the applied compressive force. These findings provide valuable insights for optimizing industrial processes involving solder microparticles, such as calendering or cold rolling. Recognizing the dominant effect of temperature on material strength is important for ensuring the reliability and performance of solder joints under varying thermal conditions. Additionally, the minimal influence of strain rate permits faster processing speeds without compromising the mechanical integrity of the solder. This balance between temperature and strain rate effects supports more efficient and effective manufacturing processes.

Moreover, through model optimization, precise values for material parameters were identified, as detailed in Tables 1–3. It should be noted that the parameter C varies depending on the initial strain rate used for curve fitting. When fitting begins with the highest strain rate, C is 0.07, whereas starting with the lowest strain rate results in C being 0.24. This discrepancy arises from the mathematical structure of the logarithmic function in the model rather than from any intrinsic material behavior, indicating the importance of the chosen fitting approach.

The yield stress values, presented in Table 2, are noteworthy. At low compression rates, these values are significantly lower than typical reference values for solder materials (i.e., 25–35 MPa at room temperature²³). At a very low strain rate, such as 10⁻³ s⁻¹ or lower, stress relaxation and creep can significantly lower the yield stress of solder materials. Under these conditions, the material behaves more like a viscoplastic than an elastoplastic material, rendering the conventional definition of yield stress less applicable. This effect is evident in Fig. S4 (ESI†), where strain in the solder continues to increase over time under constant loads, even at low levels of applied force. Slow deformation through mechanisms such as atomic diffusion and dislocation motion contributes to creep, while stress relaxation results from the gradual dissipation of built-up stress as atoms in the solder's crystal structure rearrange. These mechanisms collectively contribute to a lower observed yield stress at very low strain rates, as the material undergoes continuous deformation without an increase in applied stress.²⁴Table 3 demonstrates a significant decrease in yield stress with increasing temperature. This reduction is attributed to increased atomic mobility and a greater tendency for creep at higher temperatures, with the crystalline structure of the solder becoming increasingly susceptible to plastic deformation.

In the latter part of the study, we extended the investigation to more complex systems, specifically examining in-line configurations. A comparison between isolated particles and particles in contact was performed both experimentally and through simulation. As the number of particles in the chain increased, the difference in compressive force compared to isolated particles grew significantly, following an asymptotic trend. This trend approaches a limit as the number of particles increases, aligning with theoretical predictions for an infinite chain, where additional particles no longer significantly alter the force distribution. This effect arises from deformation constraints that intensify with an increasing number of neighbouring particles in contact.

Additionally, the simulations provided an in-depth view of pressure distributions, which would be exceedingly difficult, if not impossible, to capture experimentally. This allowed us to examine the impact of particle arrangement and temperature on contact pressures within compressed solder microparticle systems. Configurations involving multiple particles, such as chains, exhibited higher plate-sphere contact pressures compared to isolated particles, primarily due to lateral deformation constraints imposed by neighboring particles. We also quantified the sphere-sphere contact pressures across different particle configurations.

These findings highlight the relative magnitudes of contact pressures at various temperatures, which is essential for understanding the formation of conductive pathways in electronic applications. The bead-like particle chain structure, as referenced in the introduction, offers advantages for creating conductive paths and other electronic applications.²⁵ Elevated temperatures promote effective solid-state bonding between microparticles by facilitating processes such as diffusion and interface softening. However, the reduction in interparticle contact pressure at higher temperatures may lessen the mechanical stability of the bonding, potentially affecting the overall durability and conductivity of the assembled structure. These results suggest directions for further exploration, which will be addressed in detail in our subsequent work.

While the study centres on solder microparticles, the same principles regarding particle confinement, lateral constraints, and progressive plastic or viscoplastic deformation are relevant to various soft matter systems. For instance, gels or elastomers containing rigid filler particles can be modelled similarly, with local contact regions behaving analogously to solder-ball junctions. These insights help guide the design and optimization of stretchable electronics, shape-morphing composites, or soft robotic actuators, where the interplay between rigid inclusions and soft matrices is pivotal.

Author contributions

Y. Harkavyi initiated the project, formulated scientific hypotheses, co-designed all experiments, and performed the experiments with results presented in Fig. 1–10. Z. Rozynek co-designed and performed experiments with results shown in Fig. 2–4 and 7–9. K. Giżyński co-designed and performed the experiments with results presented in Fig. 4–10. Y. Harkavyi wrote the first version of the manuscript. All authors took part in discussions toward the finalization of the manuscript. Y. Harkavyi administered the submission and the review process.

Declaration of generative AI and AI-assisted technologies in the writing process

During the preparation of this work, we utilized an AI-powered writing assistant, Grammarly, solely to enhance readability and language clarity. Following the use of this tool, we meticulously reviewed and edited the content. Therefore, we take full responsibility for the content of the publication.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This research was funded by the Polish National Science Centre through OPUS (grant no. 2019/33/B/ST5/00935 and 2022/45/B/ST5/03529) and SONATA (grant no. 2019/35/D/ST5/03613) programs. We wish to thank CADENAS P.S.A. in Poland for giving us access to the company's research infrastructure and for providing materials. We also extend our gratitude to Marek Woźniak for preparing the 3D rendering visualizing the experimental setup (Fig. 1a).

References

1. Z. Rozynek, Y. Harkavyi and K. Giżyński, Fabrication of 1D particle structures outside a liquid environment using electric and capillary interactions: from fundamentals to applications, Mater. Des., 2022, 223, 1–11.
2. S. Zhang, Y. Liu, Y. Qian, W. Li, J. Juvert, P. Tian, J.-C. Navarro, A. W. Clark, E. Gu, M. D. Dawson, J. M. Cooper and S. L. Neale, Manufacturing with light – micro-assembly of opto-electronic microstructures, Opt. Express, 2017, 25(23), 28838–28850.
3. F. Klocke and C. Wagner, Coalescence behaviour of two metallic particles as base mechanism of selective laser sintering, CIRP Ann., 2003, 52(1), 177–180.
4. N. Suetsugu and E. Iwase, Conduction Conditions for Self-Healing of Metal Interconnect Using Copper Microparticles Dispersed with Silicone Oil, Micromachines, 2023, 14(2), 1–9.
5. X. He, S. B. Wang, Y. X. Wang, L. Liu, Y. W. Dong and Y. Yao, Viscoplastic behavior of bulk solder material under cyclic loading and compression of spherical joint-scale granules, J. Mater. Sci.: Mater. Electron., 2021, 32(15), 20640–20650.
6. H. C. Lin, C. Kung and R. S. Chen, Evaluations of the BGA solder ball shape by using energy method, CMC-Comput. Mat. Contin., 2007, 6(1), 43–50.
7. M. A. Haq, M. A. Hoque, J. C. Suhling and P. Lall, Determination of Anand Parameters From Creep Testing of SAC305 Solder Joints, ASME 2020 International Technical Conference and Exhibition on Packaging and Integration of Electronic and Photonic Microsystems, 2020.
8. M. A. Haq, M. A. Hoque, J. C. Suhling and P. Lall, Anand Parameters for Eutectic Tin-Bismuth Solder, 20th InterSociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), IEEE Electr. Network, 2021, pp. 926–932.
9. M. Motalab, Z. J. Cai, J. C. Suhling and P. Lall, Ieee, Determination of Anand constants for SAC Solders using Stress–Strain or Creep Data, 13th IEEE InterSociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), IEEE, San Diego, CA, 2012, pp. 910–922.
10. L. Zhang, J. G. Han, Y. Guo and C. W. He, Anand model and FEM analysis of SnAgCuZn lead-free solder joints in wafer level chip scale packaging devices, Microelectron. Reliab., 2014, 54(1), 281–286.
11. J. F. Liu, V. P. W. Shim, V. B. C. Tan and T. K. Lee, Dynamic Testing of Solder Joint Strength under Compression, Tension and Shearing, 2007 9th Electronics Packaging Technology Conference, 2007, pp. 380–385.
12. T. T. Nguyen, D. Yu and S. B. Park, Characterizing the Mechanical Properties of Actual SAC105, SAC305, and SAC405 Solder Joints by Digital Image Correlation, J. Electron. Mater., 2011, 40(6), 1409–1415.
13. Y. L. Lin, D. M. Wang, W. M. Lu, Y. S. Lin and K. L. Tung, Compression and deformation of soft spherical particles, Chem. Eng. Sci., 2008, 63(1), 195–203.
14. H. Y. Bu, Q. Li, S. H. Li and M. N. Li, Comparison of Modified Johnson–Cook Model and Strain-Compensated Arrhenius Constitutive Model for 5CrNiMoV Steel during Compression around Austenitic Temperature, Metals, 2022, 12(8), 17.
15. M. Bazilchuk, T. Sumigawa, T. Kitamura, Z. L. Zhang, H. Kristiansen and J. Y. He, Contact area measurement of micron-sized metal-coated polymer particles under compression, Int. J. Mech. Sci., 2020, 165, 7.
16. F. Dutka, Z. Rozynek and M. Napiórkowski, Continuous and discontinuous transitions between two types of capillary bridges on a beaded chain pulled out from a liquid, Soft Matter, 2017, 13(27), 4698–4708.
17. N. S. Selyutina and Y. V. Petrov, Comparative Analysis of Dynamic Plasticity Models, Rev. Adv. Mater. Sci., 2018, 57(2), 199–211.
18. R. Darveaux, M. Johnson and C. Reichman, Solder Joint Ductility, Int. Microelectron., 2012, 2012(1), 1046–1056.
19. S. T. Jenq, Y. S. Chiu, R. J. Lin and Y. S. Lai, The stress–strain relationship of Sn₆₃Pb₃₇ and SAC305 solder materials at elevated temperature condition, 2010 5th International Microsystems Packaging Assembly and Circuits Technology Conference, 2010, pp. 1–4.
20. J. Xu, X. Zhu, D. Shan, B. Guo and T. G. Langdon, Effect of grain size and specimen dimensions on micro-forming of high purity aluminum, Mater. Sci. Eng., A, 2015, 646, 207–217.
21. W. J. Plumbridge and C. R. Gagg, Effects of strain rate and temperature on the stress–strain response of solder alloys, J. Mater. Sci.: Mater. Electron., 1999, 10(5), 461–468.
22. Y. Wang, X. Zeng, H. Chen, X. Yang, F. Wang and L. Zeng, Modified Johnson–Cook constitutive model of metallic materials under a wide range of temperatures and strain rates, Results Phys., 2021, 27, 104498.
23. H. Ma and J. C. Suhling, A review of mechanical properties of lead-free solders for electronic packaging, J. Mater. Sci., 2009, 44(5), 1141–1158.
24. N. Zhang, F. Yang, Y. Shi and F. Guo, Compression creep of 63Sn37Pb solder balls, Acta Mater., 2011, 59(8), 3156–3163.
25. Z. Rozynek, Y. Harkavyi, Ø. G. Martinsen and K. Giżyński, Fabrication of a new type of electrically conductive micro-tracks via mechanical compression of beaded structures, Mater. Des., 2025 DOI:10.1016/j.matdes.2025.113985.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01499e

---