 Open Access Article
Open Access ArticleThe underappreciated role of nonspecific interactions in the crystallization of DNA-coated colloids†
Hunter
Seyforth
a,
Sambarta
Chatterjee
b,
Thomas E.
Videbæk
 a,
Manodeep
Mondal
a,
William M.
Jacobs
*b and
W. Benjamin
Rogers
a,
Manodeep
Mondal
a,
William M.
Jacobs
*b and
W. Benjamin
Rogers
 *a
*a
aMartin A. Fisher School of Physics, Brandeis University, Waltham, MA 02453, USA. E-mail: wrogers@brandeis.edu
bDepartment of Chemistry, Princeton University, Princeton, NJ 08544, USA. E-mail: wjacobs@princeton.edu
First published on 11th March 2025
Abstract
Over the last decade, the field of programmable self-assembly has seen an explosion in the diversity of crystal lattices that can be synthesized from DNA-coated colloidal nanometer- and micrometer-scale particles. The prevailing wisdom has been that a particular crystal structure can be targeted by designing the DNA-mediated interactions, to enforce binding between specific particle pairs, and the particle diameters, to control the packing of the various species. In this article, we show that other ubiquitous nonspecific interactions can play equally important roles in determining the relative stability of different crystal polymorphs and therefore what crystal structure is most likely to form in an experiment. For a binary mixture of same-sized DNA-coated colloidal micrometer-scale particles, we show how changing the magnitudes of nonspecific steric and van der Waals interactions gives rise to a family of binary body-centered tetragonal crystals, including both cesium–chloride and copper–gold crystals. Simulations using pair potentials that account for these interactions reproduce our experimental observations quantitatively, and a theoretical model reveals how a subtle balance between specific and nonspecific forces determines the equilibrium crystal structure. These results highlight the importance of accounting for nonspecific interactions in the crystal-engineering design process.
1 Introduction
Self-assembly is a powerful approach for making materials with complex microstructures, whereby individual components spontaneously organize due to interparticle interactions.1 In recent years, DNA has emerged as a useful tool to design and control the interactions between colloidal particles owing to the sequence-specific nature of DNA base pairing.2–4 This approach has been used to assemble a rich diversity of crystal lattices from both DNA-coated nanoparticles5–8 and DNA-coated micrometer-scale particles.9–13 Across this wide spectrum of length scales and crystal structures, the conventional approach has focused on controlling the specific, DNA-mediated attractions,14,15 along with the particle diameters, in order to specify the formation of a given assembly or stabilize a particular crystal lattice.Beyond the specific DNA-mediated attractions, however, other surface forces can in principle also play a crucial role in dictating the outcome of colloidal crystallization. Prominent examples include screened-Coulomb repulsion between like-charged particles, steric repulsion between polymer-grafted particles (including DNA-coated particles), and van der Waals (vdW) attraction between particles dispersed in a solvent.16,17 Although these nonspecific interactions are often overlooked, they can play equally important roles in stabilizing a certain crystal polymorph, especially in cases where there are multiple competing crystal structures with similar free energies. Indeed, recent reports demonstrate how rationally controlling the steric repulsion between DNA-coated nanoparticles can lead to the formation of different crystals,18 including crystals that have been notoriously difficult to assemble, like those isostructural to sodium chloride (NaCl).7,10
In this paper, we show how nonspecific interactions affect the assembly of micrometer-scale DNA-coated colloids. In particular, we show that the interplay between specific DNA-mediated attraction, nonspecific vdW attraction, and nonspecific steric repulsion favors the self-assembly of body-centered tetragonal (BCT) crystals, rather than crystals with cubic unit cells. We find that the BCT unit-cell dimensions depend sensitively on the relative magnitude and range of the nonspecific interactions, which we tune by varying the molecular weight of the polymer brush on the particle surface, the particle diameter, and the mixing of complementary grafted DNA strands. Using simulations, we confirm that pair potentials that account for these design choices give rise to equilibrium BCT crystals in quantitative agreement with experiments. Then, to understand these observations, we develop a theory to predict the relative stability of different crystal lattices for particles with both specific and nonspecific attraction. Taken together, our results showcase how nonspecific interactions can play an important role in dictating the equilibrium crystal structures, as well as how they can be controlled by tuning various experimental parameters. Our results might also help to explain why seemingly similar experimental systems produce different crystal structures,10,12,13,19 and why some predicted structures have remained inaccessible.20
2 Results and discussion
2.1 Characterizing the crystal structures for various polymer-brush lengths
We synthesize DNA-coated colloids with a range of polymer-brush molecular weights using a combination of physical grafting and click chemistry by following a modified version of ref. 21 (see ESI† for more details). Initially, we use polystyrene colloidal particles with 600-nm diameters and four different polyethylene oxide (PEO) block molecular weights, Mw = 6.5, 11, 34, and 67 kDa. We fluorescently dye the two particle species (referred to as A and B) different colors to distinguish their compositional order within the crystal phase. The ssDNA sequence is 65 bases long with a 7 base-long region at the end that is complementary between the two sequences. The net result is a binary suspension of same-sized particles coated with a dense brush of PEO polymers, which are end-grafted with single-stranded DNA (Fig. 1A).We characterize the binary crystals that self-assemble by determining the two-dimensional radial distribution functions (RDFs) of their surface crystallographic planes. We first assemble crystals at a constant temperature just below their melting point (see ESI† for a detailed protocol). We then lower the sample to room temperature at a ramp rate of 0.05 °C every two hours until most of the free monomers have been consumed by the growing crystals, so that we can transfer it to a confocal fluorescence microscope to image the crystal symmetry and composition. Next, we characterize the structures of roughly one hundred single crystals (Fig. 1B) by finding the particle centers using standard image-analysis routines22 and computing the two-dimensional RDFs. Two examples for crystals with the longest and shortest polymer lengths are shown in Fig. 1C. Because the particles are neither index matched nor density matched to the solvent, we image the surface facet that is parallel to the coverslip–water interface.
We classify the structure of each crystal by examining the measured RDF for A–B particle pairs, gAB(r), which provides a unique fingerprint. Specifically, we compare the measured RDF to a look-up table of RDFs for low-index crystallographic planes of body-centered tetragonal crystals. The look-up table comprises a variety of binary body-centered tetragonal crystals with various aspect-ratio unit cells, which we characterize by a dimensionless parameter C that lies between 0 and 1. If C = 0, the crystal has a cubic unit cell that is isostructural to cesium chloride (CsCl); if C = 1, the crystal again has a cubic unit cell, but this time is isostructural to copper gold (CuAu). Intermediate values of C correspond to crystals with non-cubic unit cells that are characterized by a nearest-neighbor A–B separation distance a0 and primitive vectors ax![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) , ayŷ, and azẑ:
, ayŷ, and azẑ:
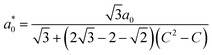 | (1a) |
 | (1b) |
 | (1c) |
Interestingly, the crystals that we assemble are neither a perfect match for CsCl nor CuAu. Moreover, their crystal structure depends on the polymer brush molecular weight Mw. For example, Fig. 1C shows the measured RDFs for binary crystals composed of 600-nm-diameter particles with Mw = 6.5 kDa and 67 kDa, as well as reference RDFs for the closest matching crystallographic planes of CsCl and CuAu. By visual inspection, we can clearly see that the two experimental RDFs are different from one another and from the reference RDFs. The differences between the experimentally determined structures are also evident in the crystal images shown in Fig. 1D. In this way, we find that all four crystals correspond to different BCT lattices with different unit-cell aspect ratios. For the particles with the shortest polymer brush, we also assemble and characterize the crystal structure for three salt concentrations ranging from roughly 50–500 mM NaCl, which has a minimal effect on the equilibrium C parameter value (see Fig. S1 and S2 in ESI†).
We hypothesize that the BCT crystal structures that we observe are stabilized by a combination of specific DNA-mediated attraction and nonspecific interactions. Prior theoretical and simulation studies using simple models of DNA-coated particles, which do not account for potential nonspecific interactions present in our experimental system, have predicted that CsCl is the thermodynamically stable crystal phase for same-sized particles with attractive interactions between A and B particles only.20,23 This prediction is due to the greater entropy of hard-sphere CsCl crystals, which have body-centered cubic (BCC) unit cells, relative to hard-sphere CuAu crystals, which have face-centered cubic (FCC) unit cells.24 However, this predicted entropic difference between CsCl and CuAu structures is smaller than the thermal energy per particle. It is therefore plausible that other interactions with similar or greater magnitude can influence the thermodynamically stable crystal structure. For example, earlier experimental results showed that CuAu crystals can be stabilized relative to CsCl by introducing a small degree of DNA hybridization between particles of the same type,23 which can only form contacts in the denser CuAu phase due to the narrow range of distances over which the DNA can hybridize. Our hypothesis follows similar reasoning, but differs in that the range of the various nonspecific interactions need not be the same as that of the specific DNA-mediated attractions. We propose that the sum total of these various surface forces, acting over a variety of different ranges, could plausibly stabilize non-cubic BCT crystal structures, which have different nearest-neighbor distances between A–A/B–B and A–B particle pairs.
2.2 Modeling microscopic interactions between DNA-coated colloids
To test this hypothesis, we first evaluate the pair-interaction free energies (referred to as ‘pair potentials’) in our experimental system using a recently developed microscopic model of the interactions between DNA-coated colloids.15 This microscopic model accounts for the free energy of DNA hybridization,25 steric repulsion between polymer brushes, and vdW attraction between colloidal particles. Importantly, the model self-consistently accounts for the excluded-volume interactions between adjacent strands, which may or may not be hybridized, by minimizing the total free energy with respect to the fraction of hybridized strands. In this way, the total free energy of interaction can be computed as a function of the distance between the DNA-coated particles. For example, Fig. 2 shows predictions of the A–A/B–B and A–B pair potentials for the two systems investigated in Fig. 1C and D at temperatures near the melting points of the corresponding crystals. Notably, each A–B pair potential has a narrow attractive well when the particle surfaces are separated by a distance comparable to twice the equilibrium polymer brush height. By contrast, the contribution to the pair potentials due to vdW attraction acts over longer distances. | ||
| Fig. 2 Predicting A–A/B–B and A–B pair potentials. (A) A schematic of a pair of DNA-coated particles, illustrating the surface-to-surface separation distance. (B) The total A–A/B–B and A–B pair potentials are calculated for the systems examined in Fig. 1C and D (600 nm-diameter particles with Mw = 6.5 or 67 kDa) plotted with respect to the separation distance between the colloidal particle surfaces (black curves). Because the DNA-hybridization contribution to the pair potential is extremely temperature sensitive, we illustrate the differences between these systems by choosing the temperature separately for each system such that the minimum of the A–B potential is approximately −5kBT. The blue curve shows the nonspecific vdW contribution to the total pair potentials. In the Mw = 6.5 kDa system, the vdW attraction is approximately 0.5kBT at the distance where the total A–B pair potential is minimized. In the Mw = 67 kDa system, the longer brush screens this interaction. | ||
These predicted pair potentials suggest that our hypothesis is indeed plausible. First, we observe that the contribution to the pair potential from vdW attraction is predicted to be independent of Mw, as the vdW interaction is determined by the colloidal particle diameter and the Hamaker constant in ref. 15. Therefore, the vdW interaction is the same for both A–A/B–B and A–B particle interactions. By contrast, the steric contribution from the polymer brush and the grafted DNA molecules depends sensitively on the polymer Mw, whereby longer polymers shift the minimum of the pair potential to larger particle separations. These differences mean that the nonspecific vdW attraction is comparable to the thermal energy for both A–A/B–B and A–B particle pairs when the brushes come into contact in the short-polymer (6.5 kDa Mw) system, whereas the vdW attraction is negligible when the brushes come into contact in the long-polymer (67 kDa Mw) system. Indeed, this weak A–A/B–B attraction between DNA-coated colloids that depends on the polymer molecular weight has been measured directly for a very similar experimental system.15
Second, we observe that the steric repulsion due to excluded volume interactions between the brushes occurs at different distances for the A–A/B–B and A–B particle pairs. This feature arises because the minimum-free-energy brush height in the microscopic model of ref. 15 depends on whether the grafted DNA is hybridized. Because the A–A/B–B particle pairs do not experience DNA-mediated attraction, the repulsion between their polymer brushes leads the pair potential to diverge at a greater separation between the particles. As we discuss below, this feature also has significant implications for the equilibrium binary crystal structure.
2.3 Comparing predicted and experimental BCT crystal structures
We next assess whether these pair potentials can explain the variations in the BCT structures that are observed in experiment. To this end, we use constant-pressure molecular dynamics simulations to predict the equilibrium crystal structure for each experimental system at room temperature, T = 25 °C (see Appendix). For each polymer length, we prepare a 1024-particle binary crystal with initial BCT C parameters ranging from 0 to 1. We then set the applied pressure to be close to zero, since the coexisting colloidal gas phase in the experiments is extremely dilute, and evolve the system under the pair potential that is predicted for the experimental design parameters. Regardless of the initial C parameter, we find that the structure converges to a unique crystal lattice for each system, which we characterize by computing the time-averaged unit-cell dimensions ax, ay, and az.Consistent with our experimental observations, these simulations predict that BCT crystals with C parameters between 0 and 1 are thermodynamically favored over both CsCl and CuAu. Moreover, the simulations predict equilibrium C parameters, computed viaeqn (1), that depend on Mw and agree nearly quantitatively with the experimentally characterized crystals (Fig. 3A and B). Both simulations and experiments show that the C value decreases from roughly 0.6 (more CuAu-like) to 0.2 (more CsCl-like) as Mw increases from 6.5 to 67 kDa. We observe a relatively narrow distribution of C for each system, indicating that all crystals for a particular system assemble the same BCT structure. Thus, based on the correspondence with our equilibrium simulations and the reproducibility of our experimental results, we conclude that the experimental C parameters reflect the equilibrium crystal structure at room temperature.
Because the vdW contribution to the pair potential is determined by the particle diameter in the microscopic model, we hypothesize that the nonspecific attraction responsible for high C parameter values can also be eliminated by reducing the size of the colloidal particles. We therefore perform the same set of experiments and simulations for the same polymer lengths but a smaller particle diameter of 430 nm. For these systems, the vdW attraction is predicted to be negligible at the distance at which the polymer brushes come into contact, regardless of the polymer Mw. As a result, we expect that the BCT crystal structures will all be close to CsCl.
Simulations and experiments confirm this expectation (Fig. 3A and B), as the equilibrium C parameter for the smaller-particle crystals is small (0.2) and nearly independent of the polymer Mw. Again we observe relatively narrow distributions of C parameters, except in the case of the shortest polymers, for which the C parameter ranges from 0.1 to 0.5 across different crystals. Yet overall, the semi-quantitative agreement between simulations and experiments is consistent regardless of the particle diameter. We attribute small discrepancies between the simulations and the experiments to our assumption that the polymer density is constant across all systems, which may not be the case in reality given that each system is synthesized separately. Nonetheless, the agreement between simulation and experiment gives us confidence that the experimental crystal structures are governed by equilibrium thermodynamics and a balance of specific and nonspecific interactions that make up the predicted pair potentials.
2.4 Predicting the stability of BCT crystal polymorphs
To gain deeper insight into the thermodynamic determinants of the observed crystal structures, we devise a theoretical model with which we can predict the equilibrium phase behavior from the microscopically modeled pair potentials. Our approach utilizes thermodynamic perturbation theory and a reference binary crystal in which A–B particle pairs are bonded via a harmonic potential. The harmonic potential uref(r) = ε + (kAB/2)(r − σ)2 is obtained from the A–B pair potential in the absence of vdW interactions, uAB, where r is the distance between the centers of the particles, σ is the distance at which uAB is minimized, ε is the value of uAB at r = σ, and kAB is the second derivative of uAB evaluated at r = σ. The free energy of a crystal with a specified BCT C parameter can be calculated exactly for this reference model. However, nonspecific interactions, which we treat perturbatively, turn out to be crucial for determining the relative free energies of the crystal structures. Complete details of these calculations are provided in the Appendix. In what follows, we describe our approach for calculating the phase behavior and highlight the essential insights that emerge.Given the predicted pair potentials, we seek the conditions for phase coexistence between a colloidal gas phase and a BCT crystal structure with a variable C parameter. To this end, we compute the free energies of these phases according to the thermodynamic perturbation theory and then equate their chemical potentials, μ, and pressures, P. At phase coexistence,
| μfluid(ηfluid) = μcrystal(Pfluid(ηfluid);C), | (2) |
We validate the predictions of our theory by comparing both the crystal melting temperatures and the equilibrium C values at room temperature with experiments. First, we predict the melting temperature for each system theoretically by finding the temperature-dependent pair potentials at which the dilute-phase packing fraction, ηfluid, that is in coexistence with the equilibrium BCT crystal is equal to the overall colloidal volume fraction in our experiments, ∼0.5%. In this way, we find that the predicted and experimentally determined melting temperatures agree semi-quantitatively, with a Pearson correlation coefficient of R = 0.98 and absolute errors less than 2 °C (see Fig. S3 in ESI†). The melting temperatures decrease monotonically with respect to increasing polymer Mw, resulting in a difference of approximately 10 °C between Mw = 6.5 and 67 kDa.
Second, we predict the BCT C parameters at room temperature and find qualitative agreement with the experimentally determined values. Although these predictions are not as accurate as the simulation results that utilize the same pair potentials, most likely due to the approximations involved in the perturbation theory, we obtain a positive correlation of R = 0.88 with respect to the experimental values (Fig. 3B). We note that the discrepancy between the predictions and the experimental measurements for the 600-nm particles with a 34-kDa polymer brush is possibly due to the very flat free-energy landscape for this system (see Fig. S4 in ESI†), which makes the predicted C values highly sensitive to potential inaccuracies in the pair-potential model, the approximations used in the BCT crystal theory, or our assumption of a constant polymer density across all systems. Yet overall, our theory reproduces the observed trends with respect to the particle diameter and the polymer Mw. We can therefore examine the theory to understand the thermodynamic driving forces that select the equilibrium BCT crystal structures.
Specifically, our theory predicts that the coexistence chemical potential is affected by the harmonic and anharmonic contributions to the crystal entropy, as well as the vdW attraction. The harmonic contribution to the entropy, which arises from the phonon modes of the reference crystal, actually favors high C parameter values, although the difference between the CuAu and CsCl phonon entropies is less than 0.1kB per particle (see Fig. S5 in ESI†). This observation may be surprising given that BCC crystals are typically expected to be entropically favored over FCC crystals.24 However, we emphasize that the harmonic reference crystal does not consider the repulsion between particles of the same type, which is accounted for by the pair potential uAA = uBB. This repulsion instead leads to an anharmonic contribution to the crystal entropy, which indeed favors low-C crystal structures in which particles of the same type are less likely to come into contact. Importantly, the probability that particles of the same type contact one another for a given C parameter depends on the distance at which uAA becomes strongly repulsive. As previously noted, this repulsion occurs at greater distances than the repulsion between particles of different types (Fig. 2), leading to an increased anharmonic entropic penalty that favors low C values. Finally, the vdW interaction lowers the chemical potential when particles of the same type are closer together, favoring larger C values as expected. Although these driving forces are individually weak compared to the thermal energy, shifting the balance among them can have large effects on the crystal structure, or potentially lead to broad distributions of C parameters, when μcoex is a weakly varying function of C (Fig. 3C).
Based on these considerations, an interesting prediction of our theory is that vdW interactions are in fact not essential to obtain BCT structures, since the harmonic contribution to the entropy also favors high C values. This prediction is supported by simulations conducted in the absence of vdW attraction (see Fig. S6 in ESI†), highlighting the complexity of crystal-structure prediction when many thermodynamic driving forces of similar magnitudes are involved. However, testing this prediction experimentally would be challenging due to the interdependence of the anharmonic contribution to the entropy and the vdW interactions, as both of these driving forces are controlled in our system by a limited set of accessible design parameters.
Overall, our theory predicts that the equilibrium BCT crystal structure is primarily determined by the balance between the anharmonic contribution to the crystal entropy and the vdW attraction. Both of these effects can be considered to be nonspecific since neither is governed by DNA-mediated interactions. Taken together, these theoretical observations explain how subtle changes to the experimentally accessible system design parameters can simultaneously affect multiple weak driving forces and tune the equilibrium BCT crystal structure.
2.5 Incorporating DNA-mediated A–A/B–B attraction
Based on our understanding of these thermodynamic driving forces, we hypothesize that alternative nonspecific attractive interactions could be used to systematically tune the BCT crystal structure. To test this idea, we devise an experiment in which the attraction between A–A/B–B particle pairs is due to DNA hybridization rather than vdW attraction. Specifically, we use a polymer brush with the largest PEO molecular weight (67 kDa) to screen the vdW attraction. We then coat the two particle species with different mixtures of the two complementary DNA sequences to induce DNA-mediated attractions between A–A/B–B particle pairs, such that one particle species is coated with mole fractions α of one sequence and (1 − α) of its complement, and the other particle species is coated with α of the complement and (1 − α) of the sequence (Fig. 4A). Therefore, both particle species should experience roughly equal A–A/B–B attraction, and the range of the A–A/B–B attraction should be comparable to the range of the A–B attraction, because both result from hybridization of the same surface-grafted DNA molecules.26 To perform simulations, we calculate pair potentials by modifying the fraction of complimentary strands on each particle species, such that the average fraction of hybridizing DNA is 2α(1 − α) on A–A/B–B particle pairs and α2 + (1 − α)2 on A–B particle pairs. We also utilize these pair potentials in a modified version of our theory to predict the equilibrium BCT C parameter as a function of α (see Fig. S7 in ESI†). | ||
| Fig. 4 Tuning the BCT crystal structure by balancing specific and nonspecific interactions. (A) 600-nm-diameter, Mw = 67 kDa particle types A and B are prepared with different strand mixing fractions, α, of two complementary DNA sequences. (B) Plotting the BCT C parameter versus α reveals a continuous shift towards CuAu-like structures as α increases. Constant-pressure simulations of the equilibrium crystal structures, conducted with pair potentials that account for the different mixing fractions (diamonds), are in good agreement with the experimental measurements (circles). Small circles show data for individual crystals; large white circles show the mean values. The broad distribution of experimentally determined C parameters at α = 0.1 likely reflects a flat μcoexversus C curve (cf.Fig. 3) near the midpoint of the continuous transition, resulting in a wide range of crystal structures with extremely similar stabilities. (C) Fluorescence micrographs of the surfaces of the crystals illustrate the continuous shift from a CsCl-like structure at α = 0 to a CuAu-like structure for α = 0.2. | ||
As anticipated, we find that increasing the strand mixing fraction α, and therefore the magnitude of the A–A/B–B attraction, induces a transition from CsCl-like to CuAu-like crystals (Fig. 4B). The experimentally observed C parameter value increases from approximately 0.1 to 0.8 upon increasing α from 0 to 0.3, and these observations are matched quantitatively by our simulation results over the same range. Importantly, this transition appears to be continuous, which is consistent with the convex μcoexversus C curves that are predicted by our theory (see Fig. S7 in ESI†). Interestingly, for α = 0.1, we observe that the interparticle spacing and crystal symmetry appear to vary locally within a single crystal domain (see Fig. S8 in ESI† for an example). We interpret this heterogeneity as the result of polymorphs with very similar free energies, leading to a large spread in the measured C parameter values at this specific mixing fraction near the midpoint of the transition from low to high average C value (Fig. 4B). This observation is also consistent with the continuous transition predicted theoretically, which results in a relatively flat μcoexversus C curve, and thus a broad distribution of near-equilibrium crystal structures, near the midpoint of this transition (Fig. 4B and C). We point out that an earlier study that used mixing of DNA sequences to induce A–A/B–B attraction lacked the spatial resolution and quantitative crystallography to identify this continuous transition.23 Nonetheless, we emphasize that the experimentally determined crystals exhibit the same compositional order as the binary crystals without strand mixing for the range of α values that we consider (Fig. 4B and C).
3 Conclusions
Taken together, our results demonstrate how nonspecific colloidal interactions can play crucial roles in determining the relative stabilities of competing crystal structures. We demonstrate that a binary mixture of same-sized, micron-scale particles can produce a diversity of BCT crystal structures that can be tuned via a variety of physically distinct modes of nonspecific attraction. In all cases, we theoretically predict a continuous transition, regardless of whether the nonspecific attraction is due primarily to vdW or DNA-mediated forces, which is consistent with the results of simulations and experiments. These results further support our conclusion that the experimentally determined BCT crystal structures reflect the equilibrium crystal structures at room temperature, and also demonstrate that subtle changes in the thermodynamic driving forces can be accurately predicted by the microscopic model.We highlight that a thorough examination of the determinants of a continuous transition from BCC to BCT to FCC versus a discontinuous transition directly from BCC to FCC could be an interesting question for future work. In particular, while it is tempting to draw direct comparisons between the phase behavior that we report and the myriad examples of DNA-mediated colloidal crystallization at the nanoscale and microscale,4,8 some of which report discontinuous transitions from BCC to FCC,27,28 making these connections is challenging owing to the wide diversity of length scales, particle shapes, conjugation strategies, and DNA motifs used across these many examples. As a result, it is difficult to conclude whether or not the resultant differences in the phase behavior are due to the fact that the vdW attraction is negligibly weak for nanometer-scale particles, that the entropic contributions to the crystal free energies are fundamentally different due to the fact that the grafted DNA molecules are comparable in size to the particle cores, or something else entirely. Determining the mechanistic details of the transitions between different crystal polymorphs therefore requires new dedicated studies designed to control for these many confounding variables.
From a materials-design perspective, our results point to new possibilities in the programmable crystallization of DNA-coated particles. Whereas the vast majority of the crystal-engineering design rules have focused primarily on the specific DNA-mediated interactions,8,29 our work motivates the development of design approaches that include and utilize both specific and nonspecific interactions. Indeed, our experimental results show that including nonspecific attraction, even in simple binary mixtures of same-sized particles, can expand the diversity of crystals that can be self-assembled to include a family of crystal structures with non-cubic unit cells. This observation begs the question: What other crystal structures might be accessible to systems of DNA-coated colloidal particles if one can design both the specific, DNA-mediated attractions and the nonspecific attractions and repulsions?
Author contributions
H. S., S. C., W. M. J., and W. B. R. conceived the research. H. S. performed the experiments. H. S., T. E. V., and M. M. analyzed the data. S. C. and W. M. J. developed the theory and simulations. All authors contributed to writing the manuscript.Data availability
Simulation, analysis, and theoretical modeling scripts are provided at https://github.com/wmjac/dnacc-binary-crystal-pub. Experimental data is available upon reasonable request.Conflicts of interest
There are no conflicts to declare.Appendices
Constant-pressure simulations
We perform molecular dynamics simulations using pair potentials computed from the microscopic model of DNA-coated colloidal particles15 at the experimental temperature T = 25 °C. For each system, we initialize binary crystals consisting of 1024 colloidal particles (512 particles of each type) in 11 different BCT crystal structures, C ∈ [0,0.1,…,1]. The initial lattice spacing is chosen such that the nearest-neighbor A–B particle pairs are separated by the distance at which the pair potential is minimized. We work in dimensionless units where the colloidal diameter is d = 1, the reduced simulation temperature is kBT = 1, and the masses of the particles are set to m = 1, so that the time unit is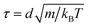 . Because the potential well is extremely narrow, we choose a small timestep equal to Δt = 5 × 10−5τ. We then perform constant-pressure (NPT) simulations, allowing the orthorhombic simulation box dimensions to fluctuate independently, at a low pressure of P = 10−4kBT/d3. We note that our results are quantitatively unchanged if the pressure is reduced to P = 10−5kBT/d3. We run the simulation for 5 × 107 timesteps to ensure that equilibrium is reached. Since the simulation box dimensions are allowed to fluctuate independently, the BCT C parameter is determined directly from the box dimensions,
. Because the potential well is extremely narrow, we choose a small timestep equal to Δt = 5 × 10−5τ. We then perform constant-pressure (NPT) simulations, allowing the orthorhombic simulation box dimensions to fluctuate independently, at a low pressure of P = 10−4kBT/d3. We note that our results are quantitatively unchanged if the pressure is reduced to P = 10−5kBT/d3. We run the simulation for 5 × 107 timesteps to ensure that equilibrium is reached. Since the simulation box dimensions are allowed to fluctuate independently, the BCT C parameter is determined directly from the box dimensions, | (3) |
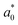 as defined in eqn (1) with a0 calculated as the equilibrium distance between nearest-neighbor A–B particle pairs in simulations. Finally, we report the BCT C parameter for each system by averaging over the final 107 timesteps of the equilibrated simulation trajectories and over all 11 initial conditions, which we empirically find to all converge to the same equilibrium crystal structure. Error bars associated with the equilibrium C values, which are calculated as the standard error of the mean of the 11 initial conditions, are typically smaller than the symbol sizes in the figures.
as defined in eqn (1) with a0 calculated as the equilibrium distance between nearest-neighbor A–B particle pairs in simulations. Finally, we report the BCT C parameter for each system by averaging over the final 107 timesteps of the equilibrated simulation trajectories and over all 11 initial conditions, which we empirically find to all converge to the same equilibrium crystal structure. Error bars associated with the equilibrium C values, which are calculated as the standard error of the mean of the 11 initial conditions, are typically smaller than the symbol sizes in the figures.
Theoretical model of BCT crystal phase coexistence
In an ordered binary crystal phase, we assume that the average spacing between nearest-neighbor particle centers is exactly r = σ. The crystal-phase packing fraction is then
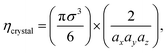 | (4) |
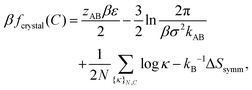 | (5) |
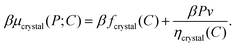 | (6) |
In the fluid phase, we use the Carnahan–Starling equation of state for a hard-sphere fluid with a mean-field correction for the short-range attractions between particles of different types,
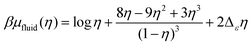 | (7) |
 | (8) |
 is the approximate width of the harmonic well.
is the approximate width of the harmonic well.
At phase coexistence, the chemical potentials and pressures of the fluid and a crystal phase are equal. Since we are assuming that the packing fraction of a given crystal phase is solely determined by the BCT parameter C, we only need to solve eqn (2) to find μcoex = μfluid = μcrystal as a function of ηfluid. The equilibrium crystal in coexistence with the fluid phase is the one with the lowest equilibrium chemical potential.
 | (9) |
By contrast, nonspecific vdW interactions affect particles in both the fluid and crystal phases. We treat the pair potential uvdW as a weak perturbation to the reference crystal structure using the λ-expansion.31 The corrections to the chemical potential and the pressure of the fluid phase are
 | (10) |
 | (11) |
For the crystal-phase calculation, we approximate the structure of the reference crystal by assuming that the particles are at their equilibrium positions in the binary lattice. The correction to the chemical potential of the crystal phase is thus
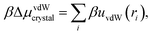 | (12) |
In practice, we incorporate these correction terms, eqn (9)–(12), and solve eqn (2) to compute μcoex as a function of C, as shown in Fig. 3C. An extension of this theory to systems with specific A–A/B–B attraction, which follows a similar perturbative approach, is presented in the ESI.†
Acknowledgements
This work was supported by the National Science Foundation (DMR-2214590) as well as the Brandeis NSF MRSEC, Bioinspired Soft Materials (DMR-2011846).Notes and references
- G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421 CrossRef CAS PubMed.
- C. A. Mirkin, R. L. Letsinger, R. C. Mucic and J. J. Storhoff, Nature, 1996, 382, 607–609 CrossRef CAS PubMed.
- A. P. Alivisatos, K. P. Johnsson, X. Peng, T. E. Wilson, C. J. Loweth, M. P. Bruchez Jr and P. G. Schultz, Nature, 1996, 382, 609–611 CrossRef CAS PubMed.
- W. M. Jacobs and W. B. Rogers, Annu. Rev. Condens. Matter Phys., 2025, 16, 443–463 CrossRef.
- S. Y. Park, A. K. R. Lytton-Jean, B. Lee, S. Weigand, G. C. Schatz and C. A. Mirkin, Nature, 2008, 451, 553–556 CrossRef CAS PubMed.
- D. Nykypanchuk, M. M. Maye, D. van der Lelie and O. Gang, Nature, 2008, 451, 549–552 CrossRef CAS PubMed.
- R. J. Macfarlane, B. Lee, M. R. Jones, N. Harris, G. C. Schatz and C. A. Mirkin, Science, 2011, 334, 204–208 CrossRef CAS PubMed.
- C. R. Laramy, M. N. O’Brien and C. A. Mirkin, Spherical Nucleic Acids, Jenny Stanford Publishing, 2020, pp. 227–289 Search PubMed.
- P. L. Biancaniello, A. J. Kim and J. C. Crocker, Phys. Rev. Lett., 2005, 94, 058302 CrossRef PubMed.
- Y. Wang, Y. Wang, X. Zheng, É. Ducrot, J. S. Yodh, M. Weck and D. J. Pine, Nat. Commun., 2015, 6, 7253 CrossRef CAS PubMed.
- M. He, J. P. Gales, É. Ducrot, Z. Gong, G.-R. Yi, S. Sacanna and D. J. Pine, Nature, 2020, 585, 524–529 CrossRef CAS PubMed.
- A. Hensley, W. M. Jacobs and W. B. Rogers, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2114050118 CrossRef CAS PubMed.
- A. Hensley, T. E. Videbæk, H. Seyforth, W. M. Jacobs and W. B. Rogers, Nat. Commun., 2023, 14, 4237 CrossRef CAS PubMed.
- W. B. Rogers and J. C. Crocker, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 15687–15692 CrossRef CAS PubMed.
- F. Cui, S. Marbach, J. A. Zheng, M. Holmes-Cerfon and D. J. Pine, Nat. Commun., 2022, 13, 1–10 Search PubMed.
- Y. Liang, N. Hilal, P. Langston and V. Starov, Adv. Colloid Interface Sci., 2007, 134, 151–166 CrossRef.
- J. N. Israelachvili, Intermolecular and surface forces, Academic Press, 2011 Search PubMed.
- R. Mao, B. Minevich, D. McKeen, Q. Chen, F. Lu, O. Gang and J. Mittal, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2302037120 CrossRef CAS.
- Y. Wang, Y. Wang, X. Zheng, É. Ducrot, M.-G. Lee, G.-R. Yi, M. Weck and D. J. Pine, J. Am. Chem. Soc., 2015, 137, 10760–10766 CrossRef CAS.
- A. V. Tkachenko, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 10269–10274 CrossRef CAS.
- J. S. Oh, Y. Wang, D. J. Pine and G.-R. Yi, Chem. Mater., 2015, 27, 8337–8344 CrossRef CAS.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310 CrossRef CAS.
- M. T. Casey, R. T. Scarlett, W. Benjamin Rogers, I. Jenkins, T. Sinno and J. C. Crocker, Nat. Commun., 2012, 3, 1209 CrossRef PubMed.
- H. Hu, P. S. Ruiz and R. Ni, Phys. Rev. Lett., 2018, 120, 048003 CrossRef CAS PubMed.
- J. SantaLucia Jr and D. Hicks, Annu. Rev. Biophys. Biomol. Struct., 2004, 33, 415–440 CrossRef PubMed.
- H. Fang, M. F. Hagan and W. B. Rogers, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 27927–27933 CrossRef CAS PubMed.
- Y. Zhang, S. Pal, B. Srinivasan, T. Vo, S. Kumar and O. Gang, Nat. Mater., 2015, 14, 840–847 CrossRef CAS.
- R. V. Thaner, Y. Kim, T. I. Li, R. J. Macfarlane, S. T. Nguyen, M. Olvera de la Cruz and C. A. Mirkin, Nano Lett., 2015, 15, 5545–5551 CrossRef CAS PubMed.
- W. B. Rogers, W. M. Shih and V. N. Manoharan, Nat. Rev. Mater., 2016, 1, 16008 CrossRef CAS.
- V. Elser, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2014, 89, 052404 CrossRef PubMed.
- J.-P. Hansen and I. R. McDonald, Theory of simple liquids: with applications to soft matter, Academic Press, 2013 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00001g |
| This journal is © The Royal Society of Chemistry 2025 |


