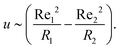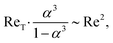Open Access Article
Open Access ArticleInertia-driven propulsion of asymmetric spinner-dimers at moderate Reynolds numbers
Zaiyi
Shen
*a,
Dongfang
Fu
a and
Juho S.
Lintuvuori
 *b
*b
aState Key Laboratory for Turbulence and Complex Systems, Department of Mechanics and Engineering Science, College of Engineering, Peking University, Beijing 100871, China. E-mail: zaiyi.shen@pku.edn.cn
bUniv. Bordeaux, CNRS, LOMA, UMR 5798, F-33400 Talence, France. E-mail: juho.lintuvuori@u-bordeaux.fr
First published on 14th April 2025
Abstract
We investigate the translational motion of rotating colloidal systems at moderate Reynolds numbers (Re), focusing on particle dimers in snowman-like configurations in three scenarios: (i) two co-rotating spheres driven by an external field, (ii) two counter-rotating spheres driven by an internal torque as a swimmer, and (iii) a single rotating spinner with a passive sphere for cargo delivery, using hydrodynamic simulations. In all three cases, the particles are bound together hydrodynamically, and the purely rotational motion of the spinners produces a net propulsion of the dimers along the axis of rotation due to symmetry breaking. We demonstrate tunable dynamics, where the propulsion direction of the co-rotating dimer can be reversed by tuning the aspect ratio and Reynolds number, as well as cargo transport where a dimer consisting of a single spinner and a passive cargo particle can have a sustained locomotion due to broken head-to-tail symmetry of the overall flow fields. These findings highlight the critical role of inertia in creating locomotion from rotational motion and offer new avenues for controlling and optimizing translational motion in colloidal assemblies through rotational degrees of freedom.
1. Introduction
Biological organisms such as bacteria, algae, and spermatozoa employ specialized propulsion strategies to navigate fluid environments.1 At the micro-scale, where the Reynolds number (Re) is typically very low, these swimmers rely on non-reciprocal motions,2,3 such as flagellar beating or ciliary strokes, to achieve net movement under conditions dominated by viscosity. However, as the physical size of a swimmer or its speed increases, inertial effects become significant, leading to fundamentally different propulsion mechanisms under higher Re conditions.4,5In recent years, growing interest in artificial micro-swimmers has highlighted the importance of understanding and harnessing fluid inertial effects.6–8 Many synthetic designs aim to replicate or abstract biological propulsion methods.9 A particularly promising strategy, in both biological and artificial systems, is to exploit rotational degrees of freedom for propulsion.10–15 Rotating structures, such as bacterial flagella or magnetically driven colloids, can generate pronounced flow fields, especially when operating in regimes not strictly confined to Re ≪ 1.16–19 Indeed, as the particle size increases or rotational frequencies become large, secondary flows arise and enable net motion in relatively simple, axisymmetric geometries that would remain stationary under purely viscous conditions (Re ≪ 1).8,20 Specifically, breaking head-to-tail symmetry along the spinning axis has been shown to lead to self-propulsion for a co-rotating colloidal snowman dimer20 and slightly asymmetric cylinders,8 when inertial flows are included. Deepening our understanding of these fluid–structure interactions offers new avenues for micro- and meso-scale robotics, targeted cargo transport, and biomedical applications.
In this paper, we explore how inertial effects enable propulsion in rotating colloids, bridging the gap between the classical Stokes-limit scenario and the more complex flow regimes at moderate Reynolds numbers (Re). We begin by validating our simulation method by examining a single rotating sphere. The result highlights the transition from purely azimuthal flows at low Re to a regime where secondary flows become significant and agree well with theoretical calculations.21 Although a single spinning sphere remains stationary across all Re due to its inherent symmetry, it has been demonstrated theoretically and numerically20 that including an additional sphere of a different size can induce net motion along the spinning axis and towards the larger sphere for a Re of up to 12.
We build on this, and consider three distinct configurations: (i) co-rotating spheres at Re ≈ 0…65, (ii) a snowman configuration of counter-rotating spinners and (iii) a driven sphere and a passive cargo particle. In all of the three cases, spontaneous motility is observed to arise from inertial hydrodynamic flows. Specifically, we show that when the Reynolds number is increased, the co-rotating dimer can reverse its direction of motion, and move towards the smaller sphere. Generally, our findings demonstrate how the size asymmetry between the spheres and inertial effects alter the flow field and drive self-propulsion.
By systematically varying the Reynolds number (Re) and geometric parameters, we identify two primary propulsion regimes: at lower Re, fluid is drawn in from the spinner poles and pulls the dimer forward. Conversely, at higher Re, increasingly strong jets emerging from the equatorial region push the spinner ahead. In summary, this study provides a comprehensive study of how rotating colloidal systems transition to inertia-dominated propulsion. It offers valuable insights for the design and optimization of future generations of active particle systems capable of operating across diverse fluidic regimes.
2. Numerical methods and validation
We employ the open-source package “Ludwig”22 to implement the lattice Boltzmann method (LBM) for simulating the system dynamics. Fluid–particle interactions are handled using the bounce-back on links method, ensuring a no-slip boundary condition on the particle surfaces. To prevent particle–particle overlap, a short-range repulsive force is applied between solid boundaries, following the approach outlined in relevant ref. 23 and 24. The cutoff of the repulsion is 0.5Δx, where Δx is the lattice spacing.All simulations for the spinner-dimer are conducted within a cubic simulation box of side length L = 20R. In the chosen simulation units, where the larger spinner has a fixed radius of R = 8Δx, while the radius of the second spinner is varied to introduce geometric asymmetry. The fluid density is set to ρ = 1.
We investigate the system at finite rotational Reynolds numbers, defined as Re = ρR2ω/μ, which quantifies the ratio of inertial to viscous forces. Here, ω represents the angular velocity of the spinner, and μ denotes the fluid viscosity, which is adjusted to achieve the desired Re values.
In the Stokes limit (Re ≪ 1), a rotating sphere generates only azimuthal flow. However, as the Reynolds number increases, a secondary flow begins to emerge.25,26 Due to inertial effects, the flow converges toward the poles and moves outward near the equator. An asymptotic analysis for small Re (Re ≪ 1) has been derived,21,25 yielding:
 | (1) |
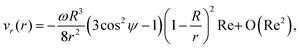 | (2) |
 | (3) |
These equations describe the azimuthal, radial, and polar velocity components of the flow induced by the rotating sphere, respectively. To validate our numerical results, we compare them against these analytical solutions. Fig. 1 shows the velocity field in the meridional plane for various Reynolds numbers. At low Re (e.g., Re = 0.0128), the flow field closely matches the analytical solution for the secondary flow (Fig. 1), and this agreement remains good for Re < 5, with only minor deviations.
As Re increases, the asymptotic assumptions become invalid, leading to significant changes in the flow behavior. A marked difference from the cross-sectional slice of the velocity field (the full flow is axisymmetric) is that the incoming flow from the polar region tends to split into two distinct streams, while the outward flow intensifies at the equator, forming a jet-like structure (Fig. 1). This effect can be attributed to the growing influence of inertia (like centrifugal effects) with increasing Re.
To quantitatively validate our numerical results, we calculated the velocity profile along the spinning pole. For Re = 0.0128 and Re = 0.8, the near-field velocity exhibits good agreement with the asymptotic solution (Fig. 2a). However, at Re = 32, the flow profile deviates from the analytical prediction because the Reynolds number is too high for the asymptotic assumptions to remain valid. In the far field, the numerical results show a faster decay compared to the analytical solution (Fig. 2a), which can be attributed to the periodic boundary conditions used in the simulations. Additionally, we determined the maximum velocity along the rotation axis and compared our data with previous studies that used other numerical methods.27 The resulting velocity-versus-Re curve shows excellent agreement with the earlier findings (Fig. 2b).
 | ||
| Fig. 2 (a) The normalized radial component of the fluid velocity along the spinning pole for Re = 0.0128, 0.8, and 32. For each Re, three curves are plotted, corresponding to simulations with computational domain sizes of L = 20R, 30R, and 40R. The black solid line represents the asymptotic solution. (b) The maximum radial velocity along the spinning pole is plotted as a function of Re. The lines correspond to results from previous numerical simulations.27 | ||
For a single spherical particle, the system maintains axisymmetry about the rotational axis and mirror symmetry across the equatorial plane. As a result, no translational motion of the sphere is expected, even when the flow becomes nonlinear at higher Reynolds numbers. However, when two spheres of different sizes form a snowman-like configuration with co-rotating axes, the dynamics change significantly and the dimer can self-propel along its spinning axis towards the larger sphere.20
At small Reynolds numbers, the flow remains predominantly azimuthal, preserving the system's symmetry and preventing any translational motion. As the rotational frequency (and thus the Reynolds number) increases, secondary flows emerge. The size difference between the two spheres breaks the equatorial-plane symmetry, triggering the onset of translational motion of the spinner-dimer. We systematically explore this behavior in three representative scenarios: (i) two co-rotating spheres driven by an external field, (ii) two counter-rotating spheres driven by an internal torque as a swimmer, and (iii) a single rotating spinner attached to a passive sphere for cargo transport.
3. Results
3.1. Two co-rotating spheres
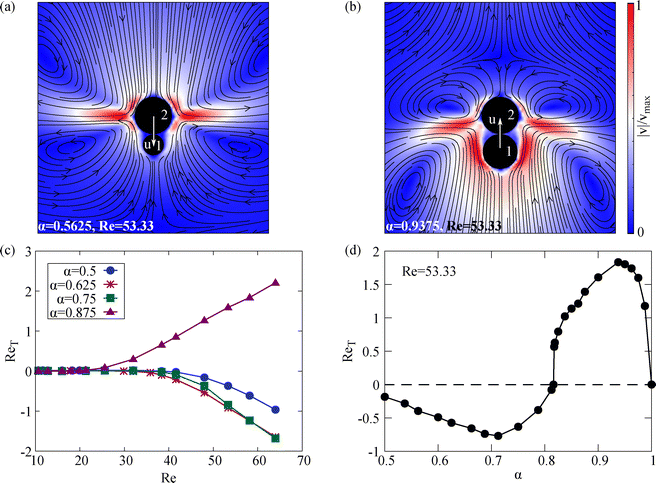
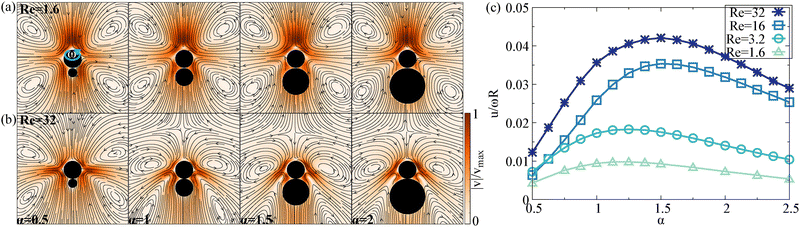
First, we examine the translational motion of two spheres with co-rotating axes and identical rotational frequencies, forming a snowman-like colloid driven by a rotating field along their common axis. The configuration is similar to ref. 20, but we extend the exploration to larger Reynolds numbers and systematically vary the aspect ratio between the sizes of the two spheres. We define the rotational Reynolds number (Re = ρR2ω/μ) and translational Reynolds number (ReT = ρRu/μ) using the radius of the larger particle (R = R2) in the dimer (Fig. 3a). The aspect ratio is given by α = R1/R2, where R1 and R2 are the radii of the smaller and larger spheres, respectively.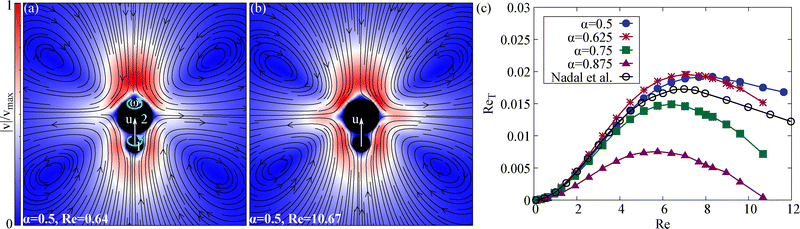 | ||
| Fig. 3 Two coaxial spherical particles rotating at the same angular velocity ω can achieve translational motion along their common axis. The streamlines for (a) Re = 0.64 and (b) Re = 10.67 are shown for a size ratio of α = 0.5. (c) The translational Reynolds number ReT is plotted as a function of the rotational Reynolds number Re for various values of α. The hollow circles represent the case of α = 0.5, as obtained by Nadal et al.20 using the finite element method in a moving reference frame. All curves exhibit the presence of an optimal Reynolds number, Re ≈ 7, which corresponds to the maximum ReT. | ||
At relatively small Reynolds numbers, the secondary flow closely follows the asymptotic behavior. Applying the analytical solution of the secondary flow field, we see that the flow velocity near the poles increases with Re when the angular velocity (ω) is fixed. Consequently, the incoming flow at the front of the larger sphere where Re is higher becomes more intense, creating a stronger pulling on the dimer. This imbalance induces translational motion from the smaller sphere toward the larger one, as illustrated in Fig. 3a, and in agreement with previous studies.20
This qualitative understanding holds for relatively small Re (Re < 10) even the secondary flow for a single particle starts to deviate from the analytical solution when Re is larger than 5 (see e.g.Fig. 1). Indeed, the flow fields generated by the dual spinners at Re = 0.64 and Re = 10.67 exhibit similar patterns (Fig. 3a and b). For an aspect ratio of α = 0.5, our results show good agreement with previous studies20 (closed blue and open black circles in Fig. 3c). The translational motion is evident from the increase of the translational Reynolds number ReT, which increases with Re (Fig. 3c). It reaches a maximum value around Re = 7, after which it begins to decline. At higher Reynolds numbers, our simulations show deviations from ref. 20, which may likely be attributed to factors such as periodic boundary effects, numerical resolution, or the surface distance between the spheres.
To gain insight into the effects of the dimer geometry, we also conducted simulations for additional aspect ratios α ≈ 0.5…0.875 (Fig. 3c). In all the cases, we observed directional movement along the spinning axis and in the direction given by the larger sphere. Furthermore, it was observed that the optimal spinning frequency for locomotion corresponds to a Reynolds number of approximately 7 for all aspect ratios considered (Fig. 3c). Furthermore, our results show that when the aspect ratio exceeds 0.625, the translational velocity decreases (Fig. 3c), suggesting that the optimal α value for maximum translational performance lies between 0.5 and 0.625. This behavior can be understood through symmetry considerations. A small α makes the configuration more similar to a single sphere with radius R2, while a larger α value gives the system a dumbbell-like shape R1 ≈ R2. At both limits, increasing the dimer symmetry reduces the flow asymmetry between the front and rear of the snowman dimer. This leads to a reduction of its net translational velocity.
Interestingly, the data in Fig. 3c show that when Re increases well beyond Re ∼ 7 the translational velocity decreases, eventually reaching zero for α ≈ 0.875 around Re ≈ 11. This suggests the possibility of reversing the direction of locomotion.
To further investigate the effects of the aspect ratio α and the spinning frequency, we extend our simulations up to Re ≈ 65 (Fig. 4). The simulations reveal that the direction of motion depends on the aspect ratio α for a given Reynolds number. For Re > 20, the spinner moves in the direction from the smaller sphere towards the larger one when α ≈ 0.875, while, for smaller values of α, the motion reverses its direction (Fig. 4c).
Unlike in lower Re, where the single particle secondary flows dominate, the flow at higher Re becomes more complex and is primarily driven by a jet originating near the equator of the larger spinner (Fig. 4a and b). This jet pushes the dimer forward, and its direction depends strongly on the geometry. For a smaller aspect ratio α, the jet is located at the equatorial region of the larger particle and slightly tilted upward, away from the smaller particle (red region in Fig. 4a). For larger α, two eddies appear near the larger spinner, and the fluid jet at the equatorial region tilts slightly downward (towards the smaller sphere). This reverses the locomotion direction from the direction towards the smaller particle (Fig. 4a) to motion in the direction of the larger colloid (Fig. 4b), when the aspect ratio is modified for a fixed Re ≈ 53.
A more detailed study at Re ≈ 53 reveals a critical α ≈ 0.82 at which the velocity direction changes (Fig. 4d). Below this critical value (α < 0.82), the colloid moves from the larger sphere to the smaller one, attaining a maximum velocity of around α = 0.7. Above this threshold (α > 0.82), the colloid reverses the direction and moves from the smaller sphere toward the larger one, reaching a maximum velocity near α = 0.94.
3.2. Two counter-rotating spheres
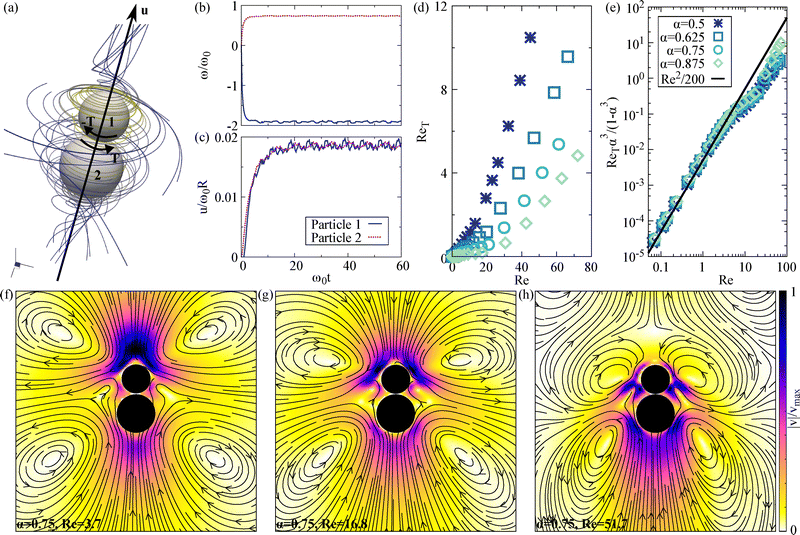
In the second scenario, we consider a torque and force-free configuration. It consists of two spheres, driven by equal but opposite internal torques (Fig. 5a). This makes the dual spinner an effective force-free swimmer. This configuration has been experimentally and theoretically shown to produce self-locomotion in viscoelastic fluids at zero Reynolds number,28,29 where more intricate coupling between rotation and translation, as well as other swimmers created stresses can be expected.30–32In this configuration, each sphere experiences an equal and opposite torque T, causing them to rotate in opposite directions (Fig. 5b). Under Stokes flow conditions, this results in an angular velocity ω1,2 = T/8πμR1,23, where R1,2 corresponds to the radii of particle 1 and particle 2, respectively. Thus the smaller particle is expected to spin faster. This holds reasonably well for the particles in the dimer as well. Considering an aspect ratio α ≡ R1/R2 = 0.75 dimer, a ratio between the spinning frequencies |ω2/ω1| ≈ 2.3 is observed (Fig. 5b), which agrees well with |ω2/ω1| ≈ 2.4 expected for isolated spinners. Consequently, the rotational Reynolds number of an isolated spinner scales as Re ∼ T/R. The corresponding inertial secondary flow of an isolated spinner is given using eqn (1)–(3). The radial component vr at polar regions, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ = 1, scales as vr ∼ Re2/R. This implies that for a fixed torque T, the smaller sphere experiences a higher Re and generates a stronger secondary flow in front of it, pulling the surrounding fluid towards itself (see e.g.Fig. 1a). As a result, one can expect that the dual-spinner swimmer translates in the direction of the smaller sphere. This agrees with the simulation results (Fig. 5a). At the steady state, both the spheres are bound together via a mutual attraction arising from the secondary flow at the polar regions and translate in the direction of the smaller sphere approximately at equal velocities (Fig. 5c).
ψ = 1, scales as vr ∼ Re2/R. This implies that for a fixed torque T, the smaller sphere experiences a higher Re and generates a stronger secondary flow in front of it, pulling the surrounding fluid towards itself (see e.g.Fig. 1a). As a result, one can expect that the dual-spinner swimmer translates in the direction of the smaller sphere. This agrees with the simulation results (Fig. 5a). At the steady state, both the spheres are bound together via a mutual attraction arising from the secondary flow at the polar regions and translate in the direction of the smaller sphere approximately at equal velocities (Fig. 5c).
A scaling argument based on the secondary flow suggests that the net force driving the swimming motion arises from the difference in the radial flow components at the front and rear of the colloidal dimer. The swimming speed can be approximated as:
Expressing this in terms of the translational Reynolds number ReT = ρRu/μ and the rotational Reynolds number Re =ρR2ω/μ, using the radius of the larger sphere (R = R2), yields:
Fig. 5d shows the behavior of ReT measured from the simulations as a function of Re for different values of α. The translational velocity increases with Re, and greater asymmetry (smaller α) yields higher swimming speeds (Fig. 5d). When we rescale the plot by α3/(1 − α3) and use a log–log format, the data for Re < 5 collapse onto a single curve (Fig. 5e), supporting our scaling analysis.
At a larger Re, the flow field deviates from the asymptotic solution. As shown in Fig. 5e, the main features related to aspect ratio still hold, but the data indicate two distinct regimes for a higher Re. For 5 < Re < 20, the dimer is pulled by the fluid at the front, though this pulling flow splits into two streams and shifts laterally as the Re increases (dark regions in Fig. 5g). Once the Re exceeds about 20, the propulsion mechanism changes. As illustrated in Fig. 5h for Re = 51.7, jets form on the side of the smaller sphere, pushing the swimmer forward. Contrary to what is observed with the forced snowman dimer (Fig. 3), no reversal of the swimming direction is observed. The internally driven force-free swimmer continues to swim along the direction given by the smaller sphere.
3.3. One rotating and one passive sphere
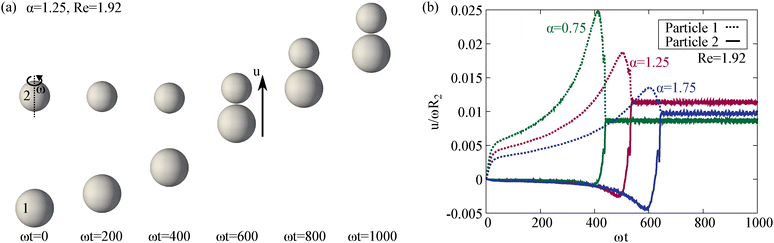
Finally we investigate the possibility of cargo transport using the inertial flow fields. We consider a single spinner at finite Re. Although a single spinner does not move on its own, including another object can break the symmetry and lead to locomotion. To test this, we placed a passive colloidal particle behind the spinner and along the spinning axis (left panel in Fig. 6a). The spinning particle creates a secondary flow that advects the fluid towards itself at the polar regions. This creates an attraction between the spinner and the cargo. Now the two particles approach each other (ωt < 600 in Fig. 6a and b). Once a contact is established, the spinner and the passive sphere translate together, moving in the direction from the passive sphere towards the spinning particle (ωt > 600 in Fig. 6a and b). This behavior is observed to hold for various sizes of the passive loads. However, the translational speed of the dimer does not vary monotonically with the aspect ratio α (the ratio of the passive sphere radius to the spinner radius). For a fixed Re ≈ 1.9, the α ≈ 1.25 dimer is observed to translate at a higher speed compared to the α ≈ 0.75 and α ≈ 1.75 dimers (Fig. 6b). This suggests that for a given Reynolds number, there exists an optimal payload size.To study the effects of the α and Reynolds number for the cargo transport in more detail, we carried out simulations of the hydrodynamically bound dimer for α ≈ 0.5…2.5 and Re ≈ 1.6, 3.2, 16, 32 (Fig. 7). Increasing the Re was observed to increase the translational speed of the dimer (Fig. 7b). The α dependence shows non-monotonic behaviour with a clear maximum (Fig. 7b). Starting from α, initially speed of the dimer increases with increasing α, for all the Reynolds numbers considered. After reaching an optimal aspect ratio α* the speed is observed to decrease. Our results show that the maximum velocity appears when α lies between 1.2 and 1.5, and this optimal value is observed to increase with Re (Fig. 7c). One should also note, that locomotion is observed for a α ≈ 1 dimer, in contrast to the externally and internally driven snowman dimers, where the symmetrical dumbbell is expected to be stationary for symmetry reasons.
To understand the non-monotonic behaviour, one can consider two competing effects. On one hand, a larger passive sphere introduces greater asymmetry, potentially enhancing the propulsion. On the other hand, a larger sphere also adds more fluid drag. These opposing influences lead to an optimal translational velocity at an intermediate aspect ratio.
Finally, the locomotion mechanism is observed to also depend on the Reynolds number. As in the previous cases, when Re is small, the locomotion is dominated by fluid pulled in at the front of the spinner (Fig. 7a), whereas at higher Re, jets formed by the spinner provide a pushing mechanism (Fig. 7b). Despite these different propulsion regimes, the optimal velocity still arises from the trade-off between propulsion and hydrodynamic drag.
4. Conclusions
Throughout this work, we have explored how rotating colloidal particles, ranging from single spinner to two-sphere assembly, behave under varying Reynolds numbers (Re). Our simulations demonstrate how the secondary flow created by spinning particles at finite Reynolds numbers can hydrodynamically bind the particles together. When a size asymmetry between the particles is introduced, locomotion along the spinning axis can be realised.We started by examining a single rotating sphere, which, due to its symmetry, experiences no net translational motion. As the rotational Reynolds number Re increases, secondary flows arise but do not break the inherent symmetry of a single sphere.
When a second spinner or a passive “cargo” is introduced, however, asymmetry emerges, and the combination becomes motile. We studied the locomotion in three distinct configurations: (i) an externally driven snowman dimer, (ii) an internally driven force and torque-free swimmer, consisting of two spinners driven by equal but opposite torques, and (iii) a spinner with a passive load particle. We carried out the exploration for various aspect ratios between the particles and a wide range of Reynolds numbers Re ≈ 0…100. Our simulations revealed that an externally driven snowman dimer can reverse its locomotion direction as a function of the aspect ratio and Reynolds number. Furthermore, cargo transport was demonstrated using a single spinner where a passive payload was hydrodynamically attached to the spinner. Here, the locomotion arises from the broken head-to-tail symmetry similarly to the externally and internally driven dimers.
Typically in experiments, confining walls are present. A single spinning sphere at finite Re is attracted to a flat no-slip wall along its spinning axis due to the inertial hydrodynamic flows.27 This is likely true for our dimers as well. Near a confining surface, the dynamics is likely dominated by an intricate balance between the wall–spinner and spinner–spinner hydrodynamics. This could lead to the dissolution of the hydrodynamically bound snowman dimers. One possibility could be to use solid particles with broken head-to-tail symmetry.8
Finally, our simulations revealed two distinct propulsion mechanisms depending on the rotational Reynolds number Re. At low Re, the propulsion mechanism is primarily a “pulling” effect where the fluid is advected primarily towards the swimmer at polar regions. At a higher Re, jet-like flows form at the equatorial region of the spinner, creating a “pushing” mechanism. Despite this transition, the same fundamental principle for the propulsion applies: breaking the head-to-tail symmetry, either by size asymmetry or by introducing a passive load, leads to a different fluid flow at the front and the rear of the dimer, resulting in a net fluid force and, consequently, sustained propulsion along the spinning axis of the particles.
Overall, these findings provide insight into designing self-propelled systems and micro-swimmers driven by rotational motion, highlighting how the aspect ratio and inertia collectively shape their hydrodynamic behavior.
Data availability
The Ludwig code used in this article can be found in the repository at https://github.com/ludwig-cf/ludwig/tree/ludwig-0.22.0.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
ZS and JSL acknowledge IdEx (Initiative d'Excellence) Bordeaux for funding and Curta cluster for computational time. JSL acknowledges support from the French National Research Agency (ANR) through Contract No. ANR-19-CE06-0012-01 and la région Nouvelle Aquitaine project GASPP. ZS acknowledges support from the Fundamental Research Funds for the Central Universities, Peking University.Notes and references
- E. Lauga and T. R. Powers, Rep. Prog. Phys., 2009, 72, 096601 CrossRef.
- E. Lauga, Annu. Rev. Fluid Mech., 2016, 48, 105–130 CrossRef.
- R. Dreyfus, J. Baudry, M. L. Roper, M. Fermigier, H. A. Stone and J. Bibette, Nature, 2005, 437, 862–865 CrossRef CAS PubMed.
- D. Klotsa, K. A. Baldwin, R. J. Hill and M. R. Swift, Phys. Rev. Lett., 2015, 115, 248102 CrossRef.
- N. J. Derr, T. Dombrowski, C. H. Rycroft and D. Klotsa, J. Fluid Mech., 2022, 952, A8 CrossRef CAS.
- D. Klotsa, Soft Matter, 2019, 15, 8946–8950 RSC.
- H. Löwen, J. Chem. Phys., 2020, 152, 040901 CrossRef.
- P. Chen, S. Weady, S. Atis, T. Matsuzawa, M. J. Shelley and W. T. Irvine, Nat. Phys., 2024, 1–9 Search PubMed.
- S. Klumpp, C. T. Lefèvre, M. Bennet and D. Faivre, Phys. Rep., 2019, 789, 1–54 CrossRef.
- E. M. Purcell, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 11307–11311 CrossRef CAS PubMed.
- B. Rodenborn, C.-H. Chen, H. L. Swinney, B. Liu and H. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, E338–E347 CrossRef CAS.
- A. Bricard, J.-B. Caussin, N. Desreumaux, O. Dauchot and D. Bartolo, Nature, 2013, 503, 95–98 CrossRef CAS PubMed.
- A. Kaiser, A. Snezhko and I. S. Aranson, Sci. Adv., 2017, 3, e1601469 CrossRef PubMed.
- M. Driscoll, B. Delmotte, M. Youssef, S. Sacanna, A. Donev and P. Chaikin, Nat. Phys., 2017, 13, 375–379 Search PubMed.
- Y. Alapan, U. Bozuyuk, P. Erkoc, A. C. Karacakol and M. Sitti, Sci. Robot., 2020, 5, eaba5726 Search PubMed.
- B. A. Grzybowski, H. A. Stone and G. M. Whitesides, Nature, 2000, 405, 1033–1036 CrossRef CAS.
- Y. Goto and H. Tanaka, Nat. Commun., 2015, 6, 5994 CrossRef CAS PubMed.
- W.-Z. Fang, S. Ham, R. Qiao and W.-Q. Tao, Langmuir, 2020, 36, 7046–7055 CrossRef CAS.
- Z. Shen and J. S. Lintuvuori, Phys. Rev. Lett., 2023, 130, 188202 CAS.
- F. Nadal, O. S. Pak, L. Zhu, L. Brandt and E. Lauga, Eur. Phys. J. E: Soft Matter Biol. Phys., 2014, 37, 1–14 CrossRef CAS.
- W. Bickley, London, Edinburgh Dublin Philos. Mag. J. Sci., 1938, 25, 746–752 CrossRef.
- kevinstratford, O. Henrich, jlintuvuori, dmarendu, qikaifzj, austin1997, shanCHEN123, ludwig cf, jurijsab, S. G. Leyva and sumeshpt, ludwig-cf/ludwig: Ludwig 0.22.0, 2024 DOI:10.5281/zenodo.12822477.
- Z. Shen, A. Würger and J. S. Lintuvuori, Eur. Phys. J. E:Soft Matter Biol. Phys., 2018, 41, 1–9 CrossRef CAS.
- Z. Shen, A. Würger and J. S. Lintuvuori, Soft Matter, 2019, 15, 1508–1521 RSC.
- E. Climent, K. Yeo, M. R. Maxey and G. E. Karniadakis, J. Fluids Eng., 2006, 129, 379–387 CrossRef.
- Z. Shen and J. S. Lintuvuori, Phys. Rev. Res., 2020, 2, 013358 CrossRef CAS.
- Q. Liu and A. Prosperetti, J. Fluid Mech., 2010, 657, 1–21 CrossRef.
- L. Kroo, J. P. Binagia, N. Eckman, M. Prakash and E. S. Shaqfeh, J. Fluid Mech., 2022, 944, A20 CrossRef CAS.
- J. P. Binagia and E. S. Shaqfeh, Phys. Rev. Fluids, 2021, 6, 053301 CrossRef.
- I. Goychuk, V. O. Kharchenko and R. Metzler, Phys. Chem. Chem. Phys., 2014, 16, 16524–16535 RSC.
- G. Li, E. Lauga and A. M. Ardekani, J. Non-Newtonian Fluid Mech., 2021, 297, 104655 CrossRef CAS.
- L. Theeyancheri, R. Sahoo, P. Kumar and R. Chakrabarti, ACS Omega, 2022, 7, 33637–33650 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2025 |