Open Access Article
Open Access ArticleWrapping nonspherical vesicles at bio-membranes†
Ajit Kumar
Sahu
,
Rajkumar
Malik
 and
Jiarul
Midya
and
Jiarul
Midya
 *
*
Department of Physics, School of Basic Sciences, Indian Institute of Technology Bhubaneswar, Jatni, Odisha-752050, India. E-mail: jmidya@iitbbs.ac.in
First published on 9th May 2025
Abstract
The wrapping of particles and vesicles by lipid bilayer membranes is a fundamental process in cellular transport and targeted drug delivery. Here, we investigate the wrapping behavior of nonspherical vesicles, such as ellipsoidal, prolate, oblate, and stomatocytes, by systematically varying the bending rigidity of the vesicle membrane and the tension of the initially planar membrane. Using the Helfrich Hamiltonian, triangulated membrane models, and energy minimization techniques, we predict multiple stable-wrapped states and identify the conditions for their coexistence. Our results demonstrate that softer vesicles bind more easily to initially planar membranes; however, complete wrapping requires significantly higher adhesion strength than rigid vesicles. As membrane tension increases, deep-wrapped states disappear at a triple point where shallow-wrapped, deep-wrapped, and complete-wrapped states coexist. The coordinates of the triple point are highly sensitive to the vesicle shape and stiffness. For stomatocytes, increasing stiffness shifts the triple point to higher adhesion strengths and membrane tensions, while for oblates, it shifts to lower values, influenced by shape changes during wrapping. Oblate shapes are preferred in shallow-wrapped states and stomatocytes in deep-wrapped states. In contrast to hard particles, where optimal adhesion strength for complete wrapping occurs at tensionless membranes, complete wrapping of soft vesicles requires finite membrane tension for optimal adhesion strength. These findings provide insights into the interplay between vesicle deformability, shape, and membrane properties, advancing our understanding of endocytosis and the design of advanced biomimetic delivery systems.
1 Introduction
Cellular transport of information and materials, a fundamental process that ensures the survival and functionality of cells, is typically facilitated by the exchange of particles across lipid membranes.1,2 The translocation across lipid-bilayer membranes depends on the size, elasticity, shape, and surface functionalization of the particles.3 Particles smaller than the thickness of the membrane can translocate, causing minimal membrane deformation,4,5 while particles larger than a few nanometers translocate through endocytosis.6 Passive endocytosis is a multistep process that begins with the attachment of the particle to the membrane, followed by wrapping and finally detachment from the membrane.7 The particle wrapping process, a key aspect of endocytosis, is ubiquitous for both living and nonliving particles, such as drug-carrying nanoparticles,8 viruses,9 and parasite invasion into host cells.10 Membrane tension, regulated by cells through remodeling, plays a critical role in endocytosis: high tension slows the internalization process, while low tension facilitates membrane invagination and efficient particle uptake.11–13 Understanding the particle wrapping process can help us optimizing biomedical applications, such as targeted drug delivery using engineered nanoparticles.14–16The wrapping of hard spherical particles at lipid membranes has been extensively investigated in experimental and theoretical studies.17–21 In general, for the wrapping of hard particles, the size and shape of the particle, the bending rigidity and tension of the membrane, and the adhesion strength of the particle–membrane have been shown to primarily control the process.22–29 In addition, the initial orientation of the anisotropic hard nanoparticles relative to the adhering membranes influences their wrapping behavior. For example, the wrapping of ellipsoidal23,30 and spherocylindrical31 nanoparticles starts with an orientation in which the major axis of the particle is parallel to the membrane surface. After half-wrapping, the orientation of the particle changes, and the major axis becomes perpendicular to the membrane surface. Unlike hard particles, soft particles can deform depending on external constraints;32,33 the deformability plays an important role in the wrapping process, in addition to the factors that apply to hard particles.
Many biologically relevant particles have anisotropic or nonspherical shapes.34,35 For example, malaria parasites are typically egg-shaped,10 mature virions can be ellipsoidal or brick-shaped,36,37 and vesicular stomatitis viruses (VSV) have bullet shapes.38 Simulations and experiments show that for ellipsoidal particles the stability of the partial-wrapped over non-wrapped and complete-wrapped states decreases when the bending rigidity of the membrane increases.39 Living particles also often have the ability to change shape and deformability throughout their life cycles. For example, murine leukemia virus (MLV) and human immunodeficiency virus (HIV) adjust their deformability through internal structural changes, significantly affecting their entry into host cells.40,41 The mature HIV viral particles are less stiff compared to the immature HIV viral particles, which hinders their complete wrapping at the host cells.41
A wide range of synthetic deformable particles with various architectures and customizable mechanical properties can be engineered for the targeted delivery of drugs, including star polymers,42,43 microgels,44,45 dendrimers,46,47 polymer-grafted nanoparticles,48,49 and vesicles.8,27,50 The deformability of these particles can be tuned through control parameters that change their molecular architecture or building blocks. For example, the deformability of microgels can be adjusted by changing the cross-link density and electric charge,51,52 of polymer-grafted nanoparticles by altering the density and length of grafted polymers,48 and of unilamellar fluid vesicles by modifying the bending rigidity and the osmotic pressure difference.53 A particularly versatile and well-characterized class of deformable particles is unilamellar vesicles.27 Free vesicles with fixed membrane areas, variable volumes, and symmetric lipid bilayer membranes assume a spherical shape and may change volumes significantly during wrapping. Nonspherical vesicles with volumes smaller than the maximal volume that can be enclosed by the vesicle membrane and potentially even asymmetric monolayer composition can have a complete zoo of shapes.54
In this work, we investigate the wrapping of single nonspherical vesicles with initial ellipsoidal, prolate, oblate, and stomatocytic shapes at initially planar membranes by systematically varying the relative stiffness of the vesicle membranes and the tension of the planar membranes. Using triangulated membranes and energy minimization techniques, we predict energetically stable wrapping states. The systematic increase in adhesion strength leads to transitions of the vesicles from non-wrapped to complete-wrapped states through intermediate shallow-wrapped and deep-wrapped states. Softer vesicles undergo both shape and orientation changes during wrapping, whereas stiffer vesicles exhibit only orientation changes. We calculate wrapping diagrams showing the energetically stable states for various membrane bending rigidities and tensions. As membrane tension increases, the deep-wrapped state becomes destabilized and eventually vanishes at a triple point, where shallow-, deep-, and complete-wrapped states coexist. Beyond the triple point, vesicles exhibit a discontinuous transition from the shallow-wrapped state to the complete-wrapped state. For initial stomatocytes, the triple point shifts to higher membrane tensions and adhesion strengths as the stiffness of the vesicles increases, while the trend is the opposite for initially oblate ones. In addition, we show that the optimal adhesion strength for the complete wrapping of soft oblate, prolate, and ellipsoidal vesicles occurs at a non-zero membrane tension, unlike rigid particles, which require zero membrane tension. This behavior is related to the shape change of the vesicles during wrapping. Our findings indicate that the initially stomatocyte, oblate and prolate vesicles preferred to be oblate in the shallow-wrapped states and stomatocyte in the deep-wrapped states.
The rest of the manuscript is organized as follows. In Section 2, we introduce the model and the numerical calculation techniques. In Sections 3.1 and 3.2, we show the deformation energy landscapes along with the typical vesicle shapes and characterize the vesicle shapes at various wrapping stages. In Section 3.3, we study the effect of vesicle deformability and in Section 3.4 of membrane tension on the stability of the wrapping states. Finally, in Section 4, we summarize and conclude our study.
2 Model and methods
To study particle wrapping in passive endocytosis, we employ a continuum membrane model, which is applicable to systems where the particle size is at least a few times larger than the thickness of the lipid bilayer membrane.55,56 In a continuum membrane model, the total energy of the system is calculated using the Helfrich Hamiltonian,57,58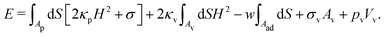 | (1) |
 | ||
| Fig. 1 (a) Schematic representation of a partial-wrapped prolate vesicle at an initially planar membrane. (b) Bending energy of vesicles as a function of reduced volume. | ||
The nonspherical shapes of the vesicles are characterized by reduced volume v = Vv/Vs, see Fig. 1(b), and Fig. S1 in the ESI.† Here, Vv is the actual volume of the vesicle with area Av, and Vs is the volume of a spherical vesicle with the same membrane area. The maximal value, v = 1, corresponds to a spherical vesicle. The values of Lagrange multipliers σv and pv depend on the vesicle shape; sudden jumps in their values indicate shape transitions; see Fig. S2 in the ESI.† The stable states for free vesicles with 0.6515 ≤ v < 1 are prolate, with 0.5915 ≤ v ≤ 0.6515 are oblate, and with v ≤ 0.5915 are stomatocytes. We refer to vesicles with v = 0.95 as ellipsoidal vesicles.59
The wrapping fraction fw = Aad/Av represents the fraction of the vesicle area that is attached to the initially planar membrane. The value of fw varies in the range 0 to 1, where fw = 0 corresponds to the non-wrapped (NW) state and fw = 1 to the complete-wrapped (CW) state. The shallow-wrapped (SW) state is defined in the range 0 < fw ≤ 0.5, and the deep-wrapped (DW) state in the range 0.5 < fw < 1. In this work, we are focusing in particular on the wrapping behavior of four vesicle shapes: stomatocyte (v = 0.55), oblate (v = 0.63), prolate (v = 0.66) and ellipsoidal (v = 0.95). The selection of vesicle shapes at the phase boundaries between the stomatocyte, oblate, and prolate can result in complex wrapping behaviors compared to prolate vesicles with reduced volumes v > 0.7, as previously reported in the literature.32
All integrals in eqn (1) are discretized using triangulated surfaces composed of vertices, edges, and facets.60,61 We initialize the energy and shape calculations with a few large triangles and then iteratively minimize the energy and refine the triangulation until the desired accuracy in energy is achieved; see Fig. S3 in the ESI.† The iterative procedure is important to avoid the need for major shape changes of finely discretized membranes, which would require a high number of minimization steps. Small triangles are used where the membrane is highly curved, and large triangles are used where it is almost planar. In addition, the edges are regularly swapped to maintain the fluidity of the membranes,62 and vertex-averaging steps ensure that neighboring triangles have similar areas. The numerical calculations are performed with the help of the freely available software Surface Evolver.63
For each of our simulations, the membrane area Av and the volume Vv of the vesicle are fixed, while the area Ap of the initially planar membrane is determined through energy minimization, which is appropriate for an ensemble with constant membrane tension. The simulations are performed by setting w = 0 and using fw as a constraint via a Lagrange multiplier  . The total energy of the system can be expressed in terms of reduced units as
. The total energy of the system can be expressed in terms of reduced units as
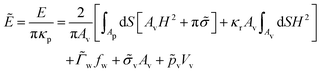 | (2) |
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) = σAv/(2πκp) is the reduced membrane tension. The bending rigidity ratio κr = κv/κp characterizes the relative deformability of the vesicle with respect to the initially planar membrane.
= σAv/(2πκp) is the reduced membrane tension. The bending rigidity ratio κr = κv/κp characterizes the relative deformability of the vesicle with respect to the initially planar membrane.
We perform simulations for different values of fw in the range 0 < fw < 1. For each value of fw, we initialized the energy minimization with different initial configurations. During this process, the vesicle can adjust its orientation and shape, while the outer patch of the initially planar membrane is constrained to remain in a plane. We calculate the reduced deformation energy as
 | (3) |
ΔẼ[fw] = ΔẼ′[fw] − ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) fw, fw, | (4) |
![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) = wAv/(πκp) is the reduced adhesion strength. To identify stable and unstable states, we fit the deformation energy ΔẼ at
= wAv/(πκp) is the reduced adhesion strength. To identify stable and unstable states, we fit the deformation energy ΔẼ at ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) = 0 using a fourth-order polynomial function. Since the energy curve is highly non-monotonic, constructing a single fitting function is challenging. Therefore, we employ a piecewise fitting approach for different ranges of fw. We apply different adhesion strengths (
= 0 using a fourth-order polynomial function. Since the energy curve is highly non-monotonic, constructing a single fitting function is challenging. Therefore, we employ a piecewise fitting approach for different ranges of fw. We apply different adhesion strengths (![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) ) to the fitted curves, and find the different global minima in the energy landscape to determine the stable states.32
) to the fitted curves, and find the different global minima in the energy landscape to determine the stable states.32
3 Results and discussion
3.1 Wrapping states and deformation energies
Fig. 2 illustrates the wrapping states of nonspherical vesicles at initially planar membranes for various wrapping fractions, fw. The wrapping process is consistently initiated in regions of the vesicle with the lowest curvature. For a stomatocyte (v = 0.55), initial attachment occurs in the “rocket” orientation, where the major axis of the vesicle is perpendicular to the initially planar membrane. As the wrapping progresses, the vesicle deforms to an oblate at fw ≃ 0.07 to minimize the deformation energy, and remains oblate within the range 0.07 ≤ fw ≤ 0.5. For fw > 0.5, the vesicle reverts to its initial stomatocytic shape, persisting in this configuration until the wrapping of the outer sphere of the stomatocyte is completed. At fw ≳ 0.75, the vesicle transforms into a vertical oblate, avoiding the high bending energy costs of the initially planar membrane associated with the wrapping of the inner sphere of the stomatocyte. Finally, at fw > 0.9, the vesicle returns to an inverted stomatocyte. Upon complete wrapping, both the vesicle and the initially planar membrane recover their original shapes.For an initially oblate vesicle (v = 0.63), the attachment to the initially planar membrane begins in a ring-shaped patch with two contact lines, as shown in Fig. 2. As the wrapping fraction fw increases, the radius of the inner contact line decreases and vanishes at fw ≈ 0.1, forming a circular patch with a single contact line, and remains oblate in the range of wrapping fractions 0.1 < fw ≲ 0.5. At higher fw values, the initially planar membrane comes into contact with the rim of the oblate, resulting in an increased bending energy cost. This energy cost induces a shape change in the vesicle from oblate to stomatocyte, which persists for 0.5 < fw ≲ 0.79. As fw increases further, the initially planar membrane needs to bend more to wrap the inner sphere of the stomatocyte, leading to a sharp increase in bending energy. To minimize the overall energy cost, the vesicle compromises its shape and reverts to a vertical oblate for fw > 0.79, maintaining this shape until it is completely wrapped. Similar shape and orientation changes are observed for prolate (v = 0.66) and ellipsoidal (v = 0.95) vesicles, as illustrated in Fig. 2.
The reduced deformation energy ΔẼ, calculated using eqn (1)–(4), as a function of the wrapping fraction fw for various reduced volumes of vesicles (v = 0.55, 0.63, 0.66 and 0.95) at a fixed relative stiffness κr = κv/κp = 1 and membrane tension ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) = 0.5 is shown in Fig. 3(a)–(d). For an initially stomatocyte (v = 0.55), ΔẼ increases with fw in the absence of adhesion energy (
= 0.5 is shown in Fig. 3(a)–(d). For an initially stomatocyte (v = 0.55), ΔẼ increases with fw in the absence of adhesion energy (![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) = 0), as shown in Fig. 3(a). The energy minimum at fw = 0 suggests that the non-wrapped (NW) state is the stable configuration. However, for adhesion strength
= 0), as shown in Fig. 3(a). The energy minimum at fw = 0 suggests that the non-wrapped (NW) state is the stable configuration. However, for adhesion strength ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) ≃ 5.3, a local minimum with the same energy appears for the first time at fw ≃ 0.21 (point ‘A’). At this adhesion strength, the vesicle undergoes a binding transition from non-wrapped (NW) to a stable shallow-wrapped (SW) state. The stable shallow-wrapped oblate states can be found for 0.21 ≲ fw ≲ 0.32. At adhesion strength
≃ 5.3, a local minimum with the same energy appears for the first time at fw ≃ 0.21 (point ‘A’). At this adhesion strength, the vesicle undergoes a binding transition from non-wrapped (NW) to a stable shallow-wrapped (SW) state. The stable shallow-wrapped oblate states can be found for 0.21 ≲ fw ≲ 0.32. At adhesion strength ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) ≃ 15.1, two energy minima at fw ≃ 0.32 (point ‘B’) and fw ≃ 0.74 (point ‘C’) have the same height, which correspond to the discontinuous transition from shallow-wrapped to deep-wrapped Wsd where oblate and stomatocyte coexist. At even higher adhesion strength,
≃ 15.1, two energy minima at fw ≃ 0.32 (point ‘B’) and fw ≃ 0.74 (point ‘C’) have the same height, which correspond to the discontinuous transition from shallow-wrapped to deep-wrapped Wsd where oblate and stomatocyte coexist. At even higher adhesion strength, ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) ≃ 33.1, the deep-wrapped stomatocytic state (point ‘D’) coexists with the complete-wrapped (CW) state at fw = 1 (point ‘E’); the envelopment transition Wdc is also discontinuous. More details about the binding transition, the shallow-to-deep wrapped transition, and the envelopment transition are discussed in the ESI.†
≃ 33.1, the deep-wrapped stomatocytic state (point ‘D’) coexists with the complete-wrapped (CW) state at fw = 1 (point ‘E’); the envelopment transition Wdc is also discontinuous. More details about the binding transition, the shallow-to-deep wrapped transition, and the envelopment transition are discussed in the ESI.†
For an oblate (v = 0.63), the reduced deformation energy ΔẼ as a function of the wrapping fraction fw is illustrated in Fig. 3(b). The first minimum in ΔẼ indicates that the binding transition Wns occurs at the adhesion strength ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) ≃ 0.8 and the wrapping fraction fw ≃ 0.16. The states within the range 0 ≤ fw ≲ 0.17 with rim patches, having two contact lines, are on the energy barrier, while the oblate states in the range 0.17 ≲ fw ≲ 0.34 with single contact line patches are stable. The shallow-to-deep-wrapped transition Wsd occurs at adhesion strength
≃ 0.8 and the wrapping fraction fw ≃ 0.16. The states within the range 0 ≤ fw ≲ 0.17 with rim patches, having two contact lines, are on the energy barrier, while the oblate states in the range 0.17 ≲ fw ≲ 0.34 with single contact line patches are stable. The shallow-to-deep-wrapped transition Wsd occurs at adhesion strength ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) ≃ 17.5, where the oblate vesicle at fw ≃ 0.34 (point ‘B’) coexists with a stomatocyte at fw ≃ 0.78 (point ‘C’). Within the deep-wrapped (DW) regime, a deep-wrapped (D1) to deep-wrapped (D2) transition Wdd is observed for
≃ 17.5, where the oblate vesicle at fw ≃ 0.34 (point ‘B’) coexists with a stomatocyte at fw ≃ 0.78 (point ‘C’). Within the deep-wrapped (DW) regime, a deep-wrapped (D1) to deep-wrapped (D2) transition Wdd is observed for ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) ≃ 28.9, where stomatocytes at fw ≃ 0.8 (point ‘D1’) coexist with vertical oblates at fw ≃ 0.96 (point ‘D2’). Finally, a continuous envelopment transition Wdc occurs with an adhesion strength of
≃ 28.9, where stomatocytes at fw ≃ 0.8 (point ‘D1’) coexist with vertical oblates at fw ≃ 0.96 (point ‘D2’). Finally, a continuous envelopment transition Wdc occurs with an adhesion strength of ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) ≃ 55.1.
≃ 55.1.
For initially prolate (v = 0.66) and ellipsoidal (v = 0.95) vesicles, the deformation energy ΔẼ as a function of fw at fixed κr = 1 and ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) = 0.5 is shown in Fig. 3(c) and (d), respectively. The binding transition for initially prolate vesicles (v = 0.66) is discontinuous due to the energy barrier associated with the shape transition from prolate to oblate. In contrast, the initially ellipsoidal vesicles (v = 0.95) exhibit a continuous binding transition as there is no energy barrier between non-wrapped and shallow-wrapped states; the initial attachment of vesicle occurs in submarine orientation where the major axis is parallel to the initially planar membrane. For both vesicles, the shallow-to-deep wrapped transition is discontinuous due to an energy barrier that arises from changes in shape and orientation of the vesicles; see Fig. 2. However, the envelopment transition is continuous for both the initially prolate (v = 0.66) and the initially ellipsoidal (v = 0.95) vesicles, as no energy barrier exists between the deep-wrapped and completely wrapped states. Although we focus here on stable states, depending on the values of κr,
= 0.5 is shown in Fig. 3(c) and (d), respectively. The binding transition for initially prolate vesicles (v = 0.66) is discontinuous due to the energy barrier associated with the shape transition from prolate to oblate. In contrast, the initially ellipsoidal vesicles (v = 0.95) exhibit a continuous binding transition as there is no energy barrier between non-wrapped and shallow-wrapped states; the initial attachment of vesicle occurs in submarine orientation where the major axis is parallel to the initially planar membrane. For both vesicles, the shallow-to-deep wrapped transition is discontinuous due to an energy barrier that arises from changes in shape and orientation of the vesicles; see Fig. 2. However, the envelopment transition is continuous for both the initially prolate (v = 0.66) and the initially ellipsoidal (v = 0.95) vesicles, as no energy barrier exists between the deep-wrapped and completely wrapped states. Although we focus here on stable states, depending on the values of κr, ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) , and
, and ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) metastable states may also appear along with the stable states.64 However, determining the vesicle shapes corresponding to these metastable states is challenging without a comprehensive understanding of the entire energy landscape.
metastable states may also appear along with the stable states.64 However, determining the vesicle shapes corresponding to these metastable states is challenging without a comprehensive understanding of the entire energy landscape.
3.2 Vesicle shapes during wrapping
The shape of a particle can be quantified using the asphericity,65,66 calculated from the principal moments (λx, λy, λz) of the gyration tensor. We define the asphericity s2 as65 | (5) |
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) . Thus, for nonspherical vesicles, s2 (>0) increases with increasing vesicle elongation.
. Thus, for nonspherical vesicles, s2 (>0) increases with increasing vesicle elongation.
Fig. 4(a) illustrates the asphericity s2 of the vesicles with various reduced volumes v as a function of the wrapping fraction fw for κr = 1 and ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) = 0.5. Initially stomatocyte vesicles (v = 0.55), resembling two connected spheres, have an asphericity close to zero. In the range 0 < fw ≲ 0.07, the vesicles retain the stomatocytic shape and s2 ≈ 0. In stable SW states with 0.07 ≲ fw ≲ 0.5, the vesicles are oblate with asphericity s2 ≃ 0.23. In the DW state, the vesicles undergo a sequence of shape transitions from stomatocytes to vertical oblates, and then back to inverted stomatocytes. This shape transition leads to a variation in asphericity from s2 ≈ 0 in the range 0.5 ≲ fw ≲ 0.75, to s2 ≃ 0.23 for 0.75 ≲ fw ≲ 0.9, and finally back to s2 ≈ 0 for fw ≳ 0.9.
= 0.5. Initially stomatocyte vesicles (v = 0.55), resembling two connected spheres, have an asphericity close to zero. In the range 0 < fw ≲ 0.07, the vesicles retain the stomatocytic shape and s2 ≈ 0. In stable SW states with 0.07 ≲ fw ≲ 0.5, the vesicles are oblate with asphericity s2 ≃ 0.23. In the DW state, the vesicles undergo a sequence of shape transitions from stomatocytes to vertical oblates, and then back to inverted stomatocytes. This shape transition leads to a variation in asphericity from s2 ≈ 0 in the range 0.5 ≲ fw ≲ 0.75, to s2 ≃ 0.23 for 0.75 ≲ fw ≲ 0.9, and finally back to s2 ≈ 0 for fw ≳ 0.9.
Initially oblate vesicles (v = 0.63) retain constant asphericity s2 ≃ 0.23 in the SW state for 0 < fw ≲ 0.5, as they retain their shapes, see Fig. 4(a). However, they transition to deep-wrapped stomatocytes for 0.5 ≲ fw ≲ 0.79, reducing asphericity to s2 ≃ 0. Within the DW state, the vesicles undergo a transition from stomatocyte to vertical oblate, returning the asphericity to s2 ≃ 0.23 for 0.79 < fw ≤ 1. In contrast, initially prolate vesicles (v ≃ 0.66), which are more elongated, have a high asphericity s2 ≃ 0.97. In SW states, 0.07 ≲ fw ≲ 0.5, they transition to oblates with s2 ≃ 0.23. In DW states, 0.5 ≲ fw ≲ 0.81, vesicles adopt stomatocytic states with s2 ≈ 0. Finally, for fw > 0.81, the vesicles return to prolates with a rotation of the major axis by 90° and asphericities s2 ≃ 0.97. For ellipsoidal vesicles (v = 0.95), the asphericity takes a value of s2 ≃ 0.1 when the vesicle adopts an oblate-ellipsoid shape in SW states for 0.1 < fw ≤ 0.5. In DW states, the vesicles maintain prolate-ellipsoidal shape for 0.5 < fw ≤ 1 with s2 ≃ 0.38.
Fig. 4(b) illustrates the effects of relative stiffness of the vesicle, κr, on the asphericity s2 for an initially oblate vesicle (v = 0.63) at membrane tension ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) = 0.5. For soft vesicles (κr ≲ 2.5), both shape and orientation changes occur during the wrapping process, resulting in variations in asphericity. Across all values of κr, the vesicles retain their oblate shape in the SW state for 0 < fw ≲ 0.5, maintaining an asphericity s2 ≃ 0.23. However, in the DW state, the soft vesicles undergo a sequence of shape transitions as the wrapping fraction increases. For example, vesicles with κr = 0.1 adopt stomatocytic shapes with s2 ≈ 0 for 0.5 ≲ fw ≲ 0.72, prolate shapes with s2 ≈ 0.97 for 0.72 ≲ fw ≲ 0.9, and vertical oblate shapes with s2 ≃ 0.23 for fw ≳ 0.95. In contrast, stiff vesicles (κr = 10) undergo only orientation changes, maintaining asphericity s2 ≃ 0.23. Similarly, the effects of membrane tension
= 0.5. For soft vesicles (κr ≲ 2.5), both shape and orientation changes occur during the wrapping process, resulting in variations in asphericity. Across all values of κr, the vesicles retain their oblate shape in the SW state for 0 < fw ≲ 0.5, maintaining an asphericity s2 ≃ 0.23. However, in the DW state, the soft vesicles undergo a sequence of shape transitions as the wrapping fraction increases. For example, vesicles with κr = 0.1 adopt stomatocytic shapes with s2 ≈ 0 for 0.5 ≲ fw ≲ 0.72, prolate shapes with s2 ≈ 0.97 for 0.72 ≲ fw ≲ 0.9, and vertical oblate shapes with s2 ≃ 0.23 for fw ≳ 0.95. In contrast, stiff vesicles (κr = 10) undergo only orientation changes, maintaining asphericity s2 ≃ 0.23. Similarly, the effects of membrane tension ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) on the asphericity of the vesicle are shown in Fig. 4(c) for an oblate (v = 0.63) with relative stiffness κr = 1 at various membrane tensions. Across a wide range of wrapping fractions fw the asphericity s2 remains nearly constant and is independent of
on the asphericity of the vesicle are shown in Fig. 4(c) for an oblate (v = 0.63) with relative stiffness κr = 1 at various membrane tensions. Across a wide range of wrapping fractions fw the asphericity s2 remains nearly constant and is independent of ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) , indicating that the shape of the vesicles is not much affected by changes in membrane tension. It decreases to s2 ≲ 0.1 for 0.6 ≲ fw ≲ 0.8, where the vesicle is a stomatocyte. For initially stomatocyte, prolate, and ellipsoidal vesicles, the effects of vesicle stiffness and membrane tension on asphericities are shown in the ESI;† see Fig. S6. The height of the center of mass of the vesicles with respect to the outer patch of the initially planar membrane can similarly indicate both shape change and orientation change during wrapping; see Fig. S7 in the ESI.†
, indicating that the shape of the vesicles is not much affected by changes in membrane tension. It decreases to s2 ≲ 0.1 for 0.6 ≲ fw ≲ 0.8, where the vesicle is a stomatocyte. For initially stomatocyte, prolate, and ellipsoidal vesicles, the effects of vesicle stiffness and membrane tension on asphericities are shown in the ESI;† see Fig. S6. The height of the center of mass of the vesicles with respect to the outer patch of the initially planar membrane can similarly indicate both shape change and orientation change during wrapping; see Fig. S7 in the ESI.†
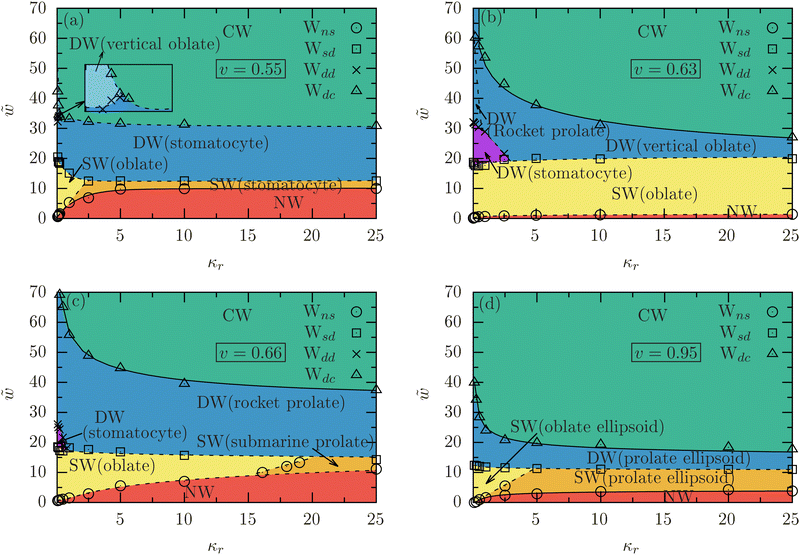
3.3 Effect of vesicle stiffness on the wrapping diagrams
Fig. 5(a)–(d) present the wrapping diagrams for various relative stiffnesses κr and reduced adhesion strengths![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) for vesicles with v = 0.55, 0.63, 0.66, and 0.95 at fixed membrane tension
for vesicles with v = 0.55, 0.63, 0.66, and 0.95 at fixed membrane tension ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) = 0.5. These wrapping diagrams were extracted from the variation of the deformation energies, ΔẼ with fw; see Fig. S4 in the ESI.† For each value of v, the binding transition Wns shifts to higher adhesion strengths
= 0.5. These wrapping diagrams were extracted from the variation of the deformation energies, ΔẼ with fw; see Fig. S4 in the ESI.† For each value of v, the binding transition Wns shifts to higher adhesion strengths ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) as κr increases, ultimately saturating at a constant value as the deformation of the vesicles is negligible for κr ≳ 10. This implies that softer vesicles adhere to the membrane more easily than stiffer ones. In contrast,
as κr increases, ultimately saturating at a constant value as the deformation of the vesicles is negligible for κr ≳ 10. This implies that softer vesicles adhere to the membrane more easily than stiffer ones. In contrast, ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) for the envelopment transition Wdc increases with decreasing κr due to the development of a sharp neck at the contact line; see Fig. 2 and 4, indicating that complete wrapping is more challenging for softer vesicles than for stiffer ones. The shape and stiffness of the vesicles also influence the nature of the binding transition, which can be continuous or discontinuous. For example, the binding transition is continuous for ellipsoidal vesicles (v = 0.95) with κr ≳ 1 and stiff (κr ≳ 1) stomatocyte (v = 0.55) vesicles, while it is discontinuous for soft (κr ≲ 1) ellipsoidal (v = 0.95), and soft (κr ≲ 2.5) stomatocyte (v = 0.55) vesicles. For initially oblate (v = 0.63) and prolate (v = 0.66) vesicles, the binding transition is discontinuous for the entire range of κr. The envelopment transition is discontinuous for initially stomatocytes and continuous for initially oblates and prolates. The shallow-to-deep-wrapped transition Wsd is always discontinuous and shows a moderate increase in
for the envelopment transition Wdc increases with decreasing κr due to the development of a sharp neck at the contact line; see Fig. 2 and 4, indicating that complete wrapping is more challenging for softer vesicles than for stiffer ones. The shape and stiffness of the vesicles also influence the nature of the binding transition, which can be continuous or discontinuous. For example, the binding transition is continuous for ellipsoidal vesicles (v = 0.95) with κr ≳ 1 and stiff (κr ≳ 1) stomatocyte (v = 0.55) vesicles, while it is discontinuous for soft (κr ≲ 1) ellipsoidal (v = 0.95), and soft (κr ≲ 2.5) stomatocyte (v = 0.55) vesicles. For initially oblate (v = 0.63) and prolate (v = 0.66) vesicles, the binding transition is discontinuous for the entire range of κr. The envelopment transition is discontinuous for initially stomatocytes and continuous for initially oblates and prolates. The shallow-to-deep-wrapped transition Wsd is always discontinuous and shows a moderate increase in ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) as κr decreases.
as κr decreases.
In the SW state, soft stomatocytes (v = 0.55) with bending rigidity ratio κr ≲ 1 adopt oblate shapes, while stiff ones with κr ≳ 2.5 retain their original shape. For intermediate stiffness, 1 ≲ κr ≲ 2.5, a discontinuous transition from stomatocyte to oblate occurs as the adhesion strength ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) increases; see Fig. 5(a). In contrast, oblate (v = 0.63) vesicles consistently maintain a “rocket” orientation for all bending-rigidity ratios; see Fig. 5(b). In the DW state, soft stomatocytes with κr < 1 transition to vertical oblates with increasing
increases; see Fig. 5(a). In contrast, oblate (v = 0.63) vesicles consistently maintain a “rocket” orientation for all bending-rigidity ratios; see Fig. 5(b). In the DW state, soft stomatocytes with κr < 1 transition to vertical oblates with increasing ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) . While soft oblate vesicles (v = 0.63) undergo a shape transition as
. While soft oblate vesicles (v = 0.63) undergo a shape transition as ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) increases, moving from stomatocyte to rocket prolate for κr ≲ 0.5 and from stomatocyte to vertical oblate for 0.5 < κr ≲ 2.5. Stiffer vesicles mainly experience an orientation change rather than a shape change. In complete wrapping, regardless of the bending-rigidity ratio, the vesicles return to their initial shapes.
increases, moving from stomatocyte to rocket prolate for κr ≲ 0.5 and from stomatocyte to vertical oblate for 0.5 < κr ≲ 2.5. Stiffer vesicles mainly experience an orientation change rather than a shape change. In complete wrapping, regardless of the bending-rigidity ratio, the vesicles return to their initial shapes.
Initially prolate vesicles (v = 0.66) with κr ≲ 16 transition to oblate in the SW state, while those with κr ≳ 20 maintain their shape, see Fig. 5(c). For intermediate stiffness values, 16 ≲ κr ≲ 20, the vesicles undergo a transition from prolate to oblate with increasing ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) . In the DW state, the vesicles with κr < 1 experience a discontinuous transition from stomatocyte to “rocket” prolate with increasing
. In the DW state, the vesicles with κr < 1 experience a discontinuous transition from stomatocyte to “rocket” prolate with increasing ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) . In contrast, stiff prolates (κr > 1) show only an orientation change, maintaining the “rocket” prolate state. Similarly, initially ellipsoidal vesicles (v = 0.95) with 1 ≲ κr ≲ 5 can exhibit a discontinuous transition from prolate to oblate in the SW state as
. In contrast, stiff prolates (κr > 1) show only an orientation change, maintaining the “rocket” prolate state. Similarly, initially ellipsoidal vesicles (v = 0.95) with 1 ≲ κr ≲ 5 can exhibit a discontinuous transition from prolate to oblate in the SW state as ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) increases; see Fig. 5(d). Softer shallow-wrapped vesicles (κr ≲ 1) remain in the oblate state throughout, while stiffer ones (κr ≳ 5) remain in the prolate state. In the DW state, all ellipsoidal vesicles adopt the prolate shape with a “rocket” orientation.
increases; see Fig. 5(d). Softer shallow-wrapped vesicles (κr ≲ 1) remain in the oblate state throughout, while stiffer ones (κr ≳ 5) remain in the prolate state. In the DW state, all ellipsoidal vesicles adopt the prolate shape with a “rocket” orientation.
Fig. 6 shows the wrapping diagrams in the κr–fw plane for the same parameter values as in Fig. 5. For stomatocytes (v = 0.55) and ellipsoidal (v = 0.95) vesicles with κr ≳ 1, initial binding to the initially planar membranes occurs at fwns = 0, indicating that the binding transition is continuous. In contrast, soft (κr ≲ 1) ellipsoidal (v = 0.95), soft (κr ≲ 1) stomatocyte (v = 0.55), prolate (v = 0.66), and oblate (v = 0.63) vesicles show discontinuous binding transitions to fwns > 0. For all reduced volumes, the wrapping fractions  and
and 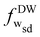 for the coexisting SW to DW states decrease weakly with increasing κr and may saturate for higher κr. For stomatocyte (v = 0.55), the wrapping fractions
for the coexisting SW to DW states decrease weakly with increasing κr and may saturate for higher κr. For stomatocyte (v = 0.55), the wrapping fractions  for the DW states that coexist with the CW state remain constant with increasing κr. For initially stomatocytes (v = 0.55), the presence of the energy barrier between the DW and CW states indicates that the envelopment transition is discontinuous. In contrast, for oblate (v = 0.63), prolate (v = 0.66), and ellipsoidal (v = 0.95) vesicles, no such energy barrier is found, indicating that the envelopment transition is continuous. The range of accessible wrapping fractions for the DW states increases slightly with increasing v.
for the DW states that coexist with the CW state remain constant with increasing κr. For initially stomatocytes (v = 0.55), the presence of the energy barrier between the DW and CW states indicates that the envelopment transition is discontinuous. In contrast, for oblate (v = 0.63), prolate (v = 0.66), and ellipsoidal (v = 0.95) vesicles, no such energy barrier is found, indicating that the envelopment transition is continuous. The range of accessible wrapping fractions for the DW states increases slightly with increasing v.
In summary, we have studied the wrapping behavior of nonspherical vesicles with different initial shapes—stomatocyte (v = 0.55), oblate (v = 0.63), prolate (v = 0.66), and ellipsoidal (v = 0.95)—by systematically varying the relative stiffness (κr) of the vesicles at a fixed reduced membrane tension ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) = 0.5. For all the vesicle shapes we have considered, the adhesion strength
= 0.5. For all the vesicle shapes we have considered, the adhesion strength ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) for the binding transition decreases with decreasing relative stiffness κr, while it increases for envelopment transition. Softer vesicles undergo a sequence of both shape and orientation changes during the wrapping process, while stiffer vesicles exhibit only orientation changes. The binding transition is discontinuous for softer stomatocyte (v = 0.55) and ellipsoidal (v = 0.95) vesicles, and continuous for the stiffer ones. For initially oblate (v = 0.63) and the prolate (v = 0.66) vesicles, the binding transition is discontinuous regardless of stiffness. The envelopment transition is continuous for initially oblate (v = 0.63), prolate (v = 0.66), and ellipsoidal (v = 0.95) vesicles, but it is discontinuous for initially stomatocyte (v = 0.55) vesicles. For all the considered vesicle shapes, the shallow-to-deep wrapped transition is always discontinuous.
for the binding transition decreases with decreasing relative stiffness κr, while it increases for envelopment transition. Softer vesicles undergo a sequence of both shape and orientation changes during the wrapping process, while stiffer vesicles exhibit only orientation changes. The binding transition is discontinuous for softer stomatocyte (v = 0.55) and ellipsoidal (v = 0.95) vesicles, and continuous for the stiffer ones. For initially oblate (v = 0.63) and the prolate (v = 0.66) vesicles, the binding transition is discontinuous regardless of stiffness. The envelopment transition is continuous for initially oblate (v = 0.63), prolate (v = 0.66), and ellipsoidal (v = 0.95) vesicles, but it is discontinuous for initially stomatocyte (v = 0.55) vesicles. For all the considered vesicle shapes, the shallow-to-deep wrapped transition is always discontinuous.
3.4 Effect of membrane tension on the wrapping diagrams
The effects of membrane tension on the wrapping diagrams are shown in Fig. 7 for stomatocyte (v = 0.55), oblate (v = 0.63), prolate (v = 0.66) and ellipsoidal (v = 0.95) vesicles, all with fixed relative stiffness κr = 1; the corresponding deformation energies are shown in Fig. S5 in the ESI.† The adhesion strength![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) for the SW-to-DW transition increases with increasing membrane tension
for the SW-to-DW transition increases with increasing membrane tension ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) , due to the increased energy cost in the neck, stabilizing SW over the DW states. As a result, the Wdc transition merges with the Wsd transition at the triple point (
, due to the increased energy cost in the neck, stabilizing SW over the DW states. As a result, the Wdc transition merges with the Wsd transition at the triple point (![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) sdct,
sdct, ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) sdct), where the SW, DW, and CW states coexist; the deformation energy landscapes at the triple points are shown in Fig. S8 in the ESI.† Beyond the triple point, the envelopment transition becomes discontinuous, with vesicles undergoing a direct transition from the SW state to the CW state. The adhesion strength
sdct), where the SW, DW, and CW states coexist; the deformation energy landscapes at the triple points are shown in Fig. S8 in the ESI.† Beyond the triple point, the envelopment transition becomes discontinuous, with vesicles undergoing a direct transition from the SW state to the CW state. The adhesion strength ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) for the binding transition does not change with increasing membrane tension
for the binding transition does not change with increasing membrane tension ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) .
.
 | ||
Fig. 7 Wrapping diagrams in the ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) – –![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) plane at κr = 1. Data is shown for nonspherical vesicles with reduced volumes (a) v = 0.55 (stomatocyte), (b) v = 0.63 (oblate), (c) v = 0.66 (prolate), (d) v = 0.95 (ellipsoidal). Stable states and transitions are indicated analogously to Fig. 5; solid lines represent continuous and dashed lines discontinuous transitions, and triple points are highlighted by red diamonds. plane at κr = 1. Data is shown for nonspherical vesicles with reduced volumes (a) v = 0.55 (stomatocyte), (b) v = 0.63 (oblate), (c) v = 0.66 (prolate), (d) v = 0.95 (ellipsoidal). Stable states and transitions are indicated analogously to Fig. 5; solid lines represent continuous and dashed lines discontinuous transitions, and triple points are highlighted by red diamonds. | ||
For oblates (v = 0.63) with a bending-rigidity ratio κr = 1, a deep-wrapped (DW1) to deep-wrapped (DW2) transition occurs at membrane tensions ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ≲ 4, where stomatocytes and oblates coexist. For
≲ 4, where stomatocytes and oblates coexist. For ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ≳ 4, vertical oblate states become unstable, and the DW1-to-DW2 transition vanishes at another triple point (
≳ 4, vertical oblate states become unstable, and the DW1-to-DW2 transition vanishes at another triple point (![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ddct,
ddct, ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) ddct), where two distinct DW states coexist with the CW state; the corresponding deformation energy landscape is shown in Fig. S9 in the ESI.† For initially stomatocytes (v = 0.55), the adhesion strength
ddct), where two distinct DW states coexist with the CW state; the corresponding deformation energy landscape is shown in Fig. S9 in the ESI.† For initially stomatocytes (v = 0.55), the adhesion strength ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) for complete wrapping gradually increases with increasing membrane tension
for complete wrapping gradually increases with increasing membrane tension ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) , since the envelope transition remains discontinuous throughout the membrane tension range
, since the envelope transition remains discontinuous throughout the membrane tension range ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) . In contrast, for oblates (v = 0.63), the envelopment transition is continuous for membrane tensions 0 <
. In contrast, for oblates (v = 0.63), the envelopment transition is continuous for membrane tensions 0 < ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ≲
≲ ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ddct and discontinuous for
ddct and discontinuous for ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) >
> ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ddct. Similarly, for prolate and ellipsoidal vesicles, the envelopment transition is continuous for membrane tensions 0 <
ddct. Similarly, for prolate and ellipsoidal vesicles, the envelopment transition is continuous for membrane tensions 0 < ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ≲
≲ ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) sdct and discontinuous for
sdct and discontinuous for ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ≳
≳ ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) sdct. Consequently, the adhesion strength
sdct. Consequently, the adhesion strength ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) for the complete wrapping initially decreases with increasing
for the complete wrapping initially decreases with increasing ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) , reaches its optimal value at the triple point, and beyond the triple point
, reaches its optimal value at the triple point, and beyond the triple point ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) increases with membrane tension
increases with membrane tension ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) . The wrapping diagram in the fw–
. The wrapping diagram in the fw–![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) plane for initially stomatocyte, oblate, prolate, and ellipsoidal vesicles for the same parameter values, as mentioned in Fig. 7, is presented in Fig. S10 in the ESI.†
plane for initially stomatocyte, oblate, prolate, and ellipsoidal vesicles for the same parameter values, as mentioned in Fig. 7, is presented in Fig. S10 in the ESI.†
The coordinates of the triple points in the ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) –
–![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) wrapping diagram are influenced by both the bending rigidity ratio κr and the reduced volume v of the vesicles. For stomatocytes (v = 0.55), the triple point (
wrapping diagram are influenced by both the bending rigidity ratio κr and the reduced volume v of the vesicles. For stomatocytes (v = 0.55), the triple point (![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) sdct,
sdct, ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) sdct) shifts to higher values of membrane tension
sdct) shifts to higher values of membrane tension ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) and adhesion strength
and adhesion strength ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) as the bending rigidity ratio κr increases; see Fig. 8(a) and Fig. S11 in the ESI.† For high κr, the almost spherical shape of the outer surface reduces the cost of wrapping energy for deep-wrapped stomatocytes, and therefore, the regions of stable DW states extend to lower adhesion strengths and higher membrane tensions
as the bending rigidity ratio κr increases; see Fig. 8(a) and Fig. S11 in the ESI.† For high κr, the almost spherical shape of the outer surface reduces the cost of wrapping energy for deep-wrapped stomatocytes, and therefore, the regions of stable DW states extend to lower adhesion strengths and higher membrane tensions ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) with increasing κr. However, as the membrane tension
with increasing κr. However, as the membrane tension ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) increases, independent of the vesicle shape, the energy cost associated with the neck for the DW states increases, increasing the stability of both the SW and the CW states compared to the DW state.
increases, independent of the vesicle shape, the energy cost associated with the neck for the DW states increases, increasing the stability of both the SW and the CW states compared to the DW state.
For an oblate (v = 0.63) and κr ≲ 3, the vesicles transition between an oblate SW and a stomatocyte DW state with increasing adhesion strength, before further transition to oblate DW or CW states, see Fig. 8(a) and Fig. S12 in the ESI.† However, unlike initial stomatocytes, increasing κr leads to decreasing tensions ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) and adhesion strengths
and adhesion strengths ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) for both triple points (
for both triple points (![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) sddt,
sddt, ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) sddt) and (
sddt) and (![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) sdct,
sdct, ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) sdct). Increasing the bending-rigidity ratio κr stabilizes the oblate states over the stomatocyte states and eventually leads to a direct transition between the oblate SW and the oblate DW or the CW states. The oblate DW state, due to its asymmetrical shape, lacks the advantages that a stomatocytic shape has, and stable states are only found for low tensions.
sdct). Increasing the bending-rigidity ratio κr stabilizes the oblate states over the stomatocyte states and eventually leads to a direct transition between the oblate SW and the oblate DW or the CW states. The oblate DW state, due to its asymmetrical shape, lacks the advantages that a stomatocytic shape has, and stable states are only found for low tensions.
The triple point (σsdct, ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) sdct) varies nonmonotonically with reduced volume v at a fixed stiffness of the vesicle κr = 1, as shown in Fig. 8(b). For 0.8 < v < 1, the triple point moves to higher membrane tensions and adhesion strengths as v decreases. This occurs because the vesicle becomes more elongated with decreasing v, increasing the stability of the deep-wrapped prolate states relative to the shallow-wrapped oblate states. In contrast, for 0.55 < v < 0.8, the vesicles tend to adopt an oblate shape in the SW state and a stomatocyte shape in the DW state. Consequently, the triple point shifts to lower membrane tensions and adhesion strengths.
sdct) varies nonmonotonically with reduced volume v at a fixed stiffness of the vesicle κr = 1, as shown in Fig. 8(b). For 0.8 < v < 1, the triple point moves to higher membrane tensions and adhesion strengths as v decreases. This occurs because the vesicle becomes more elongated with decreasing v, increasing the stability of the deep-wrapped prolate states relative to the shallow-wrapped oblate states. In contrast, for 0.55 < v < 0.8, the vesicles tend to adopt an oblate shape in the SW state and a stomatocyte shape in the DW state. Consequently, the triple point shifts to lower membrane tensions and adhesion strengths.
In summary, we have investigated the wrapping behavior of nonspherical vesicles with different initial shapes—stomatocyte (v = 0.55), oblate (v = 0.63), prolate (v = 0.66), and ellipsoidal (v = 0.95)—by systematically varying the reduced tension (![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ) of an initially planar membrane at a fixed bending rigidity ratio κr = 1. The adhesion strength
) of an initially planar membrane at a fixed bending rigidity ratio κr = 1. The adhesion strength ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) for the binding transition remains constant with increasing membrane tension
for the binding transition remains constant with increasing membrane tension ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) . The stability of the shallow-wrapped state increases with increasing
. The stability of the shallow-wrapped state increases with increasing ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) . At high membrane tension
. At high membrane tension ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) , the deep-wrapped state disappears at a triple point where the shallow-wrapped, deep-wrapped, and completely wrapped states coexist. For initially oblate vesicles (v = 0.63), an additional triple point is observed where two distinct deep-wrapped states (DW1 and DW2) coexist with the completely wrapped state. We have shown the coordinates of the triple point is influenced by both the bending rigidity ratio κr and the reduced volume v of the vesicles. For initially oblate (v = 0.63), prolate (v = 0.66), and ellipsoidal (v = 0.95) vesicles, the triple point marks the minimum adhesion strength
, the deep-wrapped state disappears at a triple point where the shallow-wrapped, deep-wrapped, and completely wrapped states coexist. For initially oblate vesicles (v = 0.63), an additional triple point is observed where two distinct deep-wrapped states (DW1 and DW2) coexist with the completely wrapped state. We have shown the coordinates of the triple point is influenced by both the bending rigidity ratio κr and the reduced volume v of the vesicles. For initially oblate (v = 0.63), prolate (v = 0.66), and ellipsoidal (v = 0.95) vesicles, the triple point marks the minimum adhesion strength ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) for complete wrapping which occurs at a finite membrane tension.
for complete wrapping which occurs at a finite membrane tension.
4 Conclusions and outlook
We calculated the shapes, orientations, and energies for the wrapping of initially prolate, oblate, and stomatocytic vesicles at initially planar membranes. A systematic variation of reduced volumes, bending rigidity ratios, and membrane tensions leads to a rich phase behavior. Whereas shallow-wrapped states are often oblate, deep-wrapped states stabilize stomatocytic shapes. Transitions between shallow-wrapped and deep-wrapped states are always discontinuous, whereas the binding and envelopment transitions can be either continuous or discontinuous depending on vesicle stiffness and membrane tension. Softer vesicles undergo major shape changes during wrapping, while stiffer ones show only orientation changes, and at high tensions, the transition can occur directly from SW to CW states. Stomatocytic shapes can, because of their near-spherical shape, stabilize deep-wrapped over shallow-wrapped states and also for initially oblate and prolate vesicles. For soft vesicles, the binding transition is shifted to lower adhesion strengths, and the envelopment transition to higher adhesion strengths, in agreement with previous studies.32,33Increasing membrane tension destabilizes deep-wrapped states that vanish at a triple point, leading to the coexistence of shallow-, deep-, and complete-wrapped states. Vesicle asphericities and triple-point coordinates can be used to systematically characterize phase diagrams as functions of elastic parameters. With increasing stiffness, the triple points between the shallow-wrapped, deep-wrapped, and complete-wrapped states shift to lower tensions and adhesion strengths for initially oblate vesicles and to higher values for initially stomatocytic vesicles. For oblate, prolate and ellipsoidal vesicles, the optimal membrane tension for uptake is finite, indicating that the adhesion strength required for complete wrapping is not the lowest for vanishing tension, as expected for hard particles.19,23,25 Because cells can regulate their membrane tension,67,68 non-spherical vesicles can favor endocytosis or shallow-wrapped states; the latter may eventually facilitate fusion and direct delivery of the vesicle volume to the cytosol.8
Vesicles are a versatile class of elastic particles, exhibiting unique behaviors not observed in particles with 3D elasticity, such as polymeric particles. In particular, in the regime of stable deep-wrapped states, vesicles show internal discontinuous shape transitions with stomatocytic states extending to higher membrane tensions. Studying initial vesicle shapes close to the phase boundaries between stomatocytic, oblate, and prolate vesicles leads to an intriguing qualitatively novel finding compared to prolate vesicles with reduced volumes v > 0.7, which we studied earlier.32 Our findings on the wrapping of nonspherical vesicles at initially planar membranes provide valuable insights for designing tailored deformable particles, with potential applications in membrane attachment, fusion, and endocytosis.
This work highlights how vesicle shape, deformability, and membrane tension influence wrapping transitions on initially planar membranes. While our current model assumes a contact potential, many realistic systems involve long-range adhesive interactions.69 Thus, future studies could include wrapping nonspherical vesicles at lipid membranes by systematically varying the range of adhesion interaction potential to mimic realistic systems. For vesicles with very low reduced volumes, large energy barriers may lead to metastable shapes,70 which can make the wrapping transitions more complex. Investigating the wrapping behavior of metastable states of such vesicles could be a valuable extension of this work. Additionally, membrane deformations induce membrane-mediated interactions, which become particularly important in crowded environments. Predicting these interaction potentials between multiple vesicles could offer insights into the aggregation behavior of virions on biomembranes. However, the knowledge we gained from this work may also contribute to biomedical applications, particularly targeted drug delivery using deformable nanoparticles.
Author contributions
JM designed the research. AKS, RM, and JM conducted the research and analyzed the data. JM and AKS drafted the manuscript.Data availability
The data used in this study are available in the main manuscript or the ESI.† Additional raw data and analysis scripts can be obtained from the corresponding author upon request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
JM thanks Thorsten Auth (Jülich) for valuable discussions and input on the wrapping behavior of vesicles on membranes. JM acknowledges funding support from the Science and Engineering Research Board (SERB/ANRF) under the MATRICS grant (grant no. MTR/2023/001538) and IIT Bhubaneswar. AKS thanks the Council of Scientific and Industrial Research (CSIR) for funding his PhD.Notes and references
- T. Pomorski, S. Hrafnsdóttir, P. F. Devaux and G. van Meer, Semin. Cell Dev. Biol., 2001, 12, 139–148 CrossRef CAS
.
- H. Sprong, P. Van Der Sluijs and G. Van Meer, Nat. Rev. Mol. Cell Biol., 2001, 2, 504–513 CrossRef CAS PubMed
.
- S. Dasgupta, T. Auth and G. Gompper, J. Phys.: Condens. Matter, 2017, 29, 373003 CrossRef CAS
.
- S. Pogodin, M. Werner, J.-U. Sommer and V. A. Baulin, ACS Nano, 2012, 6, 10555–10561 CrossRef CAS PubMed
.
- M. Werner, J. Bathmann, V. A. Baulin and J.-U. Sommer, ACS Macro Lett., 2017, 6, 247–251 CrossRef CAS PubMed
.
- B. S. Joshi, M. A. de Beer, B. N. G. Giepmans and I. S. Zuhorn, ACS Nano, 2020, 14, 4444–4455 CrossRef CAS
.
- A. Hubbard, Curr. Opin. Cell Biol., 1989, 1, 675–683 CrossRef CAS
.
- S. Kube, N. Hersch, E. Naumovska, T. Gensch, J. Hendriks, A. Franzen, L. Landvogt, J.-P. Siebrasse, U. Kubitscheck and B. Hoffmann,
et al.
, Langmuir, 2017, 33, 1051–1059 CrossRef CAS PubMed
.
- T. Wiegand, M. Fratini, F. Frey, K. Yserentant, Y. Liu, E. Weber, K. Galior, J. Ohmes, F. Braun and D.-P. Herten,
et al.
, Nat. Commun., 2020, 11, 32 CrossRef CAS
.
- S. Dasgupta, T. Auth, N. S. Gov, T. J. Satchwell, E. Hanssen, E. S. Zuccala, D. T. Riglar, A. M. Toye, T. Betz, J. Baum and G. Gompper, Biophys. J., 2014, 107, 43–54 CrossRef CAS PubMed
.
- Q. Yu, S. Dasgupta, T. Auth and G. Gompper, Nano Lett., 2020, 20, 1662–1668 CrossRef CAS PubMed
.
- T. A. Masters, B. Pontes, V. Viasnoff, Y. Li and N. C. Gauthier, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 11875–11880 CrossRef CAS
.
- P. Sens and M. S. Turner, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 031918 CrossRef PubMed
.
- M. J. Mitchell, M. M. Billingsley, R. M. Haley, M. E. Wechsler, N. A. Peppas and R. Langer, Nat. Rev. Drug Discovery, 2021, 20, 101–124 CrossRef CAS PubMed
.
- W. H. De Jong and P. J. Borm, Int. J. Nanomed., 2008, 3, 133–149 CrossRef CAS
.
- C. Barbe, J. Bartlett, L. Kong, K. Finnie, H. Q. Lin, M. Larkin, S. Calleja, A. Bush and G. Calleja, Adv. Mater., 2004, 16, 1959–1966 CrossRef CAS
.
- C. Van Der Wel, A. Vahid, A. Šarić, T. Idema, D. Heinrich and D. J. Kraft, Sci. Rep., 2016, 6, 32825 CrossRef CAS PubMed
.
- M. Raatz, R. Lipowsky and T. R. Weikl, Soft Matter, 2014, 10, 3570–3577 RSC
.
- M. Deserno and T. Bickel, Europhys. Lett., 2003, 62, 767 CrossRef CAS
.
- R. Lipowsky and H.-G. Döbereiner, Europhys. Lett., 1998, 43, 219 CrossRef CAS
.
- S. van der Ham, J. Agudo-Canalejo and H. R. Vutukuri, ACS Nano, 2024, 18, 10407–10416 CrossRef CAS PubMed
.
- A. Azadbakht, B. Meadowcroft, T. Varkevisser, A. Šarić and D. J. Kraft, Nano Lett., 2023, 23, 4267–4273 CrossRef CAS PubMed
.
- S. Dasgupta, T. Auth and G. Gompper, Nano Lett., 2014, 14, 687–693 CrossRef CAS
.
- W. Jiang, B. Y. Kim, J. T. Rutka and W. C. Chan, Nat. Nanotechnol., 2008, 3, 145–150 CrossRef CAS
.
- S. Dasgupta, T. Auth and G. Gompper, Soft Matter, 2013, 9, 5473–5482 RSC
.
- A.-S. Smith and U. Seifert, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 061902 CrossRef PubMed
.
- U. Seifert, Adv. Phys., 1997, 46, 13–137 CrossRef CAS
.
- A. H. Bahrami, Soft Matter, 2013, 9, 8642–8646 RSC
.
- A. Scotti, M. F. Schulte, C. G. Lopez, J. J. Crassous, S. Bochenek and W. Richtering, Chem. Rev., 2022, 122, 11675–11700 CrossRef CAS
.
- C. Huang, Y. Zhang, H. Yuan, H. Gao and S. Zhang, Nano Lett., 2013, 13, 4546–4550 CrossRef CAS
.
- A. Sharma, Y. Zhu, E. J. Spangler and M. Laradji, J. Chem. Phys., 2022, 156, 234901 CrossRef CAS
.
- J. Midya, T. Auth and G. Gompper, ACS Nano, 2023, 17, 1935–1945 CrossRef CAS PubMed
.
- X. Yi, X. Shi and H. Gao, Phys. Rev. Lett., 2011, 107, 098101 CrossRef PubMed
.
- Y. Hatano, M. Yoshida, F. Uno, S. Yoshida, N. Osafune, K. Ono, M. Yamada and S. Nii, J. Electron Microsc., 2001, 50, 113–124 CrossRef CAS PubMed
.
- D. K. Cureton, R. H. Massol, S. Saffarian, T. L. Kirchhausen and S. P. J. Whelan, PLoS Pathog., 2009, 5, e1000394 CrossRef PubMed
.
- R. C. Condit, N. Moussatche and P. Traktman, Adv. Virus Res., 2006, 66, 31–124 CrossRef CAS
.
- J. Liu, S. Corroyer-Dulmont, V. Pražák, I. Khusainov, K. Bahrami, S. Welsch, D. Vasishtan, A. Obarska-Kosińska, S. R. Thorkelsson, K. Grünewald, E. R. J. Quemin, B. Turoňová and J. K. Locker, Nat. Struct. Mol. Biol., 2024, 31, 1105–1113 CrossRef CAS PubMed
.
- P. Ge, J. Tsao, S. Schein, T. J. Green, M. Luo and Z. H. Zhou, Science, 2010, 327, 689–693 CrossRef CAS PubMed
.
- X. Liu, T. Auth, N. Hazra, M. F. Ebbesen, J. Brewer, G. Gompper, J. J. Crassous and E. Sparr, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2217534120 CrossRef CAS PubMed
.
- H.-B. Pang, L. Hevroni, N. Kol, D. M. Eckert, M. Tsvitov, M. S. Kay and I. Rousso, Retrovirology, 2013, 10, 4 CrossRef CAS PubMed
.
- N. Kol, M. Gladnikoff, D. Barlam, R. Z. Shneck, A. Rein and I. Rousso, Biophys. J., 2006, 91, 767–774 CrossRef CAS PubMed
.
- C. Likos, H. Löwen, M. Watzlawek, B. Abbas, O. Jucknischke, J. Allgaier and D. Richter, Phys. Rev. Lett., 1998, 80, 4450 CrossRef CAS
.
- J. M. Ren, T. G. McKenzie, Q. Fu, E. H. Wong, J. Xu, Z. An, S. Shanmugam, T. P. Davis, C. Boyer and G. G. Qiao, Chem. Rev., 2016, 116, 6743–6836 CrossRef CAS PubMed
.
- M. Brugnoni, A. Scotti, A. A. Rudov, A. P. Gelissen, T. Caumanns, A. Radulescu, T. Eckert, A. Pich, I. I. Potemkin and W. Richtering, Macromolecules, 2018, 51, 2662–2671 CrossRef CAS
.
- F. A. Plamper and W. Richtering, Acc. Chem. Res., 2017, 50, 131–140 CrossRef CAS
.
- J. Chen, D. Zhu, B. Lian, K. Shi, P. Chen, Y. Li, W. Lin, L. Ding, Q. Long and Y. Wang,
et al.
, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2220787120 CrossRef CAS
.
- U. Boas and P. M. Heegaard, Chem. Soc. Rev., 2004, 33, 43–63 RSC
.
- J. Midya, Y. Cang, S. A. Egorov, K. Matyjaszewski, M. R. Bockstaller, A. Nikoubashman and G. Fytas, Nano Lett., 2019, 19, 2715–2722 CrossRef CAS PubMed
.
-
D. Vlassopoulos and G. Fytas, From polymers to colloids: engineering the dynamic properties of hairy particles, in High Solid Dispersions, 2010, pp. 1–54 Search PubMed
.
- I. Hoffmann, C. Hoffmann, B. Farago, S. Prévost and M. Gradzielski, J. Chem. Phys., 2018, 148, 104901 CrossRef
.
- T. Höfken, U. Gasser, S. Schneider, A. V. Petrunin and A. Scotti, Macromol. Rapid Commun., 2024, 45, 2400043 CrossRef
.
- C. Strauch and S. Schneider, Soft Matter, 2023, 19, 938–950 RSC
.
- D. Vorselen, F. C. MacKintosh, W. H. Roos and G. J. Wuite, ACS Nano, 2017, 11, 2628–2636 CrossRef CAS PubMed
.
- U. Seifert, Adv. Phys., 1997, 46, 13–137 CrossRef CAS
.
- R. Groza, K. V. Schmidt, P. M. Müller, R. Ronchi, C. Schlack-Leigers, U. Neu, R. Puchkov, D. Dimova, C. Matthaeus, J. Taraska, T. R. Weikl and H. Ewers, Nat. Commun., 2024, 15, 2767 CrossRef CAS PubMed
.
- N. Baruah, J. Midya, G. Gompper, A. K. Dasanna and T. Auth, Biophys. J., 2025, 124, 740–752 CrossRef CAS PubMed
.
- W. Helfrich, Z. Naturforsch., C, 1973, 28, 693–703 CrossRef CAS PubMed
.
- H. Deuling and W. Helfrich, J. Phys., 1976, 37, 1335–1345 CrossRef CAS
.
- W. Góźdź, Langmuir, 2007, 23, 5665–5669 CrossRef PubMed
.
- W. Pezeshkian, M. König, T. A. Wassenaar and S. J. Marrink, Nat. Commun., 2020, 11, 2296 CrossRef CAS PubMed
.
-
G. Gompper and D. M. Kroll, Statistical Mechanics of Membranes and Surfaces, World Scientific, 2004, pp. 359–426 Search PubMed
.
- D. Kroll and G. Gompper, Science, 1992, 255, 968–971 CrossRef CAS PubMed
.
- K. A. Brakke, Exp. Math., 1992, 1, 141–165 CrossRef
.
- H. Noguchi, A. Sakashita and M. Imai, Soft Matter, 2015, 11, 193–201 RSC
.
- J. Midya, M. Rubinstein, S. K. Kumar and A. Nikoubashman, ACS Nano, 2020, 14, 15505–15516 CrossRef CAS PubMed
.
- H. Noguchi and G. Gompper, Phys. Rev. Lett., 2004, 93, 258102 CrossRef
.
- E. Sitarska and A. Diz-Muñoz, Curr. Opin. Cell Biol., 2020, 66, 11–18 CrossRef CAS
.
- M. P. Sheetz and J. Dai, Trends Cell Biol., 1996, 6, 85–89 CrossRef CAS
.
- M. Raatz and T. R. Weikl, Adv. Mater. Interfaces, 2017, 4, 1600325 CrossRef
.
- A. H. Bahrami and G. Hummer, ACS Nano, 2017, 11, 9558–9565 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00150a |
| This journal is © The Royal Society of Chemistry 2025 |