Hyper-auxeticity and the volume phase transition of polymer gels

Abstract

Thermoresponsive hydrogels exhibit reversible deswelling at the volume phase transition (VPT), associated to a minimum of the Poisson's ratio ν. Recent numerical investigations uncovered the occurrence of a hyper-auxetic transition (HAT) (ν = −1) for low-crosslinked hydrogels at low temperature, accompanied by a critical-like behavior. Here, we perform extensive numerical simulations to unveil the relation between these two transitions. We find that the HAT occurs at different temperatures T up to a maximum value of the crosslinker concentration c, thus being clearly distinct from the VPT, taking place at fixed T for all values of c. Our results provide novel fundamental insights on the interplay between network collapse and mechanical properties of these fascinating materials.

---

Introduction

Chemical hydrogels are covalently crosslinked polymer chains dispersed in a water-based solvent, offering versatility in synthesis and functionality, driving both scientific inquiry and practical applications.^1,2 Thermoresponsive hydrogels, like those based on poly(N-isopropylacrylamide) (pNIPAM), have gathered significant attention for their reversible swelling behavior induced by a change of temperature T. This is due to a variation of the affinity between polymer and solvent, usually water, which decreases, becoming more hydrophobic, upon increasing T.³ Experimental studies on neutral and charged pNIPAM hydrogels have elucidated this phenomenon, revealing a volume phase transition (VPT) and its theoretical underpinnings within the Flory–Rehner theory of swelling.^4,5

Mechanical instabilities are found to accompany the transition,^6–9 showcasing intriguing elastic properties and the onset of auxetic response, where materials expand perpendicularly with respect to the applied strain, yielding a negative Poisson's ratio that is a signature of auxetic behavior.^10–12 Auxetic materials often captivated the interest of researchers for their theoretical implications and practical applications, arising either from material topology or from the proximity to a thermodynamic transition.^13–21 In general, when approaching the lowest limit of mechanically stable unconstrained solids (ν = −1), a condition that we name as hyper-auxeticity, the bulk modulus K tends to zero, suggesting the presence of very large volume fluctuations from a thermodynamic viewpoint.¹⁶ However, according to the mean field theory of polymer networks, the relationship K + 4/3G = 0 is expected to hold at the VPT,^22,23 implying a positive ν within linear elasticity theory, as ν = (3K − 2G)/[2(3K + G)], where G is the shear modulus. This prediction is however inconsistent with experimental observations. While simulations could aid in reconciling this disparity, so far most computational studies concerning the VPT of hydrogels have overlooked the interactions between polymers and solvents and the link between thermodynamic and mechanical response.^24–27

Recent numerical works^28,29 have uncovered hyper-auxetic behavior of polymer networks in good solvent, hence mostly repulsive systems. This condition is met under a slight tension and by reduction of the crosslinker concentration c, leading to the occurrence of a thermodynamic criticality, that is referred to as hyper-auxetic transition (HAT).²⁹ However, in that case, the role played by the attraction and the influence of the deswelling phenomenon on the elastic properties remained unexplored. In the present work, we fill this gap by performing extensive computer simulations to investigate the occurrence of the HAT in polymer networks experiencing temperature-induced shrinking in a wide range of phase diagram and for several values of the crosslinker concentration. To this aim, we rely on a widespread bead-spring model of polymer networks^30,31 and we model implicitly the presence of the solvent via a solvophobic interaction³², that was previously shown to quantitatively reproduce the features of the networks across the VPT.³³ Our findings reveal the presence of an attraction-induced HAT consistent with the Ising universality class, which vanishes with increasing c. In addition, we are able to clearly distinguish the solvent-mediated network collapse driven by the VPT and the hyper-auxetic criticality, which at low enough c takes place in different regions of the phase diagram. This is in contrast to the VPT, which always occurs at a fixed temperature, that is dictated by the underlying monomer-solvent affinity. Our study thus establishes a clear relationship between thermodynamic and mechanical properties of polymer networks, paving the way to their fine control in experiments.

Methods

We simulate hydrogels using the well-established Kremer–Grest model for monomer–monomer interactions.^30,31 The network comprises polymer strands connected by four-valence crosslinkers. The majority of initial configurations are prepared by adding monomers at the equilibrium bond length in a diamond-like crystalline structure (ordered systems), while for one case we also perform self-assembly of patchy particles (disordered systems).^34–36 We implicitly account for the solvent by introducing an attractive term between all polymer beads in the network, known as the solvophobic potential,³² where the strength of the monomer–monomer attractive interactions is controlled by the solvophobic parameter parameter α, which plays the role of an effective temperature. We anticipate our findings to align with those of explicit solvent simulations, as demonstrated previously for microgel particles.³⁷ Additional details about the models can be found in the ESI.†

We perform molecular dynamics simulations in the isothermal–isobaric (NPT) ensemble of the hydrogels at different c, P and α values using the LAMMPS package,³⁸ and its Nosé–Hoover thermostat and barostat implementation, either in unperturbed conditions or under uniaxial strain. We choose a timestep of δt = 0.003 in reduced units. We then calculate the bulk modulus directly from volume V fluctuations as 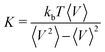, where k_b is the Boltzmann constant, while the Young modulus and the Poisson's ratio are computed through their definitions in strain-stress simulations 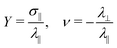, where σ_‖ and λ_‖,_⊥ are respectively the stress and the strain either parallel or perpendicular with respect to the deformation axis. We verified that including the tangential components of stress, as outlined in general linear elasticity theory (see, for instance,³⁹), does not affect our results, as expected for the homogeneous uniaxial extension of compressible solids at constant pressure. Equilibrium simulations consist in an equilibration run lasting for 10⁵ steps followed by a production run of 2 × 10⁷ steps. Strain–stress simulations consist in uniaxial deformations of different amounts, followed by equilibrium simulations spanning 10⁶ steps. We perform deformations in each of the three spatial dimensions in separate runs and then average the results. We observe an overall isotropic response of the system, which can be attributed to the large system size relative to its mesh size.⁴⁰ The time unit is defned as , where m is the monomer mass and ε sets the energy scale. In addition to the hydrogels, we also perform simulations in the isothermal-isochoric (NVT) ensemble of chains of various lengths interacting with the same potential, in order to unveil the role of the VPT.

Results

Hyper-auxeticity in solvent-mediated networks

We start by investigating the onset of auxetic behavior in the presence of attraction. For this purpose, we analyze the equation of state of the ordered system with 1% crosslinking, varying tension (or negative pressure −P) for different temperatures (quantified by the attraction strength α). The corresponding findings are reported in Fig. 1(a). Notably, as the effective attraction between particles increases, the change in the density of the network becomes more abrupt, leading to a discontinuous transition between two states, characterized by a low and a high density, respectively, when α > 0.5. Given the resemblance to a classical liquid–gas transition, we examine in more detail the system behavior at α = 0.5 for different pressures. Our analysis of the elastic moduli reveals a non-monotonic behavior of the bulk K and Young Y moduli as pressure changes, reported in the ESI† (Fig. S1), that reflects the behavior of the Poisson's ratio ν, shown in Fig. 1(b). First, ν decreases with decreasing P, reaching negative values, and then it increases again at larger tensions. Notably, these two behaviors are distinguished by a minimum where ν = −1, marking the mechanical stability limit.^41,42 We identify this condition as a hyper-auxetic point, that in addition to the mechanical instability, is characterized by huge density fluctuations, reminiscent of critical-like behavior. To quantify this behavior in the hypothesis of the occurrence of a second-order critical point, we follow the typical approach used to study gas–liquid phase separation in atomic and molecular systems.^43,44 We thus monitor the behavior of the characteristic order parameter M, defined as a combination of density and energy of the system, whose probability distribution reveals the presence of coexisting phases or critical behavior, even when structural differences are subtle or absent, as in liquids and polymeric systems.⁴³ Hence, M = ρ + se_X, where s is a mixing parameter and X identifies the type of energy employed in the analysis. In particular, we either employ the total energy e_t or the energy of the non-bonded particles e_nb only, as in our previous studies.^28,29 By examining the probability distribution of this order parameter rescaled to zero-mean and unitary variance Π(M), we compare it to the theoretical Ising behavior and find a good agreement for the critical temperature α^1%_HAT = 0.5064, between the predicted and calculated histograms with both observables, as shown in Fig. 1(c). We ascribe the differences between the results obtained with either e_t or e_nb to the intrinsic difficulties in finding these distributions in computational studies and to the weak correlation between energy and density for the considered low-density polymer network. Moreover, we observe a weaker correlation between the total energy and the density compared to the non-bonded energy. As a result, a larger mixing parameter s in modulus is required to reproduce the double-peak distribution. Our results thus suggest that the HAT transition observed in the presence of attraction is of the Ising universality class, deepening the analogy to a gas–liquid phase separation. We note in passing that the auxetic behavior observed here, originating from a thermodynamic transition, differs fundamentally from the geometric mechanisms typical of most auxetic metamaterials. This phenomenon is driven by the collective stretching of polymer chains under negative pressure, leading to a simultaneous and uniform entropy increase, as predicted by single-chain models within the Langevin approximation and discussed in detail in ref. 28.

Fig. 1 (a) Equation of state representing negative pressure P as a function of number density ρ for different attraction strengths α for the c = 1% system, obtained in equilibrium simulations. (b) Poisson's ratio ν as a function of P for the c = 1% diamond (blue circles) and 1%_diso (orange squares) systems at α = 0.5 and 0.425, repectively. (c) Normalized probability distribution Π(M) of the order parameter M = ρ + se_X, using either total energy e_t (blue line) or non-bonded particles energy e_nb (orange line), curves are rescaled to zero-mean and unitary variance. Results are for the c = 1% diamond network at α_HAT = 0.5064, reweighted to P = 9.319 × 10⁻⁴ with the mixing parameter s = −3.2, −0.8 for the two energies, respectively. The dashed gray line indicates Ising-like fluctuations.

To provide robustness to our findings, we perform a similar analysis also for the disordered c = 1% network (1%_diso). We thus evaluate the equation of state, reported in the ESI† (see Fig. S2), establishing the critical-like temperature α^1%diso_HAT = 0.425, that is notably distinct from the corresponding diamond network one. We then compute the elastic properties, confirming the occurrence of the HAT where ν = −1 at an intermediate pressure, as also shown in Fig. 1(b). Similarly to our previous studies at α = 0,^28,29 we thus confirm that the topology of the network does not play a role for the existence of the HAT, ruling out a possible geometric origin. In addition, we perform additional simulations of a larger diamond network with c = 1% to show that the present results are independent of system size. This is reported in the ESI,† where Fig. S3 shows the onset of criticality and the presence of the HAT also for the larger system.

Hyper-auxeticity and the volume phase transition

We now aim to compare these results with previous measurements on hydrogels, reporting the occurrence of auxetic behavior.¹⁰ Indeed, at first sight, it may appear that the hyper-auxetic transition (HAT) is merely an amplification of the negative Poisson's ratio observed in experiments.¹⁰ However, a more quantitative analysis is needed to verify this assumption, specifically examining the relationship between the two transitions: the HAT and the VPT. To address this issue, we report the hydrogel swelling curve for the c = 1% diamond network in Fig. 2, where the cubic root of volume V^1/3, analogous to an effective size of the hydrogel, is plotted as a function of α, which acts as an effective temperature, for different studied pressures. First, we focus on P = 0, that is the case representative of microgels in experiments, and observe that, as usual, the effective size smoothly decreases with increasing α, showing an inflection point at the VPT, namely at α_VPT ≃ 0.65.³⁴ However, upon decreasing P, we find that deswelling happens in two steps. At first, there is a decrease which progressively hits the HAT point at α_HAT ∼ 0.5, above which V^1/3 becomes discontinuous, as already observed in the pressure-density equation of state of Fig. 1(a). Representative snapshots of the hydrogel around the HAT are also reported in Fig. 2, showing the spinodal-like character of the transition. Indeed, the high density state is far from homogeneous and a further compaction only happens at larger α. This second deswelling step finally recovers the VPT behavior at high temperatures, where for all pressures the deswelling curves are virtually indistinguishable from one another. These results clearly indicate that the HAT driving the auxetic response of the system is a distinct phenomenon from the VPT.

Fig. 2 Top: Swelling curve for the c = 1% ordered network. Cubic root of the volume as a function of effective temperature α for different P as indicated in the legend. The vertical gray line indicates the location of the VPT. Bottom: Snapshots of the c = 1% system at P = −9.05 × 10⁻⁴ around the HAT, for α = 0.48 (left) and 0.56 (right), respectively. Monomers and crosslinkers are shown in violet and dark blue, respectively.

Influence of crosslinking on hyper-auxetic behavior

We now aim to unveil the HAT and VPT underlying nature and mutual interplay in greater detail. Let us first examine the occurrence of the HAT for various crosslinker concentrations. We explore diamond networks with c = 0.5, 1, 2, 3, 5 and 7.5% and investigate their elastic behavior in order to identify the conditions corresponding to the minimum Poisson's ratio ν_min. We first retrieve the corresponding pressure P_min, that, as expected, increases in absolute value for stiffer networks. Then, we calculate ν as a function of α for each network in order to determine whether the system is able to reach ν_min = −1 independently of crosslinker concentration. The results of this extensive analysis are summarized in Fig. 3(a), where only some of the investigated c values are reported to improve visualization. Our findings reveal the occurrence of hyper-auxeticity at a given α_HAT, associated to ν_min ≈ −1, up to crosslinker concentrations c ≃ 3%, while networks with higher c are still found to exhibit a minimum in ν, at a characteristic temperature that we call α_min, which however does not reach the HAT condition any longer, since ν_min > −1. Indeed, in analogy with previous results obtained for α = 0²⁸ and for microgels,⁴⁵ we find that ν_min increases with the stiffness of the network, approaching the HAT condition only at sufficiently low c. It is now interesting to look at the α_HAT and α_min dependence on crosslinker concentration, which is reported in Fig. 3(b). It is evident that α_HAT continuously turn to α_min, progressively increasing with the system connectivity and finally tending to α_VPT ∼ 0.65 at high c. Hence, while the HAT terminates at a finite c value, we provide evidence that its echo, characterized by the presence of a minimum in ν at even larger c, converges to the temperature of the VPT as crosslinker concentration increases. This is why a minimum in ν is detected even in microgels,^12,45,46 a feature here confirmed for hydrogels at P = 0, as also shown for the c = 3% network in Fig. 3(a). Interestingly, we previously detected the existence of the HAT at α = 0 in the c = 0.35% network²⁸ in the absence of attraction. Although in that case we found comparable phenomenology with the present investigation, here we notice that the two phenomena appear to be continuous from the behavior of α_HAT in Fig. 3(b). However, the underlying order parameter in that case was found to be strictly ρ + e_nb, so that differences between the attractive and repulsive case need to be further investigated.

Fig. 3 HAT and VPT. (a) Poisson's ratio as a function of effective temperature α for ordered systems with c = 1, 2, 3, 5, 7.5% and corresponding P = 9.25 × 10⁻⁴, 3.5 × 10⁻³, 7.9 × 10⁻³, 1.8 × 10⁻², 4.25 × 10⁻². The horizontal line indicates the hyper-auxetic threshold, when ν_min = −1, while the vertical line marks α_VPT, i.e., the occurrence of the VPT. (b) Top: effective temperature of chains phase separation α_c as a function of chain length l; bottom: HAT effective temperature, corresponding to the minimum in ν, as a function of c. Filled circles indicate HAT points where ν = −1 (α_HAT), while stars represent points where ν ≳ −1 (α_min). Both curves tend to the VPT effective temperature α_VPT (horizontal line), as c and l increase.

Relation to phase separation in polymer chains

Having discussed the HAT, we now address the underlying nature of the VPT. We thus consider simple polymer chains featuring the same interactions as the hydrogels and evaluate the occurrence of gas (chain poor)–liquid (chain rich) phase separation at a given critical temperature α_c, as detailed in the ESI† (see Fig. S4), for systems of different chain lengths l from monomers (l = 1) to very long chains (l ∼ 500). We find that, as expected, the various systems phase separate at a temperature which depends on l. In particular, a larger temperature is needed for monomers and small chains, while connectivity enhances the tendency to phase separate, thus lowering the critical temperature as l increases. Remarkably, for long enough chains, i.e. l ≳ 100, we find that phase separation occurs at a constant value α_c ∼ α_VPT. Given the presence of very long chains in any microgel or hydrogel realization, either in experiments or in simulations, this finding explains the almost universal value of α_VPT and of the corresponding temperature in experiments, that occurs independently of c for PNIPAM-based systems in the absence of co-monomers. This is simply due to the solvophobic interactions between polymer and water, which drives the phase separation and is mitigated by the presence of crosslinks within the network, which transforms the critical-like behavior into a smooth and reversible deswelling process.

Conclusions

In summary, the present study elucidates the multifaceted relationship between critical swelling, hyper-auxeticity, and volume phase transition in thermoresponsive polymer networks. Through extensive numerical simulations in equilibrium and under uniaxial deformation, we demonstrate that the hyper-auxetic transition represents a clearly distinct phenomenon from the VPT, that is essentially driven by the phase separation of polymer chains, echoing the coil-to-globule transition of single chains. By analyzing the swelling curves of the hydrogels, we are indeed able to discern a distinct two-step process at slightly negative pressures, whereby an initial compression leads to the onset of a hyper-auxetic point before a further volume decrease takes place, toward the generic VPT regime. Furthermore, our investigation spanning a wide range of crosslinker concentrations uncovers hyper-auxetic behavior up to a finite c ≃ 3%, while higher crosslinker concentrations exhibit increasing stiffness without reaching the mechanical instability. The convergence of the hyper-auxetic transition with the VPT as system connectivity increases underscores the complex nature of polymer network behavior. The present study provides a useful framework for the understanding of previous and future experimental observations thanks to the establishment of a clear link between thermodynamic and mechanical properties of polymer networks. Specifically, we anticipate that our predictions could be experimentally validated through mechanical analysis of low-crosslinked polymer networks subjected to progressively increasing tensile stress at varying temperature. By clarifying the conditions under which the HAT occurs, the present results call for further experimental and computational exploration of elastic and thermodynamic properties of polymer networks, both at negative and at positive pressures, paving the way for the development of novel materials with controlled auxetic properties.

Author contributions

AN and EZ designed research, performed research and wrote the paper.

Data availability

Data for this article, are available at Zenodo at https://doi.org/10.5281/zenodo.15348839.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Alberto Fernandez-Nieves and José Ruiz-Franco for insightful discussions. We gratefully acknowledge the CINECA award under the ISCRA initiative, for the availability of high-performance computing resources and support. We also acknowledge funding from the European Union - NextGenerationEU, through the ICSC-Centro Nazionale di Ricerca in High-Performance Computing, Big Data and Quantum Computing-(Grant No. CN00000013, CUP J93C22000540006, PNRR Investimento M4.C2.1.4).

Notes and references

1. Polymer gels, ed. D. DeRossi, K. Kajiwara, Y. Osada and A. Yamauchi, Springer, New York, NY, 1991.
2. Polymeric and self assembled hydrogels, ed. X. J. Loh and O. A. Scherman, Royal Society of Chemistry, Cambridge, England, 2012.
3. M. C. Koetting, J. T. Peters, S. D. Steichen and N. A. Peppas, Mater. Sci. Eng., R, 2015, 93, 1–49.
4. A. Onuki, Theory of phase transition in polymer gels, Springer, Berlin Heidelberg, 1993, pp 63–121.
5. M. S. Dimitriyev, Y.-W. Chang, P. M. Goldbart and A. Fernández-Nieves, Nano Fut., 2019, 3, 042001.
6. T. Tanaka, S.-T. Sun, Y. Hirokawa, S. Katayama, J. Kucera, Y. Hirose and T. Amiya, Nature, 1987, 325, 796–798.
7. E. S. Matsuo and T. Tanaka, Nature, 1992, 358, 482–485.
8. Y.-W. Chang, M. S. Dimitriyev, A. Souslov, S. V. Nikolov, S. M. Marquez, A. Alexeev, P. M. Goldbart and A. Fernández-Nieves, Phys. Rev. E, 2018, 98, 020501.
9. M. Shibayama, Soft Matter, 2025, 21, 1995–2009.
10. S. Hirotsu, J. Chem. Phys., 1991, 94, 3949–3957.
11. C. Li, Z. Hu and Y. Li, Phys. Rev. E, 1993, 48, 603–606.
12. N. Boon and P. Schurtenberger, Phys. Chem. Chem. Phys., 2017, 19, 23740–23746.
13. R. Lakes, Science, 1987, 235, 1038–1040.
14. K. E. Evans, Endeavour, 1991, 15, 170–174.
15. S. Xinchun and R. S. Lakes, Phys. Status Solidi B, 2007, 244, 807.
16. G. N. Greaves, A. L. Greer, R. S. Lakes and T. Rouxel, Nat. Mater., 2011, 10, 823–837.
17. Z. G. Nicolaou and A. E. Motter, Nat. Mater., 2012, 11, 608–613.
18. M. Ciarletta, M. Fabrizio and V. Tibullo, Math. Models Methods Appl. Sci., 2013, 37, 2864–2871.
19. P. M. Pigowski, J. W. Narojczyk, K. W. Wojciechowski and K. V. Tretiakov, Soft Matt., 2017, 13, 7916–7921.
20. D. R. Reid, N. Pashine, J. M. Wozniak, H. M. Jaeger, A. J. Liu, S. R. Nagel and J. J. de Pablo, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E1384–E1390.
21. M. Hanifpour, C. F. Petersen, M. J. Alava and S. Zapperi, Eur. Phys. J. B, 2018, 91, 1–8.
22. T. Tanaka, S. Ishiwata and C. Ishimoto, Phys. Rev. Lett., 1977, 38, 771–774.
23. T. Tanaka, Phys. Rev. Lett., 1978, 40, 820–823.
24. F. A. Escobedo and J. J. de Pablo, J. Chem. Phys., 1996, 104, 4788–4801.
25. F. A. Escobedo and J. J. de Pablo, J. Chem. Phys., 1997, 106, 793–810.
26. F. Escobedo and J. De Pablo, Mol. Phys., 1997, 90, 437–443.
27. P. K. Jha, J. W. Zwanikken, F. A. Detcheverry, J. J. de Pablo and M. Olvera de la Cruz, Soft Matter, 2011, 7, 5965.
28. A. Ninarello, J. Ruiz-Franco and E. Zaccarelli, Nat. Commun., 2022, 13, 527.
29. A. Ninarello, J. Ruiz-Franco and E. Zaccarelli, J. Chem. Phys., 2023, 159, 23.
30. G. S. Grest and K. Kremer, Phys. Rev. A, 1986, 33, 3628–3631.
31. G. S. Grest and K. Kremer, Macromolecules, 1990, 23, 4994–5000.
32. T. Soddemann, B. Dünweg and K. Kremer, Eur. Phys. J. E, 2001, 6, 409–419.
33. A. Ninarello, J. J. Crassous, D. Paloli, F. Camerin, N. Gnan, L. Rovigatti, P. Schurtenberger and E. Zaccarelli, Macromolecules, 2019, 52, 7584–7592.
34. N. Gnan, L. Rovigatti, M. Bergman and E. Zaccarelli, Macromolecules, 2017, 50, 8777–8786.
35. V. Sorichetti, V. Hugouvieux and W. Kob, Macromolecules, 2021, 54, 8575–8589.
36. V. Sorichetti, A. Ninarello, J. Ruiz-Franco, V. Hugouvieux, E. Zaccarelli, C. Micheletti, W. Kob and L. Rovigatti, J. Chem. Phys., 2023, 158, 7.
37. F. Camerin, N. Gnan, L. Rovigatti and E. Zaccarelli, Sci. Rep., 2018, 8, 14426.
38. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171.
39. L. D. Landau, L. P. Pitaevskii, E. M. Lifshitz and A. M. Kosevich, Theory of elasticity, Butterworth-Heinemann, Oxford, England, 1984, 3rd edn.
40. M. J. Grill, J. Kernes, V. M. Slepukhin, W. A. Wall and A. J. Levine, Soft Matter, 2021, 17, 10223–10241.
41. G. W. Milton, J. Mech. Phys. Solids, 1992, 40, 1105–1137.
42. R. Lakes, Adv. Mater., 1993, 5, 293–296.
43. N. B. Wilding and A. D. Bruce, J. Phys.: Condens. Matter, 1992, 4, 3087–3108.
44. P. G. Debenedetti, F. Sciortino and G. H. Zerze, Science, 2020, 369, 289–292.
45. L. Rovigatti, N. Gnan, A. Ninarello and E. Zaccarelli, Macromolecules, 2019, 52, 4895–4906.
46. P. Voudouris, D. Florea, P. van der Schoot and H. M. Wyss, Soft Matter, 2013, 9, 7158.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00251f

---