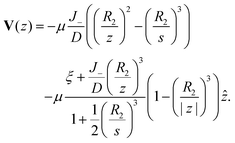DOI:
10.1039/D5SM00270B
(Paper)
Soft Matter, 2025, Advance Article
Blockage effects in the chemotaxis of diffusiophoretic particles
Received
13th March 2025
, Accepted 9th May 2025
First published on 9th May 2025
Abstract
Transport mechanisms at the micro- and nano-scale play an essential role in regulating intracellular organization. Recent work indicates that directed motion of constituents inside cells can emerge through diffusiophoretic transport, in which colloidal particles move under the influence of chemical gradients. Here, we examine how blockers—passive or actively consuming—reshape those gradients and thereby influence the motion of diffusiophoretic particles. By combining analytical solutions with finite element simulations, we first show that a single blocker can distort a background gradient enough to create or eliminate stagnation points, significantly modifying particle transport. We then introduce a second, explicitly sized blocker at one of these stagnation points and measure how its finite radius alters the diffusiophoretic velocity field for a test particle. Even moderate changes in the second blockers size can cause noticeable shifts in the substrate distribution, highlighting the importance of accounting for explicit particle radii under crowded or consumption-driven conditions. Our findings underscore that subtle geometric variations—such as the radii and positions of two or more blockers—can profoundly affect diffusiophoretic motion, providing a more complete picture of how blocking and crowding phenomena shape intracellular transport.
1. Introduction
Intracellular structure and dynamics are crucial for function and regulation in biological systems. Micro- and nano-scale transport mechanisms play an important role in the spatiotemporal organization of cellular sub-components. For instance, motor proteins and self-organizing metabolic systems are well known. Transport of intracellular matter by purely physical means has been less explored, though recent studies reveal that diffusiophoretic mechanisms can arise from metabolic inhomogeneities or ATP-consuming protein systems. In particular, theoretical work has shown how metabolite gradients may impart nonmotor forces on nanoscale complexes,1 while experiments on an ATPase system demonstrate purely friction-mediated cargo transport in the absence of dedicated motors.2 These findings underscore that nonequilibrium processes beyond canonical motor-based pathways can substantially shape intracellular organization.
Micro-scale self-propelled objects has been a rapidly expanding field in soft matter physics due to wide-ranging applications in cell biology and medicine. Numerous studies have shown that surface distortions generated by harnessing external energy can lead to self-propulsion of robotic microswimmers.3–5 Equally intriguing is the directed self-motion of particles in a bath of passive solute, where interfacial phoretic effects play a role: examples include charge gradients (electrophoresis),6 thermal gradients (thermophoresis),7 surface tension gradients (Marangoni effects),8,9 and concentration gradients (diffusiophoresis).10–12 This paper focuses on chemotaxis of bacterial microcompartments (BMCs) driven by non-ionic diffusiophoresis and hydrodynamics.
Anderson et al.13,14 originally proposed harnessing diffusiophoretic transport in solutions with substrate concentration gradients. However, in a simple background gradient, particles can only move in a single direction and rate determined by the local gradient. If, however, the particle itself creates the concentration gradient, the velocity can be tuned independently of any external substrate profile. This self-generated mechanism, called “self-diffusiophoresis”, was extensively studied by Golestanian et al.15,16 One common realization is Janus particles, featuring a catalytic coating on one hemisphere, which results in an osmotic pressure imbalance that propels the particle. Experiments by Howse et al.17 provided early evidence, followed by extensive confirmations,10–12,18–21 and numerous applications ranging from drug delivery to chemotaxis in bacterial microcompartments.22 Recent theoretical developments have shown that phoretic Janus particles can exhibit complex dynamics such as trapped states, spirals, and orbital motion under radial concentration gradients, indicating intricate interactions between chemical gradients and particle surface properties.23 Furthermore, the spatial and temporal optimization of solute sources and sinks has been demonstrated to enable precise control of diffusiophoretic banding, underscoring the potential for sophisticated manipulation of colloidal distributions.24
Recent research has refined our understanding of diffusiophoresis, with investigations into particle size and shape,11,16 new theoretical models,12,17 and a variety of possible applications: targeted drug delivery,25 separations, purification, and environmental remediation.26,27
Bacterial microcompartments (BMCs) are proteinaceous shells that encapsulate enzymes for specific metabolic pathways. They can respond to changing conditions (e.g., pH, temperature, substrate availability). One such response mechanism is diffusiophoresis, where substrate gradients induce the movement of BMCs. Recent work22 suggests this is crucial for chemotaxis in BMCs, with potential biotechnological and medical applications.
In this context, BMCs can migrate toward regions of higher substrate concentration for their metabolic pathways. The substrate-BMC surface interaction causes local depletion of substrate, leading to a chemical potential gradient and net fluid flow that drives the BMC toward higher concentrations. For instance, Steinkühler et al.28 showed that Salmonella enterica BMCs move up gradients of propanediol, an important substrate for the propendiol utitlization (Pdu) pathway. In experiments, they were able to fabricate Pdus with and without active enzymes that consumed propanediol. The non-consuming Pdus aggregate, while Pdus with consumption help sustain motion by preventing large-scale aggregation.
Besides fundamental interest, controlling BMC chemotaxis has broad implications. For example, in biotechnology, steering BMCs toward abundant substrate could optimize metabolic pathways. In medical or environmental scenarios, engineered BMCs might degrade toxins or pollutants by navigating toward higher concentrations of these harmful compounds.
In many intracellular settings, substrate gradients can arise from background sources or from local consumption, and each scenario has been studied individually. However, the impact of partial or complete “blockage”—defined here as the obstruction of substrate flux by intermediate cellular structures, such as larger BMCs or organelles situated between the chemical gradient source and the particle of interest—has received less attention. In this work, we develop a theoretical framework that explicitly accounts for blockage in both consuming and non-consuming cases. Our findings reveal that even passive blockers can significantly reshape local gradients, leading to substantial alterations in the transport behavior of diffusiophoretic particles.
This article is organized as follows. First, we describe the coupled background-consumption system, emphasizing how blockers or obstacles influence the concentration field in a crowded intracellular context. We then present the diffusion, hydrodynamic, and reaction models used for both analytical and numerical calculations. A detailed analysis of the concentration field and velocity of a test BMC in the presence of both passive and active blockers is provided. Finally, we discuss broader implications of these blocking effects for intracellular transport.
2. Setup and modeling
2.1. Setup and reaction model
As shown in Fig. 1, spherical particles of varying radii approximate enzymatic BMCs dispersed in a spherical vesicle of radius 50R, where R = 60 nm is the smallest BMC used in simulations. The system is immersed in an aqueous solvent of density ρ = 103 kg m−3 and viscosity η = 8.9 × 10−4 Pa s, at temperature T = 300 K. Substrate molecules (e.g., 1,2-propanediol) are introduced from the +z side with a boundary concentration c0 + ξz at the vesicle surface, where c0 = 50 mol m−3, and diffuse with coefficient D = 2 × 10−10 m2 s−1. The substrate-BMC interaction potential U is assumed to be attractive. Phoretic mobility is set to μ = −2.64 × 10−37 m5 s−1. A concise list of these parameter values used throughout the calculations and simulations is provided in Table 1.
 |
| | Fig. 1 Schematics of the setup for a central BMC with radius R2 = 5R = 300 nm, vesicle size 50R = 3 μm, and zero consumption J− = 0. | |
Table 1 Parameters used in the model
| Parameter |
Value |
Description |
| R |
60 nm |
Smallest BMC radius |
| s |
50R |
Vesicle radius |
| ρ |
103 kg m−3 |
Solvent density |
| c0 |
10 mol m−3 |
Initial concentration |
| D |
2 × 10−10 m2 s−1 |
Diffusion coefficient |
| η |
8.9 × 10−4 Pa s |
Viscosity |
| T |
300 K |
Temperature |
| μ |
− 2.64 × 10−37 m5 s−1 |
Diffusiophoretic mobility |
| J− |
1 × 10−2 mol m−2 s−1 |
Concentration flux |
| ξ |
10 × 106 mol m−4 |
Concentration gradient |
When BMCs are active, they consume substrate via a flux J− = −J−![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) . For passive BMCs, J− = 0.
. For passive BMCs, J− = 0.
2.2. Diffusion model
We use the continuity equation and Ficks law:16| |
∂tc + ∇·J = 0, J = −D∇c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − − ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βDc∇U βDc∇U![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + + ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cv, cv,
| (1) |
where v is the substrate (fluid) velocity, D = 2 × 10−10 m2 s−1 its diffusivity, and β = 1/(kBT). In steady state, ∂tc = 0, so| |
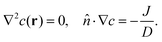 | (2) |
We note that for small Péclet number, the advective term cv can be neglected in simulations.
2.3. Hydrodynamic model
Since BMCs are at the micrometer scale with negligible inertia, the flow is in the Stokes regime.16 We also assume the fluid is incompressible:| | |
η∇2v = ρ∇U + ∇p, ∇·v = 0,
| (3) |
where η = 8.9 × 10−4 Pas and ρ = 1000 kg m−3. Combining the diffusive and hydrodynamic equations yields the “slip” velocity—the fluid velocity in the region where the substrate interacts with the particle—of vS = −μ∇||c(rS). This velocity depends on the component of the concentration gradient parallel to the surface and the diffusiophoretic mobility16| |
 | (4) |
where h is a coordinate in the interaction layer that represents the distance from the particle surface. This expression for vS assumes no-slip at the surface of the particle, as well as small curvature effects in the interaction layer.16 As described in Section 2.1, we chose μ = −2.64 × 10−37 m5 s−1 based on experiments done with Salmonella enterica BMCs in Steinkühler et al.,22 noting that a negative μ corresponds to an attractive substrate-BMC potential.
2.4. Translational diffusiophoretic velocity
In the low Reynolds number regime, net drift arises by balancing the overall Stokes drag with the contributions from surface phoretic slip:29| |
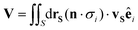 | (5) |
For a sphere of radius R, 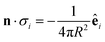 , so
, so
| |
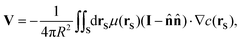 | (6) |
where we are integrating over the surface of the BMC.
3. Results and discussion
3.1. Linear concentration gradient with blockage but no consumption
As shown in Fig. 2, we consider a spherical vesicle of radius s containing a BMC of radius R1 as well as a spherical obstructing object situated at the geocenter of the vesicle (referred to as “blocker” henceforth) of radius R2. The blocker could be either another BMC, or some other organelles within the cell. To further simplify the problem, we assume the following:
 |
| | Fig. 2 Schematics of a linear concentration gradient ξ without consumption. A BMC (radius R1, mobility μ1 = μ) is blocked by a larger object (radius R2) at the center. | |
• The BMC can only be along one diameter line of the vesicle. We then set the spherical coordinate system to have the θ = 0/θ = π axis be along that line. The BMC is |z| away from the geocenter of the blocker (and thus the center of the coordinates).
• Since we are studying the blocking effects of the blocker on the BMC, we assume that the BMC is not blocking itself and can be treated as a point particle in the system (only as a “test” particle).
The substrate is introduced in such a way that the concentration on the surface of the vesicle to be c0 + ξs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, where c0 is some external reference concentration, and ξ the linear concentration gradient. We can then relate the steady-state concentration profile c(r) = c(r,θ) with the flux by the Laplace's equation
θ, where c0 is some external reference concentration, and ξ the linear concentration gradient. We can then relate the steady-state concentration profile c(r) = c(r,θ) with the flux by the Laplace's equation
and the following boundary conditions
| |
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ·∇c(R2,θ) = 0 ·∇c(R2,θ) = 0
| (8) |
| |
c(s,θ) =c0 + ξs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. θ.
| (9) |
The general solution could be expanded in terms of Legendre polynomials
| |
 | (10) |
where
l is a non-negative integer. When
l = 0, we have −
B0R2−2 = 0, so
B0 = 0. When
l > 0, we obtain
| |
 | (11) |
Substituting
(11) into
(9) and
(10) gives
| |
 | (12) |
Then we have
| |
 | (14) |
Therefore
| |
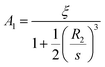 | (15) |
And the concentration profile is given as
| |
 | (16) |
We then arrive at the concentration profile along the
z-axis
| |
 | (17) |
and the diffusiophoretic transport velocity of the BMC along the
z-axis of
| |
 | (18) |
The result shows larger blocker size increases blockage effects. When
R2 → 0 we recover the classic no-blockage linear concentration gradient results
c(
r,
θ) =
c0 +
ξr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif)
cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ and
V(
z) = −
ξμẑ.
3.2. Computational model
To compare to our analytical results, we solved for c(z) and V(z) using finite element methods (COMSOL Multiphysics 6.0). One important aspect of accurately modeling diffusiophoretic transport in a crowded intracellular environment is the correct treatment of the boundary conditions at each surface. In particular, we must capture how substrate flux interacts with objects that either block diffusion or actively consume substrate. We achieve this by imposing a Neumann boundary condition for passive “blockers” with zero flux, and an assigned consumption flux for “active” blockers. Meanwhile, the test BMC experiences phoretic slip determined by the local substrate gradient. Handling these interactions consistently requires that each domain boundary—vesicle, blocker, and BMC—be explicitly included in the finite element mesh. By refining the mesh around these boundaries, we ensure that the sharp gradients forming near active or blocking surfaces are resolved, which is crucial for matching the analytical predictions in simpler geometries. Moreover, because we treat each boundary distinctly, the same numerical approach can extend to scenarios where multiple blockers have varying radii or consumption rates, making the model highly flexible for future studies.
In Fig. 3, we examine the steady-state concentration profiles along the z-axis for various blocker radii in the absence of consumption. Without a blocker (R2 = 0), the profile is purely linear, reflecting the imposed background gradient. Introducing a blocker creates a distortion in the concentration field: substrate accumulation occurs on the side of the blocker facing the source (positive z), while depletion appears on the side facing away. Although these concentration deviations are modest in magnitude, they are more pronounced for larger blocker radii, suggesting that the blocker size amplifies local gradient perturbations.
 |
| | Fig. 3 Comparison between analytical and numerical data of the concentration profile along z axis without consumption for various blocker radii. The lines end at the surface of the blocker, since the concentration is not defined within the boundaries of the blocker. The lines at the extreme values of z represent concentration profiles for the largest blocker, and each successive concentration lines corresponds to decreasing radius. | |
These gradient distortions have a major impact on particle motion, as shown in Fig. 4. Since the diffusiophoretic velocity is proportional to the surface gradient of the concentration, even small changes near the blocker significantly alter the motion of the test BMC. Specifically, the test particles velocity sharply decreases as it approaches the blocker surface, ultimately approaching zero at contact due to the no-flux boundary condition. This slowing effect occurs on both sides of the blocker, and its spatial profile becomes increasingly sharp with larger blocker sizes: smaller blockers induce a more gradual dropoff, while larger blockers localize the effect near the surface. Thus, the blocker not only deforms the background gradient but also attenuates transport over a broader spatial region. Notably, the theoretical predictions match the finite element simulations closely, confirming the validity of the analytical model even under varying blocker sizes.
 |
| | Fig. 4 Comparison of analytical and numerical data on the diffusio- phoretic transport velocity profile of tester BMC along z axis without consumption for various blocker radii. | |
3.2.1. Linear concentration gradient with blockage and consumption. With all other conditions remaining unchanged in Fig. 2, we add a consumption flux J− = −J−![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) on the BMC surface. Our equations then take the form
on the BMC surface. Our equations then take the form| |
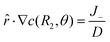 | (20) |
| | |
c(s,θ) = c0 + ξscosθ
| (21) |
which could also be expanded in terms of Legendre polynomials like (10).When l = 0
| |
 | (22) |
| |
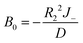 | (23) |
| |
 | (24) |
(10) and (21) give
| |
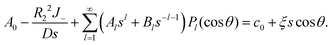 | (25) |
Similar to the case without consumption, only l = 0 and 1 remain. Solving the remaining undetermined coefficients gives
| |
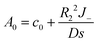 | (26) |
| |
 | (27) |
Also, from
(24),
| |
 | (28) |
Hence,
| |
 | (29) |
| |
 | (30) |
Then, the concentration profile takes the form
| |
 | (31) |
(for
c(
z) replace
r by |
z| and
r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif)
cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ by
z), and the diffusiophoretic transport velocity takes the form
| |
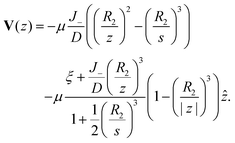 | (32) |
As
J− → 0, we recover the no-consumption result. Larger
R2 and
J− intensify blocking.
In Fig. 5–7, we extend the analysis to include substrate consumption at the surface of the blocker. Fig. 5 shows that the consumption flux creates a strong local depletion zone around the blocker, dramatically altering the concentration field compared to the no-consumption case. In the passive case (Fig. 3), we observed an accumulation of substrate on the front side of the blocker (facing the source) and depletion on the rear side. By contrast, with consumption active, we now see depletion on both the front and rear sides of the blocker relative to the 0R case. This outcome makes sense physically: local substrate consumption around the blocker surface reduces concentration everywhere nearby, regardless of orientation relative to the background gradient.
 |
| | Fig. 5 Cross-sectional concentration in units of mol m−3 (under consumption flux J−, for R2 = 0, 5R, 10R, 15R, 20R, and 30R, from top left to bottom right). | |
 |
| | Fig. 6 Concentration profile along z axis, passing through the geometric center of blocker, with consumption flux J− = 10−2 mol m−2 s−1. | |
 |
| | Fig. 7 Diffusiophoretic transport velocity profile of tester BMC along z axis, passing through the geometric center of blocker, with consumption flux J− = 10−2 mol m−2 s−1. | |
However, the consumption-driven case also introduces a qualitatively new feature: the emergence of a negative concentration gradient near the blocker surface. In the passive (non-consuming) case, even in depleted regions, the concentration gradient merely flattened (approaching zero slope) but never actually reversed. In contrast, under consumption, the depletion becomes strong enough that the local concentration decreases with increasing distance from the blocker along the source direction. This reversal of the concentration gradient causes the diffusiophoretic slip velocity to change sign, leading directly to the formation of a stagnation point where particle motion halts.
The corresponding transport effects are shown in Fig. 6 and 7. In Fig. 6, the substrate concentration lines now bend sharply inward toward the blocker, reflecting the strong consumption sink. As a result, the diffusiophoretic velocity profile in 7 shows a dramatic reversal: particle velocities first increase toward the source-facing side, then cross zero near the blocker and reverse direction. Stagnation appears prominently for smaller blocker sizes, such as 5R, but disappears for larger blockers. For blocker radii above approximately 15R, the local depletion is insufficient to fully invert the gradient, and thus no stagnation point forms along the z-axis.
Based on these observations, a central blocker radius of 5R was chosen for the two-blocker configuration studied in Section 3.2. This radius places the second BMC close to the stagnation point, enabling a clean test of how finite-size effects perturb the delicate local balance between background gradients and consumption-driven depletion. In contrast, for larger blockers where no stagnation forms, placing a second BMC would be less physically meaningful. Thus, the choice of 5R ensures that the system is maximally sensitive to the interplay between gradient distortion, substrate consumption, and finite-size blocking effects.
3.3. Two-blocker system: variation in BMC radius and impact on test BMC
In this section, we extend our investigation by introducing a second BMC whose finite radius is explicitly taken into account, thereby moving beyond the point-particle approximation. To recap, we continue to work under a linear background concentration gradient ξ along the z axis, with a central “blocker” of radius 5R actively consuming substrate at flux J−. As in previous sections, this consumption produces a stagnation point behind the blocker, which marks a balance between the background gradient and the consumption-induced gradients.
We first identify the stagnation point that forms for a blocker of radius 5R. At this specific point on the z axis, the net flux of substrate in the absence of other particles cancels out, giving zero velocity for a test particle. Since we examine solutions in the steady state, we place a second, consuming BMC at the point where its position will not change with time. Unlike the test particle considered in earlier sections, this second BMC is assigned a finite, variable radius (e.g., R, 2R, etc.) in order to capture additional surface effects that may arise from realistic BMC sizes. The setup is shown in Fig. 8.
 |
| | Fig. 8 Two blocker setup for computation, with central blocker radius 5R and secondary blocker radius 2.5R. The flow lines represent the steady state velocity of the fluid inside the vesicle, which is coupled to the concentration of the substrate. | |
With both the central blocker (radius 5R) and the second BMC (at the stagnation point, with explicit radius) now present, we introduce a test particle to measure how the local gradients and flows are altered. We sample the test particles velocity at various positions along the z axis, ranging from well upstream of the blocker (close to the background source) to well downstream. As the second BMCs radius increases, its surface further distorts the substrate distribution originally shaped by the blocker. By comparing test-particle velocities across these different radii, we can quantify how an explicitly sized BMC modifies the competing gradients in a consumption-driven environment.
Fig. 9 compares the test particles velocity v along the z-axis for several radii of a second BMC, explicitly placed at the previously identified stagnation point for a blocker of radius 5R. In contrast to the point-particle assumption, this second BMC now occupies a finite volume—ranging here from 0.5R up to 5R. We keep the central blocker fixed at radius 5R with a substrate consumption flux J−, maintaining the same overall geometry but allowing the second BMC to more strongly or weakly reshape local gradients depending on its size. As shown in the left portion of the figure (negative z), increasing the second BMCs radius tends to smooth the large negative dip in velocity near the blockers consumption zone, indicating that a larger body at the stagnation point can partially redistribute substrate flux before it reaches the test particle.
 |
| | Fig. 9 Test BMC diffusiophoretic transport velocity V(z) for two-blocker system. The central blocker has radius 5R and the second blocker varies in radius. Both blockers have consumption rate J− = 10−2 mol m−2 s−1. The near-vertical lines close to z = 0 represent the velocity profile for a test particle in between the two blockers, where the consumption of both blockers causes a steep gradient in concentration. | |
Moving beyond z = 0, the velocity becomes positive and eventually decays, but the curves reflect distinct pathways through which the test particle crosses the transition region influenced by both the blocker and the second BMC. In general, a larger second BMC more strongly perturbs the gradient: it can block or redirect flux lines around its finite surface, leading to modest differences in the velocity profile relative to smaller-radius cases. The net effect is that explicit particle sizes add another layer of crowding complexity, exemplifying how intracellular structures of varying radii can jointly dictate the directions and magnitudes of diffusiophoretic transport under simultaneous background gradient and consumption.
4. Conclusions
We have analyzed blocking effects in chemotactic systems influenced by both background gradients and enzymatic consumption in bacterial microcompartments. Our fully analytical model, validated by numerical simulations, captures the key features of these interactions, including stagnation points that shift with blocker size and consumption rate. These findings provide insights into how local substrate gradients can be significantly reshaped by actively consuming obstacles, deepening our understanding of intracellular transport in crowded or complex environments.
Beyond the immediate comparison with analytical solutions, our numerical framework illuminates how local geometric features of the intracellular landscape can drive emergent behaviors. In realistic cell environments, organelles, cytoskeletal filaments, and other compartments can create spatially complex barriers or partial obstructions to substrate diffusion, effectively sculpting chemical gradients. Our results suggest that even modest blocker sizes, when strategically located relative to a substrate source, can substantially redirect flow lines, leading to local “hot spots” or “shadows” of substrate concentration. This altered distribution may enable otherwise passive compartments to exhibit directed motion or accumulation patterns purely by virtue of how they reshape the local environment. Consequently, such findings have broad relevance for understanding how non-motor transport pathways might coordinate macromolecular organization inside cells or within synthetic vesicular systems, highlighting the potential for controlling microscale transport by simply introducing carefully placed blockers or tuned consumption rates.
Interestingly, our theoretical findings—in which the introduction of enzymatic consumption generates new stagnation points that can promote localized clustering—stand in apparent contrast to experimental observations by Steinkühler et al.28 In their work, BMCs with active enzymatic activity actually reduced large-scale aggregations, rather than causing them. This discrepancy suggests that while our model accurately captures how local gradients are altered by consumption, it may not include other important effects that can disrupt or prevent clustering in a real cellular environment. Possibilities include hydrodynamic coupling, additional regulatory factors, or highly dynamic substrate turnover rates that differ from the simplified steady-state flux used here.
Consequently, the presence of stagnation points from balancing a background gradient with a self-induced (consumption) gradient may not, by itself, explain the reduced clustering observed experimentally. Future refinements to the model could incorporate time-varying substrate fields, complex fluid flows, or other cellular processes that interfere with the formation or persistence of stagnation points. Such extended models might reconcile our theoretical predictions with the experimental evidence showing that enzymatic activity can help disperse BMCs, ultimately revealing more nuanced mechanisms behind organization and transport in crowded intracellular environments.
Our theoretical findings suggest several experimental routes for validation and further exploration. Experiments could be designed using microfluidic devices or synthetic vesicle systems, where blockers—represented by inert particles or enzymatically active microcompartments—are strategically positioned within a chemically controlled environment. Measuring the local substrate concentrations and the resulting trajectories of smaller bacterial microcompartments (BMCs) would provide direct insights into blockage-induced alterations of diffusiophoretic transport. Additionally, systematically varying blocker size and substrate consumption rates in these controlled setups could experimentally confirm the presence and movement of predicted stagnation points. These experiments would not only test the validity of our model but also refine understanding of diffusiophoretic behavior in crowded biological environments.
Data availability
Data for this article, including COMSOL files and Python code used to generate plots are available on Github at https://github.com/maf6763/chemotaxis_data.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work has been supported by the Department of Energy (DOE), Office of Basic Energy Sciences under Contract DEFG02-08ER46539. We thank Neha Kamat for useful discussions.
Notes and references
- R. P. Sear, Phys. Rev. Lett., 2019, 122, 128101 CrossRef CAS.
- B. Ramm, A. Goychuk, A. Khmelinskaia, P. Blumhardt, H. Eto, K. A. Ganzinger, E. Frey and P. Schwille, Nat. Phys., 2021, 17, 850–858 Search PubMed.
- W. Hu, G. Z. Lum, M. Mastrangeli and M. Sitti, Nature, 2018, 554, 81–85 CrossRef CAS PubMed.
- H. Yang, B. S. Yeow, Z. Li, K. Li, T.-H. Chang, L. Jing, Y. Li, J. S. Ho, H. Ren and P.-Y. Chen, Sci. Rob., 2019, 4, 33 Search PubMed.
- C. Li, G. C. Lau, H. Yuan, A. Aggarwal, V. L. Dominguez, S. Liu, H. Sai, L. C. Palmer, N. A. Sather, T. J. Pearson, D. E. Freedman, P. K. Amiri, M. O. de la Cruz and S. I. Stupp, Sci. Rob., 2020, 5, 49 Search PubMed.
- A. Nourhani, V. H. Crespi, P. E. Lammert and A. Borhan, Phys. Fluids, 2015, 27, 092002 CrossRef.
- L. Baraban, R. Streubel, D. Makarov, L. Han, D. Karnaushenko, O. G. Schmidt and G. Cuniberti, ACS Nano, 2013, 7, 1360–1367 CrossRef CAS.
- Z. Mao, G. Shimamoto and S. Maeda, Colloids Surf., A, 2021, 608, 125561 CrossRef CAS.
- M.-H. Hsieh, H.-J. Wei, K.-H. Chen, H.-C. Wang, C.-H. Yu, T.-H. Lu, Y. Chang and H.-W. Sung, Biomaterials, 2021, 271, 120748 CrossRef CAS PubMed.
- X. Zheng, B. ten Hagen, A. Kaiser, M. Wu, H. Cui, Z. Silber-Li and H. Löwen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 032304 CrossRef.
- M. Wu, H. Zhang, X. Zheng and H. Cui, AIP Adv., 2014, 4, 031326 CrossRef.
- F. Yang, S. Qian, Y. Zhao and R. Qiao, Langmuir, 2016, 32, 5580–5592 CrossRef CAS.
- J. L. Anderson, Annu. Rev. Fluid Mech., 1989, 21, 61–99 CrossRef.
- J. L. Anderson and D. C. Prieve, Langmuir, 1991, 7, 403–406 CrossRef CAS.
- R. Golestanian, T. B. Liverpool and A. Ajdari, Phys. Rev. Lett., 2005, 94, 220801 CrossRef.
- R. Golestanian, T. B. Liverpool and A. Ajdari, New J. Phys., 2007, 9, 126 CrossRef.
- J. R. Howse, R. A. L. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Phys. Rev. Lett., 2007, 99, 048102 CrossRef PubMed.
- B. Sabass and U. Seifert, J. Chem. Phys., 2012, 136, 064508 CrossRef PubMed.
- N. Sharifi-Mood, J. Koplik and C. Maldarelli, Phys. Fluids, 2013, 25, 012001 CrossRef.
- J. de Graaf, G. Rempfer and C. Holm, IEEE Trans. NanoBiosci., 2015, 14, 272–288 Search PubMed.
- A. Mozaffari, N. Sharifi-Mood, J. Koplik and C. Maldarelli, Phys. Fluids, 2016, 28, 053107 CrossRef.
- J. Steinkühler, C. H. Abrahamson, J. Agudo-Canalejo, R. Golestanian, D. Tullman-Ercek and N. P. Kamat, bioRxiv, 2022, preprint, N/A Search PubMed.
- P. Bayati and S. A. Mallory, ACS Nano, 2024, 18, 23047–23057 CrossRef CAS PubMed.
- R. R. Raj, C. W. Shields and A. Gupta, Soft Matter, 2023, 19, 892–904 RSC.
- D. Zhang, S. Liu, J. Guan and F. Mou, Front. Bioeng. Biotechnol., 2022, 10, 1002171 CrossRef.
- R. Guha, X. Shang, A. L. Zydney, D. Velegol and M. Kumar, J. Membr. Sci., 2015, 479, 67–76 CrossRef CAS.
- A. Kar, R. Guha, N. Dani, D. Velegol and M. Kumar, Langmuir, 2014, 30, 793–799 CrossRef CAS PubMed.
- J. Steinkühler, C. H. Abrahamson, J. Agudo-Canalejo, R. Golestanian, D. Tullman-Ercek and N. P. Kamat, bioRxiv, 2022, preprint, N/A Search PubMed.
- H. A. Stone and A. D. T. Samuel, Phys. Rev. Lett., 1996, 77, 4102–4104 CrossRef CAS.
Footnote |
| † These authors contributed equally to this work. |
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article b,
Ahis Shresthac and
Monica Olvera de la Cruz
b,
Ahis Shresthac and
Monica Olvera de la Cruz abcd
abcd

![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) . For passive BMCs, J− = 0.
. For passive BMCs, J− = 0.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
− ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βDc∇U
βDc∇U![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+ ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cv,
cv,
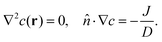

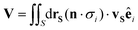
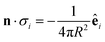 , so
, so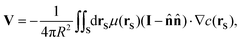

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, where c0 is some external reference concentration, and ξ the linear concentration gradient. We can then relate the steady-state concentration profile c(r) = c(r,θ) with the flux by the Laplace's equation
θ, where c0 is some external reference concentration, and ξ the linear concentration gradient. We can then relate the steady-state concentration profile c(r) = c(r,θ) with the flux by the Laplace's equation![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ·∇c(R2,θ) = 0
·∇c(R2,θ) = 0
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ.
θ.




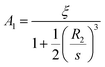



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and V(z) = −ξμẑ.
θ and V(z) = −ξμẑ.

![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) on the BMC surface. Our equations then take the form
on the BMC surface. Our equations then take the form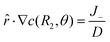

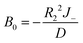

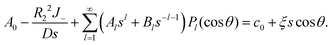
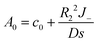





![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ by z), and the diffusiophoretic transport velocity takes the form
θ by z), and the diffusiophoretic transport velocity takes the form