 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Interaction of grain morphology and intergranular friction on grain packing†
Samuel
Martin
 a and
Marcia A.
Cooper
a and
Marcia A.
Cooper
 *b
*b
aJ. Mike Walker ‘66 Department of Mechanical Engineering, Texas A&M University, 3123 TAMU, USA
bJ. Mike Walker ‘66 Department of Mechanical Engineering, Department of Materials Science and Engineering, Affiliated, Texas A&M University, College Station, TX 77845, USA. E-mail: macoope@tamu.edu
First published on 30th May 2025
Abstract
The bulk density of loosely packed grains is determined by grain morphology and the intergranular friction coefficient. Creating simulated grain packings with realistic packing densities is the first step in performing predictions of granular material behavior at higher compaction stresses. Our novel approach performs jamming simulations at near-zero pressure where the surface properties are decoupled from the elastic properties to explore the interaction between grain morphology and intergranular friction. We use bonded particle model (BPM) grain representations with different subparticle resolutions to vary their morphological properties. Our investigation uses both regular- and irregular-shaped BPM grains to develop a relationship between grain morphology, intergranular friction, and the jamming limit that applies to simulated and physical grains. The relationship prescribes a friction coefficient for use in simulations of grain packing that considers the effect of morphology.
1 Introduction
Energy transport occurs across the contact networks in granular systems and is critically influenced by intergranular phenomena. Contact networks form when ensembles of material grains are compressed or packed together under small forces (e.g. gravity)—transitioning from a flowing state to a rigid state with an irregular mesostructure and emergent bulk properties. In this disordered jammed state, the mesostructure of the material grains has a packing fraction that can only be increased by grain rearrangement with additional force application. The bulk properties emerge from the force chain structure1 and characterize the mesostructure strength,2–4 fracture behavior,5–9 conductivity,10 and many other phenomena of interest in granular systems.The bulk density at which a disordered ensemble of material grains jam is sensitive only to their external surface characteristics. In this near-zero pressure regime, the intergranular forces and grain deformation are negligible and the grains act as rigid bodies. Laboratory experiments and computational simulations show numerous grain morphological properties influence the jamming limit, including grain size distribution,11 grain shapes,12–16 surface roughness,17–20 and friction coefficients.15,21–23 When seeking relationships of grain packing behavior it is common to employ concepts of hard-core excluded volume—the amount of space in the vicinity of a grain inaccessible to other grains.24–28 For an ensemble of grains, the excluded volume depends on their shape and arrangement resulting in an increasing excluded volume with decreasing grain sphericity.27 However, while the concept of excluded volumes has enabled rigorous mathematical treatments of convex grain packings, and can be numerically applied to concave grains,29 models that relate grain packing fraction to grain shape and the other two important factors in physical granular material systems—grain surface roughness and friction—remain an outstanding challenge.30
For convex grain shapes with friction, Yuan et al.24 showed that in the limit of infinite friction, the jamming limit is a function of excluded volume, and for finite friction, the granular packing fraction can be normalized such that it is a function of friction only. While this relationship from Yuan et al.24 results in accurate predictions of the jamming packing fraction, it is restricted to convex grains due to the use of a mean field approach relating packing fraction at infinite friction through a fitting function to a dimensionless, orientation-averaged excluded volume. This approach was not suitable for representing dimer grains with concave regions. For both physical and simulated grains, concave regions at the external boundary are common and inherently present in current granular materials research, e.g., entangled granular media.31
Depending on the scale of the concave regions on a grain surface, characterizations of surface roughness or shape can become convolved. In general, our ability to fully characterize grain surface characteristics are limited by current imaging and X-ray technology capabilities—0.1–10 micron voxel or pixel resolution—which is insufficient to capture the full spectrum of self-affine surface irregularities. There are numerous methods of DEM grain discretization that seek to precisely recreate the grain geometry, such as spherical harmonic functions,32–36 level set algorithms,37 and sphere clumping.38,39 Simulations using such methods can resolve small length scales at equivalent computational costs, which allows them to achieve much smaller differences in grain morphology. Recognizing the inherent discrepancies in reconstructing all scales of physical grains, Mollon et al.40 considered the interplay of surface roughness and friction for simulating the triaxial compression of physical grains. They utilize Fourier shape descriptors based on 2D projections from high-resolution images of physical grains to reconstruct grains in a hybrid discrete element method (DEM) using polygons. By limiting the number of Fourier shape descriptors, the grains become smoother which—under certain conditions that were beyond the jamming limit—can be replaced by increasing friction.
In contrast, a common method to reconstruct physical grains is using clumps—which may be connected by finite strength bonds as in the case of bonded particle models (BPM). BPM clumps (representing a material grain) formed from an ensemble of non-overlapping spherical elements (referred to as subparticles) have a surface roughness based on the relative subparticle size and grain size. Several studies have shown BPM grains have lower jamming limits than laboratory experiments of the same material.7,9 Clemmer et al.20 demonstrated that the jamming limit of BPM spheres varies significantly with surface roughness. They found that spherical BPM grains containing about 5000 frictionless spherical subparticles jammed at packing fractions of 0.584 to 0.598, depending on subparticle packing methodology, compared to the expected value for spheres of 0.64.12
Our motivation stems from the current challenges that exist in modeling the compression of granular materials: (1) experimental methods to image physical grains are inherently linked to the resolution limits of the method (e.g., scanning electron microscope, optical microscopes, particle size analyzer, micro-computed X-ray tomography), (2) computational grain reconstruction is subject to the typical tradeoffs between feature resolution, computational time, and numerical precision, and (3) no study has attempted to link the three critical grain characteristics of shape, surface roughness, friction to grain packing behavior. We hypothesize that a relationship exists between these three grain morphological descriptors which are best studied within the disordered jamming regime since the elastic behavior of the grains is decoupled from the intergranular behaviors. If a physical system can be simulated in the low-pressure regime with imperfect grain reconstructions and an effective friction parameter, it suggests a better initial condition for higher pressure simulations than current methods7 that produce packings in the absence of friction.
To investigate the interaction of shape, surface roughness, and friction on disordered jamming packing fraction, BPM simulations using regular-shaped and irregular-shaped grains reconstructed from data collected by typical granular material characterization methods are performed. Laboratory measurements of the jamming limit demonstrate how experimental and computational data can be considered similarly. First, Section 2 presents laboratory measurements of the jamming packing fraction of silica sand, which is selected as an exemplar material system having irregular grain shapes and is widely used in geotechnics literature.8,41–43 Sections 3–5 describe the process to simulate grain jamming using reconstructions of different grain types. Section 3 discusses the creation of libraries of BPM grains with regular- and irregular-shaped grain envelopes. Two methods of subparticle packing are used for regular-shaped grains to obtain comparatively rough and smooth surfaces. The morphological properties of all BPM grains and our physical silica sand grains are computed in Section 4. Then jamming simulations are performed as described in Section 5 and the impact of grain morphological properties on the jamming limit is discussed in Section 6. All simulations were performed using LAMMPS 3 Nov 202244 on a local computer with an AMD Ryzen 3945WX processor running Ubuntu 22.04 as well as the Texas A&M High Performance Research Computing cluster Grace.
Finally, a statistical examination of the simulated and laboratory measurements is performed in Section 7 to correlate the jamming packing fraction with grain morphology and intergranular friction. A relationship is developed that accounts for the change in morphological properties of the BPM grain representation by decreasing the friction coefficient, thereby establishing a tool to improve computational outcomes when seeking a direct comparison to real material behaviors. Even the jamming behavior of experimental data can be correlated to physical grain morphology using this relationship.
2 Jamming in physical grains with irregular shapes
Laboratory experiments measured the jamming packing fraction of silica sand (CAS# 14808-60-7, purchased from GFS Chemicals). The particle size distributions (PSD) for two lots of silica sand (Fig. 1) were measured using a LA-960V2 Horiba Particle Size Analyzer (LA-960S, RRID: SCR_022202). Both PSDs were equivalent within 1%, ranged in size from 152 μm to 777 μm, and had a mean size of 343 μm.The laboratory jamming experiments are compliant with ASTM D7481-18 Standard (Method A)45 which included measuring a small mass of particles with a scale, pouring the particles into a container, measuring the height of the particle system, and calculating the volume of the jammed particle system. The experimental setup, illustrated in Fig. 2, included a 35.10 mm tall by 31.20 mm inner diameter borosilicate glass cylinder that was open at the top and closed at the bottom by a 3D printed polylactic acid (PLA) base mounted to an optical table. The diameter of the glass cylinder was measured using a Neiko 01417A caliper with an accuracy of ±0.2 mm. The silica sand sample was weighed using a Mettler Toledo LA84E balance with an accuracy of ±0.0001 g and poured into the glass container using a funnel. The funnel was maneuvered during pouring to ensure the top surface of the silica sand was as level as possible.
Images of the sample perpendicular to the axis of the cylinder were captured with a Basler acA2440-75um camera and a Basler C23-2518-5M lens with a 3.18 mm lens tube as shown in Fig. 3. The camera has an image size of 2048 × 2448 pixels, resulting in a field of view of 31.36 mm by 37.49 mm with an optical density of 64.9 px per mm at 104 mm from the end of the lens. The bed height is calculated by post-processing images of the poured silica sand using the Canny operation from the OpenCV Python library.46 The found edges are annotated in Fig. 3. The height of the top surface was computed by averaging the height of the lower and upper edges of the uneven top surface. This optical measurement of particle bed height resulted in a volume measurement precision (less than ±0.005 cm3) which exceeded the ASTM standard recommended measurement precision (±0.6 cm3).
 | ||
| Fig. 3 (a) Representative image from experiments of Table 1. (b) Results of edge finding. Red lines correspond to the glass and sample edges and are labeled with their corresponding distance from the bottom of the glass container. The images have an optical density of 64.9 px mm−1. | ||
Five replicates were performed (Table 1) with an average measured density of 1.567 ± 0.033 g cm−3. Contributions to uncertainty include the identification of the top particle surface, vessel diameter, and sample mass. The average jamming packing fraction of ϕJ = 0.591 was calculated assuming a solid density of 2.65 g cm−3 for silica.47 This measured value is used again in Section 6.
| Trial | Mass (g) | Density (g cm−3) |
|---|---|---|
| 1 | 29.2085 | 1.532 ± 0.032 |
| 2 | 30.2597 | 1.577 ± 0.053 |
| 3 | 29.4492 | 1.586 ± 0.033 |
| 4 | 25.9499 | 1.588 ± 0.030 |
| 5 | 27.8265 | 1.551 ± 0.019 |
| Average | 28.5388 | 1.567 ± 0.033 |
3 Assembling BPM grain libraries
The following sections describe the process to create four different types of computationally reconstructed grains. Reconstructing BPM grains begins by defining their overall shape with regular- and irregular-shaped envelopes. The grain envelopes are then filled with subparticles that are bonded together to represent a continuum material. Section 3.1 describes the process of defining the bounding grain envelopes. Section 3.2 defines the subparticle contact behavior which applies to the subparticle packing of the grain envelopes and later, the subparticle interactions between contacting grains. Section 3.3 packs and bonds the subparticles within the grain envelope. Finally, libraries for the regular- and irregular-shaped grains are defined in Section 3.5.3.1 Defining BPM grain shape
The process of creating BPM grains begins by establishing their grain envelopes. Spheres were selected as the regular-shaped grain envelope as they have been extensively studied in the literature.11,12,20,48 The regular-shaped grain envelope is produced using the geometric equation for a sphere with the desired radius.The irregular-shaped envelopes are extracted from micro-CT images of silica sand using a North Star Imaging X50 μCT with a voxel resolution of 13 μm for an nominal imaging resolution of 26.4 pixels per mean grain diameter (Fig. 1). The micro-CT image stack included 250 images of an ensemble of silica sand grains confined in a 0.64-cm diameter Kapton® tube. A single image from the image stack is shown in Fig. 4a. Grain envelopes are extracted in 3D from the entire 250-image micro-CT tiff stack but 2D images are provided here for method description. First, individual grains are identified and extracted from the image stack using the scikit-image library in Python.49 The extraction process began by thresholding the images to identify pixels representing material, Fig. 4b and then applying a distance transformation to label individual grains, Fig. 4c. A minimum separation distance of 9 pixels—117 μm which is slightly smaller than the minimum grain diameter—between peaks avoided assigning multiple labels to highly irregular grains. Finally, a watershed operation assigned each remaining pixel of material to the corresponding grain label, Fig. 4d. The pixels within individual grain envelopes are isolated and saved to data files. Analysis of the micro-CT tiff stack resulted in 638 unique grain envelopes for the irregular-shaped grains.
3.2 Subparticle contact model
In preparation for packing the grain envelopes with subparticles and (later) packing a volume with grains, the contact model governing BPM grain subparticle interactions is defined.50–52 In this work, the Hertzian contact model (eqn (1) and (2)) determines the Hertz contact force Fhz from the normal and tangential forces that arise from the relative motion of contacting subparticles.11,17,21 | (1) |
| Fthz ≤ μFnhz | (2) |
The resulting normal force Fnhz between two contacting subparticles with radii ri and rj depends on the effective normal stiffness ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) n and their overlap δ along unit vector nij; whereas the resulting tangential force Fthz depends on the effective tangential stiffness
n and their overlap δ along unit vector nij; whereas the resulting tangential force Fthz depends on the effective tangential stiffness ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) t and the tangential displacement vector Δst.52,53 The normal and tangential stiffnesses are related to the macroscale material properties E and ν.52 Additionally, this model limits the tangential force between subparticles to less than or equal to the product of the normal force between subparticles and the coefficient of friction, μ. Damping forces are determined from a global viscous damping coefficient of γ = 0.001 N m s−1, the effective mass between two subparticles (sp)—equal to msp for our monodisperse subparticles with volume and diameter Vsp = πdsp3/6, and density ρsp = 0.001 g cm−3—and their normal and tangential velocity vectors, vn and vt respectively.
t and the tangential displacement vector Δst.52,53 The normal and tangential stiffnesses are related to the macroscale material properties E and ν.52 Additionally, this model limits the tangential force between subparticles to less than or equal to the product of the normal force between subparticles and the coefficient of friction, μ. Damping forces are determined from a global viscous damping coefficient of γ = 0.001 N m s−1, the effective mass between two subparticles (sp)—equal to msp for our monodisperse subparticles with volume and diameter Vsp = πdsp3/6, and density ρsp = 0.001 g cm−3—and their normal and tangential velocity vectors, vn and vt respectively.
3.3 Constructing a BPM grain
Each regular- and irregular-shaped BPM grain is constructed by deleting subparticles within a large initial subparticle packing that are external to the superimposed grain envelope.54 First, large packings of frictionless monodisperse spherical subparticles are created.11 The subparticles are randomly placed in a periodic domain and isostatically compressed (nominally 10−4% strain per increment) under low pressure until the particles jam which occurred within a specified maximum number of time steps (Fig. 5a and b). Pressures along the three coordinate directions are monitored every 5 increments of strain and used to guide the incremental domain compression in each coordinate direction. Once the system jams, the slight overlapping of particles push the others away and we observe small pressure oscillations about the final value that decay in response to the global damping. This process is consistent with a slow compression from a dilute state (similar to Method I55). The compressive pressure is p/E = 10−5 where E = 10 GPa represents an appropriate order of magnitude elastic modulus for the physical material.56 Subparticle interactions are controlled by the contact model (Section 3.2 with μ = 0).Once packed, subparticles with their centroid external to a superimposed grain envelope are deleted as illustrated in Fig. 5c for a regular-shaped grain. Fig. 6 illustrates the process for an irregular-shaped grain where the grain envelope retains a pixelated shape from the micro-CT segmentation whereas the final BPM grain resembles a clump of monodisperse subparticles. The grain solid volume fraction ϕG is estimated from the mean-field subparticle packing (spp) solid volume fraction—the volume filled by nspp subparticles each with volume Vsp divided by the domain volume Vspp (eqn (3)).
 | (3) |
 | ||
| Fig. 6 Illustration of the process to create an irregular-shaped BPM grain. The 3D process is illustrated with 2D projections. (a) A 2D cross-section of an irregular-shaped grain envelope extracted from the labeled envelopes in Fig. 4d. (b) Cross-section of packed subparticles of dsp = 0.100 within the envelope. The boundaries of the envelope are shown in red. Subparticles that appear to be outside of the envelope are centered in the grain at a different slice located either into or out of the page. (c) 3D rendering of the entire irregular-shaped BPM grain. | ||
For the regular-shaped grains, the external boundary was further smoothed by the damped oscillation of a spherical wall of stiffness E around the packed subparticles.20 This smoothing step rearranges the subparticles from the rough external boundary shown in Fig. 7a to the smoother external boundary shown in Fig. 7b. Since the subparticle packing is modified in this smoothing process, eqn (3) is no longer appropriate and a (new) maximum value of ϕG is calculated by Monte Carlo integration using 106 randomly placed integration points within a spherical region.
 | ||
| Fig. 7 (a) Image of a regular-shaped (rough) BPM grain. (b) Image of a regular-shaped (rough) BPM grain. | ||
3.4 Assigning BPM grain bond parameters
Next, the subparticles are bonded with an average coordination number of 12 using the LAMMPS bpm_rotational bond style and saved to a molecule file. Fig. 5d shows a representative bond network which was assigned microscale bond properties using the relationships published by Martin and Cooper54 and the desired macroscale properties E and ν. In this work, the BPM grains are effectively rigid and therefore the macroscale values of E and ν represent an appropriate order of magnitude representing the physical material.563.5 Assembling a library of BPM grains
Individual BPM grains are constructed with varying parameters of subparticle diameter dsp and grain shape as listed in Table 2 forming a library of each BPM grain type. The regular-shaped (rough) and regular-shaped (smooth) libraries at each value of dsp contained a single BPM grain. The range of dsp is intended to capture a range of grain resolutions while keeping computational times reasonable. The irregular-shaped libraries at each value of dsp initially contained 638 unique BPM grains (Section 3.1) which were only created with the two highest resolutions studied, dsp ≤ 0.100.| d sp | BPM grain types | ||
|---|---|---|---|
| Irregular | Regular (rough) | Regular (smooth) | |
| 0.083 | ■ | ■ | ■ |
| 0.100 | ■ | ■ | ■ |
| 0.125 | ■ | □ | |
| 0.143 | ■ | □ | |
| 0.167 | ■ | □ | |
| 0.200 | ■ | ■ | |
The subparticle diameter dsp is a unitless value that is proportional to the mean grain diameter as illustrated in Fig. 8a for a regular-shaped spherical grain and in Fig. 8b for an irregular-shaped grain. Using the dump image command in LAMMPS, the mean diameter of the BPM grains is determined from equivalent circle diameter D2D for a 2D projection at the maximum cross-sectional area. D2D (with units of subparticle diameter) is scaled57 by the ratio of the physical grain Feret diameter as determined from the micro-CT image stack (units of μm) and the reconstructed grain Feret diameter (units of subparticle diameter) resulting in a BPM grain mean diameter DG in physical units ready for comparison to the experimental particle size distribution.
| DG = D2D(LG/L2D) | (4) |
The PSD is calculated from the 683 BPM grains (dsp = 0.100) of Section 3.1 and is plotted with the experimentally measured PSD of the physical silica sand grains in Fig. 1. The narrower PSD of the irregular-shaped BPM grains compared to the physical silica sand grains may be caused by accidental mergers of some small grains and splitting of very large grains in the segmentation process (Fig. 4). To better represent the experimental PSD, BPM grains were removed from the irregular-shaped library until the root mean squared error (RMSE) between the irregular-shaped BPM grain library and experimental PSDs was less than 3%. This cut-off was selected to allow for a larger number of grains in irregular-shaped library despite the limited number in the tails of the PSD. The resulting library of irregular-shaped BPM grains contains 154 unique grains (i.e., unique shapes associated with the corresponding grain envelopes) with good agreement to the silica sand PSD in Fig. 1. Furthermore, a random sampling (duplicates were allowed) of as few as 30 BPM grains consistently matched the experimental PSD with an RMSE of less than 5%.
In the following sections, the jamming simulations are performed using 50 grains from the 154 unique grain envelopes (having a subparticle diameter of dsp). Despite the relatively small number of grains, the corresponding number of total subparticles in the simulation domain is approximately 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 subparticles for 50 regular-shaped (smooth) grains with dsp = 0.083 and approximately 32
000 subparticles for 50 regular-shaped (smooth) grains with dsp = 0.083 and approximately 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 subparticles for 50 regular-shaped (rough) grains with dsp = 0.10.
000 subparticles for 50 regular-shaped (rough) grains with dsp = 0.10.
4 Morphological characterization of grains
The process to characterize the morphological properties of the BPM grains and the physical silica sand grains is now presented. Characterizing grain morphology across scales is complex—especially if also considering the diagnostic resolution limitations when observing physical grains and the numerical costs associated with computational grain reconstruction. While excluded volumes have been shown to correlate grain shape and friction with packing behavior, the concept of excluded volumes generally does not apply to small-scale surface roughness and the calculation of excluded volume becomes increasingly difficult thereby requiring numerical methods for moderately complex particle shapes with random orientations.25,26 Alternatively, Fourier descriptors can capture features across a wide spectrum of scales and have provided important insights on the scale of grain features needed to capture interactions between roughness and friction—but the technique has not yet been applied to 3D images of grains (e.g., micro-CT image stacks).40,58 In our work, developing an optimum set of morphological descriptors is outside the scope as we investigate the interaction of shape and friction using both physical and computationally reconstructed grains. The chosen descriptors should be readily accessible by general practitioners for practical application to both simulated and physical grains. Thus, it is straightforward to employ three commonly used morphological properties which are computed using 2D projections of 3D grains:23,59–64 surface roughness, χRH, sphericity, χS, and roundness, χRD.4.1 2D projections for analysis
Each BPM grain in the libraries of Table 2 and the 20 physical silica sand grains are characterized from their 2D projected images (Fig. 9a and b). Images of the BPM grain 2D projections of Section 3.5 (at maximum cross-sectional area) are exported from LAMMPS with a resolution of 1920 pixels × 1080 pixels and a zoom factor of 2 for an average resolution of 900 pixels per grain diameter (or alternatively reported by the corresponding scaling of pixels to subparticle diameter px/dsp). Images of the physical silica sand grains (Fig. 9b) were captured on an Olympus DXS500 optical microscope (DXS500, RRID: SCR_022202) with bright field illumination. Since the micro-CT-imaged grains had a relatively low resolution (26.4 pixels per mean grain diameter), higher resolution microscope images enabled equivalent image resolution with the BPM grain analysis—however, the collected 2D projection may not correspond to the grain orientation with maximum cross sectional area. The microscope image projections were 1194 × 1194 pixels and used 416–693× magnifications for a nominal resolution of 700 pixels per grain diameter.The next sections describe the steps similarly performed on the BPM grain and physical grain projected images (both in units of image pixels) to quantify roughness, sphericity, and roundness using the automated approach of Zheng et al.64 (Fig. 10). The process starts by calculating the grain centroid and grain surface contour using the Canny command in OpenCV46 (Fig. 9c).
4.2 Roughness
The surface roughness is calculated with eqn (5) and applies to the smallest length scale of our examined morphological properties.64 It depends on the distance y from the centroid to point k, which lies on the grain surface s (green contour of Fig. 10a) or the fitted grain surface f (blue contour of Fig. 10a), for all![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) points along the surfaces.
points along the surfaces. | (5) |
The surface contours were determined using the lowess function (a non-parametric locally weighted scatter plot smoother) from Statsmodels65 in Python. The smoothing function fitted a surface to the radial distance from the centroid as a function of angle θ using an averaging distance of D2D/2. This averaging distance produced contours that preserved the features of the irregular-shaped grains while preventing individual subparticles from being treated as corners in the regular-shaped grains when dsp ≤ 0.100. This step is necessary as otherwise χRH would be zero and each subparticle along the grain surface would be added later to the calculation of roundness.
4.3 Sphericity
While numerous definitions of sphericity have been proposed over the past century,59,66–68 sphericity simply describes the shape on the length scale of the entire grain and refers to how closely the grain resembles a sphere.59 The definition of sphericity proposed by Kuo et al.69 is given in eqn (6) and depends on the equivalent circle diameter D2D (eqn (4)), and the diameter of the minimum circumscribing circle D2D,c (red circle of Fig. 10b). | (6) |
4.4 Roundness
Roundness characterizes the shape of the grain corners and describes the shape at an intermediate length scale. The formula proposed by Wadell59 appears in eqn (7) and is the ratio of the average corner radius,![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) , to the radius of the maximum inscribing circle, D2D,i/2 (green circle of Fig. 10b).
, to the radius of the maximum inscribing circle, D2D,i/2 (green circle of Fig. 10b). | (7) |
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) is given by eqn (8) and involves a summation over all corner radii Ck observed in the grain projection.
is given by eqn (8) and involves a summation over all corner radii Ck observed in the grain projection. | (8) |
Using the previously determined maximum inscribing circle, roundness circles are fit64 to the corners of the fitted surface using a threshold of 0.5 pixels for corner identification (Fig. 10c). Due to the numerical nature of this fitting process, there is an error tolerance of 2% for fitting roundness circles, as recommended in Zheng et al.64 This error tolerance allows χRD values slightly greater than 1 to be computed (but they are rounded to 1).
4.5 Summary
The morphological properties for each BPM grain type of Table 2 and the physical silica sand grains appear in Tables 3–5. The morphological properties reported for the regularly shaped grain types are from the single BPM grain in the libraries at each dsp. The morphological properties reported for the irregularly-shaped grain types are an average over all 154 unique BPM grains in the libraries at each dsp. For both regular- and irregular-shaped BPM grains, increasing dsp (decreasing subgrain resolution) increases roughness. Additionally, increasing dsp (and increasing roughness) correlates with a decrease in roundness—except for the irregular-shaped BPM grains where roundness appears nominally constant over the limited range of dsp. Sphericity exhibits a non-monotonic but nominally decreasing trend with increasing dsp. The decrease in both χS and χRD for the regular-shaped (rough) BPM grains indicates they are deviating from an ellipsoid shape with unity aspect ratio.59| d sp | χ S | χ RD | χ RH | μ | ϕ J |
|---|---|---|---|---|---|
| a Data for dsp = 0.050 is from Clemmer et al.20 | |||||
| 0.200 | 0.878 | 0.617 | 0.055 | 0.00 | 0.624 ± 0.007 |
| 0.20 | 0.551 ± 0.014 | ||||
| 0.40 | 0.518 ± 0.010 | ||||
| 0.167 | 0.856 | 0.793 | 0.046 | 0.00 | 0.600 ± 0.009 |
| 0.20 | 0.528 ± 0.016 | ||||
| 0.143 | 0.913 | 0.799 | 0.043 | 0.00 | 0.596 ± 0.009 |
| 0.20 | 0.522 ± 0.009 | ||||
| 0.40 | 0.505 ± 0.006 | ||||
| 0.125 | 0.959 | 0.832 | 0.033 | 0.00 | 0.548 ± 0.015 |
| 0.20 | 0.485 ± 0.018 | ||||
| 0.40 | 0.488 ± 0.010 | ||||
| 0.100 | 0.966 | 0.923 | 0.030 | 0.00 | 0.571 ± 0.007 |
| 0.20 | 0.537 ± 0.014 | ||||
| 0.40 | 0.516 ± 0.011 | ||||
| 0.083 | 0.979 | 1.000 | 0.020 | 0.00 | 0.570 ± 0.007 |
| 0.20 | 0.534 ± 0.017 | ||||
| 0.40 | 0.513 ± 0.007 | ||||
| 0.050a | 0.993 | 1.000 | 0.007 | 0.00 | 0.584 |
| d sp | χ S | χ RD | χ RH | μ | ϕ J |
|---|---|---|---|---|---|
| a Data for dsp = 0.050 is from Clemmer et al.20 | |||||
| 0.200 | 0.968 | 0.829 | 0.036 | 0.00 | 0.620 ± 0.005 |
| 0.20 | 0.550 ± 0.009 | ||||
| 0.40 | 0.526 ± 0.015 | ||||
| 0.167 | 0.955 | 0.941 | 0.036 | 0.00 | 0.618 ± 0.001 |
| 0.143 | 0.982 | 1.000 | 0.028 | 0.00 | 0.601 ± 0.005 |
| 0.125 | 0.962 | 1.000 | 0.022 | 0.00 | 0.597 ± 0.004 |
| 0.100 | 0.993 | 1.000 | 0.016 | 0.00 | 0.596 ± 0.009 |
| 0.20 | 0.553 ± 0.007 | ||||
| 0.40 | 0.548 ± 0.014 | ||||
| 0.083 | 0.991 | 1.000 | 0.013 | 0.00 | 0.619 ± 0.009 |
| 0.20 | 0.580 ± 0.007 | ||||
| 0.40 | 0.565 ± 0.010 | ||||
| 0.050a | 0.999 | 1.000 | 0.003 | 0.00 | 0.599 |
| d sp | χ S | χ RD | χ RH | μ | ϕ J |
|---|---|---|---|---|---|
| 0.100 | 0.688 | 0.642 | 0.069 | 0.00 | 0.509 ± 0.010 |
| 0.20 | 0.461 ± 0.011 | ||||
| 0.40 | 0.435 ± 0.010 | ||||
| 0.083 | 0.684 | 0.641 | 0.060 | 0.00 | 0.504 ± 0.012 |
| 0.20 | 0.445 ± 0.005 | ||||
| 0.40 | 0.422 ± 0.013 | ||||
| Exp. | 0.723 | 0.652 | 0.033 | 0.138‡ | 0.591 ± 0.012 |
5 Simulating BPM grain jamming
Grain jamming simulations were performed using 50 grains extracted from the BPM grain libraries and considering intergranular friction μ in the contact model of Section 3.2 as indicated in Table 2. Fig. 11 illustrates a representative initial and jammed configuration of irregular-shaped BPM grains. The grains are packed as described in Section 3.3 except with a different stopping criteria. Jamming is achieved when the total kinetic energy of the grain packing (gp) is less than ngpρspVsp × 10−18 J, where ngp is the total number of subparticles in all the grains within the grain packing domain Vgp. This criteria ensured the total system kinetic energy contributed negligible pressure in comparison to the bond and subparticle compression. No statistically significant variations in ϕJ were observed with a stopping criteria of 10−13 J or less.The jamming packing fraction ϕJ relates the density of the grain packing ρgp to the maximum density of the subparticle packing ρspp from eqn (3).
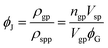 | (9) |
This method does not require the explicit calculation of the grain volume from the original grain envelope as the effect of dsp is studied and the possibility of double counting subparticles between contacting grains is eliminated. The rigid subparticle arrangements and relative subparticle size assigned to each BPM grain affect the resulting morphological parameters, that along with the subparticle friction parameter, determine the resulting grain packing fraction.
Prior literature has shown that periodic boundary conditions with as few as 6470 and 5071 grains constitute an representative element volume for elastic property determination. Since elastic properties are dependent on the particle arrangement, our simulation domains using 50 grains can be considered suitable. To minimize the possibility that jammed packing fraction correlates to the initial subparticle packing or is the result of a small simulation domain, the results are presented as averages and standard deviations of multiple realizations each with a unique selection of grains—5 realizations for the regular-shaped BPM grain jamming simulations varying rotational orientation and 10 realizations for the irregular-shaped BPM grain jamming simulations.
6 Results of jamming simulations and comparison to experiments
The jamming densities are now presented in the context of BPM grain resolution dsp, intergranular friction μ, and the calculated grain morphological parameters. The results for regular-shaped BPM grains are discussed, followed by those for irregular-shaped BPM grains. Then, the discussion is extended to consider the irregular-shaped BPM grain simulations with the laboratory experiments.Fig. 12 presents the simulation results of ϕJ for regular-shaped BPM grains with μ = 0 and varying dsp where the solid symbols correspond to the regular-shaped (rough) BPM grains and the open symbols correspond to the regular-shaped (smooth) BPM grains. The data also appear in Tables 3 and 4, respectively. The results for the regular-shaped (smooth) grains demonstrate that as dsp increases, ϕJ initially decreases slightly and then begins to increase. A similar trend occurs for the regular-shaped (rough) grains, however the initial decrease in ϕJ is significantly larger. At small dsp, the initial behavior of decreasing ϕJ with increasing dsp corresponds to relatively small changes in χS and χRD near unity while χRH increases significantly. In this region, the use of subparticles to construct the BPM grains introduces roughness but with a limited effect on grain shape. Additionally, χRH is the only quantity that is varying significantly in this region, suggesting it is the primary reason for the BPM spheres to deviate from the theoretical limit of ϕJ = 0.64 for perfectly smooth spheres.
 | ||
| Fig. 12 Plot of ϕJ for regular-shaped BPM grains with μ = 0 and varying dsp. Solid symbols correspond to regular-shaped (rough) BPM grains. Open symbols correspond to regular-shaped (smooth) BPM grains. Error bars show one standard deviation of ϕJ. Data for dsp = 0.050 is from Clemmer et al.20 Data tabulated in Tables 3 and 4. | ||
For dsp ≥ 0.125 in Fig. 12, ϕJ increases as the regular-shaped BPM grains become less spherical. Prior works12,14,72 have shown ϕJ increases when the aspect ratio of an ellipsoid diverges from 1. For both rough and smooth grains, χRD markedly decreases with increasing dsp while χRH continues to increase by a comparatively greater amount. The inflection in ϕJ for regular-shaped (rough, smooth) grains occurs between 0.083 ≤ dsp ≤ 0.143 and appears to correlate with the relative importance of decreasing χRD with increasing χRH. The lower mean value and increased standard deviation for the regular-shaped (rough) data at dsp = 0.125 suggests that the minimum in jamming packing fraction may be due to the discretization itself. We sought to mitigate any effects of repeated samplings of the regular-shaped BPM grain libraries (which contained a single grain) by randomly setting its rotation when included in the jamming simulations. However, perhaps the dsp = 0.125 regular-shaped (rough) grain had specific subparticle arrangements or features that allowed them to jam more readily. Additional simulations with 0.083 ≤ dsp ≤ 0.143 could further refine the effect on ϕJ.
Fig. 12 also contains data (triangle markers) from Clemmer et al.20 as it is the only other study that also investigated the jamming of rougher and smoother BPM spheres, to the best of our knowledge. Their data fits with the observed trend for rougher grains but is found to jam at a lower density than our work for the smoother grains which may be due to a difference in packing methodologies. Clemmer et al. began by packing frictionless spherical particles to a density of 0.57 at a pressure one order of magnitude lower than that used in this work. Then, that arrangement was used as the initial configuration for their jamming simulations, which may have caused the BPM grains to arrange differently than when compressed from a lower initial density. In contrast, our method begins from a lower initial density which allows many opportunities for clusters of grains to form before the system jams, enhancing the effect of grain morphology. These opportunities for BPM grain collisions better mimic the pouring process of real granular materials and are expected to provide a more realistic initial arrangement than beginning from a nearly jammed configuration.
The effects of μ on ϕJ are presented in Fig. 13a for the regular-shaped (rough) grains and in Fig. 13b for the regular-shaped (smooth) BPM grains. The results of the jamming simulations appear in Tables 3 and 4 and show nominal trends of decreasing ϕJ with increasing μ at constant dsp. This finding is consistent with the literature.21–23 Additionally, increasing μ results in a larger decrease in ϕJ when dsp is large. This results in the ϕJ of regular-shaped (rough) grains seeming to converge towards a single value whereas the ϕJ of regular-shaped (smooth) grains appears to diverge. The increased effect of μ on grains with larger dsp suggests that there is an interaction between χRH and μ.
Finally, Fig. 14 plots ϕJ with μ for the smallest two sizes of dsp for the irregular-shaped BPM grains as open symbols and regular-shaped (rough) BPM grains as solid symbols. Data for the irregular-shaped BPM grains appear in Table 5. As with the regular-shaped (rough, smooth) grains, the irregular-shaped grains also exhibit a decreasing ϕJ with increasing μ or decreasing dsp. The increase in ϕJ with increasing dsp is accompanied by increases in χRH although the effect is small given the small difference in dsp values.
The results for the silica sand laboratory experiments appear in Table 5 and appear as a horizontal line in Fig. 14 due to the range of values reported in the literature for the μ of silica sand.73–75 The physical silica sand grains achieve a higher ϕJ than the irregular-shaped BPM grains. While the mean difference between the physical silica sand and irregular-shaped BPM grain PSDs was 3%, the physical silica sand grains had a higher percentage of grains in both tails of the PSD while the irregular-shaped BPM grains had a higher percentage of grains in the middle of the PSD. This broader size distribution of the physical silica sand grains compared to the irregular-shaped BPM grain likely contributed to their higher ϕJ. Additionally, based on the lower χS and χRD of the physical grains compared to the irregular-shaped BPM grains, we conclude that even with dsp = 0.083 the irregular-shaped BPM grains are not adequately resolved. Further decreases in dsp are expected to produce morphological properties that approach those of the physical silica sand grains resulting in ϕJ for the irregular-shaped BPM grains approaching ϕJ of the laboratory experiments. Despite being under-resolved for direct comparison to the experimental data, the BPM grains all showed a dependency of ϕJ on the quantified morphological parameters and intergranular friction which suggests they can be correlated. Based on literature,73 a μ of 0.138 was assigned for the physical grains in Table 5 in order to use this data point in our linear regression analysis of Section 7.
7 Relationship between jamming limit, grain morphological properties, and friction
We now study whether a single relationship can correlate the disordered grain packing behavior of frictional grains with a range of morphological properties. The BPM grain jamming simulations (Tables 3–5) provide a unique dataset given the parametric variation in grain resolution (dsp), varying roughness on a nominally similar shaped grains (e.g., regular-shaped (rough/smooth) BPM grains), and the comparatively large library of irregular-shaped BPM grains. Additionally, each BPM grain type was used in repeated jamming realizations to obtain summary data describing mean system behavior. For extended applicability, our data is combined with literature12,20,23,76 shown in Table 6 to form an augmented data set incorporating 5 independent studies and 71 unique data points. These literature data were selected as their grains could also be characterized in terms of sphericity, roundness, and roughness by: (1) using eqn (6) and (7) with the definitions for ellipse cross-section area and mean radius of curvature for the smooth ellipses used by Donev et al.;12 (2) using the methods of Section 4 for the BPM grain images published by Clemmer et al.;20 or (3) using the reported values for the frictional grains in the experiments of Farrell et al.23 and the smooth frictional spheres in the DEM simulations of Silbert et al.76| Source | χ S | χ RD | χ RH | μ | ϕ J |
|---|---|---|---|---|---|
| a Morphological properties reported by the cited study are used. | |||||
| Donev12 | 1.000 | 1.000 | 0.000 | 0.00 | 0.640 |
| 0.667 | 0.333 | 0.000 | 0.00 | 0.640 | |
| 0.500 | 0.250 | 0.000 | 0.00 | 0.715 | |
| 0.400 | 0.200 | 0.000 | 0.00 | 0.690 | |
| 0.333 | 0.167 | 0.000 | 0.00 | 0.670 | |
| 0.286 | 0.143 | 0.000 | 0.00 | 0.650 | |
| 0.952 | 0.476 | 0.000 | 0.00 | 0.655 | |
| 0.909 | 0.455 | 0.000 | 0.00 | 0.670 | |
| 0.800 | 0.400 | 0.000 | 0.00 | 0.700 | |
| 0.556 | 0.278 | 0.000 | 0.00 | 0.710 | |
| 0.444 | 0.222 | 0.000 | 0.00 | 0.695 | |
| 0.500 | 0.579 | 0.000 | 0.00 | 0.700 | |
| 0.600 | 0.630 | 0.000 | 0.00 | 0.710 | |
| 0.800 | 0.634 | 0.000 | 0.00 | 0.700 | |
| 0.950 | 0.546 | 0.000 | 0.00 | 0.660 | |
| 0.900 | 0.584 | 0.000 | 0.00 | 0.675 | |
| 0.650 | 0.644 | 0.000 | 0.00 | 0.710 | |
| 0.550 | 0.608 | 0.000 | 0.00 | 0.705 | |
| 0.400 | 0.499 | 0.000 | 0.00 | 0.680 | |
| 0.340 | 0.440 | 0.000 | 0.00 | 0.665 | |
| 0.300 | 0.396 | 0.000 | 0.00 | 0.650 | |
Farrella![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23 23 |
1.000 | 1.000 | 0.000 | 0.66 | 0.551 |
| 0.940 | 0.940 | 0.000 | 0.88 | 0.540 | |
Silberta![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 76 76 |
1.000 | 1.000 | 0.000 | 0.00 | 0.639 |
| 1.000 | 1.000 | 0.000 | 0.00 | 0.638 | |
| 1.000 | 1.000 | 0.000 | 0.01 | 0.634 | |
| 1.000 | 1.000 | 0.000 | 0.10 | 0.614 | |
| 1.000 | 1.000 | 0.000 | 0.20 | 0.595 | |
| 1.000 | 1.000 | 0.000 | 0.50 | 0.574 | |
| 1.000 | 1.000 | 0.000 | 1.00 | 0.556 | |
| 1.000 | 1.000 | 0.000 | 10.00 | 0.544 | |
| Clemmer20 | 1.000 | 1.000 | 0.000 | 0.15 | 0.598 |
| 1.000 | 1.000 | 0.000 | 0.30 | 0.583 | |
| 0.993 | 1.007 | 0.007 | 0.00 | 0.584 | |
| 0.999 | 1.001 | 0.003 | 0.00 | 0.599 | |
A series of linear regressions using the ordinary least squares (OLS) function in Statsmodels65 are performed on the augmented dataset. In each linear regression study, specific terms were evaluated for their ability—as measured by the coefficient of determination, R2—to correlate with the jamming limit. To begin, data from Donev et al.12 for smooth, frictionless ellipsoids are used to study the effect of χS on ϕJ. A quadratic polynomial (eqn (10)) using χS to model ϕJ yielded good agreement (R2 = 0.975) with the reported ϕJ data. Fig. 15a plots the regression and the inset plot shows the fitted relation of eqn (10) with the data.
| ϕJ,pred = −0.542χS2 + 0.684χS + 0.498 | (10) |
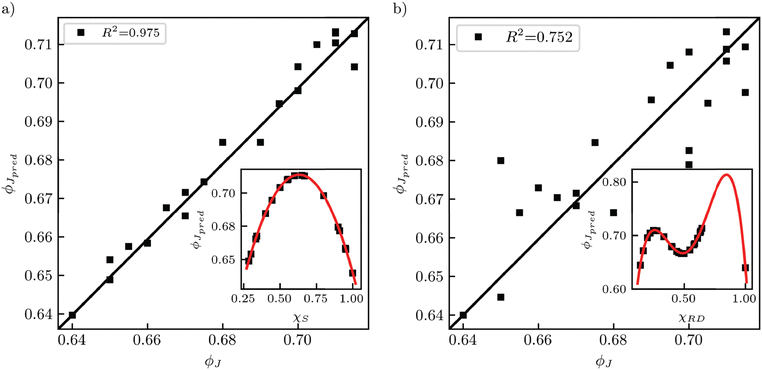 | ||
| Fig. 15 Plots of reported ϕJ,predversus ϕJ for the smooth, frictionless ellipse data from Donev et al.12 using (a) a quadratic polynomial in χS (eqn (10)) or (b) a quartic polynomial in χRD (eqn (11)). Inset plots show the data reported for ϕJ (Table 6) plotted as a function of χS and χRD along with the fitted relations of eqn (10) and (11) in red. | ||
Second, the data from Donev et al.12 is used to study the effect of χRD on ϕJ. A quartic polynomial (eqn (11)) using χRD to model ϕJ yielded moderate agreement (R2 = 0.752) with the reported ϕJ data. Fig. 15b plots the regression and the inset plot shows the fitted relation of eqn (11) with the data.
| ϕJ,pred = −11.614χRD4 + 24.704χRD3 − 17.668χRD2 + 4.994χRD + 0.225 | (11) |
Thus, ϕJ depends more on χS than χRD simply based on the number of model terms in eqn (10) and (11). Alternatively, χS appears to be a good predictor while χRD appears to be a poor predictor of ϕJ.
The third regression study considered the effect of χRH and μ on ϕJ. Yuan et al.24 showed that normalized jamming packing fraction, ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) J, for different shapes of smooth convex grains depends only on friction through a master curve with scaling parameters of μ* = 0.1635 and α = 1.07. Here,
J, for different shapes of smooth convex grains depends only on friction through a master curve with scaling parameters of μ* = 0.1635 and α = 1.07. Here, ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) J scales the ϕJ values between the limits of ϕJ(μ = 0) and ϕJ(μ = ∞) (eqn (12)).
J scales the ϕJ values between the limits of ϕJ(μ = 0) and ϕJ(μ = ∞) (eqn (12)).
 | (12) |
The limiting value of ϕJ(μ = ∞) is unknown for our BPM grains—yet is calculated from eqn (12) assuming the same μ* = 0.1635 and α = 1.07 fitting parameters and the BPM grain data at ϕJ(μ = 0.4, dsp). Then, the functional form of eqn (12) was fit to our BPM data yielding fitted values of μ* = 3.7 and α = 1 as shown in Fig. 16. It is observed that μ alone is insufficient to fully characterize the effect on packing behavior. For example, the regular-shaped (rough) grains consistently have higher ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) J for μ = 0.2 than the regular-shaped (smooth) grains. Mollon et al.40 demonstrated that for hybrid DEM, which creates grains with smoother surfaces than the corresponding grain envelope, surface roughness and μ could be varied to produce the same intergranular behavior. This suggests there is a similar relationship with χRH as μ. Based on these findings, the terms 1/(1 + μ) and 1/(1 + χRH) were incorporated into our statistical analysis along with first and second-order terms of μ and χRH.
J for μ = 0.2 than the regular-shaped (smooth) grains. Mollon et al.40 demonstrated that for hybrid DEM, which creates grains with smoother surfaces than the corresponding grain envelope, surface roughness and μ could be varied to produce the same intergranular behavior. This suggests there is a similar relationship with χRH as μ. Based on these findings, the terms 1/(1 + μ) and 1/(1 + χRH) were incorporated into our statistical analysis along with first and second-order terms of μ and χRH.
 | ||
Fig. 16 Plot of ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) J (eqn (12)) versus μ. The solid markers correspond to regular-shaped (rough) BPM grains while the hollow markers correspond to regular-shaped (smooth) BPM grains. The black line shows the relationship J (eqn (12)) versus μ. The solid markers correspond to regular-shaped (rough) BPM grains while the hollow markers correspond to regular-shaped (smooth) BPM grains. The black line shows the relationship ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) J = 1/(1 + (μ/μ*)α). J = 1/(1 + (μ/μ*)α). | ||
Fourth, the augmented dataset was examined by methodically adding and combining terms containing all three morphological properties and μ to predict ϕJ. The process began from the form of a quadratic polynomial of χS (eqn (10)) and continued incorporating terms discussed previously until a fitted relationship with the fewest terms that achieved an R2 of at least 0.90 was identified. This regression produced an 8-term polynomial for the predicted jamming limit, ϕJpred, shown in eqn (13) of order 4 that has an R2 value of 0.943 and a P value of 9.04 × 10−37.
 | (13) |
This equation uses 4 commonly reported grain morphological properties and produces a relationship that performs well for a range of regular- and irregular-shaped grains. The results of this regression were analyzed for linearity between the dependent and independent variables, multicollinearity of the dependent variables, normalcy of residuals, autocorrelation of the residuals, and homoscedasticity. The tests for multicollinearity showed that χS and χRD were moderately correlated. This correlation was expected since the fitted surface used an averaging distance of DG/2 to prevent individual subparticles from being identified as corners. We conclude that these 4 parameters contain useful information for predicting ϕJ since 3 of the 4 parameters studied exhibit no multicollinearity and the remaining variable only exhibits moderate multicollinearity with a single other parameter. The relationship of eqn (13) performs well with data from all sources as shown in Fig. 17. Averaging the morphological properties of all 154 irregular-shaped BPM grains for each dsp resulted in a strong agreement between the simulation results and predicted values as shown in Fig. 17. The use of a single projection for each regular-shaped BPM grain is likely the cause of the relatively high variance for our regular-shaped BPM grain data. The laboratory-measured ϕJ (Section 2), shown by the red hollow circle in Fig. 17, with morphological properties extracted from the irregular-shaped silica sand particles (Fig. 9b) has a relatively poor fit compared to the other data. The point shifts to the right due to changes in its computed morphological properties when the averaging distance used to create the fitted surface shown in Fig. 10a is reduced. Future work could investigate the optimal fitted surface averaging distance when performing measurements of physical and BPM grain morphological properties. Additionally, the process of creating 2D projections from BPM grains could be analyzed to ensure the relative rotation of the grains is representative of how physical grains are oriented in the optical microscope.
 | ||
| Fig. 17 Plot of jamming limit versus predicted value for the augmented data set. The data from Donev et al.12 is shown as square markers. The data from Farrell et al.23 is shown as × symbols. The data from Silbert et al.76 is shown as diamond markers. The data from Clemmer et al.20 is shown as triangular markers. Data from the regular-shaped BPM grains presented in this work is shown in solid circles. Data from the irregular-shaped BPM simulations is shown as hollow circles. The red markers correspond to data from laboratory experiments, while the black markers correspond to data from simulations. | ||
As expected from our findings fitting the ellipses (eqn (10)), the terms χS and χS2 are present in eqn (13). The findings of Mollon et al.40 show that χRH and μ have similar effects is supported by the interactions of χS2 with 1/(1 + μ) and 1/(1 + χRH). χRH also appears in 4 of the 8 terms in eqn (13), illustrating that it is a critical property for predicting ϕJ which is consistent with prior literature.77,78χRD only appears in a single term, interacting with all three other morphological parameters, demonstrating there is some interaction of morphological properties across length scales.
The importance of eqn (13) is that now users can specify an effective value of μ in their simulations given the details for their simulated grain morphology and the desired ϕJ. BPM grains do not jam at the same ϕJ when using μ for the real material because the spherical subparticles cause the BPM grains to have different morphological properties than the corresponding envelopes. μ is an independent parameter for the simulations as the morphological properties are determined when the BPM grains are created. Eqn (13) can use those morphological properties and a desired value of ϕJ to solve for the corresponding value of μ. However, μ is limited to positive values. Thus, it is important to use small values of dsp when simulating real materials with low μ values, as there is a limited range of variance in grain morphology that can be accounted for by decreasing μ.
8 Summary and future work
This study explored the interaction of grain morphology and intergranular friction on grain packing in the low-pressure jamming regime. A methodology to calculate grain shape descriptors of sphericity, roundness, and roughness were applied to physical grains and computationally reconstructed grains. Using the bonded particle discrete element method (BPM), computationally reconstructed grains were generated for regular-shaped (smooth, rough) and irregular-shaped grains with varying levels of subparticle discretization thereby directly influencing the shape descriptors. Experiments on physical grains and jamming simulations on the BPM grains were performed to predict the jamming packing fraction at low pressure where the intergranular behaviors are effectively decoupled from the elastic grain behaviors. Varying the intergranular friction in the BPM jamming simulations of the different BPM grain types yielded a large dataset for studing the interaction of grain morphological parameters, intergranular friction, and packing fraction.In general, increasing the subparticle diameter resulted in a decrease in the jamming limit that is correlated with increasing roughness and decreasing roundness. For large subparticle diameters, the regular-shaped BPM grains decreased in sphericity and the jamming packing fraction increased which has also been observed in smooth ellipses that vary from a unity aspect ratio. The exact relationship between the jamming limit and subparticle diameter of regular-shaped BPM grains varied based on whether the grains were created with a subparticle packing methodology that produced a smoother or rougher outer surface. The regular-shaped (smooth) BPM grains exhibited larger values of sphericity and roundness than the regular-shaped (rough) BPM grains with equal subparticle diameter. Increasing intergranular subparticle friction had the expected result of decreasing the jamming packing fraction.
Our results were combined with literature data to develop a correlation amongst 5 independent studies and 71 unique data points. By intentionally choosing to include the three commonly reported grain morphological parameters of sphericity, roundness, and surface roughness in our correlation, the method can be applied similarly to experimental and computationally reconstructed grains. As noted, reliance on 2D projections for calculating the shape descriptors certainly omits some details of the 3D grains yet the chosen descriptors should be readily accessible by general practitioners for straightforward application to both simulated and physical grains. This relationship allows researchers to use the morphological properties of their grains to determine an effective value of intergranular subparticle friction that will cause the BPM grains to jam at a desired density and is the first study to systematically and quantitatively explore the interactions of grain morphology and intergranular friction on grain packing behavior.
Author contributions
Samuel Martin: conceptualization, methodology, software, validation, formal analysis, investigation, data curation, writing – original draft, writing – review & editing, visualization. Marcia Cooper: conceptualization, methodology, resources, writing – review & editing, visualization, supervision, funding acquisition.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The author acknowledges the characterization part of this work was performed at Texas A&M University Materials Characterization Core Facility (RRID:SCR_022202). This work contains data from simulations performed using the Texas A&M High Performance Research Computing cluster Grace.References
- M. E. Cates, J. P. Wittmer, J.-P. Bouchaud and P. Claudin, Phys. Rev. Lett., 1998, 81, 1841 CrossRef CAS.
- G. Vreeman, C. Wang, C. M. Reddy and C. C. Sun, Cryst. Growth Des., 2021, 21, 6655–6659 CrossRef CAS.
- Y. Yu, L. Zhao, X. Lin, Y. Wang and Y. Feng, Int. J. Pharm., 2020, 577, 119023 CrossRef CAS PubMed.
- A.-S. Persson and G. Alderborn, Eur. J. Pharm. Biopharm., 2018, 125, 28–37 CrossRef CAS.
- J. T. Clemmer and M. O. Robbins, Phys. Rev. E, 2023, 108, 034902 CrossRef CAS.
- J. T. Clemmer and M. O. Robbins, Phys. Rev. Lett., 2022, 129, 078002 CrossRef CAS.
- Y. Guo, R. Liu, P. Chen, B. Zhou, G. Hu, C. Han, K. Lv and S. Zhu, Compos. Sci. Technol., 2022, 222, 109378 CrossRef CAS.
- J. Wang and H. Yan, Int. J. Numer. Anal. Methods Geomech., 2013, 37, 832–854 CrossRef.
- R. Fu, X. Hu and B. Zhou, Comput. Geotech., 2017, 91, 179–191 CrossRef.
- M. A. Cooper, W. W. Erikson and M. S. Oliver, Mech. Mater., 2021, 162, 104026 CrossRef.
- J. M. Monti, J. T. Clemmer, I. Srivastava, L. E. Silbert, G. S. Grest and J. B. Lechman, Phys. Rev. E, 2022, 106, 034901 CrossRef PubMed.
- A. Donev, I. Cisse, D. Sachs, E. A. Variano, F. H. Stillinger, R. Connelly, S. Torquato and P. M. Chaikin, Science, 2004, 303, 990–993 CrossRef PubMed.
- S. Torquato and Y. Jiao, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2009, 80, 041104 CrossRef PubMed.
- A. Donev, R. Connelly, F. H. Stillinger and S. Torquato, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2007, 75, 051304 CrossRef PubMed.
- É. Kaeshammer, L. Borne, F. Willot, P. Dokládal and S. Belon, Comput. Mater. Sci., 2021, 190, 110247 CrossRef.
- Y. Kallus, Soft Matter, 2016, 12, 4123–4128 RSC.
- H. Ikeda, C. Brito, M. Wyart and F. Zamponi, Phys. Rev. Lett., 2020, 124, 208001 CrossRef.
- I. Zuriguel, A. Garcimartín, D. Maza, L. A. Pugnaloni and J. M. Pastor, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2005, 71, 051303 CrossRef PubMed.
- K. To, P.-Y. Lai and H. K. Pak, Phys. Rev. Lett., 2001, 86, 71 CrossRef.
- J. T. Clemmer, J. M. Monti and J. B. Lechman, Soft Matter, 2024, 20, 1702–1718 RSC.
- M. P. Ciamarra, R. Pastore, M. Nicodemi and A. Coniglio, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2011, 84, 041308 CrossRef PubMed.
- V. B. Nguyen, T. Darnige, A. Bruand and E. Clement, Phys. Rev. Lett., 2011, 107, 138303 CrossRef.
- G. R. Farrell, K. M. Martini and N. Menon, Soft Matter, 2010, 6, 2925–2930 RSC.
- Y. Yuan, Y. Jiao, Y. Wang and S. Li, Phys. Rev. Res., 2021, 3, 033084 CrossRef.
- A. Baule, R. Mari, L. Bo, L. Portal and H. A. Makse, Nat. Commun., 2013, 4, 2194 CrossRef.
- R. Melnyk, A. Trokhymchuk and A. Baumketner, J. Mol. Liq., 2022, 368, 120672 CrossRef.
- W. Xu, G. Yang, P. Lan and H. Ma, Comput. Mater. Continua, 2016, 52, 25–40 Search PubMed.
- S. Torquato and Y. Jiao, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2013, 87, 022111 CrossRef.
- N. Gravish and D. I. Goldman, Fluids, Colloids Soft Mater., 2016, 341–354 Search PubMed.
- K. Kamrin, K. M. Hill, D. I. Goldman and J. E. Andrade, Annu. Rev. Fluid Mech., 2024, 56, 215–240 CrossRef.
- K. Karapiperis, S. Monfared, R. B. D. Macedo, S. Richardson and J. E. Andrade, Granular Matter, 2022, 24, 91 CrossRef.
- E. J. Garboczi, Cem. Concr. Res., 2002, 32, 1621–1638 CrossRef CAS.
- H. Liang, Y. Shen, J. Xu and X. Shen, Front. Phys., 2021, 9, 744319 CrossRef.
- X. Wang, Z.-Y. Yin, H. Xiong, D. Su and Y.-T. Feng, Int. J. Numer. Meth. Eng., 2021, 122, 5626–5655 CrossRef.
- Y. T. Feng, Comput. Methods Appl. Mech. Eng., 2021, 379, 113750 CrossRef.
- W. Xu, M. Jia, W. Guo, W. Wang, B. Zhang, Z. Liu and J. Jiang, Cem. Concr. Res., 2023, 164, 107048 CrossRef CAS.
- W. Xu, K. Zhang, Y. Zhang and J. Jiang, Water Resour. Res., 2022, 58, e2021WR031433 CrossRef.
- X. Garcia, L. T. Akanji, M. J. Blunt, S. K. Matthai and J. P. Latham, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2009, 80, 021304 CrossRef PubMed.
- J. Zhao, S. Li, R. Zou and A. Yu, Soft Matter, 2012, 8, 1003–1009 RSC.
- G. Mollon, A. Quacquarelli, E. Andò and G. Viggiani, Granular Matter, 2020, 22, 1–16 CrossRef.
- T. Zhang, C. Zhang, J. Zou, B. Wang, F. Song and W. Yang, Comput. Geotech., 2020, 122, 103542 CrossRef.
- M. Wu, J. Wang and F. Wu, Adv. Powder Technol., 2022, 33, 103599 CrossRef.
- M. B. Cil and K. A. Alshibli, C. R. Mec., 2015, 343, 133–142 CrossRef.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore and T. D. Nguyen, et al. , Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- ASTM Standard D7481-18, Standard Test Methods for Determining Loose and Tapped Bulk Densities of Powders using a Graduated Cylinder, ASTM International, West Conshohocken, PA, 2018.
- Itseez, Open Source Computer Vision Library, https://github.com/itseez/opencv, 2015.
- D. R. Lide, CRC handbook of chemistry and physics, CRC press, 2004, vol. 85 Search PubMed.
- J. D. Bernal and J. Mason, Nature, 1960, 188, 910–911 CrossRef.
- S. van der Walt, J. L. Schönberger, J. Nunez-Iglesias, F. Boulogne, J. D. Warner, N. Yager, E. Gouillart, T. Yu and Scikit-image contributors, PeerJ, 2014, 2, e453 CrossRef PubMed.
- N. V. Brilliantov, F. Spahn, J.-M. Hertzsch and T. Pöschel, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, 5382 CrossRef CAS PubMed.
- L. E. Silbert, D. Ertas, G. S. Grest, T. C. Halsey, D. Levine and S. J. Plimpton, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2001, 64, 051302 CrossRef CAS PubMed.
- H. P. Zhang and H. A. Makse, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2005, 72, 011301 CrossRef CAS.
- N. V. Brilliantov, F. Spahn, J.-M. Hertzsch and T. Pöschel, Phys. Rev. E:Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, 5382–5392 CrossRef CAS.
- S. Martin and M. A. Cooper, Comput. Part. Mech., 2024, 11, 1463–1485 CrossRef.
- A. P. Santos, I. Srivastava, L. E. Silbert, J. B. Lechman and G. S. Grest, Front. Soft Matter, 2024, 3, 1326756 CrossRef.
- W. Pabst and E. V. A. Gregorová, Ceram.-Silik., 2013, 57, 167–184 CAS.
- B. Butler, E. Lam, C. Johnson, G. Turner, D. Lewis, K. Xie and J. Paramore, PowderMet2022: International Conference on Powder Metallurgy & Particulate Materials, 2022.
- G. Mollon and J. Zhao, Comput. Methods Appl. Mech. Eng., 2014, 279, 46–65 CrossRef.
- H. Wadell, J. Geol., 1932, 40, 443–451 CrossRef.
- P. J. Barrett, Sedimentology, 1980, 27, 291–303 CrossRef.
- M. Fan, D. Su and X. Chen, Acta Geotech., 2024, 1–24 Search PubMed.
- W. Fei, G. A. Narsilio and M. M. Disfani, Powder Technol., 2019, 355, 770–781 CrossRef CAS.
- T. Kanada, Precis. Eng., 1997, 20, 117–122 CrossRef.
- J. Zheng and R. D. Hryciw, Geotechnique, 2015, 65, 494–506 CrossRef.
- S. Seabold and J. Perktold, 9th Python in Science Conference, 2010.
- J. K. Mitchell, K. Sogaet al., Fundamentals of Soil Behavior, John Wiley & Sons, New York, 2005, vol. 3 Search PubMed.
- J. Rodriguez, J. Johansson and T. Edeskär, Nordic Geotechnical Meeting: 09/05/2012-12/05/2012, 2012, pp. 207–218.
- J. C. Santamarina and G.-C. Cho, Advances in geotechnical engineering: The Skempton conference: Proceedings of a three day conference on advances in geotechnical engineering, organised by the Institution of Civil Engineers and held at the Royal Geographical Society, London, UK, on 29–31 March 2004, 2004, pp. 604–617.
- C.-Y. Kuo and R. B. Freeman, Transp. Res. Rec., 2000, 1721, 57–65 CrossRef.
- A. A. Gusev, J. Mech. Phys. Solids, 1997, 45, 1449–1459 CrossRef.
- N. Audry, B. Harthong and D. Imbault, Powder Technol., 2023, 429, 118871 CrossRef CAS.
- F. M. Schaller, M. Neudecker, M. Saadatfar, G. W. Delaney, G. E. Schröder-Turk and M. Schröter, Phys. Rev. Lett., 2015, 114, 158001 CrossRef PubMed.
- K. Senetakis, M. R. Coop and M. C. Todisco, Soils Found., 2013, 53, 746–755 CrossRef.
- J. W. Dickey, PhD thesis, Massachusetts Institute of Technology, 1966.
- S. G. Vilt, N. Martin, C. McCabe and G. Kane Jennings, Tribol. Int., 2011, 44, 180–186 CrossRef CAS.
- L. E. Silbert, Soft Matter, 2010, 6, 2918–2924 RSC.
- H. Ikeda, C. Brito, M. Wyart and F. Zamponi, Phys. Rev. Lett., 2020, 124, 208001 CrossRef CAS PubMed.
- I. Zuriguel, A. Garcimartín, D. Maza, L. A. Pugnaloni and J. M. Pastor, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 051303 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00332f |
| This journal is © The Royal Society of Chemistry 2025 |










