 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ion specific effects on the rheology of cellulose nanofibrils in the presence of salts†
Ravisara
Wattana
 a,
Daehwan
Park
b and
Chinedum O.
Osuji
a,
Daehwan
Park
b and
Chinedum O.
Osuji
 *c
*c
aDepartment of Materials Science and Engineering, University of Pennsylvania, Philadelphia, Pennsylvania 19104, USA
bDepartment of Chemistry & Cosmetics, Jeju National University, 102 Jejudaehak-ro, Jeju-si, Jeju-do 63234, Republic of Korea
cDepartment of Chemical and Biomolecular Engineering, University of Pennsylvania, Philadelphia, Pennsylvania 19104, USA. E-mail: cosuji@seas.upenn.edu
First published on 8th May 2025
Abstract
Cellulose nanofibrils (CNFs) are high-aspect-ratio semiflexible filaments that can modify the rheology of fluids in which they are suspended. This work addresses the role of ionic strength in the rheology of CNF suspensions and the ion-specific nature of such rheology. Salt-free CNF suspensions exhibit viscoelastic, shear-thinning behavior. The concentration dependences of the storage modulus and specific viscosity exhibit similar power-law relationships in two regimes, G′ ∼ ηsp ∼ ca, with exponents of a ≈ 1 and a ≈ 5 below and above, respectively, a critical concentration of roughly 0.5 wt% that delineates “dilute” and “semi-dilute” characteristics. In the semi-dilute regime, salt addition increases the elastic modulus due to increased filament–filament association enabled by electrostatic screening of the repulsive interactions between weakly charged filaments. In the dilute regime, the intrinsic viscosity decreases with ionic strength, reflecting the adoption of more compact conformations at the single-filament level due to screened electrostatics. At a fixed ionic strength, both storage modulus and intrinsic viscosity show a marked dependence on ion identity, for which ion hydration enthalpy is used as a proxy. The storage modulus decreases with the enthalpy of hydration, whereas the intrinsic viscosity increases. Notably, the orderings of both parameters mimic the ion sequence of the Hofmeister series. This highlights a strong correlation between the ability of different ions to modify the hydrogen-bonding-network structure of water and their ability to screen inter- and intra-filament electrostatic interactions. This work provides new insight into ion-specific effects in CNF suspension rheology that can be used to rationally modify the properties of CNF-based complex fluids.
1. Introduction
Cellulosic nanomaterials such as cellulose nanofibrils (CNFs) and cellulose nanocrystals (CNCs) are versatile and useful materials in various contexts. Sourced from naturally abundant biomass, these materials can be chemically modified readily and are attractive from a sustainability perspective. These characteristics drive their use in applications ranging from traditional paper production to biomedical devices,1–7 and the fabrication of a variety of functional hydrogels8,9 and microcapsules.10,11 They are also of interest for engineering complex fluids.12,13 In particular, the high aspect ratio of CNFs makes it an effective rheology modifier at low volume fractions.14,15 Chemical modification of cellulose by (2,2,6,6-tetramethyl-piperidin-1-yl)oxyl (TEMPO) oxidation converts some fraction of hydroxyl groups to carboxylates (Fig. 1). At neutral pH, TEMPO-oxidized CNFs are weakly negatively charged, but otherwise hydrophobic materials.16,17 At appropriate volume fractions, they form physical gel networks via electrostatic interactions and physical entanglement that are conceptually similar to polyelectrolyte gel networks18 with intriguing yielding and aging responses.19Fig. 1 provides a schematic illustration of such a network. TEM and SEM images highlight the high aspect ratio and semi-flexible character of CNFs, here with diameters of 5.5 ± 1.4 nm and contour lengths exceeding 1000 nm. As with any other colloidal systems, the rheology of CNF suspensions is a function of inter-particle interactions, which can be modified by the addition of other species, including surfactants and dissociated ions from dissolved salts, polymers, or other colloids.20–22 | ||
| Fig. 1 TEMPO-oxidized cellulose nanofibrils (CNFs): (A) chemical structure, (B) illustration of a three-dimensional network structure, (C) TEM image, and (D) SEM image. | ||
From a generic perspective, the presence of dissolved salts in charged colloidal and macromolecular systems has significant implications for their rheological properties in aqueous media. Dissociated salt ions modify the electrostatic interactions between the colloidal and/or macromolecular components of a system, which leads to conformational changes, or changes in the state of aggregation, and concomitant modifications in the rheology of the system. This is seen in polyelectrolyte complexes, for example, as shown in the alginate–chitosan system.23 The presence of ionic species can have significant effects on the rheology of cellulose nanomaterials, with well-known impacts of ionic strength on physiochemical properties and behavior, manifested by solubility, dissolution, and aggregation,24–26 conductivity and zeta-potential,27,28 gelation,29–35 and polymer adsorption.36,37 Interestingly, unmodified CNFs are reported to be sensitive to the presence of salts at very small concentrations, ∼1 mM, despite the absence of charged or ionizable groups present on TEMPO-modified CNFs. The sensitivity has been linked to the effect of ions on the hydrogen bonding structure of water, and specifically, to the effect on CNF hydration, which thereby impacts the nature of fibril–fibril contacts.38
The strength and range of inter-particle interactions can be used to gauge the stability in colloidal suspensions by tallying contributions from electrostatic and dispersion forces.39,40 Dissolved ions screen electrostatic interactions between charged colloidal particles due to the formation of electrical double layers. The modification to inter-particle potential is often described by the Derjaguin–Landau–Verwey–Overbeek (DLVO) theory, which considers the valency and concentration of ions. While DLVO theory is agnostic of ion identity, ion-specific effects were first introduced in protein dissolution as the conical example to understand the stability, or solubility, of proteins in aqueous media, as captured by the Hofmeister series (HS).41–46 Such an effect has been subsequentially encountered in other systems, including gelatin,47–52 collagen,53 DNA,54 polymer solutions,55,56 polyelectrolyte films,57 emulsions,58 and nanoparticles.59–62 As illustrated in Fig. 2, the HS describes the varying ability of different ions to stabilize or destabilize globular proteins in aqueous media. At a coarse level, this phenomenon has been linked to the order-inducing (kosmotropic) or disorder-inducing (chaotropic) effects of different ions on the water structure (and therefore on the hydrophobic effect) as primarily correlated with their charge density and therefore proxied by their hydrated radii and hydration enthalpies. The correlations are inverted for cations and anions – weakly hydrated cations and strongly hydrated anions are more chaotropic, whereas strongly hydrated cations and weakly hydrated anions are more kosmotropic. While this coarse-level description is useful in many scenarios, it sidesteps the role of non-additive and specific ion-solute interactions, counter-ion identity, protein charge, concentration dependence, and other contributions to ion-specific effects.63–65 Nevertheless, it captures some important broad trends. For example, the lower charge density and greater polarizability of anions relative to cations lead to larger observable anion-specific effects, and studies regarding ion-specific effects more often focus on anion than cation identity.65
 | ||
| Fig. 2 Hofmeister series (HS), ion specificity series or lyotropic sequences for conventional protein precipitation. | ||
Here, we investigate the ion-specificity in terms of the effect of added salts on the rheology of TEMPO-oxidized aqueous CNF suspensions. Neat CNF suspensions display distinct dilute and semi-dilute regimes, separated by a critical concentration of roughly 0.5 wt%. Increasing the salt concentration leads to a decrease in intrinsic viscosity and an increase in gel modulus in the dilute and semi-dilute regimes, respectively. These changes are due to screened electrostatic interactions which permit more compact single-filament conformations, and increased filament–filament contact, respectively. We study cation specific effects using a variety of chloride salts of monovalent cations in both the dilute and semi-dilute regimes. Clear trends emerge in both the dilute and semi-dilute regimes. The intrinsic viscosity decreases and storage modulus increases as it progresses along the Hofmeister series from kosmotropic to chaotropic cations. The storage modulus appears exponentially dependent on the enthalpy of hydration of the cation. We attribute these effects to the role of hydration shell-bound water in moderating the electrostatic screening that drives changes in filament conformation and association – larger hydration shells and tighter binding of waters limit the electrostatic interaction between the cation and the negatively charged carboxylate groups on CNFs, leading to a more diffuse double layer and less screening of electrostatic repulsion between CNFs. These findings highlight the non-trivial impact of ion identity in dictating the rheology of CNF suspensions and provide potential routes for optimizing the formulation of CNF-containing complex fluids.
2. Materials and methods
2.1 Sample preparation
All CNF samples were prepared from a stock 1.1 wt% aqueous suspension of (2,2,6,6-tetramethylpiperidin-1-yl)oxyl or TEMPO-modified CNF suspension obtained from the Process Development Center at the University of Maine. The CNF charge density is specified at 1.5 meq g−1 of dry material. Samples of varying compositions were prepared by either slowly concentrating the stock suspension using a rotary evaporator or diluting it with Milli-Q water, followed by vortex mixing. Nine chloride salts were examined to elucidate the monovalent and divalent cationic effects while four sodium salts were explored to probe the monovalent anion effect. All salts were obtained from Sigma-Aldrich as anhydrous high purity powders (>99.99%, trace metals basis). The investigated monovalent chloride salts are lithium chloride (LiCl), sodium chloride (NaCl), potassium chloride (KCl), rubidium chloride (RbCl), and cesium chloride (CsCl). The sodium salts are sodium fluoride (NaF), sodium iodide (NaI), and sodium bromide (NaBr). The dichloride salts include magnesium chloride (MgCl2), calcium chloride (CaCl2), strontium chloride (SrCl2), and barium chloride (BaCl2). Stock solutions of 100 mM concentration were prepared by salt dissolution in Milli-Q water and diluted to desired concentrations. Salt-containing CNF samples were prepared by combining appropriate quantities and concentrations of CNF suspensions with salt solutions, followed by vortex mixing. Air bubbles were removed by gentle centrifugation at 1500 rpm for 5 minutes and left overnight quiescently before rheological measurements.2.2 Characterization
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m). Measurements of gels or high concentration suspensions were performed with a cone-and-plate geometry of 50 mm diameter and 0.04 rad cone-angle. Samples were thermostated at 20 °C and a thin layer of mineral oil was used at the sample–air interface to minimize water evaporation during the measurements. The samples were pre-sheared at 2 s−1 for 300 s and then left quiescently for another 300 s. Amplitude sweep measurements were conducted at ω = 10 rad s−1 to determine the strain limit of the linear viscoelastic region (LVR) for the purpose of conducting frequency sweep measurements thereafter. An ascending strain sweep followed by a descending run was used to remove any sample history, prior to frequency dependent measurements. Frequency sweep measurements at strain amplitudes within the LVR were then performed, with ascending and descending ramps to verify data reproducibility.
m). Measurements of gels or high concentration suspensions were performed with a cone-and-plate geometry of 50 mm diameter and 0.04 rad cone-angle. Samples were thermostated at 20 °C and a thin layer of mineral oil was used at the sample–air interface to minimize water evaporation during the measurements. The samples were pre-sheared at 2 s−1 for 300 s and then left quiescently for another 300 s. Amplitude sweep measurements were conducted at ω = 10 rad s−1 to determine the strain limit of the linear viscoelastic region (LVR) for the purpose of conducting frequency sweep measurements thereafter. An ascending strain sweep followed by a descending run was used to remove any sample history, prior to frequency dependent measurements. Frequency sweep measurements at strain amplitudes within the LVR were then performed, with ascending and descending ramps to verify data reproducibility.
3. Results and discussion
3.1 Viscoelasticity of neat CNF suspensions
At concentrations lower than 1.1 wt%, the neat CNF suspensions are viscoelastic fluids, with G′′ > G′ over all observed frequencies. Above 1.1 wt%, they are more gel-like with G′ > G′′ and a largely frequency-independent elastic modulus, as seen in Fig. 3B. Full dynamic moduli of both amplitude and frequency dependence are shown in Fig. 1S (ESI†). Flow curves (Fig. 3C) show a transition from purely Newtonian to shear-thinning behavior upon increasing the CNF concentration. Zero-shear viscosities, η0, are obtained from fits of the data using the Cross model (eqn (1)). | (1) |
 | ||
| Fig. 3 (A) Photographs of CNF suspension samples at concentrations indicated. (B) Frequency dependent elastic moduli measured at a strain amplitude, γ = 5% for neat CNF suspensions of different concentrations (0.1 to 4.5 wt% as indicated). (C) Steady-flow curves of neat CNF suspensions (0.1 to 1.1 wt% as indicated). Solid lines are fits of the data using the Cross model (eqn (1)). | ||
The concentration dependences of the storage modulus at ω = 10 rad s−1 and the specific viscosity were examined, as shown in Fig. 4. The specific viscosity was calculated based on zero shear viscosities as ηsp = (η0 − ηs)/ηs, where ηs is the viscosity of the solvent, i.e. water. The data reveal two distinct regimes of apparent power-law behavior, G′ ∼ ηsp ∼ ca. The exponent a ≈ 1 at low concentrations and a ≈ 5 at high concentrations, with a crossover at cc ≈ 0.5 wt%. The behavior in the semi-dilute regime, c > cc, is broadly similar to that seen in prior work by Jowkarderis and van de Ven, who reported an exponent of 4.5 for elasticity measured at 6.28 rad s−1,3 and by Pettersson et al., who reported an exponent of 5.2, for carboxymethylated cellulose nanofibrils measured at roughly 0.1 rad s−1.66 It is worth noting, however, that a broad range of exponents have been observed in prior work67 and that these exponents are typically larger than the 2–2.5 expected from classical theories for semi-flexible filamentous networks.68 More recent work by Hill, however, suggests an exponent between 11/3 and 7.69 The sensitivity of the measured storage modulus to the frequency in these weak gels results in a decrease in the concentration scaling exponent upon increasing the frequency. The use of moduli measured at different frequencies may account for some of the variation in reported exponents in the literature, beyond non-trivial effects due to differences associated with the degree of crystallinity, aspect ratio, and surface charge of variously sourced CNFs studied.
The linear concentration dependence of specific viscosity is expected in the dilute regime for any colloidal particle, independent of shape. At higher concentrations, hydrodynamic interactions give rise to exponents larger than unity. For our system, the exponent a ≈ 5 is larger than would be expected for semiflexible polymers below entanglement concentrations. We consider it likely that non-trivial filament–filament interactions (electrostatic repulsion; hydrophobic association) are responsible for the larger exponent. We are not aware of prior studies that address the concentration dependence of zero shear viscosity of CNFs in the semi-dilute regime. These can be somewhat challenging studies due to the difficulty of accurately measuring zero shear viscosities in this regime due to the onset of shear thinning at very low shear rates that preclude direct observation of the Newtonian plateau and, therefore, impose the need to fit rheometric data to extract the zero-shear viscosity. Concomitantly, viscometric experiments are prohibitively long. Nevertheless, we observe qualitatively good agreement between viscometric and rheometric data in the crossover region.
3.2 Viscoelasticity of CNF suspensions with NaCl
Fig. 5 shows images of 0.55 wt% CNF suspensions with various concentrations of NaCl ranging from 25 to 500 mM. For salt concentrations below 50 mM, the sample formed clear gels. At 50 mM, the gel formed was of sufficient strength to resist gravitational flow upon sample inversion (Fig. 5A). Above this salt concentration, the suspensions become somewhat cloudy, and the gels lost their mechanical integrity. The results are consistent with an initial increase of modulus due to modest screening of electrostatic repulsion that enabled filament–filament interactions to form a stronger gel. However, excessive salt addition leads to gel collapse as stronger filament–filament association leads to flocculation and precipitation of aggregates. Our results highlight that there is a window within which an increase in ionic strength can modify the mechanical properties of CNF networks in a notably predictable fashion without causing large-scale aggregation and, therefore, without loss of optical clarity. Fig. 5C intriguingly shows exponential dependence of storage modulus on the salt concentration in the observed 0–50 mM NaCl range. This exponential dependence can be contrasted with linear70 and logarithmic71 dependences observed in other complex fluids. While the ionic strength dependence of gel modulus nominally originates in the reduction of longer range electrostatic repulsion and emergent relevance of short range van der Waals attraction as described by DLVO theory, in practice, the scaling of modulus with ionic strength is less straightforward to describe.3.3 Intrinsic viscosity of CNFs in the presence of NaCl
We investigated the intrinsic viscosity of our CNFs using viscometric measurements in the dilute regime. The intrinsic viscosity ([η] in eqn (2)) is the coefficient of proportionality that captures the ability of a particle to alter the suspension viscosity in relation to its concentration. It is therefore a direct function of the shape of the particle. For solid spherical particles, [η] = 5/2. Analytical and numerical results are available for short-fibers as a function of aspect ratio.72 Particle shape can also correspond to intrinsic viscosity via packing efficiency as a function of aspect ratio.73 For CNFs, prior work has shown that there is a direct correlation between the intrinsic viscosity and the aspect ratio,74 and work by Isogai et al. suggested a correlation ρ[η] ∼ sb, where ρ and s are the mass density and aspect ratio, and b ≈ 1.9.75 | (2) |
The concentration dependence of the reduced viscosity, ηred = ηsp/c, was linearly extrapolated to c = 0 to yield the intrinsic viscosity (Fig. 6A). The dependence of [η] on the salt concentration, cs, is shown in Fig. 6B. [η] decreases by a factor of almost 3× in going from neat CNF suspensions to 5 mM NaCl samples. There is no indication that salt addition shortens or otherwise alters the physical dimensions of CNFs, and so the aspect ratio, as strictly defined by the ratio of contour length to diameter, remains unchanged. A naïve interpretation in the context of the Isogai correlation therefore fails, necessarily. Recognizing that the preceding arguments do not incorporate the rigidity or conformational freedom of the CNF explicitly, i.e. separately from the aspect ratio, it is sufficient to recognize a change in the effective aspect ratio. We infer that, physically, the effective shape of CNFs has changed – a reduction in intrinsic viscosity is consistent with the adoption of a less extended structure, which would likely result from screened electrostatics that liberate internal modes of motion in individual filaments. The zeta potential results, shown in Fig. 3S (ESI†), further support the reduction in screened electrostatics as more salt is added at a fixed CNF concentration. This is schematically illustrated in Fig. 6C. Effectively, the filament becomes less stiff. The reduction in the intrinsic viscosity on salt addition mirrors that seen in polyelectrolyte solutions on salt addition.76
The intrinsic viscosity of polyelectrolytes in solution displays sigmoidal dependence on the salt concentration.77 This reflects a smooth transition from a low salt limit (cs = 0) to a high salt limit (cs → ∞), at a characteristic salt concentration, or inflection point, cips, as shown in the Boltzman sigmoidal equation, eqn (3), where H is an adjustable scalar. Data and the corresponding fit are shown in Fig. 7(A). The upper limit ([η] = 417 ml g−1) is the intrinsic viscosity of the CNF suspension in the absence of an additional salt.
 | (3) |
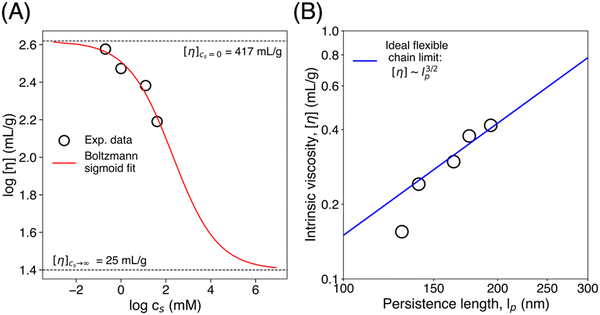 | ||
| Fig. 7 (A) The logarithmic intrinsic viscosity dependence on the logarithmic values of salt concentrations. The solid line is the Boltzmann sigmoidal curve (eqn (3); R2 = 0.95). (B) Intrinsic viscosity as a function of persistence length with a solid line indicating a 3/2 power-law as a visual guide. Persistence lengths were extracted from the WLC model fit (eqn (4) and (5)). | ||
The ionic strength dependence can be modeled to yield information on the persistence length of the CNFs. The intrinsic viscosity of a polymer scales as the reciprocal of the overlap concentration, (c*), which is the concentration within the pervaded volume, so  where M is the mass of an individual chain in solution, Φ is a polymer specific numerical factor, and R is the root mean-square end–end distance which is directly proportional to the radius of gyration.78 The mean square end–end distance for semi-flexible polymers is well represented by the worm-like chain (WLC) model as 〈R2〉 = 2lp2[L/lp − (1 − es −L/lp)]. The WLC model provides a smooth interpolation between fully flexible, and fully rigid or rod-like polymer backbones corresponding to the limits
where M is the mass of an individual chain in solution, Φ is a polymer specific numerical factor, and R is the root mean-square end–end distance which is directly proportional to the radius of gyration.78 The mean square end–end distance for semi-flexible polymers is well represented by the worm-like chain (WLC) model as 〈R2〉 = 2lp2[L/lp − (1 − es −L/lp)]. The WLC model provides a smooth interpolation between fully flexible, and fully rigid or rod-like polymer backbones corresponding to the limits  and
and  where L and lp are the contour and persistence lengths, respectively. The intrinsic viscosity is therefore correlated with the chain persistence length as shown in eqn (4).
where L and lp are the contour and persistence lengths, respectively. The intrinsic viscosity is therefore correlated with the chain persistence length as shown in eqn (4).
[η] ≈ ![[capital Phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c1.gif) [2lp2[L/lp − (1 − e−L/lp)]]3/2 [2lp2[L/lp − (1 − e−L/lp)]]3/2 | (4) |
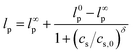 | (5) |
3.4 Ion specific intrinsic viscosity of CNF suspensions
We examined the intrinsic viscosity of CNFs in the presence of various chloride salts, with different monovalent cations. The data are shown in Fig. 8. We observe that [η] increases as we traverse a sequence of cations, from Cs+ to Li+ that inversely follows the Hofmeister series. Fig. 8B shows this dependence on ion-identity in terms of the enthalpy of hydration, with intrinsic viscosity increasing with the enthalpy of hydration. The data suggest that more extended CNF conformations are present for more strongly hydrated cations like Li+. This dependence of conformation on hydration enthalpy is consistent with the expectation that more strongly hydrated cations are less effective in screening electrostatic interactions. This loss of effectiveness can be understood simply in terms of the ability or inability of hydrated ions to closely approach charged surfaces82 such as the negatively charged CNF surface. An alternate way to view this is that close association of the ion with the charged surface requires a loss of water from the ion's hydration shell. Small, high charge-density and low polarizability species such as Li+ distort the water structure more significantly and have larger hydrated diameters than larger, lower charge density species. Static light scattering experiments were unable to resolve statistically meaningful differences in the radius of gyration of CNFs in the presence of neighboring monovalent cations along the Hofmeister sequence. Data are shown in Table 2S and Fig. 4S (ESI†) with their 95% confidence intervals. The data, however, do show a statistically meaningful difference between the extracted radius of gyration of neat CNF and CNF/CsCl suspensions, i.e. corresponding to expected maximum and minimum dimensions from the intrinsic viscosity. | ||
| Fig. 8 (A) Reduced viscosity of dilute CNF suspensions as a function of CNF concentration, in the presence of chloride salts with the indicated monovalent cations. (B) Corresponding intrinsic viscosities of CNFs as a function of cation hydration enthalpy. The noted enthalpy of hydration values are tabulated and absolute values listed in Table 2S (ESI†).83 (C) Schematic illustration of simplified representations of a change of a single CNF shape due to the ability to share or lose cations’ hydration shells indicated in light blue borderlines on the ions. | ||
3.5 Ion specific viscoelasticity of CNF suspensions
Fig. 9(A) shows data from dynamic rheological characterization of CNF suspensions in the semi-dilute regime with 25 mM concentration of salts of varying identity. The suspensions are all soft gels and exhibit frequency dependence in their response, but with G′ > G′′ and, therefore, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ < 1 (Fig. 9B) over the observed frequency range. The storage modulus decreases upon traversing the sequence from Cs+ to Li+, i.e. upon increasing the hydration enthalpy or ion charge density. As shown in Fig. 5, an increase in the concentration of a given salt (NaCl) leads to an increase of gel modulus, as screened electrostatic repulsion enables greater fibril–fibril association. We surmise that the decrease of modulus in Fig. 9 at a fixed salt concentration but changing ion identity (increasing hydration enthalpy) is associated with weaker inter-fibril association, or conversely, stronger repulsion due to decreased charge screening. This is consistent with the interpretation yielded from viscometry data, though the implications in terms of the measured quantities are different – a higher intrinsic viscosity, but a lower gel modulus. Fig. 9B shows that there is an apparent exponential dependence of the elastic modulus on the cation hydration enthalpy. This mirrors the exponential dependence of the gel modulus on the salt concentration seen in Fig. 5C for only NaCl presented. This suggests that the nominal ionic strength I can be corrected using the hydration enthalpy ΔHh to yield an effective ionic strength, Ieff, that captures the role of salt addition agnostic of ion identity. Viewed another way, the difference in the effectiveness of electrostatic screening for ions of different charge densities can be accounted for by a term involving the hydration enthalpy, G′ ∼ exp[f(I,ΔHh)] = exp[f(Ieff)].
δ < 1 (Fig. 9B) over the observed frequency range. The storage modulus decreases upon traversing the sequence from Cs+ to Li+, i.e. upon increasing the hydration enthalpy or ion charge density. As shown in Fig. 5, an increase in the concentration of a given salt (NaCl) leads to an increase of gel modulus, as screened electrostatic repulsion enables greater fibril–fibril association. We surmise that the decrease of modulus in Fig. 9 at a fixed salt concentration but changing ion identity (increasing hydration enthalpy) is associated with weaker inter-fibril association, or conversely, stronger repulsion due to decreased charge screening. This is consistent with the interpretation yielded from viscometry data, though the implications in terms of the measured quantities are different – a higher intrinsic viscosity, but a lower gel modulus. Fig. 9B shows that there is an apparent exponential dependence of the elastic modulus on the cation hydration enthalpy. This mirrors the exponential dependence of the gel modulus on the salt concentration seen in Fig. 5C for only NaCl presented. This suggests that the nominal ionic strength I can be corrected using the hydration enthalpy ΔHh to yield an effective ionic strength, Ieff, that captures the role of salt addition agnostic of ion identity. Viewed another way, the difference in the effectiveness of electrostatic screening for ions of different charge densities can be accounted for by a term involving the hydration enthalpy, G′ ∼ exp[f(I,ΔHh)] = exp[f(Ieff)].
 | ||
Fig. 9 (A) Dynamic rheology of CNFs in the presence of chloride salts with indicated monovalent cations at 25 mM. (B) Hydration enthalpy dependence on storage modulus (G′: ◇) and loss factor (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ: □) at w = 10 rad s−1. The noted enthalpy of hydration is tabulated and absolute values listed in Table 2S (ESI†).82 (C) Cole–Cole plot of the CNF dynamic modulus in the absence and the presence of chloride salts with indicated monovalent cations at 25 mM. The solid line represents an ideal Maxwell fluid, a fluid with a single relaxation time, for which δ: □) at w = 10 rad s−1. The noted enthalpy of hydration is tabulated and absolute values listed in Table 2S (ESI†).82 (C) Cole–Cole plot of the CNF dynamic modulus in the absence and the presence of chloride salts with indicated monovalent cations at 25 mM. The solid line represents an ideal Maxwell fluid, a fluid with a single relaxation time, for which  where where  is a characteristic modulus for the system. is a characteristic modulus for the system. | ||
Fig. 9C displays Cole–Cole plots, i.e. the loss modulus G′(ω) as a function of the storage modulus G′(ω). The neat suspension exhibits near Maxwell type behavior as reflected in the semi-circular trace,  , where here the largest value
, where here the largest value  is taken as characteristic of the system for this representation.84,85 The 25 mM-salt-containing samples, however, display progressive departures from Maxwell behavior, with an increase in relaxation times and broadening of relaxation time distributions inferred, on going from Li+ to Cs+. Data are shown for additional salt concentrations in Fig. 2S (ESI†). Experiments conducted on a range of cations and anions revealed a consistent correlation between the elastic modulus and the ion hydration enthalpy, with the modulus decreasing upon increasing the hydration enthalpy. This is seen in data shown in Fig. 10 for three investigated systems, viz. chloride salts (MCl), sodium salts (NaY), and dichloride salts (MCl2), examining the effects of monovalent cations (M+), monovalent anions (Y−), and divalent cations (M2+), respectively.
is taken as characteristic of the system for this representation.84,85 The 25 mM-salt-containing samples, however, display progressive departures from Maxwell behavior, with an increase in relaxation times and broadening of relaxation time distributions inferred, on going from Li+ to Cs+. Data are shown for additional salt concentrations in Fig. 2S (ESI†). Experiments conducted on a range of cations and anions revealed a consistent correlation between the elastic modulus and the ion hydration enthalpy, with the modulus decreasing upon increasing the hydration enthalpy. This is seen in data shown in Fig. 10 for three investigated systems, viz. chloride salts (MCl), sodium salts (NaY), and dichloride salts (MCl2), examining the effects of monovalent cations (M+), monovalent anions (Y−), and divalent cations (M2+), respectively.
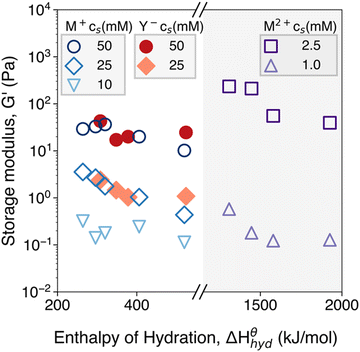 | ||
| Fig. 10 Hydration enthalpy dependence of chloride salts (MCl) with monovalent cations (M+: ○ 50 mM, ◇ 25 mM, ▽ 10 mM), sodium salts (NaY) with monovalent anions (Y−: ● 50 mM, ◆ 25 mM), and dichloride salts (MCl2) with divalent cations (M2+: □ 2.5 mM, △ 1.0 mM) on the storage modulus of CNF suspensions. The storage moduli were extracted from the frequency sweep measurements in the LVR at ω = 10 rad s−1. The enthalpy of hydration values are tabulated and absolute values are obtained from W. E. Dasent's Inorganic Energetics.82 | ||
The ability of short-range ion solvation effects to alter colloidal interactions has been observed in a variety of systems, as described earlier. Work by van der Linden et al. examining the role of such non-DLVO effects on gelation of colloidal silica observed significant changes in gelation time for different monovalent cations, using simple inversion tests.61 Gelation times were the longest for Li+ and the shortest for Cs+, with a strong power law dependence with the salt concentration. The effects were rationalized in terms of ion-specific hydration forces that dominate inter-particle interactions at length scales similar to those of the hydrated ions. The hydration forces represent energy barriers to particle association due to repulsion between structured water layers on or near particle surfaces, due to the hydrophilicity of the surface, or the presence of counterions. This effective hydration potential is a decreasing exponential function of particle separation and decreases with the salt concentration. Quantitative analysis of gelation times yielded estimates for the hydration potential and showed that the potential decreases in a sequence matching the Hofmeister series, but without a quantitative correlation with potentially relevant characteristics of the ionic species, such as hydration enthalpy. These arguments are broadly consistent with our observations – suppression of inter-particle interactions by strongly hydrated species can be seen as a consequence of reduced electrostatic screening.
4. Conclusion
In summary, we examined the behavior of CNF suspensions in water using a combination of viscometry and dynamic shear rheology measurements. At very low concentrations of 0.1 wt% the suspensions appear Newtonian across the range of shear rates considered but exhibit shear thinning at progressively lower shear rates for concentrations in excess of this value. Similarly, the suspensions are viscoelastic fluids at low concentrations, and viscoelastic solids at high concentrations. The concentration dependence of zero shear viscosity and shear moduli establishes a transition from dilute to semi-dilute behavior at around a critical concentration of 0.5 wt%. Addition of NaCl to suspensions in the dilute regime resulted in a decrease in intrinsic viscosity. For suspensions in the semi-dilute regime, NaCl addition results in the formation of clear, uniform gels up to a concentration as high as 50 mM, beyond which CNF aggregation resulted in heterogeneous and opaque samples. The gels show an exponential dependence of elastic modulus on the salt concentration over the range in which clear, uniform gels were observed. These results are consistent with the screening of electrostatic interactions between CNFs that leads to the adoption of more compact conformations of individual CNFs in dilute solution and fibril–fibril association in the semi-dilute regime, leading to a reduction of intrinsic viscosity and persistence length, and an increase in elastic modulus, respectively.The response of CNF suspensions to salt addition showed clear dependence on ion identity. At a given salt concentration, the intrinsic viscosity increases, and the gel modulus decreases, for variation of monovalent cations from a low to high charge density, i.e. from Cs+ to Li+, in direct accordance with the Hofmeister sequence. This demonstrates that the efficacy of electrostatic screening is tightly coupled to the ion identity. These effects are well correlated with ion hydration enthalpies, and remarkably, the elastic modulus shows a clear decreasing exponential dependence on absolute hydration enthalpy. It suggests that the decrease in electrostatic screening by higher charge density species may be rationalized in terms of an effective ionic strength leading to G′ ∼ exp[f(I,ΔHh)] = exp[f(Ieff)]. These results shed new light on the manner in which electrostatic screening governs the conformation and rheology of CNFs in suspensions and have potentially significant implications for the design and optimization of complex fluids and materials containing CNFs. The observed concentration-dependent behavior of CNF suspensions, coupled with the impact of salt addition on electrostatic screening, can be leveraged in applications such as drug delivery, food, cosmetics, and coatings, where the rheological properties of suspensions are crucial. The ability to control CNF conformation and fibril–fibril interactions via the salt concentration and ion identity could enable the tailoring of material properties for specific uses, such as creating uniform gels with controlled elasticity or enhancing the stability and flow behavior of suspensions in diverse formulations.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
R. W. and C. O. O. acknowledge financial support from the Royal Thai Government Scholarship, and the Center for Engineering MechanoBiology (CEMB) under the National Science Foundation (NSF) grant number CMMI-1548571 at the University of Pennsylvania. D. P. acknowledges support on this work from the 2025 National University Development Project grant of Jeju National University funded by the Ministry of Education of the Republic of Korea. We extend our appreciation to Martin Rios, a participant in the 2022 Summer Research Experience for Teachers (RET) program, for assisting with initial data collection on the viscometer. We acknowledge the use of facilities supported by NSF grant number NNCI-2025608 at the Singh Center for Nanotechnology and the University of Pennsylvania Materials Research Science and Engineering Center (MRSEC) under grant number DMR-2309043. We would also like to thank Dr. Jedtanut Thussananutiyakul and Dr. Kyle Vining for their assistance in providing the zeta potential measurements.References
-
T. Heinze, O. A. El Seoud and A. Koschella, Cellulose Derivatives: Synthesis, Structure, and Properties, Springer Series on Polymer and Composite Materials (SSPCM), Springer, 2018 DOI:10.1007/978-3-319-73168-1
.
- L. Jowkarderis and T. G. M. van de Ven, Cellulose, 2014, 21, 2511–2517 CrossRef CAS
.
- L. Jowkarderis and T. G. M. van de Ven, Carbohydr. Polym., 2015, 123, 416–423 CrossRef CAS PubMed
.
- D. Miyashiro, R. Hamano and K. Umemura, Nanomaterials, 2020, 10, 186 CrossRef CAS PubMed
.
- C. Salas, T. Nypelö, C. Rodriguez-Abreu, C. Carrillo and O. J. Rojas, Curr. Opin. Colloid Interface Sci., 2014, 19, 383–396 CrossRef CAS
.
- A. K. Mohanty, M. Misra and L. T. Drzal, J. Polym. Environ., 2002, 10, 19–26 CrossRef CAS
.
- D. Klemm, B. Heublein, H. P. Fink and A. Bohn, Angew. Chem., Int. Ed., 2005, 44, 3358–3393 CrossRef CAS PubMed
.
- D. Park, J. W. Kim and C. O. Osuji, ACS Appl. Eng. Mater., 2024, 2, 772–780 CrossRef CAS
.
- D. Park, C. O. Osuji and J. W. Kim, Small Methods, 2023, 7, 2201195 CrossRef CAS PubMed
.
- A. P. Dhand, R. Poling-Skutvik and C. O. Osuji, Soft Matter, 2021, 17, 4517–4524 RSC
.
- G. Kaufman, S. Mukhopadhyay, Y. Rokhlenko, S. Nejati, R. Boltyanskiy, Y. Choo, M. Loewenberg and C. O. Osuji, Soft Matter, 2017, 13, 2733–2737 RSC
.
- M. C. Li, X. Y. Liu, K. H. Lv, J. S. Sun, C. L. Dai, B. Liao, C. Z. Liu, C. T. Mei, Q. L. Wu and M. Hubbe, Prog. Mater. Sci., 2023, 139, 101187 CrossRef CAS
.
- M. A. Khan, K. Lv, J. S. Sun, H. K. Shen, Y. X. Zhang, A. A. Noor, S. M. Lalji, C. Z. Liu and M. C. Li, Geoenergy Sci. Eng., 2025, 244, 213524 CrossRef CAS
.
- X. X. Sun, Q. L. Wu, S. Lee, Y. Qing and Y. Q. Wu, Sci. Rep., 2016, 6, 31654 CrossRef CAS PubMed
.
- N. Quennouz, S. M. Hashmi, H. S. Choi, J. W. Kim and C. O. Osuji, Soft Matter, 2016, 12, 157–164 RSC
.
- A. Isogai, T. Saito and H. Fukuzumi, Nanoscale, 2011, 3, 71–85 RSC
.
- T. Saito, S. Kimura, Y. Nishiyama and A. Isogai, Biomacromolecules, 2007, 8, 2485–2491 CrossRef CAS PubMed
.
- S. F. Souza, M. Mariano, M. A. De Farias and J. S. Bernardes, J. Colloid Interface Sci., 2019, 538, 228–236 CrossRef CAS PubMed
.
- R. Poling-Skutvik, E. McEvoy, V. Shenoy and C. O. Osuji, Phys. Rev. Mater., 2020, 4, 102601(R) CrossRef
.
- M. A. Hubbe, P. Tayeb, M. Joyce, P. Tyagi, M. Kehoe, K. Dimic-Misic and L. Pal, BioResources, 2017, 12, 9556–9661 CAS
.
- A. I. Koponen, Cellulose, 2020, 27, 1879–1897 CrossRef CAS
.
- M. C. Li, Q. L. Wu, R. J. Moon, M. A. Hubbe and M. J. Bortner, Adv. Mater., 2021, 33, 21 Search PubMed
.
- A. Varadarajan, L. T. Kearney, J. K. Keum, A. K. Naskar and S. Kundu, Biomacromolecules, 2023, 24, 2730–2740 CrossRef CAS PubMed
.
- Z. J. Liu, C. Zhang, R. G. Liu, W. S. Zhang, H. L. Kang, P. P. Li and Y. Huang, Cellulose, 2016, 23, 295–305 CrossRef CAS
.
- T. Phan-Xuan, A. Thuresson, M. Skepö, A. Labrador, R. Bordes and A. Matic, Cellulose, 2016, 23, 3653–3663 CrossRef
.
- T. C. Cao and M. Elimelech, J. Colloid Interface Sci., 2021, 584, 456–463 CrossRef CAS PubMed
.
- S. Shafiei-Sabet, W. Y. Hamad and S. G. Hatzikiriakos, Cellulose, 2014, 21, 3347–3359 CrossRef CAS
.
- A. Wang, Z. Y. Yuan, C. P. Wang, L. M. Luo, W. F. Zhang, S. Geng, J. L. Qu, B. Wei and Y. B. Wen, Biomacromolecules, 2020, 21, 1471–1479 CrossRef CAS PubMed
.
- N. Almeida, L. Rakesh and J. Zhao, Food Hydrocolloids, 2014, 36, 323–331 CrossRef CAS
.
- N. Almeida, L. Rakesh and J. Zhao, Carbohydr. Polym., 2014, 99, 630–637 CrossRef CAS PubMed
.
- N. Mittal, T. Benselfelt, F. Ansari, K. Gordeyeva, S. V. Roth, L. Wågberg and L. D. Söderberg, Angew. Chem., Int. Ed., 2019, 58, 18562–18569 CrossRef CAS PubMed
.
- L. Valencia, E. M. Nomena, S. Monti, W. Rosas-Arbelaez, A. P. Mathew, S. Kumar and K. P. Velikov, Nanoscale, 2020, 12, 15652–15662 RSC
.
- K. M. Z. Hossain, V. Calabrese, M. A. da Silva, S. J. Bryant, J. Schmitt, J. H. Ahn-Jarvis, F. J. Warren, Y. Z. Khimyak, J. L. Scott and K. J. Edler, Polymers, 2021, 13, 951 CrossRef CAS PubMed
.
- Y. Song, B. Kim, J. D. Park and D. J. Lee, Carbohydr. Polym., 2023, 300, 120262 CrossRef CAS PubMed
.
- K. Kobayashi, N. Isobe, R. Kusumi, J. Nemoto and M. Wada, Biomacromolecules, 2024, 25, 864–870 CrossRef CAS PubMed
.
- V. Arumughan, H. D. Özeren, M. Hedenqvist, M. Skepö, T. Nypelö, M. Hasani and A. Larsson, Langmuir, 2023, 39, 15014–15021 CrossRef CAS PubMed
.
- V. Arumughan, T. Nypelö, M. Hasani, H. Brelid, S. Albertsson, L. Wågberg and A. Larsson, Colloids Surf., A, 2021, 626, 127006 CrossRef CAS
.
- S. Arola, Z. N. Kou, B. J. M. Rooijakkers, R. Velagapudi, M. Sammalkorpi and M. B. Linder, Cellulose, 2022, 29, 6109–6121 CrossRef CAS
.
- C. A. S. Batista, R. G. Larson and N. A. Kotov, 2015, 350.
- M. Boström, D. R. M. Williams and B. W. Ninham, Phys. Rev. Lett., 2001, 87, 168103 CrossRef PubMed
.
- M. Lund, P. Jungwirth and C. E. Woodward, Phys. Rev. Lett., 2008, 100, 258105 CrossRef PubMed
.
- H. I. Okur, J. Hladílková, K. B. Rembert, Y. Cho, J. Heyda, J. Dzubiella, P. S. Cremer and P. Jungwirth, J. Phys. Chem. B, 2017, 121, 1997–2014 CrossRef CAS PubMed
.
- J. R. Feng, Y. Zhao, L. Z. Jiang, Y. Zhang and X. N. Sui, Food Hydrocolloids, 2024, 149, 109577 CrossRef CAS
.
- Y. X. Liu, X. Y. Li, J. M. Liu, L. K. Wei, Y. H. Liu, F. P. Lu, W. H. Wang, Q. G. Li and Y. Li, Food Hydrocolloids, 2022, 133, 107976 CrossRef CAS
.
- Y. Q. Lei, H. Ouyang, W. Peng, X. W. Yu, L. Jin and S. G. Li, Gels, 2022, 8, 259 CrossRef CAS PubMed
.
- Y. H. Cho, Y. J. Zhang, T. Christensen, L. B. Sagle, A. Chilkoti and P. S. Cremer, J. Phys. Chem. B, 2008, 112, 13765–13771 CrossRef CAS PubMed
.
- C. D. Qiao, J. L. Zhang, X. G. Ma, W. L. Liu and Q. Z. Liu, Int. J. Biol. Macromol., 2018, 107, 1074–1079 CrossRef CAS PubMed
.
- V. Ball, J. Phys. Chem. B, 2019, 123, 8405–8410 CrossRef CAS PubMed
.
- B. H. Wu, M. Siglreitmeier, C. Debus, D. Schwahn, H. Cölfen and V. Pipich, Macromol. Biosci., 2018, 18, 1800018 CrossRef PubMed
.
- X. J. Wang, C. D. Qiao, K. Song, S. Jiang and J. S. Yao, Colloids Surf., B, 2021, 206, 111944 CrossRef CAS PubMed
.
- X. J. Wang, C. D. Qiao, S. Jiang, L. B. Liu and J. S. Yao, Colloids Surf., B, 2022, 217, 112674 CrossRef CAS PubMed
.
- S. Das, L. Giri and S. Majumdar, Eur. Polym. J., 2023, 189, 111961 CrossRef CAS
.
- A. M. Oechsle, M. Landenberger, M. Gibis, S. B. Irmscher, R. Kohlus and J. Weiss, Int. J. Biol. Macromol., 2015, 79, 518–526 CrossRef CAS PubMed
.
- S. Cruz-León, W. Vanderlinden, P. Müller, T. Forster, G. Staudt, Y. Y. Lin, J. Lipfert and N. Schwierz, Nucleic Acids Res., 2022, 50, 5726–5738 CrossRef PubMed
.
- K. Sakota, D. Tabata and H. Sekiya, J. Phys. Chem. B, 2015, 119, 10334–10340 CrossRef CAS PubMed
.
- S. Z. Moghaddam and E. Thormann, J. Colloid Interface Sci., 2019, 555, 615–635 CrossRef CAS PubMed
.
- T. Klacic, K. Bohinc and D. Kovacevic, Macromolecules, 2022, 55, 9571–9582 CrossRef CAS PubMed
.
- J. C. Courtenay, Y. Jin, J. Schmitt, K. M. Z. Hossain, N. Mahmoudi, K. J. Edler and J. L. Scott, Langmuir, 2021, 37, 6864–6873 CrossRef CAS PubMed
.
- T. Oncsik, G. Trefalt, M. Borkovec and I. Szilagyi, Langmuir, 2015, 31, 3799–3807 CrossRef CAS PubMed
.
- C. Kaulen and U. Simon, RSC Adv., 2018, 8, 1717–1724 RSC
.
- M. van der Linden, B. O. Conchuir, E. Spigone, A. Niranjan, A. Zaccone and P. Cicuta, J. Phys. Chem. Lett., 2015, 6, 2881–2887 CrossRef CAS PubMed
.
- C. Sögaard, K. Kolman, M. Christensson, A. B. Otyakmaz and Z. Abbas, Colloids Surf., A, 2021, 611, 125872 CrossRef
.
- W. Kunz, Curr. Opin. Colloid Interface Sci., 2010, 15, 34–39 CrossRef CAS
.
- A. Salis and B. W. Ninham, Chem. Soc. Rev., 2014, 43, 7358–7377 RSC
.
- B. B. Kang, H. C. Tang, Z. D. Zhao and S. S. Song, ACS Omega, 2020, 5, 6229–6239 CrossRef CAS PubMed
.
- A. Naderi, T. Lindström and T. Pettersson, Cellulose, 2014, 21, 2357–2368 CrossRef CAS
.
- O. Nechyporchuk, M. N. Belgacem and F. Pignon, Biomacromolecules, 2016, 17, 2311–2320 CrossRef CAS PubMed
.
- F. C. Mackintosh, J. Kas and P. A. Janmey, Phys. Rev. Lett., 1995, 75, 4425–4428 CrossRef CAS PubMed
.
- R. J. Hill, Biomacromolecules, 2008, 9, 2963–2966 CrossRef CAS PubMed
.
- P. Schexnailder, E. Loizou, L. Porcar, P. Butler and G. Schmidt, Phys. Chem. Chem. Phys., 2009, 11, 2760–2766 RSC
.
- Y. Feng, M. Taraban and Y. B. Yu, Soft Matter, 2012, 8, 11723–11731 RSC
.
- W. Pabst, E. Gregorová and C. Berthold, J. Eur. Ceram. Soc., 2006, 26, 149–160 CrossRef CAS
.
- S. Mueller, E. W. Llewellin and H. M. Mader, Geophys. Res. Lett., 2011, 38, L13316 Search PubMed
.
- S. Iwamoto, S.-H. Lee and T. Endo, Polym. J., 2014, 46, 73–76 CrossRef CAS
.
- R. Tanaka, T. Saito, H. Hondo and A. Isogai, Biomacromolecules, 2015, 16, 2127–2131 CrossRef CAS PubMed
.
- B. E. Conway, J. Polym. Sci., 1955, 18, 257–274 CrossRef CAS
.
- A. Eich and B. A. Wolf, ChemPhysChem, 2011, 12, 2786–2790 CrossRef CAS PubMed
.
-
M. Rubinstein and R. H. Colby, Polymer physics, Oxford University Press, Oxford, New York, 2003 Search PubMed
.
- T. Odijk, J. Polym. Sci., Polym. Phys. Ed., 1977, 15, 477–483 CrossRef CAS
.
- J. Skolnick and M. Fixman, Macromolecules, 1977, 10, 944–948 CrossRef CAS
.
- A. Brunet, C. Tardin, L. Salomé, P. Rousseau, N. Destainville and M. Manghi, Macromolecules, 2015, 48, 3641–3652 CrossRef CAS
.
- K. P. Gregory, G. R. Elliott, H. Robertson, A. Kumar, E. J. Wanless, G. B. Webber, V. S. J. Craig, G. G. Andersson and A. J. Page, Phys. Chem. Chem. Phys., 2022, 24, 12682–12718 RSC
.
-
W. E. Dasent, Inorganic energetics: an introduction, Cambridge University Press, Cambridge, 2nd edn, 1970 Search PubMed
.
- D. J. Bischoff, T. Lee, K. S. Kang, J. Molineux, W. O. Parker, J. Pyun and M. E. Mackay, Nat. Commun., 2023, 14, 7553 CrossRef CAS PubMed
.
- J. K. Song, N. Holten-Andersen and G. H. Mckinley, Soft Matter, 2023, 19, 7885–7906 RSC
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00339c |
| This journal is © The Royal Society of Chemistry 2025 |



