 Open Access Article
Open Access ArticleInvestigating polymer infiltration kinetics in nanoporous metal scaffolds using UV-vis spectroscopy†
Weiwei Kong‡
 a,
Chuyi Pan‡ab,
Rongyue Lin
a,
Chuyi Pan‡ab,
Rongyue Lin a,
Mengjie Fanc,
John M. Vohs
a,
Mengjie Fanc,
John M. Vohs *c and
Russell J. Composto
*c and
Russell J. Composto *a
*a
aDepartment of Materials Science and Engineering, University of Pennsylvania, Philadelphia, PA, USA. E-mail: composto@seas.upenn.edu
bDepartment of Chemistry, University of Pennsylvania, Philadelphia, PA, USA
cDepartment of Chemical and Biomolecular Engineering, University of Pennsylvania, Philadelphia, PA, USA
First published on 15th July 2025
Abstract
This work demonstrates that the optical response of nanoporous gold (NPG) is directly related to the infiltration extent (IE) of the polymer. Infiltration of poly(2-vinylpyridine) (P2VP) into NPG with a pore radius (Rp) of 34 nm was investigated at 140 °C. The UV-vis spectra of the NPG display plasmon absorption peaks due to the Au ligaments that depend on the height of the P2VP infiltration front in the NPG film. During infiltration, the absorption peak position shifts to longer wavelengths, while the peak height, width, and area increase monotonically with time. For P2VP with molecular weights (Mw) from 85 kDa to 940 kDa, the time to reach 80% of the IE (τ80%) scales as M1.35w, in good agreement with in situ spectroscopic ellipsometer results. AFM and XPS support the strong attraction of P2VP for the Au surface and pores as demonstrated by wetting of P2VP over surface ligaments and a shift of the 4f orbital from the N on P2VP to higher binding energy, respectively. Using nanorods configured as a “T” to model ligament geometry, discrete dipole approximation (DDA) simulations capture the optical properties of the P2VP/NPG nanocomposite during infiltration and confirm experimental results. The evolution of the P2VP/NPG optical properties is attributed mainly to an increase in the effective refractive index within the pores. This study presents UV-vis spectroscopy as an alternative method for studying polymer infiltration into nanoporous metal scaffold films.
Introduction
Polymer nanocomposites (PNCs) have garnered significant attention due to their unique combination of organic and inorganic components,1–3 leading to a range of applications as coating,4,5 membranes6,7 and actuators.8 PNCs with a high inorganic nanofiller content have received much attention because of their ability to improve mechanical properties.9,10 However, creating PNCs with a high loading of nanofiller (>50 vol%) is challenging because the thermodynamics of mixing typically favor nanofiller aggregation and as a result undesirable materials heterogeneity. Various approaches have been developed to enhance nanofiller loading capacity and distribution using pre-fabricated scaffolds, in situ polymerization, nanoparticle assemblies. Examples include the infiltration of polymers into anodized aluminum oxide (AAO) membranes,11–16 in situ polymerization with graphene-based nanofillers,17,18 nanoparticle assemblies,19–29 and nanoporous gold (NPG).30,31 In our previous studies,30,31 we fabricated polymer-infiltrated NPG (PING), with a high nanofiller loading of approximately 50 vol%, by infiltrating a polymer melt into a nanoporous gold scaffold. During the fabrication of the PING composite, polymer kinetics were investigated under conditions of moderate confinement, where chain size was slightly less than the pore diameter. Recent attention11,13,15,30–46 has been given to polymer kinetics under confinement because spatial limitations can alter polymer conformations, thus affecting thermal properties and melt viscosity. For instance, studies have shown that polymers inside channels exhibit an enhanced glass transition temperature (Tg) as compared to the bulk.23–25,30,47 Infiltration kinetics has garnered special interest due to its potential to precisely control properties such as optical response, mechanical performance, and surface topography through careful management of the extent of polymer infiltration.25–27,30,31 Research on polymer kinetics in confined channels is important for fabricating new membranes that respond to stimuli and facilitate ion conductivity.To quantify polymer infiltration into porous media, several techniques have been used, including cross-section SEM,16 small angle X-ray scattering (SAXS),13 dielectric spectroscopy (DS),11,12,14,15,48–51 and spectroscopic ellipsometry (SE).23–28,30,31,47 Cross-section SEM can directly image polymer height inside confined pores. At 130 °C, Hu and Cao studied the infiltration of a polyethylene (PE) melt inside AAO templates (length = 60 μm, diameter = 200 nm).16 The kinetics of infiltration was determined by measuring the PE growth front position (H) as a function of infiltration time.16 The infiltration height was proportional to the square root of infiltration time,16 such that H(t) ∼ 0.28t0.5, where the units of H and t are 10−6 m and s, respectively. This scaling is consistent with the Lucas–Washburn equation, indicating that the PE melt within the AAO behaves like a simple fluid.16 Drawbacks of SEM include the need for image analysis to locate the growth front, and polymer degradation under the electron beam.52
SAXS has also been used to monitor polymer infiltration.13 Shin et al. utilized time-resolved SAXS to observe the capillary rise of polystyrene (PS) within an AAO membrane.13 In this approach, the integrated intensity (Q) was used to extract the volume fractions of pore (Φρ) and alumina (ΦAO) using Q ∼ [ΦU(ρAO)2 + ΦF(ρAO − ρPS)2]ΦρΦAO, where ρ is the electron density, and ΦF and ΦU are the volume fraction of filled and unfilled pores such that ΦF + ΦU = 1.13 The total flux (J) is given by
 | (1) |
Dielectric spectroscopy (DS) is used to measure the dielectric properties of materials. A layer of gold acts as the upper electrode, while the substrate serves as the lower electrode.54–56 DS measures the complex dielectric permittivity (ε*) as a function of frequency (w) and temperature (T). The measured ε*(w, T) are fitted through the Havriliak and Negami (HN) equation:
 | (2) |
 | (3) |
Spectroscopic ellipsometry (SE) has been widely utilized for measuring polymer infiltration.25,26,30,31 SE detects the change in light polarization in the s-plane and p-plane after light reflects from the front and back surfaces of a film.57 The polarization change is represented by the amplitude ratio Ψ and phase difference Δ. Optical properties, such as refractive index, extinction coefficient, and optical anisotropy, can be obtained using models to fit the Ψ and Δ at various wavelengths.57 SE has been used in our previous infiltration studies of polystyrene (PS) and poly(2-vinylpyridine) (P2VP) into NPG.30,31 Because a laser is the probing radiation, the sample heating chamber does not require a vacuum like in SEM and SAXS. Thus, SE lends itself to in situ measurements. Disadvantages include modeling the infiltration front as a sharp boundary and the use of fitting parameters to determine Ψ and Δ, which can introduce uncertainties that depend on the model and parameter constraints.
In this manuscript, we present UV-vis as a reliable and facile tool to measure polymer infiltration into nanoporous gold (NPG). Specifically, the localized surface plasmon resonance (LSPR) can be used to characterize PNCs containing metallic nanoparticles (NPs) as well as metallic nanoporous membranes. For Au NPs and membranes, the LSPR adsorption frequency depends on the separation of AuNPs (ligaments), as well as their orientation58 and volume fraction.59 For metallic films, the LSPR depends on film thickness and valence electron density.60 For spherical Au NPs, the LSPR is in the visible range,61 and undergoes a slight red shift in peak position as particle diameter increases. For Au nanorods, the LSPR exhibits longitudinal and transverse modes due to oscillations of free electrons along each axis.62 Whereas the transverse LSPR is relatively insensitive to the aspect ratio (AR) of nanorods, the longitudinal LSPR increases as the aspect ratio increases.63,64 In contrast to discrete Au NPs, the NPG membrane exhibits a bicontinuous structure of gold ligaments.31,65 The NPG exhibits unique optical properties66–70 because the bicontinuous structure limits the motion of the conducting electrons71 resulting in LSPR absorption in the visible range.72 The optical response depends on ligament aspect ratio70 and pore diameter.72 Detsi et al. showed that the transmittance peak wavelength position increases from 560 to 580 nm as AR of the ligaments increases from 1.2 to 1.8.70 In this study, Detsi et al. modeled the optical response of the Au ligaments using a single Au nanorod with an AR from 2.5 to 9.5. Notably, the two plasmonic modes in NPG arise from longitudinal and transverse LSPR in the ligaments rather than resonant absorption from the film thickness. Lang et al. observed a red shift in the LSPR as pore diameter increases.72 Previous studies on unfilled NPG and water-filled NPG provide important background for our investigation of the optical response of NPG when the pores are partially and completely filled with polymer.
There are considerations before applying UV-vis to study polymer infiltration into nanoporous scaffolds. First, the nanoporous scaffold must be metallic and exhibit a localized surface plasmon resonance (LSPR). Second, typical polymers do not absorb light in the same range as the LSPR. As a result, the absorbance of polymers is generally separated from that of the metallic ligaments in the scaffold, which typically absorb light in the 500 to 1000 nm range, depending on the size and aspect ratio of the ligaments.70 One caveat is that polymers with conjugated backbones, such as polythiophene,73 absorb light in visible or near-IR range. For polymers that have absorbance overlapping with the LSPR, spectrum deconvolution can be performed when applying the UV-vis method. The UV-vis method has one significant advantage compared to spectroscopic ellipsometry (SE). Namely, SE is limited to study ∼100 nm thick metallic scaffolds because SE relies on measuring the change in polarization by light reflected from the nanocomposite films.30,31 In contrast, because UV-vis measures the transmission and absorbance of light, micron-thick NPG films can be characterized. In general, UV-vis spectroscopy can serve as a complementary technique to the more commonly used SE measurements.
Here, we measure the optical properties of NPG during polymer infiltration using UV-vis spectroscopy. The initial sample geometry is a bilayer of a NPG foil (ca. 120 nm) over a poly(2-vinyl pyridine) (P2VP) film (ca. 120 nm) deposited on a glass substrate.30 During infiltration, the absorbance peak redshifts from 517 nm to 521 nm, increases in intensity and broadens. The infiltration extent (IE) of P2VP into the NPG is determined from the peak height, width, and area. In our previous study of P2VP,31 the scaling of IE with molecular weight Mw was measured using in situ SE. Using UV-vis spectroscopy, the time for 80% IE is found to scale as M1.35w, in good agreement with SE results.31 Using AFM and XPS, the strong attraction of P2VP for Au is evidenced by the observed wetting of P2VP on the NPG surface and a shift to higher binding energy of the 4f orbital of N in the 2VP monomer. Using nanorods arranged in a “T” formation to model ligament absorption, discrete dipole approximation (DDA) simulations more accurately capture the optical properties during infiltration than a single rod. Changes in the optical properties of P2VP/NPG during infiltration are primarily due to an increase in the effective refractive index within the pore. This study presents UV-vis spectroscopy as a facile method to quantify polymer infiltration into a nanoporous metal scaffold. Understanding the optical responses of nanoporous metallic scaffolds during and after polymer infiltration allows for the precise design of partially and completely filled polymer composites, which can potentially be applied as membranes for separations.
Materials and methods
Preparation of nanoporous Au/P2VP bilayer
Poly(2-vinyl pyridine) (P2VP) is dissolved in butanol (≥99.9%, Sigma-Aldrich), and stirred overnight. P2VP polymers with narrow polydispersity are used as received. The radius of gyration (Rg) is calculated by where the Kuhn length (b) is 1.8 nm, the number of Kuhn segments (N) is
where the Kuhn length (b) is 1.8 nm, the number of Kuhn segments (N) is  and the Kuhn monomer molar mass is 720 Da.74 The confinement parameter is defined as the ratio of Rg to Rpore, where Rpore = 34 nm as characterized in the previous study.75 The molecular weight, radius of gyration and confinement parameter for P2VP are shown in Table 1.
and the Kuhn monomer molar mass is 720 Da.74 The confinement parameter is defined as the ratio of Rg to Rpore, where Rpore = 34 nm as characterized in the previous study.75 The molecular weight, radius of gyration and confinement parameter for P2VP are shown in Table 1.
| Sample | Mw (Da) | Rg (nm) | Γ = Rg/Rpore |
|---|---|---|---|
| P2VP-85k | 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
7.98 | 0.23 |
| P2VP-302k | 302![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
15.05 | 0.44 |
| P2VP-643k | 643![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
21.96 | 0.65 |
| P2VP-940k | 940![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
26.55 | 0.78 |
The P2VP solutions (2.4 wt%) are spin-coated (4000 rpm, 60 seconds, Laurell Technologies) onto 1 × 1 cm2 cleaned glass substrates and dried at 70 °C for 10 minutes to remove residual solvent. All films were smooth and homogeneous as-cast. Film thickness was measured with a white-light reflectometer (Filmetrics F3-UV) and ranged from 80–150 nm. P2VP is infiltrated into nanoporous gold (NPG) with pore radius (Rpore) of 34 nm and thickness of 120 nm, as characterized in our previous publication.75 The NPG membrane is deposited on top of the P2VP film. The resulting bilayer is then dried at 70 °C on a hot plate for 5 minutes to remove residual H2O. For more information about the preparation of the bilayer samples, please refer to our earlier publications.30,31 These bilayers are annealed on a Mettler heating stage at 140 °C under consistent Argon flow and then characterized by UV-Vis spectroscopy. The precision of the Mettler heating stage is 0.01 °C.
Ultraviolet-visible (UV-vis) spectroscopy
Absorbance spectra are obtained using a Varian Cary Win 5000 UV-VIS-NIR Spectrophotometer with a wavelength range of 200–1000 nm. Measurements of the absorbance are taken with a frequency of 2 nm per sweep at each infiltration time. The P2VP:NPG bilayer, atop a glass substrate, is annealed at 140 °C for different annealing times until complete infiltration is observed. The absorbance spectra of glass are included in the ESI,† and are subtracted from the bilayer absorbance spectra during data analysis.Atomic force microscopy (AFM)
Surface topography of the P2VP:NPG before and after full infiltration are measured using AFM. Tapping mode AFM is performed using Bruker Icon AFM with tips (TAP300AL-G-50 radius of curvature <10 nm, Ted Pella). The images collected are 1 × 1 μm2. The surface properties images are processed using Gwyddion software.In situ spectroscopic ellipsometry (SE)
Spectroscopic ellipsometry (SE) (J.A. Woollam, Alpha SE) is used to measure the refractive index of the P2VP bilayer/composite during the infiltration process. The SE wavelength range is 380–900 nm. A Linkam THMSEL350V heating stage is used for heating. The precision of the heating stage is 0.1 °C with respect to the set temperature. The heating rate is 30 °C min−1. The samples are heated to 70 °C and held at this temperature for 5 minutes to ensure system equilibrium. Then, the sample is heated at a rate of 30 °C min−1 and then held at 140 °C to study infiltration. Because the bulk P2VP has Tg around 100 °C, temperatures higher than 100 °C will induce polymer infiltration into NPG. As a result, the infiltration time refers to the time after the heating plate reaches 100 °C. The heating stage takes ca. 1.3 min to ramp from 100 °C to 140 °C. During infiltration, the temperature is stably held at 140 °C. Effective medium approximation (EMA) Model with two material constitutes is used to capture the change in refractive index within the NPG as polymer fills the pores and approaches the top surface. Details of SE modeling are presented in our previous publications.30,31 The infiltration extent (IE) is given by IE = (nt − ni)/(nf − ni). The initial refractive index, ni, the refractive index prior to the P2VP infiltration and the final refractive index, nf, is the refractive index after complete infiltration.X-ray photoelectron spectroscopy (XPS)
XPS is used to quantify the binding energy of elements in NPG and NPG with polymer before and after it is completely infiltrated. X-ray photoelectron spectroscopy (XPS) was performed in an ultrahigh vacuum chamber equipped with a hemispherical electron energy analyzer (Leybold–Heraeus) collecting at all angles. The incident energy of the Al-Kα X-ray source is 1486.6 eV (VG Microtech). The sampling depth is about 3 nm. To provide insight into the attraction at the P2VP/Au interface, XPS is used to quantify the shift in binding energy of the 4f electrons of Au.Discrete dipole approximation (DDA) simulations
The discrete dipole approximation (DDA) is used to determine the optical properties of the unfilled, partially filled and filled NPG. The MATLAB toolbox containing DDA with surface interaction (DDA-SI) is used.71 The optical properties are the extinction coefficient, localized surface-plasmon resonance (LSPR) wavelength, and LSPR absorption strength, calculated using the MATLAB toolbox.71,76 Because P2VP and air do not exhibit plasmonic resonances and have negligible absorption in the visible range, the dominant contribution to the optical response from the composite is the LSPR from the Au ligaments. Although the dielectric properties of the polymer within the pores influence the plasmonic response, their contribution to direct absorption is minimal over the wavelength range of interest. Thus, in our simulations, we model only the Au ligament structure to represent the NPG. A T-shape structure formed by two nanorods more accurately captures the experimental LSPR absorption spectra compared to a single nanorod, as illustrated in Fig. S13 (ESI†). Fig. 1 shows the T-shape structure used to model the NPG and the incident UV-vis radiation propagating in the z direction. This structure captures the plasmon hybridization of the unfilled NPG as well as the reduction in intensity upon infiltrating a polymer into the pore.77,78 As shown in Fig. 1, the nanorods have a radius of 25 nm, a length of 125 nm, and aspect ratio of 2.5. These dimensions match the size of the ligaments in the experimental system.Results and discussion
Transmittance spectra of NPG filled with air, water and P2VP
Plasmon absorption in the ligaments of the NPG depends on dielectric constant within the pore. The transmittance of unfilled NPG, water-filled NPG and P2VP-filled NPG was compared at constant pore radius, 34 nm. The NPG:P2VP nanocomposite was fabricated by annealing a NPG/P2VP bilayer at 140 °C for 3 h to achieve complete filling.30 Fig. 2 compares the room temperature transmittance spectra for NPG:air, NPG:water and NPG:P2VP. The transmittance minimum for NPG:air is weak because of the high reflectivity of the gold in the visible region, which reduces the absorbed (A) and transmitted (T) intensities. When the absorbance is weak (Fig. S9, ESI†), the transmittance spectra better represent the optical response because T = 10−A.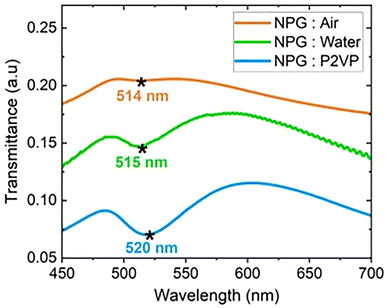 | ||
| Fig. 2 Transmittance of NPG filled with air (unfilled), water and P2VP at 25 °C. The asterisk denotes the shift of the transmittance peak minimum from 514 to 515 to 520 nm as the pore media changes from air (orange) to water (green) to P2VP (blue). The oscillations in NPG:water result from the background subtraction of the Kapton tape.79 Data are shifted to facilitate comparison of spectra. | ||
At the transmission minimum, the intensity decreases and the position redshifts as the refractive index of the medium in the pore increases. Fig. 2 shows that the NPG transmittance spectra minima (i.e., absorbance peak maxima) exhibits a redshift. For the unfilled pores, the minimum is weak and appears at 514 nm. For NPG:water, the transmittance peaks become stronger relative to the minimum. Compared to air (n = 1), the NPG has a lower reflectivity when filled with water (n = 1.33 @ wavelength = 528 nm).80 Because the refractive index difference between gold and water is smaller than gold and air. The NPG:water also undergoes a small red shift from 514 nm to 515 nm due to the increase in the refractive index in the pores. The oscillations at higher wavelengths are due to the background subtraction from the Kapton tape (Fig. S9, ESI†).79 For NPG:P2VP (n = 1.54), the transmittance peaks are stronger than those observed in the NPG:air and NPG:water systems because the reflectivity from the NPG decreases further. For NPG:P2VP, the transmittance minimum appears at 520 nm, indicating a red shift compared to air and water. Interpreting the transmission spectra in terms of absorption, these studies show that the absorption peak exhibits a red shift and grows in intensity as the refractive index of the media in the pores increases.
Absorbance spectra during P2VP infiltration into NPG
As P2VP infiltrates the NPG film from below, the refractive index of the NPG composite increases with time. Motivated by the previous section, which explored how the transmission spectra of nanoporous gold (NPG) are influenced by the medium filling the pores, we investigated the absorbance spectra of NPG during the infiltration of P2VP-643k. This was done at a temperature of 140 °C, with annealing times ranging from 0 to 300 minutes, as illustrated in Fig. 3. At 0 min, corresponding to an NPG/P2VP bilayer on glass, the absorbance peak lies at 517 nm, slightly redshifted compared to the NPG:air sample (514 nm, Fig. 2). This shift is attributed to the interface between NPG and P2VP, as discussed in the mechanism section. With increasing time, the peak shifts to 520 nm after 10 min and reaches 521 nm at 300 min (full infiltration). The absorbance peak also broadens and increases in intensity, consistent with an increase in the dielectric constant inside the pores. Similar redshifts in the absorbance peak and intensity increases were observed for NPG:P2VP-85k, NPG:P2VP-302k, and NPG:P2VP-940k (ESI,† Fig. S10), indicating a common trend during polymer infiltration.In addition to increasing the dielectric constant in the pore, the absorption peak position and intensity can be affected by strong coupling between the media and the gold surface. For example, the localized surface plasmon resonance (LSPR) of Au shifts to longer wavelengths with stronger intensity when conjugated with poly(vinyl pyrrolidone) (PVP) through electron doping in the valence band.81 P2VP is expected to be a stronger electron-donator compared to PVP because PVP:Au has a lower Au–Au coordination number than P2VP:Au, namely, 7.5 ± 0.7 and 8.3 ± 0.7, respectively.82 As a result, when P2VP binds to gold, an increase in electron doping in the gold leads to an enhancement of the LSPR, consistent with UV-vis observations. In a later section, the interfacial electron doping of NPG:P2VP will be studied using XPS.
Analysis of absorbance spectra and comparison of infiltration kinetics with SE results
In this section, we relate the absorbance characteristics, namely peak height, peak width and peak area to the extent of P2VP infiltration into the NPG. Using data from Fig. 3, Fig. 4a shows that the relative peak height initially increases rapidly at early times and then more slowly after 100 min. This behavior mimics the increase in pore refractive index measured by in situ SE in our previous publication.30,31 From the absorption spectra, the initial peak height (hi) and final peak height (hf) can be used to determine the infiltration extent, IE = (h0 − hi)/(hf − hi). The time dependence of IE calculated from UV-vis spectra is shown in Fig. 4b. Similarly, the IE was determined from the peak width and peak area as shown in ESI,† Fig. S12. The IE determined from these three approaches (height, width, area) agrees with each other within experimental uncertainty. In the following analysis, only the peak height will be considered. For NPG:P2VP-643k, Fig. 4b compares IE determined by UV-vis (red) and in situ SE75 (black) methods. The IE values are in good agreement from 0 to ca. 0.85. For IE greater than ca. 0.85, the UV-vis results exhibit a slightly greater value of IE compared to the SE results. This difference may be attributed to the sensitivity of the plasmon absorption peak to the P2VP wetting the pores ahead of the growth front. Because SE uses a two-layer EMA model, the IE may be slightly less than that measured by UV-vis because it ignores the P2VP wetting ahead of the growth front, which is particularly important near the top surface (i.e., IE > 0.85). At long times (i.e., 300 min), the IE values converge as expected for completely filled NPG. This behavior is consistent with the closing of the gap between the wetting front (P2VP adsorption on pores) and growth front (P2VP backfilling through coated pores) during late stages of infiltration.Using data like Fig. 4b for Mw = 85k, 302k, 643k and 940k Da, the time to reach 80% IE (τ80%) is determined and plotted in Fig. 5 for the UV-vis (red) and in situ SE (black) methods. The τ80% values at each Mw are in statistical agreement according to their standard deviations. In previous studies using in situ SE, τ80% was found to scale with Mw as 1.40 ± 0.03, whereas the UV-vis approach yields a scaling of 1.35 ± 0.04. This good agreement indicates that the UV-vis approach is an accurate method to determine infiltration kinetics in metallic scaffolds. In this section, we demonstrated that UV-vis is a simple method to determine the kinetics of polymer infiltration into NPG and that the results agree with the more common in situ SE method.
 | ||
| Fig. 5 The 80% infiltration times for P2VP with molecular weights of 85k, 302k, 643k and 940k at 140 °C. The in situ SE infiltration times are from our previous study.75 The UV-vis (red) and in situ SE (black) measurements are in good agreement. Reprinted (adapted) with permission from Macromolecules, 2025, 58(10), 5058–5070. Copyright 2025 American Chemical Society. | ||
Surface characterization of NPG after complete filling by P2VP
The previous section demonstrated that the plasmon resonance peak can be used to quantify polymer infiltration kinetics in a nanoporous metal scaffold. Here, we characterize the near surface region of the NPG:P2VP. For strongly attractive polymer/wall interactions, such as P2VP with gold, simulations show that P2VP forms a strongly adsorbed wetting layer on gold surfaces,75 which reduces chain mobility and slows infiltration dynamics. The present study provides new experimental insights into the attraction of P2VP for the Au ligaments.P2VP forms a thin wetting layer over the top NPG surface after complete infiltration. Fig. 6a and b show AFM height images of the NPG:P2VP-643k surface before and after complete infiltration, respectively. Fig. 6a shows the ligaments (bright) and pores (dark) of the NPG. The length and width of the ligaments are approximately 130 nm × 50 nm, respectively. The RMS roughness is 10.2 nm for the unfilled case. Upon annealing for 5 h at 140 °C to ensure complete infiltration (cf. Fig. 3b), the topmost surface of the NPG no longer shows distinct ligaments. This observation differs from polystyrene (PS) infiltration into NPG where ligaments remain distinct, indicating that PS doesn’t completely wet the top surface.31 Fig. 6b shows a topography map suggesting that the NPG ligaments are partially covered by P2VP, evidenced by the circular, high features on the surface. Correspondingly, the RMS roughness decreases from 10.2 nm to 3.4 nm, indicating a smoother surface compared to the pre-infiltrated NPG surface. Although the fully infiltrated NPG is less rough than the unfilled scaffold, the surface retains some roughness because of the P2VP droplets that cover the ligaments at the surface (Fig. 6b). The morphology of the completed infiltrated P2VP scaffold agrees with our previous results.75 Fig. S1–S3 (ESI†) show the corresponding AFM images of P2VP bilayers at Mw = 85k, 302k, and 940k Da before and after complete infiltration. Fig. S4–S7 (ESI†) show the corresponding phase images. All images are consistent with a smoother surface after complete infiltration. To confirm that the surface is wet by P2VP, Fig. S8 (ESI†) compares the water contact angles (WCA) of fully infiltrated NPG:P2VP (63°) and NPG:PS (70°). These values are consistent with surfaces of pure P2VP and a mixture of PS and Au, respectively, as noted in ESI,† Fig. S8.
XPS provides insight into the electronic structure of gold atoms in contact with the vinyl pyridine units from P2VP. XPS measures the binding energy of electrons, with a sampling depth of about 3 nm. Fig. 6c shows the binding energies of the core–shell 4f5/2 and 4f7/2 electrons before (gold) and after (blue) complete P2VP infiltration into NPG. The pristine NPG has 4f5/2 binding energy at 87.63 eV, while the 4f7/2 binding energy lies at 84.02 eV. These values are in good agreement with literature.82 Upon infiltration with P2VP, the corresponding binding energies decrease to 87.15 eV and 83.56 eV, a shift of 0.48 eV and 0.46 eV relative to the pristine case. The reduction in binding energies is consistent with a change in the chemical environment spatial redistribution of the valence electrons which create a change in the binding energies of the core electrons. We attribute this shift to electron repulsion in the valence shell, consistent with electron donation from P2VP to Au.83,84 The decrease in core–shell binding energies can be attributed to the strong interaction between P2VP and Au. The electron-donating behavior of P2VP originates from the alkyl chains adjacent to the nitrogen atom,82 making nitrogen more electronegative, thus enhancing the interaction between the 2VP monomer and Au at the interface. In summary, the wetting of P2VP on Au ligaments is consistent with the decrease in the binding energy of Au 4f electrons attributed to the attraction between Au atoms and adsorbed P2VP although the change in the UV-vis spectra during P2VP infiltration is mainly due to an increase in the dielectric constant within the pore, the interfacial interactions between P2VP and Au can also affect the LSPR spectra. Further studies are needed to explore the influence of interfacial interactions and NPG absorbance. In the next section, the discrete dipole approximation (DDA) and the effective medium approximation (EMA) are used to model the optical response of NPG during polymer infiltration.
Analysis of absorption spectra of NPG filled with air, water and P2VP
The discrete dipole approximation (DDA) was used to determine the adsorption spectra of unfilled, partially filled, and filled NPG. As shown in Fig. 1, two perpendicular nanorods forming a T were used to capture the Au ligament structure. Although previous research used a single nanorod;70 the present studies suggest that a “T” structure could better capture LSPR. The “T” provides a simple representation of the NPG ligament structure while also introducing plasmon hybridization effects, which reduces the sensitivity of the LSPR to changes in the surrounding dielectric medium.77 For comparison, the DDA simulations for a single nanorod are presented in Fig. S13 (ESI†). The longitudinal LSPR is highly sensitive to polymer infiltration and will be the primary focus of DDA simulations. To test DDA and the “T” model, Fig. 7 shows the absorption spectra of NPG in air (n = 1.0), water (n = 1.33), and P2VP (n = 1.54). As the refractive index in the pore increases from n = 1.0 to n = 1.54, the peak shifts towards higher wavelengths, namely 515, 521, and 522 nm, respectively. Because the absorbance spectra scale with the inverse of the transmission spectra, we can compare the DDA with experimental results. The DDA spectra are in qualitative agreement with the transmittance spectra from NPG in the same medium as shown in Fig. 2, with peak positions at 514 (air), 515 (water), and 520 (P2VP) nm, respectively. The difference between the UV-vis and DDA spectra near 700 nm is attributed to the scattering contribution in the former. The peak height also increases as the refractive index within the pore increases. Namely, the peak height increases from 0.264 to 0.581, and then further to 0.815 (arbitrary units), respectively, in qualitative agreement with experimental results shown in Fig. 2. These simulations show that the absorption peak position and intensity of NPG depend on the refractive index of the media within the pore.Converting the DDA absorption spectra to infiltration extent of P2VP
To investigate the relationship between P2VP infiltration and absorbance, the optical properties of NPG:P2VP composites at different infiltration extents (IE) were calculated for wavelengths from 400 to 700 nm. As shown in Fig. 8a, the total height (TH) of the T shape is 150 nm (left). The infiltrated height (IH) is set manually, and the surrounding medium has a refractive index of 1.54. IE is given by 100% × (IH/TH). For example, Fig. 8a (middle) shows a partial infiltration case for IE = 0.5, where bottom region is P2VP (purple) and the top region is surrounded by air (n = 1.0). Fig. 8a (right) shows the case of complete infiltration, IE = 1. As IE increases from 0 to 1, Fig. 8b shows that the absorption peak shifts from 515 to 522 nm, and the peak width and intensity broaden and increase, respectively. The simulation results qualitatively agree with the experimental observations in Fig. 3. Noticeably, the left shoulder of the absorption coefficient spectra remains constant at ∼470 nm during infiltration, in agreement with results in Fig. 3, while the red-shifted right shoulder broadens the peak, consistent with previous experiments.63,64 Interestingly, the work by Detsi et al. also shows a relatively constant left shoulder and a shift in the right shoulder as the NPG aspect ratio (AR) increases.70 Namely, as AR increases from 3.8 to 5.1,70 the transmittance peak becomes broader and deeper. The left shoulder (transverse) undergoes a blue shift of ∼3 nm whereas the right shoulder (longitudinal) undergoes a red shift of ∼32 nm.70 The two shoulders in the transmittance spectra originate from the absorption minima in the UV-vis spectra.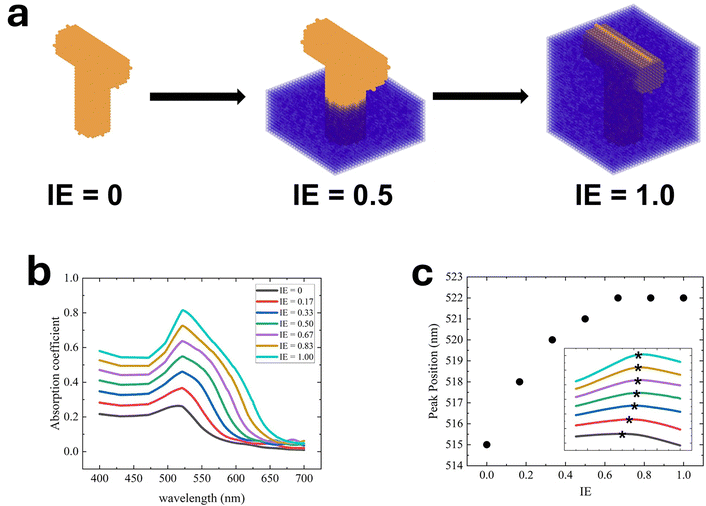 | ||
| Fig. 8 (a) Schematic of the T-shaped Au nanorod structure (gold) corresponding to infiltration extents (IE) of 0, 0.5, and 1.0. IE is defined as the infiltrated height relative to the total height of the T-shaped structure (150 nm). The medium representing P2VP is shown in purple. (b) DDA calculation of the absorption spectra for unfilled (IE = 0), partially filled (0.17, 0.33, 0.50, 0.67, 0.83), and filled (1.0) states. (c) The peak position versus infiltration extent for unfilled, partially filled and filled states. The inset highlights the peak shift between 490 nm to 540 nm for data in Fig. 8b. | ||
The increase in the refractive index of the surrounding medium also accounts for the red shift of the LSPR adsorption peak. Fig. 8c shows the peak position as a function of infiltration extent. Initially, as IE increases from 0 to 0.5, the peak position increase is large, from 515 nm to 521 nm. However, as IE increases from 0.5 to 1.0, the shift is much less, increasing from 521 nm to 522 nm. Interestingly, the peak position approaches a constant value of 522 nm near IE = 0.67, before complete infiltration (IE = 1.0) is reached. However, the adsorption peak width and shape continue to evolve for IE = 0.67, 0.83, and 1.0. The decoupling of peak position and absorption intensity as a function of IE requires further investigation.
Correlation between experimental and DDA simulated infiltration extents
Although the DDA simulations do not explicitly include infiltration time, this section shows that the DDA simulations correlate with UV-vis measurements of IE, which are time-dependent. Whereas the DDA simulation correlates adsorption peak position with IE (Fig. 8c), UV-vis experiments measure peak height as a function of infiltration time, as shown in Fig. 4a. As the height of the medium surrounding the “T” structure increases (i.e., IE increases), the DDA absorption peak position, width, and height increase. As shown in Fig. 3, the UV-vis absorption spectra evolve similarly as a function of time. This observation suggests that the IE from DDA can be correlated with experimental measurements of IE. For the UV-vis method, peak height initially increases rapidly and more slowly as infiltration time increases. As shown in Fig. 4b, the scaling of IE with infiltration time is similar. To build upon the DDA peak position analysis in Fig. 8c, the peak height, full width at half maximum (FWHM), and area under the curve (AUC) are quantified and analyzed. As shown in Fig. 9, the peak height (a.u.) increases linearly from 0.264 to 0.815 as IE increases from 0 to 1 with a slope of 0.55 ± 0.01. The AUC and FWHM also increase linearly as IE increases (ESI,† Fig. S15). By using the linear scaling of peak height, AUC, and FWHM as a function of IE, the absorbance spectra can be determined. In summary, DDA simulations of the absorbance spectra show that the peak height, area under the curve (AUC), and full width at half maximum (FWHM) increase linearly with infiltration extent, as illustrated in Fig. 9 and Fig. S15 (ESI†). These relationships support the conclusion that changes in the absorbance spectra during infiltration correlate with an increase in the refractive index as the polymer growth front approaches the surface of the “T” structure (DDA) or NPG (UV-vis).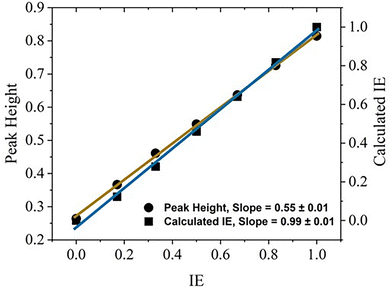 | ||
| Fig. 9 DDA peak height (solid circles; left y-axis) of “manually” infiltrated T-shaped nanorods (e.g., Fig. 8a) and calculated infiltration extent (solid squares; right y-axis) as a function of infiltration extent (IE). The linear fit for the peak height yields a slope of 0.55 ± 0.01 with Pearson's r = 0.99962 and R-square (COD) = 0.99925. Infiltration extent is defined as the infiltration height of the medium relative to the total height of the “T” model (150 nm). For the DDA spectra, the area under the curve (AUC) and full width at half maximum (FWHM) also increase linearly with infiltration extent, as shown in Fig. S15 (ESI†). The correlation between the calculated IE and IE is good, with a slope of 0.99 and a standard error of 0.01. | ||
To further investigate the relationship between peak shape and IE, the manually set IE from the DDA simulations (Fig. 8c) are compared with the calculated IE as shown in Fig. 9. Using the peak height (h) values from Fig. 8a, the calculated IE is given by IEC = (h − h0)/(hf − h0), where h0 = 0.264 and hf = 0.815. The calculated IE increases linearly as IE increases, with a slope of 0.99 ± 0.01. The agreement between the calculated and manually set IE confirms that the absorbance peak captures polymer infiltration kinetics. Similar comparisons were also conducted for AUC and FWHM, leading to similar results with a linear slope close to 1 (Fig. S16, ESI†). This DDA analysis demonstrates that UV-vis absorption spectra can effectively quantify polymer infiltration in a metallic scaffold, like the nanoporous gold used in this study.
Conclusion
This paper demonstrates that UV-vis spectroscopy is a facile method to measure polymer infiltration into nanoporous gold (NPG). At 140 °C, P2VP (Mw = 85–940 kDa) is infiltrated into an NPG film with pore radius of 34 nm. The absorption spectra exhibit a maximum due to the transverse local surface plasmon resonance from the ligaments in the NPG. During annealing, the adsorption peak height and width increase, and the peak position undergoes a red shift. The main reason for this behavior is attributed to an increase in the refractive index within the pores as the P2VP growth front approaches the NPG surface. The peak height, width, and area under the curve (AUC) are found to correlate with the infiltration extent (IE) of P2VP into NPG. UV-vis measurements show that the time for P2VP to reach 80% (τ80%) infiltration scales as M1.35w, in good agreement with SE results. Moreover, the τ80% values at each Mw are in good agreement with SE results. This comparison shows that plasmonic absorption can be used to measure the kinetics of polymer infiltration in NPG. These studies also show that the absorption characteristics (height, width, AUC) are directly proportional to the IE.AFM and XPS surface studies support strong wetting of P2VP for the Au surface and pores, as demonstrated by wetting of P2VP over surface ligaments and a shift to higher binding energy of the core shell 4f electrons in Au, respectively. Further studies are needed to quantify the effect of vinyl pyridine adsorption on the surface plasmon resonance of Au. For example, XPS can be used to measure the binding energy of the valence electrons in unfilled NPG and completely filled NPG. Because the valence electrons are the source of the LSPR,57 a shift in the binding energy would indicate that the NPG/polymer interface can influence absorption beyond the dominant effect due to the increase in the refractive index (dielectric constant) within the pore.
To model ligaments in the NPG, we use nanorods arranged in a “T” configuration. Discrete dipole approximation (DDA) simulations of absorption are conducted over a range of 400 to 700 nm to capture the transverse localized surface plasmon resonance (LSPR) from the NPG. The infiltration extent is manually set by filling the area around the rod with polymer from the bottom (IE = 0) to the top (IE = 1) of the “T”. The peak shift, height, width and AUC as a function of increasing IE are found to capture UV-vis experiments, even though time is not explicitly included in the DDA simulation. These results show that the effective medium refractive index of the T-shaped nanorods and polymer captures changes in the absorption spectra of the NPG. Whereas this study involves a polymer that strongly absorbs to gold, future studies of hydrophobic polymers will provide insight into the dominant contribution to changes in the absorption peak, namely the refractive index within the pore versus the interfacial effects due to polymer adsorption on the pore walls. Grafting polymer onto the pore wall would be an alternative approach to modify the plasmonic properties of the NPG. The present study presents UV-vis spectroscopy as a facile method for studying polymer infiltration into nanoporous metal films. By understanding the optical responses of polymer infiltration of a NPG scaffold, filled and partially filled polymer composites can be precisely fabricated with potential applications as actuators and separation membranes.
Author contributions
R. J. C. and W. K. conceived and planned for the project. C. P. and W. K. developed the experimental procedure and conducted all experimental measurements (besides XPS) and analysis. R. L. and W. K. conducted all simulation development and analysis. M. F. conducted the XPS experiments. W. K., C. P., R. L. wrote the manuscript. R. J. C., and J. M. V. edited the manuscript. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the ESI.†Acknowledgements
Experimental studies (CP, WK, RJC) were funded by the National Science Foundation's (NSF) Division of Materials Research under grant DMR-1905912 and DMR-2407300. Partial support was received from ACS/PRF 62482-ND7 (WK, RJC). W. K. acknowledges support from the Vagelos Institute for Energy Science and Technology (VIEST) through the 2023-24 VIEST Graduate Fellowship. C. P. acknowledges support from the Vagelos Integrated Program in Energy Research (VIPER). W. K. and C. P. also acknowledge characterization facilities in Singh Center for Nanotechnology, which is supported by the NSF Nanotechnology Coordinated Infrastructure Program under grant NNCI-2025608 and the Laboratory for Research on the Structure of Matter under grant MRSEC DMR-2309043. The authors would like to thank Professor Eric Detsi for insightful suggestions about modeling the UV-vis spectra.References
- A. C. Balazs, T. Emrick and T. P. Russell, Nanoparticle Polymer Composites: Where Two Small Worlds Meet, Science, 2006, 314, 1107–1110 CrossRef CAS PubMed.
- J. Kim, et al., Estimation of the concentration of nano-carbon black in tire-wear particles using emission factors of PM10, PM2.5, and black carbon, Chemosphere, 2022, 303, 134976 CrossRef CAS.
- E. Guth, Theory of Filler Reinforcement, J. Appl. Phys., 1945, 16, 20–25 CrossRef CAS.
- C. R. Bilchak, Y. Huang, B. C. Benicewicz, C. J. Durning and S. K. Kumar, High-Frequency Mechanical Behavior of Pure Polymer-Grafted Nanoparticle Constructs, ACS Macro Lett., 2019, 8, 294–298 CrossRef CAS PubMed.
- P. Rittigstein and J. M. Torkelson, Polymer-nanoparticle interfacial interactions in polymer nanocomposites: confinement effects on glass transition temperature and suppression of physical aging: Polymer-Nanoparticle Interfacial Interactions, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 2935–2943 CrossRef CAS.
- C. R. Bilchak, et al., Polymer-Grafted Nanoparticle Membranes with Controllable Free Volume, Macromolecules, 2017, 50, 7111–7120 CrossRef CAS.
- T. C. Merkel, et al., Ultrapermeable, Reverse-Selective Nanocomposite Membranes, Science, 2002, 296, 519–522 CrossRef CAS PubMed.
- Y. Liu, et al., Electro-thermal actuation in percolative ferroelectric polymer nanocomposites, Nat. Mater., 2023, 22, 873–879 CrossRef CAS PubMed.
- U. G. K. Wegst, H. Bai, E. Saiz, A. P. Tomsia and R. O. Ritchie, Bioinspired structural materials, Nat. Mater., 2015, 14, 23–36 CrossRef CAS PubMed.
- M. A. Meyers, J. McKittrick and P.-Y. Chen, Structural Biological Materials: Critical Mechanics-Materials Connections, Science, 2013, 339, 773–779 CrossRef CAS PubMed.
- Y. Yao, et al., Complex dynamics of capillary imbibition of poly(ethylene oxide) melts in nanoporous alumina, J. Chem. Phys., 2017, 146, 203320 CrossRef PubMed.
- C.-H. Tu, J. Zhou, H.-J. Butt and G. Floudas, Absorption Kinetics of cis-1,4-Polyisoprene in Nanopores by In Situ Nanodielectric Spectroscopy, Macromolecules, 2021, 54, 6267–6274 CrossRef CAS.
- K. Shin, et al., Enhanced mobility of confined polymers, Nat. Mater., 2007, 6, 961–965 CrossRef CAS PubMed.
- C.-H. Tu, M. Steinhart, H.-J. Butt and G. Floudas, In Situ Monitoring of the Imbibition of Poly(n-butyl methacrylates) in Nanoporous Alumina by Dielectric Spectroscopy, Macromolecules, 2019, 52, 8167–8176 CrossRef CAS.
- C.-H. Tu, J. Zhou, M. Doi, H.-J. Butt and G. Floudas, Interfacial Interactions During In Situ Polymer Imbibition in Nanopores, Phys. Rev. Lett., 2020, 125, 127802 CrossRef CAS PubMed.
- G. Hu and B. Cao, Flows of Polymer Melts through Nanopores: Experiments and Modelling, J. Therm. Sci. Technol., 2013, 8, 363–369 CrossRef.
- H. Kim, A. A. Abdala and C. W. Macosko, Graphene/Polymer Nanocomposites, Macromolecules, 2010, 43, 6515–6530 CrossRef CAS.
- D. Hou, et al., Simultaneous Reduction and Polymerization of Graphene Oxide/Styrene Mixtures To Create Polymer Nanocomposites with Tunable Dielectric Constants, ACS Appl. Nano Mater., 2020, 3, 962–968 CrossRef CAS.
- Y.-R. Huang, et al., Polymer nanocomposite films with extremely high nanoparticle loadings via capillary rise infiltration (CaRI), Nanoscale, 2015, 7, 798–805 RSC.
- Y. Jiang, J. L. Hor, D. Lee and K. T. Turner, Toughening Nanoparticle Films via Polymer Infiltration and Confinement, ACS Appl. Mater. Interfaces, 2018, 10, 44011–44017 CrossRef CAS.
- Y. Qiang, S. S. Pande, D. Lee and K. T. Turner, The Interplay of Polymer Bridging and Entanglement in Toughening Polymer-Infiltrated Nanoparticle Films, ACS Nano, 2022, 16, 6372–6381 CrossRef CAS PubMed.
- Y. Qiang, K. T. Turner and D. Lee, Role of Polymer–Nanoparticle Interactions on the Fracture Toughness of Polymer-Infiltrated Nanoparticle Films, Macromolecules, 2023, 56, 122–135 CrossRef CAS.
- J. L. Hor, et al., Nanoporous Polymer-Infiltrated Nanoparticle Films with Uniform or Graded Porosity via Undersaturated Capillary Rise Infiltration, ACS Nano, 2017, 11, 3229–3236 CrossRef CAS PubMed.
- J. L. Hor, H. Wang, Z. Fakhraai and D. Lee, Effects of polymer–nanoparticle interactions on the viscosity of unentangled polymers under extreme nanoconfinement during capillary rise infiltration, Soft Matter, 2018, 14, 2438–2446 RSC.
- J. L. Hor, H. Wang, Z. Fakhraai and D. Lee, Effect of Physical Nanoconfinement on the Viscosity of Unentangled Polymers during Capillary Rise Infiltration, Macromolecules, 2018, 51, 5069–5078 CrossRef CAS.
- R. B. Venkatesh and D. Lee, Conflicting Effects of Extreme Nanoconfinement on the Translational and Segmental Motion of Entangled Polymers, Macromolecules, 2022, 55, 4492–4501 CrossRef CAS.
- R. B. Venkatesh and D. Lee, Interfacial Friction Controls the Motion of Confined Polymers in the Pores of Nanoparticle Packings, Macromolecules, 2022, 55, 8659–8667 CrossRef CAS.
- R. B. Venkatesh, et al., Effect of polymer–nanoparticle interactions on solvent-driven infiltration of polymer (SIP) into nanoparticle packings: a molecular dynamics study, Mol. Syst. Des. Eng., 2020, 5, 666–674 RSC.
- T. Ren, et al., Increase in the effective viscosity of polyethylene under extreme nanoconfinement, J. Chem. Phys., 2024, 160, 024909 CrossRef CAS PubMed.
- S. M. Maguire, et al., Effect of Nanoscale Confinement on Polymer-Infiltrated Scaffold Metal Composites, ACS Appl. Mater. Interfaces, 2021, 13, 44893–44903 CrossRef CAS PubMed.
- W. Kong, et al., Capillary filling dynamics of polymer melts in a bicontinuous nanoporous scaffold, J. Chem. Phys., 2024, 160, 044904 CrossRef CAS PubMed.
- R. Kimmich, N. Fatkullin, C. Mattea and E. Fischer, Polymer chain dynamics under nanoscopic confinements, Magn. Reson. Imaging, 2005, 23, 191–196 CrossRef CAS PubMed.
- R. Mangal, S. Srivastava and L. A. Archer, Phase stability and dynamics of entangled polymer–nanoparticle composites, Nat. Commun., 2015, 6, 7198 CrossRef PubMed.
- J. L. Keddie, R. A. L. Jones and R. A. Cory, Size-Dependent Depression of the Glass Transition Temperature in Polymer Films, Europhys. Lett., 1994, 27, 59–64 CrossRef CAS.
- J. Choi, N. Clarke, K. I. Winey and R. J. Composto, Fast Polymer Diffusion through Nanocomposites with Anisotropic Particles, ACS Macro Lett., 2014, 3, 886–891 CrossRef CAS PubMed.
- M. Tarnacka, et al., The Impact of Molecular Weight on the Behavior of Poly(propylene glycol) Derivatives Confined within Alumina Templates, Macromolecules, 2019, 52, 3516–3529 CrossRef CAS.
- M. D. Ediger and J. A. Forrest, Dynamics near Free Surfaces and the Glass Transition in Thin Polymer Films: A View to the Future, Macromolecules, 2014, 47, 471–478 CrossRef CAS.
- H. M. Schneider, P. Frantz and S. Granick, The Bimodal Energy Landscape When Polymers Adsorb, Langmuir, 1996, 12, 994–996 CrossRef CAS.
- F. Lange, et al., Large-Scale Diffusion of Entangled Polymers along Nanochannels, ACS Macro Lett., 2015, 4, 561–565 CrossRef CAS PubMed.
- C. Roth and J. Dutcher, Mobility on Different Length Scales in Thin Polymer Films, in Soft Materials, ed. A. Marangoni and J. Dutcher, CRC Press, 2004, pp. 1–38 DOI:10.1201/9780203027004.ch1.
- J. Choi, et al., Universal Scaling of Polymer Diffusion in Nanocomposites, ACS Macro Lett., 2013, 2, 485–490 CrossRef CAS PubMed.
- S. Askar, T. Wei, A. W. Tan and J. M. Torkelson, Molecular weight dependence of the intrinsic size effect on Tg in AAO template-supported polymer nanorods: a DSC study, J. Chem. Phys., 2017, 146, 203323 CrossRef PubMed.
- G. J. Schneider, Dynamics of nanocomposites, Curr. Opin. Chem. Eng., 2017, 16, 65–77 CrossRef.
- S. Gam, et al., Macromolecular Diffusion in a Crowded Polymer Nanocomposite, Macromolecules, 2011, 44, 3494–3501 CrossRef CAS.
- L. Bocquet, Nanofluidics coming of age, Nat. Mater., 2020, 19, 254–256 CrossRef CAS PubMed.
- A. Bansal, et al., Quantitative equivalence between polymer nanocomposites and thin polymer films, Nat. Mater., 2005, 4, 693–698 CrossRef CAS PubMed.
- H. Wang, et al., Dramatic Increase in Polymer Glass Transition Temperature under Extreme Nanoconfinement in Weakly Interacting Nanoparticle Films, ACS Nano, 2018, 12, 5580–5587 CrossRef CAS PubMed.
- A. Serghei, D. Chen, D. H. Lee and T. P. Russell, Segmental dynamics of polymers during capillary flow into nanopores, Soft Matter, 2010, 6, 1111 RSC.
- A. Serghei, et al., Density Fluctuations and Phase Transitions of Ferroelectric Polymer Nanowires, Small, 2010, 6, 1822–1826 CrossRef CAS PubMed.
- A. Serghei, W. Zhao, X. Wei, D. Chen and T. P. Russell, Nanofluidics with phase separated block-copolymers: glassy dynamics during capillary flow, Eur. Phys. J.: Spec. Top., 2010, 189, 95–101 CAS.
- A. Houachtia, et al., Nanofluidics Approach to Separate between Static and Kinetic Nanoconfinement Effects on the Crystallization of Polymers, Nano Lett., 2015, 15, 4311–4316 CrossRef CAS PubMed.
- Y. Guohua, Z. Dezhang, P. Haochang, X. Hongjie and C. Shoumian, Beam Induced Degradation Effect in Ion Beam Analysis of Polymer, Chin. Phys. Lett., 1991, 8, 472–475 CrossRef.
- W. Schnabel, Polymer Degradation: Principles and Practical Applications, Hanser [u.a.], München, 1981 Search PubMed.
- S. Alexandris, G. Sakellariou, M. Steinhart and G. Floudas, Dynamics of Unentangled cis-1,4-Polyisoprene Confined to Nanoporous Alumina, Macromolecules, 2014, 47, 3895–3900 CrossRef CAS.
- C. Politidis, S. Alexandris, G. Sakellariou, M. Steinhart and G. Floudas, Dynamics of Entangled cis-1,4-Polyisoprene Confined to Nanoporous Alumina, Macromolecules, 2019, 52, 4185–4195 CrossRef CAS.
- S. Alexandris, et al., Interfacial Energy and Glass Temperature of Polymers Confined to Nanoporous Alumina, Macromolecules, 2016, 49, 7400–7414 CrossRef CAS.
- J. D. Bagley, H. Dennis Tolley and M. R. Linford, Reevaluating the conventional approach for analyzing spectroscopic ellipsometry psi/delta versus time data. Additional statistical rigor may often be appropriate: reevaluating the standard analysis of ellipsometry psi/delta/time data, Surf. Interface Anal., 2016, 48, 186–195 CrossRef CAS.
- M. J. A. Hore, A. L. Frischknecht and R. J. Composto, Nanorod Assemblies in Polymer Films and Their Dispersion-Dependent Optical Properties, ACS Macro Lett., 2012, 1, 115–121 CrossRef CAS PubMed.
- M. J. A. Hore and R. J. Composto, Nanorod Self-Assembly for Tuning Optical Absorption, ACS Nano, 2010, 4, 6941–6949 CrossRef CAS PubMed.
- J. Ji, Z. Li, W. Sun and H. Wang, Surface plasmon resonance tuning in gold film on silver nanospheres through optical absorption, Sens. Bio-Sens. Res., 2020, 30, 100374 CrossRef.
- K. M. Mayer and J. H. Hafner, Localized Surface Plasmon Resonance Sensors, Chem. Rev., 2011, 111, 3828–3857 CrossRef CAS PubMed.
- J. Cao, T. Sun and K. T. V. Grattan, Gold nanorod-based localized surface plasmon resonance biosensors: a review, Sens. Actuators, B, 2014, 195, 332–351 CrossRef CAS.
- X. Huang, S. Neretina and M. A. El-Sayed, Gold Nanorods: From Synthesis and Properties to Biological and Biomedical Applications, Adv. Mater., 2009, 21, 4880–4910 CrossRef CAS PubMed.
- V. Sharma, K. Park and M. Srinivasarao, Colloidal dispersion of gold nanorods: historical background, optical properties, seed-mediated synthesis, shape separation and self-assembly, Mater. Sci. Eng., R, 2009, 65, 1–38 CrossRef.
- T. Fujita, L.-H. Qian, K. Inoke, J. Erlebacher and M.-W. Chen, Three-dimensional morphology of nanoporous gold, Appl. Phys. Lett., 2008, 92, 251902 CrossRef.
- F. Yu, et al., Simultaneous Excitation of Propagating and Localized Surface Plasmon Resonance in Nanoporous Gold Membranes, Anal. Chem., 2006, 78, 7346–7350 CrossRef CAS PubMed.
- J. Biener, et al., Nanoporous Plasmonic Metamaterials, Adv. Mater., 2008, 20, 1211–1217 CrossRef CAS.
- L. H. Qian, X. Q. Yan, T. Fujita, A. Inoue and M. W. Chen, Surface enhanced Raman scattering of nanoporous gold: smaller pore sizes stronger enhancements, Appl. Phys. Lett., 2007, 90, 153120 CrossRef.
- M. C. Dixon, et al., Preparation, Structure, and Optical Properties of Nanoporous Gold Thin Films, Langmuir, 2007, 23, 2414–2422 CrossRef CAS PubMed.
- E. Detsi, M. Salverda, P. R. Onck and J. Th. M. De Hosson, On the localized surface plasmon resonance modes in nanoporous gold films, J. Appl. Phys., 2014, 115, 044308 CrossRef.
- V. L. Y. Loke, M. Pinar Mengüç and T. A. Nieminen, Discrete-dipole approximation with surface interaction: computational toolbox for MATLAB, J. Quant. Spectrosc. Radiat. Transfer, 2011, 112, 1711–1725 CrossRef CAS.
- X. Lang, L. Qian, P. Guan, J. Zi and M. Chen, Localized surface plasmon resonance of nanoporous gold, Appl. Phys. Lett., 2011, 98, 093701 CrossRef.
- I. Fuks-Janczarek, et al., Specific features of UV-vis absorption spectra of cis- and trans-polythiophenes, Spectrochim. Acta, Part A, 2006, 64, 264–271 CrossRef CAS PubMed.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, Oxford, New York, 2003 Search PubMed.
- W. Kong, et al., Polymer–Wall Interactions Slow Infiltration Dynamics in Bicontinuous, Nanoporous Structures, Macromolecules, 2025, 58(10), 5058–5070 CrossRef CAS.
- B. T. Draine and P. J. Flatau, Discrete-Dipole Approximation For Scattering Calculations, J. Opt. Soc. Am. A, 1994, 11, 1491 CrossRef.
- M. Omrani, H. Mohammadi and H. Fallah, Ultrahigh sensitive refractive index nanosensors based on nanoshells, nanocages and nanoframes: effects of plasmon hybridization and restoring force, Sci. Rep., 2021, 11, 2065 CrossRef CAS PubMed.
- A. M. Funston, C. Novo, T. J. Davis and P. Mulvaney, Plasmon Coupling of Gold Nanorods at Short Distances and in Different Geometries, Nano Lett., 2009, 9, 1651–1658 CrossRef CAS PubMed.
- S. Rout, et al., Nanoporous gold nanoleaf as tunable metamaterial, Sci. Rep., 2021, 11, 1795 CrossRef CAS PubMed.
- S. Underwood and P. Mulvaney, Effect of the Solution Refractive Index on the Color of Gold Colloids, Langmuir, 1994, 10, 3427–3430 CrossRef CAS.
- R. Ishida, S. Hayashi, S. Yamazoe, K. Kato and T. Tsukuda, Hydrogen-Mediated Electron Doping of Gold Clusters As Revealed by In Situ X-ray and UV–vis Absorption Spectroscopy, J. Phys. Chem. Lett., 2017, 8, 2368–2372 CrossRef CAS PubMed.
- A. Matsuo, S. Hasegawa, S. Takano and T. Tsukuda, Electron-Rich Gold Clusters Stabilized by Poly(vinylpyridines) as Robust and Active Oxidation Catalysts, Langmuir, 2020, 36, 7844–7849 CrossRef CAS PubMed.
- H. Tsunoyama and T. Tsukuda, Magic Numbers of Gold Clusters Stabilized by PVP, J. Am. Chem. Soc., 2009, 131, 18216–18217 CrossRef CAS PubMed.
- K. Juodkazis, XPS studies on the gold oxide surface layer formation, Electrochem. Commun., 2000, 2, 503–507 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00423c |
| ‡ Those authors contributed equally to this project. |
| This journal is © The Royal Society of Chemistry 2025 |





