Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Advancing carbon dioxide capture: investigation into the kinetics and efficiency of absorption in molten calcium oxide–chloride†
Melissa
Hall
,
Sean P.
Rigby
and
George Z.
Chen
 *
*
Department of Chemical and Environmental Engineering, Faculty of Engineering, University of Nottingham, University Park, Nottingham NG7 2RD, UK. E-mail: george.chen@nottingham.ac.uk
First published on 24th October 2024
Abstract
One promising carbon capture technology is the absorption of carbon dioxide (CO2) by molten salt, specifically the molten mixture of calcium oxide and chloride (CaO + CaCl2, COC), as it solves some of the key issues with alternative methods, including thermal stability and capture efficiency. The kinetics of CO2 absorption in a column of COC is examined by deriving a simple kinetic model and determining the kinetic constants under various conditions. The model emphasises the importance of the oxide anion (O2−) concentration and CO2 partial pressure in driving the absorption rates. Applying this model to reported experimental data on CO2 absorption with varying molten salt height, or CaO wt% in molten CaCl2 produced values for the kinetic constants with high accuracy. The fastest rate of absorption, with a rate constant of 0.00313 L mol−1 min−1 was achieved at a 15 cm molten salt height. Conversely, the slowest rate, 0.00062 L mol−1 min−1, occurred at 20 wt% CaO in CaCl2. Comparative analysis with conventional amine-based CO2 capture systems reveals a slower absorption rate for the molten salt. Nonetheless, there are further elements which need to be explored to perform a full comparison with the amine system, for example the desorption kinetics or absorption capacity. This reinforces the need for further research into molten salt absorption kinetics to gain a more holistic understanding of this technology and enable an optimal process design for further assessment of the feasibility and scalability of molten salt-based CO2 capture in current and future processes. Ultimately, this will promote the adoption of carbon capture technology, cultivating more sustainable practices in industry.
Sustainability spotlightThe urgent need to address climate change necessitates innovative carbon capture technologies to reduce greenhouse gas emissions. This paper investigates the molten salt absorption of carbon dioxide, through the development of a kinetic model to advance understanding of the chemistry of this process. Unlike conventional methods, molten salt absorption is free from toxic chemicals and can operate at high temperatures without the need to cool flue gases, thereby enhancing energy efficiency. This research supports the UN Sustainable Development Goals (SDGs), notably SDG 7 (Affordable and Clean Energy) and SDG 13 (Climate Action), by promoting sustainable industrial practising and cutting carbon emissions. The findings encourage further exploration of molten salt carbon capture, which if successful, will offer more cost-effective and viable solutions to carbon sequestration technologies, thereby enhancing sustainable development and environmental protection. |
Introduction
The global impact of climate change is intensifying, as evidenced by frequent and severe weather events such as flooding, wildfires, and heatwaves.1 Greenhouse gas emissions trap heat in the atmosphere, accelerating the planet's temperature towards the 1.5 °C warming threshold target established by the Paris Climate Agreement. If current emission rates continue, this target could be exceeded within the next decade, leading to catastrophic consequences including the destruction of ecosystems, rising sea levels, resource shortages, and the eradication of livelihoods.2Carbon dioxide (CO2) is a major greenhouse gas. Despite it absorbing less heat per molecule than other air pollutants, it remains in the atmosphere for longer. As of January 2024, CO2 levels were at 423 ppm, a 150% increase since 1750, surpassing the natural increase observed at the end of the last ice age 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 years ago.3
000 years ago.3
In addition, rapid urbanisation and growing populations are amplifying energy and resource demands, whilst efforts are being made to decarbonise industries and operate more sustainably. Therefore, capturing harmful emissions is imperative to achieving these goals, highlighting the importance of capture technology in ongoing research.4
Carbon capture technology can be implemented at the emission point, or through Direct Air Capture (DAC). DAC has intense energy requirements, as it involves cooling, compressing, and separating ambient air to remove the CO2. Furthermore, the CO2 concentration in the ambient environment is more dilute than at the point of emission, necessitating high gas flows and very specific adsorbents.5
Emission point capture can be achieved with various mechanisms, including adsorption, absorption, or membrane technology. Solid adsorption technology uses an adsorbent material to concentrate CO2 on the surface. Desorption of CO2 is then achieved by altering the temperature, pressure, composition, or a combination of these.6 One common adsorbent is a metal oxide, such as a calcium oxide–calcium carbonate (CaO–CaCO3) system. This technology can produce high-purity CO2 and requires less energy for regeneration, however material costs are high, and adsorbent efficiency is limited due to the observed rate of carbonation decreasing once the surface is covered with a product layer of calcium carbonate.7 In 2006, Grasa and Abanades illustrated the decrease in CO2 uptake for a calcium oxide (CaO) sorbent, with a significant reduction in the first ten cycles, and a residual conversion of 7–8% for the remaining hundreds of cycles.8 This explains the preference for other methods, and lack of industry implementation of this technology.
Absorption-based technology uses a liquid solvent to selectively dissolve CO2 from the gas mixture.7 Amine scrubbing is widely used in industry due to its fast absorption rate and high capacity. Emission gases are passed through a liquid solution of amines in an absorption column, which selectively absorbs the CO2. The CO2-rich amine solution is then separated in a stripping column, and the amine is regenerated using temperature or pressure swing methods. These methods, however, are energy-intensive, increasing operational costs.9 A key concern is that despite the amine solution not being inherently corrosive, the capture process produces carbamate and bicarbonate compounds. These compounds reduce the solution's alkalinity due to the presence of carbonic acid. The corrosion caused by this acid exceeds the effects of hyaluronic acid, leading to equipment degradation, shorter design lives, and increased maintenance.10 The carbamate compound will gradually decompose due to the presence of CO2, oxygen (O2), nitrous oxides (NOx), sulphur dioxide (SO2) and high temperatures during regeneration. This poses significant challenges to the reduction in CO2 capture capacity, requiring more frequent regeneration cycles and regular solvent replacement.11 Additionally, concerns arise about the environmental risks associated with amine solutions. Amines can be absorbed by water droplets in the purged gas or emitted directly into the atmosphere in gaseous form. Gupta et al. investigated aerosol emissions during post-combustion CO2 capture and concluded that 80 tons of MEA will enter the atmosphere per 1 million tons of CO2 captured when using a 30 wt% MEA aqueous solution.12
A similar gas–liquid absorption process is high-temperature carbon capture, using molten salt. This process involves the partial dissolution of CaO into a molten salt, where the solution absorbs CO2 by reacting with CaO to form calcium carbonate (CaCO3). This occurs in an absorption chamber.
Carbonation reaction between calcium oxide and carbon dioxide
| CaO + CO2 → CaCO3 | (1) |
To recover the CO2, the molten carbonate salt is stripped by raising the temperature (decarbonation) in a second reactor chamber. Fig. 1 highlights the Gibbs energy change (ΔG°) of eqn (1), demonstrating that the reaction reverses at temperatures higher than 900 °C. This temperature swing facilitates the absorption and desorption processes of the CO2, while the recovered solid oxide is reused for further CO2 absorption, closing the ab-/desorption cycle. In 2013, Olsen and Tomkute demonstrated a high CO2 capture rate using a CaO sorbent, with no sorbent deterioration after several cycles of CO2 capture.13 This combination of high efficiency, regeneration abilities, and its applicability with high-temperature sources makes it an attractive solution to some of the disadvantages of alternative methods. Notably, evidence supporting molten salt absorption is often obtained under laboratory conditions, and commercial-scale application is still absent.14 This introduces complexities surrounding scaling up and operating in non-ideal conditions. Johnsen et al. highlighted that scale-up ratios are 3–15 times larger than previous CO2 recovery systems, and emerging technologies will likely have ratios of a greater order of magnitude due to the increase in flue gas volumes to be treated.15 In addition to CaCl2–CaO, some other metal oxide in molten salts have been explored for CO2 capture, due to their advantageous thermodynamic properties. Examples include magnesium oxide (MgO) and fluoride (LiF or NaF) based sorbents which have demonstrated high absorption efficiencies.13
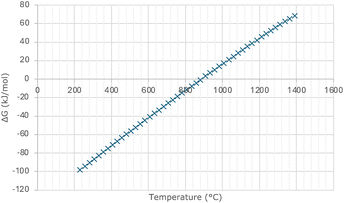 | ||
| Fig. 1 Gibbs energy change of eqn (1) as a function of temperature. | ||
Table 1 compares the key properties of solid absorption, amine scrubbing and molten salt carbon capture technologies. A molten salt system offers high capture capacities, competitive costs and the temperature range means the full heat of reaction can be utilised, eliminating the need to cool the flue gas stream prior to absorption. This emphasises the need for further research and understanding of this process. The derivation of the reaction kinetics and subsequent investigation into the application of these equations to experimental data has not been extensively explored in previous literature, presenting a significant gap in current investigations. Existing carbon capture kinetic studies primarily focus on solid or amine absorption systems. While the fluid-based nature of the amine system provides some insight into the predicted molten salt mechanism, it is not a direct representation. Research by Iveland et al. presents a kinetic model for CO2 absorption in a molten CaO–CaF2–CaCl2 system, providing a simplified framework using CO2 concentration, temperature, CaO wt%, and molten salt surface area. However, the generalisability of this model is limited, and conclusions may not be directly transferable to other systems.27
| Metal oxide | Amine scrubbing | Molten salt | |
|---|---|---|---|
| Capture capacity (g CO2 per kg sorbent) | 149.6 | 135.0 | 250.0 |
| Energy consumption (GJ per tCO2) | 11 | 4.26 | 8.8 |
| Cost analysis (USD per tCO2) | 26 | 32–114 | 30 |
| Adsorption/absorption temperature (°C) | 450–850 | 40–70 | 500–700 |
| Desorption temperature (°C) | 700–1000 | 100–150 | 885–950 |
This paper reports our preliminary findings from an ongoing programme that aims to develop a suitable kinetic model applicable across a broad range of molten salt compositions. Such a model can presumably provide a more holistic understanding of the kinetic behaviour so that more reliable prediction of the CO2 absorption rate and capacity can be achieved. This will enable investigations into scaling up the technology and its potential implementation in decarbonizing current and future processes. Such advancements would positively impact the sustainability of various processes, aligning with legislation and intended emission targets.
Experimental
The kinetic model was developed by analysing relevant ionisation and reaction equations in the molten salt process. The gas–liquid interaction resembles that of an amine carbon capture system, as supported by Iveland et al.,27 therefore similar studies of gas–liquid absorption aided in the derivation.28–33The absorption of CO2 into molten salt was simulated in Excel using lab-scale experimental data. The Excel ‘Solver’ tool was used to determine the kinetic constants and minimise discrepancies between the estimated and actual values. This method is widely adopted for non-linear analysis and calculation of kinetic parameters in research, often achieving high accuracy.27,31,32
Kinetic model derivation
The kinetic model describes the rate of CO2 absorption into molten salt, building upon established chemical principles, and is based on the following assumptions:(1) The overall reaction system follows second-order kinetics as shown in eqn (1). This is supported by Zheng et al.'s working hypothesis of the carbonation reaction, aligning with that of a solid-state CaO system.30,34
(2) The formed calcium carbonate continuously dissolves in the molten salt.26,35 This dissociation leaves reactive CaO at the surface, and explains the rapid reaction.
(3) Hu et al. emphasised the affinity of oxide ions for CO2, and this is represented in eqn (2), leading to carbonate ion formation in the molten environment, contributing to the overall CO2 absorption.36
(4) Simplification is achieved by assuming constant (or unity) activities for the calcium ions and calcium carbonate.
Relevant chemical equations in the molten salt-CO2 system:
Dissociation of CaO
| Ca2+ + O2− ⇌ CaO | (2) |
Oxide anions react with carbon dioxide
| CO2 + O2− → CO32− | (3) |
Calcium oxide reacts with carbon dioxide
| CaO + CO2 → Ca2+ + CO32− | (4) |
Dissociation of calcium carbonate
| Ca2+ + CO32− ⇌ CaCO3 | (5) |
Equilibrium constant for calcium oxide dissociation
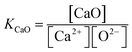 | (6) |
Equilibrium constant for calcium carbonate
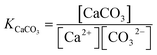 | (7) |
Rate of reaction representing eqn (4)
| rCO2 = k2[CaO]pCO2 | (8) |
Rate of reaction representing eqn (3)
| rCO2 = k1[O2−]pCO2 | (9) |
The overall rate of CO2 absorption:
Overall rate of CO2 absorption
| rCO2 = k1[O2−]pCO2 + k2[CaO]pCO2 | (10) |
However, simplification of eqn (10) can be achieved with assumption eqn (4):
Simplified rate of CO2 absorption
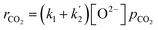 | (11) |
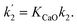
It is worth noting that the derivation above remains valid if Ca or Ca2+ is replaced by another alkaline earth metal or its cation, e.g. Mg/Mg2+ and Ba/Ba2+. For alkali metals and cations, similar equations can be derived. Due to limited time, space and literature data, this study has focused on Ca/Ca2+ or CaO/CaCl2 leaving other candidates to future research. Another point is that O2− and CaO are considered as the absorbents for CO2, whilst other absorbents may also be present in the molten salt. If so, these seem to have an insignificant effect because the simulations discussed below achieved highly satisfactory results.
Application of experimental data
Research data was sourced from the paper entitled “Investigation of High-temperature CO2 capture by CaO in CaCl2 Molten salt”.25 This study provides valuable data on CO2 absorption from a simulated flue gas in a controlled lab-scale environment, and is supported by subsequent studies, affirming the reliability of their methodology and results.37 The data utilised depicts the CO2 percentage in the gas outlet plotted against time under varying conditions. Specifically, the selected experimental data looks at varying the molten salt melt heights, and CaO wt% in CaCl2.Data manipulation
Various calculations were conducted to determine the theoretical rate of CO2 absorption. Often in kinetic analysis, simplification is achieved by assuming no molar transfer into and out of the salt, such as shown in Iveland et al.'s derivation.27 However, studies of gas–liquid systems such as Rushdi and Thamer's on an amine–CO2 system accounts for this molar transfer.38 Arifin et al. suggested that in cases where the carbonation occurs rapidly at the gas–liquid interface, the calcium carbonate will leave this interface quickly, dissolving back into the molten salt, therefore this justifies the assumption of no molar transfer in our system.39Data extraction
Numerical data, focusing on CO2 volume percentage in the gas outlet against time in minutes during the absorption phase, was extracted using the Webplot Digitizer Tool.Experimental CO2 absorption
The theoretical amount of CO2 absorbed was calculated by subtracting the CO2 volume percentage of the gas exiting, from the inlet CO2 volume percentage.Assumption of the ideal gas law was employed to calculate the molar fraction of CO2 (yCO2) absorbed from the gas stream. The total number of moles sequestered at each time point (t) is calculated using eqn (12) and (13).
Molar fraction of CO2
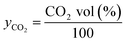 | (12) |
Moles absorbed (Mt) at time (t). ṅ = molar flow (mol min−1).
| Mt,CO2 = (yCO2 × ṅ × t) + Mtprev,CO2 | (13) |
Therefore, the rate of absorption (Rt) is:
Rate of absorption at time (t) in mol min−1.
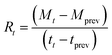 | (14) |
CaO concentration
The stoichiometry in eqn (4) means the decrease in CaO concentration can be calculated by:CaO concentration at time (t) given in mol L−1. V = volume of salt (L)
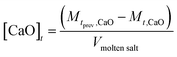 | (15) |
Partial pressure of CO2
The partial pressure of CO2 (pCO2) is calculated using:Partial pressure of CO2
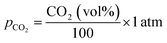 | (16) |
Oxide concentration and predicted rate of absorption
The oxide concentration can be found based on the stoichiometry of eqn (2).The predicted rate of absorption is calculated by applying the derived kinetic model.
Kinetic constants k1 and k2
The square of the error between the experimental and theoretical absorption rates was calculated, and the total error across the absorption range was determined. The Excel ‘Solver’ tool was then used to perform iterative calculations to minimise the overall sum of squared errors, with the objective function set to minimise the total error. The reaction kinetic constants (k1 and k2) were treated as the adjustable parameters, iteratively adjusting with the goal of producing the best of fit of the model to the experimental data. The only constraints applied were that k1 and k2 must be greater than or equal to zero, allowing solver to explore the parameter space, whilst ensuring physically meaningful values were assigned for the constants.Results & discussion
Kinetic model derivation
The derived kinetic model for CO2 absorption into a molten salt system is based on various assumptions aimed at simplifying the overall equation. One key assumption is considering the activity of the calcium ions and calcium carbonate as unity due to the high mobility and ionic nature of the molten salt ions; as supported by studies such as that of Zhang et al.40 Another assumption equates the CaO concentration to KCaO[O2−], resulting in a second-order reaction that accounts only for the oxide anion concentration and CO2 partial pressure. This assumption can be considered an oversimplification of the system, as studies such as Zhang et al.'s conclude that the concentration of oxide anions is not necessarily equivalent to the concentration of the CaO in the system, based on electrochemical measurements.41Similarly, application of Le Chatelier's principle to eqn (2) suggests that as the oxide anion concentration decreases when reacting with CO2, the CaO concentration would increase, due to the equilibrium position shifting to replenish the consumed oxide anions. However, eqn (4) shows that CaO is consumed due to the reaction with CO2, therefore the net effect on the calcium oxide concentration is likely to be an overall reduction. The extent of this decrease needs to be determined in future investigations.
The kinetic model shares similarities with an amine–CO2 system, and this is valid for several reasons. The overall reaction of CO2 with the amine material is similar to that with molten salt, and the formation of carbamate as an intermediate resembles carbonate formation. The simplified rate expression for an amine-based absorption system also resembles that of a molten salt–CO2 interaction, where the CO2 absorption rate is proportional to the concentrations of amine and CO2.31 This analysis reinforces the derived kinetic model's validity, while also highlighting its simplification of the system's chemistry by ignoring factors like compound dissociation, equilibrium balances, and the zwitterion mechanism which control the amine–CO2 kinetics.
Despite these simplifications, the model offers a reliable framework for estimating CO2 absorption rates, and this can be applied to experimental data. This satisfies some of the goals of this paper and provides a foundation for more research.
Experimental data application
The kinetic model was successfully applied to experimental data, yielding high accuracy in predicting the rate of CO2 absorption under varying conditions of CaO wt% in CaCl2, or the molten salt height. During data conversion for analysis, assumptions were made either for simplification or due to insufficient information in the selected sources. One key assumption is the constant volume of the molten salt melt, which is accounted for in calculations of the oxide anion concentration. Based on the characteristics of an ionic liquid medium, this can be taken as a reasonable assumption. The ionic medium has low-density ions with large gaps between them, and when CO2 is absorbed, the oxide ions react to form carbonate ions, a larger molecular anion consisting of 3 oxygens and 1 carbon. This molecule occupies the pre-existing gaps between the ions in the molten salt, and therefore we can take the volume change as negligible.Varying the molten salt height
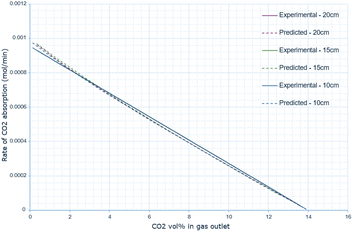
The derived rate equation was successfully applied to experimental data of varying molten salt heights. Fig. 2–4 outline that increasing the oxide concentration initially causes a rapid increase in the rate of CO2 absorption, which eventually plateaus. Notably, the calculated rate of absorption for all salt heights never exceeds 0.001 mol min−1, and the predicted rate follows the same pattern: initially underestimating the rate of absorption for a given oxide anion concentration, then achieving high accuracy, and finally overestimating the rate of CO2 absorption. The calculated error is greater at higher oxide concentrations, corresponding to the start of absorption. Furthermore, the maximum error varies with salt height, with the lowest value at 10 cm (8.0 × 10−10), and the largest at 15 cm with (14.0 × 10−10).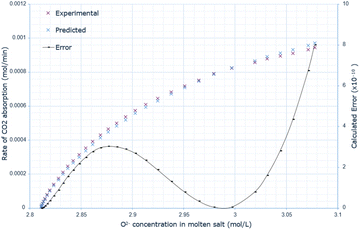 | ||
| Fig. 2 Predicted rate of absorption vs. actual at 10 cm molten salt height, compared to oxide anion concentration, with absolute error calculated at each data point. | ||
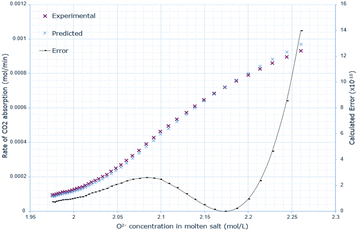 | ||
| Fig. 3 Predicted rate of absorption vs. actual at 15 cm molten salt height, compared to oxide anion concentration, with absolute error calculated at each data point. | ||
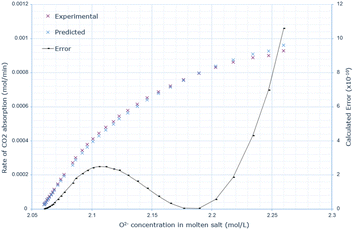 | ||
| Fig. 4 Predicted rate of absorption vs. actual at 20 cm molten salt height, compared to oxide anion concentration, with absolute error calculated at each data point. | ||
Analysing Fig. 5 highlights how the rate of absorption changes across the CO2 vol% in the gas outlet, exhibiting a linear relationship. Regarding the experimental data, Table 2 shows that for all salt heights, the parameters of the derived linear model are identical. The parameters for the predicted calculation however vary slightly, but this variation is minor.
| Salt height | Experimental | Predicted | ||
|---|---|---|---|---|
| Gradient (10−5) | Intercept (10−4) | Gradient (10−5) | Intercept (10−4) | |
| 10 cm | −6.81 | 9.53 | −6.93 | 9.58 |
| 15 cm | −6.81 | 9.53 | −7.03 | 9.66 |
| 20 cm | −6.81 | 9.53 | −6.93 | 9.58 |
The predicted rate of absorption also follows the same pattern of discrepancy, underestimating the rate of absorption at higher CO2 vol% (corresponding to a lower oxide anion concentration) and overestimating it at a lower CO2 vol% in the outlet gas (corresponding to a higher oxide anion concentration).
Varying CaO in CaCl2 weight percentage
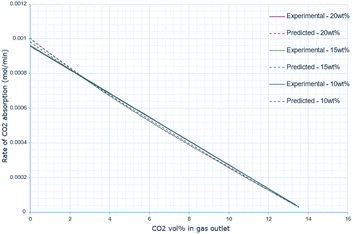
A similar pattern to the molten salt height variations is seen across Fig. 6–8. In the 15 wt% CaO experiment, the rate of absorption exceeds 0.001 mol min−1, but in all other experiments, it remains below this value. Furthermore, the same conclusion prevails: an increase in oxide anion concentration causes a greater rate of absorption, but there is a larger change in absorption at lower concentrations, which eventually plateaus. The kinetic model underestimates the rate of absorption at lower concentrations before overestimating it at higher anion concentrations for all CaO wt% in CaCl2. The maximum error increases most from 10 wt% to 15 wt% CaO, increasing by a factor of 3.4. The error then further increases from 15 wt% to 20 wt% CaO.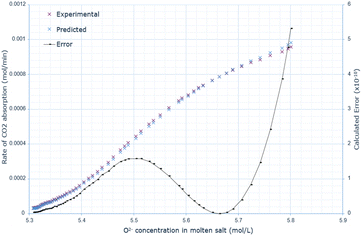 | ||
| Fig. 6 Predicted rate of absorption vs. actual at 10 wt% CaO in CaCl2, compared to oxide anion concentration, with error calculated at each data point. | ||
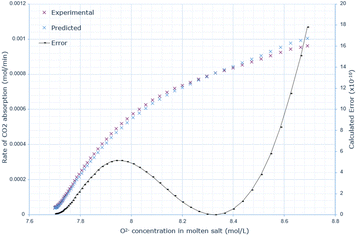 | ||
| Fig. 7 Predicted rate of absorption vs. actual at 15 wt% CaO in CaCl2, compared to oxide anion concentration, with error calculated at each data point. | ||
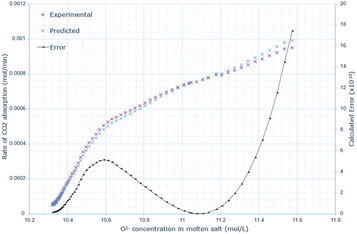 | ||
| Fig. 8 Predicted rate of absorption vs. actual at 20 wt% CaO in CaCl2, compared to oxide anion concentration, with error calculated at each data point. | ||
The predicted rate of absorption using the kinetic model has the same pattern of discrepancy as before, underestimating the rate of absorption at higher CO2 vol% (corresponding to a lower oxide anion concentration) and overestimating it at a lower CO2 vol% in the outlet gas (corresponding to a higher oxide anion concentration). Compared with the experimental data, the predicted gradient is always larger than the experimental, highlighting that the predicted change in the rate of absorption as the CO2 vol% increases is being overestimated (Fig. 9).
The data indicates that increasing the wt% of CaO in the molten salt initially increases the efficiency of carbon dioxide conversion, however this then decreases after 15 wt% (Table 3).
| CaO wt% in CaCl2 | Experimental | Predicted | ||
|---|---|---|---|---|
| Gradient (10−5) | Intercept (10−4) | Gradient (10−5) | Intercept (10−4) | |
| 10 | −6.84 | 9.58 | −6.92 | 9.61 |
| 15 | −6.87 | 9.62 | −7.02 | 9.68 |
| 20 | −6.84 | 9.58 | −7.01 | 9.65 |
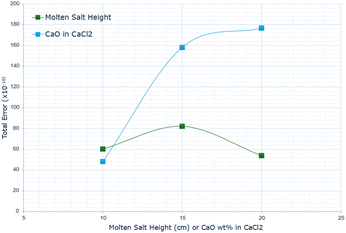
Fig. 11 outlines the total error for each derived graph, displaying a dramatic difference in the total error, increasing as the wt% in CaO increases. This is likely due to the changes in the physical conditions of the molten salt, such as the viscosity affecting diffusivity.
Despite this, the overall error is relatively low, highlighting that good accuracy has been achieved here, however this is not as high as for the molten salt height data.
Kinetic constant's and error analysis
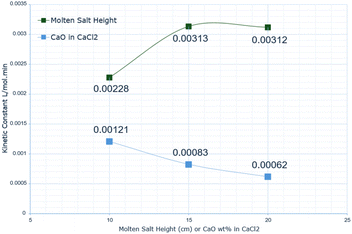
Fig. 10 shows how the kinetic constants vary with the molten salt height, showing an initial increase from 10 cm to 15 cm by a factor of 1.37. This then essentially plateaus from 15 cm to 20 cm, remaining at 0.00312 L mol−1 min−1. This increase in the rate constant with increasing height can be explained by mass transfer conditions. When the salt height is lower, the gas–liquid contact time is shorter, so the CO2 molecules are less likely to absorb into the melt. A plateau in the kinetic constant after 15 cm can be explained by the kinetic equation. The rate of absorption depends on the oxide anion concentration; when the volume increases (due to the height increasing), there are fewer reactant ions in the same given volume, so interactions between the oxide anion and CO2 molecules at the gas–liquid interface are less likely. Subsequently, there is less absorption. A simulation study, in HYSYS, of amine absorption of CO2 identified a similar trend, where increasing the column height increases CO2 removal, but after a certain point, the calculations diverge, indicating a potential maximum.42Further investigation into this would be beneficial for optimising the melt height and volume, however, overall, the discrepancy between the predicted and experimental data is relatively low across all molten salt heights, indicating that the model is accurate under these conditions.
For the CaO wt% in molten salt, there is an almost linear decrease in the kinetic constant from 10 wt% to 20 wt% CaO in CaCl2, corresponding to a gradient of 6.0 × 10−5. The largest absorption constant is at 15 cm salt height, whereas the smallest is at 20 wt% CaO. The reduction in conversion efficiency was attributed to factors such as agglomeration of the sorbent, therefore leading to a reduction in the available surface area of the absorbent and reducing the reaction efficiency.24 This explanation can be applied to the reduced absorption rate with increasing CaO concentration; however, it appears that the relationship between conversion efficiency and the rate of CO2 absorption is not a direct correlation, based on the differing results between 10 and 15 wt%. Higher concentrations of CaO can lead to mass transfer limitations, due to the increased number of reactant oxide anions promoting the carbonate formation, but this reduces the surface availability for CO2 absorption. The higher concentration also causes the viscosity to increase, therefore diffusion of the carbonate particles is slower, reducing the number of surface reactants.26 Iveland et al. strengthened this argument by highlighting that calcium carbonate can start to precipitate at higher concentrations, therefore the continuous dissolution of the reaction product becomes limited, reducing the availability of reactive sites.35 These effects are unaccounted for in the kinetic model, and therefore may explain the discrepancy at higher CaO concentrations.
Fig. 11 highlights the total calculated error across the entire absorption range. It was previously noted for the CaO in CaCl2 that the maximum error increased significantly between the 10 wt% and 15 wt% data, but this plateaus from 15 wt% to 20 wt%. When summing up the total error, there is an additional increase in the total discrepancy between the model's predicted and actual rate of absorption, indicating that the model's accuracy decreases with increasing CaO wt% in CaCl2.
For the molten salt height, the trend for the total error remains consistent with that of the maximum error between actual and predicted absorption rates. There is an initial increase in the discrepancy between 10 cm and 15 cm salt height, followed by a decrease between 15 cm and 20 cm. The main difference in terms of the behavioural pattern is that the total error at 20 cm molten salt height is lower than at 10 cm.
Notably, in nearly all cases of varying salt height, the overall error is less than the overall error for the CaO wt% in CaCl2 experiments.
Across all datasets analysed, there's a consistent trend of underestimation of the CO2 absorption rate at lower concentrations and overestimation at higher concentrations. This pattern is also observed in Iveland et al.'s study at 5 wt% CaO.27 One explanation for this is that at the start of the absorption process, the actual oxide anion concentration is smaller than the calculated value, which would shift the data point to align with the general trend. Conversely, at lower concentrations, the actual concentration is larger than the calculated value, and if rectified, the data point would fit the general trend.
Alternatively, this suggests a shift in the governing kinetics during the absorption reaction. In the analysis of an amine–CO2 system, Pawalak discussed the Hatta number, a criterion for whether a reaction takes place in the liquid film or in the liquid bulk, and the infinite enhancement factor, which represents the ratio of the reaction rate on a catalytic surface to the reaction rate in the absence of the catalyst when the surface is saturated with reactant molecules. Depending on the value of the Hatta number and the ratio of the infinite enhancement factor to the Hatta number, the second-order absorption rate can vary to between a fast pseudo-first-order regime, a fast intermediate regime, or an instantaneous regime. The first-order regime, for example, exists when the amine is present in excess relative to CO2. As the absorption reaction proceeds, this condition would change due to the reactant being used up, and therefore the governing regime would vary as the reaction continues.43 Based on the parallel nature of the kinetic mechanisms, this may also occur in the salt, so further research would be beneficial.
The average total error across all datasets examined equals 9.64 × 10−7%, demonstrating that the derived kinetic model is highly accurate. Although the overall error remains very low, there are slightly larger discrepancies at the start and end of the absorption process due to complex mechanisms in the system that are not fully captured. Similar trends have been observed in both amine–CO2 systems and analogous molten salt studies, suggesting the need to account for changing physical properties, concentrations, or governing mechanisms.27,43
Across all datasets analysed, the largest discrepancy occurs at the highest CaO concentration, with an average absolute error of 12.19 × 10−10. As CaO is likely to have the greatest impact on the kinetics, this trend is understandable. Initial interpretations of the data outlined that an almost identical plot could be achieved when varying the CaO concentration separate from the oxide anion concentration, but the lack of information on the equilibrium constant (KCaO) limits the accuracy of utilising this in the study. Coupled with the fact that the exact values for the change in CaO concentration are unknown, representative results would not be achievable by including this analysis, hence its omission. This further reinforces the areas for improvement in the kinetic model's accuracy and robustness.
Wider impact
The derived kinetic model has been successfully applied to experimental data, demonstrating high accuracy and adaptability under various reaction conditions. However, it is acknowledged that this is a simplified representation of the molten salt mechanism, and improvements can be made by considering mass-transfer processes, potential changes in the governing kinetics, or including the concentration of CaO. The kinetic constants derived agree with published values, such as Iveland et al.'s study, which determined a value of 7.7 × 10−5 msalt s−1, therefore enhancing the reliability of the derived values.27Comparing the kinetic constants between a molten salt and amine system reveals a slower reaction rate for molten salt absorption. For instance, at a 15 cm salt height, the molten salt system's kinetic constant is 0.00313 L mol−1 min−1, whereas a MDEA amine system is significantly faster at 6.71 m3 kmol−1 s−1.44 Crucially, the kinetic constant alone does not provide a complete reflection of the overall efficiency and effectiveness of a CO2 capture system. Other factors such as the absorption capacity, solvent reusability, energy for solvent regeneration, and the environmental impact of the solvent must also be considered. This necessitates a more holistic assessment of the process to make more representative comparisons, such as in a lifecycle assessment or measurements of the desorption kinetics.
Despite this, the derived reaction kinetics provide crucial insights into the CO2 absorption rate into molten salt systems. This will aid in preliminary designs and techno-economic assessments for implementing a molten salt carbon capture system into a process. This understanding of the key operating parameters affecting absorption will aid optimisation and understanding of the suitability of the technology in various processes.
Through quantification of the derived kinetic constants, plant designers can make informed decisions on the viability and performance of integrating the molten salt carbon capture system into a process. This supports the development of new, efficient carbon capture technologies for energy-intensive industries, thereby improving their sustainability.
Conclusions and recommendations
This paper has presented an initial kinetic representation of the molten salt absorption of carbon dioxide, offering valuable insight into the behaviour of this system. The model is applicable to experimental data and demonstrates high accuracy in determining the kinetic constants for the absorption process, with the findings reported by Iveland et al. (2024) confirmed due to the similarity in the derived values.27 The largest value for the kinetic constant representing the rate of CO2 absorption was at a 15 cm molten salt height, calculated at 0.00313 L mol−1 min−1, while the lowest was 0.00062 L mol−1 min−1 at 20 wt% CaO in CaCl2. The analysis of the constants has outlined variability in the rate of absorption when altering the salt height or the CaO concentration, aiding in determining the optimum conditions for maximising the rate of absorption. While the study outlined a slower rate of absorption in the molten salt compared with an amine system, further research would be beneficial to gain a more holistic understanding of the system, such as the desorption behaviour. Despite this, the model has provided an initial basis for future investigations and highlights that the oxide anion concentration and partial pressure of CO2 are major elements of the overall absorption reaction. The study is limited due to the lack of varied experimental data and the simplification of the reaction kinetics, yet the derived model can be beneficial in performing comparisons between carbon capture systems and deducing the feasibility of molten salt systems in future decarbonisation efforts. Referring to the aims and objectives, these have been successfully achieved, and the chosen methodology ran smoothly. Despite this, recommendations have been provided to improve the model and lead to a better understanding of the complex mechanisms present in the molten salt system.Recommendations
One method of improving the accuracy of the derived model is through derivation of the equilibrium constant for CaO (KCaO) to determine the behaviour of the concentration in the system. On the other hand, the model could be more universally applicable if the molten salt height and CaO content can be treated as independent variables. Furthermore, potential investigation into other parameters, such as the Hatta or infinite enhancement factor, may represent the varying regime throughout the absorption process, depicting a more accurate model of the process. Temperature dependence is another factor affecting the reaction kinetics, so further investigations could explore these variables. Similarly, applying the kinetic model to a wider variety of data, such as pilot plant data or where other independent variables are explored, would improve the reliability of the model, and highlight other aspects of the reaction not fully captured in the current equation. Finally, the absorption kinetics is only one portion of the entire process, so deriving kinetics for the desorption would also be suitable. Graphical data suggests the kinetics to be much faster, and once this is understood, a more complete view of the process would be achieved, supporting the implementation of molten salt carbon capture technology.A particularly promising prospect is that after or even before more experimental data become available, the model may be further improved upon consideration of different influential factors including temperature, pressure, and convection or sonication. Further development of the model can also benefit from the aid of sophisticated computer modelling tools such as the neural network function in Matlab or other machine learning or AI empowered capabilities.
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
MH carried out the actual work and prepared the first version of the manuscript. GZC proposed the molten salt absorption research as part of an overall MEng Research and Design Project entitled Mega Methanol Plant that was co-supervised by SR and GZC. All authors contributed to the discussion and revision of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The EPSRC and Innovate UK are acknowledged for financial support to our past and on-going molten salts research (EP/J000582/1; GR/R68078; 10017140).Notes and references
- NASA, Extreme Weather and Climate Changed, Climate Change: Vital Signs of the Planet, 2016, available from: https://climate.nasa.gov/extreme-weather/ Search PubMed.
- M. Poynting, World's first year-long breach of key 1.5C warming limit, BBC News, 2024 Feb 8 [cited 2024 Mar 1], available from: https://www.bbc.co.uk/news/science-environment-68110310 Search PubMed.
- NASA, Carbon Dioxide Concentration | NASA Global Climate Change, Climate Change: Vital Signs of the Planet, NASA, 2023 [cited 2024 Mar 3], available from: https://climate.nasa.gov/vital-signs/carbon-dioxide/ Search PubMed.
- K. Narine, J. Mohabir, N. Koylass, N. Samaroo, S. Singh-Gryzbon and A. Baboolal, et al., Climate smart process design for current and future methanol production, J. CO2 Util., 2021, 44, 101399 CrossRef CAS . Available from: https://www.sciencedirect.com/science/article/pii/S2212982020310295?casa_token=cTG4Hnwr8cYAAAAA:rfEdvFD3jlBSRfA3-DP1UJKitQXlueFNMxrzuhRO2-LN5-6VnrE26Ye0lBsCyz99bAEGR4lDCmg.
- K. Lebling, N. McQueen, M. Pisciotta and J. Wilcox, Direct Air Capture: Resource Considerations and Costs for Carbon Removal, World Resources Institute, 2021 [cited 2023 Nov 27], available from: https://www.wri.org/insights/direct-air-capture-resource-considerations-and-costs-carbon-removal Search PubMed.
- P. A. Saenz Cavazos, E. Hunter-Sellars, P. Lacomi, S. R. McIntyre, D. Danaci and D. R. Williams, Evaluating Solid Sorbents for CO2 capture: Linking Material Properties and Process Efficiency via Adsorption Performance, Front. Energy Res., 2023, 11, 1167043 CrossRef.
- U. Khan, C. C. Ogbaga, O. A. O. Abiodun, A. A. Adeleke, P. P. Ikubanni and P. U. Okoye, et al., Assessing absorption-based CO2 capture: Research progress and techno-economic assessment overview, Carbon Capture Sci. Technol., 2023, 8(100125), 100125 CrossRef CAS . Available from: https://www.sciencedirect.com/science/article/pii/S2772656823000295?via%3Dihub.
- G. S. Grasa and J. C. Abanades, CO2 Capture Capacity of CaO in Long Series of Carbonation/Calcination Cycles, Ind. Eng. Chem. Res., 2006, 45(26), 8846–8851 CrossRef CAS.
- T. Wilberforce, A. Baroutaji, B. Soudan, A. H. Al-Alami and A. G. Olabi, Outlook of carbon capture technology and challenges, Sci. Total Environ., 2019, 657(0048–9697), 56–72 CrossRef CAS PubMed.
- F. Meng, Y. Meng, T. Ju, S. Han, L. Lin and J. Jiang, Research Progress of Aqueous Amine Solution for CO2 capture: a Review, Renewable Sustainable Energy Rev., 2022, 168(112902), 112902 CrossRef CAS . Available from: https://www.sciencedirect.com/science/article/abs/pii/S1364032122007845?via%3Dihub.
- F. Vega, A. Sanna, B. Navarrete, M. M. Maroto-Valer and V. J. Cortés, Degradation of amine-based solvents in CO2 capture process by chemical absorption, Greenhouse Gases: Sci. Technol., 2014, 4(6), 707–733 CrossRef CAS.
- V. Gupta, P. Mobley, J. Tanthana, L. Cody, D. Barbee and J. Lee, et al., Aerosol emissions from water-lean solvents for post-combustion CO2 capture, Int. J. Greenhouse Gas Control, 2021, 106(103284), 103284 CrossRef CAS.
- E. Olsen and V. Tomkute, Carbon Capture in Molten Salts, Energy Sci. Eng., 2013, 1(3), 144–150 CrossRef CAS.
- Q. Zhu, Y. Zeng and Y. Zheng, Overview of CO2 Capture and Electrolysis Technology in Molten salts: Operational Parameters and Their Effects, Ind. Chem. Mater., 2023, 1(1), 595–617 RSC.
- K. Johnsen, K. Helle and T. Myhrvold, Scale-up of CO2 capture processes: The role of Technology Qualification, Energy Procedia, 2009, 1(1), 163–170 CrossRef CAS.
- M. Dunstan, F. Donat, A. Bork, C. Grey and C. Muller, CO2 Capture at Medium to High Temperature Using Solid Oxide-Based Sorbents: Fundamental Aspects, Mechanistic Insights, and Recent Advances, Chem. Rev., 2021, 121(20), 12681–12745 CrossRef CAS PubMed.
- C. Abanades, G. Grasa, M. Alonso, N. Rodriguez, E. J. Anthony and L. M. Romeo, Cost Structure of a Postcombustion CO2 Capture System Using CaO, Environ. Sci. Technol., 2007, 41(15), 5523–5527 CrossRef PubMed.
- J. C. Abanades, Y. A. Criado and H. I. White, Direct Capture of Carbon Dioxide from the Atmosphere Using Bricks of Calcium Hydroxide, Cell Rep. Phys. Sci., 2023, 4(4), 101339 CrossRef CAS . Available from: https://www.sciencedirect.com/science/article/pii/S2666386423001042.
- G. T. Rochelle, Thermal Degradation of Amines for CO2 Capture, Curr. Opin. Chem. Eng., 2012, 1(2), 183–190 CrossRef CAS . Available from: https://www.sciencedirect.com/science/article/abs/pii/S2211339812000081.
- P. Panja, B. McPherson and M. Deo, Techno-Economic Analysis of Amine-based CO2 Capture Technology: Hunter Plant Case Study, Carbon Capture Sci. Technol., 2022, 3, 100041 CrossRef CAS.
- X. Li, S. Wang and C. Chen, Experimental Study of Energy Requirement of CO2 Desorption from Rich Solvent, Energy Procedia, 2013, 37, 1836–1843 CrossRef CAS.
- I. M. Bernhardsen and H. K. Knuutila, A Review of Potential Amine Solvents for CO2 Absorption process: Absorption capacity, Cyclic Capacity and pKa, Int. J. Greenhouse Gas Control, 2017, 61, 27–48 CrossRef CAS . Available from: https://www.sciencedirect.com/science/article/abs/pii/S1750583616304911.
- G. Ozin, Molten Salts Help Capture Carbon at High Temperatures, Advanced Science News, 2022 [cited 2024 Jun 6], available from: https://www.advancedsciencenews.com/molten-salts-help-capture-carbon-at-high-temperatures/#:%7E:text=Thecentralscienceunderpinningthe Search PubMed.
- P. N. Lerøen, Carbon Capture in Molten Salts: an Extensive Survey of Chemical Systems with MgO as Sorbent, Norwegian University of Life Sciences, 2020 Search PubMed.
- V. Tomkute, A. Solheim and E. Olsen, Investigation of High-Temperature CO2 Capture by CaO in CaCl2 Molten Salt, Energy Fuels, 2013, 27(9), 5373–5379 CrossRef CAS.
- H. S. Nygård, M. Hansen, Y. Alhaj-Saleh, P. Palimąka, S. Pietrzyk and E. Olsen, Experimental Evaluation of Chemical Systems for CO2 Capture by CaO in Eutectic CaF2-CaCl2, AIMS Energy, 2019, 7(5), 619–633 Search PubMed.
- S. G. Iveland, A. Westbye, J. M. Marchetti, E. Olsen and H. S. Nygard, A Kinetic Model of CO2 Absorption in Molten CaO-CaF2-CaCl2, Electrochemistry, 2024, 92(4), 043014 CrossRef CAS.
- J. Zhang, A. R. Teixeira, H. Zhang and K. F. Jensen, Determination of Fast gas-liquid Reaction Kinetics in Flow, React. Chem. Eng., 2019, 5(1), 51–57 RSC.
- Q. Huang, Y. Li, X. Jin, D. Zhao and G. Z. Chen, Chloride ion enhanced thermal stability of carbon dioxide captured by monoethanolamine in hydroxyl imidazolium based ionic liquids, Energy Environ. Sci., 2011, 4(6), 2125 RSC.
- T. Sema, A. Naami, Z. Liang, H. Shi, A. V. Rayer and K. Z. Sumon, et al., Part 5b: Solvent chemistry: Reaction Kinetics of CO2 absorption into reactive amine solutions, Carbon Manage., 2012, 3(2), 201–220 CrossRef CAS.
- A. V. Rayer, P. D. Mobley, M. Soukri, T. R. Gohndrone, J. Tanthana and J. Zhou, Absorption rates of carbon dioxide in amines in hydrophilic and hydrophobic solvents, Chem. Eng. J., 2018, 348, 514–525 CrossRef CAS.
- L. Pino, V. Recupero and A. Hernández, A Useful Excel-Based Program for Kinetic Model Discrimination, ChemEngineering, 2018, 2(4), 57 CrossRef CAS.
- Q. Huang, Y. Li, X. B. Jin, D. Zhao and G. Z. Chen, Chloride ion enhanced thermal stability of carbon dioxide captured by monoethanolamine in hydroxyl imidazolium based ionic liquids, Energy Environ. Sci., 2011, 4, 2125–2133 RSC.
- H. Zheng, Y. He, Y. Zhu, L. Liu and X. Cui, Novel procedure of CO2 capture of the CaO sorbent activator on the reaction of one-part alkali-activated slag, RSC Adv., 2021, 11(21), 12476–12483 RSC . Available from: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC8696962/#:%7E:text=InthepresenceofCO.
- S. G. Iveland, E. Olsen, A. Westbye and H. S. Nygård, Experimental Validation of Carbon Capture in Molten Salts at Low CO2 Concentrations (1-5 Vol%), in Social Science Research Network, RELX Group, Netherlands, 2022 [cited 2024 Jun 6], available from: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4271541#:%7E:text=Fortheexperimentswith1,andXCaO%3D0.50%2Crespectively Search PubMed.
- L. Hu, Y. Song, J. Ge, J. Zhu and S. Jiao, Capture and electrochemical conversion of CO2 to ultrathin graphite sheets in CaCl2-based melts, J. Mater. Chem. A, 2015, 3(42), 21211–21218, 10.1039/C5TA05127D.
- V. Tomkute, A. Solheim and E. Olsen, CO2 capture by CaO in molten CaF2-CaCl2: Optimization of the process and cyclability of CO2 capture, Energy Fuels, 2014, 28, 5345–5353 CrossRef CAS.
- S. Rushdi and E. Thamer, Investigation of overall mass transfer coefficient of CO2 absorption in to aqueous blended Monoethanolamine (MEA), Diethanolamine (DEA) and Triethanolamine (TEA) measured in Bubble column Reactor solution, IOP Conf. Ser.: Mater. Sci. Eng., 2020, 870, 012056 CAS.
- Z. Arifin, M. Zainuri, Y. Cahyono and Darminto, The influence of temperature and gas flow rate on the formation CaCO3 vaterite phase, IOP Conf. Ser.: Mater. Sci. Eng., 2018, 395, 012004, DOI:10.1088/1757-899X/395/1/012004.
- K. Zhang, Development of Molten Salt Promoted Metal Oxide based Absorbents for CO2 Separation, Doctoral Dissertations, 2014May 3, vol. 327, available from, https://digitalcommons.lib.uconn.edu/dissertations/327 Search PubMed.
- C. Zhang, D. Rappleye, A. Nelson, S. Simpson and M. Simpson, Electroanalytical Measurements of Oxide Ions in Molten CaCl2 on W electrode, J. Electrochem. Soc., 2021, 168(9), 097502 CrossRef CAS.
- L. E. Øi, Aspen HYSYS Simulation of CO2 Removal by Amine Absorption from a Gas Based Power Plant, The 48th Scandinavian Conference on Simulation and Modeling (SIMS 2007); 30-31 October; 2007; Göteborg (Särö), 2007 Dec 21, (027), pp. 73–81 Search PubMed.
- H. Kierzkowska-Pawlak, Determination of Kinetics in Gas-Liquid Reaction Systems. An Overview, Ecol. Chem. Eng. S, 2012, 19(2), 175–196 CAS.
- T. Sema, A. Naami, Z. Liang, G. Chen, R. Gao and R. Idem, et al., A novel reactive 4-diethylamino-2-butanol solvent for capturing CO2 in the aspect of absorption capacity, cyclic capacity, mass transfer, and reaction kinetics, Energy Procedia, 2013, 37, 477–484 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4su00354c |
| This journal is © The Royal Society of Chemistry 2025 |