Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Enabling ionic transport in Li3AlP2: the roles of defects and disorder†
Ji Huab,
Alexander G. Squiresc,
Jędrzej Kondekefg,
Michael J. Johnsona,
Arthur B. Youdd,
Pooja Vadhvaa,
Partha P. Paul hi,
Philip J. Withers
hi,
Philip J. Withers i,
Marco Di Michielh,
Dean S. Keeble
i,
Marco Di Michielh,
Dean S. Keeble j,
Michael Ryan Hansen
j,
Michael Ryan Hansen ef,
David O. Scanlon
ef,
David O. Scanlon *bc and
Alexander J. E. Rettie
*bc and
Alexander J. E. Rettie
 *ab
*ab
aElectrochemical Innovation Laboratory, Department of Chemical Engineering, University College London, London, UK, WC1E 7JE. E-mail: a.rettie@ucl.ac.uk
bThe Faraday Institution, Quad One, Harwell Science and Innovation Campus, Didcot, OX11 0RA, UK. E-mail: d.scanlon@bham.ac.uk
cSchool of Chemistry, University of Birmingham, Edgbaston, Birmingham, B15 2TT, UK
dDepartment of Chemistry, University College London, London, WC1H 0AJ, UK
eInstitute of Physical Chemistry, University of Münster, Corrensstrasse 28/30, 48149 Münster, Germany
fInstitute of Inorganic and Analytical Chemistry, University of Münster, Corrensstrasse 28, Münster, 48149, Germany
gInternational Graduate School for Battery Chemistry, Characterization, Analysis, Recycling and Application (BACCARA), University of Münster, Münster, 48149, Germany
hESRF – The European Synchrotron, 71 Avenue des Martyrs, Grenoble, 3800, France
iHenry Royce Institute, Department of Materials, The University of Manchester, Manchester, M139PL, UK
jDiamond Light Source Ltd., Diamond House, Harwell Science and Innovation Campus, Didcot, OX11 0DE, UK
First published on 17th January 2025
Abstract
Lithium phosphides are an emerging class of Li+ ion conductors for solid state battery applications. Despite potentially favorable characteristics as a solid electrolyte, stoichiometric crystalline Li3AlP2 has been reported to be an ionic insulator. Using a combined computational and experimental approach, we investigate the underlying reasons for this and show that ion transport can be induced via defects and structural disorder in this material. Lithium vacancies are shown to promote diffusion, and a low barrier to Li+ hopping of 0.2–0.3 eV is revealed by both simulations and experiment. However, polycrystalline pellets exhibit low ionic conductivity (≈10−8 S cm−1) at room temperature, attributed to crystalline anisotropy and the presence of resistive grain boundaries. These aspects can be overcome in nanocrystalline Li3AlP2, where ionic conductivity values approaching 10−6 S cm−1 and low electronic conductivities are achieved. This approach, leveraging both defects and structural disorder, should have relevance to the discovery of new, or previously overlooked, ion conducting materials.
1 Introduction
All solid-state batteries have the potential to offer high energy density and safety – crucial aspects for next generation energy storage technologies.1 These devices require solid electrolyte (SE) materials which must have high ionic and low electronic conductivities and wide electrochemical stability windows, and be easily processible.2 Thus, strategies to discover and optimise SEs that simultaneously meet these stringent criteria are of great interest.High ionic conductivity (σion > 1 mS cm−1) and facile densification at room temperature have been realised in several Li-ion SE families: sulfides,3,4 halides5 and recently, phosphide Zintl phases.6,7 Named after Eduard Zintl who first studied them,8,9 these are solid-state compounds formed between metals from groups 1 and 2 and elements from groups 13 and 14. Such materials exhibit characteristics that should produce good SE candidates, namely: a tendency towards open framework structures (beneficial for ion transport), as well as being poor electronic conductors (semiconducting).10 Additionally, the phosphide anion is relatively large and polarisable; aspects thought to be favourable for facile ion migration and room temperature deformability.11,12
The reported ternary Li–M–P phases (M = Al, Si, Ga, Sn)6,7,13,14 by Fässler and co-workers support this rationale. The most lithium-rich member in the Li–Al–P phase space, Li9AlP4 achieved σion ≈ 3 mS cm−1 at room temperature, with a computational study confirming low barriers to ion migration in Li–M–P compounds.15 Despite its similarity to Li9AlP4 in AlP4 structural motifs, 50 at% Li content and 3D ion migration pathways (Fig. 1), stoichiometric Li3AlP2 was recently reported to be an ionic insulator by impedance spectroscopy.16
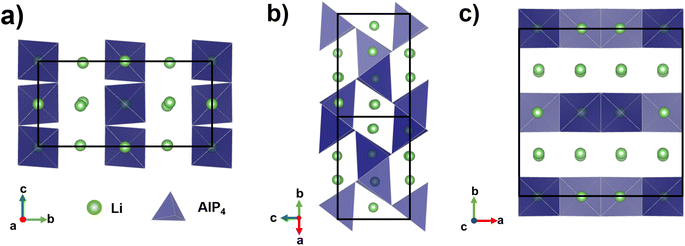 | ||
| Fig. 1 Crystal structure of orthorhombic Li3AlP2,16 the unit cell is shown in solid black lines. AlP4 tetrahedra are shown in blue and Li atoms in green. Li+ layers in the a and c axes are notable in (a) and (c). Intralayer Li+ channels are highlighted in (b). | ||
Strategies to introduce vacancies or excess mobile ions are commonly employed to increase the σion of SE materials.17,18 Additionally, the disordered or nanocrystalline materials produced via high energy ball milling have recently expanded the toolbox to realise new SEs. This has been demonstrated in the ternary lithium halides: mechanosynthesised Li3YCl6 exhibited diffraction patterns with broad peaks – consistent with nanocrystallinity – and high σion values,5 and in the case of Li3ErI6, where the as-milled phase had a higher σion compared to the material after thermal annealing.19 Similar phenomena has been reported for some sulfide electrolytes, namely Li6PS5I and Li4PS4I, where nanocrystalline materials outperformed their microcrystalline counterparts.20,21 Although whether this kind of disorder is positively or negatively correlated with σion is highly material-specific,22 the utility of ball milling to access non-equilibrium ion conducting phases is clear. To the best of our knowledge, the effects of non-stoichiometry or structural disorder on ionic conduction in ternary phosphides have not been reported so far.
Here, we investigate defect engineering approaches as a means of improving the solid electrolyte properties of Li3AlP2. First, calculations are performed to evaluate the defect chemistry and Li ion transport in this material. Vacancy assisted Li-ion hopping is shown to be the most favourable mechanism with a low activation energy, but a low native defect concentration and anisotropy appear to limit ionic transport. We then synthesise non-stoichiometric nanocrystalline and crystalline powders via mechanical ball milling and thermal treatments. Although a low microscopic hopping barrier is confirmed experimentally in crystalline Li3AlP2, a poor macroscopic conductivity is measured on pellets by impedance spectroscopy. Nanocrystalline Li3AlP2 materials are shown to exhibit at least one order of magnitude higher ionic conductivity than their crystalline counterparts while maintaining low electronic conductivity. This result is attributed to both a disruption of slow inter-layer ion transport and reduced grain boundary resistance. These results further our understanding of materials design strategies for SEs and suggest structurally disordered analogues of crystalline materials are worthy of (re-)investigation via combined theoretical and experimental approaches. Although our focus here is SEs, ternary,23 and higher,24 metal phosphides have also shown promise as high-capacity electrode materials that could benefit from such strategies to improve ion transport.
2 Methodology
2.1 Computational methods
DFT calculations were carried out using the Vienna Ab initio Simulation Package (VASP) with Projector Augmented Wave (PAW) pseudopotentials.25–28 Nudged elastic band (NEB) and ab initio molecular dynamics (AIMD) simulations were performed using the GGA functional PBEsol.29 Band structures, density of states, and defect formation energies were calculated using the hybrid functional HSE06.30,31 A 450 eV energy cutoff for the plane wave basis set was used, and was increased by 30% for calculations which allowed for the cell volume to change. A Γ-centered Monkhorst–Pack k-point grid with a density of 0.27 Å−1 was used to sample reciprocal space. Defect, AIMD and NEB calculations were all carried out in supercells with cell lengths greater than 10 Å to minimise interactions between periodic-images (full methodological details for the defect calculations can be found in the ESI†). Self-consistent field cycles were deemed converged when energy differences between successive cycles fell within 1 × 10−6 eV and structural relaxations were deemed converged when forces on all atoms fell below 0.005 eV per atom (this tolerance was increased to 0.01 eV per atom for the NEB calculations). For each AIMD simulation, two equilibration stages were performed, first using a 2 ps NVE run with temperature rescaling every 50 steps, followed by a 2 ps NVT run. The production NVT simulations were run for 95 ps.Mean squared displacements from the AIMD trajectories were calculated using the KINISI software package.32,33 CPLAP was used for calculating chemical potential limits.34 Self-consistent Fermi energies, transition level diagrams and defect concentrations were calculated using the py-sc-fermi software package.35 Ancillary analysis used the doped,36,37 scipy,38 numpy,39 pandas,40 ASE,41 pymatgen,42 sumo43 and phonopy44,45 python libraries.
2.2 Synthesis
All chemical handling was performed in an Ar-filled glovebox (MBraun, <1 ppm H2O and O2), because of flammable/air-sensitive precursors, intermediate and final products. To produce Li3AlP2 powders, stoichiometric amounts of lithium metal wire (3.2 mm dia., Alfa Aesar, 99.8%), aluminium powder (Alfa Aesar, 325 mesh, 99.5%) and red phosphorous powder (Sigma-Aldrich, ≥97.0) were mixed in a mortar and pestle before ball milling in a tungsten carbide (WC) milling jar containing three WC balls, dia. 15 mm each. A planetary ball mill (Retsch PM 100) was used to mill the materials at 350 rpm (10 min on and 3 min off) for 36 hours total. Before annealing, crucibles and ampules were dried in a drying oven overnight and transferred to a glovebox for assembly. The milled powders were loaded into an alumina crucible (Almath) and carefully placed in fused silica (Multi-lab) ampule followed by an alumina cap. The fused silica ampule was then evacuated and flame-sealed under 3–6 mTorr. These assemblies were annealed upright at three different temperatures: 300, 500, and 700 °C for 12 h in a box furnace (Carbolite-Gero CWF 1200).2.3 X-ray diffraction
Lab-based X-ray diffraction (LXRD) and synchrotron X-ray diffraction (SXRD) were carried out to check the phase purity and obtain crystallographic information. LXRD was conducted using a Rigaku Smartlab SE diffractometer with a Mo X-ray source (wavelength = 0.71 Å). The 2θ angle scanning range was from 5° to 40° with a scan speed of 0.8° min−1. Air-sensitive Li3AlP2 powder was protected from air and moisture by sealing Kapton tape against the top of the sample holder in an Ar-filled glovebox. SXRD experiments were performed at the European Synchrotron Radiation Facility (ESRF; ID15A,46 wavelength = 0.2479 Å) for as-milled and 300 °C annealed samples, and at Diamond Light Source (I15, wavelength = 0.1722 Å) for 500 °C annealed samples. All powder samples were flame-sealed under 3–6 mTorr in borosilicate glass capillary tubes (Capillary Tube Supplies Ltd., outer dia. 1.5 mm). The crystal structure and simulated diffraction patterns were analysed using VESTA software.47 Rietveld refinement was conducted using TOPAS software (version 7.21).2.4 Pair distribution function (PDF) analysis
X-ray scattering measurements were performed at the ESRF (beamline ID15A) using powder samples flame-sealed in fused silica capillaries (identical sample preparation to the SXRD experiments detailed in Section 2.3). The wavelength of X-rays were 0.2479 Å and 0.1239 Å for the 300 °C and 500 °C annealed samples respectively. pyFAI48 software was used for integration and background subtraction. The transformation from S(Q) to G(r) was done using PDFgetX3 (ref. 49) software, with maximum momentum transfer vector Qmax = 15 Å−1 and small box modelling of the local structure performed with PDFgui software.502.5 Nuclear magnetic resonance spectroscopy
Single-pulse 6Li, 27Al and 31P magic-angle spinning (MAS) NMR experiments to investigate the local structure were performed on a Bruker DSX 500 spectrometer equipped with a wide-bore superconducting magnet operating at 500.39 MHz (11.75 T) using a VTN broadband probe and zirconia rotors with outer dia. 4 mm packed under Ar atmosphere. Larmor frequencies of the studied nuclei were 73.6 MHz (6Li), 130.3 MHz (27Al), 202.5 MHz (31P). A MAS frequency of 10.00 kHz were used for all nuclei. MAS NMR experiments for all samples were performed using the following pulse lengths, flip angles: 5.50 μs, 90° (6Li), 2.00 μs, 90° (27Al), 4.00 μs, 45° (31P). To ensure quantitative spectra the following relaxation delays were used: 180 s (6Li), 2 s (27Al), 30 s (31P). The obtained MAS NMR spectra were referenced to 6Li-enriched Li2CO3 (0.1 ppm), 1 M Al(NO3)3 (0 ppm) and 1 M H3PO4 (0 ppm) for 6Li, 27Al, and 31P respectively.Single-pulse static 7Li NMR experiments with varying temperature were performed on a Bruker Advance III 300 spectrometer equipped with a wide-bore magnet which operates at 300.15 MHz (7.05 T) using a VTN broadband probe and zirconia rotors with outer dia. 4 mm packed under Ar atmosphere. All experiments were conducted at a resonance frequency of 116.6 MHz (7Li) with a pulse length of 2.50 μs for a 90° pulse, corresponding to a nutation frequency of 100 kHz. The temperature of the sample was regulated by using a nitrogen gas flow and electrical heating. In the temperature range between 165–210 K, a heated nitrogen dewar tank was used; between 200–300 K, an Air Jet XR compressor-based cooling system from SP Scientific (FTS Systems); between 300–420 K, an uncooled nitrogen gas flow was used. 1H NMR spectra of methanol (176–290 K) and ethylene glycol (320–440 K) were recorded to calibrate the temperature with the occurring shifts in signal frequency. Extrapolation of the indicated temperature versus recorded chemical shift function was used to calibrate temperature points below the freezing point of methanol.
The full width at half maximum (FWHM) were extracted from the varying temperature static 7Li NMR spectra in order to obtain activation energies (Ea) for Li+ ion transport, using the Hendrickson–Bray equation given by:
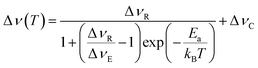 | (1) |
2.6 Cell fabrication
Solid-state electrochemical characterisation was performed using a cylindrical cell where pressure could be applied, based on the design reported by Randau et al.51 In a typical experiment, 0.15 g of powder was added to the PEEK cell chamber (8 mm dia.) and uniaxially pressed (pressure = 130 MPa, measured using a load cell) to form a pellet between two stainless steel plungers that functioned as ion-blocking electrodes. This process resulted in an approximate pellet density of 1.5 g cm−3 (>80% of theoretical). To assemble the Li|SE|Li cell configuration, lithium metal discs (Goodfellow, 0.1 mm thickness) were punched to 7 mm in diameter and placed either side of the pellet.2.7 Electrochemical and electronic characterisation
A potentiostat (ref. 600+, Gamry) was used for electrochemical and electronic measurements in the cells described previously at room temperature in an Ar-filled glovebox. Electrochemical impedance spectroscopy (EIS) was conducted using a 10–50 mV perturbation voltage range over a frequency range of 0.1–1 MHz. The EIS data were fit using an equivalent circuit model (ECM) assisted by Kramers–Kroenig analysis as well as the distribution of relaxation times (DRT) method52 using DRTtools software.53 Based on the bulk resistance (R) obtained through EIS measurements, the σtot was calculated through eqn (2),
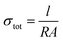 | (2) |
| σtot = σion + σe | (3) |
3 Results and discussion
3.1 Computational investigation of crystalline Li3AlP2
First reported by Juza and Schulz in 1952,54 Li3AlP2 consists of alternating corner and edge-sharing AlP4 tetrahedra that form a layered structure perpendicular to the b axis with pure Li layers separated by mixed Li/Al slabs (Fig. 1). The 3D connectivity of the Li+-containing channels and layers suggest facile ion diffusion may be possible in this structure. The crystal structure has been indexed as orthorhombic, both as Ibca (no. 73)54 and Cmce (no. 64),16 – this study assumes the symmetry of Cmce (no. 64) to be consistent with the latest literature. Table 1 shows a comparison between the lattice parameters predicted by the two functionals as compared to experiment. Generally, PBEsol slightly overestimated the lattice parameters while HSE06 underestimated them, but all values are within 1% of the experimental lattice parameters.| PBEsol (Å) | HSE06 (Å) | Experiment (Å) | |
|---|---|---|---|
| a | 11.56 | 11.44 | 11.51 |
| b | 11.80 | 11.66 | 11.76 |
| c | 5.84 | 5.77 | 5.82 |
Our electronic structure calculations (Section S1 in the ESI†) confirmed previous results for this compound,16,55 i.e., a direct band gap with magnitude in agreement with the experimentally measured absorption onset of ≈2.4 eV.56 However, phonon, defect and molecular dynamics calculations had not been performed for Li3AlP2. Phonon calculations indicated a stable phase with the phonon band structure shown in Fig. S1.2 in the ESI.†
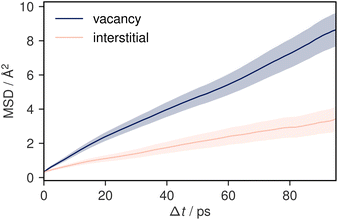
To understand potential diffusion mechanisms in orthorhombic Li3AlP2, we performed two AIMD simulations, a system containing a lithium vacancy and a system containing a lithium interstitial. The lithium mean squared displacements (MSD) for the two systems simulated for 95 ps at 900 K are shown in Fig. 2. The MSD for the vacancy system rises more quickly with time, suggesting faster diffusion in the lithium deficient system than the lithium-rich system and vacancy diffusion as the dominant transport mechanism in Li3AlP2. To obtain more insight into the diffusion processes in the vacancy containing cell, we assigned lithium site occupancies over the simulation timescale and tracked which sites the hops occur between. We can assign these hops as either intra- or inter-layer, and more specifically as between the Li-layer and the mixed Li/Al layer, or within them. This yields three types of hop: between the sites in the mixed layer, between the sites in the lithium layer, or hopping from one layer to the other. The frequency of each of these hops over the simulation timescale is plotted in Fig. 3. It is immediately clear from these simulations that the transport in Li3AlP2 is anisotropic, with the vast majority of hops occurring within the Li-layer, only relatively rarely did lithium hop between layers.
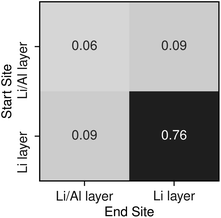 | ||
| Fig. 3 Transition frequencies between the different lithium sites in a Li3AlP2 supercell containing a single vacancy taken from a 95 ps AIMD simulation at 900 K. | ||
To further confirm and characterise the anisotropic lithium transport in Li3AlP2, we calculated climbing-image nudged elastic band (NEB) simulations on each symmetry-independent vacancy hop in crystalline Li3AlP2. The calculated energy profile for these hops are shown in Fig. 4. In general, the barriers were highest for the hops between layers and lower for hops within them, in line with the observed anisotropy in the AIMD simulations. The intralayer hopping within the mixed Li/Al layer had the lowest barrier, however, the higher energy of the end points relative to those within the lithium layer explained why this hop is less frequent in the AIMD simulation: even though the barrier was lower for hopping in the Li/Al layer, lithium vacancy formation in the mixed layer was less energetically favourable, and so these sites were less likely to be depopulated, reducing the occurrence of this hopping process. For comparison, the direct interstitial hopping barrier was greater that 1 eV, and an interstitialcy mechanism returned a barrier of 0.58 eV (Fig. S1.3 in the ESI†).
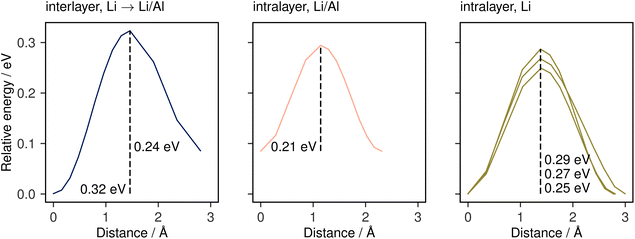 | ||
| Fig. 4 Climbing-image NEB barriers calculated for each symmetrically distinct near-neighbour vacancy-mediated Li-diffusion pathway in Li3AlP2 categorised by the identity of the end-member lithium sites. These pathways are shown schematically in the ESI, Fig. S1.3.† | ||
The assumption of vacancy-mediated transport in Li3AlP2 is predicated on lithium vacancies being a major defect species in Li3AlP2. To confirm this, we characterised the defect chemistry in Li3AlP2 as a function of elemental chemical potentials.57 Under all conditions, the highest concentration point-defects were lithium interstitials and vacancies approximately corresponding to Frenkel-defect dominated defect chemistry. All defects with concentrations above 1 × 108 cm−3 under lithium-poor conditions are shown in Fig. 5. This result again supports the possibility of vacancy dominated transport. However, it is worth noting that these defect concentrations correspond to less than 0.01% of lithium sites being vacant and of the interstitial sites being occupied, i.e., despite the reasonably low barriers for vacancy hopping, Li3AlP2 is fully ordered and, under a thermodynamic regime, has low defect concentrations.
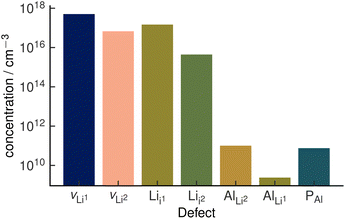 | ||
| Fig. 5 Defect concentrations in orthorhombic Li3AlP2 calculated under thermodynamic equilibrium. The two unique Li sites are discretised with the notation site Li1 and site Li2. Site Li1 refers to the lithium site in the Li layer. Site Li2 refers to the lithium site in the mixed Li/Al layer. The positions of the two interstitial sites are shown in the ESI, Fig. S1.† | ||
Taken together, this computational analysis pointed to two potential limiting factors for facile long-range conductivity in Li3AlP2: diffusion and defect formation anisotropy results in effective 2D transport in a system which on visual inspection may be assumed to have 3D transport. This may increase grain boundary resistance by introducing strong grain-orientation dependence on transport and in addition, low defect concentrations in an ordered system results in an effective low carrier concentration, further limiting conductivity. Therefore, strategies to improve ionic conductivity in Li3AlP2 should aim to overcome these limitations, disrupting the anisotropic diffusion pathways and increasing the charge carrier concentrations.
3.2 Experimental investigation of Li3AlP2
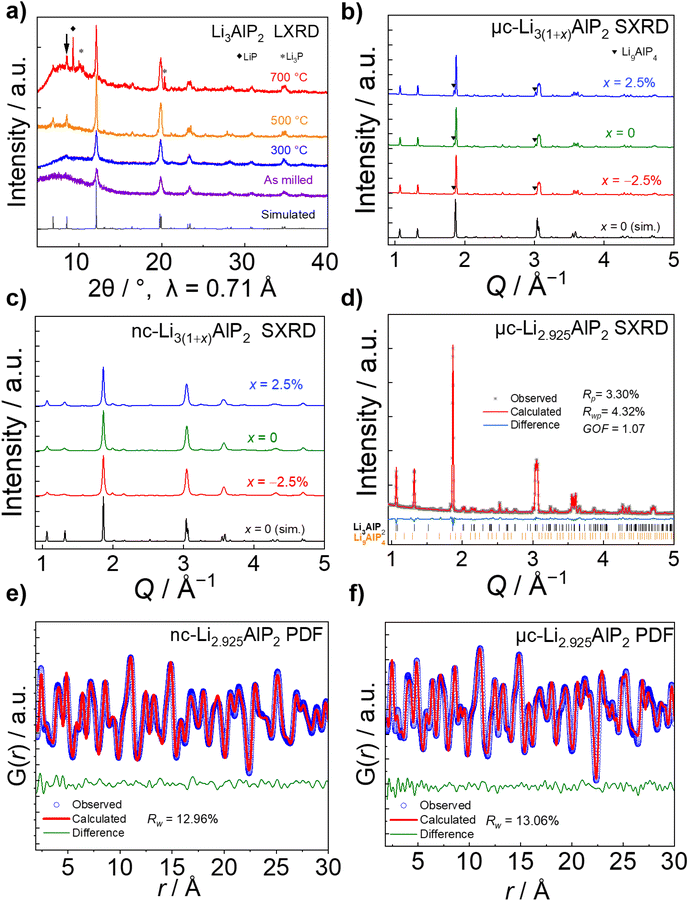
Using SXRD, the as-milled material was shown to exhibit multiple secondary phases and a broad background that were not observable by LXRD (Fig. S2.1 in the ESI†). Due to the phase inhomogeneity of this sample, it was not analysed further. In contrast, Li3AlP2 was obtained as the majority phase in both 300 °C and 500 °C treated samples (Fig. 6b and c).
No crystalline secondary phase was observed for 300 °C-treated Li3(1+x)AlP2 powders (Fig. 6c), but the peaks were noticeably broad, suggesting nanocrystallinity, i.e., nanocrystalline domains in an amorphous matrix. Rietveld refinement using the Scherrer equation58 was performed, resulting in an estimated crystallite size of ≈23 nm. In addition to the orthorhombic Li3AlP2 phase, a Li9AlP4 minor phase was detected for samples annealed at 500 °C, whose intensity decreased with decreasing x (Fig. 6b). Rietveld refinement (Fig. 6d) was carried out for the most phase-pure sample: Li2.925AlP2, resulting in a Li9AlP4 phase fraction of ≈3.5 wt%. Application of the Scherrer equation in this case resulted in a domain size > 170 nm, indicating micron-scale crystallites as expected59 (all crystallographic and refinement parameters can be found in Section S2 in the ESI†).
Based on the above analyses, the samples annealed at 500 °C and 300 °C will be identified as microcrystalline (μc-Li3(1+x)AlP2) and nanocrystalline (nc-Li3(1+x)AlP2) respectively for the remainder of the manuscript. The disordered nature of nc-Li3(1+x)AlP2 motivated us to probe the local structure and the presence of any non-crystalline phases in these samples by pair-distribution-function (PDF) analysis and solid state NMR spectroscopy.
PDF analyses (Fig. 6e and f) revealed similar local structures for nc- and μc-Li3(1+x)AlP2 that could both be well-represented by the long range orthorhombic crystal structure. Full refinement details can be located in Section S7 in the ESI.† In nanocrystals and nanocrystalline materials, the coherence length can be estimated by modelling the PDF intensity with increasing r, as atomic correlations dissipate beyond the spatial extent of the crystalline nanodomains.60,61 Attempts to extract this quantity resulted in a lower limit of ≈20 nm for domains in nc-Li3(1+x)AlP2, consistent with the results of Rietveld refinement.
The obtained MAS NMR spectra are presented in Fig. 7 for 6Li, 27Al and 31P. Orange vertical lines at marked chemical shifts were added to the 6Li, 27Al and 31P spectra to indicate the resonances corresponding to the crystalline Li3AlP2 phase,16 as well as green vertical lines to mark sample impurities and their relative shift. Spinning sidebands are marked with asterisks in all spectra. For clarity, the most phase-pure Li3(1+x)AlP2 samples (x = −2.5%) are presented in the main text, with data for all samples contained in the ESI (Fig. S3.1†).
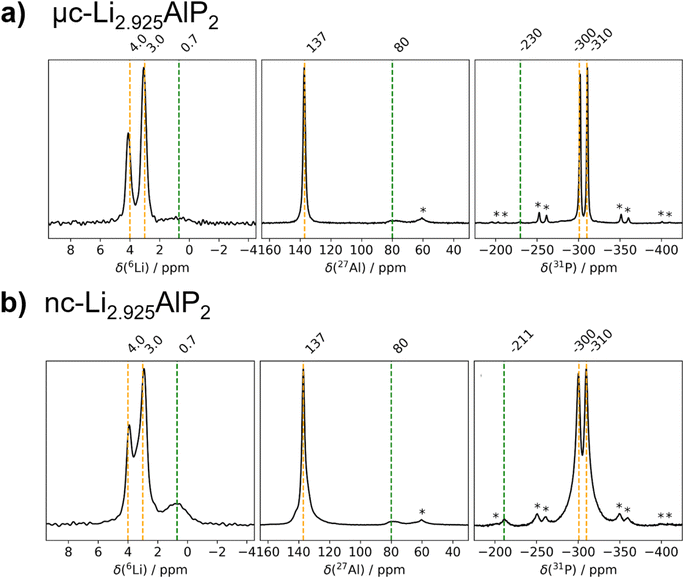 | ||
| Fig. 7 6Li, 27Al and 31P MAS NMR spectra of Li3(1+x)AlP2. (a) μc-Li2.925AlP2 and (b) nc-Li2.925AlP2 recorded with a MAS frequency of 10.0 kHz (11.75 T). | ||
As can be seen in Fig. 7, three distinct Li signals are present in all 6Li MAS NMR spectra. Two of these, with 6Li chemical shifts of 4.0 and 3.0 ppm, are attributed to the two nonequivalent crystallographic positions for Li in the Li3AlP2 crystal structure. However, depending on the annealing temperature and as a result thereof the level of crystallinity, the two Li signals become better resolved in the micro-crystalline compared to the nanocrystalline sample (Fig. 7a). A third 6Li signal at 0.7 ppm is also present, resulting from an unknown impurity. The intensity of this peak is much higher for the nc-Li2.925AlP2 sample (Fig. 7b). It can be also noted that the 6Li signal at 0.7 ppm is much less intense in the μc-Li2.925AlP2 compared to other microcrystalline compositions (Fig. S3 in ESI†). This is in agreement with SXRD refinement results (Fig. 6d) and suggests the lithium deficient sample has the least amount of impurities among all μc-Li3(1+x)AlP2 powders.
In the 27Al MAS NMR spectra presented in Fig. 7, the 27Al signal at 137 ppm may be assigned to the single nonequivalent Al position of the crystal structure for Li3AlP2.16 The 27Al chemical shift is in agreement with aluminum in a tetrahedrally coordinated position as previously reported,62 whereas the 27Al signal linewidths reflect the sample crystallinity, i.e., the linewidth decreases with annealing temperature. In addition, 27Al signals at 80 ppm for the samples in Fig. 7 can be observed. These signals can be attributed to sample impurities and were observed in all samples at similar chemical shifts (Fig. S3 in ESI†). Similar to the 6Li data, μc-Li2.925AlP2 has the weakest impurity peaks compared to all other samples.
In the 31P MAS NMR spectra presented in Fig. 7, two 31P resonances at −300 and −310 ppm can directly be assigned to the two crystallographic nonequivalent phosphorous positions in the Li3AlP2 crystal lattice. Once again a clear narrowing and splitting of signals can be observed due to increased crystallinity. This can be even better seen in the 31P MAS NMR spectra presented in (Section S3 in ESI†) for stoichiometric samples. Different impurity peaks can be identified for both the samples presented in Fig. 7, as well as those in (Fig S3.1 in ESI†). Once again it can be noted that the μc-Li2.925AlP2 sample shows only one impurity peak at −230 ppm with very low intensity.
From the fact that all probed nuclei show impurities it can be speculated that there is a secondary Li–Al–P phase with a different stoichiometry compared to Li3AlP2. This is in agreement with SXRD detecting Li9AlP4 minor phase, although assignment of the impurity peaks to a specific phase was not possible from the MAS NMR spectra. It is likely these are minor amorphous Li–Al–P phases and could describe the amorphous matrix expected in the case of nanocrystalline materials.
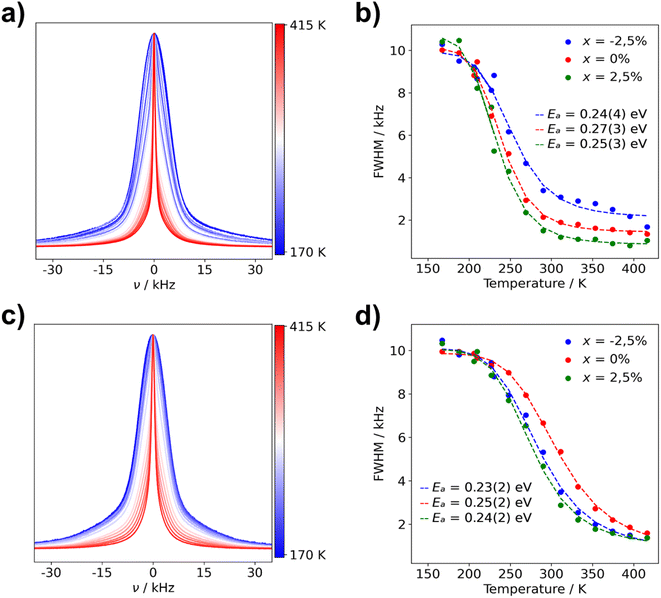 | ||
| Fig. 8 Normalized static 7Li NMR spectra and FWHM of Li3(1+x)AlP2 for (a) μc-Li2.925AlP2 7Li NMR spectra (b) μc-Li3(1+x)AlP2 FWHM fit with eqn (1) and (c) nc-Li2.925AlP2 (d) nc-Li3(1+x)AlP2 FWHM fit with eqn (1). The used color gradient ranges from blue (low temperatures) to red (high temperatures) to indicate the change of lineshapes with temperature. | ||
The FWHM are plotted against temperature in Fig. 8 for all microcrystalline (b) and nanocrystalline (d) samples. Data were fit using eqn (1) (marked with dashed lines in plots) in order to calculate activation energies (Ea) for Li+ ion transport. Obtained activation energies for microcrystalline, nanocrystalline and the as-milled samples can be located in Table S4.1 in the ESI.† Ea values for all samples are within their margin of error (0.2–0.3 eV), regardless of composition and annealing treatment. These NMR data are in strong agreement with the calculated NEB barriers. This indicates that the dominant microscopic Li+ ionic transport mechanism is the same in all samples and pertains to the majority phase: Li3AlP2.
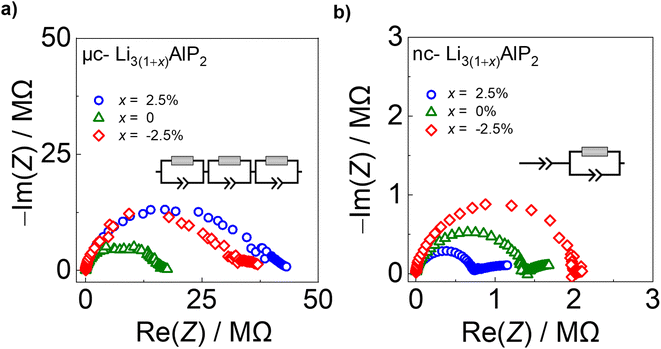 | ||
| Fig. 9 Electrochemical impedance spectra for (a) μc-Li3(1+x)AlP2 and (b) nc-Li3(1+x)AlP2 with equivalent circuit models inset. | ||
In contrast, nc-Li3AlP2 materials exhibited single semi-circles in the Nyquist plots with smaller impedances, which decreased with increasing x value and could be fit with one R-CPE unit (Fig. 9b). These results suggest a simplified and faster ionic conduction pathway compared to the microcrystalline counterparts. These samples' σe values were low (≈10−8 S cm−1), with corresponding transference numbers >0.90 assuming all ion conduction was due to Li.
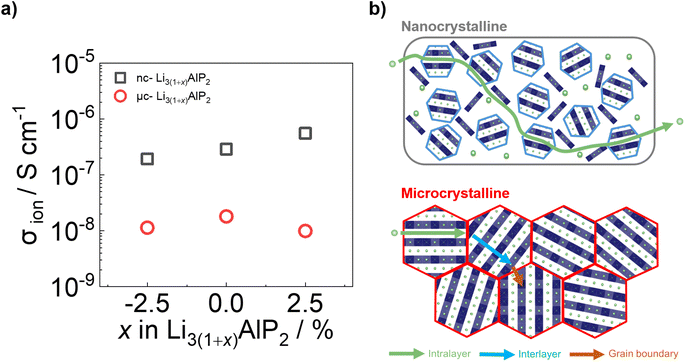
Time-dependent current decay experiments gave low values of σe (Fig. S6.1 in the ESI†). These measurements were used to determine samples' ionic conductivity using eqn (3) (Fig. 10a). We first consider μc-Li3(1+x)AlP2, which had σion values of ≈10−8 S cm−1 at room temperature. The comparable orders of magnitudes for σion and σe resulted in low transference numbers (=σion/σtot) assuming all ion conduction was due to Li.
 | ||
| Fig. 10 (a) Ionic conductivities and (b) cartoon schematics for ion transport processes in nc-Li3AlP2 and μc-Li3AlP2 materials. | ||
These values of σion (although too low for solid electrolyte applications) are appreciable, in contrast to the study of Restle et al., who found stoichiometric μc-Li3AlP2 to be an ionic insulator with capacitor-like behaviour observed using EIS.16 This difference may be due to different annealing procedures: while we used evacuated fused silica ampules, Restle et al., used welded metal cans under an Ar atmosphere. Indeed, different synthetic results were obtained: those authors observed phase-pure material after annealing at 700 °C, while at this temperature we observed impurity phases (Fig. 6a). We speculate that our annealing step under static vacuum facilitated greater loss of volatile elements during annealing, producing Li3AlP2 materials with higher concentrations of Li vacancies based on our computational analyses and thus, appreciable σion. However, targeting samples with greater Li deficiency (Li2.925AlP2) or surplus (Li3.025AlP2) both resulted in a reduction in σion by a factor of 2 (Fig. 10a), principally due to detrimental effects on grain boundary transport (Section S5 in the ESI†). We also note that σion had no relationship to the Li9AlP4 impurity content from SXRD (Fig. 6b).
Approximately 10× greater σion values were observed for nc-Li3AlP2 materials, approaching 10−6 S cm−1 (Fig. 10a). Thus, both bulk and grain boundary resistances were greatly decreased in nanocrystalline form, where the long-range crystal structure is disrupted and grain boundaries removed (Fig. 10b). We note that the ionic conductivities for nc-Li3AlP2 are comparable to initial reports for Li agyrodites,68 which, using site disorder strategies among others,69 have since achieved σion ≈ 10−2 S cm−1 at room temperature. The reason for the positive trend of σion with nominal Li content, x in Fig. 10a is not entirely clear. It is uncorrelated with the amount of amorphous minor component present in the MAS NMR spectra (Section S3 in the ESI†), but is positively correlated with the intensities of low angle diffraction peaks (Fig. 6b): (020) and (200), corresponding to spacings between layers (Fig. 1c). This observation hints that some degree of layer integrity is beneficial to overall σion and a complex relationship between intermediate-range order and ion transport in Li3AlP2.
4 Conclusions
In summary, we performed a computational and experimental investigation of ion transport in Li3AlP2. Defect calculations indicated that lithium ion transport via vacancies was more favorable than an interstitialcy mechanism. Hopping between Li sites was shown to have a relatively low energy barrier however, low native defect concentrations and anisotropy were also observed in simulations.Li3(1+x)AlP2 (x = −2.5, 0, 2.5%) powders were produced via ball milling of the elements followed by thermal annealing treatments. In several cases, minor impurity phases could only be detected using SXRD and solid-state NMR spectroscopy, highlighting the need for detailed characterisation of these materials. Microcrystalline, orthorhombic Li3AlP2 was achieved after heat treatment at 500 °C and facile Li+ hopping was confirmed by dynamic NMR experiments (Ea ≈ 0.25 eV). However, cold-pressed pellets exhibited low σion values (≈10−8 S cm−1), and EIS analyses were consistent with slow transport in the bulk and at grain boundaries. Both may be a result of the strongly anisotropic ion migration pathways in the crystal structure.
Improved ionic conductivities were realised for nanocrystalline Li3(1+x)AlP2 samples produced by annealing at only 300 °C. Broader features in NMR spectroscopy and X-ray diffraction were seen, suggesting a disordered, nanocrystalline Li3AlP2 phase. PDF analysis revealed similar local motifs between the microcrystalline and nanocrystalline materials, with a domain size of ≈20 nm estimated in the latter. σion values in the range 10−7 to 10−6 S cm−1 were determined on pellets by EIS that increased with x, while σe remained low. EIS spectra could be fit with a single relaxation feature, suggesting weaker bulk anisotropy and grain boundary effects as a result of structural disorder.
To conclude, both defect and disorder engineering was shown to positively affect ion transport in the Li3AlP2 system. Aliovalent doping to produce a greater number of vacancies (e.g., substitution of M4+ ions on the Al3+ site) and tuning of structural disorder via optimisation of synthetic conditions would be interesting avenues for future study. Additionally, there are limited studies on the electrochemical stability windows of phosphide-based solid electrolytes,70 and further work in this area would be of great value. Our work should motivate the study of other compounds with anisotropic crystal structures, even those whose stoichiometric crystalline phases that do not exhibit desirable electrochemical properties in the solid-state.
Data availability
Synchrotron-based X-ray scattering data are available through repositories at ESRF (https://doi.esrf.fr/10.15151/ESRF-ES-953231276) and Diamond Light source (CY35411). Experimental (EIS and Lab based XRD, NMR) and computational calculation datasets to support the finding of this article are available from the Zenodo repository (https://doi.org/10.5281/zenodo.14714635).Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors acknowledge the application of Beamlines ID15A at The European Synchrotron (ESRF, MA-5431, https://data.esrf.fr/doi/10.15151/ESRF-ES-953231276) as well as I15 at Diamond Light Source (CY35411) in the completion of this work. JH and AR gratefully acknowledge the Faraday Institution LiSTAR programme (FIRG014, EP/S003053/1) for funding and UCL for start-up funds. PPP and PJW are grateful for funding by EPSRC for the International Centre to Centre Collaboration with the ESRF grant reference EP/W003333/1 and the Henry Royce Institute established through EPSRC grants EP/R00661X/1, EP/P025498/1 and EP/P025021/1. JK is a member of the International Graduate School for Battery Chemistry, Characterization, Analysis, Recycling and Application (BACCARA), which is funded by the Ministry for Culture and Science of North Rhine-Westphalia, Germany. MJJ acknowledges HORIBA-MIRA, UCL and EPSRC (EP/R513143/1) for a CASE studentship. The computations described in this article were performed using University of Birmingham's BlueBEAR HPC service, the Baskerville Tier 2 HPC service (https://www.baskerville.ac.uk/; funded by the EPSRC and UKRI through the World Class Labs scheme (EP/T022221/1) and the Digital Research Infrastructure programme (EP/W032244/1)), and the Sulis Tier 2 HPC platform hosted by the Scientific Computing Research Technology Platform at the University of Warwick (funded by EPSRC Grant EP/T022108/1 and the HPC Midlands+ consortium). Through our membership of the UK's HPC Materials Chemistry Consortium, which is funded by the UK Engineering and Physical Sciences Research Council (EPSRC; EP/L000202, EP/R029431, EP/T022213), this work also used ARCHER2 UK National Supercomputing Services. We are also grateful to the UK Materials and Molecular Modelling Hub for computational resources, which is partially funded by EPSRC (EP/T022213/1, EP/W032260/1 and EP/P020194/1).Notes and references
- J. Janek and W. G. Zeier, Nat. Energy, 2023, 8, 230–240 Search PubMed.
- T. Famprikis, P. Canepa, J. A. Dawson, M. S. Islam and C. Masquelier, Nat. Mater., 2019, 18, 1278–1291 CrossRef CAS PubMed.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, Nat. Mater., 2011, 10, 682–686 CrossRef CAS PubMed.
- Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, Nat. Energy, 2016, 1, 1–7 Search PubMed.
- T. Asano, A. Sakai, S. Ouchi, M. Sakaida, A. Miyazaki and S. Hasegawa, Adv. Mater., 2018, 30, 1803075 Search PubMed.
- S. Strangmüller, H. Eickhoff, D. Müller, W. Klein, G. Raudaschl-Sieber, H. Kirchhain, C. Sedlmeier, V. Baran, A. Senyshyn, V. L. Deringer, L. V. Wüllen, H. A. Gasteiger and T. F. Fässler, J. Am. Chem. Soc., 2019, 141, 14200–14209 CrossRef PubMed.
- T. M. Restle, C. Sedlmeier, H. Kirchhain, W. Klein, G. Raudaschl-Sieber, V. L. Deringer, L. van Wüllen, H. A. Gasteiger and T. F. Fässler, Angew. Chem., Int. Ed., 2020, 59, 5665–5674 CrossRef CAS PubMed.
- E. Zintl and G. Brauer, Z. Phys. Chem. B, 1933, 20, 245–271 Search PubMed.
- E. Zintl and W. Dullenkopf, Z. Phys. Chem. B, 1932, 16, 183–194 Search PubMed.
- R. Nesper, Prog. Solid State Chem., 1990, 20, 1–45 Search PubMed.
- Y. Wang, W. D. Richards, S. P. Ong, L. J. Miara, J. C. Kim, Y. Mo and G. Ceder, Nat. Mater., 2015, 14, 1026–1031 CrossRef CAS PubMed.
- J. C. Bachman, S. Muy, A. Grimaud, H. H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Chem. Rev., 2016, 116, 140–162 CrossRef CAS PubMed.
- H. Eickhoff, S. Strangmüller, W. Klein, H. Kirchhain, C. Dietrich, W. G. Zeier, L. V. Wüllen and T. F. Fässler, Chem. Mater., 2018, 30, 6440–6448 CrossRef CAS.
- S. Strangmüller, D. Müller, G. Raudaschl-Sieber, H. Kirchhain, L. van Wüllen and T. F. Fässler, Chem.–Eur. J., 2022, 28, e20210421 CrossRef PubMed.
- Z. Min, C. Yang, G. H. Zhong and Z. Lu, ACS Appl. Mater. Interfaces, 2022, 14, 18373–18382 CrossRef CAS PubMed.
- T. M. Restle, J. V. Dums, G. Raudaschl-Sieber and T. F. Fässler, Chem.–Eur. J., 2020, 26, 6812–6819 CrossRef CAS PubMed.
- J. B. Goodenough, Solid State Ionics, 1997, 94, 17–25 Search PubMed.
- A. G. Squires, D. O. Scanlon and B. J. Morgan, Chem. Mater., 2020, 32, 1876–1886 CrossRef CAS.
- R. Schlem, T. Bernges, C. Li, M. A. Kraft, N. Minafra and W. G. Zeier, ACS Appl. Energy Mater., 2020, 3, 3684–3691 CrossRef CAS.
- A. Jodlbauer, J. Spychala, K. Hogrefe, B. Gadermaier and H. M. R. Wilkening, Chem. Mater., 2024, 36, 1648–1664 Search PubMed.
- M. Brinek, C. Hiebl and H. M. R. Wilkening, Chem. Mater., 2020, 32, 4754–4766 CrossRef CAS PubMed.
- R. Schlem, C. F. Burmeister, P. Michalowski, S. Ohno, G. F. Dewald, A. Kwade and W. G. Zeier, Adv. Energy Mater., 2021, 11, 2101022 CrossRef CAS.
- H. Tan, L. Sun, Y. Zhang, K. Wang and Y. Zhang, Adv. Sustain. Syst., 2022, 6, 2200183 CrossRef CAS.
- W. Li, Y. Li, J.-H. Wang, S. Huang, A. Chen, L. Yang, J. Chen, L. He, W. K. Pang and L. Thomsen, et al., Energy Environ. Sci., 2024, 17, 5387–5398 Search PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B:Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 Search PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 Search PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- A. R. McCluskey, S. W. Coles and B. J. Morgan, J. Chem. Theory Comput., 2025, 21(1), 79–87 CrossRef CAS PubMed.
- A. R. McCluskey, A. G. Squires, J. Dunn, S. W. Coles and B. J. Morgan, J. Open Source Softw., 2024, 9, 5984 CrossRef.
- J. Buckeridge, D. Scanlon, A. Walsh and C. Catlow, Comput. Phys. Commun., 2014, 185, 330–338 CrossRef CAS.
- A. G. Squires, D. O. Scanlon and B. J. Morgan, J. Open Source Softw., 2023, 8, 4962 CrossRef.
- S. R. Kavanagh, A. G. Squires, A. Nicolson, I. Mosquera-Lois, A. M. Ganose, B. Zhu, K. Brlec, A. Walsh and D. O. Scanlon, J. Open Source Softw., 2024, 9, 6433 Search PubMed.
- I. Mosquera-Lois, S. R. Kavanagh, A. Walsh and D. O. Scanlon, npj Comput. Mater., 2023, 9, 25 CrossRef CAS.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt and SciPy 1.0 Contributors, Nat. Methods, 2020, 17, 261–272 Search PubMed.
- C. R. Harris, K. J. Millman, S. J. Van Der Walt, R. Gommers, P. Virtanen, D. Cournapeau, E. Wieser, J. Taylor, S. Berg and N. J. Smith, et al., Nature, 2020, 585, 357–362 CrossRef CAS PubMed.
- W. McKinney, Proceedings of the 9th Python in Science Conference, 2010, pp. 56–61 Search PubMed.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002 Search PubMed.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- A. M Ganose, A. J Jackson and D. O Scanlon, J. Open Source Softw., 2018, 3, 717 Search PubMed.
- A. Togo, L. Chaput, T. Tadano and I. Tanaka, J. Phys. Condens. Matter, 2023, 35, 353001 CrossRef CAS PubMed.
- A. Togo, J. Phys. Soc. Jpn., 2023, 92, 012001 CrossRef.
- G. B. M. Vaughan, R. Baker, R. Barret, J. Bonnefoy, T. Buslaps, S. Checchia, D. Duran, F. Fihman, P. Got, J. Kieffer, S. A. J. Kimber, K. Martel, C. Morawe, D. Mottin, E. Papillon, S. Petitdemange, A. Vamvakeros, J.-P. Vieux and M. Di Michiel, J. Synchrotron Radiat., 2020, 27, 515–528 CrossRef CAS PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- J. Kieffer and D. Karkoulis, J. Phys.: Conf. Ser., 2013, 202012 CrossRef.
- P. Juhás, T. Davis, C. L. Farrow and S. J. L. Billinge, J. Appl. Crystallogr., 2013, 46, 560–566 CrossRef.
- C. L. Farrow, P. Juhas, J. W. Liu, D. Bryndin, E. S. Božin, J. Bloch, T. Proffen and S. J. L. Billinge, J. Phys. Condens. Matter, 2007, 19(7), 335219 CrossRef CAS PubMed.
- S. Randau, D. A. Weber, O. Kötz, R. Koerver, P. Braun, A. Weber, E. Ivers-Tiffée, T. Adermann, J. Kulisch, W. G. Zeier, F. H. Richter and J. Janek, Nat. Energy, 2020, 5, 259–270 CrossRef CAS.
- P. Vadhva, J. Hu, M. J. Johnson, R. Stocker, M. Braglia, D. J. L. Brett and A. J. E. Rettie, ChemElectroChem, 2021, 8, 1930–1947 CrossRef CAS.
- T. H. Wan, M. Saccoccio, C. Chen and F. Ciucci, Electrochim. Acta, 2015, 184, 483–499 CrossRef CAS.
- R. Juza and W. Schulz, Z. Anorg. Allg. Chem., 1952, 269, 1–12 CrossRef CAS.
- M. Dadsetani and S. Namjoo, J. Mod. Phys., 2011, 2, 929–933 CrossRef CAS.
- K. Kuriyama, J. Anzawa and K. Kushida, J. Cryst. Growth, 2008, 310, 2298–2300 Search PubMed.
- S. Zhang and J. Northrup, Phys. Rev. Lett., 1991, 67, 2339–2342 CrossRef CAS PubMed.
- P. Scherrer, Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse, 1918, 1918, 98–100 Search PubMed.
- U. Holzwarth and N. Gibson, Nat. Nanotechnol., 2011, 6, 534 CrossRef CAS PubMed.
- A. S. Masadeh, E. S. Božin, C. L. Farrow, G. Paglia, P. Juhas, S. J. L. Billinge, A. Karkamkar and M. G. Kanatzidis, Phys. Rev. B:Condens. Matter Mater. Phys., 2007, 76, 115413 Search PubMed.
- T. Zhao, A. N. Sobolev, X. Martinez de Irujo Labalde, M. A. Kraft and W. G. Zeier, J. Mater. Chem. A, 2024, 12, 7015–7024 Search PubMed.
- O. H. Han, H. K. C. Timken and E. Oldfield, J. Chem. Phys., 1998, 89, 6046 CrossRef.
- B. B. Duff, S. J. Elliott, J. Gamon, L. M. Daniels, M. J. Rosseinsky and F. Blanc, Chem. Mater., 2023, 35, 27–40 Search PubMed.
- J. T. S. Irvine, D. C. Sinclair and A. R. West, Adv. Mater., 1990, 2, 132–138 Search PubMed.
- C. Ma, K. Chen, C. Liang, C.-W. Nan, R. Ishikawa, K. More and M. Chi, Energy Environ. Sci., 2014, 7, 1638–1642 RSC.
- A. R. Genreith-Schriever, J. P. Parras, H. J. Heelweg and R. A. De Souza, ChemElectroChem, 2020, 7, 4718–4723 Search PubMed.
- A. R. Symington, M. Molinari, J. A. Dawson, J. M. Statham, J. Purton, P. Canepa and S. C. Parker, J. Mater. Chem. A, 2021, 9, 6487–6498 RSC.
- H.-J. Deiseroth, J. Maier, K. Weichert, V. Nickel, S.-T. Kong and C. Reiner, Z. Anorg. Allg. Chem., 2011, 637, 1287–1294 Search PubMed.
- L. Zhou, N. Minafra, W. G. Zeier and L. F. Nazar, Accounts Chem. Res., 2021, 54, 2717–2728 Search PubMed.
- Z. Min, C. Yang, G.-H. Zhong and Z. Lu, ACS Appl. Mater. Interfaces, 2022, 14, 18373–18382 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta04347b |
| This journal is © The Royal Society of Chemistry 2025 |