Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Capacity-weighted figures-of-merit for battery transport metrics†
CJ
Sturgill
 a,
Christopher
Sutton
a,
Christopher
Sutton
 a,
Julian
Schwenzel
a,
Julian
Schwenzel
 b and
Morgan
Stefik
b and
Morgan
Stefik
 *a
*a
aDepartment of Chemistry and Biochemistry, University of South Carolina, Columbia, SC 29201, USA. E-mail: morgan@stefikgroup.com
bFraunhofer Institute of Advanced Manufacturing Technology and Advanced Materials IFAM, Wiener Strasse 12, 28359 Bremen, Germany
First published on 18th December 2024
Abstract
New battery materials with improved transport are needed. Typical measurements yield widely varying voltage-dependent diffusivities and reporting practices are diverse. Some materials (e.g. first-order phase change) have most redox occur at a specific voltage and may be sufficiently represented by singular transport metrics. Many rapid intercalation materials, however, exhibit second-order phase transitions with redox over a broad voltage range. How should such cases be compared? The use of capacity-weighted average values is suggested where voltage-dependent metrics are consolidated into representative descriptors as figures-of-merit. Examples are elaborated where differential capacity (dQ/dV) is used to derive a weighting function to calculate a diffusivity figure-of-merit (DQav). Furthermore, it is shown that galvanostatic techniques can provide transport values with even capacity-weighting such that their mean value (DTav) is capacity-weighted. Though equivalent conceptually, the latter approach avoids derivative noise and subjective smoothing. Computational diffusion values can similarly include capacity-weighted figures-of-merit. Lastly, diffusivity uncertainty is addressed which is dominated by surface area error due to the second-power dependence. Best-practices can reduce the diffusivity error from ∼40% to ∼2% using appropriate BET sorbents or SAXS with thickness measurements. These perspectives improve the comparison of battery materials with a diffusivity figure-of-merit that supports performance-ranking with attention to uncertainty.
Introduction
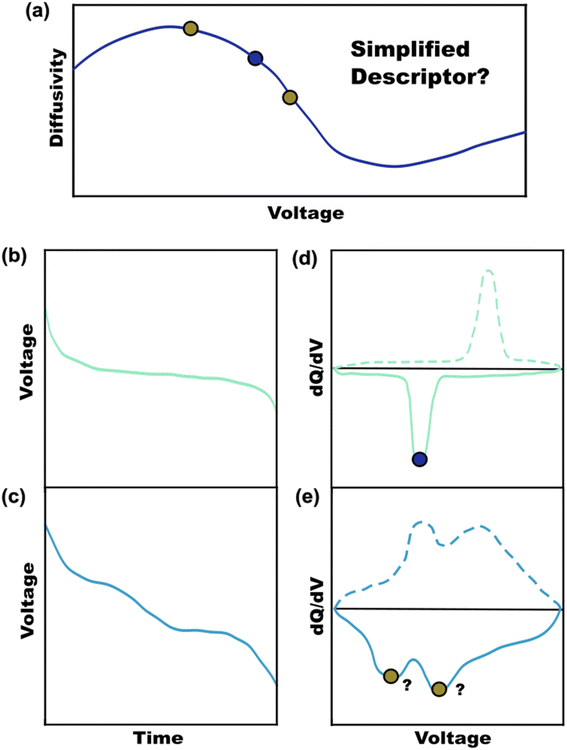
Battery publications have rapidly increased over the past 20 years with a plethora of new materials with improved transport characteristics.1 Battery performance is ultimately linked to the ionic and electronic transport characteristics of the active materials used.2,3 While there is considerable tunability via electrode optimizations (additives, particle size, thickness, porosity) these often come with tradeoffs.4 Volume used for components other than active material necessarily lower the cell-level energy density. Thus, there are benefits with active materials that have improved ionic and/or electronic transport characteristics which require less downsizing and a smaller fraction of non-active materials to reach performance targets. Figures-of-merit (FOM) are representative metrics that are intended to quantitatively rank a given attribute. FOMs such as ionic diffusivity are important for comparing materials directly without the additional convolved effects of the electrode architecture.5,6 Diffusivity values are readily measured with techniques such as intermittent current interruption (ICI),7,8 galvanostatic intermittent titration technique (GITT),9,10 potentiostatic intermittent titration technique (PITT),11,12 and electrochemical impedance spectroscopy (EIS).13,14 These techniques are generally used to measure voltage-dependent diffusivity values across a voltage range with varying state-of-charge (SOC) (Fig. 1a).15 The resulting diffusivity values can vary by an order of magnitude or more for a given material as a function on the voltage/SOC. Please note that first order phase change materials have a single voltage when two phases are present under equilibrium as expressed in Gibb's Phase Rule. Rather here we focus on second order phase change materials where the equilibrium potential of the single phase depends solely upon the SOC. The relative ranking of different materials is simple when one sample exhibits higher diffusivity across the whole voltage range. In contrast, comparing samples with intersecting diffusivities requires additional consideration.The ranking of sample diffusivities is enabled by using a representative FOM. There is not, however, universal agreeance in the literature for how to rank materials in terms of diffusivity. Some publications emphasize maximum diffusivity values16,17 while others focus on specific SOCs18,19 or the voltage(s) of maximum differential capacity (dQ/dV).20,21 A FOM must be representative of overall sample performance. First-order phase change materials exhibit a voltage plateau with a corresponding sharp peak in differential capacity (Fig. 1b and d).22,23 The diffusivity value corresponding to this principal voltage may be a sufficient FOM for such first-order samples, though it may not be clear how each phase contributes towards diffusion. A range of rapid-intercalation materials exhibit second-order phase transitions where diffusivity FOMs are particularly elusive. Such second-order materials do not phase separate during lithiation, but rather exhibit a continuum of lattice distortions. This feature can enable improved longevity by limiting cracking and minimizes voltage hysteresis by avoiding first-order phase transitions.24 Example second-order materials include T-Nb2O5 (ref. 24 and 25) and a range of Wadsley–Roth niobates such as TiNb2O7,6,26–29 Nb16W5O55,30,31 and MoNb12O33 (ref. 32 and 33) to name a few. Some intercalation materials also transition from first-order to second-order behavior with downscaling the particle sizes.34,35 Regardless of the type of phase change, it is prudent to use near-equilibrium conditions (low enough current densities) for diffusion measurements to avoid deviations that depend on the electrode structure. Second-order transitions tend to be associated with a sloped voltage profile (not a plateau) where the corresponding differential capacity plot has broad features, sometimes with multiple peaks and a non-zero baseline (Fig. 1c and e).22,23 Varying crystallinity in battery materials can also influence broadening with charge storage, making a single voltage no longer representative.6,36,37 In these cases, selecting a single diffusivity value would generally fail to account for the full range of behaviors exhibited during battery usage. Complete voltage-dependent profiles benefit battery simulations but are inconvenient as a FOM for ranking materials. A suitable FOM should derive a single value that reflects the full range of voltage-dependent diffusivity values with an appropriate weighting for the relative importance of each measured value.
Capacity-weighted figures-of-merit
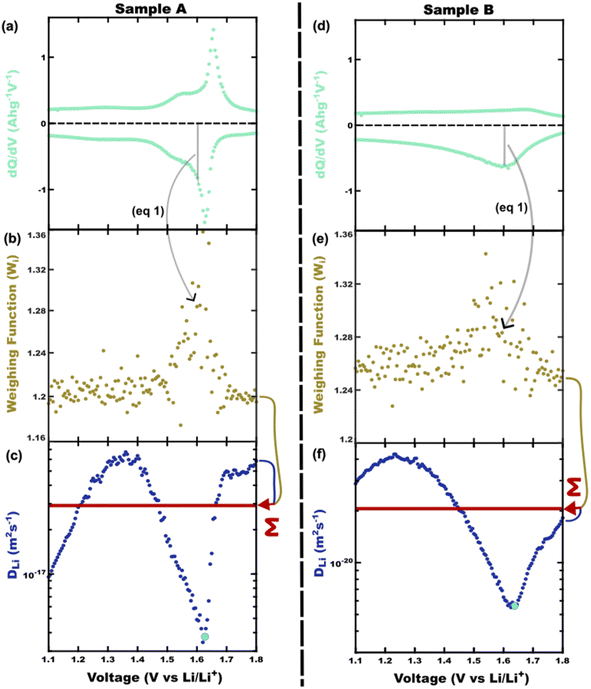
A capacity-weighted average diffusivity is suggested in this perspective where the collection of voltage-dependent diffusivities are consolidated into a single descriptor as a representative FOM. Intercalation materials with second-order transitions in particular need a better diffusivity FOM since they exhibit a continuum of lattice configurations during lithiation, each with different diffusivity values. Capacity-weighting here is intended to scale each measured diffusivity value in proportion to its relative contribution towards the total charge stored. In this way, dominant redox features (dQ/dV peaks) have higher weighting than minor redox features (dQ/dV shoulders) when combining voltage-dependent diffusivities. Naturally this data reduction involves information loss with the benefit that the resulting FOM enables simple ranking of materials in a more wholistic and non-arbitrary way. One benefit of such a weighted average is that the resulting FOM preserves the same units and magnitude as the complete dataset. Two approaches will be elaborated in the next sections with different numerical methods for implementing such capacity-weighted average diffusivities.A material's differential capacity (dQ/dV) can be used to derive a capacity-weighting function to evaluate an average diffusivity FOM. This method scales each measured diffusivity value according to the incremental amount of charge passed (both are voltage-dependent) to weight all diffusivity values according to their relative contribution towards overall charge storage. Two samples are presented conceptually using this approach: a fully-crystalline Sample A and a defect-rich crystalline Sample B.6 Example data will be considered for a well-known intercalation material that exhibits second-order phase changes upon lithiation, TiNb2O7. The sample details are irrelevant for the FOM discussion; however, the presented TiNb2O7 samples were annealed at 1100 °C and 700 °C. The differential capacity plots indicate distinctly different trends of charge storage as a function of voltage (Fig. 2a and d). The corresponding ICI derived diffusivity values as a function of voltage are shown in Fig. 2c and f. Despite both samples having a peak of differential capacity, both samples also have a significant fraction of charge storage spread across the entire voltage range measured. It follows that the diffusivity values for all of these voltages would be overlooked if reporting diffusivity from a single-voltage alone. The capacity-weighting terms (Wi) for the i-ith voltage are calculated as the piecewise integrals under the dQ/dV curve as scaled by the full integral:
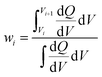 | (1) |
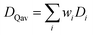 | (2) |
 | ||
| Fig. 2 The differential capacity can be combined with the complete set of diffusivity values to derive a representative descriptor. Two examples are presented (Samples A and B) side-by-side. Each point on the (a and d) dQ/dV plot yields a capacity-weighting term (gray shaded area, eqn (1)). Each (b and e) weight value, Wi(V), is multiplied by the respective diffusivity value, Di(V), (c and f) and summed (red arrow) to yield the capacity-weighted diffusivity (DQav) as a figure-of-merit (red line). In both these cases, the diffusivity at peak dQ/dV (DQP, green dot) is quite different from the more complete DQav descriptor. | ||
Comparing the diffusivity values of Sample A at the voltage of peak charge storage (DQp, Fig. 2c and f green dots) to the DQav reveals an 87% error with the single-point reporting approaches. This comparison highlights the amount of information missed when reporting diffusivity values from second-order materials measured at a single-voltage. Derivative calculations such as dQ/dV naturally amplify the noise of the underlying galvanostatic data. It is typical for dQ/dV plots to require curve smoothing which can bring a subjective component to the numerical analysis (ESI Fig. S2†). Furthermore, the data coordinates along the voltage axis can differ between the dQ/dV values and the ICI diffusivity values, requiring interpolation and the associated error when aligning the voltage coordinates. Thus, transforming dQ/dV into a weighting function enables the calculation of a capacity-weighted average diffusivity with the possibility of requiring subjective curve smoothing and interpolation.
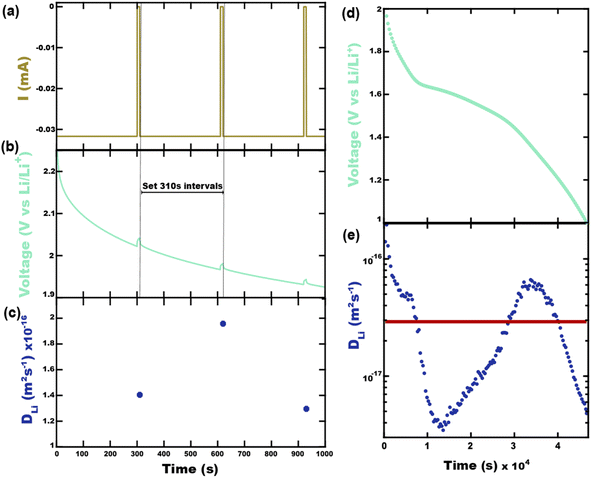
It will be shown that galvanostatic measurements of diffusivity values (ICI/GITT) naturally yield values that are evenly weighted in terms of capacity. In contrast to voltage-controlled methods such as PITT, galvanostatic measurements are carried out with current-control. ICI, for example, typically employs a constant current for a fixed duration in between temporary interruptions to open circuit conditions (Fig. 3a). The voltage is measured continuously throughout ICI measurements to derive the pseudo-open-circuit-potential, resistance, diffusion resistance, and diffusivity (Fig. 3b), vide infra. These four values are evaluated once for each transient interruption (Fig. 3c) where the complete measurement contains numerous evaluated points in time (Fig. 3d and e). Given that ICI uses a constant current with fixed time intervals there is the same amount of charge passed between each interruption stage. From this perspective, all measured values are evenly capacity-weighted. Table 1 clarifies this mathematical fact using Sample A with the first three interruptions enumerated. Here the fixed interval of ΔQ between time-samples is apparent despite the varying ΔQ/ΔV and ΔV values. Since the values are evenly capacity-weighted in this fashion, a mean value (DTav, “time-averaged”) is also capacity-weighted (Table 1 and Fig. 3e red line):
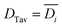 | (3) |
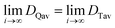 | (4) |
| Intervals | 1 | 2 | 3 | — | Sum | Mean |
|---|---|---|---|---|---|---|
| Δt (s) | 310 | 310 | 310 | — | 4.66 × 104 | — |
| ΔQ/ΔV (mA h g−1 V−1) | 8.32 | 26.9 | 41.7 | — | 3.47 × 104 | — |
| ΔV (V) | 2.33 × 10−1 | 7.20 × 10−2 | 4.65 × 10−2 | — | 1.90 | — |
| ΔQ (mA h g−1) | 1.94 | 1.94 | 1.94 | — | 291 | — |
| Weight | 6.67 × 10−3 | 6.67 × 10−3 | 6.67 × 10−3 | — | 1.00 | — |
| Diffusivity (m2 s−1) | 1.40 × 10−16 | 1.96 × 10−16 | 1.30 × 10−16 | — | — | 2.92 × 10−17 |
| Cell resistance (Ω) | 238 | 176 | 150 | — | — | 87.9 |
| Diffusion resistance (Ω s−0.5) | 133 | 91.7 | 76.5 | — | — | 38.5 |
Rather, the differences between DQav and DTav in practice are in their numerical evaluation. The calculation of DQav using dQ/dV values involves derivative noise and subjective curve smoothing. In contrast, the calculation of DTav does not involve subjective factors but does require the use of ICI/GITT.
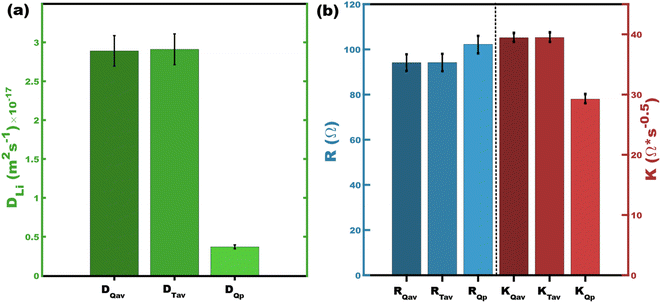
These two numerical methods are next compared to values from the peaks in differential capacity. Fig. 4a compares three different methods of presenting diffusivity values. Both DQav and DTav are closely related by both employing capacity-weighting but are different in terms of the numerical methods. Their corresponding values are nearly identical with 0.69% difference for the presented Sample A datasets. It is noteworthy that using dQ/dV derived from the ICI data would yield the exact same result as time averaging (Fig. S1,†DQav = DTav). As pointed out above, the use of DQp disregards most of the measured diffusivity values and is inherently a less representative value for intercalation materials with second-order phase transitions (Fig. 4a). Extending this concept further, the same sort of capacity-weighted averages can be determined for other ICI/GITT metrics such as the diffusion resistance (K) or cell resistance (R) (Table 1 and Fig. 4b). Analogously capacity-weighted values of ionic conductivity or electrical conductance could similarly be calculated. We argue that using representative FOMs is important when comparing existing and newly discovered battery materials that exhibit second order phase transitions.
Computational diffusivity
Analogous to experimental reporting of diffusivity noted above, it is important that computational simulations also include a range of SOCs for second-order phase change materials to derive descriptors that are representative of overall performance. Here capacity-weighted diffusivities can be calculated using eqn (3) when numerous diffusivity values are calculated with evenly spaced lithium stoichiometries. Recent mechanistic studies of Nb-based Wadsley–Roth materials have highlighted the role of local and long-range structural changes during lithium insertion.38,39 There are broadly two computational methods for diffusion analysis: (1) the calculation of activation energies for specific microscopic pathways and (2) molecular dynamics to derive the mean-squared displacement. Calculating activation energies with e.g. nudged elastic band (NEB) requires first identifying the lowest energy Li–interstitial sites via enumeration of all possible configurations. In the case of such Wadsley–Roth structures, this appears limited to low lithium concentrations due to the combinatorial expansion of the calculations with higher SOCs. Regarding the second route, ab initio Molecular Dynamics (AIMD) simulations can calculate lithium dynamics explicitly over a range of concentrations. With AIMD simulations of structures with a wide range of activation energies (e.g. Wadsley–Roth structures) the selection of simulation temperature is crucial to enable all relevant pathways within the simulated timeframe.39 The resulting AIMD diffusivity values can be scaled to the experimental temperature using the Einstein relationship.40 Doing this analysis over a wide ranging SOCs is challenging due to the number of equivalent configurations and the computational cost of DFT. A simplified way to address the SOC phase transitions is by first determining the relevant short-range configurational order using cluster expansion and preserve that in AIMD simulations. Furthermore, machine learning potentials (MLPs) can bypass the need for running DFT within MD simulations. This accelerates the MLP-based AIMD calculations by orders of magnitude without sacrificing accuracy. Notably there are available foundation models (MACE-MP0, CHGNet, and M3GNet)41–43 that can be used “out of the box” without training or fine-tuning. A broader, long-term challenge for computational simulations is addressing long-range diffusion including complications such as structural heterogeneity and crystalline defects such as grain/phase boundaries, point defects, and stacking faults. This is a grand challenge for computational approaches to identify preferred configurations amongst a many-parameter landscape and then significantly expand the number of atoms and compute-time. Regardless of future improvements, existing computational techniques can be used to calculate capacity-weighted diffusivities.Uncertainty considerations
The minimization of uncertainty is essential when comparing FOMs. Diffusivity calculations such as ICI/GITT/PITT/EIS all combine an electrochemical response time (s) with the diffusion length (m) to derive the m2 s−1 units of diffusivity; correspondingly, all diffusivity calculations have these two inputs as sources of error. The time constant here is determined by a potentiostat, often with much less than a single percent of error (∼0.1%) for the response time.44 In contrast, the diffusion length measurement not only typically has the largest percent error but also has an outsized effect on the diffusivity uncertainty owing to its second-power dependance.45,46 This squaring of the diffusion length in eqn (5) doubles the resulting percent error in the reported diffusivity value. For the sake of alignment with popular gas physisorption reporting, the diffusion length is often parameterized into diffusivity calculations via the mass-specific surface area (A). For example, the ICI method calculates each diffusivity value (D) as: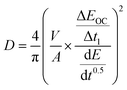 | (5) |
The Brunauer–Emmett–Teller (BET) method of analysis for sample surface area by gas physisorption are commonplace. The possible sources of error include the sorbent selection, the model, and the analysis. It is becoming increasingly known that N2 as a physisorption gas can lead to ∼20% error47–49 in sample surface area due to its quadrupole moment which would correspond to ∼40% error in the derived diffusivity metrics. In contrast, Ar as a sorbent has a spherical geometry, an ability to access smaller micropores, and no quadrupole moment which enables Ar BET to often have ∼0.6% error.47,48,50 This improved accuracy with Ar BET corresponds to ∼1.2% error in the resulting diffusivity values which is sufficiently accurate for meaningful ranking. It should be noted that model and analysis error can also be substantial where a recent round robin study with 61 labs analyzing the same 18 isotherms led to 7.1–31% difference in the interpreted surface areas.49 A challenge with BET measurements for batteries is the general need for ∼1 m2 of sample surface area which for micron scale particles with ∼1 m2 g−1 of specific surface area corresponds to significant ∼1 gram quantity of sample. Furthermore, BET analysis typically takes one to two days for sample degassing and subsequent analysis. Thus, BET with Ar gas is a best-practice method capable of enabling accurate diffusivity calculations.
Best-practices of Porod analysis of X-ray scattering data can also yield similarly accurate specific surface area measurements from few hr measurements on milligram sample quantities. In brief, here small-angle X-ray scattering (SAXS) data are acquired with absolute intensity units and background subtraction where analysis of the Porod region (qPorod > qFourier) contains information about the sample surface.51,52 It is important to note that calculating absolute intensity units requires accurate measurement of the beam brightness, the scattered intensity, and the sample thickness. A Porod plot is typically used (Iabsq4vs. q) where the constant value of Iabsq4 in the high-q limit corresponds to the surface area to volume ratio (Σ):53
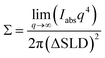 | (6) |
The sample's scattering length density relative to vacuum (ΔSLD) can be determined using an online NIST calculator based on atomic scattering factors.54 The Σ value can then be used to calculate the mass specific surface area (S):
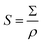 | (7) |
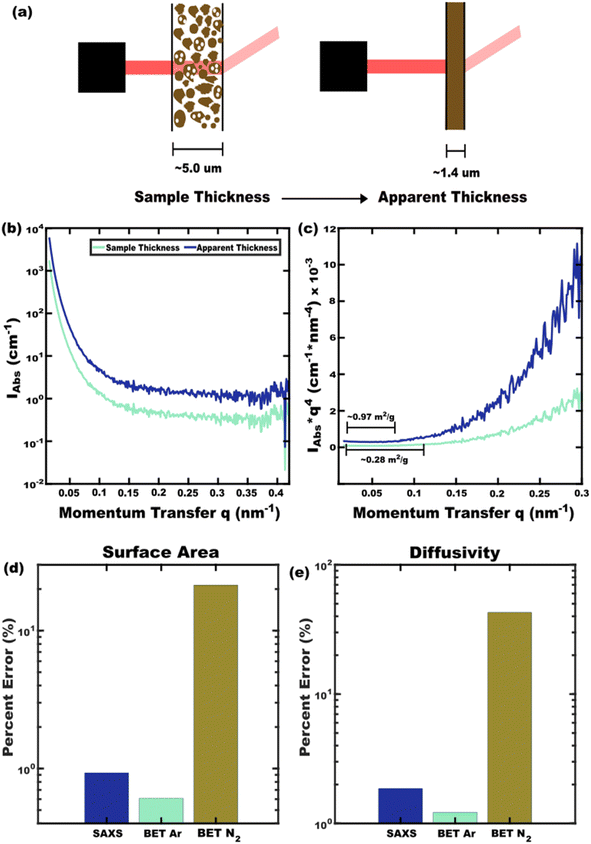 | ||
| Fig. 5 SAXS analysis with (b) absolute scattering intensity can yield specific surface area when analyzing the (c) Porod region of a Porod plot. Here a typical (a) large source of error is the use of measured sample thickness rather than the more accurate effective sample thickness determined by X-ray transmission. Similarly, N2 BET leads to significant (d) error in specific surface area whereas Ar BET or SAXS can be more accurate. The propagation of this error (e) to diffusivity values is important to consider when ranking materials. Nominal error values all obtained from ref. 48. | ||
The diffusion length has also been measured with a diversity of other methods such as electron microscopy.21 Electron microscopy has the benefit of being model-free, however care must be taken to avoid detection bias, human bias, and to include frequent instrument calibration with NIST standards under the same imaging conditions. Furthermore, being a localized measurement, the best-practice with microscopy also requires an abundance of measurements to calculate the average diffusion length (minimum radius) with minimal error-of-the-mean.
The comparison of diffusivity FOMs benefits from error minimization. The error in specific surface areas by BET and SAXS methods are presented in Fig. 5d. While local measurements by electron microscopy can also be used to derive surface area, ensemble methods such as BET or SAXS are preferrable for representative metrics. The present best-practices for surface area analysis include Ar-based BET and SAXS analysis with apparent-thickness. These two techniques yield similarly accurate specific surface areas. The corresponding error in diffusivity values are shown in Fig. 5e which are suitable for material ranking when best practices are used. As researchers continue to discover and test the diffusivity of new battery materials, the ability to rank these values will become increasingly important in terms of correlating material structures to their properties. As a preliminary demonstration, capacity-weighted diffusivities were calculated from published datasets for related materials that each exhibit second-order phase changes upon lithiation (Table 2).21,33,61,62 Previously noted diffusivity trends with block size and Ta/Nb replacement are apparent in the DQav values which remain commensurate to the underlying Di(V) values as expected.21,33 Such ranking benefits from both a comprehensive diffusivity FOM and error-minimization with best-practices for surface area analysis.
| Material | Electrochemical technique | Diffusion length assessment (error) | D Qav (m2 s−1) | Diffusivity errora | Reference |
|---|---|---|---|---|---|
| a Diffusivity error propagated from diffusion length error. b Diffusion length error calculated as the error-of-the-mean reported value. c Diffusion length error estimated based on ref. 47–49. | |||||
| Nb16W5O55 | PITT | SEMb (2.4%) | 1.35 × 10−16 | 4.8% | 21 |
| Nb14W3O44 | PITT | SEMb (2.5%) | 7.29 × 10−17 | 5.0% | 21 |
| Nb12WO33 | PITT | SEMb (1.8%) | 5.02 × 10−17 | 3.6% | 21 |
| Ta12MoO33 | ICI | SAXS (5.1%) | 7.63 × 10−18 | 10.2% | 33 |
| T-Nb2O5 | EIS | N2 BETc (∼20%) | 7.06 × 10−18 | ∼40% | 61 |
| Nb12MoO33 | ICI | SAXS (0.83%) | 6.30 × 10−18 | 1.66% | 33 |
| TiNb2O7 | GITT | N2 BETc (∼20%) | 5.54 × 10−18 | ∼40% | 62 |
Conclusion
Battery materials with improved ionic and electronic transport are necessary for a future with fast-charging anodes. Most transport metrics are reported over a range of voltages with varied reporting methods. For first order phase change materials, most redox occurs at one voltage, allowing that voltage to appropriately represent the material's transport characteristics. However, second-order phase change materials exhibit redox over a broad range of voltages where alternative reporting methods are needed to capture the range of behaviors. Using a capacity-weighted average, the voltage dependent data is combined into one representative value. Capacity-weighted figures-of-merit (DQav) can be derived using a weighing function based on differential capacity (dQ/dV). In addition, galvanostatic techniques supply transport values with even capacity-weighting such that the mean value (DTav) is inherently capacity-weighted. Both FOMs are equivalent mathematically, but DTav avoids data smoothing and interpolation necessary for the dQ/dV approach. Computational simulation of diffusivity can also be tailored to a capacity-weighted figures-of-merit. Uncertainty associated with diffusivity is heavily influenced by surface area error due to its second-power dependence. Using best-practice BET or SAXS methods can reduce the diffusivity error from ∼40% to ∼2%. This collection of perspectives improves material comparisons necessary for performance-ranking and understanding structure–property relationships.Data availability
Data for this perspective, including Sample A's and Sample B's corrected open circuit potential (EOC), ICI diffusivity, ICI resistance, and ICI diffusion resistance, are available at Open Science Framework at https://osf.io/6q2rh/?view_only=5560214975354f9fbb043a79b57918c9.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
CJ S., C. S., and M. S. acknowledge DOE support (DE-SC0023377). This work made use of the South Carolina SAXS Collaborative.References
- J. Ma, Y. Li, N. S. Grundish, J. B. Goodenough, Y. Chen, L. Guo, Z. Peng, X. Qi, F. Yang, L. Qie, C.-A. Wang, B. Huang, Z. Huang, L. Chen, D. Su, G. Wang, X. Peng, Z. Chen, J. Yang, S. He, X. Zhang, H. Yu, C. Fu, M. Jiang, W. Deng, C.-F. Sun, Q. Pan, Y. Tang, X. Li, X. Ji, F. Wan, Z. Niu, F. Lian, C. Wang, G. G. Wallace, M. Fan, Q. Meng, S. Xin, Y.-G. Guo and L.-J. Wan, J. Phys. D: Appl. Phys., 2021, 54, 183001 CrossRef CAS.
- C. Heubner, K. Nikolowski, S. Reuber, M. Schneider, M. Wolter and A. Michaelis, Batteries Supercaps, 2021, 4, 268–285 CrossRef CAS.
- M. E. Houck, A. S. Groombridge, M. F. L. D. Volder and A. M. Boies, Cell Rep. Phys. Sci., 2023, 4, 101410 CrossRef CAS.
- R. Borah, F. R. Hughson, J. Johnston and T. Nann, Mater. Today Adv., 2020, 6, 100046 CrossRef.
- A. Vu, Y. Qian and A. Stein, Adv. Energy Mater., 2012, 2, 1056–1085 CrossRef CAS.
- C. Sturgill, I. Milisavljevic, S. C. Wechsler, M. Muhit, H.-C. Zur Loye, S. Misture and M. Stefik, Chem. Mater., 2024 Search PubMed , Submitted.
- Y.-C. Chien, H. Liu, A. S. Menon, W. R. Brant, D. Brandell and M. J. Lacey, Nat. Commun., 2023, 14, 2289 CrossRef CAS PubMed.
- L. Yin, Z. Geng, Y.-C. Chien, T. Thiringer, M. J. Lacey, A. M. Andersson and D. Brandell, Electrochim. Acta, 2022, 427, 140888 CrossRef CAS.
- W. Weppner and R. A. Huggins, J. Electrochem. Soc., 1977, 124, 1569 CrossRef CAS.
- J. Kim, S. Park, S. Hwang and W.-S. Yoon, J. Electrochem. Sci. Technol., 2021, 13, 19–31 CrossRef.
- M. D. Levi, E. Markevich and D. Aurbach, Electrochim. Acta, 2005, 51, 98–110 CrossRef CAS.
- J. Li, F. Yang, X. Xiao, M. W. Verbrugge and Y.-T. Cheng, Electrochim. Acta, 2012, 75, 56–61 CrossRef CAS.
- F. Mansfeld and U. Bertocci, Electrochemical Corrosion Testing, ASTM International100 Barr Harbor Drive, PO Box C700, West Conshohocken, PA, 1981, pp. 1–411 Search PubMed.
- M. El-Azazy, M. Min and P. Annus, Electrochemical Impedance Spectroscopy, BoD – Books on Demand, 2020 Search PubMed.
- C. Deng and W. Lu, J. Power Sources, 2020, 473, 228613 CrossRef CAS.
- M. Wang, Z. Yao, Q. Li, Y. Hu, X. Yin, A. Chen, X. Lu, J. Zhang and Y. Zhao, J. Energy Chem., 2022, 69, 601–611 CrossRef CAS.
- X. Jin, Y. Deng, H. Tian, M. Zhou, W. Tang, H. Dong, X. Zhang and R. Liu, Green Energy Environ., 2024, 9, 1257–1266 CrossRef CAS.
- J. L. Allen, X. Ren, C. K. Nguyen, D. C. Horn, H. H. Sun and D. T. Tran, ChemElectroChem, 2023, 10, e202300267 CrossRef CAS.
- B. Babu and M. M. Shaijumon, Electrochim. Acta, 2020, 345, 136208 CrossRef CAS.
- J. Zheng, R. Xia, C. Sun, N. Yaqoob, Q. Qiu, L. Zhong, Y. Li, P. Kaghazchi, K. Zhao, J. E. ten Elshof and M. Huijben, Small, 2023, 19, 2301967 CrossRef CAS PubMed.
- L. D. Salzer, B. Diamond, K. Nieto, R. C. Evans, A. L. Prieto and J. B. Sambur, ACS Appl. Energy Mater., 2023, 6, 1685–1691 CrossRef CAS.
- W. Van Den Bergh and M. Stefik, Adv. Funct. Mater., 2022, 32, 2204126 CrossRef CAS.
- Y. Gogotsi and R. M. Penner, ACS Nano, 2018, 12, 2081–2083 CrossRef CAS PubMed.
- S. C. Wechsler, A. Gregg and M. Stefik, Adv. Funct. Mater., 2024, 34, 2312839 CrossRef CAS.
- E. Lim, C. Jo, H. Kim, M.-H. Kim, Y. Mun, J. Chun, Y. Ye, J. Hwang, K.-S. Ha, K. C. Roh, K. Kang, S. Yoon and J. Lee, ACS Nano, 2015, 9, 7497–7505 CrossRef CAS PubMed.
- K. J. Griffith, I. D. Seymour, M. A. Hope, M. M. Butala, L. K. Lamontagne, M. B. Preefer, C. P. Koçer, G. Henkelman, A. J. Morris, M. J. Cliffe, S. E. Dutton and C. P. Grey, J. Am. Chem. Soc., 2019, 141, 16706–16725 CrossRef CAS PubMed.
- A. A. Voskanyan, K. Jayanthi and A. Navrotsky, Chem. Mater., 2022, 34, 10311–10319 CrossRef CAS.
- S. Sun, L. Qin, Y. Sun and C. Guo, Energy Fuels, 2024, 38, 2463–2471 CrossRef CAS.
- R. Tao, G. Yang, E. C. Self, J. Liang, J. R. Dunlap, S. Men, C.-L. Do-Thanh, J. Liu, Y. Zhang, S. Zhao, H. Lyu, A. P. Sokolov, J. Nanda, X.-G. Sun and S. Dai, Small, 2020, 16, 2001884 CrossRef CAS PubMed.
- Y. Yang and J. Zhao, Adv. Sci., 2021, 8, 2004855 CrossRef CAS PubMed.
- K. J. Griffith, K. M. Wiaderek, G. Cibin, L. E. Marbella and C. P. Grey, Nature, 2018, 559, 556–563 CrossRef CAS PubMed.
- X. Zhu, J. Xu, Y. Luo, Q. Fu, G. Liang, L. Luo, Y. Chen, C. Lin and X. S. Zhao, J. Mater. Chem. A, 2019, 7, 6522–6532 RSC.
- M. A. A. Muhit, S. C. Wechsler, Z. J. L. Bare, C. Sturgill, N. Keerthisinghe, M. A. Grasser, G. Morrison, C. Sutton, M. Stefik and H.-C. zur Loye, Chem. Mater., 2024, 36, 10626–10639 CrossRef CAS.
- D. D. Robertson, H. Cumberbatch, D. J. Pe, Y. Yao and S. H. Tolbert, ACS Nano, 2024, 18, 996–1012 CrossRef CAS PubMed.
- J. F. Liu, Y. He, W. Chen, G. Q. Zhang, Y. W. Zeng, T. Kikegawa and J. Z. Jiang, J. Phys. Chem. C, 2007, 111, 2–5 CrossRef CAS.
- W. Van Den Bergh, S. Wechsler, H. N. Lokupitiya, L. Jarocha, K. Kim, J. Chapman, K. E. Kweon, B. C. Wood, S. Heald and M. Stefik, Batteries Supercaps, 2022, 5, e202200056 CrossRef CAS.
- T. Brezesinski, J. Wang, S. H. Tolbert and B. Dunn, Nat. Mater., 2010, 9, 146–151 CrossRef CAS PubMed.
- C. P. Koçer, K. J. Griffith, C. P. Grey and A. J. Morris, J. Am. Chem. Soc., 2019, 141, 15121–15134 Search PubMed.
- C. P. Koçer, K. J. Griffith, C. P. Grey and A. J. Morris, Chem. Mater., 2020, 32, 3980–3989 CrossRef PubMed.
- A. Van der Ven, Z. Deng, S. Banerjee and S. P. Ong, Chem. Rev., 2020, 120, 6977–7019 CrossRef CAS PubMed.
- I. Batatia, P. Benner, Y. Chiang, A. M. Elena, D. P. Kovács, J. Riebesell, X. R. Advincula, M. Asta, M. Avaylon, W. J. Baldwin, F. Berger, N. Bernstein, A. Bhowmik, S. M. Blau, V. Cărare, J. P. Darby, S. De, F. Della Pia, V. L. Deringer, R. Elijošius, Z. El-Machachi, F. Falcioni, E. Fako, A. C. Ferrari, A. Genreith-Schriever, J. George, R. E. A. Goodall, C. P. Grey, P. Grigorev, S. Han, W. Handley, H. H. Heenen, K. Hermansson, C. Holm, J. Jaafar, S. Hofmann, K. S. Jakob, H. Jung, V. Kapil, A. D. Kaplan, N. Karimitari, J. R. Kermode, N. Kroupa, J. Kullgren, M. C. Kuner, D. Kuryla, G. Liepuoniute, J. T. Margraf, I.-B. Magdău, A. Michaelides, J. H. Moore, A. A. Naik, S. P. Niblett, S. W. Norwood, N. O'Neill, C. Ortner, K. A. Persson, K. Reuter, A. S. Rosen, L. L. Schaaf, C. Schran, B. X. Shi, E. Sivonxay, T. K. Stenczel, V. Svahn, C. Sutton, T. D. Swinburne, J. Tilly, C. van der Oord, E. Varga-Umbrich, T. Vegge, M. Vondrák, Y. Wang, W. C. Witt, F. Zills and G. Csányi, arXiv, 2024, preprint, arXiv:2401.00096, DOI:10.48550/arXiv.2401.00096..
- C. Chen and S. P. Ong, Nat. Comput. Sci., 2022, 2, 718–728 Search PubMed.
- B. Deng, P. Zhong, K. Jun, J. Riebesell, K. Han, C. J. Bartel and G. Ceder, Nat. Mach. Intell., 2023, 5, 1031–1041 Search PubMed.
- ECS News: Understanding and Validating Potentiostat DC Accuracy. https://www.electrochem.org/ecsnews/understanding-and-validating-potentiostat-dc-accuracy/(accessed 2024-07-17).
- S. D. Kang and W. C. Chueh, J. Electrochem. Soc., 2021, 168, 120504 CrossRef.
- S. D. Kang, J. J. Kuo, N. Kapate, J. Hong, J. Park and W. C. Chueh, J. Electrochem. Soc., 2021, 168, 120503 CrossRef CAS.
- M. Thommes, K. Kaneko, A. V. Neimark, J. P. Olivier, F. Rodriguez-Reinoso, J. Rouquerol and K. S. W. Sing, Pure Appl. Chem., 2015, 87, 1051–1069 CrossRef CAS.
- C. Schlumberger, C. Scherdel, M. Kriesten, P. Leicht, A. Keilbach, H. Ehmann, P. Kotnik, G. Reichenauer and M. Thommes, Microporous Mesoporous Mater., 2022, 329, 111554 CrossRef CAS.
- J. W. M. Osterrieth, J. Rampersad, D. Madden, N. Rampal, L. Skoric, B. Connolly, M. D. Allendorf, V. Stavila, J. L. Snider, R. Ameloot, J. Marreiros, C. Ania, D. Azevedo, E. Vilarrasa-Garcia, B. F. Santos, X.-H. Bu, Z. Chang, H. Bunzen, N. R. Champness, S. L. Griffin, B. Chen, R.-B. Lin, B. Coasne, S. Cohen, J. C. Moreton, Y. J. Colón, L. Chen, R. Clowes, F.-X. Coudert, Y. Cui, B. Hou, D. M. D'Alessandro, P. W. Doheny, M. Dincă, C. Sun, C. Doonan, M. T. Huxley, J. D. Evans, P. Falcaro, R. Ricco, O. Farha, K. B. Idrees, T. Islamoglu, P. Feng, H. Yang, R. S. Forgan, D. Bara, S. Furukawa, E. Sanchez, J. Gascon, S. Telalović, S. K. Ghosh, S. Mukherjee, M. R. Hill, M. M. Sadiq, P. Horcajada, P. Salcedo-Abraira, K. Kaneko, R. Kukobat, J. Kenvin, S. Keskin, S. Kitagawa, K. Otake, R. P. Lively, S. J. A. DeWitt, P. Llewellyn, B. V. Lotsch, S. T. Emmerling, A. M. Pütz, C. Martí-Gastaldo, N. M. Padial, J. García-Martínez, N. Linares, D. Maspoch, J. A. Suárez del Pino, P. Moghadam, R. Oktavian, R. E. Morris, P. S. Wheatley, J. Navarro, C. Petit, D. Danaci, M. J. Rosseinsky, A. P. Katsoulidis, M. Schröder, X. Han, S. Yang, C. Serre, G. Mouchaham, D. S. Sholl, R. Thyagarajan, D. Siderius, R. Q. Snurr, R. B. Goncalves, S. Telfer, S. J. Lee, V. P. Ting, J. L. Rowlandson, T. Uemura, T. Iiyuka, M. A. van der Veen, D. Rega, V. Van Speybroeck, S. M. J. Rogge, A. Lamaire, K. S. Walton, L. W. Bingel, S. Wuttke, J. Andreo, O. Yaghi, B. Zhang, C. T. Yavuz, T. S. Nguyen, F. Zamora, C. Montoro, H. Zhou, A. Kirchon and D. Fairen-Jimenez, Adv. Mater., 2022, 34, 2201502 CrossRef CAS PubMed.
- Y. Shen, K. Schäfer, S. Brandt, K. Li and W.-C. Cheng, Microporous Mesoporous Mater., 2022, 344, 112210 CrossRef CAS.
- O. Spalla, S. Lyonnard and F. Testard, J. Appl. Crystallogr., 2003, 36, 338–347 CrossRef CAS.
- Z. Lu, D. Rébiscoul, T. Narayanan and T. Zemb, J. Appl. Crystallogr., 2022, 55, 1154–1163 CrossRef CAS PubMed.
- G. Porod, Kolloid-Z., 1951, 124, 83–114 CrossRef CAS.
- NIST: Scattering Length Density Calculator. https://www.ncnr.nist.gov/resources/activation/(accessed 2024-04-19).
- NIST: X-ray Form Factor, Attenuation, and Scattering Tables. https://physics.nist.gov/PhysRefData/FFast/html/form.html (accessed 2024-04-19).
- South Carolina SAXS Collaborative (SCSC). http://saxs.sc.edu (accessed 2024-08-14).
- Cornell High Energy Synchrotron Source (CHESS). https://www.chess.cornell.edu/(accessed 2024-08-14).
- Berkeley Lab: Advanced Light Source (ALS). https://als.lbl.gov/(accessed 2024-08-14).
- Argonne National Lab: Advanced Photon Source (APS). https://www.aps.anl.gov/(accessed 2024-08-14).
- Stanford Synchrotron Radiation Lightsource (SSRL). https://www-ssrl.slac.stanford.edu/(accessed 2024-08-14).
- M. V. Reddy, R. Jose, A. Le Viet, K. I. Ozoemena, B. V. R. Chowdari and S. Ramakrishna, Electrochim. Acta, 2014, 128, 198–202 CrossRef CAS.
- F. Yu, S. Wang, R. Yekani, A. La Monaca and G. P. Demopoulos, J. Energy Storage, 2024, 95, 112482 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta06041e |
| This journal is © The Royal Society of Chemistry 2025 |