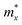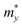Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Exploring the photoactive properties of promising MXenes for water splitting†
Diego
Ontiveros
 ,
Francesc
Viñes
,
Francesc
Viñes
 and
Carmen
Sousa
and
Carmen
Sousa
 *
*
Departament de Ciència de Materials i Química Física & Institut de Química Teòrica i Computacional (IQTCUB), Universitat de Barcelona, c/ Martí i Franquès 1-11, 08028, Barcelona, Spain. E-mail: c.sousa@ub.edu
First published on 19th November 2024
Abstract
The photoactive properties and effectiveness of a selected group of ten terminated MXenes—Sc2CT2, Y2CT2 (T = Cl, Br, S, and Se), Y2CI2 and Zr2CO2—has been deeply studied by means of density functional theory (DFT). Here it is demonstrated that the studied MXenes exhibit robust energetic and dynamical stability, having all an indirect bandgap, while most of them with values within the visible spectrum, and also exhibiting suitable band alignment for the water splitting reaction. The charge density distribution of the valence band maximum (VBM) and conduction band minimum (CBM) is found to be separated across different layers with low overlaps, below 30%. Most MXenes present high charge carrier mobilities with favourable electron–hole disparities, with Sc2CBr2 also presenting directional charge carrier transport. Additionally, these materials show strong optical absorption (∼105 cm−1) in the visible spectrum, translating to promising solar-to-hydrogen (STH) efficiency theoretical limits, up to 23%. Overall, the combination of all these features positions MXenes among the optimal materials for efficient photocatalytic water splitting.
1. Introduction
The continual rise in global energy consumption and concerns regarding environmental contamination make imperative to prioritize the development of renewable energy resources that are neither dependent on fossil fuels nor emit greenhouse gases.1,2 Hydrogen (H2), a carbon-zero-emission fuel, possessing high calorific value, high energy density, and excellent energy storage capacity, has the potential to significantly contribute at addressing the pressing sustainability and global warming challenges that mankind is currently facing.3,4 The interest in H2 production stems not only from its properties but also from its capability to be produced from renewable and abundant resources, such as water (H2O). This occurs in the so-called water splitting process, where water is broken down into H2 and oxygen (O2) using a catalyst to facilitate the cleavage, given the high energy demand of the process. On the other hand, solar energy represents an inexhaustible, clean, and renewable energy source, and has attracted widespread attention, presenting itself as a viable option for driving the water splitting reaction, with materials acting as photocatalysts for the process.5,6For a material to be photoactive in a specific reaction, it needs to be a semiconductor with a bandgap larger than the redox potential of the targeted reaction, which is 1.23 eV for water splitting. Ideally, this bandgap should fall within the visible light spectrum so that sunlight could be effectively utilized in its most intense spectrum region. Additionally, the band edges of this bandgap—i.e. the valence band maximum (VBM) and conduction band minimum (CBM)—must be properly aligned, with the VBM positioned below the oxidation potential and the CBM above the reduction potential of the reaction.7 In this context, the search for new materials that meet these conditions has been accelerated in the last years. One of the promising candidates for accomplishing the water splitting photocatalysis is the MXene family of materials. Being one of the most prominently emerging 2D nanomaterials in the last decade, MXenes have become a worldwide research hub due to their unique characteristics and wide application in many fields, including energy storage and electronics, where they excel in supercapacitors and batteries, as well as environmental applications such as water purification and CO2 capture. MXenes are even making strides in biomedical applications, offering potential in areas like drug delivery, biosensing, and tissue engineering due to their biocompatibility and tuneable properties.8–10 MXenes are a family of few-layered transition metal (TM) carbides and nitrides, with Mn+1Xn chemical formula, where M is an early TM from groups III to VI—i.e. Sc, Y, Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, and W—, X can be carbon or nitrogen, and n = 1–4.9,11 Depending on their synthesis route, the chemical environment, and the physical conditions they are exposed to, MXenes can have their surface easily functionalized with a termination, Tx, updating the general chemical formula to Mn+1XnTx. The usual synthesis of MXenes involves selectively etching A elements from bulk layered MAX materials precursors, Mn+1AXn, where A is typically a group XIII-XVI element.12 The etching process is commonly carried out using a hydrofluoric acid (HF) solution,13 which produces terminations such as –O, –F, –OH, and –H.14 Nevertheless, recent studies employing synthetic methods based on molten salts have reported new MXenes terminated with –S, –Se, –Te, –NH, –Cl, –Br, and –I, as well as pristine MXenes with no termination.15,16
Given this vastly wide compositional and structural variability, the experimental exploration of the MXene family as adequate photocatalysts can be an expensive and time-consuming task. For that reason, computational tools and methodologies aided at accelerating this process and gaining a deeper understanding of the photoactive nature of these materials.17–20 Through high-throughput comprehensive computational screenings, more than 4000 MXenes structures have been previously evaluated for their photoactive properties, with a focus on bandgap and band alignment. This analysis identified ten promising MXenes for photocatalytic water splitting, exhibiting suitable bandgaps and band alignments.19,20 Note that, while the bandgap size and alignment of the valence and conduction bands are necessary requirements for photocatalytic water splitting, as aforementioned, they alone do not account for the entirety of the process,7 and other aspects, including optical absorption,21 exciton formation and carrier mobility,17 can bias the full process. In this work, we selected the ten most promising MXenes from the previously mentioned computational screenings, mainly Zr2CO2, Sc2CT2, Y2CT2 (T = –Cl, –Br, –S, and –Se), and Y2CI2, for further computational evaluation to assess their efficiency as photoactive catalysts. Particular MXenes with group III TMs have already garnered significant attention for their electronic and photoactive properties.18,22,23 However, there remains a lack of studies exploring certain terminations, such as –Br or –I halides and –S or –Se chalcogenides. The present study addresses this gap by also considering these less-explored terminations, while providing new insights into their potential for water splitting photocatalysis. The conducted electronic structure calculations, along with the analysis of optical absorption, solar-to-hydrogen efficiency, charge distribution, and carrier mobilities, reveal that the Zr2CO2 and group III halide-terminated MXenes demonstrate superior photocatalytic properties compared to their chalcogen-terminated counterparts. While our results demonstrate that the MXenes have suitable electronic structures and band alignments for photocatalytic water splitting, a comprehensive understanding of the hydrogen evolution reaction (HER) and oxygen evolution reaction (OER) mechanisms, with the corresponding Gibbs free energy profile—including active sites at terminations or edges, adsorption dynamics, and reaction pathways in the excited state—requires further investigation, likely involving the use of hybrid functionals and powerful computational resources. Such studies would complement our current findings and guiding the design of efficient MXene-based photocatalysts.
2. Computational details
2.1. Structural models
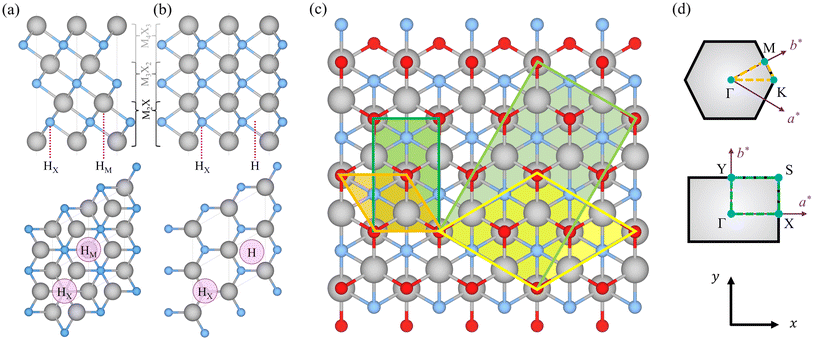
Pristine MXene structures, with Mn+1Xn chemical formula, consist of M and X atom intercalated close-packed layers, with the number of layers depending on the n number. Two possible stackings emerge for such systems; ABC stacking, see Fig. 1a, with the M layers in two different relative positions, or ABA stacking, see Fig. 1b, with the M layers in the same relative position along the vacuum direction. The terminated MXenes, Mn+1XnTx, are initially built by adding the Tx atoms to the relaxed pristine MXene structures, sampling different surface hollow sites, as indicated in Fig. 1. The explored sites are: the metal hollow in ABC stacking, HM, located above an underlying metal atom, the simple hollow in ABA stacking, H, placed with no atoms underneath, the carbon or nitrogen hollows, HX, with an underlying X atom for both stackings, and a mixture of HM (H) and HX on opposite MXene surfaces for ABC (ABA) stacking, HMX. By combining stacking and hollow sites, each terminated MXene has six possible structures, see Fig. 2. This site notation will be used in the oncoming discussion.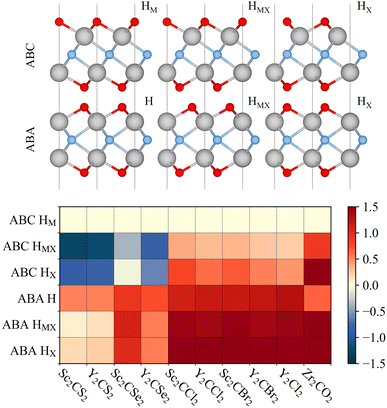 | ||
| Fig. 2 Side view of the six possible terminated MXene structures (upper panel), using the same colour code as in Fig. 1. Relative energies, ΔE, in eV, with respect to the ABC HM structure (bottom panel) for the possible terminated MXene geometries for the studied cases. | ||
These structures were modelled using a p(1 × 1) hexagonal unit cell, as in Fig. 1c. The slab models were represented with 30 Å of vacuum perpendicular to the MXene 2D surface, which previous studies and present tests revealed to be enough to avoid self-interaction,24,25 and provided a good precision to the band alignment and vacuum energy calculations.19 The structures investigated in this study are derived from a selection of 10 promising MXenes identified through previous high-throughput computational screening aimed at assessing MXenes for photocatalytic water splitting.19,20 These include Sc2CT2, Y2CT2 (T = –Cl, –Br, –S, and –Se), Y2CI2 and Zr2CO2, which already exhibit an adequate band alignment, and our subsequent investigation aims to delve deeper into their photoactive effectiveness in the water splitting process.
2.2. Methods
The electronic structure of the considered MXenes has been studied in the framework of density functional theory (DFT).26,27 Calculations were carried out using the Vienna ab initio simulation package (VASP),28 employing the Perdew–Burke–Ernzerhof (PBE)29 exchange–correlation functional within the generalized gradient approximation (GGA).30 Additionally, to achieve a more reliable estimation of the bandgap and electronic structure, further calculations were performed using the PBE0 hybrid functional, including a 25% of non-local Fock exchange.31,32 During the calculations, atomic core electrons and their interaction with valence electrons were represented using projector augmented wave (PAW) pseudopotentials,33 while the valence electrons were described using a planewave basis set with an optimal kinetic energy cutoff of 415 eV, considering spin-polarization. The geometry optimizations were considered converged when the forces acting on the nuclei were all below 0.01 eV Å−1 and a 10−6 eV threshold was chosen as the electronic convergence criterion. All atomic positions and cell parameters were allowed to relax during the optimizations. Optimal Γ-centred 7 × 7 × 1 Monkhorst–Pack34k-points grids were employed for the Brillouin zone integration.The PBE0 bandstructure calculations using planewaves require high computational resources, and so, such calculations were carried out using the Fritz-Haber Institute ab initio materials simulation (FHI-AIMS) package,35 an all-electron program that uses numerical atomic orbitals (NAOs) as basis set. The self-consistent field and optimization criteria for FHI-AIMS are set equivalent to the ones used in VASP, to maintain the same computational playground, and a light Tier-1 level was used as the basis set. The bandstructure was explored along the Γ → K → M → Γ path, see Fig. 1d.
To assess the dynamical stability of MXenes, the phonon spectra were calculated using PHONOPY,36 based on the force constants computed by density functional perturbational theory within VASP (VASP-DFPT),37 using a 4 × 4 × 1 supercell and a reduced 3 × 3 × 1 k-points grid. From each phonon spectrum, the artificial mode corresponding to the vertical translation of the slab was disregarded from the analysis.
2.3. Photocatalytic properties
To further evaluate the photoactive qualities and effectiveness of the selected MXenes, a set of properties have been computed as check-points to be fulfilled.7 Firstly, for a material to be photoactive in a given photoelectrocatalytic reaction, its band edges—i.e. the valence band maximum (VBM) and conduction band minimum (CBM)—must suitably align with respect the half-reaction potentials of the redox reaction, with the VBM and CBM being below or exceeding the oxidation and reduction potentials, respectively. In the context of photocatalytic water splitting, the reduction (H+/H2) and oxidation (H2O/O2) absolute potentials are −4.44 eV and −5.67 eV, respectively.38 The band alignment is calculated from the Fermi level, EF, and the bandgap, Eg:| EVBM = EF − Vv ECBM = EVBM + Eg | (1) |
An ideal photocatalyst would present a low exciton recombination rate, which can be fostered by a good separation between the created charge carriers. This can be estimated by calculating the electron and hole effective masses, m*, and charge carrier mobility, μ. When the electron, μe, and hole, μh, mobilities are significantly different, it is an indication that one charge carrier type is dispersing more rapidly than the other, potentially resulting in their spatial separation throughout the material, and eventually enhancing the overall efficiency of the charge carrier dynamics. Additionally, the directionality of the charge carriers can also influence their separation. The effective mass can be estimated as:
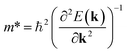 | (2) |
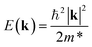 | (3) |
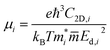 | (4) |
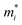 is the carrier effective mass along the direction of motion i and
is the carrier effective mass along the direction of motion i and 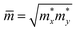 represents the geometric average of effective masses along x- and y-directions. C2D,i = [∂2ET/∂δ2]/So is the elastic modulus under uniaxial strain along a given i direction, with ET being the total energy of the system, δ the uniaxial strain along the transport direction, and So the area of the equilibrium unit cell. Finally, Ed,i designates the deformation potential constant of holes and electrons in the VBM and CBM, respectively, along the transport direction, and is defined as ∂Eedge/∂δ, where Eedge is the VBM or CBM energy. Both C2D,i and Ed,i can be estimated by parabolic and linear fitting of the variables involved, respectively. For the charge carrier mobility calculations, an orthogonal unit cell was used, see Fig. 1c, which facilitates the selection of two perpendicular directions. In MXenes, these directions are typically referred to as zigzag and armchair directions, which in our chosen unit cell, correspond to the x and y axes, respectively.
represents the geometric average of effective masses along x- and y-directions. C2D,i = [∂2ET/∂δ2]/So is the elastic modulus under uniaxial strain along a given i direction, with ET being the total energy of the system, δ the uniaxial strain along the transport direction, and So the area of the equilibrium unit cell. Finally, Ed,i designates the deformation potential constant of holes and electrons in the VBM and CBM, respectively, along the transport direction, and is defined as ∂Eedge/∂δ, where Eedge is the VBM or CBM energy. Both C2D,i and Ed,i can be estimated by parabolic and linear fitting of the variables involved, respectively. For the charge carrier mobility calculations, an orthogonal unit cell was used, see Fig. 1c, which facilitates the selection of two perpendicular directions. In MXenes, these directions are typically referred to as zigzag and armchair directions, which in our chosen unit cell, correspond to the x and y axes, respectively.
In the quest for a low exciton recombination, another property to consider is the charge density separation between the VBM and CBM. In this work, to give a quantitative numerical estimation of this spatial separation, we computed the overlap integral between both densities:
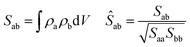 | (5) |
An optimal condition to use sunlight as an energy vector for the photocatalytic reaction is a bandgap within the visible range (1.8–3.1 eV), but, in order to fully harvest this sunlight, another key component is the absorption of light in the visible spectrum. This is studied here by means of the frequency-dependent dielectric function, ε(ω), defined as:
| ε(ω) = εr(ω) + iεi(ω) | (6) |
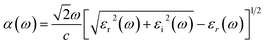 | (7) |
The solar-to-hydrogen (STH) efficiency has been also estimated. This is a key parameter for evaluating the efficiency of converting solar light into hydrogen fuel. In here one computes the upper limit of the STH, as based on a previous work,43 assuming 100% efficiency of the catalytic reactions. The STH can be decomposed into light absorption, ηabs, and carrier utilization, ηcu, efficiencies, which take the form of the following equations:
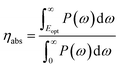 | (8) |
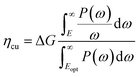 | (9) |
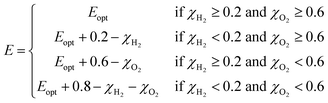 | (10) |
| ηSTH = ηabs·ηcu | (11) |
For Janus structures, with a difference between vacuum levels of the two surfaces, Δϕ, like for S- and Se-terminated MXenes, the intrinsic electric field does positive work for the separation of photon excited electrons and holes during the processing of photocatalytic water splitting, and therefore it should be added into the total energy. Hence, the corrected STH efficiency of photocatalytic water splitting for 2D materials with intrinsic electric field, 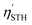 , is defined as:
, is defined as:
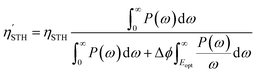 | (12) |
3. Results and discussion
3.1. Structure stability
To assess the most stable structure from the six possible ones for each studied MXene, the relative energy of the different conformations is computed with respect to the ABC HM structure. The results, presented in Fig. 2, show how all systems prefer the ABC stacking with the termination in the metal hollows, HM, except from S- and Se-terminated MXenes, for which the HMX termination arrangement is more stable, consistent with other theoretical studies.47 The forthcoming discussion and results will be based on these most stable structures.Concerning the group III S-terminated MXenes, previous theoretical studies reported the existence of a slightly more stable distorted phase.48,49 In an attempt to confirm these findings, we optimized these systems applying a 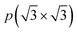 R30° larger unit cell, as depicted in Fig. 1c, to allow for symmetry breaking. After introducing an initially random distortion and re-optimizing the system, we observed that for S- and Se-terminated cases, the structure with the minimum energy indeed corresponded to a distorted phase, as shown in Fig. 3, in accordance with the mentioned literature. However, the differences in energy per MXene unit between the regular and distorted phases were found to be almost negligible in all cases, similar to findings by Zhu et al.,47 with deviations of approximately −0.03 eV and −0.02 eV for distortions in Sc2CS2 and Sc2CSe2, respectively, and at most −0.13 eV for both Y2CS2 and Y2CSe2 MXenes, thus well within the standard DFT accuracy. Therefore, while these distorted phases will still be discussed in the following, the primary focus will remain on the regular structures, as one can safely regard these as competitive domains.
R30° larger unit cell, as depicted in Fig. 1c, to allow for symmetry breaking. After introducing an initially random distortion and re-optimizing the system, we observed that for S- and Se-terminated cases, the structure with the minimum energy indeed corresponded to a distorted phase, as shown in Fig. 3, in accordance with the mentioned literature. However, the differences in energy per MXene unit between the regular and distorted phases were found to be almost negligible in all cases, similar to findings by Zhu et al.,47 with deviations of approximately −0.03 eV and −0.02 eV for distortions in Sc2CS2 and Sc2CSe2, respectively, and at most −0.13 eV for both Y2CS2 and Y2CSe2 MXenes, thus well within the standard DFT accuracy. Therefore, while these distorted phases will still be discussed in the following, the primary focus will remain on the regular structures, as one can safely regard these as competitive domains.
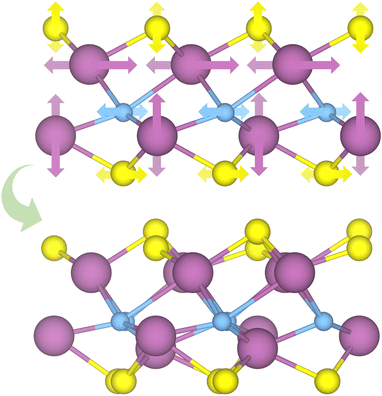 | ||
| Fig. 3 Schematic representation of the distortion movement from the regular HMX structures to the new distorted phases. The darker and lighter arrows mark the front or back atoms, respectively. | ||
Table 1 gathers the lattice parameter, a, and width, d, for all studied MXenes, including the distorted ones, marked with a d-prefix on their names. The computed values are in good agreement with other computational estimates,47,50,51 and also with experimentally synthesised systems similar to those here studied, like stacked Sc2CCl2 MXene sheets.52 The Zr2CO2 MXene presents the lowest lattice parameter among the studied cases, and within the group III MXenes, Y-MXenes have slightly larger cell parameters compared to their Sc counterparts, owing to the larger atomic radius of Y. Halide-terminated MXenes display significantly larger widths than chalcogen-terminated ones, exceeding them by more than 1 Å on average, with Y2CI2 exhibiting the largest thickness. Additionally, it is observed that the distortion found on the chalcogen-terminated MXenes leads to a slight increase in MXene width compared to the regular structures.
| MXene | a (Å) | d (Å) | E coh (eV) | E form (eV) |
|---|---|---|---|---|
| Zr2CO2 | 3.30 | 4.70 | −7.68 | −10.97 |
| Sc2CS2 | 3.77 | 4.67 | −5.52 | −4.97 |
| Y2CS2 | 4.09 | 4.82 | −5.52 | −4.87 |
| Sc2CSe2 | 3.84 | 4.98 | −5.16 | −4.21 |
| Y2CSe2 | 4.15 | 5.19 | −5.17 | −4.16 |
| Sc2CCl2 | 3.45 | 5.81 | −5.41 | −7.84 |
| Y2CCl2 | 3.72 | 6.20 | −5.42 | −7.77 |
| Sc2CBr2 | 3.52 | 6.12 | −5.09 | −6.74 |
| Y2CBr2 | 3.77 | 6.55 | −5.13 | −6.84 |
| Y2CI2 | 3.88 | 6.97 | −4.77 | −5.32 |
| d-Sc2CS2 | 6.55 | 4.80 | −5.52 | −5.00 |
| d-Y2CS2 | 7.09 | 5.03 | −5.54 | −4.99 |
| d-Sc2CSe2 | 6.66 | 5.14 | −5.16 | −4.23 |
| d-Y2CSe2 | 7.18 | 5.41 | −5.19 | −4.29 |
To evaluate the thermodynamical stability of the studied MXenes, we calculated the cohesive, Ecoh, and formation, Eform, energies, see Table 1, and compared them to similar 2D materials that have been shown to be stable. Both Ecoh and Eform energies can be extracted from the following expressions:
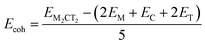 | (13) |
| Eform = EM2CT2 − (2E(M) + E(C) + 2E(T)) | (14) |
The formation energies show similar patterns, with the Zr2CO2 MXene standing out among the others. Here, halide-terminated MXenes exhibit more negative formation energies than chalcogen-terminated ones, suggesting that the former are thermodynamically more stable than the latter with respect to their reference materials. For the distorted structures of chalcogen-terminated MXenes, the formation and cohesive energies remain very similar to those of their regular structures, as the distortion does not result in a significant gain in stability. Overall, the large negative values in the formation and cohesive energies indicate the structural stability and strong bonding formation of these MXene structures.
To further investigate their plausible viability, the dynamical stability of the resulting optimal MXenes was put under scrutiny, and their phonon spectra were estimated. Fig. 4 presents the results for the regular structures while the distorted phases are displayed in Fig. S1 of the ESI.† None of the phonon modes display significant negative frequencies, suggesting the overall stability of the materials. This finding aligns with phonon calculations reported in other references for MXene systems.17,18,57 Note that while small imaginary frequencies below 30 cm−1 near the Γ point were observed for S- and Se-terminated MXenes, these can be safely attributed to numerical noise due to the vacuum region or the employed k-point mesh.58–60 While the previous phonon spectrum calculations confirmed the dynamical stability of the studied MXenes in their ground state, it is crucial to also assess their stability in excited states to better understand their behaviour under photocatalytic conditions. To this end, we selected the Zr2CO2 MXene for further investigation and performed phonon calculations in the excited triplet state. The phonon spectra exhibited all positive frequencies, see Fig. S2 of the ESI,† indicating that Zr2CO2 remains dynamically stable when photoexcited.
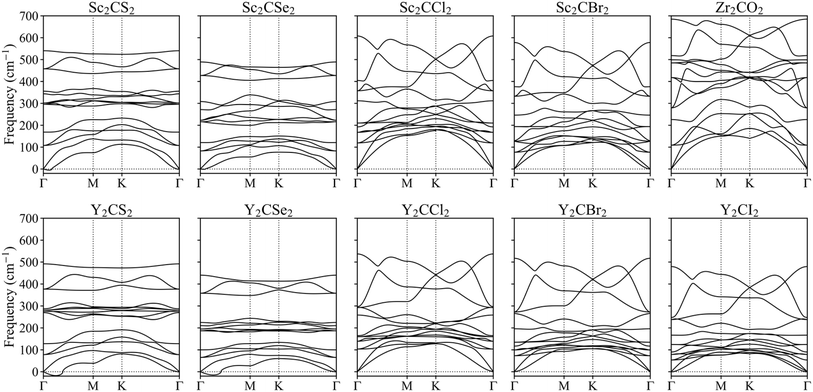 | ||
| Fig. 4 Phonons spectra along the Γ → K → M → Γ k-points paths for the studied MXenes, using a regular p(1 × 1) unit cell. | ||
Although this study focuses on the intrinsic photocatalytic properties of MXenes, it is well-documented that light irradiation can induce surface defects or generate new electronic states in MXenes, which may influence their stability and photocatalytic efficiency. For example, it has been observed that oxygen vacancies or other point defects can form on MXene surfaces,61 potentially altering electronic states and band alignment. Similarly, corrosion or degradation of the material may occur under certain conditions or environments.62 Additionally, the generation of mid-gap states due to surface defects could impact on charge separation and recombination processes.63 Thus, further research is required to investigate these effects under more realistic photocatalytic conditions.
3.2. Electronic structure
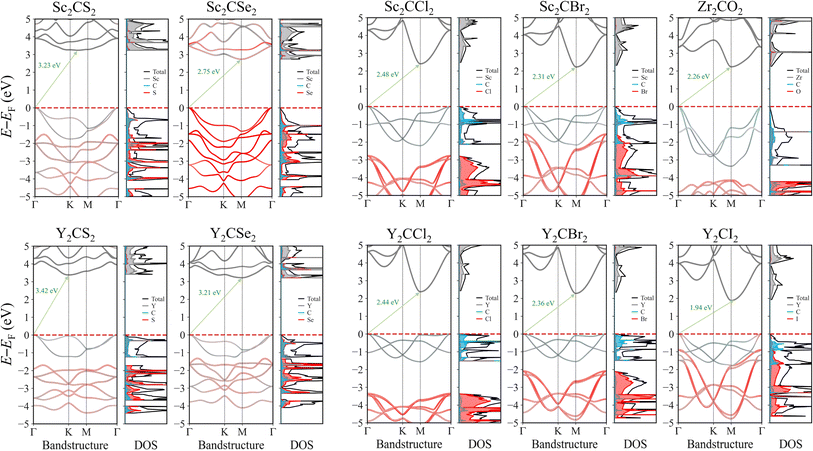
The electronic properties of MXenes were investigated through bandstructure and density of states (DOS) calculations. Since the PBE exchange–correlation functional, as many other low-rung functionals, are known to systematically underestimate the bandgap energies,32 as happen with the here explored MXenes, see Table 2, the electronic structure calculations were conducted using the PBE0 hybrid functional, known to deliver estimates comparable to reference GW while being computationally more affordable.20 The bandstructure and DOS for each MXene case is presented in Fig. 5, while for the four distorted MXene structures the results are found on Fig. S3 of the ESI.† All the selected promising cases exhibit a bandgap larger than 1.23 eV, which is necessary for photocatalysing the water splitting process. Most of these systems have a bandgap within the visible region, while the chalcogen-terminated MXenes show bandgap values that are slightly shifted towards the UV region. For the distorted structure MXene cases, the electronic structure remains very similar, with bandgap values also being comparable, although slightly reduced, likely due to the creation of new electronic states when the symmetry is broken. These new states appear just above the VBM and below the CBM, leading to a minor decrease in the overall bandgap.| MXene | E PBEg | E PBE0g | E PBE0g,D | E opt | E b | Ŝ ab (%) |
|---|---|---|---|---|---|---|
| Zr2CO2 | 0.87 | 2.26 | 3.34 | 2.87 | 0.47 | 27.92 |
| Sc2CS2 | 1.58 | 3.23 | 3.83 | 3.34 | 0.49 | 35.22 |
| Y2CS2 | 1.84 | 3.42 | 3.43 | 2.93 | 0.50 | 38.56 |
| Sc2CSe2 | 1.21 | 2.75 | 3.48 | 3.15 | 0.33 | 31.92 |
| Y2CSe2 | 1.70 | 3.21 | 3.73 | 2.99 | 0.74 | 34.59 |
| Sc2CCl2 | 0.95 | 2.48 | 2.77 | 2.30 | 0.47 | 26.26 |
| Y2CCl2 | 1.01 | 2.44 | 2.43 | 1.89 | 0.54 | 31.72 |
| Sc2CBr2 | 0.79 | 2.31 | 2.74 | 2.31 | 0.44 | 27.19 |
| Y2CBr2 | 0.94 | 2.36 | 2.37 | 1.85 | 0.52 | 30.75 |
| Y2CI2 | 0.59 | 1.94 | 2.35 | 1.79 | 0.56 | 25.26 |
| d-Sc2CS2 | 1.39 | 3.01 | 3.22 | 2.93 | 0.29 | 19.11 |
| d-Y2CS2 | 1.67 | 3.20 | 3.37 | 2.65 | 0.72 | 27.72 |
| d-Sc2CSe2 | 1.05 | 2.56 | 2.96 | 2.54 | 0.42 | 30.54 |
| d-Y2CSe2 | 1.45 | 2.94 | 3.32 | 2.65 | 0.67 | 27.09 |
When inspecting the bandstructures, it can be seen how the bandgap normally goes from the VB Γ to the CB M point, whereas in regular S-terminated MXenes, the bandgap implies the VB Γ point to (or close to) the CB K point. This last aspect is amended in the distorted structures, where all MXenes systematically present also a Γ → M transition. This feature underscores the indirect nature of the bandgap. The impact of an indirect bandgap on photocatalytic efficiency involves a balance between light absorption and charge carrier dynamics. While direct bandgaps typically enable stronger light absorption, indirect bandgaps can result in lower recombination rates, leading to longer carrier lifetimes. This extended lifetime enhances charge separation and improves the overall efficiency of photocatalytic processes. Such characteristics make indirect bandgaps advantageous in cases where carrier longevity is crucial for the desired reactions.64,65
Thanks to the atomic projections of the bandstructures and DOS, one can also discern how the VB and CB are distributed. The first bands of the VB mainly have contributions from the C and TM layers, sometimes separated by a gap from the lower energy bands, which are primarily contributed by the termination atoms. On the other hand, the CB is dominated by the d orbitals of the TM.
3.3. Band alignment
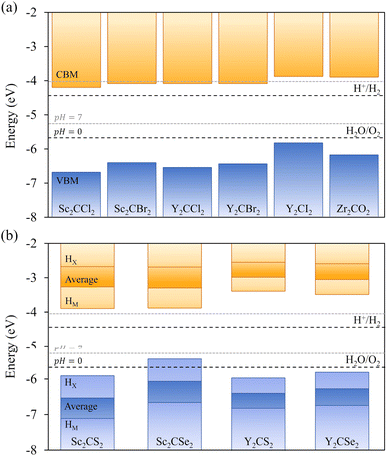
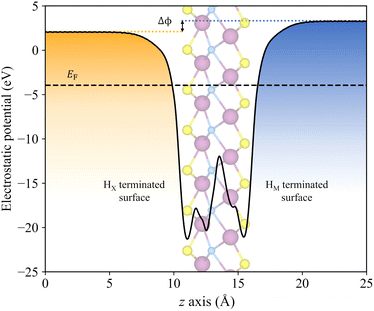
As above-mentioned, one crucial requirement for a suitable photocatalyst for the water splitting reaction is an adequate band alignment of the band edges with respect to the reaction oxidation/reduction potentials. In other words, the VBM location in the energy spectrum needs to be lower than the oxidation potential of H2O/O2, and the CBM position must exceed the reduction potential of H+/H2. These conditions are easily met by the studied candidates, see Fig. 6. Considering that S- and Se-terminated MXenes exhibit an HMX-type structure, each exposed surface is topologically different, with different chemical environments. This variation between surfaces renders them as Janus materials. As a result, the electrostatic potential in the vacuum region on each side of the slab differs, generating an intrinsic electric field.66 An example of this phenomenon is illustrated in Fig. 7, with Δϕ representing the difference between the vacuum energies on each surface. For such MXenes with the termination on HMX positions, the electrostatic potential of the surface in which the chalcogen is adsorbed on the HX site is lower than when it is located on the HM site, generating an intrinsic electric field from the HX towards the HM terminated surface. The previous has also an effect on the band alignment, since each surface will have its own band edge positioning. In Fig. 6b the band alignment of each surface is displayed for the HMX Janus-like cases. Note that in thin 2D materials, the effect of the intrinsic field may not be crucial, yet here the average band alignment between both faces is provided, as if dipole corrections were not considered and the electrostatic potential was averaged in the vacuum level.Another important factor to consider is the pH, since the redox potentials are affected by pH conditions (−5.67 + 0.059·pH eV for the oxidation and −4.44 + 0.059·pH eV for the reduction). Usually, these potentials are given at standard conditions of pH = 0, and so, at very strong acidic conditions, indicated by the black dashed lines in Fig. 6, but here one should also consider a neutral case when pH = 7, marked by the grey dashed lines. In all cases, including the symmetric HM structures and both faces of the Janus HMX geometries, there is suitable band alignment for the overall water splitting reaction at pH = 0, with the sole exception of the Sc2CSe2 HX face, which only fulfils the H+/H2 reduction potential alignment. Note that the intrinsic electric field present in these S- and Se-terminated MXenes facilitates the spatial separation of photoexcited electrons and holes. Given that the electric field direction goes from the HX to the HM terminated surface, electrons accumulate on the HX face, and holes on the HM face. This distribution helps separating the oxidation and reduction photocatalytic processes onto the faces, and in the case of Sc2CSe2, the HX face, which is only capable of photocatalysing the HER process, will be enhanced by the accumulation of holes in that region.
When increasing the pH to 7, this just mentioned feature disappears, and the Sc2CSe2 MXene becomes capable of photocatalysing the overall process, as the other chalcogen-terminated MXenes do for the entire 0–7 pH range. However, this is not the case for some halide-terminated MXenes. When the pH is increased to 7, the Sc and Y cases terminated in –Cl and –Br lose, although by little, their ability to photocatalyze the HER process since the CBM barely falls below the reduction potential, although they would be capable of so at slightly acidic conditions. This highlights the ability to modulate which reaction occurs or is triggered based on the pH conditions, which can be convenient in the actual photocatalytic process setup.
For the distorted MXenes, see Fig. S4 of the ESI,† the band alignments correspond well with their respective regular structures, with the Sc2CSe2 HX face still presenting suitable band alignment only for the HER process at pH = 0. When increasing to pH = 7, similar conclusions can be withdrawn as in the non-distorted cases, since they still maintain the overall water splitting capabilities. However, in the distorted structure of Sc2CSe2, the CBM of the HM face significantly decreases its energy, falling slightly below the reduction potential, reducing the efficiency on the HER photocatalysis, yet still maintaining suitable band alignment for OER.
3.4. Charge density
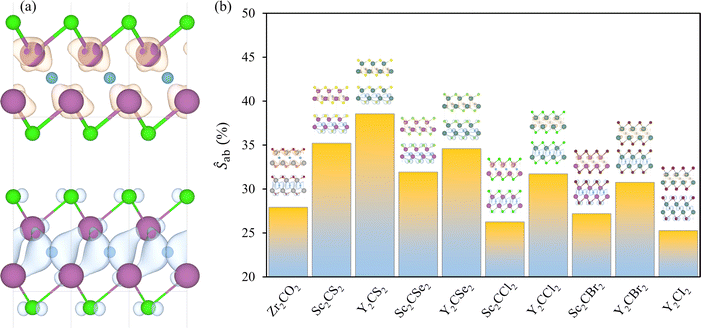
Efficient photocatalysts typically exhibit significant charge density separation between the VBM and CBM, which facilitates the effective separation and migration of photogenerated electron–hole pairs, thereby reducing recombination rates. Here, the VBM and CBM charge densities were gained for the investigated cases, encompassed in Fig. S5 of the ESI.† The halide-terminated MXenes and Zr2CO2 present the VBM distributed along the p orbitals of the C atoms, with minor contributions from the p orbitals of the terminations, while the CBM is centred around the TM layers, as seen in the example of Sc2CCl2 in Fig. 8a, in line with the orbital distribution observed in the projected DOS of Fig. 5. For the chalcogen-terminated MXenes, the asymmetry between the surfaces is also reflected in the charge density distribution. The VBM is more concentrated around the HX face, predominantly around the C and Tx atoms, while the CBM is more centrally located, with major contributions from the TM and C layers.Aside from providing a qualitative interpretation of the charge densities, a quantitative approach is tackled by computing the spatial overlap integral between the VBM and CBM charge densities, see Fig. 8b, with values listed in Table 2. This metric estimates the percentage of overlap between the charge densities at both band edges. The lowest overlaps are observed for Zr2CO2, Sc2CBr2, Sc2CCl2, and Y2CI2, in descending order, with all showing an overlap of less than 28%. The remaining MXenes present larger overlaps, exceeding 30%, with the highest overlap observed in Y2CS2. In general, Y-MXenes exhibit greater overlap compared to their Sc-MXene counterparts, likely due to the larger size of Y atoms and the more diffuse nature of their 4d orbitals compared to the 3d orbitals of Sc. In terms of the distorted cases, see Fig. S6 of the ESI,† the deformation benefits the spatial separation of charge densities, as indicated by the significantly reduced overlap percentages. The broken symmetry enables a new charge redistribution, which appears to favour the separation between the VBM and CBM.
In thin 2D monolayer materials like the MXenes studied here, achieving effective charge separation is challenging. This difficulty is why many researchers couple these materials with other semiconductors to form heterojunctions that better separate charges.67 Still, the observed localization in different layers and low overlapping percentage of the VBM and CBM charge densities is a notable finding.
3.5. Charge carriers mobility
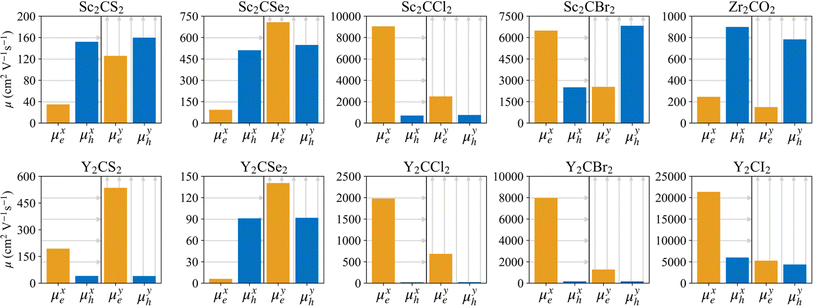
A photoinduced electron/hole pair will drift for a certain average lifetime before recombining. To ensure efficient photocatalysis, it is crucial to have a prolonged average lifetime for the charge carriers. This requires effective separation of the photogenerated electron and hole pairs to prevent rapid recombination. The separation is influenced by the relative mobilities of the electron and hole. Consequently, semiconductors with unequal electron and hole mobility often offer longer charge carriers lifetimes. Furthermore, a system with direction-dependent mobility can further facilitate charge carrier separation.The charge carrier mobilities for the electrons and holes have been calculated and listed in Table 3, along with their corresponding effective masses, elastic constants, and deformation potentials needed in their calculation, vide supra. These values were calculated along two perpendicular directions, x and y, which correspond to the zigzag and armchair directions, as stated in the computational details. As observed in the bandstructures from Fig. 5, two bands converge at the VBM, providing the created hole with two distinct migration channels. This dual-channel system implies the consideration of both valence bands in terms of charge carrier mobility. Consequently, the hole migrating through the valence band with lesser k-space curvature is referred to as the heavy hole, hH, while the one migrating through the more curved valence band is denoted as the light hole, hL. An example of the fittings used to obtain the C2D and Ed parameters is given in Fig. S7 of the ESI† for the example of Y2CCl2. To provide a more visual representation of the mobilities between e–h and their directionality, we have also represented these values as a bar plot in Fig. 9.
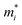 is the carrier effective mass along the i transport direction, as a fraction w.r.t to a free electron. C2D,i is the elastic constant in i transport direction in units of N m−1, Ed,i is the deformation potential constant, given in eV, and μi is the carrier mobility, in cm2 V−1 s−1 at T = 300 K. The e, hH, and hL carriers denote the electron, heavy hole, and light hole, respectively
is the carrier effective mass along the i transport direction, as a fraction w.r.t to a free electron. C2D,i is the elastic constant in i transport direction in units of N m−1, Ed,i is the deformation potential constant, given in eV, and μi is the carrier mobility, in cm2 V−1 s−1 at T = 300 K. The e, hH, and hL carriers denote the electron, heavy hole, and light hole, respectively
| MXene | Carrier | C 2D,x | C 2D,y | E d,x | E d,y | μ x | μ y | ||
|---|---|---|---|---|---|---|---|---|---|
| Zr2CO2 | e | 0.27 | 2.11 | 10.94 | 4.92 | 244.97 | 148.99 | ||
| hH | 0.43 | 0.43 | 274.39 | 267.44 | 5.95 | 6.25 | 898.22 | 782.72 | |
| hL | 0.19 | 0.19 | 0.95 | 1.31 | 183![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 662.10 662.10 |
93![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 597.25 597.25 |
|||
| Sc2CS2 | e | 3.42 | 2.55 | −2.25 | −1.38 | 34.80 | 125.75 | ||
| hH | 0.72 | 0.73 | 83.64 | 84.47 | 4.73 | 4.61 | 152.08 | 159.70 | |
| hL | 0.44 | 0.44 | −0.31 | −0.52 | 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 182.33 182.33 |
33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 884.35 884.35 |
|||
| Y2CS2 | e | 1.85 | 1.95 | −1.41 | −0.82 | 193.54 | 535.00 | ||
| hH | 0.82 | 0.82 | 63.24 | 63.19 | 7.02 | 7.06 | 40.39 | 39.75 | |
| hL | 0.55 | 0.55 | 2.16 | 2.50 | 959.91 | 712.61 | |||
| Sc2CSe2 | e | 2.02 | 2.04 | 2.06 | −0.74 | 92.90 | 707.25 | ||
| hH | 0.60 | 0.60 | 76.02 | 75.21 | 2.97 | 2.85 | 510.77 | 547.71 | |
| hL | 0.31 | 0.32 | −3.83 | −3.78 | 1118.25 | 1126.69 | |||
| Y2CSe2 | e | 5.01 | 1.55 | 3.80 | 1.42 | 6.04 | 140.46 | ||
| hH | 0.73 | 0.74 | 57.10 | 57.25 | 5.00 | 4.95 | 90.94 | 91.69 | |
| hL | 0.43 | 0.43 | −0.83 | −0.72 | 9766.42 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 839.73 839.73 |
|||
| Sc2CCl2 | e | 0.25 | 1.19 | 1.58 | 1.38 | 9042.74 | 2488.56 | ||
| hH | 1.77 | 1.77 | 147.82 | 145.27 | 1.20 | 1.15 | 692.65 | 747.72 | |
| hL | 0.42 | 0.41 | −4.19 | −4.17 | 1031.93 | 1042.20 | |||
| Y2CCl2 | e | 0.23 | 0.96 | 3.46 | 2.88 | 1978.55 | 684.51 | ||
| hH | 3.74 | 3.81 | 121.33 | 121.19 | 2.98 | 2.85 | 20.60 | 22.08 | |
| hL | 0.50 | 0.50 | −2.32 | −2.50 | 1905.93 | 1640.70 | |||
| Sc2CBr2 | e | 0.25 | 1.22 | 1.87 | 1.34 | 6487.19 | 2537.44 | ||
| hH | 1.09 | 1.09 | 143.19 | 142.30 | 1.02 | 0.61 | 2503.32 | 6827.16 | |
| hL | 0.30 | 0.30 | −5.71 | −5.51 | 1061.61 | 1142.40 | |||
| Y2CBr2 | e | 0.22 | 0.96 | 1.76 | 2.10 | 7972.61 | 1278.38 | ||
| hH | 2.34 | 2.40 | 120.57 | 118.26 | 1.64 | 1.64 | 171.43 | 165.57 | |
| hL | 0.41 | 0.41 | −3.42 | −3.35 | 1289.80 | 1328.13 | |||
| Y2CI2 | e | 0.21 | 1.02 | 1.08 | 1.01 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 368.14 368.14 |
5259.49 | ||
| hH | 0.83 | 0.85 | 112.50 | 118.79 | −0.75 | −0.90 | 6003.60 | 4360.91 | |
| hL | 0.22 | 0.22 | −6.26 | −6.35 | 1250.76 | 1301.68 |
In general, the mobility of electrons in MXenes varies significantly depending on the x or y direction. For the S- and Se-terminated MXenes, with an HMX structure, electron mobility is higher along the y-direction compared to the x-direction, while, for the rest, displaying HM structures, this trend is reversed, presenting higher electron mobilities along the x-direction. Despite these directional differences in electron mobility, heavy holes tend to maintain consistent mobility across both directions, with the exception of the Sc2CBr2 system, where the heavy holes are more mobile in the y-direction. This exceptionality in Sc2CBr2 actually makes it particularly effective for charge separation, as it demonstrates both a significant disparity in electron and hole mobilities within the same direction and a clear direction-dependent mobility, with electrons favoring migration along the x-direction while holes prefer the y-direction. The other halide-terminated MXenes also deserve attention due to their large electron–hole mobility disparities, especially along the x-direction where electrons typically have higher mobilities. A similar pattern is observed in the Zr2CO2 MXene, although in this case, the holes are the ones exhibiting higher mobilities.
Light holes, while not necessarily the preferred pathway for hole migration due to the tendency of holes to occupy higher energy bands, in this case heavy holes, still play an important role in the overall charge carrier dynamics and need to be considered. These light holes exhibit significantly higher mobilities compared to the heavy ones, often by orders of magnitude, due to their lower effective masses and reduced deformation potentials. Notable exceptions to this trend are found in Y2CI2 and Sc2CBr2 MXenes. The higher mobility of light holes further facilitates charge separation, particularly in materials such as Zr2CO2, Sc2CS2, and Y2CSe2, where the significant imbalance between the electron and light-hole mobilities enhances the effectiveness of charge separation. In the distorted phases of the S- and Se-terminated MXenes, see Table S1 and Fig. S8 of the ESI,† the mobility values differ slightly, but the general trends and ratios remain consistent with the non-distorted structures. Electrons tend to have higher mobilities in the x-direction than in the y-direction, heavy holes maintain relatively isotropic mobilities, and light holes continue to exhibit greater anisotropy and higher mobility values.
Despite the growing interest in MXenes due to their promising photocatalytic applications, the literature on the charge carrier mobilities of these materials remains relatively sparse. Among the various MXenes explored, the majority have not yet been comprehensively studied in this regard, underscoring the novelty and significance of the present computational investigation. To date, detailed mobility data are primarily available only for Zr2CO2 and Sc2CCl2 MXenes.17,51,67–71 Even if reported mobility values for these MXenes vary somewhat across different studies, the overall trends and directionality of charge carriers remain consistent both within these studies and in comparison to our findings. Notably, our results align particularly well with those reported in ref. 51 for Sc2CCl2 and ref. 67 for Zr2CO2.
One might consider that the IEF of the S- and Se-terminated MXenes may influence mobility, however, in this case, the IEF is oriented along the z-direction, meaning it does not directly affect the present mobility values calculated in the x and y directions. Nevertheless, the presence of the IEF is critical for enhancing the separation of photogenerated electrons and holes across the two surfaces of the MXenes, thereby facilitating the charge separation. To estimate the intensity of the IEF, we calculated the electrostatic potential difference (Δϕ) between the two surfaces of the MXenes. The IEF can then be expressed as EIEF = Δϕ/ed, as previously used for other Y-based Janus MXenes.18 For the regular Sc2CS2, Y2CS2, Sc2CSe2, and Y2CSe2 MXenes, the obtained IEF values, in V Å−1, are 0.26, 0.17, 0.24, and 0.18, respectively. The distorted phases yield similar IEF values of 0.27, 0.25, 0.25, and 0.21 V Å−1, respectively. Overall, the distorted structures exhibit slightly higher IEF values, with Sc-MXenes showing greater values compared to Y-MXenes in both the regular and distorted cases.
3.6. Optical properties
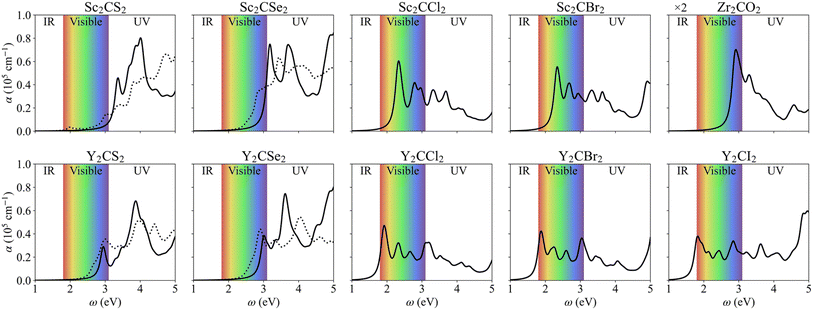
Optical absorption is another crucial factor influencing the photocatalytic effectiveness of a material. An effective photocatalyst must be capable of absorbing a substantial portion of either visible or UV light—the primary components of solar radiation—, efficiently converting this absorbed light into hole–electron photogenerated pairs, which eventually separate and promote the photocatalytic process. Here, we explored the light harvesting properties of the studied MXenes by determining the optical absorption coefficient, see Fig. 10, derived from the dielectric functions, see Fig. S9 of the ESI.† Our calculations showed very low εzz components, a common feature in 2D materials,72 so the results presented and discussed are from in-plane polarization (εxx + εyy)/2, parallel to the MXene xy plane.Most MXenes demonstrate good absorption in the visible spectrum, around 105 cm−1 in all cases, with the first absorption peak occurring within the visible region. However, some S- and Se-terminated MXenes exhibit a slight shift into the UV range, corresponding to their slightly larger bandgaps. The optical gaps, including excitonic effects calculated using the GW-BSE formalism, are listed in Table 2. Notably, even if Y-based MXenes typically have similar or even larger electronic bandgaps compared to Sc-based ones, their corresponding optical gaps are consistently smaller. When distorted, the electronic bandgap diminishes, and so does the optical gap, making these structures slightly more efficient with visible light absorption. From the GW-BSE optical spectra and the minimum direct electronic bandgap transition, the exciton binding energy can be estimated, shown in Table 2. This value represents the energy required to dissociate an exciton into its constituent electron and hole charge carriers, providing insights into the ease of charge separation. The Eb values for regular structured MXenes are mostly comprised between 0.4 and 0.6 eV, similar to those found in other reported MXenes and transition metal dichalcogenides,42 with Sc2CSe2 and Y2CSe2 breaking that rule with values of 0.33 eV and 0.74 eV, respectively. Regarding the distorted MXenes, Sc2CS2 becomes the system with lowest Eb (0.29 eV), while Y-based MXenes present values over 0.6 eV. In this sense, the most promising materials are those with the lowest Eb, as they facilitate the easiest dissociation of excitons. This makes regular Sc2CSe2 and distorted Sc2CS2 MXenes most optimal among the studied systems.
The STH conversion efficiency is also an important parameter when evaluating the efficiency of converting solar energy into hydrogen fuel for the water-splitting reaction. Here the upper limit of the STH efficiency has been estimated at pH = 0 and 7. The results at pH = 0 are encompassed in Table 4, and show that the light absorption efficiency, ηabs, of the studied 2D materials have a close relationship with their bandgap, in that a bandgap increase is accompanied by a decrease in light absorption efficiency. The halide-terminated Y-based MXenes exhibit the highest absorption efficiency and carrier utilization efficiency, resulting in superior STH efficiencies ranging from 21 to 23% for Cl- and Br-terminated structures. Notably, Y2CI2 presents the worst STH efficiency among the halide-terminated Y-MXenes due to its low OER overpotential and carrier utilization, however, its high absorption efficiency compensates this, leading to an STH efficiency of 12.2%. Sc-based MXenes with halide terminations follow closely, achieving an STH efficiency around 11%. Finally, the chalcogen-terminated MXenes, due to their large optical gap, show low absorption and STH efficiencies, not exceeding 3%. Nevertheless, in their distorted phases, the reduced bandgap enhances the absorption efficiency and so raises STH efficiencies up to 6.5%. The intrinsic electric field correction has minimal impact on both regular and distorted Janus S- and Se-MXenes. At pH = 7, as detailed in Table S2 of the ESI,† the Cl- and Br-terminated MXenes lose their photocatalytic ability for the HER, making STH calculation not possible. The other cases remain unaffected, except for Y2CI2, where the adjusted overpotentials improve the carrier utilization, increasing STH efficiency to 21.4%.
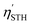 representing the efficiency of light absorption, carrier utilization, STH, and corrected STH, respectively, given in percentage
representing the efficiency of light absorption, carrier utilization, STH, and corrected STH, respectively, given in percentage
| MXene | Δϕ | χ H2 | χ O2 | η abs | η cu | η STH | |
|---|---|---|---|---|---|---|---|
| Zr2CO2 | 0.00 | 0.53 | 0.51 | 8.3 | 30.3 | 2.5 | 2.5 |
| Sc2CS2 | 1.20 | 1.77 | 1.44 | 2.6 | 34.4 | 0.9 | 0.9 |
| Y2CS2 | 0.83 | 1.89 | 1.13 | 7.2 | 37.8 | 2.7 | 2.7 |
| Sc2CSe2 | 1.19 | 1.76 | 0.95 | 4.1 | 35.7 | 1.5 | 1.4 |
| Y2CSe2 | 0.91 | 1.86 | 1.04 | 6.2 | 37.2 | 2.3 | 2.3 |
| Sc2CCl2 | 0.00 | 0.22 | 1.03 | 24.6 | 44.9 | 11.0 | 11.0 |
| Y2CCl2 | 0.00 | 0.35 | 0.86 | 41.8 | 50.8 | 21.3 | 21.3 |
| Sc2CBr2 | 0.00 | 0.37 | 0.72 | 24.2 | 44.8 | 10.9 | 10.9 |
| Y2CBr2 | 0.00 | 0.36 | 0.77 | 43.8 | 51.5 | 22.6 | 22.6 |
| Y2CI2 | 0.00 | 0.56 | 0.15 | 46.6 | 26.2 | 12.2 | 12.2 |
| d-Sc2CS2 | 1.31 | 1.76 | 1.32 | 7.3 | 37.9 | 2.8 | 2.7 |
| d-Y2CS2 | 1.24 | 1.95 | 1.26 | 13.4 | 40.8 | 5.5 | 5.2 |
| d-Sc2CSe2 | 1.29 | 1.57 | 1.05 | 16.7 | 42.1 | 7.0 | 6.5 |
| d-Y2CSe2 | 1.14 | 1.70 | 1.14 | 13.4 | 40.8 | 5.5 | 5.2 |
Overall, the most favourable solar-to-hydrogen efficiency is found for halide-terminated Y-MXenes, with STH values comparable to other Y-based MXenes,18 and considerably higher than WX2 (X = S, Se), which top at 9%.73
4. Conclusions
In the present study, first-principles calculations were employed to investigate the photoactive properties of a selection of ten MXenes—Zr2CO2, Sc2CT2, Y2CT2 (T = Cl, Br, S, and Se), and Y2CI2—in the context of water splitting. Distorted phases for the S- and Se-terminated MXenes were also considered and were found to exhibit properties that were generally very similar to their regular counterparts. Based on their cohesive and formation energies, and phonons spectra, this subset of MXenes are found to be energetically and dynamically stable. All the selected MXenes are also shown to be semiconductors with an indirect bandgap that falls within the visible or near UV range (the latter for chalcogen-terminated cases), making them suitable for photocatalysis.Moreover, their band alignment is appropriate for water splitting photocatalysis. This band alignment can be adjusted by pH changes, with the HER reaction being switched off at pH = 7 for halide-terminated MXenes. The intrinsic electric field in the HMX S- and Se-terminated Janus structures enhances charge carrier separation by accumulating electrons on the HX face and holes on the HM face. Typically, the VBM of the studied MXenes is distributed along the p orbitals of the C atoms, with minor contributions from the p orbitals of the terminations, while the CBM is primarily centered around the TM layers. The selected MXenes present good properties for charge carrier separation, with MXenes presenting a disparity between the electrons and hole mobilities, with electrons showing anisotropic mobilities. Moreover, in Sc2CBr2, we found direction-dependent mobilities, with electrons favoring migration along the x-direction and holes preferring the y-direction.
These MXenes possess an optical gap that falls within the optimal range of the solar spectrum for efficient light absorption, while also sufficiently wide to provide the necessary photogenerated energy to overcome the potential barrier for water splitting, as evidenced by the optical absorption and STH efficiency calculations. Achieving spatial separation of charge density in thin 2D materials is challenging, and the VBM and CBM overlap values of around 30%, along with the somewhat high exciton binding energies observed in the studied MXenes, may act as inhibitors to their optimal photocatalytic effectiveness. However, MXenes can be coupled with other 2D materials to form heterojunctions, which have been shown to reduce exciton binding energies and further separate the VBM and CBM states.71
Accordingly with the exhibited results, the presented MXenes show promising properties for high-performance photocatalytic water splitting. In particular, the halide-terminated MXenes and Zr2CO2 demonstrate superior properties compared to the chalcogen-terminated variants. These include greater stability, enhanced absorption in the visible light range, reduced charge density overlap, improved charge carrier mobility, and higher STH efficiency. The present research can provide insightful and helpful information, laying the grounds for future computational and experimental design of MXene-based photocatalysts. Indeed, the findings of this study provide a strategic guide for future experimental research on MXenes for photocatalytic water splitting. By identifying MXenes with optimal band alignment, robust stability, and high solar-to-hydrogen efficiency potential, this theoretical framework narrows down the selection of candidates for synthesis and testing. The calculated bandgaps and charge carrier mobilities for the proposed optimal MXene compositions offer key parameters that can be used to refine synthesis conditions, modify terminations, or engineer heterostructures to enhance photocatalytic performance.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The authors acknowledge financial support from the Spanish Ministerio de Ciencia e Innovación and Agencia Estatal de Investigación through research grants PID2021-126076NB-I00 and TED2021-129506B-C22, plus the unit of excellence María de Maeztu CEX2021-001202-M granted to the IQTCUB. The Generalitat de Catalunya is acknowledged for 2021SGR00079 funding. Computational resources were provided by Consorci de Serveis Universitaris de Catalunya (CSUC) with partial financial support from Universitat de Barcelona, while Red Española de Supercomputacion (QHS-2023-2-0017 and QHS-2023-3-0012) is gratefully acknowledged for supercomputing time. F. V. thanks the ICREA Academia Award 2023 Ref. Ac2216561, and D. O. thanks Universitat de Barcelona for a predoctoral contract (PREDOCS-UB).References
- N. S. Lewis, Science, 2007, 315, 798–801 CrossRef CAS PubMed.
- D. Larcher and J. M. Tarascon, Nat. Chem., 2015, 7, 19–29 CrossRef CAS PubMed.
- J. A. Turner, Science, 2004, 305, 972–974 CrossRef CAS PubMed.
- G. Squadrito, G. Maggio and A. Nicita, Renewable Energy, 2023, 216, 119041 CrossRef CAS.
- K. Maeda and K. Domen, J. Phys. Chem. Lett., 2010, 1, 2655–2661 CrossRef CAS.
- T. Hisatomi and K. Domen, Nat. Catal., 2019, 2, 387–399 CrossRef CAS.
- Á. Morales-García, F. Viñes, C. Sousa and F. Illas, J. Phys. Chem. Lett., 2023, 14, 3712–3720 CrossRef PubMed.
- Q. Zhong, Y. Li and G. Zhang, Chem. Eng. J., 2021, 409, 128099 CrossRef CAS.
- Y. Gogotsi, Chem. Mater., 2023, 35, 8767–8770 CrossRef CAS.
- B. Anasori and Y. Gogotsi, Graphene 2D Mater., 2023, 8, 39–41 CrossRef.
- M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Adv. Mater., 2011, 23, 4248–4253 CrossRef CAS PubMed.
- M. Alhabeb, K. Maleski, B. Anasori, P. Lelyukh, L. Clark, S. Sin and Y. Gogotsi, Chem. Mater., 2017, 29, 7633–7644 CrossRef CAS.
- M. Naguib, O. Mashtalir, J. Carle, V. Presser, J. Lu, L. Hultman, Y. Gogotsi and M. W. Barsoum, ACS Nano, 2012, 6, 1322–1331 CrossRef CAS PubMed.
- M. A. Hope, A. C. Forse, K. J. Griffith, M. R. Lukatskaya, M. Ghidiu, Y. Gogotsi and C. P. Grey, Phys. Chem. Chem. Phys., 2016, 18, 5099–5102 RSC.
- V. Kamysbayev, A. S. Filatov, H. Hu, X. Rui, F. Lagunas, D. Wang, R. F. Klie and D. V. Talapin, Science, 2020, 369, 979–983 CrossRef CAS PubMed.
- H. Ding, Y. Li, M. Li, K. Chen, K. Liang, G. Chen, J. Lu, J. Palisaitis, P. O. Å. Persson, P. Eklund, L. Hultman, S. Du, Z. Chai, Y. Gogotsi and Q. Huang, Science, 2023, 379, 1130–1135 CrossRef CAS PubMed.
- Z. Guo, J. Zhou, L. Zhu and Z. Sun, J. Mater. Chem. A, 2016, 4, 11446–11452 RSC.
- S. Y. Zhang, N. P. Shi, C. K. Wang and G. P. Zhang, Phys. Chem. Chem. Phys., 2024, 26, 412–420 RSC.
- D. Ontiveros, F. Viñes and C. Sousa, J. Mater. Chem. A, 2023, 11, 13754–13764 RSC.
- D. Ontiveros, S. Vela, F. Viñes and C. Sousa, Energy Environ. Mater., 2024, 7, e12774 CrossRef CAS.
- Y. M. Ding, X. Nie, H. Dong, N. Rujisamphan and Y. Li, Nanoscale Adv., 2020, 2, 2471–2477 RSC.
- J. H. Liu, X. Kan, B. Amin, L. Y. Gan and Y. Zhao, Phys. Chem. Chem. Phys., 2017, 19, 32253–32261 RSC.
- S. Guo, H. Lin, J. Hu, Z. Su and Y. Zhang, Materials, 2021, 14, 4739 CrossRef CAS PubMed.
- C. Ougherb, T. Ouahrani, M. Badawi and Á. Morales-García, Phys. Chem. Chem. Phys., 2022, 24, 7243–7252 RSC.
- A. Jurado, Á. Morales-García, F. Viñes and F. Illas, J. Phys. Chem. C, 2021, 125, 26808–26813 CrossRef CAS PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, 864–871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, 1133–1138 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 47, 558–561 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew and W. Yue, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8800–8802 CrossRef PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- X. Hai, J. Tahir-Kheli and W. A. Goddard III, J. Phys. Chem. Lett., 2011, 2, 212–217 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196 CrossRef CAS.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- X. Gonze and C. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10355–10368 CrossRef CAS.
- S. Trasatti, Pure Appl. Chem., 1986, 58, 955–966 CrossRef CAS.
- S. H. Mir, V. K. Yadav, J. K. Singh and J. K. Singh, ACS Omega, 2020, 5, 14203–14211 CrossRef CAS PubMed.
- M. S. Hybertsen and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 5390–5413 CrossRef CAS PubMed.
- S. Albrecht, L. Reining, R. Del Sole and G. Onida, Phys. Rev. Lett., 1998, 80, 4510–4513 CrossRef CAS.
- Z. Jiang, Z. Liu, Y. Li and W. Duan, Phys. Rev. Lett., 2017, 118, 266401 CrossRef PubMed.
- C. F. Fu, J. Sun, Q. Luo, X. Li, W. Hu and J. Yang, Nano Lett., 2018, 18, 6312–6317 CrossRef CAS PubMed.
- C. A. Gueymard, D. Myers and K. Emery, Sol. Energy, 2002, 73, 443–467 CrossRef.
- Y. Zheng, Y. Jiao, M. Jaroniec and S. Z. Qiao, Angew. Chem., 2014, 54, 52–65 CrossRef PubMed.
- C. C. L. McCrory, S. Jung, J. C. Peters and T. F. Jaramillo, J. Am. Chem. Soc., 2013, 135, 16977–16987 CrossRef CAS PubMed.
- H. Zhu, N. Qiu, G. Fang and S. Du, RSC Adv., 2023, 13, 21690–21702 RSC.
- L. Zhang, C. Tang, C. Zhang and A. Du, Nanoscale, 2020, 12, 21291–21298 RSC.
- M. Li, O. Omisakin and J. Young, Nanoscale, 2022, 14, 6970–6980 RSC.
- M. Khazaei, M. Arai, T. Sasaki, C.-Y. Chung, N. S. Venkataramanan, M. Estili, Y. Sakka and Y. Kawazoe, Adv. Funct. Mater., 2013, 23, 2185–2192 CrossRef CAS.
- L. Zhou, Y. Zhang, Z. Zhuo, A. J. Neukirch and S. Tretiak, J. Phys. Chem. Lett., 2018, 9, 6915–6920 CrossRef CAS PubMed.
- S. J. Hwu, R. P. Ziebarth, S. von Winbush, J. E. Ford and J. D. Corbett, Inorg. Chem., 1986, 25, 283–287 CrossRef CAS.
- H. Shin, S. Kang, J. Koo, H. Lee, J. Kim and Y. Kwon, J. Chem. Phys., 2014, 140, 114702 CrossRef PubMed.
- H. M. Shodja, F. Ojaghnezhad, A. Etehadieh and M. Tabatabaei, Mech. Mater., 2017, 110, 1–15 CrossRef.
- F. Ersan, E. Aktürk and S. Ciraci, Phys. Rev. B, 2016, 94, 245417 CrossRef.
- P. Hess, Nanoscale Horiz., 2021, 6, 856–892 RSC.
- Y. Jiang, Y. Zhang, Q. Huang, L. Hao and S. Du, J. Mater. Res. Technol., 2020, 9, 14979–14989 CrossRef CAS.
- K. Gaál-Nagy, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 024309 CrossRef.
- I. Pallikara, P. Kayastha, J. M. Skelton and L. D. Whalley, Electron. Struct., 2022, 4, 033002 CrossRef CAS.
- V. Wang, G. Tang, Y. C. Liu, R. T. Wang, H. Mizuseki, Y. Kawazoe, J. Nara and W. T. Geng, J. Phys. Chem. Lett., 2022, 13, 11581–11594 CrossRef CAS PubMed.
- J. D. Gouveia and J. R. B. Gomes, Phys. Rev. Mater., 2022, 6, 024004 CrossRef CAS.
- H. Liang and J. Liu, ChemCatChem, 2022, 14, e202101375 CrossRef CAS.
- T. Su, X. Ma, J. Tong, H. Ji, Z. Qin and Z. Wu, J. Mater. Chem. A, 2022, 10, 10265–10296 RSC.
- X. Zhang, J. X. Shen, W. Wang and C. G. Van De Walle, ACS Energy Lett., 2018, 3, 2329–2334 CrossRef CAS.
- S. A. Razek, M. R. Popeil, L. Wangoh, J. Rana, N. Suwandaratne, J. L. Andrews, D. F. Watson, S. Banerjee and L. F. J. Piper, Electron. Struct., 2020, 2, 023001 CrossRef.
- E. S. Sim, H. Nam, C. Kim and Y. C. Chung, Sustainable Mater. Technol., 2022, 34, e00502 CrossRef CAS.
- X. Xu, X. Wu, Z. Tian, M. Zhang, L. Li and J. Zhang, Appl. Surf. Sci., 2022, 599, 154014 CrossRef CAS.
- R. Sun, C. L. Yang, M. S. Wang and X. G. Ma, Appl. Surf. Sci., 2022, 591, 153232 CrossRef CAS.
- Y. He, M. Zhang, J. J. Shi, Y. L. Cen and M. Wu, J. Phys. Chem. C, 2019, 123, 12781–12790 CrossRef CAS.
- H. Zhang, G. Yang, X. Zuo, H. Tang, Q. Yang and G. Li, J. Mater. Chem. A, 2016, 4, 12913–12920 RSC.
- R. Zhang, F. Zhuang, R. Zhou, J. Ma, H. Li, K. Wang, X. Ye and G. Hao, J. Phys. Chem. Solids, 2022, 171, 111014 CrossRef CAS.
- T. Ketolainen and F. Karlicky, J. Mater. Chem. C, 2022, 10, 3919–3928 RSC.
- L. Ju, M. Bie, X. Tang, J. Shang and L. Kou, ACS Appl. Mater. Interfaces, 2020, 12, 29335–29343 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta06852a |
| This journal is © The Royal Society of Chemistry 2025 |