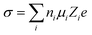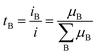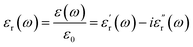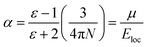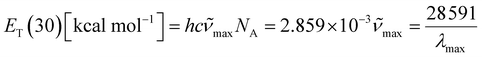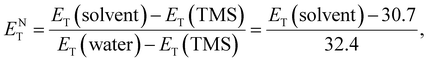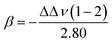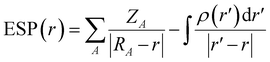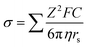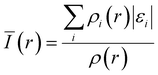Enabling rational electrolyte design for lithium batteries through precise descriptors: progress and future perspectives

Abstract

The rational design of new electrolytes has become a hot topic for improving ion transport and chemical stability of lithium batteries under extreme conditions, particularly in cold environments. Traditional research on electrolyte innovations has relied on experimental trial-and-error methods, which are highly time-consuming and often imprecise, even with well-developed theories of electrochemistry. Thus, researchers are increasingly turning to computational methods. Ab initio calculations and advancements in computer science, such as machine learning (ML), offer a more efficient way to screen potential electrolyte candidates. To accurately evaluate these candidates, precise descriptors that accurately reflect specific properties and reliably predict electrochemical performance are highly needed. This review summarizes and compares the most-used descriptors (e.g., donor number and dielectric constant) alongside critical properties (Lewis basicity and polarity). Additionally, several potential descriptors (e.g., local ionization energy) are explored. A comprehensive comparison of these descriptors is provided, and principles for developing new, more effective descriptors are proposed. This review aims to guide efficient electrolyte design and inspire the discovery of better descriptors for high-performance lithium batteries.

---

Baichuan Cui

Baichuan Cui obtained his Master of Engineering degree from Nankai University in 2024. He is currently pursuing a PhD degree at the Department of Chemistry, City University of Hong Kong. Supervised by Prof. Jijian Xu, he has continued his research on lithium batteries and his research interests are fundamental electrolyte design and functional gel polymer electrolytes.

Jijian Xu

Jijian Xu received B.S. and PhD degrees from Zhejiang University in 2014 and 2019. He worked as a Postdoc at the University of Maryland from 2019–2022 and was then promoted to Assistant Research Scientist. He is currently an assistant professor in the Department of Chemistry at City University of Hong Kong. Dr Xu's research interests focus on developing advanced electrolytes and electrode materials for high-energy batteries. He has authored more than 80 peer-reviewed papers in Nature, Nature Energy, etc.

---

1 Introduction and scope

The global pursuit of carbon neutrality highlights the urgent need for revolutionary green energy storage transformation to support a sustainable future. Central to this transformation is the widespread adoption of renewable energy systems and large-scale energy storage, such as the expansion of the electric vehicle (EV) industry. Lithium batteries play a key role in achieving these goals, but to address increasing demands for improved energy density, safety, wide temperature operation and longevity, further advancements are required.¹

As a core component of lithium batteries, electrolytes are as critical as electrode materials in determining battery performance. Electrolytes influence battery performance in two major ways: (i) conducting Li⁺ cations between the cathodes and anodes, and (ii) contributing to formation of cathode–electrolyte interphase (CEI) and solid-electrolyte-interphase (SEI) layers, which protect electrode materials and ensure stable cycling. The exploration of new electrolyte components is ongoing,² with many alternative chemicals proposed that offer benefits but also present challenges.^3,4 Identifying optimal electrolyte components requires an efficient method to balance these properties.

Historically, battery research relied on experimental screening and testing of numerous candidates, which, while reliable, is time-consuming and costly. Advances in computational chemistry provide researchers with a more efficient solution (e.g., density functional theory (DFT) calculation and molecular dynamic (MD) simulation). These methods allow researchers to predict physicochemical properties, making it possible to identify promising electrolyte candidates for subsequent experimental validation. Furthermore, the revolutionary advanced artificial intelligence (AI) and machine learning (ML) have shown incredible capability to process massive data and generate insights, making them critical tools for exploring new materials for next-generation batteries.^5–8 While tools such as DFT and MD simulations are already well-developed, there is still a blank to be filled by a systematic comprehension of the various descriptors, which were developed to link the basic characteristics of chemicals and the actual performance of electrolytes.

To enable large-scale computational screening of electrolyte components (e.g., solvents), precise descriptors are highly needed. Specifically, “finding the actuating mechanisms of a certain property or function and describing it in terms of a set of physically meaningful parameters” interprets the definition of descriptors very well by Ghiringhelli et al.⁹ Ideally, descriptors should rely solely on the microscopic properties of molecules while effectively reflecting the macroscopic properties of the compounds in a coherent order. Establishing the relationship between the “bottom” and the “top” of the physicochemical properties of electrolytes is crucial. Yao et al.¹⁰ utilized the dielectric constant to identify weak solvation electrolytes. Namely, they used 1,4-dioxane solvent, which possesses ultra-low solvating power and moderate Li salt solubility, to promote the formation of ion pairs at a standard concentration for an anion-derived SEI. Xu et al.¹¹ further proposed the combined use of the donor number (DN) and dielectric constant to screen soft solvents, aiming to balance between ionic conductivity and desolvation energy. Solvents with relatively high dielectric constants and low DN were chosen for optimized electrolytes, enabling outstanding full cell performance across a wide temperature range (−60 °C to +60 °C). Wu et al.¹² categorized solvents using electrostatic potential (ESP), which is closely determined by the electron distribution and can reflect both the salt dissociation ability and Li⁺ cation coordination strength. They proposed an ESP_max–ESP_min map for identifying different types of solvents, and a criterion for ideal antisolvents (|ESP_min| ≪ ESP_max) was also validated. Jin et al.¹³ proposed that weak solute–solvent interaction is a potential solution for low-temperature electrolytes because it can facilitate the desolvation kinetics of Li⁺ ions, which is the limiting step of the interfacial process. While current descriptors, such as donor number, dielectric constant, and Lewis basicity, have proven useful, they often fail to capture the full spectrum of properties required for accurate predictions across different electrolyte systems. Many descriptors are highly specific to particular electrolyte sets, limiting their broader applicability across different battery chemistries. Another significant limitation is that most available descriptors focus on isolated properties (e.g., ionic conductivity and viscosity) rather than providing a holistic view of the electrolyte's performance. This often results in a mismatch between predicted and actual performance in real-world applications. For instance, descriptors that capture ion transport may overlook interfacial stability, which is critical for long-term cycling. The inherent complexity of electrolyte systems—where ion solvation, transport, and interfacial reactions are interwoven—makes it unrealistic to rely on a single descriptor for accurate predictions. Furthermore, many existing descriptors are empirical or semi-empirical, lacking the precision needed for predictive models.

In this review we begin with a brief introduction to the principles of ionic transportation and solvation structures, laying the foundation for electrolyte design. Building on this, we then summarize the key descriptors that have been reported for optimizing electrolyte design. We discuss the foundational aspects of these descriptors and their interrelationship, showing that a single descriptor is insufficient. It is found that the current descriptors can reflect certain solvation properties of electrolytes quite accurately; mismatches often occur in their predictions. Based on the most effective descriptors, several potential properties of electrolytes are proposed to be possible descriptors for better electrolyte design.

2 Basic principles of electrolyte design

2.1 Ions in electrolyte: solvation chemistry and ionic transport

Solvation involves two different yet complementary mechanisms. The first is, a universal and non-specific solvent–solute interaction that exists in most solutions. This interaction is homogeneous, isotropic, and continuum-based, with its intensity primarily determined by the macroscopic properties of the solvent, such as its dielectric constant. The second mechanism involves short-range and specific chemical interactions between the solvent and solute – acting as a Lewis base and acid – contributing to the formation of primary solvation complexes or so-called solvation complexes.¹⁴ The solvation structure of lithium batteries is critical in determining the transport mechanisms of Li⁺ ions and the formation of SEI–CEI layers.

The ion–dipole interactions drive the formation of Bernal–Fowler solvation shells. Li⁺ cations are coordinated with several solvent molecules through coordination bonds following the electron donating/accepting process. As shown in Fig. 1a, in dilute electrolytes, sufficient free solvent molecules enable Li⁺ to be fully coordinated, effectively offsetting the electric field generated by each ion's charge. This scenario produces a low energy barrier, and Li⁺ ions can migrate relatively freely. As the salt concentration increases to a moderate level, the number of free solvent molecules decreases, generating two major structures: solvent-separated ion pairs (SSIPs) and contact ion pairs (CIPs). SSIPs refer to a structure in which a Li⁺ ion is surrounded by solvent molecules and is separated from the coupling anion, whereas CIPs refer to a structure in which Li⁺ ion and anions are held together by electrostatic interactions and are surrounded by the solvent molecules to form mutual solvation shells.¹⁵ The formation of CIPs has been proven to enhance the stability of the SEI because the existence of anions in the solvation shell of Li⁺ can elevate the proportion of the inorganic components in the SEI (e.g., LiF and Li₂O). As the salt concentration continues to increase, the interaction between ions becomes more pronounced, resulting in the formation of aggregations (AGG) – where an anion coordinates with two or more Li⁺ ions – and even nano-heterogeneity, which are commonly investigated in high concentration electrolytes (HCEs). It is noteworthy that the formation of these coordinates does not strictly follow expected concentration behaviours; different lithium salts show distinct tendencies to form specific complexes, regardless of the concentration level. For example, LiPF₆, lithium bis(fluorosulfonyl)imide (LiFSI), and lithium bis(trifluoromethanesulphonyl)imide (LiTFSI) tend to dissociate and form SSIPs in dilute solutions, whereas lithium triflate (LiCF₃SO₃) and lithium trifluoroacetate (LiCF₃CO₂) tend to associate and form AGGs even at significantly diluted concentrations.^16,17 This behavior can be attributed to the difference in the salts' charge distribution, molecular structure, and coordination bonding energy, which can be predicted accurately with DFT calculations.¹⁸

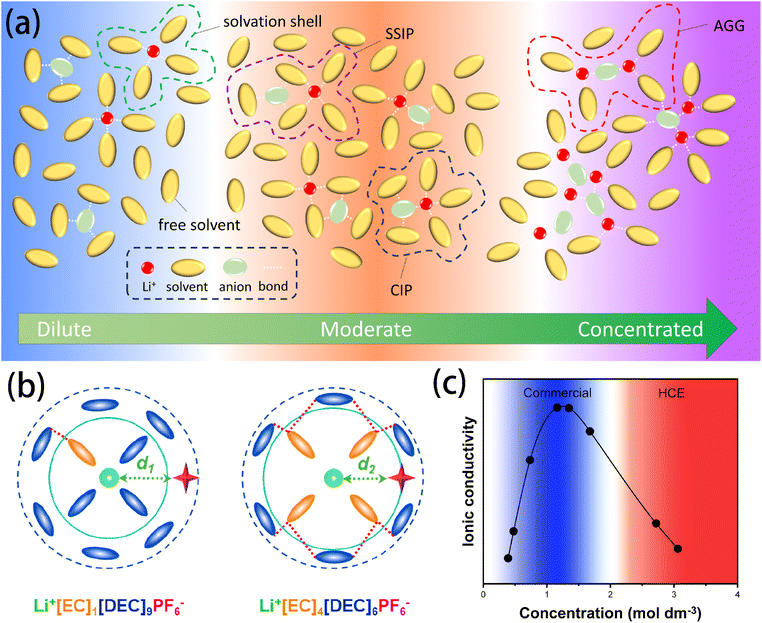Fig. 1 (a) Schematic illustration of the solvation structures in electrolytes at varying concentrations. (b) Schematic diagram of the solvation structure of the electrolyte with LiPF₆ : EC : DEC molar ratios of (left) 1 : 1 : 9 and (right) 1 : 4 : 6. Reprinted with permission from ref. 22. Copyright 2023 American Chemical Society. (c) Typical ionic conductivity curve of the Li salt–aprotic solvent mixture. Data reused and reprinted from ref. 16. Copyright 2015 the Electrochemical Society.

Understanding the solvation structure is crucial for rational electrolyte design. For instance, Schroder et al. found that anions – especially fluorinated ions or species with at least one lone pair (e.g., tributylamine and bis(oxalato)borate (BOB)) – have strong interactions with the solvent's H atoms via hydrogen bonding. This insight provides guidance for electrolyte design from the anion's aspect.¹⁹ Namely, the hydrogen bonding effect between anions and solvents can be utilized to enhance the electrochemical stability of the solvents, thereby reducing their decomposition at the electrode.^20,21 Moreover, Wang et al.²² discovered weak solvent–solvent interactions in ethylene carbonate (EC)–diethyl carbonate (DEC)-based electrolytes, which was suggested to be critical for the stabilization of electrolytes by enlarging the orbital gaps of the Li⁺(EC)_x(DEC)_y complex and decreasing its reduction vulnerability (Fig. 1b).

Salt concentration closely influences the ionic conductivity of electrolytes. Intuitively, a higher salt concentration in lithium salts suggests more Li⁺ ions, which would lead to increased ionic conductivity. However, in practice, it is found that simply increasing the salt concentration does not linearly improve the ionic conductivity of the electrolyte (Fig. 1c). Instead, the ionic conductivity drops significantly at exceptionally high salt concentration. On the one hand, the increased viscosity caused by the depletion of free solvent molecules hinders the transport of Li⁺ cations;²³ on the other hand, the transport mechanism of Li⁺ cations in electrolytes has been observed to change as the concentration is elevated.^16,24,25

2.2 Basic requirements for ideal electrolytes

2.2.1 Wide electrochemical stability window. Electrochemical stability against oxidative and reductive decomposition is an important performance indicator of electrolytes because it is a prerequisite for achieving high energy density batteries. The energy levels of the highest occupied molecular orbit (HOMO) and lowest unoccupied molecular orbit (LUMO) of an electrolyte component are used to reflect the reactivity of its valence electrons at oxidative and reductive potentials, respectively²⁶ (Fig. 2a). Conventionally, the difference value between the LUMO and HOMO is defined as the electrochemical window (ECW) and used as a preliminary indicator for the electrochemical stability of electrolytes in a battery system.²⁷

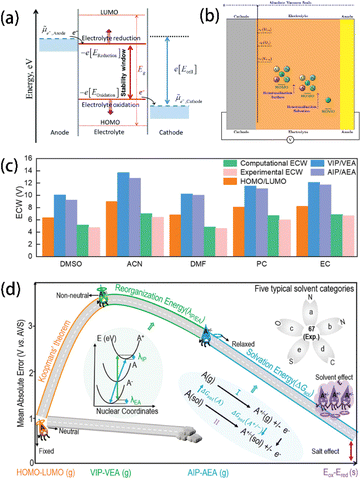Fig. 2 (a) Schematic open-circuit energy diagram of an aqueous electrolyte. Reprinted with permission from ref. 26. Copyright 2010 American Chemical Society. (b) Schematic showing the renormalization of the HOMO level of the solvent due to solvation and interactions with the cathode surface. Reprinted with permission from ref. 29. Copyright 2019 American Chemical Society. (c) Differences in ECWs (in V) of 5 common solvents evaluated by HOMO/LUMO, VIP/VEA, and AIP/AEA methods. (d) Illustration of the improvement of ECW prediction methods concerning reorganization energy and solvation energy via the thermodynamic cycle approach. The inset shows a schematic diagram of the energies of neutral and charged molecules for nuclear coordinates. Reprinted with permission from ref. 35. Copyright 2023 John Wiley and Sons.

Plenty of studies have been carried out to utilize the HOMO, LUMO, and ECW of electrolytes as descriptors to predict their electrochemical stability due to the simplicity of calculating them.²⁷ However, studies have proved that simply obtaining the HOMO and LUMO values from theoretical calculations is not a sufficiently accurate predictor of the redox properties of electrolyte components since more complicated interactions exist in real electrolyte solutions. For example, Peljo et al.²⁸ proposed that describing the redox potentials of an electrolyte using the HOMO and LUMO is problematic because the HOMO and LUMO assume that the molecules are isolated and noninteracting. Instead, a more accurate approach involves using the potentials of electrolyte reduction at negative potentials and the potentials of electrolyte oxidation at positive potentials to describe the electrochemical stability of electrolytes. Similarly, Pande et al.²⁹ pointed out that the HOMO, which assumes that the molecules are isolated from the environment, induces unneglectable errors. As the solvent HOMO levels are renormalized after the formation of solvation shells, new descriptors based on Gutmann's donor and acceptor numbers of the solvent were proposed to be more accurate for the fast screening of electrolyte solvents (Fig. 2b).

Chen et al.²⁷ found that HOMO and LUMO values generated from the traditional isolated molecule/ion models show significant deviations from the experimental value due to the omission of the solvation structures.^28,30,31 In contrast, the calculation models that consider the solvation effect show a better agreement with the experimental observations.^30,32,33 It was also demonstrated that simply considering the dielectric constant does not provide accurate descriptions of the charge transfer between molecules and atoms. Therefore, artificially constructing the ion–solvent complexes becomes a feasible way to reveal the charge transfer properties more deeply. In particular, Fadel et al.³⁴ found that the formation of the charge-transfer complexes between anions and solvents can significantly reduce the ionization potentials of the ion–solvent combination system from the higher values of the isolated ion/molecule systems (Fig. 2c). This work provides a new solution for the precise description of the electrochemical stability of electrolytes. Similarly, Wang et al.³⁵ suggested that traditional methods for ECW calculation based on the assumption that the molecules maintain their isolated neutral states have a large inaccuracy due to their neglection of the charge transfer between neutral reactant molecules and the electron and nucleus reconstruction (Fig. 2d). To address this, they introduced two correction terms – reorganization energy (λ) and solvation-energy (ΔG_sol), and further improved the vertical ionization potential (VIP)/vertical electron affinity (VEA) and adiabatic ionization potential (AIP)/adiabatic electron affinity (AEA) methods. Their approach was reported to be more accurate than traditional ECW computation because it considers the charge transfer between molecules, reducing the mean – average error (MAE) of the 68 solvents' oxidation potentials from 3.25 V to less than 0.68 V, showing a clear advantage over the traditional HOMO/LUMO method. Furthermore, 308 common solvents were screened by this corrected method, revealing two promising candidates (carbamic fluoride and 2-oxo-1,3-dioxolane-4-carbonitrile) with ECWs larger than 6 V, making them suitable for high-voltage battery applications.

2.2.2 Fast ion transport over a wide temperature range. Sufficient ionic conductivity of the bulk electrolyte plays a crucial role in determining the rate capabilities of batteries. The ionic conductivity arises from the transport of Li⁺ cations and the anions following the equation:
where n_i is the free ion number, μ_i is the ionic mobility, Z_i is the valence order of ionic species i, and e is the unit charge of electrons. At elevated temperatures, although the ionic conductivity can be increased by the enhanced ionic mobility,³⁶ the interfacial reactions between electrolyte and electrode materials are facilitated, which accelerates the consumption of electrolyte and thus promotes the capacity degradation and gas evolution;^37,38 at low temperature, the viscosity of the electrolytes increase and they might even solidify, resulting in a significant decrease in ionic conductivity. Moreover, the sluggish diffusion, desolvation, and charge transport in SEI/CEI interphases at low temperatures also result in the loss of capacity and rate capability under XFC conditions.³⁹

The transference number is often an overlooked parameter but it is important to optimize electrolyte performance.^24,40 It is defined as the proportion of B's contribution to the conduction:

As Li+ cations are more heavily coordinated by solvent molecules, leading to slower movement compared to less coordinated anions, the tLi+ in the electrolytes is generally lower than 0.5. Importantly, it is the transference number and conductivity that determine the flux of Li+ (σLi = σ × tLi+). A low tLi+ results in a larger concentration polarization, accelerating the battery performance degradation by enlarging the voltage change and internal resistance.41 Therefore, anchoring or impeding the movement of anions in electrolyte is widely carried out to increase the tLi+ of electrolyte and obtain a better battery performance.42,43 Xu et al.44 investigated the influence of anion–solvent interaction on the solvation structure. It was found that a strong interaction between the anion and solvents can effectively limit the mobility of anions and thus increase tLi+. By using a partially fluorinated ether solvent, bis(3-fluoropropyl)ether (BFPE), which possesses a strong interaction with (fluorosulfonyl)(trifluoro-methanesulfonyl)imide (FTFSI) anions, the tLi+ was improved to 0.86, resulting in an average CE above 99% at −30 °C. The improvement of ion transport properties should not merely focus on ionic conductivity, which contributes to the rate capability, but also on the challenging task of regulating the solvation structures of cations and anions. By tailoring the interactions between Li+, solvents and anions, interfacial reactions can be purposefully controlled to form a stable SEI and realize improved performance under extreme conditions.

2.2.3 Anion-derived SEI/CEI interphases. In addition to the bulk properties, electrolytes that can form a stable SEI on high-capacity anodes such as lithium metal or silicon and robust CEI on high-voltage cathodes are highly needed. The formation of a SEI film involves two coexisting processes: (1) the chemical reduction of electrolyte components on the anode surface due to the low electrode potential of lithium metal, and (2) the electrochemical reduction of the desolvated solvent molecules/anions from the solvation shell around Li⁺ cations. The desolvation of Li⁺ cations is a rate-controlling step of lithium metal batteries, especially under low temperature conditions.^45–47 The composition of the SEI, formed by the decomposition products of the desolvated solvation shell, plays a critical role in determining the cycling stability. A wide range of research has confirmed that the inorganic/organic component ratio in the SEI influences the mechanical properties and ion transport capabilities in many ways.^48–52 Particularly, it has been found that the increase in inorganic components in the SEI (e.g., Li₂O, Li₃N, and LiF) that are produced from the reductive decomposition of anions can effectively enhance the mechanical strength of the SEI and facilitate its ion conduction. A mainstream strategy to enrich the SEI with inorganic decomposition products continues to dominate the field. Therefore, the rational design of solvation structures remains a critical mission for electrolyte chemists. For example, Li et al.⁴⁸ used tris(pentafluorophenyl)borane (TPFPB) as an anion acceptor, in which the electron-deficient boron atoms attract the FSI anions and then increase the number of Li⁺ coordinated with FSI. Such a transition of the AGG mode promoted the decomposition of FSI to form Li₂S, which increased the inorganic composition ratio in the SEI (Fig. 3a and b). Similarly, Ding et al.⁴⁹ incorporated low-dielectric-constant cosolvent with HCE to enhance the cation–anion interaction in electrolytes. This work showed that the cosolvent with weak coordination with Li⁺ could construct a low-dielectricity environment around Li⁺ and facilitate the interactions between Li⁺ and the anions (Fig. 3c). With such modifications, positively charged AGGs were found to dominate the solvation structure, and thus, more FSI participated in the decomposition, forming an anion-derived SEI.

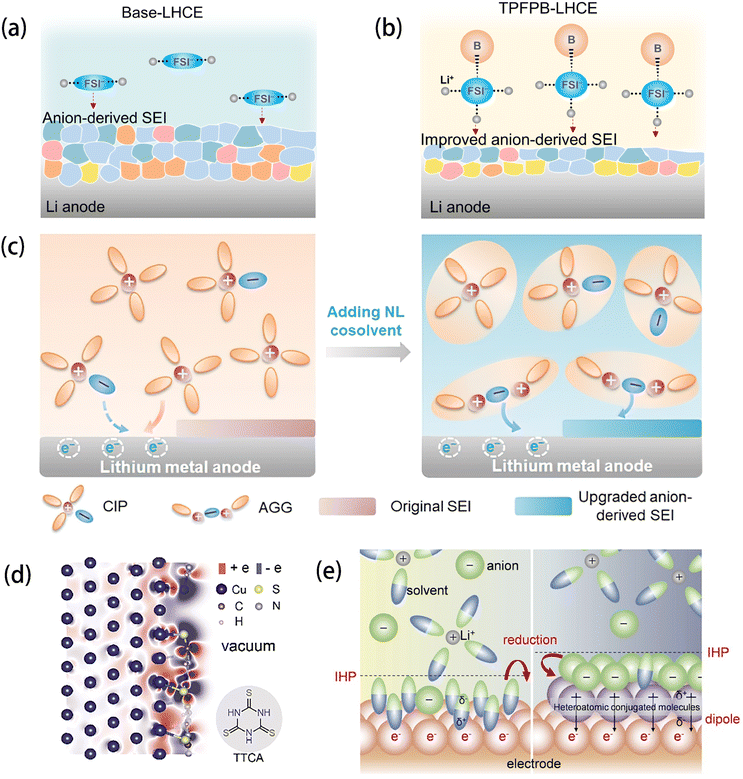Fig. 3 Schematic diagram of the electrolyte structure of FSI and the correspondingly formed SEI in (a) base-LHCE and (b) TPFPB-LHCE. Reprinted with permission from ref. 48. Copyright 2021 John Wiley and Sons. (c) Schematics showing the working mechanism of non-solvating and low-dielectricity (NL) cosolvent on the solvation structures and the SEI formation process. Reprinted with permission from ref. 49. Copyright 2021 John Wiley and Sons. (d) Charge density difference image of TTCA adsorbed on the Cu(111) surface and the structural formula of TTCA. (e) Schematic illustration of the working mechanism of the surficial dipole layer in IHP and its effect on SEI formation. Reprinted with permission from ref. 53. Copyright 2023 John Wiley and Sons.

Besides molecular engineering of the electrolyte components, some approaches have been carried out on the anode side to increase the inorganic component ratio. Fan et al.⁵³ introduced a layer of heteroatomic conjugated molecules, namely, trithiocyanuric acid (TTCA), onto the surface of the copper (Cu) current collector (Fig. 3d) to build a surficial dipole which can uniformly absorb the anions (TFSI) in the inner Helmholtz plane (IHP) and then produce an inorganic SEI via the reduction of the anions (Fig. 3e). By this measure, the deposition uniformity of Li on Cu foil was significantly increased, and superior cycling stability was realized.

2.3 Theoretical prediction of electrolyte properties

Most innovations in electrolyte formulae still rely on trial-and-error approaches based on numerous experiments. The development of computer technology and computational chemistry (i.e., DFT calculations,^54,55 MD simulations,⁵⁶ and machine learning (ML)⁵⁷), however, have opened up a new track for scientists to design electrolytes much more efficiently.^58–60 For example, Wu et al.⁶¹ screened 190 binary mixtures of 20 electrolyte solvents with seven σ-descriptors (S₁ to S₇) – which were derived from the charge density distribution of molecules – by DFT and a conductor-like screening model for realistic solvent (COSMO-RS) calculations (Fig. 4a). The resultant data were then used to train the multiple linear regression machine learning models to predict the binding energies of Li⁺ cations and TFSI anions, showing high accuracy in predicting solvent solvation abilities (Fig. 4b). Using ab initio molecular dynamics (AIMD) and DFT calculations, Qin et al.⁶² investigated the formation mechanisms of LiF on graphite electrodes. In this work, a multi-molecular model of the graphite surface in EC/EMC electrolyte was constructed to find the relationship between thermodynamic free energy and electrode potential. An electrochemical stability diagram was obtained (Fig. 4c) based on the calculation results showing that the thermodynamic free energy tends to decrease more significantly as the electrode potential decreases when more Li atoms exist in the system. LiF formation on graphite electrodes was found to be facilitated by the production of intermediate LiHF, which tends to be solvated by solvents at the graphite–electrolyte interface rather than directly deposited onto metal electrode surfaces (Fig. 4d). In another study, Liao et al.⁶³ trained the Gaussian process regression (GPR) ML models based on the CEI stability data of 28 single and dual additives in the LiNi_0.5Mn_1.5O₄‖graphite battery system (Fig. 4e and f). Their model successfully predicted the electrochemical performance of the 125 binary electrolyte compositions (i.e., final area specific impedance (ASI), impedance rise (ΔASI), and final specific capacity (Q)), identifying 6 optimal formulae (Fig. 4g, h, and i). Experimental validation revealed a promising new binary formulation: 1 wt% LiBOB + 1 wt% succinic anhydride. These studies show the power of computational methods as a practical and precise assistant of electrolyte design.

Fig. 4 (a) Schematics of the ML strategy for predicting Li⁺ and TFSI ion binding energies. (b) Comparison between the binding energies of Li⁺ and TFSI ions calculated with DFT and predicted by the multiple linear regression ML model. Reprinted with permission from ref. 61. Copyright 2024 Royal Society of Chemistry. (c) Electrochemical stability diagram of graphite–electrolyte interfacial models including 0Li, 1Li, and 2Li. (d) Gibbs free energy diagram of LiF formation. (c) and (d) reprinted with permission from ref. 62. Copyright 2024 American Chemical Society. (e) Schematics of the ML-guided design of the experiment workflow for electrolyte additive discovery. (f) Sequential method for developing ML models to predict and recommend new electrolyte additives. ASI, ΔASI, and Q denote the final area-specific impedance, impedance rise, and final specific capacity, respectively. Parity plot of GPR-predicted (g) ASI, (h) ΔASI, and (i) Q versus measured values for the training set of 28 additive and baseline solvents. Reprinted with permission from ref. 63.

Overall, DFT calculations and MD simulations have become powerful tools for researchers to understand the electrochemical processes more clearly and design electrolytes more efficiently. Based on these, ML can be even more powerful in boosting the discovery of brand-new electrolyte compositions at an unprecedented speed. Wang et al.⁶⁴ systematically reviewed the challenges for developing ML-based battery chemistry, in which the importance of accurate descriptors for material and electrolyte's properties is strongly emphasized. They proposed four key requirements for ideal descriptors for material properties: reproducibility, validity, distinguishability, and simplicity.

Machine learning (ML) has emerged as a powerful tool for accelerating electrolyte design, but its widespread adoption faces key challenges related to accuracy, interpretability, and practical implementation. The accuracy of ML models heavily depends on the availability of high-quality, diverse, and representative datasets. In the context of electrolyte screening, obtaining sufficient experimental data or reliable simulation results is often challenging due to the high costs and time-intensive nature of data generation. Limited or biased datasets can lead to inaccurate predictions and poor generalization of unseen compounds, undermining the utility of ML in discovering novel electrolytes. The choice of ML algorithms also plays a critical role in determining predictive performance. Advanced techniques, such as deep learning, excel at capturing intricate relationships within data but typically require large datasets, which are not always available in electrolyte research. Conversely, simpler models, such as linear regression or decision trees, may perform well with limited data but often lack the capacity to model complex chemical interactions. Striking the right balance between model complexity and data availability remains a central challenge.

To advance ML-based electrolyte design, two critical considerations must be addressed: (1) building high-quality datasets with interpretable descriptors. Accurate predictions require datasets that reliably capture electrolyte properties, either through experimental measurements or computational calculations. Selecting or developing interpretable descriptors – such as those grounded in physical or chemical principles – is essential to improve both the quality of datasets and the reliability of predictions. (2) Developing interpretable ML models. Interpretability is crucial for understanding the mechanisms driving ML predictions and for gaining scientific insights into electrolyte performance. Approaches such as SHapley Additive exPlanations (SHAP)⁶⁵ and Local Interpretable Model-Agnostic Explanations (LIME) enable researchers to identify the contributions of individual features to predictions. Such tools not only enhance trust in ML models but also provide guidance for rational electrolyte design. Despite the computational demands of some ML approaches, these challenges highlight the importance of integrating domain knowledge, high-quality data, and interpretable methodologies to fully realize the potential of ML in electrolyte research. By addressing these issues, ML can become an indispensable tool for accelerating the discovery of next-generation electrolytes with improved performance and stability.

3 Emerging descriptors for electrolyte design

The development of AI and ML techniques has revolutionized the search for new electrolyte formulae by enabling the screening of a large number of candidates with computers instead of experiments. Many studies have shown the accuracy of DFT calculations for basic properties of electrolytes, such as the dipole moment and dielectric constant based on various models and systems.^66–69 However, the complexity of the ion–solvent interactions in electrolytes imposes challenges in finding a single parameter that captures all relevant properties. Additionally, DFT calculations are inherently limited by their vacuum environment assumption. In recent years, various new or corrected descriptors have been proposed for accurate prediction of the Li⁺ solvation structure.⁵ It is of significant importance to understand their definitions, advantages, and shortcomings. What is more, the ion–solvent coordination structure and strength were found to be important in determining the solvation/desolvation process, SEI formation, and so on. All the interactions among Li⁺ cations, anions, and solvent molecules are fundamentally carried out by the transfer and interaction of electrons, so the development of precise descriptors for solvating properties of electrolytes should be based on the accurate description of electronic transport between molecules and ions. This section introduces the major descriptors that effectively describe the electronic properties such as polarity, Lewis basicity, and coordination energy, while discussing their development and implications for electrolyte design.

3.1 Polarity

Polarity refers to the charge distribution within a molecule, where the positive and negative charge centers are unevenly separated in an electric field. Polarity is an important parameter that determines the solubility and miscibility of solvents. Following the general rule of “like-dissolves-like”, polar solutes usually have high solubility in polar solvents, and nonpolar solutes dissolve in nonpolar solvents. In the context of electrolyte design, high polarity is typically desired for Li⁺-solvating solvents, and a low polarity is favored for non-solvating solvents (also known as diluents) for localized high-concentration electrolytes (LHCEs). The polarity of each component serves as a key descriptor for predicting the solubility behaviors and resulting solvation structures.^70–72 Therefore, it is important to understand the nature of polarity for the rational design of high-performance electrolytes.

3.1.1 Dielectric constant. Due to the difference between the electronegativities in different elements, electrons in a molecule tend to accumulate near the more electronegative atoms. This uneven distribution leads to the classification of molecules as either polar or non-polar, depending on whether the centers of the positive and negative charges coincide (Fig. 5a and b). The polarity of a molecule is primarily determined by its structure, and its electric dipole moment (μ) defines the polarity of a molecule based on the following equation:

μ = q·d

where q is the amount of charge on one side and d is the length of the dipole.

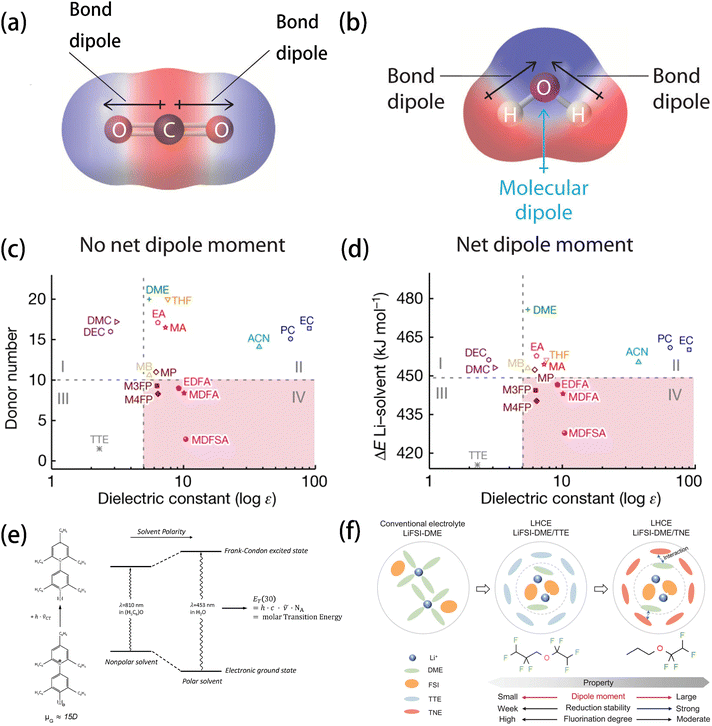Fig. 5 Charge distribution of (a) CO₂ and (b) H₂O showing the origin of dipoles of non-polar and polar molecules, respectively. Reprinted with permission from ref. 74. Diagram of (c) DN and (d) Li⁺–solvent binding energy from DFT calculations versus the experimental dielectric constant. Reprinted with permission from ref. 11. Copyright 2023 Springer Nature. (e) Qualitative illustration of a solvent's influence on the intramolecular charge-transfer visible absorption of the standard betaine dye no. 30 (μ_G > μ_E) and definition of the E_T(30) values as its molar electron transition energies. Reprinted with permission from ref. 90. Copyright 2005 Royal Society of Chemistry. (f) Illustration of the solvation structures of LiFSI/DME, LiFSI/DME-TTE, and LiFSI/DME-TNE electrolytes and the differences in properties between TTE and TNE diluent molecules. Reprinted with permission from ref. 99. Copyright 2024 John Wiley and Sons.

A molecule's dipole moment μ is a microscopic quantity, whereas the dielectric constant ε measures a macroscopic property. The definition of the dielectric constant (relative permittivity, ε_r) is the ratio of the electric displacement D to the electric field strength E when an external field is applied to the substance, denoted as:

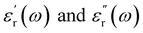where ε₀ is the vacuum permittivity, and are the real part and the imaginary part of permittivity ε(ω) at electric field frequency ω. The correlation between the dielectric constant and dipole moment is described by using the Clausius–Mossotti equation:
where α represents the polarizability of the molecule, N is the number of atoms (or ions) per unit volume, and E_loc is the local electric field. According to the equation, ε is positively correlated with μ. Therefore, the molecular structure of a solvent largely determines its dielectric constant and then influences its solubility of Li⁺ cations.

In electrolyte design, the dielectric constant is commonly used to distinguish solvating solvents and non-solvating solvents (also called anti-solvents). As the conductive lithium salts need to be dissociated into Li⁺ cations and anions, solvents with higher polarity can induce stronger charge separation. This allows the solvent molecules to interact with Li⁺ cations and anions, attracting the Li⁺ cations and the anions with their region of negative and positive charge, respectively. For a given salt, a higher dielectric constant enables the solvent to dissolve the salt at a higher concentration. As a result, solvents with high dielectric constants (e.g., linear carbonates, cyclic carbonate, ethers, etc.) are promising to realize higher concentrations of the conductive salt and maximize ionic conductivity. However, simply increasing the salt concentration is not always advantageous. As the salt concentration in the electrolyte increases, more solvent molecules will coordinate with the Li⁺ cations and anions, leading to higher viscosity.

The dielectric constant has played an important role in screening and selecting solvating and non-solvating solvents for the different types of electrolytes. For example, in Xu et al.'s work, solvents with high dielectric constants, combined with low DN values and low Li⁺–solvent binding energies were identified as ideal candidates for soft solvating electrolyte with fast ionic transport even at low-temperature, enabling stable operation across a wide temperature range (−60 to +60 °C)¹¹ (Fig. 5c and d). In another study, fluorobenzene (FB), which possesses a low dielectric constant due to its symmetric structure, was used as a diluent for LHCE, in which triethyl phosphate (TEP) functioned as a flame retardant.⁷³ The addition of FB not only significantly reduced the viscosity of the electrolyte and improved its ionic conductivity but also maintained excellent non-flammability. Chen et al.'s study revealed that solvation effects reduce the binding energy of Li⁺–solvents, Li⁺–anions, and solvent–solvent complexes. As the dielectric constant of the solvent increases, the solvation effects strengthen, significantly lowering the binding energy of these coordinates in solution compared to those in a vacuum.⁷⁴ Being a macroscopic quantity that has a well-founded database, the dielectric constant has an advantage over the microscopic molecular properties, whose values largely depend on the calculation methods and their inherent accuracy. The dielectric constant has been and is still one of the most widely used descriptors for predicting the solvation-related properties of electrolytes, while its capability of describing specific interactions such as coordination might be relatively limited compared to other descriptors.

The molecular dipole moment and dielectric constant are two mainstream and conventional descriptors for measuring the polarity of solvents. The “like-dissolves-like” principle, long used and verified for regular solutions, remains a fundamental guideline for predicting the solubility of many compounds.^75,76 This “like-dissolves-like” principle has good validity in systems where only unspecific interactions are present, and it is less effective in explaining solvation processes involving specific interactions, such as ion–solvent interactions in battery electrolytes. As more and more specific interactions have been discovered (especially the ion–solvent interaction of battery electrolytes), the macroscopic definition of solvent polarity becomes insufficient for fully describing complex solvation processes.⁷⁷ Another issue of using these descriptors is that the local polar structures in molecules can sometimes be overlooked. Although the dipole moment is conventionally used for predicting the solubility of solvents via DFT calculation, near-zero values can be obtained in some symmetric molecules (e.g., DME, DEE, and oxalic acid) due to the offset of local dipoles. Therefore, Lu et al.^78–80 proposed the molecular polarity index (MPI) to define the polarity of molecules by measuring the heterogeneity of surficial molecular charge, overcoming the disadvantage of the former.

3.1.2 Normalized molar electron transition energy. While the physicochemical properties describing the polarity of molecules (i.e., dielectric constant and dipole moment) are commonly used to predict the solvation ability of solvents, they often lead to significant inaccuracy. For example, the dielectric constant and dipole moment of tetrahydrofuran (THF) are 7.6 and 1.63 D, respectively, whereas 1,2-difluorobenzene has higher values of 14.26 and 2.53 D, respectively. Despite this, 1,2-difluorobenzene exhibits a lower ability to solvate lithium ions compared to THF.^81,82 This discrepancy highlights the need for new descriptors to better reveal the specific interactions between Li⁺ and solvent molecules.

Numerous studies have sought to develop more accurate scaling parameters for solvent polarity based on various pieces of evidence.¹⁴ For example, Winstein's and Grunwald's Y-scale⁸³ and Beron's Ω-scale⁸⁴ based on the kinetic measurements of chemical processes; Dimroth's E_T-scale,⁸⁵ and Brownstein's S-scale⁸⁶ based on the solvatochromic shifts in electronic spectra; Allerhand and Schleyer's G-scale⁸⁷ based on the stretching frequencies of specific chemical bonds, etc. have all been proposed as effective measurements of solvent polarity.

Efforts to find a single parameter capable of accurately describing the polarity of solutions, especially in systems with multiple solvation mechanisms, have produced linear correlations only in limited cases.⁸⁸ One such scale is Kosower's⁸⁹Z-value – defined as the transition energy for the 1-ethyl-carbomethoxypyridium iodide complex – to measure the polarity of solvents. Z-Values have a good linear correlation with other polarity scales, such as the Y-values of Winstein-Grunwald, and have the advantage of wide availability. In addition, the Z-value is sensitive to temperature (decreases as temperature increases) and varied significantly with changes in electrolyte concentration, making it a more accurate reflection of solvent polarity. This scale is particularly useful for distinguishing between solvents with similar dielectric constants. Namely, protonic solvents consistently exhibit more polar behaviour than aprotic solvents even when their dielectric constants are comparable.

In 1963, Dimroth et al.^85,90,91 defined the concept of molar electron transition energies (E_T(30)) of standard pyridinium-N-phenoxide betaine dye measured in solvents, establishing a polarity scale for solvents based on the following equation (x):

where [small nu, Greek, tilde]_max and λ_max are the wavelength and wavenumber of the maximum of the long-wavelength, solvatochromic, intramolecular charge transfer absorption band of the standard betaine dye, and h, c, and N_A are Planck's constant, the speed of light, and Avogadro's constant, respectively. This method utilizes the high sensitivity of the long-wavelength intramolecular charge-transfer UV-vis absorption of the pyridinium-N-phenoxide betaine dyes to small changes in solvent polarity⁹² (Fig. 5e). To transform this scale into SI units, the dimensionless normalized molar electron transition energy (E^N_T) was introduced by Reichardt et al. in 1983, defined as
which uses water and tetramethylsilane (TMS) as the most polar and nonpolar reference solvents, respectively.^93,94 In his work,⁹⁰ Reichardt summarized the E_T(30) and E^N_T values of 362 solvents, which showed strong compatibility with other polarity scales. For example, the E_T(30) values show such an excellent linear correlation with Kosower's Z values⁹⁵ that they were regarded as interchangeable. What is more, the E_T(30) values also show a good linear correlation with the Gibbs energy of activation (δΔG*) of the solvolysis of 2-chloro-2-methylpropane – another polarity scale derived from kinetics of solvation, indicating that the solvatochromic descriptor E_T(30) and the kinetic descriptor δΔG* are both effective measures of the solute–solvent interactions. Therefore, E^N_T was proposed by Reichardt to be a precise descriptor of solvent polarity, particularly in highly polar electrolytes, due to its capability to reflect intermolecular attraction among the components.⁹⁰

The concept of LHCE using anti-solvents as a diluent was first proposed by Chen et al.^96–98 and testified by many researchers^99–102 to be effective in reducing the overall viscosity of electrolyte while retaining the solvation structure and high ionic conductivity with a high salt concentration.¹⁰³ LHCEs offer the advantage of enabling the prior reduction of anions, which facilitates the formation of the anion-derived SEI resulting in stable Li deposition on the anode. However, the use of non-solvating diluents often compromises ionic conductivity due to the inferior Li⁺ solubility of commonly used diluents (e.g., fluorinated compounds). By using the polarity as an indicator of solubility, Yang et al.⁹⁹ designed an LHCE in which 1-(1,1,2,2-tetrafluoroethoxy)propane (TNE) was used as the diluent. The propoxy and tetra fluoroethyl groups in the TNE molecule enhanced its polarity. Thus, they formed a strong coordination with the major solvent DME, weakening the coordination between the DME solvent and Li⁺ (Fig. 5f). Consequently, the proportion of FSI anions in the solvation shell was increased, thereby improving the robustness and ionic conductivity of the SEI. Similarly, Nan et al.¹⁰⁴ proposed using low-polarity solvents to reduce charge transfer impedance (R_ct) at the electrode–electrolyte interfaces, particularly at low temperatures. It was found that the low-polarity solvents (e.g., ethyl methyl carbonate, EMC) exhibit weaker ion–dipole interactions than the higher-polarity ones, resulting in a lower R_ct. What is more, EMC was found to be able to form partially dissociated salt domains with high ratios of CIPs and AGGs, which facilitated the formation of an anion-derived SEI and enabled an improved performance over a wide temperature range from −40 °C to 50 °C.

For electrolytes, E^N_T has been proposed to be an ideal descriptor for the miscibility of a solvent with another (e.g., an anti-solvent with the solvating solvent). Compared to the traditional methods for predicting the miscibility of two liquids by using their dielectric constants or dipole moments, E^N_T has the advantage of high quantitative accuracy because it is defined as the enthalpy change after mixing the isolated components. A higher E^N_T indicates that polar molecules more strongly attract the solvent, thus implying a higher miscibility with the highly polar electrolyte.

3.2 Lewis basicity

Although the polarity of solvents can reflect the solubility to a large extent, it does not capture everything. For example, nitromethane and dimethylformamide (DMF) have very similar dielectric constants, and the ion-pairing ability in nitromethane is much greater than that in DMF.¹⁰⁵ For electrolyte design, Lewis basicity could be a useful addition to the consideration of polarity, ensuring a more complete and accurate understanding of solvent behavior.

3.2.1 Scales for measuring Lewis basicity. G. N. Lewis defined an acid and base as “a basic substance is one which has a lone pair of electrons which may be used to complete the stable group of another atom,” and “and an acidic substance is one which can employ a lone pair from another molecule in completing the stable group of its own atoms”.¹⁰⁶ The Lewis basicity of molecules is closely related to the chemical reactivity properties.^14,107 For electrolytes in lithium batteries, where Li⁺ is typically the only solvated cation, the Lewis basicity of solvents plays a crucial role in determining the solvating ability and solvation structures of Li⁺ cations. As such, it has been considered a core descriptor for electrolyte design. Although the definition of Lewis basicity is simple, accurately measuring it across different chemical compounds has proven complex. Therefore, many approaches have been developed to set a reliable scale for Lewis basicity.¹⁰⁸

In 1941, Gordy and Stanford reported the relationship between the O–D group's vibrational band shift in infrared spectra of solvents and their physicochemical properties (i.e., dipole moment, dielectric constant, basicity, solubility, electro-negativity, etc.). According to their research, the chemical shift of the O–D band's absorption band exhibits little correlation with the dipole moment of the solvents but shows a positive linear relationship with their basicity constants (K_b).^109,110

In 1968, Kagiya et al.¹¹¹ proposed a measuring scale for the electron-donating/accepting ability of liquid organic solvents. This scale is based on the position of the O–D or C=O absorption band in infrared spectra, where the relative differences in these positions were defined as the electron-donating or the electron-accepting power, expressed by using the following equations:

Electron donating power: Δν_D = ν_D(benzene) − ν_D(compound)

Electron accepting power: Δν_A = ν_A(benzene) − ν_A(compound)

Although these scales can effectively measure the Lewis basicity of solvents, their function is limited by the experimental procedures. In the case where a solvate is coordinated by multiple solvent molecules, dual interactions occur, complicating the determination of which absorption band should be used. Therefore, a more practical and accurate scale is needed. Over the years, many basicity scales have been proposed, each with its own advantages and shortcomings.^105,112,113 In the following discussion, we focus on the two most widely used scales: Gutmann's donor number and Kamlet–Taft's β-scale.

3.2.2 Gutmann's donor number (DN). In 1976, Gutmann introduced the DN and acceptor number (AN) to describe the nucleophilicity and electrophilicity of solvents, respectively.¹¹⁴ By interpreting solute–solvent interactions as acid–base reactions, solvation can be interpreted as a nucleophilic attack by the solvent, which donates an electron pair to the low-electron density region of the solute. The DN is defined as the dimensionless enthalpy change at room temperature for a 1 : 1 adduct formation between antimony(V) pentachloride (SbCl₅) and a solvent at low concentration in the non-coordinating main solvent 1,2-dichloroethane,^114,115 and its definition formula is:

DN = −ΔH_DN [kcal mol⁻¹]

The DN is a particularly useful tool for electrolyte design. Solvents with a high DN have strong nucleophilicity and tend to coordinate strongly with Li⁺ cations, while anti-solvents with a low DN which do not coordinate with Li⁺ cations are used as diluents to reduce electrolyte viscosity. Ding et al.⁴⁹ chose solvents with a low DN and low dielectric constant as anti-solvents for LHCE. Eight solvents were mapped in a Li⁺ binding energy-dielectric constant diagram (Fig. 7a), showing that solvents with lower dielectric constants and binding energies, such as hexane and benzene, are ideal non-solvating cosolvents. By using non-solvating cosolvents, more CIP and AGG were formed instead of free FSI anions. The enhanced Li⁺–anion binding strength increased the proportion of anion-derived inorganic compounds in the SEI, resulting in an effectively improved CE and inhibited lithium dendrite growth.^97,116–118 Chen et al.¹¹⁹ investigated the common descriptors (i.e., ε, μ, and DN) of over 500 solvent compositions. The comparison results show that the DN, rather than ε and μ, correlates more strongly with the coordination structures of Li⁺. By introducing critical DN values, a model was developed to describe the transition from LHCE to conventional dilute electrolytes (Fig. 6a). Miranda-Quintana et al.¹¹⁵ introduced an approach for computing DN values with DFT based on a series of rational approximations, achieving an acceptable accuracy with the experimental measurement results (Fig. 6b). The introduction of such a convenient and accurate DN calculation method provides researchers with a more reliable tool to predict the solvation properties of electrolyte solvents. Just as shown in Xu et al.'s work,¹¹ the Li⁺–solvent coordination energy of various solvents closely correlates with their DN values (Fig. 5c and d), indicating that the DN has a close relationship with the solvating ability of solvents.

Fig. 6 (a) Schematics of the change in free energy for the transition from LHCE to conventional dilute electrolyte. DN_c refers to the critical DN threshold value (∼10). Reprinted with permission from ref. 119. Copyright 2023 American Chemical Society. Copyright 2022 Springer Nature. (b) Comparison between the experimental DN and the corresponding energy changes for implicit solvation approaches. The red circles denote the results for the implicit expressions after a linear regression fit (−ΔE_impp^ert) and the blue squares the hardness perturbation term (−ΔE^lin_exp). The black solid implies full agreement. Reprinted with permission from ref. 115. Copyright 2021 Elsevier. Schematic of the correlations (c) between β and the CE and (d) between E^N_T and the miscibility of lithium metal batteries employing different electrolytes. Reprinted with permission from ref. 82. (e) Plot of DN/37 (DN*) against Kamlet–Taft's β. Reprinted with permission from ref. 123. Copyright 2018 Springer Nature.

3.2.3 Kamlet–Taft's Lewis basicity. In 1976, Kamlet and Taft introduced β and α for scaling a solvent's hydrogen bond acceptor basicity¹²⁰ and donor acidity,¹²¹ respectively. β, referred to as Kamlet–Taft Lewis basicity – β_KT closely aligns with the DN because they are both determined by the most negative atom's charge and electron orbitals of the solvent molecule.¹²²β_KT measures the hydrogen-bond acceptor strength of solvents by comparing the displacement of the solvatochromic shifts between the reference solvents 4-nitroaniline (1) and N,N-diethyl-4-nitroaniline (2), denoted as:

β _KT was reported to not only correlate with the coordination strength of Li⁺ in electrolytes⁸² but it was also able to partially determine the coulombic efficiency (CE) of Li‖Cu cells. Using β_KT (Fig. 6c) and E^N_T (Fig. 6d) together, Moon et al.⁸² screened non-fluorinated non-solvating solvents for diluents. A lower β_KT was preferred because it indicates a low Lewis basicity that prevents coordinating with Li⁺ cations, while a moderately higher E^N_T was targeted for better miscibility with solvating solvents. However, Waghorne et al.¹²³ pointed out that while the DN measures the Lewis basicity of isolated molecules, β_KT measures the hydrogen bond accepting strength of bulk liquids. The DN and β_KT of 110 compounds show a good trend coincidence, indicating that both scales reveal the Lewis basicity of molecules precisely. However, exceptions were observed among the nitrogen-containing bases (i.e., amines and anilines) and alcohols, reflecting differences between the DN and β_KT in their definitions (Fig. 6e). Recently, Waghorne compared several Lewis basicity scales (e.g., DN, β_KT and Catalán's SB/SA scale^124,125). It was found that all three scales strongly depend on the partial charge of the most negative atom and the energy of the electron donor orbital.¹²⁶ Hydrogen bonding significantly impacts the contribution of individual solvent molecules' properties to the bulk basicity. While the bulk basicity of non-hydrogen bond solvents is a simple function related to the molecule structure, significant deviations between the calculated and experimental basicity patterns were found in the case of hydrogen bond-containing solvents. It was supposed that the Lewis basicity of bulk solvents is not only contributed by the molecules' properties but also the hydrogen bonds.^120,127,128 The DN values reported in various literature studies have serious discrepancies. While experimental error is a factor, the primary issue is that the DN is traditionally meant for solutes rather than solvents. Gal et al.¹²⁹ realized that the DN can be approximatively used for solvents only for dilute solutions, in which the solute and solvent molecules form weak associations. They recommended using the negative of the adduct formation enthalpy of boron trifluoride in dichloromethane (DCM) as an alternative scale of solvents' Lewis basicity, which showed high accuracy in both experiments and ab initio calculations. Anion's Lewis basicity also influences the interfacial stability of Li⁺ cations. Scaling with DN, Ugata et al.¹³⁰ compared the Raman spectra of the electrolyte solutions containing different lithium salts. The anions' coordination with Li⁺ cations is enhanced as the Lewis basicity of anions increases, leading to an increased proportion of free solvent in the solution.

Overall, β_KT is a reliable descriptor for scaling the Lewis basicity of electrolyte solvents, comparable to the DN, but its distinct definition from the DN occasionally brings discrepancies in specific cases. An in-depth study on the origin of the similarity and distinction between β_KT and the DN is expected to guide chemists to use them with greater confidence and fewer mistakes.

3.3 Coordination energy

It has recently become widely accepted that a high proportion of inorganic components (e.g., LiF and Li₃N) in the SEI and CEI can reduce the interfacial impedance and increase the cycling stability. Strong coordination between solvent and Li⁺ cations can facilitate ion dissociation and create a robust Li⁺–solvent solvation shell. The coordination energy between Li⁺ cations and solvents can be calculated according to the following equation:

Coordination energy = −[E(Li⁺–solvent) − E(Li⁺) − E(solvent)]

This simple equation enables researchers to obtain the binding strength between Li⁺ cations and solvents quickly. However, it should be noted that the salt concentration of electrolyte solution has an important impact on the desolvation energy barrier. A higher concentration could indicate a stronger binding between Li⁺ cations and solvent molecules due to the increased coordination number.¹³¹ Therefore, compared to simply calculating the coordination energy of an isolated Li⁺–solvent system, building models of multiple-solvent coordination is necessary for improving the simulation accuracy of concentrated electrolytes.

Electrolyte design thus requires minimizing the coordination energy between Li⁺ and solvent molecules to allow anions to penetrate into the solvation shell so that inorganic-rich SEI and CEI films can be formed. Jin et al.¹³ verified that the sluggish desolvation of Li⁺ cations at the electrode surface predominantly contributes to the kinetic barrier of Li⁺ transport at low temperatures. To address this, a low-affinity solvent 1,3-dioxolane was used, which effectively facilitated the desolvation process and improved the low-temperature performance of the lithium metal battery. Sodeyama et al.¹³² employed a cluster model for DFT calculations to calculate the coordination energy between Li⁺ cation and 25 solvents. A database was built based on these calculation results, which includes parameters such as HOMO and LUMO energy, dipole moment, Mulliken charge of an oxygen (nitrogen) atom, and distance between the Li⁺ cation and oxygen (nitrogen) atom. The data-driven prediction of the coordination energy and melting points of 103 solvent molecules(Fig. 7b) shows that the exhaustive search with the linear regression (ES-LiR) technique provided the most accurate estimation of these properties (Fig. 7c).

Fig. 7 (a) Solvent diagram concerning relative binding energy towards Li⁺ and the dielectric constant. Reprinted with permission from ref. 49. (b) Weight diagram of the accurate top 25 combinations of descriptors for the coordination energy prediction. (c) Coordination energies of 103 solvent molecules with true values (calculated by the first-principles method) and estimated values (calculated by data-driven techniques) of MLR, LASSO, and ES-LiR (the least error combination of the descriptors). Reprinted with permission from ref. 132. (d) The energy rank of the six pairwise interactions in LHCE.

The interaction between the diluent and solvation shell can significantly influence the desolvation process and the oxidation stability of LHCE. In LHCE, diluent can disrupt the Li⁺–solvent/anion coordination via dipole–dipole interactions.¹³³ Wu et al.¹³⁴ screened diluents that can form weak but sufficient diluent–anion interactions with Li⁺ coordination energy (Fig. 7d). While a high value of the positive maximum of electrostatic potential energy (E_max ≥ 25 kcal mol⁻¹) can ensure sufficient diluent–anion interaction to prevent phase separation, an excessive diluent-solvation shell interaction may lead to the de-coordination of solvent/anions from Li⁺, which aggravates the electrolyte decomposition. Consequently, 2H,3H-decafluoropentane (HFC) with the lowest Li⁺-coordination energy and a moderately high E_max, was found to improve the oxidation stability and cycling performance of the lithium metal battery. Xu et al.¹¹ screened multiple solvents with ε, DN, and ΔE_{Li⁺–solvent}. Methyl 2,2-difluoro-2 (fluorosulfonyl)acetate with a low DN and ΔE_{Li⁺–solvent} was chosen as a “soft” solvating solvent due to its weak coordination with Li⁺ cations, permitting TFSI anions to participate in the solvation shell and promote the formation of an inorganic-rich SEI.

3.4 Electrochemical potential (ESP)

Although the dielectric constant and donor number can reflect solvent molecules' polarity and Lewis basicity, many exceptions have been observed. For example, 1,4-dioxane has a higher DN (14.8 kcal mol⁻¹) than acetonitrile (14.1 kcal mol⁻¹) but a lower solubility of lithium LiFSI. This highlights the need for a more accurate descriptor to better reflect the dissolving properties of solvents, which is essential for the efficient screening of electrolyte solvents.

The ESP of a molecule describes the molecular reactivity and is closely influenced by the molecular structures. The definition

where Z_A is the charge on nucleus A, located at R_A, and ρ(r) is the electronic density of the molecule¹³⁵ enables ESP to be obtained based on DFT calculations. Murray et al.¹³⁶ found a good correlation between the minimum ESP (V_min) and solvatochromic hydrogen bond acceptor parameter (β) of molecules, indicating that the ESP of gaseous molecules can be used as a descriptor for solvents' ability to accept protons or donate electrons in solutions.

Wu et al.¹² suggested that ESP can accurately describe the interaction between solvents and Li⁺ cations. Specifically, the lowest negative ESP (ESP_min) and the highest positive ESP (ESP_max) were used to design electrolyte solvents. As shown in Fig. 8a, the difference between the ESP_max and ESP_min of a molecule reflects its polarity, making it a good indicator of the solubility and nucleophilicity of solvent molecules. As an electron donor, a solvent's ability to lose electrons is related to its coordinating ability with Li⁺. Electrons' tendency to accumulate near electronegative atoms such as O and N (Fig. 8b) makes solvating solvents generally have a strong charge polarization, enabling them to coordinate Li⁺ cations via electron donation easily, leading to a high solubility. In contrast, the homogeneous charge distribution in anti-solvent molecules resists the electron donation, inhibiting their ability to coordinate with Li⁺ cations. The ESP_min − ESP_max diagrams show that each type of solvent accumulates in a specific ESP region (Fig. 8c and d), indicating that ESP is a powerful tool for describing solvents' solvation behaviours. While ESP_max and ESP_min correlate with the solvent polarity and Li⁺ binding energy, low |ESP_min| and high ESP_max values are indicative of the non-solvating nature of antisolvents.

Fig. 8 (a) ESP distribution of 1,1,2,2-tetrafluoroethyl-2,2,3,3-tetrafluoropropylether (TTE) and 1-(1,1,2,2-tetrafluoroethoxy)propane (TNE) molecules. Reprinted with permission from ref. 99. Copyright 2024 John Wiley and Sons. (b) Calculated ESP maps of organic solvents under vacuum conditions. (c) DFT-calculated ESP of various solvents under vacuum conditions. (d) ESP of fluorinated solvents. Reprinted with permission from ref. 12. Copyright 2023 John Wiley and Sons. (e) ESP comparison and design scheme with molecular structures of 1,2-dimethoxylethane (DME, left), 1,4-dimethoxylbutane (DMB, middle), and fluorinated 1,4-dimethoxylbutane (FDMB, right). Reprinted with permission from ref. 137. Copyright 2020 Springer Nature.

As a common electrolyte solvent, 1,2-dimethoxylethane (DME) has high solvating capability, but its inferior oxidation stability hinders its application for high-voltage cathode batteries. Yu et al.¹³⁷ designed a modified solvent by lengthening the alkyl chain of DME and introducing –F groups to improve the molecule's robustness towards oxidation. Grafting F atoms onto the chain of 1,4-dimethoxylbutane (DMB) caused negative charge accumulation around the O and F atoms (Fig. 8e), improving its stability. Simply increasing the chain length, however, did not significantly change the charge distribution. A new Li–F coordination was thus introduced and led to a higher anion content in the Li⁺ solvation shell. In another study,¹³⁸ fluorinated 1,2-diethoxyethanes (DEE) was investigated, revealing that a partially fluorinated group (–CHF₂) could coordinate Li⁺ cations strongly compared to a fully fluorinated group (–CF₃). This was attributed to the lower ESP_min of the –CHF₂ group, which enhances polarity through its local dipole effect.

3.5 Solvation shell radius

Ionic conductivity, a critical indicator for the rate capability of electrolytes, is challenging to calculate computationally. However, understanding the transport mechanisms of Li⁺ cations is instructive for realizing fast ion transport.

Dissolved Li⁺ cation transport occurs through two mechanisms: the (1) vehicular mechanism and (2) structural diffusion mechanism.^139,140 According to the formula of ionic conductivity in electrolyte solutions:

A larger radius of the solvation shell will lead to a lower ionic conductivity. Ue et al. found that the Walden product of electrolyte solutions, which indicates the ion transport ability, has a good reciprocal relationship with the anions' radius¹⁴¹ (Fig. 9a). Thus, smaller anions are preferred to increase the Li⁺ mobility. Lu et al. proposed that solvent molecules forming smaller solvation shells are ideal for building a secondary solvation shell that pulls out the Li⁺ in the primary solvation sheath to create a fast ion-conduction ligand channel and facilitate Li⁺ transport¹⁴² (Fig. 9b–d). In addition, low solvation energy and a low Li⁺ transport energy barrier (E_trans) in electrolyte solution were used to screen out fluoroacetonitrile FAN, which not only accelerated Li⁺ transport but also facilitated the formation of the LiF-rich SEI by allowing the anions to participate in the primary solvation shell.

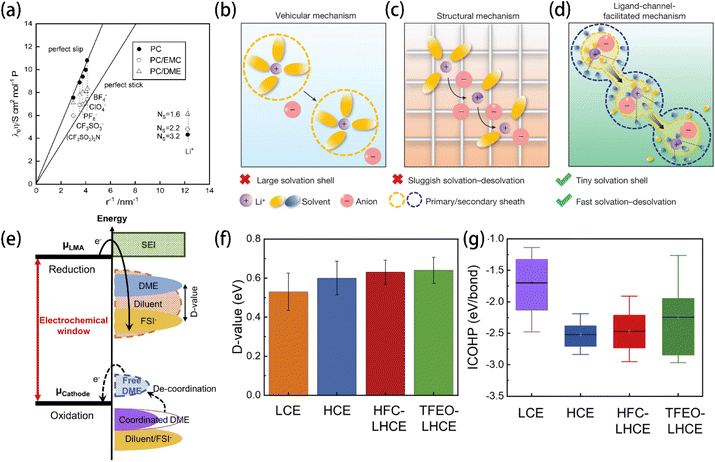Fig. 9 (a) Relationship between the Walden product and the reciprocal of the ionic radius. Reprinted with permission from ref. 141. Copyright 1995 the Electrochemical Society. Schematic illustrations of Li⁺ transport behaviors with the (b) vehicular mechanism, (c) structural diffusion mechanism, and (d) ligand-channel-facilitated mechanism. Reprinted with permission from ref. 142. Copyright 2024 Springer Nature. (e) Schematic open-circuit energy diagram of an LHCE. μ_LMA and μ_Cathode are the anode and cathode electrochemical potentials, respectively. (f) D values and (g) ICOHP of the electrolytes investigated in ref. 134. Reprinted with permission from ref. 134. Copyright 2023 Elsevier.

4 Potential descriptors for electrolyte design

4.1 Local ionization energy (Ī)

While the HOMO is commonly used to describe the oxidative stability of electrolyte components since it indicates the most energetic molecular orbits, Bulat et al.¹⁴³ suggested that the actual location of the most energetic electron is different from the HOMO. Instead, they argued that the local ionization energy at the molecule's surface can reflect its electrophilicity more accurately. Introduced by Sjoberg et al. in 1990,^144,145 average ionization energy represents the energy required to remove an electron at point r in the space from a molecule, and is expressed by using the following equation:
where ρ_i(r) and ε_i are the electron density and energy of species i at the r point, respectively. Bulat et al. showed that surficial Ī(r) not only reflects the molecule's chemical reactivity but also correlates with many other properties, including kinetic energy density, local temperature,^146,147 atomic shell structure,^148,149 electronegativity,¹⁵⁰ local polarizability, hardness,¹⁴⁵ and ESP.¹⁴⁶ Moreover, the average ionization potential has been shown to effectively improve the accuracy of ECW calculation.^34,151 Understanding the local ionization energy of solvent molecules and anions is expected to play a significant role in precisely predicting the solvation structures and properties, making it a valuable tool in electrolyte design.

4.2 E _LUMO difference (D)

The energy levels of molecules' HOMO and LUMO have long been used to reflect the oxidation and reduction stabilities, respectively. A lower HOMO energy indicates that the electrolyte component does not lose its valence electron at higher oxidative potential, and a higher LUMO energy indicates that the electrolyte component accepts external electrons at a lower reductive potential. However, almost no compound can remain stable under the extremely low potential of a lithium metal electrode, resulting in the inevitability of solvent decomposition that forms an organic SEI. Fortunately, the difference between the LUMO energies of solute anions (E_LUMO(anion)) and solvent (E_LUMO(solvent)), referred to as the D value (Fig. 9e), was proposed as an indicator of the reduction preference on the anode surface.¹³⁴ A more positive D value indicates that the anion of lithium salt, instead of the electrolyte solvent, tends to be reduced and decompose prior to the solvent molecules. Therefore, a higher proportion of anion-derived components, rather than solvent-derived components, will be produced in the SEI film. The introduction of the D value reminds one that it is not necessary to require electrolyte solvents to be completely stable to form an inorganic-rich SEI. Instead, prioritizing the reduction of anions over solvents is crucial for ensuring anodic stability. This rule is instructive for designing electrolytes that promote the formation of an inorganic-rich SEI.

4.3 Integrated crystal orbital Hamilton population (ICOHP)

As an indicator of the Li–O interactions in the solvation shell, the ICOHP of the Li–solvent complex reflects the coordination strength between Li⁺ and solvent molecules.^152,153 The bonding and antibonding interactions are presented by the negative and positive sides of the partial crystal orbital Hamilton populations (pCOHPs), respectively.¹⁵⁴ A low ICOHP value indicates a strong coordination and a robust solvation shell, which benefits the oxidative stability. HFC with both a high D-value (Fig. 9f) and low ICOHP (Fig. 9g) was identified for LHCE and showed an excellent cycling stability by forming an FSI-derived SEI.

4.4 Relative solvating power (χ)

The DN and ε are limited in reflecting the solvating ability of different solvents because they overlook the denticity and steric hindrance of solvent molecules. Particularly, the large radius of antinomy in the reference compound (SbCl₅) prevents detailed information of the molecular structure from being revealed by the DN. Relative solvating power (χ) is defined as the ratio of the coordination percentages of a test solvent to that of a reference solvent, and can be expressed as the following equation:
χ shows higher capability revealing the overall effect of molecular structures on solvation. Su et al.¹⁵⁵ used ethyl methyl carbonate (EMC) as a reference solvent by setting its χ value to 1 and determined the χ values of a series of solvents according to their diffusion coefficients. These χ values of the solvents showed good correlation with the CE of cells, validating the accuracy of this descriptor in predicting the solvation structure of electrolytes.

4.5 Dual local softness (Δs_k)

The high-temperature stability of electrolytes is relatively less studied than low-temperature performance. However, the accelerated interfacial reactions of electrolyte solvents play a critical role in the safety and performance degradation of lithium batteries. Meng et al.¹⁵⁶ proposed the dual local softness (Δs_k) as a descriptor that reflects the high-temperature stability of electrolyte solvents more accurately than the HOMO and LUMO. Δs_k is defined as the product of two descriptors: the condensed dual descriptor Δf_k and molecular softness S, which identifies the sites that are most vulnerable to nucleophilic or electrophilic attacks, respectively.¹⁵⁷ A positive Δs_k value indicates a nucleophilic characteristic of the molecular site, and a negative Δs_k value indicates an electrophilic characteristic of the molecular site. The closer Δs_k is to 0, the lower the reactivity of the solvent will be. DFT calculations show that as the terminal alkyl chain lengths of the solvent molecules increase, the Δs_k value becomes closer to 0, indicating a lower high-temperature reactivity. Combined with the screening for high ε, low-reactivity electrolyte solvents were found, and an excellent capacity retention at high temperatures (≥55 °C) was achieved.

5 Summary and perspectives

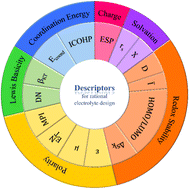
Designing electrolytes that enable fast ion transport and high electrochemical stability in lithium batteries requires rapid screening and identification of optimal electrolyte components. Advances in computer science and computational chemistry have facilitated this process, but understanding the relationship between atomic behaviors and macroscopic properties remains challenging. Identifying descriptors that reveal solvation, coordination, and redox characteristics is crucial for rational electrolyte design. Fig. 10 and Table 1 provide a comprehensive overview of these descriptors. The multiplicity of solvents' functions (i.e., solvating, dissolving, conducting, and maintaining stability) induces difficulty in predicting the overall performance of solvents with any single descriptors. However, just as presented in Fig. 10, each category of properties can be well described by several descriptors, respectively. The responsibility of researchers is to decipher the similarities and distinctions between every couple of descriptors that reflect the same properties, while developing new descriptors that compensates for the disadvantages of the traditional ones will also be valuable.

Fig. 10 Overview of the emerging descriptors for rational electrolyte design.

Table 1 Major features of the reviewed descriptors

Property	Descriptor	Features
Polarity	μ	Adv.: microscopically computable and can be used to predict the solubility of solvents by using their molecular structures
		Disadv.:large inaccuracy is generated from the isolated models that do not take into account intermolecular interactions
	ε	Adv.: easy to be experimentally measured and has a large existing database, reflecting the bulk properties of solvents
		Disadv.: does not take into account intermolecular interactions, and the validity of prediction largely depends on the model used for DFT calculations and MD simulations
	E ^NT	Takes into account the charge transfer between solvent and solute and better agrees with experimental results
	MPI	Adv.: reveals the overlooked local polarity of symmetric molecules and large molecules
Lewis basicity	DN	Adv.: simple definition and high accuracy, reflects the electron donating/accepting interactions between solute and solvent, and DFT computable via appropriate models
		Disadv.: measures isolated molecules; does not take into account hydrogen bonding effects; only applicable for solvents of dilute solution
	β KT	Adv.: measures the bulk of liquid; takes into account hydrogen bonding effects; has a high correlation with Li^+ coordination energy; reflects the coulombic efficiency of cells
		Disadv.: mismatch with DN values for certain nitrogen-containing compounds
Coordination energy	E coord	Adv.: reflects the coordination strength between Li^+ and solvents, which influences the solvation shell structure largely
	ICOHP	Adv.: DFT is computable based on molecular orbit theories, which more accurately predicts the coordination strength and solvation structure
Charge distribution	ESP	Adv.: high accuracy, single-molecule determined, contour plottable for intuitive comparison; bi-axis plottable for fast screening
Solvation shell structure	r s	Adv.: DFT computable for the prediction of Li^+ transport speed; it is simple for fast screening
	χ	Adv.: takes into account the influence of molecular structures of solvents; high accuracy
		Disadv.: non-computable and requires advanced IR-DOSY characterization
Redox stability	HOMO/LUMO	Adv.: simple definition enables estimation of electrolyte component redox stability
		Disadv.: the isolated-molecule approximation neglects the interactions between the components, resulting in large inaccuracy
	Ī	Adv.: corrects the intramolecular position where oxidation takes place to realize higher prediction of oxidation stability and many other properties
	D	Adv.: reflects the preference of reduction on the anode by correlating the LUMO energies of solvent and solute
	Δsk	Adv.: more precisely reflects the high-temperature reactivity of solvent molecules

---

Molecular polarity, predicted by the dielectric constant and dipole moment, helps distinguish between solvating solvents and non-solvating anti-solvents. However, these parameters only reflect nonspecific interactions. In contrast, the normalized molar electron transition energy, determined by energy transitions during solvation, indicates polarity differences that the dielectric constant cannot.

The solvation of Li⁺ involves electron transfer between electrophilic Li⁺ and nucleophilic solvents, determined by their electron donating/accepting abilities (Lewis basicity). The DN and β_KT are successful scales for Lewis basicity. The DN, defined by the enthalpy change of coordination, accurately scales nucleophilicity, while β_KT, based on solvatochromic measurements, better reflects hydrogen bonding effects, which significantly influence solution properties.

Relative solvating power quantitatively measures the ratio of each component in the solvation shell. Additionally, the coordination energy between Li⁺, anions, and solvents helps predict the solvation shell composition, determining the organic/inorganic ratio of the SEI and CEI. ESP of molecules closely correlates with Lewis basicity and polarity, providing a more accurate and flexible description of ion–solvent interactions. ESP_max and ESP_min can be used to screen solvents for specific properties. The solvation shell radius significantly affects Li⁺ transport speed, with smaller anion volumes increasing Li⁺ mobility.

Each descriptor has its advantages and limitations, encouraging the discovery of new descriptors for accurate and efficient electrolyte design. For example, local ionization energy closely estimates redox stability, the D value predicts the reduction sequence of anions and solvents, and ICOHP measures the coordination strength between Li⁺ and solvents. Based on these findings, we summarize the following principles for ideal descriptors in future explorations:

(i) A descriptor shall have a clear and accurate definition to avoid discrepancies in reference data due to misconceptions.

(ii) A descriptor shall be applicable to a wide range of chemical systems, allowing as many types of interactions to be considered as possible.

(iii) A descriptor shall be computable with high accuracy and low computational cost to enable fast and efficient screening of electrolyte components.

Descriptors are crucial for examining the solvation and transport properties of electrolyte compositions, enabling better performance through rational design. However, using a single descriptor does not capture all interactions among cations, anions, solvents, and diluents. Thus, it is more important to flexibly combine different descriptors to predict solvation and transport properties than to develop new ones. Only with a deep understanding of the relationships between descriptors can novel electrolytes be invented and innovative methodologies created.

Accelerating the exploration of new electrolyte formulations requires more than simply screening descriptors. While each descriptor has a clear definition that enables accurate calculations, academia still lacks a unified standard for using these descriptors to evaluate electrolyte performance. For instance, the HOMO and LUMO are widely used to assess the redox stability of solvents. However, comparing two solvents can be challenging when their HOMO and LUMO values are derived from distinct studies, as differences in calculation methods (e.g., functionals and basis sets in DFT calculations) often lead to inconsistencies. This issue, likely affecting all calculation-based descriptors, stems from the diversity of computational approaches and parameters in use. Although calculation accuracy is influenced by computational power—which is not easily standardized across research—there is a clear need for databases or standards. Such resources could define acceptable ranges for common descriptors or provide conversion rules between results from different computational methods. These tools would allow researchers to benchmark their results against published data without wasting resources on redundant calculations. Establishing a unified standard for evaluating electrolyte performance would bring significant benefits to both academic and industrial research. One promising outcome is the potential for AI-assisted design of novel compounds. Given that AI models have already been used to design and predict proteins—far more complex structures than electrolyte solutions¹⁵⁸—it is reasonable to anticipate breakthroughs in discovering unprecedented electrolyte formulations.

Previous research has highlighted discrepancies between calculated descriptors and experimental data, as well as inconsistencies among different descriptors for the same property. For instance, as discussed in the text, there is a mismatch between the DN and β_KT values for certain nitrogen-containing bases. Additionally, the HOMO and LUMO descriptors often fail to accurately reflect the actual locations where electron donation or acceptance occurs. These discrepancies can be partially attributed to differences in how similar descriptors are defined. For example, the DN is defined as the enthalpy change associated with the formation of a solvation adduct with SbCl₅ in dichloroethane, whereas β_KT originates from the solvatochromic shifts in specific solvents. Such fundamental differences in definition can lead to variations in results, making it essential for researchers to carefully consider the context and applicability of the descriptors they use.

To address these issues, two key actions are required. First, researchers aiming to use descriptors for property predictions must thoroughly understand the definitions and assumptions underlying those descriptors, ensuring that the prerequisites for their use align with the intended application. Second, there is a critical need to develop new descriptors that can be applied under universal conditions. While it is neither feasible nor necessary for a single descriptor to capture all properties, it is both achievable and valuable to create descriptors that reliably assess specific properties across diverse compounds. For example, the relative solvating power proposed by Su et al.¹⁵⁵ has demonstrated strong validity in reflecting the CE of electrolytes. Similarly, the D value introduced by Wu et al.¹³⁴ offers a convenient and precise measure of the reduction preference of electrolyte components. These examples illustrate the importance of tailoring descriptors to specific applications, particularly in the context of electrolyte design.

In summary, to accelerate the efficient design of electrolytes, researchers should focus not only on the correct use of existing descriptors but, more importantly, on the invention of new descriptors specifically tailored for electrolyte research. This dual approach will enhance the predictive power and practical utility of descriptors in this critical field.

Data availability

No primary research results, software or code have been included and no new data were generated or analysed as part of this review.

Author contributions

BC: writing-original draft; JX: writing-review & editing, supervision, and project administration.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 52402312), the Environment and Conservation Fund (ECF Project 20/2023), and a Grant from the City University of Hong Kong (Project No. 9610641).

References

1. M. Armand and J. M. Tarascon, Nature, 2008, 451, 652–657.
2. Y. Yang, W. Yang, H. Yang and H. Zhou, eScience, 2023, 3, 100170.
3. O. V. Bushkova, T. V. Yaroslavtseva and Y. A. Dobrovolsky, Russ. J. Electrochem., 2017, 53, 677–699.
4. S. Tan, Y. J. Ji, Z. R. Zhang and Y. Yang, ChemPhysChem, 2014, 15, 1956–1969.
5. Z. Wang, L. Wang, H. Zhang, H. Xu and X. He, Electron, 2024, e41.
6. N. Prasad, A. Mandyam, C. Chivers, M. Draugelis, C. W. Hanson, B. E. Engelhardt and K. Laudanski, J. Pers. Med., 2022, 12, 661.
7. S. Hu and C. Huang, Batteries, 2023, 9, 228.
8. K. Hatakeyama-Sato, T. Tezuka, Y. Nishikitani, H. Nishide and K. Oyaizu, Chem. Lett., 2018, 48, 130–132.
9. L. M. Ghiringhelli, J. Vybiral, S. V. Levchenko, C. Draxl and M. Scheffler, Phys. Rev. Lett., 2015, 114, 105503.
10. Y.-X. Yao, X. Chen, C. Yan, X.-Q. Zhang, W.-L. Cai, J.-Q. Huang and Q. Zhang, Angew. Chem., Int. Ed., 2021, 60, 4090–4097.
11. J. Xu, J. Zhang, T. P. Pollard, Q. Li, S. Tan, S. Hou, H. Wan, F. Chen, H. He, E. Hu, K. Xu, X.-Q. Yang, O. Borodin and C. Wang, Nature, 2023, 614, 694–700.
12. Y. Wu, Q. Hu, H. Liang, A. Wang, H. Xu, L. Wang and X. He, Adv. Energy Mater., 2023, 13, 2300259.
13. C.-B. Jin, N. Yao, Y. Xiao, J. Xie, Z. Li, X. Chen, B.-Q. Li, X.-Q. Zhang, J.-Q. Huang and Q. Zhang, Adv. Mater., 2023, 35, 2208340.
14. N. B. Chapman and J. Shorter, Advances in Linear Free Energy Relationships, Springer, Boston, MA, 1972.
15. W. A. Henderson, F. McKenna, M. A. Khan, N. R. Brooks, V. G. Young Jr and R. Frech, Chem. Mater., 2005, 17, 2284–2289.
16. Y. Yamada and A. Yamada, J. Electrochem. Soc., 2015, 162, A2406.
17. D. M. Seo, O. Borodin, D. Balogh, M. O'Connell, Q. Ly, S.-D. Han, S. Passerini and W. A. Henderson, J. Electrochem. Soc., 2013, 160, A1061.
18. P. Johansson, Phys. Chem. Chem. Phys., 2007, 9, 1493–1498.
19. K. W. Schroder, A. G. Dylla, L. D. C. Bishop, E. R. Kamilar, J. Saunders, L. J. Webb and K. J. Stevenson, J. Phys. Chem. Lett., 2015, 6, 2888–2891.
20. Y. Yamada, K. Furukawa, K. Sodeyama, K. Kikuchi, M. Yaegashi, Y. Tateyama and A. Yamada, J. Am. Chem. Soc., 2014, 136, 5039–5046.
21. Y. Yamada, K. Usui, C. H. Chiang, K. Kikuchi, K. Furukawa and A. Yamada, ACS Appl. Mater. Interfaces, 2014, 6, 10892–10899.
22. Y. Wang, Z. Cao, Z. Ma, G. Liu, H. Cheng, Y. Zou, L. Cavallo, Q. Li and J. Ming, ACS Energy Lett., 2023, 8, 1477–1484.
23. D. E. Goldsack and R. Franchetto, Can. J. Chem., 1977, 55, 1062–1072.
24. K. Xu, Chem. Rev., 2004, 104, 4303–4418.
25. Y. Yamada, J. Wang, S. Ko, E. Watanabe and A. Yamada, Nat. Energy, 2019, 4, 269–280.
26. J. Hou, M. Yang, D. Wang and J. Zhang, Adv. Energy Mater., 2020, 10, 1904152.
27. M. Chen, J. Zhang, X. Ji, J. Fu and G. Feng, Curr. Opin. Electrochem., 2022, 34, 101030.
28. P. Peljo and H. H. Girault, Energy Environ. Sci., 2018, 11, 2306–2309.
29. V. Pande and V. Viswanathan, J. Phys. Chem. Lett., 2019, 10, 7031–7036.
30. O. Borodin, W. Behl and T. R. Jow, J. Phys. Chem. C, 2013, 117, 8661–8682.
31. J. B. Haskins, C. W. Bauschlicher Jr and J. W. Lawson, J. Phys. Chem. B, 2015, 119, 14705–14719.
32. H. Maeshima, H. Moriwake, A. Kuwabara and C. A. J. Fisher, J. Electrochem. Soc., 2010, 157, A696.
33. H. Roohi and K. Ghauri, Thermochim. Acta, 2016, 639, 20–40.
34. E. R. Fadel, F. Faglioni, G. Samsonidze, N. Molinari, B. V. Merinov, W. A. Goddard Iii, J. C. Grossman, J. P. Mailoa and B. Kozinsky, Nat. Commun., 2019, 10, 3360.
35. D. Wang, T. He, A. Wang, K. Guo, M. Avdeev, C. Ouyang, L. Chen and S. Shi, Adv. Funct. Mater., 2023, 33, 2212342.
36. D. E. Goldsack and R. C. Franchetto, Can. J. Chem., 1978, 56, 1442–1450.
37. Y. Zhu, W. Li, L. Zhang, W. Fang, Q. Ruan, J. Li, F. Zhang, H. Zhang, T. Quan and S. Zhang, Energy Environ. Sci., 2023, 16, 2825–2855.
38. T. Zheng, A. S. Gozdz and G. G. Amatucci, J. Electrochem. Soc., 1999, 146, 4014.
39. X. Dong, Y.-G. Wang and Y. Xia, Acc. Chem. Res., 2021, 54, 3883–3894.
40. K. M. Diederichsen, E. J. McShane and B. D. McCloskey, ACS Energy Lett., 2017, 2, 2563–2575.
41. C. Qiu, G. He, W. Shi, M. Zou and C. Liu, J. Solid State Electrochem., 2019, 23, 1887–1902.
42. Z. Li, Y. Zheng, C. Liao, S. Duan, X. Liu, G. Chen, L. Dong, J. Dong, C. Ma, B. Yin, W. Yan and J. Zhang, Adv. Funct. Mater., 2024, 34, 2404427.
43. B. Cui, Z. Xiao, S. Cui, S. Hao, S. Liu, X. Gao and G. Li, ACS Appl. Mater. Interfaces, 2023, 15, 41537–41548.
44. J. Xu, V. Koverga, A. Phan, A. min Li, N. Zhang, M. Baek, C. Jayawardana, B. L. Lucht, A. T. Ngo and C. Wang, Adv. Mater., 2024, 36, 2306462.
45. T. Ma, Y. Ni, Q. Wang, W. Zhang, S. Jin, S. Zheng, X. Yang, Y. Hou, Z. Tao and J. Chen, Angew. Chem., Int. Ed., 2022, 61, e202207927.
46. Q. Li, S. Jiao, L. Luo, M. S. Ding, J. Zheng, S. S. Cartmell, C.-M. Wang, K. Xu, J.-G. Zhang and W. Xu, ACS Appl. Mater. Interfaces, 2017, 9, 18826–18835.
47. Q. Li, D. Lu, J. Zheng, S. Jiao, L. Luo, C.-M. Wang, K. Xu, J.-G. Zhang and W. Xu, ACS Appl. Mater. Interfaces, 2017, 9, 42761–42768.
48. T. Li, X.-Q. Zhang, N. Yao, Y.-X. Yao, L.-P. Hou, X. Chen, M.-Y. Zhou, J.-Q. Huang and Q. Zhang, Angew. Chem., Int. Ed., 2021, 60, 22683–22687.
49. J.-F. Ding, R. Xu, N. Yao, X. Chen, Y. Xiao, Y.-X. Yao, C. Yan, J. Xie and J.-Q. Huang, Angew. Chem., Int. Ed., 2021, 60, 11442–11447.
50. G. Park, K. Lee, D.-J. Yoo and J. W. Choi, ACS Energy Lett., 2022, 7, 4274–4281.
51. Q.-K. Zhang, X.-Q. Zhang, J. Wan, N. Yao, T.-L. Song, J. Xie, L.-P. Hou, M.-Y. Zhou, X. Chen, B.-Q. Li, R. Wen, H.-J. Peng, Q. Zhang and J.-Q. Huang, Nat. Energy, 2023, 8, 725–735.
52. Y. Xiao, R. Xu, L. Xu, J. F. Ding and J. Huang, Energy Mater., 2021, 1(2), 100013.
53. Y. Fan, R. Li, R. Yi, L. Zheng, J. Wang, R. Huang, Z. Gong, Z. Li, J. Qi, X. Liu, X. Fan, Y. Shen and L. Chen, Cell Rep. Phys. Sci., 2023, 4, 101324.
54. M. D. Bhatt and C. O'Dwyer, Curr. Appl. Phys., 2014, 14, 349–354.
55. Q. He, B. Yu, Z. Li and Y. Zhao, Energy Environ. Mater., 2019, 2, 264–279.
56. Y. Sun, T. Yang, H. Ji, J. Zhou, Z. Wang, T. Qian and C. Yan, Adv. Energy Mater., 2020, 10, 2002373.
57. N. Yao, X. Chen, Z.-H. Fu and Q. Zhang, Chem. Rev., 2022, 122, 10970–11021.
58. M. H. Huang, Y. D. Wang, Q. Hou and H. F. Xiang, Prog. Chem., 2023, 35, 1847–1863.
59. M. D. Bhatt and C. O'Dwyer, Phys. Chem. Chem. Phys., 2015, 17, 4799–4844.
60. M. A. Makeev and N. N. Rajput, Curr. Opin. Chem. Eng., 2019, 23, 58–69.
61. L.-T. Wu, Y.-T. Zhan, Z.-L. Li, P.-T. Chen, B. J. Hwang and J.-C. Jiang, J. Mater. Chem. A, 2024, 12, 15792–15802.
62. X. Qin, A. Bhowmik, T. Vegge and I. E. Castelli, ACS Appl. Mater. Interfaces, 2024, 16, 29347–29354.
63. C. Liao, B. Wang, H. Doan, S.-B. Son, D. Abraham, S. Trask, A. Jansen and K. Xu, 2024, Preprint (Version 1) available at Research Square.
64. Z. Wang, L. Wang, H. Zhang, H. Xu and X. He, Nano Convergence, 2024, 11, 8.
65. Y. Nohara, K. Matsumoto, H. Soejima and N. Nakashima, Presented in Part at the Proceedings of the 10th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, Niagara Falls, NY, USA, 2019.
66. A. Dal Corso, S. Baroni and R. Resta, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 49, 5323–5328.
67. A. Courtot-Descharles, F. Pires, P. Paillet and J. L. Leray, Microelectron. Reliab., 1999, 39, 279–284.
68. Z. Tang, C. Chang, F. Bao, L. Tian, H. Liu, M. Wang, C. Zhu and J. Xu, Polymers, 2021, 13, 284.
69. M. Cossi and V. Barone, J. Chem. Phys., 2001, 115, 4708–4717.
70. A. Martin, P. L. Wu, Z. Liron and S. Cohen, J. Pharm. Sci., 1985, 74, 638–642.
71. L. Dong, Y. Liu, K. Wen, D. Chen, D. Rao, J. Liu, B. Yuan, Y. Dong, Z. Wu, Y. Liang, M. Yang, J. Ma, C. Yang, C. Xia, B. Xia, J. Han, G. Wang, Z. Guo and W. He, Advanced Science, 2022, 9, 2104699.
72. Z. Tian, Y. Zou, G. Liu, Y. Wang, J. Yin, J. Ming and H. N. Alshareef, Advanced Science, 2022, 9, 2201207.
73. Z. Xu, K. Deng, S. Zhou, Z. Liu, X. Guan and D. Mo, ACS Appl. Mater. Interfaces, 2022, 14, 48694–48704.
74. X. Chen, X. Q. Zhang, H. R. Li and Q. Zhang, Batteries Supercaps, 2019, 2, 128–131.
75. I. Montes, C. Lai and D. Sanabria, J. Chem. Educ., 2003, 80, 447.
76. B. Zhuang, G. Ramanauskaite, Z. Y. Koa and Z.-G. Wang, Sci. Adv., 2021, 7, eabe7275.
77. D. Rak and M. Sedlák, J. Phys. Chem. B, 2019, 123, 1365–1374.
78. Z. Liu, T. Lu and Q. Chen, Carbon, 2021, 171, 514–523.
79. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
80. T. Lu, J. Chem. Phys., 2024, 161(8), 082503.
81. D.-J. Yoo, S. Yang, K. J. Kim and J. W. Choi, Angew. Chem., Int. Ed., 2020, 59, 14869–14876.
82. J. Moon, D. O. Kim, L. Bekaert, M. Song, J. Chung, D. Lee, A. Hubin and J. Lim, Nat. Commun., 2022, 13, 4538.
83. A. H. Fainberg and S. Winstein, J. Am. Chem. Soc., 1956, 78, 2770–2777.
84. J. A. Berson, Z. Hamlet and W. A. Mueller, J. Am. Chem. Soc., 1962, 84, 297–304.
85. K. Dimroth, C. Reichardt, T. Siepmann and F. Bohlmann, Justus Liebigs Ann. Chem., 1963, 661, 1–37.
86. S. Brownstein, Can. J. Chem., 1960, 38, 1590–1596.
87. A. Allerhand and P. v. R. Schleyer, J. Am. Chem. Soc., 1963, 85, 371–380.
88. C. Reichardt, Angew Chem. Int. Ed. Engl., 1965, 4, 29–40.
89. E. M. Kosower, J. Am. Chem. Soc., 1958, 80, 3253–3260.
90. C. Reichardt, Chem. Rev., 1994, 94, 2319–2358.
91. C. Reichardt, Chem. Soc. Rev., 1992, 21, 147–153.
92. C. Reichardt, Pure Appl. Chem., 2004, 76, 1903–1919.
93. C. Reichardt and E. Harbusch-Görnert, Liebigs Ann. Chem., 1983, 1983, 721–743.
94. C. Reichardt, Org. Process Res. Dev., 2007, 11, 105–113.
95. G. E. Bennett, PhD thesis, The University of Texas at Austin, 1995.
96. S. Chen, J. Zheng, D. Mei, K. S. Han, M. H. Engelhard, W. Zhao, W. Xu, J. Liu and J.-G. Zhang, Adv. Mater., 2018, 30, 1706102.
97. S. Chen, J. Zheng, L. Yu, X. Ren, M. H. Engelhard, C. Niu, H. Lee, W. Xu, J. Xiao, J. Liu and J.-G. Zhang, Joule, 2018, 2, 1548–1558.
98. L. Yu, S. Chen, H. Lee, L. Zhang, M. H. Engelhard, Q. Li, S. Jiao, J. Liu, W. Xu and J.-G. Zhang, ACS Energy Lett., 2018, 3, 2059–2067.
99. X.-T. Yang, C. Han, Y.-M. Xie, R. Fang, S. Zheng, J.-H. Tian, X.-M. Lin, H. Zhang, B.-W. Mao, Y. Gu, Y.-H. Wang and J.-F. Li, Small, 2024, 20, 2311393.
100. M. J. Hossain, Q. Wu, E. J. Marin Bernardez, C. D. Quilty, A. C. Marschilok, E. S. Takeuchi, D. C. Bock, K. J. Takeuchi and Y. Qi, J. Phys. Chem. Lett., 2023, 14, 7718–7731.
101. J. Li, S. Sui, X. Zhou, K. Lei, Q. Yang, S. Chu, L. Li, Y. Zhao, M. Gu, S. Chou and S. Zheng, Angew. Chem., Int. Ed., 2024, 63, e202400406.
102. H. Zheng, Y. Zhong, C. Gu, X. Wang and J. Tu, Batteries Supercaps, 2024, 7, e202400238.
103. X. Cao, H. Jia, W. Xu and J.-G. Zhang, J. Electrochem. Soc., 2021, 168, 010522.
104. B. Nan, et al., Enhancing Li⁺ Transport in NMC811∥Graphite Lithium-Ion Batteries at Low Temperatures by Using Low-Polarity-Solvent Electrolytes, Angew. Chem., Int. Ed., 2022, 61, e202205967.
105. W. R. Fawcett, J. Phys. Chem., 1993, 97, 9540–9546.
106. G. N. Lewis, Valence and the Structure of Atoms and Molecules, Chemical Catalog Company, Incorporated, 1923.
107. C. Laurence, J. Graton and J.-F. Gal, J. Chem. Educ., 2011, 88, 1651–1657.
108. T. M. Krygowski, E. Milczarek and P. K. Wrona, J. Chem. Soc., Perkin Trans. 2, 1980, 1563–1568.
109. W. Gordy and S. C. Stanford, J. Chem. Phys., 1940, 8, 170–177.
110. W. Gordy and S. C. Stanford, J. Chem. Phys., 1941, 9, 204–214.
111. T. Kagiya, Y. Sumida and T. Inoue, Bull. Chem. Soc. Jpn., 2006, 41, 767–773.
112. A. J. Parker, U. Mayer, R. Schmid and V. Gutmann, J. Org. Chem., 1978, 43, 1843–1854.
113. M. Munakata, S. Kitagawa and M. Miyazima, Inorg. Chem., 1985, 24, 1638–1643.
114. V. Gutmann, Electrochim. Acta, 1976, 21, 661–670.
115. R. A. Miranda-Quintana and J. Smiatek, J. Mol. Liq., 2021, 322, 114506.
116. C. V. Amanchukwu, X. Kong, J. Qin, Y. Cui and Z. Bao, Adv. Energy Mater., 2019, 9, 1902116.
117. M. L. Gordin, F. Dai, S. Chen, T. Xu, J. Song, D. Tang, N. Azimi, Z. Zhang and D. Wang, ACS Appl. Mater. Interfaces, 2014, 6, 8006–8010.
118. L. Xiao, Z. Zeng, X. Liu, Y. Fang, X. Jiang, Y. Shao, L. Zhuang, X. Ai, H. Yang, Y. Cao and J. Liu, ACS Energy Lett., 2019, 4, 483–488.
119. J. Chen, H. Zhang, M. Fang, C. Ke, S. Liu and J. Wang, ACS Energy Lett., 2023, 8, 1723–1734.
120. M. J. Kamlet and R. W. Taft, J. Am. Chem. Soc., 1976, 98, 377–383.
121. R. W. Taft and M. J. Kamlet, J. Am. Chem. Soc., 1976, 98, 2886–2894.
122. W. E. Waghorne, Pure Appl. Chem., 2020, 92, 1539–1551.
123. W. Earle Waghorne and C. O'Farrell, J. Solution Chem., 2018, 47, 1609–1625.
124. J. Catalán, C. Díaz, V. López, P. Pérez, J.-L. G. De Paz and J. G. Rodríguez, Liebigs Ann., 1996, 1996, 1785–1794.
125. J. Catalán and C. Díaz, Liebigs Ann., 1997, 1997, 1941–1949.
126. W. E. Waghorne, J. Solution Chem., 2024, 53, 747–760.
127. J. E. Gordon, J. Am. Chem. Soc., 1972, 94, 650–651.
128. M. C. Duboc, Spectrochim. Acta, Part A, 1974, 30, 431–439.
129. J.-F. Gal, P.-C. Maria, M. Yanez and O. Mo, J. Mol. Liq., 2023, 370, 120997.
130. Y. Ugata, R. Tatara, J.-y. Ock, J. Zhang, K. Ueno, M. Watanabe and K. Dokko, J. Phys. Chem. C, 2023, 127, 3977–3987.
131. H. Ji, Z. Wang, Y. Sun, Y. Zhou, S. Li, J. Zhou, T. Qian and C. Yan, Adv. Mater., 2023, 35, 2208590.
132. K. Sodeyama, Y. Igarashi, T. Nakayama, Y. Tateyama and M. Okada, Phys. Chem. Chem. Phys., 2018, 20, 22585–22591.
133. F. Ren, Z. Li, J. Chen, P. Huguet, Z. Peng and S. Deabate, ACS Appl. Mater. Interfaces, 2022, 14, 4211–4219.
134. Z. Wu, R. Li, S. Zhang, L. lv, T. Deng, H. Zhang, R. Zhang, J. Liu, S. Ding, L. Fan, L. Chen and X. Fan, Chem, 2023, 9, 650–664.
135. K. B. Lipkowitz and D. B. Boyd, Reviews in Computational Chemistry, John Wiley Sons. Inc., New York, NY, vol. 3, 1991.
136. J. S. Murray, S. Ranganathan and P. Politzer, J. Org. Chem., 1991, 56, 3734–3737.
137. Z. Yu, H. Wang, X. Kong, W. Huang, Y. Tsao, D. G. Mackanic, K. Wang, X. Wang, W. Huang, S. Choudhury, Y. Zheng, C. V. Amanchukwu, S. T. Hung, Y. Ma, E. G. Lomeli, J. Qin, Y. Cui and Z. Bao, Nat. Energy, 2020, 5, 526–533.
138. Z. Yu, P. E. Rudnicki, Z. Zhang, Z. Huang, H. Celik, S. T. Oyakhire, Y. Chen, X. Kong, S. C. Kim, X. Xiao, H. Wang, Y. Zheng, G. A. Kamat, M. S. Kim, S. F. Bent, J. Qin, Y. Cui and Z. Bao, Nat. Energy, 2022, 7, 94–106.
139. J. Self, K. D. Fong and K. A. Persson, ACS Energy Lett., 2019, 4, 2843–2849.
140. D. J. Siegel, L. Nazar, Y.-M. Chiang, C. Fang and N. P. Balsara, Trends Chem., 2021, 3, 807–818.
141. M. Ue and S. Mori, J. Electrochem. Soc., 1995, 142, 2577.
142. D. Lu, R. Li, M. M. Rahman, P. Yu, L. Lv, S. Yang, Y. Huang, C. Sun, S. Zhang, H. Zhang, J. Zhang, X. Xiao, T. Deng, L. Fan, L. Chen, J. Wang, E. Hu, C. Wang and X. Fan, Nature, 2024, 627, 101–107.
143. F. A. Bulat, J. S. Murray and P. Politzer, Comput. Theor. Chem., 2021, 1199, 113192.
144. P. Sjoberg, J. S. Murray, T. Brinck and P. Politzer, 100 Years of CSC in the Pages of CJC, Can. J. Chem., 2017, 1(1), 1440–1443.
145. P. Politzer, J. S. Murray and F. A. Bulat, J. Mol. Model., 2010, 16, 1731–1742.
146. F. A. Bulat, M. Levy and P. Politzer, J. Phys. Chem. A, 2009, 113, 1384–1389.
147. P. W. Ayers, R. G. Parr and A. Nagy, Int. J. Quantum Chem., 2002, 90, 309–326.
148. Á. Nagy, R. G. Parr and S. Liu, Phys. Rev. A, 1996, 53, 3117–3121.
149. P. Politzer, J. S. Murray, M. E. Grice, T. Brinck and S. Ranganathan, J. Chem. Phys., 1991, 95, 6699–6704.
150. P. Politzer, Z. Peralta-Inga Shields, F. A. Bulat and J. S. Murray, J. Chem. Theory Comput., 2011, 7, 377–384.
151. J. Wang and Y. Wang, J. Phys. Chem. B, 2024, 128, 1943–1952.
152. S. Perez Beltran, X. Cao, J.-G. Zhang and P. B. Balbuena, Chem. Mater., 2020, 32, 5973–5984.
153. V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466.
154. R. Nelson, C. Ertural, J. George, V. L. Deringer, G. Hautier and R. Dronskowski, J. Comput. Chem., 2020, 41, 1931–1940.
155. C.-C. Su, M. He, R. Amine, T. Rojas, L. Cheng, A. T. Ngo and K. Amine, Energy Environ. Sci., 2019, 12, 1249–1254.
156. T. Meng, S. Yang, Y. Peng, P. Li, S. Ren, X. Yun and X. Hu, Adv. Energy Mater., 2024, 2404009.
157. C. Morell, A. Grand and A. Toro-Labbé, J. Phys. Chem. A, 2005, 109, 205–212.
158. The Nobel Prize in Chemistry 2024, https://www.nobelprize.org/prizes/chemistry/2024/summary/, (accessed Thu. 21 Nov 2024, 2024).

---