 Open Access Article
Open Access ArticleRoom-temperature barocaloric effect in [Fe(pap-5NO2)2] spin-crossover material†
David Gracia *ab,
Vera Cuartero
*ab,
Vera Cuartero ac,
Catalin Popescu
ac,
Catalin Popescu d,
Adelais Trapali
d,
Adelais Trapali e,
Talal Mallah
e,
Talal Mallah e,
Marie-Laure Boillote,
Javier Blasco
e,
Marie-Laure Boillote,
Javier Blasco ab,
Gloria Subías
ab,
Gloria Subías ab and
Marco Evangelisti
ab and
Marco Evangelisti ab
ab
aInstituto de Nanociencia y Materiales de Aragón (INMA), CSIC-Universidad de Zaragoza, 50009 Zaragoza, Spain. E-mail: davidg@unizar.es
bDepartamento de Física de la Materia Condensada, Universidad de Zaragoza, Calle Pedro Cerbuna 12, 50009 Zaragoza, Spain
cDepartamento de Ciencia y Tecnología de Materiales y Fluidos, EINA, Universidad de Zaragoza, Calle María de Luna 3, 50018 Zaragoza, Spain
dCELLS – ALBA Synchrotron, 08290 Cerdanyola del Valles, Barcelona, Spain
eInstitut de Chimie Moléculaire et des Matériaux d’Orsay, CNRS UMR 8182, Université Paris-Saclay, 17, avenue des Sciences, 91400 Orsay, France
First published on 13th May 2025
Abstract
We examine the pressure dependence of the spin-crossover transition in [Fe(pap-5NO2)2] that occurs near room temperature. We employ a combination of high-pressure calorimetry and powder X-ray diffraction measurements, conducted both under variable-pressure and variable-temperature conditions. Both methods indicate that the spin-crossover transition shifts linearly to higher temperatures with increasing pressure, while simultaneously exhibiting an increase in the width of the thermal hysteresis. We report a giant barocaloric effect, revealing isothermal entropy changes in the 70–79 J kg−1 K−1 range and adiabatic temperature changes between 20 and 26 K for a pressure change of 2.0 kbar. Although the effect diminishes under reversible conditions, it remains substantial, with values of 70 J kg−1 K−1 and 14 K, respectively.
1 Introduction
Solid-state refrigeration is emerging as a promising alternative to traditional refrigeration systems that operate on the compression and expansion of greenhouse gases.1,2 This technology is based on the principle of the caloric effects, which refer to the reversible thermal changes in isothermal entropy, ΔST, and adiabatic temperature, ΔTad, following the application (or removal) of an external field. In particular, the BaroCaloric Effect (BCE) allows certain materials to respond to changes in the hydrostatic pressure, Δp. Recently, near-room-temperature barocaloric refrigeration has gained significant attention, primarily due to the observation of larger values of ΔST and ΔTad than those found in other caloric materials.3–5 For scalable barocaloric refrigeration to become a reality, it is crucial to identify materials that undergo first-order solid–solid phase transitions that are highly sensitive to pressure, while being accompanied by high entropy and volume changes. Furthermore, maintaining a low thermal hysteresis ensures optimal performance during pressure cycling.6Spin-CrossOver (SCO) compounds have been identified as excellent barocaloric materials.7 SCO transitions typically occur in octahedrally coordinated FeII complexes with a 3d6 electronic configuration. These transitions involve a shift between a diamagnetic Low-Spin (LS, s = 0) state and a paramagnetic High-Spin (HS, s = 2) state.8,9 A notable characteristic of these transitions is the large unit-cell volume change that arises due to the reversible shortening (lengthening) of the FeII bond lengths during the SCO process.10 This property makes SCO transitions particularly sensitive to changes in pressure.11 In recent years, large BCE responses have been predicted to take place at the SCO transition temperature of various FeII compounds.12–15 However, only a limited number of SCO compounds have been thoroughly explored using high-pressure calorimetry techniques.16–20
Here, we focus on the FeII Schiff-base SCO compound [Fe(pap-5NO2)2] (Fig. 1), with chemical formula C24H16FeN6O6, where the ligand Hpap-5NO2 is the condensation product of pyridine-2-carbaldehyde with 2-hydroxy-5-nitroaniline. As previously reported,21 [Fe(pap-5NO2)2] showcases a highly cooperative first-order SCO transition that occurs around room temperature. This transition is marked by a significant volume change occurring between two isostructural monoclinic phases (space group C2/c). Upon heating, the monoclinic unit cell undergoes an abrupt expansion of the b axis coupled to a shrinkage of the a axis, and an increase of the monoclinic distortion. Differential Scanning Calorimetry (DSC) measurements conducted at ambient pressure have estimated a total entropy change of ΔSSCO ≈ 56 J kg−1 K−1 during the SCO transition. In this work, we utilize high-pressure calorimetry and Synchrotron X-ray Powder Diffraction (SXRPD) measurements to investigate the pressure dependence of the thermal and structural properties throughout the SCO transition in [Fe(pap-5NO2)2]. The SXRPD experiments are performed under isothermal and variable-pressure conditions. Additionally, X-ray Powder Diffraction (XRPD) patterns are collected at our home laboratory under variable temperature and ambient-pressure conditions. Using calorimetric and structural data, we have identified a remarkably large BCE near ambient temperature in [Fe(pap-5NO2)2].
 | ||
| Fig. 1 View of the molecular structure of [Fe(pap-5NO2)2], (oxygen atoms, red; nitrogen atoms, blue), H atoms were removed for clarity. | ||
2 Materials and methods
The polycrystalline [Fe(pap-5NO2)2] powder sample was prepared under dry and anaerobic conditions by an experimental procedure based on a previously employed route.21 Specifically, Hpap-5NO2 (129 mg, 0.53 mmol) was dissolved in 30 mL of a DCM/MeOH (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 v/v) solution containing 73.9 μL of Et3N (53.6 mg, 0.53 mmol). The obtained mixture was layered with 10 mL of MeOH, to which 10 mL of FeBF4·6H2O (89.5 mg, 0.265 mmol) methanolic solution was carefully placed on top. [Fe(pap-5NO2)2] was obtained as needle-like violet crystals within approximately 10 days, which were carefully collected via cannula filtration and further washed with aliquots of MeOH (63 mg, 44%). The resulting powder was checked with XRPD measurements (Fig. S1†), using a Philips PANalytical X'Pert Pro MPD diffractometer at Cu Kα radiation, equipped with a fast detector within the 5–43° 2θ range. A soft grinding was applied to the dry samples to homogenize and reduce the grain size.
2 v/v) solution containing 73.9 μL of Et3N (53.6 mg, 0.53 mmol). The obtained mixture was layered with 10 mL of MeOH, to which 10 mL of FeBF4·6H2O (89.5 mg, 0.265 mmol) methanolic solution was carefully placed on top. [Fe(pap-5NO2)2] was obtained as needle-like violet crystals within approximately 10 days, which were carefully collected via cannula filtration and further washed with aliquots of MeOH (63 mg, 44%). The resulting powder was checked with XRPD measurements (Fig. S1†), using a Philips PANalytical X'Pert Pro MPD diffractometer at Cu Kα radiation, equipped with a fast detector within the 5–43° 2θ range. A soft grinding was applied to the dry samples to homogenize and reduce the grain size.
Variable-pressure isothermal SXRPD measurements were conducted at the Materials Science and Powder Diffraction (MSPD) beamline of the ALBA synchrotron.22 Polycrystalline sample was dispersed in Daphne oil 7373 and loaded in a membrane-free diamond anvil cell for the experiments. We used Daphne oil 7373 as the pressure transmitting medium because above room temperature it remains hydrostatic up to ∼22 kbar.23 Pressure was determined using the NaCl equation of state.24 The sample temperature was controlled by a combination of a resistive heater and a K-type thermocouple. Data were collected across the pressure range from 0 to 6 kbar along with three distinct isotherms ranging from 310 to 330 K, using a monochromatic beam with wavelength 0.4246 Å and a spot size of 15 μm × 15 μm at full width at half-maximum. For each isotherm, fresh sample was loaded in the membrane-free diamond anvil cell. A SX165 Rayonix MarCCD detector was used to collect the diffraction patterns. They were measured in the angular 2θ range from 2° to 14°, and integrated into conventional X-ray diffraction patterns using the software DIOPTAS.25 Additionally, variable-temperature isobaric XRPD characterization at ambient pressure was performed, covering the temperature range from 220 to 370 K with a Rigaku D-Max system using Cu Kα1,2 wavelengths. Le Bail refinements were executed using the Fullprof program,26 with refined parameters including the 2θ offset and unit-cell parameters to assess volume changes between the LS and HS phases.
High-pressure calorimetry experiments were carried out using a custom-built calorimeter implemented inside a piston-cylinder CuBe high-pressure cell. A Surface Mount Device (SMD) resistor of 1 kΩ (±1% tolerance) was utilized both as sample-holder and pressure sensor, while Daphne oil 7373 served as the hydrostatic pressure-transmitting medium. The entire system was housed in a liquid-nitrogen-based cryostat, Oxford Instruments OptistatDN, which operates within the temperature range from 77 to 400 K. The sample, in powder form, was mixed in a 50–50% ratio with Apiezon H grease to create a slurry weighing a few milligrams. Magnetization measurements, collected with a Quantum Design PPMS DynaCool equipped with the vibrating sample magnetometer option, discarded adverse effects on [Fe(pap-5NO2)2] from the use of Apiezon H (Fig. S2†). The temperature dependence of the isobaric heat capacity at various pressures was derived from continuously recording the temperature of the sample with a K-type thermocouple (±0.75% accuracy) in contact with the sample, complemented by a Pt100 sensor (class A with ±0.15 K tolerance) positioned outside the pressure cell. These sets of data, hereafter denoted as thermograms,27 were collected in arbitrary units during heating and cooling ramps of ±5 K min−1. Absolute values were obtained by calibrating the ambient-pressure data with previously reported DSC measurements with a TA Instruments Q-20a.21 An indirect estimation of ΔST and ΔTad was performed in accordance with standard thermodynamic formulations.28
3 Results and discussion
3.1 X-ray powder diffraction at ambient pressure
As anticipated, [Fe(pap-5NO2)2] undergoes a thermally induced transition between the LS and HS phases as it approaches approximately 300 K at ambient pressure.21 Fig. 2 shows examples of XRPD patterns collected before and after the SCO transition. The monoclinic C2/c structure is preserved upon heating. At the SCO transition temperature, we observe a notable isobaric volume change of ΔVp = 48 ± 4 Å3 for Z = 4 (Fig. 3), which corresponds to 2.3% of the total volume. The volume thermal expansion coefficient, defined as
 | (1) |
Assuming that at the SCO transition temperature the transformation from spin states s = 0 to s = 2 is fully realized, the magnetic entropy change is given by ΔSm = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(2s + 1) = 25 J kg−1 K−1.21 Therefore, the remaining entropy (∼30 J kg−1 K−1) up to the total entropy change at the SCO transition, determined from DSC measurements,21 must be attributed to the entropy change associated with crystal lattice vibrations and molecular distortions. This contribution is estimated as
ln(2s + 1) = 25 J kg−1 K−1.21 Therefore, the remaining entropy (∼30 J kg−1 K−1) up to the total entropy change at the SCO transition, determined from DSC measurements,21 must be attributed to the entropy change associated with crystal lattice vibrations and molecular distortions. This contribution is estimated as
 | (2) |
![[small beta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c3.gif) and
and ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) represent the average thermal expansion and isothermal compressibility near the SCO transition, respectively.29 To determine
represent the average thermal expansion and isothermal compressibility near the SCO transition, respectively.29 To determine ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) , we have investigated the pressure dependence of the SCO transition by SXRPD measurements.
, we have investigated the pressure dependence of the SCO transition by SXRPD measurements.
3.2 Synchrotron powder X-ray diffraction at variable pressure
The isothermal variable-pressure SXRPD measurements were conducted alongside three isotherms at 310, 320 and 330 K. At ambient pressure, for each isotherm, [Fe(pap-5NO2)2] exhibited characteristics consistent with its pure HS phase. As the pressure was increased, the SCO transition to the LS phase was induced. This behavior is depicted in Fig. 4 for the isotherm recorded at 320 K, as a matter of illustration. As can be seen, a change of pressure of ∼1.5 kbar under compression, namely from 1.7 to 3.2 kbar, induces a complete transformation between the HS and LS states. Conversely, a similar but reversed change of ∼1.3 kbar under decompression, from 1.4 to 0.1 kbar, drives the complete transformation from LS to HS states.To evaluate the pressure hysteresis, we display the isothermal pressure–volume, p–V, dependence of [Fe(pap-5NO2)2] at the three measured temperatures during both compression and decompression in Fig. 5(a–c). Volume data are presented only when the material is in a single phase due to the uncertainty associated with extracting reliable unit-cell parameters from the powder patterns within the phase coexistence region. Nevertheless, we could approximately determine the molar fraction of each phase when a coexistence of HS and LS phases was identified, as illustrated in Fig. 5(d) for 320 K (see Fig. S3† for the molar fraction plots at 310 and 330 K). As clearly seen, the pressure required to trigger the transition rises with increasing temperature, accompanied by a notable pressure hysteresis. The variations of the lattice parameters during the s = 2 to s = 0 transformation under pressure are qualitatively like those of the SCO thermal process (Fig. S4†).21
The isothermal compressibility has been calculated as
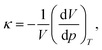 | (3) |
Finally, applying eqn (2) to the values obtained from the combined SXRPD/XRPD experiments allows calculating the lattice entropy change, ΔSv = 27 ± 3 J kg−1 K−1. This result aligns well with the anticipated values derived from the DSC estimations,21 validating our approach.
3.3 High-pressure calorimetry
We measured several thermograms, dQ/dT, under isobaric conditions up to p = 2.0 kbar (Fig. 6). For each pressure, a sharp, dominant peak identifies the transition between the LS and HS phases. The thermograms were systematically scanned twice as the first thermal cycle resulted in a significant irreversibility (representative data in Fig. S5†), as previously observed.21 The data shown in Fig. 6 correspond to the measurements collected during the second thermal cycle. Most likely, the irreversibility is ascribed to the sample microstructure as the volume change at the phase transition should impose a realigning torque on the crystallites during the first cycle.32 The irreversibility is strongly suppressed on subsequent cycles and restored after each pressure change. In addition to the main peak, we observe satellite anomalies (Fig. 6). These are likely rooted in the same microstructural characteristics. When the SCO phenomenon is accompanied by strong cooperativity, as in [Fe(pap-5NO2)2], the ensuing phase transition is highly influenced by the anisotropy of properties and shape of the sample crystallites. This relationship has been elegantly demonstrated through optical microscopy on single-crystal samples of similar materials.33 It is essential to note that we carefully prepared our samples without significant grinding to preserve the integrity of the spin-crossover features.34 Therefore, it is not surprising that our precise measurements, taken at relatively slow rates, have detected these secondary anomalies. Crucially, these anomalies represent less than 5% of the total entropy content, which remains consistent across different isobaric runs, underscoring the reliability of the results. The increase in pressure plays a significant role in stabilizing the LS state, which is characterized by a smaller volume. This increase also causes the endothermal and exothermal peaks to shift to higher temperatures, in accordance with the predictions of the Clausius–Clapeyron equation and the observation of a positive ΔVp during heating.35 | ||
| Fig. 6 Isobaric thermograms of [Fe(pap-5NO2)2] at different pressures, during heating (endothermal) and cooling (exothermal), upon baseline subtraction. | ||
We present the complete phase diagram for [Fe(pap-5NO2)2] (Fig. 7), integrating data from both high-pressure calorimetry and variable-pressure SXRPD measurements. The transition temperatures are identified at the peaks of the thermograms as well as at the even mixtures (50%) of both phases in the variable-pressure SXRPD measurements. The SCO transition shifts linearly to higher temperatures as pressure increases. Notably, the slope of temperature with respect to pressure, denoted as dT/dp, varies between the LS to HS and HS to LS transitions. In the first case, i.e., isobaric heating and isothermal decompression, the value obtained is (dT/dp)heat = 22 ± 2 K kbar−1. Conversely, in the second case, i.e., isobaric cooling and isothermal compression, the slope is (dT/dp)cool = 10 ± 1 K kbar−1. This disparity results in an increase in thermal hysteresis with rising applied pressure. This behavior contrasts with what is typically observed in most barocaloric materials, where thermal hysteresis tends to diminish with increasing pressure. However, the phenomenon seen in [Fe(pap-5NO2)2] has been documented in other studies involving SCO materials,36,37 and can be attributed to the interplay between the effects of applied pressure, which acts on both the ligand field and the strength of the elastic interactions.38
3.4 Determination of the barocaloric effect
The isobaric entropy is determined using calorimetric data and the volume thermal expansion at ambient pressure (p = p0). This is achieved by applying the expression:28
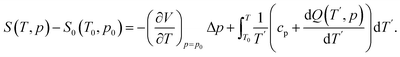 | (4) |
The first term in eqn (4) is used to calculate the pressure dependence of the heat capacity from absolute zero up to the reference temperature T0 = 270 K, utilizing the Maxwell relations. A value of
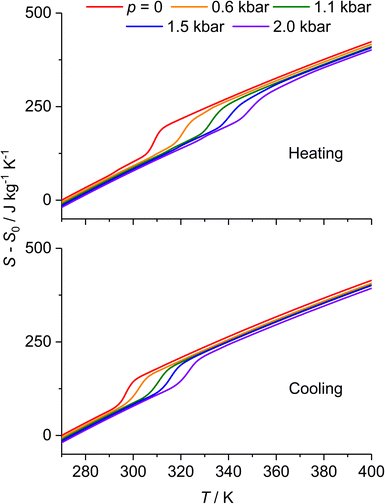 | ||
| Fig. 8 Isobaric entropy of [Fe(pap-5NO2)2] at several pressures during heating (top) and cooling (bottom). | ||
From the entropy curves, we compute the isothermal entropy change, ΔST, and the adiabatic temperature change, ΔTad, for any pressure change Δp = p − p0 ≈ p during both compression (represented by cooling entropy curves) and decompression (represented by heating entropy curves), as follows
| ΔST = [S(T, p) − S(T, p0)]T | (5) |
| ΔTad = [T(S, p) − T(S, p0)]S. | (6) |
Notably, maxima in both |ΔST| and |ΔTad| are observed when the pressure change induces the SCO transition (Fig. 9). For Δp = 2.0 kbar, |ΔST| reaches 79 ± 4 J kg−1 K−1 on decompression and 70 ± 4 J kg−1 K−1 on compression, with the primary contribution stemming from the entropy change ΔSSCO. In conjunction, for the same pressure change, |ΔTad| ranges between 20 ± 2 and 26 ± 2 K for compression and decompression, respectively. The asymmetry of the BCE arises from the difference in slope between (dT/dp)heat and (dT/dp)cool.
 | ||
| Fig. 9 Irreversible isothermal entropy change ΔST (top) and adiabatic temperature change ΔTad (bottom), during compression and decompression, for [Fe(pap-5NO2)2]. | ||
For practical applications, evaluating the BCE under cycling conditions is crucial. The condition of reversibility is achieved only when the pressure exceeds the reversibility pressure, denoted as prev, i.e., the minimum pressure necessary to overcome the thermal hysteresis, ΔThyst. Note that pressures slightly above prev are typically needed to achieve a reversible ΔTad.6 The reversibility pressure can be estimated using the expression prev = ΔThyst/(dT/dp)cool, where (dT/dp)cool represents the slope of the phase diagram during cooling or compression. For [Fe(pap-5NO2)2], an estimated value of prev is approximately 1.2 kbar. Next, we compute the reversible values of the BCE figures of merit for the pressure change of Δp = 2.0 kbar (Fig. 10). The isothermal entropy change, ΔSrevT, is calculated as the overlap between ΔST obtained upon compression and decompression.17,39 The adiabatic temperature change is deduced as follows,6
| ΔTrevad = [T(Scool, p) − T(Sheat, p0)]S. | (7) |
It is noteworthy that the thermal hysteresis observed in [Fe(pap-5NO2)2] leads to a reduction of the BCE during cycling. This is particularly pronounced in the adiabatic temperature change, which exhibits a substantial decrease from over 20 K to a reversible change of ΔTrevad = 14 ± 2 K. Conversely, the isothermal entropy change shows a minor reduction in its maximum value, decreasing from 79 to 70 J kg−1 K−1 for Δp = 2.0 kbar, as depicted in Fig. 10.
As a benchmark for evaluating the barocaloric efficiency of a material, the Coefficient of Refrigerant Performance (CRP) is often utilized. This is defined by CRP = |ΔSrevTΔTrevad/W|, where the input work W can be approximated by W = 1/2pΔV. For [Fe(pap-5NO2)2], the CRP yields 0.7 under a pressure change of Δp = 2.0 kbar.
Barocaloric materials exhibit a complex landscape of structural compositions. For those keen on comparing the efficiency metrics typical of various material classes, we recommend exploring recent review publications.4,40 One noteworthy addition to the field is [Fe(pap-5NO2)2], which enhances the category of SCO materials proposed as effective barocaloric refrigerants. The values of ΔST and ΔTad observed in [Fe(pap-5NO2)2] surpass those found in most SCO compounds.12–16,41 However, this area of research has experienced rapid advancements, with very promising candidate SCO materials being reported since 2021. For a comprehensive overview, Table 1 outlines the current state-of-the-art in barocaloric SCO compounds, showcasing the calculated reversible values of key figures of merit. To enhance clarity and enable a more straightforward comparison, Table 1 also includes representatives from other families of barocaloric materials, namely superionic conductors, plastic crystals, molecular crystals, hybrid organic–inorganic perovskites and shape-memory alloys. While [Fe(pap-5NO2)2] exhibits the lowest BCE when compared to SCO compounds with smaller thermal hysteresis,17,19 it stands out due to its operational temperatures (Tmax) being closer to room temperature, underscoring its potential in practical applications.
| ΔSrevT | ΔTrevad | CRP | Tmax | Δp | Ref. | |
|---|---|---|---|---|---|---|
| Fe3(bntrz)6(tcnset)6 | 115 | 30 | 1.7 | 360 | 2.0 | 17 |
| Fe[HB(tz)3]2 | 92 | 2 | 1.3 | 334 | 0.15 | 18 |
| [Fe(L)(NCS)2] | 114 | 16 | 2.0 | 280 | 1.0 | 19 |
| [Fe(pz)2(BH3CN)2] | 103 | 0 | 0 | 342 | 1.0 | 20 |
| [Fe(pap-5NO2)2] | 70 | 14 | 0.7 | 310 | 2.0 | This work |
| AgI | 60 | 18 | 1.2 | 395 | 2.5 | 42 |
| NPG | 510 | 30 | 1.0 | 330 | 5.7 | 43 and 44 |
| C60 | 32 | 10 | 1.3 | 260 | 1.0 | 45 |
| (C10H21NH3)2MnCl4 | 250 | 12 | 0.9 | 315 | 1.0 | 46 |
| (MnNiGe)0.91(FeCoGe)0.09 | 19 | 4 | 0.1 | 290 | 1.0 | 47 |
4 Conclusions
We have investigated the barocaloric properties of the [Fe(pap-5NO2)2] Schiff-base compound, which is characterized by a first-order SCO transition occurring near room temperature. Through calorimetry and powder X-ray diffraction experiments at different pressures, we have observed giant BCE figures of merit as large as ΔST = 79 J kg−1 K−1 and ΔTad = 26 K for a pressure change of Δp = 2.0 kbar. The presence of hysteresis results in a decrease in the reversible BCE during the cycling process, with ΔSrevT = 70 J kg−1 K−1 and ΔTrevad = 14 K at Δp = 2.0 kbar. This highlights the impact of thermal hysteresis on the barocaloric performance of this class of materials, showcasing the complexities involved in its thermal behavior.Data availability
All data presented in this article can be retrieved from DIGITAL.CSIC at https://doi.org/10.20350/digitalCSIC/16990.Author contributions
David Gracia (writing – original draft, data curation, validation, investigation, methodology, formal analysis), Vera Cuartero (methodology, data curation, validation, investigation, formal analysis, writing – review & editing), Catalin Popescu (data curation, validation), Adelais Trapali (data curation, validation), Talal Mallah (conceptualization, investigation), Marie-Laure Boillot (supervision, validation, investigation, writing – review & editing), Javier Blasco (data curation, validation, investigation), Gloria Subías (funding acquisition, supervision, data curation, validation, investigation, formal analysis, writing – review & editing), Marco Evangelisti (conceptualization, supervision, writing – review & editing, data curation, validation, investigation).Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by MICIU/AEI/10.13039/501100011033 and ERDF/UE (PID2021-124734OB-C21, CEX2023-001286-S), Gobierno de Aragón (E11-23R, E12-23R) and Fundación IberCaja and Universidad de Zaragoza (JIUZ2023-CIE-05). D. G. acknowledges financial support from the Gobierno de Aragón through a doctoral fellowship. The authors acknowledge the Servicio General de Apoyo a la Investigación from Universidad de Zaragoza, ALBA synchrotron for granting beamtime (experiment no. 2023027379), and MSPD beamline staff for experimental and technical support.References
- X. Moya, S. Kar-Narayan and N. D. Mathur, Nat. Mater., 2014, 13, 439–450 CrossRef CAS.
- I. Takeuchi and K. Sandeman, Phys. Today, 2015, 68, 48–54 CrossRef CAS.
- D. Boldrin, Appl. Phys. Lett., 2021, 118, 170502 CrossRef CAS.
- P. Lloveras and J. L. Tamarit, MRS Energy Sustainability, 2021, 8, 3–15 Search PubMed.
- L. Mañosa and A. Planes, Appl. Phys. Lett., 2020, 116, 050501 CrossRef.
- A. Aznar, P. Lloveras, M. Barrio, P. Negrier, A. Planes, L. Mañosa, N. D. Mathur, X. Moya and J. L. Tamarit, J. Mater. Chem. A, 2020, 8, 639–647 Search PubMed.
- K. G. Sandeman, APL Mater., 2016, 4, 111102 CrossRef.
- P. Gütlich and H. A. Goodwin, Spin Crossover in Transition Metal Compounds I, Springer Science & Business Media, New York City, 2004 Search PubMed.
- M. Nishino, Y. Singh, K. Boukheddaden and S. Miyashita, J. Appl. Phys., 2021, 130, 141102 CrossRef CAS.
- P. Guionneau, Dalton Trans., 2014, 43, 382–393 RSC.
- P. J. von Ranke, Appl. Phys. Lett., 2017, 110, 181909 CrossRef.
- P. J. von Ranke, B. P. Alho, R. M. Ribas, E. P. Nobrega, A. Caldas, V. S. R. de Sousa, M. V. Colaço, L. F. Marques, D. L. Rocco and P. O. Ribeiro, Phys. Rev. B, 2018, 98, 224408 CrossRef CAS.
- P. J. von Ranke, B. P. Alho and P. O. Ribeiro, J. Alloys Compd., 2018, 749, 556–560 CrossRef CAS.
- P. J. von Ranke, B. P. Alho, E. P. Nobrega, A. Caldas, V. S. R. de Sousa, M. V. Colaço, L. F. Marques, G. M. Rocha, D. L. Rocco and P. O. Ribeiro, J. Magn. Magn. Mater., 2019, 489, 165421 CrossRef CAS.
- P. J. von Ranke, B. P. Alho, P. H. S. da Silva, R. M. Ribas, E. P. Nobrega, V. S. R. de Sousa, A. M. G. Carvalho and P. O. Ribeiro, Phys. Status Solidi B, 2021, 258, 2100108 Search PubMed.
- S. P. Vallone, A. N. Tantillo, A. M. dos Santos, J. J. Molaison, R. Kulmaczewski, A. Chapoy, P. Ahmadi, M. A. Halcrow and K. G. Sandeman, Adv. Mater., 2019, 31, 1807334 CrossRef PubMed.
- M. Romanini, Y. Wang, K. Gürpinar, G. Ornelas, P. Lloveras, Y. Zhang, W. Zheng, M. Barrio, A. Aznar, A. Gràcia-Condal, B. Emre, O. Atakol, C. Popescu, H. Zhang, Y. Long, L. Balicas, J. L. Tamarit, A. Planes, M. Shatruk and L. Mañosa, Adv. Mater., 2021, 33, 2008076 CrossRef CAS PubMed.
- J. Seo, J. D. Braun, V. M. Dev and J. A. Mason, J. Am. Chem. Soc., 2022, 144, 6493–6503 CrossRef CAS PubMed.
- M. Seredyuk, R. Li, K. Znovjyak, Z. Zhang, F. J. Valverde-Muñoz, B. Li, M. C. Muñoz, Q. Li, B. Liu, G. Levchenko and J. A. Real, Adv. Funct. Mater., 2024, 2315487 CrossRef CAS.
- R. Li, Z. Zhang, Y. S. Bibik, I. A. Gural'skiy, I. V. Zatovsky, Z. Liu, Q. Li, B. Li, G. Levchenko and B. Liu, Appl. Phys. Lett., 2024, 124, 122202 CrossRef CAS.
- O. Iasco, E. Riviere, R. Guillot, M. Buron-Le Cointe, J. F. Meunier, A. Bousseksou and M. L. Boillot, Inorg. Chem., 2015, 54, 1791–1799 CrossRef CAS.
- F. Fauth, I. Peral, C. Popescu and M. Knapp, Powder Diffr., 2013, 28, S360–S370 CrossRef CAS.
- K. Yokogawa, Jpn. J. Appl. Phys., 2007, 46, 3636 CrossRef CAS.
- P. I. Dorogokupets and A. Dewaele, High Pressure Res., 2007, 27, 431 CrossRef CAS.
- C. Prescher and V. B. Prakapenka, High Pressure Res., 2015, 35, 223–230 CrossRef CAS.
- J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55–69 CrossRef.
- D. J. David, Anal. Chem., 1964, 36, 2162–2166 CrossRef CAS.
- E. Stern-Taulats, A. Gràcia-Condal, A. Planes, P. Lloveras, M. Barrio, J. L. Tamarit, S. Pramanick, S. Majumdar and L. Mañosa, Appl. Phys. Lett., 2015, 107, 152409 CrossRef.
- R. Sandrock and G. M. Schneider, Bunsenges. Phys. Chem., 1983, 87, 197–201 CrossRef CAS.
- M. Mikolasek, M. D. Manrique-Juarez, H. J. Shepherd, K. Ridier, S. Rat, V. Shalabaeva, A. C. Bas, I. E. Collings, F. Mathieu, J. Cacheux, T. Leichle, L. Nicu, W. Nicolazzi, L. Salmon, G. Molnár and A. Bousseksou, J. Am. Chem. Soc., 2018, 140, 2970–8979 CrossRef.
- J. Laisney, H. J. Shepherd, L. Rechignat, G. Molnár, E. Rivière and M. L. Boillot, Phys. Chem. Chem. Phys., 2018, 20, 15951–15959 RSC.
- S. Brooker, Chem. Soc. Rev., 2015, 44, 2880–2892 RSC.
- H. Fourati, E. Milin, A. Slimani, G. Chastanet, Y. Abid, S. Triki and K. Boukheddaden, Phys. Chem. Chem. Phys., 2018, 20, 10142–10154 RSC.
- M. S. Haddad, W. D. Federer, M. W. Lynch and D. N. Hendrickson, Inorg. Chem., 1981, 20, 131–139 CrossRef CAS.
- H. B. Callen, Thermodynamics and an Introduction to Thermostatistics, John Wiley & Sons, New Jersey, 1991 Search PubMed.
- E. König, G. Ritter, J. Waigel and H. A. Goodwin, J. Chem. Phys., 1985, 83, 3055–3061 CrossRef.
- V. Ksenofontov, H. Spiering, A. Schreiner, G. Levchenko, H. A. Goodwin and P. Gütlich, J. Phys. Chem. Solids, 1999, 60, 393–399 CrossRef CAS.
- K. Babilotte and K. Boukheddaden, Phys. Rev. B, 2020, 101, 174113 CrossRef CAS.
- B. Emre, S. Yüce, E. Stern-Taulats, A. Planes, S. Fabbrici, F. Albertini and L. Mañosa, J. Appl. Phys., 2013, 113, 213905 CrossRef.
- L. Cirillo, A. Greco and C. Masselli, Therm. Sci. Eng. Prog., 2022, 33, 101380 CrossRef.
- P. J. von Ranke, B. P. Alho, P. H. S. da Silva, R. M. Ribas, E. P. Nobrega, V. S. R. de Sousa, M. V. Colaço, L. F. Marques, M. S. Reis, F. M. Scaldini, L. B. L. Escobar and P. O. Ribeiro, J. Appl. Phys., 2020, 127, 165104 CrossRef CAS.
- A. Aznar, P. Lloveras, M. Romanini, M. Barrio, J.-L. Tamarit, C. Cazorla, D. Errandonea, N. D. Mathur, A. Planes and X. Moya, Nat. Commun., 2017, 8, 1851 CrossRef PubMed.
- P. Lloveras, A. Aznar, M. Barrio, P. Negrier, C. Popescu, A. Planes, L. Mañosa, E. Stern-Taulats, A. Avramenko and N. D. Mathur, Nat. Commun., 2019, 10, 1803 Search PubMed.
- B. Li, Y. Kawakita, S. Ohira-Kawamura, T. Sugahara, H. Wang, J. Wang, Y. Chen, S. I. Kawaguchi, S. Kawaguchi and K. Ohara, Nature, 2019, 567, 506–510 Search PubMed.
- J. Li, D. Dunstan, X. Lou, A. Planes, L. Mañosa, M. Barrio, J.-L. Tamarit and P. Lloveras, J. Mater. Chem. A, 2020, 8, 20354–20362 RSC.
- J. Li, M. Barrio, D. J. Dunstan, R. Dixey, X. Lou, J. L. Tamarit, A. E. Phillips and P. Lloveras, Adv. Funct. Mater., 2021, 31, 2105154 CrossRef CAS.
- Y. Kuang, J. Qi, H. Xu, B. Yang, B. Li, Z. Li, H. Yan, Y. Zhang, C. Esling and X. Zhao, Scr. Mater., 2021, 200, 113908 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: XRPD patterns (Fig. S1); magnetic properties with and without Apiezon H (Fig. S2); pressure dependence of HS and LS molar fractions (Fig. S3); pressure dependence of unit-cell parameters (Fig. S4); isobaric thermograms for multiple thermal cycles (Fig. S5). See DOI: https://doi.org/10.1039/d5ta00033e |
| This journal is © The Royal Society of Chemistry 2025 |







