Mapping the configuration space of half-Heusler compounds via subspace identification for thermoelectric materials discovery

Abstract

Half-Heuslers are a promising family for thermoelectric (TE) applications, yet most of their chemistries remain experimentally unexplored. In this work, we introduce a distinct computational high-throughput screening approach designed to identify underexplored yet promising material subspaces and apply it to half-Heusler TEs. We analyze 1126 half-Heuslers satisfying the “18 valence electron rule”, including 332 predicted semiconductors, using electronic structure calculations, semi-empirical transport models, and TE quality factor β. Unlike conventional filtering workflows, our approach employs statistical analysis of candidate material groups to uncover collective trends, providing robust insights and minimizing reliance on uncertain predictions for individual compounds. Our findings link n-type performance to ultra-high mobility at conduction band edges and p-type performance to high band degeneracy. Statistical correlations reveal elemental subspaces associated with high β. We identify two primary (Y- and Zr-containing) and two secondary (Au- and Ir-containing) subspaces that reinforce key physical design principles, making them promising candidates for further exploration. These recommendations align with previous experimental results on yttrium pnictides. Inspired by these insights, we synthesize and characterize rare-earth gold stannides (REAuSn), finding Sc_0.5Lu_0.5AuSn to exhibit ultra-low thermal conductivity (0.9–2.3 Wm⁻¹ K⁻¹ at 650 K). This work demonstrates alternative strategies for high-throughput screening under predictive uncertainty and offers tools and design strategies for optimizing half-Heusler chemistries for TE performance.

---

1 Introduction

Half-Heuslers are a family of face-centered-cubic crystals with chemical formula ABC where A and B are transition metals and C is a p-block element. These elements crystallize in space group F4̄3m, with the more electronegative metal (B) occupying the FCC sublattice and A and C forming a rocksalt structure.¹ The 18 valence electron half-Heuslers are of particular interest in semiconductor applications due to their anticipated band gaps and stability,^2,3 but only 188 have been realized experimentally as listed in the Inorganic Crystal Structure Database (ICSD).⁴ These compounds show promise for applications such as topological insulators and thermoelectrics (TEs).^5–10 Yet, the 188 experimentally realized half-Heuslers represent only a small subset of all possible 18 valence electron chemistries. Thus, the half-Heusler space offers a vast range of unique intermetallic chemistries and transport properties that have yet to be characterized. To fill this gap, we introduce a modified high-throughput materials screening workflow that is designed to identify subspaces, or families of related compounds, that are promising search spaces for new TEs.

The disparate properties required for good performance, as described by TE figure of merit zT, make TEs a challenging case for computational materials discovery. Figure of merit zT is a composite parameter that involves both intrinsic (e.g., intrinsic mobility and thermal conductivity^11,12) and extrinsic (e.g., temperature and carrier concentration^13,14) properties. Prediction of intrinsic properties relies on models for electron and phonon transport and scattering.¹⁵ The need to evaluate transport coefficients and other relevant material properties has motivated the design of “funnel” workflows, where candidate materials are passed through computational filters one by one.^16–19

Computational approaches to predicting transport properties, however, involve trade-offs between accuracy and cost, ranging from semi-empirical models,²⁰ to constant relaxation time Boltzmann transport equations,²¹ to fully first-principles mode-resolved calculations of scattering rates.²² Fully first-principles approaches show the highest predictive capacity but are not amenable to screening large material sets. Semi-empirical models, by contrast, are suited for evaluating large material sets and have been successfully applied to TE materials discovery,^12,14,23 though their approximate nature limits quantitative precision.

These trade-offs challenge high-throughput screening workflows that rely on traditional “funnel” approaches. In standard funnel workflows, a large pool of candidate materials is sequentially narrowed by applying computational filters based on predefined criteria. Materials passing all filters are recommended for synthesis and experimental validation. While this approach can be effective, it has notable pitfalls. Early stage reliance on computationally inexpensive, approximate filters introduces uncertainty that propagates through later stages. These workflows also often rely on rank-ordered lists of performance descriptors,^{14,17,24–28} placing emphasis on the accuracy of individual predictions, over identifying broader patterns across the material space. Rank-ordering individual compounds with a predicted figure of merit is a natural first step when the predictive model is reliable and the objective clear. It enables direct prioritization and the identification of potentially exceptional candidates. However, it is sensitive to computational uncertainties and factors not captured in the model (e.g., defects and microstructures), making individual property predictions less reliable. As a result, rank ordering can lead to false positives, where materials appear optimal due to noise rather than intrinsic merit, particularly for cases like TE materials search where one seeks materials that are exceptions to the rule.

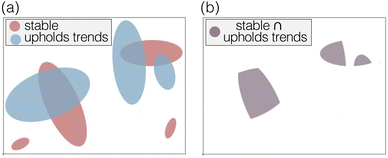
To address these challenges, we present an alternative high-throughput screening approach centered on identifying promising subspaces within a broad materials space. Subspace identification, unlike rank ordering, targets families where properties trend favorably across many candidates, even if individual compounds are not best-in-class. Consistent trends across a family, despite noisy individual predictions, suggest a deeper physical basis for good performance. As a result, subspace-based discovery is more robust to noise, statistically meaningful and offers a more reliable path to experimentally viable materials. We employ the dimensionless TE quality factor, β,²⁰ alongside evaluations of the electronic structure, thermodynamic stability, and transport properties to target key subspaces within the half-Heusler family (Fig. 1a). Instead of sequential filtering, we apply statistical analysis across the dataset to reveal robust, chemistry-based patterns, leveraging the collective behavior of groups over less reliable individual predictions. Our method uniquely integrates physical insights with computational screening, considering material stability, novelty, and future synthesis compatibility. We focus on element-based regions of half-Heusler chemical space where high TE performance aligns with stable chemistries, providing actionable insights for experimental synthesis. This intersection of performance and stability is visually represented in Fig. 2. Such element-based subspaces provide advantages in their practicality, particularly for strategies like alloying to enhance properties.^29–34

Fig. 1 Overview of the approach for identifying promising elemental subspaces in half-Heusler thermoelectric materials. (a) The method resembles a funnel approach but integrates parallel assessments of stability, performance, and statistical significance to identify optimal subspaces. (b) Elements evaluated for potential chemical substitution.

Fig. 2 Half-Heusler subspaces of interest are identified by (a) identifying chemical spaces associated with physical, interpretable trends (blue) and chemical spaces that harbor stable compounds (pink). (b) The intersection of these regions defines a unique and promising elemental subspace.

We analyze an extensive set of 1126 candidate half-Heuslers with the formula ABC, satisfying the 18-valence electron rule. These candidates were generated by selecting elements across the periodic table (Fig. 1b), of which 332 are predicted to be semiconductors. To date, the majority of half-Heusler workflows start from considering only known chemistries or those that exist in databases,⁸ or limit the search to a narrow set of elements,⁵ and often downselect through filters. In contrast, our study leverages the full dataset of 332 semiconductors to identify trends, distinguish desirable n-type and p-type characteristics for half-Heuslers, and establish statistical links to promising elemental subspaces. We find that excellent n-type performance is linked to ultra-high mobility at conduction band edges, while strong p-type behavior stems from high band degeneracy. We show that elemental subspaces statistically linked to high β reinforce physical design principles, validating known high-performance compounds and revealing four promising, underexplored subspaces for TE discovery. The underexplored subspaces include two primary (i) yttrium- and (ii) zirconium-containing chemistries, and two secondary (iii) gold- and (iv) iridium-containing chemistries. Guided by these recommendations, we present experimental work on rare earth gold stannides which yields low to ultra-low thermal conductivity half-Heusler alloys.

2 Methods

2.1 Chemical replacements

In order to methodically consider an expansive variety of theoretical half-Heusler compounds, all elements with known electronegativities from groups 3 to 17 were utilized as possible inputs to the half-Heusler structure (Fig. 1b). Transition metals were split between groups 3–7 and groups 8–12, with the former as chemical replacements for half-Heusler atom A and the latter groups' elements as atom B. An important constraint applied to this work was the requirement of a net 18 valence electrons per half-Heusler system. In such systems, atom A acts as a cation and donates all of its valence electrons to the covalently bonded and anionic BC pair. When these elements share and transfer electrons in this manner and with a net 18 valence electron count, the half-Heusler Aⁿ⁺(BC)ⁿ⁻ has a completely filled d-shell. This gap in energies before the next available orbital contributes to the likelihood of 18 valence electron half-Heuslers being semiconductors, a necessity for thermoelectric applications.^2,3,35 This 18 electron constraint in combination with the groups of elements considered led to an initial pool 1126 half-Heuslers for this work.

2.2 Structural relaxation and electronic properties

First-principles calculations were performed with density functional theory (DFT) using the Vienna Ab Initio Simulation Package (VASP)³⁶ with Projector Augmented Wave (PAW) pseudopotentials.³⁷ The Perdew–Burke–Ernzerhof (PBE)³⁸ exchange correlation functional was used for structural relaxation. A plane wave cut off of 400 eV was utilized on an 8 × 8 × 8 Monkhorst–Pack sampled k-grid for relaxation. With these parameters, all computed total energies are converged to within 0.01 eV across the chemistries considered. The total energy and total force convergence criteria for structural relaxations were 10⁻⁵ eV and 0.01 eV Å⁻¹, respectively.

The PBE exchange–correlation functional and the Modified–Becke–Johnson (mBJ) meta-GGA functional²⁶ were utilized to evaluate the band structure along a high-symmetry k-point path. Band gaps from both results were analyzed, and the mBJ band structure was kept in cases where only the PBE band gap closed but the mBJ gap did not. A high density k-grid, 14 × 14 × 14 Γ-centered, was utilized in order to converge electronic properties for trend analysis across all half-Heuslers calculated to have a band gap. Such calculations also utilized total energy criteria of 10⁻⁵ eV and total force convergence criteria of 0.01 eV Å⁻¹.

2.3 Thermoelectric quality factor

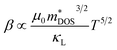
Thermoelectric quality factor, β, is a strong indicator of intrinsic thermoelectric performance.²⁰ As seen in eqn (1), β is directly evaluated from the ratio of electronic transport parameters to lattice thermal conductivity, where μ₀ is the intrinsic carrier charge mobility, is the density of states (DOS) effective mass, κ_L is the lattice thermal conductivity and T is temperature. Intrinsic carrier charge mobility is evaluated from a semi-empirical model utilizing m_DOS, band degeneracy, and bulk modulus.²⁰m_DOS is evaluated utilizing the density of states from a high k-point density DFT calculation as described in Section 2.2 and using a single parabolic band approximation. Bulk modulus is evaluated by fitting the Birch–Murnaghan equation of state.³⁹κ_L is also evaluated from a semi-empirical model and uses bulk modulus, number of atoms in the primitive unit cell, density, volume, mass, and average coordination number as inputs.¹⁹

2.4 Phase stability

The thermodynamic stabilities of 332 half-Heuslers with band gaps were evaluated against all competing ternaries and binaries available on the Inorganic Crystal Structure Database (ICSD)⁴ through convex hull analysis. Due to the half-Heusler space being largely unexplored experimentally, some compounds had no known competing binaries. In these cases, lowest energy competing phases from Materials Project (MP) were used to construct a convex hull. The lowest-energy elemental phase structures from MP were also retrieved for each compound.

Total energy calculations were performed for all competing phases. The majority of parameters for these calculations were generated from Pymatgen's MPRelaxSet,⁴⁰ but the energy convergence criterion was lowered to 10⁻⁶ eV and a total force convergence criterion of 0.01 eV Å⁻¹ (as used in our geometry optimizations described in Section 2.2) was added. Compounds directly on the hull (distance = 0 eV) were marked as stable and compounds off the hull were marked to be unstable. Ranges of chemical potentials for which the predicted stable compounds remain stable were found by visualizing each stable system in chemical potential space.

2.5 Synthesis

The ScAuSn, LuAuSn and Sc_0.5Lu_0.5AuSn samples were prepared first using arc-melting of constituent elements (Sc 99.8%, Lu 99.9%, Au 99.99%, and Sn 99.99%) under an ultra-pure argon atmosphere. The ingots were remelted and flipped several times to ensure homogeneity. The arc-melted materials were subsequently ground using an agate mortar and sintered in the induction hot press under conditions 700 °C, 40 MPa, 15 min for ScAuSn and 625 °C, 40 MPa, 60–90 min for LuAuSn and Sc_0.5Lu_0.5AuSn.

2.6 Measurement

The crystal structure was studied with X-ray diffraction using a Bruker D2 Phaser device with a Cu radiation source. Rietveld refinement was performed with FullProf software. Density was measured with geometrical methods; for all the samples, the values were ∼90% or higher. The resistivity and Hall effect were studied on a custom-built apparatus⁴¹ using the Van der Pauw technique. The current supplied was 150 mA, while the magnetic field amounted to 1 T. The Seebeck coefficient was also studied on a home-built apparatus.⁴² Thermal conductivity was calculated from relation κ = dC_pD, where d stands for the density, C_p denotes heat capacity approximated from the Dulong–Petit law, while D is the diffusivity coefficient measured with the commercial Netzsch 467 apparatus. Throughout the analysis, lattice thermal conductivity was obtained using the Franz–Wiedemann law, where the Lorenz number was calculated as shown in ref. 43.

3 Results and discussion

3.1 Trends in transport and thermoelectric quality factor

To identify the features of half-Heuslers associated with promising performance, Fig. 3 highlights several key trends observed in our computational dataset for both n-type and p-type performance. These trends are based on the 332 half-Heuslers (out of a total of 1126) that exhibit a non-zero band gap (see Section 2.2). As described by eqn (1), high intrinsic mobilities (μ_o), large density of states (DOS) effective masses , and low lattice thermal conductivities (κ_L) are desirable for achieving a high thermoelectric (TE) quality factor. However, the expression for β conceals additional complexities. DOS effective masses and mobilities are interconnected and influenced by band effective masses and band degeneracies. Optimally, a large DOS effective mass is achieved through multiple bands (high degeneracy) with low effective masses, which helps preserve high carrier mobilities, rather than by a single, heavy band. To explore these interdependencies, Fig. 3 systematically examines pairwise relationships, offering insights that can guide the identification of promising subspaces. Correlation matrices of n- and p-type data corresponding to Fig. 3 are available (ESI Fig. S1†).

Fig. 3 When the thermoelectric figure of merit, β, is visualized with respect to its components, distinct trends emerge for n-type and p-type performance. For n-type materials, (a) high β values occur exclusively at low m_DOS and high electron mobility. (b) As their band edge degeneracy is almost always fixed at N_b = 3, high β compounds must consistently exhibit low band mass . (c) For a given m_DOS, compounds with lower lattice thermal conductivity achieve higher β. For p-type materials, (d) the highest β values are less concentrated at lower m_DOS. (e) Valence band degeneracy, particularly combined with low at the valence band edge, correlates strongly with high β_p. (f) While the lowest performing compounds tend to have the highest κ_L, the p-type association between κ_L and β_p is also less pronounced than in n-type.

Fig. 3a illustrates the variation of β_n with the DOS effective mass. The data reveal an inverse relationship, where high DOS effective masses correspond to lower thermoelectric (TE) quality factors. Notably, the highest β values are observed in compounds with the lowest DOS effective masses. Each point in Fig. 3a is shaded based on the calculated electron mobility (μ_e), highlighting that compounds with low but high β_n achieve their superior predicted performance due to exceptionally high electron mobilities. Fig. 3b also plots β_n against the DOS effective mass, here with points colored by the band degeneracy (N_b) at the conduction band edge, with nearly the entire dataset sharing a degeneracy of 3. This visualization reveals that the high mobilities are linked to small band effective masses, as lower must come from a small given fixed N_b. An exception to this trend is observed in the cluster of four compounds (VFeSb, ZrIrP, WCoIn, and TaIrSn) that exhibit the maximal CBM degeneracy of 9. These compounds achieve high β despite moderate values, owing to their correspondingly low band masses.

These trends can be further understood through the common structural features of half-Heusler conduction bands: the placement of the conduction band minimum (CBM) at the point X of the fcc lattice Brillouin zone, coupled with strongly curved bands.^1,44 The CBM placement limits the n-type band degeneracy to 3, the multiplicity of the X point in the first Brillouin zone, or a theoretical maximum of 9 if each ion contributes an equivalent band at that point.^35,44 As seen in Fig. 3b, 286 of the 332 semiconductors considered here exhibit a total conduction band degeneracy of 3 (see Table S1 and Fig. S2 of the ESI†). This is much lower than the degeneracies seen in p-type half Heuslers (Fig. 3e). This limitation implies that achieving a high DOS effective mass – often regarded as beneficial for maximizing the thermoelectric quality factor β – in practice necessitates a large band effective mass and hinders mobility. Consequently, low DOS and band effective masses emerge as the primary, intertwined factors correlating with higher β for n-type performance.

To examine the influence of lattice thermal conductivity κ_L on predicted quality factor β_n, Fig. 3c again plots β_n against , but with compounds color-coded by the inverse of their predicted lattice thermal conductivity, with darker colors corresponding to lower κ_L. Achieving low lattice thermal conductivity in half-Heuslers is a well-documented challenge,^45–47 and our computational results reflect this. The predicted κ_L values span a wide range, from 0.2 to 98 W mK⁻¹, with a median of 18 W mK⁻¹ and first and third quartiles at 12 and 26 W mK⁻¹, respectively. These values contrast starkly with the < 1 W mK⁻¹ achieved by state-of-the-art thermoelectric materials above room temperature. It is worthwhile to explore how this range of κ_L impacts the observed trends. Fig. 3c shows that, for a given DOS effective mass, higher β_n values are generally associated with lower lattice thermal conductivities. The lighter color band, corresponding to compounds with relatively high κ_L, forms an envelope beneath the data points. As κ_L decreases (indicated by darker colors), the data points shift away from this envelope toward higher β_n. Since all compounds share the same crystal structure, they also share many identical parameters in the lattice thermal conductivity model. As a result, κ_L is primarily governed by the elemental masses and the bulk modulus. We find variations in κ_L relative to elemental masses to highlight the influence of bulk moduli (Fig. S3 and Table S3†).

Unlike n-type thermoelectric (TE) quality factors, p-type performance reveals much weaker correlations between β_p and the valence band DOS effective mass . Hole mobility (Fig. 3d) is much more limited than that of electrons in n-type systems. Instead, Fig. 3e indicates that high β can be achieved by higher DOS masses arising from high band degeneracy. Additionally, the highest lattice thermal conductivities (Fig. 3f) tend to be paired with low β_n, but the distinct layers of higher TE quality factor seen with lower κ_L in n-type are not carried over in p-type. Rather, Fig. 3d reveals that high β_p values are most strongly associated with small band effective masses combined with large valence band degeneracies as predictors of good performance.

The significance of band degeneracy for p-type performance can also be traced to the characteristics of half-Heusler band structures. While the conduction band minimum (CBM) is consistently located at the point X, the valence band maximum (VBM) can occur at Γ, W, or L within the first Brillouin zone.^1,48 This diversity in band edge placement, combined with the higher multiplicities of W and L (6 and 4, respectively) compared to X (3), allows for a broader range of band degeneracies in the valence band (see Table S2 and Fig. S2 in the ESI†), especially when multiple of these extrema lie close in energy. As a result, the p-type data span compounds with (i) high DOS effective masses from high valence band degeneracy and low band masses, (ii) low DOS masses from low degeneracy and low band masses, and (iii) intermediate cases. Fig. 3e shows that higher β_p values are achievable at a given DOS effective mass with increasing band degeneracy.

Overall, this analysis yields distinct design rules for identifying promising chemical subspaces for n- and p-type performance. For n-type, we seek materials with sharp conduction band edges that yield low band effective mass and therefore high mobility. For p-type, we look for materials with high valence band degeneracy characterized by degenerate energy eigenstates across any of the Γ, W, or L points of the Brillouin zone. Such degeneracy, when coupled with steeper band edges when feasible, achieves high β_p. For both carrier types, we further seek compounds with lower κ_L where possible, as this can only increase TE quality factor β more. Below, we utilize these design rules across all calculated half-Heusler semiconductors to inform subspace identification.

3.2 Phase stability

With an understanding of desirable transport properties for n- and p-type established, we next carry out phase stability analysis across the full space of 332 semiconducting half-Heuslers. We use convex hull analyses of all 332 semiconductors (described in Section 2.4) from computed formation energies and visualize the predicted compounds' stability in chemical potential space. The convex hull is the lower envelope of phase formation energies versus composition; phases on the hull are stable, while those above it are unstable or metastable. Hull analysis reveals stable phases within a composition space as well as nearby competing phases.

A summary of all half-Heusler chemistries that lie on the convex hull is presented in Fig. 4. Fig. 4 is organized into 4 groups of N_A–N_B–N_C, where N refers to the group number of the periodic table shared between elements A, B, or C. The chemistries are first organized by the group number of element A, then B, and finally C. Compounds not included in Fig. 4 are predicted to be unstable. Of the 332 half-Heuslers considered, 93 (marked in purple blocks) are predicted to be stable. We note that the 12 compounds marked as “stable, other phase known” were predicted to be thermodynamically stable here as half-Heuslers but are only experimentally known in other phases (several are predicted stable in other studies as well⁴). These compounds may be false positives; alternatively targeted synthesis strategies may be effective for ultimately realizing them. Additionally, we note one false negative result: VRuSb, calculated as unstable but experimentally known as a half-Heusler.

Fig. 4 Subset of 332 semiconductors analyzed for phase stability, including 93 compounds predicted to be thermodynamically stable. Purple blocks represent compounds calculated to lie on the convex hull, those with check marks are experimentally known while circles are those unreported in experiment. Horizontal lines mark half-Heuslers predicted stable in this work but experimentally realized in another structure. Light grey blocks correspond to compounds that lie off the calculated hull. Dark grey blocks show compounds that were not considered for this analysis.

There are 38 chemistries that are not experimentally known but predicted here to be stable labeled as “stable, unknown in experiment”. While computational analyses of their properties exist, the majority of their thermodynamic stabilities had not been previously assessed; here, they are predicted to be stable and our findings align with existing computational literature where available. This label also includes 6 chemistries not reported in the literature either experimentally or computationally: YRhTe, AcNiAs, AcNiSb, AcNiP, HfAuIn, and LaHgIn. These predicted compounds are sparsely distributed throughout the chemical space, but reflect comparatively less explored chemical trends, such as actinide containing, B-site gold containing, or atypical p-block elements such as Te, In, and P.

It is interesting to analyze trends across the stability analysis, to provide an understanding of the chemistries that tend to be stable and those that do not. For example, in Fig. 4 the block IV–IX–XV appears to be heavily explored and largely composed of stable compounds including well-known thermoelectric half-Heuslers HfCoSb and ZrIrSb. Across multiple blocks, we see that nearly all Sb-containing half-Heuslers are stable, and also have been previously reported in the literature.

It is also interesting to understand the compounds that are predicted to be unstable, given the goal of identifying comparatively underexplored but promising subspaces that contain realizable chemistries. For instance, Fig. 4 shows that chemistries with C-elements P, Pb, or Si often lie off the convex hull. This instability frequently arises from competing 1 : 1 : 1 stoichiometric phases, typically in the orthorhombic Pnma structure. Examples include ScNiP and TaCoSi, which have higher formation energies than their experimentally known Pnma counterparts.⁴ Additionally, LaNiP and YNiP remain off the convex hull due to hexagonal P6₃/mmc phases, while YPtP has a more favorable ternary in hexagonal P6m2.

As for the unstable group of Pb-based compounds seen in Fig. 4, here we often observe a competing AB binary. Favorable compounds HfPt, TiNi, TiPt, and ZrPt effectively exclude HfPtPb, TiNiPb, TiPtPb, and ZrPtPb respectively from the convex hull. In comparison, these competing AB-element binaries exhibit higher formation energies for largely stable groups of half-Heuslers such as the IV–IX–XV group.

Fig. 5 shows two example stable chemistries, ZrIrSb and ScAuSn, visualized in chemical potential space. In chemical potential space, a chemical potential of element i, Δμ_i, that is closer to 0 indicates element i-rich conditions while a more negative Δμ_i value indicates element i-poor conditions. This visualization gives further insight to the stability of each predicted-stable compound, including the bounding phases and the thermodynamic conditions under which it may be likely to form.

Fig. 5 Phase stability diagram of (a) ZrIrSb and (b) ScAuSn. Blue faces correspond to competing phases closest in composition to the A-element, orange faces correspond to competing phases closest to the B-element, and green faces correspond to competing phases closest in composition to C-element Bi. The red dots mark the invariant points at which the half-Heusler is in equilibrium with competing phases.

3.3 Subspace identification

3.3.1 Statistical testing. To begin identifying promising subspaces within half-Heusler chemistries, Barnard's exact test was used to assess correlations between TE quality factor β and elements in the A, B, and C sublattices, as well as BC element pairs. Known for its precision in small-sample comparisons, Barnard's test provides robust insights into specific elements most strongly associated with high or low β and therefore TE behavior. Alternative statistical methods were attempted but deemed unsuitable due to specific limitations. For example, chi-squared and Mutual Information tests require larger sample sizes (e.g., n > 1000, compared to our dataset of 332 semiconductors), and ANOVA assumes linear trends and homogeneous variance between groups. Fisher's exact test, though designed for small sample sizes, was also excluded because it conditions only on contingency tables with fixed marginal totals, unlike Barnard's test, which considers all possible tables.

Barnard's test was performed on all A, B, and C elements, as well as all BC element pairs, from the set of half-Heuslers predicted to have a non-zero band gap. As the test requires categorical data, compounds were classified as “high” or “low” β for n-type and p-type materials. High β values were defined as those in the top 20%, with the remainder categorized as low. The p-values for each element are shown in Fig. 6, where bar shading indicates the frequency with which compounds containing each element are classified as high β. The significance threshold for associations was set at p = 0.05.

Fig. 6 Statistical analysis results using Barnard's exact test. Frequency coloring represents the proportion of times an element was associated with high β values. The y-axis shows log₁₀(1/p), so that the statistically significant elements yield the largest bars. Subfigures (a–c) show n-type data for A elements, B elements, and lowest p-value BC pairs, respectively. Subfigures (d–f) present p-type data for the same groups. Horizontal lines denote the significance threshold (0.05), and vertical lines mark the cutoff beyond which elements are not statistically significant.

Fig. 6 shows the results of the analysis for A element, B element, and BC element subspaces. The results for C elements are shown in ESI Fig. S4† as there are fewer significant elements, and ultimately we will conclude that BC pair subspaces encompass the strongest C element subspaces. The analysis reveals several elements that achieve statistical significance in their associations with β. For n-type, the A-elements La, Y, Cr, V, Ti, Zr, and W show significant p-values (Fig. 6a), while Au among the B-elements (Fig. 6b) also stand out. For pairwise BC elements (Fig. 6c), PtP, IrAs, PtSb, HgAl, RhTe, CoS, FeSb, AuSi, AuSn emerge as significant. In p-type materials, significant A-elements include Y, Ti, Mo, Cr, Zr, and Ac (Fig. 6d); significant B-elements are Tc and Fe (Fig. 6e); and significant BC pairs are IrTl, OsPb, PtTl, AuTl, RuPb, OsSn, NiTl, PtSb, NiAl, and AuSn (Fig. 6f).

It is essential to note that Barnard's exact test identifies significant associations but does not inherently indicate the direction of these correlations (i.e., whether the association is with high or low β). To address this, we analyzed each element's contingency table by comparing the proportion of high-versus low-β compounds. Elements with a statistically stronger association to high β were retained and are visualized as darker bars in Fig. 6. For n-type performance, the most significant A-elements then become La, Y, Zr, and W; Au is the significant B-element. BC pairs PtP and IrAs immediately stand out. Several BC pairs, PtSb, HgAl, RhTe, CoS, FeSb, AuSi, and AuSn, are unique in that they achieve statistical significance despite having only moderate high-β frequencies (50%). While these frequencies are lower than those of the most significant individual elements, they contrast with the broader population of compounds lacking these pairs, which are predominantly low-β. These BC combinations highlight that certain B elements like Fe or Pt, though not significant alone, can be associated with high β when paired with specific C elements such as FeSb and PtSb. For p-type performance, significant A-elements with high β are Y, Mo, Cr, and Ac; Tc is the B-element. Pairs IrTl, OsPb, PtTl, AuTl, RuPb, OsSn, and NiTl stand out for high β in the BC elements. As with n-type analysis, PtSb, NiAl, and AuSn achieve significance but have only a 50% frequency in high-β compounds. By contrast, statistically elements such as Cr, V, and Ti for n-type, and Ti, Zr, and Fe for p-type, are excluded as their light shading indicates stronger correlations with low β.

We note that Fig. 6 shows the presence of elements frequently associated with high β values (dark colored bars) but without statistically significant p-values (p > 0.05). For example, Hg and Ir as B elements for n-type (Fig. 6b and c), and Al as B element for p-type (Fig. 6e) exhibit this behavior. The most common explanation for this behavior is that, although these chemistries correlate with high β, they are typically associated with small sample sizes. Their infrequent occurrence within the dataset results in greater variability and reduced statistical power. Consequently, their associations with high β are less likely to achieve significance in Fig. 6 despite their apparent relevance.

Lastly, we note that subspaces defined by descriptors other than elemental species are also viable in principle. For example, we examined subspaces based on elemental group numbers and group number differences (ESI Fig. S5†). However, these groupings do not exhibit the strong correlations observed in the element-specific perspective. Although alternative descriptors may exist, the pronounced trends in elemental chemistry, and their connection to underlying physical insights (see the next subsection), support the focus on element-based subspaces here. A key advantage of these subspaces is the direct identification of promising elements, which can then be targeted for alloying strategies, as alloyed half-Heuslers have demonstrated the highest thermoelectric potential to date. However, it is important to acknowledge that not all physical properties can be fully captured through elemental subspaces alone, highlighting the potential need for additional refinement or complementary descriptors in future studies.

3.3.2 Applying transport trends to significant elements. Next, we analyze the elements frequently found in high-β compounds. While Barnard's test evaluates whether the presence of a specific element increases the likelihood of high performance, this analysis identifies instead the elements most likely to be present in a high-performing compound. Additionally, we assess whether these elements align with the transport trends established in Section 3.1. This approach ensures the observed correlations reflect reproducible and interpretable physical mechanisms that offer meaningful insights into transport behavior.

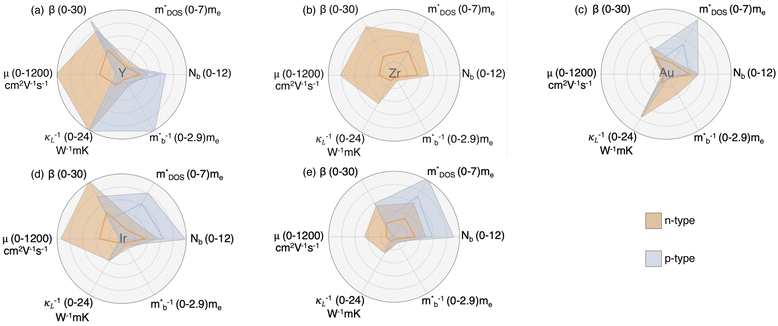
Fig. 7 provides a detailed visualization of the transport trends identified in Fig. 3. Each marker represents a compound, with marker size corresponding to the magnitude of quality factor β. Colored markers denote elements frequently appearing in the top 20%, while gray markers represent elements that are either infrequent in the top 20% or associated with lower-performing compounds outside this range. Solid colored markers denote elements that were also identified as statistically significant with Barnard's test, while cross-hatched markers highlight elements not identified as statistically significant. To better understand effective BC pairings, we examine the individual contributions of B and C elements rather than showing BC pairs directly (Fig. S6†), since most high-performing BC combinations can be inferred from their constituent elements. This element-level perspective helps identify patterns that support known BC pairs and suggest promising new combinations.

Fig. 7 Visualization of the distribution of transport properties among all 332 half-Heusler semiconductors. Half Heusler n-type performance is visualized by (a) A-element, (b) B-element, and (c) C-element, and p-type performance is also visualized by (d) A-element (e) B-element and (f) C-element. Marker size corresponds to the value of TE quality factor β, a reference to classic TE material PbTe is supplied in (a). Compounds with predicted values of β in the top 20% are marked in color, while lower β value compounds are marked in gray. The top 20% compounds contain many of the elements that show statistical significance (shaded) as well as additional elements (shaded and cross-hatched).

From Fig. 7, we first note that the majority of the strongest elements in the top 20% overlap substantially with those found using Barnard's exact test. Panels (a–c) illustrate the predicted n-type trend, where high electron mobility and low lattice thermal conductivity drive superior thermoelectric (TE) performance. As expected, the highest-performing compounds are clustered in the upper-right corner. Panels (d–f) depict the p-type trend, highlighting the roles of low band mass, low lattice thermal conductivity, and high band degeneracy. The broader distribution of the largest markers in Fig. 7d–f reflects the influence of band degeneracy, which allows high β values to arise across the parameter space rather than being confined to the upper-right corner. Even so, Fig. 7d contains a series of yttrium-based compounds, all sharing the same degeneracy, that consistently achieve higher β values as they progress from the lower left to the upper right.

An important takeaway from Fig. 7 is that the statistically significant A elements identified in Fig. 6 dominate the top 20% of compounds for both n-type and p-type half-Heuslers (Fig. 7a and d), as indicated by the prevalence of solid colored markers over cross-hatched ones. Combined with the higher prevalence of significant A elements compared to B elements or BC pairs (Fig. 6), these findings suggest that TE performance is strongly driven by the A element. In contrast, top-performing compounds show greater variability in B and C, suggesting a lesser role. Half-Heusler compounds exhibit distinctive orbital hybridization (Section 2.1), where the B and C atoms form a covalently bonded zinc blende – like sublattice that acts as an effective anion, while the A-site element largely retains its elemental character and likely allowing it to exert a greater influence.

This structural feature motivates a perspective in which half-Heuslers are viewed as combinations of an A element and a BC pair, rather than fully independent sites. This A + BC framework not only aligns with known alloying strategies, such as the well-studied TaFeSb-based or ZrCoBi-based systems, but also offers design rules for optimization.^33,49,50 For example, although Fe alone is not significant, its pairing with Sb is; this insight can guide exploration of adjacent chemistries like CoSb, which appears in high-performing systems such as ZrCoSb, outperforming well-known compounds like NbFeSb and VFeSb. Similarly, the BC pair AuSn, though largely unexplored, emerges as statistically significant and comparable in performance to established Pt-containing systems, suggesting opportunities to substitute Au for Pt in systems like YPtSn. However, since B-site chemistry and specific BC pairings can significantly influence performance—even if B or C elements alone do not—our search strategy must extend beyond A-element subspaces to also include B-element and BC-pair subspaces. By identifying robust A and B subspaces that are compatible with a broad range of C elements, we can map out flexible, experimentally viable design spaces for half-Heusler optimization.

Considering n-type semiconductors in detail, all statistically significant A and B elements associated with high β appear in Fig. 7a and b, including A-site elements La, Y, W, and Zr; the B-site element Au. All significant BC pairs appear in Fig. 7b and c; however, PtSb and HgAl are single-compound cases, and while Si and Sn are not significant as individual C elements, they often pair with Au in high-performing chemistries. Additional elements, shown with cross-hatching, also occur frequently in high-β compounds and fall into two main categories: (i) those present in both high- and low-β compounds, and (ii) those frequently found in high-β compounds but underrepresented in the dataset, limiting statistical significance. For most cross-hatched elements, their presence in the top-performing compounds seems incidental, as many poor-performing compounds also contain these elements (case (i)). An exception is Ir, which, despite not meeting the threshold for statistical significance as a B element alone due to limited data, consistently appears in high-β compounds. Its relevance is supported both by its presence in a significant BC pair (IrAs) and by its contribution to high electron mobility when occupying the B site.

In the case of p-type semiconductors, Fig. 7d–f highlight all elements identified as statistically significant and associated with high β. BC pairs containing Tl make up some of the largest β compounds in this analysis, followed by PtSb, NiAl, and AuSn. Many other elements also appear frequently in top-performing compounds but are not statistically significant due to their broader presence in low-performing thermoelectrics. Among these, B elements Au and Ir stand out for their repeated appearance in high-β systems, particularly as part of key BC pairs. As shown in Fig. 7e, Au-containing chemistries follow expected trends for high p-type performance, with low and reduced κ. Ir-based half-Heuslers, meanwhile, exhibit unusually high valence band degeneracy. These observations suggest that combining A-site elements like Y with Au-based BC pairs, as well as identifying A + BC chemistries analogous to Tl-containing systems, may be a fruitful strategy for discovering and optimizing p-type half-Heuslers.

In summary, all elements identified as strongly associated with high β using Barnard's test align with the physical trends driving high performance in both n- and p-type semiconductors and frequently appear in the top 20% of compounds. Specifically, for n-type, we focus on the A-elements La, Y, W, and Zr and the B-element Au. BC pairs PtP, IrAs, RhTe, CoS, FeSb, AuSi, and AuSn remain of interest. For p-type, key species are the A-elements Ac, Cr, and Y along with the B-element Tc. BC pairs IrTl, OsPb, PtTl, AuTl, RuPb, OsSn, NiTl, PtSb, NiAl, and AuSn also remain of interest here.

3.3.3 Filtering elements by stability, toxicity, and novelty. The considerations above identify elemental spaces of interest from which our promising subspaces are to be selected. As the goal is to identify promising, element-based subspaces for utilizable half-Heuslers, we now incorporate the phase stability analysis provided in Section 3.2. As shown in Fig. 2, it is practically of interest to identify the overlap between areas that are promising in terms of their physical trends and likely to yield stable compounds that are, when possible, in comparatively less explored regions of phase space.

In n-type, the consideration of physical trends (Fig. 7a–c) in conjunction with stability analyses identifies a more refined set of elements. More specifically, La and W are removed from consideration due to their being part of very few stable chemistries, especially those that are not already extensively explored. BC pairs PtP, CoS, and AuSi are similarly removed from further consideration. This leaves IrAs, RhTe, FeSb, and AuSn as high-performing BC candidates; however, FeSb-based half-Heuslers are already well-characterized in the literature. Thus, Y and Zr emerge as versatile A-site elements that span many top-performing BC pairs, while Au and Ir stand out for their strong performance both individually as B elements and within high-performing BC combinations. In p-type (Fig. 7d–f), Ac, Cr, Tc, and several BC pairs (IrTl, OsPb, PtTl, AuTl, RuPb, OsSn, NiTl, and NiAl) are also removed due to yielding extremely limited stable chemistries (Fig. 4); Ac, Tc, and Tl are also particularly less desirable by default given their toxicity and/or radioactivity. This leaves BC pairs PtSb and AuSn; however, PtSb is also well characterized in the literature. Thus A-element Y is pursued for its strong p-type potential and compatibility with high-performing BC pairs like AuSn, while Au and Ir are retained as B elements to enable design of AuSn-like chemistries and IrTl-analogues with improved synthesis viability. This refined selection highlights the balance between statistical significance, transport properties, and material stability.

3.3.4 Selection and analysis of promising subspaces. With clear insights into transport trends, elemental significance, and stability, we finalize an efficient selection of promising subspaces guided by an A + BC design perspective. The chosen subspaces are illustrated in Fig. 8. Primary subspaces center on A-elements Y and Zr (Fig. 8a and b), which not only show strong statistical links to high β—Y in both n- and p-type and Zr in n-type—but also encompass a wide range of high-performing BC pairs. Secondary subspaces feature B-elements Au and Ir (Fig. 8c and d), which are prevalent across top-performing compounds both as individual B elements and as part of high-β BC pairs. Together, these selected A and B element subspaces span a diverse set of C-element combinations, enabling broad coverage of the chemical space and offering a targeted yet flexible platform for A + BC-based half-Heusler discovery.

Fig. 8 Spider plot visualization of elemental subspaces: primary subspaces are (a) yttrium containing chemistries, and (b) zirconium containing chemistries. Secondary subspaces are (c) gold, and (d) iridium containing chemistries compared to (e) all stable compounds. Different properties are plotted with respect to their relationship with β, so that maximum shading indicates higher performance. Blue corresponds to p-type performance and orange to n-type. Darker shaded lines are plotted along the average values and lighter shading indicates the standard deviation for all stable compounds considered containing that element.

The visualization of these subspaces in Fig. 8 embodies key components of β that drive high TE performance in both n-type and p-type materials. Each subspace is summarized using data from all associated chemistries predicted to be thermodynamically stable. The darker lines follow the average for these compounds and the lighter shading extends to each standard deviation. In the Y-based subspace, high β is driven by lower lattice thermal conductivity, a rare trait in half-Heusler desirable for TE efficiency (Fig. 8a). As predicted, Y achieves superior electronic transport properties as a result of exceptionally high electron mobilities despite low DOS effective mass (n-type), and a combination of low band mass and high degeneracy for p-type. An advantage of Y is that it is predicted to be a high performance subspace, independent of whether the material turns out to be natively n or p-type. It is also compatible with top n-type BC pairs RhTe and AuSn, as well as to n- and p-type BC pair, AuSn. For Zr, n-type β is again enhanced by particularly high electron mobility (Fig. 8c). Zr is also frequently compatible with remaining top BC pairs IrAs and FeSb. These primary subspaces form the basis for a range of high-performing thermoelectric materials, and their compatibility with both strong BC pairs and diverse alloying elements provides flexibility for further tuning and optimization.

The Au-based subspace demonstrates more modest overall statistics but includes notable standout properties. Half-Heuslers in the Au-based subspace, for example, show a low lattice thermal conductivity which benefits both carrier types. The interplay between a high DOS effective mass and low lattice thermal conductivity benefits p-type TE quality factor specifically, but the high DOS effective mass limits carrier mobility and adversely affects electronic transport (Fig. 8c). Even so, its chemistries with particularly low lattice thermal conductivity exhibit some of the highest β values across the whole dataset. Additionally, BC pairs AuSi and AuTl were excluded due to limited stability and synthesis feasibility, but continued exploration of the Au subspace enables pairing with alternative C elements like Al, which offers comparable κ_L performance to Sn (Fig. 7f). The Ir-based subspace stands out for its exceptionally high electron mobility in n-type applications, while p-type performance is once again driven by high band degeneracy. Although IrTl pairs were excluded due to synthesis limitations, the Ir subspace remains valuable, offering rich opportunities for substitution and alloying—for example, with Sb demonstrating similar performance to Tl (Fig. 7f). This nuanced understanding of how different elements influence TE performance enables a targeted approach to optimize chemistries for both n-type and p-type materials, while also guiding the intentional exploration of the most promising groups within the largely uncharacterized half-Heusler space.

Table 1 summarizes the stable half-Heusler candidates identified through our subspace-driven approach. Additional details are available in ESI Tables 1–3† for compounds marked by*. These compounds exhibit high intrinsic performance, strong potential for novelty, representation of a diverse range of A-site elements and BC pairings within the 18-electron half-Heusler space, and favorable trends in thermodynamic stability. Notably, several candidates—such as NbIrGe, ZrIrBi, and YPtSb—exhibit particularly strong intrinsic performance, illustrating how targeted subspace selection can uncover both established and previously unexplored high-performing half-Heuslers.

Table 1 Summary of stable half-Heusler candidate materials captured in the subspaces

Subspace	Compound	Carrier type	β
Au	HfAuAl	n	5.684
Au	HfAuIn	n	6.915
Ir	HfIrSb	n	12.742
Ir	NbIrGe	p	48.052
Ir	NbIrSn	p	16.052
Au	ScAuSn	n	4.864
Ir	TaIrGe	p	8.485
Ir	TaIrSn	n	28.408
Ir	TiIrAs	n	21.5
Ir	TiIrBi	n	3.467
Ir	TiIrSb	n	2.381
Ir	VIrGe	p	7.882
Ir	VIrSi	p	7.156
Y, Au	YAuSn	n	17.698
Y	YNiBi	p	32.497
Y	YNiSb	p	20.98
Y	YPtBi	p	22.748
Y	YPtSb	n	32.755
Y	YRhTe	p	18.882
Zr, Au	ZrAuAl	n	11.602
Zr	ZrCoAs	p	4.991
Zr	ZrCoBi	p	6.367
Zr	ZrCoSb	p	4.813
Zr	ZrFeTe	p	2.528
Zr, Ir	ZrIrAs	n	17.353
Zr, Ir	ZrIrBi	n	61.934
Zr, Ir	ZrIrSb	p	7.585
Zr	ZrNiPb	n	22.131
Zr	ZrNiSn	n	3.24
Zr	ZrPtSn	n	3.407
ZR	ZrRhAs	p	7.957
Zr	ZrRhBi	p	15.043
Zr	ZrRhSb	p	9.249
Zr	ZrRuTe	p	6.284

---

3.4 Validation and experiments

3.4.1 Literature based validation. In this section we compare our theoretically selected subspaces to experimental literature data. Several well-known high-performing half-Heuslers—including ScPtSb, YPtSb, ScRhTe, NbFeSb, TaFeSb, VFeSb, and ScAuSn—appear within our broader analysis,.^4,5,51–54 Their presence supports the validity of our approach and underscores the potential of our subspace framework to uncover similarly high-performing chemistries. The chosen subspaces intentionally emphasize less-explored, novel combinations that share key chemical and performance features with these known compounds, enabling targeted exploration of analogs that may offer comparable or improved thermoelectric behavior while expanding the discovery space. These subspaces not only encompass the top-performing chemistries computationally identified in this study, but also accurately account for trends in their transport properties. For example, well-known p-type YNiSb and YPtSb fall into the yttrium-based half-Heusler phases highlighted for low thermal conductivity. Several of the representatives of this family have been reported with promising thermoelectric properties. YPtSb,^54–56 YNiBi,⁵⁷ YNiSb,⁵⁴ and YPdSb⁵⁴ exhibited in experiment low lattice thermal conductivities of 2–4 Wm⁻¹ K¹ range, 2.5, 2.3, and 2.4 Wm⁻¹ K⁻¹, respectively. These values are significantly lower than those for other well known half-Heusler thermoelectrics in their pristine form at 300 K, e.g. for ZrNiSn,⁵⁸ TiNiSn,⁵⁸ ZrCoBi,³³ and VFeSb,⁵⁹ which exhibit lattice thermal conductivity of 8–13 Wm⁻¹ K⁻¹.

Reaching out to other properties, our calculations predicted extremely high mobility at 300 K for YPtSb: 2200 cm² V⁻¹ s⁻¹. One of the experimental reports confirms the prediction within the order of magnitude, reporting even higher mobility at room temperature, 4000 cm² V⁻¹ s⁻¹.⁶⁰ Here, it is worth noting that other experimental reports for YPtSb indicate lower mobility (164 cm² V⁻¹ s⁻¹ (ref. 55) and 300 cm² V⁻¹ s⁻¹ (ref. 56)), which may stem from large susceptibility of transport properties to disorder, typical for half-Heusler compounds.^61–63 When it comes to overall performance, YPtSb, for which one of the highest β is predicted here, was shown in experiment to have a zT of 0.6 at 1000 K in a single-sample study.⁵⁵ This, in combination with our identification of yttrium subspaces, suggests that there may be additional promising materials to be identified in these subspaces, given efforts of optimization by doping, alloying and other more intricate techniques.

It is also of interest to consider well-known TE materials not present in the selected subspaces, such as n-type NbCoSn. Although this compound ranks highly in our dataset, its high performance is an exception among typically low-performing chemistries based on the A-element. Conversely, some known compounds like n-type TaCoSn and p-type HfPtSn appear in the bottom third of our dataset when ranked. These observations indicate that while elemental subspaces capture broad performance trends, some compounds may lie outside these patterns and require additional descriptors for selection. Further, our computational analysis predicts idealized performance based on intrinsic properties, assuming optimal carrier type and concentration. Many of the known half-Heusler TEs may have been identified for their performance without targeted doping and optimization.

Our findings imply that higher performance may be achievable with less-explored species, provided carrier type and concentration are optimized. For example, while Zr compounds like ZrCoBi, ZrCoSb, and ZrPtSn are typically reported for p-type behavior, we predict high potential for n-type performance in Zr containing compounds. Specifically, we predict exceptional n-type performance for ZrIrSb, though achieving this will likely require specific synthesis and doping strategies. Fig. 5a shows a large stability region for ZrIrSb, indicated a variety of thermodynamic environments under which the material may be synthesized. Promising synthesis strategies likely lie in cation-rich regions of phase space, near phase boundaries with ZrSb and Zr₅Sb₃, to suppress V_Zr and achieve optimal performance.

3.4.2 Our experimental studies. The above experimental considerations focus on prior results for yttrium pnictides with a transition metal from the tenth group of the periodic table (Ni, Pd, and Pt). Our calculations similarly predict interesting properties for the less known group of rare-earth gold stannides (REAuSn), explored here as a testament to the chemistries encompassed by the subspaces identified in this work. While several Y- and Zr-based compounds are already known as decent thermoelectrics, e.g. ZrNiSn,⁶¹ ZrCoBi,³³ YPtSb,⁵⁵ YNiSb,⁶⁴ the Au-subspace appears uncharted and further motivates our experimental exploration. Thus, from the Au-based secondary subspace, we anticipated uniquely low lattice thermal conductivity for REAuSn half-Heuslers.

We first synthesized ScAuSn, which we predicted to be a narrow band gap semiconductor (E_g ≈ 100 meV, see Table S3†) and stable (Fig. 4 and 5b). The experimental low electrical resistivity and low Seebeck coefficient (Fig. 9b and c) are in concert with the predicted band structure. The measured room temperature mobility (ca. 30 cm² V⁻¹ s⁻¹) is also within a factor of two of the theoretical value for the valence band (17 cm² V⁻¹ s⁻¹). The lattice thermal conductivity for ScAuSn drops from 11 to 8 Wm⁻¹ K⁻¹ from RT to 575 K, which is in agreement with our predicted value of 8 Wm⁻¹ K⁻¹ at RT; see Fig. 9d.

Fig. 9 Experimental studies of rare-earth gold stannides revealed uniquely low thermal conductivity. Panel (a) displays almost single-phase XRD; panel (b) demonstrates similar semimetallic resistivity for all the samples. Sc_0.5Lu_0.5AuSn has the lowest ρ due to decent mobility and rather high carrier concentration, see Table 2. Panel (c) shows Seebeck coefficient, while (d) presents thermal conductivity – κ_tot with full symbols and κ_L with open symbols. Two dashed lines represent upper and lower limit of κ_L depending on the Lorenz number (see the text for details†).

The next natural step would be an attempt to synthesize the heavier counterpart in the series of rare-earth gold stannides: YAuSn, thereby also incorporating Y from the primary subspace. For this material we predicted that, consistent with many other yttrium-bearing half-Heuslers, it will show ultra low lattice thermal conductivity and good overall TE performance (ESI Table S4†). As indicated in Fig. 4, although computationally predicted to be stable, experimentally this compound is known to crystallize in hexagonal symmetry (space group P6₃mc) instead of the half-Heusler structure.⁶⁵ Given that the two phases are energetically competitive, a targeted synthesis approach addressing the possible multi-phase behavior could be explored to stabilize the half-Heusler phase.

Fortunately, the heaviest rare-earth element (Lu) is able to substitute yttrium, leading to LuAuSn crystallizing in a half-Heusler structure.⁶⁵ Hence, we synthesized LuAuSn, and obtained a semimetal with carrier concentration even higher than for ScAuSn; see Table 2 for values of carrier concentration at RT and Fig. 9b for resistivity. Accordingly, values of mobility at 300 K for LuAuSn are revealed to be rather low (4 cm² V⁻¹ s⁻¹) compared to the Sc-based counterpart; cf.Table 2. The lattice thermal conductivity showed a relatively steady value of 9 Wm⁻¹ K⁻¹ between 300 K and 650 K (see Fig. 9d).

Table 2 Carrier concentration (n_H), Hall mobility (μ_H), and mean sound velocity (v_s) for the synthesized rare-earth stannides

	n H [1/cm^3]	μ H [cm^2 V^−1 s^−1]	v s [m s^−1]
ScAuSn	2.6 × 10^20	31	2906
Sc0.5Lu0.5AuSn	9.5 × 10^20	19	2191
LuAuSn	1.7 × 10^21	4	2217

---

In order to optimize the properties measured for each 1 : 1 : 1 chemistry and more fully characterize the promising REAuSn space, we took the opportunity of making a heavily strained alloy between the gold stannides: Sc_0.5Lu_0.5AuSn. The so-obtained material turned out to be single phase (see Fig. 9a for XRD), with lattice parameter of 6.491 Å – close to the average of the parent ternaries.⁶⁵ The carrier concentration was also close to the average values of ScAuSn and LuAuSn (Table 2). Interestingly, despite significant differences in masses and sizes between Sc and Lu, the mobility maintained relatively high values of 19 cm² V⁻¹ s⁻¹ at RT (Table 2). Most importantly, we observed strong suppression of phonon transport. When we used the standard procedure for calculating the Lorenz number from Seebeck coefficient,⁴³ the lattice thermal conductivity dropped to 1.1 Wm⁻¹ K⁻¹ at 650 K. This is an ultra-low value compared to other half-Heusler thermoelectrics, including many best performing compounds.^66,67

Here, however, it is worth noting that for Sc_0.5Lu_0.5AuSn the majority contribution to thermal conductivity comes from the electronic component. In systems of that kind, precise estimation of lattice thermal conductivity may be difficult due to imperfections of the Franz–Wiedemann Law, see e.g. ref. 68. The Lorenz number generally is known to be in range 1.5–2.44 × 10⁻⁸ WΩ K².⁴³ The lower values are typical for intrinsic semiconductors. With increasing conductivity, the Lorenz number also increases; the top limit is relevant for metals.

To ensure transparency of our results, we calculated the upper and lower limit of κ_L, using the smallest and the largest available Lorenz numbers respectively. The range of possible κ_L values are visualized by dashed lines on Fig. 9d. At the highest temperature of measurement, κ_L calculated as such ranges between 0.9 Wm⁻¹ K⁻¹ and 2.3 Wm⁻¹ K⁻¹. We acknowledge that both LuAuSn and Sc_0.5Lu_0.5AuSn exhibit unusual thermal conductivity behavior at approximately 500 K and 475 K, respectively. Typically such drops in thermal conductivity can be related to subtle changes in structure or phase transitions, but more detailed structural analysis (e.g. high temperature synchrotron diffraction) would be necessary to fully understand this behavior.

To get a preliminary insight into the origin of this interesting finding, we measured sound velocities (v_s). The results are displayed in Table 2 and reveal that rare-earth gold stannides show relatively low v_s, down to ca. 2200 m s⁻¹ for LuAuSn and Sc_0.5Lu_0.5AuSn. This is indicative of soft bonding in the studied group. Here, it is worth mentioning that in recent years v_s values of 2800 m s⁻¹ for ZrCoBi³³ and 2500 m s⁻¹ for RNiSb compounds (R = Er, Tm, Lu)⁶⁹ were considered among the lowest for half-Heusler phases. In summary, we succeeded in obtaining low to ultra-low thermal conductivity due to point-defect disorder and extremely soft bonding for Sc_0.5Lu_0.5AuSn, as guided by the design rules and trends across chemistry identified in this work.

4 Conclusions

In this study, we examine 332 semiconducting ABC half-Heusler compounds, analyzing their electronic structure, stability, and transport properties critical for optimal thermoelectric performance. Our modified screening approach emphasizes patterns across families of materials rather than relying on individual material predictions. This strategy is especially valuable for transport properties – derived from semi-empirical models at the high-throughput scale – and allows us to extract robust trends and link them to chemical composition for tuning half-Heusler properties.

Such trends yield insights into desirable properties for different polarity semiconductors. For n-type materials, we seek half-Heuslers with sharp conduction band edges that yield low band effective mass, which directly contributes to high electron mobility. This characteristic is preferred over a high DOS effective mass due to the limited conduction band edge degeneracy typical of half-Heuslers. In p-type materials, uniquely high valence band degeneracy, achievable through various positions of valence band edge extrema, emerges as the most desirable trait. Such degeneracy, when combined with steep valence band edges where possible, is also favored over simple DOS effective mass trends. For both carrier types, we seek materials with lower lattice thermal conductivity (κ_L) to further maximize the thermoelectric quality factor, β.

Using these insights, we statistically identify promising elemental subspaces. Our analysis highlights A-elements Y and Zr as well as B-element Ir for n-type thermoelectric materials as a result of high electron mobility. Both n- and p-type performance in Y, as well as secondary subspace based on B-element Au, are driven by low lattice thermal conductivity. B-element Ir is notable for its subset of exceptionally high TE quality factors, driven by ultra-high valence band degeneracy in p-type. Our subspace framework not only recovers known high-performing half-Heuslers, validating its effectiveness, but also provides a versatile foundation for continued design and optimization within the broader half-Heusler chemical landscape. The design rules provided by this approach led to the synthesis of Sc_0.5Lu_0.5AuSn, a compound with uniquely low lattice thermal conductivity attributed to the presence of Lu and Au. Our findings offer valuable insights for the continued exploration of half-Heusler compounds. The subspace approach combines insights from proven high-performance compounds with opportunities to explore new chemistries, identifying drivers of TE performance and guiding element-specific optimization of half-Heusler transport properties.

Data availability

The data supporting this article have been included as part of the ESI and are also available at: https://github.com/ertekin-research-group/halfheusler-space.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

All authors acknowledge support from U.S. National Science Foundation Harnessing the Data Revolution program under Grant No. NSF OAC 2118201. AP and EE acknowledge support from the NSF DIGI-MAT program, Grant No. NSF 1922758. KC, MW, and EST acknowledge support from NSF 2350519. Computational resources were provided by the Advanced Cyberinfrastructure Coordination Ecosystem: Services Support (ACCESS) program through Bridges-2 at the Pittsburgh Supercomputing Center, allocation TG-MAT220011P.

Notes and references

1. T. Graf, C. Felser and S. S. Parkin, Prog. Solid State Chem., 2011, 39, 1–50.
2. W. Y. S. Lim, D. Zhang, S. S. F. Duran, X. Y. Tan, C. K. I. Tan, J. Xu and A. Suwardi, Front. Mater., 2021, 8, 745698.
3. R. Nesper, Z. Anorg. Allg. Chem., 2014, 640, 2639–2648.
4. G. Bergerhoff, R. Hundt, R. Sievers and I. Brown, J. Chem. Inf. Comput. Sci., 1983, 23, 66–69.
5. R. Gautier, X. Zhang, L. Hu, L. Yu, Y. Lin, T. O. Sunde, D. Chon, K. R. Poeppelmeier and A. Zunger, Nat. Chem., 2015, 7, 308–316.
6. K. Ciesielski, I. Wolanska, K. Synoradzki, D. Szymanski and D. Kaczorowski, Phys. Rev. Appl., 2021, 15, 044047.
7. K. Ciesielski, K. Synoradzki, I. Wolanska, P. Stachowiak, L. Kepinski, A. Jezowski, T. Tolinski and D. Kaczorowski, J. Alloys Compd., 2020, 816, 152596.
8. J. Carrete, N. Mingo, S. Wang and S. Curtarolo, Adv. Funct. Mater., 2014, 24, 7427–7432.
9. S. Chadov, X. Qi, J. Kübler, G. H. Fecher, C. Felser and S. C. Zhang, Nat. Mater., 2010, 9, 541–545.
10. H. Lin, L. A. Wray, Y. Xia, S. Xu, S. Jia, R. J. Cava, A. Bansil and M. Z. Hasan, Nat. Mater., 2010, 9, 546–549.
11. R. Chasmar and R. Stratton, Int. J. Electron., 1959, 7, 52–72.
12. F. A. Bipasha, L. C. Gomes, J. Qu and E. Ertekin, Front. Electron. Mater., 2022, 2, 1059684.
13. G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114.
14. J. Qu, V. Stevanović, E. Ertekin and P. Gorai, J. Mater. Chem. A, 2020, 8, 25306–25315.
15. P. Gorai, V. Stevanović and E. S. Toberer, Nat. Rev. Mater., 2017, 2, 1–16.
16. W. Chen, J.-H. Pöhls, G. Hautier, D. Broberg, S. Bajaj, U. Aydemir, Z. M. Gibbs, H. Zhu, M. Asta and G. J. Snyder, et al. , J. Mater. Chem. C, 2016, 4, 4414–4426.
17. P. Gorai, P. Parilla, E. S. Toberer and V. Stevanovic, Chem. Mater., 2015, 27, 6213–6221.
18. G. K. Madsen, J. Am. Chem. Soc., 2006, 128, 12140–12146.
19. S. A. Miller, P. Gorai, B. R. Ortiz, A. Goyal, D. Gao, S. A. Barnett, T. O. Mason, G. J. Snyder, Q. Lv and V. Stevanović, et al. , Chem. Mater., 2017, 29, 2494–2501.
20. J. Yan, P. Gorai, B. Ortiz, S. Miller, S. A. Barnett, T. Mason, V. Stevanović and E. S. Toberer, Energy Environ. Sci., 2015, 8, 983–994.
21. G. K. Madsen and D. J. Singh, Comput. Phys. Commun., 2006, 175, 67–71.
22. A. M. Ganose, J. Park, A. Faghaninia, R. Woods-Robinson, K. A. Persson and A. Jain, Nat. Commun., 2021, 12, 2222.
23. J. Qu, C. E. Porter, L. C. Gomes, J. M. Adamczyk, M. Y. Toriyama, B. R. Ortiz, E. S. Toberer and E. Ertekin, J. Mater. Chem. A, 2021, 9, 26189–26201.
24. S. Bhattacharya and G. K. Madsen, Phys. Rev. B:Condens. Matter Mater. Phys., 2015, 92, 085205.
25. T. Jia, Z. Feng, S. Guo, X. Zhang and Y. Zhang, ACS Appl. Mater. Interfaces, 2020, 12, 11852–11864.
26. A. D. Becke and E. R. Johnson, J. Chem. Phys., 2006, 124, 174104.
27. S. Wang, Z. Wang, W. Setyawan, N. Mingo and S. Curtarolo, Phys. Rev. X, 2011, 1, 021012.
28. L. Xi, S. Pan, X. Li, Y. Xu, J. Ni, X. Sun, J. Yang, J. Luo, J. Xi and W. Zhu, et al. , J. Am. Chem. Soc., 2018, 140, 10785–10793.
29. G. Joshi, X. Yan, H. Wang, W. Liu, G. Chen and Z. Ren, Adv. Energy Mater., 2011, 1, 643–647.
30. S. Li, H. Zhu, J. Mao, Z. Feng, X. Li, C. Chen, F. Cao, X. Liu, D. J. Singh and Z. Ren, et al. , ACS Appl. Mater. Interfaces, 2019, 11, 41321–41329.
31. P. Luo, C. Lin, Z. Li, J. Zhang and J. Luo, ACS Appl. Energy Mater., 2023, 6, 10070–10077.
32. G. Rogl, P. Sauerschnig, Z. Rykavets, V. Romaka, P. Heinrich, B. Hinterleitner, A. Grytsiv, E. Bauer and P. Rogl, Acta Mater., 2017, 131, 336–348.
33. H. Zhu, R. He, J. Mao, Q. Zhu, C. Li, J. Sun, W. Ren, Y. Wang, Z. Liu and Z. Tang, et al. , Nat. Commun., 2018, 9, 2497.
34. A. Sagar, A. Bhardwaj, M. Lamba, A. Novitskii, V. Khovaylo and S. Patnaik, Bull. Mater. Sci., 2024, 47, 146.
35. W. G. Zeier, J. Schmitt, G. Hautier, U. Aydemir, Z. M. Gibbs, C. Felser and G. J. Snyder, Nat. Rev. Mater., 2016, 1, 1–10.
36. G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169.
37. P. E. Blöchl, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 17953.
38. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
39. F. Birch, Elastic Properties and Equations of State, 1988, vol. 26, pp. 31–90.
40. S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319.
41. K. A. Borup, E. S. Toberer, L. D. Zoltan, G. Nakatsukasa, M. Errico, J.-P. Fleurial, B. B. Iversen and G. J. Snyder, Rev. Sci. Instrum., 2012, 83, year.
42. S. Iwanaga, E. S. Toberer, A. LaLonde and G. J. Snyder, Rev. Sci. Instrum., 2011, 82, year.
43. H.-S. Kim, Z. M. Gibbs, Y. Tang, H. Wang and G. J. Snyder, APL Mater., 2015, 3, year.
44. S. Guo, S. Anand, M. K. Brod, Y. Zhang and G. J. Snyder, J. Mater. Chem. A, 2022, 10, 3051–3057.
45. W. Xie, A. Weidenkaff, X. Tang, Q. Zhang, J. Poon and T. M. Tritt, Nanomaterials, 2012, 2, 379–412.
46. X. Yan, G. Joshi, W. Liu, Y. Lan, H. Wang, S. Lee, J. Simonson, S. Poon, T. Tritt and G. Chen, et al. , Nano Lett., 2011, 11, 556–560.
47. S. Sakurada and N. Shutoh, Appl. Phys. Lett., 2005, 86, 082105.
48. M. T. Dylla, A. Dunn, S. Anand, A. Jain and G. J. Snyder, Research, 2020, 6375171.
49. H. Zhu, J. Mao, Y. Li, J. Sun, Y. Wang, Q. Zhu, G. Li, Q. Song, J. Zhou and Y. Fu, et al. , Nat. Commun., 2019, 10, 270.
50. A. Grytsiv, V. Romaka, N. Watson, G. Rogl, H. Michor, B. Hinterleitner, S. Puchegger, E. Bauer and P. Rogl, Intermetallics, 2019, 111, 106468.
51. J. Yu, C. Fu, Y. Liu, K. Xia, U. Aydemir, T. C. Chasapis, G. J. Snyder, X. Zhao and T. Zhu, Adv. Energy Mater., 2018, 8, 1701313.
52. Y. Huang, K. Hayashi and Y. Miyazaki, Acta Mater., 2022, 237, 118186.
53. C. B. Evers, C. G. Richter, K. Hartjes and W. Jeitschko, J. Alloys Compd., 1997, 252, 93–97.
54. J. Oestreich, U. Probst, F. Richardt and E. Bucher, J. Phys.: Condens. Matter, 2003, 15, 635.
55. G. Li, K. Kurosaki, Y. Ohishi, H. Muta and S. Yamanaka, Jpn. J. Appl. Phys., 2013, 52, 041804.
56. S. Ouardi, G. H. Fecher, C. Felser, J. Hamrle, K. Postava and J. Pištora, Appl. Phys. Lett., 2011, 99, 211904.
57. S. Li, H. Zhao, D. Li, S. Jin and L. Gu, J. Appl. Phys., 2015, 117, year.
58. H. Hohl, A. Ramirez, W. Kaefer, K. Fess, C. Thurner, C. Kloc and E. Bucher, MRS Online Proceedings Library (OPL), 1997, vol. 478, p. 109.
59. D. Young, P. Khalifah, R. J. Cava and A. Ramirez, J. Appl. Phys., 2000, 87, 317–321.
60. C. Shekhar, S. Ouardi, A. K. Nayak, G. H. Fecher, W. Schnelle and C. Felser, Phys. Rev. B:Condens. Matter Mater. Phys., 2012, 86, 155314.
61. H. Xie, H. Wang, C. Fu, Y. Liu, G. J. Snyder, X. Zhao and T. Zhu, Sci. Rep., 2014, 4, 6888.
62. H.-H. Xie, J.-L. Mi, L.-P. Hu, N. Lock, M. Chirstensen, C.-G. Fu, B. B. Iversen, X.-B. Zhao and T.-J. Zhu, CrystEngComm, 2012, 14, 4467–4471.
63. D. Gnida, K. Ciesielski and D. Kaczorowski, Phys. Rev. B, 2021, 103, 174206.
64. M. J. Winiarski and K. Bilińska, Intermetallics, 2019, 108, 55–60.
65. C. P. Sebastian, H. Eckert, S. Rayaprol, R.-D. Hoffmann and R. Pöttgen, Solid State Sci., 2006, 8, 560–566.
66. W. Li, S. Ghosh, N. Liu and B. Poudel, Joule, 2024, 1274–1311.
67. K. Xia, C. Hu, C. Fu, X. Zhao and T. Zhu, Appl. Phys. Lett., 2021, 118, year.
68. A. A. Shawon, W. Guetari, K. Ciesielski, R. Orenstein, J. Qu, S. Chanakian, M. T. Rahman, E. Ertekin, E. Toberer and A. Zevalkink, Chem. Mater., 2024, 1908–1919.
69. K. Ciesielski, K. Synoradzki, I. Veremchuk, P. Skokowski, D. Szymański, Y. Grin and D. Kaczorowski, Phys. Rev. Appl., 2020, 14, 054046.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ta00397k

---