Open Access Article
Open Access ArticleMaximizing thermoelectric performance in SnTe through strategic co-doping, nanostructuring, and topological insights†
Peramaiyan
Ganesan
 *a,
Chandra Shekar
Gantepogu
a,
Sidharth
Duraisamy
a,
Phillip
Wu
*a,
Chandra Shekar
Gantepogu
a,
Sidharth
Duraisamy
a,
Phillip
Wu
 a,
Gwo-Tzong
Huang
a,
Muhammad Yusuf
Fakhri
a,
Kuei-Hsien
Chen
b,
Yang-Yuan
Chen
a,
Gwo-Tzong
Huang
a,
Muhammad Yusuf
Fakhri
a,
Kuei-Hsien
Chen
b,
Yang-Yuan
Chen
 a and
Maw-Kuen
Wu
*a
a and
Maw-Kuen
Wu
*a
aInstitute of Physics, Academia Sinica, Taiwan. E-mail: mkwu@phys.sinica.edu.tw; kutty.peram@gmail.com; Fax: +886-2-27896750; Tel: +886-2-27896716
bInstitute of Atomic and Molecular Sciences, Academia Sinica, Taiwan
First published on 21st February 2025
Abstract
Enhancing thermoelectric performance through doping is a pivotal strategy, optimizing carrier concentration, reducing energy band separation, and decreasing thermal conductivity. This study delves into the thermoelectric and magneto-transport properties of SnTe single crystals, recognized for their topological insulator characteristics. SnTe's unique electronic states, featuring highly conductive surface states protected by crystal symmetry, significantly boost electrical conductivity while maintaining low thermal conductivity. Consequently, a high thermoelectric figure of merit (ZT) of approximately 0.71 is achieved at 873 K along the (111) direction. By fine-tuning carrier concentration and employing nanostructuring techniques, we enhanced the ZT of pristine SnTe to 0.75 at 811 K. Additionally, we explored the co-doping effects of Mg, Ag, and Bi on the thermoelectric properties of self-compensated polycrystalline SnTe. Bi-doping effectively reduces carrier concentration, promotes valence band convergence, and lowers thermal conductivity. The co-doping of Bi and Ag induces valence band convergence, further amplified by Mg doping, resulting in high power factors of 20.7 and 22.8 μW cm−1 K−2 at 872 K in Sn0.94Ag0.03Bi0.06Te and Sn0.86Ag0.03Mg0.08Bi0.06Te, respectively. The all-scale hierarchical structure and elemental doping significantly reduce lattice thermal conductivity to ultra-low values of 0.135 and 0.123 W m−1 K−1 at 873 K in Sn0.94Ag0.03Bi0.06Te and Sn0.86Ag0.03Mg0.08Bi0.06Te, respectively. These combined effects yield high ZT values of approximately 1.6 and 2.01 at 873 K in Sn0.94Ag0.03Bi0.06Te and Sn0.86Bi0.06Ag0.03Mg0.08Te, respectively. Moreover, we conducted de Haas–van Alphen (dHvA) studies to further elucidate the topological surface state properties of SnTe. These investigations enabled us to extract critical parameters such as the cyclotron effective mass, Fermi surface area, and Fermi velocity, offering deeper insights into the electronic structure and enhancing our understanding of the material's unique characteristics. Our findings highlight the significant potential of co-doping and nanostructuring strategies in advancing the thermoelectric performance of SnTe, paving the way for the development of high-efficiency thermoelectric materials.
Introduction
Thermoelectric materials are pivotal in converting heat directly into electricity and vice versa, making them highly attractive for power generation, especially amid the current energy crisis. Applications of thermoelectric materials include waste heat recovery from industrial processes, automotive exhaust systems, and power generation in remote sensors and small-scale generators in the mid-temperature range (300–600 K), as well as power generation in space missions (radioisotope thermoelectric generators), high-efficiency waste heat recovery in steel and glass manufacturing, and geothermal energy conversion in the high-temperature range (600–1000 K).1–7 The efficiency of these materials is determined by the figure of merit (ZT), which depends on the Seebeck coefficient (S), electrical conductivity (σ), and total thermal conductivity (κtot), comprising electronic (κe) and lattice (κL) components. Optimizing the intertwined parameters of S and σ in the power factor (PF = S2σ) and κe is challenging, as they rely on carrier transport, necessitating carrier optimization strategies to enhance the power factor. However, increasing carrier concentration typically reduces S, limiting PF values. To address this, strategies such as band sharpening, band convergence, minority carrier blocking, and resonant state doping have been developed to intrinsically improve PF. Conversely, κL, which depends solely on phonon transport, can be significantly reduced through methods like alloying, nanostructuring,8 and incorporating nano precipitates.9–19Topological insulators (TIs) are promising candidates for thermoelectric applications due to their unique electronic properties. TIs have gapless surface states protected by time-reversal symmetry, which can contribute to high electrical conductivity while maintaining low thermal conductivity. The band inversion in TIs, driven by strong spin–orbit coupling, leads to a warped bulk electronic structure. This warping can enhance thermoelectric performance by reducing the transport mass and effectively increasing valley degeneracy.1,20–23 Materials like Bi2Te3 and Sb2Te3 are well-known TIs exhibiting excellent thermoelectric properties.24–26 These materials have been extensively studied for their potential in thermoelectric devices. Techniques such as alloying, strain engineering, and nanostructuring can be used to optimize the thermoelectric performance of TIs.27–29 SnTe (tin telluride) stands out due to its unique combination of properties. As a topological crystalline insulator (TCI), SnTe exhibits protected surface states that arise from its crystal symmetry.30,31 These surface states are robust against certain types of perturbations, making SnTe a promising candidate for applications in quantum computing and spintronics. On the thermoelectric front, SnTe is notable for its potential to convert waste heat into electricity. However, its thermoelectric performance has traditionally been limited by high hole carrier concentration, which results in a low Seebeck coefficient and high thermal conductivity.32,33 The energy separation between the light and heavy valence bands in SnTe, approximately 0.35 eV,34 can indeed pose a challenge for achieving a high power factor. This separation can limit the effective mass of the carriers and reduce the density of states near the Fermi level, which in turn affects the Seebeck coefficient and electrical conductivity. Both SnTe and PbTe have a cubic crystal structure at room temperature. However, SnTe undergoes a ferroelectric transition at low temperatures, while PbTe remains an incipient ferroelectric.35 In terms of band gap, SnTe has a direct band gap of approximately 0.18 eV,34 whereas PbTe has a slightly larger band gap of about 0.31 eV.36 Thermoelectrically, PbTe has historically shown superior performance with higher ZT values compared to SnTe. This is primarily due to PbTe's lower lattice thermal conductivity and better optimization of carrier concentration.37 Despite these advantages, the toxicity of lead limits the large-scale application of PbTe, making SnTe a more environmentally friendly alternative. The importance of using low-toxicity elements in thermoelectric materials arises from the need to ensure safety during synthesis, usage, and disposal, mitigating health risks and environmental pollution. To define and categorize low-toxicity elements, we referenced regulatory standards from agencies like the Environmental Protection Agency (EPA) and European Chemicals Agency (ECHA), reviewed scientific literature, and assessed biocompatibility and environmental impact. The selection of Mg, Ag, and Bi as dopants in SnTe was guided by their low toxicity, environmental friendliness, and ability to enhance thermoelectric properties. Recent research has focused on enhancing the thermoelectric properties of SnTe through various methods, including Bi doping and alloying with elements such as Ag, Mn, Zn, Cu, In, Se, Ge, Pd, (Ag, Mg), and CdSe.32,34,38–51 These strategies help to reduce carrier concentration and adjust the energy offset of the valence bands, thereby improving the thermoelectric figure of merit. Notably, Ag and Mg co-doping in SnTe has demonstrated significant band engineering effects, achieving a figure of merit of approximately 1.55 at 865 K.47 Additionally, MnCdTe2 alloying in SnTe has shown a remarkable figure of merit of about 1.97 at 900 K.40 However, the low average ZT and the use of toxic elements pose challenges for practical applications. Furthermore, advancements in nanostructuring and the incorporation of nano precipitates have shown promise in reducing lattice thermal conductivity, while emerging techniques like strain engineering and resonant state doping continue to push the boundaries of thermoelectric performance.
Our work thoroughly investigated the thermoelectric properties of both single and polycrystalline SnTe. We extracted key parameters such as the cyclotron effective mass, density of states effective mass, Fermi velocity, quantum mobility, and scattering lifetime from the de Haas–van Alphen quantum oscillations. Our directional studies on SnTe crystals revealed low lattice thermal conductivity along the [111] direction. Additionally, we demonstrated that nanostructuring is an effective approach for SnTe, leading to an enhanced average ZT compared to single-crystal SnTe. To further improve the ZT, we doped SnTe with Ag, Mg, and Bi, achieving a remarkable ZT of about ≈2.01 at 873 K in Sn0.86Ag0.03Mg0.08Bi0.06Te. Mg tunes carrier concentration, Ag boosts electrical conductivity, and Bi promotes valence band convergence, collectively improving performance while maintaining safety and sustainability.
The X-ray diffraction (XRD) patterns for the pristine and doped SnTe samples, shown in Fig. S1(a),† were obtained using Cu Kα radiation. The diffraction peaks correspond to the cubic rock-salt structure with a space group of Fm-3m, indicating that the main phase remains SnTe after doping. Significant shifts in diffraction peaks, as seen in Fig. S1(b),† are due to the incorporation of various dopants. To examine phase evolution and impurities, temperature-dependent synchrotron XRD was performed with a wavelength of 0.62 Å for Sn0.94Ag0.03Bi0.06Te and Sn0.86Ag0.03Mg0.08Bi0.06Te, as shown in Fig. 1. In Ag and Bi-doped SnTe, both Bi and Ag5Te3 precipitates are present. The Bi peak disappears above 523 K, indicating that Bi precipitates dissolve at higher temperatures, while the Ag5Te3 peak persists up to 873 K, showing its stability at elevated temperatures. In the Sn0.86Ag0.03Mg0.08Bi0.06Te sample, both MgTe and Ag5Te3 precipitates are observed, with the intensity of the MgTe (100) peak increasing up to 573 K and then decreasing, almost disappearing at 923 K. The intensity of the (100) peak of the MgTe precipitate gradually increases, reaching a maximum at 573 K, and then decreases, almost disappearing at 923 K. In samples doped with Ag, Bi, and Mg, the combined effects of these dopants are evident, with shifts in primary peaks reflecting changes in lattice parameters and additional peaks indicating the presence of Ag5Te3 and MgTe secondary phases. These structural changes and impurity phases, confirmed by the shifts in diffraction peaks, are crucial for understanding and optimizing the thermoelectric properties of SnTe.
The scanning transmission electron microscopy (STEM) image in Fig. 2(a) reveals MgTe nanoparticles with sizes ranging from 1.3 nm to 10 nm, indicating a uniform distribution within the matrix. Fig. 2(b) highlights the presence of MgTe precipitates, marked by white circles, suggesting successful doping and precipitation. In Fig. 2(c), the yellow rectangle designates the area of the main SnTe matrix where Fast Fourier transform (FFT) analysis was performed, with the inset displaying the FFT pattern, confirming the crystalline nature of the SnTe matrix. Fig. 2(d)–(f) present inverse FFT profiles for the (022), (113), and (111) planes, respectively, confirmed by d-spacing measurements. These profiles reveal lattice strain and dislocation defects within the material. The red arrows in these images point to specific features indicating these defects, while the insets show diffraction patterns that further corroborate the presence of these structural anomalies. The presence of MgTe precipitates is further confirmed by Energy Dispersive X-ray Spectroscopy (EDS) measurements, as shown in ESI Fig. S2.† The grain size distribution of Sn0.86Ag0.03Mg0.08Bi0.06Te sample is shown in Fig. S3.† The EDS analysis provides elemental mapping and composition data, verifying the distribution and concentration of MgTe within the sample. These observations suggest that the doping process has introduced significant lattice strain and defects, which could influence the thermoelectric properties of the material.
The thermoelectric properties of single crystal and polycrystalline SnTe were systematically compared to understand the influence of nanostructuring and to elucidate the intrinsic thermoelectric properties of SnTe. The electrical conductivity (σ) as a function of temperature (T) (Fig. 3(a)) shows that both single crystal and polycrystalline SnTe exhibit a decreasing trend with increasing temperature. However, the single crystal SnTe maintains a higher electrical conductivity across the temperature range, attributed to its higher carrier concentration (4.73 × 1020 cm−3) compared to the polycrystalline sample (5.26 × 1019 cm−3). The Seebeck coefficient (S) versus temperature (Fig. 3(b)) indicates an increasing trend for single-crystal and polycrystalline SnTe. Interestingly, the polycrystalline SnTe shows a higher Seebeck coefficient than the single crystal SnTe, which can be linked to the differences in carrier concentration and scattering mechanisms. The thermal conductivity (κ) as a function of temperature (Fig. 3(c)) is divided into electronic (κe) and lattice (κL) components. The polycrystalline SnTe exhibits lower thermal conductivity than the single crystal sample across the temperature range. This is likely due to increased phonon scattering at grain boundaries and defects in the polycrystalline structure. Additionally, the thermoelectric properties were studied along the [010] and [111] crystallographic directions, revealing that the [111] direction shows lower thermal conductivity than the [010] direction, which is consistent with reported phonon transport studies on SnTe. These studies highlight the strong anharmonicity in SnTe's phonon spectra, influenced by its resonant bonding and crystal structure, leading to different phonon lifetimes and scattering mechanisms along various crystallographic directions. The local off-centering of Sn2+ ions along the 〈111〉 direction creates significant lattice distortions and scattering centers, reducing thermal conductivity in this direction. In contrast, the 〈010〉 direction experiences fewer distortions and less scattering, resulting in higher thermal conductivity.35,52–54 The polycrystalline SnTe shows lower κL of 0.47 W m−1 K−1 at 500 K, but an increased trend at higher temperatures due to bipolar contribution. While the complete phase transition to a rhombohedral structure (full ferroelectric phase) occurs below 114 K (Fig.S6(a)†), these local ferroelectric domains persist in the cubic phase above 114 K, all the way to high temperatures. Studies have confirmed these local domains at room temperature,52 significantly influencing SnTe's thermal and electrical properties. The interplay between cubic and ferroelectric phases could introduce phonon Berry curvature, resulting in phenomena like the nonlinear phonon Hall effect, further modulating heat transport. This transition at 112 K in the MT (magnetization vs. temperature) curve for the polycrystalline sample aligns well with our resistivity findings (Fig.S6(b)†). It indicates that the phase transition is indeed affecting the magnetic properties. The fact that it's less pronounced in the single crystal but still visible suggests that the structural transition impacts both types but is more accentuated in polycrystalline due to increased scattering at grain boundaries and defects. Such observations highlight the intricate interplay between structural phase transitions and magnetic properties, which can be pivotal for understanding the material's full range of behaviors and potential applications. By ruling out carrier concentration dependent phase transition speculation,55 our findings provide a clearer focus on the intrinsic structural influences at play. The figure of merit (ZT) versus temperature (Fig. 3(d)) demonstrates that ZT values increase with temperature for both single crystal and polycrystalline SnTe. However, the polycrystalline SnTe achieves higher ZT values compared to the single crystal SnTe, indicating superior thermoelectric performance. The average ZT of polycrystalline SnTe is about 0.29 for the temperature range of 300 to 811 K and 0.34 for 500 to 811 K.
The weighted mobility (μW) versus T (Fig. 3(e)) shows a decreasing trend with increasing log(T) for both types of SnTe. The single crystal SnTe maintains higher mobility, which can be attributed to fewer grain boundaries and defects, leading to less scattering of charge carriers. The temperature dependence of the weighted mobility provides insights into the scattering mechanisms at play. The temperature dependence of the weighted mobility reveals that for single crystal SnTe, the mobility follows a T−2 dependence up to the mid-temperature range, indicating significant phonon-boundary scattering and transitions to a T−1 dependence at high temperatures, where phonon–phonon Umklapp scattering becomes dominant. In contrast, polycrystalline SnTe exhibits a T−1.4 dependence up to the mid-temperature range, suggesting boundary and defect scattering, and a T−2.05 dependence at high temperatures, likely due to grain boundary and defect scattering. The log(κL) versus log(T) plot (Fig. 3(f)) presents the lattice thermal conductivity as a function of temperature on a logarithmic scale for a single crystal. The linear fit applied to the data indicates that single-crystal SnTe has lower lattice thermal conductivity along the (111) direction than the (010) direction, confirming the anisotropic phonon dispersion and further supporting directional-dependent scattering mechanisms.
In this study, we investigated the de Haas–van Alphen (dHvA) oscillations in SnTe single crystals along the (010) crystallographic direction, as shown in Fig. 4(a). The magnetization measurements were conducted at low temperatures, and the data were analyzed using the Lifshitz–Kosevich (L–K) fit to extract key electronic properties. The L–K formula accounts for multiple valleys, increasing the effective mass by providing more available states for carriers.56 The cyclotron effective mass  of the charge carriers in single crystal SnTe was determined to be 0.09 me (Fig. 4(b)) from de Haas–van Alphen (dHvA) measurements at 3 K, indicating that the charge carriers are light and contribute to higher mobility. Measurements along the [010] and [111] crystallographic directions yielded consistent values for the cyclotron effective mass, confirming the isotropic nature of the band structure in SnTe. Consequently,
of the charge carriers in single crystal SnTe was determined to be 0.09 me (Fig. 4(b)) from de Haas–van Alphen (dHvA) measurements at 3 K, indicating that the charge carriers are light and contribute to higher mobility. Measurements along the [010] and [111] crystallographic directions yielded consistent values for the cyclotron effective mass, confirming the isotropic nature of the band structure in SnTe. Consequently, 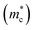 can be reliably equated to
can be reliably equated to  in this material. However, different thermal conductivities observed along these directions indicate anisotropic lattice dynamics. For pristine polycrystalline SnTe, the density of states (DOS) effective mass
in this material. However, different thermal conductivities observed along these directions indicate anisotropic lattice dynamics. For pristine polycrystalline SnTe, the density of states (DOS) effective mass  was estimated to be 0.173 me using the Snyder57,58 formula at 300 K. This difference highlights the impact of crystallographic structure and temperature on the effective mass. The consistency between the effective masses obtained using different methods and conditions indicates a robust electronic structure across different modelling approaches.
was estimated to be 0.173 me using the Snyder57,58 formula at 300 K. This difference highlights the impact of crystallographic structure and temperature on the effective mass. The consistency between the effective masses obtained using different methods and conditions indicates a robust electronic structure across different modelling approaches.
The scattering lifetime was found to be approximately 1.899 × 10−23 s at 3 K and 1.845 × 10−23 s at 4 K (Fig. 4(c)). The quantum mobility was calculated to be 3368 cm2 V−1 s−1 at 3 K and 3281 cm2 V−1 s−1 at 4 K, confirming the efficient transport properties of the charge carriers in SnTe. This is in close agreement with the Hall mobility of about 3221 cm2 V−1 s−1 at 3 K. Fig. 4(d) shows the Fast Fourier Transform (FFT) analysis of the dHvA oscillations revealed frequencies of 37 T for the (010) direction and 52 T for the (111) direction, corresponding to Fermi surface areas of 3.528 × 10−3 Å−2 and 4.958 × 10−3 Å−2, respectively. The Fermi vectors were found to be 0.033 Å−1 for the (010) direction and 0.039 Å−1 for the (111) direction, with corresponding velocities of 4.31 × 105 m s−1 and 5.11 × 105 m s−1. These values suggest that the charge carriers experience relatively infrequent scattering events, indicative of high crystal quality and low impurity levels. The extracted parameters align with those reported in the literature,31 indicating the presence of a nontrivial Berry phase and confirming the existence of topological surface states in SnTe,30 as supported by studies such as the one by Dybko et al.31 Notably, we observed that the DOS effective mass for single crystal SnTe is significantly higher (0.648 me) than polycrystalline SnTe (0.174 me) at 300 K. Despite an order of magnitude difference in carrier concentration, the Seebeck coefficient remains relatively stable, measuring 24 μV K−1 for single crystal and 25 μV K−1 for polycrystalline SnTe at 300 K. This stability suggests that the intrinsic electronic properties are optimized through the material's unique characteristics. The presence of topological surface states and a Dirac cone in single crystal SnTe, which introduces linear band dispersion, likely contributes to the higher DOS effective mass. These topological surface states enhance the electronic properties by providing additional electronic pathways, which are more pronounced in the single crystal form due to the absence of grain boundaries and defects. Given that the Seebeck coefficient remains consistent across both forms, efforts should be focused on minimizing lattice thermal conductivity to improve thermoelectric performance. These observations collectively suggest that the nanostructuring process has introduced significant lattice strain and defects, which play a crucial role in influencing the thermoelectric properties of SnTe along with topological surface states. Interestingly, polycrystalline SnTe demonstrates better ZT values than single-crystal SnTe. However, the single crystal SnTe still shows comparable ZT, benefiting from higher carrier concentration, better crystallinity, and lower lattice thermal conductivity. This highlights the robust thermoelectric performance of SnTe across different structural forms.
Fig. 5 illustrates the thermoelectric properties of polycrystalline Sn1.03Te with various dopants. The electrical conductivity (σ) of all samples decreases with temperature, indicating a degenerate semiconductor character, as shown in Fig. 5(a). Self-compensated SnTe exhibits high electrical conductivity of approximately 7670 S cm−1, with a carrier mobility of around 908 cm2 V−1 s−1. Ag-doping enhances conductivity at high temperatures by increasing the carrier concentration from 5.27 × 1019 cm−3 to 1.89 × 1020 cm−3. In contrast, the conductivity of Sn0.95Mg0.08Te decreases to 2347 S cm−1, though it maintains decent σ at high temperatures. Combined doping with Ag (3 atm%), Bi (6 atm%), and Mg (8 atm%) in Sn1.03Te further reduces conductivity to 1703 S cm−1 due to lower carrier concentration and enhanced carrier scattering. Fig. 5(b) shows that Mg doping results in a higher Seebeck coefficient than singly and doubly doped SnTe. Combined doping with Ag, Mg, and Bi balances these effects, resulting in high Seebeck coefficients. This combination achieves a high power factor of approximately 22.8 μW cm−1 K−2 at 872 K, as shown in Fig. 5(c). Fig. 5(d) illustrates the variation in carrier concentration (nh) and mobility (μh) for different dopings. Excess Sn significantly reduces the hole concentration while maintaining high carrier mobility. Notably, in Mg-doped SnTe, nh is significantly decreased to 4.80 × 1019 cm−3 with mobility of 293 cm2 V−1 s−1. Since Mg is likely to be 2+ like Sn, it mitigates the formation of Sn vacancies, which helps maintain a lower carrier concentration and enhances the Seebeck coefficient. In triply doped Sn0.86Ag0.03Mg0.08Bi0.06Te, the carrier concentration slightly increases to 9.9 × 1019 cm−3, while maintaining a mobility of 112.07 cm2 V−1 s−1.
Our research has demonstrated an enhanced power factor in doped SnTe, primarily due to an increased Seebeck coefficient. However, the precise mechanisms behind this improvement were not fully understood. To gain deeper insights, we conducted a detailed analysis using Pisarenko plots and density of states (DOS) effective mass calculations. We utilized the Pisarenko plot methodology reported by Riddhimoy Pathak et al.,47 which accounts for contributions from both light and heavy hole valence bands. The Pisarenko curve plots the room temperature Seebeck coefficients of SnTe and its doped variants against carrier concentration, considering contributions from both light and heavy hole valence bands with varying energy gaps, as shown in Fig. 6(a). The energy difference between the light and heavy bands is approximately 0.35 eV.47 For pristine SnTe, the Seebeck value follows the single-band contribution. Bi-doped SnTe matches the curve for a 0.27 eV energy difference, while Ag and Bi co-doped SnTe shows a Seebeck value well above the single band contribution. Mg doping significantly decreases the energy difference, aligning closely with 0.10 eV. The triply-doped Ag, Mg, and Bi in SnTe also aligns closely with 0.10 eV, better than singly and doubly co-doped SnTe. Additionally, Bi doping, whether with Mg, Ag, or both, subtly decreases the energy difference, contributing to the overall enhancement of thermoelectric properties.
 | ||
| Fig. 6 (a) Pisarenko plot showing the Seebeck coefficient versus carrier concentration for SnTe, considering contributions from both light and heavy hole valence bands with varying energy gaps (ΔE ≈ 0.35 eV, 0.28 eV, 0.27 eV and 0.10 eV).47 (b) Density of states effective mass for pristine and doped SnTe samples. Ag, Mg, and Bi doping increase the effective mass, with Mg doping alone showing a significant increase. | ||
The DOS effective mass  was calculated using the expression reported by Snyder et al., as shown in Fig. 6(b). For pristine SnTe (Sn1.03Te), the DOS effective mass is 0.173 me. When doped with Ag, the DOS effective mass increases to 0.319 me, and with Mg doping alone, it further increases to 0.353 me. Bi-doping results in a lower DOS effective mass of 0.167 me. Co-doping with Ag and Bi increases the DOS effective mass to 0.325 me, while Mg and Bi co-doping results in a DOS effective mass of 0.327 me. Ag and Mg co-doping significantly increases the DOS effective mass to 0.605 me, and triply doping with Ag, Mg, and Bi further increases it to 0.627 me. Importantly, the carrier concentration of all samples is in the range of 4.8 to 9.9 × 1019 cm−3, which is not significantly different from pristine Sn1.03Te. This consistency in carrier concentration allows us to attribute the observed changes in band structure primarily to the doping effects. Mg doping significantly decreases the energy difference between the lighter and heavier bands, thereby increasing the DOS effective mass. This is consistent with the estimated effective mass values. The combined doping strategies of Ag, Mg, and Bi further enhance the thermoelectric properties by optimizing the band structure. These findings highlight the importance of doping strategies in tuning the electronic properties of SnTe for improved thermoelectric performance.
was calculated using the expression reported by Snyder et al., as shown in Fig. 6(b). For pristine SnTe (Sn1.03Te), the DOS effective mass is 0.173 me. When doped with Ag, the DOS effective mass increases to 0.319 me, and with Mg doping alone, it further increases to 0.353 me. Bi-doping results in a lower DOS effective mass of 0.167 me. Co-doping with Ag and Bi increases the DOS effective mass to 0.325 me, while Mg and Bi co-doping results in a DOS effective mass of 0.327 me. Ag and Mg co-doping significantly increases the DOS effective mass to 0.605 me, and triply doping with Ag, Mg, and Bi further increases it to 0.627 me. Importantly, the carrier concentration of all samples is in the range of 4.8 to 9.9 × 1019 cm−3, which is not significantly different from pristine Sn1.03Te. This consistency in carrier concentration allows us to attribute the observed changes in band structure primarily to the doping effects. Mg doping significantly decreases the energy difference between the lighter and heavier bands, thereby increasing the DOS effective mass. This is consistent with the estimated effective mass values. The combined doping strategies of Ag, Mg, and Bi further enhance the thermoelectric properties by optimizing the band structure. These findings highlight the importance of doping strategies in tuning the electronic properties of SnTe for improved thermoelectric performance.
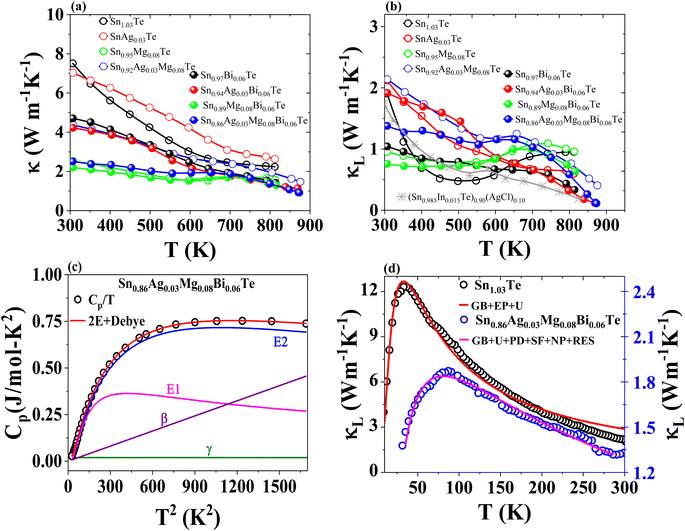
The thermal conductivity of SnTe and its doped variants with Ag, Mg, and Bi is shown in Fig. 7. Pristine Sn1.03Te shows a room temperature thermal conductivity of about 7.95 W m−1 K−1, which is lower than reported values. It decreases significantly with temperature up to 650 K and then starts to increase due to bipolar contribution (Fig. 7(a)). Ag doping slightly increases the total thermal conductivity due to enhanced electronic thermal conductivity. Mg doping results in a very low total thermal conductivity of about 2.48 W m−1 K−1, with an upward trend above 600 K and a decline after 700 K. Bi doping alone shows a remarkable reduction in κtot without bipolar contribution, attributed to reduced electronic thermal conductivity, point defects, and Bi precipitates. Co-doping with Ag and Bi significantly reduces thermal conductivity, particularly at high temperatures, due to point defects, large mass and strain field fluctuations, and Bi and Ag5Te3 precipitates. Ag5Te3 is known for its intrinsically low thermal conductivity, primarily due to its complex crystal structure and low sound velocity.59 Mg and Bi co-doping results in an almost flat thermal conductivity trend from 300 K to 811 K with a suppressed bipolar contribution. The combination of Ag, Mg, and Bi doping reduces κtot to 0.91 W m−1 K−1 at 873 K, with κL as low as 0.123 W m−1 K−1, as shown in Fig. 7(b), this reduction is comparable to the values obtained in (Sn0.985In0.015Te)0.90(AgCl)0.10, as shown in Fig. 7(b) of the referenced study.60 It is clear that MgTe, Sn, Bi, and Ag5Te3 precipitates contribute to reducing κL.
To further understand such ultralow κL, we conducted Debye–Callaway61,62 and Debye–Einstein model63 analyses. The Debye–Einstein model was specifically chosen for Cp analysis because it effectively captures the contributions of both acoustic and optical phonon modes, which are crucial for understanding the phonon scattering mechanisms in doped SnTe. Optical phonon modes introduce additional phonon scattering and impede the normal transport of acoustic phonons with similar frequencies, resulting in low κL. The temperature-dependent Cp data is fitted well with one Debye mode and two Einstein modes (Fig. 7(c)). From the fitted parameters (given in Table S1†), the Debye temperature (θD) is estimated to be 126.6 K. We extended the thermal conductivity analysis using average sound velocity (1658 m s−1)47 and θD to understand the influence of different phonon scattering mechanisms on the ultralow κL of the (Ag, Mg, and Bi) co-doped SnTe. The measured κL below 300 K is fitted based on the Debye–Callaway model, as shown in Fig. 7(d), by considering phonon scattering mechanisms such as the Umklapp process (U), boundary scattering (B), point-defect scattering related to mass and strain field fluctuations (PD), nanoparticle scattering (NP), stacking faults scattering (SF), and resonant scattering (RES). The model is selected due to its comprehensive approach to phonon transport, providing a robust framework for analyzing complex materials. However, it has limitations arising from simplifying assumptions, such as the phonon dispersion relation, which may not fully capture the material's complexity. Additionally, the model's accuracy heavily depends on precisely determined scattering parameters, with minor inaccuracies potentially leading to significant deviations. Discrepancies between experimental and modelled values, especially at low temperatures, may occur due to these assumptions, inhomogeneities in doping concentration and distribution, and experimental measurement errors. The phonon mean free path of SnTe is about 10 nm.64 In Sn0.86Ag0.03Mg0.08Bi0.06Te, MgTe nanoprecipitates with sizes varying from 1.3 nm to 10 nm are effective in scattering phonons and thus reducing κL. Additionally, the presence of Ag5Te3 precipitates, a low thermal conductivity material, further contributes to the reduction in thermal conductivity. The Debye–Einstein model analysis revealed two Einstein modes and one Debye mode, indicating the presence of optical phonon modes that introduce additional phonon scattering. These combined effects of nanoprecipitates, precipitates of low thermal conductivity materials, and the presence of optical phonon modes result in the observed ultralow κL in our doped SnTe samples. These findings provide a comprehensive understanding of the factors contributing to reduced thermal conductivity, which is crucial for optimizing the thermoelectric performance of SnTe.
Fig. 8(a) shows the thermoelectric figure of merit (ZT) for SnTe and its doped variants (Ag, Mg, and Bi) as a function of temperature, highlighting the enhanced performance due to doping. Fig. 8(b) compares the average ZT values of these doped SnTe compounds over two temperature ranges (300–870 K and 500–870 K) with other reported SnTe materials, demonstrating the superior thermoelectric efficiency of the doped SnTe variants. This indicates that doping SnTe with these elements significantly improves its thermoelectric properties, making it a promising material for thermoelectric applications. Notably, Sn0.92Ag0.03Mg0.08Te shows a ZT of about ≈1.55 at 865 K, consistent with reported data. Pristine nanostructured SnTe exhibits better average ZT than other reported values. Ag and Bi doping enhances ZT, similar to Ag and Mg doping, but with less impressive average ZT. Mg doping significantly increases average ZT, achieving a peak ZT of about ≈2 at 873 K and an average ZT of ≈0.66 between 300–873 K. We fairly reproduced the thermoelectric data as shown in Fig. S4.† Fig. S5† shows the thermogravimetric curve of Sn0.86Ag0.03Mg0.08Bi0.06Te. The 5% of weight loss above 823 K to 873 K does not show any significant changes in thermoelectric transport data.
 | ||
| Fig. 8 Thermoelectric performance comparison of doped SnTe compounds: (a) ZT values as a function of temperature for various doped SnTe variants,65 and (b) average ZT values over different temperature ranges compared with other reported materials. | ||
To understand the doping effects on the topological characteristics, we performed a resistivity analysis of pristine and doped polycrystalline SnTe, revealing significant insights into their topological characteristics. The resistivity model used in this analysis is 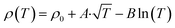 , where ρ0 represents the residual resistivity, A corresponds to weak antilocalization (WAL) effects, and B corresponds to weak localization (WL) or electron–electron interactions (EEI) effects. This model is based on the weak antilocalization theory described in detail by Hikami, Larkin, and Nagaoka (1980).66,67 Pristine SnTe exhibits high intrinsic conductivity (ρ0 = 7.39 × 10−7 Ω m), strong weak antilocalization (WAL) effects (A = 3 × 10−7 Ω m), and pronounced weak localization (WL) effects (B = −5.68 × 10−7 Ω m), indicating robust topological surface states and quantum interference effects typical of topological insulators. Interestingly, pristine SnTe shows a metal–insulator (M–I) transition at approximately 12.5 K, indicating the presence of complex interactions and possible disorder even in the pristine sample, as shown in Fig. S7.† In contrast, doped SnTe shows increased residual resistivity (ρ0 = 4.23 × 10−6 Ω m) due to introduced disorder and impurities but retains weak antilocalization effects (A = 1.52 × 10−7 Ω m), suggesting the preservation of some topological characteristics. The weaker WL effects (B = −2.29 × 10−7 Ω m) and the observation of an M–I transition at approximately 10 K in doped SnTe highlight the significant impact of disorder introduced by doping, disrupting conductive pathways and altering electronic behavior.
, where ρ0 represents the residual resistivity, A corresponds to weak antilocalization (WAL) effects, and B corresponds to weak localization (WL) or electron–electron interactions (EEI) effects. This model is based on the weak antilocalization theory described in detail by Hikami, Larkin, and Nagaoka (1980).66,67 Pristine SnTe exhibits high intrinsic conductivity (ρ0 = 7.39 × 10−7 Ω m), strong weak antilocalization (WAL) effects (A = 3 × 10−7 Ω m), and pronounced weak localization (WL) effects (B = −5.68 × 10−7 Ω m), indicating robust topological surface states and quantum interference effects typical of topological insulators. Interestingly, pristine SnTe shows a metal–insulator (M–I) transition at approximately 12.5 K, indicating the presence of complex interactions and possible disorder even in the pristine sample, as shown in Fig. S7.† In contrast, doped SnTe shows increased residual resistivity (ρ0 = 4.23 × 10−6 Ω m) due to introduced disorder and impurities but retains weak antilocalization effects (A = 1.52 × 10−7 Ω m), suggesting the preservation of some topological characteristics. The weaker WL effects (B = −2.29 × 10−7 Ω m) and the observation of an M–I transition at approximately 10 K in doped SnTe highlight the significant impact of disorder introduced by doping, disrupting conductive pathways and altering electronic behavior.
Our comprehensive study reveals significant enhancements in the thermoelectric performance of SnTe through strategic doping and nanostructuring, capitalizing on its topological insulator properties. The highly conductive surface states of SnTe, protected by crystal symmetry, contribute to high electrical conductivity while maintaining low thermal conductivity. Doping with Mg, Ag, and Bi optimizes carrier concentration, induces valence band convergence, and reduces thermal conductivity through solid solution point defects and nanoprecipitates. Mg plays a crucial role in band engineering, increasing the density of states (DOS) effective mass, and reducing thermal conductivity, particularly at low temperatures. However, its impact on thermal conductivity is less significant at high temperatures. In contrast, Bi doping effectively reduces thermal conductivity across a broader temperature range, while also optimizing carrier concentration, reducing the energy difference between valence bands, and introducing lattice strain. Ag enhances the effective mass  , and when combined with Mg, it further increases the DOS effective mass more effectively than either element alone. HRTEM and synchrotron X-ray diffraction measurements support the presence of MgTe nanoprecipitates and Ag5Te3 and MgTe secondary phases. These synergistic effects result in high power factors and substantial improvements in the thermoelectric figure of merit (ZT), with peak values reaching approximately ≈2 at 873 K. Additionally, de Haas–van Alphen (dHvA) studies provided deeper insights into the topological surface state properties of SnTe, further elucidating its unique electronic structure. Our dHvA oscillation studies confirm the isotropic electronic band structure, whereas thermal transport studies reveal the anisotropic phonon transport. These findings underscore the potential of co-doping and nanostructuring strategies in developing high-efficiency thermoelectric materials, paving the way for future advancements in thermoelectric technology.
, and when combined with Mg, it further increases the DOS effective mass more effectively than either element alone. HRTEM and synchrotron X-ray diffraction measurements support the presence of MgTe nanoprecipitates and Ag5Te3 and MgTe secondary phases. These synergistic effects result in high power factors and substantial improvements in the thermoelectric figure of merit (ZT), with peak values reaching approximately ≈2 at 873 K. Additionally, de Haas–van Alphen (dHvA) studies provided deeper insights into the topological surface state properties of SnTe, further elucidating its unique electronic structure. Our dHvA oscillation studies confirm the isotropic electronic band structure, whereas thermal transport studies reveal the anisotropic phonon transport. These findings underscore the potential of co-doping and nanostructuring strategies in developing high-efficiency thermoelectric materials, paving the way for future advancements in thermoelectric technology.
Data availability
The data that support the findings of this study are available from the corresponding author, upon reasonable request. The data include [brief description of data types, such as raw data, processed data, ESI,†etc.]. Due to [any reasons for restrictions, such as privacy or ethical concerns], certain data are not publicly available but can be shared under specific conditions.Author contributions
P. G. designed the project, prepared the samples, and P. G. and S. D. performed thermoelectric transport measurements. C. G. conducted the powder X-ray diffraction and magnetization measurements. P. G. and S. D. conducted TEM experiments and analyzed magnetization data. M. Y. F. performed the diffusivity measurement. P. W. supervised, reviewed, and edited the manuscript. G. T. H. performed the synchrotron X-ray diffraction measurements. Y. Y. conceptualized the project and provided material processing facilities. K. H. C. provided the facility for the diffusivity measurement. P. G. contributed to data analysis, writing the original draft, review, and editing. M. K. contributed to conceptualization, investigation, resources, supervision, funding acquisition, review, and editing.Conflicts of interest
The authors declare no competing interests.Acknowledgements
The authors thank Taiwan’s Ministry of Science and Technology (MOST) for the research startup grant (MOST110-2112-M-001-063) and Center for Sustainability Science, Academia Sinica [project AS-SS-112–01]. Phillip M. Wu acknowledges the support from the National Science and Technology Council of Taiwan grant number NSTC 113-2112-M-001-022-MY2. We extend our sincere gratitude to the Core Facility Center of National Cheng Kung University for the FIB facility and the Institute of Physics, Academia Sinica, for providing the X-ray diffraction measurement facilities. Our thanks also go to Dr Sankar Raman for the crystal growth facilities and Dr Ou Min-Nan for the Lau-X-ray diffraction facility.References
- I. Petsagkourakis, K. Tybrandt, X. Crispin, I. Ohkubo, N. Satoh and T. Mori, Sci. Technol. Adv. Mater., 2018, 19, 836–862 CrossRef CAS PubMed
.
- B. Ma, H. Ren, F. Zhang, Z. Peng, H. He, M. Cui, Z. Ge, B. Li, W. Wu, P. Liang, Y. Xiao, X. Chao, Z. Yang and D. Wu, Small, 2023, 19, 2206439 CrossRef CAS PubMed
.
- K. Biswas, Z. Ren, Y. Grin, K. H. Lee, T. Mori and L. Chen, Appl. Phys. Lett., 2022, 121, 070401 CrossRef CAS
.
- Y. Pei, X. Shi, A. LaLonde, H. Wang, L. Chen and G. J. Snyder, Nature, 2011, 473, 66–69 Search PubMed
.
- K. Song, A. N. M. Tanvir, M. O. Bappy and Y. Zhang, Small Sci., 2024, 2300359 CrossRef
.
- J. P. Heremans, V. Jovovic, E. S. Toberer, A. Saramat, K. Kurosaki, A. Charoenphakdee, S. Yamanaka and G. J. Snyder, Science, 2008, 321, 554–557 CrossRef CAS PubMed
.
- Y. Xiao, D. Wang, B. Qin, J. Wang, G. Wang and L.-D. Zhao, J. Am. Chem. Soc., 2018, 140, 13097–13102 CrossRef CAS PubMed
.
- Q. Zhang, B. Liao, Y. Lan, K. Lukas, W. Liu, K. Esfarjani, C. Opeil, D. Broido, G. Chen and Z. Ren, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 13261–13266 CrossRef CAS PubMed
.
- Q. Zhang, B. Liao, Y. Lan, K. Lukas, W. Liu, K. Esfarjani, C. Opeil, D. Broido, G. Chen and Z. Ren, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 13261–13266 CrossRef CAS PubMed
.
- D. Sarkar, T. Ghosh, A. Banik, S. Roychowdhury, D. Sanyal and K. Biswas, Angew. Chem., Int. Ed., 2020, 59, 11115–11122 CrossRef CAS PubMed
.
- R. Pathak, D. Sarkar and K. Biswas, Angew. Chem., Int. Ed., 2021, 60, 17686–17692 CrossRef CAS PubMed
.
- Z. Liu, W. Gao, H. Oshima, K. Nagase, C.-H. Lee and T. Mori, Nat. Commun., 2022, 13, 1120 CrossRef CAS PubMed
.
- Y. Xiao, D. Wang, Y. Zhang, C. Chen, S. Zhang, K. Wang, G. Wang, S. J. Pennycook, G. J. Snyder, H. Wu and L.-D. Zhao, J. Am. Chem. Soc., 2020, 142, 4051–4060 CrossRef CAS PubMed
.
- M. Samanta and K. Biswas, J. Am. Chem. Soc., 2017, 139, 9382–9391 CrossRef CAS PubMed
.
- H. Wu, C. Chang, D. Feng, Y. Xiao, X. Zhang, Y. Pei, L. Zheng, D. Wu, S. Gong, Y. Chen, J. He, M. G. Kanatzidis and L.-D. Zhao, Energy Environ. Sci., 2015, 8, 3298–3312 RSC
.
- J.-S. Liang, X.-L. Shi, Y. Peng, W.-D. Liu, H.-Q. Yang, C.-Y. Liu, J.-L. Chen, Q. Zhou, L. Miao and Z.-G. Chen, Adv. Energy Mater., 2022, 12, 2201086 CrossRef CAS
.
- Y. Luo, S. Cai, X. Hua, H. Chen, Q. Liang, C. Du, Y. Zheng, J. Shen, J. Xu, C. Wolverton, V. P. Dravid, Q. Yan and M. G. Kanatzidis, Adv. Energy Mater., 2019, 9, 1803072 CrossRef
.
- Z. Liu, J. Sun, J. Mao, H. Zhu, W. Ren, J. Zhou, Z. Wang, D. J. Singh, J. Sui, C.-W. Chu and Z. Ren, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5332–5337 CrossRef CAS PubMed
.
- Y. Zheng, Q. Zhang, X. Su, H. Xie, S. Shu, T. Chen, G. Tan, Y. Yan, X. Tang, C. Uher and G. J. Snyder, Adv. Energy Mater., 2015, 5, 1401391 CrossRef
.
- M. Y. Toriyama and G. J. Snyder, Mater. Horiz., 2024, 11, 1188–1198 RSC
.
- L. Müchler, F. Casper, B. Yan, S. Chadov and C. Felser, Phys. Status Solidi RRL, 2013, 7, 91–100 CrossRef
.
- D. Baldomir and D. Faílde, Sci. Rep., 2019, 9, 6324 CrossRef PubMed
.
- N. Xu, Y. Xu and J. Zhu, npj Quantum Mater., 2017, 2, 51 CrossRef
.
- Y. L. Chen, J. G. Analytis, J.-H. Chu, Z. K. Liu, S.-K. Mo, X. L. Qi, H. J. Zhang, D. H. Lu, X. Dai, Z. Fang, S. C. Zhang, I. R. Fisher, Z. Hussain and Z.-X. Shen, Science, 2009, 325, 178–181 CrossRef CAS PubMed
.
- D. Hsieh, Y. Xia, D. Qian, L. Wray, F. Meier, J. H. Dil, J. Osterwalder, L. Patthey, A. V Fedorov, H. Lin, A. Bansil, D. Grauer, Y. S. Hor, R. J. Cava and M. Z. Hasan, Phys. Rev. Lett., 2009, 103, 146401 CrossRef CAS PubMed
.
- H. Zhang, C.-X. Liu, X.-L. Qi, X. Dai, Z. Fang and S.-C. Zhang, Nat. Phys., 2009, 5, 438–442 Search PubMed
.
- Y. Lu, Y. Zhou, W. Wang, M. Hu, X. Huang, D. Mao, S. Huang, L. Xie, P. Lin, B. Jiang, B. Zhu, J. Feng, J. Shi, Q. Lou, Y. Huang, J. Yang, J. Li, G. Li and J. He, Nat. Nanotechnol., 2023, 18, 1281–1288 CrossRef CAS PubMed
.
- Z.-H. Zheng, X.-L. Shi, D.-W. Ao, W.-D. Liu, M. Li, L.-Z. Kou, Y.-X. Chen, F. Li, M. Wei, G.-X. Liang, P. Fan, G. Q. (Max) Lu and Z.-G. Chen, Nat. Sustain., 2023, 6, 180–191 CrossRef
.
- P. Ghaemi, R. S. K. Mong and J. E. Moore, Phys. Rev. Lett., 2010, 105, 166603 CrossRef PubMed
.
- T. H. Hsieh, H. Lin, J. Liu, W. Duan, A. Bansil and L. Fu, Nat. Commun., 2012, 3, 982 CrossRef PubMed
.
- K. Dybko, M. Szot, A. Szczerbakow, M. U. Gutowska, T. Zajarniuk, J. Z. Domagala, A. Szewczyk, T. Story and W. Zawadzki, Phys. Rev. B, 2017, 96, 205129 CrossRef
.
- M. Zhou, Z. M. Gibbs, H. Wang, Y. Han, C. Xin, L. Li and G. J. Snyder, Phys. Chem. Chem. Phys., 2014, 16, 20741–20748 RSC
.
- S. Misra, B. Wiendlocha, J. Tobola, F. Fesquet, A. Dauscher, B. Lenoir and C. Candolfi, J. Mater. Chem. C, 2020, 8, 977–988 RSC
.
- S. Misra, B. Wiendlocha, J. Tobola, F. Fesquet, A. Dauscher, B. Lenoir and C. Candolfi, J. Mater. Chem. C, 2020, 8, 977–988 RSC
.
- K. R. Knox, E. S. Bozin, C. D. Malliakas, M. G. Kanatzidis and S. J. L. Billinge, Phys. Rev. B:Condens. Matter Mater. Phys., 2014, 89, 14102 CrossRef
.
- Z. M. Gibbs, A. LaLonde and G. J. Snyder, New J. Phys., 2013, 15, 075020 CrossRef CAS
.
- B. Jia, D. Wu, L. Xie, W. Wang, T. Yu, S. Li, Y. Wang, Y. Xu, B. Jiang, Z. Chen, Y. Weng and J. He, Science, 2024, 384, 81–86 CrossRef CAS PubMed
.
- A. Banik, U. S. Shenoy, S. Saha, U. V Waghmare and K. Biswas, J. Am. Chem. Soc., 2016, 138, 13068–13075 CrossRef CAS PubMed
.
- L. Zhao, J. Wang, J. Li, J. Liu, C. Wang, J. Wang and X. Wang, Phys. Chem. Chem. Phys., 2019, 21, 17978–17984 RSC
.
- F. Li, X. Liu, S.-R. Li, X.-F. Zhang, N. Ma, X.-J. Li, X.-Y. Lin, L. Chen, H. Wu and L.-M. Wu, Energy Environ. Sci., 2024, 17, 158–172 RSC
.
- Y. Liu, X. Zhang, P. Nan, B. Zou, Q. Zhang, Y. Hou, S. Li, Y. Gong, Q. Liu, B. Ge, O. Cojocaru-Mirédin, Y. Yu, Y. Zhang, G. Chen, M. Wuttig and G. Tang, Adv. Funct. Mater., 2022, 32, 2209980 CrossRef CAS
.
- A. Banik, B. Vishal, S. Perumal, R. Datta and K. Biswas, Energy Environ. Sci., 2016, 9, 2011–2019 RSC
.
- G. Tan, F. Shi, J. W. Doak, H. Sun, L.-D. Zhao, P. Wang, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Energy Environ. Sci., 2015, 8, 267–277 RSC
.
- A. Banik, U. S. Shenoy, S. Anand, U. V Waghmare and K. Biswas, Chem. Mater., 2015, 27, 581–587 CrossRef CAS
.
- U. S. Shenoy and D. K. Bhat, J. Mater. Chem. C, 2020, 8, 2036–2042 RSC
.
- G. Tan, F. Shi, S. Hao, H. Chi, L.-D. Zhao, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, J. Am. Chem. Soc., 2015, 137, 5100–5112 CrossRef CAS PubMed
.
- R. Pathak, D. Sarkar and K. Biswas, Angew. Chem., Int. Ed., 2021, 60, 17686–17692 CrossRef CAS PubMed
.
- Y. Kawami, X. Q. Tran, T. Yamamoto, S. Yoshioka, Y. Murakami, S. Matsumura, K. Nogita and J. Zou, Adv. Mater., 2024, 2410508 CrossRef CAS PubMed
.
- C. Nie, C. Wang, Y. Xu, Y. Liu, X. Niu, S. Li, Y. Gong, Y. Hou, X. Zhang, D. Zhang, D. Li, Y. Zhang and G. Tang, Small, 2023, 19, 2301298 CrossRef CAS PubMed
.
- L. Wang, S. Chang, S. Zheng, T. Fang, W. Cui, P. Bai, L. Yue and Z.-G. Chen, ACS Appl. Mater. Interfaces, 2017, 9, 22612–22619 CrossRef CAS PubMed
.
- Z. Ma, J. Lei, D. Zhang, C. Wang, J. Wang, Z. Cheng and Y. Wang, ACS Appl. Mater. Interfaces, 2019, 11, 33792–33802 CrossRef CAS PubMed
.
- L. Aggarwal, A. Banik, S. Anand, U. V Waghmare, K. Biswas and G. Sheet, J. Mater., 2016, 2, 196–202 Search PubMed
.
- K. V Mitrofanov, A. V Kolobov, P. Fons, M. Krbal, T. Shintani, J. Tominaga and T. Uruga, Phys. Rev. B, 2014, 90, 134101 CrossRef
.
- C. W. Li, O. Hellman, J. Ma, A. F. May, H. B. Cao, X. Chen, A. D. Christianson, G. Ehlers, D. J. Singh, B. C. Sales and O. Delaire, Phys. Rev. Lett., 2014, 112, 175501 CrossRef CAS PubMed
.
- M. Iizumi, Y. Hamaguchi, K. F. Komatsubara and Y. Kato, J. Phys. Soc. Jpn., 1975, 38, 443–449 CrossRef CAS
.
-
D. Shoenberg, Magnetic Oscillations in Metals, Cambridge University Press, 1984 Search PubMed
.
- G. J. Snyder, A. Pereyra and R. Gurunathan, Adv. Funct. Mater., 2022, 32, 2112772 CrossRef CAS
.
- K. H. Lee, S. Kim, J.-C. Lim, J. Y. Cho, H. Yang and H.-S. Kim, Adv. Funct. Mater., 2022, 32, 2203852 CrossRef CAS
.
- X. Zhang, Z. Chen, S. Lin, B. Zhou, B. Gao and Y. Pei, ACS Energy Lett., 2017, 2, 2470–2477 CrossRef CAS
.
- L. Wang, M. Hong, Q. Sun, Y. Wang, L. Yue, S. Zheng, J. Zou and Z.-G. Chen, ACS Appl. Mater. Interfaces, 2020, 12, 36370–36379 CrossRef CAS PubMed
.
- J. Callaway and H. C. von Baeyer, Phys. Rev., 1960, 120, 1149–1154 CrossRef CAS
.
- J. Callaway, Phys. Rev., 1959, 113, 1046–1051 CrossRef CAS
.
- I. K. Dimitrov, M. E. Manley, S. M. Shapiro, J. Yang, W. Zhang, L. D. Chen, Q. Jie, G. Ehlers, A. Podlesnyak, J. Camacho and Q. Li, Phys. Rev. B, 2010, 82, 174301 CrossRef
.
- B. Yang, S. Li, X. Li, Z. Liu, D. Li, H. Zhong and S. Feng, Intermetallics, 2021, 136, 107257 CrossRef CAS
.
- G. Tan, L.-D. Zhao, F. Shi, J. W. Doak, S.-H. Lo, H. Sun, C. Wolverton, V. P. Dravid, C. Uher and M. G. Kanatzidis, J. Am. Chem. Soc., 2014, 136, 7006–7017 CrossRef CAS PubMed
.
- S. Hikami, A. I. Larkin and Y. Nagaoka, Prog. Theor. Phys., 1980, 63, 707–710 CrossRef
.
- W. Niu, M. Gao, X. Wang, F. Song, J. Du, X. Wang, Y. Xu and R. Zhang, Sci. Rep., 2016, 6, 26081 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ta00582e |
| This journal is © The Royal Society of Chemistry 2025 |




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)