 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unraveling Li-ion transport mechanisms in high-entropy anion-disordered argyrodites via machine-learned interatomic potentials†
Myeongcho
Jang‡
ab,
Kanguk
Park‡
a,
Hun-Gi
Jung
 acd,
Kyung Yoon
Chung
acd,
Kyung Yoon
Chung
 ac,
Joon Hyung
Shim
ac,
Joon Hyung
Shim
 *b,
Ohmin
Kwon
*b,
Ohmin
Kwon
 *ae and
Seungho
Yu
*ae and
Seungho
Yu
 *ac
*ac
aEnergy Storage Research Center, Korea Institution of Science and Technology, Seoul 02792, Republic of Korea. E-mail: shyu@kist.re.kr
bSchool of Mechanical Engineering, Korea University, 145 Anam-ro, Seongbuk-gu, Seoul 02841, South Korea. E-mail: shimm@korea.ac.kr
cDivision of Energy & Environment Technology, KIST School, Korea University of Science and Technology, Seoul 02792, Republic of Korea
dDepartment of Energy Science and KIST-SKKU Carbon-Neutral Research Center, Sungkyunkwan University, Suwon 16419, Republic of Korea
eLiB Materials Research Group, Research Institute of Industrial Technology and Science (RIST), POSCO Global R&D Center, Songdogwahak-ro 100, Yeonsu-gu, Incheon, 21985, Republic of Korea. E-mail: omkwon0823@posco-inc.com
First published on 28th April 2025
Abstract
Lithium argyrodite sulfide solid electrolytes are widely used in all-solid-state batteries owing to their high ionic conductivity. Recently, high-entropy argyrodites formed by anion disorder in Li6PS5Cl have emerged as promising superionic conductors. However, the details of the Li-ion conduction mechanism in high-entropy argyrodites have yet to be fully elucidated. In this study, the Li-ion conduction mechanism is systematically investigated through first-principles calculations and molecular dynamics simulations using machine-learned interatomic potentials (MLIPs). The calculations indicate that high-entropy Li6PS5Cl argyrodites improve site energy uniformity and facilitate inter-cage jumps, significantly enhancing Li-ion conductivity. Ionic conductivity was further improved with increased disorder in Cl-rich argyrodites, but a critical threshold was observed with the addition of Cl. By leveraging MLIPs, a detailed analysis of the conduction mechanism was efficiently conducted, and a systematic investigation of ionic conductivity through entropy variation was performed. These findings highlight the reliability and effectiveness of MLIPs in facilitating the design and analysis of novel high-entropy superionic argyrodites.
1. Introduction
Li-ion batteries have garnered significant attention as energy storage systems for electric vehicles; however, their limitations in energy density and safety have driven the development of next-generation batteries.1 All-solid-state batteries (ASSBs) incorporating solid electrolytes (SEs) are widely regarded as among the most promising candidates for next-generation batteries, owing to their combination of high energy density and improved safety.2,3 ASSBs facilitate the utilization of high-energy-density electrode chemistries, such as metallic Li anodes, anode-less configurations, and thick composite cathodes.4 Additionally, ASSBs significantly enhance safety by replacing flammable and volatile liquid electrolytes with nonflammable SEs.5Among the various types of SEs, sulfide-based SEs have been widely studied due to their high ionic conductivity, comparable to that of liquid electrolytes.5,6 Several sulfide SEs, including thio-LISICON-type Li10GeP2S12, glassy Li2S–P2S5 type Li7P3S11, and argyrodite-type Li5.5PS4.5Cl1.5, have exhibited high ionic conductivity above 10 mS cm−1 at room temperature.7,8 The lithium argyrodite family, Li6PS5X (X = Cl, Br), is regarded as one of the most promising sulfide SEs due to its high ionic conductivity, low cost, and good compatibility in ASSBs.9,10 Since the discovery of argyrodite SEs in 2008, comprehensive studies have been conducted on their synthesis, ionic conduction mechanisms, structural design, defect chemistry, interfacial stability, and applications in ASSBs.11–13
Ionic substitution in argyrodite SEs has significantly enhanced ionic conductivity by facilitating inter-cage jumps for long-range migration.14 For example, Li vacancy formation through excess halogen anions in Li6PS5Cl increased ionic conductivity to approximately 10 mS cm−1 for Li5.5PS4.5Cl1.5 (cold-pressed state),15 while anion mixing with Br also enhanced the ionic conductivity.16–18 Additionally, Li site disorder induced by aliovalent substitution with M4+ in Li6+xMxP1−xS5I and Li6+xMxSb1−xS5I (M = Si, Ge, Sn) significantly enhanced ionic conductivity, achieving 14.8 mS cm−1 for Li6.6Sb0.4Si0.6S5I19 and 16 mS cm−1 for Li6.5Sb0.5Ge0.5S5I.20 Recently, high-entropy argyrodites have been investigated to enhance ion migration through the redistribution of localized ionic sites.21–25 The mixture of various cation and anion substitutions in argyrodites increased conformational entropy and facilitated inter-cage jumps, achieving an ionic conductivity of 13.2 mS cm−1 for Li[P0.25Si0.25Ge0.25Sb0.25]S5I21 and 14.05 mS cm−1 for Li6.67[P0.16Si0.16Ge0.5Sb0.16]S5I.25
Ionic substitutions have enhanced the ionic conductivity of argyrodite SEs, but they introduce trade-offs, including higher costs due to expensive metals, increased weight from heavy elements, incompatibility with the Li anode, and more complex fabrication processes due to additional elements. Therefore, conventional Li6PS5Cl and its Cl-rich phases, Li6−xPS5−xCl1+x, have regained attention due to their low cost, good compatibility in ASSBs, and a high ionic conductivity of approximately 10 mS cm−1. Various compositions have been investigated, and increasing disorder in high-entropy phases effectively enhances ionic conductivity.14 However, the Li-ion conduction mechanism in high-entropy Li6PS5Cl and Li6−xPS5−xCl1+x argyrodites has yet to be fully elucidated through computational analysis. Although several theoretical studies have analyzed Li-ion migration in high-entropy argyrodites,26–28 a comprehensive investigation of the detailed composition of high-entropy phases has not been conducted.
In this study, machine-learned interatomic potentials (MLIPs) were utilized to investigate high-entropy argyrodites. The lithium-ion conduction mechanisms in high-entropy argyrodites were systematically investigated, while comprehensive maps of ionic conduction across detailed compositions were generated using MLIPs. The calculation results show that higher entropy, achieved by increasing S/Cl site inversion in Li6PS5Cl, facilitates long-range Li-ion migration, with maximum ionic conductivity at 50% site inversion. Site energy distribution analysis revealed that increased anion disorder broadens the potential energy landscape, enhancing inter-cage migration. Additionally, high-entropy argyrodites with excess Cl incorporation exhibit a sharp decline in Li-ion conductivity beyond the critical threshold, indicating the additional impact of Li vacancies on conductivity. Overall, this study efficiently analyzed the conduction mechanism in high-entropy argyrodites using MLIPs, demonstrating their reliability and effectiveness in investigating and designing novel superionic conductors.
2. Methods
First-principles calculations were performed using density functional theory (DFT) as implemented in the Vienna ab initio Simulation Package.29 The projector augmented wave method30 and the generalized gradient approximation with the Perdew–Burke–Ernzerhof functional31 were used for the calculations. A plane-wave cutoff energy of 550 eV was used for the plane-wave basis, and the k-point grids included a k-point density of at least 1000 per atom. Ionic position relaxations were conducted until the force was less than 0.03 eV Å−1, while the electronic self-consistency loops were converged to a value of 10−5 eV. The simulation cells were generated based on the experimental structural configurations. Ab initio molecular dynamics (AIMD) simulations were conducted to evaluate Li-ion diffusivity, employing an NVT ensemble with a Nosé–Hoover thermostat, an energy cut-off of 350 eV, and a Γ-point-only k-point grid.The Moment Tensor Potential (MTP) formalism was used to obtain machine-learned interatomic potentials (MLIPs) from AIMD simulations.32–35 AIMD calculations were performed for crystalline and amorphous argyrodite phases (Li6−xPS5−xCl1+x, x = 0, 0.5, 1.0), elemental phases (Li, P, and S), and lithium binary halide (LiCl). For the crystal argyrodite phases, all possible site disorders between the 4a and 4d sites were considered, and the structure with the lowest energy was used for the AIMD calculations, while fully ordered Li6PS5Cl and Li5.5PS5Cl1.5 structures were also included. AIMD calculations for the crystal argyrodite phases were performed at four different temperatures (300, 600, 900, and 1200 K) and at three strain levels (−5%, 0%, and 5%). After the heating step (0.5 K fs−1) and equilibration (20 ps at the target temperature), an additional 10 ps of simulations were run, with snapshots extracted every 0.1 ps. This resulted in a total of 1200 training structures (100 snapshots × 4 temperatures × 3 strains) for each crystal argyrodite phase. Amorphous argyrodite structures were also obtained using a melt-and-quench process at three strain levels (−5%, 0%, and 5%), which involved a pre-melting step at 4000 K for 10 ps, melting at 2000 K for 20 ps, and quenching to 300 K for 17 ps at a rate of 100 K ps−1. The structure snapshots were extracted every 0.1 ps during the melting and quenching steps, resulting in a total of 1110 training structures (370 snapshots × 3 strains). Additionally, AIMD calculations for elemental phases and lithium binary halide were performed by increasing the temperature to 1000 K. After the heating step (0.5 K fs−1) to 300 K and 10 ps of equilibration at 300 K, structure snapshots were extracted every 0.2 ps during the heating to 1000 K for 42 ps.
Single-point DFT static calculations were performed using the optB88-vdW functional for the training structures. Using DFT static calculation results from 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 550 argyrodite and 840 precursor structures, the MTP training was performed for the Li–P–S–Cl four-element system for Li6−xPS5−xCl1+x argyrodites. The MTP training was performed with a cutoff radius of 6 Å and a maximum level of 10, using fitting weights of 100
550 argyrodite and 840 precursor structures, the MTP training was performed for the Li–P–S–Cl four-element system for Li6−xPS5−xCl1+x argyrodites. The MTP training was performed with a cutoff radius of 6 Å and a maximum level of 10, using fitting weights of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.01 for energy, force, and stress, respectively. The MTP training was validated using the mean absolute errors (MAEs) of total energies, forces, and stresses. A schematic workflow of the MTP training process is illustrated in Fig. S1.†
0.01 for energy, force, and stress, respectively. The MTP training was validated using the mean absolute errors (MAEs) of total energies, forces, and stresses. A schematic workflow of the MTP training process is illustrated in Fig. S1.†
Classical molecular dynamics (MD) simulations were performed using the trained interatomic potentials with the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) package.36 The MD simulations were performed on 4 × 4 × 4 supercell structures under the NPT ensemble for 10 ns at target temperatures. The mean squared displacement (MSD) of Li ions over time was calculated to determine the diffusion coefficient, D,
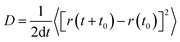 | (1) |
 | (2) |
The configurational entropy, ΔSconf, of the argyrodite phases was calculated using the mole fraction of each atom in the Wyckoff 4a and 4d sites, based on the following equation:
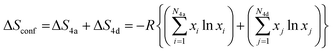 | (3) |
Site energy distributions were calculated to examine the enhancement of ionic conductivity along inter-cage jump sites, using the method described in earlier work.38 Calculations were carried out using a unit cell, with a Li atom placed on the T2, T4, and T5 Wyckoff sites.39 A single-point calculation was performed for all sites, while the charge was externally adjusted to maintain neutrality. The calculated site energies were analyzed using kernel density estimation and normalized by dividing by the number of Wyckoff sites.
3. Results
MLIP was obtained for the Li–P–S–Cl four-element system (Li6−xPS5−xCl1+x) and validated by calculating the root mean square errors (RMSEs) of energy and force relative to values obtained using DFT, as shown in Fig. S2.† The RMSEs for energy and force are 7.5 meV per atom and 0.37 eV Å−1 for the Li–P–S–Cl system, which are consistent with previously reported values in the literature.40,41 The MD simulation using MLIPs was performed with supercells of argyrodite structures, following a convergence test of cell size, as shown in Fig. S3.† The MSD value for Li6PS5Cl at 300 K was obtained using MLIPs, and it converged as the cell size increased to a 4 × 4 × 4 supercell (3328 atoms), which is consistent with previous studies.41High-entropy argyrodites were achieved through anion disorder between the 4a and 4d sites, as shown in Fig. 1, leading to high ionic conductivity.16,22,42,43 In the structure of Li6PS5Cl without anion disorder (Fig. 1a), Cl occupies the face centered positions of the cube (Wyckoff 4a), while S occupies the PS4 tetrahedral sites (Wyckoff 16e) and the center of the cage-like Li polyhedron (Wyckoff 4d). The configurational entropy, ΔSconf, for the 4a and 4d sites is zero in the ordered Li6PS5Cl structure, but increases with the mixing of S and Cl across the 4a and 4d sites, as shown in Fig. 1b. The ΔSconf in Li6PS5Cl can be further increased by introducing excess Cl, forming Li6−xPS5−xCl1+x (0 ≤ x ≤ 1).
The configurational entropy of Li6−xPS5−xCl1+x, arising from S/Cl inversion at the 4a and 4d sites, generally falls within the medium entropy range (1 R ≤ ΔSconf < 1.5 R). Achieving higher configurational entropy values beyond 1.5 R would require additional multi-element substitutions involving both cation and anion sites.16,22 Nevertheless, this study focuses on anion-disordered Li6−xPS5−xCl1+x, where configurational entropy is maximized through S/Cl site inversion, and the system approaches the high entropy threshold 1.5 R. Using the MLIP, Li-ion conduction was systematically investigated with anion disorder at the 4a and 4d sites, while the entropy term was thoroughly incorporated to better understand the role of disorder degree in achieving high conductivity.
The thermodynamic phase stability of high-entropy argyrodites was assessed by calculating the energy above the convex hull for Li6−xPS5−xCl1+x phases with varying degrees of S/Cl site inversion. As shown in Fig. S4,† the phase stability decreases as the degree of site inversion increases, suggesting that a high degree of inversion may be thermodynamically unfavorable. Notably, argyrodites with maximized configurational entropy were found to be metastable, indicating that such phases may still be experimentally accessible under favorable synthesis conditions.
Li-ion migration in Li6PS5Cl under different degrees of anion disorder was investigated using MLIP for the supercell system, as shown in Fig. 2 and S5.† The isosurfaces of the Li-ion probability densities were plotted to visualize the Li-ion trajectories during a 10 ns molecular dynamics (MD) simulation at 300 K. The structure of Li6PS5Cl without anion disorder in Fig. 2a (corresponding to zero ΔSconf) exhibited localized Li-ion migration with negligible inter-cage jumps. As the degree of S/Cl site inversion increases to 25% and further to 50% (Fig. 2b and c, respectively), the Li-ion trajectories become more interconnected between the cages, suggesting long-range Li diffusion that results in high ionic conductivity. The substitution of Cl with S at the 4d site weakens the electrostatic attraction with adjacent Li ions, enabling greater Li mobility and facilitating migration to neighboring cages.
As the degree of S/Cl site inversion increases to 75% and further to 100% (indicating that the 4d sites are predominantly occupied by Cl), the Li-ion trajectories become less connected between cages, indicating a decrease in ionic conductivity. With the substitution of Cl at the 4d sites exceeding 50%, the electrostatic attraction is further weakened, leading to expanded cages and a transformation in their shape. At 100% S/Cl site inversion, all 4d sites are occupied by Cl, leading to localized Li-ion migration, with Li ions appearing to occupy more ordered sites (Fig. 2d). This phenomenon is closely related to the entropy arising from anion disorder between the 4a and 4d sites. The ΔSconf is maximized by mixing 50% of Cl with S at the 4d sites in Li6PS5Cl, which exhibits the most active inter-cage jumps. The decrease in ΔSconf leads to more ordered arrangements, causing Li ions to remain localized at low-energy sites, thereby restricting their migration to adjacent sites.
The detailed analysis of the ionic conduction mechanism as a function of ΔSconf induced by anion disorder was conducted using MLIP, as shown in Fig. 3. Li-ion conductivity in Li6PS5Cl was calculated using a 10 ns MD simulation at 300 K by varying the S/Cl site inversion from 0% to 100% in 3.125% intervals, as shown in Fig. 3a. Li-ion conductivity increases as the degree of site inversion increases, reaching a maximum of approximately 15 mS cm−1 near 50% site inversion, and declines with further inversion. As predicted by the Li-ion migration trajectories in Fig. 2, higher ΔSconf resulting from S and Cl mixing at the 4a and 4d sites facilitates Li-ion migration, achieving the highest ionic conductivity at the maximum ΔSconf. In Fig. 3b, Li-ion conductivity is plotted as a function of ΔSconf, with the color of each data point corresponding to that in Fig. 3a. As ΔSconf increases, ionic conductivity increases linearly, indicating a strong correlation between ionic conductivity and ΔSconf in Li6PS5Cl.
The self-part of the van Hove correlation function, Gs, was calculated for Li6PS5Cl to analyze Li-ion migration with increasing S/Cl site inversion, as shown in Fig. 3c. Most Li ions remain near their initial positions in the absence of disorder, and intra-cage jumps of approximately 3 Å are observed, as shown in Fig. 3c. As the degree of S/Cl site inversion increases, the transition to larger r values occurs more rapidly, indicating long-range Li-ion migration (>5 Å) through inter-cage jumps. The Gs values are presented as a function of the degree of site inversion in Fig. S6,† indicating that increasing anion disorder facilitates Li-ion migration across the cage, resulting in higher ionic conductivity. The occurrence of larger r values in the Gs plot decreases above 50% site inversion, confirming the reduction in Li-ion conductivity beyond the maximum entropy point shown in Fig. 3a. The Gs plot for Li6PS5Cl with 100% S/Cl site inversion, where all 4d sites are occupied by Cl, verifies the low ionic conductivity by demonstrating localized Li-ion migration.
High ionic conductivity was achieved through long-range Li-ion migration via inter-cage jumps, as illustrated in Fig. 4a, including direct inter-cage jumps between T2 sites and inter-cage jumps between T5 sites through the intermediate T4 site. Inter-cage jumps were directly counted during the MD simulations, where Li-ion displacements exceeding 3 Å from their initial positions were considered transitions between distinct cages, as shown in Fig. 4b. The frequency of inter-cage Li-ion hopping was examined as a function of ΔSconf to assess the effect of configurational disorder on long-range Li-ion mobility. During the 10 ns MD simulation at 300 K, the number of Li-ion hops to adjacent sites was measured at various degrees of S/Cl site inversion. Consistent with the Gs plots in Fig. 3c and S6,† Li6PS5Cl with low anion disorder exhibits fewer Li-ion hops compared to systems with higher disorder, due to restricted migration within intra-cage regions. The number of Li-ion hops increases with greater anion disorder, reaching its maximum at the highest value of ΔSconf, suggesting that additional Li-ion hops are facilitated through inter-cage jumps in high-entropy systems.
The enhanced Li-ion migration at high ΔSconf was further investigated by analyzing the site energy distributions in the structure, using a method previously employed to examine ionic conduction through site disorder.38,44 Site energy distributions of Li ions along the inter-cage migration paths (T2, T4, and T5 sites) were calculated by varying the degree of S/Cl site inversion, as shown in Fig. 4c and S7.† The site energy distribution describes the potential energy of Li ions along their migration sites and is limited to a narrow region when the sites are more ordered and exhibit lower energy. The site energy distribution broadens as disorder is introduced, due to the more uniform potential energy landscape of Li ions resulting from increased site similarity caused by the disorder. In the site energy distribution for low anion disorder with low ΔSconf, the site energy of each site exhibits a distinct and narrow region with reduced overlap. However, the site energy distributions for the T2, T4, and T5 sites begin to overlap as ΔSconf increases, allowing Li ions to experience a more continuous energy landscape with lowered barriers to migrate to other sites. The site energy distributions exhibit the greatest overlap at the maximum ΔSconf, indicating that Li-ion migration can be substantially enhanced in this state.
High-entropy argyrodites formed by anion disorder in Li6PS5Cl significantly increase ionic conductivity, and further enhancement of entropy can be achieved through excess chlorine incorporation, forming Li6−xPS5−xCl1+x (0 ≤ x ≤ 1). Using MLIP, Li-ion conduction in Cl-rich phases was investigated as a function of the degree of S/Cl site inversion, as shown in Fig. 5. The ΔSconf values were calculated as a function of additional Cl in Li6−xPS5−xCl1+x (0 ≤ x ≤ 1, with an interval of 0.125), as shown in Fig. 5a, assuming that the additional Cl occupies the 4d sites (e.g., for Li5.5PS4.5Cl1.5 with an additional 0.5 Cl, at least 0.5 Cl can be positioned at the 4d sites, indicating a minimum of 50% S/Cl site inversion). For each composition, ΔSconf was calculated by varying the degree of S/Cl site inversion in 12.5% intervals, starting from the minimum site inversion value. For example, Li6PS5Cl was evaluated over nine site inversion degrees from 0% to 100%, while Li5.5PS4.5Cl1.5 was evaluated over five site inversion degrees from 50% to 100%. In Fig. 5a, the ΔSconf values were presented as a bar chart for each composition, showing the maximum and minimum values, with green bars representing the 25% to 75% range and the average values indicated by a red line. The ΔSconf increases with additional Cl incorporation up to x = 0.25 and exhibits a slight decline beyond this point, while it significantly decreases above x = 0.5, as most 4d sites become occupied by Cl, thereby reducing disorder.
The effect of ΔSconf on Li-ion migration was further investigated for Cl-rich phases using MD simulations at 300 K for 10 ns, as shown in Fig. 5b–d. The MD calculations were performed for compositions in Li6−xPS5−xCl1+x (0 ≤ x ≤ 1, with an interval of 0.125), with the degree of S/Cl site inversion varied in 12.5% intervals, starting from the minimum site inversion value. In Fig. 5b, Li-ion conductivity increases with a small amount of additional Cl incorporation, consistent with the trends of ΔSconf with increasing Cl content, indicating that enhanced disorder facilitates Li-ion migration. Li-ion conductivity increases with additional Cl incorporation, reaching a maximum near the composition of x = 0.5 (Li5.5PS4.5Cl1.5). As the Cl content increases to x = 0.5, the increase in entropy facilitates more active inter-cage jumps, while the formation of Li vacancies due to additional Cl further reduces the activation barrier for Li migration.45 Beyond x = 0.5, Li-ion conductivity exhibits a sharp decline, consistent with previous experimental studies.46,47 This pronounced decline contrasts with the gradual decreasing trend of ΔSconf in Fig. 5a, indicating that ΔSconf is not the only factor influencing Li-ion conductivity, as additional Li vacancies also play a role. The Li vacancies formed by Cl incorporation in Li6−xPS5−xCl1+x can reduce the extent of concerted Li-ion migration by removing Li ions from the migration pathways, leading to a substantial decrease in ionic conductivity.
In Fig. 5c, Li-ion hopping was further examined to investigate the significant decline in ionic conductivity in Cl-rich phases. The Li-ion hopping away from its initial position to neighboring sites (jump length > 3 Å) was counted during MD simulations for Cl-rich phases. As predicted from the low ionic conductivity in Cl-rich phases, the number of Li-ion hops substantially decreases with compositions with more than 0.5 additional Cl incorporation. Therefore, Li vacancies, along with the level of Cl incorporation, are important factors in achieving high ionic conductivity in Li6−xPS5−xCl1+x. In Fig. 5d and S8,† the ionic conductivity data from Fig. 5b are presented in detail as functions of both Cl incorporation and the degree of S/Cl site inversion, using a heat map and a contour map. The contour map in Fig. 5d visually displays a region of reduced ionic conductivity, with a critical threshold at 0.5 Cl incorporation.
The effects of Li vacancies on ionic conductivity in Cl-rich phases were further investigated by restoring the deficient Li, as shown in Fig. 6a. For Li-deficient phases Li6−xPS5−xCl1+x, Li-ion conductivity slightly increases with Cl content, reaching a maximum at x = 0.5, and then decreases sharply (shown as blue dots and line). After Li compensation in the phases Li6PS5−xCl1+x, the Li-ion conductivity exhibits similar trends, but the curves show a gradual change without a significantly reduced region (shown as red dots and line). The scattered ionic conductivity values for each composition result from variations in the degree of S/Cl site inversion, whereas the averaged values exhibit a more coherent behavior. These ionic conductivities show a stronger correlation with the trend of ΔSconf in Fig. 5a, compared to the ionic conductivity of Li-deficient phases. These findings suggest that the ΔSconf resulting from anion disorder in Cl-rich phases can be a significant factor in determining ionic conductivity, while additional Li vacancies introduced by Cl incorporation also affect Li-ion migration, particularly exhibiting a critical threshold for ionic conductivity in Li-deficient phases above x = 0.5.
The improved ionic conductivity through Li vacancy compensation was analyzed using the isosurfaces of the Li-ion probability densities, as shown in Fig. 6b. The Li-ion trajectories for the Li-deficient phase Li5.375PS4.375Cl1.625 (x = 0.625) were obtained during 10 ns MD simulations at 300 K and compared with those of the Li-added phase Li6PS4.375Cl1.625. Consistent with the ionic conductivities in Fig. 6a, the Li-deficient phases exhibit more fragmented Li-ion trajectories along the migration paths, suggesting a weakening of concerted Li-ion migration due to Li vacancies. In contrast, the modified phases with restored Li vacancies exhibit more connected Li-ion trajectories, consistent with the enhanced ionic conductivity. Additionally, the radial distribution function (RDF) plot in Fig. S9† indicates that the bonds of Li with Cl in the 4d cages become less localized at a specific length and shift to larger values after Li replenishment, suggesting that Li ions are weakly bonded to the cages, thereby facilitating their movement.
4. Conclusions
High-entropy argyrodites with anion disorder have emerged as promising superionic conductors; however, the details of the Li-ion conduction mechanism have yet to be fully elucidated. In this study, the Li-ion conduction mechanism is systematically investigated through first-principles calculations and molecular dynamics simulations using MLIPs. The calculation results show that increasing S/Cl site inversion in Li6PS5Cl enhances inter-cage connectivity and long-range diffusion. Higher ΔSconf facilitates long-range Li-ion migration, with maximum ionic conductivity at 50% S/Cl site inversion, while excessive inversion leads to localization and reduced conductivity. Site energy distribution analysis revealed that increased anion disorder broadens the potential energy landscape and causes site energy overlap, which results in lower migration barriers and enhanced inter-cage migration.In addition, high-entropy argyrodites with excess Cl incorporation in Li6−xPS5−xCl1+x (0 ≤ x ≤ 1) were investigated, revealing that ΔSconf initially increased but then dropped significantly due to Cl saturation at 4d sites. Li-ion conductivity followed a similar trend, sharply declining beyond the critical threshold of x = 0.5, indicating the additional impact of Li vacancies on conductivity. After Li compensation in Li6−xPS5−xCl1+x, Li-ion conductivity changes more gradually without a significantly reduced region and shows a stronger correlation with ΔSconf, indicating that anion disorder is a key factor in ionic conductivity, while Li vacancies introduced by Cl incorporation also play an important role. Overall, a detailed analysis of the conduction mechanism in high-entropy argyrodites was efficiently conducted using MLIPs. This study highlights the reliability and effectiveness of MLIPs in guiding the design and analysis of novel high-entropy superionic argyrodites.
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Myeongcho Jang: conceptualization, formal analysis, investigation, and writing – original draft. Kanguk Park: investigation, visualization, and methodology. Hun-Gi Jung: investigation. Kyung Yoon Chung: resources. Joon Hyung Shim: supervision. Ohmin Kwon: supervision. Seungho Yu: conceptualization, supervision, and writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the institutional program of the Korea Institute of Science and Technology (No. 2E33941 and 2V10640); by the Development Program of Core Industrial Technology, funded by the Ministry of Trade, Industry & Energy of Korea (No. 20007045); by the National Research Council of Science & Technology (NST) grant by the Korea government (MSIT) (No. GTL24011-000); by the National Supercomputing Center with supercomputing resources including technical support (KSC-2023-CRE-0406).References
- Y. Tian, G. Zeng, A. Rutt, T. Shi, H. Kim, J. Wang, J. Koettgen, Y. Sun, B. Ouyang, T. Chen, Z. Lun, Z. Rong, K. Persson and G. Ceder, Chem. Rev., 2020, 121, 1623–1669 CrossRef.
- A. Manthiram, X. Yu and S. Wang, Nat. Rev. Mater., 2017, 2, 1–16 Search PubMed.
- S. Randau, D. A. Weber, O. Kötz, R. Koerver, P. Braun, A. Weber, E. Ivers-Tiffée, T. Adermann, J. Kulisch, W. G. Zeier, F. H. Richter and J. Janek, Nat. Energy, 2020, 5, 259–270 CrossRef CAS.
- T. Schmaltz, F. Hartmann, T. Wicke, L. Weymann, C. Neef and J. Janek, Adv. Energy Mater., 2023, 13, 2301886 CrossRef CAS.
- J. Wu, S. Liu, F. Han, X. Yao and C. Wang, Adv. Mater., 2021, 33, 2000751 CrossRef CAS.
- C. Wang, J. Liang, Y. Zhao, M. Zheng, X. Li and X. Sun, Energy Environ. Sci., 2021, 14, 2577–2619 RSC.
- L. Zhou, N. Minafra, W. G. Zeier and L. F. Nazar, Acc. Chem. Res., 2021, 54, 2717–2728 CrossRef CAS.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, Nat. Mater., 2011, 10, 682–686 CrossRef CAS PubMed.
- L. Zhou, K.-H. Park, X. Sun, F. Lalère, T. Adermann, P. Hartmann and L. F. Nazar, ACS Energy Lett., 2018, 4, 265–270 CrossRef.
- R. P. Rao and S. Adams, Phys. Status Solidi A, 2011, 208, 1804–1807 CrossRef CAS.
- J.-S. Park, C.-H. Jo and S.-T. Myung, Energy Storage Mater., 2023, 61, 102869 CrossRef.
- H. J. Deiseroth, S. T. Kong, H. Eckert, J. Vannahme, C. Reiner, T. Zaiß and M. Schlosser, Angew. Chem., Int. Ed., 2008, 120, 767–770 CrossRef.
- C. Yu, F. Zhao, J. Luo, L. Zhang and X. Sun, Nano Energy, 2021, 83, 105858 CrossRef CAS.
- D. Wang, H. Shi, S. Wang, X. Wu, W. Jiang, S. Liang and Z. Xu, Coord. Chem. Rev., 2024, 508, 215776 CrossRef CAS.
- W. D. Jung, J.-S. Kim, S. Choi, S. Kim, M. Jeon, H.-G. Jung, K. Y. Chung, J.-H. Lee, B.-K. Kim, J.-H. Lee and H. Kim, Nano Lett., 2020, 20, 2303–2309 CrossRef CAS.
- S. Li, J. Lin, M. Schaller, S. Indris, X. Zhang, T. Brezesinski, C. W. Nan, S. Wang and F. Strauss, Angew. Chem., Int. Ed., 2023, 62, e202314155 CrossRef CAS.
- S. V. Patel, S. Banerjee, H. Liu, P. Wang, P.-H. Chien, X. Feng, J. Liu, S. P. Ong and Y.-Y. Hu, Chem. Mater., 2021, 33, 1435–1443 CrossRef CAS.
- P. Wang, S. Patel, H. Liu, P. H. Chien, X. Feng, L. Gao, B. Chen, J. Liu and Y. Y. Hu, Adv. Funct. Mater., 2023, 33, 2307954 CrossRef CAS.
- L. Zhou, A. Assoud, Q. Zhang, X. Wu and L. F. Nazar, J. Am. Chem. Soc., 2019, 141, 19002–19013 CrossRef CAS PubMed.
- Y. Lee, J. Jeong, H. J. Lee, M. Kim, D. Han, H. Kim, J. M. Yuk, K.-W. Nam, K. Y. Chung, H.-G. Jung and S. Yu, ACS Energy Lett., 2021, 7, 171–179 CrossRef.
- J. Lin, G. Cherkashinin, M. Schafer, G. Melinte, S. Indris, A. Kondrakov, J. r. Janek, T. Brezesinski and F. Strauss, ACS Mater. Lett., 2022, 4, 2187–2194 CrossRef CAS.
- W. Li, Z. Chen, Y. Chen, L. Zhang, G. Liu and L. Yao, Adv. Funct. Mater., 2024, 34, 2312832 CrossRef CAS.
- Y. Li, S. Song, H. Kim, K. Nomoto, H. Kim, X. Sun, S. Hori, K. Suzuki, N. Matsui, M. Hirayama, T. Mizoguchi, T. Saito, T. Kamiyama and R. Kanno, Science, 2023, 381, 50–53 CrossRef CAS PubMed.
- B. Ouyang and Y. Zeng, Nat. Commun., 2024, 15, 973 CrossRef CAS.
- J. Lin, M. Schaller, S. Indris, V. Baran, A. Gautam, J. Janek, A. Kondrakov, T. Brezesinski and F. Strauss, Angew. Chem., Int. Ed., 2024, 63, e202404874 CrossRef CAS PubMed.
- J. Lee, S. Ju, S. Hwang, J. You, J. Jung, Y. Kang and S. Han, ACS Appl. Mater. Interfaces, 2024, 16, 46442–46453 CrossRef CAS.
- J. H. Kim, B. Jun, Y. J. Jang, S. H. Choi, S. H. Choi, S. M. Cho, Y.-G. Kim, B.-H. Kim and S. U. Lee, Nano Energy, 2024, 124, 109436 CrossRef CAS.
- P.-H. Chien, B. Ouyang, X. Feng, L. Dong, D. Mitlin, J. Nanda and J. Liu, Chem. Mater., 2023, 36, 382–393 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- I. S. Novikov, K. Gubaev, E. V. Podryabinkin and A. V. Shapeev, Mach. learn.: sci. technol., 2020, 2, 025002 Search PubMed.
- J. Li, M. Zhou, H. H. Wu, L. Wang, J. Zhang, N. Wu, K. Pan, G. Liu, Y. Zhang, J. Han, X. Liu, X. Chen, J. Wan and Q. Zhang, Adv. Energy Mater., 2024, 14, 2304480 CrossRef CAS.
- R. Jalem, M. L. H. Chandrappa, J. Qi, Y. Tateyama and S. P. Ong, Energy Adv., 2023, 2, 2029–2041 RSC.
- J. Qi, S. Banerjee, Y. Zuo, C. Chen, Z. Zhu, M. H. Chandrappa, X. Li and S. P. Ong, Mater. Today Phys., 2021, 21, 100463 CrossRef CAS.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. In't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, B. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- Z. Deng, Z. Zhu, I.-H. Chu and S. P. Ong, Chem. Mater., 2017, 29, 281–288 CrossRef CAS.
- Y. Zeng, B. Ouyang, J. Liu, Y.-W. Byeon, Z. Cai, L. J. Miara, Y. Wang and G. Ceder, Science, 2022, 378, 1320–1324 CrossRef CAS.
- S. T. Kong, H. J. Deiseroth, C. Reiner, Ö. Gün, E. Neumann, C. Ritter and D. Zahn, Chem.–Eur. J., 2010, 16, 2198–2206 CrossRef CAS PubMed.
- J. W. Lee, J. H. Kim, J. S. Kim, Y. J. Jang, S. H. Choi, S. H. Choi, S. M. Cho, Y.-G. Kim and S. U. Lee, J. Mater. Chem. A, 2024, 12, 7272–7278 RSC.
- H. J. Lee, H. Kim, S. Ji, K. Choi, H. Choi, W. Lim and B. Lee, Adv. Energy Mater., 2024, 14, 2402396 CrossRef CAS.
- F. Strauss, J. Lin, A. Kondrakov and T. Brezesinski, Matter, 2023, 6, 1068–1070 CrossRef CAS.
- H. Guo, J. Li, M. Burton, J. Cattermull, Y. Liang, Y. Chart, G. J. Rees, J. Aspinall and M. Pasta, Cell Rep. Phys. Sci., 2024, 5, 102228 CrossRef CAS.
- T. Jeon, G. H. Cha and S. C. Jung, J. Mater. Chem. A, 2024, 12, 993–1002 RSC.
- W. Li, M. Li, S. Wang, P.-H. Chien, J. Luo, J. Fu, X. Lin, G. King, R. Feng, J. Wang, J. Zhou, R. Li, J. Liu, Y. Mo, T.-K. Sham and X. Sun, Nat. Nanotechnol., 2025, 20, 265–275 CrossRef CAS.
- Y. J. Choi, S.-I. Kim, M. Son, J. W. Lee and D. H. Lee, Nanomaterials, 2022, 12, 4355 CrossRef CAS.
- C. Yu, Y. Li, M. Willans, Y. Zhao, K. R. Adair, F. Zhao, W. Li, S. Deng, J. Liang, M. N. Banis, R. Li, H. Huang, L. Zhang, R. Yang, S. Lu, Y. Huang and X. Sun, Nano Energy, 2020, 69, 104396 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ta02205c |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |






