Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Negative linear compressibility and complex phase behaviour in 7Li2CO3†
Christopher J.
Ridley
 *ab,
Fabio
Orlandi
*ab,
Fabio
Orlandi
 b,
Craig L.
Bull
b,
Craig L.
Bull
 bc,
Nicholas P.
Funnell
bc,
Nicholas P.
Funnell
 b,
Jasmine K.
Hinton
b,
Jasmine K.
Hinton
 a,
Robin S.
Perry
bd,
Stephen
Hull
a,
Robin S.
Perry
bd,
Stephen
Hull
 b and
Rebecca
Wurr‡
b and
Rebecca
Wurr‡
 b
b
aNeutron Scattering Division, Oak Ridge National Laboratory, Oak Ridge, TN, USA. E-mail: ridleycj@ornl.gov
bISIS Neutron and Muon Source, Rutherford Appleton Laboratory, Chilton, Didcot OX11 0QX, UK
cSchool of Chemistry, University of Edinburgh, David Brewster Road, Edinburgh EH9 3FJ, UK
dLondon Centre for Nanotechnology and Department of Physics and Astronomy, University College London, Gower Street, London WC1E 6BT, UK
First published on 14th May 2025
Abstract
We present a combination of neutron powder-diffraction measurements demonstrating negative linear compressibility and irregular thermal expansion in 7Li2CO3. This is shown to be due to an interplay between the tilting of the rigid carbonate group and the shear strain in the unit cell, which leads to a first-order transition from monoclinic to hexagonal symmetry. The phase evolution is shown to be highly sensitive to the level of hydrostaticity in the sample. Under hydrostatic conditions, the sample begins transformation at 8.5 GPa leading to a change from tetrahedral to octahedral Li coordination. Symmetry adapted basis mode analysis, combined with density functional theoretical (DFT) calculations and Raman spectroscopy, is used to show that this transition is reverse proper ferroelastic in nature.
Introduction
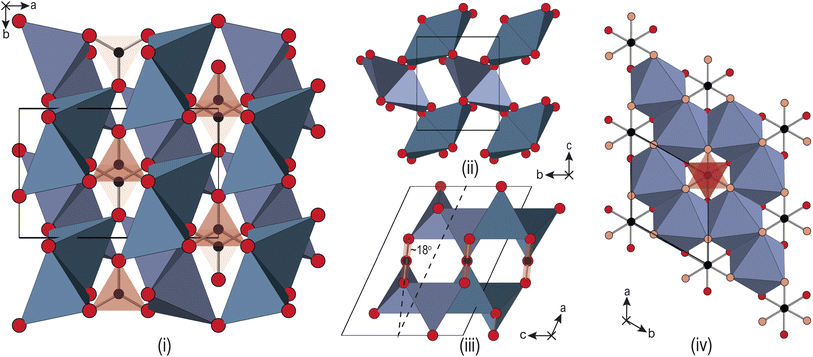
Alkali metal-carbonates are a family of industrially important materials. They are used in the production of detergents, glass and ceramic manufacture, pharmaceuticals, and in energy applications. Li2CO3 is the largest global source of Li-metal, predominantly used for the production of cathode materials such as LiCoO2, for the manufacture of Li-ion batteries. Li2CO3 is also used as the dominant electrolyte component in molten-carbonate fuel cells (forming a eutectic with K2CO3), which are of growing interest for generating power and capturing CO2 from the flue gases emitted by natural gas power plants, or other carbon-intensive processes.1 Other applications include CO2 sensing,2 and as a non-metallic catalyst for diamond synthesis.3The crystallographic structure of Li2CO3 at ambient conditions was first reported by Zemann4 from single-crystal X-ray diffraction (XRD), and later reconfirmed by Effenberger and Zemann.5 The symmetry is C2/c (see Fig. 1), with the main structural feature being a staggered off-set arrangement of CO32− groups along the c-axis. This forms layers along the a-axis, separated by layers of slightly distorted, tetrahedrally coordinated Li atoms. The tetrahedra each have one shared-edge within the layers, and two shared-corners between the layers, one of which meets at the shared edge of another pair of tetrahedra. This forms a canted bow-tie arrangement within the layers of Li–O tetrahedral units, with the bow-ties alternating in orientation with translation along the c-axis.
The related compound, Na2CO3, is well known for being the only incommensurately modulated alkali-carbonate in the γ-phase at room temperature.6 This transforms to a commensurately modulated δ-phase below 170 K, with both modulated phases possessing the same monoclinic average symmetry (C2/m).7 On heating, the amplitude of the modulation drops to zero, transforming to the β-phase above 620 K, maintaining monoclinic symmetry (C2/m). With further heating above 763 K, the hexagonal (P63/mmc) α-phase forms.8,9 Doping with Li, LiNaCO3 forms a triclinic structure which has a complex phase diagram driven by differing tetrahedrally coordinated Li+ and distorted square-pyramidal coordinated Na+ ions.10 The triclinic phase transforms to a hexagonal phase above 448 K,10,11 with an order–disorder transition to another hexagonal phase above 633 K, resulting in two distinct CO32− environments.12 Upon doping with K, forming LiKCO3, the Li is forced into a LiO5 pyramidal coordination, alongside the KO9 polyhedra, maintaining monoclinic symmetry.13,14
Studies into the effects of high-temperature on the structure of Li2CO3 are complicated by its chemical-reactivity, and the formation of eutectics with trace impurities. Differential thermal-analysis (DTA) performed under either a CO2 atmosphere or air showed a clear heat-effect at approximately 683 K prior to melting at 993 K, indicative of a solid–solid transition.15 In air, additional features in the DTA suggested the formation of a eutectic with Li2O, indicating that the loss of CO2 from the sample causes premature decomposition.15 This effect was observed again in a later study by Klement Jr and Cohen,16 with the sample in air. A structural study, using high-temperature powder XRD, further considered the effects of sample history and atmosphere on the occurrence of a possible solid–solid transition.17 Khlapova and Kovaleva17 concluded that Li2CO3 exists in three crystalline forms under ambient conditions: the stable monoclinic α-form, the metastable β-form (of unknown symmetry) which may be recovered from the melt (melting temperature 993 K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18) where the sample isn't subsequently exposed to moisture or CO2, and the γ-form upon heating above 681 K. However, the presence of 0.91% trace impurities in the sample may explain these transitions, potentially with a ternary eutectic with Na2CO3 and K2CO3 as suggested by Stober.18
18) where the sample isn't subsequently exposed to moisture or CO2, and the γ-form upon heating above 681 K. However, the presence of 0.91% trace impurities in the sample may explain these transitions, potentially with a ternary eutectic with Na2CO3 and K2CO3 as suggested by Stober.18
The predominant interest in the application of high-pressure to the alkali-metal carbonates is in the search for an sp3-bonded structure, analogous to those observed for alkaline-earth carbonates.19 Both Na2CO3 and K2CO3 have been shown to have rich high-pressure phase-diagrams.20–24 While some of the early DTA work considered the application of modest hydrostatic pressures to Li2CO3,16 it has received relatively little attention compared with the other carbonates. The focus in the literature is on the use of the material as a non-metallic catalyst for diamond synthesis, with a view to increasing the purity of the end-product.3 Grzechnik et al.25 also considered this, and were the first to study the structural changes in Li2CO3 with pressure. A new high-pressure hexagonal phase (P63/mcm) was identified, see Fig. 1(iii) and (iv), with phase coexistence between 10–18 GPa. However, there were a number of additional features observed in the diffraction patterns, suggesting that there may be unidentified phases in the lower pressure regime, up to 6 GPa. Likely limited by the appearance of unindexed peaks, Grzechnik et al.25 did not report any structural analysis of the high pressure data prior to the phase transition.
In the synthesis of Li-based cathode materials, such as Ni-doped LiCoO2 compounds, the presence of unreacted Li2CO3 can be problematic, resulting in additional cation disorder resulting in rapid capacity fade.26 The application of high-pressure during synthesis has the potential to lead to better conversion, though a better understanding of how Li2CO3 itself behaves under pressure is needed first. The present study uses neutron powder-diffraction data, combined with Raman spectroscopy and computation, to better understand the structural properties of this material under high-pressures and -temperatures.
Experimental details
Polycrystalline Li2CO3 with 99.95 at% 7Li was supplied by Oak Ridge National Laboratory (ORNL, USA). The isotopic 7Li enrichment reduces the level of neutron absorption, improving the measured signal. No crystalline impurities were observed in the neutron diffraction patterns at ambient conditions, demonstrating high chemical-purity in the bulk compound. Single crystals of natural 6/7Li2CO3 were grown using a modified floating zone technique. Neutron diffraction measurements were performed using the PEARL diffractometer at the ISIS Neutron and Muon Source,27 and the SNAP diffractometer at Oak Ridge National Laboratory. Vibrational spectroscopy calculations were performed using the plane-wave DFT package, CASTEP 23.1.28 ISODISTORT and the ISOTROPY suite were used for the symmetry mode analysis.29,30 Full experimental details are available in the ESI.†31–39Results and discussion
Structural changes upon heating
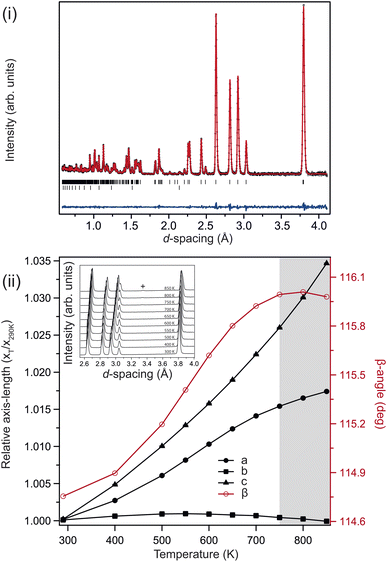
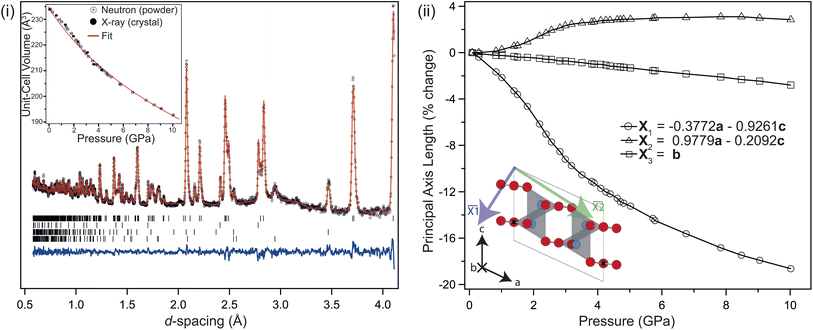
Fig. 2(i) shows the neutron powder-diffraction pattern from the sample at ambient conditions; no traces of crystalline impurity were observed, and refining the monoclinic (C2/c) structure against these data results in an good fit. The refined model is listed in Table 1. The lattice parameters compare favourably with previous reports.26 The sample maintained this monoclinic structure over the full temperature range investigated 4–850 K, the refined structures at 4 K and 850 K are also listed in Table 1. Upon heating, the unit cell preferentially expands in the ac-plane, with an increase in the β-angle, and the b-axis remaining essentially invariant, reducing slightly at higher temperatures, see Fig. 2(ii). This is clearly seen in the diffraction patterns, see inset Fig. 2(ii), with the splitting of the (![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 02) and (111) reflections at approximately 3 Å. The (111) reflection is close to invariant, while the (
02) and (111) reflections at approximately 3 Å. The (111) reflection is close to invariant, while the (![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 02) shifts significantly to higher d-spacing on heating.
02) shifts significantly to higher d-spacing on heating.
| NPD | NPD | NPD | DFT | |
|---|---|---|---|---|
| Temperature (K) | 298 | 850 | 4 | — |
| a-axis (Å) | 8.3613(3) | 8.5104(4) | 8.3453(4) | 8.3248 |
| b-axis (Å) | 4.97652(15) | 4.9780(2) | 4.9747(3) | 4.9777 |
| c-axis (Å) | 6.1957(2) | 6.4130(3) | 6.1601(3) | 6.1543 |
| β-angle (°) | 114.761(2) | 115.979(2) | 114.6978(15) | 114.303 |
| Volume (Å3) | 234.104(14) | 244.23(2) | 232.34(2) | 232.42 |
| Li-x | 0.6970(5) | 0.6819(8) | 0.6962(3) | 0.6971 |
| Li-y | 0.0535(8) | 0.0533(9) | 0.0533(5) | 0.0520 |
| Li-z | 0.3351(6) | 0.3081(10) | 0.3342(4) | 0.3364 |
| C-y | 0.0652(5) | 0.0770(6) | 0.0665(3) | 0.0654 |
| O1-x | 0.1470(2) | 0.1423(3) | 0.14691(12) | 0.1472 |
| O1-y | 0.9369(3) | 0.9423(4) | 0.9355(2) | 0.9345 |
| O1-z | 0.3132(3) | 0.3057(3) | 0.31335(14) | 0.3135 |
| O2-y | 0.3209(5) | 0.3313(6) | 0.3233(3) | 0.3220 |
| ρ (g cm−3) | 2.096 | 2.010 | 2.112 | 2.112 |
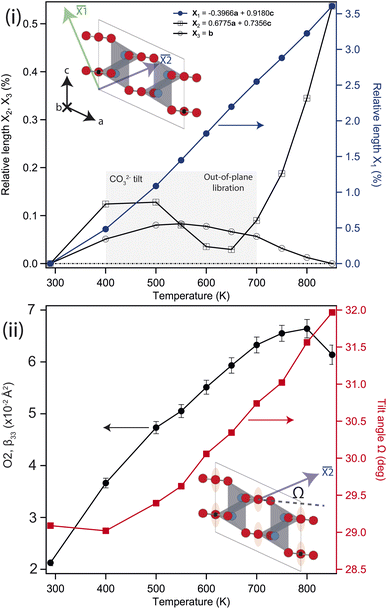
Above 750 K two additional reflections were observed at 2.37 & 3.35 Å, corresponding to the formation of Li2O and Si from labile Li reacting with the quartz ampule. These peaks remained in the diffraction pattern after cooling back to ambient conditions, confirming that the sample had started to decompose rather than transform to a high-temperature phase. Above 550 K the b-axis begins to contract with further heating, while the unit-cell volume continues to expand. There is a clear change in the volumetric thermal-expansion at this temperature (see ESI†). If the principal axes of expansion are considered, see Fig. 3(i), it is clear that while ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 1 expands as expected, there are other interesting features within the ac-plane, and along
1 expands as expected, there are other interesting features within the ac-plane, and along ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 3 (the b-axis), suggestive of some competing effects within the structure. Initially, both
3 (the b-axis), suggestive of some competing effects within the structure. Initially, both ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 2 and
2 and ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 3 show very little response with heating, with both expanding no more than 0.1% by 500 K, and
3 show very little response with heating, with both expanding no more than 0.1% by 500 K, and ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 2 then contracting back to the room temperature value by 600 K.
2 then contracting back to the room temperature value by 600 K.
Above approximately 650 K, ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 2 begins to expand while
2 begins to expand while ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 3 slowly contracts, eventually falling back to the room temperature value at the highest temperature considered. The contraction of
3 slowly contracts, eventually falling back to the room temperature value at the highest temperature considered. The contraction of ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 2 is driven by the tilting of the rigid CO32− groups, which starts to change significantly above 400 K, see Fig. 3(ii). This also contributes to the larger expansion along
2 is driven by the tilting of the rigid CO32− groups, which starts to change significantly above 400 K, see Fig. 3(ii). This also contributes to the larger expansion along ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 1. The upturn in
1. The upturn in ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 2 above 600 K is subsequently caused by increased CO32− out-of-plane libration, which similarly results in the slow contraction of
2 above 600 K is subsequently caused by increased CO32− out-of-plane libration, which similarly results in the slow contraction of ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 3 at higher temperatures still, and is apparent in the refined anisotropic displacement parameter (ADP), β33, for O2, see Fig. 3(ii). This has a coupled effect in β33 for the Li atom, which may be thought of as a symmetric stretch of the tetrahedral unit. While the ADPs along the other unit-cell axes show an as-expected growth with temperature, the β33 parameters for Li and O2 show significant changes, with their values growing 3–4 times larger than either β11, and β22 at 800 K. The tilt and libration of the CO32− therefore contribute competing effects to the expansion/contraction of
3 at higher temperatures still, and is apparent in the refined anisotropic displacement parameter (ADP), β33, for O2, see Fig. 3(ii). This has a coupled effect in β33 for the Li atom, which may be thought of as a symmetric stretch of the tetrahedral unit. While the ADPs along the other unit-cell axes show an as-expected growth with temperature, the β33 parameters for Li and O2 show significant changes, with their values growing 3–4 times larger than either β11, and β22 at 800 K. The tilt and libration of the CO32− therefore contribute competing effects to the expansion/contraction of ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 2.
2.
The carbonate group itself was determined to adopt the ideal geometry, within error, with a O1–C–O2 bond angle of 120.3(2)° at 300 K. The two C–O1 bond lengths were determined to be 1.2901(14) Å, and the single C–O2 bond length to be 1.268(3) Å. The O1–C–O2 bond angle remained constant on heating, within error, while the C–O1 bonds contracted, and the C–O2 bonds elongated, resulting in C–O2 being larger than C–O1. The polarising nature of the Li+ on the delocalised electrons in the CO32− group is smaller than group-II carbonates, but it is still expected that the shorter C–O bond belongs to the O coordinated to fewer Li+, in this case O2 (note this is defined as O1 in work of Effenberger and Zemann5). These data suggest that approaching decomposition, it is this shorter C–O oxygen which eventually forms an oxide ion with Li, and the initially less delocalised O1 atoms which form CO2.
An additional measurement was performed at 4 K, where the sample was observed to maintain monoclinic symmetry. A simple two point analysis of the changes in the unit cell, suggests that the principal axes contract as expected on cooling.
High-pressure phase transitions: how many are there?
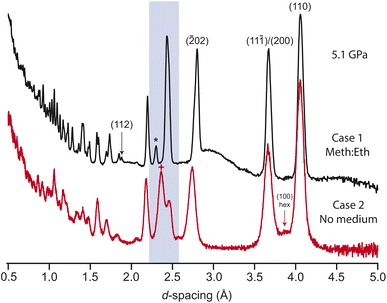
The previous study observed a series of phase transitions, of unknown symmetry or structure, with increasing pressure up to 6 GPa.25 It is possible that these phases are not thermodynamically stable, instead being induced through non-hydrostatic pressure conditions. We have investigated this further through varying the ratio of pressure-medium to sample in the gasket. Three cases were tested: (1) the sample was firmly packed into the gasket, with the remaining voids in the sample space filled with pressure medium; (2) the sample was initially pelletised, and then compressed without pressure medium; (3) the sample was loosely packed into the gasket, with a greater volume of pressure medium.In case 1, a single unaccounted-for reflection was observed to grow into the diffraction patterns at ∼2.32 Å above ∼3.8 GPa (see Fig. 4 and ESI†). Additionally, the intensity of the (112) reflection is seen to grow significantly in intensity, unaccounted for by the current crystallographic model. The additional reflection is unindexed by the existing cell, or alternative cells common to other alkali-metal carbonates. Loss of the c-glide and C-centering were also checked; the peak remains unindexed against metrically similar monoclinic cells with C2, P2, P21, P21/c symmetry. It may be related to the (2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) reflection of the high-symmetry hexagonal phase, though at significantly lower pressures (reported above 10 GPa
0) reflection of the high-symmetry hexagonal phase, though at significantly lower pressures (reported above 10 GPa![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25). Attempts to freely index the new pattern suggest that a loss of C-centering, an increase in β-angle, and a ∼2.5× elongation of the c-axis may fit the data, though no structure could be found.
25). Attempts to freely index the new pattern suggest that a loss of C-centering, an increase in β-angle, and a ∼2.5× elongation of the c-axis may fit the data, though no structure could be found.
In case 2, the pelletisation led to no adverse changes in the initial pattern (see ESI†), with no significant broadening or preferred orientation. As the pressure is increased the sample peaks are initially seen to broaden and reduce in intensity, consistent with growing levels of strain. Several reflections are seen to shift at different rates to those in case 1. For example, the cluster of reflections (31![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )/(020)/(11
)/(020)/(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) )/(002) merge together, as in case 1, but the (002) reflection then shifts to much lower d-spacing with a larger relative intensity, see Fig. 4. The hexagonal phase is also induced at lower pressures than in the hydrostatic case. If the positions of the (200)/(110) are compared between case 1 and 2, the hexagonal phase is seen to emerge at a significantly lower pressure of approximately 5.2 GPa. A similar effect is seen in the Raman data. The diamond anvil cell (DAC) loading is tightly packed with sample (similar to case 1), and the structural change is clearly mirrored in the Raman spectra, onset above approximately 5 GPa (see ESI†). The allowed Raman modes in each phase were confirmed through DFT phonon calculations (the CASTEP output for these is included as ESI†). Experimentally, there remain some features that are forbidden in the hexagonal symmetry, suggesting that when highly strained the sample locally retains some monoclinic character.
)/(002) merge together, as in case 1, but the (002) reflection then shifts to much lower d-spacing with a larger relative intensity, see Fig. 4. The hexagonal phase is also induced at lower pressures than in the hydrostatic case. If the positions of the (200)/(110) are compared between case 1 and 2, the hexagonal phase is seen to emerge at a significantly lower pressure of approximately 5.2 GPa. A similar effect is seen in the Raman data. The diamond anvil cell (DAC) loading is tightly packed with sample (similar to case 1), and the structural change is clearly mirrored in the Raman spectra, onset above approximately 5 GPa (see ESI†). The allowed Raman modes in each phase were confirmed through DFT phonon calculations (the CASTEP output for these is included as ESI†). Experimentally, there remain some features that are forbidden in the hexagonal symmetry, suggesting that when highly strained the sample locally retains some monoclinic character.
In case 3, the sample reflections behave similarly to case 1, but with no additional reflections observed (see ESI†). Comparing the relative intensity of the nearest expected reflection between the over- and under-packed cases demonstrates that, even with differing signal to background, the reflection is clearly absent. In all three cases, the sample fully reverts to the ambient monoclinic structure on pressure release. It is therefore clear that the sample is highly sensitive to the level of deviatoric stress in the pressure environment. As the additional peak cannot be accounted for with any obvious loss of symmetry, it is possibly the result of domain structure in the sample, only apparent where the powder density is increased above a critical threshold. The single-crystal XRD measurements confirmed that the monoclinic structure is stable where the pressure conditions are hydrostatic, with no unindexed reflections.
This sensitivity to non-hydrostatic pressure is consistent with the observations of Grzechnik et al.,25 who used a DAC to apply pressure under non-hydrostatic conditions. The uniaxial strain field in a DAC is very different to that in a toroidal anvil assembly. In the latter, it has been shown that a pellet of NaCl at 6 GPa can sustain uniaxial stresses of the order 0.3 GPa.40 Li2CO3, having a slightly larger shear-modulus than NaCl, is expected to sustain higher levels than this. A DAC loading is geometrically more uniaxial, and this results in a very different evolution of the structure. This is evidenced by the fact that at 5 GPa we see the early onset of the hexagonal structure, which is not observed in the previous DAC measurements. It would be an interesting future study to consider the effects of uniaxial stress on a single-crystal.
The data discussed in the remainder of this study were collected from loadings where the gaskets were packed less firmly, loaded with a larger volume of pressure medium (as per case 3). The sample is therefore considered to be under hydrostatic conditions up to 10.5 GPa, the limit of methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethanol (4
ethanol (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by volume) at room temperature.41Fig. 5(i) shows a representative high-pressure data set from Li2CO3 at 4.1 GPa. The monoclinic phase was found to be stable up to 8.5 GPa. Beyond this, additional reflections appeared in the pattern corresponding to the hexagonal phase, most notably the (100) reflection at approximately 3.88 Å. The monoclinic and hexagonal phases coexisted, with the hexagonal phase-fraction increasing up to approximately 10 GPa, beyond which the sample was purely hexagonal.
1 by volume) at room temperature.41Fig. 5(i) shows a representative high-pressure data set from Li2CO3 at 4.1 GPa. The monoclinic phase was found to be stable up to 8.5 GPa. Beyond this, additional reflections appeared in the pattern corresponding to the hexagonal phase, most notably the (100) reflection at approximately 3.88 Å. The monoclinic and hexagonal phases coexisted, with the hexagonal phase-fraction increasing up to approximately 10 GPa, beyond which the sample was purely hexagonal.
Negative linear compressibility
The change in unit-cell volume (inset, Fig. 5(i), residual plot in ESI†) is described using a Rydberg–Vinet equation of state (EOS), with V0 = 234.24(14) Å3, B0 = 31.5(8) GPa and Bp = 5.0(3), in good agreement with the ambient pressure unit-cell volume listed in Table 1. While the unit-cell volume is well approximated by the EOS, it isn't able to fully reproduce the measured changes below 3 GPa, where there is a clear inflexion in the data, reproduced by both the neutron and XRD measurements. Looking at the percentage length change in the principal axes with pressure, see Fig. 5(ii);![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 3 compresses almost linearly, while
3 compresses almost linearly, while ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 1 compresses non-linearly, and
1 compresses non-linearly, and ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 2 expands non-linearly. The balance struck between the nonlinear expansion and contraction of
2 expands non-linearly. The balance struck between the nonlinear expansion and contraction of ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 2 and
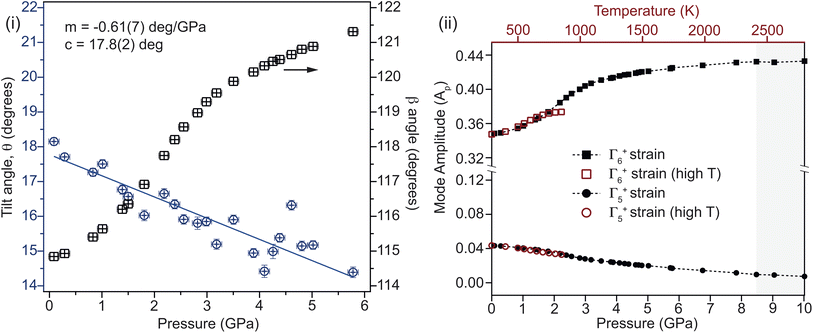
2 and ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 1 respectively causes an unusual form to the pressure–volume curve below 4 GPa, which is also seen in the data collected from the single crystal XRD. The cause of this non-linear compression is the interplay between unit-cell shear and tilting of the rigid CO32− groups within the cell. The tilt of the group relative to the a-axis is shown in Fig. 6. The linear reduction in tilt-angle results in an effective expansion along the a-axis, while the non-linear increase in β-angle (equivalent to shear) counteracts this. At higher pressures, the shear dominates, and the unit-cell volume reduces following the expected Rydberg–Vinet trend. The resultant negative compressibility along the a-axis is −3.18 TPa−1 over the 7 GPa range.
1 respectively causes an unusual form to the pressure–volume curve below 4 GPa, which is also seen in the data collected from the single crystal XRD. The cause of this non-linear compression is the interplay between unit-cell shear and tilting of the rigid CO32− groups within the cell. The tilt of the group relative to the a-axis is shown in Fig. 6. The linear reduction in tilt-angle results in an effective expansion along the a-axis, while the non-linear increase in β-angle (equivalent to shear) counteracts this. At higher pressures, the shear dominates, and the unit-cell volume reduces following the expected Rydberg–Vinet trend. The resultant negative compressibility along the a-axis is −3.18 TPa−1 over the 7 GPa range.
The Li–O tetrahedral volume reduces by ∼19.4% up to 10 GPa. The distortion index (deviation in bond length away from the average Li–O bond length) shows no obvious change outside of error up to the on-set of the transition, but then increases from approximately 0.02 to 0.06 between 8 and 10 GPa, as the Li coordination becomes increasingly octahedral.
Symmetry analysis of the monoclinic–hexagonal transition
The high-pressure form of Li2CO3 formed above 8.5 GPa is hexagonal (space group: P63/mcm), see Fig. 1(iv), with edge-shared Li–O6 octahedra in the ab-plane. These build face-shared columns along the c-axis forming an 8-membered ring of Li–O6 octahedra around each CO32− group, the central C-atoms of which now sit on the Wyckoff 2a (0,0,1/4) site. The transition from monoclinic to hexagonal is seen to occur gradually, with phase coexistence over a range of ∼ 2 GPa, becoming phase pure hexagonal above ∼ 10 GPa. The transition is therefore, first-order in nature.In addition, the low-symmetry monoclinic structure forms a group-subgroup relationship with the high-symmetry hexagonal phase. This allows us to decompose the structure of the low symmetry phase in terms of the amplitudes of a series of symmetry adapted distortion modes. This was done assuming that the unit cell of the low symmetry phase is obtained by applying the transformation matrix (−a − 2b, a, c; origin 000) to the hexagonal unit cell. Decomposing the structure in this way shows that there are three order-parameters, Γ5+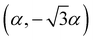 , Γ3+ (β), Γ6+
, Γ3+ (β), Γ6+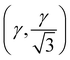 . We demonstrate later that Γ3+ and Γ6+ are the two primary order-parameters of the phase transition. Γ6+ is dominated by the shear of the unit cell coupled with the tilting of the CO32− group, while Γ3+ has no strain component, instead relating to the change in Li coordination. Γ5+ is therefore a secondary order parameter, related to the change in centering of the CO32− groups and orthorhombic strain. The transition is ferroelastic, due to the appearance of a spontaneous shear strain in the low symmetry phase.
. We demonstrate later that Γ3+ and Γ6+ are the two primary order-parameters of the phase transition. Γ6+ is dominated by the shear of the unit cell coupled with the tilting of the CO32− group, while Γ3+ has no strain component, instead relating to the change in Li coordination. Γ5+ is therefore a secondary order parameter, related to the change in centering of the CO32− groups and orthorhombic strain. The transition is ferroelastic, due to the appearance of a spontaneous shear strain in the low symmetry phase.
Which order parameter is primary?
Further symmetry analysis allows us to consider the coupling between all the distortion modes;42,43 the coupling between the three order parameters is trilinear (αβγ), acting as a cubic term in the free-energy expansion. This is consistent with, though not a requirement for, the transition being first-order. Furthermore, the transition may be considered as ferroelastic, as the shear strain in the unit cell shares the symmetry of one of the primary order parameters (Γ6+). However, it isn't clear whether the transition may be considered as proper (where the spontaneous strain is the primary order parameter), as the Γ6+ order parameter has contributions from both homogeneous shear-strain and the tilting of the CO32− group. The other primary order parameter (Γ3+) has no strain component. From diffraction measurements alone, it is not possible to determine whether the acoustic instability (shear strain) drives the optic instability (CO32− tilting), or vice versa.DFT calculations were used to disentangle these effects. By considering the relative energetic-stability of structures sequentially deformed from the high-symmetry phase, we are able to show that the transition is proper. The computational model was validated through three methods: the relaxed structure from DFT is first compared with that from the 4 K neutron measurements (see Table 1); the pressure dependence of the unit-cell parameters were compared with those determined from experiment; the calculated Raman spectra were compared with those measure experimentally. These were in good agreement with those reported previously in the literature.44–47 All three of these confirm that the pseudopotentials provide an accurate portrayal of the sample over a range of pressures and distortions, reproducing the observed negative linear compressibility (see ESI†). Additionally, the effect of hydrostatic pressure on the final calculated enthalpies of the monoclinic and hexagonal phases shows that the hexagonal phase becomes favourable above 5 GPa (see ESI†). This is in reasonable agreement with the observed onset transition pressure of 8.5 GPa.
Through selectively varying the amplitude of each distortion mode we are able to determine which of these are the true driver for the transition. For these calculations, the volumetric (Γ1+) strain was fixed to the values determined for the ambient structure. Fig. 7 shows the results of the calculated final energies for these distorted structures. Fig. 7 shows that Γ5+ is a ‘hard’ mode, with a single minimum around zero mode-amplitude. Γ3+ and Γ6+ are both found to be ‘soft’ modes, with an energy minimum at non-zero mode-amplitude, and are therefore both primary order-parameters. However, when the strain component of Γ6+ is set to zero, the mode is switched to being ‘hard’. Additionally, where only the strain component of Γ6+ is varied, it remains ‘soft’. This shows that the carbonate group tilt is secondary, and that it is the shear strain that drives the transition, such that it is a proper ferroelastic. DFT also confirms that Γ5+ is a secondary order parameter induced by Γ3+/Γ6+ through the trilinear invariant described previously. Formally, the transition may be considered ‘reverse ferroelastic’, where the low symmetry monoclinic structure transforms to a higher density, higher symmetry, hexagonal form on applied pressure. An improper example of this is seen in Pb3(PO4)2, where local displacement of the Pb atoms break the symmetry.48 This is in contrast to the related compound Na2CO3, which shows a second-order proper ferroelastic transition, from monoclinic to hexagonal on heating.9
Comparing the effects of pressure and temperature
The effects of temperature and pressure are similar for both Γ5+ and Γ6+ strain modes, though over different energy scales (see Fig. 6(ii)). The former reduces with increasing pressure and temperature, while the latter increases in a highly non-linear manner (see ESI†). Comparing the mode decomposition results between the temperature and pressure data allows for an estimation of the temperature at which the transition would occur at ambient pressure. This would not be expected to occur below 2400 K which is far in excess of the melting temperature for Li2CO3 at ambient pressure. Additionally, this implies that heating the sample to 850 K effectively reduces the transition pressure by ∼2 GPa. Additional high-pressure and -temperature data are needed to draw a more complete comparison.It is required that the magnitude of the order parameters reduce to zero in the high-symmetry phase, discontinuously in the case of a first-order transition. On the approach to the transition, a gradual reduction in magnitude is indicative of a reduction in stability of the low symmetry phase. In the case of Li2CO3, both primary order parameters are found to increase in magnitude on approach to the transition, showing that an increase in distortion of the cell is initially more energetically favourable. This implies that there are competing effects within the structure. Fig. 7 shows that while Γ6+ shear strain is the ‘soft’ component, the addition of CO32− tilting softens the mode further. This suggests that the energetic coupling between these two components is complex, and that while the tilt is not the primary driver of the transition, it certainly has a strong affect on how the structure evolves before it. Given the observed effects of non-hydrostatic pressure, it is possible that uniaxial strain tunes this balance differently, resulting in a new phase which is closely related to the known monoclinic structure.
Conclusion
The elusive temperature behaviour of this important mineral, Li2CO3, has been reinvestigated. We have shown that the temperature and hydrostatic pressure have similar effects, with an interesting interplay between the lattice behaviour and the carbonate group tilt on heating, leading to non-linear behaviour in the lattice expansion. We find no evidence of additional high temperature phases, only the eventual decomposition of the carbonate, resulting in a partial reaction between the Li and the quartz holder.The effects of high pressure on the structure and phase transformation of Li2CO3 have been investigated in detail through combining neutron diffraction and XRD with Raman spectroscopy and DFT calculations. We have demonstrated that there are only two stable phases of Li2CO3 under hydrostatic conditions, and we have further proven that the material is extremely sensitive to non-hydrostatic conditions.
Under hydrostatic pressure conditions Li2CO3 demonstrates negative linear compressibility, a phenomenon not typically expected in such simple minerals, but strongly related to the ferroelastic nature of the phase.49 This is driven by the tilting of the rigid carbonate groups in the structure, competing with the shearing of the unit cell. This leads to a first order phase transition to a hexagonal structure, starting above 8.5 GPa, where the lithium becomes octahedrally coordinated. While the tilting of the carbonate groups is critical to the negative linear compressibility, the transition is accompanied by a large shear strain. The nature of this phase transition was analysed through combining symmetry analysis with DFT calculation, decoupling these two observed changes in the structure, demonstrating that it is a proper ferroelastic transition. This being the case, where one of the primary order-parameters is the shear of monoclinic unit cell, the high sensitivity to externally applied shear-strains is understandable.
The tunability of Li2CO3 under both hydrostatic and non-hydrostatic pressure has implications for the synthesis of LiCoO2, and other cathode materials. Applying pressure can enable the formation of new phases, often with stoichiometries which are unstable at ambient conditions. This has the potential for improving battery performance, enhancing stability and capacity. The use of pressure may also have interesting applications in the synthesis of novel ‘lattice-engineered’ compounds, as an alternative to ball-milling,50 and on new techniques for extracting Li, and the carbonate itself, from other precursors.51
For example, high-pressure and -temperature conditions can be used to stabilise new structures which can be recovered back to ambient conditions, such as the case with FePO4.52,53 This can fundamentally alter the ability for Li to intercalate within a material, and the resultant diffusion pathways. LiFePO4 is a well known example of a ‘two-phase’ Li-intercalation compound, where the Li-concentration results in a phase-transformation in the parent compound.54 Pressure can be used to balance the material towards one phase or another in tandem. Negative linear compressibility has the counterintuitive effect of elongating crystal structures along one or more of the principal axes. This could for example, be engineered to either open or close a particular pathway. Aside from diffusion and intercalation, a structural phase transition can alter coordination environments, which may influence the likelihood of unintended reactions within the material during charge/discharge or synthesis, affecting charge capacity.55
Data availability
Data for this article, including the neutron powder diffraction data, are available at https://doi.org/10.5286/ISIS.E.RB2010781 and https://doi.org/10.14461/oncat.data/2536722. Further data supporting this article have been included as part of the ESI,† and crystallographic data for Li2CO3 has been deposited at the CCDC.Author contributions
The conceptualisation was performed by C. J. R. The formal analysis was performed by C. J. R. and F. O. The investigation was performed by C. J. R., R. W., J. H., C. L. B. and N. P. F. The original draft was prepared by C. J. R. and was reviewed and edited by C. L. B., F. O., S. H. and N. P. F. Single crystals of the sample were prepared by R. S. P.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the Science and Technology Facilities Council for providing neutron beamtime on the PEARL instrument at the ISIS Neutron and Muon Source,56 and are grateful to Claire Talbott and Adam Sears (Pressure and Furnace Section, ISIS Neutron and Muon Source) for their assistance in running the high-temperature measurements. We also thank the Materials Characterisation Laboratory at the ISIS Neutron and Muon Source for access to the single-crystal XRD facilities. We acknowledge the computing resources provided the STFC Scientific Computing Department's SCARF cluster. A portion of this research used resources at the Spallation Neutron Source, a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory.57 The beam time was allocated to the SNAP instrument on proposal number IPTS-28913 and IPTS-34329. This research used resources of the Compute and Data Environment for Science (CADES) at the Oak Ridge National Laboratory, which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC05-00OR22725.Notes and references
- T. A. Barckholtz, K. M. Taylor, S. Narayanan, S. Jolly and H. Ghezel-Ayagh, Appl. Energy, 2022, 313, 118553 CrossRef CAS
.
- N. Imanaka, T. Murata, T. Kawasato and G. ya Adachi, Sens. Actuators, B, 1993, 13, 476–479 CrossRef CAS
.
- Y. N. Pal’yanov, A. G. Sokol, Y. M. Borzdov, A. F. Khokhryakov, A. F. Shatsky and N. V. Sobolev, Diamond Relat. Mater., 1999, 8, 1118–1124 CrossRef
.
- J. Zemann, Acta Crystallogr., 1957, 10, 664–666 CrossRef CAS
.
- H. Effenberger and J. Zemann, Z. Kristallogr. - Cryst. Mater., 1979, 150, 133–138 CrossRef CAS
.
- C. J. De Pater and R. B. Helmholdt, Phys. Rev. B, 1979, 19, 5735 CrossRef CAS
.
- M. Dušek, G. Chapuis, M. Meyer and V. Petricek, Acta Crystallogr., Sect. B:Struct. Sci., 2003, 59, 337–352 CrossRef PubMed
.
- F. Tuinstra, Z. Kristallogr. - Cryst. Mater., 1986, 177, 155–164 CrossRef CAS
.
- I. P. Swainson, M. T. Dove and M. J. Harris, J. Phys.: Condens. Matter, 1995, 7, 4395 CrossRef CAS
.
- A. V. Yatsenko, S. G. Zhukov, V. A. D’yakov, A. Etz, W. Molleman and H. Schenk, Mater. Res. Bull., 1995, 30, 739–744 CrossRef CAS
.
- A. V. Yatsenko, S. G. Zhukov, V. A. D’yakov and H. Schenk, Acta Crystallogr., Sect. C:Cryst. Struct. Commun., 1996, 52, 1–3 CrossRef
.
- S. G. Zhukov, A. V. Yatsenko, V. V. Chernyshev, V. A. D’yakov, R. L. Loux and H. Schenk, Z. Kristallogr. - Cryst. Mater., 1999, 214, 255–258 CrossRef CAS
.
- Y. Idemoto, J. W. Richardson Jr, N. Koura, S. Kohara and C.-K. Loong, J. Phys. Chem. Solids, 1998, 59, 363–376 CrossRef CAS
.
- A. Kirfel, H. Euler, B. Barbier, E. Hägele and H. Klapper, Z. Kristallogr. - Cryst. Mater., 2000, 215, 744–751 CrossRef CAS
.
- A. Reisman, J. Am. Chem. Soc., 1958, 80, 3558–3561 CrossRef CAS
.
- W. Klement Jr and L. H. Cohen, Ber. Bunsenges. Phys. Chem., 1975, 79, 327–334 CrossRef
.
- A. N. Khlapova and E. S. Kovaleva, J. Struct. Chem., 1967, 7, 528–532 CrossRef
.
-
H. C. Stober, Analytical Profiles of Drug Substances, Elsevier, 1986, vol. 15, pp. 367–391 Search PubMed
.
- D. N. Sagatova, N. E. Sagatov, P. N. Gavryushkin, M. V. Banaev and K. D. Litasov, Cryst. Growth Des., 2021, 21, 6744–6751 CrossRef CAS
.
- Ž. Čančarevič, J. Schön and M. Jansen, Z. Anorg. Allg. Chem., 2006, 632, 1437–1448 CrossRef
.
- P. N. Gavryushkin, S. V. Rashenko, A. F. Shatskiy, K. D. Litasov and A. I. Ancharov, J. Struct. Chem., 2016, 57, 1485–1488 CrossRef CAS
.
- P. N. Gavryushkin, A. Behtenova, Z. I. Popov, V. V. Bakakin, A. Y. Likhacheva, K. D. Litasov and A. Gavryushkin, Cryst. Growth Des., 2016, 16, 5612–5617 CrossRef CAS
.
- P. N. Gavryushkin, A. Bekhtenova, S. S. Lobanov, A. Shatskiy, A. Y. Likhacheva, D. Sagatova, N. Sagatov, S. V. Rashchenko, K. D. Litasov, I. S. Sharygin, A. F. Goncharov, V. B. Prakapenka and Y. Higo, Minerals, 2019, 9, 599 CrossRef CAS
.
- P. N. Gavryushkin, N. E. Sagatov, D. N. Sagatova, A. Bekhtenova, M. V. Banaev, E. V. Alexandrov and K. D. Litasov, Cryst. Growth Des., 2023, 23, 6589–6596 CrossRef CAS
.
- A. Grzechnik, P. Bouvier and L. Farina, J. Solid State Chem., 2003, 173, 13–19 CrossRef CAS
.
- B. Ying, J. R. Fitzpatrick, Z. Teng, T. Chen, T. W. B. Lo, V. Siozios, C. A. Murray, H. E. Brand, S. Day, C. C. Tang, R. S. Weatherup, M. Merz, P. Nagel, S. Schuppler, M. Winter and K. Kleiner, Chem. Mater., 2023, 35, 1514–1526 CrossRef CAS PubMed
.
- C. L. Bull, N. P. Funnell, M. G. Tucker, S. Hull, D. J. Francis and W. G. Marshall, High Pressure Res., 2016, 36, 493–511 CrossRef
.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr. - Cryst. Mater., 2005, 220, 567–570 CrossRef CAS
.
- B. J. Campbell, H. T. Stokes, D. E. Tanner and D. M. Hatch, J. Appl. Crystallogr., 2006, 39, 607–614 CrossRef CAS
.
- H. T. Stokes, D. M. Hatch and B. J. Campbell, ISODISTORT, ISOTROPY Software Suite Online, Accessed: April 2025, https://iso.byu.edu.
- O. Arnold, J. C. Bilheux, J. M. Borreguero, A. Buts, S. I. Campbell, L. Chapon, M. Doucet, N. Draper, R. Ferraz Leal, M. A. Gigg, V. E. Lynch, A. Markvardsen, D. J. Mikkelson, R. L. Mikkelson, R. Miller, K. Palmen, P. Parker, G. Passos, T. G. Perring, P. F. Peterson, S. Ren, M. A. Reuter, A. T. Savici, J. W. Taylor, R. J. Taylor, R. Tolchenov, W. Zhou and J. Zikovsky, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156–166 CrossRef CAS
.
- J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55–69 CrossRef
.
- M. J. Cliffe and A. L. Goodwin, J. Appl. Crystallogr., 2012, 45, 1321–1329 CrossRef CAS
.
- G. Shen, Y. Wang, A. Dewaele, C. Wu, D. E. Fratanduono, J. Eggert, S. Klotz, K. F. Dziubek, P. Loubeyre, O. V. Fat’yanov, P. D. Asimow, T. Mashimo, R. M. M. Wentzcovitch and other members of the IPPS task group, High Pressure Res., 2020, 40, 299–314 CrossRef
.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188–5192 CrossRef
.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed
.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. Howard and H. Puschmann, Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS
.
- G. M. Sheldrick, Acta Crystallogr., Sect. A:Found. Adv., 2015, 71, 3–8 CrossRef PubMed
.
- L. J. Bourhis, O. V. Dolomanov, R. J. Gildea, J. A. K. Howard and H. Puschmann, Acta Crystallogr., Sect. A:Found. Adv., 2015, 71, 59–75 CrossRef CAS PubMed
.
- S. Klotz, J. M. Besson and G. Hamel, High Pressure Res., 2006, 26, 277–282 CrossRef
.
- S. Klotz, L. Paumier, G. L. March and P. Munsch, High Pressure Res., 2009, 29, 649–652 CrossRef CAS
.
- D. M. Hatch and H. T. Stokes, J. Appl. Crystallogr., 2003, 36, 951–952 CrossRef CAS
.
-
H. T. Stokes, D. M. Hatch and B. J. Campbell, INVARIANTS, ISOTROPY Software Suite Online, accessed: April 2025, https://stokes.byu.edu/iso/isotropy.php
.
- N. Koura, S. Kohara, K. Takeuchi, S. Takahashi, L. A. Curtiss, M. Grimsditch and M.-L. Saboungi, J. Mol. Struct., 1996, 382, 163–169 CrossRef CAS
.
- M. H. Brooker and J. B. Bates, J. Chem. Phys., 1971, 54, 4788–4796 CrossRef CAS
.
- Y. Hase and I. V. P. Yoshida, Spectrochim. Acta A, 1978, 35, 377–378 Search PubMed
.
- Y. Hase and I. V. P. Yoshida, Spectrochim. Acta A, 1978, 35, 379 CrossRef
.
- R. J. Angel and U. Bismayer, Acta Crystallogr., Sect. B:Struct. Sci., 1999, 55, 896–901 CrossRef PubMed
.
- A. B. Cairns and A. L. Goodwin, Phys. Chem. Chem. Phys., 2015, 17, 20449–20465 RSC
.
- Y. Zhu, Y. Chen, J. Chen, J. Yin, Z. Sun, G. Zeng, X. Wu, L. Chen, X. Yu and H. Luo,
et al.
, Adv. Mater., 2024, 36, 2312159 CrossRef CAS PubMed
.
- S. Wang, N. J. Szymanski, Y. Fei, W. Dong, J. N. Christensen, Y. Zeng, M. Whittaker and G. Ceder, Inorg. Chem., 2024, 63, 13576–13584 CrossRef CAS PubMed
.
- C. W. Wilson, C. J. Ridley, S. G. MacLeod and C. L. Bull, High Pressure Res., 2021, 41, 14–26 CrossRef CAS
.
- C. L. Bull, C. J. Ridley, N. P. Funnell, C. W. Wilson and S. G. MacLeod, Mater. Adv., 2021, 2, 5096–5104 RSC
.
- D. Li and H. Zhou, Mater. Today, 2014, 17, 451–463 CrossRef CAS
.
- H. Du, Y. Wang, Y. Kang, Y. Zhao, Y. Tian, X. Wang, Y. Tan, Z. Liang, J. Wozny and T. Li,
et al.
, Adv. Mater., 2024, 36, 2401482 CrossRef CAS PubMed
.
- C. J. Ridley, S. Hull, C. L. Bull and N. P. Funnell, Structural anomalies in lithium carbonate, STFC ISIS Neutron and Muon Source, 2020, DOI:10.5286/ISIS.E.RB2010781.
- C. J. Ridley and J. K. Hinton, Negative linear compressibility and complex phase behaviour in 7Li2CO3, SNS ORNL, 2025, DOI:10.14461/oncat.data/2536722.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ta02325d |
| ‡ Present address: Department of Physics, King's College London, London WC2R 2LS, UK. |
| This journal is © The Royal Society of Chemistry 2025 |