Probing the orientation and membrane permeation of rhodamine voltage reporters through molecular simulations and free energy calculations†
Yajing
Qi
 a,
Lap Yan
Fung
a,
Christophe
Chipot
a,
Lap Yan
Fung
a,
Christophe
Chipot
 *bcd and
Yi
Wang
*bcd and
Yi
Wang
 *a
*a
aDepartment of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong SAR, China. E-mail: yiwang@cuhk.edu.hk
bLaboratoire International Associé Centre National de la Recherche Scientifique et University of Illinois at Urbana Champaign, Unité Mixte de Recherche no. 7019, Université de Lorraine, 54506 Vandoeuvre-lès-Nancy, France. E-mail: Christophe.Chipot@univ-lorraine.fr
cTheoretical and Computational Biophysics Group, Beckman Institute, and Department of Physics, University of Illinois at Urbana Champaign, Urbana, IL 61801, USA
dDepartment of Biochemistry and Molecular Biology, University of Chicago, Chicago, IL 60637, USA
First published on 3rd January 2025
Abstract
The transmembrane potential of plasma membranes and membrane-bound organelles plays a fundamental role in cellular functions such as signal transduction, ATP synthesis, and homeostasis. Rhodamine voltage reporters (RhoVRs), which operate based on the photoinduced electron transfer (PeT) mechanism, are non-invasive, small-molecule voltage sensors that can detect rapid voltage changes, with some of them specifically targeting the inner mitochondrial membrane. In this work, we conducted extensive molecular dynamics simulations and free-energy calculations to investigate the physicochemical properties governing the orientation as well as membrane permeation barriers of three RhoVRs. Our results indicate that the positioning of the most polarized functional group relative to the hydrophobic molecular wire dictates the alignment of RhoVRs with the membrane normal, thereby, significantly affecting their voltage sensitivity. Free-energy calculations in different membrane systems identify significantly higher barriers against the permeation of RhoVR 1 compared to SPIRIT RhoVR 1, explaining their distinct subcellular localization profiles. Subsequent free-energy calculations of the distinguishing components from the two different RhoVRs provide additional insight into the physicochemical properties governing their membrane permeation. The connection between chemical composition and membrane orientation, as well as permeation behaviors of RhoVRs revealed by our calculations provides general guiding principles for the rational design of PeT-based fluorescent dyes with enhanced voltage sensitivity and desired subcellular distribution.
Introduction
The membrane potential (Vmem) is a crucial instructive signal that regulates a wide range of cellular behaviors.1 Measurement of Vmem traditionally employs the patch clamp technique, where a microelectrode is directly attached to a cell of interest. However, the invasiveness, low throughput, as well as low spatial resolution significantly limits the application of this approach.2 Over the past few decades, the development of voltage-sensitive dyes (VSDs) has revolutionized our ability to measure Vmem and monitor the electrical activity of living cells. These small-molecule voltage sensors generally fall into two categories: slow- and fast-response dyes.3 Slow dyes typically make use of the voltage-dependent accumulation of lipophilic ions in a membrane, or, their redistribution between its two leaflets. Compared with fast dyes, they provide higher sensitivity, but suffer from slower response time and may introduce a capacitive load that disrupts normal membrane and cellular functions.4 Prominent examples of fast dyes are electrochromic dyes3 that operate based on the molecular Stark effect: the electric field directly interacts with the chromophore, causing small wavelength shifts in its excitation and emission spectra. As a result, these VSDs have excellent response speed, although their best sensitivity is achieved in the wings of the spectra, preventing the majority of their excitation and emission photons from being utilized.3VSDs based on the photo-induced electron transfer (PeT) mechanism are another class of fast dyes: these amphiphilic compounds consist of an electron donor–accepter pair covalently connected by a molecular linker, where the electron transfer from the donor to the acceptor competes with fluorescence in a voltage-dependent manner.4–6 Compared with electrochromic or slow dyes described above, PeT-based voltage sensors are fast, have no capacitive loading, and allow the efficient use of photons for excitation and emission. A representative family of PeT-based voltage sensors, namely, the VoltageFluor (VF) dyes, feature an aniline-based electron donor at one end of a phenylenevinylene linker and a sulfonated fluorescein as the electron acceptor at the other end.7 The polarity of the sulfonated fluorescein head and the hydrophobicity of the aniline-phenylenevinylene tail renders the molecule amphiphilic. Upon inserting into the plasma membrane, the tail of a VF dye is buried within the outer leaflet, while its head is exposed to water. At hyperpolarizing potentials, PeT in the VF dye is promoted and fluorescence is quenched; at depolarizing potentials, PeT is inhibited and fluorescence is enhanced. Such voltage sensitivity of a PeT-based dye has been modeled by the equation:7
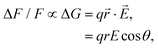 | (1) |
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) and the displacement vector
and the displacement vector ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) of the transferred electron.
of the transferred electron.
Eqn (1) dictates that the voltage sensitivity of a PeT-based dye strongly depends on its orientation within the membrane: at θ = 0° the VSD perfectly aligns with the membrane normal and the distance traveled by the electron along the transmembrane electric field reaches its maximum (r), resulting in the largest ΔF/F. Based on this relation and employing molecular dynamics (MD) simulations, we previously modeled the orientation of several VF dyes in a POPC bilayer, which led to the development of disulfoVF (dsVF) with an improved alignment with the membrane normal and a significantly higher voltage sensitivity than its predecessor, monosulfoVF (msVF).8 However, a major limitation of these VF dyes is their excitation and emission profiles in the cyan to green region of the visible spectrum, which precludes their concurrent usage with optical indicators such as green fluorescent proteins. Another family of PeT-based VSDs, namely, rhodamine voltage reporters (RhoVRs),9 address this issue by employing a tetramethylrhodamine-based fluorophore.10 These red-shifted dyes have demonstrated a sensitivity comparable to the most sensitive VF dye.9 Notably, among various synthesized RhoVRs, RhoVR 1, which features the phenylenevinylene molecular linker at the 5′-, rather than the typically explored 4′-position of the rhodamine aryl ring,11–13 exhibits the highest voltage sensitivity. Such a difference is somewhat surprising, as the RhoVR featuring a 4′-substituted tetramethylrhodamine, hereon referred to as RhoVR 1–4′, appears to produce an overall ‘more symmetric’ molecule than its 5′-substituted counterpart (Fig. 1). A higher degree of symmetry about its molecular wire is expected to improve alignment with the membrane normal and the voltage sensitivity of a given PeT-based VSD. Therefore, the cause underlying the different performances of the 5′- and 4′-substituted RhoVRs demands further investigation.
While the majority of PeT-based VSDs target the plasma membrane, a variant of RhoVR 1, namely, SPIRIT RhoVR 1, has been re-programmed to target the inner mitochondrial membrane.6 SPIRIT RhoVR 1 is obtained by masking the carboxylate of RhoVR 1 as an acetoxymethyl ester.6 Once inside the mitochondrion, esterases hydrolyze SPIRIT RhoVR 1, trapping the resulting RhoVR 1 in the inner mitochondrial membrane, where it can monitor the mitochondrial electrochemical potential via the PeT mechanism. Based on their distinct target destinations, RhoVR 1 and SPIRIT RhoVR 1 have very opposite requirements on their plasma membrane permeability: the former needs to minimize this permeability to prevent dye internalization, while the latter should enhance it to enable intracellular accumulation. Due to the permanent positive charge borne by the rhodamine xanthene moiety and a negatively charged carboxylate moiety as part of its sarcosine amide group, RhoVR 1 carries a zero net charge. In contrast, SPIRIT RhoVR 1, for which the carboxylate moiety has been replaced by an ester moiety, is +1 charged. Based solely on net-charge considerations, it may appear that RhoVR 1 should have a greater membrane permeability than SPIRIT RhoVR 1, since the hydrophobic interior of a lipid bilayer is known to pose significant barriers against charged species.14–16 This apparent paradox may be explained by a charge delocalization over the rhodamine aromatic rings. Indeed, a previous study on several permanently charged rhodamine cations has shown that they are highly permeable in artificial membranes.17 However, to the best of our knowledge, no measurement of the actual free-energy barriers against plasma membrane permeation of the aforementioned RhoVRs has been made, precluding quantitative analysis of their permeation mechanism, which could guide rational design efforts to fine-tune the intracellular distribution of RhoVRs and other PeT-based VSDs.
In this work, we report extensive molecular dynamics simulations of three RhoVRs, namely, RhoVR 1, RhoVR 1–4′, and SPIRIT RhoVR 1. Through comparative orientation analysis of the three dyes, we show that placing its most polar functional group and its molecular wire at para positions of the rhodamine aryl ring significantly improves the orientation of a RhoVR dye in lipid membranes. RhoVR 1 with such a structural arrangement exhibits a significantly smaller θ than RhoVR 1–4′ in a POPC bilayer as well as a model mammalian membrane. This result, which emphasizes the symmetry in the position of its most polar functional group about the molecular wire, is consistent with our previous findings on the VF dye family,18 and should apply in general to PeT-based VSDs. Employing well-tempered metadynamics combined with the extended adaptive biasing force (WTM-eABF) method,19,20 we further determined the membrane permeation free-energy profiles for RhoVR 1 and SPIRIT RhoVR 1 as well as two components distinguishing these two VSDs. Our calculations consistently reveal lower free-energy barriers against the permeation of SPIRIT RhoVR 1 than RhoVR 1, corresponding to permeation rates approximately three orders of magnitude higher for the former VSD. These results confirm that the localized negative charge on the sarcosine carboxylate moiety dominates the barrier against RhoVR 1 permeation, while the absence of this carboxylate moiety and the delocalization of a positive charge over its rhodamine xanthene moiety grants SPIRIT RhoVR 1 a significantly higher membrane permeability than RhoVR 1. Moreover, analysis of the whole molecules versus their two distinguishing components reveals distinct major contributors to free-energy barriers against the permeation of the two RhoVRs, shedding further light onto structural considerations in the design of PeT-based VSDs with different subcellular destinations.
Methods
Simulation protocols and force-field parameters
We conducted equilibrium MD simulations on RhoVR 1, SPIRIT RhoVR 1, and RhoVR 1–4′ in three lipid bilayers: pure POPC, mixed POPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CHL at a 2
CHL at a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio, and a model mammalian membrane. The pure POPC bilayer consists of 42 POPC molecules per leaflet, while the mixed POPC:CHL bilayer contains 38 POPC and 19 cholesterol molecules per leaflet. Following the addition of water molecules, both systems contain approximately 28
1 molar ratio, and a model mammalian membrane. The pure POPC bilayer consists of 42 POPC molecules per leaflet, while the mixed POPC:CHL bilayer contains 38 POPC and 19 cholesterol molecules per leaflet. Following the addition of water molecules, both systems contain approximately 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms, with the dimensions 54 × 54 × 94 Å3. A pre-equilibrated mammalian membrane from our previous work,21 built based on coarse-grained simulations by Ino et al.,22 is adopted here. This model mammalian membrane includes 26 lipid species with a total of 256 lipid molecules, of which 81 are cholesterol. After solvation, this system contains ∼49
000 atoms, with the dimensions 54 × 54 × 94 Å3. A pre-equilibrated mammalian membrane from our previous work,21 built based on coarse-grained simulations by Ino et al.,22 is adopted here. This model mammalian membrane includes 26 lipid species with a total of 256 lipid molecules, of which 81 are cholesterol. After solvation, this system contains ∼49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms, with the dimensions 80 × 80 × 75 Å3. In all three lipid bilayers, sodium and chloride ions are used to maintain electric neutrality with an ion concentration of 0.15 M. A single RhoVR molecule was manually inserted into a given bilayer by aligning it with the membrane normal along the z-axis and replacing one overlapping lipid molecule. For each simulation system, a 200
000 atoms, with the dimensions 80 × 80 × 75 Å3. In all three lipid bilayers, sodium and chloride ions are used to maintain electric neutrality with an ion concentration of 0.15 M. A single RhoVR molecule was manually inserted into a given bilayer by aligning it with the membrane normal along the z-axis and replacing one overlapping lipid molecule. For each simulation system, a 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-step energy minimization followed by a 10-ns equilibration in the isobaric-isothermal ensemble were performed. Each system was then run in three replicas of 1-μs simulations, resulting in an aggregate simulation time of 27 μs.
000-step energy minimization followed by a 10-ns equilibration in the isobaric-isothermal ensemble were performed. Each system was then run in three replicas of 1-μs simulations, resulting in an aggregate simulation time of 27 μs.
All simulations were performed using the CHARMM36 force field for lipids,23 the CGenFF force field for small molecules24,25 and the TIP3P water model.26 The initial parameters for RhoVRs were generated using the CGenFF program,27 which assigned penalty scores to indicate the reliability of the predicted parameters. The RhoVR parameters thus obtained had charge penalties up to 60.1 and dihedral penalties up to 207.0, necessitating further optimization, which was achieved with ffTK28 employing a fragment-based divide-and-conquer approach. Specifically, the conjugated xanthene ring sharing the +1 charge of the tetramethylrhodamine was the focus of the charge optimization. Geometry optimization at the MP2/6-31G(d) level revealed a symmetric, planar tricyclic ring system, consistent with previous density functional theory calculations.29 Therefore, during its charge optimization, we maintained the symmetry of the xanthene ring by enforcing that the corresponding atom pairs were given the same atom types and atomic charges. Simulations of the parameterized tetramethylrhodamine component (Fig. S1a, ESI†) in a water box were conducted for 10 ns at room temperature, during which the planar structure of the tricyclic ring was preserved. All geometry optimizations were performed at the MP2/6-31G(d) level except for the anionic fragment (Fig. S1e, ESI†), which was optimized at the MP2/6-31+G(d) level. Charge optimizations were conducted at the HF/6-31G(d) level. The dihedrals were optimized by scanning and fitting the energies at the MP2/6-31G(d) level for neutral and positively charged fragments of the molecules or the MP2/6-31+G(d) level for its anionic fragment. All quantum chemical calculations were conducted using Gaussian 09.30
Potential of mean force (PMF) calculations and data analysis
To explore the energetics of RhoVR membrane permeation, we employed the WTM-eABF method,19,31 which combines two powerful enhanced-sampling approaches: well-tempered metadynamics (WTM)32–34 and extended adaptive biasing force (eABF).35–38 The combination of the two methods enables efficient estimation of free-energy landscapes, and is particularly suitable for complex processes such as membrane permeation.14,19,39,40 The collective variable (CV) for the WTM-eABF calculation was chosen as the z-projection of the distance between the center of mass of the sarcosine-based tertiary amide and that of the bilayer, which was determined from the position of the phosphorous atoms of POPC as well as the oxygen atoms of cholesterol. Sampling ranges and window divisions for each system are listed in Table S1 (ESI†). Briefly, three to five windows were used to enhance sampling efficiency, with an overlap of 2 to 5 Å between adjacent windows and a bin width of 0.2 Å for each window. The threshold beyond which the bias was applied was set to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps, while the standard deviation between the actual and the extended CV was set to 0.05 Å and the oscillation period for the fictitious particle to 100 ns. To strike a balance between enhanced sampling and controlled exploration of the conformational space, WTM calculations are typically performed with a bias temperature in the range of 1000 to 8000 K.14,20,34 Following Harris et al.,14 the WTM part of our calculation was performed with a bias temperature of 3000 K. A hill width of 5.0 Å and a hill weight of 0.1 kcal mol−1 were employed. All PMFs w(z) were symmetrized about the bilayer center (z = 0) through antisymmetrizing the gradients. The uncertainty in w(z) was estimated as the average deviation of the z < 0 and z > 0 halves of the unsymmetrized PMF from the symmetrized PMF.
000 steps, while the standard deviation between the actual and the extended CV was set to 0.05 Å and the oscillation period for the fictitious particle to 100 ns. To strike a balance between enhanced sampling and controlled exploration of the conformational space, WTM calculations are typically performed with a bias temperature in the range of 1000 to 8000 K.14,20,34 Following Harris et al.,14 the WTM part of our calculation was performed with a bias temperature of 3000 K. A hill width of 5.0 Å and a hill weight of 0.1 kcal mol−1 were employed. All PMFs w(z) were symmetrized about the bilayer center (z = 0) through antisymmetrizing the gradients. The uncertainty in w(z) was estimated as the average deviation of the z < 0 and z > 0 halves of the unsymmetrized PMF from the symmetrized PMF.
Following the work by Harris et al. investigating the membrane permeation of ionizable molecules,14,41 the above WTM-eABF calculations were repeated for RhoVR 1 with its carboxylate moiety protonated (Table S1, ESI†). The PMFs of the deprotonated and the protonated RhoVR 1 were then combined to estimate its permeability based on the pH partition hypothesis.14 Specifically, this hypothesis assumes that permeant molecules in different protonation states traverse a membrane independently. The effective permeability of the permeant can then be expressed as  , where fs denotes the fraction of each species, i.e., fd for deprotonated RhoVR 1 and fp for protonated RhoVR 1, as determined by Henderson–Hasselbalch equilibrium.42 The specific permeability (Ps) for individual protonation states follows the Kramers–Smoluchowski treatment for steady-state flux across free energy barriers:43–45
, where fs denotes the fraction of each species, i.e., fd for deprotonated RhoVR 1 and fp for protonated RhoVR 1, as determined by Henderson–Hasselbalch equilibrium.42 The specific permeability (Ps) for individual protonation states follows the Kramers–Smoluchowski treatment for steady-state flux across free energy barriers:43–45
 | (2) |
In this work, the above equation is only used to estimate the relative permeabilities of SPIRIT RhoVR 1 and RhoVR 1, where the two VSDs are assumed to have similar diffusion coefficients that drop out of eqn (2) in estimating the ratio of their membrane permeabilities. For SPIRIT RhoVR 1, which does not have ionizable groups, eqn (2) is applied on the single PMF obtained from its WMT-eABF calculation. For RhoVR 1, the PMFs used in the above equation correspond to ws obtained directly from WTM-eABF, where ws(±L/2) = 0 for both the deprotonated and the protonated RhoVR 1. Nonetheless, to reflect their different population fractions, the PMF of the protonated RhoVR 1 is shifted by the free energy cost ΔG of protonating RhoVR 1 at pH 7 when it is displayed in the same figure as the PMF of the deprotonated RhoVR 1. With a predicted pKa of 3.746 for the N-methylhippuric acid moiety, the corresponding ΔG is estimated by:
| ΔG = ln(10)kBT(pH − pKa). | (3) |
All equilibrium MD simulations were performed with NAMD 2.14, while the WTM-eABF calculations were performed with NAMD 3.0.47,48 The temperature was kept at 310 K with the stochastic velocity rescaling method, with a damping coefficient of 1 ps−1. Langevin piston was applied to control the pressure at 1.01325 bar.49 Short-range electrostatic potential and van der Waals (vdW) potential were smoothed at 12 Å, where the vdW potential was switched by a force-switching protocol. Particle-mesh Ewald algorithm was applied to determine the long-range electrostatic potential, with a grid spacing of 1 Å.50 The SETTLE algorithm was employed to constrain water molecules to their equilibrium geometry,51 and covalent bonds involving hydrogens were constrained to their equilibrium lengths using the RATTLE algorithm.52 The equations of motion were integrated with the r-RESPA multiple time-stepping algorithm, with short-range and long-range interactions calculated every 2 and 4 fs, respectively.53 The alignment and positioning of RhoVRs within a given membrane were characterized using several parameters (Fig. 1): the angle θ between the z-axis and a vector pointing from the diethylaniline nitrogen to the center of mass of the tricyclic ring in the tetramethylrhodamine head, the tilt angles of vectors  and
and  , the angle φ between these two vectors, the distance between the center of mass of RhoVRs and the bilayer along the z-axis (CoMz), as well as the number of water molecules within 2.4 Å of the RhoVRs. The three-dimensional occupancy maps of water molecules were computed using the VolMap plugin54 of VMD based on the central window (−15 < z < 15 Å) of the WTM-eABF calculations.
, the angle φ between these two vectors, the distance between the center of mass of RhoVRs and the bilayer along the z-axis (CoMz), as well as the number of water molecules within 2.4 Å of the RhoVRs. The three-dimensional occupancy maps of water molecules were computed using the VolMap plugin54 of VMD based on the central window (−15 < z < 15 Å) of the WTM-eABF calculations.
Results
Position of its most polar functional group dictates RhoVR orientation
All RhoVRs contain an aniline-based electron donor, a phenylenevinylene molecular linker, and a rhodamine-based head that serves both as the fluorophore and the electron acceptor (Fig. 1). The three VSDs investigated in this work differ either in the relative positions of their tetramethylrhodamine-based heads with respect to the diethylaniline-phenylenevinylene tails, or, in their functional groups at the 2′-position of the rhodamine aryl ring, hereon referred to as the anchors of these molecules (labeled as R in Fig. 1a). Unless otherwise specified, the carboxylate moiety of the sarcosine anchor in RhoVR 1 is modelled in the deprotonated (−1 charged) state based on its predicted pKa of 3.7.46 Following the PeT mechanism, the orientation of the three RhoVRs within the membrane is expected to strongly influence their voltage sensitivity (eqn (1)). To explore their dynamics and orientation within a membrane and understand how lipid compositions influence their voltage sensitivities, we conducted triplicated 1-μs MD simulations on the three RhoVR variants in a pure POPC bilayer, a mixed POPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CHL bilayer at a 2
CHL bilayer at a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
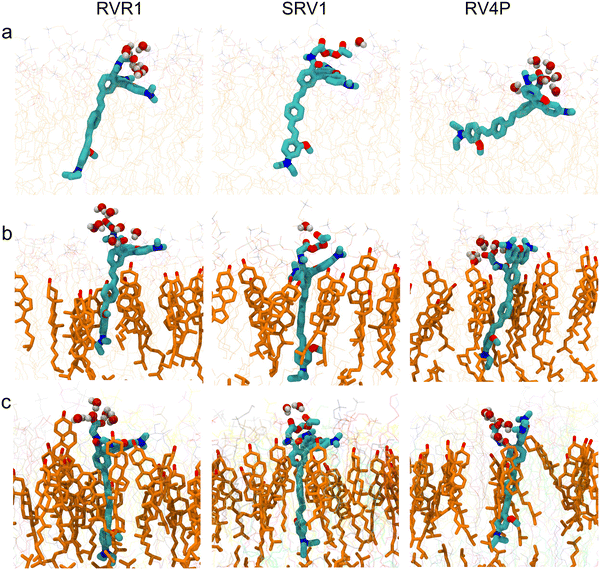
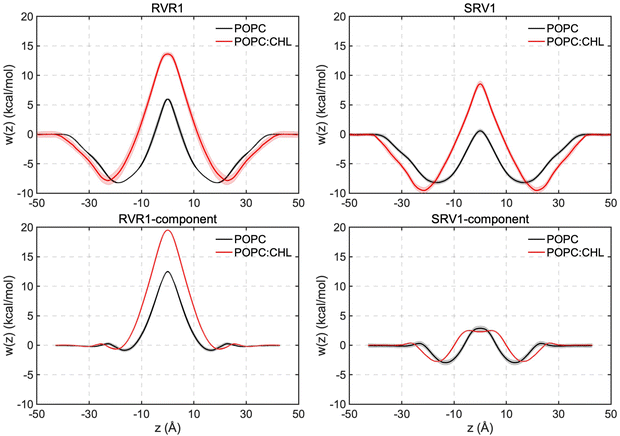
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio, and a model mammalian membrane. The trajectories representing an aggregate time of 27 μs reveal that all three RhoVRs localize to the lipid–water interface, with their hydrophobic tails embedded within the membrane and their rhodamine-based heads exposed to water (Fig. 2 and Fig. S2, ESI†).
1 molar ratio, and a model mammalian membrane. The trajectories representing an aggregate time of 27 μs reveal that all three RhoVRs localize to the lipid–water interface, with their hydrophobic tails embedded within the membrane and their rhodamine-based heads exposed to water (Fig. 2 and Fig. S2, ESI†).
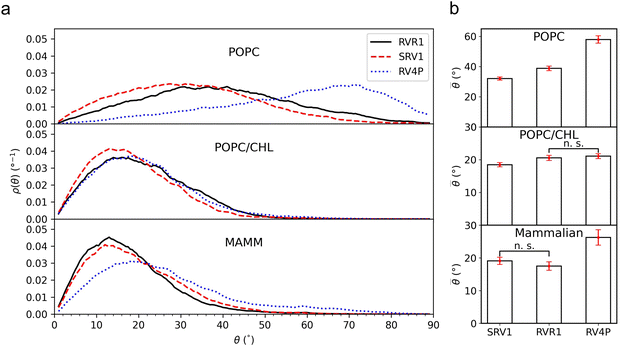
Following our previous work,18 we define the tilt angle, θ, as the angle between the membrane normal (z-axis) and a vector pointing from the diethylaniline nitrogen to the center of mass of the tricyclic ring in the tetramethylrhodamine head (Fig. 1d). The distributions of θ for all three RhoVRs across different membrane systems are reported in Fig. 3, with their mean values, standard errors and correlation times determined from MD trajectories given in Table 1. Overall, RhoVR 1 and SPIRIT RhoVR 1 are found to bear close similarities in their θ distributions across all investigated membrane systems. In contrast, RhoVR 1–4′ displays notably different alignment with the membrane normal than the other two RhoVRs, except in POPC:CHL where its mean tilt angle is statistically indistinguishable from RhoVR 1. In the pure POPC bilayer, RhoVR 1–4′ exhibits a mean tilt angle of 57.9°, approximately 20° greater than RhoVR 1. This distinction can be explained by the different positions of the sarcosine anchor in these two molecules: given its negative charge, this hydrophilic anchor needs to maximize its exposure to water; the 4′-positioned phenylenevinylene linker in RhoVR 1–4′ dictates that the entire molecule must tilt significantly to meet such a requirement (Fig. 2). In contrast, the 5′-positioned linker in RhoVR 1 and SPIRIT RhoVR 1 allows them to maintain an “upright” orientation that readily enables the solvation of the sarcosine-based anchors. The more favorable alignment of RhoVR 1 with the membrane normal, therefore, contributes to its greater voltage sensitivity (47% ΔF/F per 100 mV) compared to RhoVR 1–4′ (26% ΔF/F per 100 mV).9
![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) ) ± standard error (eθ) of the tilt angle θ measured from three replicas of 1-μs simulations of a RhoVR dye in a given lipid environment. The integrated autocorrelation time τ (ns) averaged over simulations of a given RhoVR dye-lipid system is also provided
) ± standard error (eθ) of the tilt angle θ measured from three replicas of 1-μs simulations of a RhoVR dye in a given lipid environment. The integrated autocorrelation time τ (ns) averaged over simulations of a given RhoVR dye-lipid system is also provided
| Membrane |
![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) ± eθ, τ ± eθ, τ |
||
|---|---|---|---|
| RVR1 | SRV1 | RV4P | |
| POPC | 38.8° ± 1.5°, 1.1 ns | 32.0° ± 1.0°, 0.6 ns | 57.9° ± 2.4°, 2.3 ns |
| POPC:CHL | 20.6° ± 0.8°, 0.8 ns | 18.5° ± 0.7°, 0.6 ns | 21.1° ± 0.7°, 0.6 ns |
| Mammalian | 17.5° ± 1.3°, 11.5 ns | 19.1° ± 1.1°, 7.5 ns | 26.3° ± 2.4°, 16.4 ns |
To further dissect the orientational differences among the three RhoVRs in a lipid membrane, we computed the tilt angles of the sarcosine-based anchor (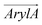 , Fig. 1d) as well as the xanthene-based tricyclic ring (
, Fig. 1d) as well as the xanthene-based tricyclic ring ( ). Unlike θ, which reflects the global molecular orientation, these two tilt angles capture the orientations of two individual segments of the RhoVRs. Since both segments in RhoVR 1 and RhoVR 1–4′ carry net charges, a “tug of war” aimed at gaining solvent exposure can be expected between them. As shown in Fig. S3 (ESI†), the angle between
). Unlike θ, which reflects the global molecular orientation, these two tilt angles capture the orientations of two individual segments of the RhoVRs. Since both segments in RhoVR 1 and RhoVR 1–4′ carry net charges, a “tug of war” aimed at gaining solvent exposure can be expected between them. As shown in Fig. S3 (ESI†), the angle between  and the z-axis falls within a range of ∼0 to 45° for RhoVR 1 and ∼0 to 40° for RhoVR 1–4′ in POPC, whereas the corresponding
and the z-axis falls within a range of ∼0 to 45° for RhoVR 1 and ∼0 to 40° for RhoVR 1–4′ in POPC, whereas the corresponding  tilts more significantly over the range of ∼20° to 90° in RhoVR 1–4′ and ∼40° to 120° in RhoVR 1. These results indicate that the sarcosine anchor is the clear “winner” of the aforementioned tug of war. Additionally, the significant tilting of
tilts more significantly over the range of ∼20° to 90° in RhoVR 1–4′ and ∼40° to 120° in RhoVR 1. These results indicate that the sarcosine anchor is the clear “winner” of the aforementioned tug of war. Additionally, the significant tilting of  in RhoVR 1 emphasizes the lipophilic nature of the tetramethylrhodamine head—angles greater than 90° correspond to orientations where the xanthene ring points towards the interior of the lipid phase (Fig. S4, ESI†). In contrast,
in RhoVR 1 emphasizes the lipophilic nature of the tetramethylrhodamine head—angles greater than 90° correspond to orientations where the xanthene ring points towards the interior of the lipid phase (Fig. S4, ESI†). In contrast, 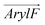 tilting rarely exceeds 90° in RhoVR 1–4′, which is again explained by the para positions of its tetramethylrhodamine head and the hydrophobic molecular wire—with the former pointing towards bilayer center, the latter would be forced into an unfavorable orientation pointing towards water (Fig. S4, ESI†). These results underscore the critical role played by anchor positions in determining the orientation of RhoVRs within a membrane environment. Scaffolds featuring the para positioning of the molecular wire and the sarcosine anchor best accommodates the amphiphilicity of these VSDs. Such a strategic arrangement minimizes compromise to the orientation of the molecular wire, resulting in a significantly smaller tilt angle for the 5′-substituted RhoVR 1 over 4′-substituted RhoVR 1–4′.
tilting rarely exceeds 90° in RhoVR 1–4′, which is again explained by the para positions of its tetramethylrhodamine head and the hydrophobic molecular wire—with the former pointing towards bilayer center, the latter would be forced into an unfavorable orientation pointing towards water (Fig. S4, ESI†). These results underscore the critical role played by anchor positions in determining the orientation of RhoVRs within a membrane environment. Scaffolds featuring the para positioning of the molecular wire and the sarcosine anchor best accommodates the amphiphilicity of these VSDs. Such a strategic arrangement minimizes compromise to the orientation of the molecular wire, resulting in a significantly smaller tilt angle for the 5′-substituted RhoVR 1 over 4′-substituted RhoVR 1–4′.
Lipid composition strongly affects RhoVR orientation
The mammalian plasma membrane is a heterogeneous bilayer containing a large variety of lipid species, including phospholipids, cholesterol, sphingolipids, as well as polyunsaturated lipids.22,55,56 As its simplified representations, pure POPC and mixed POPC:CHL are frequently used to mimic the mammalian membrane. Here, apart from a pure POPC bilayer, we simulated RhoVRs in a mixed POPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CHL bilayer at a 2
CHL bilayer at a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio, as well as in a mammalian membrane model that contains over 20 lipid species, with the molar percentage of cholesterol comparable in the latter two membranes. As shown in Fig. 2 and 3, these simulations clearly demonstrate the influence of bilayer composition on RhoVR orientation. In particular, the presence of cholesterol increases the membrane thickness, resulting in an “ordering” effect that stabilizes and enhances the alignment of RhoVRs with the membrane normal. For instance, the tilt angle of RhoVR 1–4′ decreases from 57.9° in pure POPC to 21.1° in POPC:CHL, and 26.3° in the mammalian membrane. Similarly, RhoVR 1 exhibits a tilt angle of 20.6° in POPC:CHL, approximately half of its value in pure POPC. Notably, the distribution of θ is much narrower in POPC:CHL and in the mammalian membrane compared to that in pure POPC (Fig. 3), indicating that the presence of cholesterol not only reduces θ, but also restricts its fluctuation. Further analysis of
1 molar ratio, as well as in a mammalian membrane model that contains over 20 lipid species, with the molar percentage of cholesterol comparable in the latter two membranes. As shown in Fig. 2 and 3, these simulations clearly demonstrate the influence of bilayer composition on RhoVR orientation. In particular, the presence of cholesterol increases the membrane thickness, resulting in an “ordering” effect that stabilizes and enhances the alignment of RhoVRs with the membrane normal. For instance, the tilt angle of RhoVR 1–4′ decreases from 57.9° in pure POPC to 21.1° in POPC:CHL, and 26.3° in the mammalian membrane. Similarly, RhoVR 1 exhibits a tilt angle of 20.6° in POPC:CHL, approximately half of its value in pure POPC. Notably, the distribution of θ is much narrower in POPC:CHL and in the mammalian membrane compared to that in pure POPC (Fig. 3), indicating that the presence of cholesterol not only reduces θ, but also restricts its fluctuation. Further analysis of 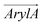 and
and 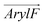 reveals an anticorrelation between their tilt angles (Fig. S3, ESI†) in mixed POPC:CHL and in the mammalian membrane, suggesting that the aforementioned tug of war is even more evident in these lipid environments. Out of all three RhoVRs, RhoVR 1–4′ experiences the largest shift in the
reveals an anticorrelation between their tilt angles (Fig. S3, ESI†) in mixed POPC:CHL and in the mammalian membrane, suggesting that the aforementioned tug of war is even more evident in these lipid environments. Out of all three RhoVRs, RhoVR 1–4′ experiences the largest shift in the 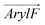 tilt angle, where its most probable value drops from around 70° in pure POPC to 25° in POPC:CHL and the model mammalian membrane. This dramatic change, which explains the largest shift in its ρ(θ), can be attributed to the para positioning of its phenylenevinylene linker and the tricyclic ring: when the former is forced to align more closely with the membrane normal, tilting of the latter is inevitably reduced. These findings are consistent with our previous studies on the VF dye family, whereby a similar improvement in dye orientation is recorded in the presence of cholesterol.18 Notably, while RhoVR orientations in POPC:CHL are highly similar to those in the mammalian membrane, the former appears to exert a slightly greater “ordering” effect on RhoVR 1–4′, resulting in statistically indistinguishable
tilt angle, where its most probable value drops from around 70° in pure POPC to 25° in POPC:CHL and the model mammalian membrane. This dramatic change, which explains the largest shift in its ρ(θ), can be attributed to the para positioning of its phenylenevinylene linker and the tricyclic ring: when the former is forced to align more closely with the membrane normal, tilting of the latter is inevitably reduced. These findings are consistent with our previous studies on the VF dye family, whereby a similar improvement in dye orientation is recorded in the presence of cholesterol.18 Notably, while RhoVR orientations in POPC:CHL are highly similar to those in the mammalian membrane, the former appears to exert a slightly greater “ordering” effect on RhoVR 1–4′, resulting in statistically indistinguishable ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) for RhoVR 1 and RhoVR 1–4′ (Fig. 3b). Therefore, while the shorter correlation time of θ in mixed POPC:CHL (Table 1) facilitates sampling of the RhovR orientation, the ranking of
for RhoVR 1 and RhoVR 1–4′ (Fig. 3b). Therefore, while the shorter correlation time of θ in mixed POPC:CHL (Table 1) facilitates sampling of the RhovR orientation, the ranking of ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) based on this bilayer may not always reflect that of the more realistic mammalian membrane.
based on this bilayer may not always reflect that of the more realistic mammalian membrane.
SPIRIT RhoVR 1 has significantly lower permeation free-energy barrier than RhoVR 1
Despite sharing the same molecular scaffold and differing only in their hydrophilic anchors, RhoVR 1 and SPIRIT RhoVR 1 exhibit distinct cellular localization profiles—while RhoVR 1 is localized to the outer leaflet of the plasma membrane, SPIRIT RhoVR 1 can penetrate the plasma membrane and reach the mitochondrion.6 Once inside the mitochondrial matrix, esterases cleave the ester on its anchor, converting SPIRIT RhoVR 1 back to RhoVR 1 and trapping it within the inner mitochondrial membrane.6 To explore the thermodynamic foundation of the distinct membrane permeabilities of the two RhoVRs, we conducted extensive free-energy calculations of both VSDs in pure POPC and mixed POPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CHL (2
CHL (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) using the WTM-eABF algorithm.19Fig. 4 shows the symmetrized free-energy profiles for each RhoVR, while unsymmetrized free-energy profiles are shown in Fig. S5 (ESI†). The shaded areas in Fig. 4 represent average deviations between these two sets of free-energy profiles (see Methods), which can be viewed as an indicator of the sampling accuracy.40,57–59 In pure POPC, the deviations are 0.7 kcal mol−1 and 0.4 kcal mol−1 for RhoVR 1 and SPIRIT RhoVR 1, respectively, suggestive of achieved convergence; the corresponding deviations are slightly larger (1.0 kcal mol−1 for RhoVR 1 and 0.5 kcal mol−1 for SIPIRT RhoVR 1) in mixed POPC:CHL. As shown in Fig. 4, both RhoVRs exhibit W-shaped free-energy profiles21,60,61 in the two bilayers, with their minima near the lipid–water interface and barriers at the bilayer center. RhoVR 1 and SPIRIT RhoVR 1 have comparably deep free-energy wells (approximately −9 to −8 kcal mol−1), reflecting the attraction between their identical hydrophobic molecular wires and the lipid phase. In contrast, the free-energy barriers at the bilayer center vary significantly between the two RhoVRs: RhoVR 1 experiences barriers that are 5.3 kcal mol−1 and 5.1 kcal mol−1 greater than those of SPIRIT RhoVR 1 in pure POPC and mixed POPC:CHL, respectively.
1) using the WTM-eABF algorithm.19Fig. 4 shows the symmetrized free-energy profiles for each RhoVR, while unsymmetrized free-energy profiles are shown in Fig. S5 (ESI†). The shaded areas in Fig. 4 represent average deviations between these two sets of free-energy profiles (see Methods), which can be viewed as an indicator of the sampling accuracy.40,57–59 In pure POPC, the deviations are 0.7 kcal mol−1 and 0.4 kcal mol−1 for RhoVR 1 and SPIRIT RhoVR 1, respectively, suggestive of achieved convergence; the corresponding deviations are slightly larger (1.0 kcal mol−1 for RhoVR 1 and 0.5 kcal mol−1 for SIPIRT RhoVR 1) in mixed POPC:CHL. As shown in Fig. 4, both RhoVRs exhibit W-shaped free-energy profiles21,60,61 in the two bilayers, with their minima near the lipid–water interface and barriers at the bilayer center. RhoVR 1 and SPIRIT RhoVR 1 have comparably deep free-energy wells (approximately −9 to −8 kcal mol−1), reflecting the attraction between their identical hydrophobic molecular wires and the lipid phase. In contrast, the free-energy barriers at the bilayer center vary significantly between the two RhoVRs: RhoVR 1 experiences barriers that are 5.3 kcal mol−1 and 5.1 kcal mol−1 greater than those of SPIRIT RhoVR 1 in pure POPC and mixed POPC:CHL, respectively.
 | ||
| Fig. 4 Membrane permeation free-energy profiles of deprotonated RhoVR 1, SPIRIT RhoVR 1 as well as their two distinct components (Fig. 1a, circled in red). | ||
Analysis of the orientation and solvation of RhoVRs sheds light onto the origin of the free-energy barriers against their membrane permeation: in order to traverse the membrane, the dyes undergo a flip-flop motion to switch from one leaflet to the other, changing their orientations near the bilayer center (Fig. S6a, ESI†). To keep charged functional groups solvated, a small retinue of water molecules constantly accompany the rhodamine-based heads of both RhoVRs during this process (Fig. S6b, ESI†). The penetration of these water molecules deep into the hydrophobic tail region of the bilayer is energetically unfavorable and may induce significant membrane deformation, thereby, resulting in barriers at the central region of the free-energy profiles. Compared with RhoVR 1, which requires about six to eight water molecules in its vicinity (within 2.4 Å) throughout its membrane permeation, the less polar head group of SPIRIT RhoVR 1 reduces this number to only two to three at the bilayer center (Fig. S6b, ESI†). Along with the reduced membrane deformation induced by SPIRIT RhoVR 1 (Fig. S7, ESI†), these distinct solvation patterns explain the ∼5 kcal mol−1 difference in the free-energy barriers against permeation of the two RhoVRs.
Given the significantly shorter correlation time of RhoVR reorientation in mixed POPC:CHL than the model mammalian membrane (Table 1), the former system is used here to investigate the impact of cholesterol on RhoVR membrane permeation. As shown in Fig. 4, the resulting free-energy profiles reveal a significant increase in the permeation free-energy barriers for both RhoVR 1 and SPIRIT RhoVR 1. Specifically, the barriers against RhoVR 1 and SPIRIT RhoVR 1 permeation increased by 7.7 kcal mol−1 and 7.9 kcal mol−1 in mixed POPC:CHL compared to pure POPC, respectively. Furthermore, the free-energy profiles in the mixed POPC:CHL environment are broader than those in pure POPC, especially near the free-energy well and the barrier, which is consistent with the increased order and thickness of the membrane. These results agree well with experimental observations that the presence of cholesterol reduces the permeability of small molecules across membranes.62–64 The increased barrier heights can be attributed to the greater resistance of the mixed POPC:CHL environment against membrane deformation caused by RhoVRs. For instance, the flip-flop transition of RhoVR 1 and SPIRIT RhoVR 1 is less sharp in the presence of cholesterol and fewer water molecules accompany the two VSDs during their permeation (Fig. S6, ESI†), suggesting that the POPC:CHL bilayer is less accommodating to such flip-flop transition of the RhoVRs than pure POPC.
Charge delocalization facilitates RhoVRs’ membrane permeation while large anchor size hinders it
Given that RhoVR 1 and SPIRIT RhoVR 1 only differ in their anchor groups, one may naturally hypothesize that the differences in their free-energy profiles arise from the structural distinction of these hydrophilic anchors. To test this hypothesis and explore the origin of their membrane permeability differences, we repeated the WTM-eABF calculations for the two anchor groups and their connecting rhodamine aryl rings. These aryl ring-attached anchors are hereon referred to as the components of the RhoVRs (circled in red in Fig. 1a). The free-energy calculations of their permeation yielded results that mirrored the trends observed for the whole molecules (Fig. 4). The RhoVR 1 component, namely, a deprotonated N-methylhippuric acid, experienced an even greater permeation barrier than the whole RhoVR 1 molecule: the former has free-energy barriers that are 6.6 kcal mol−1 and 5.9 kcal mol−1 larger than the latter in POPC and POPC:CHL, respectively. This somewhat surprising result indicates that the difference in size of the two permeants (the entire RhoVR 1 and its component), which clearly favors the smaller permeant, is outweighed by other factors favoring the whole molecule. One such factor is the hydrophobic diethylaniline-phenylenevinylene tail that contributes to the −9 to −8 kcal mol−1 free-energy well in the RhoVR 1 PMF. In addition, while the xanthene ring in the tetramethylrhodamine head carries a positive charge, the delocalization of this charge appears to have significantly reduced the associated permeation free-energy barrier, in line with previous experimental as well as computational studies.17,65 The neutralizing effect of the tetramethylrhodamine xanthene ring, which sets the net charge of the entire RhoVR 1 molecule to zero, may, therefore, also contribute to its lower free-energy barrier than the −1 charged component alone.Unlike RhoVR 1, the SPIRIT RhoVR1 component has a zero net charge and encounters relatively small free-energy barriers during its own permeation (Table 2). Interestingly, compared to an entire SPIRIT RhoVR1, the free-energy barrier of this component is slightly more pronounced (2.3 kcal mol−1 higher) in pure POPC, and significantly reduced (6.0 kcal mol−1 lower) in POPC:CHL. Such a dependence on the lipid composition and the zero net charge of the SPIRIT RhoVR1 anchor hint to a permeation barrier that is of a distinct nature from RhoVR 1: steric hindrance due to its relatively large and flexible anchor appears to be a major contributor to the above trend. Specifically, as it crosses a lipid membrane, SPIRIT RhoVR 1 is frequently recorded in an “open” conformation, where by its anchor extends in the opposite direction of the tetramethylrhodamine head, resulting in an angle of φ ≈ 90° between them (Fig. S8, ESI†). An alternative, “closed” conformation (φ ≈ 55°), in which the anchor group folds back onto the tetramethylrhodamine, is also recorded. Unlike SPIRIT RhoVR 1, RhoVR 1 exclusively adopts a closed conformation throughout its membrane permeation (Fig. S8, ESI†). Therefore, anchor group aside, the rest of the molecular scaffold in SPIRIT RhoVR 1 appears to introduce two competing effects: while the hydrophobicity of the diethylaniline-phenylenevinylene tail deepens the free-energy well (Fig. 4), the increased number of conformations and size of the whole molecule, especially its bulky tetramethylrhodamine-based head, add to the steric hindrance that raises the free-energy barrier. In pure POPC, where the lipids are more disordered, the former effect appears to dominate, yielding a reduced barrier for SPIRIT RhoVR 1 than for its component alone. Conversely, in the mixed POPC:CHL bilayer, where the membrane environment is less accommodating to the flip-flop transition of the VSD, the latter effect dominates instead, raising the barrier against the permeation of an entire SPIRIT RhoVR 1.
| Membrane | RhoVRs | w(0) | w(zvalley) | z valley (Å) |
|---|---|---|---|---|
| POPC | RVR1 | 5.9 | −8.2 | ±18.6 |
| SRV1 | 0.6 | −8.2 | ±16.4 | |
| RVR1 component | 12.5 | −0.9 | ±16.8 | |
| SRV1 component | 2.9 | −3.0 | ±13.2 | |
| RVR1 protonated | −2.1 | −8.1 | ±17.2 | |
| POPC:CHL | RVR1 | 13.6 | −7.9 | ±23.0 |
| SRV1 | 8.5 | −9.5 | ±21.6 | |
| RVR1 component | 19.5 | −0.6 | ±19.6 | |
| SRV1 component | 2.5 | −2.8 | ±16.6 | |
| RVR1 protonated | 8.6 | −7.7 | ±22.6 |
Protonation lowers free-energy barriers against RhoVR 1 membrane permeation
With a pKa of 3.7,46 the N-methylhippuric acid moiety of RhoVR 1 is predominantly deprotonated at pH 7, motivating free-energy calculations of the deprotonated RhoVR 1 in the previous section. Despite an overall zero net charge, the permeation of RhoVR 1 in this protonation state encounters significant free-energy barriers, which has been linked to the number of water molecules solvating its negatively charged carboxylate moiety during membrane permeation (Fig. 5). Protonation of this carboxylate moiety may, therefore, reduce the polarity of RhoVR 1, lowering its permeation barrier. To quantitatively investigate this scenario, we have repeated the WTM-eABF calculations (Table S1, ESI†) for the protonated RhoVR 1, which carries a +1 net charge due to its cationic tetramethylrhodamine xanthene moiety. The average deviations between the symmetrized and unsymmetrized free-energy profiles (0.7 kcal mol−1 in POPC and 0.8 kcal mol−1 in POPC:CHL) are comparable with those obtained for the deprotonated RhoVR 1. The protonated RhoVR 1 encounters no permeation barrier in pure POPC, and a 8.6 kcal mol−1 barrier in POPC:CHL (Fig. 6 and Table 2), which is significantly lower than that for the deprotonated RhoVR 1 (5.9 kcal mol−1 and 13.6 kcal mol−1 in pure POPC and POPC:CHL, respectively). These results confirm that once the localized negative charge on the carboxylate moiety is neutralized, the delocalized positive charge on the tetramethylrhodamine xanthene moiety, in conjunction with a hydrophobic molecular wire, does not present any significant barrier against SPIRIT RhoVR 1 permeation.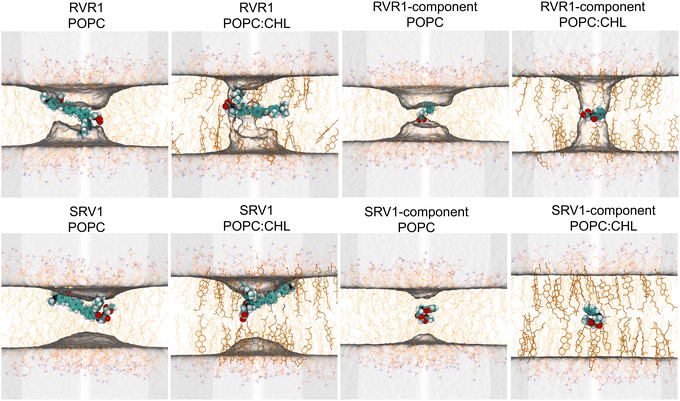 | ||
| Fig. 5 Average water occupancy (shown as isosurfaces with an isovalue of 3%) computed from the WTM-eABF trajectories of a given permeant with −5 Å < z < 5 Å. | ||
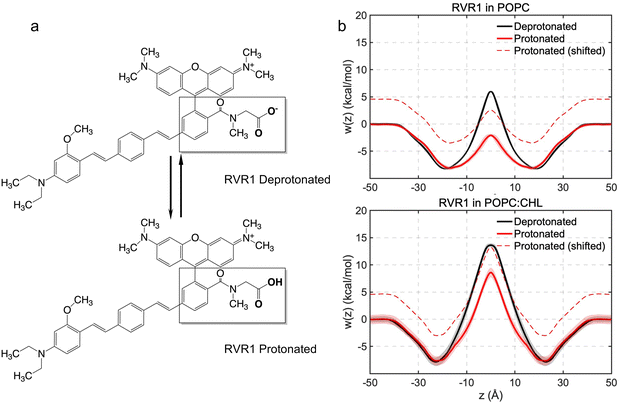 | ||
| Fig. 6 (a) Deprotonated and protonated forms of RhoVR 1. (b) Free-energy profiles of protonated RhoVR 1 with and without the shift of ΔG computed using eqn (3). The free-energy profiles of deprotonated RhoVR 1 are also plotted for reference. | ||
At pH 7, the less permeable, deprotonated form of RhoVR 1 has a population fraction of 99.95%, while the more permeable, protonated form has a fraction of 0.05%. As shown by Harris et al.,14 one way to visualize this population difference is to shift the permeation free-energy profiles of the protonated RhoVR 1 by a value corresponding to the free-energy cost of protonating its carboxylate moiety (eqn (3)). With this cost estimated to be ΔG = 4.6 kcal mol−1 (eqn (3)), the shifted free-energy profiles of protonated RhoVR 1 now exhibit higher barriers than SPIRIT RhoVR 1 in both pure POPC (2.5 kcal mol−1vs. 0.6 kcal mol−1) and POPC:CHL (13.2 kcal mol−1vs. 8.5 kcal mol−1). Given that the deprotonated RhoVR 1 already encounters greater permeation barriers than SPIRIT RhoVR 1 in both POPC and POPC:CHL, the above comparison implies that once the fractions of its two protonation states are taken into account, RhoVR 1 should have an overall lower permeability than SPIRIT RhoVR 1 in both bilayers. This observation is readily verified by calculating the permeability ratios between the two RhoVRs: assuming that all RhoVR variants have similar position-dependent diffusion coefficient profiles, D(z) drops out of eqn (2); taking SPIRIT RhoVR 1 in pure POPC as the reference and setting arbitrarily its permeability to 1, we measure the relative permeabilities of the RhoVR variants with respect to this reference. As shown in Table 3, consistent with the aforementioned comparison of their free-energy profiles, the permeability of protonated RhoVR 1 (without accounting for its population fraction) slightly exceeds SPIRIT RhoVR 1. When the fractions of its two protonation states are used as weighting factors based on the pH partition hypothesis,14 the overall permeability of RhoVR 1 is found to be about three orders of magnitude lower than SPIRIT RhoVR 1. This difference rationalizes the distinct distribution profiles of RhoVR 1 and SPIRIT RhoVR 1 recorded experimentally, with the former localized to the plasma membrane and the latter reaching its intracellular target.6
| Membrane | SRV1 | RVR1 (deprotonated) (fd = 99.95%) | RVR1 (protonated) (fp = 0.05%) | RVR1 (pH partition) |
|---|---|---|---|---|
| POPC | 1.0 | 7.8 × 10−4 | 1.6 | 1.6 × 10−3 |
| POPC:CHL | 1.1 × 10−5 | 1.9 × 10−9 | 1.0 × 10−5 | 7.3 × 10−9 |
Discussion
The working mechanism of PeT-based VSDs dictates that their voltage sensitivity depends strongly on how effectively these molecules align themselves with the membrane normal. Previous experimental and computational studies of dsVF, a PeT-based dye that places its two sulfonate moieties symmetrically at the meta positions of its fluorescein headgroup, have highlighted the importance of a symmetric molecular scaffold in improving the VSD's alignment with membrane normal.8,18 Upon a first look, RhoVR 1–4′, which more evenly distributes its mass about its molecular wire, is more symmetric than RhoVR 1, as the phenylenevinylene linker and the tricyclic xanthene ring are in the para rather than the meta positions of the rhodamine aryl ring in RhoVR 1–4′ (Fig. 1). Our simulations of the three RhoVRs clearly show that it is not such an overall mass distribution, but the position of its most polar functional group relative to the molecular wire that dictates the orientation of a RhoVR. The more symmetric, para positioning of the sarcosine-based anchors with respect to the phenylenevinylene linker enables RhoVR 1 and SPIRIT RhoVR 1 to readily expose their anchors to water without significant tilting. In stark contrast, the 4′-position of the molecular wire in RhoVR 1–4′ dictates that greater tilting is needed to maximize the solvation of the sarcosine moiety. These results indicate that while the tetramethylrhodamine xanthene ring and the sarcosine amide carry the same magnitude of net charge, the contribution of the former to the RhoVR orientation is outweighed by the latter, consistent with the reduced polarity of the former due to its delocalized charge. It should be added that molecular orientation is certainly not the only factor contributing to the voltage sensitivity of a PeT-based VSD. Any change in the molecular scaffold may, in principle, be accompanied by changes in the molecular orbitals and their energy levels,66 which may affect the free-energy change upon electron transfer and account for the improved membrane orientation of certain PeT-based dyes with lower-than-expected voltage sensitivity recorded in previous experiments.5 Nonetheless, reducing tilt angles of PeT-based VSDs within a membrane remains a key consideration in their molecular design. Our results on RhoVRs clearly indicate that such a design should focus on maximizing the symmetry regarding the position of their polar anchor groups.With a permanent positive charge on its tetramethylrhodamine xanthene moiety and a negatively charged carboxylate in its sarcosine anchor, RhoVR 1 is a zwitterion. Its zero net charge stands in clear contrast to the VF family of PeT-based VSDs: msVF and dsVF are −2 and −3 charged, respectively. While the VF dyes’ net charges result in understandably large barriers against their internalization, the nature of RhoVR 1's membrane permeation barrier is less clear. Our free-energy calculations of RhoVR 1 and SPIRIT RhoVR 1 suggest that the negatively charged carboxylate moiety in the former dye molecule makes the dominating contribution to its poor membrane permeability. Charge delocalization over the tetramethylrhodamine xanthene ring significantly reduces the polarity of the rhodamine-based head, resulting in fewer water molecules in its vicinity compared to the charged sarcosine (Fig. 2). Consistent with previous experimental and computational studies,17,65 this result suggests that charge delocalization over a given moiety lowers its membrane permeation free-energy barrier compared to one with a well-localized net charge. While the protonated RhoVR 1 also shows reduced polarity and lowered permeation barrier than the deprotonated RhoVR 1, the mere 0.05% population fraction of its protonated form renders the overall permeability of RhoVR 1 three orders of magnitude lower than that of SPIRIT RhoVR 1. Therefore, membrane permeation wise, the uncharged RhoVR 1 encounters barriers typical of a charged permeant rather than a neutral one, while SPIRIT RhoVR 1 behaves as if its net charge were negligible. Considering that it is the net charge of the whole molecule that dictates any electrostatics-driven accumulation, the above results suggest that the total charge and its distribution over the molecule are two separate physicochemical properties that can both be manipulated to achieve the desired subcellular distribution of a VSD: being an overall neutral molecule and carrying a localized negative charge effectively protects RhoVR 1 from internalization, while a delocalized positive net charge allows SPIRIT RhoVR 1 to cross the plasma membrane and directs it towards the negatively charged mitochondrion.
The high permeability of the +1 charged SPIRIT RhoVR 1 obtained in our work is in line with previous artificial membrane permeability assays17 for a series of rhodamine-based cations, although the unusually high membrane permeability of several cations reported therein, which have carboxylate moieties directly attached to their rhodamine aryl rings, may have been caused by the formation of neutral spirocycles.67 Unlike RhoVR 1, where the negatively charged carboxylate in its sarcosine anchor produces a permeation free-energy barrier even greater than that of the whole molecule, the neutral component containing the SPIRIT RhoVR 1 anchor can readily permeate both POPC and POPC:CHL bilayers. When this neutral component joins the rest of the dye, the permeation barrier for the entire compound strongly depends on the lipid composition—since the relatively bulky anchor of SPIRIT RhoVR 1 may adopt two different conformations (Fig. S8, ESI†), the rigidity of the membrane becomes particularly relevant. In the more disordered and accommodating POPC environment, SPIRIT RhoVR 1 encounters a negligible barrier, whereas in the more ordered POPC:CHL medium, it meets a barrier ∼8 kcal mol−1 higher. Steric hindrance encountered in this mixed POPC:CHL bilayer, therefore, appears to be a major contributor to the free-energy barrier against SPIRIT RhoVR 1 permeation. This result suggests that manipulating anchor size and flexibility may enable the fine-tuning of the membrane permeability of SPIRIT RhoVR 1 and other PeT-based VSDs with an intracellular target. MD simulations and free-energy calculations as presented in this work can be readily employed to facilitate these efforts.
Conclusions
In this study, we have carried out extensive equilibrium MD simulations and WTM-eABF free-energy calculations to elucidate the orientation and permeation energetics of three RhoVRs in different membrane environments. With RhoVR 1–4′ found to exhibit the poorest alignment with the membrane normal, our results underscore the critical role played by the relative positioning of the hydrophilic anchor and the long hydrophobic molecular wire in determining the orientation of PeT-based VSDs. Rather than symmetrizing the mass distribution of the entire dye, placing its most polar functional group symmetrically about its molecular wire reduces its tilt angle, which may lead to an improved voltage sensitivity. Comparison of our simulations conducted in model membranes with and without cholesterol have highlighted the pronounced influence of the latter on the orientation of RhoVRs. Given that cellular membranes likely consist of microdomains with varied cholesterol contents,68 the same RhoVR may exhibit distinct voltage sensitivities in different lipid microdomains. Enriching these PeT-based VSDs in domains with high cholesterol contents may, therefore, constitute another strategy to improve their voltage sensitivities. Along this line, whether there exists a connection between the orientation of RhoVRs in a given membrane model and their partitioning preference for its particular lipid composition remains to be further investigated.Our free-energy calculations have captured the energetics of membrane permeation by RhoVR 1, SPIRIT RhoVR 1 as well as two components from these dyes in pure POPC and mixed POPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CHL (2
CHL (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) bilayers. The resulting PMFs exhibit a characteristic “W” shape, where the central barriers of deprotonated RhoVR 1 and SPIRIT RhoVR 1 differ by ∼5 kcal mol−1. This difference in free-energy barriers arises from charge delocalization in the tetramethylrhodamine headgroup of RhoVRs, which significantly reduces the barrier against permeation of the +1 charged SPIRIT RhoVR 1. Based on the PMFs for both the deprotonated and the protonated RhoVR 1 and the pH partition hypothesis, we estimate that the permeation rates of RhoVR 1 are approximately three orders of magnitude lower than SPIRIT RhoVR 1, explaining why the latter is able to reach the mitochondrion, while the former remains confined to the outer leaflet of the plasma membrane.6 Along with a negative-inside potential of about 160 mV across the inner mitochondrial membrane,69 the above results explain the distinct cellular distribution profiles of RhoVR 1 and SPIRIT RhoVR 1. Notably, in the presence of cholesterol, the latter VSD encounters a non-trivial barrier of 8.5 kcal mol−1, which arises, at least in part, from its relatively bulky and flexible anchor group. With PeT-based dyes increasingly utilized to sense organelle transmembrane potentials,70 manipulating their anchor size and flexibility should enable greater control over the intracellular distribution of these small-molecule voltage sensors.
1) bilayers. The resulting PMFs exhibit a characteristic “W” shape, where the central barriers of deprotonated RhoVR 1 and SPIRIT RhoVR 1 differ by ∼5 kcal mol−1. This difference in free-energy barriers arises from charge delocalization in the tetramethylrhodamine headgroup of RhoVRs, which significantly reduces the barrier against permeation of the +1 charged SPIRIT RhoVR 1. Based on the PMFs for both the deprotonated and the protonated RhoVR 1 and the pH partition hypothesis, we estimate that the permeation rates of RhoVR 1 are approximately three orders of magnitude lower than SPIRIT RhoVR 1, explaining why the latter is able to reach the mitochondrion, while the former remains confined to the outer leaflet of the plasma membrane.6 Along with a negative-inside potential of about 160 mV across the inner mitochondrial membrane,69 the above results explain the distinct cellular distribution profiles of RhoVR 1 and SPIRIT RhoVR 1. Notably, in the presence of cholesterol, the latter VSD encounters a non-trivial barrier of 8.5 kcal mol−1, which arises, at least in part, from its relatively bulky and flexible anchor group. With PeT-based dyes increasingly utilized to sense organelle transmembrane potentials,70 manipulating their anchor size and flexibility should enable greater control over the intracellular distribution of these small-molecule voltage sensors.
Data availability
Force field parameters of RhoVRs and their components simulated in this article are available at https://github.com/yjqimia/RhoVRs.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the PROCORE-France/Hong Kong Joint Research Scheme (F-CUHK402/21). Y. W. is also supported by projects 14301417 and AoE/P-705/16 from the Hong Kong Research Grants Council as well as direct grants from the Chinese University of Hong Kong. C. C. is indebted to the Agence Nationale de la Recherche (grants LOR-AI and ProteaseInAction) and to the CNRS for its International Emerging Actions initiative with Hong Kong.References
- M. Levin, Molecular Bioelectricity: How Endogenous Voltage Potentials Control Cell Behavior and Instruct Pattern Regulation in Vivo, Mol. Biol. Cell, 2014, 25, 3835–3850 CrossRef PubMed.
- M.-L. Chang Liao, T. P. De Boer, H. Mutoh, N. Raad, C. Richter, E. Wagner, B. R. Downie, B. Unsöld, I. Arooj and K. Streckfuss-Bömeke, et al., Sensing Cardiac Electrical Activity With a Cardiac Myocyte-Targeted Optogenetic Voltage Indicator, Circ. Res., 2015, 117, 401–412 CrossRef CAS PubMed.
- L. M. Loew, Design and Use of Organic Voltage Sensitive Dyes, Adv. Exp. Med. Biol., 2015, 859, 27–53 CrossRef PubMed.
- E. W. Miller, Small Molecule Fluorescent Voltage Indicators for Studying Membrane Potential, Curr. Opin. Chem. Biol., 2016, 33, 74–80 CrossRef CAS PubMed.
- P. Liu and E. W. Miller, Electrophysiology, Unplugged: Imaging Membrane Potential with Fluorescent Indicators, Acc. Chem. Res., 2020, 53, 11–19 CrossRef CAS PubMed.
- P. E. Z. Klier, J. G. Martin and E. W. Miller, Imaging Reversible Mitochondrial Membrane Potential Dynamics with a Masked Rhodamine Voltage Reporter, J. Am. Chem. Soc., 2021, 143, 4095–4099 CrossRef CAS PubMed.
- E. W. Miller, J. Y. Lin, E. P. Frady, P. A. Steinbach, W. B. Kristan and R. Y. Tsien, Optically Monitoring Voltage in Neurons by Photo-Induced Electron Transfer through Molecular Wires, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 2114–2119 CrossRef CAS PubMed.
- R. U. Kulkarni, H. Yin, N. Pourmandi, F. James, M. M. Adil, D. V. Schaffer, Y. Wang and E. W. Miller, A Rationally Designed, General Strategy for Membrane Orientation of Photoinduced Electron Transfer-Based Voltage-Sensitive Dyes, ACS Chem. Biol., 2017, 12, 407–413 CrossRef CAS PubMed.
- P. E. Deal, R. U. Kulkarni, S. H. Al-Abdullatif and E. W. Miller, Isomerically Pure Tetramethylrhodamine Voltage Reporters, J. Am. Chem. Soc., 2016, 138, 9085–9088 CrossRef CAS PubMed.
- Y.-L. Huang, A. S. Walker and E. W. Miller, A Photostable Silicon Rhodamine Platform for Optical Voltage Sensing, J. Am. Chem. Soc., 2015, 137, 10767–10776 CrossRef CAS PubMed.
- A. Minta, J. P. Kao and R. Y. Tsien, Fluorescent Indicators for Cytosolic Calcium Based on Rhodamine and Fluorescein Chromophores, J. Biol. Chem., 1989, 264, 8171–8178 CrossRef CAS PubMed.
- S. C. Dodani, Q. He and C. J. Chang, A Turn-On Fluorescent Sensor for Detecting Nickel in Living Cells, J. Am. Chem. Soc., 2009, 131, 18020 CrossRef CAS PubMed.
- T. Egawa, K. Hirabayashi, Y. Koide, C. Kobayashi, N. Takahashi, T. Mineno, T. Terai, T. Ueno, T. Komatsu and Y. Ikegaya, et al., Red Fluorescent Probe for Monitoring the Dynamics of Cytoplasmic Calcium Ions, Angew. Chem., Int. Ed., 2013, 52, 3874–3877 CrossRef CAS PubMed.
- J. Harris, C. Chipot and B. Roux, How Is Membrane Permeation of Small Ionizable Molecules Affected by Protonation Kinetics?, J. Phys. Chem. B, 2024, 128, 795–811 CrossRef CAS PubMed.
- J. C. Gumbart and C. Chipot, Decrypting Protein Insertion through the Translocon with Free-Energy Calculations, Biochim. Biophys. Acta, Biomembr., 2016, 1858, 1663–1671 CrossRef CAS PubMed.
- R. Elber, Defect Formation and Peptide Permeation across Phospholipid Membranes, J. Phys. Chem. B, 2023, 127, 7810–7818 CrossRef CAS PubMed.
- H. Fischer, M. Kansy, A. Avdeef and F. Senner, Permeation of Permanently Positive Charged Molecules through Artificial Membranes – Influence of Physico-Chemical Properties, Eur. J. Pharm. Sci., 2007, 31, 32–42 CrossRef CAS PubMed.
- C. K. Lam, L. Y. Fung and Y. Wang, Orientation and Membrane Partition Free Energy of PeT-Based Voltage-Sensitive Dyes from Molecular Simulations, J. Phys. Chem. B, 2024, 128, 2734–2744 CrossRef CAS PubMed.
- H. Fu, X. Shao, W. Cai and C. Chipot, Taming Rugged Free Energy Landscapes Using an Average Force, Acc. Chem. Res., 2019, 52, 3254–3264 CrossRef CAS PubMed.
- H. Fu, H. Chen, X. Wang, H. Chai, X. Shao, W. Cai and C. Chipot, Finding an Optimal Pathway on a Multidimensional Free-Energy Landscape, J. Chem. Inf. Model., 2020, 60, 5366–5374 CrossRef CAS PubMed.
- C. H. Tse, J. Comer, S. K. Sang Chu, Y. Wang and C. Chipot, Affordable Membrane Permeability Calculations: Permeation of Short-Chain Alcohols through Pure-Lipid Bilayers and a Mammalian Cell Membrane, J. Chem. Theory Comput., 2019, 15, 2913–2924 CrossRef CAS PubMed.
- H. I. Ingólfsson, M. N. Melo, F. J. van Eerden, C. Arnarez, C. A. Lopez, T. A. Wassenaar, X. Periole, A. H. de Vries, D. P. Tieleman and S. J. Marrink, Lipid Organization of the Plasma Membrane, J. Am. Chem. Soc., 2014, 136, 14554–14559 CrossRef PubMed.
- J. B. Klauda, R. M. Venable, J. A. Freites, J. W. O’Connor, D. J. Tobias, C. Mondragon-Ramirez, I. Vorobyov, A. D. J. MacKerell and R. W. Pastor, Update of the CHARMM All-Atom Additive Force Field for Lipids: Validation on Six Lipid Types, J. Phys. Chem. B, 2010, 114, 7830–7843 CrossRef CAS PubMed.
- W. Yu, X. He, K. Vanommeslaeghe and A. D. MacKerell Jr., Extension of the CHARMM General Force Field to Sulfonyl-Containing Compounds and Its Utility in Biomolecular Simulations, J. Comput. Chem., 2012, 33, 2451–2468 CrossRef CAS PubMed.
- K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes and I. Vorobyov, et al., CHARMM General Force Field: A Force Field for Drug-like Molecules Compatible with the CHARMM All-Atom Additive Biological Force Fields, J. Comput. Chem., 2010, 31, 671–690 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of Simple Potential Functions for Simulating Liquid Water, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- K. Vanommeslaeghe, E. P. Raman and A. D. MacKerell, Automation of the CHARMM General Force Field (CGenFF) II: Assignment of Bonded Parameters and Partial Atomic Charges, J. Chem. Inf. Model., 2012, 52, 3155–3168 CrossRef CAS PubMed.
- C. G. Mayne, J. Saam, K. Schulten, E. Tajkhorshid and J. C. Gumbart, Rapid Parameterization of Small Molecules Using the Force Field Toolkit, J. Comput. Chem., 2013, 34, 2757–2770 CrossRef CAS PubMed.
- D. L. Silva, K. Coutinho and S. Canuto, Electronic Spectroscopy of Biomolecules in Solution: Fluorescein Dianion in Water, Mol. Phys., 2010, 108, 3125–3130 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, et al., Gaussian 09, Revision D.01., 2009 Search PubMed.
- H. Fu, H. Zhang, H. Chen, X. Shao, C. Chipot and W. Cai, Zooming across the Free-Energy Landscape: Shaving Barriers, and Flooding Valleys, J. Phys. Chem. Lett., 2018, 9, 4738–4745 CrossRef CAS PubMed.
- H. Grubmüller, Predicting Slow Structural Transitions in Macromolecular Systems: Conformational Flooding, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 2893–2906 CrossRef PubMed.
- J. F. Dama, M. Parrinello and G. A. Voth, Well-Tempered Metadynamics Converges Asymptotically, Phys. Rev. Lett., 2014, 112, 240602 CrossRef PubMed.
- A. Barducci, G. Bussi and M. Parrinello, Well-Tempered Metadynamics: A Smoothly Converging and Tunable Free-Energy Method, Phys. Rev. Lett., 2008, 100, 020603 CrossRef PubMed.
- E. Darve, D. Rodríguez-Gómez and A. Pohorille, Adaptive Biasing Force Method for Scalar and Vector Free Energy Calculations, J. Chem. Phys., 2008, 128, 144120 CrossRef PubMed.
- A. Lesage, T. Lelièvre, G. Stoltz and J. Hénin, Smoothed Biasing Forces Yield Unbiased Free Energies with the Extended-System Adaptive Biasing Force Method, J. Phys. Chem. B, 2017, 121, 3676–3685 CrossRef CAS PubMed.
- H. Fu, X. Shao, C. Chipot and W. Cai, Extended Adaptive Biasing Force Algorithm. An On-the-Fly Implementation for Accurate Free-Energy Calculations, J. Chem. Theory Comput., 2016, 12, 3506–3513 CrossRef CAS PubMed.
- J. Hénin, G. Fiorin, C. Chipot and M. L. Klein, Exploring Multidimensional Free Energy Landscapes Using Time-Dependent Biases on Collective Variables, J. Chem. Theory Comput., 2010, 6, 35–47 CrossRef PubMed.
- H. Chen and C. Chipot, Enhancing Sampling with Free-Energy Calculations, Curr. Opin. Struct. Biol., 2022, 77, 102497 CrossRef CAS PubMed.
- C. Chipot, Predictions from First-Principles of Membrane Permeability to Small Molecules: How Useful Are They in Practice?, J. Chem. Inf. Model., 2023, 63, 4533–4544 CrossRef CAS PubMed.
- Z. Yue, C. Li, G. A. Voth and J. M. J. Swanson, Dynamic Protonation Dramatically Affects the Membrane Permeability of Drug-like Molecules, J. Am. Chem. Soc., 2019, 141, 13421–13433 CrossRef CAS PubMed.
- P. A. Shore, B. B. Brodie and C. A. M. Hogben, The Gastric Secretion of Drugs: A pH Partition Hypothesis, J. Pharmacol. Exp. Ther., 1957, 119, 361–369 CAS.
- H. A. Kramers, Brownian Motion in a Field of Force and the Diffusion Model of Chemical Reactions, Physica, 1940, 7, 284–304 CrossRef CAS.
- M. Smoluchowski, Drei Vorträge über Diffusion, Brownsche Molekularbewegung und Koagulation von Kolloidteilchen, Pisma Mariana Smoluchowskiego, 1927, 2, 530–594 Search PubMed.
- J. M. Diamond and Y. Katz, Interpretation of Nonelectrolyte Partition Coefficients between Dimyristoyl Lecithin and Water, J. Membr. Biol., 1974, 17, 121–154 CrossRef CAS PubMed.
- X. Pan, H. Wang, C. Li, J. Z. H. Zhang and C. Ji, MolGpka: A Web Server for Small Molecule pKa Prediction Using a Graph-Convolutional Neural Network, J. Chem. Inf. Model., 2021, 61, 3159–3165 CrossRef CAS PubMed.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kalé and K. Schulten, Scalable Molecular Dynamics with NAMD, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- J. C. Phillips, D. J. Hardy, J. D. C. Maia, J. E. Stone, J. V. Ribeiro, R. C. Bernardi, R. Buch, G. Fiorin, J. Hénin and W. Jiang, et al., Scalable Molecular Dynamics on CPU and GPU Architectures with NAMD, J. Chem. Phys., 2020, 153, 044130 CrossRef CAS PubMed.
- S. E. Feller, Y. Zhang, R. W. Pastor and B. R. Brooks, Constant Pressure Molecular Dynamics Simulation: The Langevin Piston Method, J. Chem. Phys., 1995, 103, 4613–4621 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, Particle Mesh Ewald: An N·log(N) Method for Ewald Sums in Large Systems, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- S. Miyamoto and P. A. Kollman, Settle: An Analytical Version of the SHAKE and RATTLE Algorithm for Rigid Water Models, J. Comput. Chem., 1992, 13, 952–962 CrossRef CAS.
- H. C. Andersen, Rattle: A “Velocity” Version of the Shake Algorithm for Molecular Dynamics Calculations, J. Comput. Phys., 1983, 52, 24–34 CrossRef CAS.
- M. Tuckerman, B. J. Berne and G. J. Martyna, Reversible Multiple Time Scale Molecular Dynamics, J. Chem. Phys., 1992, 97, 1990–2001 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual Molecular Dynamics, J. Mol. Graphics, 1996, 14(33–38), 27–28 Search PubMed.
- J. L. Sampaio, M. J. Gerl, C. Klose, C. S. Ejsing, H. Beug, K. Simons and A. Shevchenko, Membrane Lipidome of an Epithelial Cell Line, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 1903–1907 CrossRef CAS PubMed.
- G. van Meer, D. R. Voelker and G. W. Feigenson, Membrane Lipids: Where They Are and How They Behave, Nat. Rev. Mol. Cell Biol., 2008, 9, 112–124 CrossRef CAS PubMed.
- M. Blazhynska, E. Goulard Coderc De Lacam, H. Chen and C. Chipot, Improving Speed and Affordability without Compromising Accuracy: Standard Binding Free-Energy Calculations Using an Enhanced Sampling Algorithm, Multiple-Time Stepping, and Hydrogen Mass Repartitioning, J. Chem. Theory Comput., 2023, 19, 3091–3101 CrossRef CAS PubMed.
- J. Comer, J. C. Gumbart, J. Hénin, T. Lelièvre, A. Pohorille and C. Chipot, The Adaptive Biasing Force Method: Everything You Always Wanted To Know but Were Afraid To Ask, J. Phys. Chem. B, 2015, 119, 1129–1151 CrossRef CAS PubMed.
- H. Fu, M. Zhou, C. Chipot and W. Cai, Overcoming Sampling Issues and Improving Computational Efficiency in Collective-Variable-Based Enhanced-Sampling Simulations: A Tutorial, J. Phys. Chem. B, 2024, 128, 9706–9713 CrossRef CAS PubMed.
- C. T. Lee, J. Comer, C. Herndon, N. Leung, A. Pavlova, R. V. Swift, C. Tung, C. N. Rowley, R. E. Amaro and C. Chipot, et al., Simulation-Based Approaches for Determining Membrane Permeability of Small Compounds, J. Chem. Inf. Model., 2016, 56, 721–733 CrossRef CAS PubMed.
- C. H. Tse, J. Comer, Y. Wang and C. Chipot, Link between Membrane Composition and Permeability to Drugs, J. Chem. Theory Comput., 2018, 14, 2895–2909 CrossRef CAS PubMed.
- M. B. Lande, J. M. Donovan and M. L. Zeidel, The Relationship between Membrane Fluidity and Permeabilities to Water, Solutes, Ammonia, and Protons, J. Gen. Physiol., 1995, 106, 67–84 CrossRef CAS PubMed.
- J. C. Mathai, S. Tristram-Nagle, J. F. Nagle and M. L. Zeidel, Structural Determinants of Water Permeability through the Lipid Membrane, J. Gen. Physiol., 2008, 131, 69–76 CrossRef CAS PubMed.
- H. Saito and W. Shinoda, Cholesterol Effect on Water Permeability through DPPC and PSM Lipid Bilayers: A Molecular Dynamics Study, J. Phys. Chem. B, 2011, 115, 15241–15250 CrossRef CAS PubMed.
- A. Kowalska and M. Makowski, Interactions between Rhodamine Dyes and Model Membrane Systems—Insights from Molecular Dynamics Simulations, Molecules, 2022, 27, 1420 CrossRef PubMed.
- L.-S. Li, Fluorescence Probes for Membrane Potentials Based on Mesoscopic Electron Transfer, Nano Lett., 2007, 7, 2981–2986 CrossRef CAS PubMed.
- D. Englert, E.-M. Burger, F. Grün, M. S. Verma, J. Lackner, M. Lampe, B. Bühler, J. Schokolowski, G. U. Nienhaus and A. Jäschke, et al., Fast-Exchanging Spirocyclic Rhodamine Probes for Aptamer-Based Super-Resolution RNA Imaging, Nat. Commun., 2023, 14, 3879 CrossRef CAS PubMed.
- E. Sezgin, I. Levental, S. Mayor and C. Eggeling, The Mystery of Membrane Organization: Composition, Regulation and Physiological Relevance of Lipid Rafts, Nat. Rev. Mol. Cell Biol., 2017, 18, 361–374 CrossRef CAS PubMed.
- A. A. Gerencser, C. Chinopoulos and M. J. Birket, et al., Quantitative measurement of mitochondrial membrane potential in cultured cells: calcium-induced depolarization and hyperpolarization of neuronal mitochondria, J. Physiol., 2012, 590, 2845–2871 CrossRef CAS PubMed.
- P. E. Z. Klier, R. Roo and E. W. Miller, Fluorescent Indicators for Imaging Membrane Potential of Organelles, Curr. Opin. Chem. Biol., 2022, 71, 102203 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tb02670e |
| This journal is © The Royal Society of Chemistry 2025 |