Charge engineering controls cooperative assembly and loading in protein host–guest complexes

Abstract

Controlling cargo loading in self-assembling protein capsules remains a key challenge in supramolecular chemistry. Inspired by nature's capacity for host–guest recognition, we engineered supercharged green fluorescent protein (GFP) cargo for controlling its encapsulation by Archaeoglobus fulgidus ferritin. Guided by molecular dynamics (MD) simulations and computational protein design, experiments confirmed that GFP charge magnitude and distribution dictate capsule assembly and loading efficiency. These data provide the first example of cooperative assembly with a ferritin capsule. Finally, we established a strategy for generating stoichiometric 1 : 1 protein host–guest complexes, confirmed by time-resolved fluorescence anisotropy. This provides a blueprint for designing ferritin host–guest complexes with enhanced homogeneity and functionality.

---

Introduction

Naturally occurring and computationally designed protein cages offer molecularly defined architectures of varied size, symmetry, and interior capacity.^1,2 The exterior surface of protein cages can be functionalized to display antigens³ or increase circulation lifetime in vivo.⁴ The cage interior can modulate chemical reactions, i.e., biomineralization or protection of cargo molecules, thereby enabling applications in catalysis,^5–7 drug delivery,^8–10 bioimaging,^11–13 and biomaterials.¹⁴ Despite these promising features, controlling the cargo loading stoichiometry in protein cages remains challenging. Conventional loading methods, including genetic fusion,^15,16 affinity-based encapsulation,¹⁷ and covalent conjugation,¹⁸ often yield heterogeneous stoichiometries that limit the applications of these systems.^19–21 Nature provides many examples of highly specific molecular recognition, where complementary size, shape, and charge drive exclusive, one-to-one binding.^22–25 Electrostatic interactions often guide the formation of protein host–guest assemblies, which is analogous to the efficient encapsulation of negatively charged genomes within cationic virus capsids.²⁶ This facile loading has allowed the encapsulation of diverse cargo, including nucleic acids, proteins, metallic nanoparticles, and dendrimers.^27–29 However, unlike other common cargo, most native guest proteins do not possess a high degree of charge to promote interactions with a capsular host, necessitating engineering approaches such as appending charged tags.^30–32 Alternatively, the surface of the cargo can be site-specifically modified to carry substantial amounts of complementary charge, a strategy termed ‘supercharging’. Supercharged proteins can possess new properties, i.e., resistance to aggregation,^33,34 enhanced enzymatic activity at higher temperatures,^35,36 improved affinity to binding partners,³⁷ and cell-membrane permeability.^38–40 Despite notable successes, in many scenarios, proteins do not withstand extensive engineering, as it can lead to loss of function (e.g., green fluorescent protein (GFP) with decreased brightness⁴¹), protein expression in inclusion bodies,³⁵ and significantly reduced thermal stability and/or binding affinity.³³ Therefore, achieving the desired supercharged state requires careful design to preserve native protein properties while still favouring encapsulation. The goal of creating protein host–guest complexes requires a deeper understanding of molecular recognition, including the interplay of charge magnitude and distribution, size, shape, and cooperativity.⁴²

Here, we explore the use of ferritin, a ubiquitous self-assembling capsular protein that sequesters iron and has served important roles in biotechnology.^{10,18,35,43,44} Ferritin is promising candidate for achieving 1 : 1 host–guest binding. In particular, Archaeoglobus fulgidus ferritin (AfFtn) exhibits ionic-strength-dependent self-assembly: the 24 mer protein cage (AfFtn₂₄) forms at neutral pH and high ionic strengths (>800 mM NaCl) but disassembles into dimers (AfFtn₂) at lower ionic strengths (<200 mM NaCl) (Fig. 1(a)). The 8-nm interior cavity of AfFtn, characterized by negative charge (pI = 4.7),⁴⁵ provides an ideal environment for cationic cargo encapsulation.⁴⁶ Previously, we demonstrated that AfFtn 24 mer formation and encapsulation of supercharged GFP(+36) and human carbonic anhydrase II (hCAII(+21)) occur under low ionic strength conditions that favor complementary electrostatic interactions.^35,43

Fig. 1 Solvent-excluded surface colored by electrostatic potential of (a) host AfFtn (PDB ID 1S3Q)⁵¹ and (b) guest GFP variants used in this work. Color scale bar is provided for visualization of electrostatic charge: negative (red); positive (blue). (a) The predominantly negatively charged electrostatic surface of AfFtn encompasses the entire cage and its symmetrical subunits. Notably, within the interior surface of each subunit, the ferroxidase center forms a concentrated region of negative charge. At the same time, small positively charged regions generated from the short helix on the C-terminus are present. Colored arrows indicate the large triangular pores. (b) The predominantly positively charged electrostatic surface for different superpositively charged GFP variants; pairs of structures differ by a rotation of 180° about a vertical axis. Positive charges are localized to both ends or one side of the GFP for the computationally designed GFP(+16)BE and GFP(+16)OS. AfFtn (a) and GFP (b) and (c) are not drawn to scale.

In this work, we make three key advances: first, we elucidate how cargo charge magnitude and distribution (Fig. 1) influence the formation of capsular host–guest complexes. Second, we develop and validate methods to control cargo loading stoichiometry, achieving precise 1 : 1 host–guest complexes as confirmed by time-resolved fluorescence anisotropy. Third, we report the first example of cooperative assembly in a ferritin capsular system. Cooperativity underpins the fidelity and efficiency in assembly.^47–49 While cooperativity has been established as an important feature of several capsular protein assemblies,^26,29,47,50 it has not been studied in ferritin, possibly due to the extreme pH values required to disassemble most ferritins. Our results reveal insights into the “all-or-nothing” behavior that underpins efficient ferritin cage formation. Together, these findings advance the fundamental understanding of supramolecular protein host–guest systems and pave the way for the rational design of ferritin-based capsules in biochemistry and biomedicine.

Results and discussion

Charge effects on AfFtn–GFP(+36) interaction investigated by molecular dynamics simulations

The previously reported encapsulation of GFP(+36) by AfFtn^43,46 motivated us to elucidate the molecular details of binding, with the goal of controlling host–guest formation. The current study focuses on understanding and improving cargo design.^52,53 Molecular dynamics (MD) simulations were conducted of GFP(+36) within a twenty-four 4-helix bundle AfFtn₁ subunit cage using an all-atom model. Two distinct binding configurations were identified, shown in Fig. 2(a) and (b). Additional details, including the equilibration process and a third configuration, are provided in ESI,† Fig. S1.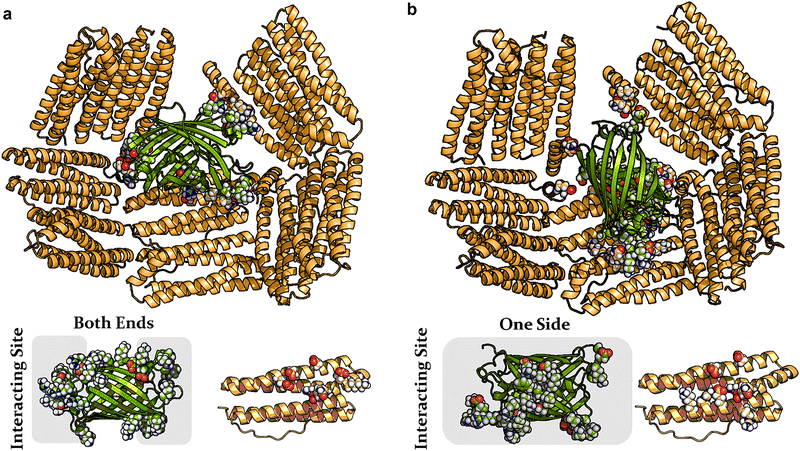

Fig. 2 Representative configurations (a) and (b) from two independent molecular dynamics simulations depicting the binding of GFP(+36) (green) within the interior of the AfFtn cage (orange). AtFtn subunits not interacting with GFP(+36) are omitted for clarity. (a) GFP(+36) is localized at the pore formed by five AfFtn dimers. Lower panel: the primary contacting residues (rendered with space-filling for both GFP and an AfFtn subunit) are mainly located at the barrel ends of GFP. (b) Similar binding pattern to (a) but with slight displacement of the GFP. The contacting residues on GFP are predominantly located on one side of the beta-barrel. Detailed pairwise residue interaction maps are provided in Fig. S1 (ESI†).

GFP(+36) preferentially binds to the highly negatively charged edges of the large triangular pores (height of 4.5 nm) within the AfFtn cage. In the first configuration (Fig. 2(a)), the 4-nm long GFP(+36) aligns along the triangular pore, almost blocking it by interacting with five nearby AfFtn dimers. These interactions involve a series of positively charged residues at both ends of the GFP barrel. GFP makes contact mainly with negatively charged residues located in the center of one helix and at the C-terminal short E-helix of AfFtn. The second configuration shown in Fig. 2(b), generated through an independent simulation, identifies that GFP(+36) adopts a similar binding position with a slight displacement. The interactions with five ferritin dimers are retained, but the interacting GFP residues now predominantly concentrate on one lateral surface (Fig. 2(b)). Consequently, additional AfFtn residues are involved, and additional residues on a second helix participate. In both configurations, the GFP(+36) side of the cylindrical barrel structure is in contact with the ferritin interior surface. This positioning reduces GFP–GFP excluded volume if multiple cargo proteins are present, potentially allowing multiple GFP occupancy within AfFtn₂₄. The simulations provide evidence that not all positive surface charges on GFP(+36) participate in binding, with interactions concentrated on one surface or at both ends of the barrel.

Based on the simulation results, we reasoned that distributing positive charges on one side or both ends of the GFP beta-barrel could be sufficient to bridge AfFtn₂ subunits and foster AfFtn₂₄ formation while using less charged GFPs. To test this hypothesis, two new GFP(+16) mutants were computationally designed and expressed, each with positive charges introduced at specific regions of the barrel. Mutations were added from the superfolder GFP (sfGFP).³³ Specifically, a variant was generated with positive charges located mainly on one side (OS) of the cylinder (GFP(+16)OS, with 15 mutations) and another with positive charges incorporated mainly at both ends (BE) of the cylinder (GFP(+16)BE, with 16 mutations), and supplementary mutations placed in the middle region to attenuate the overall positive charge (Fig. 1 and Fig. S17, ESI†). Dynamic light scattering (DLS) measurements indicated that the two new GFP variants are monomeric, with sizes nearly identical to GFP(+36) (Fig. 4).

Cooperative assembly depends on guest charge magnitude and distribution

To investigate the requirements of guest charge magnitude and positioning on AfFtn host–guest assembly, the loading of GFP with net charges of +9, +14, +28, or +36 at pH 7.6 were examined (Fig. 1). The newly designed GFP(+16) variants were also tested to understand the effect of charge distribution. AfFtn₂ in low ionic strength buffer (20 mM sodium phosphate, pH 7.6) was mixed with GFP variants at a 12 : 1 (AfFtn₂ : GFP) molar ratio in the same buffer. Staining the purified GFP samples with SYBR Gold confirmed the lack of nucleic acid contaminants (ESI,† Fig. S2), which was important for accurately assessing AfFtn encapsulation.

Encapsulation was verified using our previously established methods, including analytical size exclusion chromatography (SEC), DLS, native gel electrophoresis, and negative-stain transmission electron microscopy (TEM).^35,43 For SEC, two wavelengths were monitored: 280 nm and 488 nm, corresponding to protein absorption and the signature GFP absorption, respectively. This two-wavelength absorbance-based approach improved quantitation beyond the 509 nm fluorescence intensity previously monitored for GFP.^35,43 For GFP(+36), GFP(+28), and GFP(+16)BE samples, two 280 nm peaks eluted via SEC (Fig. 3(a)). The first peak appeared at the expected AfFtn₂₄ elution volume and contained GFP absorbance at 488 nm, indicating AfFtn assembly and association with GFP. The later peak corresponded to unassembled AfFtn₂ without 488 nm absorbance. As we previously observed,^35,43 unencapsulated GFP was unable to elute unless a high ionic strength buffer (20 mM sodium phosphate, 800 mM NaCl, pH 7.6) was used to dissipate interactions with the anionic SEC column resin. For GFP(+9), GFP(+14), and GFP(+16)OS, only AfFtn₂ eluted on SEC, and no GFP absorbance was observed, suggesting that all three GFPs failed to template ferritin 24 mer assembly (Fig. 3(a)). Notably, GFP(+16)BE at 6 μM induced AfFtn assembly (vs. 2 μM for GFP(+36) and GFP(+28)). This was likely due to a lower affinity of ferritin to GFP(+16)BE compared to the more highly charged variants. However, no assembly was formed when even higher concentrations (10 μM) of GFP(+9), GFP(+14), and GFP(+16)OS were applied (ESI,† Fig. S3).

Fig. 3 GFP cargo charge magnitude and positioning affect supramolecular protein host–guest assembly. (a) SEC traces of AfFtn₂ mixed with GFP variants at a 12-to-1 molar ratio. 2 μM of GFP was used, except for GFP(+16)BE, in which 6 μM was used. The first peak eluting near 12.5 mL corresponded to AfFtn₂₄, and AfFtn₂ eluted near 16.5 mL. Co-elution of GFP absorbance at 488 nm (green trace) with the AfFtn₂₄ absorbance at 280 nm (blue trace) confirmed AfFtn–GFP association. (b) Native gel electrophoretic mobility assay of AfFtn with GFP(+28) for different stoichiometric ratios of AfFtn₂ : GFP(+28). [AfFtn₂] = 7.2 μM and [GFP] was varied. Left: Fluorescence imaging of gel. Green bands correspond to GFP. Right: The same gel after Coomassie blue staining shows protein (ferritin and GFP). Overlap between green and blue bands is consistent with GFP encapsulation.

Native gel electrophoresis was used to confirm cargo encapsulation and examine the impact of host–guest stoichiometry. GFP(+36), GFP(+28), and GFP(+16)BE comigrated with the AfFtn₂₄ band, which was separated from the AfFtn₂ band (Fig. 3(b) and ESI,† Fig. S4). Little encapsulation was observed for GFP(+9), GFP(+14) and GFP(+16)OS at all tested ratios (ESI,† Fig. S5). Upon increasing the AfFtn₂: GFP(+28) ratio, the assembly appeared to undergo a transition at a ratio of 12 : 4 (Fig. 3(b)); for ratios of 12 : 5 and 12 : 6, the encapsulated fluorescence signal was dim compared to the lower ratios, and more GFP(+28) was trapped in the loading well. This transition behavior was only observed for GFP(+28). Micrographs collected using confocal laser scanning microscopy revealed that at the 12 : 6 ratio, AfFtn₂–GFP(+28) assembled into micrometer-sized puncta, while no puncta were observed for the 12 : 1 ratio (ESI,† Fig. S6).

DLS measurements confirmed that the SEC-purified complexes that formed upon mixing AfFtn₂ with GFP(+36), GFP(+28), or GFP(+16)BE exhibited hydrodynamic diameters of 12.5, 12.6, and 13.2 nm, respectively; these are similar to the diameter determined for AfFtn 24 mer in the absence of GFP (13.2 nm) (Fig. 4). The hydrodynamic diameter of the AfFtn–GFP(+16)OS mixture was predominantly 8 nm, which was slightly larger than AfFtn₂. Much larger particles (>1000 nm) were formed for solutions containing AfFtn₂ and either GFP(+9) or GFP(+14) (ESI,† Fig. S7), indicating that both of these GFP variants induce weak, nonspecific electrostatic interactions with ferritin and form less-ordered micron-sized particles instead of promoting AfFtn₂₄ assembly that is typical of the more highly charged GFP variants. TEM micrographs provided further evidence that GFP-induced AfFtn assemblies possess similar size and morphologies to the AfFtn₂₄ cage formed in the high ionic strength buffer (ESI,† Fig. S8).

Fig. 4 Molecular volume distributions obtained from dynamic light-scattering measurements of solutions with AfFtn₂, GFP variants (dotted line), and AfFtn₂ : GFP mixtures (solid line), each with a 12 : 1 ratio. AfFtn₂₄ (purple) in the high ionic strength buffer is consistent with the diameter of the 24 mer. AfFtn–GFP(+36), AfFtn–GFP(+28), and AfFtn–GFP(+16)BE complexes purified by SEC each had a similar distribution and average hydrodynamic diameters as that of AfFtn₂₄. The average diameter observed for the AfFtn–GFP(+16)OS system (red solid line) was slightly larger than that of AfFtn₂ (purple dotted line).

The SEC, gel electrophoresis, DLS, and TEM data consistently supported that GFP(+36), GFP(+28), and GFP(+16)BE induced AfFtn₂₄ assembly, while GFP(+9), GFP(+14), and GFP(+16)OS did not. Both GFP(+16) variants and GFP(+14) possess nearly identical charges, yet only GFP(+16)BE nucleated ferritin assembly. This matches our expectations following the MD simulations, that charge distribution of GFP cargo spanning multiple AfFtn subunits is a key feature associated with forming the ordered protein assembly. While other weak interactions such as van der Waals forces and hydrogen bonding may contribute at short range, our data strongly support electrostatics as the primary driver of GFP-induced AfFtn assembly.

Based on concentrations determined using UV/Vis absorbances after SEC-purification (see Methods), the 12 : 1 AfFtn₂ : GFP input ratio consistently yielded an average of 2–3 GFP proteins encapsulated per ferritin cage for each of three variants that induce assembly. These results are consistent with the MD simulation observation that each GFP molecule binds up to five AfFtn dimers at one of the four triangular pores. We posit that the primary role of GFP in inducing AfFtn assembly is to bridge AfFtn dimers and mediate the unfavorable interdimer electrostatic repulsion, which prevents 24 mer formation at low ionic strength conditions at pH 7.6.⁵⁴

To test this hypothesis, the buffer pH was lowered to pH 5.8 so as to protonate acidic residues on the interior surface of AfFtn. As expected, a significant fraction (∼20%) of the AfFtn₂₄ (2 μM, pH 5.8) remained assembled at 0 mM NaCl concentration (ESI,† Fig. S9). The AfFtn₂ peak was isolated by SEC and mixed with all GFP variants used in this study at 12 : 1. Surprisingly, all the positively charged GFP variants, including GFP(+9), GFP(+14), and GFP(+16)OS, were encapsulated by ferritin at pH 5.8, as verified by SEC and TEM (Fig. S9 and S10, ESI†). This could be explained by two considerations: (1) protonation of the polyhistidine tag of GFP variants increased their overall positive charge, and (2) the charge requirement on GFP for inducing ferritin assembly was lowered due to the decreased repulsive inter-dimer interactions. The negatively charged eGFP (−8 at physiological pH) remained excluded at pH 5.8, indicating that an overall positive charge associated with the guest protein (not only the His tag residues) was required for GFP encapsulation.

In addition, from UV-Vis absorbance measurements and SEC, the average number of GFP(+36) molecules per AfFtn₂₄ at pH 5.8 was determined to be 1.2, in agreement with the 12 : 1 input ratio. This indicated that most assemblies were 12-to-1 complexes, though a smaller number may contain two guest molecules. We attribute the decreased guest encapsulation relative to that observed at pH 7.6 to the screening of unfavorable ferritin inter-dimer electrostatic interactions at the acidic pH, and as a result, fewer GFP molecules were required to stabilize the assembly.

Constructing 12-to-1 host–guest complexes

Controlling host–guest stoichiometry is a desirable feature for many supramolecular assemblies. An exclusive 12-to-1 loading ratio (producing a 24 mer with one encapsulated guest molecule) should enable the formation of homogenous assembly products. We next sought to achieve 12-to-1 host–guest complexes, i.e., “1-to-1 binding”. Because the calculated GFP loading was based on a bulk measurement, a more precise method was needed for distinguishing between loading a single GFP vs. multiple GFP molecules within each ferritin cavity. Multiple GFP molecules in close proximity produce homo-Förster resonance energy transfer (homoFRET),^55,56 which occurs when there is spectral overlap between the emission and absorption features of neighboring fluorescent molecules. Energy transfer to GFP with an alternate orientation can happen on a timescale shorter than GFP rotation, resulting in a short (ns) component in anisotropy decay.⁵⁷ HomoFRET and other spectroscopic features were assessed via time-resolved fluorescence anisotropy, which was measured using a time-correlated single photon counting (TCSPC) system.

The fluorescence lifetimes of GFP(+36) alone in solution and within the ferritin assembly were 2.6 ns and 2.5 ns, respectively, indicating that the chromophore and surrounding beta-barrel structure of GFP(+36) were not substantially altered by ferritin encapsulation. The anisotropy data were fit with a bi-exponential decay (see Methods and ESI† for equations and details of the fit). The decay showed two components of 0.2 ns and 12.1 ns for GFP(+36) alone (Fig. 5(a)). The 12.1 ns component corresponds to GFP Brownian rotational motion and is similar to the previously reported value.⁵⁸ The shorter sub-ns time was associated with the instrument response, which consistently appeared in all the samples, with and without AfFtn. This component was not considered homoFRET and was not included in subsequent analysis. If an additional fast anisotropy decay component was found and was shorter than that observed for the free GFP fluorescence lifetime, this was associated with homoFRET and an indicator of multiple interior GFPs. If it was longer than the free GFP fluorescence anisotropy time (12 ns), this was associated with no homoFRET and served as a measure of rotational diffusion for GFP associated with ferritin.

Fig. 5 Time-resolved fluorescence anisotropy of AfFtn–GFP. (a) GFP(+36) in the low ionic strength buffer, pH 7.6. The observed decay time (12.1 ns) is consistent with the rotational diffusion of GFP. (b) SEC-purified AfFtn–GFP(+36) at pH 7.6. (c) SEC-purified AfFtn–GFP(+36) at pH 5.8. From the fits, three decay times were obtained and associated with instrument response, homoFRET, and rotation. (d) AfFtn–GFP(+36) assembly at pH 7.6, 500 mM NaCl. (e) AfFtn–GFP(+36) assembly at pH 7.6, 175 mM NaCl. In (d) and (e), both anisotropy decays were fit biexponentially with only instrument response and rotation diffusion of the assembly with no homoFRET observed. This suggested that a 12-to-1 complex was formed under both conditions. The t = 0 was set by the timing of the excitation laser pulse, and the data acquisition started around 6 ns. Each experiment was conducted in triplicate, and the sum files were plotted. In all samples, [GFP] = 1 μM. In each case, the anisotropy was fit with a multiexponential model equation (see Methods). Conditions and fitted fluorescence anisotropy parameters with uncertainties are summarized in ESI,† Table S1.

A multiexponential decay was fit to the time-resolved anisotropy for the AfFtn–GFP(+36) assembly formed at pH 7.6 at a 12 : 1 ratio and purified by SEC (Fig. 5(b)). The fastest component was associated with the instrument response. The second component was associated with the rapid fluorescence depolarization and had a time constant of 1.4 ns, which was shorter than the rotational diffusion time of GFP(+36). As the possibility of ultrafast tumbling of GFP within ferritin is unlikely, this decay time was consistent with homoFRET as found in myosin VI dimerization and assembly of calcium–calmodulin-dependent protein kinase-II,^55,56 confirming that multiple GFP(+36) molecules were encapsulated inside ferritin. These anisotropy data corroborated SEC, DLS, gel, and TEM results. The rotational correlation time of a ferritin holo-cage has been determined to be approximately 165 ns, using a ruthenium–ligand complex with a long excited-state lifetime.⁵⁹ Similarly, in our system, the rotational diffusion time of the AfFtn–GFP(+36) assembly was considered unmeasurable and much longer than both the GFP(+36) fluorescence lifetime and the 50 ns experimental time window. The long rotational diffusion time was consistent with GFP(+36) associating and co-rotating with the 480 kDa ferritin cage. Molecular simulations show diminished mobility of GFP(+36) molecules within the ferritin cage, as GFP(+36) loading increases (ESI,† Fig. S11). This tight packing is consistent with the observation of homoFRET.

Time-resolved anisotropy measurements further confirmed that fewer GFPs were encapsulated within each 24 mer when samples were constructed at pH 5.8 (Fig. 5(c)). Similar to the assembly formed at pH 7.6, the anisotropy decay was fit to a multiexponential decay model. Namely, the amplitude associated with the exponential decay of the homoFRET component for the AfFtn–GFP(+36) complex was 50% less at pH 5.8 than at pH 7.6 (Fig. 5(b)).^56,60 The timescale of homoFRET (2.3 ns) was almost two times longer, although still comparable to the GFP fluorescence lifetime, consistent with less efficient energy transfer due to increased average distances between GFP(+36) molecules inside ferritin. This spectroscopic technique was further applied to confirm the formation of 12-to-1 host–guest complexes when homo-FRET was undetected.

To achieve 12-to-1 host–guest complexes at pH 7.6, we increased the ionic strength of the buffer, which screens interdimer repulsions and host–guest interactions. The salt concentration almost quantitatively affected the loading stoichiometry (ESI,† Fig. S12). At 500 mM NaCl, only 0.7 GFP(+36) molecule was encapsulated per 24 mer ferritin on average. Because AfFtn self-assembles into 24 mer under high ionic strength conditions, multiple GFP(+36) molecules could potentially get encapsulated within one cage while other cages remain empty. The time-resolved anisotropy experiment disproved this hypothesis of multiply occupied cages as the anisotropy decay of this sample was well fit to a bi-exponential decay model (Fig. 5(d)). The absence of the fast anisotropy decays indicates there was no appreciable homoFRET and suggested that only one GFP(+36) molecule was encapsulated per cage and confirmed the formation of 12-to-1 complexes. The rotational diffusion time was again unmeasurable, though GFP(+36) molecules were expected to be less tightly bound to the AfFtn cage (Fig. 5(d)), due to screening of AfFtn–GFP(+36) interactions at high ionic strength.

Theoretically, some host–guest interactions could be restored at a lower ionic strength while the 12-to-1 complex remains stable. After preparing the sample in 500 mM NaCl buffer, it was subjected to on-column buffer exchange into 50, 125, or 175 mM NaCl concentrations. After reducing the NaCl concentration to 50 and 125 mM, the average number of guests occupied per cage increased, but this was not observed with 175 mM NaCl. The size of the AfFtn–GFP(+36) complex measured by DLS also remained unchanged at this ionic strength after overnight incubation, suggesting the stability of the complex under this condition (ESI,† Fig. S13). At 175 mM NaCl concentration, the anisotropy decay was also fit biexponentially with only instrument response and rotational diffusion and lacked the fast homoFRET component (Fig. 5(e)). The slow rotational component was flatter compared to the one found in Fig. 5(d) at 500 mM, supporting a stronger host–guest association in AfFtn–GFP(+36) at the lower ionic strength. In the TEM micrographs of the 12-to-1 ratio at 500 mM NaCl, some cages were empty, and some were partially filled, consistent with the morphologies of empty AfFtn₂₄ and GFP(+36) loaded AfFtn₂₄, respectively (ESI,† Fig. S14). These experimental results supported the formation of a 12-to-1 complex at 175 mM NaCl and indicate that the 12-to-1 AfFtn–GFP(+36) complex is stable at intermediate ionic strengths.

Modulation of cargo loading in host–guest complexes

Having established 12-to-1 host–guest complexation, we next explored the limits of guest loading by preparing AfFtn₂ : GFP ratios ranging from 12 : 1 to 12 : 6 and analyzing by SEC (Fig. 6). For GFP(+36), the peak area ratio between that of assembled AfFtn₂₄ and total AfFtn (AfFtn₂₄ and AfFtn₂) increased with increasing relative amount of GFP until, at the 12 : 5 input ratio, the dimer peak nearly disappeared, and AfFtn subunits were assembled into the 24 mer (Fig. 6(a) and (b)). The measured GFP loading for each AfFtn₂ : GFP input ratio was determined and summarized in Fig. 6(b). Increasing the GFP(+36) concentration not only yielded more assembly but also increased the average number of cargo encapsulated per assembly. Maximally, 4–5 GFP(+36) molecules were encapsulated per ferritin 24 mer. As measured with DLS, the hydrodynamic diameter distribution and the average (13 nm) of the 24 mer peak purified by SEC was invariant with respect to the variation of the AfFtn₂ : GFP input ratio (ESI,† Fig. S15). This invariance is consistent with ferritin assembly retaining native morphology, where the interior cavity limits the total cargo volume; the DLS data provided additional evidence that GFP(+36) is encapsulated within ferritin instead of attaching to the outer surface of the 24 mer. Computational modeling, while minimizing steric clashes, was able to position as many as 5 GFP(+36) guest molecules within the AfFtn₂₄ host (Fig. 6(g)). Although GFP molecules have little freedom to move within the host, all three loading configurations (3, 4, 5 interior GFPs) are allowed. We reason that electrostatic interactions between GFP(+36) and the ferritin interior surface likely attenuate repulsive interactions between encapsulated GFPs, enabling stable multivalent loading within the ferritin cage.

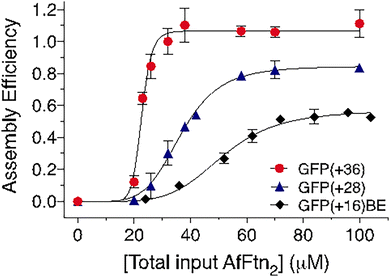
Fig. 6 Varying loading densities and assembly efficiencies with supercharged GFP guests mixed at different ratios in pH 7.6 buffer. Top panels: SEC traces (normalized to the highest intensity) with increasing (a) GFP(+36), (c) GFP(+28), and (e) GFP(+16)BE to AfFtn₂ ratios. Blue: absorbance at 280 nm; green: absorbance at 488 nm. Enlarged (a), (c), and (e) can be found in ESI.† (b), (d) and (f) Number of GFPs encapsulated per AfFtn₂₄ at each mixing ratio (green circle, right vertical axis). Area under 24 mer peaks was divided by total peak area of 24 mer and dimer peaks to yield assembly efficiency (blue square, left vertical axis). [AfFtn₂] = 24 μM, 36 μM, and 72 μM, for GFP(+36), GFP(+28), and GFP(+16)BE, respectively (N ≥ 2). (g) Representative model configurations for N = 3, 4, and 5 GFP(+36) molecules (from left to right) within the AfFtn₂₄ host.

As with AfFtn–GFP(+36), the efficiency of 24 mer assembly increased with increasing GFP(+28) concentration (Fig. 6(c) and (d)). However, the efficiency plateaued at loading ratios of 12 : 4 to 12 : 6, with roughly 20% of ferritin remaining in the dimer form (Fig. 6(c) and (d)). The average number of GFP(+28) molecules encapsulated per host increased slightly when a higher ratio of GFP(+28) was used (Fig. 6(d)). The maximum loading of GFP(+28) was 3–4 molecules per AfFtn₂₄, indicating that one less GFP(+28) molecule was encapsulated compared to GFP(+36). For GFP(+16)BE, the assembly efficiency remained lower than 50% at all tested stoichiometries (Fig. 6(e) and (f)). A constant loading of three GFP(+16)BE guests encapsulated per AfFtn₂₄ was observed (Fig. 6(f)).

Somewhat surprisingly, guest molecules with higher charge exhibited higher loading within the AfFtn cage. The higher cargo loading may result from a higher binding affinity between AfFtn and GFP(+36) during assembly as well as increased likelihood of initiating the assembly process. Higher charges also mean more potential complementary contacting residues between host and guest, allowing GFP(+36) to adopt multiple electrostatically complementary configurations within the host as additional GFP(+36) molecules bind and become encapsulated. In contrast, GFP(+16)BE has a more limited set of complementary configurations, and the number of guest molecules per host remained unchanged with respect to the attempts to increase the loading (Fig. 6(f)).

Charge influence on host–guest assembly efficiency

We noticed during the complexation process that only fully assembled 24 mer products and excess dimer were observed via SEC without evidence of intermediate oligomerization. We hypothesized that GFP-induced AfFtn assembly resembles the highly cooperative formation of protein cages from individual protein building blocks, which has not been investigated with ferritin systems.^20,26,61 To determine the degree of cooperativity and the assembly efficiency of AfFtn in the presence of each GFP variant, AfFtn₂ was titrated into solutions where the total GFP concentration was kept constant at [GFP] = 10 μM (Fig. 7) during the course of the titration. The assembly efficiency for each value of [AfFtn₂] was assessed by SEC. Because the GFP variants only elute with the 24 mer under low ionic strength conditions, GFP absorption at 488 nm upon elution was used to monitor AfFtn assembly. Assembly efficiency was defined as GFP_Ftn/GFP_tot, where GFP_Ftn is the amount of GFP encapsulated within AfFtn₂₄ (Fig. 7). GFP_tot was determined separately by loading the same volume of only 10 μM GFP in the high ionic strength buffer, for which GFP elutes from the analytical SEC column. Quantification of GFP_Ftn and GFP_tot in each case was obtained by integrating the area under the SEC elution curve. The resulting assembly efficiency curves were fitted to a Hill equation (Fig. 7; see Methods).

Fig. 7 Assembly efficiency as a function of AfFtn concentration in the presence of the indicated GFP variants at pH 7.6. For each titration, [GFP] = 10 μM. [Total input AfFtn₂] is determined prior to mixing with GFP. Assembly efficiency of the 24 mer is obtained as the fraction of GFP that eluted from the SEC column (N = 3; see Methods). Curves are fitted to a two-state cooperative Hill model for assembly (see Methods). For each GFP variant, the maximum assembly efficiency increases with the surface charge of the guest GFP.

The Hill coefficient (cooperativity exponent) n and the apparent dissociation constants of the AfFtn assembly in the presence of each of the GFP variants are: GFP(+36), n = 12.7, K_D = 22.7 μM; GFP(+28), n = 5.4, K_D = 36.7 μM; and GFP(+16)BE, n = 5.2, K_D = 51.5 μM (Fig. 7). All three variants induced cooperative supramolecular assembly of AfFtn. GFP(+36) showed a remarkably high degree of cooperativity that aligns with the expected theoretical value of n = 12 for all-or-none assembly of the 24 mer from AfFtn dimers. Cooperative assembly is also observed for the other two variants; interpretation of the exponent is less clear, and the smaller values n = 5–6 may result from coalescence of partially assembled structures. The maximal value of the encapsulation efficiency increases with the magnitude of the charge on these positively charged GFP variants. This trend explains the high efficiencies of AfFtn₂₄ formation induced by GFP(+36) and GFP(+28), close to 100% and 85%, respectively. In contrast, GFP(+16)BE had a lower assembly efficiency of 57%. These reduced values align qualitatively with the lower GFP loading observed for GFP(+28) and GFP(+16)BE (Fig. 6(d) and (f)) compared to that of GFP(+36) (Fig. 6(b)). The assembly efficiency for GFP(+36) saturates near [AfFtn₂] = 40 μM or [AfFtn₂]/[GFP] = 4 (Fig. 7). Assuming AfFtn is present as the 24 mer, this ratio corresponds to a loading of 3 GFP per 24 mer, similar to the loading of 3–4.5 presented in Fig. 6(b). K_D is lowest (least dissociation) for GFP(+36) and increases with decreasing GFP charge, consistent with the GFP variants fostering AfFtn subunit association via complementary electrostatic interactions. The correlation between cargo charge density and assembly efficiency has been previously observed in gold nanoparticle encapsulation by virus-like particles, where charge regulation also played a role in determining assembly efficiency.⁶²

Conclusions

We investigated ferritin complexation with supercharged GFP guest molecules to assess loading capacity, binding affinity, cooperativity and efficiency of assembly. Introducing positive charges on the GFP cargo promoted AfFtn assembly. Charge discrimination was prominent at pH 7.6: GFP(+36) and GFP(+28) were encapsulated by AfFtn but guests with lower charges (GFP(+9) and GFP(+14)) were not. The results showed that complementary charges can induce protein–protein interactions but not necessarily ferritin assembly and encapsulation. Notably, at pH 5.8, all the positively charged GFP variants exhibited encapsulation by AfFtn. Computational simulations identified key electrostatic inter-residue contacts between a GFP(+36) molecule and up to five ferritin dimers at a 3-fold symmetric axis. The simulation results also suggested that cargo GFP might be encapsulated by distributing positive surface charge at the ends of the beta-barrel, and this was verified experimentally using a rationally designed “charges at both ends” variant, GFP(+16)BE. Cargo charge magnitude is known to play a role in encapsulation efficiency,²⁹ but the distinct assembly profiles for GFP(+36), GFP(+28), and GFP(+16)BE were unexpected. All three GFP variants were encapsulated by ferritin cooperatively, a key feature shared with other supramolecular assemblies, including native and artificial biological and inorganic systems.^{27,47,50,63,64} The assembly efficiency for GFP(+36) was 100%, meaning that all input GFP(+36) molecules were encapsulated by AfFtn at micromolar concentrations. In the presence of GFP(+36), AfFtn exhibited the highest effective intersubunit affinity (K_D = 22.7 μM) and demonstrated high cooperativity (n = 12.7), consistent with the value expected for all-or-none formation of the host AfFtn₂₄. Comparing this cooperativity value to other examples of electrostatically driven protein complexes, the ferritin-GFP model system achieves nearly the same cooperativity as the high-symmetry (T = 4) VLP assembly induced by a 19 nm gold nanoparticle (n = 15)²⁹ and shows higher cooperativity than computationally designed self-assembling protein nanomaterials (n = 7.1)⁵⁰ and single-stranded RNA packaging by cowpea chlorotic mottle virus (n = 3).⁶⁵ To our knowledge, this is the first direct evidence of cooperative assembly in a ferritin capsular system. Additionally, it was determined that 3–5 GFP(+36) could be loaded per ferritin 24 mer compared to a loading of 3 per ferritin for GFP(+28) and GFP(+16)BE at all loading ratios. These results indicate that enhancing guest electrostatic charge can increase the cargo loading. We showed that it is possible to achieve the elusive 1-to-1 AfFtn₂₄–GFP(+36) host–guest complex by fine-tuning the strength of host–guest interactions by modulating ionic strength and verified this experimentally using time-resolved fluorescence anisotropy measurements. The absence of anisotropy decay via homoFRET on 1–2 ns timescale and the corresponding persistence of anisotropy on tens-of-ns timescale, confirmed the presence of a single GFP(+36) within the host cavity. Our findings identify routes for encapsulating a wide range of wildtype and engineered protein cargo within A. fulgidus ferritin by manipulating host–guest and host–host cooperativity through guest charges (binding affinity), pH, and ionic strength. This work also highlights design principles for guest molecules that enable supramolecular host–guest assembly. Similar to what we have done with guest modifications, protein charge resurfacing can be extended to the host,^66,67 and by controlling the size, shape, charge distribution, and loading of the guest, protein host–guest complexes with novel properties can be realized to support a broad set of applications.

Materials and methods

AfFtn purification

AfFtn wildtype (UniProtKB O29424) was expressed and purified with slight modifications to previously published methods.³⁵ AfFtn plasmid was transformed in BL21(DE3) cells (New England Biolabs) and cultured overnight in LB supplemented with 100 μg mL⁻¹ ampicillin at 37 °C. The cultures were transferred to 1 L LB supplemented with ampicillin at the same concentration at 37 °C until OD₆₀₀ reached 0.6. The cells were then induced with 1 mM IPTG for 4 h at 37 °C and pelleted by centrifugation (10 min, 6 krpm, 4 °C). The pellet was resuspended in a 20 mM sodium phosphate, 20 mM NaCl, pH 7.6 buffer and treated with lysozyme (1 mg mL⁻¹ final concentration), Benzonase nuclease (1 μL per gram of cell pellet, Millipore Sigma) with 2 mM MgCl₂ final concentration, sonication (amplitude of 20, 1 s on, 1 s off, 10 min processing time), and centrifugation (30 min, 13 krpm, 4 °C). The supernatant was heat shocked for 10 min at 80 °C and centrifuged for 30 min at 9 krpm and 4 °C. The solution was concentrated and injected through a 0.22 μm filter to a HiLoad 16/60 Superdex 200 size exclusion chromatographic column in high ionic strength buffer (20 mM sodium phosphate, 800 mM NaCl, pH 7.6). AfFtn dimer concentration was determined using an extinction coefficient at 280 nm of ε_Ftn,280 = 6.8 × 10⁴ M⁻¹ cm⁻¹ (AfFtn₂).

Supercharged GFP purification

Genes for the corresponding constructs were obtained as follows: GFP(+36) was purchased from DNA 2.0 (now ATUM); GFP(+28), GFP(+14), and GFP(+9) were gifts from David Liu (Plasmids 89 250, 89 252, and 89 247); GFP(+16)OS was purchased from ATUM; and GFP(+16)BE was made via Gibson assembly on a plasmid purchased from ATUM. Supercharged GFPs were expressed and purified with slight modifications to our previous publication.⁴³ Briefly, bacterial cultures were grown overnight at 37 °C in LB, then transferred to 1 L LB and cultivated until OD₆₀₀ reached 0.6. Induction with 1 mM IPTG followed for 4 h at 37 °C. Cells were harvested, stored at −20 °C, and later lysed with lysozyme and sonication. After centrifugation, purification was achieved with Ni²⁺–NTA spin columns, cation exchange chromatography (except for GFP(+9) and eGFP), and size exclusion chromatography equilibrated with PBS. Purity was confirmed by SDS-PAGE, and protein concentration was determined using the extinction coefficient at 488 nm: ε_GFP,488 = 4.7 × 10⁴ M⁻¹ cm⁻¹ (supercharged GFP variants), ε_eGFP,488 = 5.3 × 10⁴ M⁻¹ cm⁻¹ (eGFP). Nucleic acids were degraded for ease of removal by adding benzonase (1 μL per gram of cell pellet) during purification. Protein solutions were stored at 4 °C until use.

AfFtn–GFP complex formation

AfFtn 24 mer was first disassembled into dimers in low ionic strength buffer (20 mM sodium phosphate, pH 7.6 or 5.8) with an overnight incubation time. AfFtn–GFP complexes were formed by mixing AfFtn₂ and GFP in a 12 : x ratio in the same low ionic strength buffer at AfFtn₂ concentrations of 24, 36, 72, or 120 μM. To test the effect of ionic strength on assembly formation, AfFtn–GFP complexes were made by mixing 72 μM of AfFtn₂ and 6 μM of GFP (a 12 : 1 AfFtn₂ : GFP ratio) in 20 mM sodium phosphate buffer at pH 7.6 at the corresponding NaCl concentrations. All samples were equilibrated at 4 °C overnight before analysis.

Analytical size exclusion chromatography (SEC)

Analytical size exclusion chromatography was done on an AKTA Pure FPLC system using a Superdex200 Increase 10/300 GL column equilibrated with the same buffer for complex formation. 200 μL or 500 μL of sample was injected, and absorbances at 280 and 488 nm were monitored. Samples were eluted at 4 °C using a flow rate of 1.0 mL min⁻¹.

Dynamic light scattering (DLS)

DLS measurements were conducted on a Malvern ZetaSizer Nano ZS with a scattering angle of 173° and an equilibration time of 60 s at rt. Samples were measured in disposable UV-cuvettes (BrandTech) with volume of 100 μL. Particle sizes were reported by averaging three measurements in distributions of volume.

Native gel electrophoresis

Native agarose gels (0.7%) were made using a buffer containing 5 mM NaCl and 20 mM sodium phosphate at pH 7.6. Samples were mixed with glycerol (final glycerol concentration 16% v/v) before loading. Gel electrophoresis was conducted at 100 V for 20 min in the dark. Imaging was performed using a Typhoon FLA7000 imager, exciting at 473 nm with a PMT setting of 700 V. Subsequently, gels were stained with Coomassie Brilliant Blue R-250.

Transmission electron microscopy

AfFtn–GFP complexes were purified with analytical SEC and concentrated. Carbon-coated copper grids were glow discharged. Samples containing [AfFtn₂₄] = 0.6–1 μM were incubated on the grid for 5 min before buffer was removed with filter paper. Grids were stained in 2% uranyl acetate for 30 s. Excess stain solution was removed using filter paper. Grids were imaged on a JEOL-1010 microscope operating at 80 kV.

Determination of GFP loading

GFP loading was determined as previously described.⁴³ Briefly, SEC fractions containing both AfFtn and GFP were collected and concentrated, and protein concentrations were determined by measuring absorbances at 280 nm and 488 nm, A₂₈₀ and A₄₈₈, using a Multizone CARY 3500 UV-Vis spectrometer. A₄₈₈ was used to determine GFP concentration. Ferritin concentration was determined by subtracting contributions to the absorbance at 280 nm due to GFP.

ε_Ftn,280b [AfFtn₂] = A₂₈₀ − ε_GFP,280b (A₄₈₈/bε_GFP,488),

where b is the photocell path length. Average GFP loaded per cage = [GFP]/[AfFtn₂₄], where [AfFtn₂₄] = [AfFtn₂]/12.

Cooperativity analysis

AfFtn₂ concentrations between 20 to 100 μM were titrated into a solution of GFP (10 μM) at pH 7.6 (20 mM sodium phosphate). The assembly efficiency at each ratio was assessed by analytical SEC. Assembly efficiency E was defined as the amount of GFP eluted (encapsulated within AfFtn₂₄), GFP_Ftn, divided by the total input of GFP, GFP_tot.

E = GFP_Ftn/GFP_tot.

Each GFP quantity, GFP_Ftn and GFP_tot, was obtained as the corresponding the area under the chromatographic curve monitored at 488 nm, and areas were determined by the UNICORN 7 software. GFP_tot was obtained by injecting samples containing only 10 μM GFP prepared in the high ionic strength buffer (20 mM sodium phosphate, 800 mM NaCl, pH 7.6) into the analytical SEC column equilibrated with the same buffer. Elution of the GFP constructs was not observed in the absence of either AfFtn or the high ionic strength buffer.

The obtained plot was fitted to the Hill equation:

Assembly efficiency = B_max × ^xnxⁿ/(K_Dⁿ + xⁿ)

where x is the input AfFtn₂ concentration, and the fitted parameters are n the Hill exponent, K_D the apparent dissociation constant, and B_max a coefficient accounting for the fact that not all GFP may be encapsulated. We note that this cooperative Hill model is a simplification but does reveal the cooperativity of the assembly.

Confocal laser scanning microscopy imaging

All samples (30 μL) were imaged on μ-slide 8-well chamber coverslips (ibidi) using an Olympus FV1000 laser scanning confocal microscope equipped with a 40× oil immersion objective (NA = 1.30, Olympus UPLN). GFP was excited by a 488 nm laser. Fiji was used for image processing.⁶⁸

TCSPC/anisotropy

Time-resolved fluorescence and anisotropy measurements were collected on a time-correlated single photon counting (TCSPC) system with a 1 cm quartz cuvette at rt. Samples were excited by the output of a picosecond diode laser (LDH-P-C Series, Picoquant) at 482 nm and 20 MHz repetition rate. Emission was collected at magic angle, VV, VH, HV, and HH polarization conditions using linear polarizers (Thorlabs LPVISE100-A) in excitation and emission and in a 90° geometry relative to excitation, selected by a long-wavelength (Schott GG495) and bandpass (Chroma HQ535/50) filter, and detected by a MCP-PMT detector (Hamamatsu R2809U) and a TCSPC PC-board (Becker & Hickl SPC-730). The overall IRF of this setup was about 120 ps. Fluorescence and anisotropy decay were fit using the FLUOFIT program (Picoquant GmbH). Flourescence polarization anisotropy r(t) was fit as a function of time t using the following sum of exponentials.
Here, the R_i, τ_i and R_infinite are parameters determined during the fitting. The smallest value τ_i is associated with the instrument response.

Surface potential calculation

Protein structures for AfFtn (PDB ID: 1S3Q)⁵¹ and GFP (PDB ID: 2B3P)⁶⁹ were obtained from the Protein Data Bank (PDB). Structures were checked for completeness, and hydrogens were added as necessary. Structures of designed variants of GFP were prepared using Charmm-GUI,⁷⁰ and oligomers of AfFtn were selected and prepared similarly (Fig. 1(a)). The prepared PDB files were submitted to the PDB2PQR server with default parameters to convert them into PQR format.⁷¹ The resulting PQR files were then used for electrostatic potential calculations with the Adaptive Poisson–Boltzmann Solver (APBS).⁷² Surface electrostatic potentials were visualized using PyMOL,⁷³ with the potentials colored from red (negative) to blue (positive).

Single GFP simulation

All simulations were done with NAMD 3.0b6 with the NPT ensemble and CHARMM36 forcefield.^74–76 The minimum distance between any atoms of the peptide and the edge of the box was 20 Å. Water molecules (TIP3P) were introduced and, to achieve charge neutrality, Na⁺ and Cl⁻ counterions were added in a manner consistent with [NaCl] = 0.15 mol L⁻¹. Additional details can be found in ESI.†

Multi GFP placement within AtFtn 24 mer

A Monte Carlo approach was employed to place N guest GFP proteins within a fixed AfFtn 24 mer host while minimizing steric clashes. For simplicity, all residues were represented as r = 6 Å radius spheres centered on their alpha carbons. Any pair of residues with a separation smaller than r = 6 Å contributed to a clash score, S.
where the sum is over all unique residue pairs i,j on distinct protein subunits, d_ij is the distance between residues i and j, and θ is the Heaviside step function, i.e., only clashes where r > d_ij contribute to S. The host molecule was positioned at the origin and held fixed, while the guest molecules underwent uniform, random translational displacements and rotations in each step. Configurations were accepted or rejected based on the Metropolis criterion, with a unitless temperature of T = 10. This process continued until a clash-free arrangement (S = 0) of guest GFP proteins within the host was achieved.

Author contributions

Z. W., J. A. B., R. G., J. G. S. and I. J. D. conceived and designed the project. Z. W. designed and performed the experiments and data analysis. D. B. Y. performed computational modelling and simulations. J. A. B. helped with protein expression and purification. R. G. performed protein design and modeling. T. T. and S. V. performed time-resolved fluorescence and anisotropy measurements. Z. W. and I. J. D. wrote the manuscript with input from all authors.

Data availability

All data supporting this study are available in the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by funding from NSF grant CHE-1905203 to IJD and JGS. ZW was supported by NIH grant R35-GM131907 to IJD. D.-B.Y. acknowledges a John G. Miller Fel-lowship from the University of Pennsylvania. J. G. S. acknowl-edges support from DOE (DE-SC0019282). Simulations and modeling were performed using allocation TG-CHE110041 from the Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS) program, which is supported by National Science Foundation grants #1548562, #2138259, #2138286, #2138307, #2137603, and #2138296. We thank Stephen Crane for help with confocal microscopy.

References

1. T. G. W. Edwardson, M. D. Levasseur, S. Tetter, A. Steinauer, M. Hori and D. Hilvert, Protein Cages: From Fundamentals to Advanced Applications, Chem. Rev., 2022, 122(9), 9145–9197,  DOI:10.1021/acs.chemrev.1c00877.
2. K. W. Pulsipher and I. J. Dmochowski, Ferritin: Versatile Host, Nanoreactor, and Delivery Agent, Isr. J. Chem., 2016, 56(9–10), 660–670,  DOI:10.1002/ijch.201600017.
3. B. Nguyen and N. H. Tolia, Protein-Based Antigen Presentation Platforms for Nanoparticle Vaccines, npj Vaccines, 2021, 6(1), 1–11,  DOI:10.1038/s41541-021-00330-7.
4. N. K. Lee, E. J. Lee, S. Kim, G. Nam, M. Kih, Y. Hong, C. Jeong, Y. Yang, Y. Byun and I.-S. Kim, Ferritin Nanocage with Intrinsically Disordered Proteins and Affibody: A Platform for Tumor Targeting with Extended Pharmacokinetics, J. Controlled Release, 2017, 267, 172–180,  DOI:10.1016/j.jconrel.2017.08.014.
5. S. Chakraborti, A. Korpi, M. Kumar, P. Stępień, M. A. Kostiainen and J. G. Heddle, Three-Dimensional Protein Cage Array Capable of Active Enzyme Capture and Artificial Chaperone Activity, Nano Lett., 2019, 19(6), 3918–3924,  DOI:10.1021/acs.nanolett.9b01148.
6. P. C. Jordan, D. P. Patterson, K. N. Saboda, E. J. Edwards, H. M. Miettinen, G. Basu, M. C. Thielges and T. Douglas, Self-Assembling Biomolecular Catalysts for Hydrogen Production, Nat. Chem., 2016, 8(2), 179–185,  DOI:10.1038/nchem.2416.
7. Y. Wang, E. Selivanovitch and T. Douglas, Enhancing Multistep Reactions: Biomimetic Design of Substrate Channeling Using P22 Virus-Like Particles, Adv. Sci., 2023, 10(13), 2206906,  DOI:10.1002/advs.202206906.
8. N. K. Lee, S. Cho and I.-S. Kim, Ferritin – a Multifaceted Protein Scaffold for Biotherapeutics, Exp. Mol. Med., 2022, 54(10), 1652–1657,  DOI:10.1038/s12276-022-00859-0.
9. X. Yu, Z. Weng, Z. Zhao, J. Xu, Z. Qi and J. Liu, Assembly of Protein Cages for Drug Delivery, Pharmaceutics, 2022, 14(12), 2609,  DOI:10.3390/pharmaceutics14122609.
10. M. Khoshnejad, H. Parhiz, V. V. Shuvaev, I. J. Dmochowski and V. R. Muzykantov, Ferritin-Based Drug Delivery Systems: Hybrid Nanocarriers for Vascular Immunotargeting, J. Controlled Release, 2018, 282, 13–24,  DOI:10.1016/j.jconrel.2018.02.042.
11. F. C. Herbert, O. R. Brohlin, T. Galbraith, C. Benjamin, C. A. Reyes, M. A. Luzuriaga, A. Shahrivarkevishahi and J. J. Gassensmith, Supramolecular Encapsulation of Small-Ultrared Fluorescent Proteins in Virus-Like Nanoparticles for Noninvasive In Vivo Imaging Agents, Bioconjugate Chem., 2020, 31(5), 1529–1536,  DOI:10.1021/acs.bioconjchem.0c00190.
12. X. Lin, J. Xie, G. Niu, F. Zhang, H. Gao, M. Yang, Q. Quan, M. A. Aronova, G. Zhang, S. Lee, R. Leapman and X. Chen, Chimeric Ferritin Nanocages for Multiple Function Loading and Multimodal Imaging, Nano Lett., 2011, 11(2), 814–819,  DOI:10.1021/nl104141g.
13. X. Lin, J. Xie, L. Zhu, S. Lee, G. Niu, Y. Ma, K. Kim and X. Chen, Hybrid Ferritin Nanoparticles as Activatable Probes for Tumor Imaging, Angew. Chem., Int. Ed., 2011, 50(7), 1569–1572,  DOI:10.1002/anie.201006757.
14. Z. Liu, J. Qiao, Z. Niu and Q. Wang, Natural Supramolecular Building Blocks: From Virus Coat Proteins to Viral Nanoparticles, Chem. Soc. Rev., 2012, 41(18), 6178–6194,  10.1039/C2CS35108K.
15. L. Esquirol, D. McNeale, T. Douglas, C. E. Vickers and F. Sainsbury, Rapid Assembly and Prototyping of Biocatalytic Virus-like Particle Nanoreactors, ACS Synth. Biol., 2022, 11(8), 2709–2718,  DOI:10.1021/acssynbio.2c00117.
16. A. O’Neil, C. Reichhardt, B. Johnson, P. E. Prevelige and T. Douglas, Genetically Programmed In Vivo Packaging of Protein Cargo and Its Controlled Release from Bacteriophage P22, Angew. Chem., Int. Ed., 2011, 50(32), 7425–7428,  DOI:10.1002/anie.201102036.
17. I. J. Minten, L. J. A. Hendriks, R. J. M. Nolte and J. J. L. M. Cornelissen, Controlled Encapsulation of Multiple Proteins in Virus Capsids, J. Am. Chem. Soc., 2009, 131(49), 17771–17773,  DOI:10.1021/ja907843s.
18. V. V. Shuvaev, M. Khoshnejad, K. W. Pulsipher, R. Yu Kiseleva, E. Arguiri, J. C. Cheung-Lau, K. M. LeFort, M. Christofidou-Solomidou, R. V. Stan, I. J. Dmochowski and V. R. Muzykantov, Spatially Controlled Assembly of Affinity Ligand and Enzyme Cargo Enables Targeting Ferritin Nanocarriers to Caveolae, Biomaterials, 2018, 185, 348–359,  DOI:10.1016/j.biomaterials.2018.09.015.
19. W. F. Rurup, F. Verbij, M. S. T. Koay, C. Blum, V. Subramaniam and J. J. L. M. Cornelissen, Predicting the Loading of Virus-Like Particles with Fluorescent Proteins, Biomacromolecules, 2014, 15(2), 558–563,  DOI:10.1021/bm4015792.
20. Y. Azuma, M. Herger and D. Hilvert, Diversification of Protein Cage Structure Using Circularly Permuted Subunits, J. Am. Chem. Soc., 2018, 140(2), 558–561,  DOI:10.1021/jacs.7b10513.
21. S. Banskota, A. Raguram, S. Suh, S. W. Du, J. R. Davis, E. H. Choi, X. Wang, S. C. Nielsen, G. A. Newby, P. B. Randolph, M. J. Osborn, K. Musunuru, K. Palczewski and D. R. Liu, Engineered Virus-like Particles for Efficient in Vivo Delivery of Therapeutic Proteins, Cell, 2022, 185(2), 250–265,  DOI:10.1016/j.cell.2021.12.021.
22. B. D. Cons, D. G. Twigg, R. Kumar and G. Chessari, Electrostatic Complementarity in Structure-Based Drug Design, J. Med. Chem., 2022, 65(11), 7476–7488,  DOI:10.1021/acs.jmedchem.2c00164.
23. X. Du, Y. Li, Y.-L. Xia, S.-M. Ai, J. Liang, P. Sang, X.-L. Ji and S.-Q. Liu, Insights into Protein–Ligand Interactions: Mechanisms, Models, and Methods, Int. J. Mol. Sci., 2016, 17(2), 144,  DOI:10.3390/ijms17020144.
24. M. Majewski, S. Ruiz-Carmona and X. Barril, An Investigation of Structural Stability in Protein-Ligand Complexes Reveals the Balance between Order and Disorder, Commun. Chem., 2019, 2(1), 1–8,  DOI:10.1038/s42004-019-0205-5.
25. K. N. Houk, A. G. Leach, S. P. Kim and X. Zhang, Binding Affinities of Host–Guest, Protein–Ligand, and Protein–Transition-State Complexes, Angew. Chem., Int. Ed., 2003, 42(40), 4872–4897,  DOI:10.1002/anie.200200565.
26. J. D. Perlmutter and M. F. Hagan, Mechanisms of Virus Assembly, Annu. Rev. Phys. Chem., 2015, 66, 217–239,  DOI:10.1146/annurev-physchem-040214-121637.
27. T. Beck, S. Tetter, M. Künzle and D. Hilvert, Construction of Matryoshka-Type Structures from Supercharged Protein Nanocages, Angew. Chem., Int. Ed., 2015, 54(3), 937–940,  DOI:10.1002/anie.201408677.
28. F. Palombarini, S. Masciarelli, A. Incocciati, F. Liccardo, E. Di Fabio, A. Iazzetti, G. Fabrizi, F. Fazi, A. Macone, A. Bonamore and A. Boffi, Self-Assembling Ferritin-Dendrimer Nanoparticles for Targeted Delivery of Nucleic Acids to Myeloid Leukemia Cells, J. Nanobiotechnol., 2021, 19(1), 172,  DOI:10.1186/s12951-021-00921-5.
29. L. He, Z. Porterfield, P. van der Schoot, A. Zlotnick and B. Dragnea, Hepatitis Virus Capsid Polymorph Stability Depends on Encapsulated Cargo Size, ACS Nano, 2013, 7(10), 8447–8454,  DOI:10.1021/nn4017839.
30. J. E. Glasgow, S. L. Capehart, M. B. Francis and D. Tullman-Ercek, Osmolyte-Mediated Encapsulation of Proteins inside MS2 Viral Capsids, ACS Nano, 2012, 6(10), 8658–8664,  DOI:10.1021/nn302183h.
31. Y. Azuma, R. Zschoche, M. Tinzl and D. Hilvert, Quantitative Packaging of Active Enzymes into a Protein Cage, Angew. Chem., Int. Ed., 2016, 55(4), 1531–1534,  DOI:10.1002/anie.201508414.
32. M. Brasch, R. M. Putri, M. V. de Ruiter, D. Luque, M. S. Koay, J. R. Castón and J. J. Cornelissen, Assembling Enzymatic Cascade Pathways inside Virus-Based Nanocages Using Dual-Tasking Nucleic Acid Tags, J. Am. Chem. Soc., 2017, 139(4), 1512–1519,  DOI:10.1021/jacs.6b10948.
33. M. S. Lawrence, K. J. Phillips and D. R. Liu, Supercharging Proteins Can Impart Unusual Resilience, J. Am. Chem. Soc., 2007, 129(33), 10110–10112,  DOI:10.1021/ja071641y.
34. J. R. Laber, B. J. Dear, M. L. Martins, D. E. Jackson, A. DiVenere, J. D. Gollihar, A. D. Ellington, T. M. Truskett, K. P. Johnston and J. A. Maynard, Charge Shielding Prevents Aggregation of Supercharged GFP Variants at High Protein Concentration, Mol. Pharmaceutics, 2017, 14(10), 3269–3280,  DOI:10.1021/acs.molpharmaceut.7b00322.
35. J. A. Bulos, R. Guo, Z. Wang, M. A. DeLessio, J. G. Saven and I. J. Dmochowski, Design of a Superpositively Charged Enzyme: Human Carbonic Anhydrase II Variant with Ferritin Encapsulation and Immobilization, Biochemistry, 2021, 60(47), 3596–3609,  DOI:10.1021/acs.biochem.1c00515.
36. I. Paik, S. Bhadra and A. D. Ellington, Charge Engineering Improves the Performance of Bst DNA Polymerase Fusions, ACS Synth. Biol., 2022, 11(4), 1488–1496,  DOI:10.1021/acssynbio.1c00559.
37. A. E. Miklos, C. Kluwe, B. S. Der, S. Pai, A. Sircar, R. A. Hughes, M. Berrondo, J. Xu, V. Codrea, P. E. Buckley, A. M. Calm, H. S. Welsh, C. R. Warner, M. A. Zacharko, J. P. Carney, J. J. Gray, G. Georgiou, B. Kuhlman and A. D. Ellington, Structure-Based Design of Supercharged, Highly Thermoresistant Antibodies, Chem. Biol., 2012, 19(4), 449–455,  DOI:10.1016/j.chembiol.2012.01.018.
38. D. B. Thompson; J. J. Cronican and D. R. Liu, Chapter Twelve – Engineering and Identifying Supercharged Proteins for Macromolecule Delivery into Mammalian Cells, in Methods in Enzymology, Protein Engineering for Therapeutics, Part B ed. K. D. Wittrup and G. L. Verdine, Academic Press, 2012, vol. 503, pp. 293–319 DOI:10.1016/B978-0-12-396962-0.00012-4.
39. J. J. Cronican, D. B. Thompson, K. T. Beier, B. R. McNaughton, C. L. Cepko and D. R. Liu, Potent Delivery of Functional Proteins into Mammalian Cells in Vitro and in Vivo Using a Supercharged Protein, ACS Chem. Biol., 2010, 5(8), 747–752,  DOI:10.1021/cb1001153.
40. B. R. McNaughton, J. J. Cronican, D. B. Thompson and D. R. Liu, Mammalian Cell Penetration, siRNA Transfection, and DNA Transfection by Supercharged Proteins, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(15), 6111–6116,  DOI:10.1073/pnas.0807883106.
41. M. Patrian, A. Shaukat, M. Nieddu, J. A. Banda-Vázquez, J. V. I. Timonen, J. P. Fuenzalida Werner, E. Anaya-Plaza, M. A. Kostiainen and R. D. Costa, Supercharged Fluorescent Protein-Apoferritin Cocrystals for Lighting Applications, ACS Nano, 2023, 17(21), 21206–21215,  DOI:10.1021/acsnano.3c05284.
42. T. G. W. Edwardson, S. Tetter and D. Hilvert, Two-Tier Supramolecular Encapsulation of Small Molecules in a Protein Cage, Nat. Commun., 2020, 11(1), 5410,  DOI:10.1038/s41467-020-19112-1.
43. K. W. Pulsipher, J. A. Bulos, J. A. Villegas, J. G. Saven and I. J. Dmochowski, A Protein–Protein Host–Guest Complex: Thermostable Ferritin Encapsulating Positively Supercharged Green Fluorescent Protein, Protein Sci., 2018, 27(10), 1755–1766,  DOI:10.1002/pro.3483.
44. J. C. Cheung-Lau, D. Liu, K. W. Pulsipher, W. Liu and I. J. Dmochowski, Engineering a Well-Ordered, Functional Protein–Gold Nanoparticle Assembly, J. Inorg. Biochem., 2014, 130, 59–68,  DOI:10.1016/j.jinorgbio.2013.10.003.
45. J. Swift, C. A. Butts, J. Cheung-Lau, V. Yerubandi and I. J. Dmochowski, Efficient Self-Assembly of Archaeoglobus Fulgidus Ferritin around Metallic Cores, Langmuir, 2009, 25(9), 5219–5225,  DOI:10.1021/la8040743.
46. S. Tetter and D. Hilvert, Enzyme Encapsulation by a Ferritin Cage, Angew. Chem., Int. Ed., 2017, 56(47), 14933–14936,  DOI:10.1002/anie.201708530.
47. P. Ceres and A. Zlotnick, Weak Protein−Protein Interactions Are Sufficient To Drive Assembly of Hepatitis B Virus Capsids, Biochemistry, 2002, 41(39), 11525–11531,  DOI:10.1021/bi0261645.
48. J. D. Perlmutter, M. R. Perkett and M. F. Hagan, Pathways for Virus Assembly around Nucleic Acids, J. Mol. Biol., 2014, 426(18), 3148–3165,  DOI:10.1016/j.jmb.2014.07.004.
49. T. A. Sobiech, Y. Zhong, D. P. Miller, J. K. McGrath, C. T. Scalzo, M. C. Redington, E. Zurek and B. Gong, Ultra-Tight Host–Guest Binding with Exceptionally Strong Positive Cooperativity, Angew. Chem., Int. Ed., 2022, 61(50), e202213467,  DOI:10.1002/anie.202213467.
50. A. J. Wargacki, T. P. Wörner, M. van de Waterbeemd, D. Ellis, A. J. R. Heck and N. P. King, Complete and Cooperative in Vitro Assembly of Computationally Designed Self-Assembling Protein Nanomaterials, Nat. Commun., 2021, 12(1), 883,  DOI:10.1038/s41467-021-21251-y.
51. E. Johnson, D. Cascio, M. R. Sawaya, M. Gingery and I. Schröder, Crystal Structures of a Tetrahedral Open Pore Ferritin from the Hyperthermophilic Archaeon Archaeoglobus Fulgidus, Structure, 2005, 13(4), 637–648,  DOI:10.1016/j.str.2005.01.019.
52. Y. Shamsudin, A. R. Walker, C. M. Jones, T. J. Martínez and S. G. Boxer, Simulation-Guided Engineering of Split GFPs with Efficient β-Strand Photodissociation, Nat. Commun., 2023, 14(1), 7401,  DOI:10.1038/s41467-023-42954-4.
53. E. Karaca, C. Prévost and S. Sacquin-Mora, Modeling the Dynamics of Protein–Protein Interfaces, How and Why?, Molecules, 2022, 27(6), 1841,  DOI:10.3390/molecules27061841.
54. K. W. Pulsipher, J. A. Villegas, B. W. Roose, T. L. Hicks, J. Yoon, J. G. Saven and I. J. Dmochowski, Thermophilic Ferritin 24mer Assembly and Nanoparticle Encapsulation Modulated by Interdimer Electrostatic Repulsion, Biochemistry, 2017, 56(28), 3596–3606,  DOI:10.1021/acs.biochem.7b00296.
55. D. Altman, D. Goswami, T. Hasson, J. A. Spudich and S. Mayor, Precise Positioning of Myosin VI on Endocytic Vesicles In Vivo, PLoS Biol., 2007, 5(8), e210,  DOI:10.1371/journal.pbio.0050210.
56. T. A. Nguyen, P. Sarkar, J. V. Veetil, S. V. Koushik and S. S. Vogel, Fluorescence Polarization and Fluctuation Analysis Monitors Subunit Proximity, Stoichiometry, and Protein Complex Hydrodynamics, PLoS One, 2012, 7(5), e38209,  DOI:10.1371/journal.pone.0038209.
57. N. Ojha, K. H. Rainey and G. H. Patterson, Imaging of Fluorescence Anisotropy during Photoswitching Provides a Simple Readout for Protein Self-Association, Nat. Commun., 2020, 11(1), 21,  DOI:10.1038/s41467-019-13843-6.
58. M. A. Hink, R. A. Griep, J. W. Borst, A. van Hoek, M. H. M. Eppink, A. Schots and A. J. W. G. Visser, Structural Dynamics of Green Fluorescent Protein Alone and Fused with a Single Chain Fv Protein, J. Biol. Chem., 2000, 275(23), 17556–17560,  DOI:10.1074/jbc.M001348200.
59. E. Terpetschnig, H. Szmacinski, H. Malak and J. R. Lakowicz, Metal–Ligand Complexes as a New Class of Long-Lived Fluorophores for Protein Hydrodynamics, Biophys. J., 1995, 68(1), 342–350,  DOI:10.1016/S0006-3495(95)80193-1.
60. C. Thaler, S. V. Koushik, H. L. Puhl, P. S. Blank and S. S. Vogel, Structural Rearrangement of CaMKIIα Catalytic Domains Encodes Activation, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(15), 6369–6374,  DOI:10.1073/pnas.0901913106.
61. A. Hernandez-Garcia, D. J. Kraft, A. F. J. Janssen, P. H. H. Bomans, N. A. J. M. Sommerdijk, D. M. E. Thies-Weesie, M. E. Favretto, R. Brock, F. A. de Wolf, M. W. T. Werten, P. van der Schoot, M. C. Stuart and R. de Vries, Design and Self-Assembly of Simple Coat Proteins for Artificial Viruses, Nat. Nanotechnol., 2014, 9(9), 698–702,  DOI:10.1038/nnano.2014.169.
62. R. Kusters, H.-K. Lin, R. Zandi, I. Tsvetkova, B. Dragnea and P. van der Schoot, Role of Charge Regulation and Size Polydispersity in Nanoparticle Encapsulation by Viral Coat Proteins, J. Phys. Chem. B, 2015, 119(5), 1869–1880,  DOI:10.1021/jp5108125.
63. J. Z. Porterfield, M. S. Dhason, D. D. Loeb, M. Nassal, S. J. Stray and A. Zlotnick, Full-Length Hepatitis B Virus Core Protein Packages Viral and Heterologous RNA with Similarly High Levels of Cooperativity, J. Virol., 2010, 84(14), 7174–7184,  DOI:10.1128/JVI.00586-10.
64. Y. Yang, T. K. Ronson, Z. Lu, J. Zheng, N. Vanthuyne, A. Martinez and J. R. Nitschke, A Curved Host and Second Guest Cooperatively Inhibit the Dynamic Motion of Corannulene, Nat. Commun., 2021, 12(1), 4079,  DOI:10.1038/s41467-021-24344-w.
65. M. Comas-Garcia, R. F. Garmann, S. W. Singaram, A. Ben-Shaul, C. M. Knobler and W. M. Gelbart, Characterization of Viral Capsid Protein Self-Assembly around Short Single-Stranded RNA, J. Phys. Chem. B, 2014, 118(27), 7510–7519,  DOI:10.1021/jp503050z.
66. J. Swift, W. A. Wehbi, B. D. Kelly, X. F. Stowell, J. G. Saven and I. J. Dmochowski, Design of Functional Ferritin-Like Proteins with Hydrophobic Cavities, J. Am. Chem. Soc., 2006, 128(20), 6611–6619,  DOI:10.1021/ja057069x.
67. C. A. Butts, J. Swift, S. Kang, L. Di Costanzo, D. W. Christianson, J. G. Saven and I. J. Dmochowski, Directing Noble Metal Ion Chemistry within a Designed Ferritin Protein, Biochemistry, 2008, 47(48), 12729–12739,  DOI:10.1021/bi8016735.
68. J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld, B. Schmid, J.-Y. Tinevez, D. J. White, V. Hartenstein, K. Eliceiri, P. Tomancak and A. Cardona, Fiji: An Open-Source Platform for Biological-Image Analysis, Nat. Methods, 2012, 9(7), 676–682,  DOI:10.1038/nmeth.2019.
69. J.-D. Pédelacq, S. Cabantous, T. Tran, T. C. Terwilliger and G. S. Waldo, Engineering and Characterization of a Superfolder Green Fluorescent Protein, Nat. Biotechnol., 2006, 24(1), 79–88,  DOI:10.1038/nbt1172.
70. S. Jo, T. Kim, V. G. Iyer and W. Im, CHARMM-GUI: A Web-Based Graphical User Interface for CHARMM, J. Comput. Chem., 2008, 29(11), 1859–1865,  DOI:10.1002/jcc.20945.
71. S. Unni, Y. Huang, R. M. Hanson, M. Tobias, S. Krishnan, W. W. Li, J. E. Nielsen and N. A. Baker, Web Servers and Services for Electrostatics Calculations with APBS and PDB2PQR, J. Comput. Chem., 2011, 32(7), 1488–1491,  DOI:10.1002/jcc.21720.
72. E. Jurrus, D. Engel, K. Star, K. Monson, J. Brandi, L. E. Felberg, D. H. Brookes, L. Wilson, J. Chen, K. Liles, M. Chun, P. Li, D. W. Gohara, T. Dolinsky, R. Konecny, D. R. Koes, J. E. Nielsen, T. Head-Gordon, W. Geng, R. Krasny, G.-W. Wei, M. J. Holst, J. A. McCammon and N. A. Baker, Improvements to the APBS Biomolecular Solvation Software Suite, Protein Sci., 2017, 27(1), 112,  DOI:10.1002/pro.3280.
73. W. L. DeLano, PyMOL: An Open-Source Molecular Graphics Tool. CCP4 Newsl, Protein Crystallogr., 2002, 40(1), 82–92.
74. J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kalé and K. Schulten, Scalable Molecular Dynamics with NAMD, J. Comput. Chem., 2005, 26(16), 1781–1802,  DOI:10.1002/jcc.20289.
75. J. C. Phillips, D. J. Hardy, J. D. C. Maia, J. E. Stone, J. V. Ribeiro, R. C. Bernardi, R. Buch, G. Fiorin, J. Hénin, W. Jiang, R. McGreevy, M. C. R. Melo, B. K. Radak, R. D. Skeel, A. Singharoy, Y. Wang, B. Roux, A. Aksimentiev, Z. Luthey-Schulten, L. V. Kalé, K. Schulten, C. Chipot and E. Tajkhorshid, Scalable Molecular Dynamics on CPU and GPU Architectures with NAMD, J. Chem. Phys., 2020, 153(4), 044130,  DOI:10.1063/5.0014475.
76. J. Huang and A. D. MacKerell Jr, CHARMM36 All-Atom Additive Protein Force Field: Validation Based on Comparison to NMR Data, J. Comput. Chem., 2013, 34(25), 2135–2145,  DOI:10.1002/jcc.23354.

---

Footnotes

† Electronic supplementary information (ESI) available: Experimental procedures, additional experimental and simulation results, figures, design and sequence of GFP(+16) variants. See DOI: https://doi.org/10.1039/d5tb01202c

‡ These authors contributed equally.

---