Exploring the triplet-to-singlet conversion mechanism in persistent luminescence: insights from a host–guest system†
Fernando Teixeira
Bueno
 a,
Tiago
de Sousa Araújo Cassiano
a,
Tiago
de Sousa Araújo Cassiano
 a,
Piotr
de Silva
a,
Piotr
de Silva
 b,
Pedro Henrique
de Oliveira Neto
b,
Pedro Henrique
de Oliveira Neto
 ac and
Leonardo Evaristo
de Sousa
ac and
Leonardo Evaristo
de Sousa
 *b
*b
aInstitute of Physics, University of Brasília, Brasília-DF, 70910-900 DF, Brazil
bDepartment of Energy Conversion and Storage, Technical University of Denmark, Anker Engelunds Vej 301, 2800 Kongens Lyngby, Denmark. E-mail: ledso@dtu.dk
cInternational Center of Physics, Institute of Physics, University of Brasilia, Brazil
First published on 20th December 2024
Abstract
The afterglow phenomenon, characterized by persistent luminescence after the cessation of external excitation, is typically a result of late phosphorescence. However, recent research has explored the possibility of producing afterglow with delayed fluorescence resulting from triplet conversion mechanisms. The main mechanism is a reverse intersystem crossing (rISC), a monomolecular phenomenon in which triplet excitons are converted into singlets. However, triplet conversion can also happen via the intermolecular pathway of triplet-to-singlet (TTS) Förster transfers. For instance, this mechanism has been used to explain afterglow in a host–guest system composed of NPB and DCJTB molecules, but the mechanism behind the photophysics of this system has not been fully characterized. Here, we provide a full theoretical study of the photophysics of NPB and DCJTB molecules, employing a methodology that accounts for vibrational and medium effects to determine the rates of various intra- and intermolecular processes that determine the behavior of this system. We identify extremely low rISC and nonradiative decay rates in NPB as responsible for simultaneously making it an efficient dual emitter and an effective donor molecule for TTS exciton transfers. We also demonstrate how morphological conditions contribute to the pairing of energy levels between NPB and DCJTB, playing a key role in allowing for efficient TTS transfers. Finally, we use kinetic Monte Carlo simulations to prove that the TTS transfer mechanism is able to produce delayed fluorescence in a timescale of tenths of seconds, well-explaining the experimental observations.
I. Introduction
The afterglow phenomenon also referred to as persistent luminescence, involves the emission of light that persists long after the external excitation source has ceased. For organic devices in particular, the occurrence of afterglow allows compounds to be used in a plethora of applications, such as light-emitting diodes, solar cells,1 textile dyeing,2,3 data encryption,4 bioimaging,5–8 warning signs and anti-counterfeiting.9Usually, afterglow is a result of late phosphorescence. As such, the efficiency of this process depends on the quantum yield of triplet generation and on the suppression of nonradiative decay pathways. For these reasons, materials that have been used as possible afterglow emitters include rare-earth-based phosphors and molecular complexes based on transition metals,10–12 as the presence of heavy atoms results in higher spin–orbit coupling and consequently higher intersystem crossing (ISC) and phosphorescence rates. However, this approach increases costs and results in less sustainable devices.
In this context, new strategies for obtaining afterglow are of interest. One such strategy consists of making use of delayed fluorescence generated by the conversion of triplet states into singlets. The most common way of achieving this is by using molecules that possess significant rates of reverse ISC (rISC).13–15 Molecules in this class usually follow a donor–acceptor architecture that induces a charge-transfer (CT) character to their first singlet state.16–18 A second, less popular approach relies on triplet conversion by means of triplet-to-singlet (TTS) Förster transfers.19–21 In this process, a triplet exciton is nonradiatively transferred from a donor molecule, resulting in a singlet exciton in an acceptor molecule.
Recently, an experimental study demonstrated the achievement of afterglow by leveraging TTS transfers between two organic compounds.22 This host–guest system was composed of NPB [N,N-di(naphtha-1-yl)-N,N-diphenylbenzidine] (1-a) embedded in a rigid PMMA [poly(methyl methacrylate)] matrix, with varying concentrations of the fluorescent dye DCJTB [4-(dicyano-methylene)-2-tert-butyl-6-(1,1,7,7-tetramethyljulolidyl-9-enyl)-4H-pyran] (1-b). NPB is a biluminescent molecule (capable of fluorescence and phosphorescence) typically used as a hole-transport material in OLEDs23–26 and DCJTB is a fluorescent emitter known as an optimal dopant for a range of devices to achieve maximum fluorescence efficiency.27–29 In this experimental setting, NPB molecules were optically excited, producing singlet excitons that were converted into triplets by ISC. It was proposed that these triplet excitons migrate to DCJTB molecules by means of TTS Förster transfers, after which they fluoresce producing an afterglow.
In this work, we perform theoretical characterization of the photophysics of NPB and DCJTB while accounting for vibrational and medium effects. We simulate absorption and emission spectra; estimate the rates of fluorescence, phosphorescence, and (r)ISC for both molecules; and compute the Förster radii for regular singlet-to-singlet transfers and TTS transfers. Finally, we use the characterization results to parameterize kinetic Monte Carlo (KMC) simulations of exciton dynamics in solid films with varying relative amounts of NPB and DCJTB. We demonstrate that rISC rates in NPB are extremely low and unable to explain the observed delayed fluorescence. In contrast, we show that TTS transfers are theoretically allowed and may outperform both phosphorescence and nonradiative decay in NPB, resulting in fluorescence-derived afterglow stemming from DCJTB molecules. Finally, we track the combination of electronic and morphological properties responsible for the occurrence of TTS transfers, while providing comparisons with available experimental data. These results shed light on the working of this less popular though highly relevant triplet conversion mechanism.
II. Methods
A. Electronic structure
The electronic structure properties of both NPB and DCJTB molecules were calculated by means of density functional theory (DFT) and time-dependent DFT (TD-DFT). The ωB97X-D functional was employed with the 6-31G(d,p) basis set. For each molecule, the functional range separation parameter was tuned non-empirically, according to the protocol presented in ref. 30. After functional tuning, optimized geometries and their respective normal mode frequencies were obtained for both compounds in their ground (S0), first singlet (S1), and triplet (T1) excited states. Calculations involving excited states were performed using the Tamm–Dancoff (TDA) approximation,31 given that it mitigates triplet instability issues,32 as well as provides accurate results in spectrum simulations.33With the use of the nuclear ensemble method,34 we simulated absorption, fluorescence, and phosphorescence spectra. Ensembles comprised of 500 conformations were sampled from the Wigner distribution at T = 300 K. The polarizable continuum model (PCM) along with the perturbative state-specific and linear-response solvation corrections were used in all excited state calculations to provide more accurate solvent corrections to the energies of electronic states.35–41 Static dielectric constants used in these simulations are listed in Table S2 (ESI†). A refractive index of 1.489 corresponding to a PMMA matrix42–44 was also used. Simulated spectra were used to estimate Förster radii and exciton transfer rates. Relevant photophysical rates were calculated using the NEMO software45 interfaced with Q-Chem 5.0.46 Spin–orbit couplings were computed with the one electron part of the Breit–Pauli Hamiltonian as implemented in Q-Chem.47–49
The general expression used for computing rates and spectra is given by37
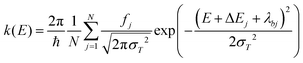 | (1) |
B. Kinetic Monte Carlo simulations
We performed kinetic Monte Carlo simulations in a 50 × 50 × 50 lattice using the Xcharge software.50 Due to the impossibility of exciton transfer between dopants and PMMA, the simulations only account for dopant molecules. Each site is randomly assigned to NPB or DCJTB, following the relative concentration of each molecule as described in Section S1 A of the ESI,† based on experimental results from ref. 22. In a similar fashion, the average intermolecular distance between dopant molecules was also estimated from their experimental concentrations. To reproduce experimental conditions, singlet excitons are generated uniquely on NPB sites. They are then allowed to move by Förster transfers.51 Such a process occurs nonradiatively with the excitation energy being transferred from one molecule to another provided the existence of an overlap between the emission and absorption spectra of the donor and acceptor molecules, respectively. The FRET rate (kF) is calculated as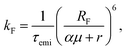 | (2) |
 | (3) |
Since we simulate optically generated excitons, triplet excitons are only created as a product of ISC. ISC rates are taken as the sum of ISC rates from S1 to the first 5 triplet states, but given the usually high internal conversion rates, we consider these transfers to effectively happen between S1 and T1. As such, once a singlet exciton is generated on NPB, it undergoes one of three possible processes: singlet-to-singlet transfer between molecules; ISC to the T1 state; or fluorescence. In the case of ISC, the resulting triplet exciton can exhibit phosphoresce, decay non-radiatively or undergo TTS transfer. Once transferred, the exciton is now in a singlet state, subject to the same possible processes as when it was first generated. For this system, the calculated average intermolecular distances prevent orbital overlap, which means that triplet excitons do not undergo energy transfer via the Dexter mechanism.54,55 The process that takes place is selected by a weighted random selection algorithm that is repeated until recombination occurs. Each simulation is run with 106 excitons.
III. Results
Before we treat the phenomenon of energy transfer, we focus on the optical characterization of each individual molecule. Experimental and simulated absorption, fluorescence, and phosphorescence peaks are shown in Table S3 (ESI†) for both NPB and DCJTB in different media. As shown in the table, there is excellent agreement between simulated and experimental maximum wavelengths for NPB's absorption, with a corresponding energy variation lower than 0.1 eV. Although it does not display the same level of agreement, its phosphorescence spectra is still in reasonable agreement, and the maximum energy difference is under 0.25 eV.In the case of DCJTB, extra care is necessary when comparing experimental and simulation results. This is so because films doped with DCJTB as emitters have been shown to exhibit a concentration-dependent red-shift due to self-polarization,56,57 similarly to what happens in solution when solvent polarity increases. As a result, it is necessary to map the different DCJTB concentrations into corresponding dielectric constants for use in calculations. To do so, we employed a procedure based on experimental data and detailed in Section S1 B (ESI†). Table S4 (ESI†) shows that this approach can reproduce the experimental red-shift of DCJTB in emission energies within reasonable agreement, with a peak to peak difference no higher than 0.15 eV.
In Fig. 1-a, the normalized fluorescence spectrum for pure NPB with dielectric constants corresponding to several DCJTB concentrations (Table S2, ESI†) is shown. Notably, NPB's experimental fluorescence spectrum peaks at around 435 nm.22 This closely aligns with the simulated spectrum, which peaks at 442 nm when no DCJTB is present (ε = 2.45). With increasing DCJTB concentration, the simulated spectrum undergoes a redshift and broadening. Turning to DCJTB, Fig. 1-b shows its fluorescence spectrum under varying concentrations. In spite of reasonable agreement, the experimental redshift is more intense than the predicted one. Our simulation shows a fluorescence peak at 586 nm for the highest concentration versus an experimental peak of 615 nm.22 It can be seen thus, that our spectrum simulations capture most of the redshift in the fluorescence spectrum that results from changes in the medium's polarity. It is worth noting that higher spectral broadening is also associated with increased solvent reorganization energies. However, since spectrum simulations do not include non-radiative decay, which quenches higher wavelength emission more strongly, the resulting simulated fluorescence spectra become broader than their experimental counterparts.
 | ||
| Fig. 1 Simulated fluorescence spectra for both NPB (a) and DCJTB (b) molecules for different DCJTB concentrations (different dielectric constants). | ||
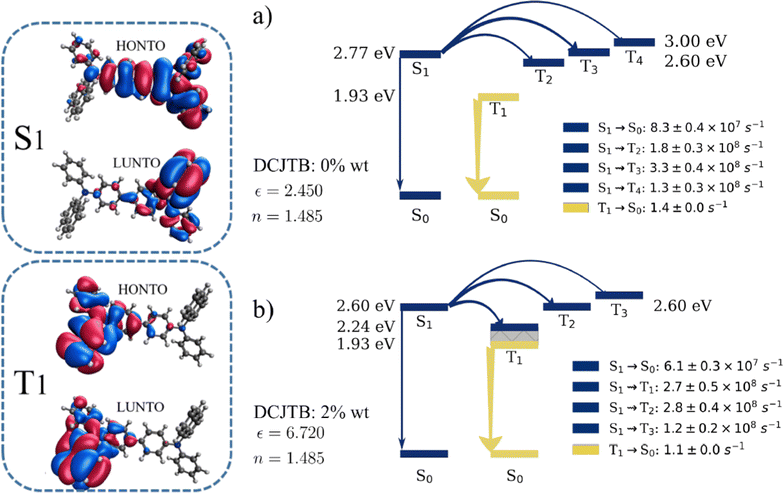
Changes in medium polarity due to the DCJTB concentration have broader implications beyond just altering the spectra. In Fig. 2, we present an energy level diagram including the most relevant electronic transitions and their corresponding rates for NPB at the lowest (Fig. 2-a) and the highest (Fig. 2-b) DCJTB concentrations (ε = 2.45 and ε = 6.72, respectively). Comparisons between these two figures show a 0.16 eV redshift in the S1 energy, which is consistent with a charge-transfer state. Natural transition orbitals (NTOs) for the S1 state are also shown in Fig. 2 and confirm the CT character of the first singlet state of NPB. The redshift of the S1 state also affects the ISC processes. At low polarity, calculations show ISC to the second, third and fourth triplet states as the most relevant, due to lower energy gaps. It is expected that internal conversion from these states down to T1 should follow, though. In the high polarity scenario, ISC to T1 occurs at a similar rate to ISC to T2 and T3 states, due to the availability of triplet states in the ensemble with energies closer to S1. After ISC, relaxation in the triplet potential energy surface – represented by the gray area in the figure – ensues. It is worth mentioning that T1 energies are unaffected by medium polarity. This is due to the localized character of the T1 state as evidenced by the NTOs shown in Fig. 2. Once in the T1 state, calculations show phosphorescence as the main deactivation pathway, beating rISC and nonradiative decay (ISC to the ground state). In Fig. S1 (ESI†), NPB's phosphorescence spectra are shown for three different DCJTB concentrations. Due to the localized character of the T1 state, these spectra are not very sensitive to changes in medium polarity. Fig. S1 (ESI†) also shows the existence of a spectral overlap between NPB phosphorescence and DCJTB absorption spectra, indicating the possibility of TTS transfers. The equivalent level diagram for DCJTB in the same concentrations can be seen in Fig. S2 (ESI†), showing that DCJTB does not present rISC either but rather an efficient nonradiative decay pathway for triplets, indicated by the T1 ![[radiolysis arrow - arrow with voltage kink]](https://www.rsc.org/images/entities/char_e116.gif) S0 transition.
S0 transition.
Fig. 3 shows how the change in the system's polarity resulting from the increasing DCJTB concentration alters different rates. In Fig. 3-a, we present the fluorescence rates for both molecules across various concentrations. Notably, these rates follow similar trends for both molecules, decreasing with concentration while remaining within the same order of magnitude. This behavior is also observed in the phosphorescence rates of NPB and DCJTB, as depicted in Fig. 3-b, despite the almost two orders of magnitude difference between them.
 | ||
| Fig. 3 Calculated fluorescence (a), phosphorescence (b) and intersystem crossing (c) rates for NPB and DCJTB as a function of DCJTB concentration. | ||
Examining the intersystem crossing rates shown in Fig. 3-c, we note that NPB exhibits rates ranging from 6.4 × 108 s−1 to 6.6 × 108 s−1, while DCJTB's go from 3.3 × 107 to 5.7 × 107 s−1, differing by one order of magnitude. The ISC rate is inherently linked to the spin–orbit coupling (SOC) of the molecule. Average coupling values were calculated for each DCJTB concentration and are shown in Fig. S3-a and b (ESI†) for both molecules. They range from 0.18 meV to 0.32 meV in NPB and from 0.05 meV to 0.09 meV in DCJTB. Furthermore, the ISC rate of NPB is also one order of magnitude larger than its fluorescence rate. This means that a singlet exciton is roughly ten times more likely to undergo ISC into a triplet state than to fluoresce. In the case of DCJTB, due to both rates being within the same order of magnitude, there is a 48% chance of ISC taking place, according to calculations.
Fig. 4-a depicts the Förster radii as a function of the DCJTB concentration for the most relevant singlet-to-singlet and TTS exciton transfers. All curves related to singlet–singlet transfer exhibit a trend of slightly decreasing radius with increasing DCJTB presence, while the TTS related radius increases with DCJTB presence. Experimental estimates of the Förster radius for singlet–singlet transfer from NPB to DCJTB place it at 36 ± 10 Å.22 Moreover, our simulations yielded a range of 51.3 Å to 49.4 Å, with an average of 50.1 ± 1.7 Å. Regarding the TTS Förster radius, the same experimental study reported it at 25.0 ± 10 Å, whereas our results placed it between 30.5 Å and 33.0 Å, averaging 32.1 ± 2.5 Å.
 | ||
| Fig. 4 (a) Förster radii for different energy transfers within the NPB-DCJTB system. (b) Förster rates to first neighbor as a function of the DCJTB concentration. | ||
Fig. 4-b displays the Förster rate between first neighbors for each transfer as a function of DCJTB concentration. A decrease in Förster radius translates into less effective transfers only if the effective interaction distance remains constant. However, intermolecular distances are affected by an increased presence of DCJTB, altering the system's morphology as detailed in Section S1 A of the ESI.† Notably, even with a slight reduction in the radius, the rates increase for every transfer. Therefore, the reduction in the average intermolecular distance offsets the decrease in spectral overlap and radiative lifetime. Although all processes are depicted together, it is worth noting that the TTS transfer rate is much lower than that of the remaining processes. However, TTS transfers do not directly compete against singlet–singlet transfers, but rather against phosphorescence and nonradiative decay for triplet excitons. At a 0.2 wt% DCJTB concentration, the TTS transfer rate to a first neighbor is 1.21 s−1, whereas the phosphorescence rate reaches 1.35 s−1. This implies that a triplet exciton in NPB has around 47% chance of undergoing TTS and 53% chance of undergoing phosphorescence. When the concentration of DCJTB reaches its maximum, these probabilities become 85% and 15% respectively, almost doubling TTS efficiency. Additionally, another potential competing event is the nonradiative decay from T1 to S0. However, at the same concentration, this event has an essentially null calculated rate. As DCJTB concentration rises, the nonradiative decay rate increases, but it remains four orders of magnitude lower than the other competing rates. Therefore, it does not significantly alter the probabilities of each event occurring in our calculations. This is attributed to the high energy of the T1 state in NPB. Incidentally, these extremely low rISC and triplet nonradiative decay rates are a decisive factor that makes NPB an excellent candidate for serving as an efficient TTS Förster donor molecule. As a matter of fact, these very same properties make NPB an efficient dual emitter when on its own. As such, if one is looking for molecules with an expected efficient TTS transfer mechanism, dual emitters are the natural candidates.
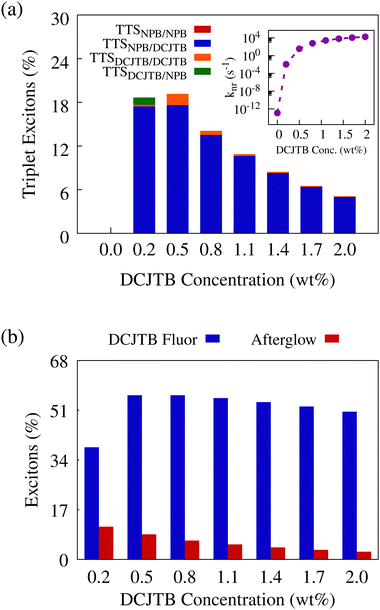
In the absence of rISC, TTS transfers are the sole mechanism for triplet excitons’ conversion into singlet states. Fig. 5-a depicts the TTS transfer efficiency as measured by the ratio between the number of excitons that underwent TTS followed by fluorescence and the number of S1 → T1 ISC events in NPB at each acceptor concentration. Notably, with higher DCJTB concentration, TTS transfers decrease from over 18% in the lowest non-null acceptor concentration to approximately 5% at a 2.0 wt% DCJTB concentration. This is the result of a combination of factors. First, the highest transfer rate is the singlet–singlet exciton transfer from NPB to DCJTB. Naturally, as the number of DCJTB molecules increases, singlet excitons in NPB are more likely to undergo the said transfer than to undergo ISC. Second, with an increase of singlet excitons in DCJTB, the small difference between fluorescence and ISC rates in that material shows approximately 40% of ISC taking place. However, due to there being no efficient rISC or TTS mechanism for triplet excitons in DCJTB, after undergoing ISC, the resulting triplet can only suffer nonradiative decay or exhibit phosphorescence. The inset plot in Fig. 5-a shows the increase of the nonradiative decay rate for triplet excitons in DCJTB as the concentration rises. Notably, the said rate can get up to 4 × 104 s−1, which is two orders of magnitude higher than the phosphorescence rate shown in Fig. 3-c. This means that any triplet exciton resulting from ISC in DCJTB has a 98% probability of decaying nonradiatively. Thus the triplet states in DCJTB would not significantly contribute to any afterglow.
Besides TTS transfers, singlet excitons in DCJTB can be generated by means of regular singlet-to-singlet Förster transfers to DCJTB. However, this happens at a completely different time scale than TTS-derived emission. In Fig. 5-b, we show the relative contribution of singlet excitons that exhibit fluorescence in different timescales in DCJTB. The blue bars account for excitons that fluoresced in DCJTB before 1 μs, which will include prompt fluorescence. The red bars account for excitons that fluoresced after the 1 μs mark. These emissions were labeled as afterglow. The average fluorescence time for each group is shown in Table S5 (ESI†), in which we can observe that excitons that fall into the afterglow category are fluorescing in the scale of fractions of a second, much larger than the other group, which fluoresce in the nanoseconds time scale. As DCJTB concentration rises, afterglow occurrence is reduced, which is observed experimentally with samples with the lowest non-null DCJTB concentration displaying the most intense afterglow. This result, coupled with the relevant nonradiative decay process of triplet excitons in this material, reveals that afterglow in this system originates not from phosphorescence, as commonly observed, but rather from highly delayed fluorescence resulting from TTS transfers from NPB to DCJTB.
IV. Conclusions
To summarize, we have investigated the photophysics of NPB/DCJTB films. All the relevant photophysical rates were estimated while accounting for vibrational and medium polarity effects. Calculations demonstrated that NPB displays very low rates of rISC and nonradiative triplet deactivation while showing significant ISC rates, which explains its effectiveness as a dual emitter. In addition, the energy alignment between NPB and DCJTB makes TTS highly competitive against phosphorescence in NPB such that when coupled with short intermolecular distances, it makes TTS transfers possible.KMC simulations in an NPB/DCJTB host–guest system for different concentrations of DCJTB allowed us to identify TTS exciton transfers as the phenomenon responsible for providing a pathway to persistent luminescence that results from delayed fluorescence instead of phosphorescence. We were also able to quantify the efficiency of the process and show that TTS-derived afterglow happens in the timescale of tenths of seconds.
Furthermore, we also determined the importance of morphological aspects when dealing with a delicate interplay of several conversion and transfer phenomena. Specifically, we show that a triplet recycling mechanism based on intermolecular interactions can play a relevant role as evidenced by the observations that as the acceptor concentration increased, the TTS efficiency was significantly altered. Finally, for higher DCJTB concentrations, the occurrence of nonradiative decay of triplet excitons is shown to be a limiting factor of the efficiency of the said afterglow. Overall, these findings open up prospects for designing new persistent luminescent materials that make use of TTS transfers as a triplet harvesting mechanism for diverse technological applications.
Data availability
The NEMO code for nuclear ensemble calulations for the computation of photophysical rates and spectra can be found at https://github.com/LeonardoESousa/NEMO. The version of the code employed for this study is version [1.2.0]. The code for visualization and analysis of NEMO ensembles can be found at https://github.com/LeonardoESousa/nemoview. The version of the code employed for this study is version [0.3.0]. The code for kinetic Monte Carlo simulations can be found at https://github.com/LeonardoESousa/Xcharge. The version of the code employed for this study is version [0.0.1]. The ensemble files supporting this article have been included as part of the ESI† and can be visualized using the NEMOview code.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors gratefully acknowledge the financial support from the Brazilian Research Councils DC (grant number 304637/2018-1) CAPES and FAPDF. P. H. O. N. gratefully acknowledge the financial support from FAPDF grant 00193-00001853/2023-15 and CNPq grant 306080/2022-2. P. d. S and L. E. d. S. gratefully acknowledge the financial support from grant no. 2032-00144B from the Independent Research Fund Denmark and from the Novo Nordisk Foundation Data Science Research Infrastructure 2022 Grant: A high-performance computing infrastructure for data-driven research on sustainable energy materials, Grant no. NNF22OC0078009.References
- P. E. Keivanidis, G. Itskos, Z. Kan, E. Aluicio-Sarduy, H. Goudarzi, V. Kamm, F. Laquai, W. Zhang, C. Brabec and G. Floudas, et al. , ACS Appl. Mater. Interfaces, 2019, 12, 2695 CrossRef PubMed.
- Y. Lu, X. Xiao, Y. Liu, J. Wang, S. Qi, C. Huan, H. Liu, Y. Zhu and G. Xu, J. Alloys Compd., 2020, 812, 152144 CrossRef.
- B. Mahltig, C. Heil, S. Kaub and J. N. Kapadiya, Commun. Dev. Assem. Text. Prod., 2024, 5, 1 Search PubMed.
- H. Sun, S. Liu, W. Lin, K. Y. Zhang, W. Lv, X. Huang, F. Huo, H. Yang, G. Jenkins and Q. Zhao, et al. , Nat. Commun., 2014, 5, 3601 CrossRef PubMed.
- Q. Miao, C. Xie, X. Zhen, Y. Lyu, H. Duan, X. Liu, J. V. Jokerst and K. Pu, Nat. Biotechnol., 2017, 35, 1102 CrossRef CAS PubMed.
- Z. Chen, K. Y. Zhang, X. Tong, Y. Liu, C. Hu, S. Liu, Q. Yu, Q. Zhao and W. Huang, Adv. Funct. Mater., 2016, 26, 4386 CrossRef CAS.
- X. Zhou, H. Liang, P. Jiang, K. Y. Zhang, S. Liu, T. Yang, Q. Zhao, L. Yang, W. Lv and Q. Yu, et al. , Adv. Sci., 2016, 3, 1500155 CrossRef PubMed.
- X. Zhen, Y. Tao, Z. An, P. Chen, C. Xu, R. Chen, W. Huang and K. Pu, Adv. Mater., 2017, 29, 1606665 CrossRef PubMed.
- S. Xu, R. Chen, C. Zheng and W. Huang, Adv. Mater., 2016, 28, 9920 CrossRef CAS PubMed.
- Z. An, C. Zheng, Y. Tao, R. Chen, H. Shi, T. Chen, Z. Wang, H. Li, R. Deng and X. Liu, et al. , Nat. Mater., 2015, 14, 685 CrossRef CAS PubMed.
- W. Zhao, Z. He, J. W. Lam, Q. Peng, H. Ma, Z. Shuai, G. Bai, J. Hao and B. Z. Tang, Chem, 2016, 1, 592 CAS.
- S. Mukherjee and P. Thilagar, Chem. Commun., 2015, 51, 10988 RSC.
- Y. Wada, H. Nakagawa, S. Matsumoto, Y. Wakisaka and H. Kaji, Nat. Photonics, 2020, 14, 643 CrossRef CAS.
- J. Gibson, A. P. Monkman and T. J. Penfold, ChemPhysChem, 2016, 17, 2956 CrossRef CAS PubMed.
- H. Noda, H. Nakanotani and C. Adachi, Sci. Adv., 2018, 4, eaao6910 CrossRef PubMed.
- K. Tvingstedt, K. Vandewal, A. Gadisa, F. Zhang, J. Manca and O. Inganas, J. Am. Chem. Soc., 2009, 131, 11819 CrossRef CAS PubMed.
- V. Coropceanu, X.-K. Chen, T. Wang, Z. Zheng and J.-L. Brédas, Nat. Rev. Mater., 2019, 4, 689 CrossRef.
- Z. R. Grabowski, K. Rotkiewicz and W. Rettig, Chem. Rev., 2003, 103, 3899 CrossRef PubMed.
- L. E. de Sousa, L. dos Santos Born, P. H. de Oliveira Neto and P. de Silva, J. Mater. Chem. C, 2022, 10, 4914 RSC.
- D. Volyniuk, V. Cherpak, P. Stakhira, B. Minaev, G. Baryshnikov, M. Chapran, A. Tomkeviciene, J. Keruckas and J. V. Grazulevicius, J. Phys. Chem. C, 2013, 117, 22538 CrossRef CAS.
- K. Bartkowski, P. Z. Crocomo, M. A. Kochman, D. Kumar, A. Kubas, P. Data and M. Lindner, Chem. Sci., 2022, 13, 10119 RSC.
- A. Kirch, M. Gmelch and S. Reineke, J. Phys. Chem. Lett., 2019, 10, 310 CrossRef CAS PubMed.
- M. D. Halls, C. P. Tripp and H. B. Schlegel, Phys. Chem. Chem. Phys., 2001, 3, 2131 RSC.
- S. A. Van Slyke, C. Chen and C. W. Tang, Appl. Phys. Lett., 1996, 69, 2160 CrossRef CAS.
- R. Zhang, C. Lee and S. Lee, Appl. Phys. Lett., 1999, 75, 2418 CrossRef CAS.
- R. Zhang, C. Lee and S. Lee, J. Chem. Phys., 2000, 112, 8614 CrossRef CAS.
- J.-S. Lu, H.-F. Chen, J.-C. Kuo, R. Sun, C.-Y. Cheng, Y.-S. Yeh, H.-C. Su and K.-T. Wong, J. Mater. Chem. C, 2015, 3, 2802 RSC.
- W. Zhou, M.-C. Wang and X. Zhao, Sol. Energy, 2015, 115, 569 CrossRef CAS.
- C. Chen, C. W. Tang, J. Shi and K. P. Klubek, Thin Solid Films, 2000, 363, 327 CrossRef CAS.
- T. Stein, L. Kronik and R. Baer, J. Am. Chem. Soc., 2009, 131, 2818 CrossRef CAS PubMed.
- S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291 CrossRef CAS.
- M. J. Peach, M. J. Williamson and D. J. Tozer, J. Chem. Theory Comput., 2011, 7, 3578 CrossRef CAS PubMed.
- A. Chantzis, A. D. Laurent, C. Adamo and D. Jacquemin, J. Chem. Theory Comput., 2013, 9, 4517 CrossRef CAS PubMed.
- L. E. de Sousa and P. de Silva, J. Chem. Theory Comput., 2021, 17, 5816 CrossRef CAS PubMed.
- J.-M. Mewes, Z.-Q. You, M. Wormit, T. Kriesche, J. M. Herbert and A. Dreuw, J. Phys. Chem. A, 2015, 119, 5446 CrossRef CAS PubMed.
- Z.-Q. You, J.-M. Mewes, A. Dreuw and J. M. Herbert, J. Chem. Phys., 2015, 143, 204104 CrossRef PubMed.
- L. E. de Sousa and P. de Silva, J. Phys. Chem. A, 2023, 127, 8200 CrossRef CAS PubMed.
- M. Caricato, B. Mennucci, J. Tomasi, F. Ingrosso, R. Cammi, S. Corni and G. Scalmani, J. Chem. Phys., 2006, 124, 124520 CrossRef PubMed.
- C. A. Guido, D. Jacquemin, C. Adamo and B. Mennucci, J. Chem. Theory Comput., 2015, 11, 5782 CrossRef CAS PubMed.
- G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 084102 CrossRef PubMed.
- M. Caricato, J. Chem. Theory Comput., 2012, 8, 4494 CrossRef CAS PubMed.
- P. Thomas, R. E. Ravindran and K. Varma, IEEE, 2012, pp. 1–4 Search PubMed.
- H. Zhang, Y. Jin and Y. Qiu, IOP Conference Series: Materials Science and Engineering, IOP Publishing, 2015, vol. 87, p. 012032.
- L.-H. Lee and W.-C. Chen, Chem. Mater., 2001, 13, 1137 CrossRef CAS.
- https://github.com/LeonardoESousa/NEMO .
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng and X. Feng, et al. , Mol. Phys., 2015, 113, 184 CrossRef CAS.
- L. Veseth, Theor. Chim. Acta, 1970, 18, 368 CrossRef CAS.
- S. Kotaru, P. Pokhilko and A. I. Krylov, J. Chem. Phys., 2022, 157, 224110 CrossRef CAS PubMed.
- P. Pokhilko, E. Epifanovsky and A. I. Krylov, J. Chem. Phys., 2019, 151, 034106 CrossRef PubMed.
- https://github.com/LeonardoESousa/xcharge .
- T. Förster, Ann. Phys., 1948, 437, 55 CrossRef.
- V. May and O. Kühn, Charge and energy transfer dynamics in molecular systems, John Wiley & Sons, 2023 Search PubMed.
- S. R. Yost, E. Hontz, S. Yeganeh and T. Van Voorhis, J. Phys. Chem. C, 2012, 116, 17369 CrossRef CAS.
- G. D. Scholes, Annu. Rev. Phys. Chem., 2003, 54, 57 CrossRef CAS PubMed.
- D. L. Dexter, J. Chem. Phys., 1953, 21, 836 CrossRef CAS.
- D. Xu, Z. Deng, Y. Xu, J. Xiao and C. Liang, Displays, 2005, 26, 185 CrossRef CAS.
- V. Bulović, A. Shoustikov, M. Baldo, E. Bose, V. Kozlov, M. Thompson and S. Forrest, Chem. Phys. Lett., 1998, 287, 455 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc03774j |
| This journal is © The Royal Society of Chemistry 2025 |