Deciphering carbon–sulfur rotational distribution in a crystalline host for enhanced red persistent organic phosphorescence

Abstract

Persistent room-temperature phosphorescence (pRTP) from organic host–guest solids has been used for autofluorescence-free high-resolution imaging. However, from the lowest triplet excited state, the radiative transition rate (k_p) decreases and the non-radiative transition rate (k_nr) increases with increasing wavelength. Therefore, the pRTP yield (Φ_p) at long wavelengths is still low. Here we report an enhanced red pRTP from dibenzo[g,p]chrysene substituted with a phenylthio group (PhSDBC) as a guest in a crystalline benzophenone host. Host–guest crystals composed of deuterated PhSDBC and benzophenone showed red pRTP with Φ_p = 28.8% and a lifetime of 1.47 s. Investigation of the correlation between experimental and calculated values of k_p and k_nr revealed that the distribution of C–S rotational conformations of PhSDBC was constrained to a narrow range in the crystalline host. In the constrained distribution, the phenylthio substituents enhanced the cooperation of spin–orbit couplings and the transition dipole moment associated with the higher singlet excited state, which resulted in the selective increase of k_p and in turn the enhanced Φ_p.

---

Introduction

Persistent room-temperature phosphorescence (pRTP), which can be observed from organic matter within 100 ms after the excitation light irradiation is stopped, is beginning to be used as a technique to obtain two-dimensional (2D) information without observing autofluorescence with a 2D photodetector.^1–3 Many works have been reported, focusing on anti-counterfeiting^4–7 and bioimaging.^8–11 Because pRTP can produce a higher instantaneous brightness than the long persistent luminescence caused by recombination after excited charge separation, attempts are being made to use pRTP for high-resolution imaging.^12,13

To fully use pRTP and extract information about emission color and lifetime, preparation of materials with highly efficient pRTP in the blue-green-red and near-infrared regions is desirable. For blue and green pRTP, host–guest molecular crystals with a pRTP yield (Φ_p) of nearly 100% have been reported.^14,15 This molecular structure displaying efficient blue and green pRTP is a motif already known in other fields, and there has been much discussion of the crystal structure of guest chromophores in crystalline hosts. Φ_p is expressed by the phosphorescence rate constant (k_p), the non-radiative deactivation rate (k_nr) from the lowest triplet excited state (T₁) of guest chromophores, and the triplet quenching rate caused by intermolecular electron transfer and exchange between the guest and host (k_q). Because k_nr increases as the square of the wavelength and k_p is inversely proportional to the cube of the wavelength, shorter wavelengths generally tend to produce higher Φ_p¹⁶ when k_q is well suppressed. Therefore, for short-wavelength colors, the use of existing chemical structures may be sufficient to obtain large Φ_p. However, in the long-wavelength region, k_nr increases while k_p does not. Therefore, it is predicted that new π structures may be necessary to control k_p and k_nr using the molecular framework in the long-wavelength region. pRTP at long wavelengths such as in the red and near-infrared regions is important for bioimaging applications because such long-wavelength light penetrates living organisms. Although materials with a pRTP peak wavelength (λ_p) exceeding 600 nm and an average pRTP lifetime (τ_p) longer than 100 ms have been reported, their Φ_p is still below 21%.^11,17–24

Molecular structures that show high fluorescence quantum yields in the red and near-infrared regions have been developed.^25,26 Therefore, a major scientific question is why is it still difficult to increase k_p above k_nr in the long-wavelength region in organic phosphorescence? In an attempt to address this question, we have pioneered computational techniques to estimate k_p and k_nr for a wide range of molecules. It has been confirmed that to statistically discuss k_p and k_nr of organic guest chromophores, it is necessary to consider the structural displacement caused by molecular vibration in the T₁ state of the chromophores.^24,27–30 An approach correlating experimental and calculation data considering the thermal distribution of molecular geometry may clarify molecular designs that can realize efficient pRTP at long wavelengths.

Here we report a phenylthio (PhS)-substituted chromophore that exhibits enhanced red pRTP and demonstrate that the structural distribution of the PhS bridge site is confined in a solid host. A dibenzo[g,p]chrysene (DBC) substituted with a PhS group is synthesized as a guest chromophore. In a benzophenone crystalline host, this chromophore shows higher Φ_p in the red region than DBC substituted with a benzoyl group, even though benzoyl substituents are often reported to enhance Φ_p in the blue and blue-green regions.¹⁴ A deuterated form of the PhS-substituted DBC shows red pRTP with Φ_p = 28.8%, τ_p = 1.47 s, and λ_p = 611 nm. The C–S rotation of the guest exhibiting the red pRTP is calculated to be free in a vacuum, but the analysis of the correlation between the experimental and calculated values of k_p as well as k_nr reveals that the distribution of such free C–S rotation at room temperature (RT) is greatly suppressed in the benzophenone host. With its limited distribution of C–S rotations, PhS substitution allows cooperative enhancement of the spin–orbit coupling (SOC) between the nth-order singlet excited state (S_n) and T₁ (n ≥ 1) and the transition dipole moment between S_n and the ground state (S₀). This cooperation leads to selective enhancement of k_p relative to k_nr, which in turn results in the increase of Φ_p.

Results and discussion

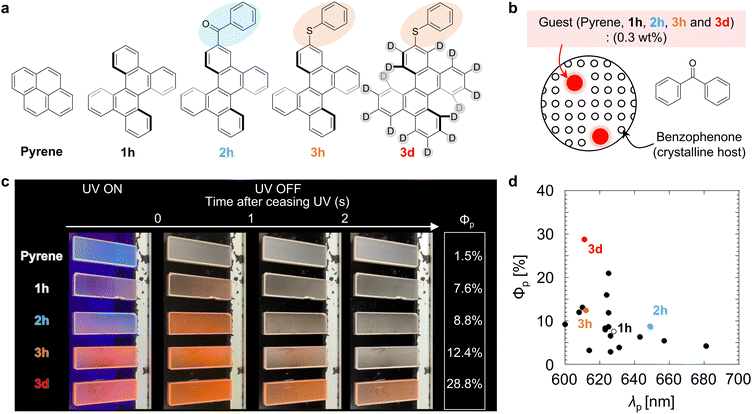
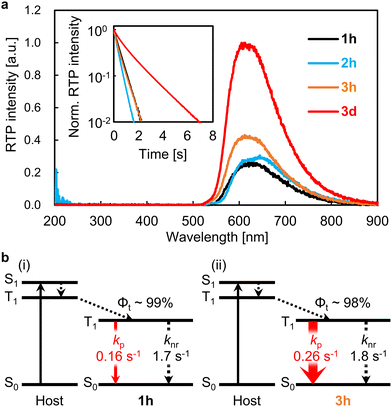
To demonstrate the enhanced red pRTP performance, the five molecules shown in Fig. 1a were examined as guest compounds. Pyrene and DBC (1h) were obtained commercially and purified by sublimation before use. Chromophore 2h was synthesized from 1h by Friedel–Crafts acylation. Chromophore 3h was synthesized from 1hvia monobromination followed by reaction with diphenyl disulfide using a palladium catalyst. The structures of 2h and 3h were confirmed by nuclear magnetic resonance and high-resolution mass spectral analyses, and the purity of 2h and 3h was confirmed by elemental analysis (Fig. S1 and S2, ESI†). Chromophore 3d was synthesized by deuteration of 1h followed by monobromination and subsequent reaction with diphenyl disulfide using a palladium catalyst (Fig. S3 and S4, ESI†). Pyrene, 1h, 2h, 3h, and 3d were each doped in crystalline benzophenone at a concentration of 0.3 wt% to prepare films denoted as pyrene, 1h, 2h, 3h, and 3d, respectively (Fig. 1b). For these films, Φ_p was measured by comparing the luminescence quantum yield upon irradiation with excitation light with the emission spectrum 20–40 ms after the excitation light irradiation was stopped (Fig. S5–S7, ESI†). Φ_p of the pyrene, 1h, 2h, 3h, and 3d films were 1.5%, 7.6%, 8.8%, 12.4%, and 28.8%, respectively, after excitation at 310 nm (Fig. 1c and Movie S1, ESI†). Φ_p of film 3d (28.8%) is the highest achieved to date among materials with τ_p ≥ 100 ms and λ_p ≥ 600 nm (Fig. 1d and Table S1, ESI†). For pyrene doped in crystalline benzophenone, Φ_p was reported to be close to 9.2%.¹¹ However, we investigated many films with different amounts of pyrene doped in benzophenone and their crystallization conditions, and found that similar phosphorescence lifetimes were observed but with much lower Φ_p (1.5%). In fact, bright red pRTP under ultraviolet (UV) light and immediately after UV light exposure was not observed in the pyrene film; a much brighter red pRTP was observed in the 1h, 2h, 3h, and 3d films (Fig. 1c and Movie S1, ESI†). It should also be noted that the absorption spectra of these thin films were comparable from 300 to 400 nm (Fig. S8a, ESI†). Observation of red pRTP soon after ceasing the UV excitation under white indoor light was reasonable considering the excitation power of the UV light and intensity of the indoor light (Fig. S8b–e, ESI†). Previous reports have shown that direct substitution of polyaromatic hydrocarbons with a benzoyl group can markedly improve Φ_p of blue to green emission.^14,31,32 However, benzoyl substitution of DBC (2h) did not enhance Φ_p compared with that of unsubstituted DBC (1h). Comparison of Φ_p of films 1h–3h confirmed that direct substitution of DBC with a PhS group enhanced red pRTP to a greater extent than benzoyl substitution.

Fig. 1 (a) Chemical structures of guest chromophores. (b) Schematic diagram of the host–guest crystal. (c) Luminescence from host–guest crystalline thin films during and after UV light irradiation under indoor lighting (0.12 mW cm⁻²). When the films were photographed separately, the emission intensity of each film appeared to vary depending on the automatic change of camera settings. To mitigate this problem, five films were photographed simultaneously using one UV light source (0.22 mW cm⁻²). (d) The performance of the films in terms of Φ_pvs. λ_p relative to previously reported materials with τ_p ≥ 100 ms.

Next, quantitative optical properties were measured to explore the origin of the enhancement of Φ_p from 1h to 3h. λ_p of the 1h, 2h, 3h, and 3d films were 628, 649, 612, and 611 nm, respectively (Fig. 2a). τ_p of the 1h, 2h, 3h, and 3d films were 0.49, 0.34, 0.48, and 1.47 s, respectively (Fig. 2a, inset). Afterglow based on thermally activated delayed fluorescence has a large initial decay by 100 ms. In contrast, pRTP with τ_p > 100 ms does not have such a large decrease in the initial stage of the afterglow decay (Fig. S9, ESI†). Therefore, bright 2D afterglow emissions can be observed using 2D photodetectors, which makes it difficult to increase the frame rate.²⁴Φ_p is commonly denoted as,

Φ_p = Φ_tk_pτ_p, (1)

where Φ_t is the efficiency of T₁ formation of the guest under photo excitation. Transient absorption measurements confirmed that the yield of the intersystem crossing from the lowest singlet excited state (S₁) to T₁ (Φ_isc) of chromophores 1h and 3h was close to 100% (Fig. S10 and Tables S2, S3, ESI†).¹⁹ In fact, when 1h and 3h were doped into an amorphous β-estradiol host with no absorption above 340 nm and the guest was directly excited with 360 nm light, Φ_p and k_p of the film with 3h was higher than those of the film with 1h (Fig. S11, ESI†). Therefore, the increase in Φ_p of 3h relative to 1h in benzophenone is thought to be due to an increase in k_p. When a benzophenone crystal host is used and the concentration of the guest is low, benzophenone mainly absorbs light. After the photo-absorption by benzophenone, T₁ of benzophenone forms with almost 100% efficiency, and then T₁ of the guest is formed by triplet–triplet energy transfer from the T₁ of benzophenone to the guest. It is believed that the yield of from S₁ of benzophenone to T₁ of the doped guest via T₁ of benzophenone (Φ_t) is nearly 100% because of Φ_isc = 100% of benzophenone and efficient triplet–triplet energy transfer from benzophenone to the guest molecules.³³ Transient absorption spectroscopy confirmed the formation of equivalent amounts of T₁ in the 1h and 3h films when the absorbance at the excitation wavelength and excitation intensity were the same for both films (Fig. S12–S14, ESI†). The value of k_p was determined by substituting Φ_t, Φ_p, and τ_p into eqn (1). Furthermore, the values of k_nr + k_q for films 1h and 3h were determined to be 2.0 and 2.1 s⁻¹, respectively, by substituting k_p into the following equation,

τ_p = 1/(k_p + k_nr + k_q), (2)

Information on k_nr + k_q and phosphorescence characteristics for 2h and 3d are summarized in the ESI† (Table S4, ESI†). Furthermore, the k_nr values at RT of the 1h and 3h films were determined to be 1.7 and 1.8 s⁻¹, respectively, from Arrhenius plots of k_nr + k_q (Fig. S15 and S16, ESI†).^27–30 Because k_nr values of 1h and 3h are equivalent in benzophenone crystals, the selective increase of k_p of 3h leads to the higher Φ_p of film 3h relative to that of film 1h. Furthermore, 3d confirmed that the decrease of k_nr caused by deuteration increased Φ_p from 12.4% to 28.8%.^2,12,34

Fig. 2 (a) pRTP spectra and decay characteristics (inset) of the 1h, 2h, 3h, and 3d films soon after ceasing excitation at 310 nm. The spectral height of the RTP spectra was set so that the area of the phosphorescence spectrum was proportional to Φ_p. (b) Jablonsky diagrams showing pRTP of (i) film 1h and (ii) film 3h.

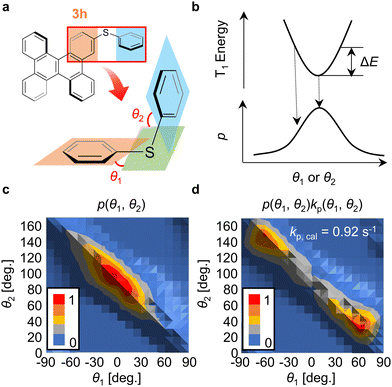
To identify the factor that causes the selective increase of k_p of 3h compared with that of 1h, the conformational distribution of 3h was considered. It is possible to estimate k_p and k_nr for many chromophores using elements from the second row of the periodic table onwards by performing quantum chemical calculations considering vibrational displacements at RT.^24,27–30 In 3h, the two dihedral angles (θ₁ and θ₂) defined in Fig. 3a vary easily at low thermal energy because of the weak C–S bonds (Fig. 3a). In this paper, θ₁ and θ₂ at RT were calculated using density functional theory (DFT) and time-dependent DFT techniques (Section S11, ESI†). Initially, the optimized structure of 3h at T₁ in a vacuum was calculated. For that structure, the potential curves in the T₁ state were calculated when θ₁ and θ₂ were changed. Using the activation energy (ΔE) of the potential curve of T₁ (Fig. 3b), the possibility of the geometry of 3h with θ₁ and θ₂ [p(θ₁, θ₂)] was calculated using the following equation (Fig. 3c),

p(θ₁, θ₂) = exp[−ΔE(θ₁, θ₂)/kT]/∑exp[−ΔE(θ₁, θ₂)/kT] (3)

where k is the Boltzmann constant and T is the temperature. It was estimated that in a vacuum, 3h allows wide distributions of θ₁ and θ₂. A histogram of k_p(θ₁, θ₂) for the distributions of θ₁ and θ₂ was calculated (Fig. S18, ESI†). The histogram of the product of k_p(θ₁, θ₂) and p(θ₁, θ₂) is presented in Fig. 3d. It was confirmed that if k_p exists in the regions of (θ₁, θ₂) ≃ (60°, 40°) and (θ₁, θ₂) ≃ (−60°, 140°), they will greatly contribute to the enhancement of k_p. By integrating this histogram, the average value of calculated k_p (k_p,cal) was estimated to be 0.92 s⁻¹. For DBC (1h), which exhibits no displacement associated with C–S rotation, k_p,cal = 0.16 s⁻¹ was calculated for the optimized structure of T₁. Thus, the quantum chemical calculations in the vacuum model for 1h and 3h revealed that the substitution of DBC with PhS increased k_p,cal by 5.8 times. However, the optical measurements of the actual films 1h and 3h showed that optically determined k_p (k_p,exp) of 3h was only 1.6 times higher that of 1h (Fig. 2b). This difference suggests that the distributions of θ₁ and θ₂ of 3h in the solid film are not as wide as those in a vacuum.

Fig. 3 (a) Depiction of the definition of θ₁ and θ₂ in 3h. (b) Relationship between the energy change (ΔE) and state probability (p) associated with the change of θ₁ and θ₂ from the optimized structure of T₁. (c) Distribution of p calculated in a vacuum for 3h with respect to θ₁ and θ₂. (d) Distribution of the product of k_p and p calculated in a vacuum for 3h with respect to θ₁ and θ₂.

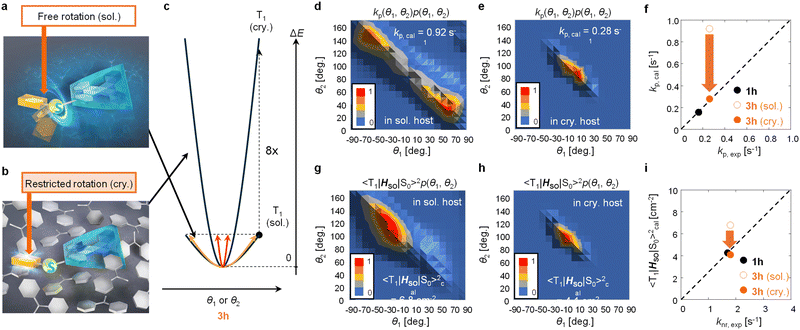
To confirm the confinement of the distributions of θ₁ and θ₂ of 3h in the crystalline film, we theoretically narrowed the distributions of θ₁ and θ₂ to confirm whether the correlation between experimental and calculation results could be improved in terms of both k_p and k_nr. A model was proposed in which when C–S rotation occurs in benzophenone crystals, the steric hindrance between the host and guest increases ΔE of the potential curve of T₁ for the same θ₁ and θ₂ displacement of 3h (Fig. 4a and 4b). For example, when ΔE increases by a factor of eight (Fig. 4c), p(θ₁, θ₂) in a vacuum converges to a narrow range based on eqn (3) (Fig. S19, ESI†). When p(θ₁, θ₂) narrows, the histogram of k_p(θ₁, θ₂)p(θ₁, θ₂) changes from that in Fig. 4d to that in Fig. 4e. From the integration of the histogram in Fig. 4e, k_p,cal was estimated to be 0.28 s⁻¹. Therefore, when considering the distributions of θ₁ and θ₂ where the host increases the guest ΔE by a factor of eight, k_p,exp and k_p,cal correlate well (Fig. 4f). The correlation of experimental and calculated values of k_nr provides further evidence that this estimate is reasonable.

Fig. 4 Estimated molecular motions of 3h in (a) solution and (b) a solid host. (c) Estimated potential surface of 3h depending on the change of θ₁ and θ₂ in solution and solid media. Histograms of normalized k_p(θ₁, θ₂)p(θ₁, θ₂) in (d) solution and (e) a crystalline host. (f) The relationship between k_p,cal and k_p,exp for 1h and 3h. Histograms of normalized 〈T₁|H_SO|S₀〉(θ₁, θ₂)²p(θ₁, θ₂) in (g) solution and (h) a crystalline host. (i) The relationship between 〈T₁|H_SO|S₀〉_cal² and k_nr,exp for 1h and 3h.

In a model in which the distributions of θ₁ and θ₂ of the guest were confined by steric hindrance with the host, the experimental and calculated values of k_nr showed a strong correlation. k_nr is proportional to the square of the SOC between T₁ and S₀ (〈T₁|H_SO|S₀〉) and also depends on the phosphorescence energy. Therefore, the difference of k_nr among guest chromophores could be approximated by 〈T₁|H_SO|S₀〉² when the phosphorescence energy does not change much between guests.^16,29 When ΔE increases by a factor of eight, the histogram of 〈T₁|H_SO|S₀〉 (θ₁, θ₂)²p(θ₁, θ₂) changes from that in Fig. 4g to that in Fig. 4h. The calculated average values of 〈T₁|H_SO|S₀〉² (〈T₁|H_SO|S₀〉_cal²) were determined to be 6.8 and 4.1 cm⁻² from the integration of Fig. 4g and h, respectively. For 1h, it was calculated that 〈T₁|H_SO|S₀〉_cal² = 4.3 cm⁻² using the optimized T₁ structure. For the distributions of θ₁ and θ₂ in a vacuum at 3h, the correlation between optically determined k_nr (k_nr,exp) and 〈T₁|H_SO|S₀〉_cal² was poor (Fig. 4i). Conversely, when considering the distributions of θ₁ and θ₂ where the host increases the ΔE of the guest by a factor of eight, a much stronger correlation between k_nr,exp and 〈T₁|H_SO|S₀〉_cal² was observed (Fig. 4i).

When considering k_p and k_nr, it is essential to include the conformational displacement of vibrations.^24,27–30 Generally, compounds up to the second row of the periodic table form strong bonds, so the changes of displacement at RT are limited.^19,24 Therefore, k_p may not change that much between soft and rigid environments. Conversely, in compounds containing elements from the third row of the periodic table or later, the bonds between the elements and carbon are generally weak, and many of the compounds display free rotation. This study demonstrated from both experimental and computational aspects of k_p and k_nr that such large free conformational changes are strongly suppressed in solid hosts, resulting in a narrow structural distribution. When the enhancement of ΔE induced by the crystalline host is much less than a factor of eight, k_p,cal is still overestimated compared with k_p,exp. The best correlation between the experimental and calculated k_p and k_nr values could be observed when considering the distribution of θ₁ and θ₂ where the host increases ΔE of the guest by a factor of eight. Not only was there a strong correlation between the experimental and calculated k_p and k_nr values of the confined 3h geometry and 1h, but also the equivalent phosphorescence energies of 1h and 3h observed experimentally were corroborated by the calculations (Fig. S17, ESI†).

The strong correlation between the experimental and calculation results obtained by considering the state distribution makes it possible to clarify the factor causing the increase of k_p of 3h relative to that of 1h. k_p is logically related to the product of the SOC between S_n and T₁ (〈S_n|H_SO|T₁〉) and the transition dipole moment of S_n and S₀ (μ_Sn–S0).^16,27,35,36 More specifically, because k_p is approximately proportional to 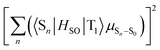, k_p increases as the product of 〈S_n|H_SO|T₁〉 and μ_Sn–S0 increases for each n. In the conformation where θ₁ approaches 0° and θ₂ approaches 90° in Fig. 4e and h, which is close to the T₁ optimized geometry of 3h. The introduction of PhS-substituents at the confined angles increases the cooperativity of 〈S_n|H_SO|T₁〉 and μ_Sn–S0 for a wide range of n (Fig. 5). On the other hand, the introduction of phenylthio-substituents in the geometry does not increase k_nr because 〈T₁|H_SO|S₀〉² of 3h (3.6 cm⁻²) is comparable to that of 1h (4.3 cm⁻²), where 〈T₁|H_SO|S₀〉² is logically proportional to k_nr. Therefore, the cooperativity of 〈S_n|H_SO|T₁〉 and μ_Sn–S0 for a wide range of n in 3h compared with the case for 1h allows the selective enhancement of k_p, which in turn leads to the increase of Φ_p of the 3h film compared with that of the 1h film. The comparable 〈T₁|H_SO|S₀〉 values of 1h and 3h contain important information on the heavy atom effect of S. When S is directly bonded to the phosphorescent chromophore, the heavy atom effect might be in play. However, similar 〈T₁|H_SO|S₀〉 values were calculated at 1h and 3h in benzophenone crystals, and the k_nr values determined by optical measurements were also comparable between them. Therefore, it can be seen that the increase in the molecular weight of S does not have the effect of significantly increasing at least 〈T₁|H_SO|S₀〉.

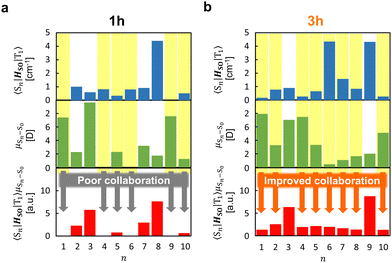Fig. 5 Relationship between 〈S_n|H_SO|T₁〉, μ_Sn–S0, and 〈S_n|H_SO|T₁〉μ_Sn–S0 from n = 1 to n = 10 in 1h (a) and 3h (b).

Green pRTP properties have often been achieved using motifs in which two benzene groups are linked by a six-membered ring containing at least one group-16 element, such as phenothiazine, 9H-thioxanthene, and thianthrene.^37–42 In terms of the group-16 element, it has been reported that the effect of sulfur on green pRTP is considerably smaller than that of selenium.^39,40 In this paper, we showed that direct substitution of sulfur into the red pRTP backbone, even without using heavy atoms such as selenium, enhances Φ_p considerably in the long-wavelength range and maintains a large τ_p compared with other substitutions. By clarifying the confined conformational distribution of the guest dye in the crystal host, we also elucidated that the Φ_p enhancement is caused by the cooperative strengthening of SOCs and the transition dipole moment associated with S_n.

Conclusions

Direct substitution of DBC with PhS produced 3h, which showed enhanced red pRTP over that of DBCs with other substituents in a crystalline benzophenone host. Deuterated DBC with a PhS substituent in a crystalline benzophenone host achieved values of τ_p = 1.47 s and Φ_p = 28.8% with λ_p = 611 nm. Correlation of experimental and calculated values of k_p and k_nr showed that the free rotation of C–S of 3h considered to occur in a vacuum is largely suppressed in the crystalline benzophenone host. For the geometry with a limited distribution of C–S rotations, the PhS group induces cooperative enhancement of the S_n–T₁ SOC and the S_n–S₀ transition dipole moment for a variety of states with n ≥ 1, which leads to the selective enhancement of k_p over k_nr. The selective enhancement of k_p results in the increase of Φ_p. In host–guest solid materials, quantum chemical calculations taking vibrations into account are necessary to elucidate the relationship between k_p, k_nr, and molecular structure. Although guest chromophores in solution show large fluctuations because of the absence of surrounding intermolecular forces at RT, thermally activated displacements are also present within the crystalline host, but their distribution is greatly constrained. There are few reports of one-to-one correspondence between k_p, k_nr, and molecular structure determined through a combination of experiments and calculations among the many recent studies on pRTP. Recently, it has been reported that the RTP from molecular crystals that are not host–guest is not due to the molecular structure, but rather to impurities present in the crystals, which has become clearer.^43–45 A thorough collaborative analysis of experiments and theories as described in this paper will contribute to identifying chromophores that emit phosphorescence and their conformations and distributions.

Author contributions

S. U. and S. H. wrote the manuscript. S. U. performed the organic synthesis with advice from B. K. S. U. performed transient absorption analysis with K. F. S. U. performed the quantum chemical calculations with the help of S. H. S. H. supervised this project.

Data availability

Detailed information on organic synthesis, optical property measurements, and quantum chemical calculations is provided in the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the assistance with high-resolution mass spectrometry measurements received from the Coordinated Center for UEC Research Facilities of the University of Electro-Communications. This work was supported by Fusion Oriented Research for disruptive Science and Technology (FOREST) of the Japan Science and Technology Agency (Grant Number JPMJFR201T) and the Japan Society for the Promotion of Science (Grant Number 24K01567).

Notes and references

1. W. Zhao, Z. He and B. Z. Tang, Nat. Rev. Mater., 2020, 5, 869–885.
2. S. Hirata, K. Totani, J. Zhang, T. Yamashita, H. Kaji, S. R. Marder, T. Watanabe and C. Adachi, Adv. Funct. Mater., 2013, 23, 3386–3397.
3. A. S. Mathew, C. A. DeRosa, J. N. Demas and C. L. Fraser, Anal. Methods, 2016, 8, 3109–3114.
4. Y. Deng, D. Zhao, X. Chen, F. Wang, H. Song and D. Shen, Chem. Commun., 2013, 49, 5751–5753.
5. P. Long, Y. Feng, C. Cao, Y. Li, J. Han, S. Li, C. Peng, Z. Li and W. Feng, Adv. Funct. Mater., 2018, 28, 1800791.
6. M. Louis, H. Thomas, M. Gmelch, A. Haft, F. Fries and S. Reineke, Adv. Mater., 2019, 31, 1807887.
7. B. Zhou, G. Xiao and D. Yan, Adv. Mater., 2021, 33, 2007571.
8. X. Zhen, Y. Tao, Z. An, P. Chen, C. Xu, R. Chen, W. Huang and K. Pu, Adv. Mater., 2017, 29, 1606665.
9. S. M. A. Fateminia, Z. Mao, S. Xu, Z. Yang, Z. Chi and B. Liu, Angew. Chem., Int. Ed., 2017, 56, 12160–12164.
10. J. Yang, X. Zhen, B. Wang, X. Gao, Z. Ren, J. Wang, Y. Xie, J. Li, Q. Peng, K. Pu and Z. Li, Nat. Commun., 2018, 9, 840.
11. F. Xiao, H. Gao, Y. Lei, W. Dai, M. Liu, X. Zheng, Z. Cai, X. Huang, H. Wu and D. Ding, Nat. Commun., 2022, 13, 186.
12. I. Bhattacharjee and S. Hirata, Adv. Mater., 2020, 32, 2001348.
13. E. H. Badriyah, K. Hayashi, B. Sk, R. Takano, T. Ishida and S. Hirata, Adv. Sci., 2023, 10, 2304374.
14. W. Ye, H. Ma, H. Shi, H. Wang, A. Lv, L. Bian, M. Zhang, C. Ma, K. Ling, M. Gu, Y. Mao, X. Yao, C. Gao, K. Shen, W. Jia, J. Zhi, S. Cai, Z. Song, J. Li, Y. Zhang, S. Lu, K. Liu, C. Dong, Q. Wang, Y. Zhou, W. Yao, Y. Zhang, H. Zhang, Z. Zhang, X. Hang, Z. An, X. Liu and W. Huang, Nat. Mater., 2021, 20, 1539–1544.
15. H. Ma, L. Fu, X. Yao, X. Jiang, K. Lv, Q. Ma, H. Shi, Z. An and W. Huang, Nat. Commun., 2024, 15, 3660.
16. S. Hirata, Appl. Phys. Rev., 2022, 9, 011304.
17. Y. Katsurada, S. Hirata, K. Totani, T. Watanabe and M. Vacha, Adv. Opt. Mater., 2015, 3, 1726.
18. B. Chen, W. Huang, X. Nie, F. Liao, H. Miao, X. Zhang and G. Zhang, Angew. Chem., Int. Ed., 2021, 60, 16970–16973.
19. K. Fukasawa, Y. Sugawara, R. Tsuru, T. Yamashita and S. Hirata, J. Phys. Chem. Lett., 2022, 13, 7788.
20. D. Li, J. Yang, M. Fang, B. Z. Tang and Z. Li, Sci. Adv., 2022, 8, eabl8392.
21. J. Jovaišaitė, S. Kirschner, S. Raišys, G. Kreiza, P. Baronas, S. Juršėnas and M. Wagner, Angew. Chem., Int. Ed., 2023, 62, e202215071.
22. X. Shen, Y. Luo, K. Chen, C. Fu, R. Liu, Y. Huang, K. Wu, J. Luoa and Z. Lu, Chem. Commun., 2023, 59, 7036–7039.
23. X. Zheng, Q. Han, Q. Lin, C. Li, J. Jiang, Q. Guo, X. Ye, W. Z. Yuan, Y. Liu and X. Tao, Mater. Horiz., 2023, 10, 197–208.
24. B. Sk and S. Hirata, Adv. Sci., 2024, 11, 2308897.
25. C. Qiang, T. Stefan, S. Sven, S. Dieter, M. Klaus, N. Akimitsu and B. Thomas, J. Am. Chem. Soc., 2019, 141, 16439–16449.
26. I. Hattori, M. Hagai, M. Ito, M. Sakai, H. Narita, K. J. Fujimoto, T. Yanai and S. Yamaguchi, Angew. Chem., Int. Ed., 2024, 63, e202403829.
27. S. Hirata, J. Phys. Chem. Lett., 2018, 9, 4251–4259.
28. S. Hirata and I. Bhattacharjee, J. Phys. Chem. A, 2021, 125, 885–894.
29. I. Bhattacharjee, K. Hayashi and S. Hirata, JACS Au, 2021, 1, 945–954.
30. B. Sk, R. Tsuru, K. Hayashi and S. Hirata, Adv. Funct. Mater., 2023, 33, 2211604.
31. M. Shimizu, R. Shigitani, M. Nakatani, K. Kuwabara, Y. Miyake, K. Tajima, H. Sakai and T. Hasobe, J. Phys. Chem. C, 2016, 120, 11631–11639.
32. Y. Zhang, Z. Wang, Y. Su, Y. Zheng, W. Tang, C. Yang, H. Tang, L. Qu, Y. Li and Y. Zhao, Research, 2021, 8096263.
33. J. Cao, M. Zhang, M. Singh, Z. An, L. Ji, H. Shi and Y. Jiang, Front. Chem., 2021, 9, 781294.
34. G. W. Robinson and R. P. Frosch, J. Chem. Phys., 1963, 38, 1187.
35. S. K. Lower and M. A. El-Sayed, Chem. Rev., 1966, 66, 199.
36. P. N. Lai, C. H. Brysacz, M. K. Alam, N. A. Ayoub, T. G. Gray, J. M. Bao and T. S. Teets, J. Am. Chem. Soc., 2018, 140, 10198.
37. P. Pander, A. Swist, R. Turczyn, S. Pouget, D. Djurado, A. Lazauskas, R. Pashazadeh, J. V. Grazulevicius, R. Motyka, A. Klimash, P. J. Skabara, P. Data, J. Soloducho and F. B. Dias, J. Phys. Chem. C, 2018, 122, 24958–24966.
38. N. A. Kukhta, R. Huang, A. S. Batsanov, M. R. Bryce and F. B. Dias, J. Phys. Chem. C, 2019, 123, 26536–26546.
39. D. R. Lee, K. H. Lee, W. Shao, C. L. Kim, J. Kim and J. Y. Lee, Chem. Mater., 2020, 32, 2583–2592.
40. W. Shao, H. Jiang, R. Ansari, P. M. Zimmerman and J. Kim, Chem. Sci., 2022, 13, 789–797.
41. W. Shao and J. Kim, Acc. Chem. Res., 2022, 55, 1573–1585.
42. M. Schmiedtchen, I. Maisuls, H. Siera, J. Balszuweit, C. Wölper, M. Giese, G. Haberhauer, C. A. Strassert and J. Voskuhl, Angew. Chem., Int. Ed., 2024, e202414326.
43. C. Chen, Z. Chi, K. C. Chong, A. S. Batsanov, Z. Yang, Z. Mao, Z. Yang and B. Liu, Nat. Mater., 2021, 20, 175–180.
44. Z. Wu, J. C. Roldao, F. Rauch, A. Friedrich, M. Ferger, F. Würthner, J. Gierschner and T. B. Marder, Angew. Chem., Int. Ed., 2022, 61, e202200599.
45. Z. Wu, C. Herok, A. Friedrich, B. Engels, T. B. Marder and Z. M. Hudson, J. Am. Chem. Soc., 2024, 146, 31507–31517.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc04829f

---