Harnessing machine learning to probe dielectrics in next generation telecommunication and automotive radar applications†
Amit Kumar
Sharma
 a,
Tai-Ming
Zheng
a,
Yen-Lun
Chiu
a,
Kao-Shuo
Chang
a,
Tai-Ming
Zheng
a,
Yen-Lun
Chiu
a,
Kao-Shuo
Chang
 a,
I-Ting
Li
a,
Jr-Jeng
Ruan
a,
I-Ting
Li
a,
Jr-Jeng
Ruan
 a,
Pin-Chao
Liao
b,
Chia-Yun
Chen
a,
Pin-Chao
Liao
b,
Chia-Yun
Chen
 a,
Jyh-Ming
Ting
a,
Jyh-Ming
Ting
 a and
Yen-Hsun
Su
a and
Yen-Hsun
Su
 *a
*a
aDepartment of Materials Science and Engineering, National Cheng Kung University, No. 1, Daxue Road, East District, Tainan City 70101, Taiwan. E-mail: yhsu@mail.ncku.edu.tw
bProgram on Semiconductor Packaging and Testing, Academy of Innovative Semiconductor and Sustainable Manufacturing, National Cheng Kung University, Tainan 70101, Taiwan
First published on 1st April 2025
Abstract
In the last decade, technological advancements in signal transmission, particularly in fifth generation (5G) and emerging sixth generation (6G) wireless technologies, have grown at an exponential rate. While 5G provides faster data speeds and improved broadband capacity, 6G is projected to operate in the terahertz (THz) frequency range, achieving transmission speeds up to one terabit per second (Tbps). However, several challenges such as transmission loss and heat generation, particularly in ceramic dielectric materials (DEMs), persist in the implementation and execution of these technologies. This study aims at addressing these challenges using machine learning (ML) and generative reinforcement learning (GRL) in predicting optimal fabrication parameters for DEMs and antenna design. By integrating genetic algorithms (GA), we demonstrated the optimization of the synthesis parameters of DEMs such as magnesium silicate (Mg2SiO4) and created databases to accurately predict desired dielectric properties and antenna configurations. Six comprehensive databases were created to predict the optimal dielectric properties and antenna configurations. These databases encompass variables such as sintering temperature, dielectric constant, and dopant concentration, enabling highly accurate predictions of material performance. Our results underscore the transformative potential of ML-driven approaches in expediting the fabrication processes of DEMs and advancing the field of next-generation wireless communication technologies.
1. Introduction
Over the past decade, innovation and technological advancements in signal transmission have grown at an exponential rate. The ongoing efforts in fifth generation (5G) and the emerging sixth generation (6G) wireless transmission technologies are paving the way for rapid communications.1 5G wireless communication technologies introduce key advantages—such as enhanced mobile broadband, delivering significantly faster data speeds of gigabits per second (Gbps), and increased capacity for mobile broadband applications, vastly improving capacity for high-bandwidth applications such as high-definition video streaming, virtual reality (VR), and augmented reality (AR)2—to meet the ever-growing demands of modern communications.3 6G technology, on the other hand, is poised to revolutionize wireless communication even further by operating in the terahertz (THz) frequency band.4 This breakthrough could enable data transmission speeds up to 1 terabit per second (Tbps), making it 1000 times faster than 5G. THz frequency is a nonionizing radiation and thus has diverse applications owing to its low photon energy of 4 MeV at 1 Hz in the THz range.5 Additionally, network latency is projected to decrease from the millisecond (in 5G) to microsecond range (in 6G), thus enhancing real-time communication modalities such as holographic communication.The primary requirements for seamless and uninterrupted transmission of the THz frequency are multiple input and multiple output antennas that facilitate high signal quality and signal capacity,6 reduced interference and improved signal-to-noise ratio,7 network slicing,8 and ultra-low latency for real-time applications9 (autonomous vehicles, remote surgery, augmented reality). A major challenge in the propagation of these technologies is transmission loss, high power consumption, and heat generation within the transmitting device.1 Dielectric materials (DEMs), particularly metal oxides, have gained significant attention in advancing the 5G and 6G technologies.10 Owing to their tunable permittivity, capacitance and tunable physical characteristics, DEMs assist in confining the transmitted electromagnetic wave, thereby improving the efficiency of the transmitting device.11 Furthermore, due to their low dissipation factor and thermal and environmental stability, DEMs can effectively transmit electromagnetic radiation with minimal signal loss across the THz frequency.12 The 5G signal transmission is also attenuated by walls and civil constructions, thus demanding signal enhancement devices that are often integrated with multiple layers of metals.13 Ceramic DEMs have emerged as a suitable alternative to overcome these challenges and facilitate seamless transmission of 5G and 6G technologies.14 However, there are numerous factors associated with the selection and fabrication of appropriate ceramic DEMs while incorporating in the antenna.
The early years of the 21st century are known for the rapid development of machine learning (ML) tools and their quick integration into various sectors such as materials science,15 metallurgy,16 engineering,17 healthcare,18 sensors,19 and comprehensive simulation-based prediction of the functional properties of appropriate nanomaterials20 applied in these sectors. Machine learning (ML) and generative artificial intelligence (GAI) have become indispensable tools for humans, enabling rapid data processing and making accurate predictions through extrapolation and interpolation.21 Operating on a limited set of input data—followed by meticulous refinement of the generated prediction—these ML and GAI tools have proven effective in performing complex simulation and predicting a wide range of possible solutions to obtain an effective fabrication parameter for desired functional properties in a nanomaterial.22 Additionally, the application of ML and GAI tools has significantly accelerated the optimization of parameters essential for precise control of thin layers at the surface and at the interface of participating materials.23
The accuracy of the output from an ML model is largely determined by the type, quantity and quality of input data, particularly for supervised learning, where the model is trained on labeled data to learn a mapping between inputs and outputs through regression or taxonomical classification. In contrast, unsupervised learning models are used to analyze and predict patterns in data without any human supervision, such as clustering.24 At the interface of the supervised and unsupervised learning lies the semi-supervised learning approach, which facilitates the handling of large datasets that are partially labeled and partially unlabeled.25 This technique seeks human intervention to guide through the learning process and improve its performance. Semi-supervised learning further enables effective utilization of ever-growing usable datasets through a combination of the above techniques. Additionally, reinforcement learning is another approach applicable to unlabeled data that functions through a self-teaching and iterative process.26 Reinforcement learning tools are essentially a trial-and-error based learning modality, and decisions are made based on rewards or penalties.
The generative reinforcement learning (GRL) model is a sophisticated extension of the reinforcement learning tool that incorporates the generative artificial neural network (GANN) model to predict and extrapolate new data points based on the input data.27,28 These data points are then evaluated by reinforcement learning. Owing to this, the GRL model often requires less human intervention and can lead to highly accurate predictions.29 Contemporary regression-based optimization and prediction models rely on linear or logistic regression methods aimed at minimizing errors through least squares estimation. It is imperative that there exists a relationship between independent and dependent variables, and thus its implementation is much suited to simpler datasets.30 Owing to its limitations, the accuracy and robustness of such models could not be validated for non-linear complex data analysis. GRL, on the other hand, is capable of handling complex multilevel datasets and determining an accurate relationship between the variables through sequential decision making and continuous adaptability to the dynamic environment.31 Integrating GRL with the ongoing materials science research could largely alleviate the laborious process of experimentally optimizing nanomaterial synthesis parameters. Furthermore, based on the output predictions, this approach could assist in rapid identification and determination of the appropriate DEM for its application in antennas for 5G and 6G transmission. In contrast to conventional high throughput screening of materials, where micro/nanomaterials often exhibit certain properties depending on the input experimental parameters, GRL has the potential to predict the synthesis parameters as per the desired crystal structure and properties.32
In this study, the GRL model is used to determine the applicability of DEMs, such as Mg2SiO4. Owing to its low dielectric constant, higher quality factor (Q × f value), and facile synthesis methods, α-Mg2SiO4 (Mg2SiO4) is a suitable candidate for 5G and 6G transmission.33,34 Additionally, previous experimental reports have shown that B-site cation replacement or doping on Mg2SiO4 at high sintering temperatures and longer sintering durations could result in a higher Q × f value, which is deemed suitable for 5G and 6G signal transmission.10 Considering the various possible alterations in Mg2SiO4 during synthesis, we have designed several databases composed of independent variables to train the GRL model and accurately predict parameters for desired characteristics. The independent variables that were used to create databases are sintering temperature, sintering time, sintering density, dielectric constant, dopant concentration, and test frequency. The choice of these parameters was based on their role in determining the phase, microstructural evolution and defect concentrations of Mg2SiO4-based ceramics, consequently influencing the dielectric properties.35–37 For example, sintering temperature governs grain growth, densification, and phase stability, which is crucial for a well-connected grain structure, minimizing porosity and interfacial scattering. Sintering time, on the other hand, determines the extent of grain coarsening and diffusion kinetics, while sintering density is associated with the sintering temperature and sintering time. Consequently, a well-defined microstructure with minimal porosity is essential for achieving low dielectric loss and maintaining a stable dielectric constant.38
The accuracy of the output prediction for the DEM is based on the Q × f value with a low dielectric constant, where a higher Q × f value indicates a narrow bandwidth, less energy loss, high efficiency, and high selectivity of filters aimed at improving the antenna performance. To better handle large data sets and achieve an accurate prediction, genetic algorithm (GA)39–41 in combination with GRL was used in this study. Four databases were created for Mg2SiO4, each representing different dopants such as Ba3(VO4)2 (database A), LiF (database B), lithium magnesium zinc borosilicate (LiMgZnBaS) (database C), and Zn2SiO4 with different Zn/Si ratios and the substitution of Zn2+ by Mg2+ (database D). These dopants were selected owing to their influence on the ceramic structure by reducing sintering temperature, improving densification and enhancing Q × f values. A separate database was created for antenna design (database E) to predict the shape and thickness of the antenna. Finally, polymers with various side chain carbon numbers and molecular weights were also evaluated using GRL to determine the optimum dielectric constant and dielectric loss in database F. The training model selectively eliminates the results varying beyond a standard average. To further improve the quality of the prediction through this model, selection, mating and mutation are employed in the GA training model.
2. Computational method
First, six different datasets with a specific set of input parameters—for synthesis of DEMs and antenna design—were prepared for optimization through the GRL machine learning approach. These input parameters were acquired experimentally and used to train the machine learning model to obtain accurate predictions. The predictions are stored in the database (viz. A, B, C, D, E, and F), each representing a separate category. Database A contains predictions for doping Mg2SiO4 with Ba3(VO2)4, database B contains predictions for doping with LiF, database C contains predictions for doping with LiMgZnBaS, database D contains predictions for substitution of Zn2+ by Mg2+ in Zn2SiO4, database E contains predictions for antenna design and database F contains predictions for the use of polymers in antenna design (details about the respective databases are provided in the Results and discussion section).The experimentally acquired parameters are used as input data into the neural network to train the GRL model. The GANN was used to generate a preliminary prediction on the input data and the results were judged based on the minimal deviations from the input data. From these predictions, randomly selected data points were chosen from each library and used as an input for the second round of training to refine the model using reinforcement learning. The accuracy of the predicted output was determined by the fitness value or quality factor (Q × f). The quality factor (Q) is defined as the inverse of the dielectric loss tangent (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ), essentially indicating storage and dissipation of electromagnetic energy. Low energy dissipation is attributed to a high quality factor.38,42Q × f (f = frequency of measurement, GHz) serves as a metric for selecting which solutions are more likely to be carried over to the next generation. The selection process determines which individuals are chosen for mating in the next generation.
δ), essentially indicating storage and dissipation of electromagnetic energy. Low energy dissipation is attributed to a high quality factor.38,42Q × f (f = frequency of measurement, GHz) serves as a metric for selecting which solutions are more likely to be carried over to the next generation. The selection process determines which individuals are chosen for mating in the next generation.
To assess the performance of the optimized output model, randomly selected data points from the initial predictions were compared to the prediction results, generating a regression curve. After optimization, the final root mean square (RMS) errors of the six databases were significantly reduced to 0.02484, 0.04484, 0.00418, 0.01874, 0.04274, and 0.001857, respectively. These databases are published under the name “Novel Dielectrics Database for Beyond 5G and 6G Telecommunication and Automotive Radar”, at https://mgi.mse.ncku.edu.tw/5g6g/. These databases are now composed of 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400, 18
400, 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480, 705
480, 705![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600, 27
600, 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 720, 7200 and 252
720, 7200 and 252![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 data entries, respectively.
000 data entries, respectively.
3. Results and discussion
Based on Darwin's Theory of Evolution, GA is a metaheuristic optimization algorithm that can perform crossover, mutation and selection operations on the input data with high robustness. Each step contributes to improving the solution to a problem over successive generations. As shown in Scheme 1, after achieving a Q × f value of Mg2SiO4, the numbers of variables and hidden layers are determined and further evaluated to obtain an accurate solution. To improve the accuracy of the training model, it is directed towards GA. GA begins by randomly generating an initial population of potential solutions. Each individual green dot represents a potential solution to the problem and is typically encoded as a vector or string of binary numbers or real values. Each individual green dot in the population is then evaluated based on a predefined fitness function (Q × f). This function quantifies how good or fit each individual solution is relative to the problem. Individuals with higher Q × f are more likely to be selected, although lower Q × f individuals may still have a chance to promote diversity within the population. This step ensures that well-performing solutions are given more opportunities to contribute to the next generation while still allowing some diversity by occasionally selecting less optimal solutions. | ||
| Scheme 1 Schematic representation of the flow of the genetic algorithm (GA) reinforcement learning algorithm model implemented in this study for predicting output. | ||
Once the individual solutions are selected, they are forwarded to the next step, mating. Two individual solutions are paired to produce offspring by combining their information. Single-point crossover, multi-point crossover, and uniform crossover are among the popular crossover approaches used during the mating step. After crossover, mutation is applied to introduce small random changes to the offspring to explore new areas of solution that might not be reachable through crossover alone and helps maintain diversity in the population. The offspring produced through crossover and mutation then replace some or all of the population from the previous generation. The best-performing individuals from the current generation are carried over. This cycle of selection, mating, mutation and replacement continues for several generations in the hidden layer until a termination condition is met. We have set the termination of the algorithm based on the satisfactory Q × f value, which is achieved through population convergence and when further improvement is unlikely. The GA model was trained based on the experimental conditions used to synthesize dielectric materials such as Mg2SiO4 through sintering temperature, dopant concentrations, sintering density and dielectric constant (see Table S1, ESI†).
GA was then applied on the input data within the databases, A, B, C, D, E, and F, with random sampling on the parameters to ensure reproducibility and reduce bias. All the input variables were used for training, with varying numbers of hidden layers (hn) and neurons (nn) (A: hn = 2, nn = 4; B: hn = 2, nn = 7; C: hn = 2, nn = 4; D: hn = 2, nn = 4; E: hn = 2, nn = 2; F: hn = 2, nn = 4), where the number of neurons was selected based on the number of input variables. An adaptive learning rate of 0.2 was implemented, while random sample seeds and the mating rate are set at 0.456 and 0.7, respectively, and a fixed mutation rate of 0.007. A uniform mating mode was selected at 0.7 to prevent premature convergence and the population number is set to 25 with one million learning iterations to ensure highly accurate output.
The results (Fig. 1a–f) show that the predicted output is scattered along the X = Y curve and linear regression R2 was determined. This indicates that the training model is able to predict results with minimal deviations from the input values. The number of iterations in the hidden layer is a key factor governing the accuracy of the prediction. Each database was then trained on these generated parameters as the independent variables and the accuracy was determined based on the Q × f value (for databases A, B, C, and D), antenna bandwidth (for database E), dielectric constant and dielectric loss (for database F).
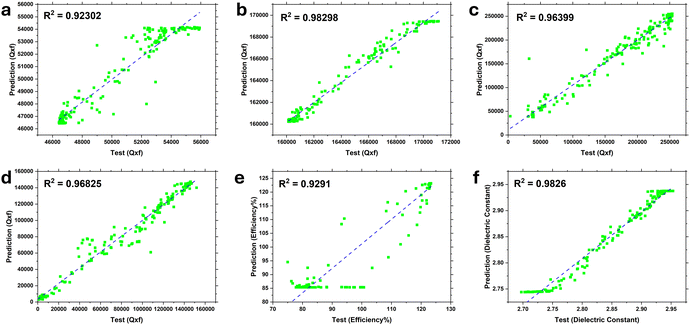 | ||
| Fig. 1 (a–f) Scatter diagram of the results obtained from the GRL model performed on the initial set of input data for each database. | ||
As shown in Table 1, database A entails parameters of Mg2SiO4-based films that are trained for Ba3(VO4)2 doping, database B entails parameters of Mg2SiO4 trained for LiF doping, database C entails parameters of Mg2SiO4 with altered Mg/Si ratio and LMZBS doping, database D entails parameters of Mg2SiO4 with altered Zn/Si ratio and MgO doping, database E entails parameters for designing antennas using metamaterials based on their shape and thickness, while database F shows polymer-based antenna design based on the number of side chain carbons, number of benzene rings, molecular weight, humidity and polymer type.
| # | Database | Independent variables | Dependent variable/output |
|---|---|---|---|
| A | Mg2SiO4-based films (26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 data entries) 400 data entries) |
Ba3(VO4)2 addition amount, sintering temperature, sintering density, dielectric constant | Q × f value |
| B | Mg2SiO4-based films (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 data entries) 480 data entries) |
LiF addition amount, sintering temperature, sintering density, dielectric constant | Q × f value |
| C | Mg2SiO4-based films (705![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 data entries) 600 data entries) |
LMZBS addition amount, Mg/Si ratio, sintering temperature, sintering density, dielectric constant, sintering time, test frequency | Q × f value |
| D | Mg2SiO4-based films (27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 720 data entries) 720 data entries) |
Zn/Si ratio, MgO addition amount, sintering temperature, dielectric constant | Q × f value |
| E | Antenna design (7200 data entries) | Antenna shape, antenna thickness | Bandwidth, lowest point, bandwidth center point, number of bands, maximum gain and efficiency |
| F | Polymer-mixed design (252![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 data entries) 000 data entries) |
Number of side chain carbons, number of benzene rings, molecular weight, humidity, polymer type | Dielectric constant, dielectric loss |
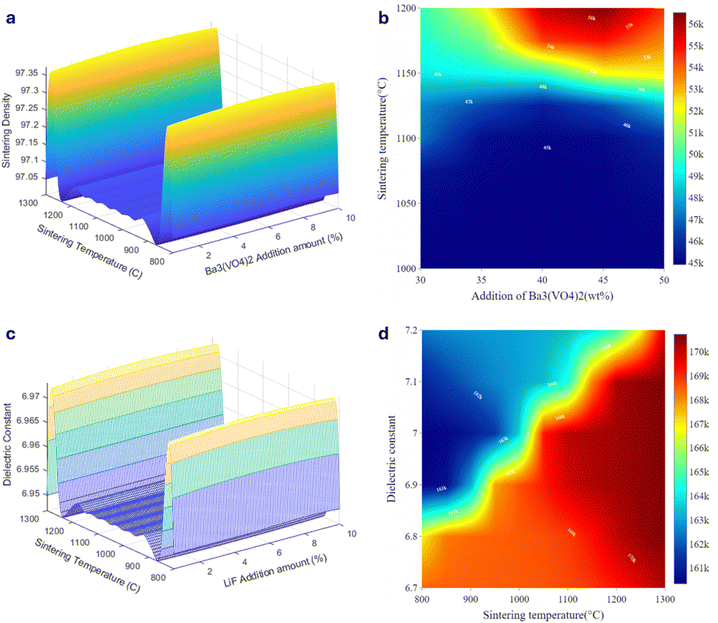
Fig. 2a shows the 3D plot of the input parameters used in database A, i.e. the amount of Ba3(VO4)2 doped on Mg2SiO4 against various sintering temperature and sintering density. Ba3(VO4)2 was chosen as a dopant for Mg2SiO4 owing to its positive temperature coefficient of resonant frequency (τf = +52 ppm °C−1), high dielectric constant, Q × f value of 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 GHz, without influencing the crystal phase of Mg2SiO4.35 The formation of Ba-V-rich second phases further enhance densification and grain connectivity, reducing sintering temperatures, and improving the overall Q × f value by reducing interfacial scattering.
000 GHz, without influencing the crystal phase of Mg2SiO4.35 The formation of Ba-V-rich second phases further enhance densification and grain connectivity, reducing sintering temperatures, and improving the overall Q × f value by reducing interfacial scattering.
Fig. 2b shows the output prediction, governed by the Q × f value, in a numerical plane distribution of the respective concentrations of Ba3(VO4)2 at a fixed sintering porosity of 97% and dielectric constant of 8.4. The results indicate that the highest Q × f is obtained at 45 wt% doping and a sintering temperature of 1200 °C. The vertical axis represents the sintering temperature and indicates that the Q × f value is less sensitive to temperature variations beyond 1160 to 1200 C. The bright red regions represent higher Q × f values, predicting the optimal combination of the dopant at respective sintering temperature.
Fig. 2c shows various concentrations of LiF used as a dopant. LiF doping is reported to reduce the sintering temperature while maintaining a high Q × f.36 As a sintering aid, LiF doping promotes densification through fluorine assisted liquid-phase sintering, reducing porosity and reducing grain growth. Sintering temperature and sintering density were used as the input parameters to determine the optimum prediction. Fig. 2d shows the relationship between sintering temperature and the dielectric constant for 2 wt% LiF doping on Mg2SiO4 performed in database B. The numerical plane distribution of Q × f in database B shows that, upon doping with LiF, the change in the dielectric constant progresses non-linearly with respect to sintering temperature. Lower sintering temperature leads to a lower dielectric constant due to incomplete densification and residual porosity, reduction in grain boundary defects, and residual stress. With the increase in the sintering temperature, the grain growth and improved packing density enhance polarization, leading to a more stable dielectric response and an enhanced Q × f value.36 Notably, a further increase in sintering temperature induces secondary phase and defect formation, thereby degrading performance.
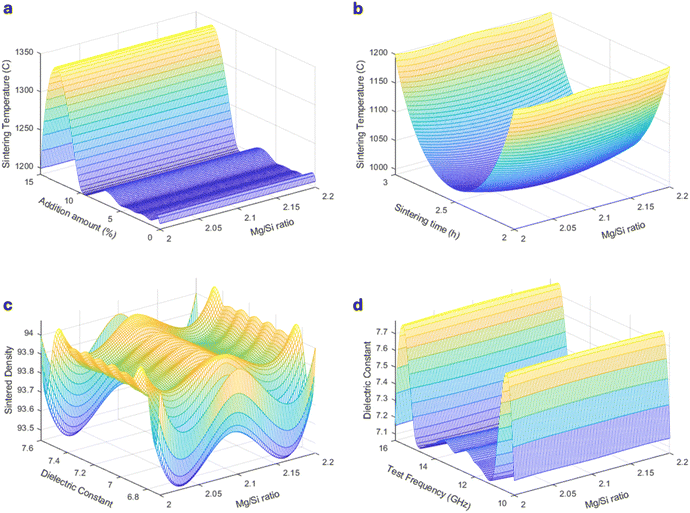
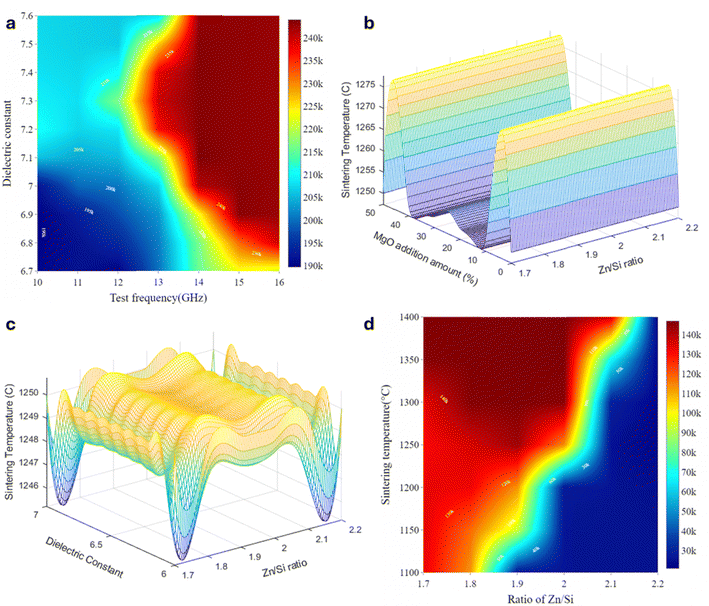
Database C is developed to predict the effect of altered Mg/Si ratio—compared to databases A and B—in terms of test frequency against the dielectric constant. The sintering temperature, sintering density, and dielectric constant are among the input parameters used to train the model (Fig. 3). The LiMgZnBaS glass additive is a low-melting modifier that influences the sintering temperature while maintaining microstructural homogeneity and a high Q × f value of the ceramic.43 With a fixed Mg/Si ratio of 2.1, 10 wt% LiMgZnBaS dopant, and sintering at 1000 °C for 2 hours with 93% porosity, the Q × f value reaches its peak at a test frequency corresponding to a dielectric constant of 7.1 to 7.5 (Fig. 4a). This enhancement can be attributed to the optimal sintering kinetics, which promote efficient densification, as well as the improved phase compatibility between Mg2SiO4 and the introduced glass phase, reducing defects and minimizing dielectric loss.
Notably, the ML-driven optimization of sintering conditions suggests that the ideal sintering temperature for the Q × f value varies with different additives. Sintering at ∼1200 °C (with Ba3(VO4)2 and LiF addition) favors the stabilization of the α-Mg2SiO4 phase, which is essential for high Q × f performance.2 Sintering at lower temperatures (∼1000 °C with LiMgZnBaS) introduces a glassy phase, facilitating densification and enhancing dielectric stability. However, excessively high sintering temperatures (>1300 °C) lead to abnormal grain growth and secondary phase formation, which correlates with the decrease in Q × f observed in our ML predictions. These results align with known Mg2SiO4 phase transformations and microstructural evolution.44
Furthermore, in database D, Zn2SiO4 with different Zn/Si ratios and the substitution of Zn2+ by Mg2+ using MgO is used to train the model against sintering temperature and the dielectric constant (Fig. 4b and c). One of the output predictions obtained for the ratio of Zn/Si against sintering temperature at a fixed dielectric constant of 6.5 and 10 wt% MgO is shown in Fig. 4d. At a 2.0 ratio of Zn/Si, the Q × f value is the highest at a 1300 °C sintering temperature.
Database E is used to train the model to determine the maximum Q × f value for different antenna shapes (polygon) and thicknesses in terms of bandwidth, lowest point, bandwidth center point, number of bands, maximum gains, and efficiency. Fig. 5a shows the output prediction of antenna shape against thickness and desired bandwidth. For 5G and 6G technologies that transmit between 0.1 and 10 THz, the predictions indicate that larger polygon shapes with a 1–3 mm thickness of antenna could assist in a stable transmission. 0.4 THz is the lowest point predicted for successful transmission in a decagon polygon shaped antenna (Fig. 5b). Furthermore, the GRL model predicts that increasing antenna polygon facilitates a higher number of bands for signal transmission (Fig. 5c), which additionally provides higher gain and efficiency (Fig. 5d).
Learning from the previous results, a polygon shaped antenna up to icosagon was further used as a model for training and the output prediction was evaluated using the fitness function (Q × f) (Fig. 6). The thickness of the antenna ranged from 0 m to 0.004 m and the Q × f value was determined using the model. It is seen that the optimal maximum Q × f bandwidth was observed in a pentagon antenna at 0.0002 m thickness, while the Q × f value for the lowest point in the antenna lies just beyond the pentagon shape and a thickness of 0.0005 m. The Q × f value shows a direct proportion with antenna shape and thickness, indicating a more focused radiation pattern with minimal side lobes, thereby reducing the signal-to-noise ratio. A similar relationship is observed for the bandwidth center point, number of bands, maximum gain, and efficiency Q × f value. This prediction indicates that the number of sides on the antenna is proportional to its efficiency in transmitting multiband frequencies increasing its versatility, signal strength and coverage.
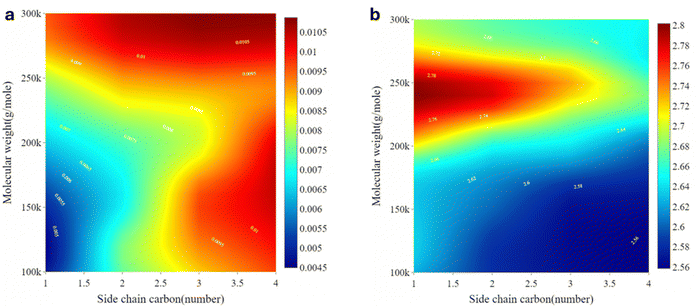
Database F was used to train the model for polymer-mixed design with side chain carbon, benzene rings, molecular weight, humidity and polymer type as independent variables. 6FDAM with ODPA was used as the model polymer with 2 benzene rings at 5% humidity and the test frequency was 3 MHz. Fig. 7a shows the plot of the side chain carbon number against the molecular weight of the polymer, predicting the highest dielectric loss Q × f value for polymers with a side chain carbon number of 4 and a molecular weight of 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. Fig. 7b shows that the Q × f value for the dielectric constant is optimal for smaller side chain carbon numbers and higher molecular weights.
000. Fig. 7b shows that the Q × f value for the dielectric constant is optimal for smaller side chain carbon numbers and higher molecular weights.
Finally, to validate the prediction from the training model, Mg2SiO4 doped with Ba3(VO2)4 and LiF were taken as examples. The experimentally determined Q × f value overlaps with the generated prediction Q × f value, as shown in Fig. S1 (ESI†). This study, thus, verifies the functional capabilities, robustness and accuracy of the databases for determining suitable synthesis parameters for the DEMs as per desired characteristics and expedite the development of 5G/6G technologies.
4. Conclusion
This study highlights the indispensable role of ML in optimizing the process of identifying the suitable DEM and determining appropriate synthesis parameters, which are instrumental in designing high efficiency antennas for 5G and 6G signal transmission. Through ML tools like GA and GRL, we have successfully developed databases based on synthesis parameters, such as dopant concentrations, sintering temperature, sintering density, dielectric constant, test frequency and antenna design. Based on the Q × f values of the databases, ML could predict 45% Ba3(VO4)2 dopant sintered at 1200 °C as suitable to synthesize Mg2SiO4 for antenna design. This sintering temperature also facilitates a stable dielectric constant of 7.1–7.5 at a fixed Mg/Si ratio, while the Zn/Si dopant requires elevated sintering temperatures and provides a lower dielectric constant. The thickness and shape of the antenna play a pivotal role in 5G and 6G signal transmission. Furthermore, low molecular weight polymers are suitable for an optimal dielectric constant of the material used for antenna design. The databases developed in this study can be used as a benchmark for predicting the appropriate parameters with desired characteristics that govern the efficiency of DEMs in 5G and 6G signal transmission. The complexity and labor-intensive nature of optimizing these parameters could be significantly reduced, thus expediting the overall process.Data availability
The authors confirm that the data supporting the findings in this study are available within the article. The databases used for this study are available at https://mgi.mse.ncku.edu.tw/5g6g. Super PCNeuron 5.0 was used to build the training model (https://www.twnfi.com/?sLang=en). Pre-trained models and original datasets can be downloaded from the aforementioned database.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
The authors are grateful for the financial support by the National Science and Technology Council (NSTC), Taiwan, under Grant No. NSTC 112-2221-E-006-052-MY3.References
- F. Salahdine, T. Han and N. Zhang, Ann. Telecommun., 2023, 78, 525–549 CrossRef.
- T.-V. Nguyen, N. P. Nguyen, C. Kim and N.-N. Dao, J. Netw. Comput. Appl., 2023, 211, 103564 CrossRef.
- P. Tiwari, V. Gahlaut, M. Kaushik, P. Rani, A. Shastri and B. Singh, Int. J. Antennas Propag., 2023, 1–19 Search PubMed.
- P. Jain, A. Gupta, N. Kumar and M. Guizani, IEEE Trans. Veh. Technol., 2023, 72, 3264–3273 Search PubMed.
- S. Shi, S. Yuan, J. Zhou and P. Jiang, iScience, 2023, 26, 107060 CrossRef PubMed.
- S. Chen, Y.-C. Liang, S. Sun, S. Kang, W. Cheng and M. Peng, IEEE Trans. Wirel. Commun., 2020, 27, 218–228 Search PubMed.
- M. Sung, S.-R. Moon, E.-S. Kim, S. Cho, J. K. Lee, S.-H. Cho, T. Kawanishi and H.-J. Song, IEEE Trans. Wirel. Commun, 2021, 28, 185–191 Search PubMed.
- A. Alharbi, M. Aljebreen, A. Tolba, K. A. Lizos, S. A. El-Atty and F. Shawki, ACM Trans. Multimedia Comput. Commun. Appl., 2022, 18, 1–18 CrossRef.
- B. Hassan, S. Baig and M. Asif, IEEE Commun. Mag, 2021, 5, 106–113 Search PubMed.
- J. Li, Y. Zhou, J. Wu and F. Liu, Ceram. Int., 2022, 48, 27973–27981 CrossRef CAS.
- Z. Li, J. Pan, H. Hu and H. Zhu, Adv. Electron. Mater., 2021, 8, 2100978 CrossRef.
- P. S. Pálvölgyi, D. Sebők, I. Szenti, E. Bozo, H. Ervasti, O. Pitkänen, J. Hannu, H. Jantunen, M. E. Leinonen, S. Myllymäki, A. Kukovecz and K. Kordas, Nano Res., 2021, 14, 1450–1456 CrossRef.
- S. Tripathi, N. V. Sabu, A. K. Gupta and H. S. Dhillon, Millimeter-wave and Terahertz Spectrum for 6G Wireless, 2021, pp. 83–121 Search PubMed.
- Y. Jiang, H. Liu, R. Muhammad, X. Luo, K. Song, M. Mao, S. Sun, H. B. Bafrooei, E. Taheri-Nassaj, Y. Iqbal, R. Sun and D. Wang, Ceram. Int., 2022, 48, 26922–26927 CrossRef CAS.
- Y. Juan, Y. Dai, Y. Yang and J. Zhang, J. Mater. Sci. Technol., 2021, 79, 178–190 CrossRef.
- T. DebRoy, T. Mukherjee, H. L. Wei, J. W. Elmer and J. O. Milewski, Nat. Rev. Mater., 2020, 6, 48–68 CrossRef.
- S. Saha, Z. Gan, L. Cheng, J. Gao, O. L. Kafka, X. Xie, H. Li, M. Tajdari, H. A. Kim and W. K. Liu, Comput. Methods Appl. Mech. Eng., 2021, 373, 113452 CrossRef.
- H. Pallathadka, M. Mustafa, D. T. Sanchez, G. Sekhar Sajja, S. Gour and M. Naved, Mater. Today Proc., 2023, 80, 2803–2806 CrossRef.
- A. Venketeswaran, N. Lalam, J. Wuenschell, P. R. Ohodnicki, M. Badar, K. P. Chen, P. Lu, Y. Duan, B. Chorpening and M. Buric, Adv. Intell. Syst., 2022, 4, 2100067 CrossRef.
- J. Liu, Y. Zhang, Y. Zhang, S. Kitipornchai and J. Yang, Mater. Des., 2022, 213, 110334 CAS.
- Y. Wang and R. D. King, Mach. Learn., 2024, 113, 8205–8232 CrossRef.
- H. Tao, T. Wu, M. Aldeghi, T. C. Wu, A. Aspuru-Guzik and E. Kumacheva, Nat. Rev. Mater., 2021, 6, 701–716 Search PubMed.
- N. J. Szymanski, Y. Zeng, H. Huo, C. J. Bartel, H. Kim and G. Ceder, Mater. Horiz., 2021, 8, 2169–2198 CAS.
- M. Alloghani, D. Al-Jumeily, J. Mustafina, A. Hussain and A. J. Aljaaf, A Systematic Review on Supervised and Unsupervised Machine Learning Algorithms for Data Science, Supervised and Unsupervised Learning for Data Science, 2020, pp. 3–21 Search PubMed.
- J. E. van Engelen and H. H. Hoos, Mach. Learn., 2020, 109, 373–440 CrossRef.
- Y. Matsuo, Y. LeCun, M. Sahani, D. Precup, D. Silver, M. Sugiyama, E. Uchibe and J. Morimoto, Neural Networks, 2022, 152, 267–275 CrossRef PubMed.
- M. Korshunova, N. Huang, S. Capuzzi, D. S. Radchenko, O. Savych, Y. S. Moroz, C. I. Wells, T. M. Willson, A. Tropsha and O. Isayev, Commun. Chem., 2022, 5, 129 CrossRef PubMed.
- W.-C. Tseng, C.-C. Kaun and Y.-H. Su, Thin Solid Films, 2022, 755, 139326 CrossRef CAS.
- S. Jang, S. Yoo and N. Kang, Comput. Aided Des., 2022, 146, 103225 CrossRef.
- F. E. Harrell, Regression Modeling Strategies, Springer International Publishing, Cham, 2015 Search PubMed.
- M. Wang, J. Zhang, P. Zhang, W. Xiang, M. Jin and H. Li, J. Manuf. Syst., 2024, 77, 946–961 CrossRef.
- H. Park, Z. Li and A. Walsh, Matter, 2024, 7, 2355–2367 CrossRef CAS.
- I. Hameed, L. Li, X. Q. Liu and X. M. Chen, J. Am. Ceram. Soc., 2022, 105, 2010–2019 CrossRef CAS.
- G. Asghar, X. Dong, S. Chae, C.-S. Yoo, J. Jeon, C. Woo, T. Y. Kim, J. Ahn, X. Zhang, H.-S. Oh, H. K. Yu and J.-Y. Choi, Mater. Lett., 2023, 337, 134009 CrossRef CAS.
- S. Meng, Z. Yue, H. Zhuang, F. Zhao and L. Li, J. Am. Ceram. Soc., 2010, 93, 359–361 CrossRef CAS.
- J. Zhang, Z. Yue, Y. Luo, X. Zhang and L. Li, J. Am. Ceram. Soc., 2016, 99, 1122–1124 CrossRef CAS.
- Z. Ye, J. Li, G. Wang, Z. Qi, G. Gan, Y. Yang and H. Zhang, Mater. Res. Express, 2019, 6, 106313 CrossRef CAS.
- Y. Liu, M. Mao, T. Ni, H. Liu, J. Fang, L. Li, H. B. Bafrooei, F. Shi, F. Hussain, D. Wang and K. Song, Ceram. Int., 2024, 50, 329–339 CrossRef CAS.
- N. Behera, Analysis of microarray gene expression data using information theory and stochastic algorithm, Handbook of Statistics, 2020, vol. 43, pp. 349–378 Search PubMed.
- G. Cosma, D. Brown, M. Archer, M. Khan and A. Graham Pockley, Expert Syst. Appl., 2017, 70, 1–19 CrossRef.
- S. M. Cabaneros and B. Hughes, Environ. Model. Softw., 2022, 158, 105529 CrossRef.
- K. X. Song, X. M. Chen and C. W. Zheng, Ceram. Int., 2008, 34, 917–920 CrossRef CAS.
- T. S. Sasikala, C. Pavithran and M. T. Sebastian, J. Mater. Sci.: Mater. Electron., 2010, 21, 141–144 CrossRef CAS.
- A. Bouibes and A. Zaoui, J. Phys. Chem. Solids, 2020, 136, 109161 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5tc00104h |
| This journal is © The Royal Society of Chemistry 2025 |