Open Access Article
Open Access ArticleInterfacial magnetic anisotropy of iron-adsorbed ferroelectric perovskites: first-principles and machine learning study†
Dameul Jeonga,
Seoung-Hun Kang *abc and
Young-Kyun Kwon
*abc and
Young-Kyun Kwon *ab
*ab
aDepartment of Physics and Research Institute for Basic Sciences, Kyung Hee University, Seoul, 02447, Korea. E-mail: ykkwon@khu.ac.kr
bDepartment of Information Display, Kyung Hee University, Seoul, 02447, Korea. E-mail: physicsksh@khu.ac.kr; ykkwon@khu.ac.kr
cMaterials Science and Technology Division, Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA
First published on 15th May 2025
Abstract
The advancement of spin-based devices as a replacement for CMOS technology demands lower spin-switching energy in ferromagnetic (FM) materials. Ferroelectric (FE) materials offer a promising avenue for influencing FM properties, yet the mechanisms driving this interplay remain inadequately understood. In this study, we investigate iron-adsorbed FE ABO3 perovskites using a combination of first-principles calculations and machine learning. Our findings reveal a universal correlation between the magnetic anisotropy energy (MAE) of iron and the induced magnetic dipole moments within the BO2 layer and basal oxygen atoms of ABO3 at the FE/FM interface. By identifying key material descriptors and achieving high predictive accuracy, this research provides a robust framework for selecting and optimizing ABO3 substrates for energy-efficient spintronic devices. These insights contribute to the rational design of novel low-power spin-based technologies.
Introduction
The miniaturization of complementary metal–oxide–semiconductor (CMOS) technology has driven the development of compact and fast electronic devices for decades. However, as device sizes approach 5 nm, quantum tunneling effects hinder the smooth flow of electrons, presenting a critical bottleneck.1 While extensive efforts have been made to overcome this limitation, a fundamental solution remains elusive.2–4 Spintronics, an emerging alternative,5–7 harnesses the electron's spin rather than its charge to operate devices, offering revolutionary potential for energy-efficient electronics. One prominent application of spintronics is spin-transfer torque magnetoresistive random-access memory (STT-MRAM), which delivers near-zero standby power and eliminates leakage currents.8,9 Despite these advantages, STT-MRAM requires substantial energy for writing and maintaining magnetic states.10 Among various approaches11–13 addressing this challenge, Intel's magnetoelectric spin–orbit (MESO) devices demonstrate significant energy savings, outperforming traditional CMOS devices by a factor of 10 to 30. MESO devices rely on spin-to-charge conversion and magnetization switching via the magnetoelectric effect of multiferroic materials, such as La-doped BiFeOi3.14 However, the practical adoption of such materials has been limited due to high costs, reliability concerns, and the scarcity of multiferroic compounds exhibiting robust ferroelectric and ferromagnetic properties at room temperature.15,16A promising strategy to overcome these challenges involves reducing the energy required for spin switching by manipulating the magnetic anisotropy energy (MAE) of ferromagnetic (FM) materials. Ferroelectric (FE) materials, with their spontaneous polarization, offer the potential to influence MAE, providing a pathway for lowering spin-switching energy. Previous studies have demonstrated the impact of FE substrates, such as BaTiO3 (BTO) and HfO2, on the MAE of FM materials.17–23 However, the interplay between the FE substrate properties and FM layer behaviors, particularly at the atomic interface, remains insufficiently understood.
Here, we present our first principles and machine learning investigation of the MAE of iron adsorbates on various FE ABO3 perovskite substrates. These substrates consist of alkaline earth metals (A = Ca, Sr, Ba) and group 4 transition metals (B = Ti, Zr, Hf). Our study identifies unique factors influencing the MAE of iron adsorbates, providing valuable insights for selecting and optimizing FE and FM materials for spintronic applications. While the MAE of FM layers on FE substrates is well-documented in terms of the spontaneous polarization of FE substrates,17,18 our findings reveal that the MAE of iron adsorbates correlates not only with the spontaneous polarization of ABO3 but also with the induced magnetic dipole moments in the BO2 layer and basal oxygen of the ABO3 octahedron near the interface. Employing machine learning, we further explore the universal behavior of FM MAE in the presence of FE layers, demonstrating that the induced magnetic moment near the interface is a critical feature explaining the FE-dependent behavior of FM MAE.
Computational methodology
We carried out ab initio calculations based on density functional theory (DFT),24,25 as implemented in the Vienna ab initio simulation package (VASP).26,27 Projector augmented wave potentials28 were employed to ensure the accurate and efficient description of the valence electrons. For the exchange–correlation functional, we used the Ceperley–Alder form29 within the local density approximation (LDA). All calculations were performed with an energy cutoff of 500 eV to ensure computational efficiency without sacrificing accuracy.To obtain reliable structural configurations, we relaxed all structures until the Hellmann–Feynman force on each atom was below 0.01 eV Å−1. The Brillouin zone was sampled using 10 × 10 × 10 k-point grids for bulk structures and 12 × 12 × 1 Γ-centered k-point grids for slab structures. We considered the spin–orbit interaction and the Berry phase approach30 to evaluate the MAE and spontaneous polarization.
To examine the universal behaviors of the MAE of iron adsorbates on different ABO3 substrates, we applied the Sure Independence Screening and Sparsifying Operator (SISSO) method.31 SISSO generates an extensive feature space encompassing all measurable quantities related to our primary interest. It then employs the sure independence screening (SIS) technique to select subspaces from their feature space and utilizes the sparsifying operator (SO) to achieve sparsity, ultimately providing an optimal n-dimensional descriptor.
During this process, we analyzed a wide range of characteristics representing the essential properties of our Fe-adsorbed ABO3 slab model. We employed both simple mathematical operations (addition, subtraction, multiplication, and division) and more complex functions (exponentials and trigonometric functions) to systematically and recursively create meaningful combinations. This thorough approach resulted in four distinct features with a complexity level of three mathematical operations. From a large collection, we selected a subspace size of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, leading to the discovery of an optimized two-dimensional descriptor that effectively captures the universal behavior of the MAE of iron adsorbed on various ABO3 compounds with full coverage.
000, leading to the discovery of an optimized two-dimensional descriptor that effectively captures the universal behavior of the MAE of iron adsorbed on various ABO3 compounds with full coverage.
It is noted that we employed LDA in all first-principles calculations, primarily due to its numerical stability when combined with spin–orbit coupling and the magnetic force theorem. To validate this choice, we computed the magnetic moment of bulk Fe using LDA, GGA, GGA+U (U = 1–3 eV), and a hybrid functional. The LDA value (2.141 μB) closely matches the experimental value (2.13 μB), while GGA and hybrid functionals significantly overestimate it, as summarized in Table S1 (ESI†). We further confirmed the robustness of our findings by recalculating MAE using GGA+U for multiple U values. Although the absolute MAE values vary slightly, the main trends, such as the appearance or absence of discrete MAE jumps, remain unchanged. These validations are detailed in Note S3 and Fig. S4 (ESI†).
Results and discussion
Perovskite is a mineral with the same crystal form as CaTiO3 (CTO), characterized by the ABX3 configuration. Its unit cell is a cube of space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (221), with cations A and B located at the vertices and body centers, respectively, and anion X at the face centers, as illustrated in Fig. 1(a). The cation A acts as a fixed shell, making its chemical and physical properties relatively less significant. However, the displacement of the B and X atoms, breaking the centrosymmetry, transforms the cube into a tetrahedral structure inducing spontaneous polarization. This displacement, which governs the FE properties of perovskites, can be controlled by modifying the electronic configuration of cation B through geometric changes in the BX6 octahedron.32 Typically, A represents an alkali or alkaline earth metal, while B represents a transition metal element.33 In this study, we considered only divalent (group 2: Ca, Sr, Ba, Ra) and tetravalent (group 4: Ti, Zr, Hf) elements for cations A and B, respectively, with oxygen as anion X.
m (221), with cations A and B located at the vertices and body centers, respectively, and anion X at the face centers, as illustrated in Fig. 1(a). The cation A acts as a fixed shell, making its chemical and physical properties relatively less significant. However, the displacement of the B and X atoms, breaking the centrosymmetry, transforms the cube into a tetrahedral structure inducing spontaneous polarization. This displacement, which governs the FE properties of perovskites, can be controlled by modifying the electronic configuration of cation B through geometric changes in the BX6 octahedron.32 Typically, A represents an alkali or alkaline earth metal, while B represents a transition metal element.33 In this study, we considered only divalent (group 2: Ca, Sr, Ba, Ra) and tetravalent (group 4: Ti, Zr, Hf) elements for cations A and B, respectively, with oxygen as anion X.
To investigate the effect of FE materials on spin switching in FM materials, we considered iron (Fe), a prime example of a magnetic material, as an adsorbate on ABO3. To gain a fundamental understanding of Fe adsorption on ABO3, we first investigated its interaction with barium titanate, BaTiO3 (BTO), a well-established FE material. Following the experimental observations revealing the interfacial structure between iron and BTO20 and iron adsorption at the atomic scale,34–36 we constructed a model structure of Fe-adsorbed BTO as follows. We created a BTO surface with the TiO2 layer and then added iron atoms to the surface one by one until a full monolayer coverage (Θ = 1) was achieved. Fig. 1(b) shows two configurations of Fe adsorption on BTO at coverage of 50% (Θ = 1/2) and 100% (Θ = 1). Note that we only considered the positive BTO polarization, under which Fe atoms are initially more readily absorbed on the B top site than under its negative polarization.
To quantitatively investigate the preferred adsorption sites for Fe atoms, we calculated the Fe atom adsorption energy Eads, defined as
| Eads = EFe/BTOtot − EBTOtot − EFetot | (1) |
We utilized the slab model, as shown in Fig. 1(b), to examine the interplay between the MAE and the spontaneous polarization of various ABO3 materials. To achieve an equilibrium interfacial structure, we fully relaxed the top three layers of the ABO3 substrate and the adsorbed Fe atoms within the same crystal symmetry. The bottom four layers were fixed to preserve the bulk structure to clearly capture the effect of spontaneous polarization on the MAE of the adsorbed Fe. The polarization direction depends on the relative displacement of BO6 octahedra within the ABO3 unit cell. When the octahedra is displaced towards the adsorbed Fe layer, the polarization becomes negative. Conversely, displacement in the opposite direction leads to positive polarization. Having established the interface between the adsorbed Fe and ABO3 substrate, we first studied the MAE of the Fe adsorbate on the unpolarized ABO3 structures with the centrosymmetric structure shown in Fig. 1(a). The MAE η is the energy required to change the direction of magnetization from the out-of-plane direction to the in-plane direction in the magnetic thin film material, defined as:
| η = Etot(S→) − Etot(S↑) | (2) |
 | (3) |
 | ||
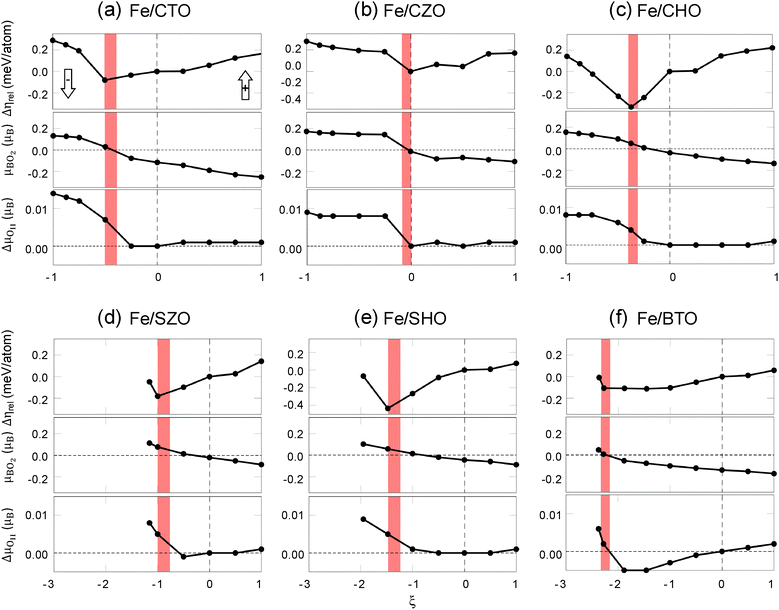
| Fig. 2 (a) The relative MAE ΔηFe, defined in eqn (3), of iron adsorbates on different ABO3 substrates (A = Ca, Sr, or Ba; B = Ti, Zr, or Hf) at full coverage. The divalent elements Ca, Sr, and Ba corresponding to the cation A are represented by solid squares, crosses, and solid circles, respectively. The tetravalent elements Ti, Zr, and Hf for the cation B are represented by blue, red, and orange colors, respectively. Dashed lines indicate quadratic fits for each B element, highlighting the classification by tetravalent elements. (b) The relative MAE Δηrel, defined in eqn (4), as a function of ξ = P/Ps for six ABO3 substrates labeled with the same symbol and color as in (a). The vertical dashed line marks ξ = 0. Three ABO3 substrates with zero spontaneous polarization are excluded. The linear behavior in SZO, SHO, and BTO contrasts with the unexpected upturns in CTO, CZO, and CHO as ξ decreases. | ||
To explore the inherent effect of the spontaneous polarization of the ABO3 substrate alone on the MAE of the adsorbed Fe, we also evaluated the relative MAE Δηrel using
| Δηrel = η(ξ) − η(0) | (4) |
We now turn our attention to the abrupt upturns in Δηrel observed in three cases (Fe/CTO, Fe/CZO, and Fe/CHO) as shown in Fig. 2(b). Notably, these upturns occur within the range of spontaneous polarization (|ξ| < 1). In contrast, the other three cases (Fe/SZO, Fe/SHO, and Fe/BTO) do not exhibit such upturns within the same polarization range. This disparity suggests the presence of factors beyond the electric field effects induced by spontaneous polarization. Specifically, our analysis reveals that the MAE upturns are predominantly influenced by interface effects, such as induced interfacial magnetic dipole moments, as described in the following. To illustrate this interface-driven effect, we analyzed how the electronic structure evolves with polarization, as detailed in Note S2 (ESI†). Fig. S3 (ESI†) presents the projected density of states (PDOS) of Fe 3d orbitals under varying polarization states. In CTO, polarization reversal leads to marked shifts and reshaping of Fe 3d peaks, indicating a strong change in orbital character and hybridization. In contrast, BTO exhibits only minimal changes in Fe 3d states. This distinction aligns with the sharp MAE jump observed in CTO and its absence in BTO, confirming that polarization-induced modification of Fe–O–metal bonding is the key factor controlling magnetic anisotropy. While LDA may underestimate absolute band alignment, it reliably captures the polarization-driven modulation of Fe orbital anisotropy that governs the observed trends.
Fig. 3 presents the relative MAE (Δηrel), the induced magnetic moments of the interface BO2 layer (μBO2), and the relative magnetic moment induced in the oxygen atom OII (ΔμOII), located just below the topmost B atom in ABO3 as depicted in Fig. 1(b), as a function of ξ for all six cases. Abrupt upturns in Δηrel are observed in the region ξ < 0 for all cases. Notably, in the first three cases (Fe/CTO, Fe/CZO, and Fe/CHO), these upturns occur within −1 < ξ < 0, whereas in the other three cases (Fe/SZO, Fe/SHO, and Fe/BTO), the upturns are observed only when ξ < − 1, beyond the spontaneous polarization range. We observed that μBO2 changes its sign near ξc, the critical ξ value where the upturns occur. Furthermore, ΔμOII exhibits a sharp change near ξc, transitioning from positive for ξ < ξc to near zero for ξ > ξc, mirroring the behavior of MAE. This emphasizes that, in practical scenarios, MAE upturns are apparent only in the first three cases within their spontaneous polarization limits. For the other three cases, external electric fields are necessary to extend polarization beyond the ξ = −1 threshold to observe similar effects.
Additionally, we found that as the A-site element becomes heavier, the critical value ξc shifts further into the negative range. This trend is attributed to the increased stability of the octahedron in ABO3 perovskites with heavier A-site elements, leading to reduced octahedral deformation. A critical degree of octahedral deformation appears to be essential for significantly enhancing the interfacial magnetic moments of both B and OII atoms, ultimately driving the observed MAE upturns. Our analysis underscores the essential role of changes in the magnetic moments of interface atoms induced by spontaneous polarization. These findings highlight the complex interplay of structural and magnetic properties in determining the MAE of adsorbed Fe in ABO3 perovskites, providing valuable insights into their multi-dimensional effects.
Building on these findings, our analysis identifies two distinct factors that contribute to the MAE of adsorbed Fe in ABO3 systems influenced by spontaneous polarization. The first factor is the “interface effect” arising from atomic displacements induced by ferroelectricity. To elucidate the atomic-level mechanism of the MAE jump, we find that polarization switching induces vertical displacements of interfacial oxygen atoms relative to the Fe layer. This structural shift modifies the Fe–B and B–OII bond lengths, thereby altering the Fe–B orbital hybridization. Since orbital hybridization determines the orbital moment anisotropy of Fe atoms, these polarization-driven adjustments at the interface ultimately lead to the observed discrete jump in MAE. As shown in Fig. S2 (ESI†), when ξ assumes a negative value, the separation between the Fe and B atoms increases. The magnetic moment of the B atom in the BO2 layer, which opposes that of the adsorbed Fe, decreases significantly in magnitude, by approximately 0.2 to 0.4 μB in the negative ξ regime. In contrast, the magnetic moment of the O atoms in the same plane, which aligns with the Fe moment, exhibits a comparatively smaller increase, typically 0.02 to 0.04 μB. This difference highlights the dominant influence of the B atoms in converting the net magnetic moment of the BO2 layer to a positive value, which amplifies the MAE by reinforcing the out-of-plane anisotropy of the Fe moment. Furthermore, the displacement of atoms in the negative ξ regime brings the OII atom closer to the B atom, as shown in Fig. 1(b), inducing a magnetic moment in OII through the proximity effect. The combined movement of the B atom and the reduced magnetic moment at the interface leads to the induction of a magnetic moment in OII, which correlates with the observed abrupt upturns in the MAE of the adsorbed Fe. The second factor is associated with the electric field directly induced by spontaneous polarization. However, this effect is relatively minor, as detailed in Note S1 (ESI†).
We employed the SISSO scheme for machine learning to identify key parameters for accurately representing Δηrel. Training the model on a 30-set dataset excluding unpolarized ABO3, we evaluated features such as the ABO3 lattice constant, polarization value, and the magnetic moments of individual atoms in the Fe adsorbate-ABO3 system under spontaneous polarization. These primary features were selected based on their direct physical relevance to MAE. The magnetic moment of Fe atoms directly influences MAE. The ABO3 lattice constant indirectly affects the local strain and site symmetry at the Fe adsorption site and thus alters the electronic structure and magnetic properties. The polarization value changes the interfacial electric field and atomic displacements, as it is widely considered a key factor that could influence MAE. Based on this physically informed selection, the SISSO algorithm systematically constructed composite descriptors and identified the optimal combination for the best correlation with the evaluated MAE values. This analysis yielded the following descriptor,
| α = (μB + μFe)(λ1μOIIμFe + λ2a6) + γ, | (5) |
Fig. 4(a) illustrates the high predictive accuracy of α for the training set of Fe adsorbates on ABO3 substrates (solid black circles), achieving R2 = 0.933 and RMSE = 0.035, where RMSE denotes the root-mean-squared error. Furthermore, the descriptor demonstrates strong predictive power for untrained data (empty red circles) with R2 = 0.898 and RMSE = 0.050. Even when applied to an extrapolated dataset of RaTiO3, which is absent from the training set, it maintains robust accuracy (R2 = 0.865, RMSE = 0.063), as indicated by the blue rhombi. The predicted MAE for RaBO3 (B = Ti, Zr, Hf) aligns closely with the trends observed in the training dataset, as depicted in Fig. 4(b), which is the same as Fig. 2(a) with additional data points for RaBO3. These results underscore the utility of our machine learning approach for predicting MAE values in diverse ABO3 compounds with Fe adsorbates. By capturing the complex interplay of interfacial magnetic moments and lattice effects, our descriptor provides a powerful tool for guiding the design of advanced ferroelectric and spintronic materials. Furthermore, the predicted discrete jump in MAE driven by interfacial structural changes is expected to be experimentally detectable via techniques such as X-ray magnetic circular dichroism (XMCD)20 or ferromagnetic resonance (FMR),44 providing a viable pathway for experimental validation of our theoretical predictions.
 | ||
| Fig. 4 (a) Relationship between the relative MAE Δηrel and the identified descriptor α given in eqn (5). Solid black circles denote the training set (R2 = 0.933), empty red circles the validation set (R2 = 0.898), and blue diamonds the test set (R2 = 0.865). (b) The relative MAE ΔηFe of Fe-adsorbed RaBO3 substrates (B = Ti, Zr, Hf) obtained from the identified descriptor α given in eqn (5), which were added to Fig. 2(a), showing that our machine learning descriptor can also be applied to the heavier A = Ra element in ABO3. | ||
Conclusions
In summary, this study addresses the challenge of controlling the magnetic anisotropy energy (MAE) in ferromagnetic (FM) materials to enable low-power spin-based devices. By exploring the influence of ferroelectric (FE) spontaneous polarization, we investigated ABO3 materials as substrates and their effects on Fe adsorbates. Our results revealed significant variations in MAE across ABO3 compounds with different A and B elements. A key finding was the unexpected jump in MAE, which was primarily driven by interface effects rather than the electric field effects associated with spontaneous polarization. This discovery underscores the critical role of the interplay between the Fe adsorbate and the ABO3 substrate at the atomic level. Leveraging machine learning, we developed a descriptor that accurately captures the physical factors affecting MAE. By incorporating the magnetic moments of interface atoms and the lattice constant, our model achieved high predictive accuracy, with R2 = 0.933 and RMSE = 0.035 on the training set. Notably, the model demonstrated strong performance when extrapolated to unseen data, including RaTiO3, achieving R2 = 0.865 and RMSE = 0.063. These results validate the robustness and generalizability of our approach, offering a predictive tool for tailoring MAE in a wide range of ABO3 compounds. Our study also highlights how the selection of A and B elements in perovskite structures significantly influences MAE. Heavier A elements, such as Sr and Ba, were found to stabilize the octahedral structure of ABO3, reducing deformation and modulating the MAE more effectively. This insight provides a pathway for engineering materials that exhibit optimal MAE characteristics, enabling faster and more energy-efficient switching in spintronic devices. For example, incorporating ABO3 compounds with A = Ca into device architectures could reduce magnetization switching times by exploiting the MAE jump, without requiring changes to the external electric field direction.Overall, these findings advance our understanding of the mechanisms underlying MAE modulation in FM materials and establish a framework for designing high-performance spintronic devices. By bridging first-principles calculations and machine learning, this work contributes to the broader field of materials science, offering strategies for the development of next-generation electronic and spintronic technologies.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
The authors have no conflicts of interest to disclose.Acknowledgements
This research was supported by the Korean government (MSIT) through the National Research Foundation of Korea (NRF-2022R1A2C1005505, NRF-2022M3F3A2A01073562, and NRF-RS-2024-00416976) and Institute for Information & Communications Technology Planning & Evaluation (IITP) (2021-0-01580). S.-H. K. is supported by the US Department of Energy (DOE), Office of Science, National Quantum Information Science Research Centers, Quantum Science Center. Our computational work was done using the resources of the KISTI Supercomputing Center (KSC-2023-CRE-0053 and KSC-2024-CRE-0211) and the resources of the Oak Ridge Leadership Computing Facility, US DOE Office of Science User Facilities. This manuscript has been coauthored by UT-Battelle, LLC, under Contract No. DE-AC0500OR22725 with the U.S. Department of Energy. The United States Government retains and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a non-exclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this manuscript or allow others to do so, for the United States Government purposes. The Department of Energy will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (https://energy.gov/downloads/doe-public-access-plan).References
- L. Wang, PhD thesis, Georgia Institute of Technology, 2006 Search PubMed.
- R. K. Ratnesh, A. Goel, G. Kaushik, H. Garg Chandan, M. Singh and B. Prasad, Mater. Sci. Semicond. Process., 2021, 134, 106002 CrossRef CAS.
- A. Samal, S. L. Tripathi and S. K. Mohapatra, Trans. Electr. Electron. Mater., 2020, 21, 443–455 CrossRef.
- C. Prasad, IEEE Trans. Electron Devices, 2019, 66, 4546–4555 CAS.
- S. A. Wolf, D. D. Awschalom, R. A. Buhrman, J. M. Daughton, S. von Molnár, M. L. Roukes, A. Y. Chtchelkanova and D. M. Treger, Science, 2001, 294, 1488–1495 CrossRef CAS PubMed.
- I. Z. Žuti, J. Fabian and S. Das Sarma, Rev. Mod. Phys., 2004, 76, 323–410 CrossRef.
- A. Fert, Rev. Mod. Phys., 2008, 80, 1517–1530 CrossRef CAS.
- S. A. Wolf, J. Lu, M. R. Stan, E. Chen and D. M. Treger, Proc. IEEE, 2010, 98, 2155–2168.
- S. Salehi, D. Fan and R. F. Demara, J. Emerg. Technol. Comput. Syst., 2017, 13, 1–16 CrossRef.
- T. Nozaki, T. Yamamoto, S. Miwa, M. Tsujikawa, M. Shirai, S. Yuasa and Y. Suzuki, Micromachines, 2019, 10, 327 CrossRef PubMed.
- Y. Gupta and L. Bhargava, Int. J. Electron. Lett., 2019, 7, 249–261 CrossRef.
- V. S. D. Eswar, K. D. Bhavani and D. Nandan, J. Phys. Conf. Ser., 1714, 2021, 012041 Search PubMed.
- H. Cai, J. Chen, Y. Zhou and W. Zhao, IEEE Trans. Circuits Syst., 2021, 68, 2633–2639 Search PubMed.
- S. Manipatruni, D. E. Nikonov, C.-C. Lin, T. A. Gosavi, H. Liu, B. Prasad, Y.-L. Huang, E. Bonturim, R. Ramesh and I. A. Young, Nature, 2019, 565, 35–42 CrossRef CAS PubMed.
- J.-C. Yang, Q. He, P. Yu and Y.-H. Chu, Annu. Rev. Mater. Res., 2015, 45, 249–275 CrossRef CAS.
- J. A. Mundy, C. M. Brooks, M. E. Holtz, J. A. Moyer, H. Das, A. F. Rébola, J. T. Heron, J. D. Clarkson, S. M. Disseler, Z. Liu, A. Farhan, R. Held, R. Hovden, E. Padgett, Q. Mao, H. Paik, R. Misra, L. F. Kourkoutis, E. Arenholz, A. Scholl, J. A. Borchers, W. D. Ratcliff, R. Ramesh, C. J. Fennie, P. Schiffer, D. A. Muller and D. G. Schlom, Nature, 2016, 537, 523–527 CrossRef CAS PubMed.
- C.-G. Duan, S. S. Jaswal and E. Y. Tsymbal, Phys. Rev. Lett., 2006, 97, 047201 CrossRef PubMed.
- C.-G. Duan, J. P. Velev, R. F. Sabirianov, W. N. Mei, S. S. Jaswal and E. Y. Tsymbal, Appl. Phys. Lett., 2008, 92, 122905 CrossRef.
- P. V. Lukashev, J. D. Burton, S. S. Jaswal and E. Y. Tsymbal, J. Phys.: Condens. Matter, 2012, 24, 226003 CrossRef PubMed.
- G. Radaelli, D. Petti, E. Plekhanov, I. Fina, P. Torelli, B. R. Salles, M. Cantoni, C. Rinaldi, D. Gutiérrez, G. Panaccione, M. Varela, S. Picozzi, J. Fontcuberta and R. Bertacco, Nat. Commun., 2014, 5, 3404 CrossRef CAS PubMed.
- D. Odkhuu, Phys. Rev. B, 2017, 96, 134402 CrossRef.
- B. F. Vermeulen, F. Ciubotaru, M. I. Popovici, J. Swerts, S. Couet, I. P. Radu, A. Stancu, K. Temst, G. Groeseneken, C. Adelmann and K. M. Spaldin, ACS Appl. Mater. Interfaces, 2019, 11, 34385–34393 CrossRef CAS PubMed.
- Y. Cheng, S. Zhao, Z. Zhou and M. Liu, Nano Res., 2023, 16, 5983–6000 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- D. M. Ceperley and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566–569 CrossRef CAS.
- N. A. Spaldin, J. Solid State Chem., 2012, 195, 2–10 CrossRef CAS.
- R. Ouyang, S. Curtarolo, E. Ahmetcik, M. Scheffler and L. M. Ghiringhelli, Phys. Rev. Mater., 2018, 2, 083802 CrossRef CAS.
- R. J. D. Tilley, Perovskites: structure-property relationships, John Wiley Sons, 2016 Search PubMed.
- H. Wei, C. Yang, Y. Wu, B. Cao, M. Lorenz and M. Grundmann, J. Mater. Chem. C, 2020, 8, 15575–15596 RSC.
- M. Wagner, P. Lackner, S. Seiler, S. Gerhold, J. Osiecki, K. Schulte, L. A. Boatner, M. Schmid, B. Meyer and U. Diebold, Phys. Rev. Lett., 2016, 117, 206101 CrossRef PubMed.
- X. Yang, Y. Yuan, Y. Peng, E. Minamitani, L. Peng, J.-J. Xian, W.-H. Zhang and Y.-S. Fu, Nanoscale, 2020, 12, 8174–8179 RSC.
- P. Fan, F. Yang, G. Qian, H. Chen, Y.-Y. Zhang, G. Li, Z. Huang, Y. Xing, L. Kong, W. Liu, K. Jiang, C. Shen, S. Du, J. Schneeloch, R. Zhong, G. Gu, Z. Wang, H. Ding and H.-J. Gao, Nat. Commun., 2021, 12, 1348 CrossRef CAS PubMed.
- S. Valencia, A. Crassous, L. Bocher, V. Garcia, X. Moya, R. O. Cherifi, C. Deranlot, K. Bouzehouane, S. Fusil, A. Zobelli, A. Gloter, N. D. Mathur, A. Gaupp, R. Abrudan, F. Radu, A. Barthélémy and M. Bibes, Nat. Mater., 2011, 10, 753–758 CrossRef CAS PubMed.
- J. R. Kim, J. Jang, K.-J. Go, S. Y. Park, C. J. Roh, J. Bonini, J. Kim, H. G. Lee, K. M. Rabe, J. S. Lee, S.-Y. Choi, T. W. Noh and D. Lee, Nat. Commun., 2020, 11, 4944 CrossRef CAS PubMed.
- M. L. Marcondes, S. S. M. Santos, I. P. Miranda, P. Rocha-Rodrigues, L. V. Assali, A. M. L. Lopes, J. P. Araujo and H. M. Petrilli, J. Mater. Chem. C, 2021, 9, 15074–15082 RSC.
- M. D. Biegalski, L. Qiao, Y. Gu, A. Mehta, Q. He, Y. Takamura, A. Borisevich and L.-Q. Chen, Appl. Phys. Lett., 2015, 106, 162904 CrossRef.
- A. Herklotz, A. T. Wong, T. Meyer, M. D. Biegalski, H. N. Lee and T. Z. Ward, Sci. Rep., 2016, 6, 26491 CrossRef CAS PubMed.
- J. Jia, X. He, A. Akhtar, G. Herranz and M. Pruneda, Phys. Rev. B, 2022, 105, 224112 CrossRef CAS.
- G. H. O. Daalderop, P. J. Kelly and M. F. H. Schuurmans, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 11919–11937 CrossRef CAS PubMed.
- M. Tortarolo, D. Goijman, M. A. Barral, S. Di Napoli, A. A. Pérez Martnez, G. Ramrez, A. Sarmiento Chavez, J. Gómez, A. Zakharova, S. E. Bayram, F. Stramaglia, C. A. F. Vaz, J. Milano and C. Piamonteze, J. Appl. Phys., 2025, 137, 014101 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5tc00250h |
| This journal is © The Royal Society of Chemistry 2025 |