Exploring the balance between spin frustration and single-ion effects in triangular Dy₃ complexes

Abstract

We report the synthesis, structures, and magnetic properties of a series of triangular Dy₃ complexes with [Dy₃(hmci)₃(MeOH)₆]·3MeOH·2MeCN·2H₂O (1) and [Dy₃(hmcb)₃(MeOH)₆]·3MeOH·1H₂O (2) (H₃hmci = 2-hydroxy-3-methoxy-5-iodobenzaldehyde hydrazone, H₃hmcb = 2-hydroxy-3-methoxy-5-bromobenzaldehyde hydrazone). These complexes adopt a calixarene-like triangular topology with phenoxide-bridged Dy³⁺ ions, leading to near-perpendicular orientation of anisotropic axes relative to the Dy₃ plane. Magnetic studies and theoretical calculations reveal rare examples of Ising spin frustration driven by dipolar interactions, while retaining a zero-field single-molecule-magnet (SMM) behavior. Furthermore, halogen substitutions at the para position of the ligands fine-tune the local crystal field environment, enabling modulation of the relaxation dynamics and slow magnetic relaxation profiles. These findings underscore the critical role of ligand design in tailoring spin frustration and optimizing the zero-field SMM performance of triangular Dy₃ complexes.

---

1. Introduction

Single-molecule magnets (SMMs) are a remarkable class of molecular materials celebrated for their ability to exhibit slow relaxation of magnetization and magnetic hysteresis at the molecular level, driven by strong magnetic anisotropy. Over the years, SMMs have shown tremendous potential for applications in quantum computing, high-density data storage, and spintronic devices.^1–6 While lanthanide-based mononuclear systems have provided fundamental insights into SMM behavior, particularly through precise control of magnetic anisotropy via chemical manipulation of crystal-field (CF) splitting, especially for Dy³⁺ ions,^7–19 further progress depends on addressing limitations imposed by spin–phonon interactions. In particular, Raman relaxation, which can hinder performance by reducing the blocking temperature, has emerged as a critical bottleneck.^20–23

In parallel, magnetic interactions between lanthanide ions in polynuclear complexes introduce additional layers of complexity and opportunities for tuning their magnetic properties.²³ These interactions influence key parameters such as blocking temperature and magnetic coercivity, often balancing the subtle dipolar and exchange contributions.^24–30

Among polynuclear complexes, triangular Dy₃ complexes have emerged as ideal models for exploring the interplay between magnetic anisotropy and intramolecular magnetic interactions.³¹ This topology offers an intriguing platform where the spatial arrangement of Dy³⁺ ions and their anisotropic axes can create unique magnetic behaviors such as vortex-like arrangements of magnetic moments, resulting in toroidal moments with nonmagnetic ground states but retaining fascinating dynamic properties like slow relaxation and quantum tunnelling.^32–36 Thus, the magnetic interactions between Dy³⁺ ions, mediated by the surrounding ligands in combination with the relative orientation of the local anisotropic axis play a critical role in determining the overall magnetic behavior and relaxation dynamics. Beyond their magnetic properties, Dy₃ triangles have also drawn attention for their potential to exhibit magnetoelectric coupling, expanding the scope of molecular materials with coupled ferroic properties.³⁷

Spin frustration in an Ising triangle, on the other hand, arises from competing antiferromagnetic interactions, which in molecular systems such as triangular trinuclear complexes, lead to nearly degenerate spin ground states.^38–40 The ideal frustrated Ising triangle requires a perfectly equilateral geometry, with principal magnetic axes perpendicular to the triangle's plane and sufficiently large Dy³⁺–Dy³⁺ distances to suppress exchange interactions. In such a configuration, dipolar interactions dominate and induce a frustrated ground state. Yet achieving this necessitates precise control over the orientation of the anisotropic axes as dipolar interactions among highly anisotropic magnetic centers play a critical role in the relaxation dynamics in polynuclear SMMs. Traditionally viewed as either negligible or detrimental, these interactions, when carefully tuned, can effectively govern transition probabilities between low-energy states.^41,42 This highlights their potential as a strategic mechanism for refining relaxation processes and tailoring magnetic properties in complex systems.

In this context, phenoxide-based ligands have been widely utilized for assembling polynuclear SMMs with high energy barriers, offering a robust framework for constructing diverse core topologies.^{2,5,16,43–50} Previously, we reported a triangular Dy₃ complex based on the H₃hnc (1,5-bis(2-hydroxy-3-methoxy-5-nitrobenzylidene)carbonohydrazide) featuring an electron-withdrawing NO₂ group in the para position.³¹ This topology features a central Dy₃ triangle with para-substituents projecting outward in a tripod-like configuration below the Dy₃ plane.

Building on this foundation, the present study extends this design by incorporating halogen substituents. In contrast to our previous work with a NO₂ π-withdrawing group, we utilize halogen substituents, known for their π-donating ability, with the aim to increase the electron density at the phenoxide oxygen and in turn modulate the magnetic anisotropy and relaxation dynamics. By examining the steric and electronic effects introduced by halogen variations, we aim to uncover how these subtle modifications govern the magnetic behavior in two novel triangular Dy₃ SMMs and in particular their spin frustration. Interestingly, despite differences in ligand substitution and the number of crystallographically distinct Dy³⁺ centers, a similar low-temperature regime observed in our earlier study is evident. This finding suggests a consistent underlying behavior in these systems. This work underscores the adaptability of the tripod-like arrangement while offering a strategic framework for optimizing SMM performance through tailored ligand design.

2. Experimental

2.1. General conditions

All chemicals and solvents were purchased from Alfa Aesar, and used as received without further purification. The 2-hydroxy-5-iodo-3-methoxybenzaldehyde was prepared according to literature procedures by o-vanillin reacting with iodine monochloride.⁵¹ The 5-bromo-2-hydroxy-3-methoxy-benzaldehyde was prepared according to literature procedures by reacting with o-vanillin, sodium acetate and bromine in glacial acetic acid.⁵² 1 H spectra were recorded on a Varian Mercury-400 (400 MHz for 1 H) spectrometer. Infrared spectra were recorded on all samples in the solid-state under ambient conditions on a Nicolet iS5 FT-IR spectrometer with iD5-ATR accessory in the 4000–400 cm⁻¹ region.

2.2. Synthesis of the ligands (H₃hmci and H₃hmcb)

2-Hydroxy-5-iodo-3-methoxybenzaldehyde/5-bromo-2 hydroxy-3-methoxy-benzaldehyde (20 mmol) was added to EtOH (100 mL), followed by the addition of carbohydrazide (10 mmol). The solution was refluxed at 70 °C for 3 hours. A white precipitate formed as the product, which was collected by filtration after removing the remaining ethanol. The precipitate was washed with water and dried under vacuum.

H₃hmci: yield = 80.4%. NMR (DMSO-d₆, 400 MHz): 10.95 (s, 2H), 8.37 (s, 2H), 7.70 (s, 2H), 7.2 (dd, 2H), 3.81 (s, 6H). IR (ATR cm⁻¹): 1699 (s), 1612 (w), 1592 (w), 1563 (m), 1530 (s), 1485 (s), 1439 (m), 1413 (m), 1350 (m), 1265 (s), 1245 (s), 1213 (s), 1143 (m), 1078 (m), 1017 (w), 943 (w), 842 (w), 832 (w).

H₃hmcb: yield: 79.2%. NMR (DMSO-d₆, 400 MHz): 10.98 (s, 2H), 8.40 (s, 2H), 7.56 (s, 2H), 7.11 (dd, 2H), 3.83 (s, 6H). IR (ATR cm⁻¹): 1605 (w), 1573 (w), 1473 (s), 1449 (m), 1439 (m), 1422 (s), 1402 (w), 1352 (m), 1318 (w), 1214 (s), 1139 (w), 1101 (w), 1074 (s), 1005 (w), 927 (m), 847 (m), 824 (s), 784 (m), 761 (s), 700 (m).

2.3. Synthesis of [Dy₃(hmci)₃(MeOH)₆]·3MeOH·2MeCN·2H₂O (1·3MeOH·2ACN·2H₂O)

To a solution of DyCl₃·6H₂O (0.125 mmol) in MeOH/MeCN (11.5 mL/3.5 mL) was added a solution of H₃hmci (0.125 mmol, 0.0762 g), and tetraethylammonium hydroxide (0.5 mmol, 0.205 mL) in MeOH/MeCN (11.5 mL/3.5 mL). The solution was stirred for 1 min and then filtered. The yellow solution was left to settle for one week, after which transparent yellow crystals of 1 were obtained by filtration, washed with ether, and dried in vacuo. Complex 1: yield = 9.31%. IR (ATR cm⁻¹): 1594 (w), 1560 (m), 1488 (s), 1456 (s), 1439 (s), 1379 (s), 1306 (m), 1231 (s), 1212 (s), 1148 (w). 1113 (m), 1078 (m), 1020 (w), 956 (w), 863 (w), 837 (w), 779 (m), 760 (s), 713 (m), 663 (m). Anal. (%) calcd for C₅₇H₇₅N₁₂Dy₃O₂₇I₆(1·6H₂O): C, 26.24; H, 2.90; N, 6.44. Found: C, 25.99; H, 2.62; N, 6.69. CCDC number: 2412859.†

2.4. Synthesis of [Dy₃(hmcb)₃(MeOH)₆]·3MeOH·1H₂O (2·3MeOH·1H₂O)

To a solution of Dy(OAc)₃·4H₂O (0.125 mmol) in MeOH (15 mL) was added a solution of H₃hmcb (0.125 mmol, 0.0645 g), and triethylamine (1 mmol, 0.139 mL) in MeOH (15 mL). The solution was stirred for 1 min and then filtered. The yellow solution was left to settle for one week, after which transparent yellow crystals of 2 were obtained by filtration, washed with ether, and dried in vacuo. Complex 2: Yield = 16.56%. IR (ATR cm⁻¹): 1596 (w), 1561 (m), 1541 (w), 1488 (s), 1456 (s), 1440 (s), 1408 (w), 1377 (s), 1304 (m), 1229 (s), 1209 (s), 1147 (w), 1079 (m), 955 (w), 839 (w), 805 (w), 786 (m), 760 (s), 721 (m), 669 (m). Anal. (%) calcd for C₅₇H₇₉N₁₂Dy₃O₂₉Br₆(2·8H₂O): C, 28.97; H, 3.37; N, 7.11. Found: C, 28.63; H, 3.03; N, 7.22. CCDC number: 2412858.†

2.5. X-ray crystallography

Single crystals of complexes 1–2 suitable for X-ray diffraction measurements were mounted on an Oxford Xcalibur Sapphire-3 CCD Gemini diffractometer employing graphite-monochromated Mo-Kα radiation (λ = 0.71073 Å), and intensity data were collected with ω scans. The data collection and reduction were performed with the CrysAlisPro software, and the absorptions were corrected by the SCALE3 ABSPACK multiscan method. The space-group determination was based on a check of the Laue symmetry and systematic absences, and it was confirmed using the structure solution. The structure was solved and refined with the Olex2 1.2-ac21 package. Anisotropic thermal parameters were used for all non-H atoms, and fixed isotropic parameters were used for H atoms.

Powder diffraction patterns were collected on a Bruker AXS D8 Advance X-ray diffractometer using Cu Kα radiation (λ = 1.5418 Å). XRD data were collected within a 2θ range of 5 to 40°.

2.6. Magnetic measurements

Magnetic susceptibility data were collected with a Quantum Design MPMS3 SQUID magnetometer working in the range 1.8–300 K with the magnetic field up to 7 Tesla. The samples were filtered and prepared immediately prior to the magnetic measurements in order to minimize any potential degradation. The data were corrected from the sample holder and the diamagnetic contributions calculated from the Pascal's constants. The AC magnetic susceptibility measurements were carried out in the presence of a 2.5 Oe oscillating field in zero or applied external DC field.

2.7. Theoretical calculations

CASSCF calculations were performed with ORCA 6.0^53,54 software using the crystallographic structures without any structural geometry optimization. For [Dy₃(hnc)₃(DMF)₆],³¹ the molecular orientation was redefined to properly account for the C₃ symmetry between the Dy³⁺ sites, ensuring that this axis was aligned along the z-direction and perpendicular to the Dy₃ plane. This redefinition was achieved by transforming the Pa3̄ (205) space group into the R3̄ (148) space group using the transformation matrix a − b, b − c, a + b + ca − b, b − c, a + b + ca − b, b − c, a + b + c as provided by the Bilbao Crystallographic Serveer.^55,56 Tolerance for energy convergence is fixed at 10⁻⁷ E_h. An active space considering the seven 4f orbitals with 9 electrons CAS (9, 7) for all the sextets (21 roots) for spin–orbit coupling using QDPT was considered. The calculations employed the def2 Ahlrichs basis sets: DKH-DEF2-TZVP for all atoms except Dy, for which the SARC2-DKH-QZVP basis set was used, and Y, for which the SARC-DKH-TZVP basis set was applied. The AUTOAUX feature was used to automatically generate auxiliary basis sets within the RIJCOSX approximation to speed up the calculations. Then, the SINGLE_ANISO and POLY_ANISO⁵⁷ program implemented in ORCA was used to obtain details about the magnetic relaxation.

3. Results and discussions

3.1. Synthesis and crystal structures

To achieve the goal of synthesizing polynuclear complexes with unique topologies, we use the o-vanillin building-block to design ligands with multiple coordination sites (Scheme 1). In our previous study, Dy-based trinuclear SMMs were successfully synthesized using Schiff base ligands incorporating several coordination pockets.³¹ Building on this foundation, the ligands in this study were strategically modified with -I and -Br substituents at the para position of o-vanillin to investigate how subtle changes in ligand chemistry influence magnetic properties while maintaining similar coordination environments.

Scheme 1 Scheme of the H₃hmci and H₃hmcb ligands.

The triangular Dy₃ complexes, [Dy₃(hmci)₃(MeOH)₆]·3MeOH·2MeCN·2H₂O (1) and [Dy₃(hmcb)₃(MeOH)₆]·3MeOH·1H₂O (2), were synthesized via straightforward one-pot reactions conditions.

Both reactions utilized a 1 : 1 molar ratio of the Dy³⁺ precursor and the corresponding Schiff-base ligand (H₃hmci or H₃hmcb) in methanolic solutions with an excess of base. Methanol served dual roles, acting as the solvent and a terminal ligand occupying coordination sites on the Dy₃ core.

For complex 1, DyCl₃·6H₂O was used as the metal precursor, and tetraethylammonium hydroxide (TEAOH, 3.8 equiv.) served as the base to facilitate the deprotonation of H₃hmci and promote the formation of the triangular assembly. While the reaction of H₃hmcb with DyCl₃·6H₂O and TEAOH yielded microcrystalline powders, substituting DyCl₃·6H₂O with Dy(OAc)₃·4H₂O and TEAOH with triethylamine (NEt₃, 8 equiv.) afforded yellow crystals of 2.

The choice of ligand substituents (–I in H₃hmci vs. –Br in H₃hcmb), the base, its quantity, and the Dy³⁺ precursor anions (although not incorporated into the structure) all influenced the crystallization behavior. Unfortunately, attempts to crystallize the system with the chlorine-ligand analogue were unsuccessful.

X-ray analysis reveals that complexes 1 and 2 crystallize in the triclinic P1̄ space group with a trinuclear complex in the asymmetric unit (Table S1, ESI†). Both structures consist of triangular [Dy₃(hmci/hmcb)₃(MeOH)₆] complexes, where three crystallographically independent Dy³⁺ ions, labelled Dy₁, Dy₂, and Dy₃, are interconnected by the central part of the ligand via three nitrogen atoms and one alkoxide moiety (Fig. 1 and Fig. S1, ESI†). The intramolecular Dy³⁺–Dy³⁺ distances range from 5.772 to 5.873 Å in 1, while slightly shorter ranges are observed in 2 (5.758 to 5.896 Å), indicating subtle structural variations (Table 1). Each Dy³⁺ ion exhibits eight-coordinate geometry, coordinated by three nitrogen and three oxygen atoms from the hmci/hmcb ligands, along with two methanol molecules. However, SHAPE analysis⁵⁸ highlights distinct differences in coordination geometries between complexes 1 and 2 (Table S2, ESI†). In 1, all Dy³⁺ ions adopt a dodecahedral geometry with varying degrees of distortion, with Dy₂ exhibiting the lowest degree of distortion. In contrast, complex 2 shows Dy₁ and Dy₂ in a dodecahedral geometry, while Dy₃ adopts a distorted biaugmented trigonal prism.

Fig. 1 (a) Molecular structures of 1. Colour code: orange, Dy; red, O; blue, N; grey, C.; purple, I. Hydrogen atoms have been omitted for clarity. (b) View from the top of the Dy₃ triangle arrangement.

Table 1 Some relevant crystallographic parameters for 1–3

Compound	Dy–O terminal (Å) out of plane	Dy–O terminal (Å) in-plane	O–Dy–O	Dy–Dy distances (Å)
1	2.184(12)	2.243(12)	116.0(5)	5.772
	2.218(12)	2.240(14)	110.6(5)	5.779
	2.166(12)	2.196(15)	110.8(5)	5.873
2	2.204(5)	2.271(5)	106.32(17)	5.758
	2.226(4)	2.255(5)	114.93(17)	5.798
	2.221(5)	2.213(4)	118.17(18)	5.896

---

Two short Dy–O(phenoxide) bonds from distinct ligands are notable in both complexes. The Dy–O bonds nearly perpendicular to the Dy₃ triangular plane measure 2.166–2.185 Å in 1 and 2.199–2.227 Å in 2, while those within the plane are slightly longer, ranging from 2.196–2.243 Å in 1 and 2.209–2.275 Å in 2. The angles between these bonds further emphasize the geometric differences, ranging from 105° to 116° in 1 and 106.25° to 118.31° in 2 (Table 1). Hydrogen bonding interactions are evident within the structures and are observed between the ligands and coordinated methanol molecules. The shortest intermolecular Dy³⁺–Dy³⁺ distance in the crystal is 7.601 Å, indicating a relatively close packing (Fig. S2, ESI†).

PXRD measurements show that the compounds rapidly lose crystallinity upon exposure to air (Fig. S3, ESI†).

3.2. Magnetic properties

The magnetic properties of the triangular complexes were investigated using SQUID magnetometry under both static and dynamic conditions.

At room temperature, the χT (χ being the molar magnetic susceptibility and T the temperature) values for complexes 1 and 2, were determined to be 42.08 cm³ K mol⁻¹ and 42.44 cm³ K mol⁻¹, respectively. These values align well with the theoretical value of 42.51 cm³ K mol⁻¹ expected for three isolated Dy³⁺ ion (⁶H_15/2) (Fig. 2).

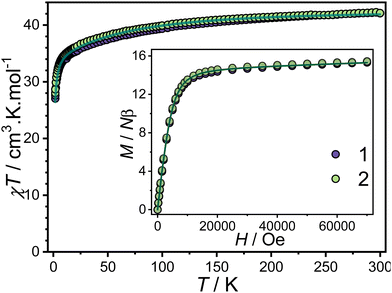Fig. 2 Temperature dependence of χT under an applied magnetic field of 1000 Oe for 1 and 2. Inset: Field dependence of the magnetization at 1.8 K. The solid lines represent the fit with POLY_ANISO.

Upon cooling, the thermal dependence of χT reveals a gradual decrease, reaching 27.04 cm³ K mol⁻¹ for 1 and 28.02 cm³ K mol⁻¹ for 2 at 1.8 K. This decrease is attributed to the thermal depopulation of the ± m_J levels, potentially combined with dominant antiferromagnetic interactions between the Dy³⁺ ions. The field-dependent magnetization curves, measured up to 70 kOe at 1.8 K, exhibit unsaturated behavior for both complexes, indicative of significant magnetic anisotropy (Fig. 2, inset). The magnetization (M) values at 70 kOe are 15.31 Nβ for 1 and 15.44 Nβ for 2, consistent with the presence of CF effects.

The magnetic hysteresis loops, measured at 1.8 K, display an opening for both complexes, suggesting the presence of slow relaxation dynamics (Fig. S4, ESI†). Notably, the hysteresis loop for complex 1 is slightly wider compared to that of complex 2, suggesting distinct relaxation profiles.

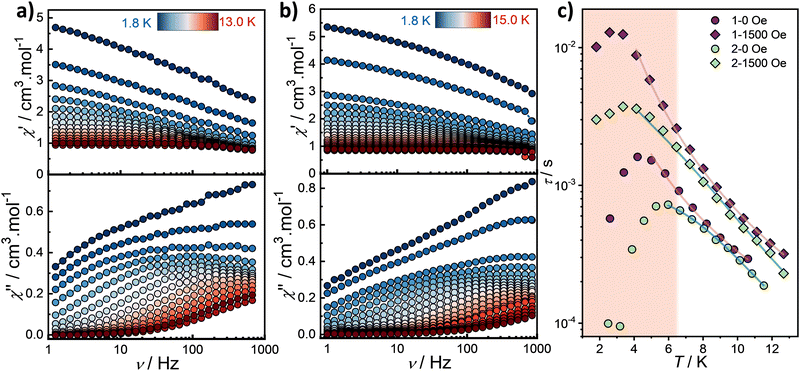
The occurrence of slow relaxation of the magnetization was investigated using alternating current (ac) measurements. Under zero dc field, both complexes exhibit a broad out-of-phase (χ′′) signal in their ac susceptibility at low temperatures, with no clearly defined maximum (Fig. 3). Upon heating, the signal sharpens, and a single peak gradually emerges up to 13 K.

Fig. 3 Frequency dependence of the in-phase (χ′) and out-of phase (χ′′) susceptibilities for 1 (a) and 2 (b) under a zero dc-field. (c) Temperature dependence of the relaxation time using the ac susceptibility data. The solid line represents the fit. The low temperature regime is highlighted in coral colour.

In the high-temperature regime, the maximum shifts to higher frequencies, as typically expected for systems exhibiting slow relaxation. However, in the low-temperature regime, the opposite behavior is observed, with the maximum shifting to lower frequencies. This unusual trend could arise from the presence of multiple Dy³⁺ crystallographic sites, strong intermolecular interactions or possibly a spin frustrated system which may affect the relaxation dynamics.

While these results are primarily attributed to an intrinsic effect of the molecular triangle, it is important to consider the potential role of intermolecular interactions. However, comparison with our previously reported [Dy₃(hnc)₃(DMF)₆] triangle which shows even larger intermolecular Dy³⁺–Dy³⁺ separations and lacks solvate molecules,³¹ suggests that these are not the dominant factor.

The observed unusual behavior is further confirmed by the Cole–Cole plots, where the data could not be satisfactorily fitted with a generalized Debye model (Fig. S5, ESI†). In the high-temperature regime, the α values remain relatively large until approximately 10 K (about 0.2), indicating a broad distribution of relaxation times (Tables S3 and S4, ESI†). This confirms that the relaxation dynamics are more complex than a simple single relaxation model. The relaxation times, τ, were estimated from the ac data. The temperature dependence of τ clearly confirms the presence of a distinct low-temperature regime, with a decrease of the relaxation time below approximately 6 and 4 K for 1 and 2, respectively (Fig. 3c). The “high-temperature” thermal dependence of τ can be fitted with a Raman process using

τ⁻¹ = CTⁿ. (1)

For complex 2, a QTM term must be included to obtain a pertinent fit (Fig. 3c). The best fit parameters are provided in Table 2 and highlight also differences in the relaxation dynamics between the two complexes. Note that inclusion a thermally activated behavior leads to unrealistic fitting parameters, suggesting that the dynamics in the high temperature regime is indeed dominated by a Raman relaxation.

Table 2 Fit parameters of the temperature dependence of the relaxation time for 1 and 2

Compound	n	C (s^−1 K^−n)	τQTM (s)	A (s^−1 K)
1 (0 Oe)	2.34 ± 0.05	14 ± 1	—	—
1 (1500 Oe)	3.06 ± 0.03	1.3 ± 0.1		—
2 (0 Oe)	4.4 ± 0.2	0.09 ± 0.04	(8.6 ± 0.4) × 10^−4	—
2 (1500 Oe)	4.6 ± 0.4	0.03 ± 0.02	—	63 ± 12

---

As the relaxation dynamics, and in particular the QTM, could be significantly influenced by dc fields, the field dependence of the ac susceptibility was investigated at 2 K (Fig. S6, ESI†). Both complexes exhibit intricate behavior, with an increase in relaxation time up to approximately 1500–2000 Oe, after which a plateau in χ′′ is observed, preventing further analysis of the relaxation time (Fig. S7, ESI†). For direct comparison between the two complexes, a dc field of 1500 Oe was selected to study its effect on the relaxation dynamics. The frequency dependence collected under this dc field reveals a comparable behavior in comparison to the zero-field data but with maximum observed at lower frequency (Fig. S8, ESI†). Subsequent Cole–Cole analysis (Fig. S9 and Tables S5 and S6, ESI†) and extraction of the relaxation time confirm an increase in relaxation time compared to the zero-field data. The temperature dependence of the relaxation time could be modelled in the high temperature regime with a Raman process for complex 1, while an additional direct process term is needed for complex 2, using the equation

τ⁻¹ = CTⁿ + AT (2)

(Fig. 3c, Table 2). Although the relaxation times for complexes 1 and 2 differ, they exhibit similar temperature-dependent profiles.

The longer relaxation time observed for complex 1 indicates enhanced axiality compared to complex 2. For a given compound, the relaxation times are comparable under zero-field and dc-field conditions at higher temperatures. At lower temperatures, a clear bifurcation between the zero-field and field-induced relaxation data becomes however apparent.

3.3. Theoretical calculations

To further investigate the relaxation dynamics and explain the observed differences between the complexes, ab initio calculations were carried out at the CASSCF level using the ORCA package.⁵³ For each Dy₃ triangles, two Dy³⁺ ions in the respective crystallographic sites were replaced by diamagnetic Y³⁺ ions, creating Dy₁, Dy₂, and Dy₃ fragments associated with each Dy³⁺ center. The results reveal substantial variations in magnetic anisotropy between the different Dy³⁺ sites, both within individual triangular complexes and across complexes 1 and 2.

To provide a clearer understanding, we first analyse the electronic structures of the different Dy³⁺ sites in complex 1, which presents the best magnetic properties. All Dy³⁺ sites exhibit substantial axiality, with g_z values around 19.3 for Dy₁ and Dy₃, and slightly higher for Dy₂ (g_z = 19.57) (Table 3). Wavefunction compositions indicate a dominant contribution (>89%) from the m_J = |±15/2〉 state for all the sites (Tables S7–S9, ESI†). However, none of the sites could be considered as perfectly axial (g_z ≈ 20). Furthermore, despite Dy₂'s slightly higher axiality, its transverse g_x and g_y components were in the same order of magnitude to those of Dy₁ and Dy₃, as confirmed by the quantitative comparison of QTM rates obtained from SINGLE_ANISO (Fig. 4). The anisotropic axes of the ground KD for the Dy³⁺ sites are nearly perpendicular to the Dy₃ triangular plane (Fig. 5a) but exhibit varying tilt angles (Table S10, ESI†). The angles between the “out-of-plane” phenoxide and “in-plane” phenoxide in association with the Dy-phenoxide bond lengths most likely influence the tilt of the anisotropic axis relative to the Dy₃ triangular plane. The tilting of the anisotropic axes relative to the Dy³⁺–Dy³⁺ intranuclear vectors varies across the Dy³⁺ sites. Dy₁ shows the most uniform tilting across both Dy₁–Dy₂ and Dy₁–Dy₃ directions, with angles remaining close to perpendicular, while Dy₃ exhibits slightly greater variation. Dy₂, on the other hand, demonstrates the largest angular deviations. These variations in tilt angles emphasize the geometric and electronic diversity among the Dy³⁺ sites, which likely influences the dipolar interactions.

Table 3 Energy of the lowest Kramers doublets (KD) and their associated g tensors on the individual Dy fragments for 1

KD	Energy (cm^−1) Dy1	g tensor Dy1	Energy (cm^−1) Dy2	g tensor Dy2	Energy (cm^−1) Dy3	g tensor Dy3
1	0	gx = 0.0117	0	gx = 0.0083	0	gx = 0.0084
		gy = 0.0023		gy = 0.0134		gy = 0.0170
		gz = 19.3067		gz = 19.5708		gz = 19.3313
2	155	gx = 0.3623	179	gx = 0.0083	140	gx = 0.3296
		gy = 0.6687		gy = 0.3186		gy = 0.6580
		gz = 15.8018		gz = 15.8432		gz = 15.3503
3	247	gx = 1.5716	253	gx = 0.7154	204	gx = 0.7776
		gy = 2.5509		gy = 1.6082		gy = 1.9322
		gz = 14.5608		gz = 14.3943		gz = 14.5719
4	333	gx = 7.9748	343	gx = 3.6996	299	gx = 5.063
		gy =6.8501		gy = 5.2254		gy = 6.1174
		gz = 4.4915		gz = 9.9122		gz = 9.1874
5	412	gx = 0.3304	418	gx = 1.4635	377	gx = 0.0843
		gy = 3.2666		gy = 5.4189		gy = 4.1231
		gz = 11.3609		gz = 10.8270		gz = 11.1017
6	497	gx = 0.0722	486	gx = 0.7708	461	gx = 1.4451
		gy = 2.3338		gy = 3.3058		gy = 3.8186
		gz = 13.3185		gz = 14.8958		gz = 10.9838
7	544	gx =1.0455	528	gx = 0.5906	502	gx = 2.0211
		gy =1.5273		gy = 1.2066		gy = 3.7924
		gz = 16.1839		gz = 17.6440		gz = 13.5665
8	589	gx = 0.1750	606	gx = 0.0717	562	gx = 0.3038
		gy = 0.3598		gy = 1.2066		gy = 0.4998
		gz = 19.1759		gz = 18.5462		gz = 19.0740

---

Fig. 4 Energy diagram for low-lying KDs and transition magnetic moment matrix elements⁵⁹ (in μB) for the connected states (only for the KD1 and KD2) for fragments 1. For each KD (n), the corresponding states (−n, n) are placed according to their magnetic moments. The horizontal arrows show the QTM transitions within each doublet, whereas the non-horizontal arrows are spin-phonon transition paths. Only the first KDs are shown here.

Fig. 5 (a) Orientation of the anisotropic axis (pink) corresponding to the ground KD in 1. (b) Energy diagram of the coupled states resulting from the dipolar interactions in 1.

Theoretical calculations also reveal differences in the CF splitting across the different centers. Specifically, the first excited KD level ranges from 140 cm⁻¹ (Dy₃) to 179 cm⁻¹ (Dy₂) (Fig. 4 and Table 3). Despite these significant splitting values, a Raman-mediated relaxation is observed, likely due to the limited axiality of both the ground and 1st excited KD for all the Dy³⁺ sites.

Although this analysis points out substantial differences between the Dy³⁺ sites, the effect of magnetic interaction was also investigated. Since the local magnetic anisotropy is stronger than the magnetic interactions and nearly perpendicular to the Dy₃ plane, this system corresponds to a case of Ising spin frustration, characterized by a six-fold degenerate ground state composed of two aligned spins and one inverted spin. To validate this, POLY_ANISO was employed to obtain details about the magnetic interactions between the Dy³⁺ sites. Given the large Dy³⁺–Dy³⁺ intramolecular distances (>5.7 Å) and the substantial number of bridging atoms, exchange interactions were neglected, and only dipolar interactions were considered.³⁴ This allows to nicely reproduce the χT vs. T and M vs. H curves (Fig. 3 and Fig. S10, ESI†). The calculated dipolar interaction matrix (Table S10, ESI†) for 1 suggests a frustrated system. The six-fold degenerate ground state, characterized by two aligned spins and one inverted spin, splits into three closely spaced doublets, located at 0, 0.023, and 0.037 cm⁻¹, whereas the excited ferromagnetic state is predicted at 0.859 cm⁻¹ (Fig. 5b and Table S12, ESI†). Such small energy differences between the three ground doublets are typically regarded as a hallmark of frustration in triangular systems.^38–40,60

The computed energy spectrum and corresponding g_z values provide critical insights into the nature of the coupled states within the Dy₃ triangle (Fig. 5b). The three low-lying doublets exhibit close g_z values ranging between 21.52 to 24.45 (Table S12, ESI†). However, their corresponding magnetic moments differ, suggesting varying degrees of spin canting in each state (Fig. 5b). In the ground state, the spins exhibit a moderate degree of canting, resulting in an intermediate magnetic moment of approximately 11.9 μB.

The second and third doublets also correspond to frustrated configurations, where the canting becomes more pronounced, leading to further reductions in the magnetic moments (5.3 μB and 3.4 μB, respectively). Lastly, the fourth state represents a ferromagnetic-like configuration, yet the spins remain canted rather than perfectly aligned, yielding a reduced magnetic moment of 20.6 μB instead of the expected ∼30 μB for three Ising-like Dy³⁺ ions with ferromagnetic coupling in the absence of canting.

In comparison to 1, the electronic structures of the Dy³⁺ centers in 2 exhibit notable disparities (Tables S13–S16, ESI†). In particular, Dy₁ exhibits the lowest axiality with a g_z value of 19.05 whereas Dy₃ shows the greatest axiality (g_z = 19.62). This trend is also reflected in the ground-state wavefunction composition where Dy₁ shows only 84% of m_J = |±15/2〉 state, in contrast to Dy₂ and Dy₃ which exhibit 92.6% and 94.4%, respectively (Tables S13–S16, ESI†). Hence, the degree of axiality progressively increases from Dy₁ to Dy₃, as also mirrored by energies of the first KD found at 111, 159 and 177 cm⁻¹ for Dy₁, Dy₂ and Dy₃, respectively. The orientation of the anisotropic axes (Fig. S11, ESI†) and their tilting relative to the Dy₃ plane are comparable to those observed in 1 (Table S10, ESI†).

However, Dy₁ exhibits notably higher computed QTM rates (Fig. S12, ESI†), further corroborated by the transverse components of the g-tensor for the ground doublet. The transverse g-tensor component, proportional to ,⁶¹ highlights the larger transverse anisotropy of Dy₁ compared to Dy₂ and Dy₃, as well as to the Dy³⁺ sites present in complex 1 (Fig. 6).

Fig. 6 Bar plot showing the transversal magnetic anisotropy determined by the computed for the different Dy³⁺ sites in 1 and 2.

It turns out that with the exception of the Dy₃ site, the transverse components are consistently greater in 2, especially for Dy₁. The enhanced transverse components in 2 likely contribute to its reduced SMM performance compared to 1.

The site-dependent influence of the halogen substituent on the Dy³⁺ electronic structure complicates the identification of a clear trend across the series, highlighting the subtle interplay of electronic and steric effects. Future studies focusing on systems with a single Dy³⁺ site could help isolate the direct impact of the halogen and potentially reveal more general trends. Additionally, investigating unsubstituted or differently substituted analogues would further elucidate these effects. On the other hand, analysis using POLY_ANISO reveals a comparable exchange spectrum between 1 and 2, with the presence of spin frustration (Fig. S13 and Table S12, ESI†).

All these findings suggest that the relaxation dynamics is predominantly of single-ion origin. Indeed, the weak degeneracy breaking of the spin-frustrated states should enable the thermal population of these states, even at low temperatures. Additionally, the conversion between the frustrated states could occur through a single spin flip on one Dy³⁺ center.³⁹ Therefore, the relaxation dynamics shall be most likely predominantly governed by single-ion effects. Furthermore, the fact that none of the Dy³⁺ sites are highly axial is also consistent with the observed Raman relaxation processes at high temperatures and further supports the single-ion origin of the magnetic dynamics in these triangular Dy₃ complexes.

Nevertheless and to our knowledge, previous examples of frustrated Dy-based Ising triangles do not show the low temperature regime in the ac relaxation profile as observed in 1 and 2. While it is tempting to attribute this behavior to distinct relaxation pathways arising from the different Dy³⁺ crystallographic sites or possible intermolecular interactions, the comparison with our previously reported Dy₃ triangle [Dy₃(hnc)₃(DMF)₆] (H₃-hnc: 1,5-bis(2-hydroxy-3-methoxy-5 nitrobenzylidene)carbonohydrazide) suggests a more complex picture. Unlike 1 and 2, this compound features a unique crystallographic Dy³⁺ site related by a C₃ axis, and also exhibits a drop in relaxation time at low temperatures (Fig. S14, ESI†). To gain further insights, we performed CASSCF calculations to elucidate the electronic structure of [Dy₃(hnc)₃(DMF)₆]. Despite differences in substituents and coordinated solvents (MeOH vs. DMF), the CF splitting appears comparable to that in 1 and 2, with a first excited KD located at 117 cm⁻¹, while the KD ground-state shows g_z = 19.51 (Table S17 and Fig. S15, ESI†). In [Dy₃(hnc)₃(DMF)₆], the alignment of the anisotropic axes is influenced by the unique crystallographic Dy³⁺ site, leading to a less pronounced tilt between the relative axes compared to 1 and 2 (Fig. S16, ESI†). When considering only dipolar interactions, the calculated energy spectrum is closely resembling those of 1 and 2, displaying three degenerated doublets and a ferromagnetic excited state around 0.86 cm⁻¹. Furthermore, the significantly large intermolecular Dy³⁺–Dy³⁺ distances in [Dy₃(hnc)₃(DMF)₆] (exceeding 15 Å) suggest that intermolecular interactions are unlikely to drive the low-temperature behavior observed across the Dy₃ triangles.

To summarize, our findings suggest that single-ion anisotropy likely governs the relaxation behavior in our systems. The moderate magnetic axiality of the Dy³⁺ centers is consistent with the observed Raman relaxation processes in the high-temperature range; however, distinct behaviors are observed across the series, including the previously reported compound. This underscores the influence of the substituent and symmetry on the relaxation dynamics. While our analysis using POLY_ANISO indicates the presence of spin frustration driven by dipolar interactions, as evidenced by the closely spaced ground doublets in the energy spectrum, the direct attribution of the unusual relaxation behavior observed at low temperatures to this phenomenon warrants further investigation, as distinct relaxation pathways arising from the different Dy³⁺ sites and/or subtle lattice effects might also contribute to this low-temperature regime. These findings emphasize the need for future research to better capture the underlying dynamics and explore potential avenues for enhancing the magnetic axiality to improve the SMM performance of such frustrated triangular Dy₃ complexes.

4. Conclusions

In this study, we have investigated a series of triangular Dy₃ tripod-like complexes that represent rare examples of Ising spin frustration in a Dy₃ triangle. The unique topology, combined with the nearly perpendicular orientation of the principal magnetic axes to the triangle's plane, leads to a frustrated ground state driven by dipolar interactions, with minimal influence from exchange interactions. This work highlights the critical importance of precise geometric and anisotropic control in achieving such frustration, providing a valuable model for understanding magnetic phenomena in triangular systems.

Remarkably, we observe a distinctive slow relaxation regime at low temperatures in both complexes. While spin frustration is present, its influence on the relaxation dynamics should be limited, with the single-ion effects dominating the high-temperature behavior, highlighting the delicate balance between these two mechanisms. However, comparison with a similar Dy₃ triangle featuring a unique Dy³⁺ ion, suggests a more intricate relaxation mechanism at low temperature. Additionally, we demonstrate that halogen substitution at the para position of the ligands influences the relaxation dynamics. The halogen substituents modulate the local crystal field, thereby affecting the magnetic anisotropy of the Dy³⁺ centers. However, this modulation exhibits site-specific variations within the Dy₃ triangle, reflecting the complex interplay of steric and electronic factors in the ligand environment.

The presence of spin frustration opens promising avenues for future exploration, particularly in fine-tuning the magnetic properties of triangular SMMs through strategic modifications of the ligand framework (including substituents) and by employing techniques such as solvent exchange or other post-synthetic modifications.

Data availability

Crystallographic data for 1 and 2 has been deposited at the Cambridge Crystallographic Data Centre as Supplementary Publication No 2412859 and 2412858.†

Conflicts of interest

There are no conflict of interest to declare.

Acknowledgements

The authors thank the University of Montpellier, CNRS. J. Long also acknowledges the support from the Institut Universitaire de France. We also gratefully acknowledge the financial support from National Chung Hsing University and the National Science and Technology Council, Taiwan 113-2113-M-005-006 to P.-H. Lin.

Notes and references

1. J. Luzon and R. Sessoli, Dalton Trans., 2012, 41, 13556–13567.
2. D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148.
3. F. Troiani and M. Affronte, Chem. Soc. Rev., 2011, 40, 3119–3129.
4. L. Bogani, A. Vindigni, R. Sessoli and D. Gatteschi, J. Mater. Chem., 2008, 18, 4750–4758.
5. R. A. Layfield and M. Murugesu, Lanthanides and Actinides in Molecular Magnetism, Wiley, 2015.
6. J.-L. Liu, Y.-C. Chen and M.-L. Tong, Chem. Soc. Rev., 2018, 47, 2431–2453.
7. R. A. Layfield, Organometallics, 2014, 33, 1084–1099.
8. C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442.
9. F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400–1403.
10. K. Randall McClain, C. A. Gould, K. Chakarawet, S. J. Teat, T. J. Groshens, J. R. Long and B. G. Harvey, Chem. Sci., 2018, 9, 8492–8503.
11. J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer, S. Gao, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 5441–5450.
12. Y.-S. Ding, N. F. Chilton, R. E. P. Winpenny and Y.-Z. Zheng, Angew. Chem., Int. Ed., 2016, 55, 16071–16074.
13. Y.-S. Ding, K.-X. Yu, D. Reta, F. Ortu, R. E. P. Winpenny, Y.-Z. Zheng and N. F. Chilton, Nat. Commun., 2018, 9, 3134.
14. Y. S. Ding, T. Han, Y. Q. Zhai, D. Reta, N. F. Chilton, R. E. P. Winpenny and Y. Z. Zheng, Chem. – Eur. J., 2020, 26, 5893–5902.
15. K.-X. Yu, J. G. Kragskow, Y.-S. Ding, Y.-Q. Zhai, D. Reta, N. F. Chilton and Y.-Z. Zheng, Chem, 2020, 6, 1777–1793.
16. V. Parmar, D. P. Mills and R. Winpenny, Chem. – Eur. J., 2021, 27, 7625–7645.
17. J. Long, A. O. Tolpygin, E. Mamontova, K. A. Lyssenko, D. Liu, M. D. Albaqami, L. F. Chibotaru, Y. Guari, J. Larionova and A. A. Trifonov, Inorg. Chem. Front., 2021, 8, 1166–1174.
18. X.-L. Ding, Y.-Q. Zhai, T. Han, W.-P. Chen, Y.-S. Ding and Y.-Z. Zheng, Chem. – Eur. J., 2021, 27, 2623–2627.
19. W. J. Xu, Q. C. Luo, Z. H. Li, Y. Q. Zhai and Y. Z. Zheng, Adv. Sci., 2024, 11, e2308548.
20. A. Lunghi, F. Totti, R. Sessoli and S. Sanvito, Nat. Commun., 2017, 8, 14620.
21. L. Escalera-Moreno, J. J. Baldoví, A. Gaita-Ariño and E. Coronado, Chem. Sci., 2018, 9, 3265–3275.
22. D. Reta, J. G. C. Kragskow and N. F. Chilton, J. Am. Chem. Soc., 2021, 143, 5943–5950.
23. Y.-C. Chen and M.-L. Tong, Chem. Sci., 2022, 13, 8716–8726.
24. M. J. Giansiracusa, E. Moreno-Pineda, R. Hussain, R. Marx, M. Martínez Prada, P. Neugebauer, S. Al-Badran, D. Collison, F. Tuna, J. van Slageren, S. Carretta, T. Guidi, E. J. L. McInnes, R. E. P. Winpenny and N. F. Chilton, J. Am. Chem. Soc., 2018, 140, 2504–2513.
25. R. J. Blagg, L. Ungur, F. Tuna, J. Speak, P. Comar, D. Collison, W. Wernsdorfer, E. J. L. McInnes, L. F. Chibotaru and R. E. P. Winpenny, Nat. Chem., 2013, 5, 673–678.
26. J. Long, F. Habib, P.-H. Lin, I. Korobkov, G. Enright, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2011, 133, 5319–5328.
27. K. Katoh, R. Asano, A. Miura, Y. Horii, T. Morita, B. K. Breedlove and M. Yamashita, Dalton Trans., 2014, 43, 7716–7725.
28. E. M. Pineda, Y. Lan, O. Fuhr, W. Wernsdorfer and M. Ruben, Chem. Sci., 2017, 8, 1178–1185.
29. J. Xiong, H.-Y. Ding, Y.-S. Meng, C. Gao, X.-J. Zhang, Z.-S. Meng, Y.-Q. Zhang, W. Shi, B.-W. Wang and S. Gao, Chem. Sci., 2017, 8, 1288–1294.
30. J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, Nat. Chem., 2011, 3, 538–542.
31. L.-W. Cheng, C.-L. Zhang, J.-Y. Wei and P.-H. Lin, Dalton Trans., 2019, 48, 17331–17339.
32. Y.-S. Meng, Y.-S. Qiao, M.-W. Yang, J. Xiong, T. Liu, Y.-Q. Zhang, S.-D. Jiang, B.-W. Wang and S. Gao, Inorg. Chem. Front., 2020, 7, 447–454.
33. L. Ungur, S.-Y. Lin, J. Tang and L. F. Chibotaru, Chem. Soc. Rev., 2014, 43, 6894–6905.
34. L. F. Chibotaru, L. Ungur and A. Soncini, Angew. Chem., Int. Ed., 2008, 47, 4126–4129.
35. J. Tang, I. Hewitt, N. T. Madhu, G. Chastanet, W. Wernsdorfer, C. E. Anson, C. Benelli, R. Sessoli and A. K. Powell, Angew. Chem., Int. Ed., 2006, 45, 1729–1733.
36. J. Luzon, K. Bernot, I. J. Hewitt, C. E. Anson, A. K. Powell and R. Sessoli, Phys. Rev. Lett., 2008, 100, 247205.
37. Y.-X. Wang, Y. Zhou, Y. Ma, P. Lu, Y.-Q. Zhang, Y. Sun and P. Cheng, Adv. Sci., 2024, 11, 2308220.
38. V. Vieru, L. Ungur and L. F. Chibotaru, J. Phys. Chem. Lett., 2013, 4, 3565–3569.
39. T. Pugh, F. Tuna, L. Ungur, D. Collison, E. J. L. McInnes, L. F. Chibotaru and R. A. Layfield, Nat. Commun., 2015, 6, 7492.
40. G. Lu, Y. Liu, W. Deng, G.-Z. Huang, Y.-C. Chen, J.-L. Liu, Z.-P. Ni, M. Giansiracusa, N. F. Chilton and M.-L. Tong, Inorg. Chem. Front., 2020, 7, 2941–2948.
41. A. P. Orlova, J. D. Hilgar, M. G. Bernbeck, M. Gembicky and J. D. Rinehart, J. Am. Chem. Soc., 2022, 144, 11316–11325.
42. M. G. Bernbeck, A. P. Orlova, J. D. Hilgar, M. Gembicky, M. Ozerov and J. D. Rinehart, J. Am. Chem. Soc., 2024, 146, 7243–7256.
43. M. Andruh, Dalton Trans., 2015, 44, 16633–16653.
44. J. Long, Y. Guari, R. A. S. Ferreira, L. D. Carlos and J. Larionova, Coord. Chem. Rev., 2018, 363, 57–70.
45. J. Long, Front. Chem., 2019, 7, 63.
46. J.-H. Jia, Q.-W. Li, Y.-C. Chen, J.-L. Liu and M.-L. Tong, Coord. Chem. Rev., 2019, 378, 365–381.
47. J. Tang and P. Zhang, Lanthanide Single Molecule Magnets, Springer Berlin Heidelberg, Berlin, Heidelberg, 2015, pp. 41–90 DOI:10.1007/978-3-662-46999-6_2.
48. S. T. Liddle and J. van Slageren, Chem. Soc. Rev., 2015, 44, 6655–6669.
49. Z. Zhu, M. Guo, X.-L. Li and J. Tang, Coord. Chem. Rev., 2019, 378, 350–364.
50. J. Long, M. S. Ivanov, V. A. Khomchenko, E. Mamontova, J.-M. Thibaud, J. Rouquette, M. Beaudhuin, D. Granier, R. A. S. Ferreira, L. D. Carlos, B. Donnadieu, M. S. C. Henriques, J. A. Paixão, Y. Guari and J. Larionova, Science, 2020, 367, 671.
51. D. Y. Kim and H. J. Kim, Org. Lett., 2021, 23, 5256–5260.
52. K. R. More and R. S. Mali, Tetrahedron, 2016, 72, 7496–7504.
53. F. Neese, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2012, 2, 73–78.
54. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606.
55. M. I. Aroyo, J. M. Perez-Mato, C. Capillas, E. Kroumova, S. Ivantchev, G. Madariaga, A. Kirov and H. Wondratschek, Z. Kristallogr., 2006, 221, 15–27.
56. M. I. Aroyo, A. Kirov, C. Capillas, J. M. Perez-Mato and H. Wondratschek, Acta Crystallogr., Sect. A: Found. Crystallogr., 2006, 62, 115–128.
57. L. F. Chibotaru and L. Ungur, The computer programs SINGLE_ANISO and POLY_ANISO, University of Leuven, 2, 2006.
58. D. Casanova, M. Llunell, P. Alemany and S. Alvarez, Chem. – Eur. J., 2005, 11, 1479–1494.
59. L. Ungur and L. F. Chibotaru, Inorg. Chem., 2016, 55, 10043–10056.
60. R. Grindell, V. Vieru, T. Pugh, L. F. Chibotaru and R. A. Layfield, Dalton Trans., 2016, 45, 16556–16560.
61. Y. Gil, A. Castro-Alvarez, P. Fuentealba, E. Spodine and D. Aravena, Chem. – Eur. J., 2022, 28, e202200336.

---

Footnote

† Electronic supplementary information (ESI) available: Additional structural and magnetic and ab initio calculations data. CCDC 2412858 and 2412859. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d5tc00334b

---